Instructional Perseverance in Early-Childhood Classrooms: Supporting Children’s Development of STEM Reasoning in a Social Justice Context

Abstract

In early childhood education (ECE) classrooms, teachers navigate practices about how to allow space for students to make sense of new STEM-based ideas. We posit that such pedagogical moves require ample in-the-moment perseverance by the instructor. In this paper, we seek to explore the nature of such instructional perseverance in ECE classrooms and how it manifests when ECE educators are supporting young children to develop their STEM reasoning, with a primary focus on the mathematics discipline in a social justice context. Working with a dataset consisting of four ECE classroom episodes, we employed an analytical framework that captured evidence of instructional perseverance. We found that the instructional perseverance of the ECE teacher was integral to the development of STEM reasoning of her young students. We present an illustrative case that details the instructional perseverance of the ECE teacher and the related STEM reasoning of her students in the context of exploring income variance by race. We argue that teacher education development must address how ECE teachers can plan for and navigate in-the-moment instructional obstacles in order to support young students’ STEM reasoning development, which positions students for productive STEM-based outcomes.

1. Introduction

Effective education about Science, Technology, Engineering and Mathematics (STEM) content in early childhood education (ECE) classrooms requires a focus on both students’ and teacher’s perseverance. From the student perspective, the importance of perseverance in problem-solving for learning with understanding is a widespread theoretical position in education [1,2] In this context, perseverance has been defined as initiating and sustaining, and re-initiating and re-sustaining, in-the-moment productive struggle in the face of obstacles, setbacks, or discouragements [1]. The processes of struggle to approach, reach, and make continued progress despite a perceived impasse put forth cognitive demands upon the learner that are conducive for the development of conceptual ideas [3,4]. This theoretical framework positions students as successful learners if and when they engage in a productive struggle to make meaning, or as they grapple with ideas that are within reach, but not yet well-formed. From the teacher’s perspective, the notion of perseverance in problem-solving takes on a different meaning. In this context, the problem-solving that teachers do refers to their in-the-moment pedagogy to better support students’ engagement with STEM-based ideas. Thus, we define the construct of instructional perseverance as initiating and sustaining, and re-initiating and re-sustaining, opportunities for students’ engagement with new ideas in the face of content-based and pedagogical obstacles, setbacks, or discouragements.

The support provided to young learners to help them persevere with challenging ideas is influenced by the instructional perseverance of the teacher, such that ECE teachers and children are in essence dependent on one another to engage in mathematical inquiry [5]. Much like a student’s perseverance requires self-regulation and overcoming setbacks during productive struggle, teachers’ instructional perseverance requires monitoring one’s pedagogical moves and overcoming instructional setbacks if and when a student needs additional support. Such instructional perseverance occurs in the moment as teachers process and respond to a student’s mathematical thinking. This is especially important in ECE settings because although these young students are capable of grappling with challenging STEM-based ideas [6], their problem-solving experiences are rooted in the ways in which they have interacted with the world prior to entering formal schooling. Thus, they require teacher guidance and feedback about how to monitor their progress and productively struggle to persevere [7]. STEM-based learning opportunities for young children should consistently foreground one discipline as the central focus, with the other disciplines adding support and enhancement in the background [8]. In our research and for this paper, we foreground the discipline of mathematics.

Supporting students’ perseverance with challenging tasks is a primary driver of learning mathematics with understanding [9], yet little is known about how to support perseverance in ECE settings. There is much research that specifies the productive teaching practices that can support student’s mathematical learning in ECE classrooms, however, we posit that such pedagogical moves require ample in-the-moment perseverance by the instructor. In this paper, we build from the theoretical framework of perseverance in problem-solving to explore the nature of instructional perseverance in ECE classrooms and how it manifests when ECE educators support young children to develop their mathematical (and STEM-based) reasoning. Next, we will review the relevant literature in the ECE and STEM reasoning development spaces, including a linkage to using social justice to develop STEM reasoning, detail our methodology, present our overall findings and an illustrative case, and discuss our findings and conclusions relative to the ECE field.

2. Literature Review

Young students’ mathematical and STEM-based knowledge is a strong predictor of later success in mathematics [10,11,12]. Situated within the theoretical framework of persevering in problem-solving to make meaning of mathematics, children’s engagement with ill-structured problems (those which require a variety of approaches, justifications, and represent complex situations [13]) simultaneously engages them in practice with vital components of STEM reasoning, such as communication, development of language, critical thinking, collaboration, persistence, and problem-solving [14]. These elements of STEM reasoning subsequently result in sense-making opportunities and positive dispositions towards STEM-related topics. These sense-making opportunities must be strategically facilitated by the classroom teacher and involve both listening to and drawing out children’s discourse about STEM content areas.

Building from the theoretical framework of perseverance in problem-solving, our work centers on the early childhood teachers’ perseverance in facilitating instruction around mathematics and justice goals during lessons that extended on STEM-related units in the classroom. Lee [15] espoused that ECE teachers need to be aware of mathematics situations in the classroom setting and have effective pedagogical and classroom/student knowledge to respond to these situations. As such, we focus on the ways in which ECE teachers support young children to demonstrate STEM reasoning through the communication of knowledge. We do this by looking at the discourse used to support instructional perseverance.

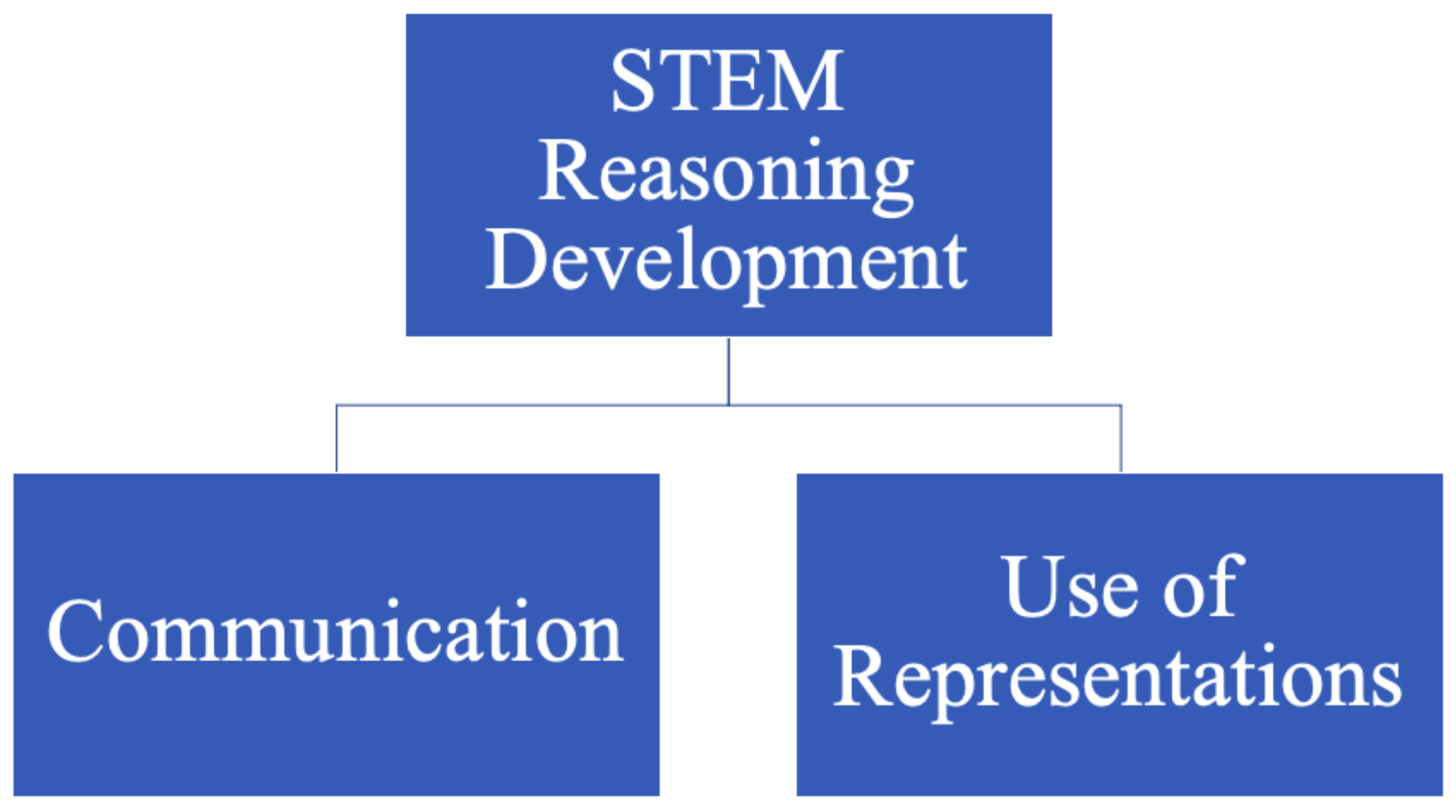
2.1. STEM Reasoning Development

STEM reasoning is developed across the disciplines of science, technology, engineering, and mathematics through problem-solving situations. As such, STEM reasoning involves communication, development of language, critical thinking, collaboration, persistence, and problem-solving with STEM content [14]. With young children, lessons focused on STEM learning goals often foreground one discipline as central to the lesson (e.g., mathematics), with the other disciplines (e.g., science, technology, and engineering) are adding support and enhancement in the background [8]. The interconnected nature of disciplines in this way helps to illuminate more real-world STEM connections for children, highlighting the ways in which children are exposed to STEM-related learning opportunities on a daily basis. Many of the concepts, practices, and needed dispositions of STEM learning are shared amongst the disciplines that are found within the acronym [8].

Central to developing STEM reasoning are the pedagogical practices of communication and representation for young learners [8] (see Figure 1). ECE teachers are critical in facilitating and focusing classroom attention on communication of STEM-related ideas and the representation of them to allow children the opportunity to construct, visualize, write, graph, and draw in an attempt to communicate reasoning, develop language, collaborate, and productively struggle with STEM-related experiences. Supported by the theoretical frame of perseverance in problem-solving, such productive struggles help develop key reasoning skills that span the scope of STEM discipline practices and dispositions. These reasoning skills later contribute to more broad generalization of ideas, explicit understanding of concepts, and continued discourse around new and challenging topics. Next, we review literature within two themes supportive of STEM reasoning development in young children: supporting communication and use of representations.

2.1.1. Supporting Communication for STEM Reasoning

One way for ECE teachers to support communication for a child’s STEM reasoning development is to focus on facilitating meaningful mathematical discourse in the classroom. The National Council of Teachers of Mathematics [16] defines mathematical discourse as “the purposeful exchange of ideas through classroom discussion, as well as through other forms of verbal, visual, and written communication” (p. 29). We center our aims in the early childhood classroom as working to develop meaningful discourse that moves student STEM reasoning forward, specifically in the areas of mathematics learning. Ball et al. [17] emphasize the teacher’s knowledge of mathematics content, pedagogical skills, and insight into classroom context as a critical piece to inform their discursive choices and in-the-moment teaching moves. As part of facilitating meaningful mathematics discourse, Imm and Stylianou [18] found that classrooms where students felt safe to share mistakes, misconceptions, and general thinking about mathematics had higher levels of discourse due to the explicit message of learning from the discourse present. Huinker and Bill [19] later position the concept of facilitating mathematical discourse as a central and influential pedagogy to support the learning of mathematics in young children. Henderson Pinter et al. [20] extend on this work, noting that teachers who plan and prepare to address misconceptions of young children through discourse are deemed effective in their practice. This also builds on the work of Imm and Stylianou [18], who found that classrooms where students felt safe to share mistakes, misconceptions, and general thinking about mathematics had higher levels of discourse due to the explicit message of learning from the discourse present. Implicitly, these researchers are describing ways ECE teachers can persevere in their instruction, situated within the theoretical framework of perseverance in problem-solving from the teacher’s perspective, to provide children with these communication supports toward developing their STEM reasoning.

Learning experiences in ECE settings should incorporate ample opportunities for mathematical discourse because discourse can act as the vehicle by which students express their ideas and understandings about their emergent mathematical and STEM-based knowledge. Engaging in mathematical discourse helps students make sense of new mathematical ideas as they connect prior knowledge to new knowledge, as well as recognize specific mathematical ideas for which they need further clarification [21]. The teacher must consider and prepare the means of discourse by analyzing the context of their classroom and the knowledge of their students to inform moves around attending to the strategies of children, interpreting children’s’ understandings, and determining how to respond to children’s’ understandings [22]. These instructional moves are informed by day-to-day teacher–child interactions, and influenced by both the content and pedagogical knowledge of the teacher [17,20]. Furthermore, Van Es and Sherin [23] propose that teachers make concerted, in-the-moment efforts to access children’s thinking that may have been otherwise missed. This describes a version of formative assessment with feedback provisioning, in which the teacher is soliciting student thinking and subsequent instruction responds to those ideas, by building on productive beginnings or addressing emerging misunderstandings [24]. Teachers can do this through verbal exchanges between the ECE teacher and students, and is particularly vital because young children are just developing a language for expressing their mathematical and STEM-based ideas. Verbal discourse in the ECE classroom provides a powerful opportunity for teachers to access student thinking to help support individual students toward the mathematical goals of the lesson [19]. Such listening and responding to student thinking can dictate whether and how teachers can persevere in their mathematics instruction. The teacher’s perseverance is especially important as children are experiencing a challenge or impasse with the STEM-based content, because teachers need to recognize these impasse moments and re-initiate and re-sustain opportunities for their students to engage with the idea from a fresh perspective.

One particular focal point within facilitating mathematical discourse that can support young children’s development of STEM reasoning is posing purposeful questions. As a formative assessment tool, teachers can pose questions strategically to surface students’ STEM reasoning and evolving understanding. Teachers can use assessing, probing, visualizing, justifying, and collaborative questioning techniques to build from what students know, develop deeper knowledge, and help students make important connections between new mathematical ideas and between STEM disciplines [19]. Smith and Sherin [25] described ways to start meaningful mathematics conversations and explorations in the classroom through assessing and advancing questions: to reveal children’s ideas and to cultivate new ideas, respectively. Research on posing purposeful questions in ECE classrooms has described how young students think about concepts like cardinality, ordinality, and number structure [26], which has motivated using ECE teacher interventions to study how young children learn about STEM-related content. Carlsen et al. [27] illuminated the ways in which ECE teachers facilitated discourse in classrooms focused on STEM-related learning goals through a designed sequence of questions and inquiries. ECE teachers prepared and enacted purposeful questions that guided children’s thinking around concepts such as estimation, weight, volume, and quantitative comparisons and the connections between them. The instructional perseverance illustrated in asking these carefully designed questions supports children in making connections between STEM-related concepts.

Challenges surrounding posing purposeful questions in ECE contexts center around teachers’ continuous efforts to attend to children’s development and perspectives during engagement with tasks [28]. ECE teachers must make careful considerations about the mathematics and other STEM-based content with which children have already engaged in their classroom and communities, children’s successes and challenges with mathematics content, and teachers’ understanding of the capabilities of children in the classroom. This presents an opportunity for teachers to persevere as they must navigate these considerations both during planning and implementation of the lesson itself.

2.1.2. Supporting Use of Representation for STEM Reasoning

One way for ECE teachers to support use of representation for a child’s STEM reasoning development is to focus on exposing children to multiple representations of the same mathematical idea. In this pedagogy, teachers provide space for students to explore various representations of mathematical thinking to deepen their understanding of concepts and procedures [16]. The goal is for students to move fluidly between representations in order to acquire, often through some productive struggle, and demonstrate understanding of problems and concepts [19]. In ECE, research shows that young students can use a myriad of concrete tools to represent and help develop their mathematical thinking, from traditional mathematics manipulatives to “loose parts” open-ended materials that can be manipulated [29,30].

While mathematical representations for young children range across the continuum of concrete (physical manipulatives), relational (pictorial representations such as circles/dots), and abstract (numbers and symbols), ECE teachers work to develop a shared understanding, and place for these representations remains varied. Throughout the process of planning, teaching, and assessing, teachers need to remain mindful of not only the definition they have constructed for representations, but also how they are modeling, creating, and connecting multi-modal representations with children [7,31]. Children will not begin to use and connect these representations all at once, so ECE teachers must continue to plan for, model, use, and encourage them in practice; these actions are all indicative of instructional perseverance and situated within the theoretical framework of perseverance in problem-solving from the teacher’s perspective.

To support use of representations with young children, ECE teachers must also elicit and use evidence of student thinking as children explore different representations and work to connect them. In this practice, teachers listen to what students say, observe their actions, and/or analyze their written work to formatively assess their understanding. Such data informs teachers’ decisions about how to adapt instruction, both in the moment and for future lessons [19]. Research in ECE classrooms has found that using formative assessment to reveal students’ thinking and inform a teacher’s decision making as young children are exploring new mathematical ideas and representations can result in deeper mathematical thinking and engagement with more specific ideas, such as emerging number knowledge and learning of patterns [26]. ECE teachers must always be looking for opportunities to reveal student thinking; this helps teachers attend, interpret, and respond to it via feedback provisioning in the moment. Eliciting student thinking also invites the idea of shaping into STEM-based classrooms such that teachers can construct interactions with children to promote sensemaking [23]. “Shaping involves teachers constructing interactions, in the midst of noticing, to gain access to additional information that further supports their noticing” (p. 23). In this way, shaping directly involves the teacher in making in-the-moment decisions, which are informed by the contextual uniqueness of the classroom.

However, Dunphey [32] found 62% of ECE teachers often have difficulty engaging children in and facilitating conversation about mathematical and STEM-based learning involving multiple representations. This illuminates the complexity of discourse and the need for ECE teachers to both conceptualize the practice in their context and persevere in using it. The willingness and ability for mathematics teachers to attend to these complexities is rooted in notions from Jazby’s [33] ecological modeling of teaching noticing, in which the importance of teachers analyzing their own interactions in the classroom environment to help orchestrate both conversations and events during lessons was discussed. Jazby noted that the teacher’s active behavior during teaching helped to foster an environment in which noteworthy discussions of mathematical ideas and/or connections to STEM-based ideas could flourish. We view such active behavior as indicative of instructional perseverance and aligned to the theoretical framework of perseverance in problem-solving from the teacher’s perspective.

Young children also need time to productively struggle with new representations of mathematical ideas to help develop their STEM reasoning. Classroom environments that support productive struggle with mathematical representations give students time and space to grapple with mathematical ideas that are not immediately apparent to them. It is often difficult for teachers to withstand students’ struggles and not intervene and “rescue” students when they are frustrated while engaging with a new idea [19] (p. 237). Although much has been written about how to support K-5 students’ productive struggles with mathematical representations, including providing adequate wait time, asking questions, acknowledging student’s contributions, and providing encouragement, there has been little scholarship situated in the Pre-K setting despite persistence being a key recommendation for Pre-K mathematics classrooms [34]. Gifford [35] noted that ECE mathematics research has been limited to thinking about children’s abilities and competence, rather than a shift to considerations for teacher pedagogical moves that can support STEM reasoning development. In ECE settings, we argue that the responsibility is on teachers to persevere in their instruction to continually nurture opportunities to learn mathematics for children; it is the teachers’ instructional perseverance that paves the way for opportunities for students to persevere with challenging mathematical representations and ideas.

2.2. Supporting STEM Reasoning Development through Social Justice

The use of STEM-based lessons naturally connects to skills such as critical thinking, critical analysis, and reflective skills that are necessary to question the world and operation of systems within it [36]. With communication and use of representations as focal points of developing STEM reasoning, we assert that children’s participation in social justice-oriented content lessons, in our case mathematics, positions learners to “read and write the world” [37]. Through the utilization of social justice to provide both contextual background and goals for learning within STEM-based lessons, students are poised to reflect on their world and experiences. From this productive positioning, students can then begin to communicate about their reasoning of STEM-based content and concepts while centering their knowledge of justice-oriented practice [38]. Moreover, engagement in STEM-based content with social justice goals promotes critical consciousness in students, even those in the early grades.

Becoming critically conscious builds from work around three components: critical reflection, political efficacy, and critical action. The first, critical reflection, acts as an impetus for engagement in critical action and calls upon students to attend to the entangled nature of social injustices within systems [39]. For teachers, their background work and planning to provide contextual information about and opportunities for noticing issues of fairness and equity (as connected to their STEM-based content lessons) can support the critical reflection component. The second component, political efficacy, is one’s perceived ability to evoke and contribute to social change [39]. Through engagement in communication and use of representations to develop reasoning, the teacher can work to position young students as capable of creating change and using their collective voice. The final element of critical consciousness, critical action, calls for action taken to evoke change in aspects of society [39]. For young children developing STEM reasoning through communication and the use of representation, this presents a natural linkage to practices they are already engaged with during STEM-based lessons, as well as practices that are considered to be appropriate for their respective ages.

In sum, the literature presents research-based and student-centered practices that can be effective in supporting young children to develop their mathematical (and STEM-based) reasoning in ECE classrooms. However, little or no research exists that focuses on how ECE educators persevere during instruction to continually provide these learning opportunities to young children, despite setbacks and discouragements. We argue that research situated in an instructional perseverance in problem-solving theoretical perspective is necessary. Foregrounding the discipline of mathematics, we remind the reader of our definition of the construct of instructional perseverance: initiating and sustaining, and re-initiating and re-sustaining, opportunities for students’ engagement with mathematical ideas in the face of mathematical and pedagogical obstacles, setbacks, or discouragements. As such, the research question that guided this exploratory study is as follows: in what ways does instructional perseverance manifest itself in an ECE classroom and how does it support children’s STEM-based (primarily mathematical) reasoning in a social justice context?

3. Methodology

The purpose of this study was to explore the nature of instructional perseverance in ECE classrooms and how it manifests when ECE educators support young children to develop their mathematical (and STEM-based) reasoning. Using case study methodology [40], we explored data from an ECE teacher’s experiences teaching Pre-K mathematics in an early childhood lab school in the southeastern United States. This allowed us to explore the case and generate insight to refine prior theoretical framing of instructional perseverance [41]. Furthermore, case study research aims to promote understanding and centers on studying authentic experiences [40].

3.1. The Case and Context

As a lab school, the school was located on the campus of a research-intensive university and served the faculty, staff, and local community. The site frequently hosted teacher candidates from the early childhood program and worked closely with university faculty for professional development. Teachers engaged in inquiry-based instruction in the form of project work [42] in which children’s study made linkages between their interests and state standards in multiple areas. Teachers were supported to study their own practice through teacher action research and job-embedded professional development that was facilitated by the director and content experts. Prior to the time of lesson implementation, the teacher had been involved in work with the school centered around professional development and leading inquiries connected to both mathematics and culturally responsive teaching practices. At the time of data collection, approximately 80 students were attending the school from ages 2 to 5. The school house a classroom for each age group, with two classrooms serving as sites for the voluntary Pre-K (prekindergarten) in the state.

The teacher was engaged in leading lessons for small groups of students who were entering Pre-K during the upcoming school year. Students in the class were four and five years old at the time of the study with three students being female and six males. Students were all native English speakers and received instruction in English. The teacher in our study had been working with the school for two years providing professional development and collaborating with other teachers prior to the study. Prior to this experience, she had worked as an elementary and early childhood educator in the public-school setting for six years. She also served as a professional development coordinator for the local school district in the area of kindergarten mathematics. At the time of data collection, she was working on her doctoral degree in early childhood curriculum and mathematics education.

Lesson Contexts

Earlier in the school year, children had engaged in projects that worked to connect with various STEM topics and social justice standards. These lessons were designed by the teacher using the standards for early learning in the state along with social justice standards from Learning for Justice [43]. These projects and their corresponding STEM foci are described below in

Table 1. STEM lesson foci.

Lesson Topic	Science Focus	Technology Focus	Engineering Focus	Mathematics Focus
Playgrounds: designing and examining locations	x	Using iPads to communicate thinking	Building and constructing a playground	Measurement, data collection, and graphing
Gardens: planting a garden, food insecurity	Growing plants, parts of plants, healthy food choices/nutrition	x	Designing a garden and structures for plants	Measurement
Jobs: examining average income by race	x	Producing a haiku deck on a computer	x	Comparing quantities

.

Each lesson topic lasted for approximately three to four days and involved children in creating their own final product by which they could communicate their learning. These products aimed to serve as a mechanism to communicate their reasoning of the topic and associated social justice goals and also to demonstrate STEM reasoning skills associated with the lessons.

3.2. Data Sources

For this paper, we draw upon four instructional episodes that occurred as part of the ECE teacher’s work with her students. These four instructional episodes represent a range of the lesson topics described in Table 1 above and were selected as they featured students working through the mathematics content and standards. Data came from video-recorded lessons and transcriptions, lesson plans, and the ECE teacher’s reflective journal [44]. Lessons were video-recorded to capture the students’ thinking and discourse around the lesson content and later transcribed. Lesson plan notes and ECE teacher reflective journals were constructed during planning, immediately following lesson implementation, and again after viewing the lesson recordings to add any additional information. Notes from lesson reflections were used to provide additional context when constructing cases and provide a rich description of the events and their connection to instructional perseverance in ECE classrooms and how this ECE teacher supported young children to develop their mathematical (and STEM-based) reasoning through lessons that center mathematics and social justice.

3.3. Data Analysis

We employed an ECE Instructional Three-Phase Perseverance Framework (ECE-3PP) to qualitatively operationalize the perseverance process from the perspective of the ECE teacher (see

Table 2. ECE Instructional Three-Phase Perseverance Framework (3PP).

Phase 0: Entrance Phase
Clarity Check (C-0)	Checked for child’s understanding of task instructions and context
Initial Obstacle Check (IO-0)	Confirmed a solution pathway was not immediately apparent for child
Phase 1: Initial Attempt Phase
Initiated Effort Establishment (IE-1)	Provided a space for child to initially engage with task
Sustained Effort Facilitation (SE-1)	Facilitated child’s exploration of task
Productive Outcome of Instructional Effort (OE-1)	Perceived child to have made progress with their STEM reasoning toward a task solution
Phase i+1: Additional Attempt Phases (after sensing i child impasses)
Initiated Effort Establishment (IE-i+1)	Provided a space for child to initially re-engage with task
Sustained Effort Facilitation (SE-i+1)	Facilitated child’s continued exploration of task
Productive Outcome of Instructional Effort (OE-i+1)	Perceived child to have made progress with their STEM reasoning toward a task solution

). This framework was adapted from the original Three-Phase Perseverance Framework that was used to operationalize the perseverance process from the student perspective [45]. Informed from the literature on facilitating meaningful mathematical discourse with young children, e.g., [17,19,22] and the development of STEM reasoning [14], the adjective “Three-Phase” refers to three main phases of ECE instruction that can help nurture young children (i.e., students) in their perseverance in problem-solving: determining the appropriateness of the mathematical situation for the child (Entrance Phase), supporting the child’s initial effort toward a solution (Initial Attempt Phase), and facilitating the child’s additional effort(s) toward a solution after a setback(s) (Additional Attempt Phase(s)).

While launching the task with the child, Phase 0: Entrance Phase captured whether the ECE teacher determined if the child understands the entirety of what the task is asking and if the child immediately knew how to solve the problem, e.g., [28]. Essentially, this phase captured the ECE teacher’s efforts to determine the appropriateness of the task and if the STEM-based challenge is both warranted and within reason for the child.

The Phase 1: Initial Attempt Phase examined whether and how the ECE teacher supported the child to initiate and sustain their effort, and the outcome of such instructional efforts as the ECE teacher facilitates the child’s exploration toward a task solution. For this study, we defined evidence of STEM reasoning (e.g., children communicating, using new language, thinking critically, collaborating, persisting, and problem-solving about/with the STEM-based content) as what constitutes a productive outcome of instructional effort. As per Spaepen et al. [8], we chose to foreground the discipline of mathematics as the primary source of evidence of STEM reasoning, although evidence from all STEM disciplines was considered. The discursive sub-practices of posing purposeful questions, using and connecting mathematical representations, eliciting and using evidence of student thinking, and supporting productive struggle help constitute supportive teacher actions in the context of the Initial Attempt Phase, e.g., [19].

In the event the child did not solve the task after making a first attempt supported by the ECE teacher, the Phase i+1: Additional Attempt Phases captured if and how the ECE teacher supported the child to find a new way to engage with the task, sustain such engagement, and the outcome of such instructional efforts as the ECE teacher assisted the child to overcome any setbacks and continue to work toward a task solution. To enter the Additional Attempt Phase (marking the end of an initial attempt and the beginning of an additional attempt), the ECE teacher must have noticed that the child reached an impasse [46] that is, the teacher sensed that the child was substantially confused or disinterested about how to move forward, e.g., [23]. Many sensed impasses were confirmed via the ECE teacher’s reflective journal entries.

The ECE teacher could continue their instructional efforts in the Phase i+1: Additional Attempt Phases by entering a Phase 3, Phase 4, etc., depending on if the child encountered more impasses and needed further perseverance support. Here, the teacher’s decision making will likely be connected to their own sense-making of this attempt, possibly from the idea of shaping [23], but also based upon their own approaches to teaching and pedagogies that inform their practice [47]. The discursive sub-practices of posing purposeful questions, using and connecting mathematical representations, eliciting and using evidence of student thinking, and supporting productive struggles help constitute supportive teacher actions in the context of the Additional Attempt Phase(s), e.g., [19].

4. Results

First, we will share our overall ECE-3PP findings across our four instructional episodes. By the nature of the ECE-3PP, these findings describe the instructional perseverance and coinciding STEM reasoning by the ECE teacher and students, respectively. We also report findings relative to students’ developing understandings based on their progress towards social justice goals of the lessons. Second, we will describe the details of one instructional episode as an illustrative case of instructional perseverance, and the coinciding evidence of students’ STEM and access to social justice goals, in an ECE classroom.

4.1. Overall Findings

We found evidence of ECE teacher instructional perseverance and coinciding students’ STEM reasoning and access to social justice goals during all four instructional episodes (see

Table 3. Overall findings of instructional perseverance and the students’ experience.

Instructional Perseverance			Students’ Experience
Instructional Episode	Sensed Impasses	ECE-3PP Attempt Phases	Evidence of STEM Reasoning	Access to Social Justice Goals
A	4	5	Connecting the length of bars on a graphical representation to a corresponding quantitative inequality (mathematics); designing a map of new playgrounds (engineering); creating video media to disseminate their thinking (technology)	Understanding the [un]fairness of playground prevalence and regional income
B	2	3	Recognizing that the statistic 1 in 5 describes the unlikely nature of achieving a desired outcome (mathematics); planning a garden to grow food (science); use digital tools to collect and analyze data (technology)	Understanding the inequity of the statistic that “1 in 5 kids in our community struggle with food insecurity”
C	4	5	Recognizing that the statistic 1 in 5 describes the unlikely nature of achieving a desired outcome (mathematics); planning a garden to grow food (science); use digital tools to collect and analyze data (technology)	Understanding the inequity of the statistic that “1 in 5 kids in our community struggle with food insecurity”
D	8	9	Connecting a quantitative inequality to more-likely and less-likely outcomes (mathematics); employing an experimental balance scale (science)	Understanding the inequity of income variance by race

). From an instructional perseverance perspective, the ECE teacher passed through the ECE-3PP Entrance Phase with her students to successfully and appropriately launch each task in all four instructional episodes. From a social justice perspective, we also found evidence of the ECE teacher supporting critical consciousness [39] in her students in all four instructional episodes. The ECE teacher did ample background work to provide contextual information and opportunities for her students to notice about fairness and equity related to their STEM-based content lessons. The ECE teacher also worked to position her students as capable of creating change using their collective voice as they engaged in communication and with different representations during the lessons.

During episode A, the ECE teacher sensed a total of four student impasses relative to the mathematical, engineering, and technological (and social justice) goals and, as a result, the ECE teacher passed through five ECE-3PP Attempt Phases in total. Coinciding with this instructional perseverance was evidence of students’ STEM reasoning and access to social justice goals, in the forms of connecting the bar length on a graphical representation to a corresponding quantitative inequality and understanding the [un]fairness of playground prevalence and regional income, respectively. During instructional episodes B, C, and D, we found similar results relative to instructional perseverance and the students’ experience: the ECE teacher sensed multiple student impasses and, thus, passed through multiple ECE-3PP Attempt Phases, and such instructional perseverance coincided with evidence of students’ STEM reasoning and access to social justice goals. See Table 3 for more details about our findings during each instructional episode.

4.2. Illustrative Case-Episode D: Exploring Income Variance by Race

The instructional goals of this lesson were for students to understand quantitative comparisons between incomes, more-likely and less-likely outcomes, employing a balance scale to reason about quantities, and connecting each of those STEM-based goals to income variance by race. During this two-day, 65 min instructional episode, we found evidence of ECE teacher instructional perseverance as she facilitated the task with five Pre-K students (S1, S2, S3, S4, S5). Our findings focus on the instructional perseverance of the ECE teacher and evidence of students’ STEM reasoning and progress towards social justice goals that coincided with such instructional perseverance. In the following paragraphs, we describe the details of ECE teacher’s instructional perseverance during this episode and include illuminating data from the ECE teacher’s reflective journal entries. See

Table 4. Summary of the Instructional Perseverance in Episode D.

Instructional Perseverance in Episode D
		Attempt Phases
Entrance Phase			1	2	3	4	5	6	7	8	9
Clarity Check (C-0)	✓	Initiated Effort Establishment (IE)	✓	✓	✓	✓	✓	✓	✓	✓	✓
Initial Obstacle Check (IO-0)	✓	Sustained Effort Facilitation (SE)	✓	✓	✓	✓	✓	✓	✓	✓	✓
		Productive Outcome of Instructional Effort (OE)	✓	✓	✗	✓	✓	✗	✓	✓	✓

for a summary of the instructional perseverance in episode D in which a check indicates the presence of the element within the attempt phase and an “x” indicates the absence of the element.

4.2.1. Entrance Phase

While launching the task with S1, S2, S3, S4, and S5, the ECE teacher passed through the Entrance Phase of instructional perseverance by confirming the students’ familiarity with the task’s context and instructions (C-0) and checking for an initial obstacle (IO-0). All students were familiar with the ideas of money and income. In her reflections, it was clear to the ECE teacher that all students had experiences with identifying numbers 0–9, making quantitative comparisons, and using proportional reasoning, but struggled to make meaning of these ideas and connections between them. Students also had not previously experienced a task with the same social justice goals as this task: income variance by race.

4.2.2. First Attempt Phase

Marking the beginning of the First Attempt Phase of instructional perseverance, the ECE teacher directed her students’ attention to some different colored toy bears and some pretend money. She helped her students initiate a way to establish their effort by modeling for them how certain colored bears can get paid different amounts of money (IE-1). By introducing these physical representations of bears and money and the action of income, the ECE teacher provided an opportunity for these students to initiate their effort with the task.

The ECE teacher facilitated a way for her students to sustain their effort by continuing to model the variance of income for different colored bears and explaining that certain colored bears would receive more money than other colored bears for certain arbitrary reasons (SE-1). The ECE teacher explained to the students, “I really like yellow, so I’m going to give the yellow bear $10…My mom’s favorite color is orange, so I’m going to give the orange bear $10…I don’t like blue or green, so I’m going to give the blue bear $7 and the green bear $7”. The ECE teacher physically distributed these amounts of money to the different colored bears and prompted the student to count the money aloud as she distributed it. Such modeling of how certain colored bears receive income based on arbitrary reasoning provided an opportunity for the students to recognize the inequity and the arbitrary source of it. The students collaboratively noticed the unequal quantities of money and immediately suggested that the bears should borrow money from each other to ensure they all have the same amount of money. S4 noticed, “[the yellow] one and [the blue] one, they’re not the same”. S2 wondered, “If only one bear has all the money, how can the other bear trade food with that?”

Since the students were critically thinking and communicating about some bears having more money than others, the ECE teacher perceived this as progress in STEM reasoning made as a result of her instructional efforts (OE-1). Still, at this point, the ECE teacher sensed a students’ impasse (i = 1) about the source of these different incomes and the underlying inequity, which drove the social justice goal. In her reflection on this moment, the ECE teacher clarified that early on, students were able to see the distribution of money as unfair when she decided to give the blue and green bears only $7 (as noted by the students disagreeing with this decision). At this point, the ECE teacher knew that the children were able to make sense of the unfairness and inequity influencing the amount of money each bear was receiving because they had already explored the concept of fairness in connection with food insecurity and access (this happened in Episode B, days earlier). This ended the ECE teacher’s First Attempt Phase of instructional perseverance.

4.2.3. Second Attempt Phase

In response to her sense of the students’ impasse around the inequity, the ECE teacher amended her instructional plan to start a Second Attempt Phase. She re-initiated a way for her students to engage with the task by refocusing the conversation on the rationale for each colored bear’s income (IE-2). She asked her students, “What do you guys think of…how I decided how much money the bears got?” The ECE teacher continued to facilitate ways for her students to think about the inequity in the context of income variance by different colored bears by asking “Was that a good way [of deciding how much money the bears got]?” (SE-2). S2 answered immediately and said, “That was a good way for the yellow and orange one, but not the other ones because you gave them $7”, which was perceived by the ECE teacher as progress in STEM reasoning (and social justice progress) toward problem-solving with a quantitative comparison that $10 and $7 were not equal (OE-2).

Still, at this point, the ECE teacher sensed a students’ impasse (i = 2) about connecting the mathematics to the inequity. In her reflection on this moment, the ECE teacher clarified that students had demonstrated the ability to compare numbers like 10 and 7 during earlier lessons and during the current lesson, she thought she could continue with the lesson by providing more purposeful questions to support students making connections between the mathematics and inequity, linking to both the mathematics and justice goals. This ended the ECE teacher’s Second Attempt Phase of instructional perseverance.

4.2.4. Third Attempt Phase

In response to her sense of the students’ impasse around connecting the mathematics to the inequity, the ECE teacher amended her instructional plan to start a Third Attempt Phase. She re-initiated a way for her students to engage with the task by focusing on the relationship between the quantities $10 and $7 (IE-3). She asked her students, “What do we know about seven and ten? What do we know about those two numbers?” Her students were unsure how to respond, so the ECE teacher continued to facilitate ways for her students to think about the inequity in the context of income variance by different colored bears by asking a purposeful question, “Is [$10 or $7] more or less than another?” (SE-3).

The students were still confused about how to compare these two quantities and S3 responded, “Maybe the bears don’t have no more dollars”. Thus, the ECE teacher sensed another student impasse (i = 3) about comparing the quantities $10 and $7 and perceived no progress in STEM reasoning as a result of her most recent instructional efforts (hence no indication of an OE code). This ended the ECE teacher’s Third Attempt Phase of instructional perseverance.

4.2.5. Fourth Attempt Phase

Motivated by the students’ lack of mathematical progress about comparing the quantities $10 and $7, the ECE teacher started her Fourth Attempt Phase by redirecting the discussion onto bears spending their money instead of earning it. The ECE teacher re-initiated a way for her students to engage with the task by stating the fact that “the bears might run out of their dollars” (IE-4). She went on to facilitate this discussion by prompting students with the question, “Which bears are going to run out of their dollars the quickest?” (SE-4). In response, S3 pointed to one of the bears with $7 and said, “This one”. This implied that S3 was critically thinking and communicating about $7 being less than $10 and was perceived by the ECE teacher as progress in STEM reasoning (OE-4).

Another student, S4, joined in and said, “If the blue one and green one have seven and the orange one and the yellow one have ten, that’s not fair. We have to do something nice”. This collaborative critical thinking and language use about the idea of fairness was also perceived by the ECE teacher as progress in STEM reasoning (and social justice progress) toward connecting the quantitative comparison that $10 and $7 were not equal to the income inequity (OE-4). However, the students went on to demonstrate some confusion about the source of the inequity: that the ECE teacher was arbitrarily deciding which colored bears received more or less money. The ECE teacher perceived this as an impasse (i = 4). In her reflections, she explained that, at this point, the students had not yet had an opportunity to think about unequal income despite equivalent jobs, which might explain their confusion. This ended the ECE teacher’s Fourth Attempt Phase of instructional perseverance.

4.2.6. Fifth Attempt Phase

In response to her sense of the students’ impasse about the inequity source, the ECE teacher started a Fifth Attempt Phase. She re-initiated a way for her students to engage with the task by clarifying that the bears all had equivalent jobs and education-levels despite different incomes (IE-5). She told her students, “All these bears have the same job…and they went to school for the same number of years. The only thing that is different about these bears is their color”. She helped facilitate a discussion about these ideas by asking students to explain to each other how each bear’s income was decided (SE-5).

Soon after, S4 began explaining to the other students and said, “The blue one and the green one, they just have seven, and the orange one and the yellow one, they had ten”. The ECE teacher asked an advancing question, “How did [I] decide how much money the bears got?” S4 replied, “If you put only seven for [the blue and green bears], they will finish it all before [the orange and yellow bears], then [the blue and green bears] will go gone”. This exchange was perceived by the ECE teacher as progress in STEM reasoning since students were voicing new language about their understandings of how $7 is less than $10 (OE-5), which was a focus of her instruction during the Fourth Attempt Phase. At this point, however, the ECE teacher perceived an impasse (i = 5) about a lack of connections between the color of the bears and their influence on the income variance, as linked to the social justice goal. This ended the ECE teacher’s Fifth Attempt Phase of instructional perseverance.

4.2.7. Sixth Attempt Phase

The ECE teacher started her Sixth Attempt Phase by re-initiating a way for her students to engage with the task by playing a game that could illustrate income variance (IE-6). The game involved students spinning a spinner to randomly earn different amounts of income. The amounts of income earned were represented by certain numbers of toy bears that each child received. She explained the rules of the game, “When it’s your turn you will spin the spinner. Whatever number you land on, you will take that many bears and you’re going to line your bears up”. The ECE teacher was trying to provide an opportunity for her students to recognize income variance unfold as different students invariably earned different income amounts based on their spins. She facilitated the gameplay by making sure each student followed the rules by spinning the spinner, recognizing the outcome, and representing their income with lined up bears (SE-6).

Although the students were taking turns at spinning the spinner and collecting bears, they were struggling to make any quantitative comparisons about the bears collected and connections to income variance. As a result, the ECE teacher sensed another impasse (i = 6) and perceived no progress in STEM reasoning made by her students during such gameplay thus far. This ended the ECE teacher’s Sixth Attempt Phase of instructional perseverance.

4.2.8. Seventh Attempt Phase

Motivated by the students’ struggles to connect quantitative comparisons to income variance during the spinner game, the ECE teacher started her Seventh Attempt Phase by re-initiating a way for her students to engage with the task by introducing a new scientific tool: a balance scale (IE-7). She facilitated the use of the balance scale to provide an opportunity for students to explore quantitative comparisons, specifically that $10 > $7 because 10 bears are heavier than 7 bears (SE-7). The students referred to the scale as “a teeter totter” and began making observations when different quantities were put on the balance scale.

When S1 and S5 experimented by placing three bears on each side of the balance scale, S2 voiced an observation that “if S1 and S5 put three bears, then the level will be the same one”. This implied that S2 was critically thinking about the comparison of these quantities and that they were equal because the scale was balanced as a result of their problem-solving experiment. This was perceived by the ECE teacher as progress in STEM reasoning (OE-7) as a result of her instructional efforts. At this point, however, the ECE teacher sensed a student impasse around not seeing connections to the social justice goal of task (i = 7), and decided to shift gears to a new instructional move. This ended the ECE teacher’s Seventh Attempt Phase of instructional perseverance.

4.2.9. Eighth Attempt Phase

The ECE teacher started her Eighth Attempt Phase by re-initiating a way for her students to engage with the task by playing a new game that could illustrate income variance by race (IE-8). This game was related to the previous spinner game, but had new rules (and new colored bears). This game involved teams of students randomly drawing a bear of a certain color and spinning a spinner to randomly determine that colored bear’s income. The ECE teacher facilitated the gameplay by revealing the rules as the students were playing, after they had each randomly drawn a bear of a certain color (SE-9). She explained, “Blue bears and yellow bears get [$2] no matter what you spin”. She went on to explain, “Red bears and green bears get $2 if you spin a 0, 1, 2, 3, 4, 5, 6, or 7…but an 8 or 9 means they only get $1”.

The students played this game by spinning the spinner and earning $2 or $1 for their bear of a certain color. As some students started to earn more money for their blue and yellow bears, other students began to recognize that the game was unfair. The team of S4 and S5 exclaimed “Oh my gosh!” in frustration when they observed S2 earn $2 for their yellow bear no matter what they spun. Several times, S4 and S5 tried to swap their red bear for a blue or yellow bear to insure they’d receive $2 no matter their spin. S2 noticed the unequal pay, stating, “Our team have much more money than that team”. Such collaboration, language use, and critical thinking was perceived by the ECE teacher as progress in STEM reasoning (OE-8) as a result of her instructional efforts. Trying to connect such quantitative reasoning to the source of the inequity, the ECE teacher asked, “How did [I] decide how much money you were getting?”, but the students were unsure how to answer. The ECE teacher sensed this as an impasse (i = 8), and this ended the ECE teacher’s Eighth Attempt Phase of instructional perseverance.

4.2.10. Ninth Attempt Phase

The ECE teacher started her Ninth Attempt Phase by focusing her students’ attention on the bear color and income differences. She re-initiated a way for her students to engage with the task by posing the assessing question, “Did all bears earn the same amount of money?” (IE-9). All the students enthusiastically replied, “No!”. The ECE teacher facilitated the discussion by asking an advancing question, “I know that some of you when you were playing the game were trying to pick certain color bears. Which color bears were you trying to get?” (SE-9). S4 answered, “We were trying to get…more money”. The ECE teacher responded, “… to pick a yellow or blue bear to get $2 no matter what you spun?” S2 answered, “Yes”. The ECE teacher then posed another advancing question, “Did you always get $2 when you got a green or red bear?” All the students answered, “No!”, and S3 shared, “That not make sense…it not make sense that S4 have $1, then I get [$2]!”.

The ECE teacher continued facilitating this discussion about income variance by bear color, and several students voiced their concerns about its unfairness. Near the end of their allotted time for the lesson, the ECE teacher admitted, “Well, that’s what happens sometimes in the real world”. S2 replied, “Then, if the bears don’t have that much money…if the bears finish all their money before [our blue and yellow bears], then maybe we can give them some of ours”. This entire collaborative discussion was perceived by the ECE teacher as progress in STEM reasoning (OE-9) because the students were critically thinking about the relationship between the income variance and unfair practices, namely that certain colored bears were arbitrarily earning more money than other colored bears. Although there was additional progress in STEM reasoning possible to make, the instructional episode was ended due to time constraints. This ended the ECE teacher’s Ninth Attempt Phase of instructional perseverance.

4.2.11. Summary

In sum, the ECE teacher traversed nine Attempt Phases of instructional perseverance with her students during episode D, with hopes of achieving both STEM reasoning and social justice goals. Our analysis helps show the perseverance of the ECE teacher to continue to support her students’ problem-solving with these challenging ideas, despite several setbacks, distractions, and discouragements along the way. Although not every learning goal was accomplished across these nine Attempt Phases, there was evidence of student progress in STEM reasoning (and social justice) progress relating quantitative comparisons to income variance by race. This suggests the outcome of STEM reasoning (and social justice) progression was made possible by the resilient instructional perseverance of the ECE teacher.

5. Discussion and Conclusions

Situated in the theoretical perspective of perseverance in problem-solving for learning with understanding, an important contribution of this work is the recognition of the existence of instructional perseverance in an ECE setting and how it might support children’s STEM reasoning development. This study shows how pedagogy focused on supporting children’s STEM reasoning development via encouraging communication and representation use can also describe the ways ECE teachers sense impasse moments during their students’ STEM-based learning experiences, pedagogically pivot to overcome such obstacles, and persevere in their student-centered instruction. Recognizing this responsive pedagogy helps iterate and build on traditional perseverance in problem-solving theory because it redefines what problem-solving can mean to consider the perspective of the teacher. The problem-solving that teachers do refers to their in-the-moment pedagogy to better support students to stay engaged with robust learning goals, and instructional perseverance describes a teacher’s tenacity while engaging in such pedagogical problem-solving. Our interpretations of the data show, in Episode D beginning with the entrance phase of the ECE-3PP, that the ECE teacher offered her students opportunities to connect prior and new knowledge through engagement with familiar ideas and contexts [19,21,22,28]. As students entered into the task, the ECE teacher used physical representations of races and income, along with purposeful questions, to move towards the mathematical and social justice goals of the lesson. These moves supported students in making sense of various representations [7,19,25,31] while also highlighting the ECE teachers’ ways of helping students engage with the task in order to make progress with their STEM reasoning.

During the times when students were confused or straying from STEM reasoning or social justice goal progression, such as the several times when the children were unsure about how to connect the quantitative inequalities to the source of the underlying inequity, the ECE teacher used shaping techniques to reveal student thinking and inform new instructional avenues toward sensemaking [23]. This pedagogy aligns with formative assessment moves coupled with feedback provisioning by surfacing students’ misconceptions and addressing certain misunderstandings in the moment. Our interpretation of the data showed multiple moves such as this, as the ECE teacher sensed eight student impasse moments during the lesson. This illustrated the ECE teacher’s attentiveness to the key moments during classroom activity that raised the need for instructional perseverance and that separated the Initial and Additional Attempt Phase(s) of Instructional Perseverance. Additionally, evidence in this study showed the ECE teacher amending her instructional plan to offer new ways for students to engage in STEM reasoning; when she facilitated conversations about comparing the quantities that represented the different incomes, introduced (and re-introduced with modifications) a game to represent income variance, encouraged exploration of the situation by posing assessing and advancing questions, and involved a variety of STEM-based tools (e.g., spinners, balance scales) to assist in facilitation of the activity. These in-the-moment moves provided fresh opportunities for students to communicate about how to use different representations of the same mathematical ideas [7,8,19,25,31] and how to connect them to the social justice goals of the lesson. Similar pedagogies were performed during the remainder of the lesson as the ECE teacher responded to eight impasses. These pedagogical pivots illustrate the ECE teacher’s attentiveness to issues encapsulated by the Additional Attempt Phase(s) of Instructional Perseverance and align to the general theoretical perspective of perseverance in problem-solving.

ECE teacher’s knowledge of the classroom context and students positioned the teacher in our study to have specialized expertise around which students could be supported to extend their thinking and at what points. It also provided the teacher with the ability to consider representations that students have prior familiarity within her instructional delivery. These insights provided the means to foster instructional perseverance and STEM reasoning over the course of the episodes. However, as we consider the progress in developing STEM reasoning with young children evident in these episodes, we must also consider the ongoing power dynamics within early childhood classrooms. Educators must attend to how they are working with children to co-construct learning experiences that are centered in environments where children can express their voice around impasses (e.g., through sharing their frustrations and needs during the lesson). Wood [48] argues that child-centered spaces should position learners as active and competent, shifting from prior conceptions of children as empty and needing to be filled with knowledge. By listening to the voices of learners, teachers can begin to craft environments in which power and agency are shared between teacher and learners. Conversely, a classroom where attention to power is not occurring may yield less robust interactions and reasoning development amongst learners.

One limitation of our work was that it did not center on this power dynamic nor how it was addressed in this particular classroom; it was outside the scope of this study. However, we contend that focusing on the ways that ECE teachers attend to the power dynamics between themselves and their students in the classroom setting is pivotal. Power itself is irremovable from daily classroom practice [49]. Jobb [50] suggests that power exists not between just the people (teachers and students), but also exists in the space these groups occupy and is under constant negation [51]. Classifying the classroom as child- or teacher-centered fails to speak to the nuances required of the space in which learning is occurring. To help address this limitation, we suggest future work to explore the early childhood classroom environment in a more holistic manner and over longer periods of time to help to pinpoint possible classroom factors that aim to support co-constructed perseverance. Rogers and Freiberg [52] espouse that teachers become co-learners in the instructional process, thereby acknowledging the simultaneous learning that occurs for teacher and student during instruction. As teachers work to sustain their own instructional perseverance, they model what perseverance looks like and the contextual considerations of perseverance for their own students. Therefore, both parties engage with the task in new ways and work together towards the development of STEM reasoning. Focusing on this collaborative development, a guiding principle for early childhood STEM development [8] may require exploring the entanglement of the teacher’s and students’ perseverance during lessons.

An additional area of future work may include teacher education and professional development around instructional perseverance. These research initiatives should introduce the construct of instructional perseverance and emphasize the ways in which teachers can reflect on their instructional perseverance when enacting STEM-based tasks to support students’ STEM-based reasoning. This could be done through increased engagement in action research as a method for professional development. Involving teachers and teacher candidates in investigating their practice and identifying moments of missed and captured opportunities to demonstrate perseverance when teaching is important to support the equitable practices in the classroom. As teachers become aware of their instructional contexts and the perseverance of their students, they are better equipped to leverage their own instructional perseverance to help set high expectations for those in their classrooms. Moreover, this focus would support Cochran-Smith’s [53] theory of teacher education for social justice, specifically ideas around interpretive frames. Providing reflective analysis of the ways in which teacher education candidates are developing asset-based views of students, inquiry approaches in teaching, and the knowledge of the sociopolitical contexts of education seeks to enhance STEM-based reasoning from simply centered on content to centered on critical consciousness.