Exploring Measurement through Coding: Children’s Conceptions of a Dynamic Linear Unit with Robot Coding Toys

Abstract

Programming activities have the potential to provide a rich context for exploring measurement units in early elementary mathematics. This study examines how a small group of young children (ages 5–6) express their emergent conception of a dynamic linear unit and the measurement concepts they found challenging. Video of an introductory programming lesson was analyzed for evidence of preconceptions and conceptions of a dynamic linear unit. Using Artifact-Centric Activity Theory as a lens for the analysis, we found that social context, gesturing, and verbal descriptions influenced the children’s understanding of a dynamic linear unit. Challenges that students encountered included developing a constructed conception of a unit, reconciling preconceptions about the meaning of a code, and socially-influenced preconceptions. This study furthers the exploration of computational thinking and mathematics connections and provides a basis for future exploration of dynamic mathematics and programming learning in early elementary education.

1. Introduction

Learning length measurement in elementary school mathematics involves quantifying the length or distance between two endpoints of an object or space. Young children must develop differing levels of thinking to understand length measurement, which involves important concepts such as comparison, seriation, unit, and iteration [1,2,3]. By recognizing that lengths of objects can be compared, children are able to understand length as a comparative attribute to distinguish objects from each other [3]. One form of comparison is seriation, the ordering of objects by length. Both comparison and seriation are intuitive to young children as they reason proportionally [1]. A foundational concept required to quantitize length measurements is an understanding and use of units. Length units are used as references to compare the length of one unit with the length of the distance being measured. A length measure is quantitized by iterating (repetition without gaps or overlaps between each unit) equal units along the length until the space being measured is exhausted [4]. These ideas form a foundation for linear measurement [5]; however, foundational topics and concepts, such as developing concepts of dynamic linear measurement, are often absent from the standards [6]. Measurement skills are nevertheless important to later mathematics learning and, more broadly, STEM learning.

Children in the United States are generally taught length measurement skills by first comparing and ordering (seriating) physical objects’ length, then measuring lengths by iterating unconventional units (e.g., hand spans, finger widths), and finally measuring with conventional tools, such as rulers [6]. Children in the United States regularly underperform in measurement knowledge on international assessments [7,8]. One possible explanation for children’s difficulty with measurement skills is that United States measurement curriculum places a heavy focus on procedures rather than also attending to children’s conceptual understanding of measurement concepts [8]. While we acknowledge the ongoing debate regarding the relationship and value of procedural and conceptual knowledge, respectively (e.g., [9,10,11]), to report on it here is outside the scope of this study. Instead, we take the position that each knowledge type has value. In alignment with this perspective, we argue that an effective approach to measurement instruction would be to engage students in activities that support both conceptual and procedural knowledge, such as exploration and discussion [10]. For example, research indicates that manipulating physical objects and understanding that a unit is a length of space positively impacts children’s unit measurement knowledge [3,12,13]. Thus, hands-on instructional activities that allow children to manipulate objects in physical space through explorative activities while engaging in discussion have the potential to improve children’s understandings of units and measurement.

One rich context for learning measurement in this way is programming activities with tangible robot coding toys that move in iterated units through space (e.g., a robot moving two forward units on a grid; see

Table 1. Examples of screen-free coding toys. From left to right, Learning Resource’s Code & Go Robot Mouse, Fisher Price’s Code-a-pillar, Learning Resource’s Botley the Coding Robot, and Primo’s Cubetto.

	Robot Mouse		Code-a-Pillar		Botley		Cubetto
Robot
Robot Codes and Movements		forward		forward		forward		forward
		rotate right 90°		turn right		rotate right 90°		rotate right 90°
		rotate left 90°		turn left		rotate left 90°		rotate left 90°
		backward				backward		backward

). Tangible coding toys are screen-free robots that move along paths or within a grid space by manipulating coding blocks (forward, backward, rotate left, rotate right). Coding toys have been used to teach various early-elementary mathematical concepts, such as spatial skills (e.g., [13,14,15,16]), sequencing (e.g., [17,18,19,20]), and measurement skills (e.g., [21,22,23]). In a recent study [24], a research group identified overlaps of mathematics concepts and skills with computational thinking as small groups of children (ages 5–6 years old) participated in programming lessons with screen-free coding toys. They found that children applied various mathematics concepts and skills, including distance and linear units, spontaneously and without teacher prompting as they engaged with the coding toys. These findings support the assertion that coding toys provide a meaningful context for learning mathematical concepts, such as measurement. Moreover, tangible coding toys provide children with a uniquely dynamic representation of measurement concepts through the toy’s real-time movements along a navigational plane.

In this paper, we expand on previous research on coding toys and early childhood mathematics and argue that interacting with coding toys provides opportunities to develop unit measurement concepts, specifically opportunities to understand length measurement from a dynamic perspective (e.g., length of a distance the robot traveled) as opposed to a static perspective (e.g., the length of a robot). We call this concept a dynamic linear unit. The goal of the present study was to explore kindergarten (ages 5–6 years old) children’s emergent conceptions of a dynamic linear unit as a foundation for learning length measurement. Our research was guided by the following two questions:

Question a:

How do kindergarten-aged children express their emergent conception of a dynamic linear unit of measure during programming activities with coding toys?

Question b:

What measurement concepts and skills are challenging for kindergarten-age children to construct during programming activities with coding toys?

1.1. Early Research on Measurement and Coding

A forebearer to current research on early childhood coding toys is Papert’s [25] Logo, a programming tool in which young children use basic codes (forward, backward, right rotation, left rotation) to manipulate a digital or physical robot turtle. Through research with Logo, Papert described children’s construction of mathematical understanding from their lived experiences. Papert argued for experiencing mathematics with one’s body and environment to support natural learning rather than undoing experiential mathematics learning in favor of rote rules.

Additionally, early research on the effects of Logo experiences on children’s mathematics learning provides evidence that interactive computer environments, such as Logo, supported students’ use of mathematical concepts, including concepts related to length measurement [26]. For example, third graders with Logo instruction were more accurate in estimating distance [27]. Researchers also found that Logo turtle instruction supported third graders’ connections between number and geometry in measurement [28]. Further, recent findings suggest that traditional measurement activities, such as counting discrete objects, transition students to counting ruler hatch marks which inadvertently supports an incorrect procedure of identifying length as marks on a ruler rather than iterated spatial units [29]. Hence, the present study proposes that programming activities with coding toys can provide a context in which students’ understanding of dynamic linear units can build their understanding of the construct of length measurement.

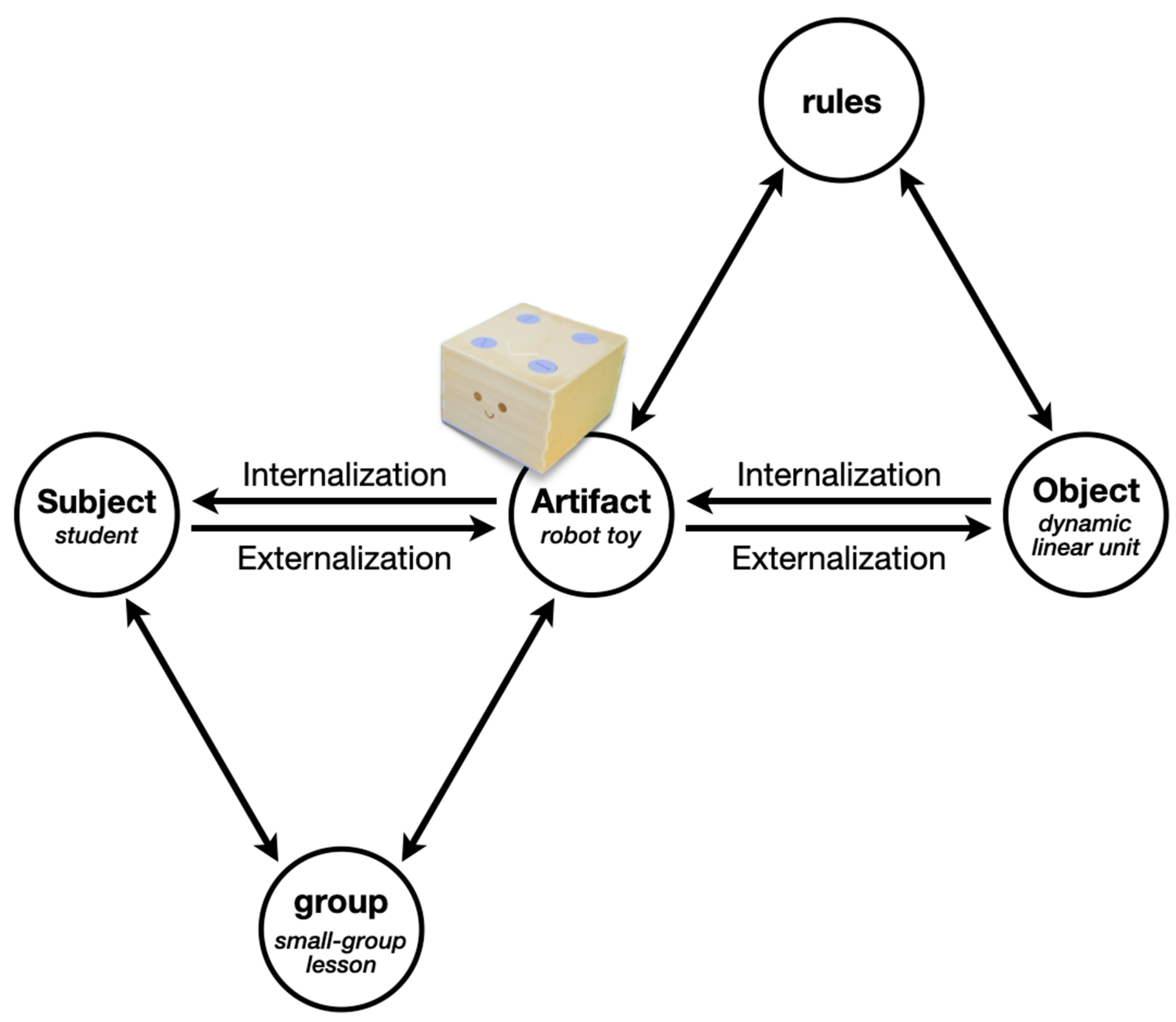
1.2. Artifact-Centric Activity Theory

We use Artifact-Centric Activity Theory as our theoretical perspective for understanding children’s expressions of the dynamic linear unit concept. Rooted in Engeström’s theories of internalization and externalization through activity among subject-object-community, Ladel and Kortenkamp’s [30] Artifact-Centric Activity Theory (ACAT) provides a perspective that centers the role of an artifact in these interactions for learning. The ACAT framework has traditionally been used in mathematics education research to examine children’s engagement with digital apps (e.g., [31,32]) and virtual manipulatives (e.g., [33,34]), however Ladel and Kortenkamp [35] have encouraged researchers to apply the ACAT framework to other instructional tools. Figure 1 shows the ACAT framework situated in our study’s complex activity system of teaching and learning. As applied to our study, the ACAT framework describes how, within the context of a teacher-led small group activity (group), interaction with a coding robot toy (the artifact) mediates a student’s (the subject) conceptualization of a dynamic linear unit (the object). This framework also depicts how the constraints imposed by mathematical principles and the artifact’s design (rules) further mediate students’ experience with the artifact and, subsequently, the student’s mathematical understandings.

The arrows in the ACAT framework indicate the expected relations between each element. For example, the bi-directional arrow connecting the group and the artifact indicates that the group engages with (i.e., manipulates, discusses, observes) and is influenced by the artifact, while the artifact also influences how the group interacts with it. Mediating factors affecting how the group interacts with the artifact stem from the artifact’s design, or rules. The double-headed arrow connecting the artifact and rules indicates how the artifact’s design impacts how a subject and group interacts with the artifact. In this study, the robot acting as the artifact operates within its design constraints, or rules. Some of the robot’s rules include how the robot is coded, which commands the robot can be given, and how the robot interprets each command.

The relations among the ACAT elements on the main axes (subject—artifact—object) are depicted with directional arrows and labeled as internalization and externalization. According to ACAT, the subject externalizes (makes visible) their thinking by engaging with the artifact, then internalizes (makes sense of, adopts) knowledge demonstrated by the artifact. As applied to this study, a student externalizes their thinking by programming or moving the robot. The student then internalizes specific knowledge by observing the robot’s program execution. As the student externalizes their thinking by programming the robot with linear commands (forward, backward), they externalize their conception of a dynamic linear unit (the object). This is possible as each linear code is executed by the robot as one consistent, iterable unit of movement. The student’s reflection on the robot’s program execution also leads to the student internalizing specific knowledge about a dynamic linear unit in relation to the robot’s demonstration of this concept. We determined the ACAT framework as an appropriate lens for three reasons. First, the lessons analyzed in this study feature the artifact (the robot coding toy) as a center of focus in a shared space among the children. Second, research on young children’s use of gestures reveal that gesture can influence learning [35,36,37]. We refer to gesture as hand movements to convey meaning. Research indicates that children communicate aspects of their knowledge with gesture that is not otherwise indicated through their speech [38]. As such, gesture provides insight into individuals’ mathematical learning process individually [37,39] and among peers [40]. The ACAT framework provides insight into social and individual interactions with the artifact to conceptualize a mathematical object (a dynamic linear unit). Finally, the ACAT framework has not been applied in a three-dimensional programming context, so this framework is a unique lens to examine tangible coding toys as an artifact.

The focus of the present study centers primarily along the ACAT framework’s main axis, as we sought in research question a to identify how children (the subject) express their emergent conception of a dynamic linear unit (the object) while using coding toys (the artifact). To address research question b, however, we could not discount the likelihood that the group context and artifact/object rules might impact students’ development of measurement concepts and skills. In short, attending the ACAT framework’s horizontal axis primarily informed our first research question, while the entirety of the framework informed our second research question.

2. Methods

2.1. Research Design

This study is part of a larger research project (anonymized) that is: (1) operationalizing what computational thinking (CT) looks like in early childhood classrooms, (2) developing CT curriculum and resources for early childhood teachers, and (3) developing early childhood CT assessments [38,41]. For the purposes of this project, we define CT as “the conceptual foundation required to solve problems effectively and efficiently (i.e., algorithmically, with or without the assistance of computers) with solutions that are reusable in different contexts” [42] (p. 151). The present study used a case study approach [43] to explore how kindergarten-aged children express their emergent conception of a dynamic linear unit of measure through activities with robot coding toys [44]. The unit of analysis was a group of four children interacting with a coding toy during two 30-min introductory programming lessons.

2.2. Participants and Setting

The participants were four kindergarten children from one classroom in a Title I public school in the western United States. They included three males (Liam, Cam, and Will; names have been changed for anonymity) and one female (Tana). Cam is Latino and speaks Spanish as a first language and English as a second language. Cam received speech services unrelated to his position as an English language learner. Liam, Will, and Tana are White and speak English as their first language. The children represented a variety of knowledge levels and were especially active in using verbal and non-verbal communication methods. All four children were present for the first lesson; Tana was absent for the second lesson. As an exploratory study, a single group was chosen to examine in depth due to the teacher’s emphasis on linear measurement with this particular group (see further explanation below in Section 2.3).

2.3. Procedures

This data set was collected to refine the larger research project’s CT curriculum. Students were divided into four groups of 4–5 by their classroom teacher. Each lesson lasted 30 min and was videotaped. For each group, a teacher-researcher who had prior experience teaching kindergarten taught the lesson and a second researcher observed and created design memos (a structured form of field notes used to inform iterative lesson design; our design memos are influenced by Sandoval’s (2014) conjecture mapping concept) [45]. The teacher-researchers drew from a common set of previously-developed lessons; however, the curriculum focus for each group was unique. For example, one teacher-researcher taught lessons with a debugging focus while another teacher-researcher paid particular attention to program construction. After each lesson, the teacher-researcher and observing researcher used the design memo to review the day’s lesson and develop plans for the subsequent lesson. The teacher-researcher who led the group in this study emphasized unit measurement and decomposition through student discussion and exploration while routinely prompting students to describe their thinking. As a result, this dataset provided a body of evidence to gain insight into children’s thinking on linear measurement.

2.4. Materials

2.4.1. Artifact Description and Rules: Cubetto Coding Toy

The present study focuses on the Cubetto robot, produced by Primo Toys (see Table 1 and Figure 2). This toy is designed for young children and utilizes a programming board with directional tiles to code forward (green tile) and backward (purple tile) linear movements, as well as right-angle rotations in clockwise (red tile) and counterclockwise (yellow tile) directions.

To program Cubetto, directional tiles fit into the programming board’s cavities, starting with the top left cavity, and continuing in a switchback pattern resembling a mirrored S. A program can contain as many as 12 codes. The board also includes a separate programming space at the bottom to program functions. The function feature was not used in the present study. When a blue “start” button is pushed, the robot enacts the program and stops when it meets an empty cavity. One of this artifact’s rules is that each programming code produces one movement. The agent’s rule for the forward code, which operates as a dynamic linear unit, is that one forward command is enacted as one 6-inch forward movement.

Cubetto travels on a grid (see Figure 3) with squares equal in width to the distance Cubetto travels in one forward or backward movement (six inches). These canvas mats, commercially produced for Cubetto, are designed similar to maps with coordinates along the top and left sides as well as designs and pictures in each square. A traditional compass rose adorns each grid’s top left square.

Figure 3 pictures the Adventure Mat, the grid used for this lesson. While these mats are not required for Cubetto to function, the grid squares provide reference points for programming the robot and the map elements provide a context for playful engagement.

2.4.2. Cubetto Coding Tasks

As part of the larger project, we developed 6, 30-min lessons for the coding toys. The lessons were designed for a teacher to work with small groups of 4–5 students. Lessons one and two are introductory in that they were designed to help children construct knowledge about programming, space, and measurement. The first objective was for children to learn that each coding block represented one movement and instructed the robot to move in a particular way, for example, the green tile represented one forward movement: the unit. The second objective was for children to use the codes and apply their understanding of a unit in order to instruct Cubetto to move along on a linear path, then on a path requiring a rotation. The lessons are designed for researchers to ask questions throughout in order to elicit both mathematical and computational elements of children’s thinking. The first two lessons were selected for this analysis in order to understand children’s emergent ideas of a dynamic linear unit, including their preconceptions early in the coding process.

2.5. Data Sources and Analysis

The data sources were videos of the group engaged in the first two coding lessons (~66 min) and their respective design memos (structured field notes used to inform iterative lesson design). We used emergent coding [46] in MAXQDA 2020, a data analysis tool, to analyze students’ actions, gestures, and verbal responses with the robot and with each other. The unit of analysis for our first and second rounds of coding were instances when individual students demonstrated a developed or constructed conception of a dynamic linear unit.

In the first round of coding, we isolated instances when the students (subject) demonstrated a constructed conception of a dynamic linear unit (object) while engaging with and referencing the robot and its materials. Next, we analyzed the isolated instances to explore how the students (subject) constructed an understanding that the robot’s movements (artifact) represent dynamic units of equal length (object). We then coded how the students applied their constructed conception of dynamic units to describe and predict future linear paths programmed into the robot (internalization/externalization for research question a). Section 3.1 reports on our findings.

The second round of coding addressed research question b. In the second round, we identified instances in the data when students demonstrated a still-developing understanding of dynamic linear units in these two introductory lessons. These challenging concepts emerged in instances when the children described or gestured with their hands to indicate what one forward command would make the robot (agent) do. After identifying these instances, we thematized them into three categories, as reported in Section 3.2.

2.6. Limitations

For the purpose of this exploratory study, we focused our analysis on a case study of one group of students. This approach allowed us to closely examine the students’ interactions and access to dynamic linear unit and measurement concepts during the introductory lessons (as they were learning how to code/program with the robot coding toys). We acknowledge the limitation of our analysis and that the results cannot be generalized to the larger sample nor to the general population of 5- and 6-year-old children. The results of this study, instead, serve to introduce dynamic units as a context for linear measurement instruction, begin to describe children’s conceptions of dynamic linear units, and examine tangible coding toys through the lens of ACAT.

3. Results

3.1. Research Question a: Expressing an Emergent Conception of a Dynamic Linear Unit of Measure

Students expressed their emergent conception of a dynamic linear unit through gestures with or mimicking the artifact, verbal descriptions about the artifact, and social interactions with each other with or about the artifact. Students externalized their thinking by using verbal descriptions and gestures to discuss the unit (i.e., one forward movement of the robot), which allowed for observable behaviors related to both their conceptualization of a dynamic linear unit as well as their preconceptions (discussed in Section 3.2). These outward expressions often arose in response to social cues, such as questions or peer discussions; hence the social context and rules around the artifact and object emerged as an important theme in this analysis.

3.1.1. Expressing an Emergent Conception of a Dynamic Linear Unit of Measure: Mimicking the Artifact with Gestures

Children used their hands and arms to simulate the robot’s movement or to move across the grid space to explain and justify their thinking. We refer to these hand and arm movements as gestures. Observing children’s gestures was particularly helpful as kindergarteners are still developing the academic vocabulary required to precisely communicate and defend their ideas. For example, tapping the mat’s squares with their fingers and bouncing their hands in the air or along the grid were common ways that participants identified units. For example, Liam tapped each of the spaces along a linear path with his finger to justify that Cubetto required three forward movements to get from the tree to the desert on the grid and to externalize his thinking to Cam, saying, “it needs three…one, two, three”. Liam then used a sweeping hand movement across the mat to trace the path. After observing Liam’s hand movements, Cam showed his understanding and agreement with Liam by displaying three fingers and saying, “it wants three spaces” (see Figure 4).

Tapping each space along the intended path and attaching a sequential number for each tap indicated that Liam interpreted the forward command as an iterable unit of distance that the robot can travel. Further, Liam’s sweeping motion along the path after tapping each square suggests that he recognizes the path as a whole, which is made up of the three units he had just counted. Cam used three fingers to identify the total number of spaces needed, however it is unclear if by “space” he considered the robot’s dynamic movement or a static grid square. Liam’s tapping and sweeping movements provided greater insight into how he visualized the agent’s dynamic movement, whereas Cam’s use of three fingers was a more abstract representation of his thinking and, as such, made it more difficult to discern his meaning.

Students’ use of gestures, such as bouncing hands and tapping spaces on the grid, provide evidence that students were making a one-to-one connection between the iterative movements of the robot and the spaces it travels. In this way, students appeared to internalize the value of the dynamic unit and were able to externalize, or apply it, to programming problems when using the artifact, Cubetto.

3.1.2. Expressing an Emergent Conception of a Dynamic Linear Unit of Measure: Verbal Descriptions about the Artifact’s Movements

The children described a unit (i.e., one forward movement of the robot) as “one space”, often reiterating that the green tile instructed Cubetto to go “just one space forward”. For example, at one point in the lesson the children appeared to connect the artifact’s (the robot’s) rule that a forward tile instructed the robot to travel one dynamic linear unit; however, up until this point, the group had only practiced this with the robot’s starting location facing the mat’s top edge. To check if students would transfer this rule if the robot were oriented differently, the teacher positioned Cubetto to face the mat’s bottom edge and programmed the programming board with one forward command. The following transcript illustrates students’ verbal descriptions of Cubetto’s rule while referencing the artifact. Screenshots associated with portions of the transcript are provided in Figure 5.

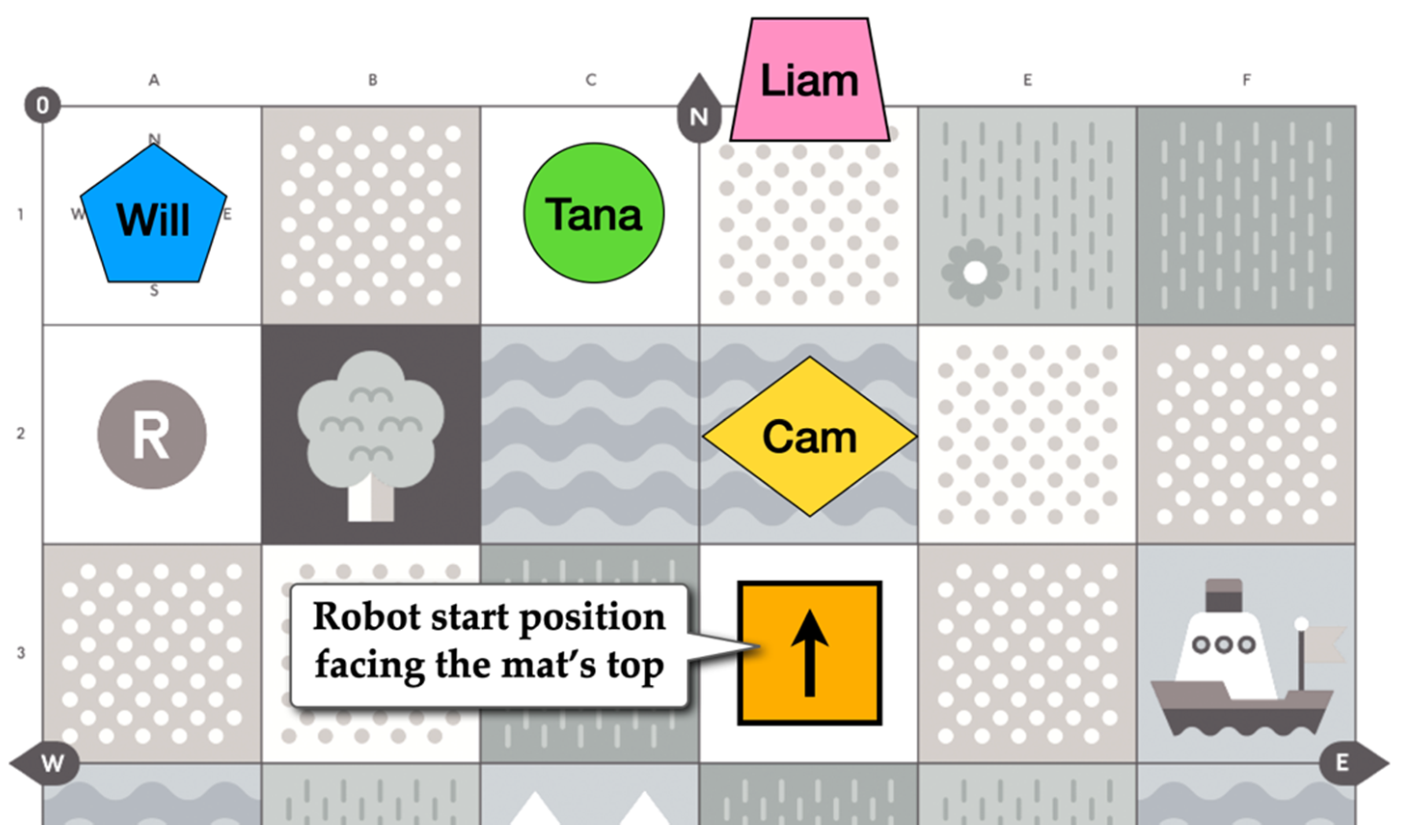
Teacher:

Now, which way is Cubetto looking?

Will:

(repeatedly taps the square in front of Cubetto, which faces the mat’s bottom edge) (see Figure 5a)

Teacher:

Cubetto’s looking that direction (points toward the mat’s bottom edge), right? See Cubetto’s face is here (taps Cubetto’s face)? (Figure 5a)

Teacher:

So, where will Cubetto go if we press the go button?

Tana:

(points to the blue square in front of Cubetto) (Figure 5b)

Will:

One space! (repeatedly slaps the square in front of Cubetto) (Figure 5c)

Teacher:

One space? You think it will go there?

Liam:

(indicates space in front of Cubetto) (Figure 5d)

Teacher:

You think it will go here (points to the square in front of Cubetto) and it won’t go here (points to the square behind Cubetto?) (Figure 5e)

Tana:

Nope.

Cam:

No.

Teacher:

Why won’t it go here? (points to the square behind Cubetto) (Figure 5e)

Will:

Because it’s facing (points behind Cubetto), um, like looking (taps square behind Cubetto). (Figure 5f)

Teacher:

The face isn’t looking there? (points to the square behind Cubetto) (Figure 5f)

Will:

(nods his head in affirmation)

The transcript above provides an example of children connecting a conception of a dynamic linear unit with the artifact’s rules for the forward command. Additionally, the transcript paints a picture of how students used verbal descriptions and hand movements in tandem to communicate their knowledge. While the children’s language used provided important insight into their thinking, the children combined language with hand movements to extend their means of communication and, as a result, shared their thinking more precisely.

Similar to its central position in the ACAT framework, the artifact is central to students’ discussions about the artifact’s rules and their application to the given scenario. For instance, the group demonstrates a recognition that one rule governing the artifact is its orientation and position in space. By attending to this rule, the children correctly anticipate where the robot will travel when programmed with one forward command.

3.1.3. Social Context: Subject-Group-Artifact Relationships for Expressing an Emergent Conception of a Dynamic Linear Unit of Measure

The social context of a small-group lesson format influenced the children’s responses, but each child maintained their own ideas of how far the robot would move for one forward command. One example of this is near the beginning of lesson one after all of the children in the group agreed that a green forward command would send the robot to a green square. To test the children’s preconception of the forward command’s rule, the teacher changed the robot’s starting position so that the robot would land on a yellow square when programmed with one forward. The teacher asked the students to predict where the robot would stop after running the program (one forward). Each child responded differently, as shown in Figure 6. Only Tana, who originally introduced the idea that the robot would land on a green square, indicated that the robot would stop on a green square. It appeared that each child was still internalizing the robot’s rules and externalized their thinking independent of the group’s original consensus.

Cam was the only child to demonstrate a constructed conception of a dynamic linear unit by indicating that the robot would move forward one space. In doing so, he indicated that he had internalized the artifact’s rule that one forward command results in one dynamic linear unit in a forward direction. Cam’s association between the forward command and a dynamic linear unit is represented by the double-headed arrow on the ACAT framework between rules and object. In contrast, Liam demonstrated an approaching conceptualization of the rules—object link by indicating that the robot would continue in a straight line until it hit another object. Liam understood that the artifact’s rules for the forward commanded resulted in a forward, linear movement. However, he had yet to grasp the unitized nature of each forward unit.

3.2. Research Question b: Challenges in Developing a Dynamic Linear Unit of Measurement

While there were instances of children expressing their emergent understanding of a unit of measure and use of iterated units to describe a distance, the analysis showed that these young children needed multiple experiences to further develop the concept of a dynamic linear unit. Participants exhibited three interpretation categories as the children constructed their understanding of one forward movement as a unit. These categories describe the children’s new and emerging understanding of the agent’s rules for enacting one forward command (a green tile representing that unit) and use of the forward unit in a dynamic way. These categories (which we call preconceptions) and their definitions are presented in

Table 2. Descriptions of the children’s preconceptions and constructed conception of a dynamic linear unit.

Category	Description	Example
Location of choice (preconception L)	The robot will travel to any location.	When asked where the green tile would send the robot, Liam indicated that the robot would stop on the compass rose (see Figure 6, Will).
Green space (preconception G)	The robot will travel to a green-colored square.	When asked where the green tile will send the robot, a child exclaimed “to the green!” and slapped an incorrect green square on the mat.
Forward travel (preconception F)	The robot will travel forward until stopped by an outside force.	When asked what the green tile will tell the robot to do, one child predicted: “it will crash into the programming board.” The programming board was a few feet in front of the robot.
Constructed Conception (C)	The length of one dynamically iterable unit of movement.	When asked where the green tile would make the robot go, a student replied: “to the space in front of it.”

. We include the constructed conception of a dynamic linear unit (discussed in the findings for Research Question a) as a point of comparison.

Each student indicated a fragile understanding of what a dynamic linear unit is. Figure 7 is a visual representation of the evidence that each child exhibited during the introductory lesson indicating their preconception (L, G, F) and constructed conception (C) of a dynamic linear unit. Each shape represents an instance in which the associated child verbally or non-verbally indicated their interpretation of what a dynamic linear unit is. The circles represent instances when the child indicated a preconception, and the hexagons represent instances when the child indicated a constructed conception. The shapes are aligned chronologically in the order of each child’s interpretation.

To illustrate, during the introductory lesson, the first evidence that Liam evidenced his interpretation of a dynamic linear unit by verbalizing that the forward command would send the robot “all over the place.” This statement was categorized as preconception L, that one forward dynamic linear unit would cause the robot to travel anywhere. Liam next indicated his understanding of the forward command’s meaning non-verbally by using his hand to tap a space on the grid that the forward command would send the robot one space forward. Liam’s nonverbal identification of where one forward would send the robot indicated a constructed conception of a dynamic linear unit.

Ordering each child’s interpretation across the lesson indicates that students frequently, though sometimes inconsistently, applied a constructed conception of a dynamic linear unit. Exploring the context of the group’s preconception and constructed conception interpretations reveals the influence of a social context (the group) and each child’s emerging understanding of how the artifact’s rules relate to the object of interest, a dynamic linear unit. This context will be explored through Will’s experience in the subsequent section.

Subject-Group-Artifact: Will’s Experience within the Small Group

We illustrate the conceptualization process of a dynamic linear unit using one student’s experience. Will’s participation in the group influenced his journey toward understanding dynamic linear units. After running a program with one forward, Cam observed that Cubetto moved one space forward on the grid and landed on a green square. When asked what the green forward command instructed Cubetto to do, Tana explained that it sent Cubetto to a green square. She made the connection between the green forward tile and the green color on the grid, trying to figure out Cubetto’s rules and its movements. “But will it always send Cubetto to a green square?” asked the teacher. Tana, Will, and Cam agreed that it would.

After repositioning Cubetto to a different starting point, the teacher asked where the robot would stop if programmed with one green forward command. Cam responded with a constructed conception (C), and Liam stated that it would stop at the end of the mat (preconception F). Will paused a moment before indicating that Cubetto would land on the compass (L), even though he previously ascertained that Cubetto would end on a green space. This may have been influenced by Cam and Liam’s predictions that contrasted their initial social agreement that Cubetto’s green forward command sends Cubetto to a green square every time (G).

After Cam’s prediction proved correct, the teacher asked how far the forward command would send Cubetto. “One space”, replied Tana. Liam responded that Cubetto would move two spaces and justified his thinking by using a gesture in which he tapped and counted the square Cubetto started on and the destination square. The teacher then asked him to explain his thinking by moving the robot. When Liam moved the robot, however, he revised his thinking to conclude that the forward command moved the robot one space. Cam gestured by pointing to the destination square, sharing a similar idea as Liam.

The teacher again repositioned Cubetto to a new location on the map and queried where Cubetto would end with one forward command. Liam, Tana, and Cam predicted correctly (C), but Will observed without response. When the teacher asked the group to explain Liam, Tana, and Cam’s answer, Will responded, “Because it goes one space”. Will appeared to consider his peers’ ideas and confidently concluded that the green forward command instructed Cubetto to move forward one space. This internalization process was influenced by his activity with Cubetto (the artifact), negotiation of the rules, and interactions with peers about Cubetto’s movements.

The final task required students to apply their understanding of the forward unit to code a linear path from the tree to the desert (see Figure 8; programmed correctly as three forwards or three green tiles). This final task required students to apply Cubetto’s rules of how the artifact operationalizes one forward command in order to correctly program a linear path. The teacher introduced the task by showing green tiles and asking what their function was. Will replied, “Go to the grass”, touching a green square with his hand (G; see Figure 6). Cam nodded in agreement. Tana countered that one green tile would send the robot one space forward, yet Will insisted again it would be sent to the grass. This final application of the unit in the context of a task could be considered a unique situation, which could explain why Will did not transfer his fragile understanding of a dynamic unit.

The reemergence of preconception G in Will’s response hints at the influence of a social context, in this case, the group. Will’s connection that the forward tile sent Cubetto to a green square (G) originated in Tana’s connection between the green tile and a green grid space. Will’s first five responses (G, L, C, C, C) were in reference to Cubetto starting in different orientations around the grid and enacting one forward unit. The next two responses (G, G) were in the context of the tree to the desert task, and the final response (G) was when he was asked at the end of the lesson what the green tile does.

4. Discussion

As reported in this article, our research team conducted a case study of a small group of four children (5–6 years old) engaged in introductory programming lessons with tangible, screen-free coding toys. Using the lens of Artifact-Centric Activity Theory (ACAT), our research objectives were (1) to describe how young children expressed their emergent conception of a dynamic linear unit of measure during programming activities with coding toys and (2) to identify the measurement concepts and skills that were challenging for young children to construct. We found that children expressed a constructed conception of a dynamic linear unit using hand and arm movements (e.g., gestures)and verbal descriptions and that children’s expressions were influenced by the coding toy (the artifact). Further, the social context of a small group working with the toy often spurred children’s outward expressions of dynamic linear unit conceptions.

Shumway et al. [24] found that in order to build a program for a robot toy, children needed to identify a unit of measure, determine the number of iterations, and then iterate the unit. In the present study, we were interested in children’s constructions of a dynamic linear unit and their expression of that knowledge [37]. Similar to our findings, children in the present study also demonstrated their knowledge of the robot’s unit of movement through gestures by pausing between hand and arm movements, mimicking the pauses between Cubetto’s forward movements, and the number of codes needed for each movement. They demonstrated their knowledge of iterated units using repeated motions of tapping their hands across squares on the grid or bouncing their hands in movements from one square to another, similar to jumps on a number line. Research on gestures and mathematics explains that children and teachers use specific and subtle hand and arm movements to construct and communicate knowledge [37], such as the example of Liam’s tapping of his fingers/hands (iterated units) and sweeping of his hand (distance from start to end) to express to Cam how many codes were needed for the program (tapping) and why (sweeping).

In addition to using their hands and arms to represent their conception of a dynamic linear unit, students often verbally described one dynamic linear unit as the robot moving “one space”. This coincides with standard length measures as iterated units, such as those marked off as spaces between the ticks on a ruler. It is unclear if the children in our study more closely aligned their understanding of a unit with the robot moving the length of a space or simply moving to an adjacent square.

We also found that the children expressed different preconceptions of a dynamic linear unit, which were also influenced by various features of the toy and its components (e.g., green coding tile equated with green space on the grid). While all of the children showed evidence of applying a conception of a dynamic linear unit in the lessons, this knowledge was fragile and still in development. Each child inconsistently reverted back to their preconceptions. This is not surprising given that research on measurement has shown that it takes time to develop (e.g., [3,5]).

A measurement preconception exhibited by Liam was his initial inclusion of the robot’s starting space as a unit rather than attending to the movement that the robot would execute. Liam originally justified his thinking by counting the grid squares but later revised his thinking after being prompted to explain his thinking by moving the robot. Similar to other studies using the ACAT framework, this instance showed how the artifact influenced Liam’s thinking and evoked a change of concept [47,48]. Liam appeared to develop a conception of a dynamic linear unit by shifting his focus from counting discrete grid squares to counting the single dynamic movement that the robot would operationalize with one forward command.

Just as Liam needed to count the length that the robot moved rather than the start and stop grid squares, it is common for individuals reading rulers to count a ruler’s hash marks rather than the spaces between the hash marks [1]. Similarly, Solomon et al. [29] reported that young children using rulers struggled to recognize the rulers’ spaces and countable units. Children using number lines also incorrectly include the starting number in their counts rather than counting on from the beginning number [49]. Length measurement and number lines are closely related as each depend on iterated units of length, or space. Tangible coding toys’ three-dimensional design provides a unique context for developing children’s conception of iterated units of space as the toys’ units are visibly iterated in the robots’ movements. The coding toy’s dynamic enactment of each unit provides a concrete representation of a unit compared to the units on a ruler or number line represented by static spaces. In this study, the ACAT framework provided a lens for understanding how the robot coding toy mediated children’s developing conception of a unit, and more specifically, a dynamic linear unit.

Our exploratory analysis describing children’s emerging understanding of dynamic linear units serves as a starting point to study how young children’s engagement with tangible coding toys can support children’s development of foundational measurement concepts, such as units. This work also provides insight into how social context influences children’s knowledge development and the challenges inherent in applying emergent knowledge in different contexts. Further, this study contributes to the ACAT research by moving from studies on two-dimensional, multi-touch technology artifacts [34,47,48] to using the framework in a three-dimensional space with a tangible technology artifact.

5. Conclusions

Linear measurement is a foundational concept in early mathematics that is related to mathematics learning in later years [5]. Despite its importance, linear measurement is often left out of early childhood math standards [6]. The present study has two implications for the teaching of linear measurement in early childhood classrooms. The first is that students require multiple hands-on opportunities to engage in linear measurement tasks in multiple contexts and settings to develop unit measurement knowledge. The second is that tangible coding toys offer a new context for students to engage in hands-on measurement activities. Tangible coding toys present a dynamic representation of linear measurement unique to existing measurement curricula. The artifact-centric lessons we examined in this study presented students with linear measurement that, instead of statically iterated lengths, emerged as the artifact’s dynamic movements. Hence, we described the robot’s linear units as dynamic linear units.

This study’s STEM education research implications apply to research and theory. This study provides an exploratory look at the conceptions of a dynamic linear unit. A larger analysis of children engaging with other tangible coding toys may reveal additional preconceptions of dynamic linear units and further inform the field of how coding toys can be used as a unique and meaningful context to build children’s mathematics knowledge and skills.

The theoretical implications for this study include a contribution to theory advancement by using the ACAT framework to describe how tangible coding toys, as artifacts, mediate children’s (subject) measurement unit conceptualization (object). To the best of our knowledge, this is the first study to examine tangible coding toys through an ACAT lens, which contributes to the ever-evolving realm of activity theory perspectives. Applying the ACAT framework permitted us to describe how children’s gestures and language evidenced children’s internalization and externalization of a dynamic linear unit and how the small group context influenced children’s conceptualization of a dynamic linear unit through engagement with the artifact.