Fuel Grain Configuration Adaptation for High-Regression-Rate Hybrid Propulsion Applications
Abstract
1. Introduction
2. Streamline Optimization Based on CFD
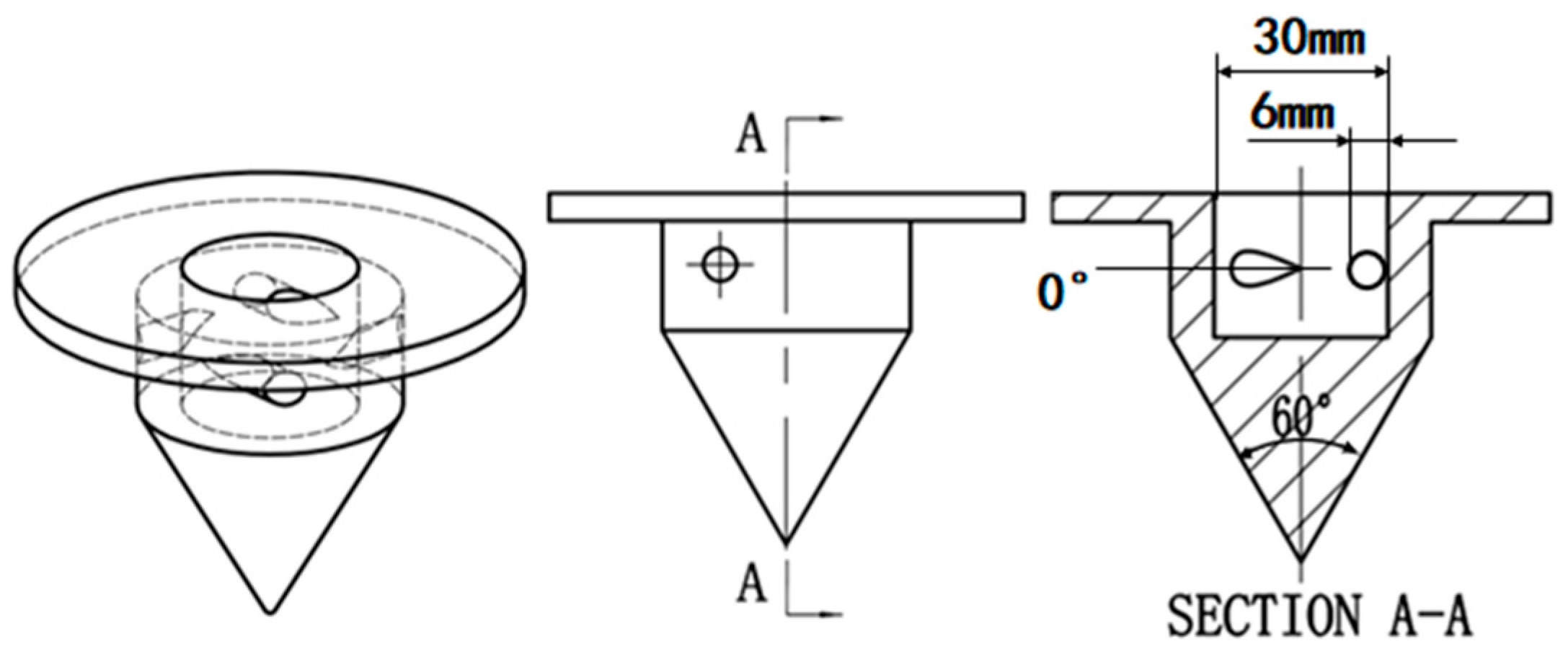
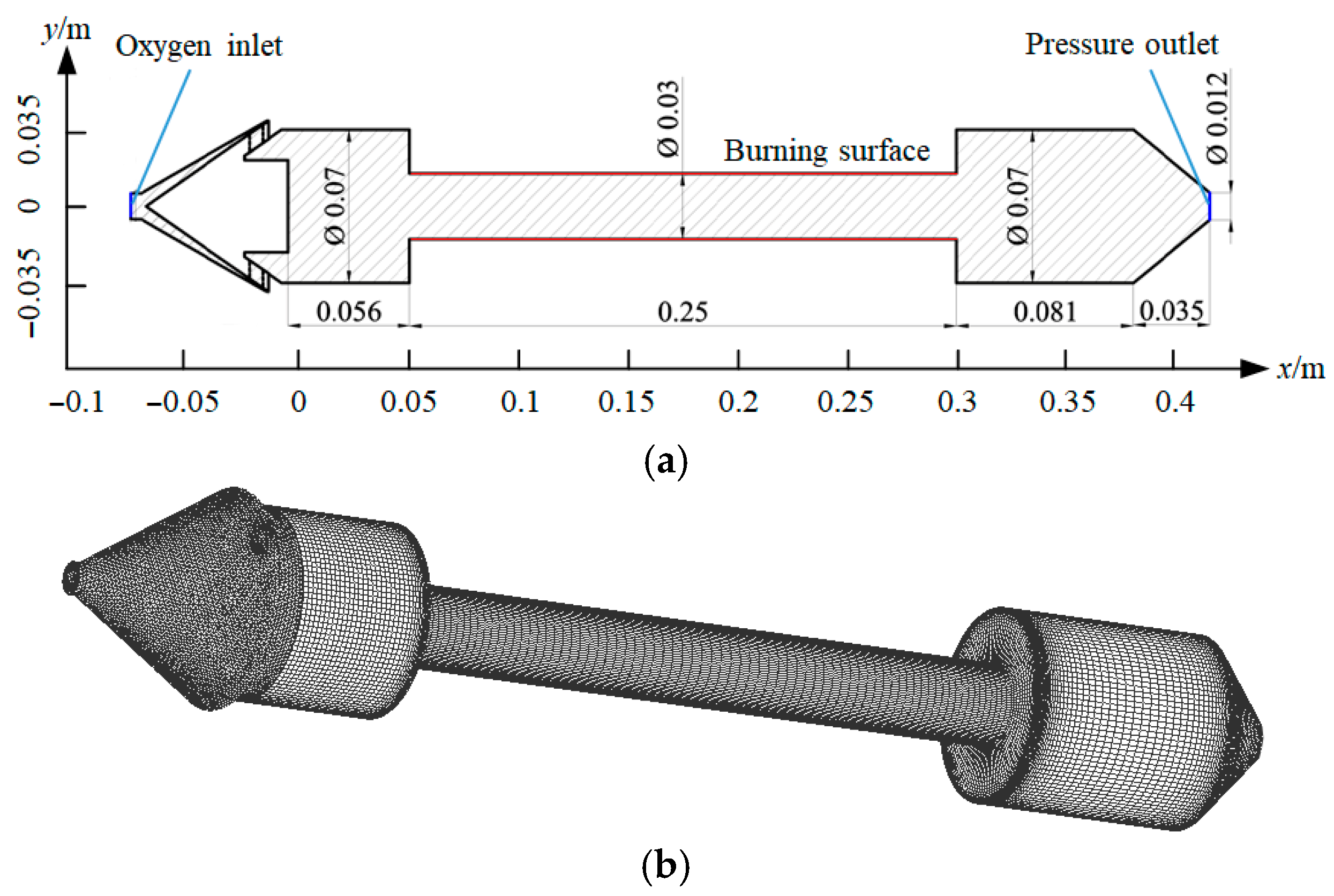
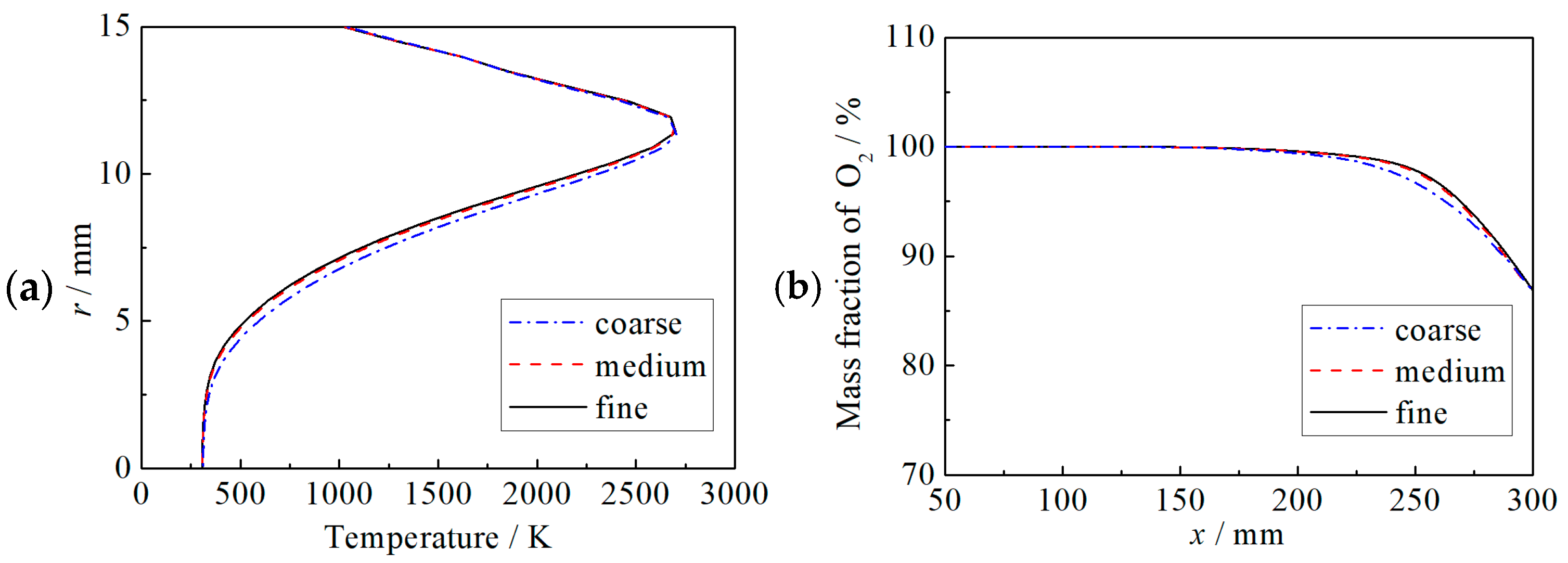
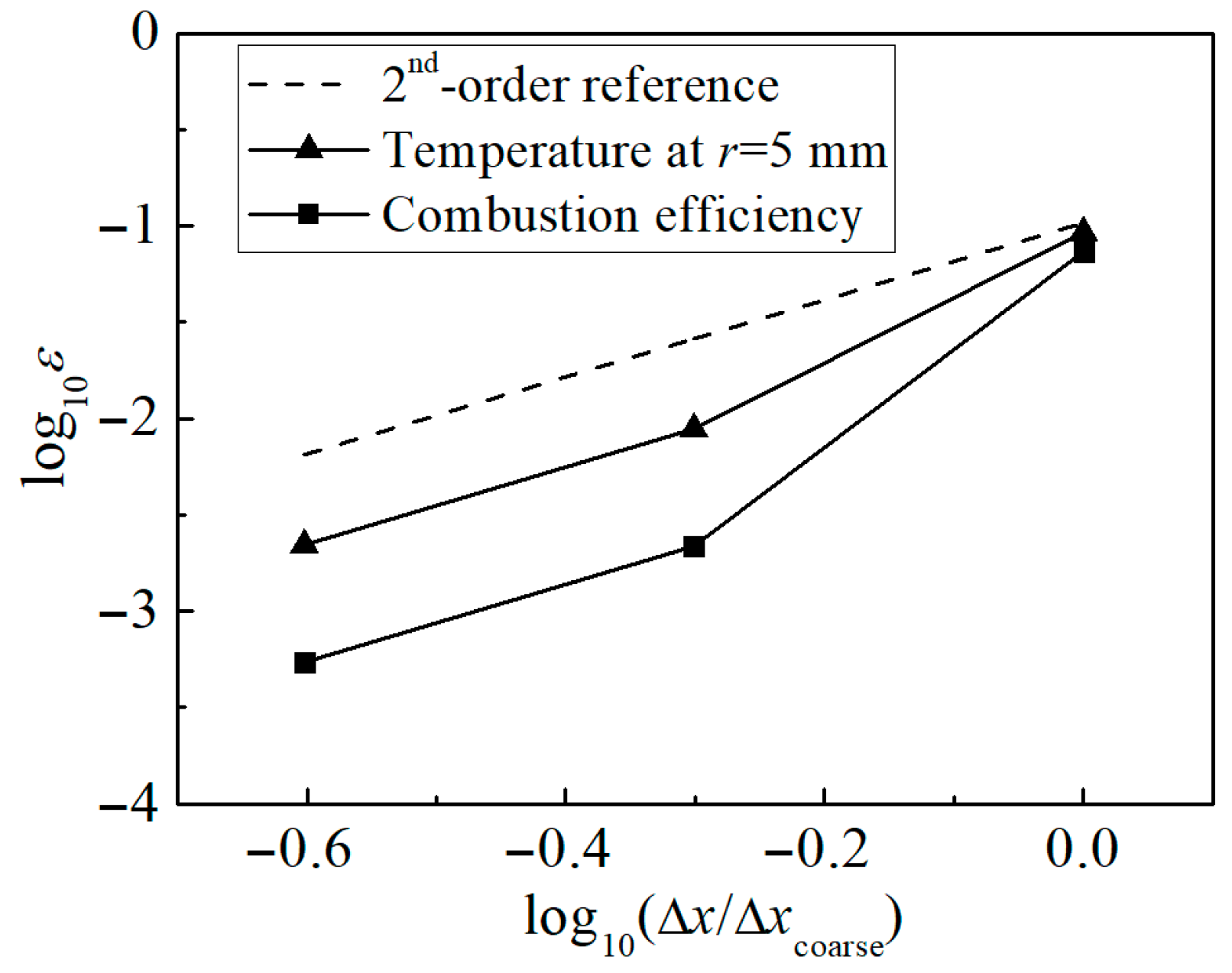
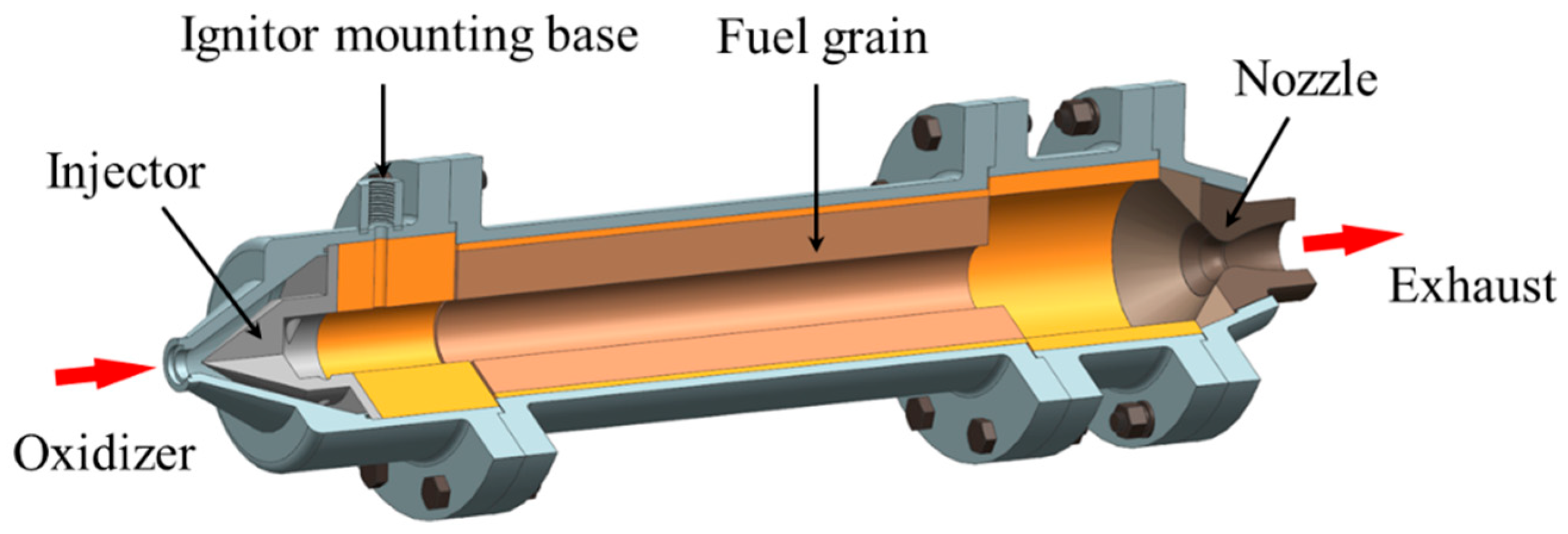
2.1. CFD Analysis
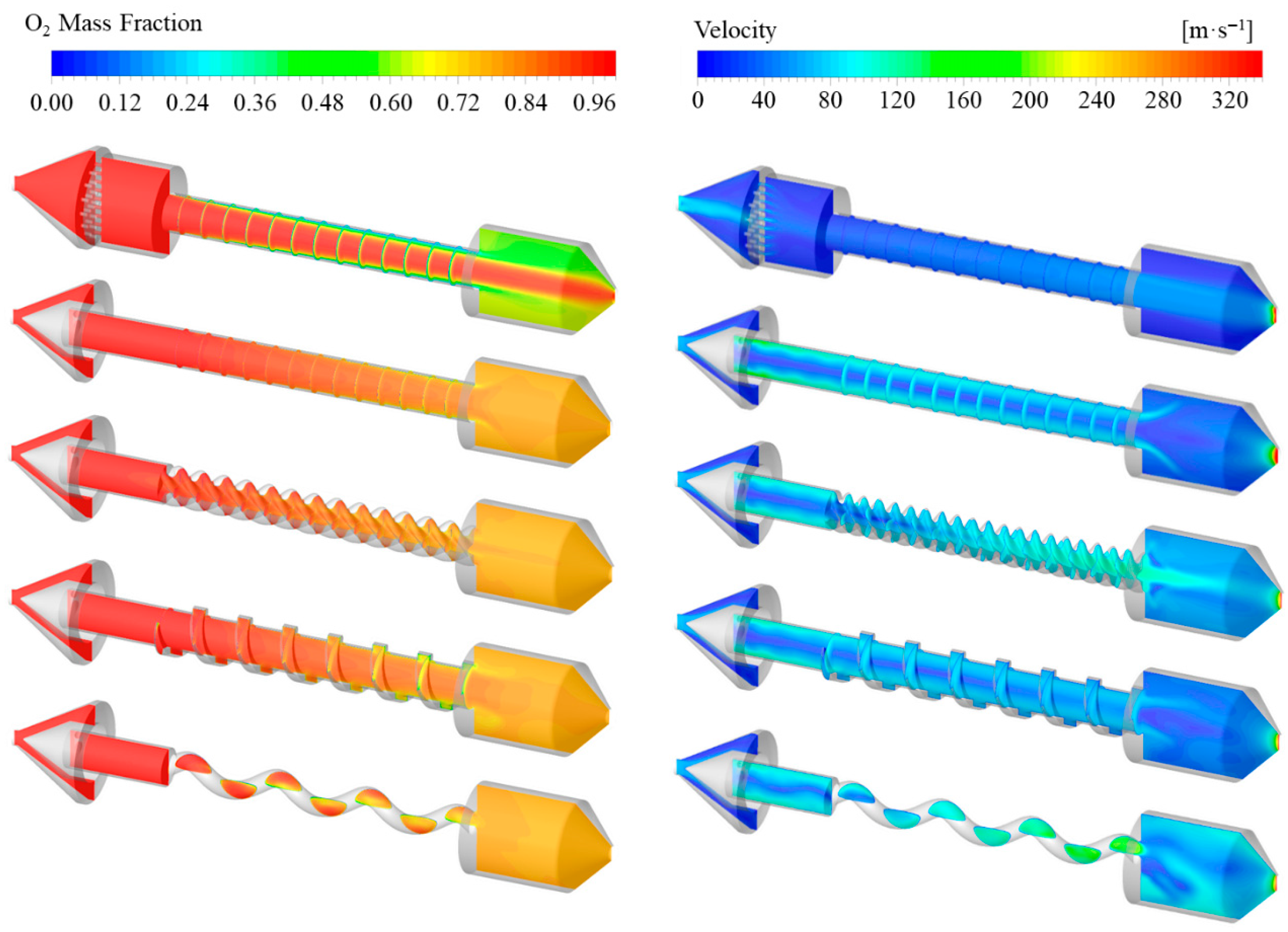
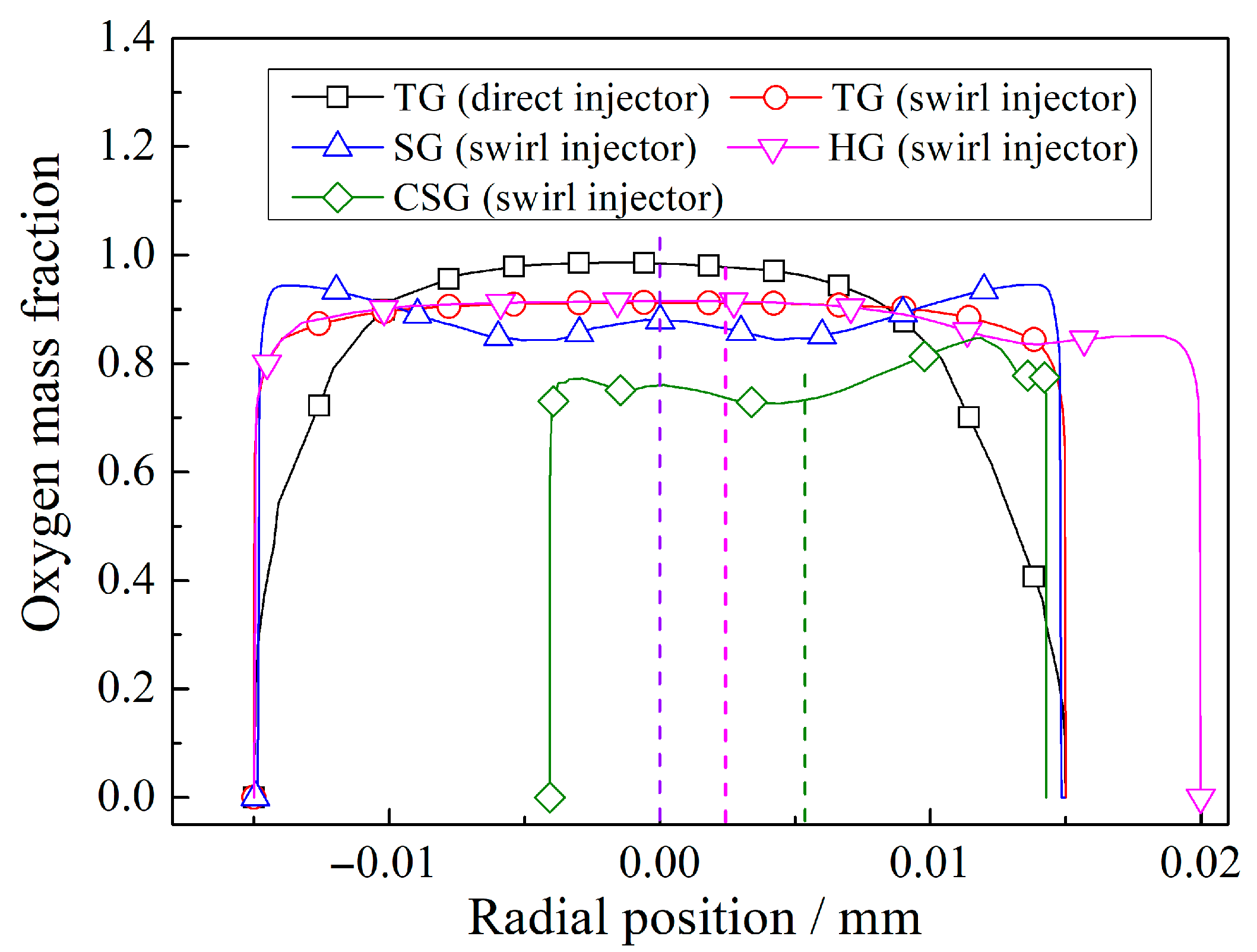
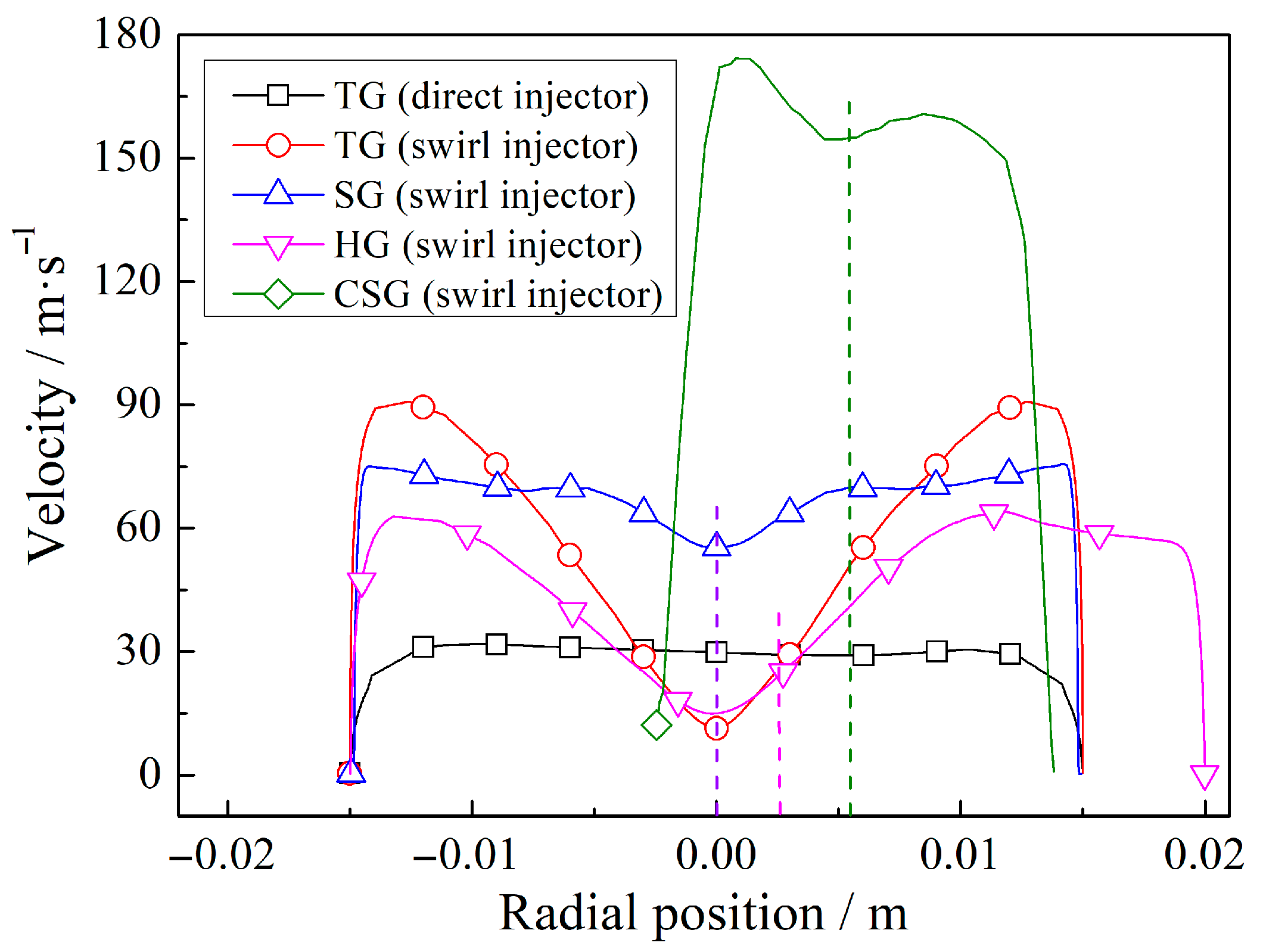
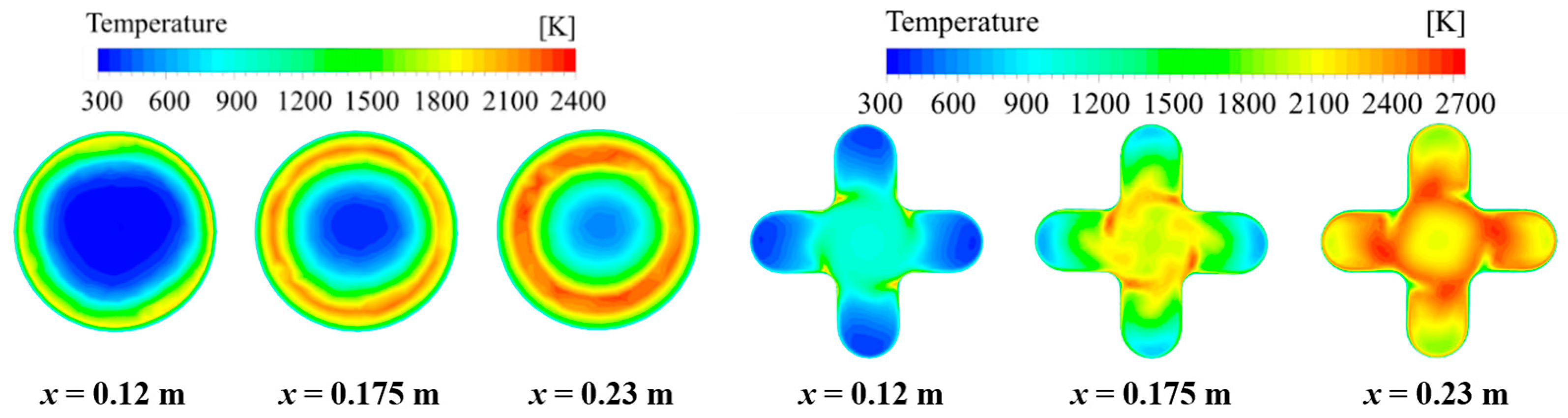
2.2. Non-Reactive Mixing Intensity for Various Grain Configurations
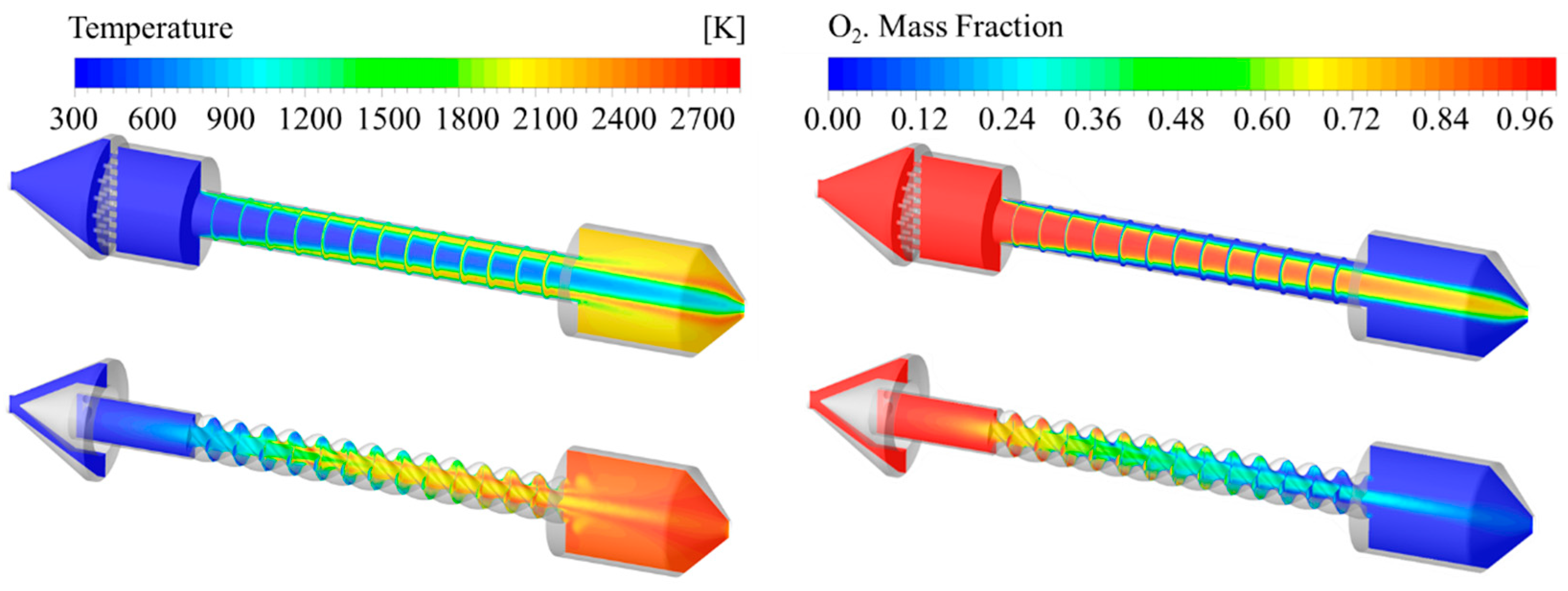
2.3. The Reacting Flow of Star-Swirl Grain Combined with a Swirl Injector
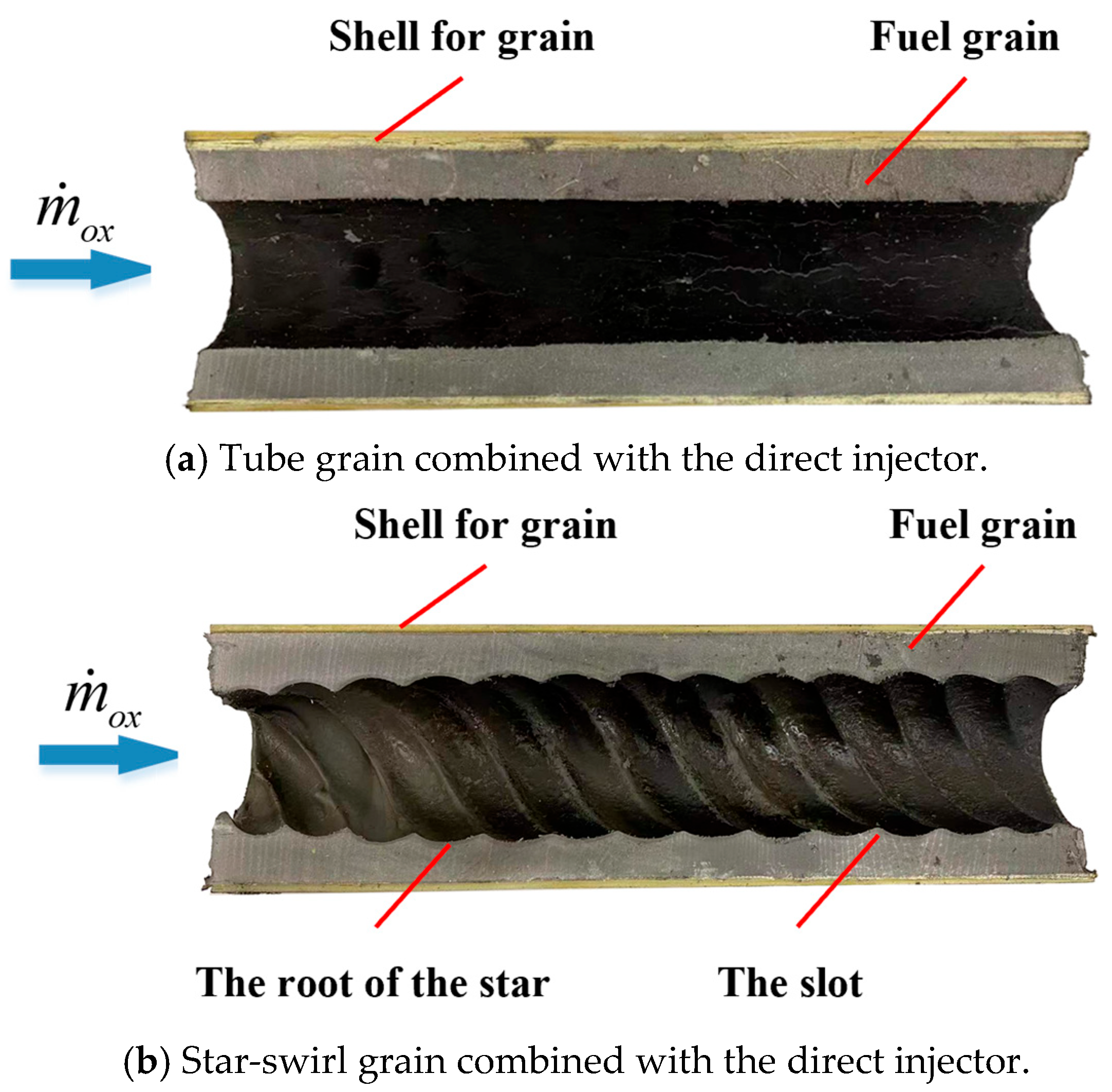
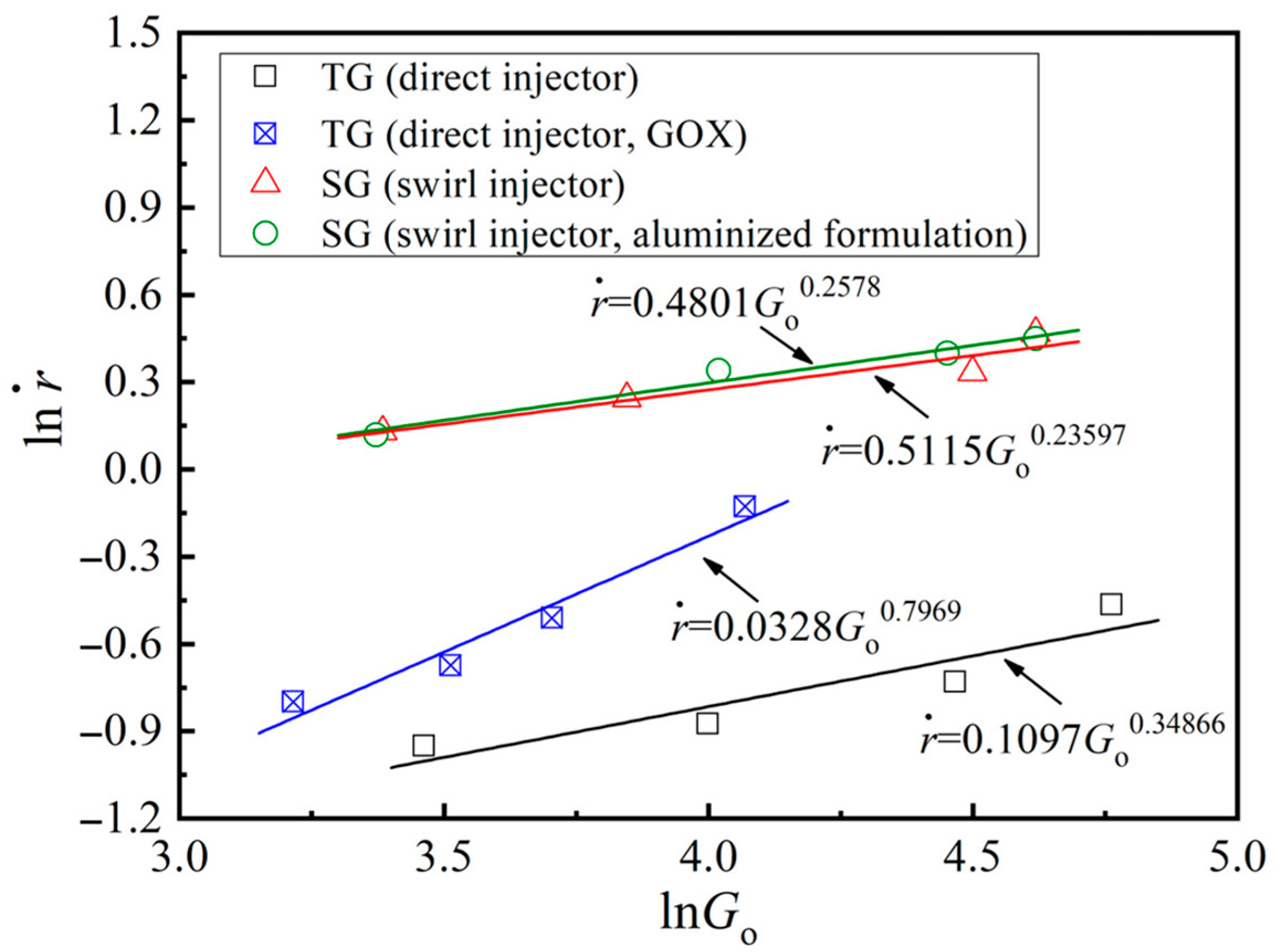
3. Regression Rate of Star-Swirl Grain
3.1. HRM Ground Test
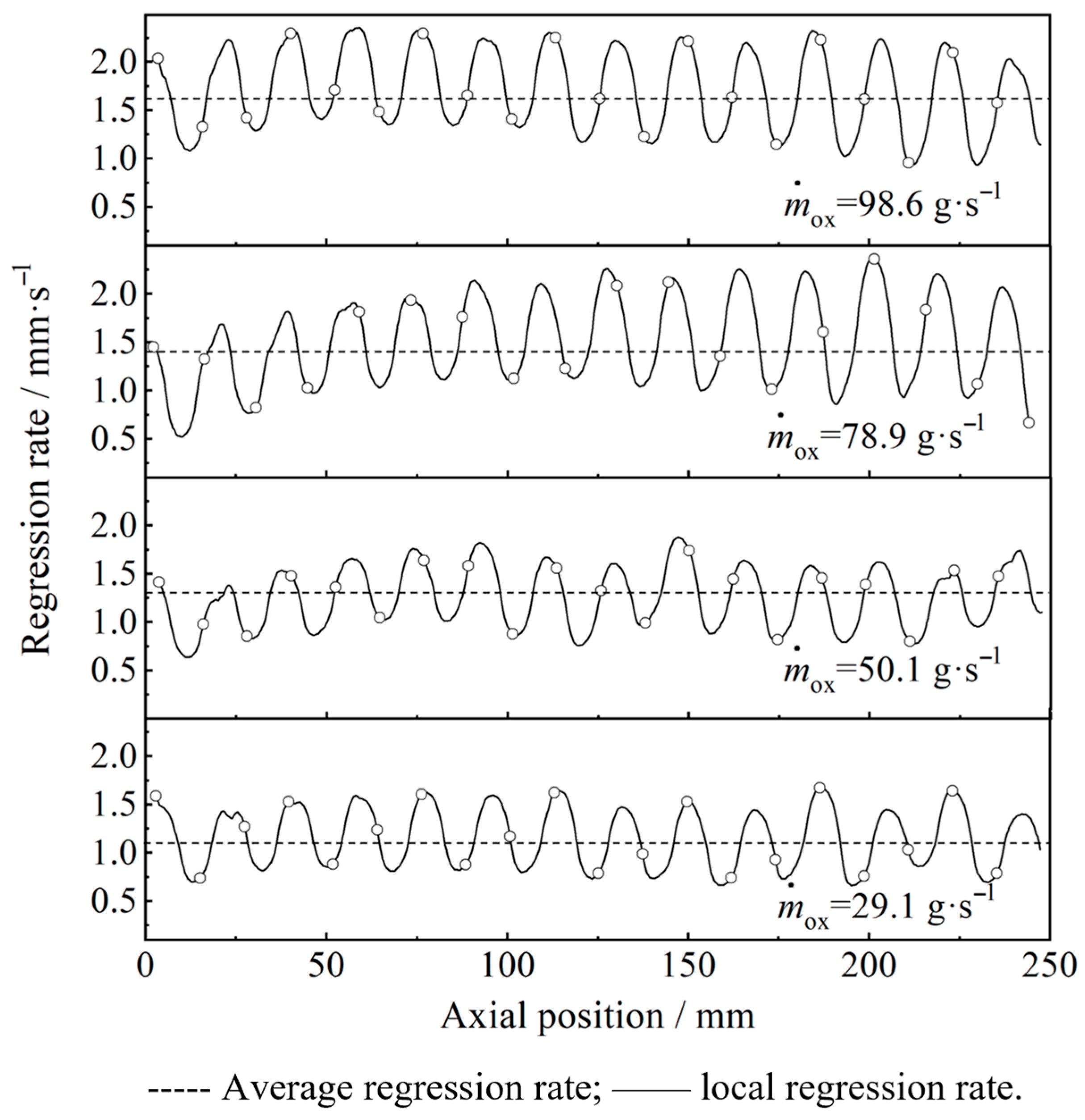
3.2. Local Regression Rate Characteristics
3.3. Spatially Averaged Regression Rate Characteristics
4. Conclusions
- (1)
- The star-swirl grain and swirl injector combination attained the highest mixing degree of 86% in CFD simulations, resulting from sustained swirl intensity and a lower diffusion scale. This configuration delivered 93% combustion efficiency at the nozzle throat, contrasting sharply with the 66% efficiency of the tube grain and direct injector under the same conditions.
- (2)
- The swirling flow with both high mixing intensity and high velocity could be formed by using the swirl injector, which would increase the mixing degree of the gaseous fuel and the oxidizer significantly. Experimental evidence confirmed that the grain configuration maintained the swirling intensity post-combustion, which was also beneficial for the mixing.
- (3)
- A spatially averaged regression rate of 1.40 mm·s−1 was achieved for the star-swirl grain and the swirl injector combination when the mass flux of N2O was 89.94 kg·m−2·s−1. This was about 191% higher than the case of the tube grain and the direct injector combination. However, there were obvious local regression rate differences between the root of the star and the slot, which should be addressed in the port geometry design.
- (4)
- It was shown that the enhancement in the regression rate was accompanied by a decrease in the combustion efficiency for the strong swirl flow condition due to the remarkable higher mass flow rate of the gasified fuels. In addition, nano-sized aluminum could enhance the regression rate but would result in lower combustion efficiency, especially for extreme fuel-rich conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Davydenko, N.A.; Gollender, R.G.; Gubertov, A.M.; Mironov, V.V.; Volkov, N.N. Hybrid Rocket Engines: The Benefits and Prospects. Aerosp. Sci. Technol. 2007, 11, 55–60. [Google Scholar] [CrossRef]
- Sun, X.; Tian, H.; Li, Y.; Yu, N.; Cai, G. Regression Rate Behaviors of HTPB-Based Propellant Combinations for Hybrid Rocket Motor. Acta Astronaut. 2016, 119, 137–146. [Google Scholar] [CrossRef]
- Marquardt, T.; Majdalani, J. Review of Classical Diffusion-Limited Regression Rate Models in Hybrid Rockets. Aerospace 2019, 6, 75. [Google Scholar] [CrossRef]
- Yuasa, S.; Ide, T.; Masugi, M.; Sakurai, T.; Shiraishi, N.; Shimada, T. Visualization of Flames in Combustion Chamber of Swirling-Oxidizer-Flow-Type Hybrid Rocket Engines. J. Therm. Sci. Technol. 2011, 6, 268–277. [Google Scholar] [CrossRef]
- Kumar, C.P.; Kumar, A. Effect of Swirl on the Regression Rate in Hybrid Rocket Motors. Aerosp. Sci. Technol. 2013, 29, 92–99. [Google Scholar] [CrossRef]
- Yuasa, S.; Yamamoto, K.; Hachiya, H.; Kitagawa, K.; Oowada, Y. Development of a small sounding hybrid rocket with a swirling-oxidizer-type engine. In Proceedings of the 37th Joint Propulsion Conference and Exhibit, Salt Lake City, UT, USA, 8–11 July 2001. [Google Scholar] [CrossRef]
- Summers, M.H.; Dennis, J.D.; Villarreal, J.K. Small-Scale Hybrid Rocket Test Stand & Characterization of Swirl Injectors. In Proceedings of the 49th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, San Jose, CA, USA, 14–17 July 2013. [Google Scholar] [CrossRef]
- Tian, H.; Li, Y.; Li, C.; Sun, X. Regression Rate Characteristics of Hybrid Rocket Motor with Helical Grain. Aerosp. Sci. Technol. 2017, 68, 90–103. [Google Scholar] [CrossRef]
- Wang, Z.; Lin, X.; Li, F.; Yu, X. Combustion Performance of a Novel Hybrid Rocket Fuel Grain with a Nested Helical Structure. Aerosp. Sci. Technol. 2020, 97, 105613. [Google Scholar] [CrossRef]
- Zhang, S.; Hu, F.; Zhang, W. Numerical Investigation on the Regression Rate of Hybrid Rocket Motor with Star Swirl Fuel Grain. Acta Astronaut. 2016, 127, 384–393. [Google Scholar] [CrossRef]
- Tian, H.; Jiang, X.; Lu, Y.; Liang, Y.; Zhu, H.; Cai, G. Numerical Investigation on Hybrid Rocket Motors with Star-Segmented Rotation Grain. Aerospace 2022, 9, 585. [Google Scholar] [CrossRef]
- Vignesh, B.; Kumar, R. Effect of Multi-Location Swirl Injection on the Performance of Hybrid Rocket Motor. Acta Astronaut. 2020, 176, 111–123. [Google Scholar] [CrossRef]
- Dubey, A.; Kumar, R.; Biswas, S. Performance estimation of hybrid rocket by varying the flow rate at multi-location swirl injector. FirePhysChem 2025, 5, 111–120. [Google Scholar] [CrossRef]
- Knuth, W.H.; Chiaverini, M.J.; Sauer, J.A.; Gramer, D.J. Solid-Fuel Regression Rate Behavior of Vortex Hybrid Rocket Engines. J. Propuls. Power 2002, 18, 600–609. [Google Scholar] [CrossRef]
- Yu, H.; Yu, X.; Chen, S.; Zhang, W.; DeLuca, L.T.; Shen, R. The Catalysis Effects of Acetylacetone Complexes on Polymer Matrix of HTPB-Based Fuels. FirePhysChem 2021, 1, 205–211. [Google Scholar] [CrossRef]
- Cardoso, K.P.; Ferrão, L.F.A.; Kawachi, E.Y.; Gomes, J.S.; Nagamachi, M.Y. Ballistic Performance of Paraffin-Based Solid Fuels Enhanced by Catalytic Polymer Degradation. J. Propuls. Power 2019, 35, 115–124. [Google Scholar] [CrossRef]
- Karabeyoglu, M.A.; Altman, D.; Cantwell, B.J. Combustion of Liquefying Hybrid Propellants: Part 1, General Theory. J. Propuls. Power 2002, 18, 610–620. [Google Scholar] [CrossRef]
- Karabeyoglu, M.A.; Cantwell, B.J. Combustion of Liquefying Hybrid Propellants: Part 2, Stability of Liquid Films. J. Propuls. Power 2002, 18, 621–630. [Google Scholar] [CrossRef]
- Kim, S.; Moon, H.; Kim, J.; Cho, J. Evaluation of Paraffin-Polyethylene Blends as Novel Solid Fuel for Hybrid Rockets. J. Propuls. Power 2015, 31, 1750–1760. [Google Scholar] [CrossRef]
- Liu, L.-L.; He, X.; Wang, Y.; Chen, Z.B.; Guo, Q. Regression Rate of Paraffin-Based Fuels in Hybrid Rocket Motor. Aerosp. Sci. Technol. 2020, 107, 106269. [Google Scholar] [CrossRef]
- Liu, L.-L.; Zhang, T.-Y.; Chen, Z.-B.; He, X.; Ji, Z. Boundary Layer Combustion of Paraffin Fuels for Hybrid Propulsion Applications. Acta Astronaut. 2022, 193, 338–345. [Google Scholar] [CrossRef]
- Hashish, A.; Paravan, C.; Verga, A. Liquefying Fuel Combustion in a Lab-Scale Vortex Flow Pancake Hybrid Rocket Engine. In Proceedings of the AIAA Propulsion and Energy Forum, Virtual Event, 9–11 August 2021. [Google Scholar] [CrossRef]
- Zhang, Z.; Lin, X.; Wang, Z.; Wu, K.J.; Luo, J.; Fang, S. Effects of swirl injection on the combustion of a novel composite hybrid rocket fuel grain. Acta Astronaut. 2022, 199, 174–182. [Google Scholar] [CrossRef]
- Xia, H.; Wu, Y.; Wang, N.; Zhang, Z.; Yang, J.; Zhang, F. Numerical analysis of influence of injection method and skeleton structure on the combustion of skeleton reinforced paraffin fuel. J. Aerosp. Power 2023, 38, 1496–1505. [Google Scholar] [CrossRef]
- Quadros, F.D.A.; Lacava, P.T. Swirl injection of gaseous oxygen in a lab-scale paraffin hybrid rocket motor. J. Propuls. Power 2019, 35, 896–905. [Google Scholar] [CrossRef]
- Tian, H.; Meng, X.; Zhu, H.; Li, C.; He, L.; Cai, G. Dynamic Numerical Simulation of Hybrid Rocket Motor with HTPB-Based Fuel with 58% Aluminum Additives. Aerospace 2022, 9, 727. [Google Scholar] [CrossRef]
- Meng, X.; Huang, H.; Chen, Y.; Yao, M.; Wang, J.; Tian, H. The Three-Dimensional Transient Simulation of Cross-Shaped Grains in Hybrid Rocket Motors. Aerospace 2025, 12, 429. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, S.-Q.; Liu, X.-L.; Liu, L.-L. Regression rate modeling of HTPB/paraffin fuels in hybrid rocket motor. Aerosp. Sci. Technol. 2022, 121, 107324. [Google Scholar] [CrossRef]
- Wang, R.; Lin, X.; Wang, Z.; Wu, K.; Zhang, Z.; Luo, J.; Li, F.; Yu, X. Combustion characteristics of a swirl-radial-injection composite fuel grain with applications in hybrid rockets. Aerospace 2023, 10, 759. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.-L.; Li, B.-B.; Chen, Z.-X.; Hu, S.-Q. Fuel Grain Configuration Adaptation for High-Regression-Rate Hybrid Propulsion Applications. Aerospace 2025, 12, 652. https://doi.org/10.3390/aerospace12080652
Liu L-L, Li B-B, Chen Z-X, Hu S-Q. Fuel Grain Configuration Adaptation for High-Regression-Rate Hybrid Propulsion Applications. Aerospace. 2025; 12(8):652. https://doi.org/10.3390/aerospace12080652
Chicago/Turabian StyleLiu, Lin-Lin, Bo-Biao Li, Ze-Xin Chen, and Song-Qi Hu. 2025. "Fuel Grain Configuration Adaptation for High-Regression-Rate Hybrid Propulsion Applications" Aerospace 12, no. 8: 652. https://doi.org/10.3390/aerospace12080652
APA StyleLiu, L.-L., Li, B.-B., Chen, Z.-X., & Hu, S.-Q. (2025). Fuel Grain Configuration Adaptation for High-Regression-Rate Hybrid Propulsion Applications. Aerospace, 12(8), 652. https://doi.org/10.3390/aerospace12080652





