Abstract
Rising temperature, drought and more-frequent extreme climatic events have been predicted for the next decades in many regions around the globe. In this framework, soil water availability plays a pivotal role in affecting vegetation productivity, especially in arid or semi-arid environments. However, direct measurements of soil moisture are scarce, and modeling estimations are still subject to biases. Further investigation on the effect of soil moisture on plant productivity is required. This study aims at analyzing spatio-temporal variations of a modified temperature vegetation wetness index (mTVWI), a proxy of soil moisture, and evaluating its effect on gross primary production (GPP) in forests. The study was carried out in Europe on 19 representative tree species during the 2000–2010 time period. Results outline a north–south gradient of mTVWI with minimum values (low soil water availability) in Southern Europe and maximum values (high soil water availability) in Northeastern Europe. A low soil water availability negatively affected GPP from 20 to 80%, as a function of site location, tree species, and weather conditions. Such a wetness index improves our understanding of water stress impacts, which is crucial for predicting the response of forest carbon cycling to drought and aridity.
1. Introduction
Climate change results in rising air temperature and changes in the frequency and distribution of precipitation [1]. More-frequent extreme events are projected for the next decades in many regions around the globe [2]. Earlier studies have suggested a significant increase in frequency and severity of droughts [1,3], especially in the Mediterranean region [4,5,6,7,8,9]. Knowledge of mechanisms through which climate variations affect forest ecosystem processes, such as productivity, phenology, regeneration, and mortality, is still partial [10,11,12]. Consequently, there is an urgent need to realize a permanent assessment of forest sensitivity to climate change [13,14].
Mediterranean forests are considered particularly susceptible to future warming and drought conditions due to their location within the transition zone between arid and temperate climates [2,15,16,17]. Several studies have reported increased plant mortality rates and die-off events, reduced seedling recruitment, long-term shifts in vegetation composition, reduced radial growth, and increased crown defoliation responses [18,19,20,21,22]. Similarly, studies carried out in boreal forests, located in regions less constrained by drought, have reported reductions in productivity and widespread increases in tree mortality because of increasing drought stress [23]. On the one hand, warming conditions might promote drought stress, reducing gross primary production (GPP, representing the sum of gross carbon uptake by plant photosynthesis) and enhancing root and tree mortality [24,25,26,27]. On the other hand, warming conditions could increase: (i) forest growth from CO2 fertilization, (ii) water use efficiency, and (iii) growing seasons duration [28,29,30,31,32].
Soil moisture plays a pivotal role in vegetation dynamics [8,33], considering that soil water availability is a crucial limiting factor for plant photosynthesis [34,35]. However, soil water content (SWC) is a critical variable depending on many factors such as precipitation amount, the duration and intensity of drought, level of soil erosion, surface runoff impacts, and rate of evapotranspiration [36,37]. Consequently, SWC is difficult to estimate both with field measurements and model estimations [38]. There are different methods to estimate SWC, such as volumetric and gravimetric methodologies [39], or remote sensing techniques [40,41]. The Soil Moisture and Ocean Salinity (SMOS) mission conducted by the European Space Agency (ESA) has the capacity to estimate soil moisture globally and routinely based on a microwave radiometer system [42]. To date, SMOS soil moisture data have provided particularly suitable long-term records of global soil moisture, even if limited to shallow soil [43].
Remote sensing can be used to generate a vast amount of information about the Earth’s surface and can be useful for suitable land-management planning. A strong relationship was found between SWC and values derived from surface temperature–vegetation index (Ts–VI) methods using optical and thermal remote sensing data as inputs [44]. Based on this method, a temperature–vegetation wetness index (TVWI) was developed to estimate SWC in a forest-dominated and topographically variable landscape in eastern Canada [45]. The integration of the normalized difference vegetation index (NDVI) and potential surface temperatures (θs) was used for an indirect assessment of soil moisture [45]. Following the concepts described above, a modified version of the temperature vegetation wetness index (mTVWI) was proposed using the complementary value of crown defoliation instead of NDVI [46]. In Europe, tree crown defoliation is monitored by the International Cooperative Programme on Assessment and Monitoring of Air Pollution Effects on Forests (ICP Forests) and is regarded as morphological damage affecting the green biomass of plants [47].
The driving hypothesis in this study is that a large variation of GPP, in response to soil water availability, depends on species, location, and weather characteristics, helping to better understand the relationship between GPP and mTVWI. Using the mTVWI, and considering GPP as a proxy for photosynthesis at the canopy level, we analyzed spatio-temporal variations of mTVWI across Europe, quantifying the impact of mTVWI and thus soil water availability on the GPP of European forests.
The analysis was carried out over the time period 2000–2010 for 19 representative tree species distributed across four bio-geographic areas using a MODIS GPP at 1 km of spatial resolution (Collection5 MOD17).
2. Materials and Methods
2.1. Data Collection
Crown defoliation data were provided by the ICP Forests network (Level I monitoring plots) for the main European tree species over the time period 2000–2010. In Europe, crown condition is the most widely applied indicator for forest health and vitality assessments [43,44,45,46,48,49,50,51]. Crown defoliation of the dominant tree species is visually estimated as the relative amount of foliage (expressed as percentage) in the tree crown compared to a reference tree of the same species with full foliage, growing in the same stand and site conditions [52,53]. Crown defoliation is estimated annually for 1623 monitoring plots of Level I according to the Manual on methods and criteria for harmonised sampling, assessment, monitoring, and analysis of the effects of air pollution on forests [53]. Mean annual values of crown defoliation were calculated for each Level I monitoring plot and for all considered species as reported in Figure S1 in the supplementary material. In particular, we considered nineteen tree species: six conifers (Larix decidua Mill., Picea abies L., Pinus halepensis Mill., Pinus nigra J.F. Arnold, Pinus pinaster Aiton, and Pinus sylvestris L.), twelve broad-leaf deciduous trees (Acer pseudoplatanus L., Alnus glutinosa Gaertn, Betula pendula Roth, Betula pubescens Ehrhart, Carpinus betulus L., Castanea sativa Miller, Fagus sylvatica L., Fraxinus excelsior L., Populus tremula L., Quercus petraea Liebl., Quercus pubescens Willd., and Quercus robur L.) and one broad-leaf evergreen species (Quercus ilex L.) distributed across four European bio-geographic areas (Boreal, Atlantic–Temperate, Continental–Temperate, Mediterranean). Furthermore, the crown defoliation database included site characteristics such as latitude, longitude, and altitude.
Mean annual temperature data (T mean, °C) were obtained from the European Climate Assessment & Dataset (ECA&D) for the time period 2000–2010. The ECA&D consists of a daily series of observations collected at several meteorological stations (>2000) throughout Europe. The nearest meteorological station to each ICP Forests site was used to provide temperature data.
GPP data (gC m−2 day−1) were provided by MOD17 product of the MODIS (MODerate Resolution Imaging Spectroradiometer) instrument aboard the Terra satellite, as modified by [54]. MOD17 is the first continuous satellite-driven dataset monitoring global vegetation productivity at 1 km of spatial resolution, providing 8-day, monthly, and annual GPP averages. The GPP component of the algorithm is estimated by a light use efficiency model and requires daily inputs of incoming photosynthetically active radiation (PAR) and climate variables [55,56,57]. The Collection5 MOD17 products, temperature, and crown defoliation data were used with a temporal resolution of 1 year, over the time period 2000–2010. All analyses were separately performed for all considered years in the 1623 plots.
2.2. Modified Temperature Vegetation Wetness Index (mTVWI)
The mTVWI [45,46] was defined as an indirect assessment of soil moisture related to NDVI and potential surface temperatures (θs). NDVI is one of the most extensively applied vegetation indices, closely associated to leaf area index (LAI), primary production [58], and the biochemical processes underlying primary production (photosynthetic activity). Following Vitale et al. (2014) [46], we used the complementary values of crown defoliation Γ, defined as 100 minus defoliation values as a proxy of NDVI.
where Defoliationplot is the mean crown defoliation value in one specific plot (in %). Γ was calculated for all considered plots and years. The potential surface temperature (θs) was calculated in two steps, as in [45]. The first step concerned the calculation of atmospheric pressure (p, in kPa), given by:
where z (in m) is the plot elevation relative to sea level. This equation is based on a simplified form of the ideal gas law for a neutrally-stratified atmosphere and a temperature of 20 °C at a standard atmosphere (i.e., 101.3 kPa).
Γ = 100 − Defoliationplot
Then, surface potential temperature θs (in K) was calculated as:
where TS is the mean annual temperature (in K), p0 is the average pressure at mean sea level (set at 100.0 kPa), R is the gas constant (i.e., 287 J kg−1 K−1), and cp is the specific heat capacity of air (~1004 J kg−1 K−1). A scatter plot between θs and Γ was generated to derive two parameters, θdry and θwet (Figure 1), for each considered year. θdry (in K) indicates low levels of water availability limiting evapotranspiration; it was calculated as the straight line passing through points A and B, where A is the point with coordinates (max Γ; max θs in max Γ) and B is the point with coordinates (max Γ in the 99th percentile of θs; 99th percentile of θs) as depicted in Figure 1 and Figure S2.
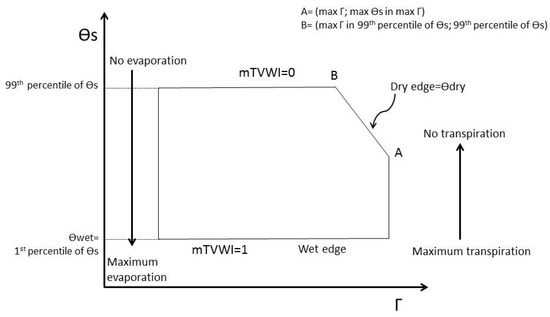
Figure 1.
mTVWI scheme based on the relationship between potential surface temperature (θs) and the complementary values of crown defoliation (Γ).
θwet (in K) indicates an unlimited amount of water available to sustain evapotranspiration, and was calculated as the 1st percentile of θs. To derive the percentiles we considered all analyzed species together (1623 monitoring plots) for each year.
Finally, we calculated the mTVWI as follows:
where mTVWI is a dimensionless quantity varying from 0 (the case where water is not available for evapotranspiration, θdry) and 1 (the case where water is freely available for evapotranspiration, θwet). Consequently, the mTVWI is an index strictly linked to forest crown defoliation (θdry), surface potential temperature, and vapor pressure deficit (VPD) conditions [46].
All the above parameters were calculated on an annual basis during the time period 2000–2010.
2.3. Statistical Analyses
Under the assumption that partial correlation is a measure of association between two variables controlling or adjusting the effect of one or more additional variables [59], partial correlation coefficients define the degree of existing correlation between two variables when the effects of one or more variables are removed [59]. Since temperature strongly affects GPP and mTVWI, possibly causing confounding effects [60,61,62], we evaluated the partial correlation between annual data of GPP and the mTVWI after that temperature effect was removed [63] over the time period 2000–2010. We also performed a pair-wise Spearman’ rank correlation analysis using rs coefficients [64], a non-parametric test to investigate both linear and non-linear correlations [59,60,65,66]. Significance was tested at p < 0.05 after Bonferroni’s correction for multiple comparisons [67]. One-way analysis of variance (ANOVA) was used to determine if there was at least one significant difference among the means of three or more independent groups. Specifically, we hypothesized that the means of mTVWI and GPP reduction in broad-leaf deciduous species significantly differed from mTVWI and GPP reduction in conifer and broad-leaf evergreen species. We used the Tukey post hoc test to find significant patterns and/or relationships (p < 0.05) between subgroups of broad-leaf deciduous, conifer, and broad-leaf evergreen species.
2.4. Impact of mTVWI on GPP
The impact of mTVWI on GPP was estimated similarly to the method proposed by [62,68] to quantify the impact of tropospheric ozone on GPP. The quantification of mTVWI influence on GPP (GPP related to water availability, GPPWater) was expressed as follows:
where GPP is the original GPP derived from the MODIS product.
Finally, we calculated the percentage variation of the original GPP in respect to GPPWater to evaluate the impacts of aridity on European tree species considered in this study for each year from 2000 to 2010.
2.5. Anomalies Analysis
The term anomaly is defined here as the difference between the value of a variable (e.g., GPP and mTVWI) for a single temporal period (year) and the grand mean of the same variable over a given time period (2000−2010). The analysis of anomalies was performed for each analyzed tree species, displaying GPP and mTVWI anomalies together in order to evaluate a recurrent pattern and to identify all deviations from the grand mean.
3. Results
3.1. Space–Time Distribution Patterns of mTVWI in Europe
The spatial distribution of the mTVWI values for the 19 plant species over the time period 2000–2010, is shown in Figure 2A–C. A north–south gradient in Europe is highlighted. Minimum mTVWI values (0–0.20) were mainly found in Southern Europe (Italy and Spain) while the maximum (0.80–1) were observed in Northeastern Europe (Belarus and Norway). In Central Europe, we found mTVWI values ranging from 0.40 to 0.80. Mediterranean evergreen oak (Q. ilex L.) showed a low mTVWI value (0.17) whilst B. pubescens, a typical Northern European species growing in wet conditions, showed a higher mTVWI value (0.87). In general, we found that broad-leaf deciduous species showed higher mTVWI values than conifers and the broad-leaf evergreen (Table S1). The analysis of variance (ANOVA) corroborated this evidence. In fact, the ANOVA and Tukey post hoc test indicated significant differences (p < 0.05) among mean mTVWI values referring to conifers, broad-leaf deciduous, and evergreen species for all years (Figure S3, Table S2). Taking into account temporal variations, Figure 3 shows the mean annual mTVWI values (±standard error, SE) over the time period 2000–2010 when considering all tree species together. We found the lowest mTVWI values in 2007 and 2008 (0.49 ± 0.01 and 0.33 ± 0.01, respectively) whilst in 2000, 2002, and 2009 we found mTVWI values ranging from 0.60 to 0.63.
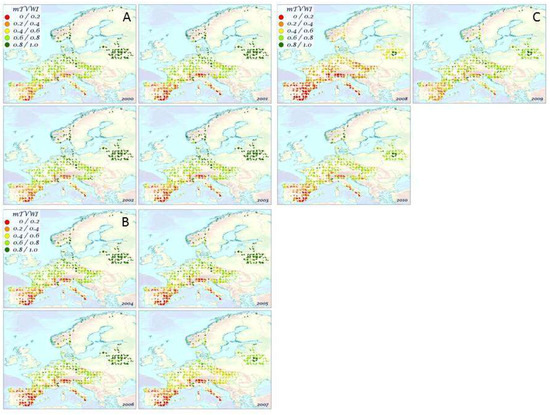
Figure 2.
Spatial distribution of the mTVWI values over the time period 2000–2010. The points show ICP Forests level I sites.
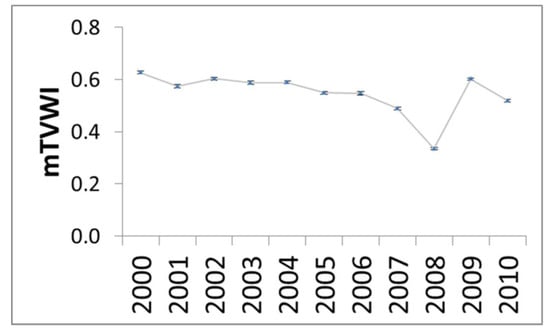
Figure 3.
mean annual values of mTVWI (±SE) over the time period 2000–2010.
3.2. Correlation between GPP and mTVWI
Partial correlation coefficients between GPP and mTVWI were significant (p < 0.05) in most of the European tree species (Table 1). In general, GPP and mTVWI correlated positively in conifers and broad-leaf evergreen species and negatively in broad-leaf deciduous species. We found positive correlation coefficients in L. decidua, P. pinaster, P. nigra, B. pendula, and Q. ilex ranging from 0.22 to 0.56 (p < 0.05). By contrast, P. sylvestris, A. pseudoplatanus, A. glutinosa, C. betulus, F. excelsior, P. tremula, Q. pubescens, and Q. robur showed negative coefficients varying from −0.24 to −0.56 (p < 0.05). Other species such as P. abies, P. halepensis, B. pubescens, C. sativa, F. sylvatica, and Q. petraea did not show significant relationships between GPP and mTVWI. Mediterranean species such as P. pinaster and Q. ilex showed the highest positive correlation coefficients between GPP and mTVWI (0.36–0.50 and 0.24–0.33, respectively). Conversely, species growing in wet conditions like P. sylvestris and P. tremula showed negative correlation coefficients between GPP and mTVWI.

Table 1.
Partial correlation coefficients (controlling for: temperature (T)) for the correlation between gross primary production (GPP) and the modified temperature vegetation wetness index (mTVWI). Bold indicates significance at p < 0.05.
Spearman rank-order correlation coefficients between GPP and mTVWI (Table 2) were in agreement with partial correlation analysis results. The GPP and mTVWI relationships were positive and statistically significant (p < 0.05) in conifers and broad-leaf evergreen species and negative in broad-leaf deciduous species. We found positive correlation coefficients in L. decidua, P. nigra, P. pinaster, and Q. ilex (the same species highlighted in the partial correlation analysis except for B. pendula) and negative coefficients in most of the analyzed species (e.g., P. sylvestris, A. pseudoplatanus, B. pubescens, F. excelsior).

Table 2.
Spearman rank-order correlation (rs) for the correlation between gross primary production (GPP) and the modified temperature vegetation wetness index (mTVWI). Bold indicates significance at p < 0.05.
3.3. Impact of mTVWI on GPP
The percentage change of GPP due to mTVWI is shown in Figure 4A–C. The largest decrease occurred in Mediterranean countries, whereas the smallest decrease occurred in Belarus and Norway for all considered years. Italy and Spain showed a GPP reduction ranging from 40 to 100%. Central Europe presented a GPP reduction ranging from 20 to 40% for all years except for 2007 and 2008, where the GPP reduction reached 80%. Northern and Northeastern Europe were characterized by a small GPP reduction (0–40%). Table 3 shows a plant species-based GPP reduction (%) for all years. Conifers showed a mean GPP reduction of nearly 50% ranging from 40% in P. sylvestris to 80% in P. halepensis, P. nigra, and P. pinaster. The broad-leaf deciduous species showed an average GPP reduction close to 40%, with some species showing higher reductions (54%, F. sylvatica and Q. pubescens) and other species with limited GPP reduction (20% B. pubescens, B. pendula, P. tremula). By contrast, Q. ilex presented values of GPP reduction close to 70% for all considered years. Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 show the average GPP reduction values over the time period 2000–2010 (standard deviations are shown in Figure S4). The largest decrease occurred in F. sylvatica, P. halepensis, P. nigra, P. pinaster, and Q. ilex, whereas the smallest decrease occurred in B. pendula and B. pubescens.
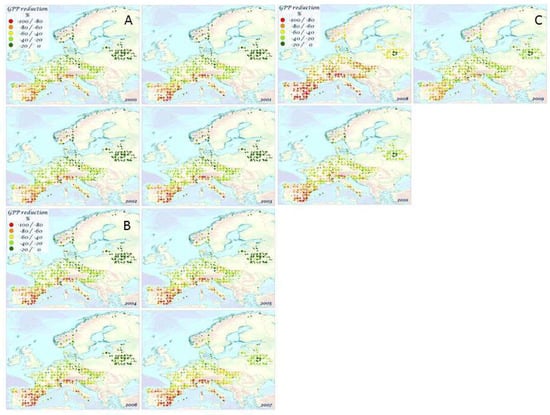
Figure 4.
The percentage change of gross primary production (GPP) due to mTVWI, a proxy of soil water availability, over the time period 2000–2010.

Table 3.
Species-specific GPP reduction (%) due to mTVWI over the time period 2000–2010 (±standard deviation).
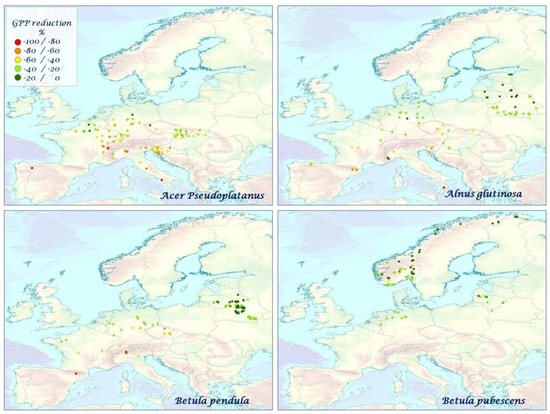
Figure 5.
The mean species–specific GPP reduction (%) for A. pseudoplatanus, A. glutinosa, B. pendula, B. pubescens over the time period 2000–2010.
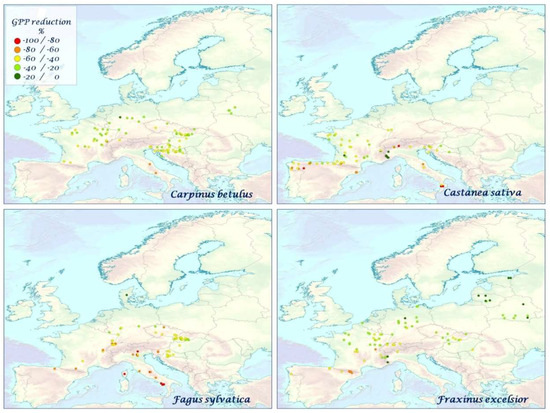
Figure 6.
The mean species–specific GPP reduction (%) for C. betulus, C. sativa, F. sylvatica, F. excelsior over the time period 2000–2010.
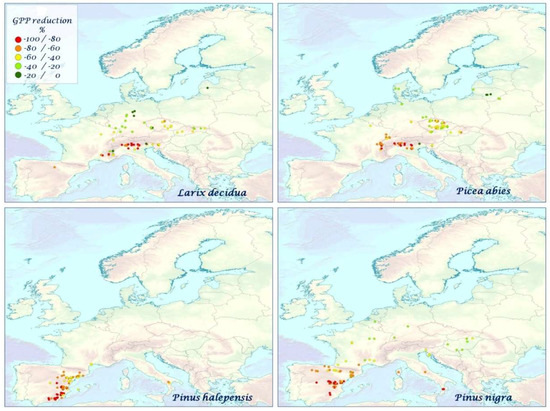
Figure 7.
The mean species–specific GPP reduction (%) for L. decidua, P. abies, P. halepensis, P. nigra over the time period 2000–2010.
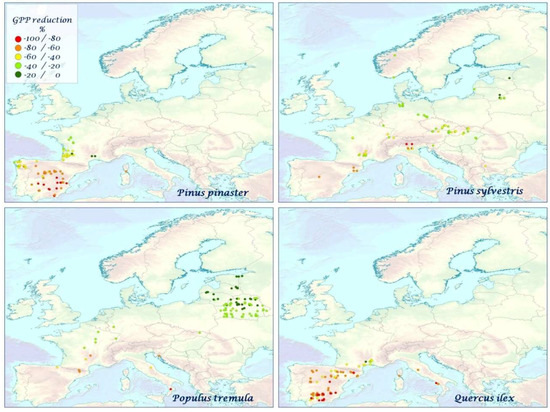
Figure 8.
The mean species–specific GPP reduction (%) for P. pinaster, P. sylvestris, P. tremula, Q. ilex over the time period 2000–2010.
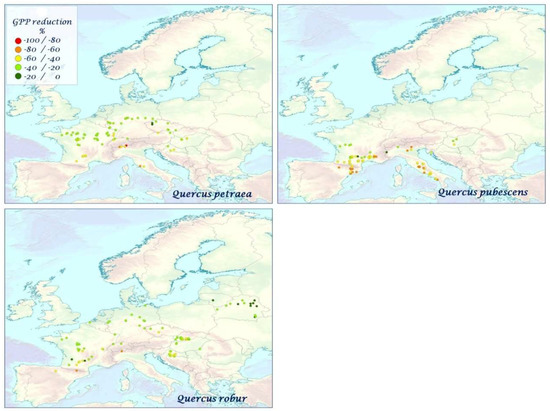
Figure 9.
The mean species–specific GPP reduction (%) for Q. petraea, Q. pubescens, Q. robur over the time period 2000–2010.
In general, we found that broad-leaf evergreen (Q. ilex) and conifer species showed higher GPP reduction values than broad-leaf deciduous (Table 3), which was also confirmed by analysis of variance (ANOVA) and Tukey post hoc tests (Figure S5, Table S3). The anomalies analysis is shown in Figure 10. We found a species-specific pattern of GPP and mTVWI anomalies in the time period 2000–2010. In general, highly negative anomalies of mTVWI (a condition of severe aridity) often correspond to a reduction of GPP. Indeed, in 2008 a highly negative deviation from the grand mean corresponds to a GPP reduction in most of the considered species (e.g., A. pseudoplatanus, F. sylvatica, P. abies, L. decidua, P. tremula). Taking into account the 2003 heat wave that affected much of Europe from June to September [69], we found a highly negative deviation from the grand mean of GPP not matching with high negative mTVWI anomalies.
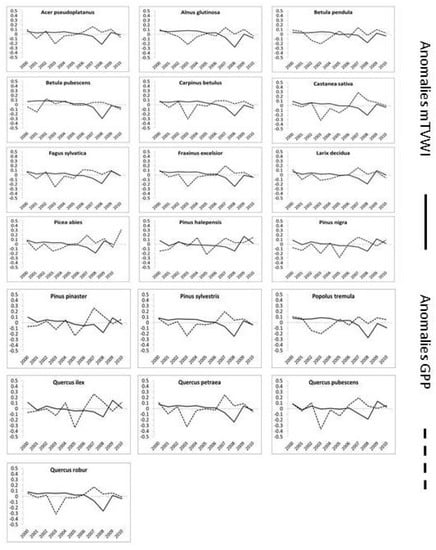
Figure 10.
Anomalies of mTVWI and GPP over the time period 2000–2010. The term anomaly is defined here as the difference between the mean of mTVWI and GPP calculated for a single year and the grand–mean of mTVWI and GPP but considering the overall time period (2000–2010).
4. Discussion
4.1. Spatial and Temporal Distribution of mTVWI
Our study assessed the impact of water availability in 19 tree species distributed across four European bio-geographic areas by using a modified temperature vegetation wetness index (mTVWI). The study focused on the impact of mTVWI, a proxy for soil water availability, on GPP. Our analyses revealed a north–south gradient of the mTVWI with minimum values in Southern Europe and maximum values in Northeastern Europe over the time period 2000–2010. Precipitation over the Northern Europe increased between 10 and 40% in the 20th century [70], whereas some parts of Southern Europe dried by up to 20% [70], reporting a geographic pattern consistent with our results. However, a north–south gradient of the mTVWI is not surprising as soil moisture and soil water availability affect vegetation growth and productivity especially in arid or semi-arid ecosystems [34]. In fact, the impact of water deficit on growth is much higher in arid and semi-arid sites in which water availability principally affects the main physiological processes of vegetation (growth, photosynthesis, carbon, and nitrogen use) than in sites with a moderate or well-balanced water supply [71,72,73,74]. A significant decrease of the mTVWI (−40% respect to others years) was observed in 2007 and 2008 over Europe. This reduction is likely related to high values of crown defoliation [75], especially in Mediterranean areas, impacting mTVWI values. Unfortunately, due to the lack of measurements of soil water content into the field conditions in our sites, it is unfeasible to compare the estimation of the index with real world measurements.
4.2. Correlations, Impacts, and Anomalies of GPP and mTVWI
Significant correlations between GPP and mTVWI were found in most of the European tree species. The highest positive coefficients were found for two Mediterranean species, Q. ilex and P. pinaster. Greater water availability allows higher stomatal conductance and thus a positive relationship between mTVWI and GPP [76]. Conversely, we found negative GPP–mTVWI relationships in other species (e.g., P. sylvestris, P. tremula) mainly growing in Central–Northern Europe. These results were well corroborated by Pasho et al. [77] in 2011, where they found a strong association between tree growth and a drought index (the standardized precipitation index) in P. sylvestris. On the other hand, other studies in Northern European countries did not find any association between SPI and crown defoliation (e.g., [78]). The different responses to drought from tree species are related to different strategies in coping with drought and local conditions of the forest stands [77]. As a function of site location and tree species, mTVWI negatively affected GPP from 20 to 80%. We found that broad-leaf evergreen (Q. ilex) and conifer species showed higher GPP reduction than broad-leaf deciduous species. A generalized increase in defoliation and mortality occurring was observed during 1987–2007 in Southern European forests (principally in Q. ilex stands), largely related to a severe drought regime [79], thus confirming our results. In agreement with our results, a high sensitivity to drought was found for broad-leaf Mediterranean forests [24]. P. pinaster, a Mediterranean species, showed high GPP reductions (50–80%) over the years, which are in line with earlier studies suggesting a high dependence of water availability in mixed pine–oak Mediterranean forests [22,80,81,82]. Probably, forests located in sites experiencing strong drought events (e.g., Southern European forests) could reduce their carbon sink efficiency and contribute to the reduction in carbon sink in the Northern Hemisphere [82,83]. However, the response of GPP to water availability significantly varied among species and locations. For example, B. pendula and B. pubescens, mainly distributed in northern temperate regions [84], showed low GPP reductions (10–30%). Conversely, F. excelsior was characterized by moderate-to-high GPP reductions (30–60%) being a water-demanding species suffering severe damages under increasing temperature [85]. Similarly, F. sylvatica showed high GPP reductions (up to 70%) likely due to its high sensitivity to drought [24]. Furthermore, an increase of crown defoliation was reported for the beech, especially in the Mediterranean area [50]. In fact, sensitivity to extreme temperature in F. sylvatica increased with the decreasing of soil water availability in the Mediterranean area [86].
Anomalies analysis showed a similar pattern of mTVWI and GPP anomalies over the time period 2000–2010, highlighting that negative anomalies of mTVWI (more aridity) induced a reduction of GPP. This result is in line with several studies (e.g., [87,88]) that reported a reduction of GPP NPP related to drought. Taking into account the 2003 heat wave, we found a highly negative deviation from the grand mean of GPP, whereas mTVWI did not show a corresponding variation. However, it should be noted that mTVWI was calculated considering temperature of the overall year (2003), whilst the peak temperatures in 2003 were found only during the growing season [68], thus impacting mainly GPP.
5. Conclusions
Models such as CMIP5 running under a higher temperature increased the potential evapotranspiration and changes in seasonal precipitation patterns and highlighted an intensification of drought events both in frequency and intensity [1,3], especially in the Mediterranean region [5,6]. Increasing climate and soil aridity are expected to cause growth decline and enhancement of mortality particularly in drought-sensitive forest species [15,16,89,90,91]. Thus, understanding and predicting the impacts of climate change on ecosystems is one of the pivotal challenges for the global change science [92,93]. As climate change is strictly dependent on the increase of the emissions of air pollutants, and consequently on air pollutant concentrations [1,3], we cannot study the impacts of climate change on soil aridity without considering air pollution impacts. Our study contributes to an assessment of GPP responses to soil water availability based on a dimensionless index—the modified temperature vegetation wetness index (mTVWI)—which is an indirect measure of soil moisture tightly linked to VPD conditions. Empirical results of this study outline a negative impact of low soil water availability on GPP, although it varied according to plant functional types, years, and bio-geographic areas. In fact, tree species can vary their ability to adjust physiological functions to soil water deficit [94,95]. Moreover, mTVWI could be used to estimate soil water availability when direct measurements and/or model estimations are lacking. Thus, its application can improve quantification of the carbon gain of forests undergoing drought promptly, to inform forest management planners of short-term climate change and its influence on the status of forest health.
Supplementary Materials
The following are available online at https://www.mdpi.com/2225-1154/7/3/42/s1, Figure S1: title, Table S1: title, Video S1: title.
Author Contributions
Conceptualization, C.P., M.V., and A.D.M.; Methodology, C.P., M.V., and F.F.; Software, C.P.; Validation, C.P. and A.A.; Formal Analysis, C.P.; Investigation, C.P. and A.A.; Resources, A.D.M.; Data Curation, C.P. and A.D.M.; Writing—Original Draft Preparation, C.P.; Writing—Review & Editing, C.P., A.A., S.F., L.S.E.P., M.V., A.D.M., F.F., A.S. and P.S.; Visualization, A.S.; Supervision, A.D.M. and E.P.; Project Administration, E.P.; Funding Acquisition, E.P.
Funding
This research received no external funding
Acknowledgments
This work was carried out within the IUFRO Task Force on Climate Change and Forest Health.
Conflicts of Interest
No conflict of interest.
References
- Dai, A. Increasing drought under global warming in observations and models. Nat. Clim. Chang. 2013, 3, 52–58. [Google Scholar] [CrossRef]
- Huang, J.; Yu, H.; Guan, X.; Wang, G.; Guo, R. Accelerated dryland expansion under climate change. Nat. Clim. Chang. 2016, 6, 166–171. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Camarero, J.J.; Azorın–Molina, C. Diverse responses of forest growth to drought timescales in the Northern Hemisphere. Glob. Ecol. Biogeogr. 2014, 23, 1019–1030. [Google Scholar] [CrossRef]
- Mavrakis, A.; Salvati, L. Analyzing the behavior of selected risk indexes during the 2007 Greek forest fires. Int. J. Environ. Res. 2015, 9, 831–840. [Google Scholar]
- Gao, X.; Giorgi, F. Increased aridity in the Mediterranean region under greenhouse gas forcing estimated from high resolution simulations with a regional climate model. Glob. Planet Chang. 2008, 62, 195–209. [Google Scholar] [CrossRef]
- Hertig, E.; Jacoboeit, J. Downscaling future climate change: Temperature scenarios for the Mediterranean area. Glob. Planet Chang. 2008, 63, 127–131. [Google Scholar] [CrossRef]
- Salvati, L.; Zitti, M.; Ceccarelli, T.; Perini, L. Building–up a synthetic index of land vulnerability to drought and desertification. Geogr. Res. 2009, 47, 280–291. [Google Scholar] [CrossRef]
- Salvati, L.; Perini, L.; Sabbi, A.; Bajocco, S. Climate aridity and land use changes: A regional-scale analysis. Geogr. Res. 2012, 50, 193–203. [Google Scholar] [CrossRef]
- Colantoni, A.; Ferrara, C.; Perini, L.; Salvati, L. Assessing Trends in Climate Aridity and Vulnerability to Soil Degradation in Italy. Ecol. Indic. 2015, 48, 599–604. [Google Scholar] [CrossRef]
- Michaletz, S.T.; Cheng, D.; Kerkhoff, A.J.; Enquist, B.J. Convergence of terrestrial plant production across global climate gradients. Nature 2014. [Google Scholar] [CrossRef]
- Cutini, A.; Manetti, M.C.; Mazza, G.; Moretti, V.; Salvati, L. Climate variability and growth rate of Pinus pinea L. in Castelporziano forest: An exploratory data analysis. Rend. Accad. Nazion. Lincei 2015, 26, 413–420. [Google Scholar] [CrossRef]
- Chu, C.; Bartlett, M.; Wang, Y.; He, F.; Weiner, J.; Chave, J.; Sack, L. Does climate directly influence NPP globally? Glob. Chang. Biol. 2016, 22, 12–24. [Google Scholar] [CrossRef]
- Salvati, R.; Salvati, L.; Ferrara, A.; Corona, P.; Barbati, A. Estimating the sensitivity to desertification of Italian forests. iForest 2014, 8, 287–294. [Google Scholar] [CrossRef]
- Zang, C.; Meier, C.H.; Dittmar, C.; Rothe, A.; Menzel, A. Patterns of drought tolerance in major European temperate forest trees: Climatic drivers and levels of variability. Glob. Chang. Biol. 2014, 20, 3767–3779. [Google Scholar] [CrossRef]
- Morales, P.; Hickler, T.; Rowell, D.P.; Smith, B.; Sykes, M.T. Changes in European ecosystem productivity and carbon balance driven by regional climate model output. Glob. Chang. Biol. 2007, 13, 108–122. [Google Scholar] [CrossRef]
- Anav, A.; Mariotti, A. Sensitivity of natural vegetation to climate change in the Euro-Mediterranean area. Clim. Res. 2011, 46, 277–292. [Google Scholar] [CrossRef]
- Barbeta, A.; Mejía-Chang, M.; Ogaya, R.; Voltas, J.; Dawson, T.E.; Penuelas, J. The combined effects of a long–term experimental drought and an extreme drought on the use of plant-water sources in a Mediterranean forest. Glob. Chang. Biol. 2014, 21, 1213–1225. [Google Scholar] [CrossRef]
- Sicard, P.; Dalstein-Richier, L. Health and vitality assessment of two common pine species in the context of climate change in southern Europe. Environ. Res. 2015, 137, 235–245. [Google Scholar] [CrossRef]
- Allen, C.D.; Macalady, A.K.; Chenchouni, H.; Bachelet, D.; McDowell, N.; Vennetier, M.; Kitzberger, T.; Rigling, A.; Breshears, D.D.; Hogg, E.H.; et al. A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. For. Ecol. Manag. 2010, 259, 660–684. [Google Scholar] [CrossRef]
- Mueller, R.C.; Scudder, C.M.; Porter, M.E.; Talbot, T.R.; Gehring, C.A.; Whitham, T.G. Differential tree mortality in response to severe drought: Evidence for long-term vegetation shifts. J. Ecol. 2005, 93, 1085–1093. [Google Scholar] [CrossRef]
- Breshears, D.D.; Cobb, N.S.; Rich, P.M.; Price, K.P.; Allen, C.D.; Balice, R.G.; Romme, W.H.; Kastens, J.H.; Floyd, M.L.; Belnap, J.; et al. Regional vegetation die–off in response to global-change-type drought. Proc. Natl. Acad. Sci. USA 2005, 102, 15144–15148. [Google Scholar] [CrossRef]
- Andreu, L.; Gutiérrez, E.; Macias, M.; Ribas, M.; Bosch, O.; Camarero, J.J. Climate increases regional tree-growth variability in Iberian pine forests. Glob. Chang. Biol. 2007, 13, 804–815. [Google Scholar] [CrossRef]
- Peng, C.; Ma, Z.; Lei, X.; Zhu, Q.; Chen, H.; Wang, W.; Liu, S.; Li, W.; Fang XZhou, X. A drought–induced pervasive increase in tree mortality across Canada’s boreal forests. Nat. Clim. Chang. 2011, 1, 467–471. [Google Scholar] [CrossRef]
- Granier, A.; Reichestein, M.; Brèda, N.; Janssens, I.A.; Falge, E.; Ciais, P.; Grünwald, T.; Aubinet, T.; Berbigier, P.; Bernhofer, C.; et al. Evidence for soil water control on carbon and water dynamics in European forests during the extremely dry year: 2003. Agric. For. Meteorol. 2007, 143, 123–145. [Google Scholar] [CrossRef]
- Friend, A.D.; Lucht, W.; Rademacher, T.T.; Keribin, R.; Betts, R.; Cadule, P.; Ciais, P.; Clark, D.B.; Dankers, R.; Falloon, P.D.; et al. Carbon residence time dominates uncertainty in terrestrial vegetation responses to future climate and atmospheric CO2. Proc. Natl. Acad. Sci. USA 2014, 111, 3280–3285. [Google Scholar] [CrossRef] [PubMed]
- Allen, C.D.; Breshears, D.D.; McDowell, N.G. On underestimation of global vulnerability to tree mortality and forest die–off from hotter drought in the Anthropocene. Ecosphere 2015, 6, 1–55. [Google Scholar] [CrossRef]
- McDowell, N.G.; Williams, A.P.; Xu, C.; Pockman, W.T.; Dickman, L.T.; Sevanto, S.; Pangle, R.; Limousin, J.; Plaut, J.; Mackay, D.S.; et al. Multi–scale predictions of massive conifer mortality due to chronic temperature rise. Nat. Clim. Chang. 2016, 6, 295–300. [Google Scholar] [CrossRef]
- Ayres, M.P.; Lombardero, M.J. Assessing the consequences of global change for forest disturbances for herbivores and pathogens. Sci. Total Environ. 2000, 262, 263–286. [Google Scholar] [CrossRef]
- Bachelet, D.; Neilson, R.P.; Hickler, T.; Drapek, R.J.; Lenihan, J.M.; Sykes, M.T.; Smith, B.; Sitch, S.; Thonicke, K. Simulating past and future dynamics of natural ecosystems in the United States. Glob. Biogeochem. Cycles 2003, 17, 1045. [Google Scholar] [CrossRef]
- Lucht, W.; Schaphoff, S.; Erbrecht, T.; Heyder, U.; Cramer, W. Terrestrial vegetation redistribution and carbon balance under climate change. Carbon Balance Manag. 2006, 1, 6. [Google Scholar] [CrossRef]
- Scholze, M.; Knorr, W.; Arnell, N.W.; Prentice, I. A climate–change risk analysis for world ecosystems. Proc. Natl. Acad. Sci. USA 2006, 103, 13116–13120. [Google Scholar] [CrossRef] [PubMed]
- Lloyd, A.H.; Bunn, A.G. Responses of the circumpolar boreal forest to 20th century climate variability. Environ. Res. Lett. 2007, 2, 045013. [Google Scholar] [CrossRef]
- Cleverly, J.; Eamus, D.; Restrepo Coupe, N.; Chen, C.; Maes, W.; Li, L.; Faux, R.; Santini, N.S.; Rumman, R.; Yu, Q.; et al. Soil moisture controls on phenology and productivity in a semi–arid critical zone. Sci. Total Environ. 2016, 568, 1227–1237. [Google Scholar] [CrossRef] [PubMed]
- Nemani, R.R.; Keeling, C.D.; Hashimoto, H.; Jolly, W.M.; Piper, S.C.; Tucker, C.J.; Myneni, R.B.; Running, S.W. Climate–Driven Increases in Global Terrestrial Net Primary Production from 1982 to 1999. Science 2003, 300, 1560–1563. [Google Scholar] [CrossRef] [PubMed]
- Murray-Tortarolo, G.; Friedlingstein, P.; Sitch, S.; Seneviratne, S.I.; Fletcher, I.; Mueller, B.; Greve, P.; Anav, A.; Liu, Y.; Ahlström, A.; et al. The dry season intensity as a key driver of NPP trends. Geophys. Res. Lett. 2016, 43, 2632–2639. [Google Scholar] [CrossRef]
- Salvati, L.; Petitta, M.; Ceccarelli, T.; Perini, L.; Di Battista, F.; Venezian Scarascia, M.E. Italy’s renewable water resources as estimated on the basis of the monthly water balance. Irr. Drain 2008, 57, 507–515. [Google Scholar] [CrossRef]
- Moretti, V.; Di Bartolomei, R.; Sorgi, T.; Aromolo, R.; Salvati, L. Soil water deficit and climate conditions during the dry season along the coastal–inland gradient in Castelporziano Forest, central Italy. Rend. Accad. Naz. Lincei 2015, 26, 283–288. [Google Scholar] [CrossRef]
- Wang, T.; Franz, T.E.; Yue, W.; Szilagyi, J.; Zlotnik, V.A.; You, J.; Chen, X.; Shulski, M.D.; Young, A. Feasibility analysis of using inverse modeling for estimating natural groundwaterrecharge from a large-scale soil moisture monitoring network. J. Hydrol. 2016, 533, 250–265. [Google Scholar] [CrossRef]
- Bittelli, M. Measuring soil water content: A review. HortTechnology 2011, 21, 293–300. [Google Scholar] [CrossRef]
- Zhang, D.; Tang, R.; Zhao, W.; Tang, B.; Wu, H.; Shao, K.; Li, Z.L. Surface Soil Water Content Estimation from Thermal Remote Sensing based on the Temporal Variation of Land Surface Temperature. Remote Sens. 2014, 6, 3170–3187. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, Y.; Shao, M.; Horton, R. Estimating soil water content from surface digital image gray level measurements under visible spectrum. Can. J. Soil Sci. 2011, 91, 69–76. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS mission: New tool for monitoring key elements of the global water cycle. Proc. IEEE Inst. Electr. Electron. Eng. 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Qiu, B.; Xue, Y.; Fisher, J.B.; Guo, W.; Berry, J.A.; Zhang, Y. Satellite chlorophyll fluorescence and soil moisture observations lead to advances in the predictive understanding of global terrestrial coupled carbon-water cycles. Glob. Biogeochem. Cycles 2018, 32, 360–375. [Google Scholar] [CrossRef]
- Moran, M.S.; Peters–Lidard, C.D.; Watts, J.M.; McElroy, J. Estimating soil moisture at the watershed scale with satellite–based radar and land surface models. Can. J. Remote Sens. 2004, 30, 805–826. [Google Scholar] [CrossRef]
- Hassan, Q.K.; Bourque, C.P.; Meng, F.R.; Cox, R.M. A wetness index using terrain–corrected surface temperature and normalized difference vegetation index derived from standard MODIS products: An evaluation of its use in a humid forest–dominated region of eastern Canada. Sensors 2007, 7, 2028–2048. [Google Scholar] [CrossRef]
- Vitale, M.; Proietti, C.; Cionni, I.; Fischer, R.; De Marco, A. Random forests analysis: A useful tool for defining the relative importance of environmental conditions on crown defoliation. Water Air Soil Pollut. 2014, 225, 1–17. [Google Scholar] [CrossRef]
- Michel, A.; Seidling, W. (Eds.) Forest Condition in Europe: 2017 Technical Report of ICP Forests. Report under the UNECE Convention on Long-Range Transboundary Air Pollution (CLRTAP); BFW Dokumentation 24/2017; BFW Austrian Research Centre for Forests: Vienna, Austria, 2017; 128p. [Google Scholar]
- Rossini, M.; Panigada, C.; Meroni, M.; Colombo, R. Assessment of oak forest condition based on leaf biochemical variables and chlorophyll fluorescence. Tree Physiol. 2006, 26, 1487–1496. [Google Scholar] [CrossRef] [PubMed]
- Fischer, R.; Lorenz, M. Forest Condition in Europe, 2011 Technical Report of ICP Forests and FutMon. Work Report of the Institute for World Forestry 2011/1; ICP Forests: Hamburg, Germany, 2011; p. 212. [Google Scholar]
- De Marco, A.; Proietti, C.; Cionni, I.; Fischer, R.; Screpanti, A.; Vitale, M. Future impacts of nitrogen deposition and climate change scenarios on forest crown defoliation. Environ. Pollut. 2014, 194, 171–180. [Google Scholar] [CrossRef]
- Ferretti, M.; Marchetto, A.; Arisci, S.; Bussotti, F.; Calderisi, M.; Carnicelli, S.; Cecchini, G.; Fabbio, G.; Bertini, G.; Matteucci, G.; et al. On the tracks of Nitrogen deposition effects on temperate forests at their southern European range—An observational study from Italy. Glob. Chang. Biol. 2014, 20, 3423–3438. [Google Scholar] [CrossRef]
- Badea, O. Manual on Methodology for Long-Term Monitoring of Forest Ecosystems Status under Air Pollution and Climate Change Influence ed; Editura Silvică: Bucharest, Romania, 2008. [Google Scholar]
- ICP Forests. International Cooperative Programme on Assessment and Monitoring of Air Pollution Effects on Forests. Manual on Methods and Criteria for Harmonized Sampling, Assessment, Monitoring and Analysis of the Effects of Air Pollution on Forests, Part I (Federal Research Center for Forestry and Forest Products; ICP Forests: Hamburg, Germany, 2010. [Google Scholar]
- Zhao, M.; Heinsch, F.A.; Nemani, R.R.; Running, S.W. Improvements of the MODIS terrestrial gross and net primary production global data set. Remote Sens. Environ. 2005, 95, 164–176. [Google Scholar] [CrossRef]
- Turner, D.P.; Ritts, W.D.; Cohen, W.B.; Gower, S.T.; Running, S.W.; Zhao, M.; Costa, M.H.; Kirschbaum, A.A.; Ham, J.M.; Saleska, S.R.; et al. Evaluation of MODIS NPP and GPP products across multiple biomes. Remote Sens Environ. 2006, 102, 282–292. [Google Scholar] [CrossRef]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.; Reeves, M.; Hashimoto, H. A continuous satellite–derived measure of global terrestrial primary production. Bioscience 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Heinsch, F.A.; Reeves, M.; Votava, P.; Kang, S.; Milesi, C.; Zhao, M.; Glassy, J.; Jolly, W.M.; Loehman, R.; Bowker, C.F.; et al. GPP and NPP (MOD17A2/A3) Products NASA MODIS Land Algorithm. In MOD17 User’s Guide; MODIS Land Team: Washington, DC, USA, 2003; pp. 1–57. [Google Scholar]
- Reed, B.C.; Brown, J.F.; VanderZee, D.; Loveland, T.R.; Merchant, J.W.; Ohlen, D.O. Measuring phenological variability from satellite imagery. J. Veg. Sci. 1994, 5, 703–714. [Google Scholar] [CrossRef]
- Stevens, J. Partial and Semipartial Correlations. 2003. Available online: www.uoregon.edu/~stevensj/MRA/partial.pdf (accessed on 2010 February 10).
- Vargas, R.; Baldocchi, D.D.; Bahn, M.; Hanson, P.J.; Hosman, K.P.; Kulmala, L.; Pumpanen, J.; Yang, B. On the multi–temporal correlation between photosynthesis and soil CO2 efflux: Reconciling lags and observations. New Phytol. 2011, 191, 1006–1017. [Google Scholar] [CrossRef]
- Heinemeyer, A.; Wilkinson, M.; Vargas, R.; Subke, J.A.; Casella, E.; Morison, J.I.L.; Ineson, P. Exploring the “overflow tap” theory: Linking forest soil CO2 fluxes and individual mycorrhizosphere components to photosynthesis. Biogeosciences 2012, 9, 79–95. [Google Scholar] [CrossRef]
- Proietti, C.; Anav, A.; De Marco, A.; Sicard, P.; Vitale, M. A multi–sites analysis on the ozone effects on Gross Primary Production of European forests. Sci. Total Environ. 2016, 556, 1–11. [Google Scholar] [CrossRef]
- Fares, S.; Vargas, R.; Detto, M.; Goldstein, A.H.; Karlik, J.; Paoletti, E.; Vitale, M. Tropospheric ozone reduces carbon assimilation in trees: Estimates from analysis of continuous flux measurements. Glob. Chang. Biol. 2013, 19, 2427–2443. [Google Scholar] [CrossRef] [PubMed]
- Ceccarelli, T.; Bajocco, S.; Perini, L.; Salvati, L. Urbanisation and Land Take of High Quality Agricultural Soils—Exploring Long–term Land Use Changes and Land Capability in Northern Italy. Int. J. Environ. Res. 2014, 8, 181–192. [Google Scholar]
- Pili, S.; Grigoriadis, E.; Carlucci, M.; Clemente, M.; Salvati, L. Towards Sustainable Growth? A Multi–criteria Assessment of (Changing) Urban Forms. Ecol. Indic. 2017, 76, 71–80. [Google Scholar] [CrossRef]
- Chen, P.Y.; Popovich, P.M. Correlation: Parametric and Nonparametric Measures; Sage Publications: Thousand Oaks, CA, USA, 2002. [Google Scholar]
- Duvernoy, I.; Zambon, I.; Sateriano, A.; Salvati, L. Pictures from the Other Side of the Fringe: Urban Growth and Peri–urban Agriculture in a Post–industrial City (Toulouse, France). J. Rural Stud. 2018, 57, 25–35. [Google Scholar] [CrossRef]
- Anav, A.; Menut, L.; Khvorostyanov, D.; Viovy, N. Impact of tropospheric ozone on the Euro-Mediterranean vegetation. Glob. Chang. Biol. 2011, 17, 2342–2359. [Google Scholar] [CrossRef]
- Beniston, M. The 2003 heat wave in Europe: A shape of things to come? An analysis based on Swiss climatological data and model simulations. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Maracchi, G.; Sirotenko OBindi, M. Impacts of Present and Future Climate Variability on Agriculture and Forestry in the Temperate Regions: Europe. Clim. Chang. 2005, 70, 117. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Cuadrat-Prats, J.M.; Romo, A. Aridity influence on vegetation patterns in the middle Ebro Valley (Spain): Evaluation by means of AVHRR images and climate interpolation techniques. J. Arid Environ. 2006, 66, 353–375. [Google Scholar] [CrossRef]
- Jump, A.S.; Hunt, J.M.; Peñuelas, J. Rapid climate change–related growth decline at the southern range edge of Fagus sylvatica. Glob. Chang. Biol. 2006, 12, 2163–2174. [Google Scholar] [CrossRef]
- Sarris, D.; Christodoulakis, D.; Körner, C. Recent decline in precipitation and tree growth in the eastern Mediterranean. Glob. Chang. Biol. 2007, 13, 1187–1200. [Google Scholar] [CrossRef]
- Martínez-Vilalta, J.; Lopez, B.C.; Adell, N.; Badiella, L.; Ninyerola, M. Twentieth century increase of Scots pine radial growth in NE Spain shows strong climate interactions. Glob. Chang. Biol. 2008, 14, 2868–2881. [Google Scholar] [CrossRef]
- ICP Forests. International Cooperative Programme on Assessment and Monitoring of Air Pollution Effects on Forests Executive Report; ICP Forests: Hamburg, Germany, 2008; printed in Germany. [Google Scholar]
- De Marco, A.; Sicard, P.; Fares, S.; Tuovinen, J.P.; Anav, A.; Paoletti, E. Assessing the role of soil water limitation in determining the Phytotoxic Ozone Dose (PODY) thresholds. Atmos. Environ. 2016, 147, 88–97. [Google Scholar] [CrossRef]
- Pasho, E.; Camarero, J.J.; de Luis, M.; Vicente-Serrano, S.M. Impacts of drought at different time scales on forest growth across a wide climatic gradient in northeastern Spain. Agric. For. Meteorol. 2011, 151, 1800–1811. [Google Scholar] [CrossRef]
- Araminiene, W.; Sicard, P.; Anav, A.; Agathokleous, E.; Stakėnas, V.; De Marco, A.; Varnagirytė-Kabašinskienė, I.; Paoletti, E.; Girgždienė, R. Trends and inter-relationships of ground-level ozone metrics and forest health in Lithuania. Sci. Total Environ. 2019, 658, 1265–1277. [Google Scholar] [CrossRef]
- Carnicer, J.; Coll, M.; Ninyerola, M.; Pons, X.; Sanchez, G.; Penuelas, J. Widespread crown condition decline, food web disruption, and amplified tree mortality with increased climate change-type drought. Proc. Natl. Acad. Sci. USA 2011, 108, 1474–1478. [Google Scholar] [CrossRef] [PubMed]
- Corcuera, L.; Camarero, J.J.; Gil-Pelegrín, E. Effects of a severe drought on Quercus ilex radial growth and xylem anatomy. Trees-Struct. Funct. 2004, 18, 83–92. [Google Scholar]
- Montserrat–Martí, G.; Camarero, J.J.; Palacio, S.; Pérez–Rontomé, C.; Milla, R.; Albuixech, J.; Maestro, M. Summer–drought constrains the phenology and growth of two coexisting Mediterranean oaks with contrasting leaf habit: Implications for their persistence and reproduction. Trees 2009, 23, 787–799. [Google Scholar] [CrossRef]
- Gutiérrez, E.; Campelo, F.; Camarero, J.J.; Ribas, M.; Muntán, E.; Nabais, C.; Freitas, H. Climate controls act at different scales on the seasonal pattern of Quercus ilex L. stem radial increments in NE Spain. Trees Struct. Funct. 2011. [Google Scholar] [CrossRef]
- Ciais, P.; Reichstein, M.; Viovy, N.; Granier, A.; Ogée, J.; Allard, V.; Aubinet, M.; Buchmann, N.; Bernhofer, C.; Carrara, A.; et al. Europe–wide reduction in primary productivity caused by the heat and drought in 2003. Nature 2005, 437, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Canadell, J.G.; Le Quéré, C.; Raupach, M.R.; Field, C.B.; Buitenhuis, E.T.; Ciais, P.; Conway, T.J.; Gillett, N.P.; Houghton, R.A.; Marland, G. Contributions to accelerating atmospheric CO2 growth from economic activity, carbon intensity, and efficiency of natural sinks. Proc. Natl. Acad. Sci. USA 2007, 104, 18866–18870. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, M.D. Betula pendula Roth (B. verrucosa Ehrh.) and B. pubescens Ehrh. J. Ecol. 1992, 80, 837–870. [Google Scholar] [CrossRef]
- Bernetti, G. Selvicoltura Speciale; Unione Tipografico-Editrice Torinese: Torino, Italy, 1995; ISBN 8802048673. [Google Scholar]
- Lebourgeois, F.; Breda, N.; Ulrich, E.; Granier, A. Climate-tree-growth relationships of European beech (Fagus sylvatica L.) in the French Permanent Plot Network (RENECOFOR). Trees 2005, 19, 385–401. [Google Scholar] [CrossRef]
- Zhao, M.; Running, S.W. Drought–induced reduction in global terrestrial net primary production from 2000 through 2009. Science 2010, 329, 940–943. [Google Scholar] [CrossRef]
- Churkina, G.; Running, S.W. Contrasting climatic controls on the estimated productivity of global terrestrial biomes. Ecosystems 1998, 1, 206–215. [Google Scholar] [CrossRef]
- Linares, J.C.; Delgado–Huertas, A.; Carreira, J.A. Climatic trends and different drought adaptive capacity and vulnerability in a mixed Abies pinsapo–Pinus halepensis forest. Clim. Chang. 2010, 105, 67–90. [Google Scholar] [CrossRef]
- Gruber, A.; Strobl, S.; Veit, B.; Oberhuber, W. Impact of drought on the temporal dynamics of wood formation in Pinus sylvestris. Tree Physiol. 2010, 30, 490–501. [Google Scholar] [CrossRef] [PubMed]
- Koepke, D.F.; Kolb, T.E.; Adams, H.D. Variation in woody plant mortality and dieback from severe drought among soils, plant groups, and species within a northern Arizona ecotone. Glob. Chang. Ecol. 2010, 163, 1079–1090. [Google Scholar] [CrossRef] [PubMed]
- Boisvenue, C.; Running, S.W. Impacts of climate change on natural forest productivity—Evidence since the middle of the 20th century. Glob. Chang. Biol. 2006, 12, 862–882. [Google Scholar] [CrossRef]
- Bonan, G.B. Forests and Climate Change: Forcings, Feedbacks, and the Climate Benefits of Forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef]
- Sperry, J.S.; Hacke, U.G.; Oren, R.; Comstock, J.P. Water deficits and hydraulic limits to leaf water supply. Plant Cell Environ. 2002, 25, 251–263. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).