A Lagrangian Ocean Model for Climate Studies
Abstract
1. Introduction
2. Materials and Methods
2.1. Fluid Parcels
2.2. Lagrangian Convective Parameterization
2.3. Model Equations
2.4. Mixing
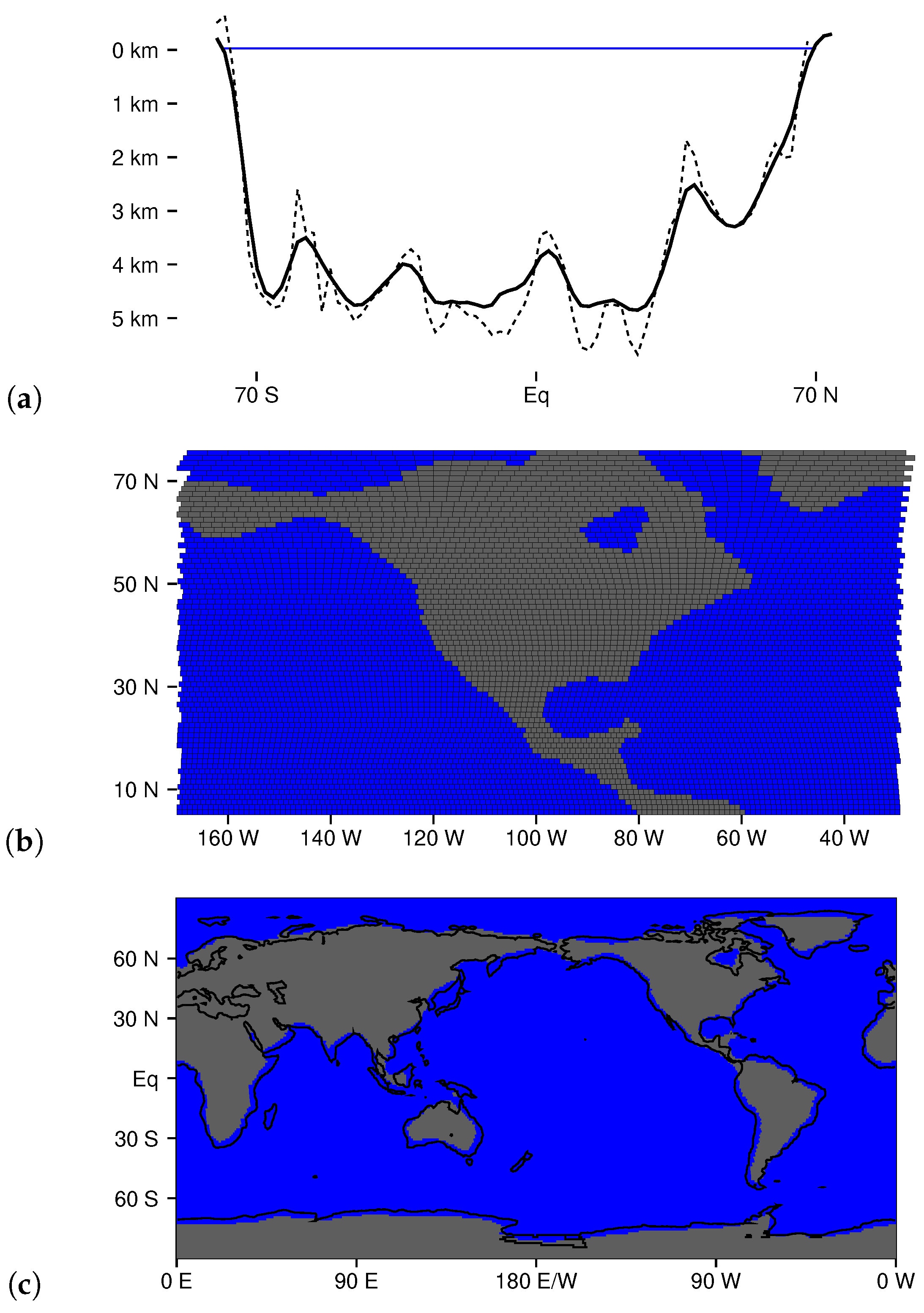
2.5. Bottom Topography and Spherical Geometry
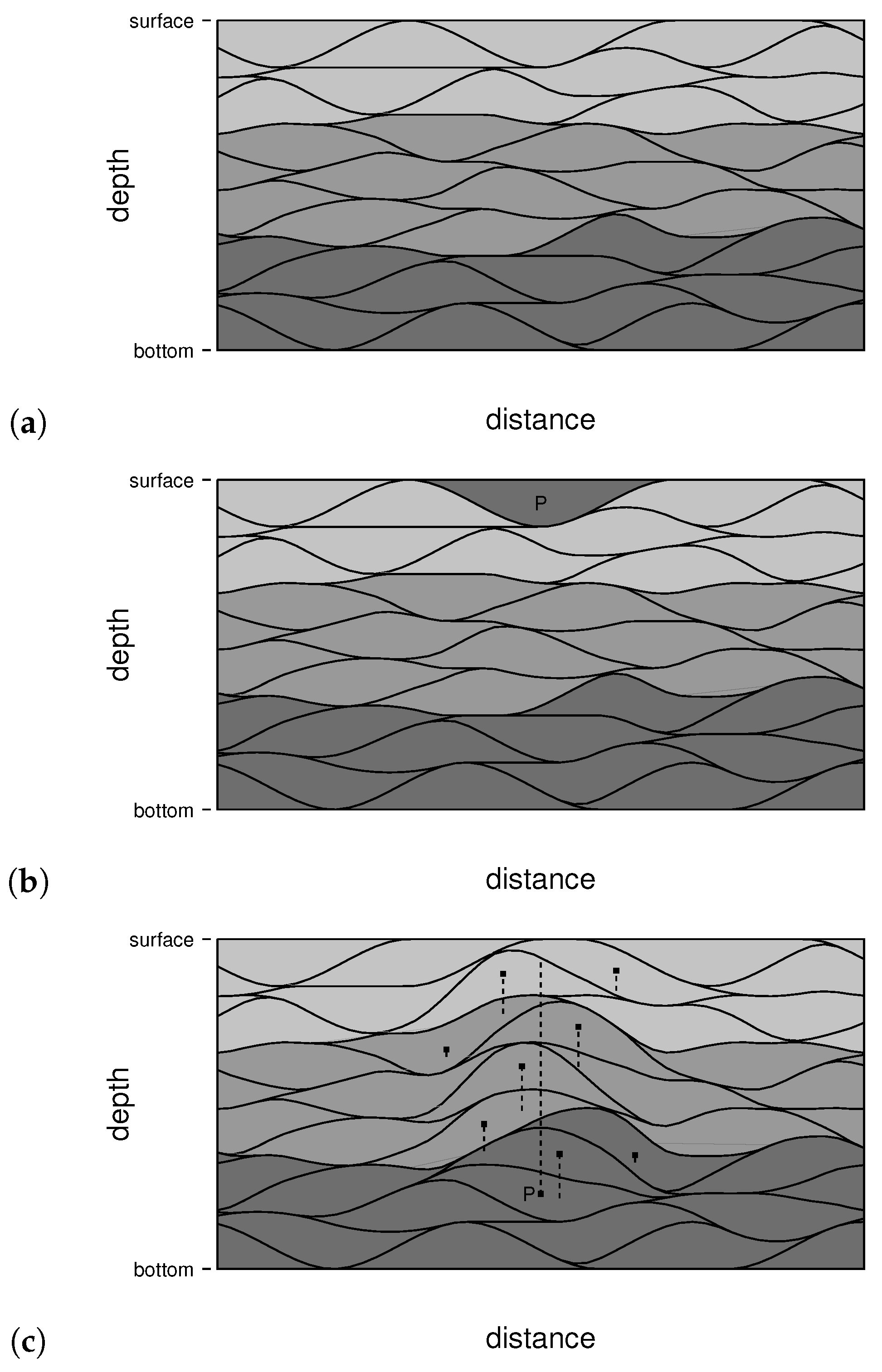
2.6. Merging and Dividing Parcels
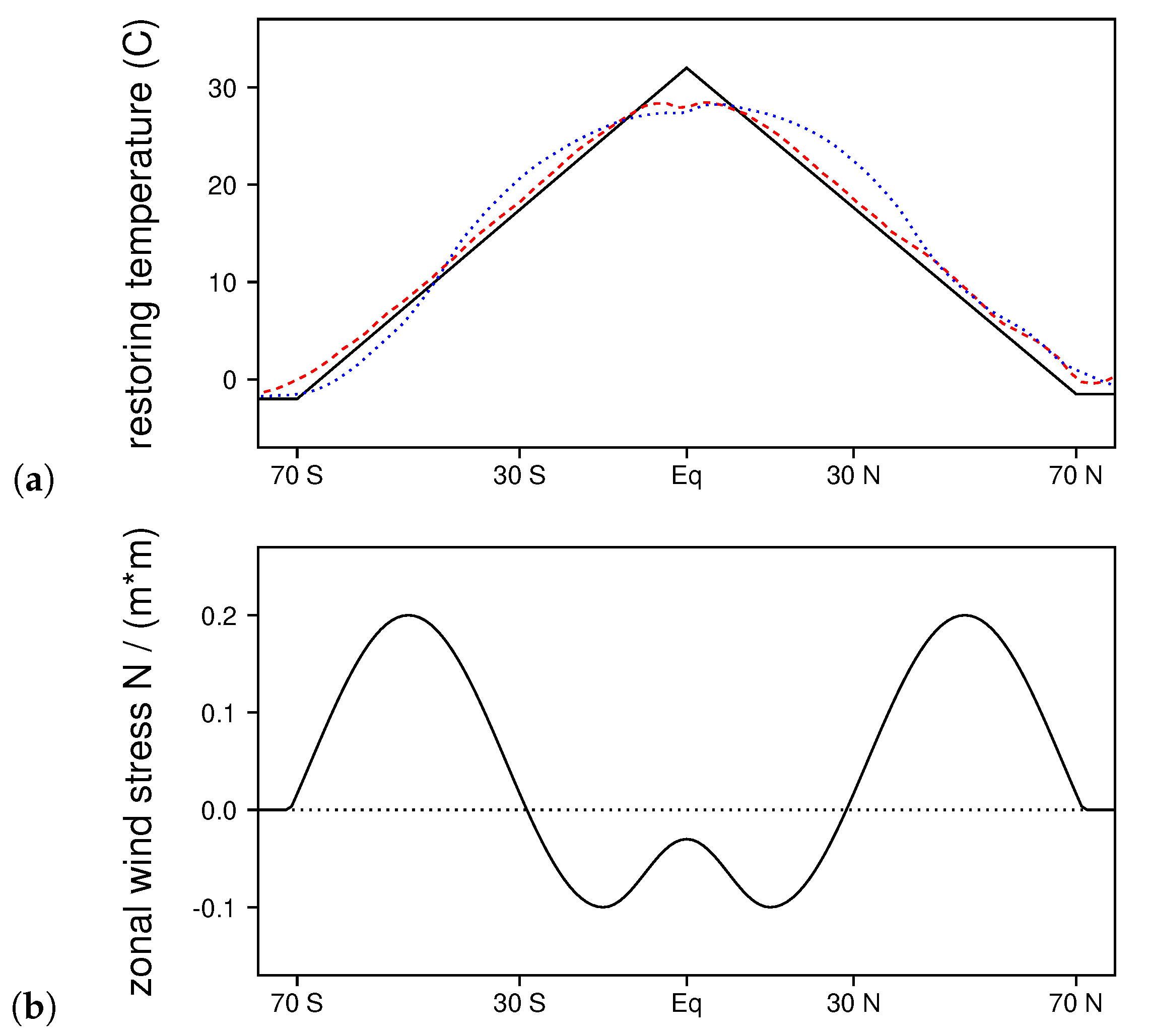
2.7. Experimental Design
3. Results
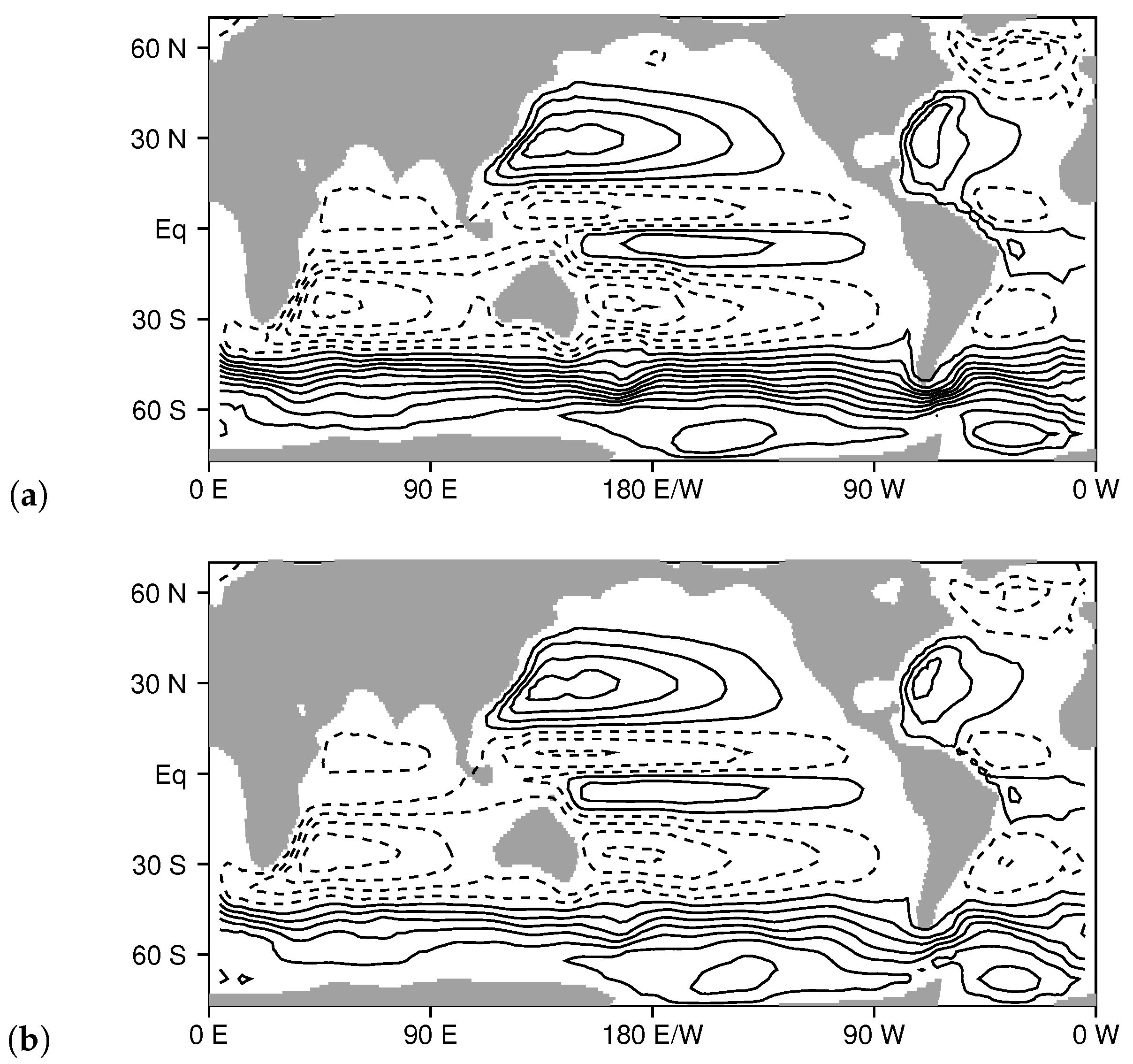
3.1. Horizontal Stream Function
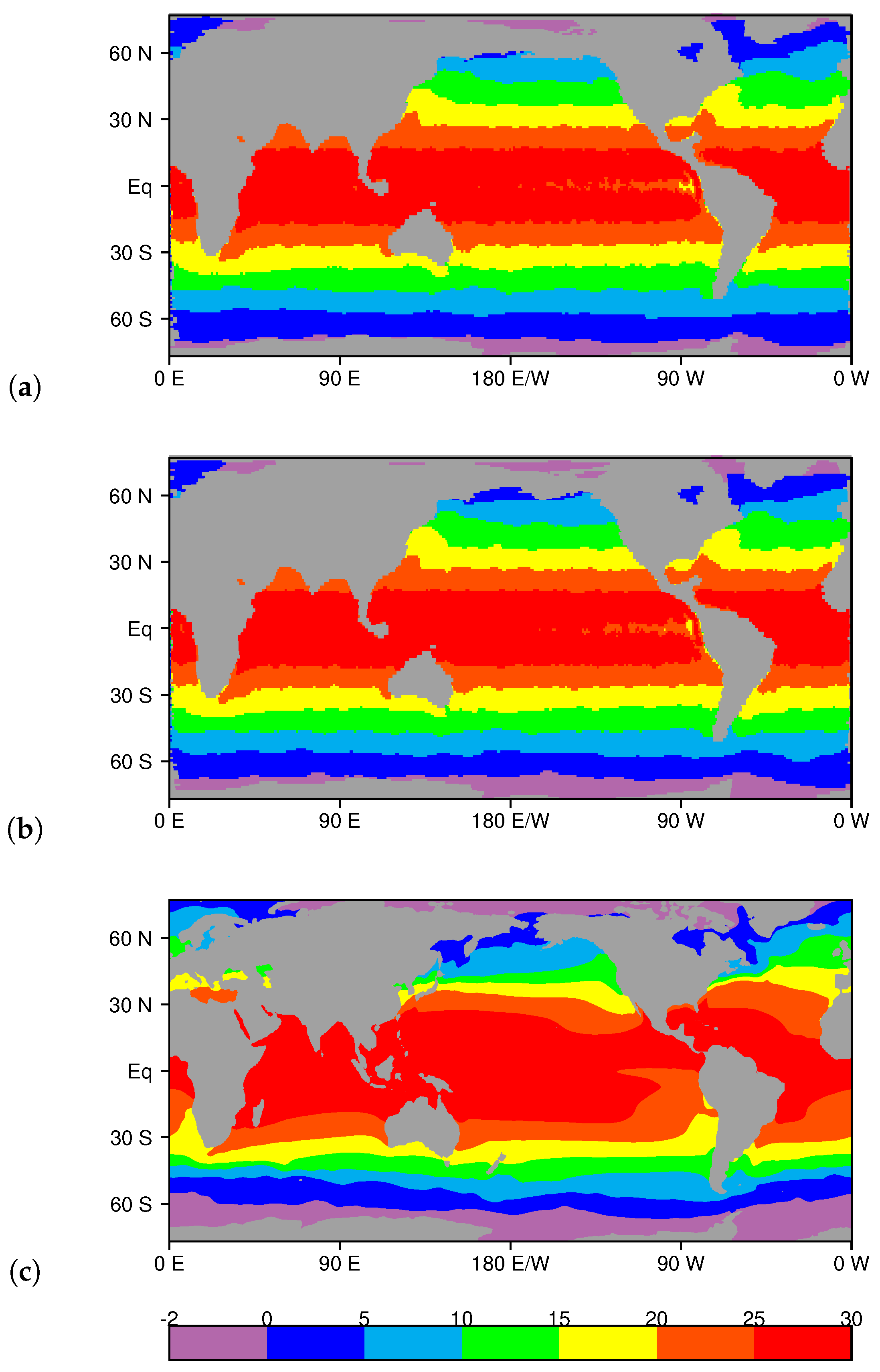
3.2. Surface Temperature Field
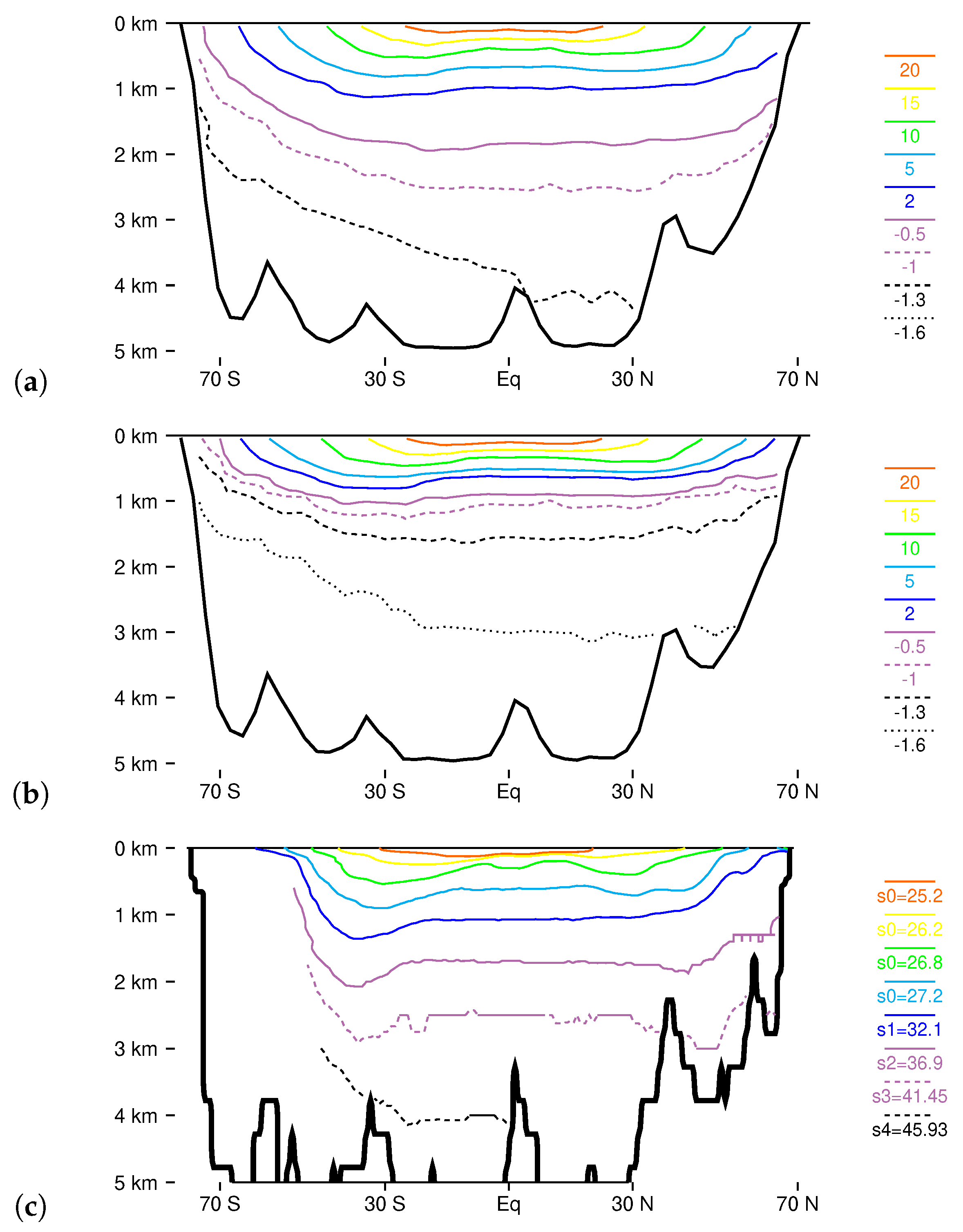
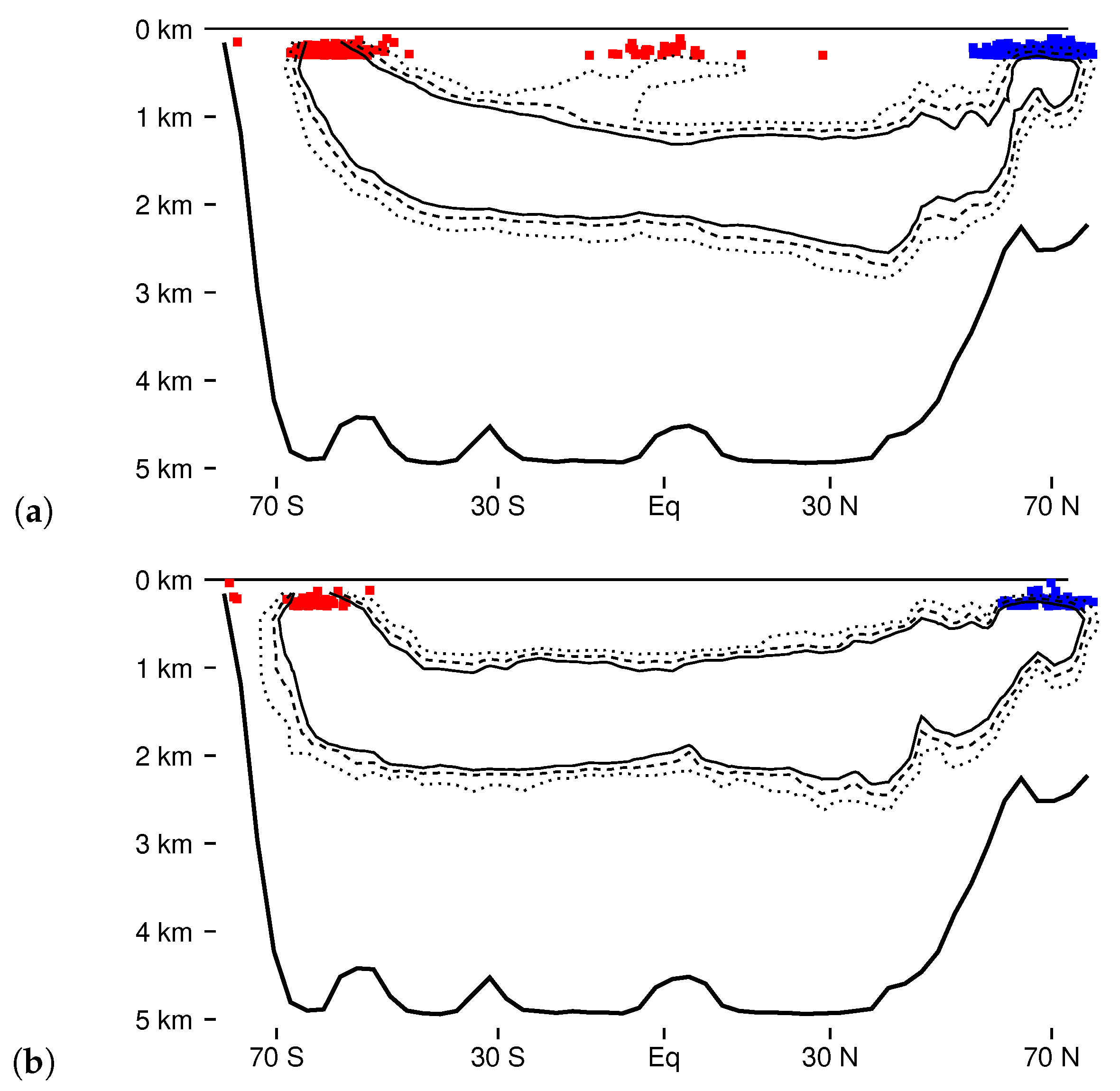
3.3. Stratification
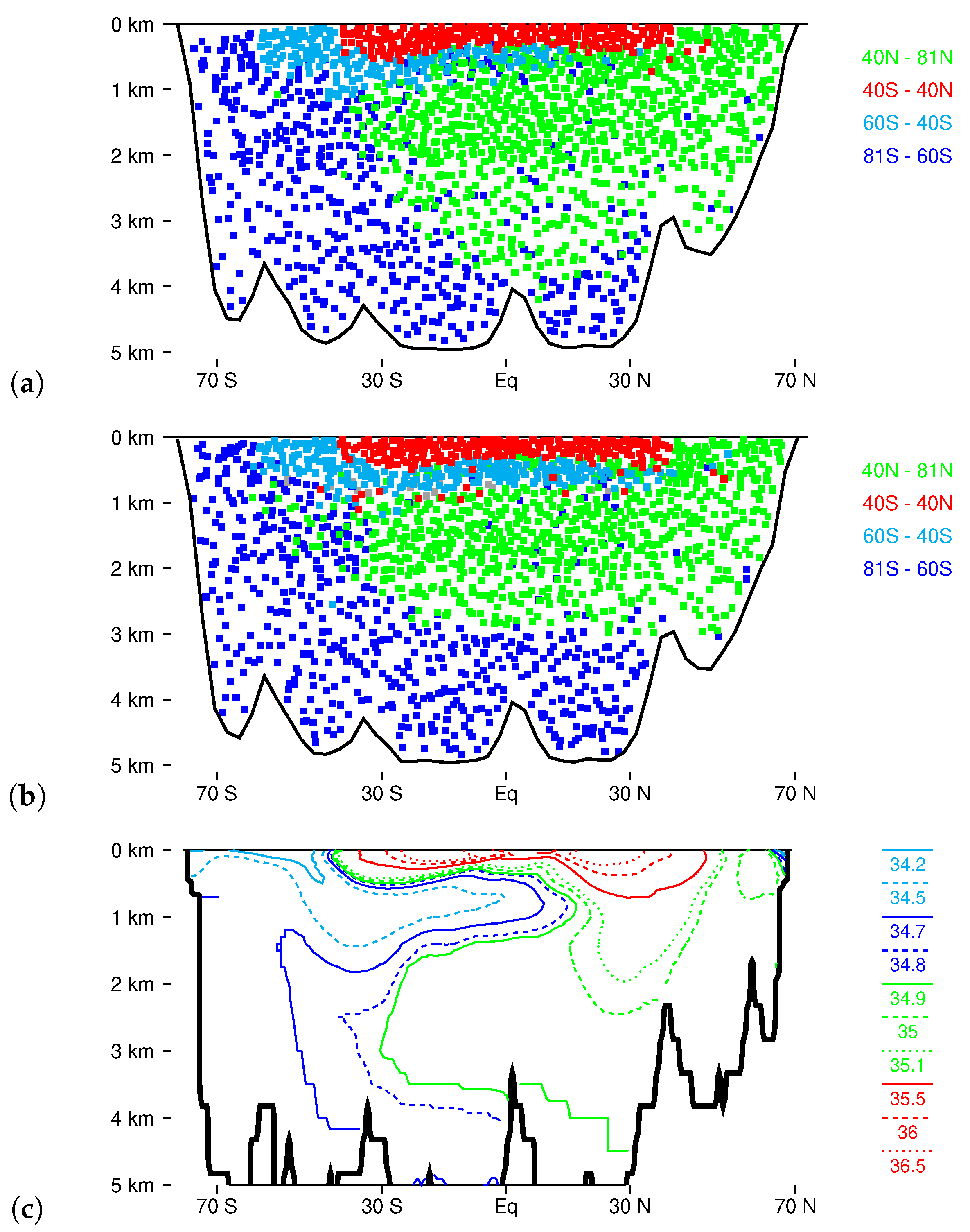
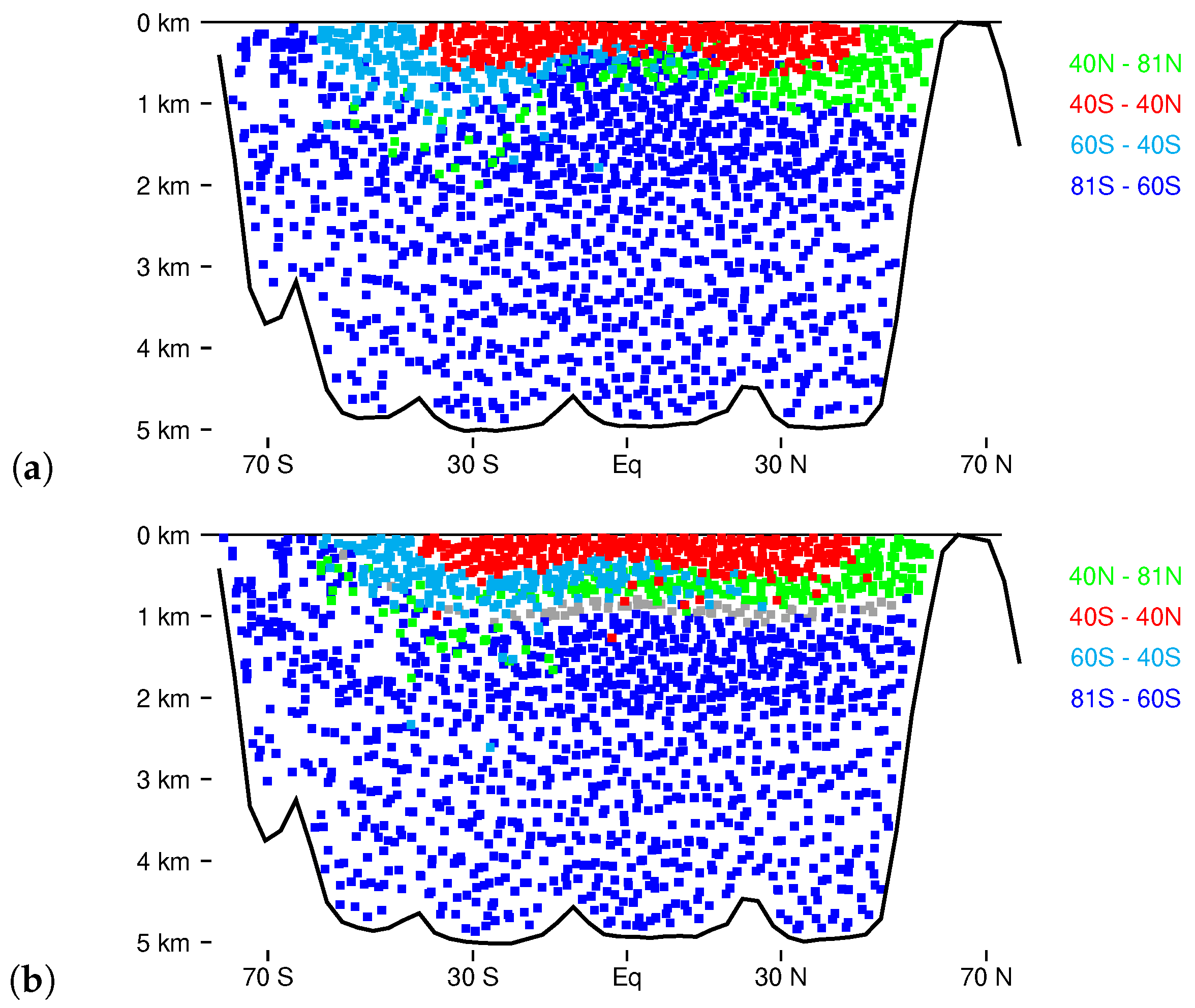
3.4. Water Mass Distributions
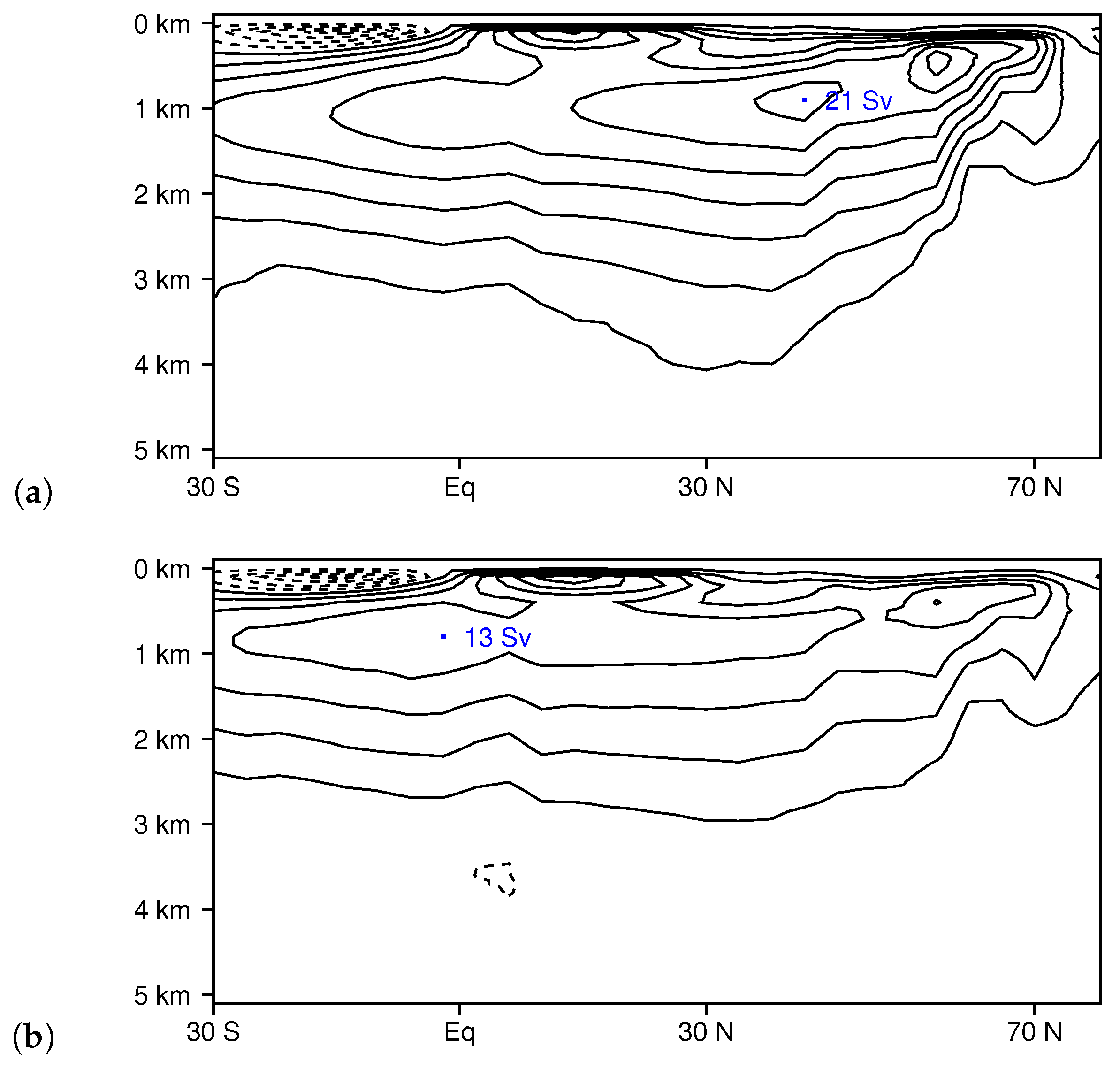
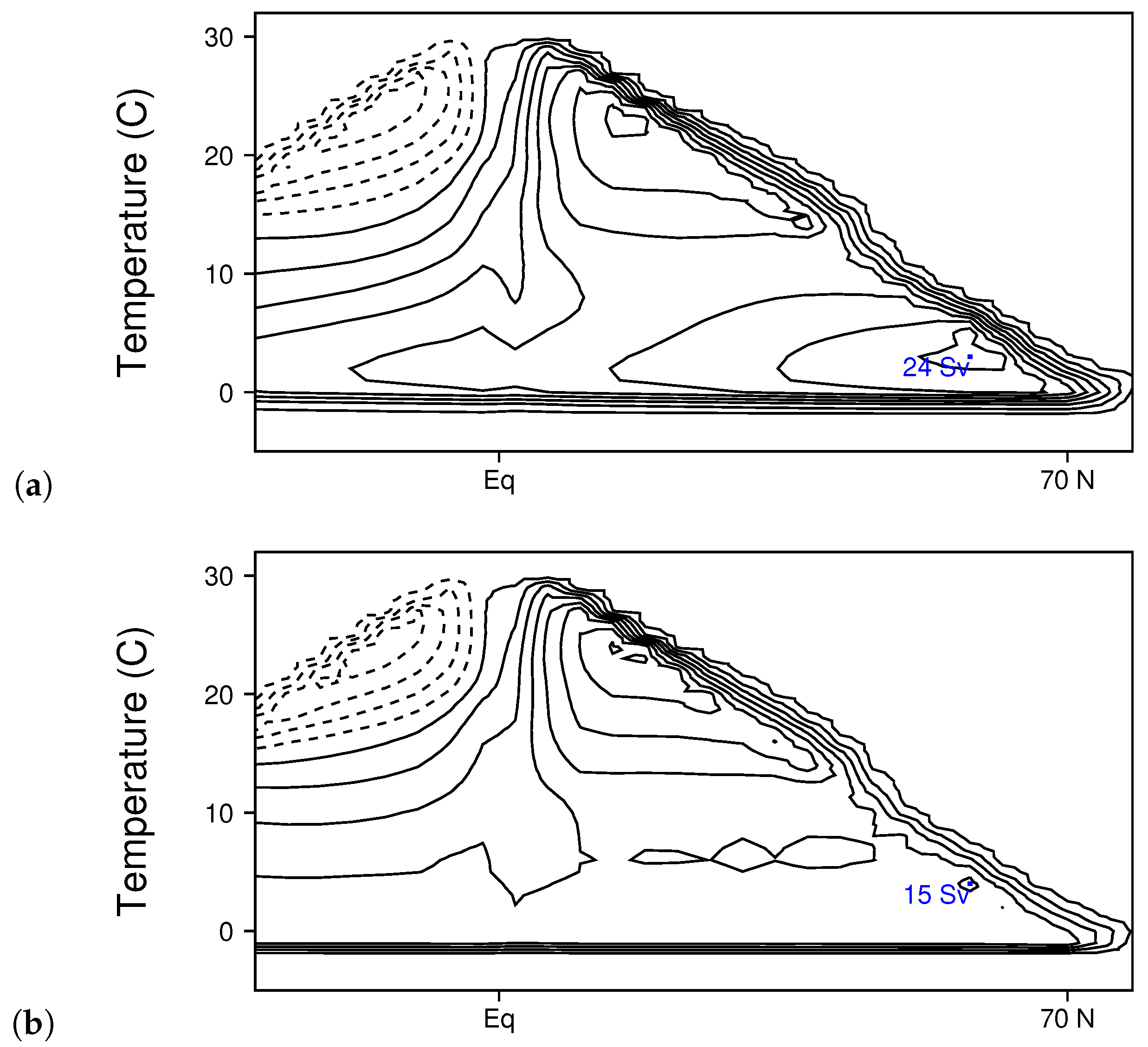
3.5. Atlantic Meridional Overturning Circulation
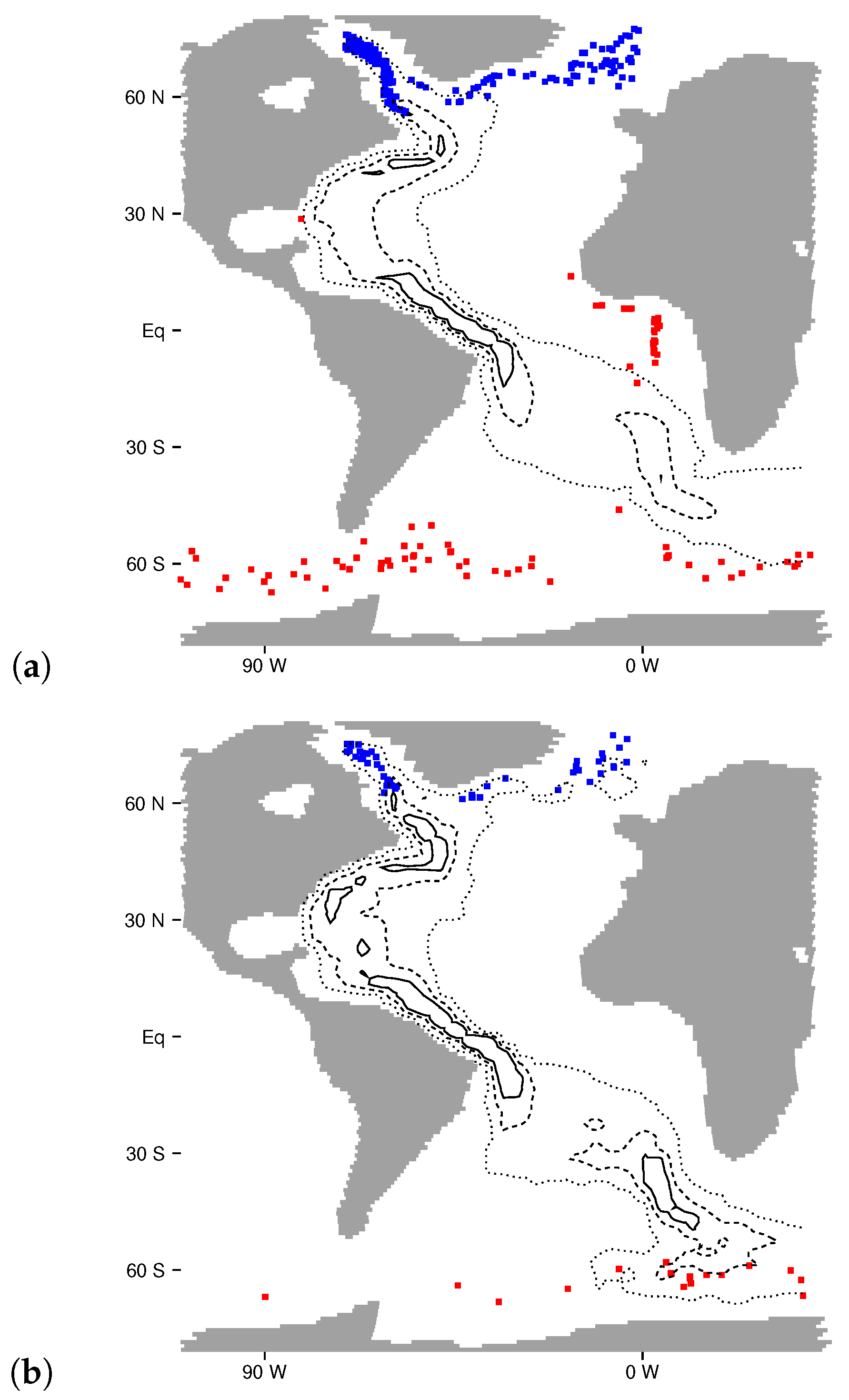
3.6. Sample Trajectory Analysis
3.7. Pacific Water Masses
4. Discussion
Funding
Conflicts of Interest
References
- Lin, J.; Brunner, D.; Gerbig, C.; Stohl, A.; Luhar, A.; Webley, P. Lagrangian Modeling of the Atmosphere; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 200. [Google Scholar]
- Bates, M.L.; Griffies, S.M.; England, M.H. A dynamic, embedded Lagrangian model for ocean climate models. Part I: Theory and implementation. Ocean Model. 2012, 59, 41–59. [Google Scholar] [CrossRef]
- Van Sebille, E.; Griffies, S.M.; Albernathey, R.; Adams, T.P.; Befloff, P.; Biastoch, A.; Blanke, B.; Chassignet, E.P.; Cheng, Y.; Cotter, C.J.; et al. Lagrangian ocean analysis: Fundamentals and practices. Ocean Model. 2018, 121, 49–75. [Google Scholar] [CrossRef]
- Haertel, P.; Boos, W.R.; Straub, K. Origins of Moist Air in Global Lagrangian Simulations of the Madden—Julian Oscillation. Atmosphere 2017, 8, 158. [Google Scholar] [CrossRef]
- Haertel, P.; Straub, K.; Fedorov, A. Lagrangian overturning and the Madden–Julian Oscillation. Q. J. R. Meteorol. Soc. 2014, 140, 1344–1361. [Google Scholar] [CrossRef]
- Haertel, P.; Straub, K.; Budsock, A. Transforming circumnavigating Kelvin waves that initiate and dissipate the Madden–Julian Oscillation. Q. J. R. Meteorol. Soc. 2015, 141, 1586–1602. [Google Scholar] [CrossRef]
- Zhang, C. Madden-julian oscillation. Rev. Geophys. 2005, 43. [Google Scholar] [CrossRef]
- Slingo, J.; Rowell, D.; Sperber, K.; Nortley, F. On the predictability of the interannual behaviour of the Madden-Julian Oscillation and its relationship with El Niño. Q. J. R. Meteorol. Soc. 1999, 125, 583–609. [Google Scholar] [CrossRef]
- Lin, J.L.; Kiladis, G.N.; Mapes, B.E.; Weickmann, K.M.; Sperber, K.R.; Lin, W.; Wheeler, M.C.; Schubert, S.D.; Del Genio, A.; Donner, L.J.; et al. Tropical intraseasonal variability in 14 IPCC AR4 climate models. Part I: Convective signals. J. Clim. 2006, 19, 2665–2690. [Google Scholar] [CrossRef]
- Hung, M.P.; Lin, J.L.; Wang, W.; Kim, D.; Shinoda, T.; Weaver, S.J. MJO and convectively coupled equatorial waves simulated by CMIP5 climate models. J. Clim. 2013, 26, 6185–6214. [Google Scholar] [CrossRef]
- Maloney, E.D.; Hartmann, D.L. Modulation of eastern North Pacific hurricanes by the Madden–Julian oscillation. J. Clim. 2000, 13, 1451–1460. [Google Scholar] [CrossRef]
- Fedorov, A.V.; Hu, S.; Lengaigne, M.; Guilyardi, E. The impact of westerly wind bursts and ocean initial state on the development, and diversity of El Niño events. Clim. Dyn. 2015, 44, 1381–1401. [Google Scholar] [CrossRef]
- Wu, M.L.C.; Schubert, S.; Huang, N.E. The development of the South Asian summer monsoon and the intraseasonal oscillation. J. Clim. 1999, 12, 2054–2075. [Google Scholar] [CrossRef]
- Neena, J.; Lee, J.Y.; Waliser, D.; Wang, B.; Jiang, X. Predictability of the Madden–Julian oscillation in the intraseasonal variability hindcast experiment (ISVHE). J. Clim. 2014, 27, 4531–4543. [Google Scholar] [CrossRef]
- Haertel, P.; Fedorov, A. The ventilated ocean. J. Phys. Oceanogr. 2012, 42, 141–164. [Google Scholar] [CrossRef]
- Griffies, S.M.; Pacanowski, R.C.; Hallberg, R.W. Spurious diapycnal mixing associated with advection in az-coordinate ocean model. Mon. Weather Rev. 2000, 128, 538–564. [Google Scholar] [CrossRef]
- Bleck, R. An oceanic general circulation model framed in hybrid isopycnic-Cartesian coordinates. Ocean Model. 2002, 4, 55–88. [Google Scholar] [CrossRef]
- Riehl, H. On the heat balance of the equatorial trough zone. Geophysica 1958, 6, 503–538. [Google Scholar]
- Zipser, E.J. The role of organized unsaturated convective downdrafts in the structure and rapid decay of an equatorial disturbance. J. Appl. Meteorol. 1969, 8, 799–814. [Google Scholar] [CrossRef]
- Haertel, P.T.; Randall, D.A. Could a pile of slippery sacks behave like an ocean? Mon. Weather Rev. 2002, 130, 2975–2988. [Google Scholar] [CrossRef]
- Daly, B.; Harlow, F.; Welch, J.; Wilson, E.; Sanmann, E. Numerical Fluid Dynamics Using the Particle-and-Force Method. Part I. the Method and Its Applications; Technical Report; Los Alamos Scientific Lag., Univ. California: Oakland, CA, USA, 1964. [Google Scholar]
- Monaghan, J.J. Smoothed particle hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Pavia, E.G.; Cushman-Roisin, B. Modeling of oceanic fronts using a particle method. J. Geophys. Res. Oceans 1988, 93, 3554–3562. [Google Scholar] [CrossRef]
- Haertel, P.T.; Randall, D.A.; Jensen, T.G. Simulating upwelling in a large lake using slippery sacks. Mon. Weather Rev. 2004, 132, 66–77. [Google Scholar] [CrossRef]
- Haertel, P.T.; Van Roekel, L.; Jensen, T.G. Constructing an idealized model of the North Atlantic Ocean using slippery sacks. Ocean Model. 2009, 27, 143–159. [Google Scholar] [CrossRef]
- Van Roekel, L.P.; Ito, T.; Haertel, P.T.; Randall, D.A. Lagrangian analysis of the meridional overturning circulation in an idealized ocean basin. J. Phys. Oceanogr. 2009, 39, 2175–2193. [Google Scholar] [CrossRef]
- Haertel, P. A Lagrangian method for simulating geophysical fluids. Lagrangian Model. Atmos. 2012, 85–98. [Google Scholar] [CrossRef]
- Gent, P.R.; Mcwilliams, J.C. Isopycnal mixing in ocean circulation models. J. Phys. Oceanogr. 1990, 20, 150–155. [Google Scholar] [CrossRef]
- Jensen, T.G. Artificial retardation of barotropic waves in layered ocean models. Mon. Weather Rev. 1996, 124, 1272–1284. [Google Scholar] [CrossRef]
- Pedlosky, J. Ocean Circulation Theory; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Cunningham, S.; Alderson, S.; King, B.; Brandon, M. Transport and variability of the Antarctic circumpolar current in drake passage. J. Geophys. Res. Oceans 2003, 108. [Google Scholar] [CrossRef]
- De Szoeke, S.P.; Yuter, S.; Mechem, D.; Fairall, C.W.; Burleyson, C.D.; Zuidema, P. Observations of stratocumulus clouds and their effect on the eastern Pacific surface heat budget along 20 S. J. Clim. 2012, 25, 8542–8567. [Google Scholar] [CrossRef]
- Döös, K.; Nycander, J.; Coward, A.C. Lagrangian decomposition of the Deacon Cell. J. Geophys. Res. Oceans 2008, 113. [Google Scholar] [CrossRef]
- Luyten, J.; Pedlosky, J.; Stommel, H. The ventilated thermocline. J. Phys. Oceanogr. 1983, 13, 292–309. [Google Scholar] [CrossRef]
- Welander, P. An advective model of the ocean thermocline. Tellus 1959, 11, 309–318. [Google Scholar] [CrossRef]
- Paparella, F.; Popolizio, M. Lagrangian numerical methods for ocean biogeochemical simulations. J. Comput. Phys. 2018, 360, 229–246. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haertel, P. A Lagrangian Ocean Model for Climate Studies. Climate 2019, 7, 41. https://doi.org/10.3390/cli7030041
Haertel P. A Lagrangian Ocean Model for Climate Studies. Climate. 2019; 7(3):41. https://doi.org/10.3390/cli7030041
Chicago/Turabian StyleHaertel, Patrick. 2019. "A Lagrangian Ocean Model for Climate Studies" Climate 7, no. 3: 41. https://doi.org/10.3390/cli7030041
APA StyleHaertel, P. (2019). A Lagrangian Ocean Model for Climate Studies. Climate, 7(3), 41. https://doi.org/10.3390/cli7030041



