The Spatial Equity of Nursing Homes in Changchun: A Multi-Trip Modes Analysis
Abstract
1. Research Background and Literature Review
2. Data Sources and Research Methods
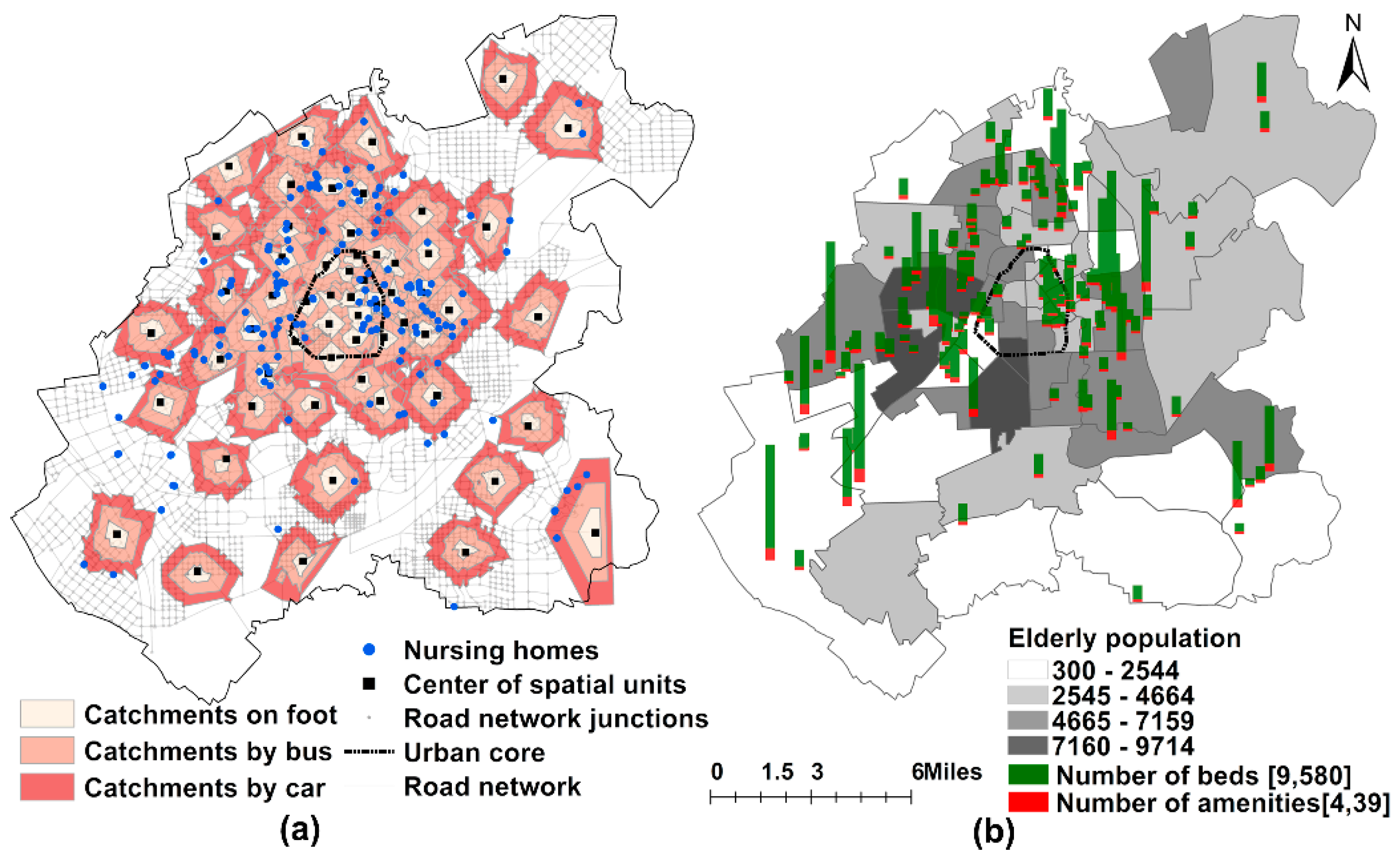
2.1. Data Sources
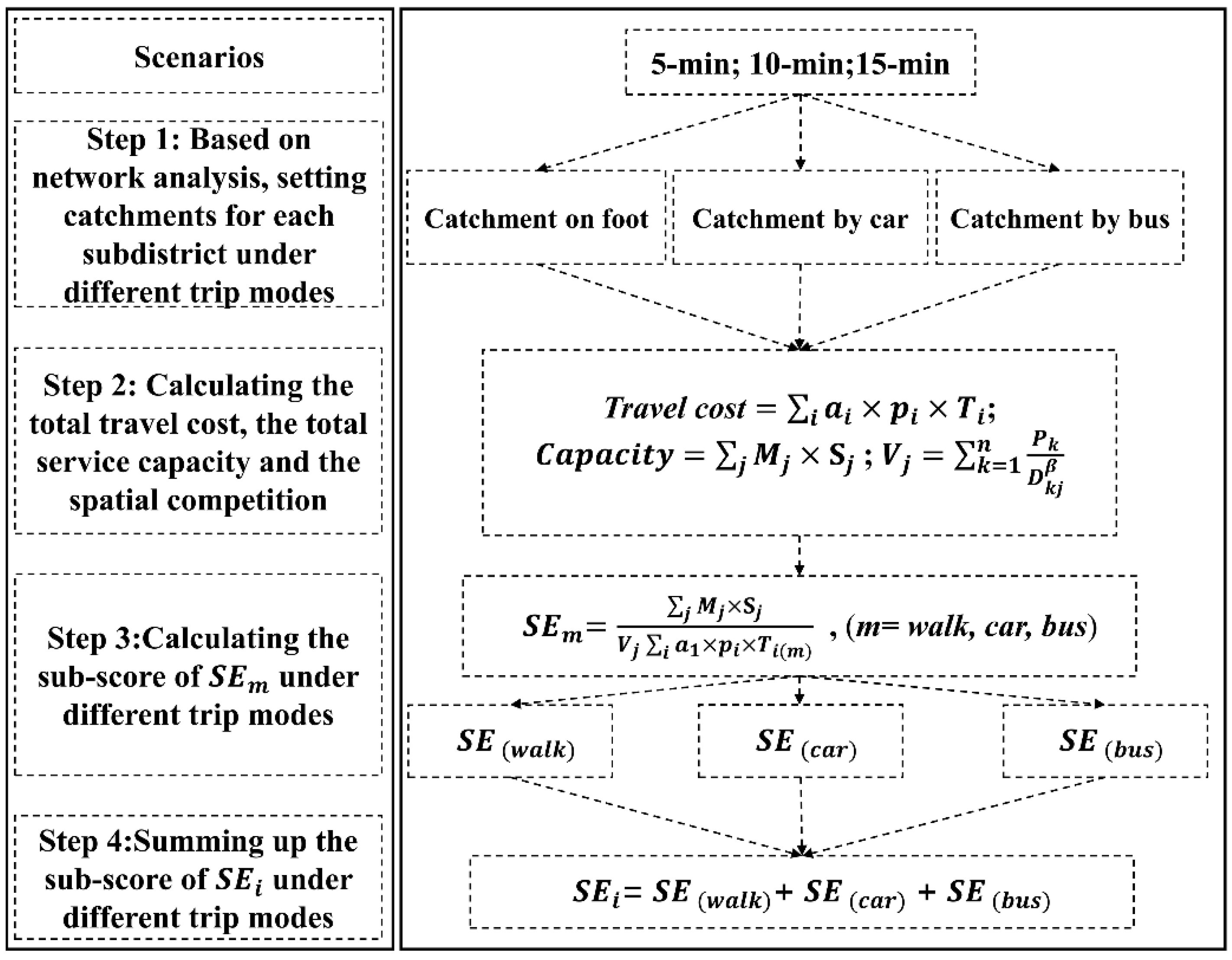
2.2. Research Methods
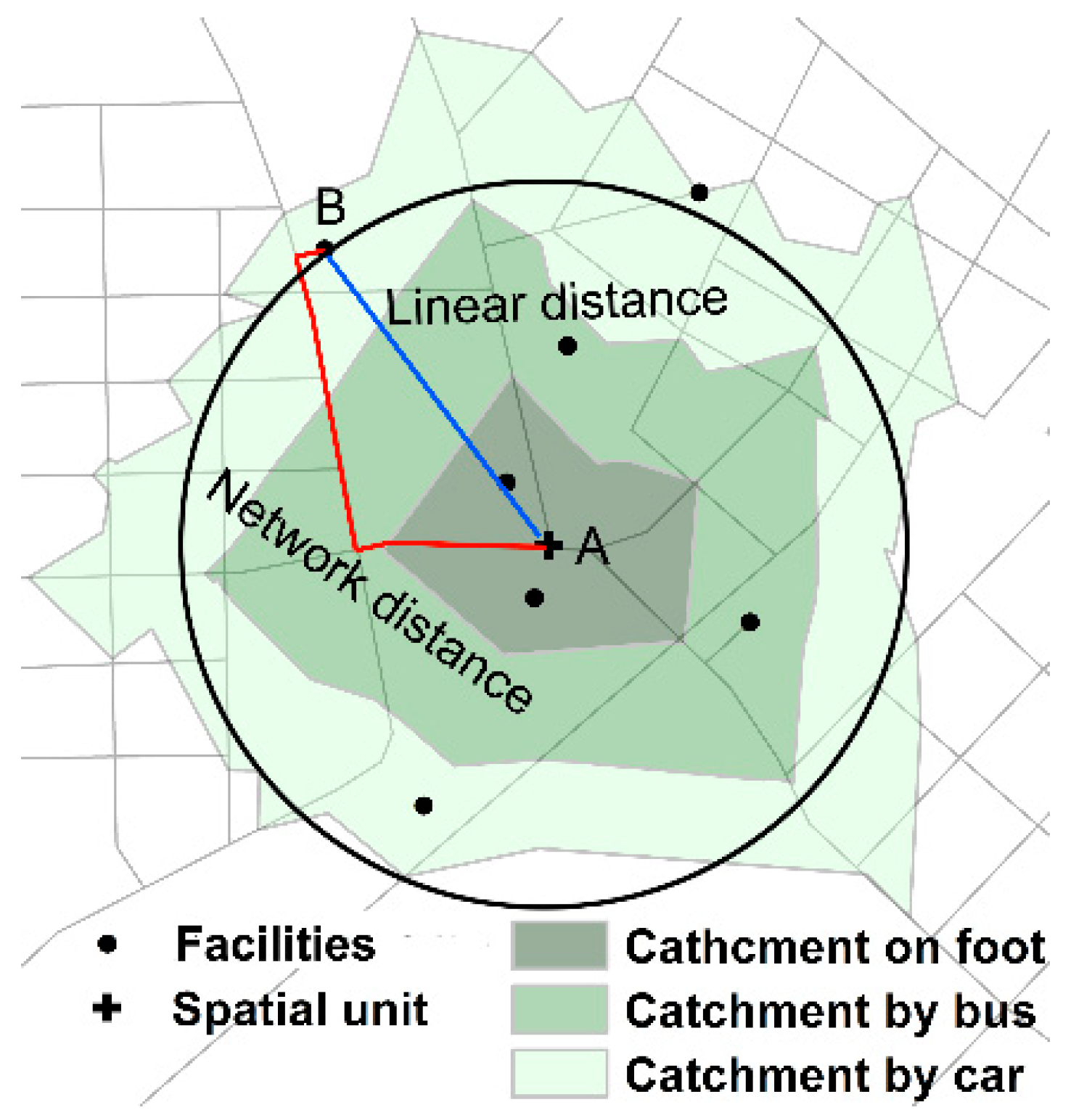
2.2.1. Improved Potential Model
2.2.2. Spatial Equity Model
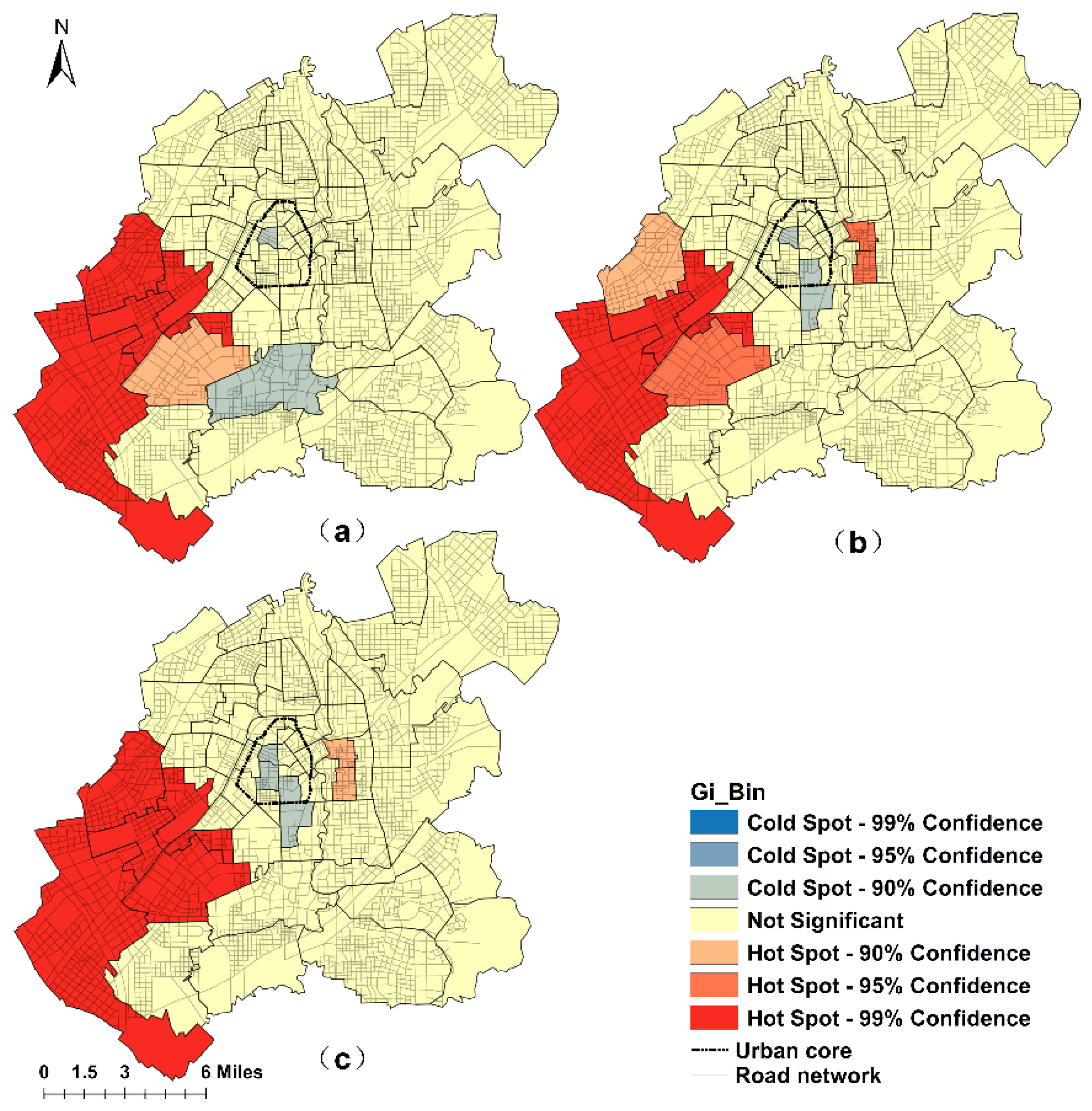
2.2.3. Hot Spot Analysis
3. Results
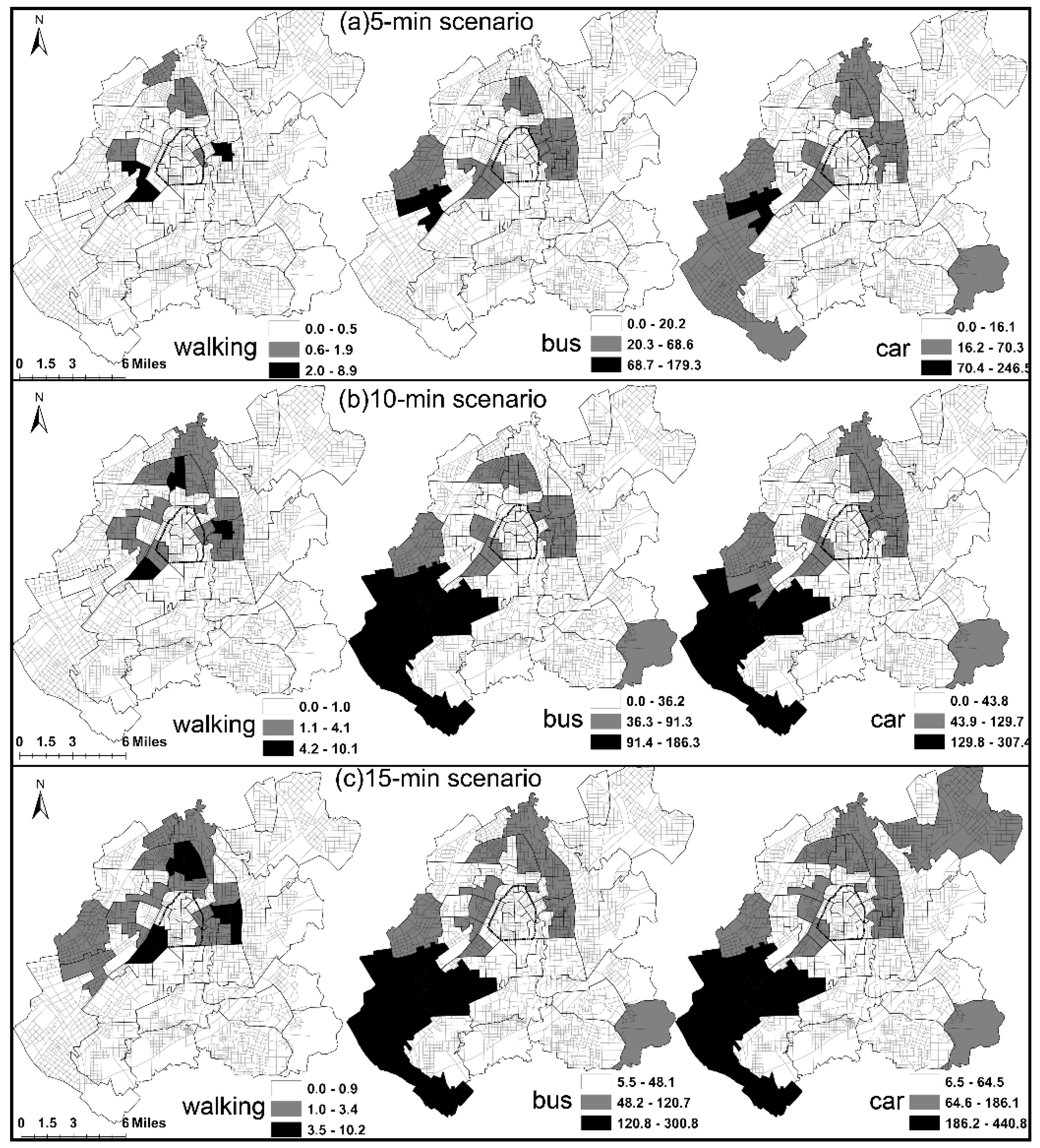
3.1. The Geography of Spatial Equity in Different Scenarios
3.2. The Influencing Factors of Spatial Equity
3.3. The Spatial Patterns of SEi in Different Scenarios
4. Conclusions and Discussions
4.1. Conclusions
4.2. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Feng, Z.; Zhan, H.J.; Feng, X.; Liu, C.; Sun, M.; Mor, V. An Industry in the Making: The Emergence of Institutional Elder Care in Urban China. J. Am. Geriatr. Soc. 2011, 59, 738–744. [Google Scholar] [CrossRef]
- Zhan, H.J.; Liu, G.; Guan, X.; Bai, H.G. Recent developments in institutional elder care in China: Changing concepts and attitudes. J. Aging Soc. Policy 2006, 18, 85–108. [Google Scholar] [CrossRef]
- Liu, Y.; Jing, Y.; Zhang, L.; Li, J.; Yin, C. Assessing Spatial Accessibility of Public and Private Residential Aged Care Facilities: A Case Study in Wuhan, Central China. ISPRS Int. J. Geo Inf. 2017, 6, 304. [Google Scholar] [CrossRef]
- Rahman, M.M.; Neema, M.N. A GIS Based Integrated Approach to Measure the Spatial Equity of Community Facilities of Bangladesh. AIMS Geosci. 2015, 1, 21–40. [Google Scholar] [CrossRef]
- Harries, K.; Smith, D.M. Geography and Social Justice. J. Econ. Issues 1994, 17, 335–344. [Google Scholar] [CrossRef]
- Chang, H.-S.; Liao, C.-H. Exploring an integrated method for measuring the relative spatial equity in public facilities in the context of urban parks. Cities 2011, 28, 361–371. [Google Scholar] [CrossRef]
- Omer, I. Evaluating accessibility using house-level data: A spatial equity perspective. Comput. Environ. Urban Syst. 2006, 30, 254–274. [Google Scholar] [CrossRef]
- Talen, E.; Anselin, L. Assessing spatial equity: An evaluation of measures of accessibility to public playgrounds. Environ. Plan. A 1998, 30, 595–613. [Google Scholar] [CrossRef]
- Tsou, K.W.; Hung, Y.T.; Chang, Y.L. An accessibility-based integrated measure of relative spatial equity in urban public facilities. Cities 2005, 22, 424–435. [Google Scholar] [CrossRef]
- Garrison, W.L. Connectivity of the interstate highway system. Pap. Reg. Sci. 2010, 6, 121–137. [Google Scholar] [CrossRef]
- Marsh, M.T.; Schilling, D.A. Equity measurement in facility location analysis: A review and framework. Eur. J. Oper. Res. 1994, 74, 1–17. [Google Scholar] [CrossRef]
- Ingram, D.R. The concept of accessibility: A search for an operational form. Reg. Stud. 1971, 5, 101–107. [Google Scholar] [CrossRef]
- Comber, A.; Brunsdon, C.; Green, E. Using a GIS-based network analysis to determine urban greenspace accessibility for different ethnic and religious groups. Landsc. Urban Plan. 2008, 86, 103–114. [Google Scholar] [CrossRef]
- Delmelle, E.C.; Casas, I. Evaluating the spatial equity of bus rapid transit-based accessibility patterns in a developing country: The case of Cali, Colombia. Transp. Policy 2012, 20, 36–46. [Google Scholar] [CrossRef]
- Dony, C.C.; Delmelle, E.M.; Delmelle, E.C. Re-conceptualizing accessibility to parks in multi-modal cities: A Variable-width Floating Catchment Area (VFCA) method. Landsc. Urban Plan. 2015, 143, 90–99. [Google Scholar] [CrossRef]
- Páez, A.; Scott, D.M.; Morency, C. Measuring accessibility: Positive and normative implementations of various accessibility indicators. J. Transp. Geogr. 2012, 25, 141–153. [Google Scholar] [CrossRef]
- Langford, M.; Higgs, G.; Fry, R. Multi-modal two-step floating catchment area analysis of primary health care accessibility. Health Place 2016, 38, 70–81. [Google Scholar] [CrossRef]
- Almohamad, H.; Knaack, A.; Habib, B. Assessing Spatial Equity and Accessibility of Public Green Spaces in Aleppo City, Syria. Forests 2018, 9, 706. [Google Scholar] [CrossRef]
- Xiao, Y.; Wang, Z.; Li, Z.; Tang, Z. An assessment of urban park access in Shanghai—Implications for the social equity in urban China. Landsc. Urban Plan. 2017, 157, 383–393. [Google Scholar] [CrossRef]
- Delbosc, A.; Currie, G. Using Lorenz curves to assess public transport equity. J. Transp. Geogr. 2011, 19, 1252–1259. [Google Scholar] [CrossRef]
- Drezner, T.; Drezner, Z.; Guyse, J. Equitable service by a facility: Minimizing the Gini coefficient. Comput. Oper. Res. 2009, 36, 3240–3246. [Google Scholar] [CrossRef]
- Vadrevu, L.; Kanjilal, B. Measuring spatial equity and access to maternal health services using enhanced two step floating catchment area method (E2SFCA)—A case study of the Indian Sundarbans. Int. J. Equity Health 2016, 15, 87. [Google Scholar] [CrossRef]
- Wang, Y.; Tu, Q.; Lai, Q.; Huang, L. Fairness or Not? Health Resources Allocation in Chongqing—Based on Theil Index. Open J. Soc. Sci. 2015, 3, 117–123. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, J.; Rosenberg, M.W. Spatial access to residential care resources in Beijing, China. Int. J. Health Geogr. 2012, 11, 32–44. [Google Scholar] [CrossRef]
- Wang, F.; Tang, Q. Planning toward Equal Accessibility to Services: A Quadratic Programming Approach. Environ. Plan. B 2013, 40, 195–212. [Google Scholar] [CrossRef]
- Luo, W.; Wang, F. Measures of Spatial Accessibility to Health Care in a GIS Environment: Synthesis and a Case Study in the Chicago Region. Environ. Plan. B 2003, 30, 865–884. [Google Scholar] [CrossRef]
- Tan, P.Y.; Samsudin, R. Effects of spatial scale on assessment of spatial equity of urban park provision. Landsc. Urban Plan. 2017, 158, 139–154. [Google Scholar] [CrossRef]
- Smoyer-Tomic, K.E.; Hewko, J.N.; Hodgson, M.J. Spatial accessibility and equity of playgrounds in Edmonton, Canada. Can. Geogr. 2004, 48, 287–302. [Google Scholar] [CrossRef]
- Yuan, G.; Qingsong, H.; Yaolin, L.; Lingyu, Z.; Haofeng, W.; Enxiang, C. Imbalance in Spatial Accessibility to Primary and Secondary Schools in China: Guidance for Education Sustainability. Sustainability 2016, 8, 1236. [Google Scholar]
- Zhang, S.; Song, X.; Wei, Y.; Deng, W. Spatial Equity of Multilevel Healthcare in the Metropolis of Chengdu, China: A New Assessment Approach. Int. J. Environ. Res. Public Health 2019, 16, 493. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Sun, F.; Che, Y. Public green spaces and human wellbeing: Mapping the spatial inequity and mismatching status of public green space in the Central City of Shanghai. Urban For. Urban Green. 2017, 27, 59–68. [Google Scholar] [CrossRef]
- Dadashpoor, H.; Rostami, F.; Alizadeh, B. Is inequality in the distribution of urban facilities inequitable? Exploring a method for identifying spatial inequity in an Iranian city. Cities 2016, 52, 159–172. [Google Scholar] [CrossRef]
- Taleai, M.; Sliuzas, R.V.; Flacke, J. An integrated framework to evaluate the equity of urban public facilities using spatial multi-criteria analysis. Cities 2014, 40, 56–69. [Google Scholar] [CrossRef]
- Gutiérrez, J.; García-Palomares, J.C. Distance-Measure Impacts on the Calculation of Transport Service Areas Using GIS. Environ. Plan. B 2008, 35, 480–503. [Google Scholar] [CrossRef]
- Apparicio, P.; Cloutier, M.-S.; Shearmur, R. The case of Montréal’s missing food deserts: Evaluation of accessibility to food supermarkets. Int. J. Health Geogr. 2007, 6, 4. [Google Scholar] [CrossRef]
- Lovett, A.; Haynes, R.; Sünnenberg, G.; Gale, S. Car travel time and accessibility by bus to general practitioner services: A study using patient registers and GIS. Soc. Sci. Med. 2002, 55, 97–111. [Google Scholar] [CrossRef]
- Fan, P.; Xu, L.; Yue, W.; Chen, J. Accessibility of public urban green space in an urban periphery: The case of Shanghai. Landsc. Urban Plan. 2016, 165, 177–192. [Google Scholar] [CrossRef]
- Liang, M.; Nekorchuk, D. Measuring spatial accessibility to healthcare for populations with multiple transportation modes. Health Place 2013, 24, 115–122. [Google Scholar]
- Sanchez, T.W. Residential location, transportation, and welfare-to-work in the United States: A case study of Milwaukee AU—Shen, Qing. Hous. Policy Debate 2005, 16, 393–431. [Google Scholar] [CrossRef]
- Xing, L.; Liu, Y.; Liu, X. Measuring spatial disparity in accessibility with a multi-mode method based on park green spaces classification in Wuhan, China. Appl. Geogr. 2018, 94, 251–261. [Google Scholar] [CrossRef]
- Hansen, W.G. How Accessibility Shapes Land Use. J. Am. Inst. Plan. 1959, 25, 73–76. [Google Scholar] [CrossRef]
- Joseph, A.E.; Bantock, P.R. Measuring potential physical accessibility to general practitioners in rural areas: A method and case study. Soc. Sci. Med. 1982, 16, 85–90. [Google Scholar] [CrossRef]
- Bureau, C.P. Changchun Comprehensive Transportation System Planning. Available online: http://www.ccghj.gov.cn/info/1069/10282.htm (accessed on 10 May 2018).
- Mcgrail, M.R.; Humphreys, J.S. Measuring spatial accessibility to primary health care services: Utilising dynamic catchment sizes. Appl. Geogr. 2014, 54, 182–188. [Google Scholar] [CrossRef]
- Luo, W.; Qi, Y. An enhanced two-step floating catchment area (E2SFCA) method for measuring spatial accessibility to primary care physicians. Health Place 2009, 15, 1100–1107. [Google Scholar] [CrossRef] [PubMed]
- Bissonnette, L.; Wilson, K.; Bell, S.; Shah, T.I. Neighbourhoods and potential access to health care: The role of spatial and aspatial factors. Health Place 2012, 18, 841–853. [Google Scholar] [CrossRef]
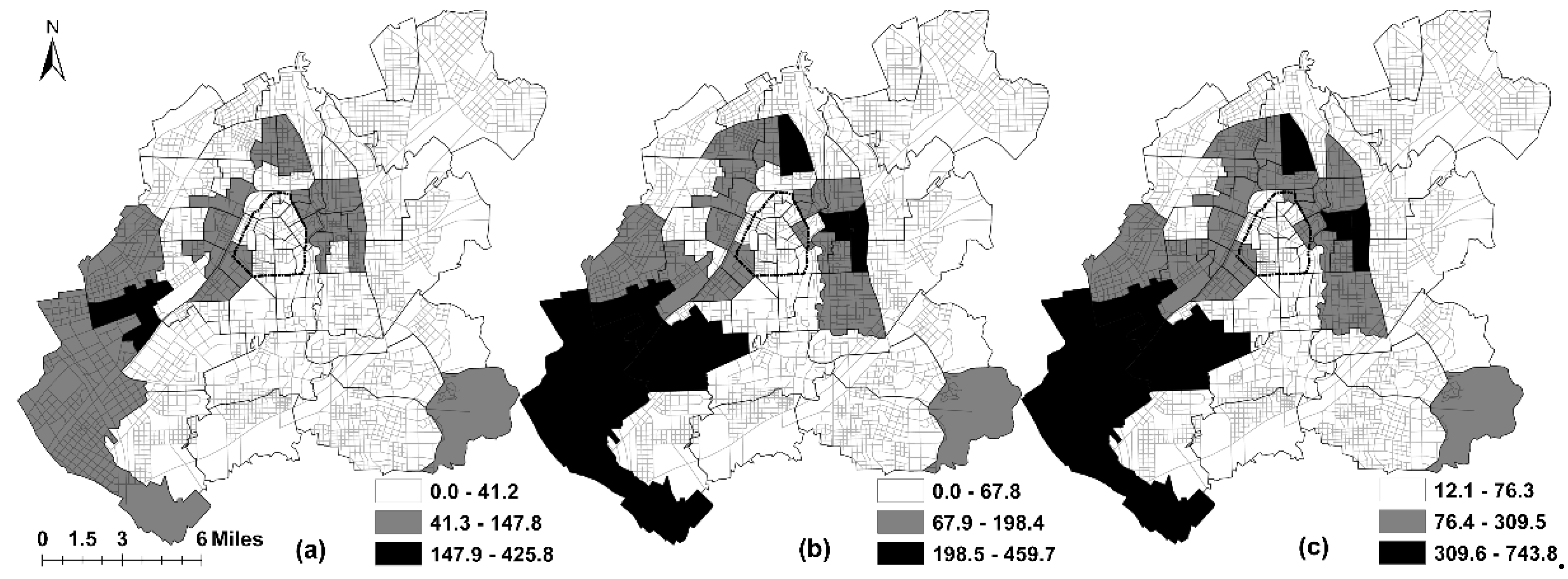
| Scenarios | SEi | |||
|---|---|---|---|---|
| Maximum | Minimum | Mean | SD | |
| 5-min | 425.8 | 0 | 40.2 | 61.7 |
| 10-min | 459.7 | 0 | 81.9 | 96.2 |
| 15-min | 743.8 | 11.9 | 130.9 | 145.7 |
| Scenarios | Variables | Coefficients | Std. Error | t | Sig. |
|---|---|---|---|---|---|
| Constant | 60.109 | 15.249 | 3.942 | 0.000 | |
| X1 | 0.045 | 0.009 | 4.959 | 0.000 | |
| 5-min | X2 | −0.010 | 0.003 | −3.270 | 0.002 |
| (R2 = 0.420) | X3 | 2.735 | 0.855 | 3.198 | 0.002 |
| Constant | 124.053 | 20.104 | 6.171 | 0.000 | |
| X1 | 0.054 | 0.009 | 5.665 | 0.000 | |
| 10-min | X2 | −0.018 | 0.004 | −4.907 | 0.000 |
| (R2 = 0.544) | X3 | 2.743 | 0.541 | 5.074 | 0.000 |
| Constant | 208.239 | 28.630 | 7.279 | 0.000 | |
| X1 | 0.073 | 0.010 | 7.092 | 0.000 | |
| 15-min | X2 | −0.034 | 0.005 | −7.057 | 0.000 |
| (R2 = 0.675) | X3 | 2.924 | 0.634 | 4.613 | 0.000 |
| X5 | −15036.260 | 5008.272 | −3.002 | 0.004 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, S.; Song, W.; Li, C.; Lu, J. The Spatial Equity of Nursing Homes in Changchun: A Multi-Trip Modes Analysis. ISPRS Int. J. Geo-Inf. 2019, 8, 223. https://doi.org/10.3390/ijgi8050223
Hu S, Song W, Li C, Lu J. The Spatial Equity of Nursing Homes in Changchun: A Multi-Trip Modes Analysis. ISPRS International Journal of Geo-Information. 2019; 8(5):223. https://doi.org/10.3390/ijgi8050223
Chicago/Turabian StyleHu, Shuju, Wei Song, Chenggu Li, and Jia Lu. 2019. "The Spatial Equity of Nursing Homes in Changchun: A Multi-Trip Modes Analysis" ISPRS International Journal of Geo-Information 8, no. 5: 223. https://doi.org/10.3390/ijgi8050223
APA StyleHu, S., Song, W., Li, C., & Lu, J. (2019). The Spatial Equity of Nursing Homes in Changchun: A Multi-Trip Modes Analysis. ISPRS International Journal of Geo-Information, 8(5), 223. https://doi.org/10.3390/ijgi8050223






