1. Introduction
Urban design is an activity to consciously transform a city, or a part of it, in order to adapt to changing boundary conditions. For instance, to house the increase in population, waste land may be transformed into a new residential quarter; or a deprived urban quarter may be revalued by creating new buildings or by reconfiguring the public space. However, urban design is a challenging task due to the complexity that is inherent to cities: they consist of many different physical elements (e.g., streets, buildings, greenery). These elements can be configured in multiple ways and must meet many criteria in order to be truly sustainable. Furthermore, the relationship between these criteria and the parameters for defining the physical elements is not linear (e.g., increasing the size of a public square does not linearly increase its attractivity). In addition, since some of the criteria are contradictory, there is no straightforward procedure to create “the” best-performing design [
1,
2]. For instance, one can hardly improve an existing street by maximizing the available space for pedestrians, cyclists, and cars at the same time. Instead, the design process can be described more as a search for trade-offs, offering the best balance of performance for all objectives [
3].
In order to avoid mistakes in the planning process, a sound understanding between the design parameters and the different performance criteria is crucial. Design decisions based on research-grounded models and methods is called evidence-based design [
4] and is generally preferred over personal ad hoc intuitions. However, not all design goals can be operationalized to the extent that a rigorous quantitative evaluation is possible which is especially the case for most criteria related to human behavior and perception. This makes urban design prone to failure, as the effects of planning decisions on social behavior are often either neglected or evaluated by the subjective experience of a few individuals. This results in what Blake (1977) [
5] described as the fiasco of modernist planning, namely to concentrate on aspects that can be quantified and neglecting the ones that cannot. Examples for the negative effects of neglecting or not properly anticipating the social and psychological aspects in urban design can for instance be found in Lawson (2001) [
6], Gehl (1987) [
7] or Jacobs (1961) [
8]. In this context, an unsolved problem for sustainable urban design is to interpret urban structures in terms of their psychological and social implications and combine this with more easily quantifiable aspects, such as energy performance or costs. This would allow for a systematic evaluation of trade-offs between urban design proposals across their multiple dimensions.
1.1. Research Questions and Scope
The main aim of this paper is to introduce a methodological framework for a quantitative evaluation of long-term planning decisions in terms of the social, psychological, and energy potentials. We chose the three aspects (social, psychological, and energy) on account of their previously mentioned relevance to urban planning. However, in the overall framework, these three aspects can be seen as examples for demonstrating the basic principle of investigating the impact of urban planning on the many different criteria that cities have to meet.
Among the multitude of urban planning related factors that affect the three aspects, we specifically focus our research on the effect of the geometry, also referred to as urban form. Urban form typically comprises the shape of the three layers: streets, plots and buildings [
9]. While non-morphological aspects (such as greenery, building materials, or land use allocation) have substantial effects on the social, psychological, and energy demand, we argue that, in particular, the understanding of the effect of the morphological aspects is crucial. First, urban form is hard to change once built—as such, urban form has long-lasting effects [
10]. Second, it is most helpful to inform the early design stages, where most of the decisions are related to the geometry of cities respective to the rules for how it is built.
In the scope of this paper, we address the questions (1) how to operationalize and test the social, psychological, and energy potential of urban form; and (2) how to identify distinct categories of urban form and evaluate the trade-offs between social, psychological, and energy potential for each category of urban form. In our methodological framework, urban form comprises the buildings represented as envelopes in level of detail 1 (i.e., simple flat roof block models without any details regarding the shape of the roof, or windows), as well as the configuration of the street network with each street being represented as two-dimensional lines connected to the neighboring streets at both ends.
The following links between urban form and the three potentials are assumed. The energy demand (for heating and cooling) strongly related to the shape and arrangement of building volumes. The social potential (which is interpreted as the accessibility of people) is strongly related to the street network since this creates the precondition to access people. The psychological potential (referred to as the physiological response to an environment as well as its subjective evaluation) is related to both the building volumes (the urban objects that are mainly restricting views) and the street network, which controls movement of cars and pedestrians and therefore influences noise and people density (liveliness). The framework chosen for this study focuses on the evaluation of aggregated psychological, social, and energy potentials of urban form. This considers the effects of urban form on the population level, as opposed to considering them on the level of the individual.
As a result of the above-mentioned scope, we define the outcome of the presented evaluation framework to be representative of capturing psychological, social, and energy potentials; thereby being fully aware of the fact that other factors (i.e., non-geometrical aspects) that can significantly influence the outcome are not considered in this study.
Nevertheless, we argue that this potential-oriented approach can meaningfully inform the planning process, especially in the early planning stages, to deal with many ‘unknown’ variables. We argue that models that would deliver a very precise result would also require very detailed information to run, which is however typically not available in the design stage. As result, the detailed models would require making intuitive assumptions about these details, which would again make these models prone to errors.
1.2. Case Studies
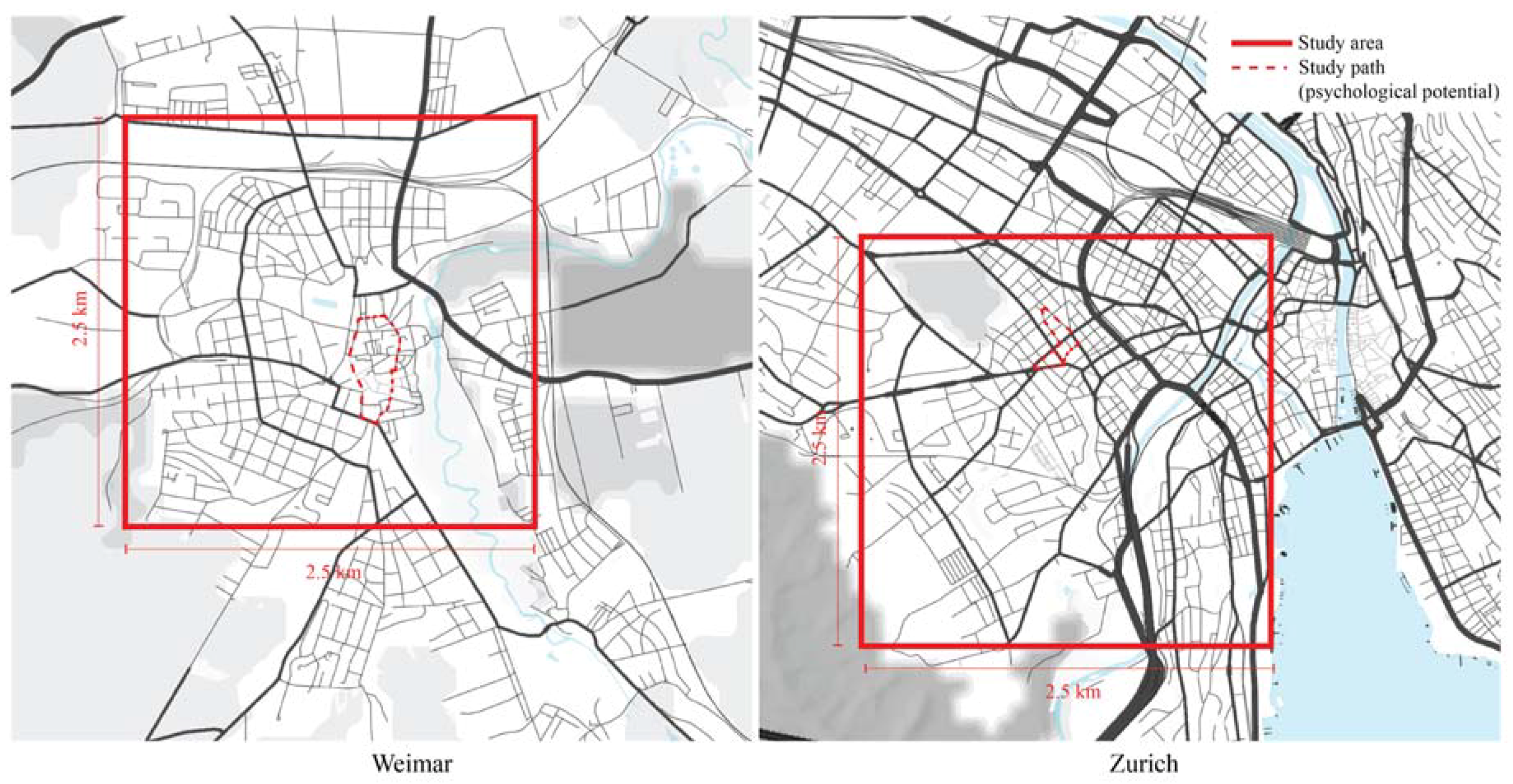
The methodological framework developed for this work was tested on two exemplary case studies: the cities of Weimar and Zurich (see
Figure 1). The aim behind studying multiple areas at once is to increase the generalizability of the findings and make it possible to apply these to new cases. However, when comparing (a) different measures and (b) the performance of urban systems varying in their size, type, or number of elements, we need to address the issue of normalization as discussed in following sections.
From the morphological perspective, both cities have common features from the development around a medieval historic center and exhibit large extensions from the 19th and 20th century. Topographically, both cities lie at a river. However, Zurich is quite hilly, while Weimar is for the most part rather flat. Furthermore, both cities are of different size (Weimar has around 60,000 inhabitants, while Zurich has about 400,000). For both cities, we chose a case study area of 2.5 × 2.5 km (6.25 km
2). The size and location of the case study areas was selected to ensure a large variation of building typologies such as detached, rowed, and courtyard buildings and their location in the urban structure (e.g., city center, suburbs). The size of the study was chosen as trade-off between the benefits of larges sites comprising higher variance of urban form and computational cost required to process and analyze the large urban datasets. The overall size of the study area was determined by the number of data points given by an underlying analysis grid used for the purpose of analyzing the trade-offs between different potentials at the same location. Since the maximum size of one grid cell has to be small enough to capture the variation in the highly location-sensitive psychological and energy potential (see respective sections for details), we end up at fine-grained, empirically calibrated analysis grid of 15 by 15 m [
11] accounting for over 55,000 cells per study area.
The data describing the Zürich building stock (i.e., building type and year of construction) was acquired by the Statistical office of Zürich and combined with the urban form model (i.e., street network and buildings in LOD1) acquired by the Planning office Zürich. In the case of Weimar, all data on urban form and land use was collected from the geoinformation platform of the German state Thuringia—geoportal-th.de. All publicly available data sources used in this research can be accessed as described in the section
Supplementary Materials.
1.3. Structure of the Article
The article is structured as follows: First, we introduce the methodological frameworks for evaluating the psychological, the social, and the energy potential of urban form. In each section, we briefly review the state of the art in the field, explain the methods, and display the key results of each section, which is a map of the potentials for each of the two cities. Second, we explore the trade-offs between the three different potentials. Therefore, we present an approach for identifying distinct urban form clusters for which we analyze their social, psychological, and energy potential. Finally, we discuss the different trade-offs between the social, psychological, and energy potential of these urban form clusters and give recommendations for future work.
2. Social Potential of Urban Form
The social consequences of planning have gained growing attention after “much of urban planning and design in the 20th century failed to deliver on its claims” [
12]. There is wide consensus that these failures are predominantly social by nature, which is often being demonstrated through segregation and ghetto formation of marginalized social groups [
13]; with consequences such at high crime rates, unemployment rates and school drop-out rates. Significant effort has been spent on linking these negative consequences to various aspects of urban form with the intention to fix the present and prevent the future failures of this kind. For instance, the studies on Crime [
14], unemployment [
15] or economic activity [
16] have repeatedly shown that allocation, typology, and configuration of urban form can be traced back to various kinds of negative social behavior. However, despite the amount of empirical evidence, it remains difficult to generalize and draw conclusions on top of them. This can be attributed to the broad use of the term “social” with almost any human activity being treated as social consequence of urban form. As an illustration, one can only speculate how the findings about negative social effect of high densities on crime rates [
17] relate to the positive social effect of high densities on innovation [
18].
We argue that what makes all the above-mentioned human types of behavior social is that they are all a result of human interactions and the mutual relationships between individuals [
19]. Hence, when measuring the social impact of urban form, we suggest focusing on the core of any social phenomena, namely the social interactions. We argue that our better understanding of the cause, which are in our case the social relationships, is the key for our understanding of its consequences (e.g., crime, innovation, unemployment).
Therefore, the aim of this section is to measure the long-term impact of urban form on the potential for social interaction. For this purpose, we adopt the Aggregated Social Accessibility (ASA) method [
20] which has been proven as particularly well suited for capturing the social potential of one specific morphological element, namely the street network configuration. Since the configurational properties of the street network remain stable over time [
21] and are hard to change, once built, the ASA is specifically useful to capture the long lasting impact of the early planning decisions. For the ASA analysis, urban form is represented as two-dimensional street network consisting only of lines and their intersections.
The social potential, as captured by the ASA expresses how many people can be accessed in public space from a given location relative to all other locations. In other words, it gives us a quantitative measure of the potential social interactions for any given location. The current limitation of the method is that it does not express the quality of the interaction. In other words, we know that there are many people to interact with, but we do not know if the environment encourages or hinders any of these potential social interactions. Despite this limitation, we argue that this quantitative model of social interaction potential is still useful for planning purposes as the additional evaluation of the interaction quality would require detailed socio-demographic data (e.g., who interacts, for what purpose) which is not available during the planning stage.
Moreover, the ASA as a measure of the fundamental potential for social interaction has been empirically linked to what we previously described as “broader social consequences”. Our previous study [
20] suggests that the access to other people is the single strongest predictor of the access to amenities encouraging walking behavior so-called walking attractors (e.g., coffee, restaurants, retail) and can potentially improve the health and quality of life at a given location. The ASA alone could explain 84% of the variance in the access to walking attractors in Weimar, which underlines the crucial role of street network configuration on humans and their activities.
2.1. Methods for Measuring Social Potential of Urban Form
In general, the ASA analysis consists of two steps. First, the pedestrian movement flows are estimated based on the configuration of the street network and then the accessibility to these movement flows is calculated for any given location. As a result, different locations or design options can be compared based on their access to movement flows giving relative potential for social interaction (here termed as social potential).
2.1.1. Urban Form and Pedestrian Movement Flows
To estimate the effect of street network configuration on pedestrian movement flows, we adopt the well-established graph-theoretical measure of flow,
betweenness centrality. This was first introduced by Freeman (1977) [
22] as measure of information flow in social networks and was later adapted for its use in spatial networks. The main contribution for bringing the graph-configurational methods to the field of architecture and urban planning needs to be attributed to the
Space Syntax researchers with Hillier & Hanson (1984) [
23] laying the theoretical foundations of this field in their seminal work
Social logic of space. In following years, the
Space Syntax scholars developed an analytical framework which was able to explain about 60% to 80% of the variance in movement flows purely based on the street network configuration. The
Space Syntax approach to represent the urban system, is built on the idea of an inverse graph, where streets (or any linear elements such as visual axes) are graph vertices and their intersections are the edges capturing the distance between the vertices. The major advantage of this rather unique representation is the fact that the relationship between two locations in the graph can be measured in addition to the metric distance, also in terms of cognitive load required to navigate. This is expressed as angular deviation and is used to approximate human route choice behavior that aims to minimize angular turns along a path.
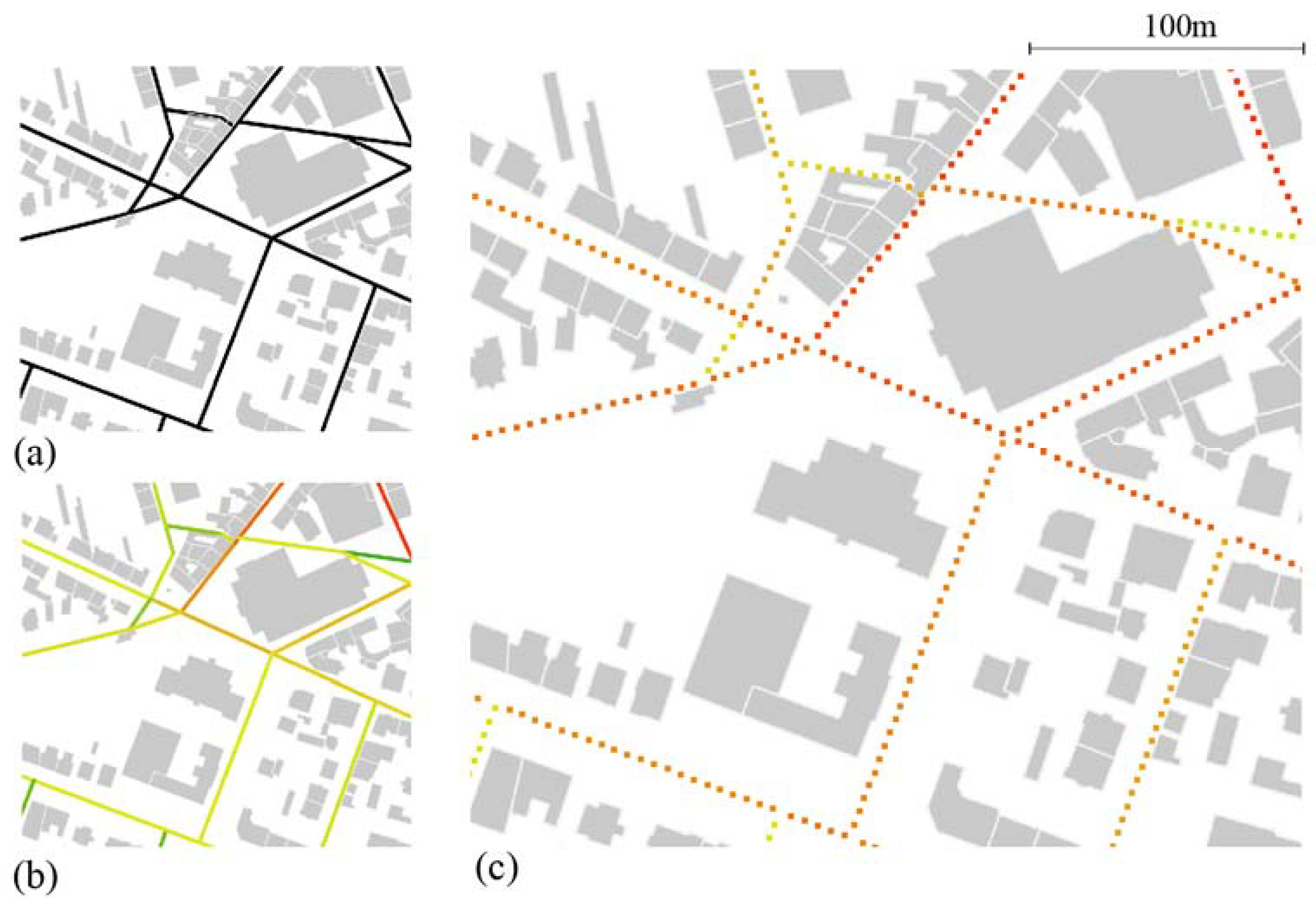
One specific
Space Syntax model utilizing the angular distance was introduced by Turner (2001) [
24]) under the name
angular segment map. It has been repeatedly proven as a strong predictor of human movement flows [
25,
26,
27]. As a result, the ASA method adopted the angular betweenness centrality as a calculation method and the segment map (see
Figure 2) as a spatial representation used to estimate the pedestrian flows. To calculate the betweenness centrality of a given street network, the analysis radius defining the maximum metric distance between pairs of street segments has to be defined. This is of high relevance as the analysis radius reflects the maximum distance assumed to be travelled based on the choice of the travel mode e.g., pedestrian, cyclist, car. For the purpose of measuring the social potential, we are mainly interested in pedestrian movement as this is most accessible in terms of social interaction.
The optimal pedestrian analysis radius used for the two case studies presented in this paper was empirically calibrated. Bielik et al. (2017) [
28] systematically investigated the relationship between analysis radius (from 100 to 2000 m) and the ability of angular betweenness centrality predict the pedestrian movement in the city of Weimar. The highest R
2 = 0.491 was measured at radius 600 m [
28]. Correspondingly, the analysis area is extended by a buffer of 600 m to avoid the negative consequences of the “
edge effect” [
29]. One specific
Space Syntax model utilizing the angular distance introduced under the name
angular segment map [
24] has been repeatedly proven as strong predictor of human movement flows. As a result, the ASA method adopted the angular betweenness centrality as a calculation method and segment map (see
Figure 2) as a spatial representation used to estimate the pedestrian flows. To calculate the betweenness centrality of given street network, the analysis radius defining the maximum metric distance between pairs of street segments has to be defined. This is of high relevance as the analysis radius reflects the maximum distance assumed to be travelled based on the selected travel mode, e.g., pedestrian, cyclist, or car. For the purpose of measuring the social potential, we are mainly interested in pedestrian movement as this is most accessible in terms of social interaction.
Finally, it must be noted that the adopted
angular segment map model for estimating pedestrian movement flows is based on few parameters. On the one hand it allows model simplicity, i.e., only information on the street network is needed to accurately predict complex human behavior [
30], but on the other hand, can be a source of bias [
31]. Therefore, these assumptions—namely that building densities follow the street network centrality and that every segment is equally important as origin and destination of movement must be cautiously evaluated prior to any analysis. In general, they tend to hold true for historically grown cities, which was also confirmed by our previous studies [
28]. Therefore, we adopt the simple
angular segment map model based purely on street segments as this has shown a high predictive power for our case studies and is more suitable for our overall goal to inform early planning stages.
2.1.2. Urban Form and the Access to Pedestrian Movement Flows
After the pedestrian movement flows in the street network are estimated, the accessibility to the estimated pedestrian flows are calculated. For this calculation we utilize the concept of accessibility as a “measure of the cost of getting from one place to another, traded off against the benefits received once the place is reached” [
32]. This concept has been operationalized by Hanse (1959) [
33] as the
Gravity function proportional to the attractiveness of all points of interest
j surrounding location
i and inversely proportional to travel cost between
i and
j (Equation (1)).
The travel costs in the
Gravity function are defined as negative exponential with the distance-decay parameter
β (the ASA method adopts this function with the distance-decay parameter
β set to 0.00217 as empirically calibrated by [
34]. A distance decay parameter β of 0.00217 in meters corresponds to 0.1813 in temporal units) controlling the attitude towards travel distance. To apply the gravity function, the location for which the accessibility is calculated, as well as the points of interest, must be defined. In our case, the starting locations can be any location connected to the street network (e.g., buildings, streets) and the points of interest are the pedestrians moving through the street network. Since the estimated distribution of pedestrians by the
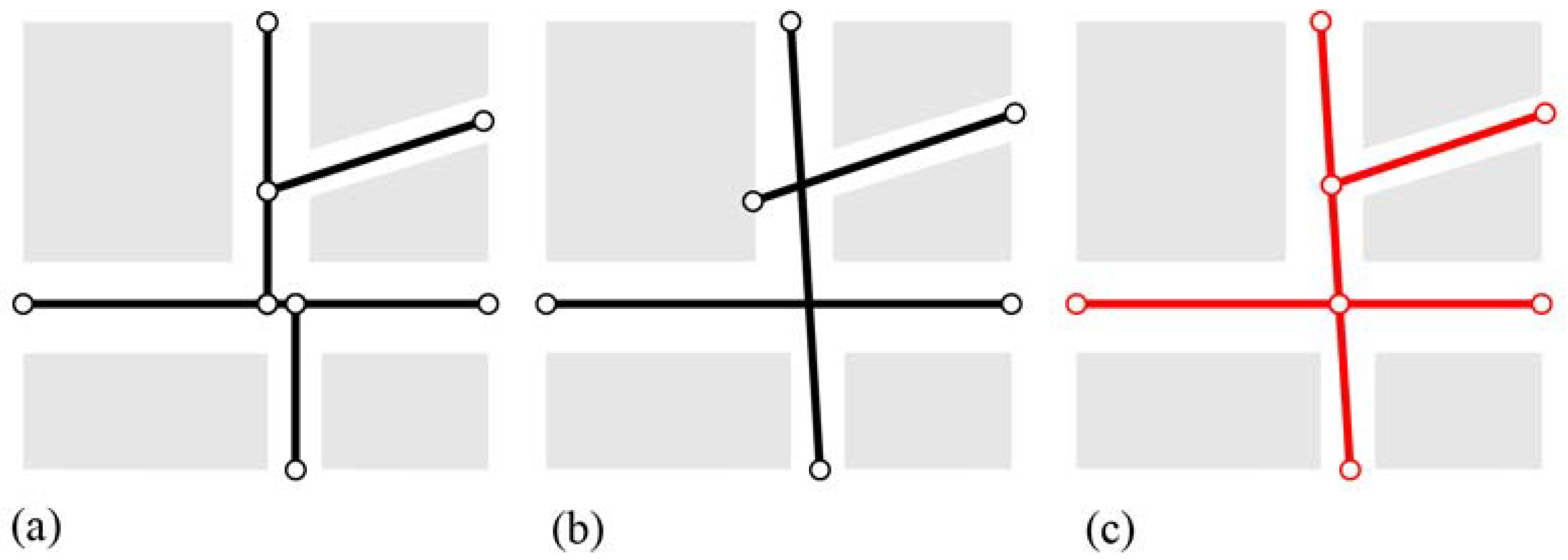
betweenness centrality is depicting continuous movement flows for each segment, these have to be discretized first (see
Figure 3). This approach was chosen to reflect that (a) the amount of people on a given street depends on the movement flow potential and the length of the street and (b) that the distance to the various sections of the same street differs and so does the accessibility of people or amenities.
The discretization parameter defining the distance between the points of interest was set to 5 m, as this setting represents a good approximation of a continual distribution of pedestrians with acceptable computation time (below 30) [
20]. The travel costs in the
Gravity function are defined as negative exponential with the distance-decay parameter
β controlling the attitude towards travel distance. To apply the gravity function, the location for which the accessibility is calculated, as well as the points of interest, must be defined. In our case, the starting locations can be any location connected to the street network (e.g., buildings, streets) and the points of interest are the pedestrians moving through the street network. Therefore, we evenly discretize all street segments into point arrays (see
Figure 3). The discretization parameter defining the distance between the points of interest was set to 5 m as this setting represents a good approximation of a continual distribution with acceptable computation time (below 30 min).
Finally, it has to be noted that the ASA method allows one not only to compare variations in social potential between different locations of one urban system, but also across several systems. Such comparison is notoriously problematic as the overall size of the urban system has a direct effect on the centrality at individual locations [
23,
35]. We argue that this problem doesn’t apply to our case as the ASA method works strictly on pedestrian radius of 600 m and is therefore not affected by the overall size of the system, which in our case covers more than 2.5 by 2.5 km.
2.2. Results of Measuring Social Potential of Urban Form
In the following section, we present the social potential scores calculated for both case studies. We mapped the ASA scores on the common analysis grid that is later used to visualize and compare the psychological, social, and energy potential of urban form. Therefore, we interpolated the ASA of the street segment points onto the grid cells (for details see the Trade-offs section).
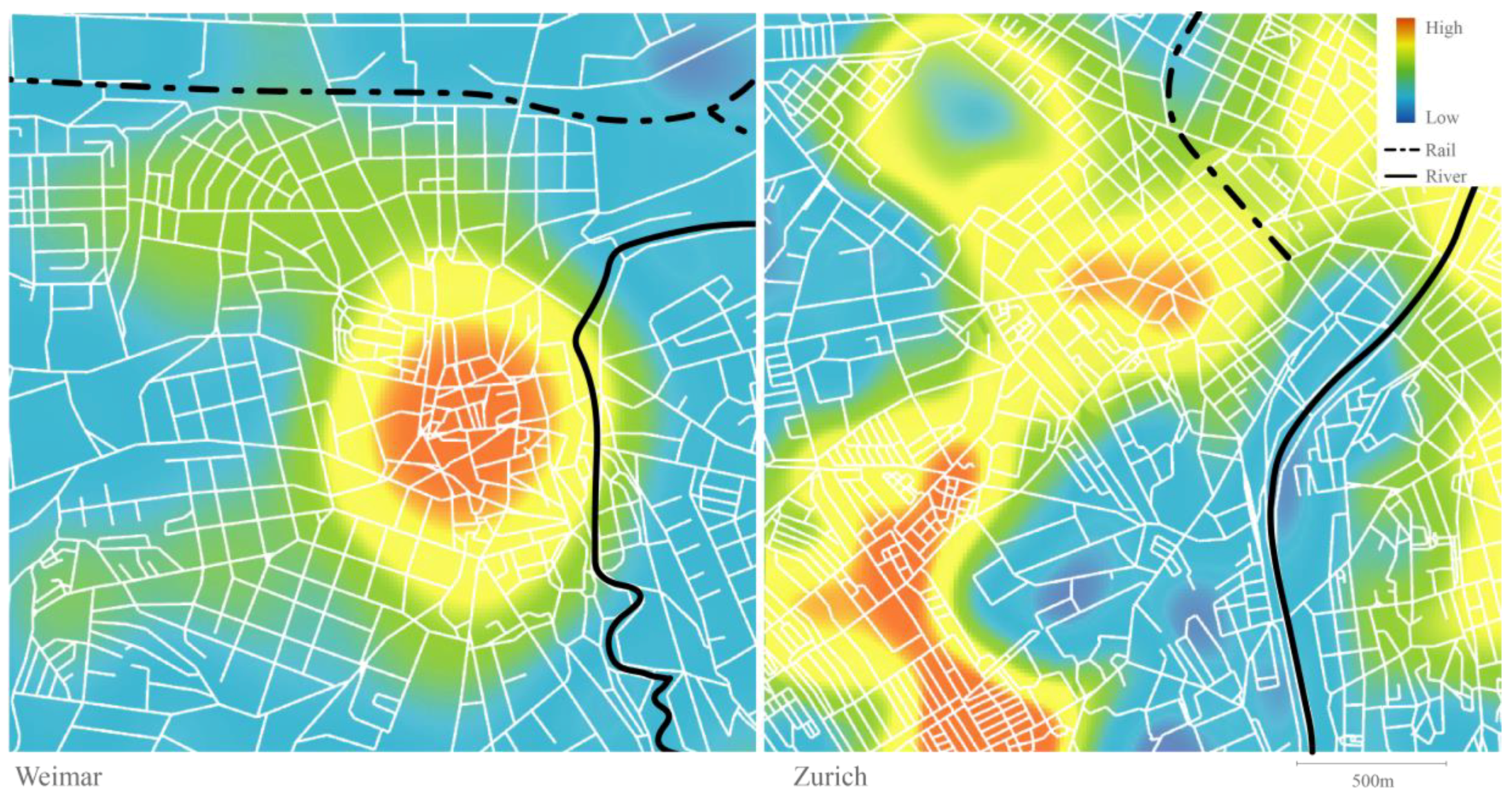
The resulting maps reveal the spatial patterns of social potential as defined by the street network configuration (see
Figure 4). In both case studies, we can observe a strong influence of natural and infrastructural barriers on the distribution of social potential, i.e., rivers and railroads are dividing both areas in the two cities not only physically, but also socially. Similarly, both cities share a rather irregular geometrical form of the social accessibility distribution. Beside these common patterns, both cities differ strongly in the number of centers accumulating social potential. Here, Weimar can be described as mono-centric with the highest values of social potential in the historical core, which are then irregularly dispersed towards the outskirts. In contrast, Zurich reveals a more polycentric pattern with the main centers being interconnected with continuous stripes of neighborhoods with high social potential.
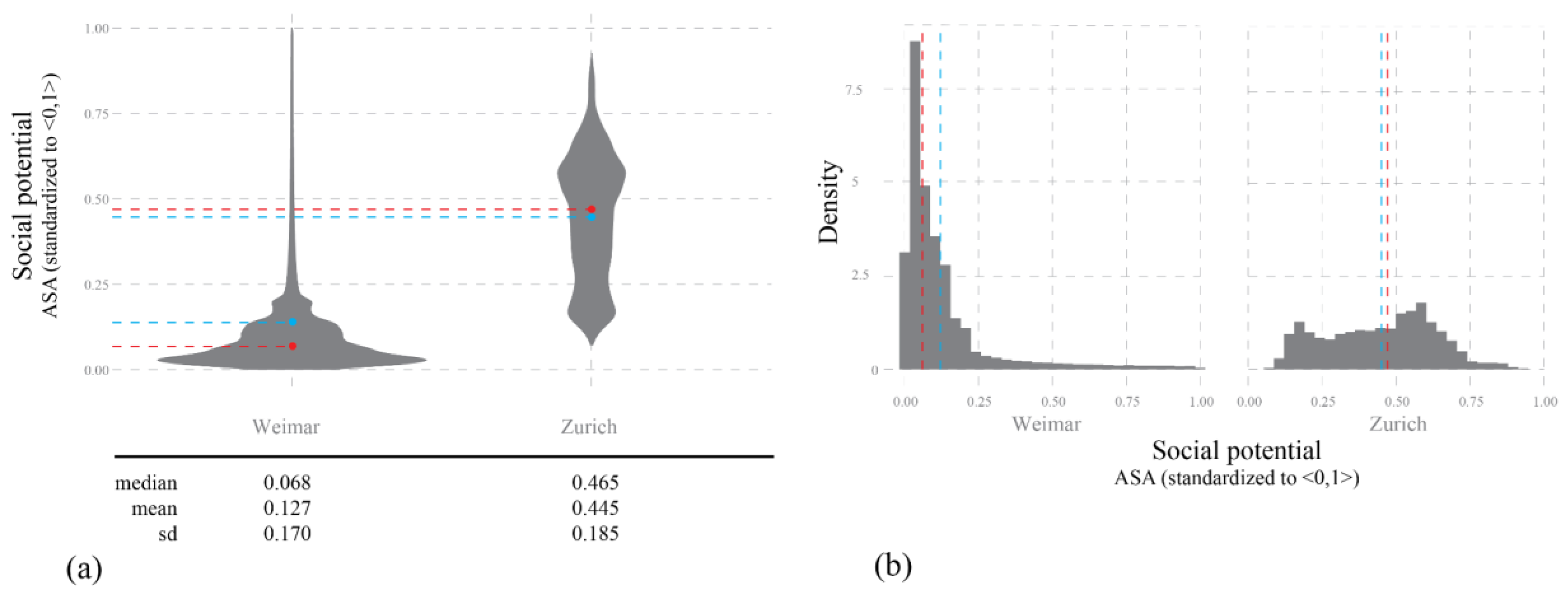
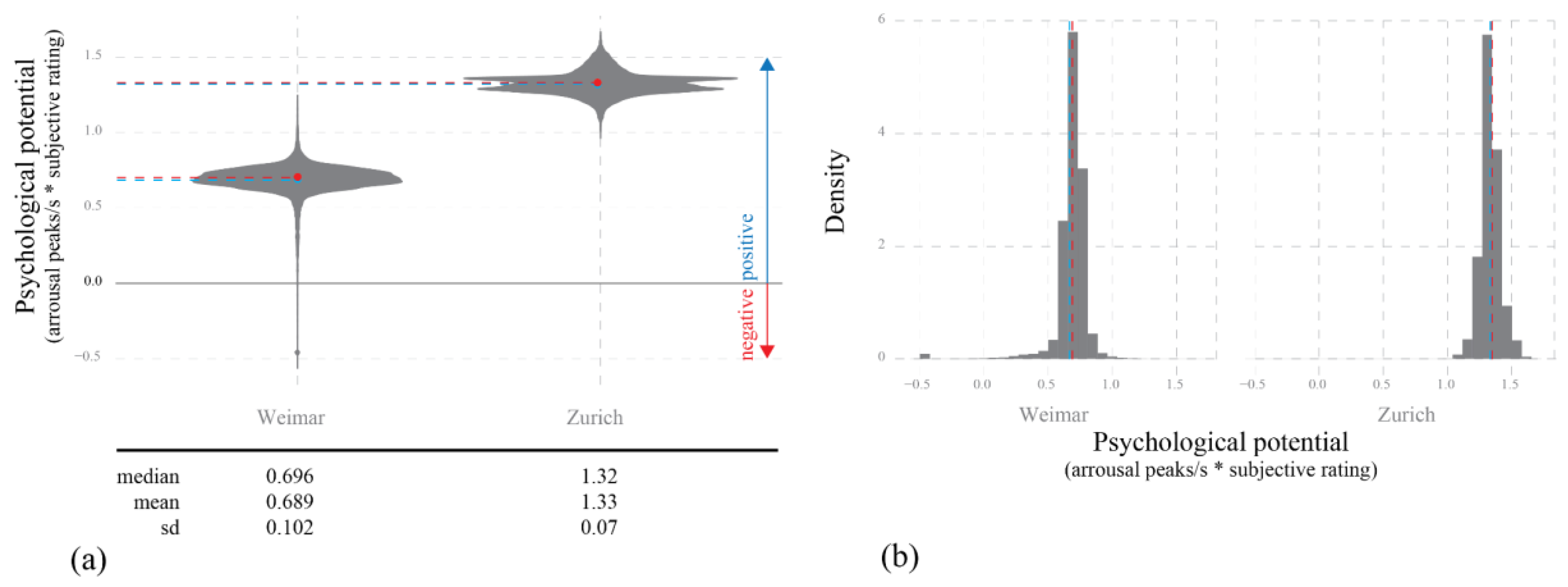
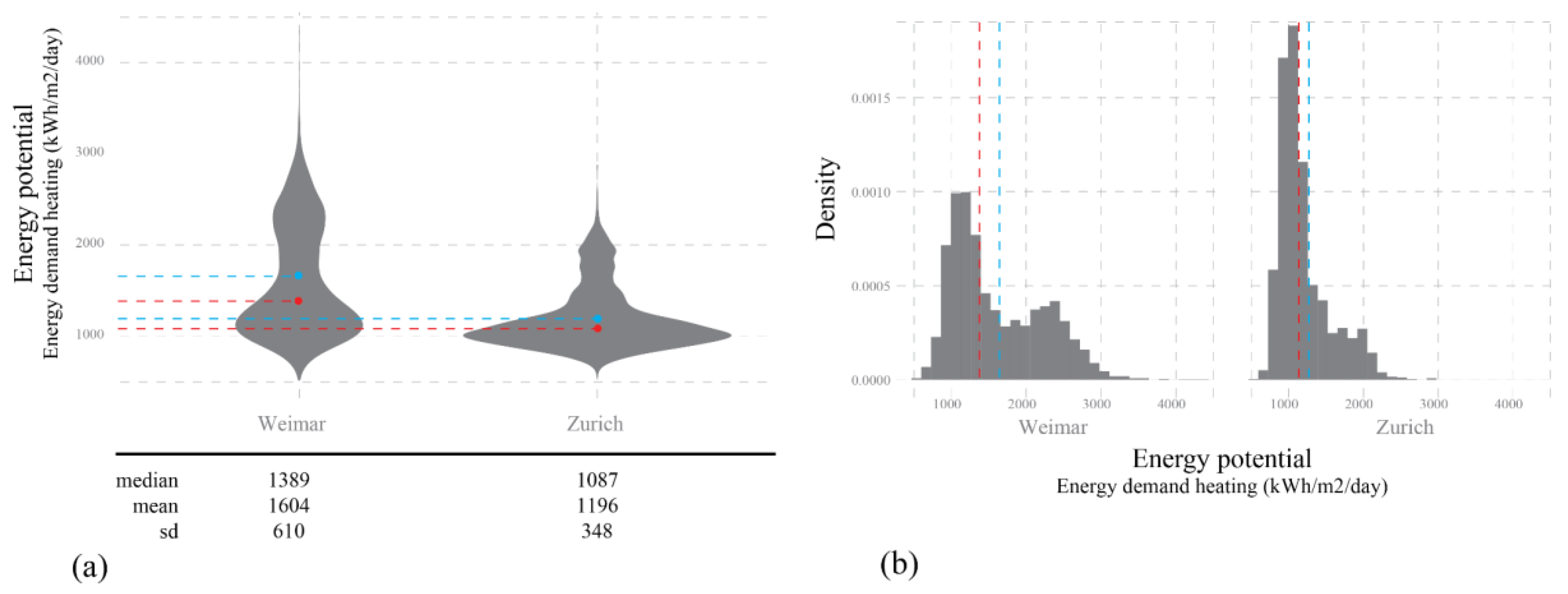
The differences between Weimar and Zurich become more obvious when we examine the descriptive statistics characterizing both distributions of the social potential. After normalizing the ASA scores into the range of [0 to 1] (the normalization base was the joined distribution for both cities, so the relative differences between them were maintained after the normalization was done), we can observe that the average and median social potential for Weimar is significantly lower (mean = 0.127 and median = 0.068) compared to Zurich (mean = 0.445 and median = 0.465). Second, the whole distribution in the Weimar case is strongly positively (right) skewed with many small values and few very high ones, whereby in Zurich we see more normally distributed social potential as depicted in the
Figure 5. This can be partially explained by smaller size of Weimar with the consequence of more of the city outskirts being covered in the analysis area as compared to Zurich. Nevertheless, even by disregarding the edge effect contributing to very small values in the Weimar case, there is still much bigger area of Zurich covered with mid to high values of social potential.
2.3. Summary
To analyze the social potential of urban form, we used the ASA method for estimating the impact of the street network configuration on the potential for social interaction. The results revealed that the two case studies share some properties, such as the non-symmetric distribution of social potential, however, they differ in their overall social performance. Here, the Zurich urban form reveals a higher social potential compared to Weimar. We argue that the different patterns of social potential are a direct consequence of their different urban form—namely the street network configuration of both cities.
3. Psychological Potential of Urban Form
If there is a psychological potential of urban form, in that psychological responses could be predicted based on a set of variables, one must define of what it consists, and distinguish which variables in the urban environment are critical for urban perception and experience, and how these variables interact. For instance, one distinction could be made between the conscious experience and subjective opinions about space, and the rapid subconscious perceptual responses to our environments on a physiological level.
On the one hand, it is clear that, to a large extent, our experience of the built environment depends on visual perception of spatial characteristics around us [
36,
37,
38]. For instance, the way buildings surround us, and the way streets connect, is a crucial factor for how we experience cities (e.g., building blocks determine movement flows and enclosure, shadows, or blocked views). On the other hand, perceptual processes happen rapidly and subconsciously. For instance, when we walk through the city, all of our senses are engaged in processing manifold sources of sensory information around us. As such, even when we do not form a subjective opinion about our experience of a place, our body will already have been affected by the sensory stimuli around us; the temperatures and humidity, illuminance, soundscapes, and so on. This interplay of dynamic environmental and individual variables makes it hard to predict responses to a planned or existing urban environment.
Both geometry-based properties (e.g., features of the form of buildings and the street network) and non-geometric properties (such as soundscapes, temperatures, illumination, and many more) influence perception; and further: that urban experience is determined by the interaction between these environmental aspects and the individual subjective environmental appraisal (e.g., liking an environment or not) and physiological responses (i.e., the way an environment affects our body).
Several methods exist to quantify perception and behavior—relevant properties of urban form, for instance, visibility analysis [
39] or the street network analysis mentioned in the previous section. The non-geometric properties are harder to define, as they mostly vary dynamically, change in time, and interact among each other (e.g., increased noise and pollution levels from higher traffic).
However, quantifying these complex relationships between environmental characteristics and urban perception and experience further would allow urban planners to calculate predictions of the ‘psychological potentials’ (subjective experience or appraisal, physiological/perceptual responses) that could be used to inform early planning stages. As such, if the complex relationships between urban form and human responses were defined quantitatively, planners could conduct quantitative analyses of their plans and predict urban experience even before the (re)development of an urban environment.
Previous research has already started untangling these complexities of urban experience, in order to more closely evaluate which environmental variables are relevant and measurable to quantify urban perception. In terms of geometric and other visual properties, Ewing and Handy (2009) [
40] defined perceptual urban design qualities’, such as visual enclosure, spatial complexity, greenery, crowding, urban soundscapes. They also identified that pavement conditions, the number of parked cars along a street and many other aspects in the environment could influence how we perceive and experience urban environments. However, few studies systematically examine and quantify these manifold environmental variables and their relationship to urban experience. For instance, Knöll et al. (2015) [
41] examined environmental appraisal in relation to different typologies of urban environments (i.e., a park, a square, a courtyard, and streets). They found that street network centralities and the field of view were linked to ratings of urban stress perception. In addition, earlier work by those authors also indicated that a key aspect of urban stress are soundscapes [
42]. Such soundscapes, e.g., caused by traffic, are also strongly related to the street network (cf. the section on social potentials). Second, to capture the effect of dynamic and non-geometric variables on urban perception, sensor-data that measures these variables in a temporal fashion would have to be linked to continuous ratings of urban appraisal or physiological responses or tested notoriously as isolated variables in the laboratory. One field where progress has been made is in the way we physiologically respond to urban environments. For instance, Roe et al., (2013) [
43] implemented a systematic laboratory study and found that physiological arousal based on electroencephalography data correlated with specific arrangements of urban scenes. Their later work included field testing and indicated that excitement measures of the electroencephalography data were higher in busy/vibrant urban environments (study with elderly persons, [
44]).
The authors argued that there are ‘neural signatures’ in the experience of different urban spaces. As such, our brain and nervous system responds distinctly to different spatial settings (e.g., urban and greenery [
45]). This is similar evident in Hijazi et al. (2016) [
46], who conducted a small-sample study in which participants wore a skin conductance wristband while roaming freely in an environment. They concluded that participants physiological response was linked to changes of a spatial scene, e.g., street intersections. This indicated that physiological responses may be sensitive to soundscapes (perhaps as environmental stressors, [
47]). However, whether the physiological changes were triggered by permanent features of the street (e.g., urban form) or dynamically changing variables (e.g., soundscapes, illumination, temperatures, and so on) could not be answered in the previous studies. However, Raja et al. (2018) [
48] pointed out that sensing and geo-tracking with mobile devices is beneficial as ‘emotional city mapping’, but advised researchers to narrow down the relative influence of each variable in human-environment interaction in a step by step fashion.
3.1. Methods for Measuring Psychological Potential of Urban Form
In the following section, we describe our methodology for developing a predictive model of physiological responses to urban form. This is based on iterative studies that examined the complexity in the field, then reduced the variables in a systematic fashion in the research laboratory to quantify their relative impact on urban perception and experience.
3.1.1. Measuring Perception
To measure physiological changes while participants experienced each environment, we used the wearable device Empatica (cf. Poh et al., (2010) [
49] for a comparison of different devices). With this device, we measured skin conductance (i.e., electro-dermal activity, EDA). As Benedek and Kaernbach (2010, p. 80) [
50] described, “electrodermal activity (EDA) refers to the variation of the electrical properties of the skin in response to sweat secretion.” EDA responds to a variety of stimuli around us, such as social interaction, spatial changes, stress, and fear, to name but a few. However, EDA is primarily a measurement of changes in the sympathetic nervous system, rather than a predictor. Two measures of EDA are central: EDA measures skin conductance level (SCL), a slowly changing tonic activity of the skin; as well as the skin conductance response (SCR), a rapidly changing, phasic activity [
50]. Higher arousals mean a higher activity of the sympathetic nervous system. In psychological research, EDA is considered to be an index of sympathetic activity, and linked to arousal, cognitive states, emotional processes and attention [
51,
52]. This relationship is unspecific; i.e., as Figner and Murphy (2010) [
53] describe, the phasic skin conductance response co-varies with arousal, but not with a certain ‘types’ of emotion (e.g., joy) or its valence.
However, since SCR does not indicate the valence, i.e., which emotions (e.g., joy) the participants experience, or how strong the respective emotions occur, we also asked for subjective evaluations of the environment. We measured subjective environmental appraisal on one dimension of pleasure: like, neutral, and dislike. Participant made continuous ratings of how they liked the scene along the path, by pressing one of the three response options on a device (here referred to as ‘clicker’). A more detailed evaluation of the environment (such as spaciousness, complexity, brightness) is in general possible, but would require a more complex study setup (rating interface) and more time and cognitive load from the participant while walking along the paths. This was demonstrated in a previous study [
54].
It has to be noted that more advanced sensors exist, including electroencephalography (EEG), for which some more less reliable techniques exist to extract excitement, frustration etc. (valence) [
55]. However, such assumptions so far have not been tested for reliability and correspondence to experience.
3.1.2. Measuring Urban Form
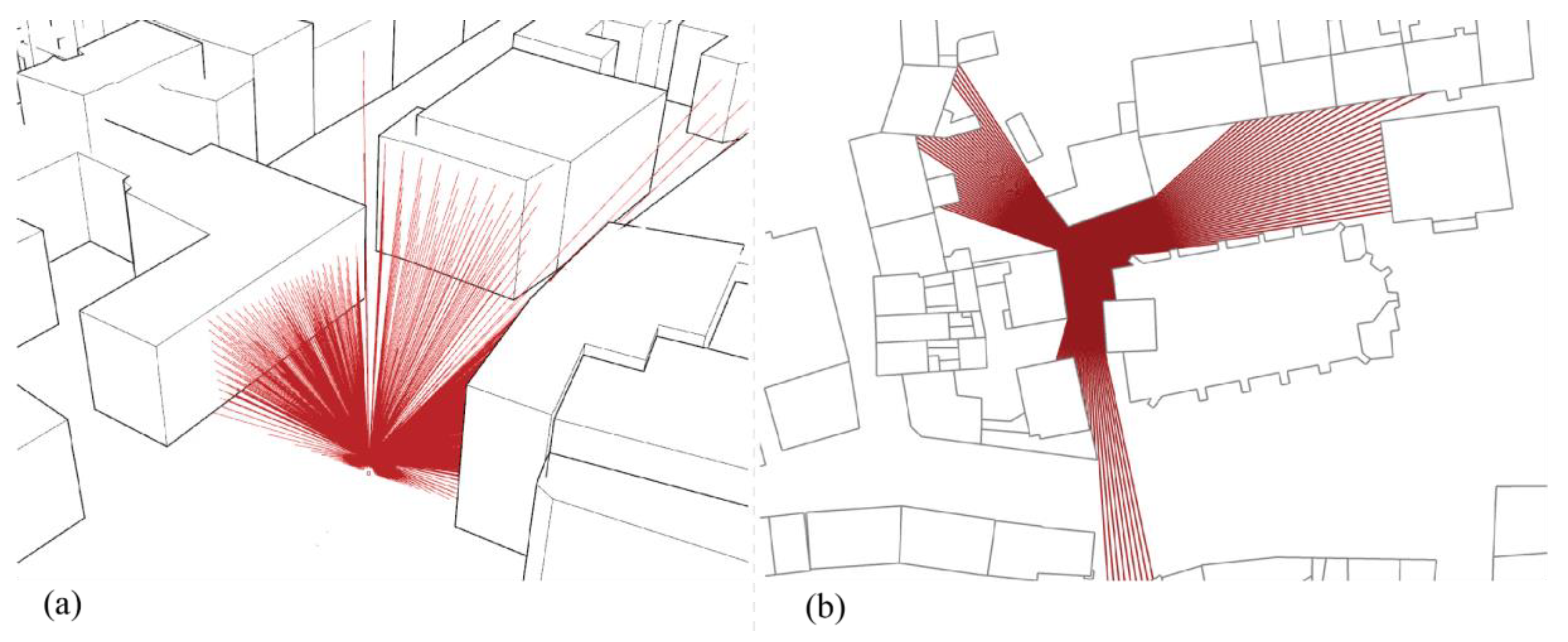
In order to measure perception, relative to urban form were used the concept of the isovist [
39]. An isovist is defined as the area that can be seen from a single vantage point. For this aim, rays are created radially around a viewpoint and intersected with the environment. From the shape and rays of the isovist different properties can be derived, such as the surface area of the isovist polygon, its perimeter, compactness (ratio of area to perimeter related to an ideal circle) or occlusivity (length of occluding edges).
Along with the two-dimensional isovist, which has already been frequently used in environment-behavior studies [
56,
57,
58], we applied the basic principles to the 3rd dimension as well. From the rays and the volume of the 3D-isovist (
Figure 6), we again derived different measures, such as volume, the longest and shortest rays, or amount of visible sky.
3.1.3. A Real to Virtual Workflow
Besides the temporally static features of urban form (isovist), there are many dynamic variables that strongly relate to the perception of urban space, such as illuminance, noise, temperature, humidity, or pollution. In order to systematically measure and analyze the influence of all these variables, we developed a ‘real-to virtual workflow’. This means that we collected perception data in different levels of abstraction of the environment, using virtual reality. The ‘real to virtual work flow’ was developed to filter out to which degree the physiological states were linked to changes in urban form [
59]. This is particularly important since field studies contain many naturally and simultaneously occurring variables, and it would be hard to distinguish the direct influence on urban form without planned comparisons.
More precisely, in the field study (study 1), every participant experiences different soundscapes, weather conditions, objects along the way. By using a 360-degree video of the path (study 2), the soundscapes, illumination, and visual scenery remained the same for each participant, while some factors, such as temperature and movement, were cancelled out. This allowed a controlled replication of the field study in the virtual laboratory, as virtual environments are feasible methods to represent the real world [
60]. Similarly, we used an abstracted geometry model to remove effects of different materials, soundscapes, illumination, and greenery to measure effects of urban form in isolation from other factors (study 3).
Figure 7 indicates the underlying idea of reducing environmental variables to enhance experimental control.
3.1.4. Experimental Set-up
For the studies, a walking path in each of the two case-cities were chosen. For study 1 (field study), the dynamic variables, such as noise (decibel, dB), dust (mg/m
3), temperature (°C), relative humidity (percentage), and illuminance (lux) were measured using a sensor backpack (Griego et al. 2017). Skin conductance data was collected with a wristband (Empatica) with the common procedures (adjustment times, usage on the nondominant hand, pre-processing, normalization of data etc.). In the field study 30 participants took part where 10 EDA signals were discarded and the remaining 20 uncorrupt EDA signals were used for data analysis. Due to technical issues and time limitations the field study with the backpack and the Empatica Device was only conducted for Zurich [
11]. A pre-study using an analogous method for Weimar can be found in Bielik et al., 2015 [
54].
For study 3, 360° videos of the paths were recorded, where some of the dynamic urban properties were absent (e.g., solar radiation, wind, temperature, humidity) others remained constant for (e.g., noise). The experiment was done using a head-mounted-display, with 30 participants in Zurich and 20 in Weimar. For study 3, videos of the abstract geometry models were created. In this study, 22 participants for the Zurich path and 27 participants for Weimar path were recruited. In both VR-based studies the participants watched a video of the path, while their physiological changes were tracked with the Empatica device. Furthermore, they used a clicker to rate whether they experienced the scenes as positive, neutral, or negative (like, neutral, dislike buttons).
The field study data collections were conducted on two days in October/November for Weimar and during three weeks in April for Zurich. We did not conduct data collections in rain, snow, etc. to protect participants from such conditions. The April and October collections were similar in illumination and temperatures. The videos for VR were recorded in similar conditions, but did contain relatively stable weather, as it otherwise would not have been feasible to record videos on those days. The geometry models were equally illuminated and did not include any weather. We did not conduct statistical analysis of the ratings to compare differences across their data collection times, but given that we collected on different times throughout a day and in similarly cold months, this variability should be equal across participants.
3.2. Results of Measuring Psychological Potential of Urban Form
3.2.1. Mapping Physiological Responses and Subjective Ratings of Appraisal
In order to interpret the skin-conductance measures, we performed the physiological arousal quantification using the common procedures to pre-process and normalize the data [
50,
51,
53]. The physiological arousal was spatially mapped on equally distributed points along the paths (
Figure 8).
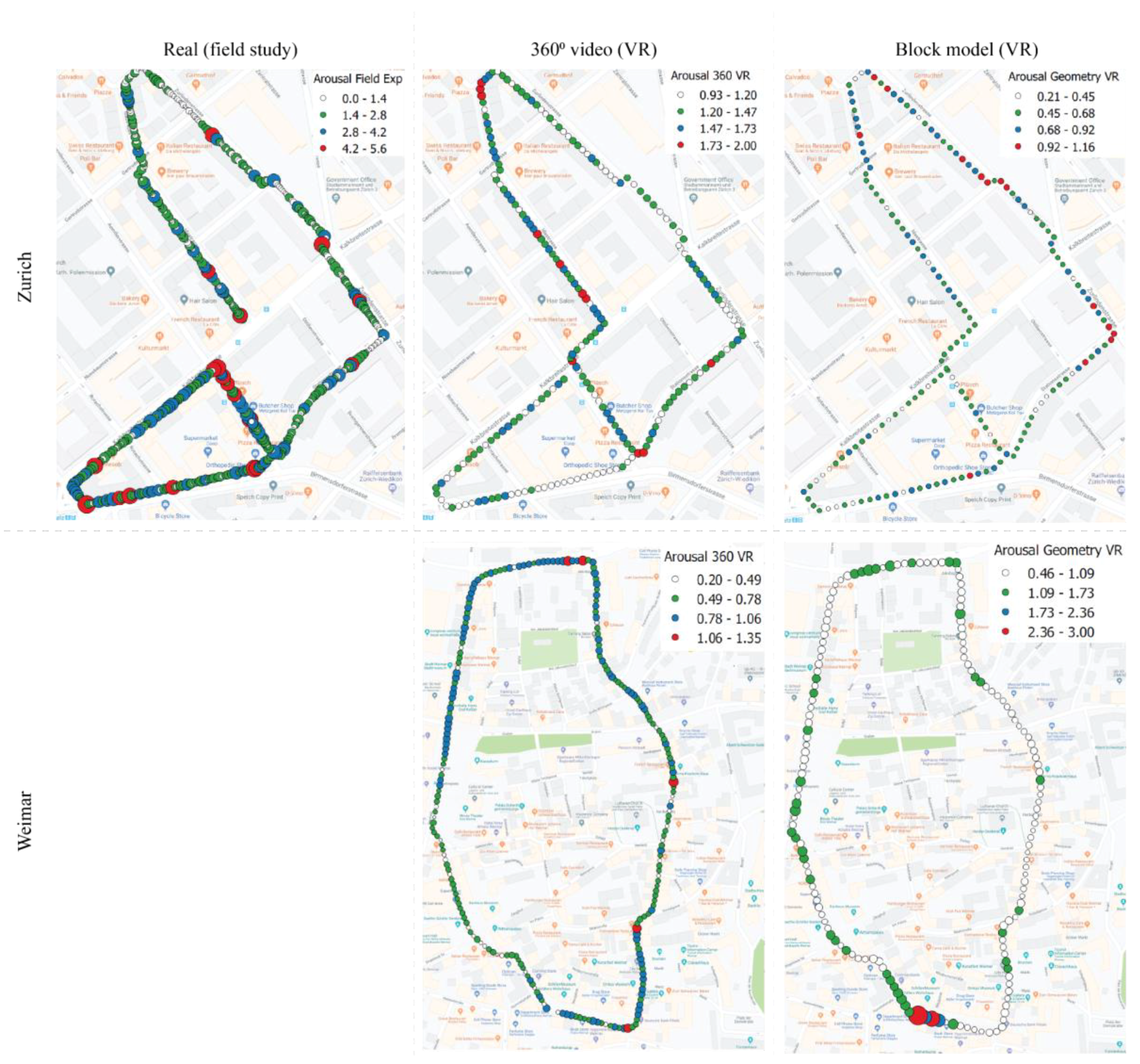
When comparing the results of the three studies (
Figure 8), two things become obvious: First, the arousal levels on average are lower with the reduction of realism. In the field study the average arousal levels are highest, followed by the 360° video and lowest in the geometry model, where the arousal level was lowest. Second, when we look at the distribution of the high and low values, there are strong differences between the three studies. In the field study, high arousals appear in areas of high traffic, while in study 2 and 3, there are fewer arousals and they mainly occur where the street geometry changed from a narrower to wider space and vise-versa. A similar effect was observed shortly before and after participants walked from one street to another. This relates to work by Koenig et al. (2014) [
61], who found that physiological responses change at intersections or changes of openness of the space.
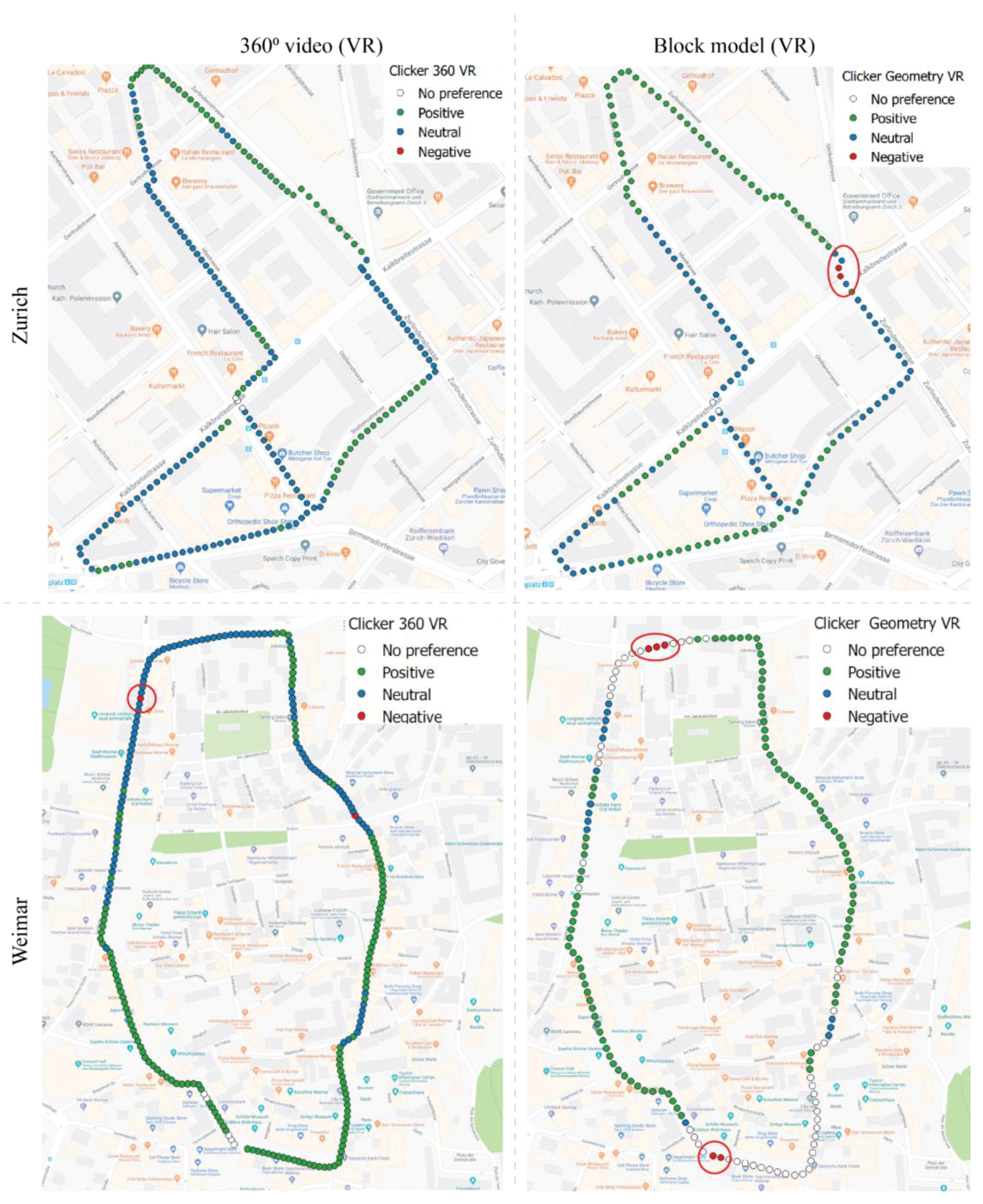
As described before, in the VR studies alongside the physiological response, we also recorded the environmental appraisal (liking or disliking a scene) using the clicker (cf. earlier). When a participant did not press one of the clicker buttons, the corresponding input was taken as no preference. The results of these subjective environmental appraisals are displayed in
Figure 9. Many participants evaluated many of the city scenes as neutral. In Zurich, positive evaluations mainly occurred in areas with green space (park or trees along the street). This result would be in line with earlier suggestions [
62] and research [
43] indicating intrinsic preferences for nature [
45]. In Weimar, the positive evaluations mainly occurred in the slightly winding streets through the historic urban structure. There were no negative ratings for Zurich from the 360°-video and only one negative rating in the geometry model at a larger junction, where, in reality, large trees enclose the space. For Weimar, there were two negative evaluations in both studies. In the 360°-video, these occurred once on a high traffic street and the other on a junction where one crosses a wide street. In the geometry model the negative evaluations occurred at a larger traffic crossing (where the open space is similarly unenclosed as in the Zurich street junction) and at the main inner-city retail streets, which most inhabitants regarded as beautiful.
3.2.2. Predictive Modelling
For identifying relationships between the physiological measures, urban form and dynamic urban properties, we chose a machine learning approach using classification (decision tree), fuzzy rule-based inference, feature selection, and clustering. A detailed description of the methods is found in Ojha et al. (2019) [
11].
In order to measure the psychological potential of urban form in terms of the valence (i.e., positive/negative subjective ratings) and size of physiological arousal, we trained the predictive model on the empirical data collected for both study paths in Zürich and Weimar. We use the predictive model to extrapolate new predictions to the over 7000 locations distributed all over the larger 2.5 × 2.5 km study area. For this purpose, we conduct a decision-tree based predictive analysis, using 2D-/3D isovists as the inputs and physiological arousals and subjective ratings as the outputs. The empirical data on the arousal and ratings is based on the results of study 2 (360-degree video) since the video minimized the effect of dynamic factors and at the same time keeps up a high degree of realism. The results show that on one hand, the measures of the street network and the 2D/3D isovists hardly predicted the physiological arousal peaks of the EDA data for perception analysis along both paths (R2 = 0.03). On the other hand, with 2D/3D isovists as the inputs the subjective environmental appraisal could be predicted for a larger area with reasonable accuracy. For the Zurich path R2 = 0.79 and for the Weimar path R2 = 0.67. However, here it needs to be mentioned that the dataset contained mostly neutral and positive ratings. So, for future studies, datasets with greater variance are needed.
We mapped the predicted scores on the common analysis grid that is later used to visualize and compare the psychological, social, and energy potential of urban form (see
Figure 10).
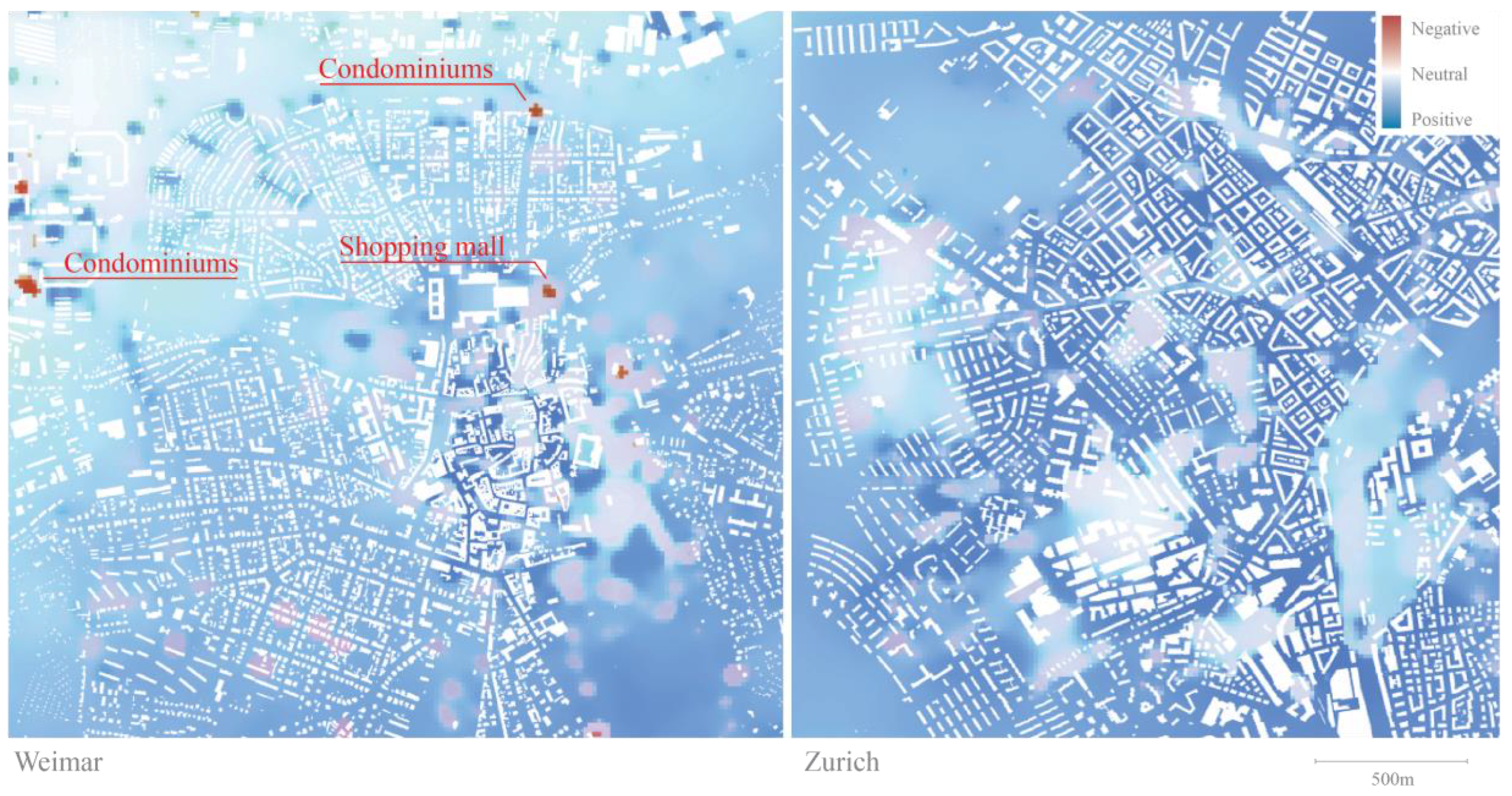
For this purpose, we interpolated over 7000 psychological potential scores onto the analysis grid cells using the Universal Kriging methods (for details see the Trade-offs section). The obtained psychological potentials show only few negative predictions for Weimar located mostly at large open spaces with not clearly defined borders such as modernistic condominium district, shopping mall or railway. For Zürich, the prediction model does not estimate any areas with negative psychological potential. In both, case studies the most positive estimations were allocated in the dense urban centers with Zürich being overall perceived more positively compered to Weimar (see
Figure 11).
3.3. Summary
In summary, we defined psychological potentials as a combination of subjective experiences/appraisal and physiological arousal by skin conductance level. This was done by recording physiological changes while participants walked along a path with different spatial characteristics in the two cities. Then, urban form was measured based on what one can see while walking. For data analysis, select machine learning methods were used to r identify complex relationships between the environment, perception and experiential data. The results indicate a minor influence of urban form on perception (strong differences between real and virtual scenes) and the low predictive power of the model for arousal. However further research could include additional data to characterize individual perception of urban spaces and better descriptors for perception-relevant features of urban form.
4. Energy Potential of Urban Form
The primary focus of the energy analysis is to simulate the impact of urban morphology on building energy performance. In a wider context, the energy demand of urban form also includes transportation, construction processes, materials, and general maintenance. While these elements also impact the overall ecological footprint of cities, we focus purely on energy demand of large building stocks in the presented analysis. A deterministic modelling approach was used to perform the energy analysis. It considers the impact of inter-building shading, building geometry, and overall building orientation, along with other important building simulation parameters such as local historic weather data and building material properties. A customized workflow was developed for this study.
4.1. State of the Art and Study Objectives
4.1.1. Impact of Urban Morphology on Building Energy Demand
The individual building shape and the surrounding environment (building density) both impact the building’s energy demand. Building shape influences the surface area to volume ratio, where external environmental conditions have a greater impact on building energy consumption in buildings with a larger external façade and roof surface area relative to the total volume. Many studies evaluate the impact of geometric form on energy demand including parametric studies using constant volumes and constant floor area parameters evaluated using single building energy performance tools such as Energy plus [
63,
64,
65].
In the study by Rodrigues (2015) [
64], over 500 different building geometric configurations were analyzed for eight different climate regions in Europe and compared by shape coefficient (C
f), south exposure coefficient (C
s), relative compactness (RC), window to wall ratio (WWR), window to floor ratio (WFR), and window to surface ratio (WSR). This study shows that none of the geometric indicators has a strong influence on the energy performance in all climate regions. However, when considering the results, RC has the most statistically significant correlation for cold climate regions in two and three-story buildings, where more compact buildings have a better thermal performance.
This finding is consistent with the study by Geletka (2012) [
63] who also performed a parametric analysis for diverse building shapes and locations. In temperate climates with relatively large WWR, RC has a strong influence on the heating demand. This study also suggests that WWR and orientation relative to south are important considerations in energy models when analyzing the effects of geometry on energy demand.
4.1.2. Urban Energy Modelling
When analyzing the effects of urban morphology on energy performance it is important to consider inter-building shading and total facade solar exposure by orientation. Various urban energy simulation tools have been developed to calculate such scenarios. A review of existing energy simulation tools, indicates that
CitySim [
66] is the most appropriate urban scale software to estimate the effects of urban morphology on energy demand [
67]. Other district scale simulation tools, such as Transient System Simulation Tool (TRNSYS) or Lawrence Berkeley National Laboratory (LBNL) District libraries from Modelica, focus more on the building heating ventilation and air conditioning (HVAC) systems and are therefore too detailed for our study.
CitySim calculates the dynamic irradiation on the exterior building surfaces to consider the effects of inter-building shading and uses a resistor-capacitor thermal model to calculate the heat transfer between the outdoor and indoor environment (Robinson, 2009), which is most suitable at this scale. Thus,
CitySim can simultaneously consider important geometric features at an urban scale including the building size, shape, orientation, and density in response to local weather data and at the appropriate level of detail.
4.1.3. Study Objectives
The primary objective of this study is to determine the best methodology to estimate the seasonal energy performance for large urban districts (2000–5000 buildings) when considering pure geometric form. Further, for such a large number of buildings, it is also important to create simplifications in the building geometry in order to perform more efficient simulations. Therefore, we also evaluate how the energy performance changes with incremental geometric modifications, such as removing shared interior building surfaces and averaging building block heights compared to detailed building geometry.
4.2. Methods for Measuring Energy Potential of Urban Form
4.2.1. Case Studies
The case study area in Zurich, Alt-Wiedikon, was a prime candidate for urban-scale energy analysis since it is primarily composed residential and mixed-use residential buildings. Residential buildings are predominantly envelope-load driven buildings and are therefore suitable for pure-geometry based energy models. Furthermore, this area has a wide variation in geometric form including courtyard, rowed, multi-tenant complex, or detached-single tenant buildings.
The input parameters for the energy models were selected based on the actual characteristics of the Zürich case study area. The same values were then applied to the Weimar building district for comparative purposes. The predominant year of construction for the building stock is from 1920–1974. A review of building material properties for the predominant year of construction was chosen from (TEP Energy, 2016) Wall U-value = 0.86 W/m2-K, Window U-value = 2 W/m2-K, Roof U-value = 0.7 W/m2-K, Floor U-value = 0.7 W/m2-K. Other input parameters required for the CitySim model were derived from a previous energy simulation of a small group of buildings in Alt-Wiedikon (Perez 2011), window g-value = 0.7, ground conductance = 0.3 W/m2-K, and infiltration rate of 0.4 ACH, minimum and maximum indoor temperature were set at 21 °C and 26 °C respectively.
4.2.2. Simulation Procedure
Despite the many advantages of
CitySim by Kämpf (2016) [
66], several steps were required to develop a usable model for such large-scale scenarios. This required custom-made geometry, local weather data, a PostgreSQL database, a post processing data parser, a more flexible visualization approach and an XML parser for ease of model modification. The energy simulation workflow and a full user-guide, models and code are located on the project repository.
4.3. Results of Measuring Energy Potential of Urban Form
The heating and cooling energy demand potential are two key indicators to measure the energy performance as they consider the heat transfer through the building envelope and thus appropriately consider the impact of geometric form. The impact of the building shape on the energy demand is normalized by gross floor area and correlated with shape coefficient (C
f) and the relative compactness, similar to Rodrigues (2015) [
64]. The shape coefficient (C
f) is the ratio of building surface area exposed to outdoor air (S) to the total building volume (V) while RC is the volume to surface area ratio relative to a rectangular reference volume (Equation (2)).
The heating energy potential is analyzed on the winter solstice while the cooling energy potential is analyzed on the summer solstice. The results of the regression analysis for Zurich and Weimar are illustrated in
Figure 12.
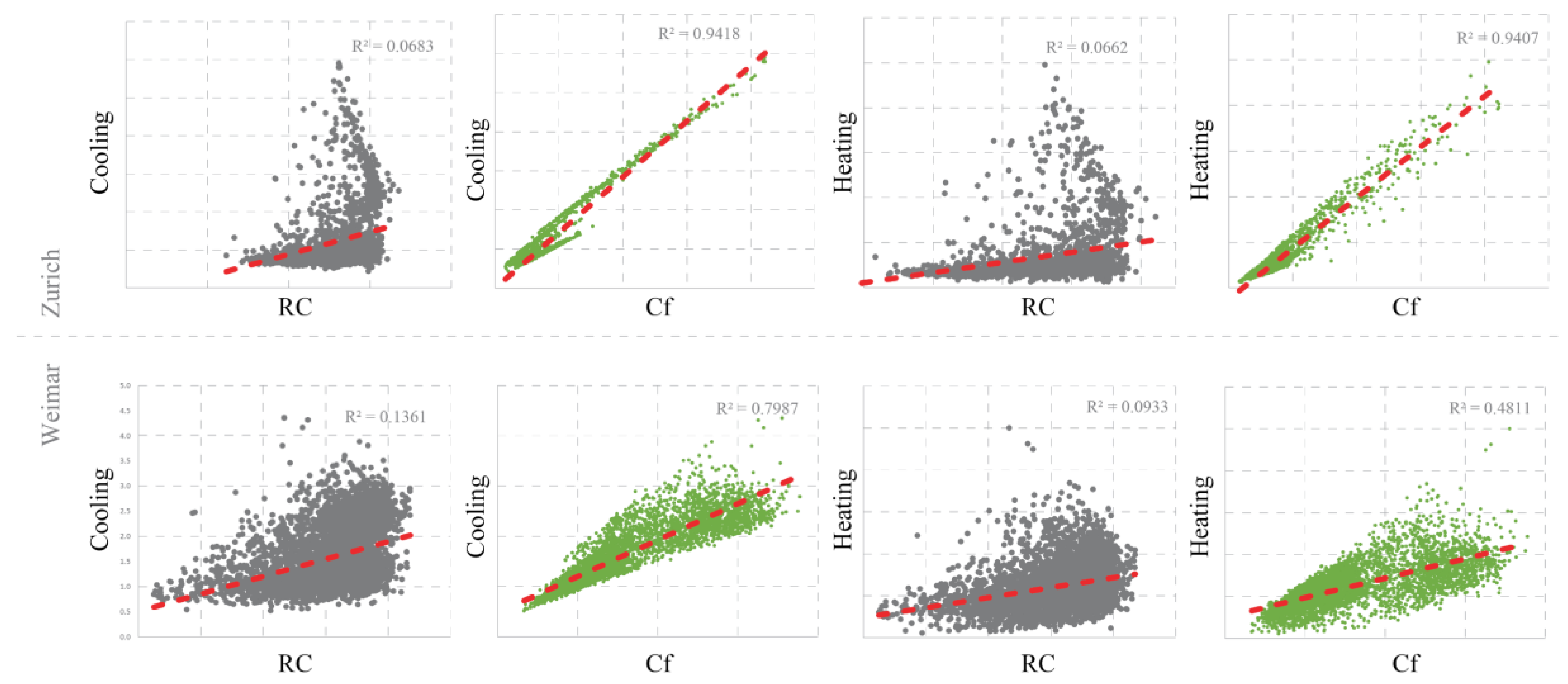
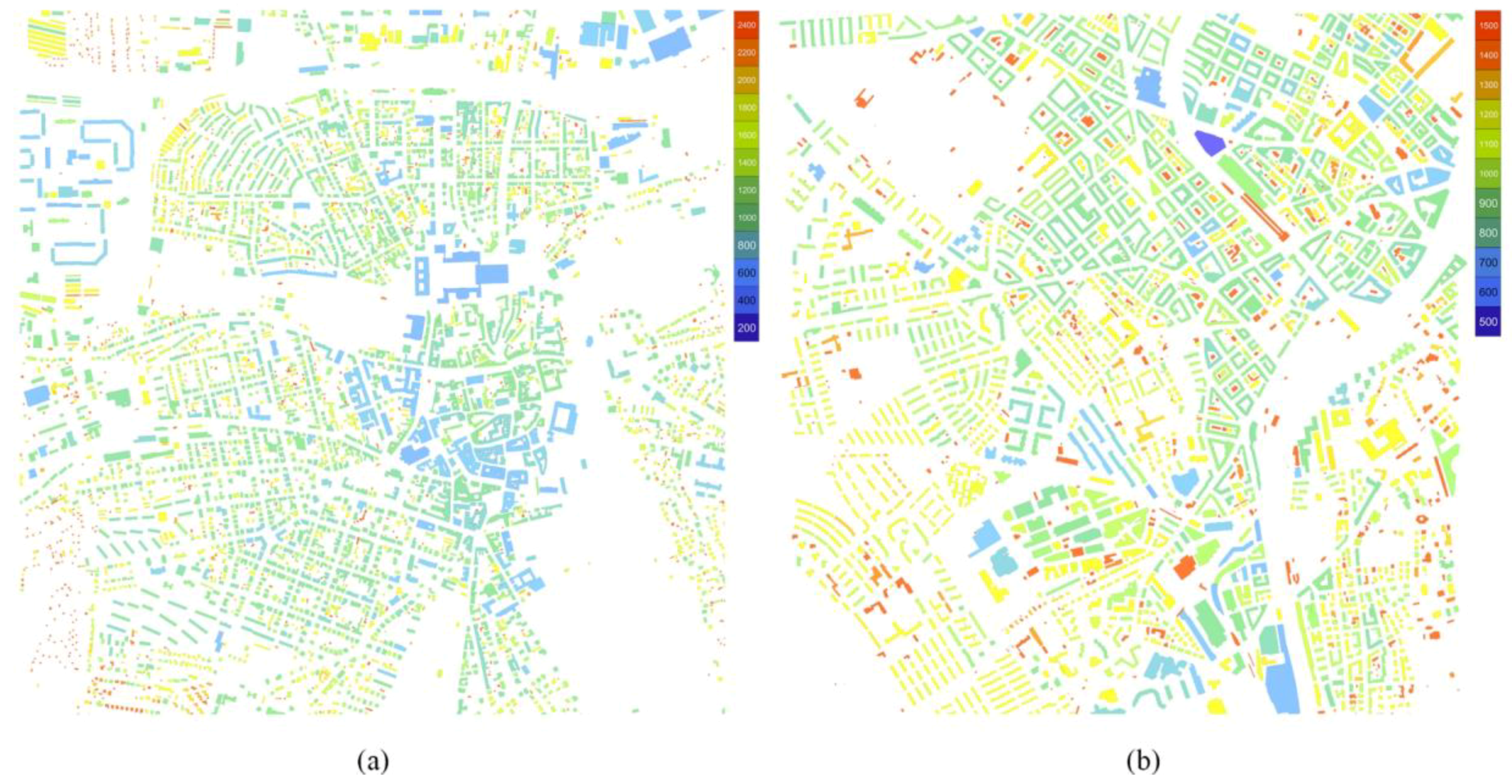
The RC shows a weak overall correlation with heating and cooling energy demand potential for both cities, however, it does indicate a general trend that more compact buildings have lower energy demand. The shape coefficient on the other hand shows a strong correlation with the heating energy use intensity for both cities with R-squared values up to 0.94 for Zurich and 0.79 for Weimar. The correlation between the shape coefficient for the cooling energy demand is however much lower for the Weimar energy model. The weaker correlations for Weimar might also correspond with the larger building sample. The heating energy use intensity are also spatially represented where the respective results for Zurich and Weimar are shown in
Figure 13.
When comparing the Weimar and Zürich studies, we conclude that the distribution of energy potential is right skewed in both cases (see
Figure 14). Overall, the building stock in Zürich has lower energy demand for heating per build floor area, which might be attributed to the more dense and compact building block typologies of Zürich compared to the large portion of Weimar buildings stock being less dense detached or semidetached housing.
4.4. Summary
The energy analysis illustrates the impact of pure geometric form on the energy demand potential of the building stock in the two case studies. In order to accurately consider both thermal and irradiation effects in the energy simulation, a simulation tool was required. Using CitySim, we were confronted with significant challenges in the modeling approach due to the size of the city model. Therefore, we created a workflow which addresses the challenges of size and complexity but are still rather time intensive for complete annual energy simulations (1 day in the model requires 10 h to simulate). The models were developed with constant input parameters for the glazing and envelope material properties in order to focus solely on the relevant urban morphological features.
5. Trade-Offs
The general goal of this research is to measure and explore the trade-offs between social, psychological, and energy potentials of urban morphologies. In the previous sections, we introduced three methods to measure these potentials and applied them to two case studies in Weimar and Zurich. In this section, we first introduce a method to aggregate the different potentials onto common analysis grid. Second, we cluster the urban form at each analysis grid cell into distinct groups which are finally used to compare the trade-offs between the social, psychological, and energy potentials across the different urban forms.
5.1. Methods for Measuring Trade-offs Between Social, Psychological, and Energy Potentials of Urban Form
5.1.1. Aggregating Urban Potentials to a Common Analysis Grid
Each of the three potentials introduced in the previous sections cover distinct qualities of the urban environment and are linked to different elements of the urban form. For the analyses, different representations are used: the psychological perception is analyzed for points in public space, the energy potential for building envelopes, and the social potential is assessed for any point in space covering both the public and the built space. Consequently, they cannot be compared directly. Therefore, we use a rectangular grid as an abstract and flexible analysis framework with each grid cell to map any analysis object (i.e., point, polygon).
A further advantage of the evenly distributed analysis grid is the possibility to analyze the continuous change in urban potentials through space as illustrated in
Figure 4,
Figure 10, and
Figure 13. This shows the potentials at specific locations where we can also plot the
“potential landscape” covering the entire study area. We divided both case study areas of 2.5 × 2.5 km into 27,889 analysis grid cells covering 15 × 15 m each. This relatively fine-grained grid was necessary to capture the high spatial variation in psychological and energy potentials.
Based on the type of the original analysis object, the mapping procedure follows two different approaches, direct mapping for polygons and interpolation of geostatistical points. For example, the former is applied to the energy potential. Here, every analysis grid cell is assigned the energy potential calculated for the building polygons directly intersecting with the grid cell. Since in some cases several building polygons can intersect with one grid cell
i, we calculate the weighted mean of their energy potential
WPE by weighting the energy potential of each polygon
PE by its area intersecting with the grid cell
A (Equation (3)). In the case that no building polygons intersect with the grid cell, no value is assigned, and it remains empty.
For the social and psychological potentials, we interpolate the original evaluation samples from their point locations to the common analysis grid cells. Even though both potentials can be directly calculated for all of the individual grid cells with no need to interpolate, this is not computationally feasible as the size of the case study areas consist of more than 55,000 analysis grid cells. To reduce the number of required evaluation samples, we analyzed the degree to which the individual potentials are spatially correlated. For this purpose, we calculated the semi-variograms (
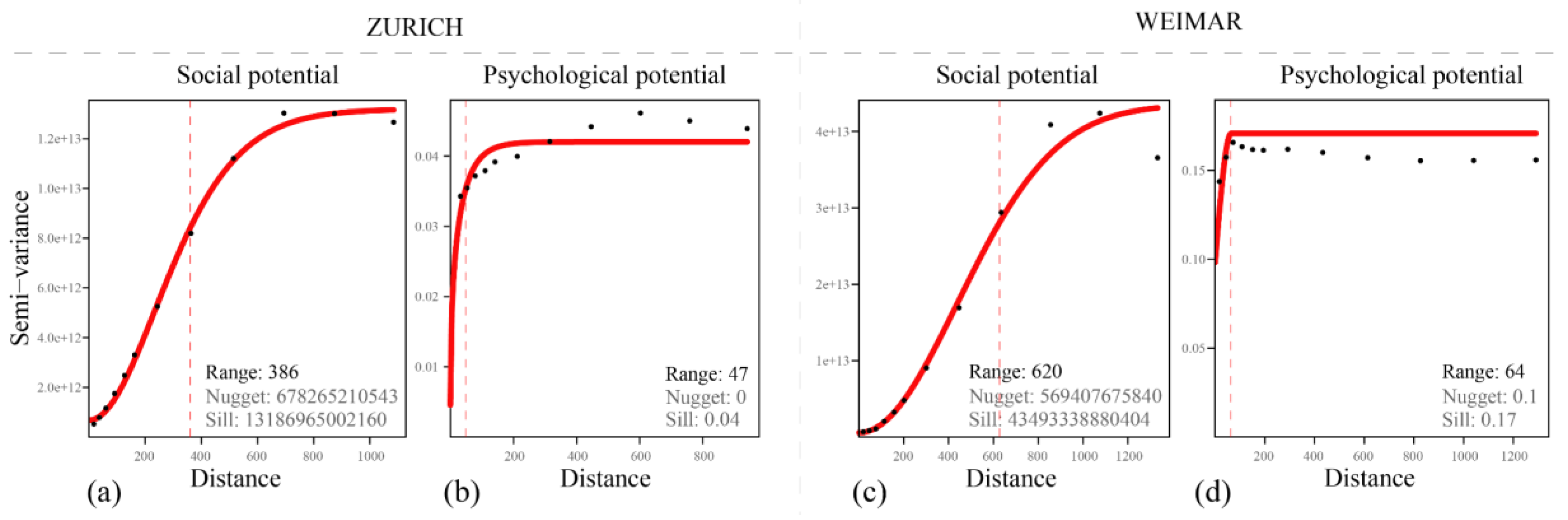
Figure 15) as a measure of how much two evaluation samples will vary in their social and psychological potential, depending on the distance between those samples.
For each semi-variogram, the range measure was calculated to identify the distance beyond which two samples are in no spatial relationship to each other. The semi-variograms confirmed that both potentials are spatially autocorrelated for psychological potential with a smaller range from 47 m to 64 m for Zurich and a larger range from 386 m to 620 m for Weimar. These results suggest that (a) the set of evaluation samples can be meaningfully reduced for computational purposes and up-sampled afterwards for visualization purposes and (b) the sampling rate should be higher for the psychological potential than for the social potential. This has been reflected in the sampling methods, with social potential calculated at the center-point and psychological potential at the center-point and the crossing of each street segment. This results in 3945 unique samples for the former and 7190 unique samples for the latter. Finally, both sample sets were interpolated from the street segments to the fine-grained grid covering the analysis area using the Universal Kriging method (For spatial interpolation we used the “automap” package by Paul Hiemstra for statistical software R. This package performs an automatic interpolation by estimating the semi-variogram).
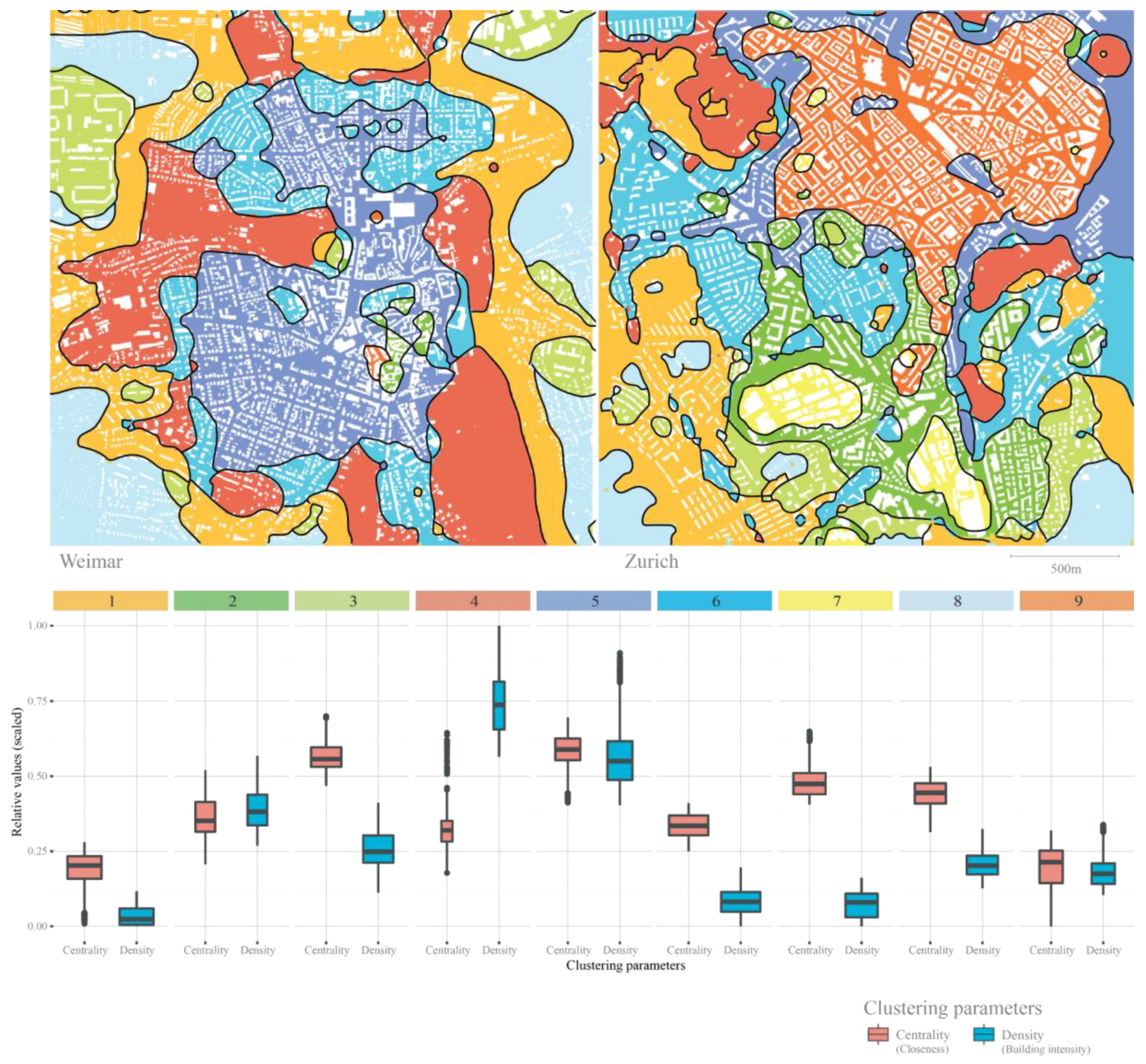
5.1.2. Classifying Urban Morphologies
To examine the trade-offs between psychological, social, and energy potentials of different urban forms, we first identified these distinct morphological clusters and assigned them to each cell of the common analysis grid. In general, the process requires (a) quantifying one or more properties of the items that is clustered and (b) measuring their similarity in terms of the distance between these properties. In this research, we describe urban form as the collection of simplified buildings and the street network. Correspondingly, we adopt the building intensity and closeness centrality as two descriptors of the properties of urban form used in the clustering process. The scope of this research extends beyond studying single urban systems and aims to present a method allowing to analyze the performance of urban form across different systems. Consequently, the clustering method introduced in this chapter needs to identify distinct urban form clusters across the two study areas. In other words, the similarly central and dense urban forms allocated in different parts of Zurich and Weimar should end up in the same cluster. This makes it possible to study how different urban form clusters are represented in each study area, and compare their overall performance and consequently draw generalizable conclusions for other case studies.
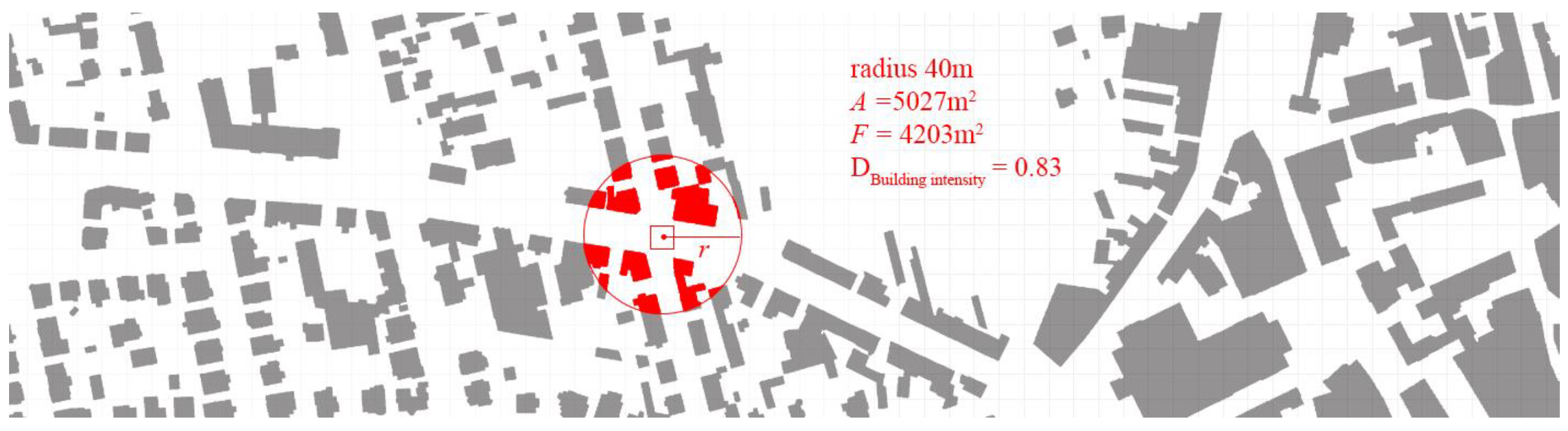
The first variable used to cluster the urban form—
building intensity—is a measure of density capturing the total gross floor area
F per floor plan area
A (Equation (4)). Since the aim is to measure the
building intensity for each analysis grid cell, we employ the adaptation of the radius based density calculation method introduced by Bielik et al. (2017) [
28]. In our case, we measure the density in a radius of 40 m (In a previous study by Bielik et al. (2017), the radius of 40 m was identified as the as the smallest radius suitable for describing the density of urban form. Below this radius measurement artefacts often cause strong bias) from the center of each grid cell (see
Figure 16). This can be seen as a measure describing the local properties of urban form (describing features that are only relevant, or experienceable for one point without taking into account relations to other parts of the city).
The second clustering variable—the street network
closeness centrality—captures how close (or integrated) any location
i relative to all other locations is in the network (Equation (5)). The formal definition of the closeness centrality comes from Sabidussi (1966) [
68] and can be interpreted as a global measure of urban form describing how its individual elements relate to each other. In order to find clusters of urban form shared by both case studies, we need to normalize the closeness centrality to make comparisons across different urban systems. For this purpose, we adopt the empirically informed normalization proposed by Hillier et al. (2012) [
35]. The resulting Equation (6) accounts for the effect of different system sizes by multiplying the original closeness centrality by number of nodes
NC (street segments) raised by an empirical coefficient of 1.2.
After measuring the local (density) and global (centrality) properties of urban form at each grid cell, we search for groups containing grid cells with similar properties using k-means clustering (the
building intensity density and
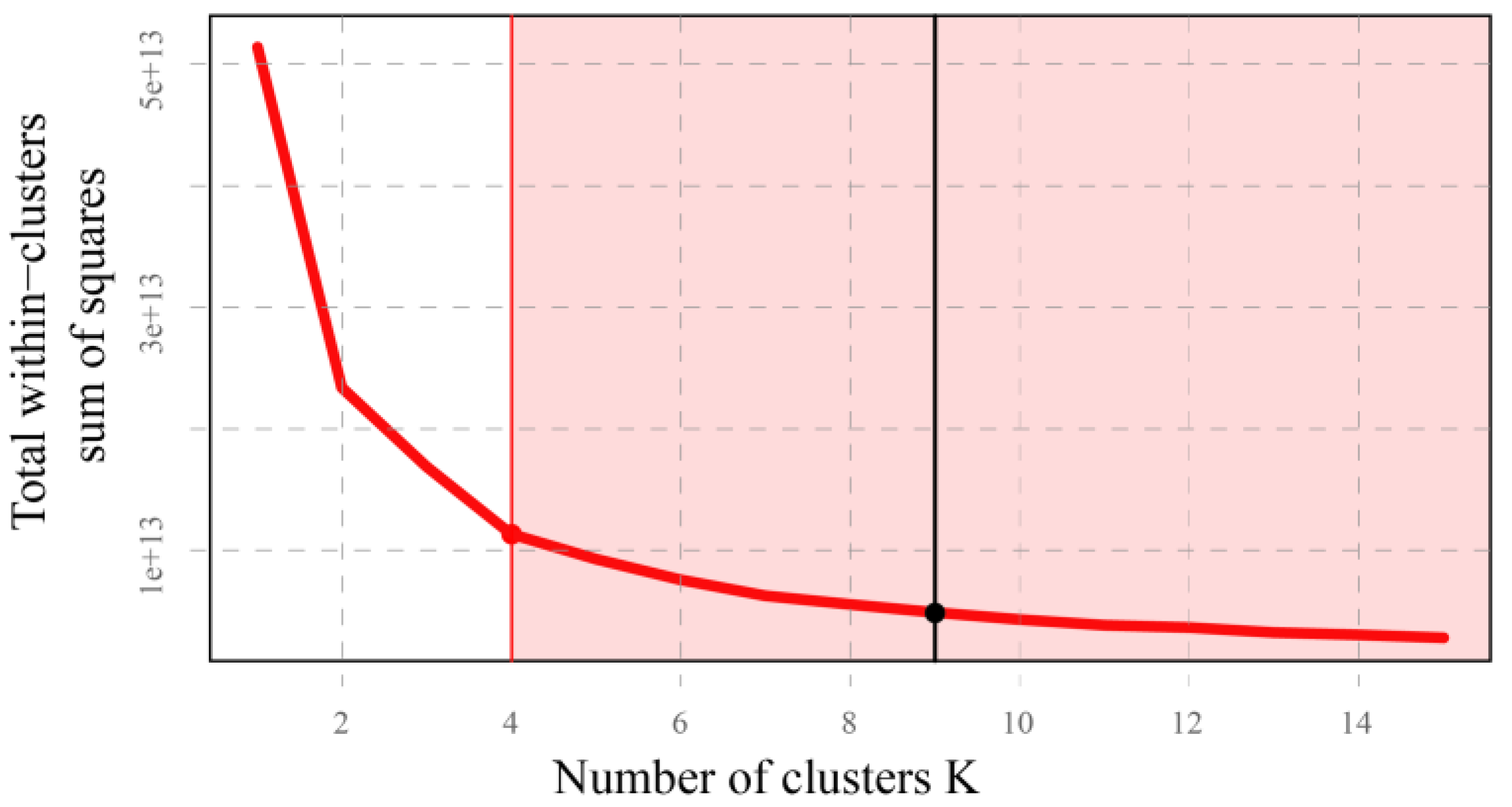
closeness centrality are transformed to the standard score to avoid the clustering being biased by the choice of the measurement unit). Since the k-means requires a priory information for the number of clusters, we determined this by the
Elbow method to view inter-cluster variation as a function of the number of clusters. The results suggest that at least four distinct clusters can be identified; all additional clusters contribute only marginally to the similarity of individual items contained in each cluster (see
Figure 17).
Even though, the four clusters are sufficient from the quantitative point of view, we identified experimentally that a higher number of clusters more appropriately reflects the established urban typology classification. This distinguishes between building types, such as detached, semidetached, and row houses, and their location in city (i.e., center, periphery). Since many of these variations were dismissed in the first four clusters, we extended this number until a minimal set of clusters (k = 9) appropriately differentiated basic urban typologies.
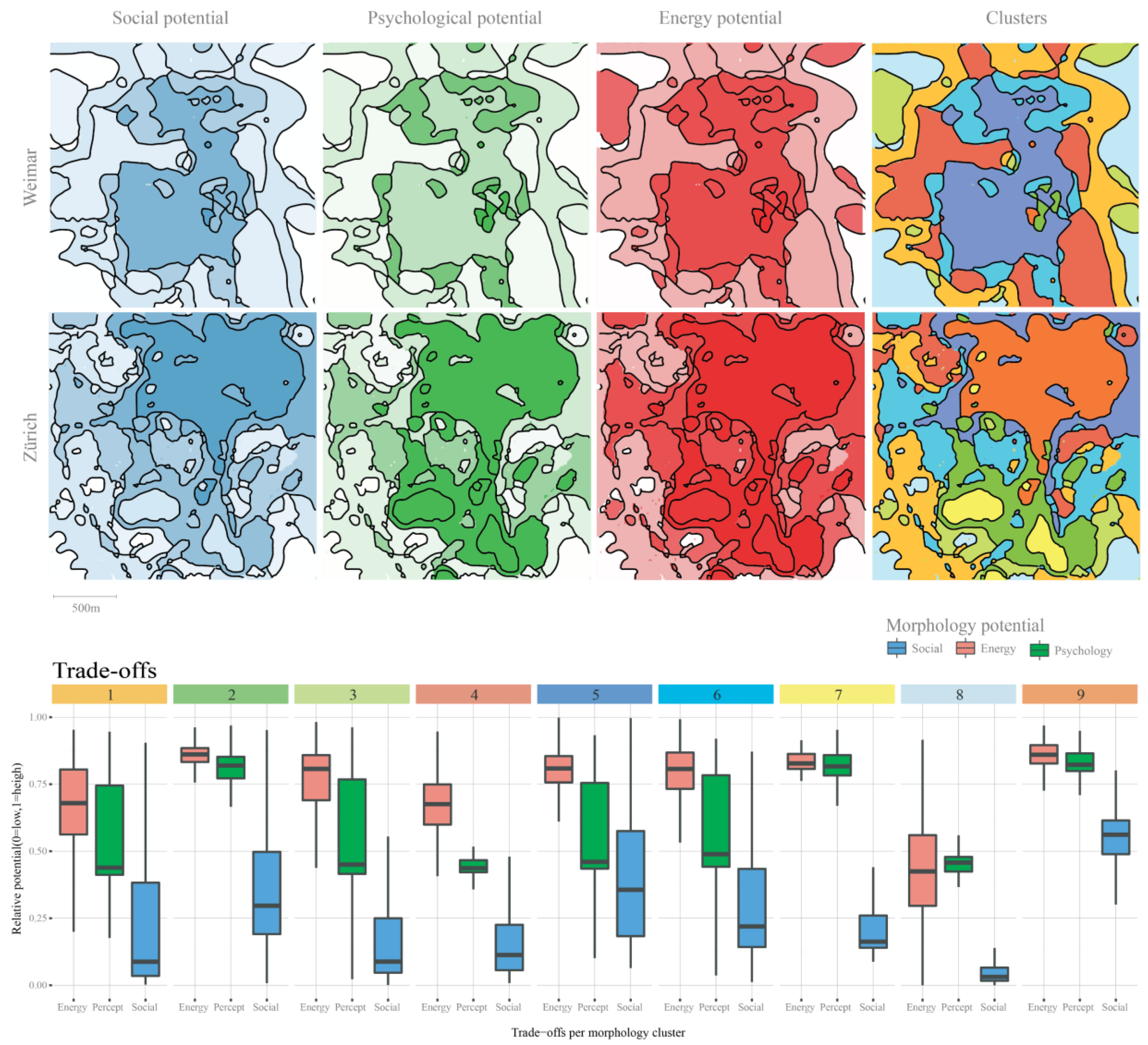
5.2. Results of Measuring Trade-offs Between Social, Psychological and Energy Potential of Urban Form
In the following we examine the spatial distribution of the clustering results and identify the trade-offs between their social, psychological, and energy potential (
Figure 10 and
Figure 13).
As shown in
Figure 18, the individual grid cells are clustered based on density and centrality as they form coherent spatial boundaries that reflect both the underlying building typology as well as the location in the city. Additionally, we conclude that eight of nine morphological clusters could be identified in both cities. Only cluster number
seven, characterized mostly by dense multi-story administrative buildings with relatively central location in Zurich, was absent in Weimar. The remaining clusters are present in each city showing consistency in the identified typologies.
In the following, we explore the general patterns of trade-offs between the social, psychological, and energy potentials for individual clusters. For this purpose, we aggregate the potentials of all grid cells from each cluster and map the average value as shown in
Figure 19. The box plots show the center of the potential distribution per cluster and its spread (For the visualization purpose we normalized all three potentials to range from 0 to 1 data (The normalization base was the joined distribution for all clusters in both cities, so the relative differences between them were maintained after the normalization was done)). The spread and the average values indicate that one cluster performs better for all three potentials and one cluster performs the worst. The remaining seven clusters show a wide variety of trade-offs with no clear way of ordering them from best to worst. The best performing cluster,
nine, is characterized by its form as central and dense inner-city street block housing. This typology has the highest average values in all three potentials and the spread of values is relatively low.
On the other hand, cluster eight consists mostly of detached sub-urban housing and has the lowest average potential values with a narrow spread. These results are not surprising as they confirm the hypotheses from qualitative literature on urban planning about devastating effects of low density sub-urban development and the positive impact of dense urban centers. Therefore, we consider these mainly as validation of our methodology. The more interesting results are to be found in clusters one to seven. Here, the effect of location is observed by keeping the building form constant and the effect of different building typologies in the same location in the city.
For the former, clusters three and six demonstrate how similar modernist condominium typologies perform differently when located at the edge of the city (cluster three) compared to the center (cluster six). Both clusters perform similarly in the energy and psychological potential as these are closely related to the local properties of the urban form. However, they are significantly different in their social potential as this depends on the location in the city structure. For the latter, clusters two and five show the influence of building typology by keeping the location constant. Both clusters spread over relatively central locations however cluster five consists of smaller, detached two to four story housing whereby cluster two is comprised of many large, compact administrative buildings. As a result, both perform similarly in the social dimension but differ in the energy and psychological dimensions.
More individual comparisons can be drawn from these results depending on the specific planning problem or the research question. One could, for instance, compare different design variations for a given location or search for appropriate locations for specific building typologies. This would however go beyond the scope of this paper, which focuses on developing and testing the methodological framework necessary for such investigations.
6. Discussion
In this paper, we present a methodological framework to assess and evaluate urban form with respect to social, psychological, and energy demand factors. Thereby, the scope is limited to identify potentials that urban geometry can offer. Although these potentials might not fully reflect the real situation, due to other confounding non-geometric factors, the potentials provide valuable information for early urban planning stages, when many strategic decisions about urban form are made. This can influence the social, psychological, and energy aspects of a district or neighborhood.
The three potentials used in the study demonstrate a method to investigate the effect of urban form on different performance criteria. We also introduce a method to create predictive models to show the performance in new situations (as it is necessary for the case of urban design). The methodological framework therefore presents an approach that is extendable by other aspects and case studies to improve the existing models.
In order to assess the social potential of urban form, we developed a model that applies graph-based measures to the geometry of the street network. With this, an approximation of how many people one potentially can reach from a certain location is calculated. The results for both case studies have clear patterns for how this social accessibility is distributed across the city where strong differences between the two cities were revealed. However, a clear limitation of the model is that it only captures the quantitative aspect of interaction (the number of encounters theoretically possible). The quality of interaction is not considered. Here, questions arise, such as who are the people that potentially meet? Would they also interact when they meet? Or do the local properties of the environment foster or hinder interaction, such as noisy streets or wide sidewalks?
The method to assess psychological potential includes a workflow to systematically investigate the effect of urban form on physiological changes and subjective ratings. The greatest challenge considered in the approach are potential influences from many different (geometrical and non-geometrical, static and dynamic) variables that influence human perception of spaces. By applying the real-to-virtual workflow, the influence of urban form on the implicit response (skin conductance) is rather low (different results in VR-Studies compared to the field study). Perhaps the measures describe urban form (2D/3D isovists) were not sufficient to capture perception-relevant features. It might also be due to physiological data itself, which strongly differs from participant to participant. Although the physiological data and physiological response was calibrated for each individual, this is an emerging technique and the technological issues of missing wristband data should be improved in the future. The predictive power for the explicit response (subjective ratings) was, on the other hand, much higher. However, the variance in the responses was much less than the physiological data (mostly neutral, some positive, and very few negative evaluations).
Finally, due to the large number of variables, one would consequently also need a large sample size. However, due to resource constraints to conduct such a study, only a limited number of studies was possible. Here future research should consider using crowd sourcing to collect data about human perception of urban spaces.
For the energy analysis, we focus on the energy demand for heating and cooling, which from an urban form perspective is mainly influenced by the relation of the exterior surfaces to the total building volume and by inter-building shading. For the analysis we used the existing tool CitySim and investigated different modelling approaches to reduce computation time. The results of the analysis confirm that large buildings with a compact shape demand less energy than small and complex building shapes.
For the future, the ecological potential could be extended by infrastructural aspects, such as transportation, renewable energy, and lifecycle of building materials. Since these are physically linked to the street network, relationships to the social potential can be expected.
Finally, we developed a methodology to investigate trade-offs between the different potentials. For this, the results of the different potentials were mapped on one common analysis grid. We used this grid to identify different types of urban form. We used building intensity and closeness centrality for a k-means clustering analysis which could identify classical urban typologies. Since both cities identified similar typologies, it would be interesting if this also holds true for other cities.
Based on the identified urban typologies, we visualized their performance, where we could identify that the different types also perform differently for the three potentials. The methodology introduced in this paper allowed us to explore the influence of building typologies and location on the social, psychological, and energy performance. We also identified two urban form types—the dense inner-city block and the low dense suburban settlement structure—which strongly represent and minimally represent all three potentials in both cities, respectively.
The framework can be used to assess strategic decisions regarding urban form during the early planning stages. It reveals potentials regarding different aspects including trade-offs regarding different types of urban form, and thus can inform urban design in order to create more sustainable cities. Due to the multiple criteria urban design must consider, the framework could be extended by other aspects (e.g., economic potential, land use potential or livability potential). Furthermore, some of the methods (especially the psychological potential and the identification of urban typologies in the trade-off section) require future work to test and improve their generalizability.
Supplementary Materials
The following data are available online at
https://zenodo.org/record/1638667 under DOI 10.5281/zenodo.1638667: 360 degree video Weimar, 360 video Zurich, 3d Model of Weimar building stock in LOD1, 3d Model of Zurich building stock in LOD1, Weimar street network, Zurich street network. The research project of which this paper is part of is documented at
https://www.esum.arch.ethz.ch/.
Author Contributions
Author Contributions: S.S., R.K., G.S. and D.D. are responsible for the funding acquisition, developed the initial research plan, contributed to the conceptualization of the research goals, and coordinated and supervised the project. M.B. developed the methodology for the evaluation of the social potential of UF. S.K., V.O., D.G. and M.B. developed the methodology for the evaluation of the psychological potential of UF. D.G. developed the methodology for the evaluation of the energy potential of UF. D.G. and S.K. carried out empirical investigations and pilot-tests for the psychological potential of UF. D.G. and M.B. collected and prepared the resources for studying the energy potential of UF. M.B. collected and prepared the resources for studying the social potential of UF. S.K., D.G., V.O. and M.B. collected and prepared the resources for studying the psychological potential of UF. V.O. and S.K. performed the formal analysis of the psychological potential dataset. D.G. performed the formal analysis of the energy potential dataset. M.B. performed the formal analysis of the social potential dataset. M.B. developed the visualizations for the social potential of UF and trade-offs. V.O. developed visualizations for the psychological potential of UF. D.G. and M.B. developed visualizations for the energy potential of UF. M.B., S.S, S.K., D.G. and V.O. contributed to writing the original draft. R.K. reviewed the original draft.
Funding
This research has been a direct collaboration between ETH Zurich and Bauhaus University Weimar and was funded by Swiss National Science Foundation (Schweizerischer Nationalfonds zur Foerderung der Wissenschaftlichen Forschung), grant number 10 0 013L_149552” and the German Research Foundation (Deutsche Forschungs- gemeinschaft), grant number DO551/21-01. Martin Bielik was party funded by Ernst-Abbe doctoral researcher funding program.
Acknowledgments
We gratefully acknowledge the guidance and supervision provide by Christoph Hölscher. We also acknowledge the great work done by Matthias Standfest in developing the data backpack used for collecting the urban environmental data. This study was further supported by student assistants Ashris Choudhury, Alessandro Forino, Ricardo Joss, Olaf Kammler, Dominik Lehmann, Asha Nariyambut Murali, Janette Sesselmann, Cheng-Kai Wang and René Weisser.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
| ASA | Aggregated social accessibility |
| EDA | Electro-dermal activity |
| HVAC | Heating ventilation and air conditioning |
| LOD1 | Level of detail one |
| RC | Relative compactness |
| SCL | Skin conductance level |
| SCR | Skin conductance response |
| UF | Urban form |
| VR | Virtual reality |
| WFR | window to floor ratio |
| WSR | window to surface ratio |
| WWR | window to wall ratio |
References
- Rittel, H.W.J.; Webber, M.M. Dilemmas in a General Theory of Planning. Policy Sci. 1973, 4, 155–169. [Google Scholar] [CrossRef]
- Simon, H.A. The structure of ill structured problems. Artif. Intell. 1973, 4, 181–201. [Google Scholar] [CrossRef]
- Radford, A.D.; Gero, J.S. On optimization in computer aided architectural design. Build. Environ. 1980, 15, 73–80. [Google Scholar] [CrossRef]
- Karimi, K.; Vaughan, L. An evidence-based approach to designing new cities: The English new towns revisited. In Explorations in Urban Design: An Urban Design Research Primer; Ashgate Publishing, Ltd.: Surrey, UK, 2014; pp. 261–274. [Google Scholar]
- Blake, P. Form Follows Fiasco: Why Modern Architecture Hasn’t Worked; Little, Brown: Boston, MA, USA, 1977. [Google Scholar]
- Lawson, B. Language of Space; Architectural Press: Oxford, UK, 2001; ISBN 0-7506-5246-2. [Google Scholar]
- Gehl, J. Life Between Buildings: Using Public Space; Van Nostrand Reinhold: New York, NY, USA, 1987; ISBN 0-442-23011-7. [Google Scholar]
- Jacobs, J. The Death and Life of Great American Cities; Random House: New York, NY, USA, 1961. [Google Scholar]
- Conzen, M.R.G. Alnwick, Northumberland: A Study in Town-Plan Analysis. Trans. Pap. Inst. Br. Geogr. 1960. [Google Scholar] [CrossRef]
- Oliveira, V. Urban Morphology: An Introduction to the Study of the Physical Form of Cities; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Ojha, V.K.; Griego, D.; Kuliga, S.; Bielik, M.; Buš, P.; Schaeben, C.; Treyer, L.; Standfest, M.; Schneider, S.; König, R.; et al. Machine learning approaches to understand the influence of urban environments on humans physiological response. Inf. Sci. 2019, 474, 154–169. [Google Scholar] [CrossRef]
- Marcus, L. Spatial Capital. J. Space Syntax 2010, 1, 30–40. [Google Scholar]
- Vaughan, L. The spatial syntax of urban segregation. Prog. Plan. 2007, 67, 205–294. [Google Scholar] [CrossRef]
- Nubani, L.; Wineman, J. The role of space syntax in identifying the relationship between space and crime. In Proceedings of the 5th Space Syntax Symposium on Space Syntax, Delft, The Netherlands, 13–17 June 2005. [Google Scholar]
- Vaughan, L. The relationship between physical segregation and social marginalisation in the urban environment. World Archit. 2005, 185, 88–96. [Google Scholar]
- Porta, S.; Strano, E.; Iacoviello, V.; Messora, R.; Latora, V.; Cardillo, A.; Wang, F.; Scellato, S. Street Centrality and Densities of Retail and Services in Bologna, Italy. Environ. Plan. B Plan. Des. 2009, 36, 450–465. [Google Scholar] [CrossRef]
- Harries, K. Property Crimes and Violence in United States: An Analysis of the influence of Population density. Int. J. Crim. Justice Sci. 2006, 1, 5. [Google Scholar]
- Carlino, G.A.; Chatterjee, S.; Hunt, R.M. Urban density and the rate of invention. J. Urban Econ. 2007, 61, 389–419. [Google Scholar] [CrossRef]
- Weber, M. The Nature of Social Action in Runciman, WG Weber: Selections in Translation; Cambridge University Press: Cambridge, UK, 1991; Volume 2, p. 111. [Google Scholar]
- Bielik, M.; König, R.; Schneider, S.; Varoudis, T. Measuring the Impact of Street Network Configuration on the Accessibility to People and Walking Attractors. Netw. Spat. Econ. 2018, 1–20. [Google Scholar] [CrossRef]
- Strano, E.; Nicosia, V.; Latora, V.; Porta, S.; Barthélemy, M. Elementary processes governing the evolution of road networks. Sci. Rep. 2012, 2, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Freeman, L.C. A set of measures of centrality based on betweenness. Sociometry 1977, 40, 35–41. [Google Scholar] [CrossRef]
- Hillier, B.; Hanson, J. The Social Logic of Space; Cambridge University Press: Cambridge, UK, 1984. [Google Scholar]
- Turner, A. Angular Analysis. In Proceedings of the 3rd International Symposium on Space Syntax, Atlanta, GA, USA, 7–11 May 2001; pp. 7–11. [Google Scholar]
- Hillier, B.; Iida, S. Network and Psychological Effects: A Theory of Urban Movement; Springer: Berlin/Heidelberg, Germany, 2005; pp. 475–490. [Google Scholar]
- Turner, A.; Dalton, R.C. A simplified route choice model using the shortest angular path assumption. In Proceedings of the 8th International Conference on GeoCompuation, Ann Arbor, MI, USA, 31 July–3 August 2005. [Google Scholar]
- Varoudis, T.; Law, S.; Karimi, K.; Hillier, B.; Penn, A. Space syntax angular betweenness centrality revisited. In Proceedings of the 2013 International Space Syntax Symposium; Seoul, South Korea, 31 October–3 November 2013. [Google Scholar]
- Bielik, M.; Emo, B.; Schneider, S.; Hölscher, C. Does urban density follow centrality? Empirical study on the influence of street network centrality on urban density and its implications for the prediction of pedestrian flows. In Proceedings of the 11th International Space Syntax Symposium, Lisbon, Portugal, 3–7 July 2017. [Google Scholar]
- Okabe, A.; Sugihara, K. Spatial Analysis along Networks: Statistical and Computational Methods; John Wiley & Sons: Chichester, UK, 2012; ISBN 978-1-119-96710-1. [Google Scholar]
- Hillier, B. The hidden geometry of deformed grids: Or, why space syntax works, when it looks as though it shouldn’t. Environ. Plan. B Plan. Des. 1999, 26, 169–191. [Google Scholar] [CrossRef]
- Ratti, C. Space syntax: Some inconsistencies. Environ. Plan. B Plan. Des. 2004, 31, 487–499. [Google Scholar] [CrossRef]
- Batty, M. Accessibility: In search of a unified theory. Environ. Plan. B Plan. Des. 2009, 36, 191–194. [Google Scholar] [CrossRef]
- Hansen, W.G. How Accessibility Shapes Land Use. J. Am. Inst. Plan. 1959, 25, 73–76. [Google Scholar] [CrossRef]
- Handy, S.L.; Niemeier, D.A. Measuring accessibility: An exploration of issues and alternatives. Environ. Plan. A 1997, 29, 1175–1194. [Google Scholar] [CrossRef]
- Hillier, B.; Yang, T.; Turner, A. Normalising least angle choice in Depthmap and it opens up new perspectives on the global and local analysis of city space. J. Space Syntax 2012, 3, 155–193. [Google Scholar]
- Appleton, J. Landscape evaluation: The theoretical vacuum. Trans. Inst. Br. Geogr. 1975, 120–123. [Google Scholar] [CrossRef]
- Herzog, T.R. A cognitive analysis of preference for urban spaces. J. Environ. Psychol. 1992, 12, 237–248. [Google Scholar] [CrossRef]
- Lynch, K. The Image of the City; MIT Press: Cambridge, MA, USA, 1960; Volume 11. [Google Scholar]
- Benedikt, M.L. To take hold of space: Isovists and isovist fields. Environ. Plan. B Plan. Des. 1979, 6, 47–65. [Google Scholar] [CrossRef]
- Ewing, R.; Handy, S. Measuring the unmeasurable: Urban design qualities related to walkability. J. Urban Des. 2009, 14, 65–84. [Google Scholar] [CrossRef]
- Knöll, M.; Li, Y.; Neuheuser, K.; Rudolph-Cleff, A. Using space syntax to analyse stress ratings of open public spaces. In Proceedings of the 10th International Space Syntax Symposium, London, UK, 13–17 July 2015; Volume 123, pp. 247–259. [Google Scholar]
- Knöll, M.; Neuheuser, K.; Vogt, J.; Rudolph-Cleff, A. Einflussfaktoren der gebauten Umwelt auf wahrgenommene Aufenthaltsqualität während der Nutzung städtischer Räume. Umw. Psychol. Ger. 2014, 35, 84–102. [Google Scholar]
- Roe, J.J.; Aspinall, P.A.; Mavros, P.; Coyne, R. Engaging the brain: The impact of natural versus urban scenes using novel EEG methods in an experimental setting. Environ. Sci. 2013, 1, 93–104. [Google Scholar] [CrossRef]
- Neale, C.; Aspinall, P.; Roe, J.; Tilley, S.; Mavros, P.; Cinderby, S.; Coyne, R.; Thin, N.; Bennett, G.; Thompson, C.W. The Aging Urban Brain: Analyzing Outdoor Physical Activity Using the Emotiv Affectiv Suite in Older People. J. Urban Health 2017, 94, 869–880. [Google Scholar] [CrossRef]
- Emo, B.; Treyer, L.; Schmitt, G.; Hoelscher, C. Towards defining perceived urban density. In Proceedings of the 35th International Conference on Education and Research in Computer Aided Architectural Design in Europe: ShoCK! Sharing of Computable Knowledge; Education and Research in Computer Aided Architectural Design in Europe (eCAADe), Rome, Italy, 22 September 2017; Volume 2, pp. 637–646. [Google Scholar]
- Hijazi, I.H.; Koenig, R.; Schneider, S.; Li, X.; Bielik, M.; Schmit, G.N.J.; Donath, D. Geostatistical analysis for the study of relationships between the emotional responses of urban walkers to urban spaces. Int. J. E Plan. Res. 2016, 5, 1–19. [Google Scholar] [CrossRef]
- Evans, G.W. Environmental Stress; CUP Archive: New York, NY, USA, 1984. [Google Scholar]
- Raja, M.; Exler, A.; Hemminki, S.; Konomi, S.; Sigg, S.; Inoue, S. Towards pervasive geospatial affect perception. GeoInformatica 2018, 22, 143–169. [Google Scholar] [CrossRef]
- Poh, M.-Z.; Swenson, N.C.; Picard, R.W. A wearable sensor for unobtrusive, long-term assessment of electrodermal activity. IEEE Trans. Biomed. Eng. 2010, 57, 1243–1252. [Google Scholar] [PubMed]
- Benedek, M.; Kaernbach, C. A continuous measure of phasic electrodermal activity. J. Neurosci. Methods 2010, 190, 80–91. [Google Scholar] [CrossRef] [PubMed]
- Boucsein, W. Electrodermal Activity; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Braithwaite, J.J.; Watson, D.G.; Jones, R.; Rowe, M. A guide for analysing electrodermal activity (EDA) & skin conductance responses (SCRs) for psychological experiments. Psychophysiology 2013, 49, 1017–1034. [Google Scholar]
- Figner, B.; Murphy, R.; Schulte-Mecklenbeck, M.; Kuehberger, A.; Ranyard, R. A Handbook of Process Tracing Methods for Decision Research: A Critical Review and User’s Guide; Psychology Press: New York, NY, USA, 2010. [Google Scholar]
- Bielik, M.; Schneider, S.; Kuliga, S.; Valášek, M.; Donath, D. Investigating the effect of urban form on the environmental appraisal of streetscapes. In Proceedings of the 10th International Space Syntax Symposium, London, UK, 13–17 July 2015; pp. 1–13. [Google Scholar]
- Aspinall, P.; Mavros, P.; Coyne, R.; Roe, J. The urban brain: Analysing outdoor physical activity with mobile EEG. Br. J. Sports Med. 2015, 49, 272–276. [Google Scholar] [CrossRef] [PubMed]
- Franz, G.; Wiener, J.M. Exploring isovist-based correlates of spatial behavior and experience. In Proceedings of the 5th International Space Syntax Symposium, Delft, The Netherlands, 13–17 June 2005. [Google Scholar]
- Kuliga, S.; Dalton, R.C.; Hölscher, C. Aesthetic and Emotional Appraisal of the Seattle Public Library and its relation to spatial configuration. In Proceedings of the Ninth International Space Syntax Symposium, Seoul, Korea, 31 October–3 November 2013. [Google Scholar]
- Stamps, A.E., III. Isovists, enclosure, and permeability theory. Environ. Plan. B Plan. Des. 2005, 32, 735–762. [Google Scholar] [CrossRef]
- Griego, D.; Kuliga, S.; Bielik, M.; Standfest, M.; Ojha, V.K.; Schneider, S.; König, R.; Donath, D.; Schmitt, G.; Miltiadis, C.; et al. ESUM Urban Sensing Handbook: Component, Assembly and Operational Guide: Sensor Backpack & 360 Videos; ETH Zurich: Zurich, Switzerland, 2017. [Google Scholar]
- Kuliga, S.F.; Thrash, T.; Dalton, R.C.; Hölscher, C. Virtual reality as an empirical research tool—Exploring user experience in a real building and a corresponding virtual model. Comput. Environ. Urban Syst. 2015, 54, 363–375. [Google Scholar] [CrossRef]
- König, R.; Scheider, S.; Hamzi, I.; Bielik, M.; Schmitt, G.; Donath, D. Using geo statistical analysis to detect similarities in emotional responses of urban walkers to urban space. In Proceedings of the 6th International Conference on Design Computing and Cognition (DCC14), London, UK, 23–25 June2014. [Google Scholar]
- Kaplan, R.; Kaplan, S. The Experience of Nature: A Psychological Perspective; CUP Archive: New York, NY, USA, 1989. [Google Scholar]
- Geletka, V.; Sedláková, A. Shape of buildings and energy consumption. Czas. Tech. 2012, 109, 124–128. [Google Scholar]
- Rodrigues, E.; Amaral, A.R.; Gaspar, A.R.; Gomes, Á. How reliable are geometry-based building indices as thermal performance indicators? Energy Convers. Manag. 2015, 101, 561–578. [Google Scholar] [CrossRef]
- Hemsath, T.L.; Alagheband Bandhosseini, K. Sensitivity analysis evaluating basic building geometry’s effect on energy use. Renew. Energy 2015, 76, 526–538. [Google Scholar] [CrossRef]
- Kämpf, J.H.; Robinson, D. Optimisation of building form for solar energy utilisation using constrained evolutionary algorithms. Energy Build. 2010, 42, 807–814. [Google Scholar] [CrossRef]
- Allegrini, J.; Orehounig, K.; Mavromatidis, G.; Ruesch, F.; Dorer, V.; Evins, R. A review of modelling approaches and tools for the simulation of district-scale energy systems. Renew. Sustain. Energy Rev. 2015, 52, 1391–1404. [Google Scholar] [CrossRef]
- Sabidussi, G. The centrality index of a graph. Psychometrika 1966, 31, 581–603. [Google Scholar] [CrossRef] [PubMed]
Figure 1.
Case study areas in two cities—Weimar, Germany and Zürich, Switzerland. Both case studies comprise 6.25 km
2 and contain the path used to study psychological potential of urban form. (Data source:
OpenStreetMaps.org and
Mapbox.com).
Figure 1.
Case study areas in two cities—Weimar, Germany and Zürich, Switzerland. Both case studies comprise 6.25 km
2 and contain the path used to study psychological potential of urban form. (Data source:
OpenStreetMaps.org and
Mapbox.com).
Figure 2.
Various street network representations used to represent the street network in the ASA model: (a) Street center line; (b) Axial map; (c) Segment map.
Figure 2.
Various street network representations used to represent the street network in the ASA model: (a) Street center line; (b) Axial map; (c) Segment map.
Figure 3.
Discretization of the street network: (a) Segment map; (b) Betweenness R600 (red = high Betweenness, green = low Betweenness); (c) Street network discretized to evenly distributed points (at 5 m distance).
Figure 3.
Discretization of the street network: (a) Segment map; (b) Betweenness R600 (red = high Betweenness, green = low Betweenness); (c) Street network discretized to evenly distributed points (at 5 m distance).
Figure 4.
Aggregated social accessibility (ASA) results (potential for social interaction) interpolated via Universal Kriging on raster grid and mapped to show the spatial distribution of social potential.
Figure 4.
Aggregated social accessibility (ASA) results (potential for social interaction) interpolated via Universal Kriging on raster grid and mapped to show the spatial distribution of social potential.
Figure 5.
Distribution of ASA (measure potential for social interaction) across the two case studies. (a) Violin plot, with highlighted median (red) and mean (blue) values; (b) histogram with highlighted median (red) and mean (blue).
Figure 5.
Distribution of ASA (measure potential for social interaction) across the two case studies. (a) Violin plot, with highlighted median (red) and mean (blue) values; (b) histogram with highlighted median (red) and mean (blue).
Figure 6.
Isovist visualized by rays. (a) perspective view of 3D isovist and (b) Top view of 2D isovist.
Figure 6.
Isovist visualized by rays. (a) perspective view of 3D isovist and (b) Top view of 2D isovist.
Figure 7.
Three levels of abstraction: (a), (b), and (c) are example images of Zurich, Switzerland in the three abstraction levels. experimental framework (field study, 360° video and geometry model) that enhances experimental control in each setting.
Figure 7.
Three levels of abstraction: (a), (b), and (c) are example images of Zurich, Switzerland in the three abstraction levels. experimental framework (field study, 360° video and geometry model) that enhances experimental control in each setting.
Figure 8.
Mapping of arousal peaks from the results of the field study, 360°-video study, and geometry model study (left to right). Arousal peaks mapped along the two experimental paths. The quantified EDA results are shown with red dots indicating more arousal peaks than the blue and green dot; white indicates a very low number of arousal peaks in the EDA data.
Figure 8.
Mapping of arousal peaks from the results of the field study, 360°-video study, and geometry model study (left to right). Arousal peaks mapped along the two experimental paths. The quantified EDA results are shown with red dots indicating more arousal peaks than the blue and green dot; white indicates a very low number of arousal peaks in the EDA data.
Figure 9.
Results from the virtual-reality studies: Subjective environmental appraisal, mapped along the two experimental paths in the 360° video (left) and block model (right), for Zürich (above) and Weimar (below). The red areas indicate negative ratings, which are surprisingly few in the virtual setting; and absent in the Zurich evaluation. The heading clicker refers to the way participants evaluated the environment, pressing the buttons like, neutral, or dislike continuously during the virtual video presentation.
Figure 9.
Results from the virtual-reality studies: Subjective environmental appraisal, mapped along the two experimental paths in the 360° video (left) and block model (right), for Zürich (above) and Weimar (below). The red areas indicate negative ratings, which are surprisingly few in the virtual setting; and absent in the Zurich evaluation. The heading clicker refers to the way participants evaluated the environment, pressing the buttons like, neutral, or dislike continuously during the virtual video presentation.
Figure 10.
Extrapolated (from path to district) predictions of the psychological potential based on the decision tree predictive model for Weimar (left) and Zurich (right). The prediction combines the subjective ratings and the physiological arousal to estimate the size and the direction of the psychological potential of urban form (from negative-dark red to positive-dark blue).
Figure 10.
Extrapolated (from path to district) predictions of the psychological potential based on the decision tree predictive model for Weimar (left) and Zurich (right). The prediction combines the subjective ratings and the physiological arousal to estimate the size and the direction of the psychological potential of urban form (from negative-dark red to positive-dark blue).
Figure 11.
Distribution of the Psychological potential (predicted arousal peaks/s combined with psychological subjective ratings) across the two case studies. Score above zero stand for positive arousal and scores below zero stand for negative arousal. (a) violin plot, with highlighted median (red) and mean (blue) values (b) histogram with highlighted median (red) and mean (blue).
Figure 11.
Distribution of the Psychological potential (predicted arousal peaks/s combined with psychological subjective ratings) across the two case studies. Score above zero stand for positive arousal and scores below zero stand for negative arousal. (a) violin plot, with highlighted median (red) and mean (blue) values (b) histogram with highlighted median (red) and mean (blue).
Figure 12.
Correlation of energy demand (winter and summer) to the relative compactness (RC) and shape coefficient (Cf) for the two cases of Zurich (top row) and Weimar (bottom row).
Figure 12.
Correlation of energy demand (winter and summer) to the relative compactness (RC) and shape coefficient (Cf) for the two cases of Zurich (top row) and Weimar (bottom row).
Figure 13.
Heating energy use intensity (kW/m2/day) for Zurich (left) and Weimar (right).
Figure 13.
Heating energy use intensity (kW/m2/day) for Zurich (left) and Weimar (right).
Figure 14.
Distribution of the Energy potential (Building energy demand for heating in kWh/m2/day). (a) Violin plot, with highlighted median (red) and mean (blue) values; (b) histogram with highlighted median (red) and mean (blue).
Figure 14.
Distribution of the Energy potential (Building energy demand for heating in kWh/m2/day). (a) Violin plot, with highlighted median (red) and mean (blue) values; (b) histogram with highlighted median (red) and mean (blue).
Figure 15.
Semi-variogram curves fitted by Universal Kriging spatial interpolation method. (a) Social potential for Zurich, (b) Psychological potential for Zurich, (c) Social potential for Weimar, and (d) Psychological potential for Weimar.
Figure 15.
Semi-variogram curves fitted by Universal Kriging spatial interpolation method. (a) Social potential for Zurich, (b) Psychological potential for Zurich, (c) Social potential for Weimar, and (d) Psychological potential for Weimar.
Figure 16.
Radius-based building intensity calculation illustrated for one analysis grid cell.
Figure 16.
Radius-based building intensity calculation illustrated for one analysis grid cell.
Figure 17.
Elbow method illustrating the relationship between the number of clusters k and the total within-clusters variation. The vertical line indicates minimal number of clusters. The black vertical line indicates the chosen number of clusters.
Figure 17.
Elbow method illustrating the relationship between the number of clusters k and the total within-clusters variation. The vertical line indicates minimal number of clusters. The black vertical line indicates the chosen number of clusters.
Figure 18.
Morphological clusters with box plots displaying the distribution of clustering parameters (i.e., closeness centrality and building intensity density) for each cluster. The box width illustrates number of elements in the cluster.
Figure 18.
Morphological clusters with box plots displaying the distribution of clustering parameters (i.e., closeness centrality and building intensity density) for each cluster. The box width illustrates number of elements in the cluster.
Figure 19.
The average social, psychological, and energy potentials mapped for each cluster (Dark color = high potential, Light color = low potential). Box plots display the distribution of potentials per cluster. The box width illustrates the number of elements in the cluster.
Figure 19.
The average social, psychological, and energy potentials mapped for each cluster (Dark color = high potential, Light color = low potential). Box plots display the distribution of potentials per cluster. The box width illustrates the number of elements in the cluster.
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).