Variations on the Theme “Definition of the Orthodrome”

Abstract

A geodesic or geodetic line on a sphere is called the orthodrome. Research has shown that the orthodrome can be defined in a large number of ways. This article provides an overview of various definitions of the orthodrome. We recall the definitions of the orthodrome according to the greats of geodesy, such as Bessel and Helmert. We derive the equation of the orthodrome in the geographic coordinate system and in the Cartesian spatial coordinate system. A geodesic on a surface is a curve for which the geodetic curvature is zero at every point. Equivalent expressions of this statement are that at every point of this curve, the principal normal vector is collinear with the normal to the surface, i.e., it is a curve whose binormal at every point is perpendicular to the normal to the surface, and that it is a curve whose osculation plane contains the normal to the surface at every point. In this case, the well-known Clairaut equation of the geodesic in geodesy appears naturally. It is found that this equation can be written in several different forms. Although differential equations for geodesics can be found in the literature, they are solved in this article, first, by taking the sphere as a special case of any surface, and then as a special case of a surface of rotation. At the end of this article, we apply calculus of variations to determine the equation of the orthodrome on the sphere, first in the Bessel way, and then by applying the Euler–Lagrange equation. Overall, this paper elaborates a dozen different approaches to orthodrome definitions.

1. Introduction

The orthodrome or great circle is the intersection of a sphere and a plane passing through the centre of the sphere. Every arc of a great circle is a geodetic line or geodesic on the sphere; so, great circles in spherical geometry are the natural analogue of lines in the plane. For any pair of distinct non-antipodal points on the sphere, there is a unique great circle that passes through both points. Every great circle through any point also passes through its antipodal point; so, there are infinite great circles through two antipodal points. The shorter of two great circle arcs between two distinct points on the sphere is the shortest path between them on the sphere.

A great circle is the largest circle that exists on any sphere. Any diameter of any great circle coincides with the diameter of the sphere, and therefore every great circle is concentric with the sphere and has the same radius. Any other circle on a sphere is called a small circle and is the intersection of the sphere with a plane that does not pass through its centre.

Some examples of great circles on the celestial sphere are the celestial horizon, the celestial equator, and the ecliptic. Great circles are also used as approximation of geodesics on the Earth’s surface for air or sea navigation, as well as on spheroidal celestial bodies. The equator of an idealised Earth is a great circle, and each meridian and its opposite meridian form a great circle. A great circle divides the Earth into two hemispheres.

The easiest way to measure the distance between two points on a map is to draw a straight line connecting the two points. In this case, the straight line is taken to be the image of a great circle, i.e., an arc of a great circle. However, a line segment on small-scale maps is generally not an image of a great circle. The exception is the gnomonic projection. Therefore, distances and azimuths measured directly from the maps will not be accurate; so, it is useful to determine the orthodromicity of a map projection. This refers to the degree of approximation of the image of the orthodrome on the map and the straight line connecting the endpoints. Orthodromicity depends on the properties of the projection and can be defined by the largest deviation of the image of the orthodrome from the direction and the difference between their length and azimuth [1].

Conformal map projections have an important property from the point of view of measuring distances and direction positions on maps. In these projections, the arc of a great circle of a sphere is not mapped into a straight line. The properties of conformality and orthodromicity cannot be fulfilled simultaneously. In cases where the non-orthodromicity of a conformal projection is particularly pronounced, the accuracy of measuring straight lines and directions is significantly reduced [2]. The assessment of the deviation of a straight line from the image of the orthodrome is important when choosing the most suitable map projection for a given area.

Although we will encounter a large number of mathematical expressions and equations in this article, for those who find such an approach slightly more difficult, let us say that the concept of an orthodrome can be described without mathematical relations. For example, let us take an orange as an approximate model of a sphere. If we put a thin rubber band on the orange so that it does not slip, it will take the shape of an orthodrome. Instead of the orange, we can use a tennis ball or any other object in the shape of a ball. In a similar way, using the equilibrium of an elastic band on a surface, Ljusternik [3] explains the geodesic. Consider the surface of a sphere. A rubber band stretched along a large circle will be in equilibrium and will describe a great circle. If we cut the sphere with a plane that does not pass through its centre, we will not be able to put the rubber band in equilibrium, and it will slip; so, the small circle is not an orthodrome [3].

To understand the following text, we will need basic knowledge of analytical, spherical and differential geometry. Spherical trigonometry formulas are applied in various areas, such as astronomy, cartography or satellite geodesy. Classical versions of these formulas can be found in the literature (e.g., [4]).

However, the basic spherical trigonometry formulas can be obtained very easily using vector algebra, as demonstrated by Krilov [5]. Hence, the idea is to approach problems related to the orthodrome from the point of view of vector algebra as well, with a small extension with terms from differential geometry. Such an approach enables a simpler and clearer exposition, freeing the reader from the often-clumsy expressions of spherical trigonometry.

Great circle navigation or orthodromic navigation (from the ancient Greek ορθός (orthós) ‘right angle’ and δρόμος (drómos) ‘road’) is the practice of navigating a vessel (ship or aircraft) along a great circle. Such routes give the shortest distance between two points on the Earth’s sphere [6]. Orthodrome properties are usually stated without proof. This led to the idea to consider different definitions of that curve on the sphere using a mathematical apparatus that is sometimes very simple and sometimes, perhaps at first glance, complicated.

In geodesy, a rotating ellipsoid is very often used for the Earth model. Geodesics on the ellipsoid are very well researched and there is a relatively extensive literary body on them [7,8,9]. Sometimes a sphere is used instead of a rotating ellipsoid as a simpler model. A geodesic on a sphere as a special case of geodesic on the ellipsoid is called the orthodrome. Research has shown that the orthodrome can be defined in an unusually large number of ways. This is why this article deals with various definitions of the orthodrome.

In the following sections, we recall the definitions of the great scientists, such as Bessel [7] and Helmert [8]. We derive the equation of the orthodrome in the geographic coordinate system and in the Cartesian spatial coordinate system. Since the orthodrome is a geodesic on a sphere, we recall the definition of a geodesic on a general surface. This definition states that it is a curve for which the geodetic curvature at every point is zero. Equivalent expressions of this statement are that at every point of this curve, the principal normal vector is collinear with the normal to the surface, that it is a curve whose binormal at every point is perpendicular to the normal to the surface, and that it is a curve whose osculation plane contains the normal to the surface at every point. This way, the well-known Clairaut theorem or Clairaut equation of a geodesic appears naturally. It is found that this equation can be written in several different forms. Since the orthodrome is a geodesic, and for such curves, corresponding differential equations have been derived in the literature but seldom solved, they are solved in this article, first, by taking the sphere as a special case of any surface, and then as a special case of a surface of revolution. At the end of this article, we apply calculus of variations to determine the equation of the orthodrome on the sphere, first in the Bessel way, and then by applying the Euler–Lagrange equation.

In all the following derivations, we assume without loss of generality, and for the sake of economy of writing, that the radius of the sphere is equal to 1.

2. Definition of the Orthodrome According to Helmert

Let us first consider how Helmert [8] approached the introduction of the concept of the orthodrome. Let us assume that all level surfaces are concentric spherical surfaces, and therefore all plumb lines are lines passing through a common centre. Any two plumb lines then have a common vertical plane, which intersects the physical surface of the Earth in a more or less wavy profile but intersects every level surface in a great circle.

The horizontal distance between two points also gives the shortest distance between the projections of both points on the corresponding level surface.

To prove this, let us divide the greatest circular arc P₀P_n (Figure 1) between the projections marked P₀ and P_n into infinitesimal segments P₀P₁, P₁P₂, P₂P₃, etc., and describe circles around P₀ with radii P₀P₁, P₁P₂, P₂P₃, etc. These circles are small circles on the sphere, which are arranged in pairs at the same distance from each other. The shortest connection between P₀ and P_n on the surface of the sphere is therefore the greatest circular arc itself, and not any other line P₀P’₁P’₂P’₃… P_n, because it alone follows the shortest distance between small spherical circles everywhere. In general:

P₀P’₁ > P₀P₁, P’₁P’₂ > P₁P₂, etc.

It is also:

P₀P’₁P’₂P’₃… P_n > P₀P₁P₂P₃… P_n.

The exception occurs only for P₀P_n > π. In that case, the shortest distance is equal to the circumference of the sphere minus P₀P_n. Therefore, P₀P_n is no longer a relative minimum since every infinitely close connection between P₀ and P_n is shorter on the small circle.

The plane of the greatest circular arc is the common vertical plane not only of the endpoints but also of all the intermediate points, because all radii are normal to the sphere and this plane passes through the centre of the sphere. It is therefore also the plane corresponding to the three infinitely close points of the greatest circular arc, i.e., the oscillating plane at the corresponding point is also a vertical plane. Because of this property of the greatest circular arc, it can also be called a geodesic on the sphere.

To explain this expression, let us imagine that the inhabitants of an arbitrarily curved surface, which is also a level surface, are given the task of drawing a straight line in terms of geodetic practice from point P₀ in a given direction.

Then, we will first lay a vertical plane from P₀ in that direction and place a point P₁ on the surface, then lay a vertical plane in P₁ through P₀ and place a point P₂ in it (Figure 1), from P₂ in the vertical plane through P₁ place a new point P₃, etc., where it is tacitly assumed that the adjacent points are so close to each other that there is no noticeable difference between the adjacent vertical planes, so that the three adjacent points lie in a plane, which, at this point, is the vertical plane of the surface (sphere).

From the above, we can conclude that in the previous sense, a geodetic line, or geodesic, has the described property in relation to its osculating plane.

3. The Orthodrome as the Intersection of a Plane Passing Through the Centre of a Sphere and the Sphere

Let a sphere of radius 1 centred at the origin of the coordinate system be defined by the following geographic parameterisation:

$$X=\cos \phi \cos \lambda , Y=\cos \phi \sin \lambda , Z=\sin \phi ,$$

(1)

where $\phi$ and $\lambda$ are the latitude and longitude, respectively, $\phi \in \left[-\pi /2,\pi /2\right]$, $\lambda \in \left[-\pi ,\pi \right]$.

Let us define the orthodrome as the intersection of a plane passing through the centre of a sphere and the sphere. Let us write the equation of the plane passing through the centre of the sphere given by (1):

$$AX+BY+CZ=0.$$

(2)

In this equation, A, B and C are three real numbers. Let us insert the expressions for X, Y and Z from (1) into Equation (2). We will obtain the equation of the orthodrome on the sphere in the geographic coordinate system in the following form:

$$A\cos \phi \cos \lambda +B\cos \phi \sin \lambda +C\sin \phi =0.$$

(3)

Let us assume that $\phi \ne \pm \pi /2$. After dividing by $\cos \phi$, Equation (3) becomes:

$$A\cos \lambda +B\sin \lambda +C\tan \phi =0.$$

(4)

If A and B are equal to zero, then Equation (4) describes the equator, $\phi =0$. Assume that at least one of A and B is not zero and divide (4) by $\sqrt{A^2+B^2}$. With the following notations:

$$\sin \beta ={\displaystyle \frac{A}{\sqrt{A^2+B^2}}}, \cos \beta =-{\displaystyle \frac{B}{\sqrt{A^2+B^2}}}, a={\displaystyle \frac{C}{\sqrt{A^2+B^2}}}$$

(5)

Equation (4) can be written in the following form:

$$\sin (\lambda -\beta )=a\tan \phi .$$

(6)

Constants a and $\beta$ can be given a simple geometric interpretation. Namely, it is easy to see that $\beta$ is the longitude of the point where the orthodrome intersects the equator, while a is the cotangent of the angle between the orthodrome and the equator at their intersection. Furthermore, with the assumption $\sqrt{A^2+B^2}\ne 0$, it is easy to determine that the orthodrome has the highest and lowest points, vertices, whose geographical coordinates are determined by $\lambda =\beta \pm \pi /2$ and $\tan \phi =1/a$.

If $A=B=0$ and $C\ne 0$, then $\phi =0$, i.e., it is the equator.

If $C=a=0$, the equation of the orthodrome (6) becomes:

$$\lambda =\beta \pm \pi ,$$

(7)

and the orthodrome is a meridian circle.

Let the great circle be given by its two points with geographic coordinates $({\phi }_1,{\lambda }_1)$ and $({\phi }_2,{\lambda }_2)$. The unit vectors corresponding to these points are as follows:

$${\overrightarrow{r}}_1=\left(\cos {\phi }_1\cos {\lambda }_1,\cos {\phi }_1\sin {\lambda }_1,\sin {\phi }_1\right)$$

$${\overrightarrow{r}}_2=\left(\cos {\phi }_2\cos {\lambda }_2,\cos {\phi }_2\sin {\lambda }_2,\sin {\phi }_2\right),$$

(8)

and the normal vector to the plane to which the orthodrome belongs will be as follows:

$$\overrightarrow{N}={\overrightarrow{r}}_1\times {\overrightarrow{r}}_2=\left(A, B, C\right),$$

(9)

where:

$$A=\cos {\phi }_1\sin {\lambda }_1\sin {\phi }_2-\cos {\phi }_2\sin {\lambda }_2\sin {\phi }_1,$$

$$B=-\cos {\phi }_1\cos {\lambda }_2\sin {\phi }_2+\cos {\phi }_2\cos {\lambda }_2\sin {\phi }_1,$$

(10)

$$C=\cos {\phi }_1\cos {\phi }_2 \mathrm{s}\mathrm{i}\mathrm{n}\left({\lambda }_2-{\lambda }_1\right).$$

We would arrive at the same result from the condition that three points with coordinates $\left(\mathrm{0,0}\right),$ $({\phi }_1,{\lambda }_1)$ and $({\phi }_2,{\lambda }_2)$ lie in a plane.

Since the centre of such a circle coincides with the centre of the sphere, and therefore with the centre of the gnomonic projection, the great circle in that projection is mapped into a line. This important property can be used to determine individual points of the orthodrome and to transfer the orthodrome to a map made in any other projection.

4. Orthodrome in the Cartesian Spatial Coordinate System

In the textbook collection of solved problems in vector analysis [10], there is the equation of the orthodrome (which does not include meridian circles):

$$\overrightarrow{r}={\displaystyle \frac{1}{\sqrt{a^2+{\sin }^2(\lambda -\beta )}}}\left[a\cos \lambda \overrightarrow{i}+a\sin \lambda \overrightarrow{j}+\sin (\lambda -\beta )\overrightarrow{k}\right],$$

(11)

where $a=const.$, $\beta =const.$, $\lambda \in \left[-\pi ,\pi \right]$. The following tasks are solved:

(a)

Prove that the orthodrome (11) lies on the unit sphere.

(b)

Prove that the orthodrome (11) lies in the plane $Ax+By+Cz=0$ passing through the origin, where $\sqrt{A^2+B^2}\ne 0$.

$$\sin \beta ={\displaystyle \frac{A}{\sqrt{A^2+B^2}}}, \cos \beta =-{\displaystyle \frac{B}{\sqrt{A^2+B^2}}}, a={\displaystyle \frac{C}{\sqrt{A^2+B^2}}}.$$

(c)

If a point with geographic coordinates $(\phi ,\lambda )$ belongs to the great circle, then:

$$\sin (\lambda -\beta )=a\tan \phi$$

(d)

Show the following:

$$\left|{\overrightarrow{r}}^{\prime }\right|=\left|{\displaystyle \frac{d\overrightarrow{r}}{d\lambda }}\right|={\displaystyle \frac{a\sqrt{a^2+1}}{a^2+{\sin }^2(\lambda -\beta )}.}$$

(12)

(e)

Show that $\beta$ is the latitude of the point where the orthodrome (11) intersects the equator.

(f)

If $T_1({\phi }_1,{\lambda }_1)$ and $T_2({\phi }_2,{\lambda }_2)$ are two points of the orthodrome, then:

$$\tan \beta ={\displaystyle \frac{\tan {\phi }_1\sin {\lambda }_2-\tan {\phi }_2\sin {\lambda }_1}{\tan {\phi }_1\cos {\lambda }_2-\tan {\phi }_2\cos {\lambda }_1}.}$$

(13)

(g)

Show that a is the cotangent of the angle between the orthodrome and the equator at their intersection.

(h)

If $T_1({\phi }_1,{\lambda }_1)$ and $T_2({\phi }_2,{\lambda }_2)$ are two points of the orthodrome, then it is as follows:

$$a={\displaystyle \frac{\sin \left({\lambda }_1-{\lambda }_2\right)}{\sqrt{{\tan }^2{\phi }_1+{\tan }^2{\phi }_2-2\tan {\phi }_1\tan {\phi }_2\cos \left({\lambda }_1-{\lambda }_2\right)}}}$$

(14)

(i)

The angle $\gamma$ between the orthodrome and the meridian passing through the point $T_1({\phi }_1,{\lambda }_1)$ is determined by the following relation:

$$\cos \gamma ={\displaystyle \frac{1}{\sqrt{a^2+1}}}\cos \left({\lambda }_1-\beta \right).$$

(15)

(j)

Show that by appropriately rotating the spatial coordinate system around the origin, the equation of the orthodrome can be transformed into the following form:

$$\overrightarrow{r}=\cos t {\overrightarrow{e}}_1+\sin t {\overrightarrow{e}}_2,$$

(16)

where ${\overrightarrow{e}}_1$ and ${\overrightarrow{e}}_2$ are two unit and mutually perpendicular vectors, $t\in \left[0, 2\pi \right]$.

5. Orthodrome as a Geodesic on a Sphere

Let the orthodrome be a geodesic on the sphere. A geodesic on a surface can be defined in several ways, e.g., it is:

(a)

A curve for which the geodetic curvature at every point is zero;

(b)

A straight line or curve where at every point the vector of its principal normal and the vector of the normal to the surface are collinear;

(c)

A straight line or curve whose binormal is perpendicular to the normal to the surface at every point;

(d)

A straight line or curve whose osculating plane contains the normal to the surface at every point.

Suppose we are looking for a curve on a sphere where at every point the vector of its principal normal $\overrightarrow{n}$ and the vector of the normal to the surface $\overrightarrow{N}$ are collinear, i.e., the following holds [11]:

$$\overrightarrow{N}=\lambda \overrightarrow{n}, \lambda \in \mathbb{R}.$$

(17)

It is obvious that there are no straight lines on a sphere; so, we will look for such curves on the sphere for which (17) holds. The normal vector $\overrightarrow{N}$ of the sphere $X^2+Y^2+Z^2=1$ at any point is equal to the radius vector $\overrightarrow{r}$ of that point:

$$\overrightarrow{N}=\overrightarrow{r}.$$

(18)

If the curve $\overrightarrow{r}=\overrightarrow{r}\left(s\right)$ is parameterised by the arc length s, then its normal vector is as follows:

$$\overrightarrow{n}={\displaystyle \frac{d^2\overrightarrow{r}}{d{s}^2}}={\overrightarrow{r}}^{″}.$$

(19)

If we insert $\overrightarrow{N}$ from (18) and $\overrightarrow{n}$ from (19) into (17) we get:

$$\overrightarrow{r}=\lambda {\overrightarrow{r}}^{″}.$$

(20)

Let us determine the parameter $\lambda$. Since $\overrightarrow{r}$ is the radius vector of a point on a sphere of radius 1, it is obvious that:

$${\overrightarrow{r}}^2=1.$$

(21)

We differentiate (21) twice:

$$2\overrightarrow{r}{\overrightarrow{r}}^{\prime }=0, {{\overrightarrow{r}}^{\prime }}^2+\overrightarrow{r}{\overrightarrow{r}}^{″}=0.$$

(22)

Since we have assumed that the curve $\overrightarrow{r}=\overrightarrow{r}\left(s\right)$ is parameterised by the arc length s, it holds that:

$${{\overrightarrow{r}}^{\prime }}^2=1$$

(23)

so it is as follows:

$$\overrightarrow{r}{\overrightarrow{r}}^{″} =-1.$$

(24)

Multiplying (20) by $\overrightarrow{r}$ and using (24) we get:

$$\lambda =-1.$$

(25)

This means that the differential equation of the orthodrome is as follows:

$${\overrightarrow{r}}^{″} + \overrightarrow{r}=\overrightarrow{0}.$$

(26)

Equation (26) is a simple second-order differential equation whose solution is as follows:

$$\overrightarrow{r}={\overrightarrow{c}}_1\cos s+{\overrightarrow{c}}_2\sin s,$$

(27)

where ${\overrightarrow{c}}_1$ and ${\overrightarrow{c}}_2$ are two constant vectors. Since the orthodrome is a curve on the sphere, (21) holds, and from there it follows that:

$$\left|{\overrightarrow{c}}_1\right|=\left|{\overrightarrow{c}}_2\right|=1 \mathrm{and} {\overrightarrow{c}}_1\perp {\overrightarrow{c}}_2.$$

(28)

Vectors ${\overrightarrow{c}}_1$ and ${\overrightarrow{c}}_2$ determine the plane that passes through the origin of the coordinate system; so, we conclude that the orthodrome, as the intersection of a sphere and a plane through its centre, is a great circle on the sphere.

Now, starting from the differential Equation (26), we will derive the equation of the orthodrome in the geographic coordinate system. Let a sphere of radius 1 with the centre at the origin of the coordinate system be defined by the geographic parameterisation (1). Let us write (1) in vector form:

$$\overrightarrow{r}=\left(\cos \phi \cos \lambda ,\cos \phi \sin \lambda ,\sin \phi \right).$$

(29)

Let the curve on the sphere be parameterised by the arc length s, i.e., let $\phi =\phi \left(s\right), \lambda =\lambda \left(s\right)$. Let us calculate the following vectors:

$${\overrightarrow{r}}^{\prime }={\displaystyle \frac{d\overrightarrow{r}}{ds}}=\left(-\sin \phi {\displaystyle \frac{d\phi }{ds}}\cos \lambda -\cos \phi \sin \lambda {\displaystyle \frac{d\lambda }{ds}},-\sin \phi {\displaystyle \frac{d\phi }{ds}}\sin \lambda +\cos \phi \cos \lambda {\displaystyle \frac{d\lambda }{ds}},\cos \phi {\displaystyle \frac{d\phi }{ds}}\right),$$

(30)

and

$$\begin{gathered} {\overrightarrow{r}}^{″}={\displaystyle \frac{d^2\overrightarrow{r}}{d{s}^2}}=\left(-\cos \phi \cos \lambda {\left({\displaystyle \frac{d\phi }{ds}}\right)}^2+\sin \phi \sin \lambda {\displaystyle \frac{d\phi }{ds}}{\displaystyle \frac{d\lambda }{ds}}-\sin \phi \cos \lambda {\displaystyle \frac{d^2\phi }{d{s}^2}}+\sin \phi \sin \lambda {\displaystyle \frac{d\phi }{ds}}{\displaystyle \frac{d\lambda }{ds}}-\cos \phi \cos \lambda {\left({\displaystyle \frac{d\lambda }{ds}}\right)}^2- \\ \cos \phi \sin \lambda {\displaystyle \frac{d^2\lambda }{d{s}^2}},-\cos \phi \sin \lambda {\left({\displaystyle \frac{d\phi }{ds}}\right)}^2-\sin \phi \cos \lambda {\displaystyle \frac{d\phi }{ds}}{\displaystyle \frac{d\lambda }{ds}}-\sin \phi \sin \lambda {\displaystyle \frac{d^2\phi }{d{s}^2}}-\sin \phi \cos \lambda {\displaystyle \frac{d\phi }{ds}}{\displaystyle \frac{d\lambda }{ds}}-\cos \phi \sin \lambda {\left({\displaystyle \frac{d\lambda }{ds}}\right)}^2+ \\ \cos \phi \cos \lambda {\displaystyle \frac{d^2\lambda }{d{s}^2}},-\sin \phi {\left({\displaystyle \frac{d\phi }{ds}}\right)}^2+\cos \phi {\displaystyle \frac{d^2\phi }{d{s}^2}}\right). \end{gathered}$$

(31)

Inserting (30) and (31) into the differential equation of the orthodrome (26), we can write it in terms of the components:

$$\cos \phi \cos \lambda -\cos \phi \cos \lambda {\left({\displaystyle \frac{d\phi }{ds}}\right)}^2+2\sin \phi \sin \lambda {\displaystyle \frac{d\phi }{ds}}{\displaystyle \frac{d\lambda }{ds}}-\sin \phi \cos \lambda {\displaystyle \frac{d^2\phi }{d{s}^2}}-\cos \phi \cos \lambda {\left({\displaystyle \frac{d\lambda }{ds}}\right)}^2-\cos \phi \sin \lambda {\displaystyle \frac{d^2\lambda }{d{s}^2}}=0,$$

(32)

$$\cos \phi \sin \lambda -\cos \phi \sin \lambda {\left({\displaystyle \frac{d\phi }{ds}}\right)}^2-2\sin \phi \cos \lambda {\displaystyle \frac{d\phi }{ds}}{\displaystyle \frac{d\lambda }{ds}}-\sin \phi \sin \lambda {\displaystyle \frac{d^2\phi }{d{s}^2}}-\cos \phi \sin \lambda {\left({\displaystyle \frac{d\lambda }{ds}}\right)}^2+\cos \phi \cos \lambda {\displaystyle \frac{d^2\lambda }{d{s}^2}}=0,$$

(33)

$$\sin \phi -\sin \phi {\left({\displaystyle \frac{d\phi }{ds}}\right)}^2+\cos \phi {\displaystyle \frac{d^2\phi }{d{s}^2}}=0.$$

(34)

Since the last equation is a differential equation with only one unknown function $\phi =\phi \left(s\right)$, we will solve that equation first. Let us start by lowering the order, i.e., let us denote:

$$p={\displaystyle \frac{d\phi }{ds}}, p^{\prime }=p{\displaystyle \frac{dp}{d\phi }}.$$

(35)

and substitute in (34). After the separation of the variables and tidying up, we will get:

$$\tan \phi d\phi ={\displaystyle \frac{pdp}{p^2-1}}.$$

(36)

Let us prepare the last equation for integration.

$${\displaystyle \frac{\sin \phi }{\cos \phi }}d\phi ={\displaystyle \frac{1}{2}}{\displaystyle \frac{-2pdp}{1-p^2}}.$$

(37)

We integrate and get:

$$-\ln \cos \phi ={\displaystyle \frac{1}{2}}\ln \left(1-p^2\right)-\ln K,$$

(38)

where K is the constant of integration. From (38), it first follows:

$${\displaystyle \frac{K}{\cos \phi }}=\sqrt{1-p^2},$$

(39)

and then:

$$p={\displaystyle \frac{d\phi }{ds}}={\displaystyle \frac{\sqrt{{\cos }^2\phi -K^2}}{\cos \phi }}.$$

(40)

From the last relation, it follows:

$$ds={\displaystyle \frac{\cos \phi d\phi }{\sqrt{{\cos }^2\phi -K^2}}}={\displaystyle \frac{\cos \phi d\phi }{\sqrt{1-K^2-{\sin }^2\phi }}}.$$

(41)

By substituting $t=\sin \phi$, $dt=\cos \phi d\phi$, we obtain:

$$ds={\displaystyle \frac{dt}{\sqrt{1-K^2-t^2}}},$$

(42)

which, after integration, gives:

$$s={\sin }^{-1}{\displaystyle \frac{t}{\sqrt{{1-K}^2}}}+L,$$

(43)

where L is the constant of integration. From (43), it finally follows:

$$\sin \phi =\sqrt{{1-K}^2}\sin s,$$

(44)

if we choose $L=0$, for $\phi =0$. We can also express the following:

$$\tan \phi ={\displaystyle \frac{\sqrt{{1-K}^2}\sin s}{\sqrt{K^2+\left(1-K^2\right){\cos }^{2}s}},}$$

(45)

which we will need later.

We still need to determine the function $\lambda =\lambda \left(s\right)$. To carry this out, multiply (32) by $\cos \lambda$, (33) by $\sin \lambda$ and add these two equations. We get:

$$\cos \phi \left(1-p^2\right)-\sin \phi p^{\prime }-\cos \phi {\left({\displaystyle \frac{d\lambda }{ds}}\right)}^2=0,$$

(46)

where we mark, as before, ${\displaystyle \frac{d\phi }{ds}}=p={\displaystyle \frac{\sqrt{{\cos }^2\phi -K^2}}{\cos \phi }}$, and since ${\displaystyle \frac{dp}{d\phi }}={\displaystyle \frac{-K^2\sin \phi }{{\cos }^2\phi \sqrt{{\cos }^2\phi -K^2}}}$, this will be

$${\displaystyle \frac{d^2\phi }{d{s}^2}}={\displaystyle \frac{dp}{ds}}=p^{\prime }=p{\displaystyle \frac{dp}{d\phi }}=-{\displaystyle \frac{K^2\sin \phi }{{\cos }^3\phi }}.$$

(47)

Inserting the expressions for $p$ and $p^{\prime }$ into (46), we obtain, after minor rearrangements:

$${\left({\displaystyle \frac{d\lambda }{ds}}\right)}^2={\displaystyle \frac{K^2}{{\cos }^4\phi }}.$$

(48)

From there, it follows to the sign:

$${\displaystyle \frac{d\lambda }{ds}}={\displaystyle \frac{K}{{\cos }^2\phi }}={\displaystyle \frac{K}{1-\left(1-K^2\right){\sin }^{2}s}}={\displaystyle \frac{\frac{K}{1-K^2}}{\frac{K^2}{1-K^2}+{\cos }^{2}s}}.$$

(49)

Finally, we have:

$$\lambda ={\displaystyle \frac{K}{1-K^2}}\int {\displaystyle \frac{ds}{\frac{K^2}{1-K^2}+{\cos }^{2}s}}={\tan }^{-1}\left(K\tan s\right)+\beta ,$$

(50)

where $\beta$ denotes the additive constant. Instead of (50), we can write:

$$\tan \left(\lambda -\beta \right)=K\tan s,$$

or

$$\sin \left(\lambda -\beta \right)={\displaystyle \frac{K\sin s}{\sqrt{K^2+\left(1-K^2\right){\cos }^{2}s}}}$$

(51)

If we compare (45) with (51), we see that:

$$\sin \left(\lambda -\beta \right)={\displaystyle \frac{K}{\sqrt{1-K^2}}}\tan \phi .$$

(52)

This is the equation of the orthodrome in the geographic coordinate system. Comparison with (6) gives the relationship between the constants:

$$a={\displaystyle \frac{K}{\sqrt{1-K^2}}}.$$

(53)

6. The Orthodrome as a Geodesic on a Sphere and the Clairaut Theorem

The geodetic curvature $K_g$ of the curve on the surface is defined at a particular point using the following relation:

$$K_g=\left(\overrightarrow{t},\overrightarrow{n}, \overrightarrow{N}\right),$$

(54)

where $\overrightarrow{t}$ is the unit vector of the tangent to the curve, $\overrightarrow{n}$ is the unit vector of the principal normal to the curve, and $\overrightarrow{N}$ is the unit vector of the normal to the surface [11]. The mixed product $\left(\overrightarrow{t},\overrightarrow{n}, \overrightarrow{N}\right)$ can be written in the following form:

$$K_g=\overrightarrow{t}\left(\overrightarrow{n}\times \overrightarrow{N}\right),$$

(55)

so, $K_g=0$ if the vectors $\overrightarrow{n}$ and $\overrightarrow{N}$ are collinear. We covered this in the previous section. However, due to the well-known property of the mixed product that it will not change if the vectors cyclically swap places, we can also write:

$$K_g=\overrightarrow{N}\left(\overrightarrow{t}\times \overrightarrow{n}\right)=\overrightarrow{N}\overrightarrow{b},$$

(56)

where we also recognised that the vector product $\overrightarrow{t}\times \overrightarrow{n}$ gives the binormal vector $\overrightarrow{b}$. Therefore, we can now say that $K_g=0$, if the vectors $\overrightarrow{b}$ and $\overrightarrow{N}$ are perpendicular. It does not matter whether the two vectors are unit vectors or not. In this sense, we continue further.

Let a sphere of radius 1 with its centre at the origin of the coordinate system be defined by the geographic parameterisation (1). Let us write (1) in vector form (29). The normal vector $\overrightarrow{N}$ to the sphere will be

$$\overrightarrow{N}={\overrightarrow{r}}_{\phi }\times {\overrightarrow{r}}_{\lambda },$$

(57)

where the first partial derivatives are as follows:

$${\overrightarrow{r}}_{\phi }={\displaystyle \frac{\partial \overrightarrow{r}}{\partial \phi }}=\left(-\sin \phi \cos \lambda ,-\sin \phi \sin \lambda ,\cos \phi \right),$$

(58)

$${\overrightarrow{r}}_{\lambda }={\displaystyle \frac{\partial \overrightarrow{r}}{\partial \lambda }}=\left(-\cos \phi \sin \lambda ,\cos \phi \cos \lambda ,0\right).$$

(59)

Let us calculate second partial derivatives:

$${\overrightarrow{r}}_{\phi \phi }={\displaystyle \frac{{\partial }^2\overrightarrow{r}}{\partial {\phi }^2}}=\left(-\cos \phi \cos \lambda ,-\cos \phi \sin \lambda ,-\sin \phi \right),$$

$${\overrightarrow{r}}_{\phi \lambda }={\displaystyle \frac{{\partial }^2\overrightarrow{r}}{\partial \phi \partial \lambda }}=\left(\sin \phi \sin \lambda ,-\sin \phi \cos \lambda ,0\right),$$

(60)

$${\overrightarrow{r}}_{\lambda \lambda }={\displaystyle \frac{{\partial }^2\overrightarrow{r}}{\partial {\lambda }^2}}=\left(-\cos \phi \cos \lambda ,-\cos \phi \sin \lambda ,0\right).$$

Let $\lambda =\lambda \left(\phi \right)$ be the equation of a curve on a sphere. Then, for this curve we can write:

$$\overrightarrow{r}\left(\phi \right)=\left(\cos \phi \cos \lambda \left(\phi \right),\cos \phi \sin \lambda \left(\phi \right),\sin \phi \right),$$

(61)

and calculate the following vectors:

$${\overrightarrow{r}}^{\prime }={\displaystyle \frac{d\overrightarrow{r}(\phi )}{d\phi }}=\left(-\sin \phi \cos \lambda -\cos \phi \sin \lambda {\displaystyle \frac{d\lambda }{d\phi }},-\sin \phi \sin \lambda +\cos \phi \cos \lambda {\displaystyle \frac{d\lambda }{d\phi }},\cos \phi \right),$$

$${\overrightarrow{r}}^{\prime }={\overrightarrow{r}}_{\phi }+{\overrightarrow{r}}_{\lambda }{\displaystyle \frac{d\lambda }{d\phi }},$$

(62)

$$\begin{gathered} {\overrightarrow{r}}^{″}={\displaystyle \frac{d^2\overrightarrow{r}(\phi )}{d{\phi }^2}}=\left(-\cos \phi \cos \lambda +\sin \phi \sin \lambda {\displaystyle \frac{d\lambda }{d\phi }}+\sin \phi \sin \lambda {\displaystyle \frac{d\lambda }{d\phi }}-\cos \phi \cos \lambda {\left({\displaystyle \frac{d\lambda }{d\phi }}\right)}^2- \\ \cos \phi \sin \lambda {\displaystyle \frac{d^2\lambda }{d{\phi }^2}},-\cos \phi \sin \lambda -\sin \phi \cos \lambda {\displaystyle \frac{d\lambda }{d\phi }}-\sin \phi \cos \lambda {\displaystyle \frac{d\lambda }{d\phi }}-\cos \phi \sin \lambda {\left({\displaystyle \frac{d\lambda }{d\phi }}\right)}^2+\cos \phi \cos \lambda {\displaystyle \frac{d^2\lambda }{d{\phi }^2}},-\sin \phi \right), \end{gathered}$$

$${\overrightarrow{r}}^{″}={\overrightarrow{r}}_{\phi \phi }+2{\overrightarrow{r}}_{\phi \lambda }{\displaystyle \frac{d\lambda }{d\phi }}+{\overrightarrow{r}}_{\lambda \lambda }{\left({\displaystyle \frac{d\lambda }{d\phi }}\right)}^2+{\overrightarrow{r}}_{\lambda }{\displaystyle \frac{d^2\lambda }{d{\phi }^2}}.$$

(63)

The osculation plane is determined by the vectors ${\overrightarrow{r}}^{\prime }$ and ${\overrightarrow{r}}^{″}$; so, we can write for the binormal vector, $\overrightarrow{b}={\overrightarrow{r}}^{\prime }\times {\overrightarrow{r}}^{″}$. The condition that the normal vector to the surface $\overrightarrow{N}={\overrightarrow{r}}_{\phi }\times {\overrightarrow{r}}_{\lambda }$ is perpendicular to the binormal vector $\overrightarrow{b}={\overrightarrow{r}}^{\prime }\times {\overrightarrow{r}}^{″}$ can be written in the following form:

$$\left({\overrightarrow{r}}_{\phi }\times {\overrightarrow{r}}_{\lambda }\right)\left({\overrightarrow{r}}^{\prime }\times {\overrightarrow{r}}^{″}\right)=0,$$

and this is identical to the following expression:

$$\left(\overrightarrow{r_{\phi }}{\overrightarrow{r}}^{\prime }\right)\left(\overrightarrow{r_{\lambda }}{\overrightarrow{r}}^{″}\right)-\left(\overrightarrow{r_{\phi }}{\overrightarrow{r}}^{″}\right)\left(\overrightarrow{r_{\lambda }}{\overrightarrow{r}}^{\prime }\right)=0.$$

(64)

Let us calculate:

$$\overrightarrow{r_{\phi }}{\overrightarrow{r}}^{\prime }=1,$$

$$\overrightarrow{r_{\lambda }}{\overrightarrow{r}}^{″}=-2\sin \phi \cos \phi {\displaystyle \frac{d\lambda }{d\phi }}+{\cos }^2\phi {\displaystyle \frac{d^2\lambda }{d{\phi }^2}},$$

$$\overrightarrow{r_{\phi }}{\overrightarrow{r}}^{″}=\sin \phi \cos \phi {\left({\displaystyle \frac{d\lambda }{d\phi }}\right)}^2,$$

$$\overrightarrow{r_{\lambda }}{\overrightarrow{r}}^{\prime }={\cos }^2\phi {\displaystyle \frac{d\lambda }{d\phi }}$$

Inserting it into (64) and assuming $\cos \phi \ne 0,$ we get:

$$-2\sin \phi {\displaystyle \frac{d\lambda }{d\phi }}-\sin \phi {\cos }^2\phi {\left({\displaystyle \frac{d\lambda }{d\phi }}\right)}^3+\cos \phi {\displaystyle \frac{d^2\lambda }{d{\phi }^2}}=0.$$

(65)

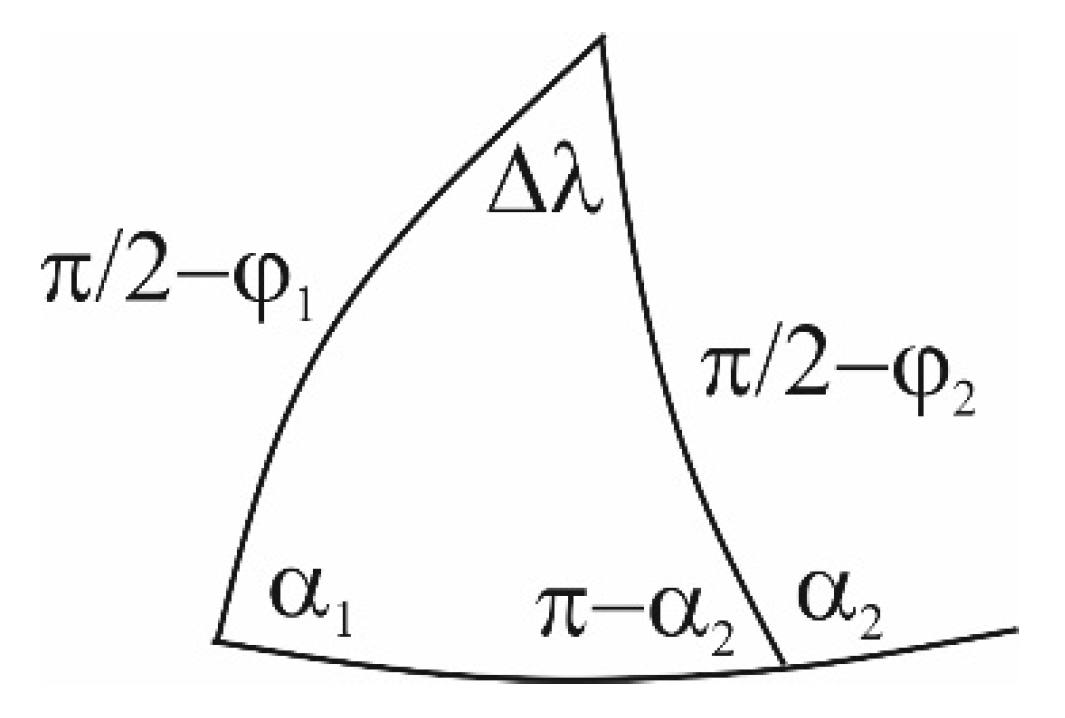
Let us introduce the azimuth α as follows (Figure 2):

$$\tan \alpha ={\displaystyle \frac{\cos \phi d\lambda }{d\phi }},$$

(66)

i.e.,

$${\displaystyle \frac{d\lambda }{d\phi }}={\displaystyle \frac{\tan \alpha }{\cos \phi }}.$$

(67)

Calculation gives:

$${\displaystyle \frac{d^2\lambda }{d{\phi }^2}}={\displaystyle \frac{\frac{\cos \phi }{{\cos }^2\alpha }\frac{d\alpha }{d\phi }+\tan \alpha \sin \phi }{{\cos }^2\phi }}.$$

(68)

Substituting (67) and (68) into (65), after minor rearrangements, we obtain:

$$-\tan \alpha \tan \phi +{\displaystyle \frac{d\alpha }{d\phi }}=0,$$

(69)

and then:

$$-\sin \alpha \sin \phi +\cos \alpha \cos \phi {\displaystyle \frac{d\alpha }{d\phi }}=0,$$

(70)

and finally:

$${\displaystyle \frac{d}{d\phi }}\left(\cos \phi \sin \alpha \right)=0,$$

(71)

i.e.,

$$\cos \phi \sin \alpha =K=const.$$

(72)

In geodesy, the last equation is called Clairaut’s theorem of the geodesic [12]. Alexis Claude Clairaut (1713–1765) was a French mathematician, astronomer and geophysicist. It is obvious that the value of the constant K must be in the range of $-1\le K\le 1$. The azimuth α is equal to zero when the orthodrome is equal to the meridian circle arc. In general, it will have the smallest value when the radius of the parallel takes the largest value, i.e., at the equator, when $\cos \phi =1$; so, the following holds:

$$\sin {\alpha }_{max}=K.$$

(73)

The largest value of angle α, i.e., $\alpha =\pi /2$, corresponds to the smallest value of $\cos \phi$; therefore:

$${\left(\cos \phi \right)}_{min}=K.$$

(74)

Therefore, the constant K in Clairaut’s theorem is equal to the radius of the northernmost and southernmost parallel that the orthodrome reaches. Clairaut’s theorem for the sphere is identical to the sine theorem in spherical trigonometry. Namely, the sine theorem can be written in the following form (Figure 3):

$$\cos {\phi }_1\sin {\alpha }_1=\cos {\phi }_2\sin {\alpha }_2.$$

(75)

Möhle [13] derived the equation of the geodesic for a surface of revolution in an analogous manner.

Let us also show that (72) is indeed the equation of an orthodrome on the unit sphere. For every curve on the sphere, the following holds (Figure 2):

$$d\phi =\cos \alpha ds$$

(76)

$$\cos \phi d\lambda =\sin \alpha ds.$$

(77)

If we divide (77) by (76), we get:

$$\cos \phi {\displaystyle \frac{d\lambda }{d\phi }}=\tan \alpha .$$

(78)

Clairaut’s Equation (72) gives:

$$\sin \alpha ={\displaystyle \frac{K}{\cos \phi }},$$

(79)

and then

$$\tan \alpha ={\displaystyle \frac{\frac{K}{\cos \phi }}{\sqrt{1-\frac{K^2}{{\cos }^2\phi }}}}={\displaystyle \frac{K}{\sqrt{{\cos }^2\phi -K^2}}}.$$

(80)

Accordingly, we can write:

$${\displaystyle \frac{d\lambda }{d\phi }}={\displaystyle \frac{K}{\cos \phi \sqrt{{\cos }^2\phi -K^2}}}.$$

(81)

From there:

$$\lambda =K\int {\displaystyle \frac{d\phi }{\cos \phi \sqrt{{\cos }^2\phi -K^2}}}={\tan }^{-1}{\displaystyle \frac{K\sin \phi }{\sqrt{{\cos }^2\phi -K^2}}}+\beta ,$$

(82)

where $\beta$ denotes the additive constant. From (82), it follows:

$$\tan \left(\lambda -\beta \right)={\displaystyle \frac{K\sin \phi }{\sqrt{{\cos }^2\phi -K^2}}},$$

(83)

or (52) or (6).

7. Different Forms of the Clairaut Theorem

The Clairaut theorem can be written in other forms:

$${\cos }^2\phi {\displaystyle \frac{d\lambda }{ds}}=K=const.$$

(84)

$$\cos \phi \sin \alpha =K$$

(85)

$${\displaystyle \frac{d\alpha }{ds}}=\tan \phi \sin \alpha$$

(86)

$${\displaystyle \frac{d\alpha }{d\lambda }}=\sin \phi .$$

(87)

Let us show the equivalence of the relations (84)–(87). For every curve on the sphere, (76) and (77) hold (Figure 2). Substituting (77) into (84), we obtain (85). Differentiating (85) with respect to s, we obtain:

$$\cos \phi {\displaystyle \frac{d}{ds}}\sin \alpha +\sin \alpha {\displaystyle \frac{d}{ds}}\cos \phi =0,$$

$$\cos \phi \cos \alpha {\displaystyle \frac{d\alpha }{ds}}-\sin \alpha \sin \phi {\displaystyle \frac{d\phi }{ds}}=0.$$

(88)

From there:

$${\displaystyle \frac{d\alpha }{ds}}=\tan \phi \tan \alpha {\displaystyle \frac{d\phi }{ds}.}$$

(89)

Considering (76), we get (86). If we insert $\sin \alpha$ from (77) into (86), we get:

$${\displaystyle \frac{d\alpha }{ds}}=\tan \phi \cos \phi {\displaystyle \frac{d\lambda }{ds}}$$

(90)

and from there, (87) follows immediately since, according to (90), it is:

$${\displaystyle \frac{d\alpha }{ds}}=\sin \phi {\displaystyle \frac{d\lambda }{ds}}$$

(91)

then because of (76), it is:

$$\cos \alpha {\displaystyle \frac{d\alpha }{ds}}=\sin \phi {\displaystyle \frac{d\phi }{ds}}{\displaystyle \frac{d\lambda }{ds}.}$$

(92)

Differentiating (77) with respect to s, we obtain:

$$\cos \alpha {\displaystyle \frac{d\alpha }{ds}}=-\sin \phi {\displaystyle \frac{d\phi }{ds}}{\displaystyle \frac{d\lambda }{ds}}+\cos \phi {\displaystyle \frac{d^2\lambda }{d{s}^2}.}$$

(93)

From the last two equations, it follows:

$$-2\sin \phi {\displaystyle \frac{d\phi }{ds}}{\displaystyle \frac{d\lambda }{ds}}+\cos \phi {\displaystyle \frac{d^2\lambda }{d{s}^2}}=0,$$

(94)

and this means that (84) holds. Since (84) follows (85), (85) follows (86), (86) follows (87), and (87) follows (84), it is shown that all four relations, (84)–(87), are equivalent.

8. The Orthodrome as a Solution of Differential Equations of a Geodesic

In differential geometry, one can find differential equations for a geodesic on any surface [11,14]:

$${\phi }^{″}=-{\Gamma }_{\phi \phi }^{\phi }{{\phi }^{\prime }}^2-2{\Gamma }_{\phi \phi }^{\lambda }{\phi }^{\prime }{\lambda }^{\prime }-{\Gamma }_{\lambda \lambda }^{\phi }{{\lambda }^{\prime }}^2$$

$${\lambda }^{″}=-{\Gamma }_{\phi \phi }^{\lambda }{{\phi }^{\prime }}^2-2{\Gamma }_{\phi \lambda }^{\lambda }{\phi }^{\prime }{\lambda }^{\prime }-{\Gamma }_{\lambda \lambda }^{\lambda }{{\lambda }^{\prime }}^2$$

(95)

where ${\Gamma }_{\phi \phi }^{\phi }$, …, ${\Gamma }_{\lambda \lambda }^{\lambda }$ are Christoffel notations of the second kind, ${\phi }^{\prime }={\displaystyle \frac{d\phi }{ds}}$, ${\phi }^{″}={\displaystyle \frac{d^2\phi }{d{s}^2}}$, ${\lambda }^{\prime }={\displaystyle \frac{d\lambda }{ds}}$, ${\lambda }^{″}={\displaystyle \frac{d^2\lambda }{d{s}^2}}$, and s is the arc length. Elwin Bruno Christoffel (1829–1900) was a German mathematician and physicist. In addition, for any curve parametrised by the arc length:

$$E{{\phi }^{\prime }}^2+2F{\phi }^{\prime }{\lambda }^{\prime }+G{{\lambda }_{\prime }}^2=1,$$

(96)

where $E$, $F$ and $G$ are first-order Gaussian quantities for the surface.

Let a sphere of radius 1 with the centre at the origin of the coordinate system be defined by the geographic parameterisation (1). For this sphere, the first-order Gaussian quantities or the coefficients of the first differential form are equal to:

$$E=1, F=0, G={\cos }^2\phi ,$$

(97)

so, the first differential form (96) takes the following form:

$${{\phi }^{\prime }}^2+{\cos }^2 \phi {{\lambda }^{\prime }}^2=1.$$

(98)

The Christoffel notations of the second kind for a sphere have these values:

$${\Gamma }_{\phi \phi }^{\phi }=0, {\Gamma }_{\phi \phi }^{\lambda }=0, {\Gamma }_{\lambda \lambda }^{\phi }=\sin \phi \cos \phi$$

$${\Gamma }_{\phi \phi }^{\lambda }=0, {\Gamma }_{\phi \lambda }^{\lambda }=-\tan \phi , {\Gamma }_{\lambda \lambda }^{\lambda }=0.$$

(99)

Substituting (99) into (95), we get:

$${\phi }^{″}=\sin \phi \cos \phi {{\lambda }^{\prime }}^2$$

(100)

$${\lambda }^{″}=2\tan \phi {\phi }^{\prime }{\lambda }^{\prime }.$$

(101)

So, geodesics on the sphere will be obtained by solving differential equations (100) and (101) with the help of relation (99). One possibility is to express ${{\lambda }^{\prime }}^2$ from relation (99) and include it in (100). This way, we would get a second-order differential equation with an unknown function $\phi =\phi \left(s\right)$, which we reduce to a first-order differential equation by lowering the order and then solve it in the usual way. We will describe a slightly shorter procedure.

Let us assume that it is:

$${\lambda }^{\prime }=0,$$

(102)

so, we immediately get that the geodesics are meridians, $\lambda =C=const.$, and then from (100) $\phi ”=0$, ${\phi }^{\prime }=K$, $\phi =Ks+L$, where $K$ and $L$ are constants. If we want $\phi =0$ for $s=0$, then we should take $L=0$. If we also want $s=\pi /2$ for $\phi =\pi /2$, we should take $K=1$.

Let us now assume that:

$${\lambda }^{\prime }\ne 0,$$

(103)

so, when we divide (101) by ${\lambda }^{\prime }$, we get:

$${\displaystyle \frac{{\lambda }^{″}}{{\lambda }^{\prime }}}=2\tan \phi {\displaystyle \frac{d\phi }{ds}},$$

(104)

and then:

$${\displaystyle \frac{{\lambda }^{″}}{{\lambda }^{\prime }}}ds=2\tan \phi d\phi ,$$

and after integration:

$$\ln {\lambda }^{\prime }=-2\ln \cos \phi +\ln K,$$

(105)

where $K$ is a constant. After the antilogarithm process, (105) becomes:

$${\lambda }^{\prime }={\displaystyle \frac{K}{{\cos }^2\phi }}$$

(106)

From relation (98), it follows:

$${{\phi }^{\prime }}^2=1-{\cos }^2\phi {{\lambda }^{\prime }}^2,$$

(107)

and then considering (106), it follows:

$${{\phi }^{\prime }}^2=1-{\displaystyle \frac{K^2}{{\cos }^2\phi },}$$

(108)

$${\phi }^{\prime }={\displaystyle \frac{\sqrt{{\cos }^2\phi -K^2}}{\cos \phi },}$$

(109)

$$ds={\displaystyle \frac{\cos \phi }{\sqrt{{\cos }^2\phi -K^2}}}d\phi ={\displaystyle \frac{\cos \phi }{\sqrt{1-K^2-{\sin }^2\phi }}}d\phi ,$$

(110)

and finally:

$$s={\sin }^{-1}{\displaystyle \frac{\sin \phi }{\sqrt{1-K^2}}}.$$

(111)

From (111), it follows:

$$\sin \phi =\sqrt{1-K^2}\sin s$$

(112)

and then:

$${\cos }^2\phi =1-{\sin }^2\phi =1-\left(1-K^2\right){\sin }^{2}s.$$

(113)

Now we can write according to (106) and (113):

$${\lambda }^{\prime }={\displaystyle \frac{K}{1-\left(1-K^2\right){\sin }^{2}s}}$$

(114)

$$\lambda =K\int {\displaystyle \frac{ds}{1-\left(1-K^2\right){\sin }^{2}s}}+\beta ,$$

(115)

where $\beta$ is the constant of integration. After integration, we get:

$$\lambda ={\tan }^{-1}\left(K\tan s\right)+\beta .$$

(116)

We can obtain a direct relationship between $\lambda$ and $\phi$ as follows. From (112) and (113), it follows:

$$\tan \phi ={\displaystyle \frac{\sin \phi }{\cos \phi }}={\displaystyle \frac{\sqrt{1-K^2}\sin s}{\sqrt{1-\left(1-K^2\right){\sin }^{2}s}},}$$

(117)

while from (116), we get (50), and from there:

$$\sin \left(\lambda -\beta \right)={\displaystyle \frac{K\sin s}{\sqrt{1-\left(1-K^2\right){\sin }^{2}s}}}.$$

(118)

Finally, from (117) and (119), we obtain (6).

We note another interesting consequence of (101), known as the Clairaut theorem. Note that Equation (101) can be written as follows:

$${\left({\cos }^2\phi {\lambda }^{\prime }\right)}^{\prime }={\cos }^2\phi {{\lambda }^{\prime }}^{\prime }-2\sin \phi \cos \phi {\lambda }^{\prime }{\phi }^{\prime }=0.$$

From there it follows:

$${\cos }^2\phi {\lambda }^{\prime }=const.$$

and:

$$\cos \phi {\displaystyle \frac{\cos \phi d\lambda }{d\phi }}=\cos \phi \sin \alpha =const.$$

which is the famous Clairaut theorem.

9. The Orthodrome as a Solution of Differential Equations of a Geodesic on a Surface of Revolution

In differential geometry, differential equations for a geodesic on any surface can be found [11,15]. If it is a surface of revolution, its equation can be written in the following form:

$$X=f\left(\phi \right)\cos \lambda , Y=f\left(\phi \right)\sin \lambda , Z=g\left(\phi \right).$$

(119)

The differential equations of the geodesic on such a surface read:

$${\phi }^{″}={\displaystyle \frac{-\left(f^{\prime }{f}^{″}+g^{\prime }{g}^{″}\right){{\phi }^{\prime }}^2+f{f}^{\prime }{{\lambda }^{\prime }}^2}{{f^{\prime }}^2+{g^{\prime }}^2}},$$

(120)

$$\lambda ”=-2{\displaystyle \frac{f^{\prime }}{f}}{\phi }^{\prime }{\lambda }^{\prime },$$

(121)

where the notation for derivatives was introduced:

$$f^{\prime }={\displaystyle \frac{df}{d\phi }}, f^{″}={\displaystyle \frac{d^{2}f}{d{\phi }^2}}, g^{\prime }={\displaystyle \frac{dg}{d\phi }}, g^{″}={\displaystyle \frac{d^{2}g}{d{\phi }^2}},$$

(122)

$${\phi }^{\prime }={\displaystyle \frac{d\phi }{ds}}, {\phi }^{″}={\displaystyle \frac{d^2\phi }{d{s}^2}}, {\lambda }^{\prime }={\displaystyle \frac{d\lambda }{ds}}, {\lambda }^{″}={\displaystyle \frac{d^2\lambda }{d{s}^2}}.$$

(123)

Since for a sphere defined by geographic parameterisation:

$$f\left(\phi \right)=\cos \phi , g\left(\phi \right)=\sin \phi ,$$

(124)

it is:

$$f^{\prime }=-\sin \phi , f^{″}=-\cos \phi ,$$

$$g^{\prime }=\cos \phi , g^{″}=-\sin \phi ,$$

(125)

so, the differential equations of geodesics on the sphere (120) and (121) pass into:

$${\phi }^{″}=\sin \phi \cos \phi {{\lambda }^{\prime }}^2,$$

$${\lambda }^{″}=2\tan \phi {\phi }^{\prime }{\lambda }^{\prime },$$

and these are differential Equations (100) and (101) from the previous section; so, they can be solved in the same way as they were solved there.

10. The Orthodrome as the Shortest Arc Length of a Curve on a Sphere Connecting Two Points According to Bessel

Let there be two points A and B on a surface. We ask ourselves what is the shortest connection between these points on the surface? For some simpler cases, it is possible to give a necessary condition. Geodesics have the local minimum property: they are curves that are the shortest connections between two points on the surface. In other words, a geodesic is the shortest connection between two sufficiently close points on the surface [11].

The problem of a geodesic as the shortest path between two points on a given surface was addressed by many scientists as early as the 18th century. Bessel provides a concise description of the work of several authors who dealt with this topic, such as Clairaut, Euler, du Séjour, Legendre, and Oriani [9].

Let us take two points A and B on the surface of the ellipsoid of revolution connected by a certain curve. Consider two adjacent points on the curve with latitudes $\phi$ and $\phi +d\phi$ and longitudes relative to A of $\lambda$ and $\lambda +d\lambda$ (measured east). Let the distance between them be ds, the azimuth of the line directed towards A be $\alpha$ (measured clockwise from north), the radius of the parallel corresponding to the latitude r, and the radius of curvature of the meridian R; then, we find:

$$\cos \alpha ds=Rd\phi ,$$

$$\sin \alpha ds=rd\lambda ,$$

which gives:

$$ds=\sqrt{R^{2}d{\phi }^2+r^{2}d{\lambda }^2}.$$

If we put:

$$p={\displaystyle \frac{d\phi }{d\lambda }} \mathrm{and} U=\sqrt{R^2{p}^2+r^2},$$

then, we have:

$$ds=Ud\lambda .$$

The distance along the curve between two points A and B is therefore:

$$s=\int Ud\lambda ,$$

where the integration is from A to B. In order for the curve to be geodesic or the shortest one, the relation between $\phi$ and $\lambda$ must be such that the value of the integral is minimal. If we slightly change that relation by replacing $\phi$ with $\phi +z$, where $z$ is an arbitrary function of $\lambda$ that vanishes at the end points (because those points lie on both curves), then the slightly changed length:

$$s^{\prime }=\int U^{\prime }d\lambda ,$$

must be longer than s for each $z$. Let us expand $U(\phi ,p)$ in a Taylor series. We will get:

$$U^{\prime }=U+{\displaystyle \frac{\partial U}{\partial \phi }}z+{\displaystyle \frac{\partial U}{\partial p}}{\displaystyle \frac{dz}{d\lambda }}+\cdots ,$$

and therefore we have:

$$s^{\prime }=s+\int \left({\displaystyle \frac{\partial U}{\partial \phi }}z+{\displaystyle \frac{\partial U}{\partial p}}{\displaystyle \frac{dz}{d\lambda }}\right)d\lambda +\cdots ,$$

where we explicitly introduce terms only up to the first order of $z$. For s to be a minimum, it should be:

$$\int \left({\displaystyle \frac{\partial U}{\partial \phi }}z+{\displaystyle \frac{\partial U}{\partial p}}{\displaystyle \frac{dz}{d\lambda }}\right)d\lambda +\cdots \ge 0$$

for all $z$. Since this must also hold if $z$ is replaced by −$z$, and since we can take $z$ so small that the first-order terms are greater than the sum of all other higher-order terms (unless the first-order terms vanish), it follows that the condition for a minimum of s is equal to:

$$\int \left({\displaystyle \frac{\partial U}{\partial \phi }}z+{\displaystyle \frac{\partial U}{\partial p}}{\displaystyle \frac{dz}{d\lambda }}\right)d\lambda =\int {\displaystyle \frac{\partial U}{\partial \phi }}zd\lambda +\int {\displaystyle \frac{\partial U}{\partial p}}dz=0.$$

Partial integration of the second integral gives:

$$z{\displaystyle \frac{\partial U}{\partial p}}-\int zd\left({\displaystyle \frac{\partial U}{\partial p}}\right).$$

and remembering that $z$ vanishes at the endpoints, we get:

$$\int z\left[{\displaystyle \frac{\partial U}{\partial \phi }}-{\displaystyle \frac{d}{d\lambda }}\left({\displaystyle \frac{\partial U}{\partial p}}\right)\right]d\lambda =0.$$

Since the integral should vanish for arbitrary $z$, it must be:

$${\displaystyle \frac{\partial U}{\partial \phi }}-{\displaystyle \frac{d}{d\lambda }}\left({\displaystyle \frac{\partial U}{\partial p}}\right)=0$$

or by multiplying by $p={\displaystyle \frac{d\phi }{d\lambda }}$

$${\displaystyle \frac{\partial U}{\partial \phi }}{\displaystyle \frac{d\phi }{d\lambda }}+{\displaystyle \frac{\partial U}{\partial p}}{\displaystyle \frac{dp}{d\lambda }}-{\displaystyle \frac{dp}{d\lambda }}{\displaystyle \frac{\partial U}{\partial p}}-{\displaystyle \frac{d}{d\lambda }}\left({\displaystyle \frac{\partial U}{\partial p}}\right)=0,$$

which, integrating with respect to λ, gives:

$$U-p{\displaystyle \frac{\partial U}{\partial p}}=const.$$

By substituting $U=\sqrt{R^2{p}^2+r^2}$, we get:

$${\displaystyle \frac{r}{\sqrt{1+\frac{R^2}{r^2}{p}^2}}}=r\sin \alpha =const.$$

which is the well-known characteristic equation of a geodesic. The Bessel derivative shown applies to an ellipsoid of revolution. If we consider a unit sphere, then $R=1$, $r=\cos \phi$; so, the last equation becomes:

$${\displaystyle \frac{{\cos }^2\phi }{\sqrt{{\cos }^2\phi +{\left(\frac{d\phi }{d\lambda }\right)}^2}}}={\displaystyle \frac{{\cos }^2\phi d\lambda }{ds}}=\cos \phi \sin \alpha =const.$$

where we recognise the Clairaut theorem for the sphere.

11. The Orthodrome as a Solution to the Euler–Lagrange Equation

The brachistochrone is one of many problems in which we want to determine a function y(x) that minimises or maximises an integral [16]:

$$J\left[y\left(x\right)\right]={\int }_a^{b}f\left(x,y\left(x\right),y^{\prime }\left(x\right)\right)dx.$$

(126)

Leonhard Euler was the first to devise a systematic method for solving such problems. Consider, for example, two points, A and B, on a sphere of radius 1 centred at the origin. We want to connect A and B by the shortest, continuously differentiable curve lying on the sphere.

Let the sphere of radius 1 centred at the origin of the coordinate system be defined by the geographic parameterisation (1). The first differential form of the mapping (1) is as follows:

$$d{s}^2=d{\phi }^2+{\cos }^2\phi d{\lambda }^2.$$

(127)

From there, we have:

$$ds=\sqrt{d{\phi }^2+{\cos }^2\phi d{\lambda }^2}.$$

(128)

Assume that $\lambda =\lambda \left(\phi \right)$. Searching for the curve that minimises the length of the arc between the points $A=\left({\phi }_1,{\lambda }_1\right)$ and $B=\left({\phi }_2,{\lambda }_2\right)$ is reduced to finding the function $\lambda =\lambda \left(\phi \right)$ that minimises the integral:

$$s={\int }_A^{B}ds={\int }_{{\phi }_1}^{{\phi }_2}\sqrt{1+{\cos }^2\phi {\left({\displaystyle \frac{d\lambda }{d\phi }}\right)}^2}d\phi$$

(129)

with the following boundary conditions:

$$\lambda \left({\phi }_1\right)={\lambda }_1, \lambda \left({\phi }_2\right)={\lambda }_2.$$

(130)

Leonhard Euler was the first person to systematise the study of variational problems. His 1744 work [17], Method for Finding Curved Lines Enjoying the Properties of Maximums or Minimums, or the Solution of Isoperimetric Problems in the Widest Sense, is a collection of 100 special problems. The book also contains a general method for solving such problems. Euler abandoned his method in favour of Lagrange’s more elegant “method of variations” after receiving Lagrange’s letter (12 August 1755). Euler also named the subject the calculus of variations in Lagrange’s honour.

This variational derivative has the same role for functionals as the partial derivative has for functions. For a relative (or local) minimum, we expect the derivative to vanish at each point, leaving us with the Euler–Lagrange equation:

$${\displaystyle \frac{\partial f}{\partial y}}-{\displaystyle \frac{d}{dx}}\left({\displaystyle \frac{\partial f}{\partial y^{\prime }}}\right)=0.$$

(131)

The Euler–Lagrange equation is only a necessary condition, in the same sense that f’(x) = 0 is a necessary but insufficient condition in mathematical analysis. For general surfaces, the resulting Euler–Lagrange equation is quite complicated. Fortunately, the Euler–Lagrange equation simplifies for some surfaces. The most important special case is the one for surfaces of revolution, i.e., surfaces obtained by rotating a plane curve about an axis. For example, the Euler–Lagrange equation for the unit sphere simplifies to:

$${\displaystyle \frac{d}{d\phi }}\left[{\displaystyle \frac{{\cos }^2\phi \frac{d\lambda }{d\phi }}{\sqrt{1+{\cos }^2\phi {\left(\frac{d\lambda }{d\phi }\right)}^2}}}\right]=0.$$

(132)

From there, it follows:

$${\displaystyle \frac{{\cos }^2\phi \frac{d\lambda }{d\phi }}{\sqrt{1+{\cos }^2\phi {\left(\frac{d\lambda }{d\phi }\right)}^2}}}=K.$$

(133)

If we solve the last equation in terms of ${\displaystyle \frac{d\lambda }{d\phi }}$ and integrate, we will get (82) and then (83), (52) or (6).

12. Conclusions

This article provides an overview of the various definitions of the orthodrome, as research has shown that this curve can be approached in about a dozen different ways, which is not common in defining technical terms in geodesy and related fields. Geodesics have been studied and are still studied by many scientists today. A geodesic on a surface is a curve for which the geodetic curvature is zero at every point. Equivalent expressions of this statement are that at every point of this curve, the vector of the principal normal is collinear with the normal to the surface, that it is a curve whose binormal at every point is perpendicular to the normal to the surface, and that it is a curve whose osculation plane contains the normal to the surface at every point. In this case, the well-known Clairaut equation of a geodesic naturally appears in geodesy. It is shown that this equation can be written in several different forms. Since corresponding differential equations for geodesics can be found in the literature, but usually without a solution, they are solved in this article. In addition, the orthodrome can also be approached using the calculus of variations since it is a question of finding the minimum length of an arc.

This article contains a large number of mathematical expressions. To understand this text, basic knowledge of analytical, spherical and differential geometry and the calculus of variations is sufficient. The simplest derivation is carried out using analytical geometry, in which the orthodrome is defined as the intersection of a sphere and a plane passing through its centre. The shortest derivation is carried out using the calculus of variations, but this requires knowledge of the basics of this part of mathematics that is usually not taught in the study of geodesy.