Best Practices for Applying and Interpreting the Total Operating Characteristic
Abstract
1. Introduction
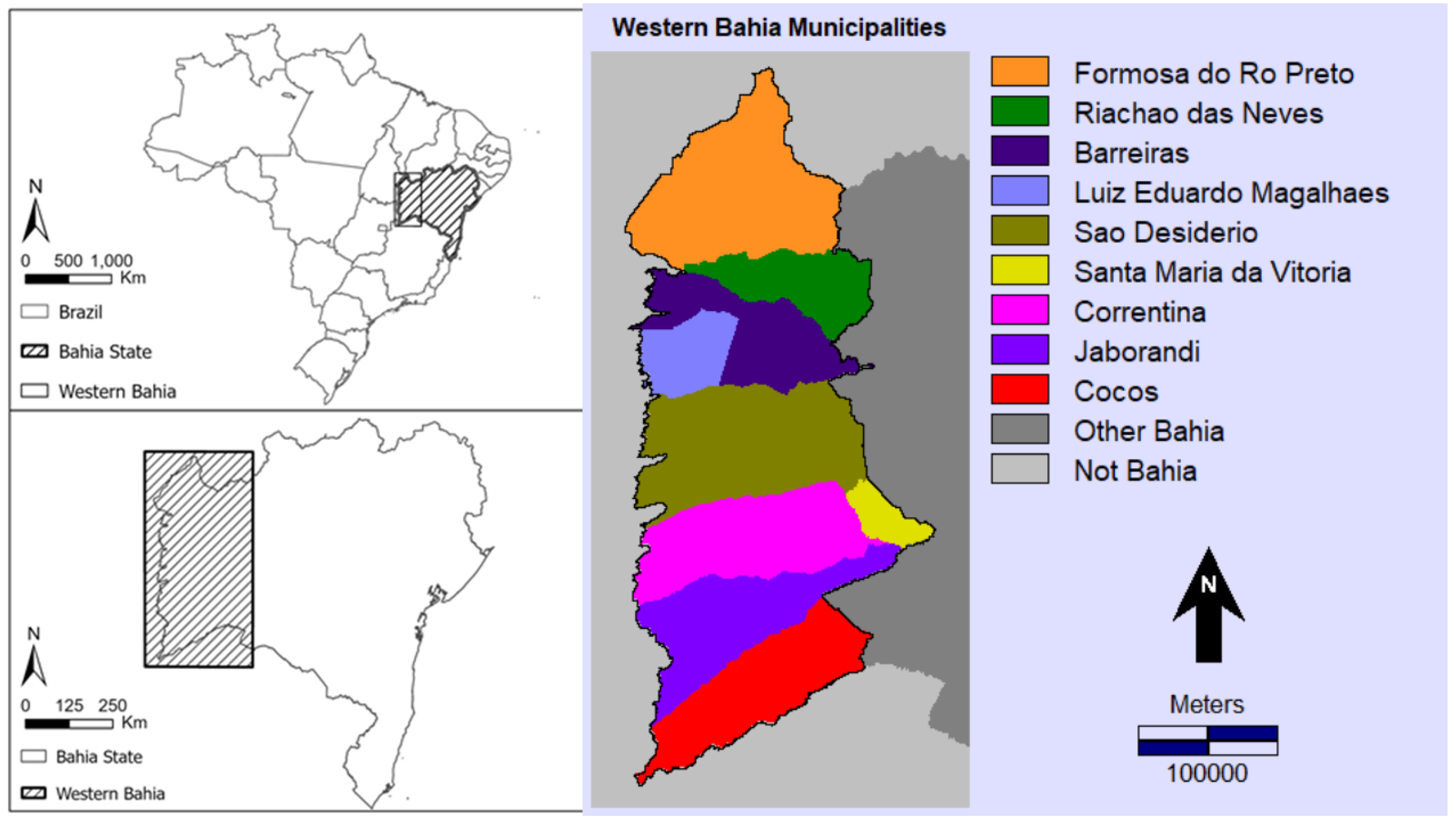
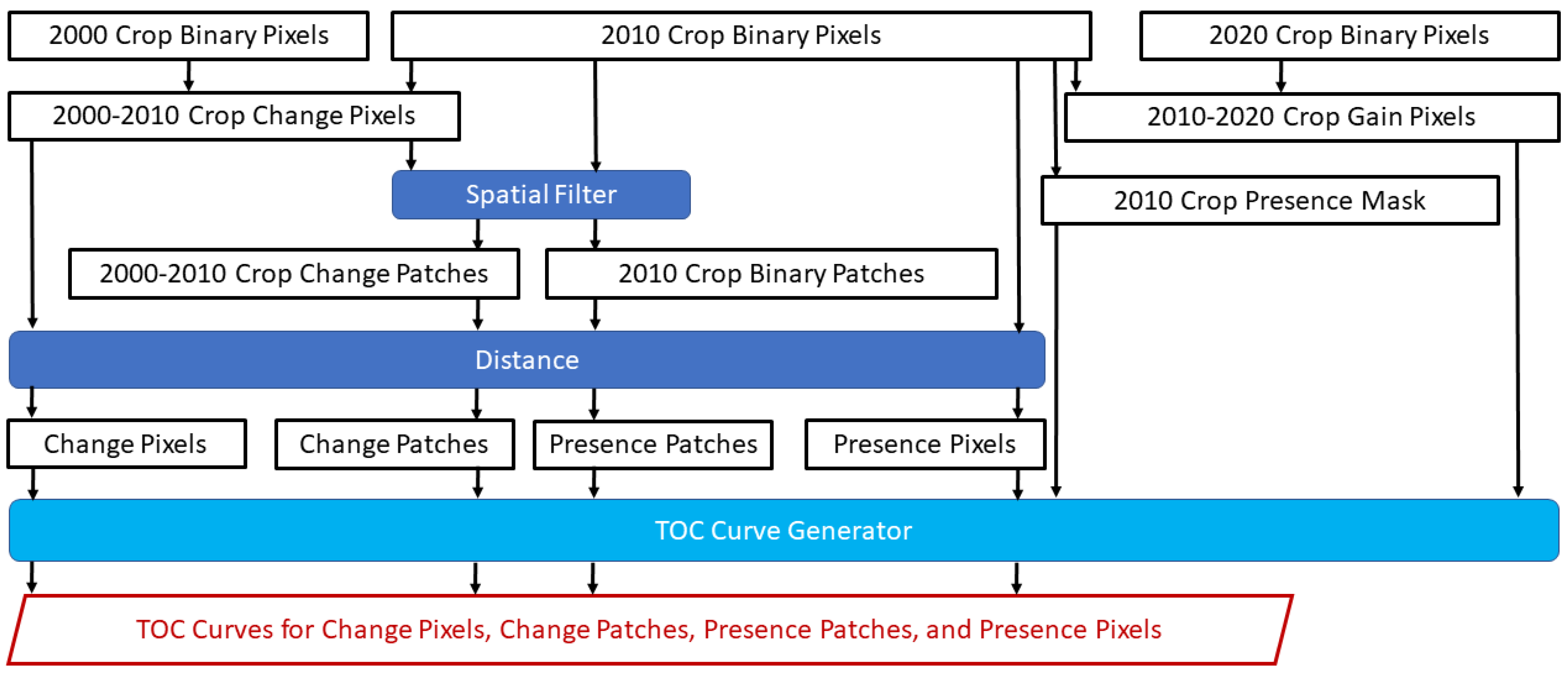
2. Materials and Methods
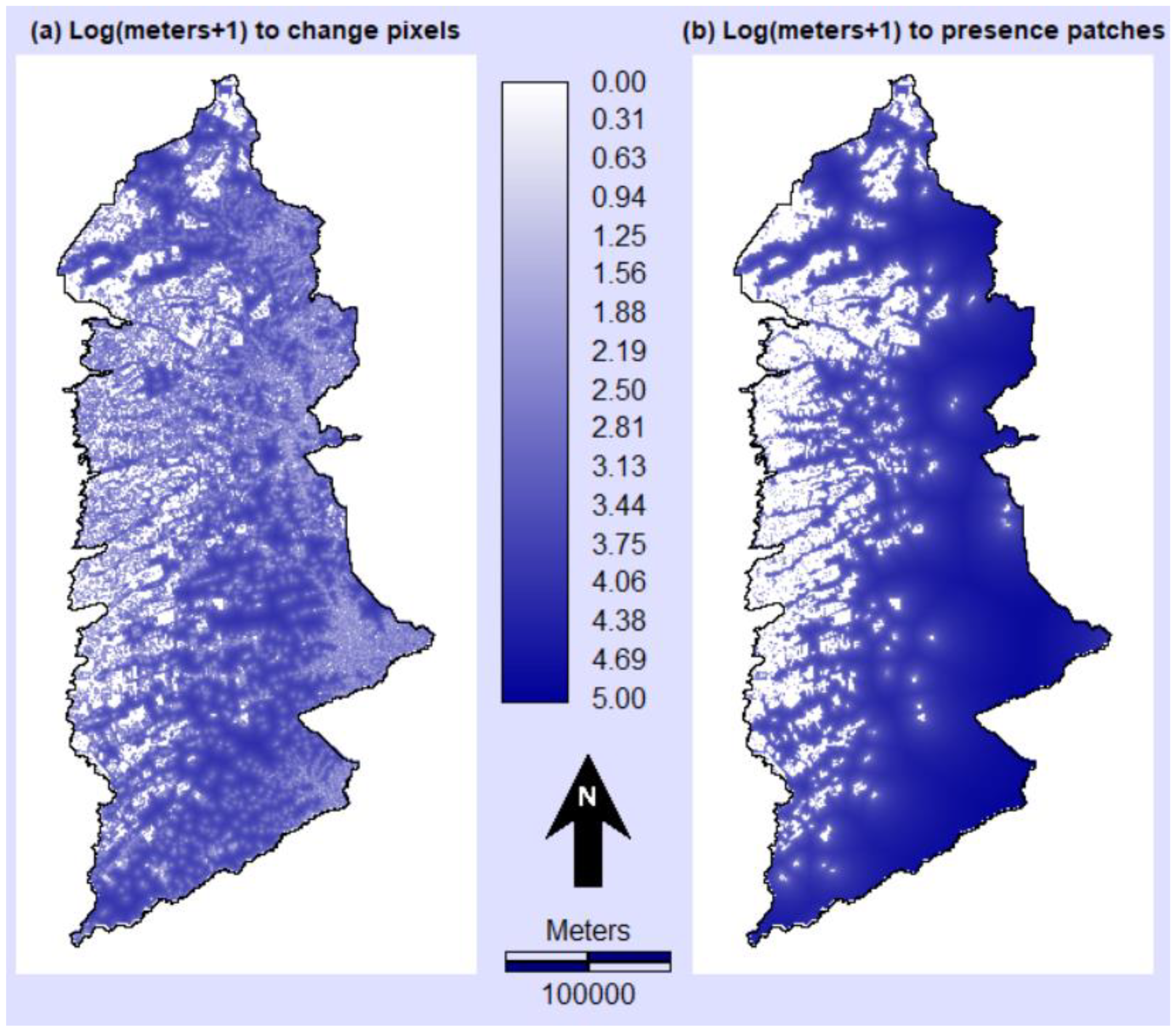
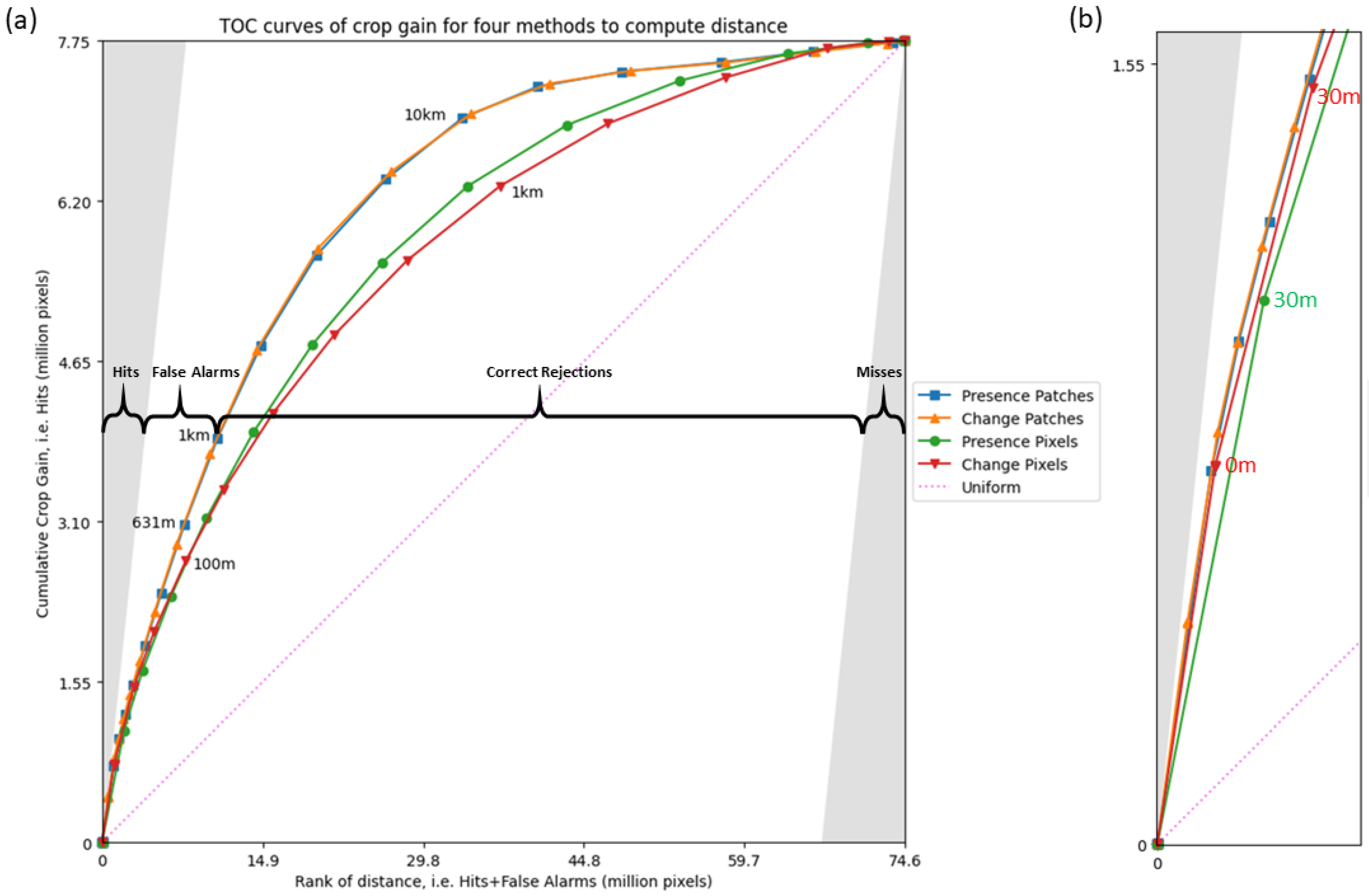
3. Results
4. Discussion
4.1. Interpretation of Results
4.2. Examples of TOC Curves in the Literature
4.3. Future Research
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pontius, R.G., Jr.; Si, K. The Total Operating Characteristic to Measure Diagnostic Ability for Multiple Thresholds. Int. J. Geogr. Inf. Sci. 2014, 28, 570–583. [Google Scholar] [CrossRef]
- Swets, J.A. Measuring the Accuracy of Diagnostic Systems. Science 1988, 240, 1285–1293. [Google Scholar] [CrossRef] [PubMed]
- Swets, J.A.; Dawes, R.M.; Monahan, J. Better DECISIONS through SCIENCE. Sci. Am. 2000, 283, 82–87. [Google Scholar]
- Saito, T.; Rehmsmeier, M. The Precision-Recall Plot Is More Informative than the ROC Plot When Evaluating Binary Classifiers on Imbalanced Datasets. PLoS ONE 2015, 10, e0118432. [Google Scholar] [CrossRef]
- Pontius, R.G., Jr. Metrics That Make a Difference: How to Analyze Change and Error; Advances in Geographic Information Science; Springer International Publishing: Cham, Switzerland, 2022; ISBN 978-3-030-70764-4. [Google Scholar] [CrossRef]
- Lobo, J.M.; Jiménez-Valverde, A.; Real, R. AUC: A Misleading Measure of the Performance of Predictive Distribution Models. Glob. Ecol. Biogeogr. 2008, 17, 145–151. [Google Scholar] [CrossRef]
- Peterson, A.T.; Papes, M.; Soberon, J. Rethinking Receiver Operating Characteristic Analysis Applications in Ecological Niche Modeling. Ecol. Model. 2008, 213, 63–72. [Google Scholar] [CrossRef]
- Hand, D.J.; Anagnostopoulos, C. When Is the Area under the Receiver Operating Characteristic Curve an Appropriate Measure of Classifier Performance? Pattern Recognit. Lett. 2013, 34, 492–495. [Google Scholar] [CrossRef]
- Cushman, S.A.; Macdonald, E.A.; Landguth, E.L.; Malhi, Y.; Macdonald, D.W. Multiple-Scale Prediction of Forest Loss Risk across Borneo. Landsc. Ecol. 2017, 32, 1581–1598. [Google Scholar] [CrossRef]
- Zhuang, H.; Chen, G.; Yan, Y.; Li, B.; Zeng, L.; Ou, J.; Liu, K.; Liu, X. Simulation of Urban Land Expansion in China at 30 m Resolution through 2050 under Shared Socioeconomic Pathways. GIScience Remote Sens. 2022, 59, 1301–1320. [Google Scholar] [CrossRef]
- Liu, X.; Liang, X.; Li, X.; Xu, X.; Ou, J.; Chen, Y.; Li, S.; Wang, S.; Pei, F. A Future Land Use Simulation Model (FLUS) for Simulating Multiple Land Use Scenarios by Coupling Human and Natural Effects. Landsc. Urban Plan. 2017, 168, 94–116. [Google Scholar] [CrossRef]
- Deng, Z.; Quan, B. Intensity Characteristics and Multi-Scenario Projection of Land Use and Land Cover Change in Hengyang, China. Int. J. Environ. Res. Public Health 2022, 19, 8491. [Google Scholar] [CrossRef] [PubMed]
- Harati, S.; Perez, L.; Molowny-Horas, R.; Pontius, R.G., Jr. Validating Models of One-Way Land Change: An Example Case of Forest Insect Disturbance. Landsc. Ecol 2021, 36, 2919–2935. [Google Scholar] [CrossRef]
- Ahmadlou, M.; Karimi, M.; Sammen, S.S.h.; Alsafadi, K. Three Novel Cost-Sensitive Machine Learning Models for Urban Growth Modelling. Geocarto Int. 2024, 39, 2353252. [Google Scholar] [CrossRef]
- Andaryani, S.; Nourani, V.; Haghighi, A.T.; Keesstra, S. Integration of Hard and Soft Supervised Machine Learning for Flood Susceptibility Mapping. J. Environ. Manag. 2021, 291, 112731. [Google Scholar] [CrossRef]
- Amato, F.; Tonini, M.; Murgante, B.; Kanevski, M. Fuzzy Definition of Rural Urban Interface: An Application Based on Land Use Change Scenarios in Portugal. Environ. Model. Softw. 2018, 104, 171–187. [Google Scholar] [CrossRef]
- Shojaei, H.; Nadi, S.; Shafizadeh-Moghadam, H.; Tayyebi, A.; Van Genderen, J. An Efficient Built-up Land Expansion Model Using a Modified U-Net. Int. J. Digit. Earth 2022, 15, 148–163. [Google Scholar] [CrossRef]
- Shafizadeh-Moghadam, H.; Minaei, M.; Pontius, R.G., Jr.; Asghari, A.; Dadashpoor, H. Integrating a Forward Feature Selection Algorithm, Random Forest, and Cellular Automata to Extrapolate Urban Growth in the Tehran-Karaj Region of Iran. Comput. Environ. Urban Syst. 2021, 87, 101595. [Google Scholar] [CrossRef]
- Wang, B.; Liang, Y.; Peng, S. Harnessing the Indirect Effect of Urban Expansion for Mitigating Agriculture-Environment Trade-Offs in the Loess Plateau. Land Use Policy 2022, 122, 106395. [Google Scholar] [CrossRef]
- Estoque, R.C.; Murayama, Y. Quantifying Landscape Pattern and Ecosystem Service Value Changes in Four Rapidly Urbanizing Hill Stations of Southeast Asia. Landsc. Ecol 2016, 31, 1481–1507. [Google Scholar] [CrossRef]
- Du, S.; Van Rompaey, A.; Shi, P.; Wang, J. A Dual Effect of Urban Expansion on Flood Risk in the Pearl River Delta (China) Revealed by Land-Use Scenarios and Direct Runoff Simulation. Nat Hazards 2015, 77, 111–128. [Google Scholar] [CrossRef]
- Viana, C.M.; Pontius, R.G., Jr.; Rocha, J. Four Fundamental Questions to Evaluate Land Change Models with an Illustration of a Cellular Automata–Markov Model. Ann. Am. Assoc. Geogr. 2023, 113, 2497–2511. [Google Scholar] [CrossRef]
- Pontius, R.G., Jr.; Castella, J.-C.; de Nijs, T.; Duan, Z.; Fotsing, E.; Goldstein, N.; Kok, K.; Koomen, E.; Lippitt, C.D.; McConnell, W.; et al. Lessons and Challenges in Land Change Modeling Derived from Synthesis of Cross-Case Comparisons. In Trends in Spatial Analysis and Modelling; Behnisch, M., Meinel, G., Eds.; Geotechnologies and the Environment; Springer International Publishing: Cham, Switzerland, 2018; Volume 19, pp. 143–164. ISBN 978-3-319-52520-4. [Google Scholar] [CrossRef]
- Pontius, R.G., Jr.; Francis, T.; Millones, M. A Call to Interpret Disagreement Components during Classification Assessment. Int. J. Geogr. Inf. Sci. 2025, 1–18. [Google Scholar] [CrossRef]
- Hand, D.J. Assessing the Performance of Classification Methods. Int Stat. Rev. 2012, 80, 400–414. [Google Scholar] [CrossRef]
- Pousa, R.; Costa, M.H.; Pimenta, F.M.; Fontes, V.C.; Brito, V.F.A.d.; Castro, M. Climate Change and Intense Irrigation Growth in Western Bahia, Brazil: The Urgent Need for Hydroclimatic Monitoring. Water 2019, 11, 933. [Google Scholar] [CrossRef]
- Souza, C.M., Jr.; Z. Shimbo, J.; Rosa, M.R.; Parente, L.L.; A. Alencar, A.; Rudorff, B.F.T.; Hasenack, H.; Matsumoto, M.; G. Ferreira, L.; Souza-Filho, P.W.M.; et al. Reconstructing Three Decades of Land Use and Land Cover Changes in Brazilian Biomes with Landsat Archive and Earth Engine. Remote Sens. 2020, 12, 2735. [Google Scholar] [CrossRef]
- Liu, Z.; Pontius, R.G., Jr. The Total Operating Characteristic from Stratified Random Sampling with an Application to Flood Mapping. Remote Sens. 2021, 13, 3922. [Google Scholar] [CrossRef]
- Pontius, R.G., Jr. Criteria to Confirm Models that Simulate Deforestation and Carbon Disturbance. Land 2018, 7, 14. [Google Scholar] [CrossRef]
- Bilintoh, T.M.; Pontius, R.G., Jr.; Liu, Z. Analyzing the Losses and Gains of a Land Category: Insights from the Total Operating Characteristic. Land 2024, 13, 1177. [Google Scholar] [CrossRef]
- Bilintoh, T.M.; Pontius, R.G., Jr.; Zhang, A. Methods to Compare Sites Concerning a Category’s Change during Various Time Intervals. GISci. Remote Sens. 2024, 61, 2409484. [Google Scholar] [CrossRef]
- Chen, S.; Feng, Y.; Ye, Z.; Tong, X.; Wang, R.; Zhai, S.; Gao, C.; Lei, Z.; Jin, Y. A Cellular Automata Approach of Urban Sprawl Simulation with Bayesian Spatially-Varying Transformation Rules. GISci. Remote Sens. 2020, 57, 924–942. [Google Scholar] [CrossRef]
- Kamusoko, C.; Gamba, J. Simulating Urban Growth Using a Random Forest-Cellular Automata (RF-CA) Model. ISPRS Int. J. Geo-Inf. 2015, 4, 447–470. [Google Scholar] [CrossRef]
- Azari, M.; Billa, L.; Chan, A. Multi-Temporal Analysis of Past and Future Land Cover Change in the Highly Urbanized State of Selangor, Malaysia. Ecol. Process 2022, 11, 2. [Google Scholar] [CrossRef]
- Chakraborti, S.; Das, D.N.; Mondal, B.; Shafizadeh-Moghadam, H.; Feng, Y. A Neural Network and Landscape Metrics to Propose a Flexible Urban Growth Boundary: A Case Study. Ecol. Indic. 2018, 93, 952–965. [Google Scholar] [CrossRef]
- Naghibi, F.; Delavar, M. Discovery of Transition Rules for Cellular Automata Using Artificial Bee Colony and Particle Swarm Optimization Algorithms in Urban Growth Modeling. ISPRS Int. J. Geo-Inf. 2016, 5, 241. [Google Scholar] [CrossRef]
- Naghibi, F.; Delavar, M.; Pijanowski, B. Urban Growth Modeling Using Cellular Automata with Multi-Temporal Remote Sensing Images Calibrated by the Artificial Bee Colony Optimization Algorithm. Sensors 2016, 16, 2122. [Google Scholar] [CrossRef]
- Singh, R.K.; Sinha, V.S.P.; Joshi, P.K.; Kumar, M. Modelling Agriculture, Forestry and Other Land Use (AFOLU) in Response to Climate Change Scenarios for the SAARC Nations. Environ. Monit. Assess. 2020, 192, 236. [Google Scholar] [CrossRef]
- Simwanda, M.; Murayama, Y. Spatiotemporal Patterns of Urban Land Use Change in the Rapidly Growing City of Lusaka, Zambia: Implications for Sustainable Urban Development. Sustain. Cities Soc. 2018, 39, 262–274. [Google Scholar] [CrossRef]


| ID | Description |
|---|---|
| 1 | Specify the purpose, particularly whether the TOC measures calibration or validation. |
| 2 | Report what is known concerning data quality. |
| 3 | Show an overlay of the maps at the time points that bound the time intervals. |
| 4 | Show maps of the independent and rank variables. |
| 5 | Compare to a non-random baseline ranking. |
| 6 | Mask pixels that are not candidates for the particular type of change. |
| 7 | Describe the sampling scheme and how the method accounts for the sampling. |
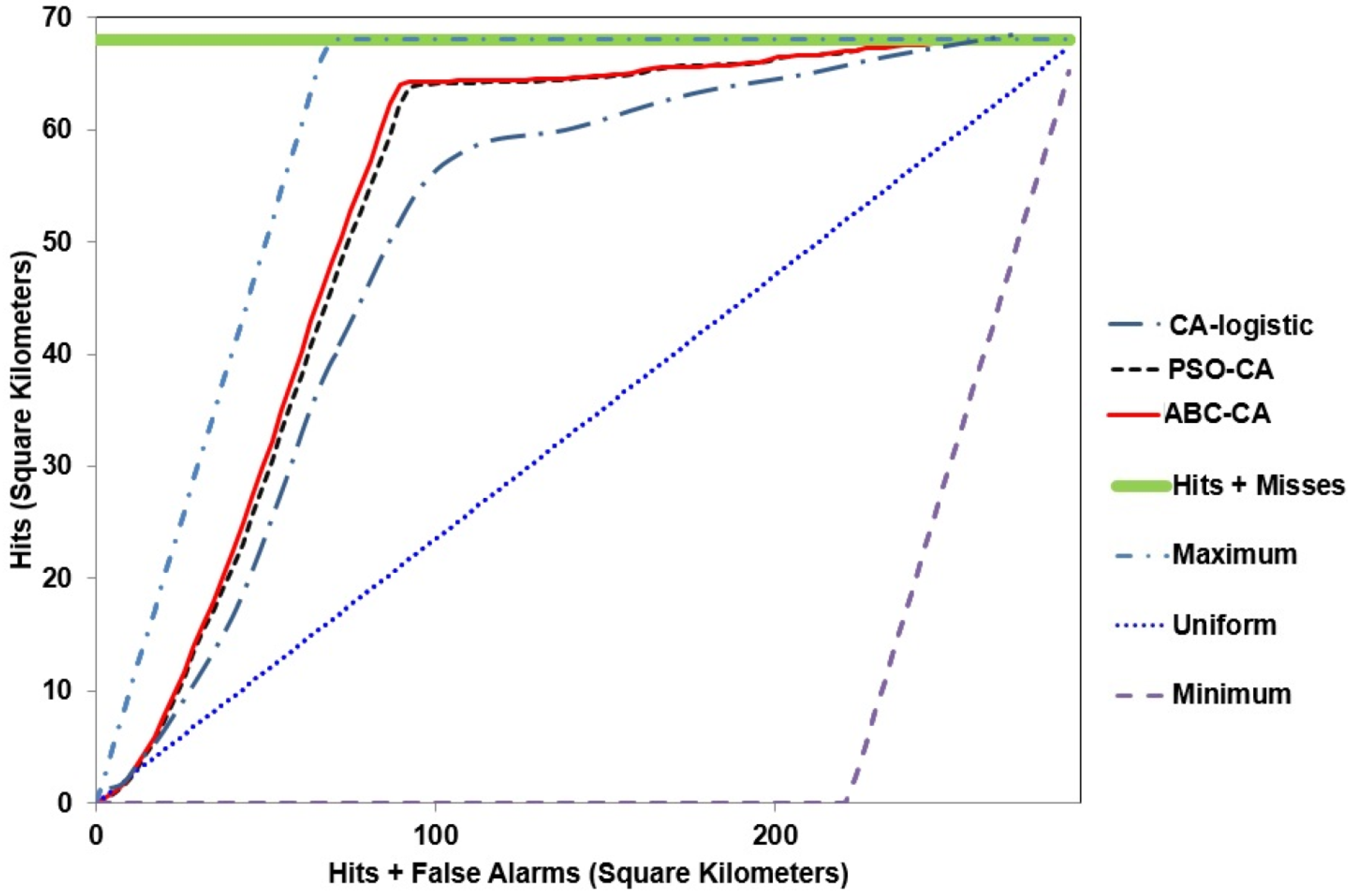
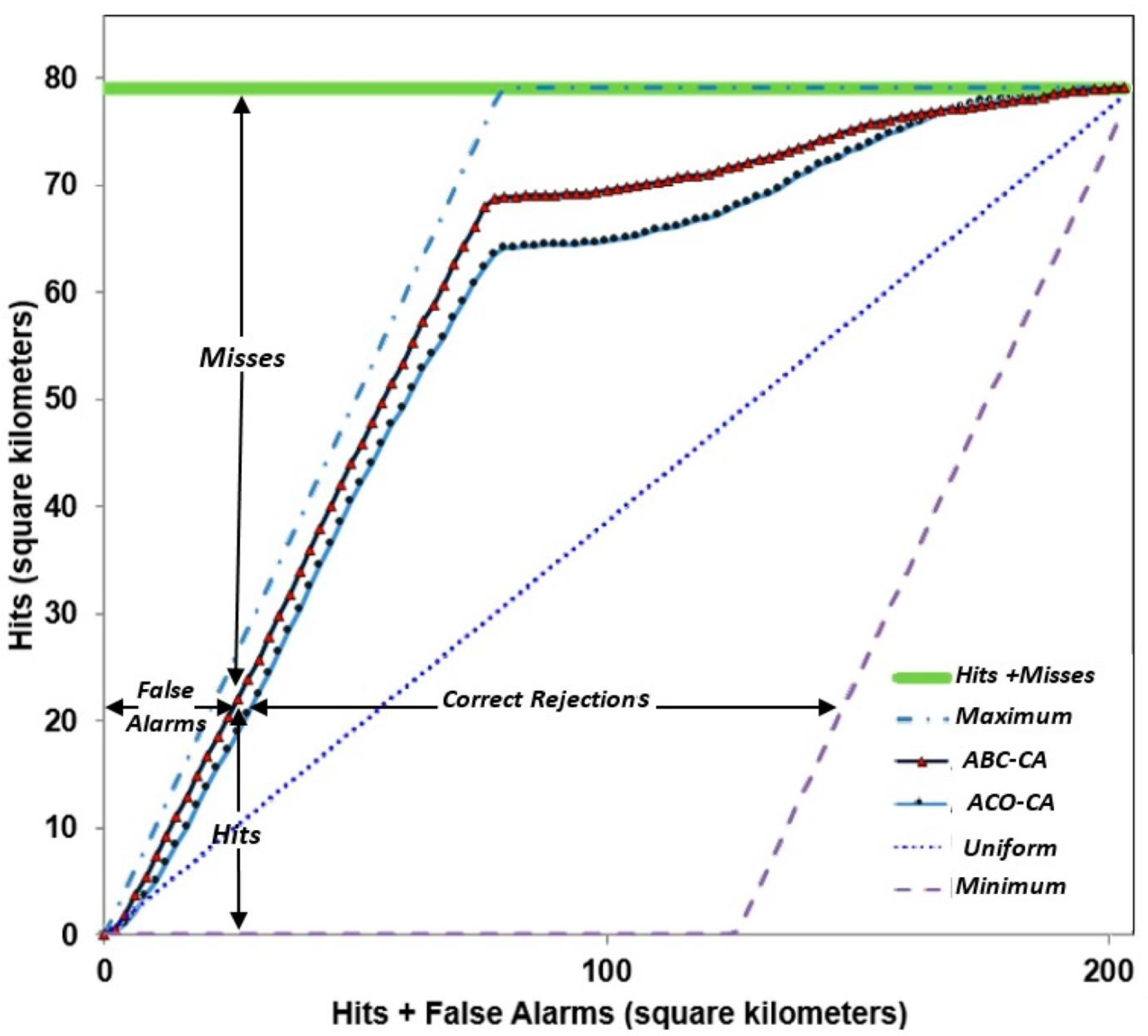
| 8 | Plot TOC curves including the baseline in the same parallelogram. |
| 9 | Consider extent reduction so the curve first touches the upper bound at the right corner. |
| 10 | Include threshold markers on the curves. |
| 11 | Label relevant thresholds, especially the threshold at the correct quantity. |
| 12 | Interpret slopes of the segments of the TOC curves relative to the uniform line. |
| 13 | Discuss the reasons for any changes in the concavity of the curves. |
| 14 | Investigate the points where TOC curves touch or cross. |
| 15 | Zoom into the origin of the TOC parallelogram to interpret early thresholds. |
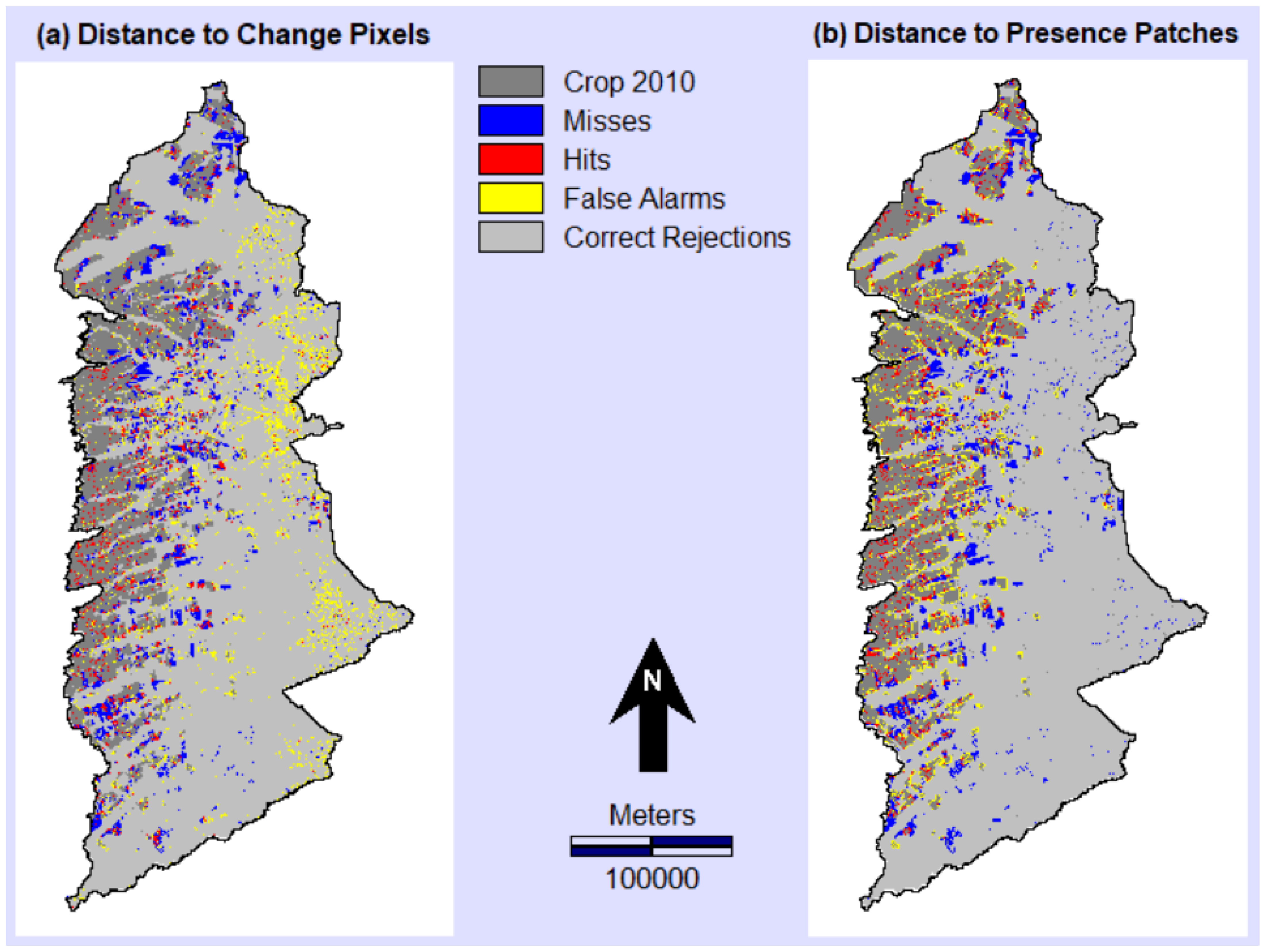
| 16 | Show maps of misses, hits, false alarms, and correct rejections for relevant thresholds. |
| 17 | Report exclusively the metric(s) that relate to the research question. |
| 18 | Test the sensitivity of results to the threshold selections. |
| 19 | Avoid stating model performance in simple universal words such as “good”. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Honnef, T.; Pontius, R.G., Jr. Best Practices for Applying and Interpreting the Total Operating Characteristic. ISPRS Int. J. Geo-Inf. 2025, 14, 134. https://doi.org/10.3390/ijgi14040134
Honnef T, Pontius RG Jr. Best Practices for Applying and Interpreting the Total Operating Characteristic. ISPRS International Journal of Geo-Information. 2025; 14(4):134. https://doi.org/10.3390/ijgi14040134
Chicago/Turabian StyleHonnef, Tanner, and Robert Gilmore Pontius, Jr. 2025. "Best Practices for Applying and Interpreting the Total Operating Characteristic" ISPRS International Journal of Geo-Information 14, no. 4: 134. https://doi.org/10.3390/ijgi14040134
APA StyleHonnef, T., & Pontius, R. G., Jr. (2025). Best Practices for Applying and Interpreting the Total Operating Characteristic. ISPRS International Journal of Geo-Information, 14(4), 134. https://doi.org/10.3390/ijgi14040134








