Abstract
This paper introduces a prospective study of the potential of spatio-temporal graphs (ST-graphs) and knowledge graphs (K-graphs) for the modelling of geographical phenomena. While the integration of time within GIS has long been a domain of major interest, alternative modelling and data manipulation approaches derived from graph and knowledge-based principles provide many opportunities for many application domains. We first survey graph principles and how they have been applied to GIS and a few representative domains to date. A comprehensive analysis of the principles behind K-graphs, respective data representation and manipulation capabilities is discussed. The perspectives offered by a close integration of ST-graphs and K-graphs are explored. The whole approach is illustrated and discussed in the context of maritime transportation.
1. Introduction
The past 30 years have seen a continuous search for modelling concepts and structures oriented to a sound integration of time within GIS [1,2,3,4]. Most of these models have been oriented to the integration, management and analysis of moving data and phenomena in space and time with a large diversity of applications in the environmental and urban domains [5]. Despite a series of conceptual and formal advances at all levels, there is still a need for novel modelling mechanisms that can provide additional data representations and analysis capabilities for moving objects and complex dynamic phenomena in space and time [6]. Continuous advances in real-time and sensor-based technologies have favoured the integration of large geographical data sets. However, this often leads to heterogeneous and complex data structures, which are not always easy to manipulate [7]. This stresses the need for novel spatio-temporal approaches adapted to the complexity of these large emerging datasets.
Over recent years, spatial and temporal graphs have been the object of major developments in many fields, thanks to a sound theoretical framework and to computational efficiency when applied to the analysis of the properties of large interconnected data sets [8]. Knowledge graphs (K-graphs) [9] offer a recent and promising paradigm that has emerged in the field of Semantic Web technologies. This approach promotes a graph-based data model that is both human and machine-readable and thus interoperable and dedicated to a semantically enriched knowledge representation by means of ontologies that offer a formal, and generally consensual, specification of the conceptualisation of a given domain.
A spatio-temporal graph (ST-graph) not only supports the representation of entities but also changes, events and processes. Connections between all these instances are specifically represented as nodes and edges, thus generating large network structures whose properties can be then analysed at different local to global levels, using specific graph operators and analytics. Moreover, graphs offer specific algorithms for browsing through the structural properties and relationships that characterise a given phenomenon (e.g., data inference [10] and knowledge extraction [11]). Last but not least, additional graph visualisation capabilities favour the observation of patterns and outliers from large evolving network structures [12,13]. Figure 1 illustrates the respective representation and computational principles behind spatio-temporal graphs and knowledge graphs. Differences in terms of data sources and application capabilities are highlighted, with these clearly showing a potential avenue for complementary approaches that not only are likely to provide extended heterogeneous data source integration but also a wider range of data analysis and visualisation capabilities and much more potential in terms of application domains.
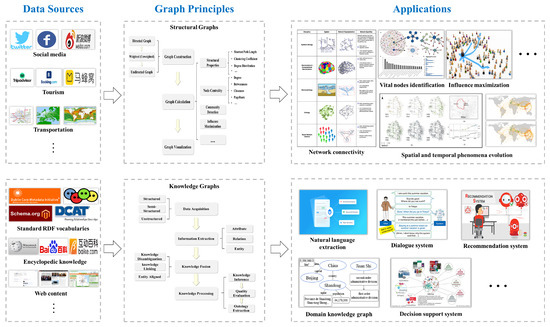
Figure 1.
ST-graph vs. K-graph frameworks.
Despite the intuitive properties and computational efficiency of graph-based models, a series of modelling issues are still pending. First, at the primitive levels, graphs can be applied using different principles. While nodes and edges are basic modelling structures, they might generate different types of graphs (e.g., connectivity graphs, bi-graphs, dual graphs, K-graphs and colored graphs), with these constraining the range of patterns that can be explored. Next, the integration of the temporal, spatial and semantic dimensions brings a series of conceptual issues that must be deal with; this is a common research issue when applying a general theory or computational technique to the field of GIS, not mentioning the problem of scale and abstraction levels. Third, the range of graph operators, graph analytics and algorithms that can be applied is relatively large, and so there is a need to have a clear picture of the current capabilities offered at the user level.
This paper reviews the formal and modelling principles behind ST-graphs and K-graphs. Their capabilities are described from the integration and representation of large and heterogeneous semantic data sources (e.g., RDF vocabularies to Web and social media contents) to the data manipulation and visualisation levels (Figure 1). The range of applications is relatively large and is discussed in the specific context of maritime information systems that illustrate how structural, temporal and semantics properties might be manipulated and analysed. This should favour a better understanding of the patterns and trends that emerge at the regional and global levels [14]. We finally introduce a few methodological directions for the methodological integration of ST-graphs and K-graphs.
The remainder of the paper is organised as follows: Section 2 introduces the main principles behind the representation of graphs, spatial, ST-graphs and K-graphs. Section 3 develops a few principles behind the representation of K-graphs, while Section 4 presents a few successful application of ST-graphs to the geographical and maritime domains. Section 5 provides methodological pathways for a modelling integration of ST-graphs and K-graphs. Finally, the conclusion summarizes the paper and outlines a few directions for further work.
2. Graphs
Graph models and structures have long been recognised as valuable means to represent many real-world applications that embed network structures. Graph principles provide valuable abstractions and mechanisms to represent and analyse many complex systems. This section introduces a brief survey of the principles behind graph structures, with a specific focus on the spatial and temporal dimensions.
2.1. Structural Graphs
Graphs have long been studied for the representation of many phenomena in different fields and disciplines. Graphs embed different structural properties that characterise a given phenomena but also provide additional opportunities to study emerging patterns at the local and global levels using either graph operators or graph analytics. The structure of a graph is relatively straightforward to represent as it is made of a finite set of nodes that form either undirected or directed sets of edges. These edges and nodes can be valued to denote additional semantics, thus extending the range of data manipulations.
Amongst the many successful applications of graph properties, the study of the relationship between the structure and function of urban spaces has been a major example of successful development. This has been the scope of space syntax studies, whose objectives are to empirically explore the relationships between the structure and function of a given urban space representing an urban network environment as a spatial graph [15]. By analysing urban network properties using local and global metrics, graph-based measures can reveal network structures, clusters and connected and disconnected areas in the city, thus providing useful insights for urban planners and decision-makers [15]. Indeed, as GIS already supports network structures, close integration between GISs and graph manipulation principles, as required by space syntax studies, have been widely facilitated, with this being one of the main reasons behind the fast growing application of space syntax studies in close connection with spatial data infrastructures.
Different graph primal representations (i.e., where nodes denote road intersections and edge connections between road intersections) have been applied to date to model the structural properties of an urban network, based on either isovists [16], axial lines [17] or convex spaces [18]. Different graph measures based on either local connectivities or global path-based properties can reveal urban structures and navigation opportunities in the urban layout and possible correlations with behavioural and social patterns. However, a few recent discussions note a lack of the theoretical grounding of these quantitative space syntax approaches and a lack of consideration of additional metrics [19], or even a lack of some additional structural properties such as the land property layout [20]. In fact, this also illustrates the fact that the current integration between graph-based and GIS approaches does not completely explore their full potential.
Not only graph-based principles have been applied to the analysis of the structural and functional properties of urban environments, but amongst many relevant examples, origin–destination simulations have been applied for the study of mobility patterns in urban systems by a combination of GIS network properties and graph-based analytics and simulations [21], the management of water distribution networks in order to identify water losses through the definition of an optimal network partitioning applied on top of a network representation [22], the study of large human communities as derived from social media and where humans are denoted as spatial entities and friendships as graph connections [23], hydrological networks [24] and graph patterns over time derived from water masses in the Mediterranean Sea [25]. Modelling the close relations between places, events and traffic patterns has been also explored using graph metrics and an experimental implementation within the Neo4j graph database [26]. This is indeed a major development as graph databases certainly provide a much more logical and methodological connection between GIS and graph capabilities than the geo-relational principles available in most GISs. Overall, these recent advances and trends highlight the interest of different research communities in the potential of graphs, thus stressing the need for a clear picture of the underlying modelling principles and processing capabilities available and of the perspectives and challenges offered by a close integration of graphs and GISs.
2.2. Spatial Graphs and Spatio-Temporal Graphs
2.2.1. Spatial Graphs
Spatial graphs describe spatial entities associated by spatial relationships. Spatial relations can denote, for instance, either topological relations or network properties that can be further qualified and valued by additional spatial semantics and metrics. Spatial graphs have been applied and embedded at different levels of granularity and scale (cf. Section 2.2.2) [27], in order, for instance, to study urban network structures at different levels of hierarchy [28,29,30]. One can remark that accessibility should not be confused with a connectivity graph, where edges denote any kind of spatial connection relation specified using, for instance, topological relationships. Approximate topological relations can be represented as in [31], for example, where degrees of connection between spatial entities are valued. In [32], a connectivity graph is applied to the context of historical cadastral maps.
2.2.2. Granularity in Graphs
The modelling of a given phenomenon implies a more or less simplified description of the reality that depends on the available knowledge and application requirements. The concept of granularity characterises the levels of abstraction and detail required for the representation of a given phenomena [33]. These levels can be organised according to a hierarchical structure that can increase or decrease the detail of the representation [34] within the limit imposed by the data. Browsing across different granularity levels is a valuable tool when one wishes to study the same phenomenon at several levels of detail. The granularity is usually broken down into three dimensions: semantic, temporal and spatial [29]. However, there are a few criteria to take into account when selecting a higher level of abstraction (i.e., spatial or temporal generalisation): this generates a loss of information, and so semantic and spatio-temporal constraints should be defined to identify which data are kept at a higher level of abstraction.
The modelling of the granularity in a graph is generally done according to two levels, node and/or edge, or via specific graph structures (e.g., bi-graph). Once a change of abstraction is modelled at the node level, this means that, at a certain level of granularity, a node actually represents a sub-graph. For example, clustering has been applied to group a series of vertices towards a single node at a higher level of abstraction [35]. Indeed, the choice of the clustering criterion depends on the modelling objectives. One might, for instance, group nodes according to some given criteria (e.g., grouping vertices into a cluster when they have the same neighbours outside the cluster, or according to some distance constraints). Abstraction can also be expressed by the selection of sub-graphs according to some spatial or semantic criteria (e.g., specific structure, node type). Regardless of how the granularity is modelled in a graph, hierarchical structures allow the selection of the appropriate level of abstraction with regard to the objective of the study. Representing a spatial graph from different points of view can help to select the sub-graphs that are relevant according to the context and thus to select the most appropriate level of granularity according to the user’s needs. Choosing a sub-graph means limiting the study to elements that compose this sub-graph. For example, in [30], the authors introduced several sub-graphs that denote transportation modes in the urban environment. Therefore, routes can be derived according to different transportation means, while the union of these graphs supports the derivation of multi-modal routes. Indeed, different levels of granularity can be generated either by establishing an abstraction via the nodes [27,36] or the edges [37] of the graph. The concept of granularity could also be associated with spatial inclusion, like in bi-graph structures [38,39], which are another way to model different levels of granularity. A bi-graph is made up of a “places” graph and a “links” graph. The “links” graph is a hypergraph that denotes the semantic relations between the represented spatial entities. A “places” graph is a forest as denoted in graph terminology that represents the entities that denote a given phenomenon, thus favouring the derivation of user-oriented views at different levels of spatial granularity.
2.2.3. Spatio-Temporal Graphs
It appears that most spatial modelling attempts oriented towards the integration of graphs have not fully considered the temporal dimension. Indeed, analysing the evolution of entities involves studying time as a component of the phenomenon considered. Time could be also taken into account by graphs using either external or internal mechanisms. For example, bi-graphs can define external dynamic rules that are not directly embedded into the graph structure. On the other hand, an ST-graph can be roughly defined as a spatial graph extended by additional temporal properties at the internal structural and representation levels. Integrating this temporal dimension stresses the need to formalise the notion of temporal abstractions and relationship in close association with the spatial concepts already identified at the spatial graph level. Temporal relations can be quantitatively valued by interval-based algebra [40] and by dependency links that appear from events, processes and changes. The temporal dimension can be introduced by either directly integrating time in the graph or a sequence of spatial graphs between which temporal relations are defined. For example, in [41], the authors introduce a graph that falls into the first category, where the nodes of the graph are clustered according to some spatial and temporal metrics (i.e., spatial distance, time differences). The objective is to detect patterns of moving objects that evolve together (i.e., moving objects patterns). Modelling actions or events in a graph was proposed in [42], but with a graph falling into the second category. Spatial configuration changes are characterised via a particular graph structure called a map tree. The evolution of a spatial configuration is modelled by temporal connections. The idea is to propose a classification of events according to the structure of the associated graphs. Many models fall into this second category of spatial graph sequences that evolve over time, and where from a spatial configuration, at each timestamp in which a change occurs, appropriate relationships are derived between the subsequent configurations. These models denote a global graph that contains the available data at a given time but also temporal connections between different times (or when these changes happen). Different generic approaches have been proposed in that direction, such as [8,43] or [44,45] (i.e., historical data available at different times), or in urban environment contexts [46]. In fact, identifying snapshots (i.e., spatial configurations at a given time) of evolution is relatively well supported for this category of graph but not immediately for graphs that integrate time intrinsically (i.e., the first category). On the other hand, the integration of different times increase the computational complexity at the processing levels. Other alternatives apply aggregation mechanisms to decrease the computational time and also the effectiveness of data manipulation processes [44,47].
2.2.4. Spatio-Temporal Graphs and Semantic Graphs
In [48], the existing duality between the spatial and the semantic components of a given object is highlighted. These two components can be broken down into several levels of granularity. Ideally, such models should therefore take into account both the spatial and temporal dimension of an object, but also its semantic component, and consider them homogeneously at the data manipulation level. In fact, additional semantic relations can be considered and should be integrated into spatial or ST-graphs using specific relations. For example, in [8], the concept of filiation, unlike as it is considered in [49], is not a spatial relationship; it is rather defined by the concept of identity and can be seen as a relationship of dependence, which is the transmission of kinship when a entity descends from another (see Figure 2).
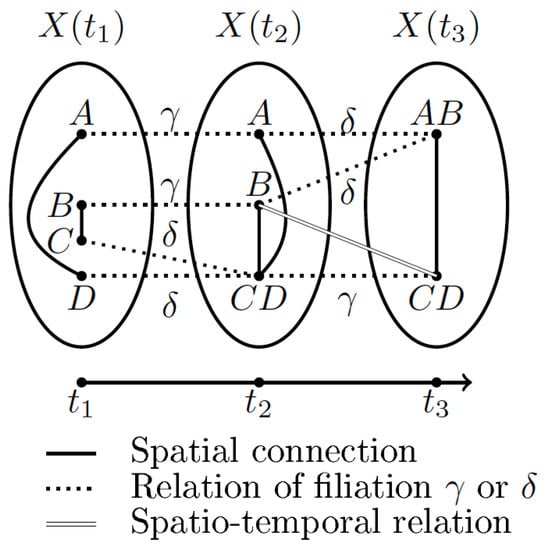
Figure 2.
A spatio-temporal graph from [8]. and are four spatial entities present at the first time . represents the set of spatial entities present at time . Spatial relations are denoted with plain lines, filiations are shown with dotted lines with labels and to denote continuations and derivations and spatio-temporal relations are shown with a double line. C and D combine at time to a new entity which derives from them. continues at while A and B combine at to a new entity .
This notion of filiation is also found in the field of ontologies, as in [50], where filiations are defined between entities based on spatial relationships and identities, and these two types of filiations are combined to obtain another level of abstraction in the typology of these filiation relationships. This model exploits the capabilities of the Semantic Web and defines a hierarchy of filiation relationships. This favours the consistency of a model based on this hierarchy and the inference of filiation relationships. This way of inferring information is a relevant example of using data that are not necessarily available in current spatial and ST-graph models.
2.2.5. Graph Analysis
One of the major challenges when characterising spatial dynamics is the modelling of change. Extracting knowledge and patterns from a spatial or ST-graph is one of the most widespread processing approaches applied to date and is based on graph theory techniques. In [41,42,51], the authors search for specific patterns. In [41], a graph clustering technique is introduced to extract entities (i.e., cliques) whose speed and space are close to each other in order to detect traffic anomalies. In [42], spatial configuration changes are detected, and in [51], actions are qualified. In both cases, each transformation as well as each action corresponds to a given structure of the graph, while the search for structural properties is also concerned with patterns. However, a key issue is not only to extract data but also to infer new information from the data.
In [52], the author combines the concept of a colored graph and logic programming to generate new crop rotations that respect a set of constraints learned from the study of agricultural plots in a pre-processing step. In [44], another example of the creation of information is presented in which the generation of an aggregate ST-graph brings out other relationships. An ST-graph represents the evolution of geo-historical observations and describes the changes and processes that constitute this evolution. The main idea is to search for temporal patterns in the graph (e.g., disappearance, re-appearance), but this implies that data quality issues such as missing data must be considered.
3. Knowledge Graphs
K-graphs have recently been the object of increased interest as they have the advantage of combining graph principles with semantic Web formalisms. This section briefly reviews the main principles of K-graphs and their potential for representing spatio-temporal phenomena.
3.1. Knowledge Graphs: Main Principles
For about 10 years, the paradigm of K-graphs, which appeared in the field of the Semantic Web, has been the subject of great interest in many research domains, which have largely exceeded its original community and the field of Artificial Intelligence from which it originates. K-graphs are associated with Linked Data, an initiative of the W3C to publish and link data on the Web (Berners-Lee T., Linked Data. Design Issues. W3C, 2006, https://www.w3.org/DesignIssues/LinkedData (accessed on 1 August 2021)). The RDF (Resource Description Framework) (RDF, RDF 1.1 Concepts and Abstract Syntax, W3C, 2014, https://www.w3.org/TR/rdf11-concepts/ (accessed on 1 August 2021)) is the basic language of the Semantic Web (or Web 3.0) and is made up of a set of languages and technologies dedicated to making the content of the Web interpretable by humans but also by machines.
In order to formally describe Web resources and their metadata, RDF is supported by a data model on top of a graph structure. RDF data are represented by a triple (subject, predicate, object), and an RDF graph is then a set of such triples. The subject of a triple can be a URI (Uniform Resource Identifier) or an empty node. A predicate represents a property always designated by a URI. The object corresponds to the value of the property (i.e., predicate). This value can be a URI, an empty node or a literal. A literal denotes a string of characters or typed data. The vertices (which play the roles of subject or object) and the oriented edges (which carry the predicates) of an RDF graph are therefore labelled (see Figure 3). The challenge for humans, and especially for machines, is to understand these labels (especially when they are represented by URIs or by their generalisation, namely IRIs (Internationalised Resource Identifiers)). This is the role of RDF vocabularies. Among them, the RDF Schema (RDFS) (RDFS, RDF Schema 1.1, W3C, 2014, https://www.w3.org/TR/rdf-schema/ (accessed on 1 August 2021)) is an RDF vocabulary that acts as a meta-vocabulary by structuring the terms of a domain by means of classes and properties. Thus, if the nodes (i.e., subjects or objects) of RDF graphs are described by RDF vocabulary classes while the edges (predicates) are described by RDF vocabulary properties, the semantics of these RDF graphs become accessible through these vocabularies by humans and machines. In order to surpass the limits to the expressiveness of RDFs, the knowledge representation language OWL (Web Ontology Language) (OWL, OWL Web Ontology Language, W3C, 2004, https://www.w3.org/TR/owl-ref/ (accessed on 1 August 2021)) has been proposed. OWL is also based on the RDF data model. An ontology in OWL is defined first by means of classes and properties that capture the concepts and relations between these concepts of the domain addressed by the ontology. Moreover, OWL proposes a set of axioms (equivalent classes, equivalent properties, equality of two resources, difference, opposite, symmetry, cardinality constraints...) that gives it superior description capabilities. It is commonly acknowledged that SPARQL (SPARQL, SPARQL Query Language for RDF, W3C, 2008, https://www.w3.org/TR/rdf-sparql-query/ (accessed on 1 August 2021)) is to RDF what SQL is to relational databases: a query language allowing users to search, create, add, delete and modify data. SPARQL is therefore the language on which the triple stores, which are the RDF database management systems, are based [53]. Triple stores rely on the SPARQL protocol to offer the possibility of creating access points, called SPARQL end points. These SPARQL end points allow a local RDF database to be accessed and queried via SPARQL queries from any client on the Web. Although the term “Knowledge Graph” was first introduced by Google (Singhal A., Introducing the Knowledge Graph: Things, not Strings, May 2012. https://googleblog.blogspot.co (accessed on 1 August 2021)) to refer to the exploitation of semantics by its search engine—without however revealing all its secrets—it owes its success more to applications such as DBPedia, Freebase, Wikidata or Yago, which provide access to open and publicly accessible K-graphs [54]. These multilingual K-graphs are all based on the linked data paradigm. The Wikidata knowledge base, for example, to date contains more than 92 million items (nodes). Wikidata is a common source of data covering a wide variety of domains, topics and communities. All of these datasets, consisting of publicly accessible RDF triplets, are part of the Linked Open Data Cloud (LOD, https://lod-cloud.net/ (accessed on 1 August 2021)). Within the LOD Cloud, more than a thousand RDF datasets are mutually referenced through the URIs they contain, thus enabling navigation from dataset to dataset, from domain to domain, from subject to subject and from node to node. This global and semantic database greatly contributes to the strength and interest of the Linked Data Web. Figure 4 shows a simple example of a K-graph.
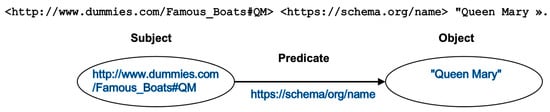
Figure 3.
An RDF triple (N-Triples notation), referring to a Web resource about the Queen Mary boat, and its graphical representation.
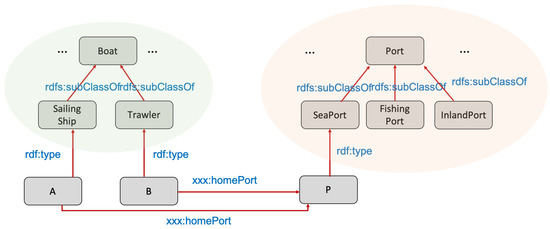
Figure 4.
A K-graph representing knowledge about a sailing ship A and a trawler B sharing the same home port P. Through the predicate rdf:type, two ontologies, available in the LOD Cloud and describing a universe of boats and ports, respectively, are referred to.
Graph theory in support of K-graphs favours the manipulation of structural properties and metrics and the application of search-based algorithms for querying, browsing, digging (for a review, see [9]) and pattern extraction [55]. As a K-graph is based on one-to-many ontologies, additional reasoning mechanisms can be applied from the Semantic Web. Immersed in the Linked Data Web, based on the same RDF model and reference vocabularies and serialisable, accessible and searchable via SPARQL, K-graphs are interoperable. They benefit from the standardisation operated by the W3C. They are easily navigable and composable. They make data from billions of linked triples and knowledge on multitudes of domains in most languages freely accessible on the Web. Finally, they are a natural support for the explicability, the provenance and therefore the traceability of facts. All this available knowledge can be used for different purposes, in different fields of application: natural language understanding, dialogue systems (questions/answers) and recommendation systems [56] in the field of tourism, energy or education [57].
3.2. Spatio-Temporal Knowledge Graphs
If existing K-graphs are complemented with edges and nodes carrying information related to space and/or time, then we can qualify these graphs as spatial and/or temporal K-graphs (or STK-graphs here, for the sake of simplicity). Similarly, if one seeks to describe objects in the real world by considering their spatial footprint or coverage, their location in time or their positioning in space and/or time in relation to each other, constructing STK-graphs is a solution to his issue. Figure 5 extends the example of Figure 4 and shows a simple STK-graph.
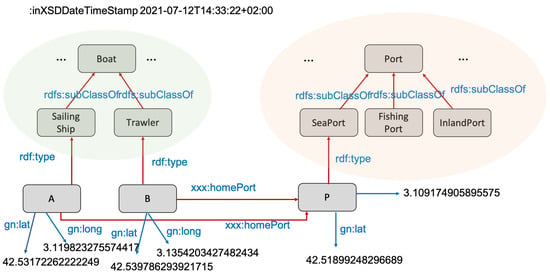
Figure 5.
An STK-graph extending the K-graph of Figure 4. Spatial knowledge (predicates in blue) has been added as the latitude and longitude coordinates of the port P and boats A and B, using the geonames ontology (https://www.geonames.org/ontology/documentation.html (accessed on 1 August 2021)) (prefix is used). We suppose that time is contextual to the K-graph and corresponds to 12 July 2021 at 2:33 p.m. and 22 s, UTC +2.
For the past 15 years, the description of temporal data in the Semantic Web has been preferably based on the W3C’s standard OWL-Time ontology (OWL, Time Ontology in OWL, W3C Candidate Recommendation, 2020, https://www.w3.org/TR/owl-time/ (accessed on 1 August 2021)). OWL-Time is an ontology dedicated to the representation of time, in which a temporal entity is either an instant or an interval (i.e., a period of time whose duration is delimited by a beginning and an end instant). OWL-Time provides a description to express dates and durations, as well as properties to characterise and access temporal data, but also seven topological binary relationships and their inverses (e.g., before, after, meets, met by, overlaps, overlapped, starts, started by, during, contains, finishes, finished by, equals), making it possible to locate, in the chronological order of a chosen reference time system, instants and intervals in relation to each other. As recommended by the OGC and W3C (SDWBP, Spatial Data on the Web Best Practices, W3C Working Group Note 28 September 2017, https://www.w3.org/TR/sdw-bp/#spatial-relations (accessed on 1 August 2021)), the description of spatial data embedded in K-graphs can be based on the ontology of the OGC GeoSPARQL standard (GeoSPARQL, A Geographic Query Language for RDF Data, OGC, 2012. https://www.ogc.org/standards/geosparql (accessed on 1 August 2021)). GeoSPARQL is both a vocabulary for representing spatial or geospatial data in RDF and an extension of the SPARQL language to formulate queries on the spatial dimension of RDF data expressed in this vocabulary. GeoSPARQL integrates a number of standards, recommendations or norms that preceded it. The GeoSPARQL ontology is based on three main classes: one represents spatial objects in all their generality; the other two, which are distinct sub-classes, correspond respectively to features and geometries, so that, among the features of a spatial object, the characteristics specific to its geometry (spatial footprint) are distinguished. The geometries described by sets of points can be voluminous and then serialised using the WKT (WKT CRS, Well-known text representation of coordinate reference systems, OGC, 2012, https://www.ogc.org/standards/wkt-crs (accessed on 1 August 2021)) or GML (GML, Geography Markup Language, OGC, 2010, https://www.ogc.org/standards/gml (accessed on 1 August 2021)) languages. GeoSPARQL includes a vocabulary of spatial topological relations established between two spatial objects and to be chosen among the three models DE-9IM [58], Egenhofer [59], and RCC8 [60]. Each binary topological relation can be queried or asserted. A set of non-topological spatial functions (e.g., Euclidean distance, convex envelope, etc.) is also provided. Directional or orientation relationships, although spatial, are not covered by the GeoSPARQL vocabulary. With regard to the spatio-temporal aspect, the coverage of the temporal dimension in GeoSPARQL queries is limited to the functions available in the SPARQL language on dates and time. The topological temporal relations taken into account by OWL-Time are excluded.
The storage of these STK-graphs is also carried out within triple stores. In [61], the authors propose a recent comparative study of the main triple stores that support GeoSPARQL. This study tests a substantial RDF dataset of more than 130 Gbytes against a benchmark composed of two series of queries (simple and complex). The Virtuoso, GraphDB and Strabon systems have proven to be very efficient here for processing queries on data sets of around 500 million RDF triplets. However, the OBDA approach implemented in the Ontop-spatial system [62] is superior due to its potential for scaling up. Ontop-spatial is an extension of the Ontop system [63]. The idea is to access geospatial data stored in relational databases from virtual geospatial RDF graphs, created using R2RML, which can be queried via GeoSPARQL queries translated into standard OpenGIS SQL (OGC, Simple Feature Access—Part 2: SQL Option, 2010, https://www.ogc.org/standards/sfs (accessed on 1 August 2021)).
The design of an STK-graph from various sources has crystallised around the entity resolution problem and the link discovery problem. The former [64,65] is tackled with non-spatial and/or spatial similarity measurements between entities and is established using the sameAs property defined in OWL. Link discovery echoes the fourth rule of the Data Web (linking data together to enrich their respective information context). It is based on various measures of similarity [66,67] adapted to the processed data. In the case of spatial data, it is possible to establish topological relationships [68], distances or orientations. Similarly, temporal topological relationships, where appropriate, can be generated. Entity resolution and link discovery are essential operations in that they make it possible, firstly, to link K-graphs (or RDF data sets) together and then to traverse them in a second stage dedicated to the exploration and exploitation of these graphs. The integration of heterogeneous data sources is currently facilitated by specific tools such as SILK [69].
Spatial and temporal data lend themselves well to visualisation capabilities. In fact, there are several works that propose an interface to visualise, by means of maps, data extracted from STK-graphs. Among them, Sextant [70] is a multifunction system that allows the visualisation and exploration of the evolution of linked spatial data, as well as the production of thematic maps or statistical diagrams. More recently, in [71], the authors proposed the building of spatio-temporal K-graphs from some vectorised historical maps about a railway network and then for changes to be visualised over time.
Driven by the objective of the European INSPIRE directive to facilitate access to open data, the National Mapping Agencies in Europe, which are the producers of official data, are also turning their attention to linked data to develop an open European Geographic K-graph on top of an open European SDI [72]. In 2014, in [73], the potential of Linked Data and K-graphs for Geographic Information Science was discussed: “The Linked Data paradigm offers a radically new perspective on structuring, publishing, discovering, accessing, and integrating data”. One of the most striking recent attempts to bring GIS closer to the LOD Cloud is [74], which proposes a deep integration of linked data into GIS, preserving the functionality, roles and strengths of each party. This framework and the underlying methodology can be seen as a geo-enrichment service within ArcGIS and a first step towards GIS with extended exploration, question/answer and recommendation capabilities, which are the primary missions of K-graphs.
Finally, when compared to ST-graphs, two types of K-graphs are also capable of representing knowledge and its evolution over time: dynamic K-graphs and contextual K-graphs. In dynamic K-graphs, time-stamps are associated with relations (edges) or even nodes and define their validity or existence period. Approaches such as temporal or dynamic K-graphs [75,76], labelled property graphs promoted by Neo4j (https://neo4j.com (accessed on 1 August 2021)) or RDF-star (RDF*) (https://w3c.github.io/rdf-star/cg-spec/editors_draft.html (accessed on 1 August 2021)) are based on graph models that are capable to capture the evolution of information or knowledge through time, in the same manner as ST-graphs. A single dynamic K-graph is generally considered, but the nodes and edges of this dynamic K-graph are embedded or are labelled with some spatial and/or temporal information indicating when they are valid (in which space and/or during which period). It should be noted that labelled property graphs or RDF-star (RDF*) are generic approaches that are not specifically dedicated to the representation of knowledge evolution within a graph, but rather allow this representation through their model. Contextual K-graphs form a dual approach that expresses a set of temporalised (valid in the time interval associated with the K-graph) and/or spatialised (valid in the space or territory associated with the K-graph) knowledge. Thus, a spatial and/or temporal context is associated with the contextual K-graph as a global label [9]. The representation of the evolution of knowledge leads to the consideration of as many spatial and/or temporal contexts (and thus contextual K-graphs) as necessary, which renders this approach more cumbersome to manage.
4. Graphs and Knowledge Graphs in the Field of Maritime Transportation
4.1. Large Maritime Graphs
Maritime transportation is a valuable example of a worldwide phenomenon with large data flows that can be comprehended using spatial, temporal and semantic graphs [77]. It provides a set of properties, either spatial, semantic or temporal, that support a valuable application example in which different categories of graphs can be applied for different representation and application purposes and an illustrative support to discuss most of the concepts and methodological proposals introduced in this paper. For instance, maritime trade routes can be derived from either liner companies or global insurance companies [78] or automated maritime geo-location infrastructures. Therefore, harbour departure and arrival records can favour the analysis of modern trade routes and flows from city to country and regional scales [79]. As illustrated in Figure 6, maritime datasets can also be integrated and aggregated using different data sources in order to provide additional semantics and processing capabilities [80]. For instance, the global cargo trajectory data available in real-time can be associated with freight status (e.g., type, length, width) and with additional maritime infrastructures such as ports and berths. This provides a sound support for the construction of a fine-grained global maritime network that can be further manipulated at either the local or the global level using graph functions and analytics, as well as GIS analysis and visualisations. From vessel departure and arrival data, origin and destination ports modelled as nodes, the underlying maritime routes are implicitly represented as links and then maritime routes. Additional semantics can be associated with these links and nodes. For instance, a weighted maritime network can be associated with trade volumes, and graph theory principles have been recently applied to mine the spatio-temporal characteristics of maritime transport network journeys [13,81].
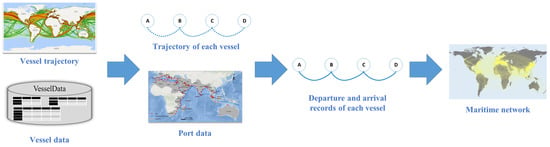
Figure 6.
Sketch map of a maritime network design.
Current research on the development of the spatio-temporal analysis of maritime transport networks generally considers maritime network structural properties through the main transportation routes and/or port connections and flows using graph theory principles. This favours, for instance, the analysis of the main maritime routes over time or some dependency relations between different ports and countries. The typical analysis of maritime networks can also study “scale-free”, “small-world” and “rich-club” characteristics that generally arise in maritime networks and that can be revealed by graph-based operators [81,82,83,84]. When studying “scale-free” maritime networks, the degree of the ports (i.e., port-to-port connections in terms of maritime traffic) might reveal a power-law distribution when most of the ports have low degree values (i.e., they are stops over a few maritime routes) while a few ports have large degree values (i.e., they are stops over many maritime routes). There are also many studies oriented towards container shipping to exhibit core–periphery patterns and “hub-and-spokes” structures that reflect spatial disparities using graph analytics [81,85,86]. Overall, it has been shown that the global maritime network has a low average shortest path length value and a high average clustering coefficient compared with other transport networks (e.g., the worldwide airport network) [87], indicating that the global maritime transport network is much more closely connected than many other networks. Close trade relations between different ports and fewer occurrences of transshipments among ports will lead to an increase in the transshipment capacity of the hub ports and promote the formation of a closer trading community around them. A series of works have developed community analysis for the maritime transport networks by combining graph operators and analytics with additional semantic graph properties [12,13,88,89]. As Figure 7 shows, in [12], it appears that the global liquefied natural gas (LNG) trade network has developed several closely connected trading communities since 2013, and ports within individual communities have gradually become more geographically spatially concentrated. By using different network topology representations and the effects of space-L (a link is created between consecutive stops in one route) and space-P (all ports that belong to the same route are connected), emerging topologies on the maritime network can be studied [90,91]. Hu et al., found that the worldwide maritime transportation network is a small-world network with power-law behaviour for both its network and topology [91]. Moreover, differences between maritime transportation networks can be also studied [77,78]. For example, in [78], the authors found that container ships follow regularly repeating paths, whereas bulk dry carriers and oil tankers move less predictably between ports. To fully consider the spatial relationships between different types of maritime transport networks, rather than aggregating all layers of networks, multi-layer network methods can be applied to study global maritime transport networks [89,92,93].
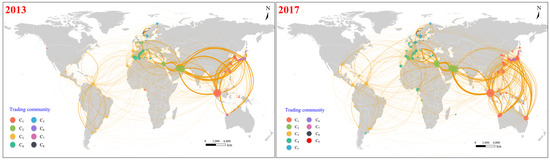
Figure 7.
Spatial distribution of ports in different trading communities [12].
The efficiency of maritime transportation has a major impact on global economic development, international politics and social and economic exchanges. Maritime transportation is also extremely vulnerable to emergencies such as natural disasters and political changes. Therefore, the quantitative evaluation of the robustness of the maritime transportation network structure and the proposal of targeted improvements are of great significance for improving the efficiency of maritime transportation [94]. Several scholars have developed some graph structural analyses and simulations to evaluate the impact on the whole network of some ports’ decline of maritime activity and flows. This helps to evaluate the degree of robustness of the whole or even local maritime networks [77,87,95,96]. These studies found that maritime networks are relatively robust to random failure while being extremely vulnerable to targeted failure. Moreover, different cargo ship networks behave heterogeneously in terms of their robustness, with the container network being the weakest and the bulk carrier network being the strongest [77]. Ensuring the stable operation of key hub ports is of great significance to ensuring the robustness of maritime transportation.
Another important area that has been explored when studying maritime networks is the study of some local and global port properties at different levels of granularity, using some centrality indices such as the degree, betweenness centrality and closeness, et al., in order to mine important ports and the way they are embedded in the whole network [77,97,98,99,100,101,102]. One can conclude that port centrality represents a port’s ability to attract both traffic from its hinterland area and services from its directly connected and indirectly connected ports [99]. Some well-known ports, such as Singapore and Hong Kong, have a high centrality, because they are strategically located in favourable intermediate geographical positions along major trade routes. Other ports have a high centrality because they are visited by a large number of ships (e.g., Shanghai) or primarily by being connected to many different ports (e.g., Antwerp) [78]. There is a certain correlation between different centrality indicators; in [102], it was found that high-scoring ports in betweenness centrality have high degree and closeness measures. Apart from the static centrality indices in mining the port importance, in [103,104], a port influence diffusion model was designed. The authors found over half of the ports in the networks were able to influence only one other port, while Rotterdam and Antwerp influenced ports in the entire network in 2013 and 2016. Figure 8 shows the hub influence and its diffusion in 2013 and 2016.
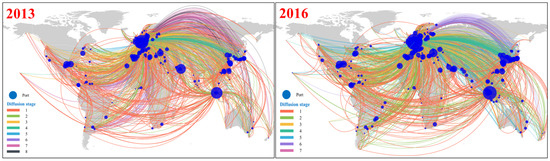
Figure 8.
Hub influence and diffusion in 2013 and 2016 [103].
With the availability of many maritime data sources, temporal analysis on maritime transport and ports that particularly influence the structural changes over time can be applied [12,92,103,104,105,106,107,108,109]. With the continuous advancement of navigation technology and the further popularisation of long-distance transportation, the scale of the maritime transport network has shown an increasing trend over time, accompanied by an increase in the number of routes of the important ports. For example, in [107], it was found that Singapore port had 159 routes passing through it in 2009 and 484 in 2016 for crude oil transport, and the increase in trade relations with ports in the Asia-Pacific region has been particularly prominent, especially with China, Japan, South Korea and Australia. Moreover, by analyzing the network character of global maritime multilayer networks and their evolution from 1977 to 2008, the authors of [92] found that maritime traffic distribution shows a place-dependent character due to the reinforced position of existing ports, and the network expands and concentrates around large hub ports over time. However, several major events have also had a great impact on maritime transport [108,110]. For example, the worldwide evolution of containerised trade reflects a general decrease in the volume of merchandise from 2008 to 2010, with this being caused by the fall in the demand within the global economy which took place during the years considered [108].
4.2. Ontology-Based and Knowledge Graph-Based Approaches in the Maritime Transport Domain
As pointed out by Katsumi and Fox [111], formal ontologies whose semantics are explicitly defined and transcribed into machine-readable languages are capable of supporting various knowledge management and reasoning services, such as semantic integration and interoperability, data validation and knowledge inference. The study by these authors lists a dozen ontologies dedicated to passenger and freight transport, with various description capacities adapted or not to a particular transport mode. Although none of these ontologies is specifically concerned with maritime transport, one can identify two main families of ontologies dedicated to the maritime transport domain in the literature: those focused on the monitoring and control of ship movements at sea, and those oriented towards the regulation and management of risks in ports and terminals.
The first category includes the work by Villa and Camossi [112], which introduces a Maritime Container Ontology (MCO) that represents ships, containers, their movements and their routes (see a excerpt in Figure 9) in order to identify and detect patterns of suspicious manoeuvres or movements using axioms described in OWL. Similarly, a semantic trajectory ontology is exploited for surveillance and control purposes in [113] in which spatial or aspatial rules, written in SWRL (the Semantic Web Rula Language (SWRL, SWRL: A Semantic Web Rule Language Combining OWL and RuleML, W3C, 2004, http://www.w3.org/Submission/SWRL/ (accessed on 1 August 2021))), allow abnormal ship behaviours to be described and alerts to be triggered. Lange et al. [114] introduce an ontology to describe and simulate the behaviour of objects involved in the management of container loading and unloading terminals.
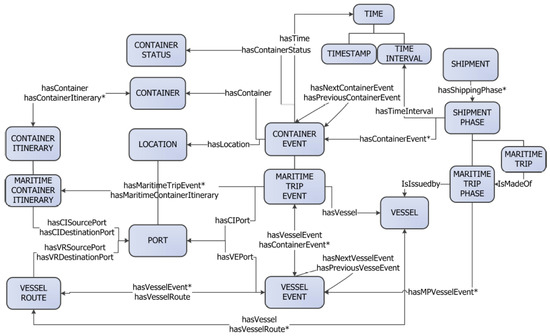
Figure 9.
An excerpt of the Maritime Container Ontology [112].
In the second category, the work by Hagaseth et al. [115] addresses the problem of the complexity of maritime transport regulations. To this end, they introduced an ontology of maritime regulations whose classes capture both the target (i.e., person or ship) to which the regulation applies, the conditions under which it applies (i.e., context) and what is required by that regulation. The complete ontology describes the documents supporting one regulation and all the rules and clauses associated with this regulation, as well as the ships, ports, weather, routes, etc. The ontology is exploited by a triple store after the conversion of its content into RDF graphs. A SPARQL query is then used to extract and reconstruct a text document corresponding to a (part of a) regulation. Pileggi et al. [116] developed a vision of port management in which several communities or actors are involved and cooperate in the general organisation and, more specifically, in the risk management process. All the knowledge (i.e., type of risks, decision makers, port, cooperation aspects, risk management, etc.) related to the interactions between these actors are described by ontologies. The Port of Hamburg (Germany) serves as a case study in the validation of this approach.
K-graphs, on the other hand, have emerged more recently in the maritime transport domain. In the field of monitoring and control, Wen et al. [117] introduced a semantic model for ship behaviour (SMSB). These semantic networks describe observable states and behaviours in navigation, at berth, at anchorage and on a defined maritime route. States are recognised and established by rules, and potential behaviours are inferred by a Dynamic Bayesian Network (DBN). Automatic Identification System (AIS (AIS, https://en.wikipedia.org/wiki/Automatic_identification_system (accessed on 1 August 2021))) data from maritime merchant traffic are used to establish typical profiles of ship behaviour in different phases (at berth, at anchor, underway, on a given route) through the DBN. In real time, ship trajectories can be annotated with the detected states and with alerts in case of the recognition of an abnormal behaviour. A visualisation of the annotated trajectories in real time is proposed. With the different states characterising the ships stored in the K-graphs, the SPARQL language can then be used to query the recorded trajectories. Zhang et al. [118] retained a K-graph approach for the monitoring and management of Dangerous Maritime Goods (DMG). K-graphs describe the types of DMGs, the packaging and the containers that carry them (see Figure 10 for an excerpt of the DMG K-graph). In addition to terminology axioms establishing inclusion or equality relationships between concepts, the SWRL language is used to establish segregation (i.e., separate exposure) and storage condition rules for each DMG.
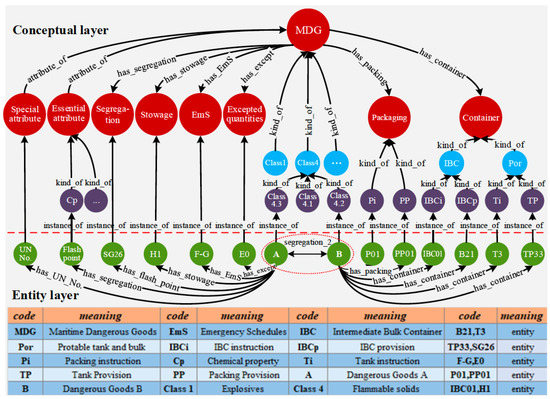
Figure 10.
An excerpt of the DMG K-graph [118].
An approach based on link prediction in dynamic K-graphs oriented to the identification of maritime navigation scenes is presented in [76]. Dynamic K-graphs capture the evolution of entities such as ships, ports and countries. Two link prediction methods (Know-Evolve [75] and TransE [119] between two entities based on neural networks are exploited and allow for the prediction of a suspicious activity (e.g., transshipment at sea between two ships) by observing their respective trajectories.
The difference between ontology-based and knowledge graph approaches is first a matter of precedence (K-graphs were introduced recently (in 2012, through Google’s Knowledge Graph), while formal ontologies have existed in Artificial Intelligence for about 30 years. As a matter of fact, K-graphs are often assimilated and confused with knowledge bases, and these are confused with ontologies. However, in contrast to a simple knowledge base or ontology, according to the definition given by [54], a knowledge graph that is immersed and built from semantic Web technologies should demonstrate capabilities to “acquire and integrate information into an ontology and to apply a reasoner to derive new knowledge”.
Beyond these emerging works highlighting the contribution of K-graphs and underlying ontologies, one can remark that there is so far little or no public RDF vocabulary specifically dedicated to maritime transport in the LOD Cloud. However, it is important that existing ontologies are listed and accessible. Thus, it appears that the ontology-based initiatives mentioned above could be extended to K-graphs and exploited by dedicated analysis techniques (i.e., querying, visualszation, machine learning, etc.), the development of which is currently booming. As with many other application domains, the development and publication of K-graphs dedicated to maritime transport would facilitate semantic interoperability and the integration of data from different sources. Similarly, linking (through discovery, whether automatic or manual) should favour a close association of these business resources described by these K-graphs to other domain resources, thus avoiding the well-known phenomena of knowledge islands formed by isolated K-graphs. Once linked to other K-graphs—in particular, those accessible in the LOD Cloud—K-graphs representing maritime transportation networks can be semantically enriched, thus offering much greater possibilities of knowledge discovery or inferences. Finally, thanks to the valuable tools now available for storing K-graphs, the accumulated data on maritime transport could be queried using much more powerful semantic queries.
5. Discussion
It clearly appears that (ST) graphs and K-graphs both encompass specific properties, implying that each has its own advantages, especially when taking into account the spatial and temporal dimensions. On the one hand, graphs offer a straightforward data model that is mainly based on a dual representation of nodes and edges, to which labels can be associated as a very first step towards semantics. The ability of graphs to propose multiple structures and properties that are generally well-fitted to the representation of real-world geographical networks is a strong point of this method. In other words, graphs concentrate on the essential factors and also offer many data manipulation capabilities thanks to the large availability of graph operations and analytics. This kind of processing can most often highlight some underlying structural properties and metrics derived from graph principles. One might also browse these graphs in search of a node, an edge or a given path or clusters, or to compare different graphs to search for particular sub-graphs or patterns. Overall, graphs have now reached a good level of maturity to be applied to different application contexts, especially the geographical context, in which many network-based structures can be represented with graph-based approaches (for a review, see [120]).
On the other side, with K-graphs, semantics takes precedence and is expressed in the vocabularies and domain ontologies at the conceptual level. The main principle lies in the graph model promoted by RDF, which, adopted de facto as a pivotal format, facilitates interoperability. Interoperability is also reinforced by the support of standard vocabularies or ontologies that can be used by machines (computers). The Linked Open Data (LOD) Cloud, which contains open and accessible K-graphs, linking together a multitude of domains, thus constitutes a global and RDF semantised database that can be browsed or traversed in search of data and knowledge but also extended by connecting one’s own graphs by means of IRI referencing.
The constant progress of RDF (triple) stores makes them capable today of competing on many points with graph database management systems or relational databases [121], while the complexity of SPARQL is proven to be similar to that of SQL [122]. Moreover, these families of data management tools are not necessarily opposed. For example, graph DBMS can be used to store and analyse K-graphs. Neo4j is a popular graph DBMS which relies on a modelling based on labelled property graphs (i.e., LPG), which is both more flexible and more compact than the classic modelling by RDF triples, but also on a query language, called Cypher, adapted to these LPGs while ensuring compatibility with RDF graphs. Moreover, the debate around LPGs and K-graphs may well fade away with the recent proposal of RDF-star (RDF*), which allows metadata to be associated to any RDF triplet while still preserving the triplet unit format. The next sub-sections discuss the respective and mutual contribution of graphs and K-graphs and the emerging opportunities when the two are associated or closely connected.
5.1. From Knowledge Graphs to Spatio-Temporal Graphs
Starting from a K-graph, one can extract an associated graph in order to analyse the structural properties and then manipulate it using specific graph operators and analytics. A promising objective is to combine the respective data representation and manipulation of both knowledge and structural graphs in order to take full advantage of the two approaches. Therefore, the approach can be implemented in a homogeneous, complementary and efficient way in which structural properties resulting from graph principles and metrics can be applied together with K-graph operations. Accordingly, this implies that an initial K-graph is available, as well as specific properties and constraints that can relate the structural and the K-graphs. In other words, this requires a domain-based ontological model, a structural-based model and indeed a relevant dataset. Practically, from a K-graph, one can identify an associated sub-graph that is constructed by extracting nodes and/or edges from the initial K-graph. After this extraction, the nodes/edges of the associated graph are not necessarily identical to the nodes and edges selected in the K-graph but may also result from a complex transformation rather than a simple projection. In the example illustrated in Figure 11, the K-graph on the top describes boats which have the same home ports. The ST-graph below describes the spatial relation of the closeness between different boats. In this example, there is no bijection between the instances and relations of the K-graph and the ST-graph. This means that data could come from different sources, but there could be an injection from the K-graph to ST-graph if the ST-graph is an extraction of the K-graph data.
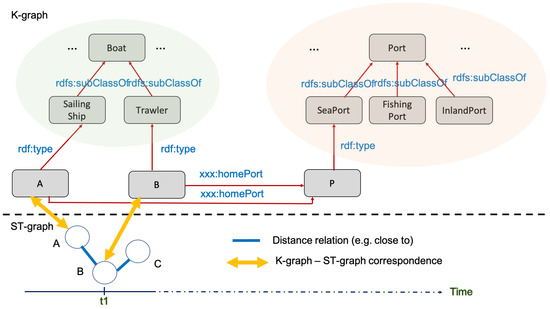
Figure 11.
Potential correspondence between K-graph and ST-graph (one timestamp).
The associated ST-graph can be used to analyse, by derivation, the K-graph, and then to produce a set of additional knowledge related to the initial K-graph. The knowledge inferred by processing the associated graph can retrospectively be integrated (i.e., made explicit) into the initial K-graph in order to increase it and to enrich the knowledge it contains. For example, the result of applying a metric to the associated graph would be added to the metadata (by means of nodes and edges) of the K-graph.
5.2. From Spatio-Temporal Graphs to Knowledge Graphs
Conversely, starting from a graph, it is possible to complete it with additional knowledge provided by K-graphs—in particular, those accessible on the LOD Cloud—in order to infer new knowledge and to complete the initial graph in a detailed manner.
Indeed, in the example given in Figure 11, the semantics related to the node classification could be inferred from the conceptual hierarchy of the K-graph to enrich the ST-graph (e.g., entity a is a sailing ship which is a boat). The conceptual hierarchy in the K-graph should be greatly more developed as that in the ST-graph, as it is only possible to assign a flattened classification for nodes, and as considering additional structural properties is not straightforward. This conceptual hierarchy could refer to an ontology that characterises the instances more accurately.
Overall, it is assumed that an initial graph that represents the model of a given application is available. For a particular node (or edge) of this graph, it is possible—for example, by relying on a search engine—to search (usually in the LOD Cloud) for a K-graph that contains a node that describes the node (or edge) of the initial graph. This identification phase can be complex and costly; it also requires the consideration of the reliability and quality of the associated K-graph discovered. This associated K-graph can then be browsed for specific additional knowledge. In the example given in Figure 11, the associated K-graph can be used to search for all the ships that have the same owner as a given ship in the initial graph. Traversing the associated K-graph can also be a matter of serendipity and allow links between nodes to be discovered that are not present in the initial graph. For example, it may be discovered that two boats represented by two nodes in the initial graph correspond to nodes in the associated K-graph that point to the same node via the “is-owned-by” edge, meaning that they have the same owner. As illustrated in the two previous examples, the explicit and direct knowledge carried by the associated K-graph is exploited. However, more broadly, other types of ontological and axiomatic knowledge (for example, by exploiting properties such as transitivity or specialisation relations), possibly expressed by rules, make it possible to make implicit knowledge explicit (i.e., to make it appear in order to eventually integrate it). At the end of this search and enrichment process via the LOD Cloud, one can decide to extend and thus enrich the initial graph with all or part of the discovered or inferred knowledge. This results in a more general process that can be described as the semantisation of graphs through K-graphs. On the other hand, it is possible that the search in the LOD Cloud is unsuccessful and that no K-graph is identified. However, if the process of semantic enrichment of the initial graph has been initiated, this implies the building of a K-graph based on an ontological representation of the domain covered by the initial graph, and then for this K-graph to be published and made accessible in the LOD Cloud.
In the example in Figure 11, the ST-graph does not consider time, but if considered, as shown in Figure 12, the mapping between K-graph instances and the ST-graph is similar. The K-graph here is static, which means that the semantics are considered to be constant or atemporal, while the dynamics are represented by the ST-graph, which shows the mobility of the boats. This is a choice, and the extension to a temporal K-graph could be done according to the same principles. The idea is still to make a mapping between the common instances of the two types of graphs. Accordingly, the ST-graph focuses on specific relations, and the possibility to complicate the graph operators by querying the K-graph remains. For example, it is possible to search for the closest boats if the issue consists of detecting the risk of impact and then looking for the port to which they belong. For the main objective (impact detection), the second question is not absolutely required, but it could be useful in a second iteration to look at a higher semantic level of detail to have this information. Furthermore, taking into account the only necessary information should improve the computational time requirements.
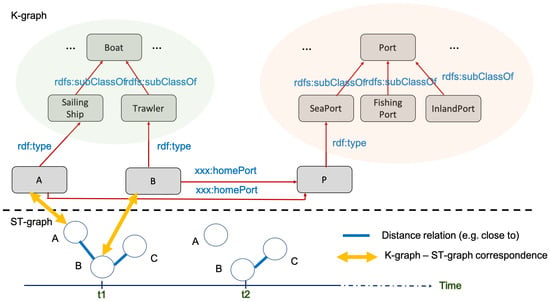
Figure 12.
Potential correspondence between K-graph and ST-graph (multiple timestamps).
6. Conclusions
Over the past few years, many modelling attempts have been developed for a sound representation of spatio-temporal phenomena. In particular, spatial and temporal graphs have been recently widely explored as alternative modelling structures for many geographical phenomena. The research developed in this paper discusses recent research advances in the application of different categories of graphs for handling spatial and temporal information.
In order to provide a modelling background, in our paper, we first introduce a brief survey of ST-graphs and K-graphs principles and capabilities and how they have been progressively applied to geographical applications. The specific example of the maritime transportation domain exemplifies how ST-graphs and K-graphs have been successfully applied to a context that provides many spatial, temporal and semantic properties, but also still raises many open avenues for further research.
An underlying important and challenging issue we have addressed in this paper is whether K-graphs can be considered as a support when specifying the semantics of the ST-graph models as a new higher level of semantics for ST-graphs. On the other hand, we also discuss how K-graphs can be associated with and enriched by an ST-graph that provides a structurally complementary view of the data. A prospective discussion of the mutual benefits of this dual approach is developed, as well as potential ways to connect these two types of graphs. It appears that an ST-graph shows a greatly simplified level of semantic that allows graphs operators to be computed more efficiently, and the K-graph makes a higher level of semantic available, allowing more complex semantic queries.
The next step is to confirm this intuition and try to use Semantic Web tools such as inference engines to automatically complete the semantics in ST-graphs and create completely new information (i.e., not already present in the initial K-graph/ST-graph). The processing carried out on these graphs thus enriched could be much more precise regarding the traversed semantics of the nodes and arcs. It would also be possible to show the potentiality of more complex queries which would not be considered without the combination of the ST-graph and K-graph. However, there will certainly be a need to further develop ST-graphs and K-graphs within integrated database frameworks that support conceptual design processes and query representation and manipulation interfaces that support a sound combination of the data representations and intuitive user-oriented functions. This is a still expected development that will imply the full involvement of the scientific community, standardisation bodies and the software industry [123].
Author Contributions
Conceptualisation, G.D.M., P.P., J.G., C.C. and F.L.; Methodology, G.D.M., P.P., J.G., C.C. and F.L.; Validation, G.D.M., P.P., J.G., C.C. and F.L.; formal analysis, G.D.M., P.P., J.G., C.C. and F.L.; Investigation, G.D.M., P.P., J.G., C.C. and F.L.; Writing—original draft preparation, G.D.M., P.P., J.G., C.C. and F.L.; Writing—review and editing, G.D.M., P.P., J.G., C.C. and F.L. All authors have read and agreed to the published version of the manuscript.
Funding
Géraldine Del Mondo, Jérôme Gensel and Christophe Claramunt are supported by the French National Research Framework MAGIS (CNRS 2340), Peng Peng and Feng Lu are supported by the National Natural Science Foundation of China (41631177, 42001391). Peng Peng is also supported by China Postdoctoral Science Foundation (2020T130644, 2019M660774). Christophe Claramunt is also supported by Chinese Academy of Sciences President’s International Fellowship Initiative (2021VTA0002).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Langran, G. A review of temporal database research and its use in GIS applications. Int. J. Geogr. Inf. Sci. 1989, 3, 215–232. [Google Scholar] [CrossRef]
- Peuquet, D. It’s About Time: A Conceptual Framework for the Representation of Temporal Dynamics in Geographic Information Systems. Ann. Assoc. Am. Geogr. 1984, 84, 441–461. [Google Scholar] [CrossRef]
- Claramunt, C.; Thériault, M. Managing Time in GIS: An Event-Oriented Approach. In Recent Advances in Temporal Databases, Proceedings of the International Workshop on Temporal Databases, Zürich, Switzerland, 17–18 September 1995; Clifford, J., Tuzhilin, A., Eds.; Workshops in Computing; Springer: Berlin/Heidelberg, Germany, 1995; pp. 23–42. [Google Scholar] [CrossRef]
- Spaccapietra, S.; Parent, C.; Damiani, M.L.; de Macedo, J.A.; Porto, F.; Vangenot, C. A conceptual view on trajectories. Data Knowl. Eng. 2008, 65, 126–146. [Google Scholar] [CrossRef]
- Siabato, W.; Claramunt, C.; Ilarri, S.; Manso-Callejo, M. A Survey of Modelling Trends in Temporal GIS. ACM Comput. Surv. 2018, 51, 30:1–30:41. [Google Scholar] [CrossRef]
- Galton, A. Space, Time and the Representation of Geographical Reality. In The Philosophy of GIS; Tambassi, T., Ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 75–97. [Google Scholar] [CrossRef]
- Yang, C.; Clarke, K.; Shekhar, S.; Tao, C.V. Big Spatiotemporal Data Analytics: A research and innovation frontier. Int. J. Geogr. Inf. Sci. 2020, 34, 1075–1088. [Google Scholar] [CrossRef]
- Del Mondo, G.; Stell, J.G.; Claramunt, C.; Thibaud, R. A Graph Model for Spatio-temporal Evolution. J. Univ. Comput. Sci. 2010, 16, 1452–1477. [Google Scholar] [CrossRef]
- Hogan, A.; Blomqvist, E.; Cochez, M.; d’Amato, C.; de Melo, G.; Gutiérrez, C.; Gayo, J.L.; Kirrane, S.; Neumaier, S.; Polleres, A.; et al. Knowledge Graphs. 2020. Available online: http://xxx.lanl.gov/abs/2003.02320 (accessed on 1 August 2021).
- Gao, J.; Qiu, P.; Yu, L.; Huang, Z.; Lu, F. An interpretable attraction recommendation method based on knowledge graph. Sci. Sin. Inf. 2020, 50, 1055–1068. [Google Scholar] [CrossRef]
- Qiu, P.; Yu, L.; Gao, J.; Lu, F. Detecting geo-relation phrases from web texts for triplet extraction of geographic knowledge: A context-enhanced method. Big Earth Data 2019, 3, 297–314. [Google Scholar] [CrossRef]
- Peng, P.; Cheng, S.; Lu, F. Characterizing the global liquefied petroleum gas trading community using mass vessel trajectory data. J. Clean. Prod. 2020, 252, 119883. [Google Scholar] [CrossRef]
- Peng, P.; Lu, F.; Cheng, S.; Yang, Y. Mapping the global liquefied natural gas trade network: A perspective of maritime transportation. J. Clean. Prod. 2021, 283, 124640. [Google Scholar] [CrossRef]
- Lu, F.; Yu, L.; Qiu, P. On geographic knowledge graph. J. Geo Inf. Sci. 2017, 6, 723–734. [Google Scholar] [CrossRef]
- Hillier, B.; Hanson, J. The Social Logic of Space; Cambridge University Press: Cambridge, UK, 1984. [Google Scholar] [CrossRef]
- Benedikt, M.L. To Take Hold of Space: Isovists and Isovist Fields. Environ. Plan. B 1979, 6, 47–65. [Google Scholar] [CrossRef]
- Turner, A.; Penn, A.; Hillier, B. An Algorithmic Definition of the Axial Map. Environ. Plan. B 2005, 32, 47–65. [Google Scholar] [CrossRef]
- Peponis, J.; Wineman, J.; Rashid, M.; Kim, S.H.; Bafna, S. On the description of shape and spatial configuration inside buildings: Convex partitions and their local properties. Environ. Plan. B 1997, 24, 761–781. [Google Scholar] [CrossRef]
- Ratti, C. Space syntax: Some inconsistencies. Environ. Plan. B 2004, 31, 487–499. [Google Scholar] [CrossRef]
- Domingo, M.; Thibaud, R.; Claramunt, C. A graph-based approach for the structural analysis of road and building layouts. Geo Spat. Inf. Sci. 2019, 22, 59–71. [Google Scholar] [CrossRef]
- Wang, Y.; Yin, H.; Chen, H.; Wo, T.; Xu, J.; Zheng, K. Origin-Destination Matrix Prediction via Graph Convolution: A New Perspective of Passenger Demand Modeling. In Proceedings of the KDD’19—25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 1227–1235. [Google Scholar] [CrossRef]
- Nardo, A.D.; Giudicianni, C.; Greco, R.; Herrera, M.; Santonastaso, G.F. Applications of Graph Spectral Techniques to Water Distribution Network Management. Water 2018, 10, 45. [Google Scholar] [CrossRef]
- Fang, Y.; Cheng, R.; Li, X.; Luo, S.; Hu, J. Effective community search over large spatial graphs. In Proceedings of the VLDB Endowment, Munich, Germany, 28 August–1 September 2017; Volume 6, pp. 1227–1235. [Google Scholar] [CrossRef]
- Leonard, L.; MacEachren, A.M.; Madduri, K. Graph-based visual analysis for large-scale hydrological modeling. Inf. Vis. 2016, 16, 2015–2216. [Google Scholar] [CrossRef]
- Petelin, B.; Kononenko, I.; Malacic, V.; Kukar, M. Frequent subgraph mining in oceanographic multi-level. Int. J. Geogr. Inf. Sci. 2019, 33, 1936–1959. [Google Scholar] [CrossRef]
- Maduako, I.; Wachowicz, M. A space-time varying graph for modelling places and events in a network. Int. J. Geogr. Inf. Sci. 2019, 33, 1915–1935. [Google Scholar] [CrossRef]
- Stell, J.G. Granulation for graphs. In Spatial Information Theory. Cognitive and Computational Foundations of Geographic Information Science. International Conference COSIT’99, Volume 1661 of Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1999; pp. 417–432. [Google Scholar] [CrossRef]
- Batty, M. Network Geography: Relations, Interactions, Scaling and Spatial Processes in GIS. In UCL Working Papers Series; Centre for Advanced Spatial Analysis: London, UK, 2003; Volume 63, ISSN 1467-1298. [Google Scholar]
- Claramunt, C.; Winter, S. Structural Salience of Elements of the City. Environ. Plan. B Plan. Des. 2007, 34, 1030–1050. [Google Scholar] [CrossRef]
- Jguirim, I.; Brosset, D.; Claramunt, C. Un Système de Génération d’Itinéraires des activités mobiles dans la ville. In Proceedings of the Actes de la 11ème Conférence Internationale Annuelle Spatial Analysis and GEOmatics, SAGEO 2015, Hammamet, Tunisia, 30 November 2015; pp. 46–59. [Google Scholar]
- Sriti, M.; Thibaud, R.; Claramunt, C. A network-based Model for representing the evolution of spatial structures. In Proceedings of the 4th ISPRS Workshop on Dynamic & Multi-Dimensional GIS, Pontypridd, UK, 5–8 September 2005; pp. 150–155. [Google Scholar]
- Rodier, X.; Couedic, M.L.; Hautefeuille, F.; Leturcq, S.; Jouve, B.; Fieux, E. From space to graphs to understand spatial changes using medieval and modern fiscal sources. In Proceedings of the 40th Annual Conference of Computer Applications and Quantitative Methods in Archaeology (CAA), Southampton, UK, 26–29 March 2012; Amsterdam University Press: Southampton, UK, 2012; pp. 424–431. [Google Scholar] [CrossRef]
- Meentemeyer, V. Geographical perspectives of space, time, and scale. Landsc. Ecol. 1989, 33, 163–173. [Google Scholar] [CrossRef]
- Frank, A.U.; Timpf, S. Multiple representations for cartographic objects in a multi-scale tree—An intelligent graphical zoom. Comput. Graph. 1994, 18, 823–829. [Google Scholar] [CrossRef]
- Auber, D.; Chiricota, Y.; Jourdan, F.; Melançon, G. Multiscale Visualization of Small World Networks. In Proceedings of the Ninth Annual IEEE Conference on Information Visualization—INFOVIS’03, Seattle, WA, USA, 19–21 October 2003; pp. 75–81. [Google Scholar] [CrossRef]
- Pinson, L.; Del Mondo, G.; Tranouez, P. Representation of interdependencies between urban networks by a multi-layer graph. In Proceedings of the 14th International Conference on Spatial Information Theory (COSIT 2019), Regensburg, Germany, 9–13 September 2019; Volume 142. [Google Scholar]
- Mainguenaud, M. Modelling the Network Component of Geographical Information Systems. Int. J. Geogr. Inf. Syst. 1995, 9, 575–593. [Google Scholar] [CrossRef]
- Walton, L.; Worboys, M.F. An Algebraic Approach to Image Schemas for Geographic Space. In Proceedings of the Spatial Information Theory, 9th International Conference, COSIT 2009, Aber Wrac’h, France, 21–25 September 2009; pp. 357–370. [Google Scholar] [CrossRef]
- Stell, J.G.; Del Mondo, G.; Thibaud, R.; Claramunt, C. Spatio-temporal Evolution as Bigraph Dynamics. In Proceedings of the Spatial Information Theory—10th International Conference, COSIT 2011, Belfast, ME, USA, 12–16 September 2011; pp. 148–167. [Google Scholar] [CrossRef]
- Allen, J.F. Towards a general theory of action and time. Artif. Intell. 1984, 23, 123–154. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J.; Wang, S.; Liu, Z.; Yuan, Q.; Yang, F. On Retrieving Moving Objects Gathering Patterns from Trajectory Data via Spatio-temporal Graph. In Proceedings of the 2014 IEEE International Congress on Big Data, Anchorage, AK, USA, 27 June–2 July 2014; pp. 390–397. [Google Scholar] [CrossRef]
- Jiang, J.; Worboys, M.F. Event-based topology for dynamic planar areal objects. Int. J. Geogr. Inf. Sci. 2009, 23, 33–60. [Google Scholar] [CrossRef]
- Stell, J.G. Granularity in change over time. In Foundations of Geographic Information Science; Duckham, M., Goodchild, M., Worboys, M., Eds.; Taylor and Francis: Abingdon, UK, 2003; pp. 95–115. [Google Scholar] [CrossRef]
- Costes, B.; Perret, J.; Bucher, B.; Gribaudi, M. An aggregated graph to qualify historical spatial networks using temporal patterns detection. In Proceedings of the 18th AGILE International Conference on Geographic Information Science, Lisbon, Portugal, 9–12 June 2015. [Google Scholar]
- Bertrand, D. Un Système d’Information Géographique pour le Suivi d’Objets Historiques Urbaines à Travers l’Espace et le Temps. Ph.D. Thesis, EHESS, Paris, France, 2015. [Google Scholar]
- Oberoi, K.S.; Mondo, G.D.; Dupuis, Y.; Vasseur, P. Modeling Road Traffic Takes Time. In Proceedings of the 10th International Conference on Geographic Information Science (GIScience 2018), Dagstuhl, Germany, 28–31 August 2018; Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik; Leibniz International Proceedings in Informatics (LIPIcs). Volume 114, pp. 52:1–52:7. [Google Scholar] [CrossRef]
- George, B.; Shekhar, S. Journal on Data Semantics XI; Chapter Time-Aggregated Graphs for Modeling Spatio-Temporal Networks; Springer: Berlin/Heidelberg, Germany, 2008; pp. 191–212. [Google Scholar] [CrossRef]
- Stell, J.G.; Worboys, M. Stratified map spaces: A formal basis for multi-resolution spatial databases. In Proceedings of the SDH’98 Proceedings 8th International Symposium on Spatial Data Handling, International Geographical, Vancouver, BC, Canada, 11–15 July 1998; pp. 180–189. [Google Scholar]
- Spéry, L.; Claramunt, C.; Libourel, T. A Spatio-Temporal Model for the Manipulation of Lineage Metadata. Geoinformatica 2001, 5, 51–70. [Google Scholar] [CrossRef]
- Harbelot, B.; Arenas, H.; Cruz, C. Continuum: A spatiotemporal data model to represent and qualify filiation relationships. In Proceedings of the 4th ACM SIGSPATIAL International Workshop on GeoStreaming, IWGS 2013, Orlando, FL, USA, 5 November 2013; Kashani, F.B., Basalamah, A., Zhang, C., Eds.; ACM: New York, NY, USA, 2013; pp. 76–85. [Google Scholar] [CrossRef]
- Sridhar, M.; Cohn, A.G.; Hogg, D.C. Benchmarking Qualitative Spatial Calculi for Video Activity Analysis. In Proceedings of the IJCAI Workshop Benchmarks and Applications of Spatial Reasoning, Barcelona, Spain, 16–18 July 2011; pp. 15–20. [Google Scholar]
- Guyet, T.; Moinard, Y.; Quiniou, R. Programmation par ensembles réponses pour simuler l’assolement d’un paysage. Rev. d’Intell. Artif. 2015, 29, 293–320. [Google Scholar] [CrossRef][Green Version]
- Wylot, M.; Hauswirth, M.; Cudré-Mauroux, P.; Sakr, S. RDF Data Storage and Query Processing Schemes: A Survey. ACM Comput. Surv. 2018, 51, 84:1–84:36. [Google Scholar] [CrossRef]
- Ehrlinger, L.; Wöß, W. Towards a Definition of Knowledge Graphs. In Proceedings of the Posters and Demos Track of the 12th International Conference on Semantic Systems—SEMANTiCS2016 and the 1st International Workshop on Semantic Change & Evolving Semantics (SuCCESS’16) Co-Located with the 12th International Conference on Semantic Systems (SEMANTiCS 2016), Leipzig, Germany, 12–15 September 2016; Volume 1695. [Google Scholar]
- Ingalalli, V.; Ienco, D.; Poncelet, P. Mining frequent subgraphs in multigraphs. Inf. Sci. 2018, 451–452, 50–66. [Google Scholar] [CrossRef]
- Ji, S.; Pan, S.; Cambria, E.; Marttinen, P.; Yu, P.S. A Survey on Knowledge Graphs: Representation, Acquisition and Applications. 2020. Available online: http://xxx.lanl.gov/abs/2002.00388 (accessed on 1 August 2021).
- Fensel, D.; Simsek, U.; Angele, K.; Huaman, E.; Kärle, E.; Panasiuk, O.; Toma, I.; Umbrich, J.; Wahler, A. Knowledge Graphs—Methodology, Tools and Selected Use Cases; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar] [CrossRef]
- Clementini, E.; Sharma, J.; Egenhofer, M. Modelling topological spatial relations: Strategies for query processing. Comput. Graph. 1994, 18, 815–822. [Google Scholar] [CrossRef]
- Egenhofer, M. A Formal Definition of Binary Topological Relationships. In Foundations of Data Organization and Algorithms, Proceedings of the 3rd International Conference, FODO 1989, Paris, France, 21–23 June 1989; Litwin, W., Schek, H., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1989; Volume 367, pp. 457–472. [Google Scholar] [CrossRef]
- Cohn, A.; Bennett, B.; Gooday, J.; Gotts, N.M. Qualitative Spatial Representation and Reasoning with the Region Connection Calculus. GeoInformatica 1997, 1, 275–316. [Google Scholar] [CrossRef]
- Ioannidis, T.; Garbis, G.; Kyzirakos, K.; Bereta, K.; Koubarakis, M. Evaluating Geospatial RDF Stores Using the Benchmark Geographica 2. 2019. Available online: http://xxx.lanl.gov/abs/1906.01933 (accessed on 1 August 2021).
- Bereta, K.; Xiao, G.; Koubarakis, M. Ontop-spatial: Ontop of geospatial databases. J. Web Semant. 2019, 58, 100514. [Google Scholar] [CrossRef]
- Calvanese, D.; Cogrel, B.; Komla-Ebri, S.; Kontchakov, R.; Lanti, D.; Rezk, M.; Rodriguez-Muro, M.; Xiao, G. Ontop: Answering SPARQL queries over relational databases. Semant. Web 2017, 8, 471–487. [Google Scholar] [CrossRef]
- Christen, P. A Survey of Indexing Techniques for Scalable Record Linkage and Deduplication. IEEE Trans. Knowl. Data Eng. 2012, 24, 1537–1555. [Google Scholar] [CrossRef]
- Christophides, V.; Efthymiou, V.; Stefanidis, K. Entity Resolution in the Web of Data; Synthesis Lectures on the Semantic Web; Theory and Technology, Morgan & Claypool Publishers: San Rafael, CA, USA, 2015. [Google Scholar] [CrossRef]
- Ngomo, A.N.; Auer, S. LIMES—A Time-Efficient Approach for Large-Scale Link Discovery on the Web of Data. In Proceedings of the 22nd International Joint Conference on Artificial Intelligence, Barcelona, Spain, 16–22 July 2011; pp. 2312–2317. [Google Scholar] [CrossRef]
- Nentwig, M.; Hartung, M.; Ngomo, A.N.; Rahm, E. A survey of current Link Discovery frameworks. Semant. Web 2017, 8, 419–436. [Google Scholar] [CrossRef]
- Bhardwaj, P.; Debruyne, C.; O’Sullivan, D. On the Overlooked Challenges of Link Discovery. In Proceedings of the 3rd International Workshop on Geospatial Linked Data and the 2nd Workshop on Querying the Web of Data Co-Located with 15th Extended Semantic Web Conference (ESWC 2018), Heraklion, Greece, 3 June 2018; Volume 2110, pp. 41–46. [Google Scholar]
- Isele, R.; Jentzsch, A.; Bizer, C. Efficient Multidimensional Blocking for Link Discovery without losing Recall. In Proceedings of the 14th International Workshop on the Web and Databases 2011—WebDB 2011, Athens, Greece, 12 June 2011. [Google Scholar]
- Nikolaou, C.; Dogani, K.; Bereta, K.; Garbis, G.; Karpathiotakis, M.; Kyzirakos, K.; Koubarakis, M. Sextant: Visualizing time-evolving linked geospatial data. J. Web Semant. 2015, 35, 35–52. [Google Scholar] [CrossRef]
- Shbita, B.; Knoblock, C.; Duan, W.; Chiang, Y.; Uhl, J.; Leyk, S. Building Linked Spatio-Temporal Data from Vectorized Historical Maps. In The Semantic Web, Proceedings of the 17th International Conference, ESWC 2020, Heraklion, Greece, 31 May–4 June 2020; Harth, A., Kirrane, S., Ngomo, A.N., Paulheim, H., Rula, A., Gentile, A.L., Haase, P., Cochez, M., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2020; Volume 12123, pp. 409–426. [Google Scholar] [CrossRef]
- Bucher, B.; Tiainen, E.; von Brasch, T.E.; Janssen, P.; Kotzinos, D.; Ceh, M.; Rijsdijk, M.; Folmer, E.; Damme, M.V.; Zhral, M. Conciliating Perspectives from Mapping Agencies and Web of Data on Successful European SDIs: Toward a European Geographic Knowledge Graph. ISPRS Int. J. Geo Inf. 2020, 9, 62. [Google Scholar] [CrossRef]
- Kuhn, W.; Kauppinen, T.; Janowicz, K. Linked Data—A Paradigm Shift for Geographic Information Science. In Geographic Information Science, Proceedings of the 8th International Conference, GIScience 2014, Vienna, Austria, 24–26 September 2014; Duckham, M., Pebesma, E., Stewart, K., Frank, A., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2014; Volume 8728, pp. 173–186. [Google Scholar] [CrossRef]
- Mai, G.; Janowicz, K.; Yan, B.; Scheider, S. Deeply integrating Linked Data with Geographic Information Systems. Trans. GIS 2019, 23, 579–600. [Google Scholar] [CrossRef]
- Trivedi, R.; Dai, H.; Wang, Y.; Song, L. Know-Evolve: Deep Temporal Reasoning for Dynamic Knowledge Graphs. In Proceedings of the 34th International Conference on Machine Learning, ICML 2017, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 3462–3471. [Google Scholar]
- Everwyn, J.; Mouaddib, A.; Zanuttini, B.; Gatepaille, S.; Brunessaux, S. Link Prediction on Dynamic Attributed Knowledge Graphs for Maritime Situational Awareness. In Proceedings of the Conférence Nationale sur les Applications Pratiques de l’Intelligence Artificielle (APIA 2019), Toulouse, France, 1–2 July 2019. [Google Scholar]
- Peng, P.; Cheng, S.; Chen, J.; Liao, M.; Wu, L.; Liu, X.; Lu, F. A fine-grained perspective on the robustness of global cargo ship transportation networks. J. Geogr. Sci. 2018, 28, 881–889. [Google Scholar] [CrossRef]
- Kaluza, P.; Kölzsch, A.; Gastner, M.T.; Blasius, B. The complex network of global cargo ship movements. J. R. Soc. Interface 2010, 7, 1093–1103. [Google Scholar] [CrossRef] [PubMed]
- Wilmsmeier, G.; Monios, J. Geographies of maritime transport. In Geographies of Maritime Transport; Edward Elgar Publishing: Cheltenham, UK, 2020. [Google Scholar] [CrossRef]
- Claramunt, C.; Ray, C.; Salmon, L.; Camossi, E.; Hadzagic, M.; Jousselme, A.; Andrienko, G.; Andrienko, N.; Theodoridis, Y.; Vouros, G. Maritime data integration and analysis: Recent progress and research challenges. Adv. Database Technol. EDBT 2017, 2017, 192–197. [Google Scholar] [CrossRef]
- Liu, C.; Wang, J.; Zhang, H. Spatial heterogeneity of ports in the global maritime network detected by weighted ego network analysis. Marit. Policy Manag. 2018, 45, 89–104. [Google Scholar] [CrossRef]
- Ducruet, C.; Notteboom, T.E. The worldwide maritime network of container shipping: Spatial structure and regional dynamics. Glob. Netw. 2012, 12, 395–423. [Google Scholar] [CrossRef]
- Liu, C.; Wang, J.; Zhang, H.; Yin, M. Mapping the hierarchical structure of the global shipping network by weighted ego network analysis. Int. J. Shipp. Transp. Logist. 2018, 10, 63–86. [Google Scholar] [CrossRef]
- Pan, J.; Bell, M.G.H.; Cheung, K.; Perera, S.; Yu, H. Connectivity analysis of the global shipping network by eigenvalue decomposition. Marit. Policy Manag. 2019, 46, 957–966. [Google Scholar] [CrossRef]
- Cazzaniga-Francesetti, D.; Foschi, A. The impact of hub and spokes networks in the Mediterranean peculiarity. In Proceedings of the 2002 IAME Annual Conference Panama, Panama City, Panama, 13–15 November 2002. [Google Scholar]
- Notteboom, T.E. Container shipping and ports: An overview. Rev. Netw. Econ. 2004, 3. [Google Scholar] [CrossRef]
- Woolley-Meza, O.; Thiemann, C.; Grady, D.; Jungbin, L.J.; Seebens, H.; Blasius, B.; Brockmann, D. Complexity in human transportation networks: A comparative analysis of worldwide air transportation and global cargo-ship movements. Eur. Phys. J. B 2011, 84, 589–600. [Google Scholar] [CrossRef]
- Ducruet, C.; Zaidi, F. Maritime constellations: A complex network approach to shipping and ports. Marit. Policy Manag. 2012, 39, 151–168. [Google Scholar] [CrossRef]
- Ducruet, C. Network diversity and maritime flows. J. Transp. Geogr. 2013, 30, 77–88. [Google Scholar] [CrossRef]
- Xu, X.; Hu, J.; Lu, F. Empirical analysis of the ship-transport network of China. Chaos Interdiscip. J. Nonlinear Sci. 2007, 17, 023129. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Zhu, D. Empirical analysis of the worldwide maritime transportation network. Phys. A Stat. Mech. Appl. 2009, 388, 2061–2071. [Google Scholar] [CrossRef]
- Ducruet, C. Multilayer dynamics of complex spatial networks: The case of global maritime flows (1977–2008). J. Transp. Geogr. 2017, 60, 47–58. [Google Scholar] [CrossRef]
- Yu, H.; Fang, Z.; Lu, F.; Murray, A.; Zhao, Z.; Xu, Y.; Yang, X. Massive automatic identification system sensor trajectory data-based multi-layer linkage network dynamics of maritime transport along 21st-century maritime silk road. Sensors 2019, 19, 4197. [Google Scholar] [CrossRef] [PubMed]
- Peng, P.; Cheng, S.; Liu, X.; Mei, Q.; Lu, F. The robustness evaluation of global maritime transportation networks. Acta Geogr. Sin 2017, 72, 2241–2251. [Google Scholar] [CrossRef]
- Ducruet, C.; Lee, S.; Ng, K.A. Centrality and vulnerability in liner shipping networks: Revisiting the Northeast Asian port hierarchy. Marit. Policy Manag. 2010, 37, 17–36. [Google Scholar] [CrossRef]
- Ducruet, C. The polarization of global container flows by interoceanic canals: Geographic coverage and network vulnerability. Marit. Policy Manag. 2016, 43, 242–260. [Google Scholar] [CrossRef]
- Bartholdi, J.; Jarumaneeroj, P.; Ramudhin, A. A new connectivity index for container ports. Marit. Econ. Logist. 2016, 18, 231–249. [Google Scholar] [CrossRef]
- Wang, Y.; Cullinane, K. Measuring container port accessibility: An application of the Principal Eigenvector Method (PEM). Marit. Econ. Logist. 2008, 10, 75–89. [Google Scholar] [CrossRef]
- Peng, P.; Yang, Y.; Lu, F.; Cheng, S.; Mou, N.; Yang, R. Modelling the competitiveness of the ports along the Maritime Silk Road with big data. Transp. Res. Part A Policy Pract. 2018, 118, 852–867. [Google Scholar] [CrossRef]
- Wang, Y.; Cullinane, K. Traffic consolidation in East Asian container ports: A network flow analysis. Transp. Res. Part A Policy Pract. 2014, 61, 152–163. [Google Scholar] [CrossRef]
- Mou, N.; Liu, C.; Zhang, L.; Fu, X.; Xie, Y.; Li, Y.; Peng, P. Spatial pattern and regional relevance analysis of the maritime silk road shipping network. Sustainability 2018, 10, 977. [Google Scholar] [CrossRef]
- Wang, Y.; Cullinane, K. Determinants of port centrality in maritime container transportation. Transp. Res. Part E Logist. Transp. 2016, 95, 326–340. [Google Scholar] [CrossRef]
- Peng, P.; Poon, J.P.; Yan, Y.; Lu, F.; Cheng, S. Global oil traffic network and diffusion of influence among ports using real time data. Energy 2019, 172, 333–342. [Google Scholar] [CrossRef]
- Peng, P.; Lu, F. Mapping the Port Influence Diffusion Patterns: A Case Study of Rotterdam, Antwerp and Singapore. In Proceedings of the International Conference on Computational Science, Amsterdam, The Netherlands, 3–5 June 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 266–276. [Google Scholar] [CrossRef]
- Fang, Z.; Yu, H.; Lu, F.; Feng, M.; Huang, M. Maritime network dynamics before and after international events. J. Geogr. Sci. 2018, 28, 937–956. [Google Scholar] [CrossRef]
- Yu, H.; Fang, Z.; Lu, F.; Murray, A.; Zhang, H.; Peng, P.; Mei, Q.; Chen, J. Impact of oil price fluctuations on tanker maritime network structure and traffic flow changes. Appl. Energy 2019, 237, 390–403. [Google Scholar] [CrossRef]
- Peng, P.; Yang, Y.; Cheng, S.; Lu, F.; Yuan, Z. Hub-and-spoke structure: Characterizing the global crude oil transport network with mass vessel trajectories. Energy 2019, 168, 966–974. [Google Scholar] [CrossRef]
- Laxe, F.G.; Seoane, M.J.; Montes, C.P. Maritime degree, centrality and vulnerability: Port hierarchies and emerging areas in containerized transport (2008–2010). J. Transp. Geogr. 2012, 24, 33–44. [Google Scholar] [CrossRef]
- Wang, L.; Zhu, Y.; Ducruet, C.; Bunel, M.; Lau, Y. From hierarchy to networking: The evolution of the “twenty-first-century Maritime Silk Road” container shipping system. Transp. Rev. 2018, 38, 416–435. [Google Scholar] [CrossRef]
- Kosowska-Stamirowska, Z. Network effects govern the evolution of maritime trade. Proc. Natl. Acad. Sci. USA 2020, 117, 12719–12728. [Google Scholar] [CrossRef]
- Katsumi, M.; Fox, M. Ontologies for transportation research: A survey. Transp. Res. Part C 2018, 89, 53–82. [Google Scholar] [CrossRef]
- Villa, P.; Camossi, E. A Description Logic Approach to Discover Suspicious Itineraries from Maritime Container Trajectories. In GeoSpatial Semantics, Proceedings of the 4th International Conference, GeoS 2011, Brest, France, 12–13 May 2011; Claramunt, C., Levashkin, S., Bertolotto, M., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6631, pp. 182–199. [Google Scholar] [CrossRef]
- Vandecasteele, A.; Napoli, A. An enhanced spatial reasoning ontology for maritime anomaly detection. In Proceedings of the 7th International Conference on System of Systems Engineering, SoSE 2012, Genova, Italy, 16–19 July 2012; pp. 247–252. [Google Scholar] [CrossRef]
- Lange, A.; Pirovano, G.; Pozzi, R.; Rossi, T. Development of a Container Terminal Simulation Ontology. Simul. Notes Eur. 2014, 24, 79–86. [Google Scholar] [CrossRef]
- Hagaseth, M.; Lohrmann, L.; Ruiz, A.; Oikonomou, F.; Roythorne, D.; Rayot, S. An Ontology for Digital Maritime Regulations. J. Marit. Res. 2016, 12, 7–18. [Google Scholar]
- Pileggi, S.; Indorf, M.; Nagi, A.; Kersten, W. CoRiMaS—An Ontological Approach to Cooperative Risk Management in Seaports. Sustainability 2020, 12, 4767. [Google Scholar] [CrossRef]
- Wen, Y.; Zhang, Y.; Huang, L.; Zhou, C.; Xiao, C.; Zhang, F.; Peng, X.; Zhan, W.; Sui, Z. Semantic Modelling of Ship Behavior in Harbor Based on Ontology and Dynamic Bayesian Network. ISPRS Int. J. Geo Inf. 2019, 8, 107. [Google Scholar] [CrossRef]
- Zhang, Q.; Wen, Y.; Zhou, C.; Long, H.; Han, D.; Zhang, F.; Xiao, C. Construction of Knowledge Graphs for Maritime Dangerous Goods. Sustainability 2019, 11, 2849. [Google Scholar] [CrossRef]
- Bordes, A.; Usunier, N.; García-Durán, A.; Weston, J.; Yakhnenko, O. Translating Embeddings for Modeling Multi-relational Data. In Proceedings of the Advances in Neural Information Processing Systems 26: 27th Annual Conference on Neural Information Processing Systems 2013, Lake Tahoe, NV, USA, 5–8 December 2013; pp. 2787–2795. [Google Scholar]
- Heidari, S.; Simmhan, Y.; Calheiros, R.N.; Buyya, R. Scalable Graph Processing Frameworks: A Taxonomy and Open Challenges. ACM Comput. Surv. 2018, 51, 60:1–60:53. [Google Scholar] [CrossRef]
- Hernández, D.; Hogan, A.; Riveros, C.; Rojas, C.; Zerega, E. Querying Wikidata: Comparing SPARQL, Relational and Graph Databases. In Proceedings of the Semantic Web—ISWC 2016—15th International Semantic Web Conference, Kobe, Japan, 17–21 October 2016; Volume 9982, pp. 88–103. [Google Scholar] [CrossRef]
- Pérez, J.; Arenas, M.; Gutiérrez, C. Semantics and complexity of SPARQL. ACM Trans. Database Syst. 2009, 34, 16:1–16:45. [Google Scholar] [CrossRef]
- Claramunt, C. Ontologies for geospatial information: Progress and challenges ahead. J. Spat. Inf. Sci. 2020, 20, 35–41. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).