Dynamic Instability of Rydberg Atomic Complexes
Abstract
:1. Introduction
2. Kinetics of Radiative Transitions for Highly Excited Atoms
2.1. Spectral Parameters of an Excited Atom
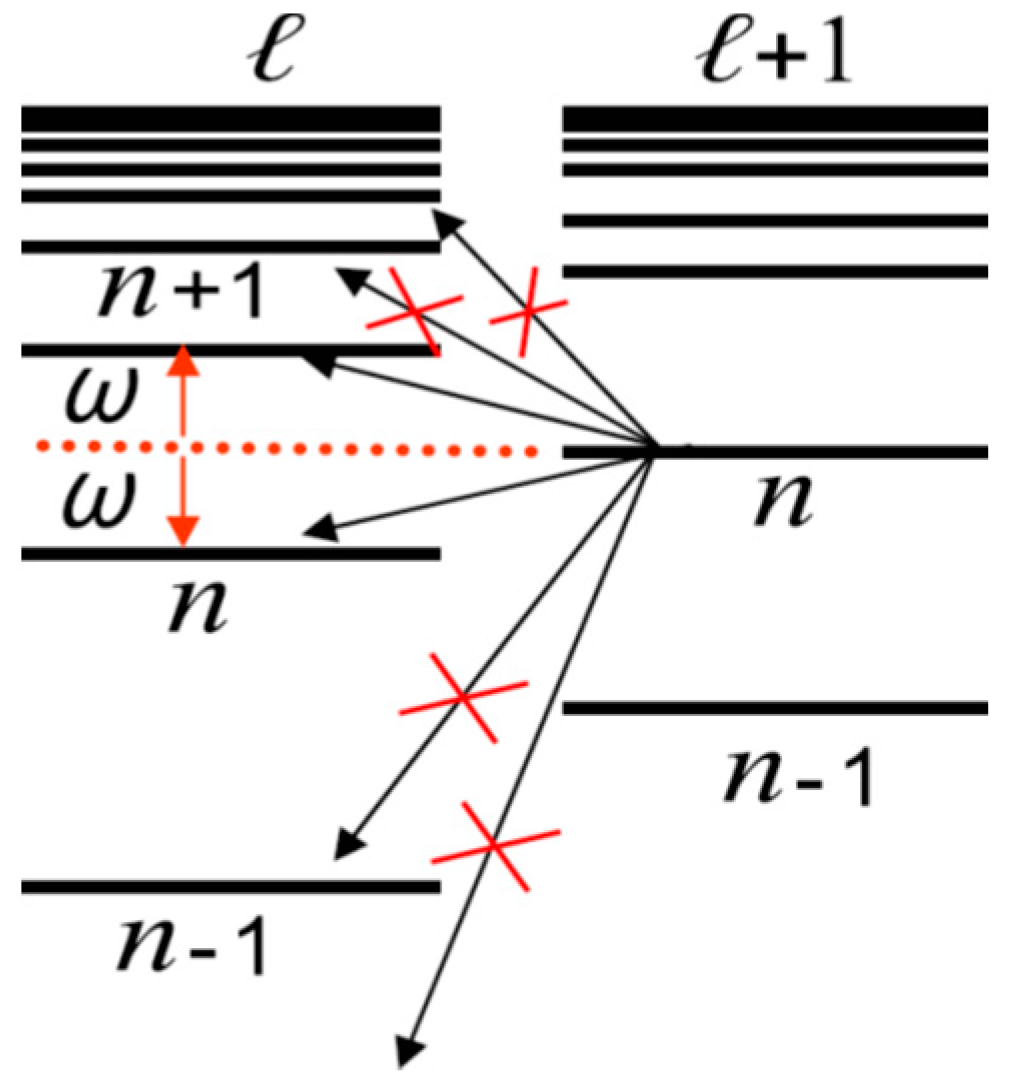
2.2. Blocking of the Spectral Transitions. Double Stark (Förster) Resonance
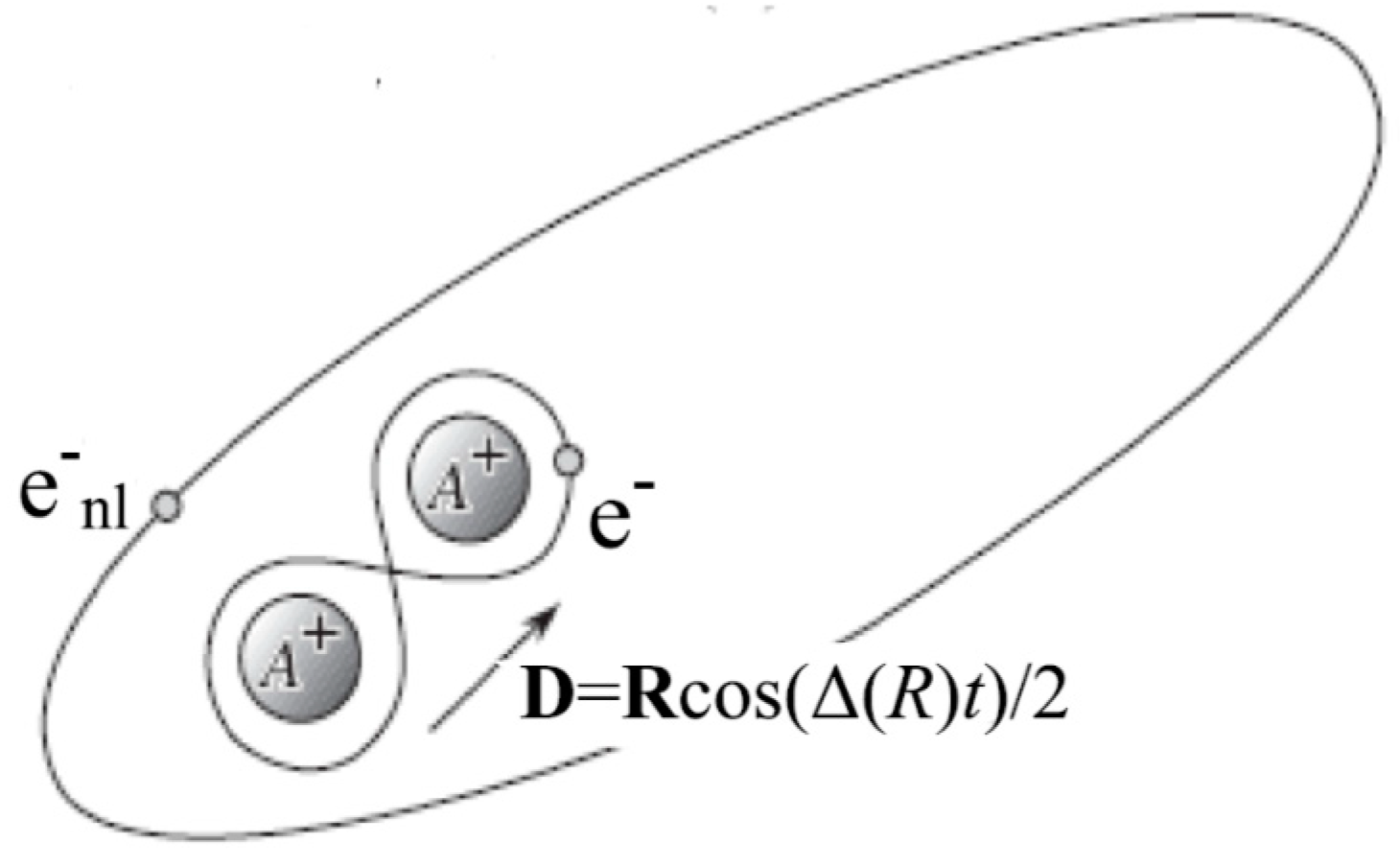
3. Rydberg Quasimolecular Complex in the Framework of the Dipole Resonance Mechanism Model
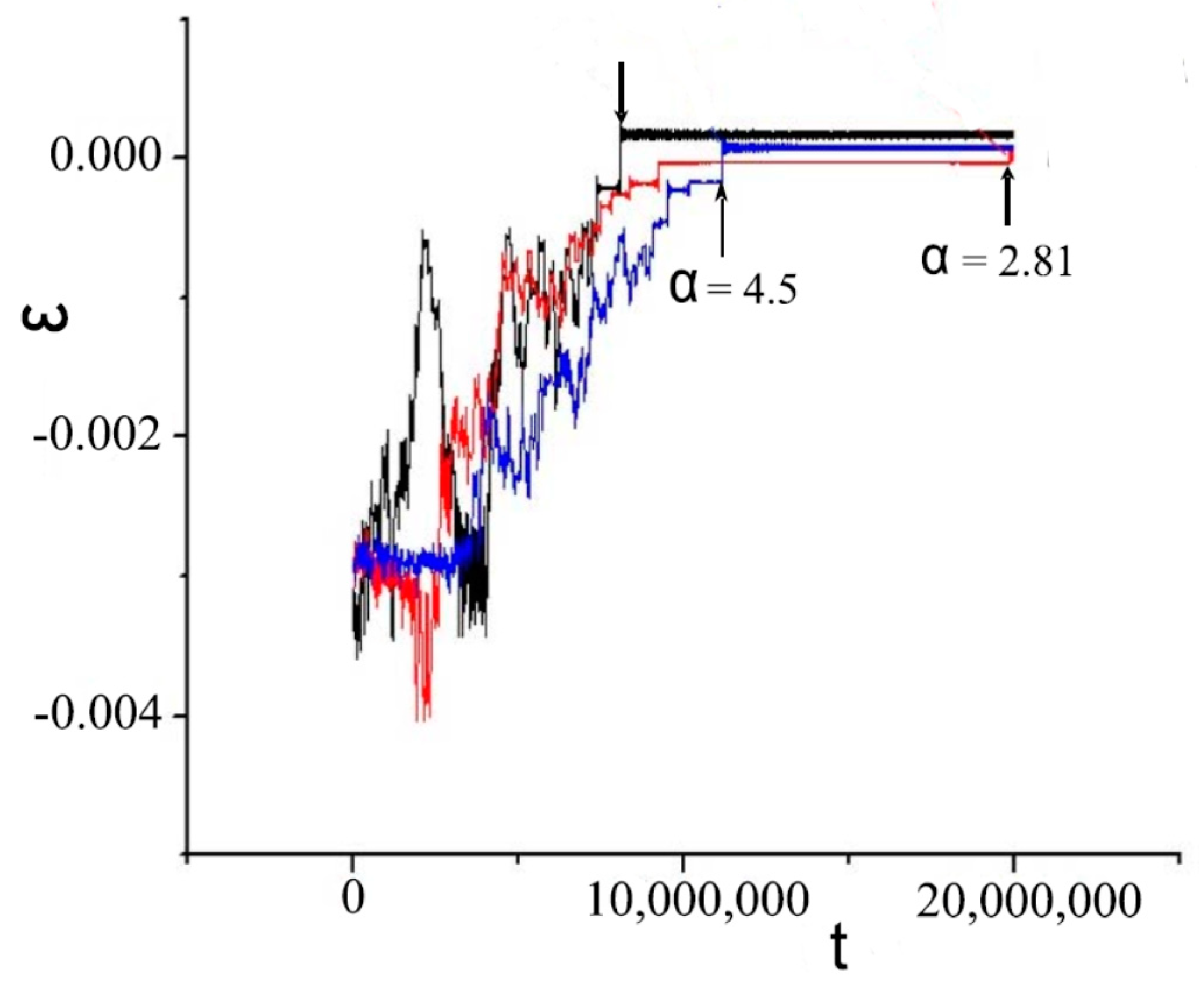
4. Rydberg Collisional Complex in Approximation of Dynamic Chaos
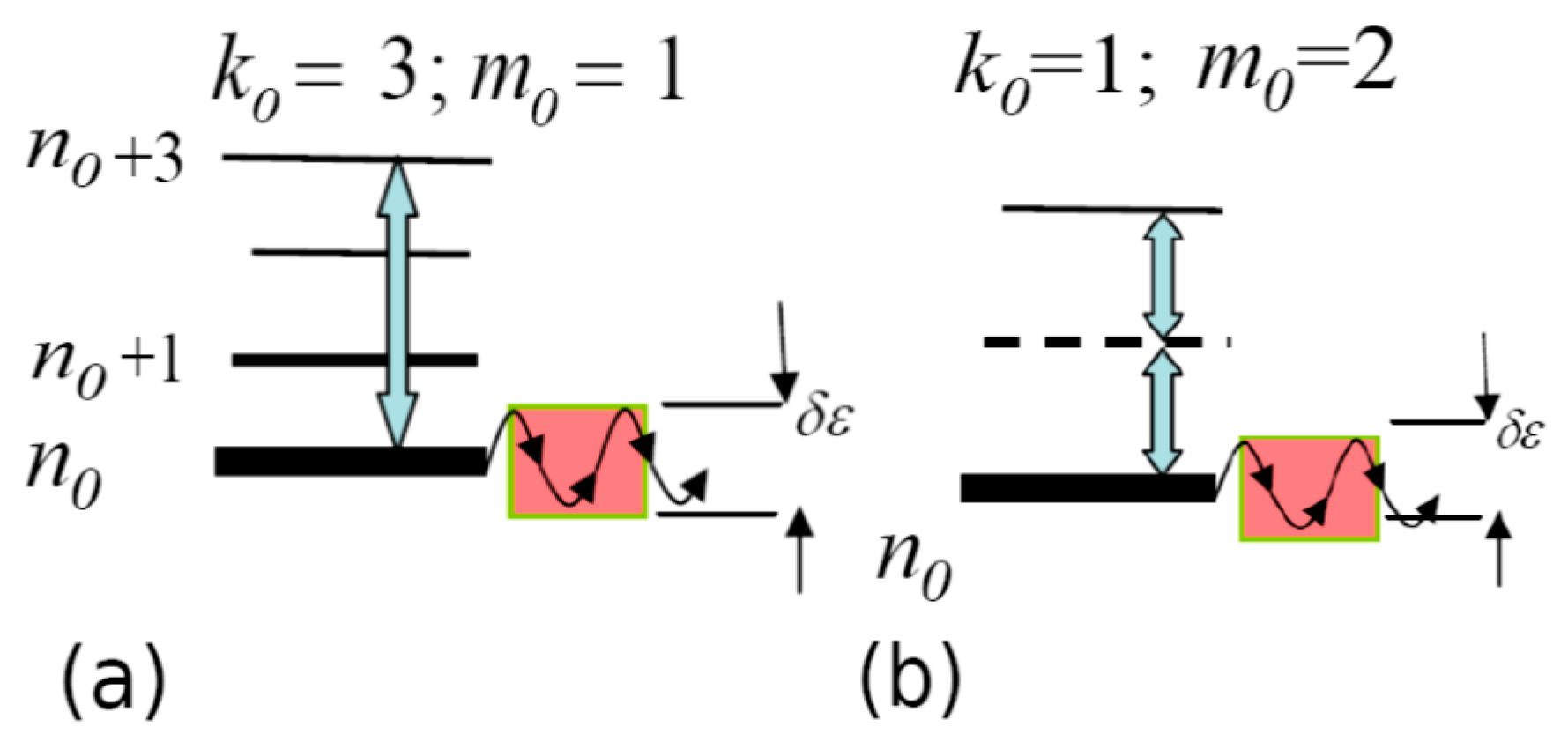
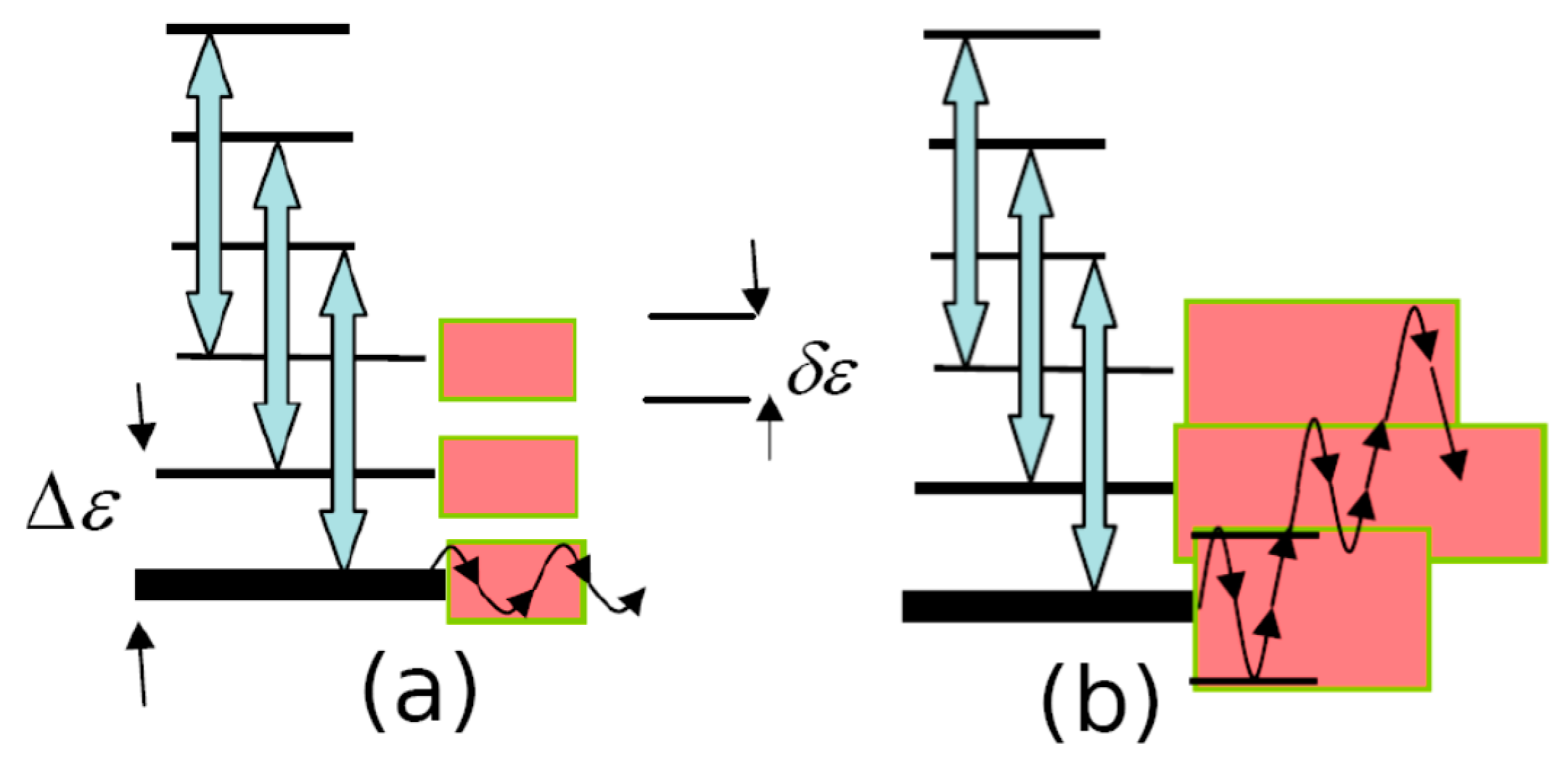
4.1. Nonlinear Dynamic Resonances and the Emergence of Deterministic Chaos
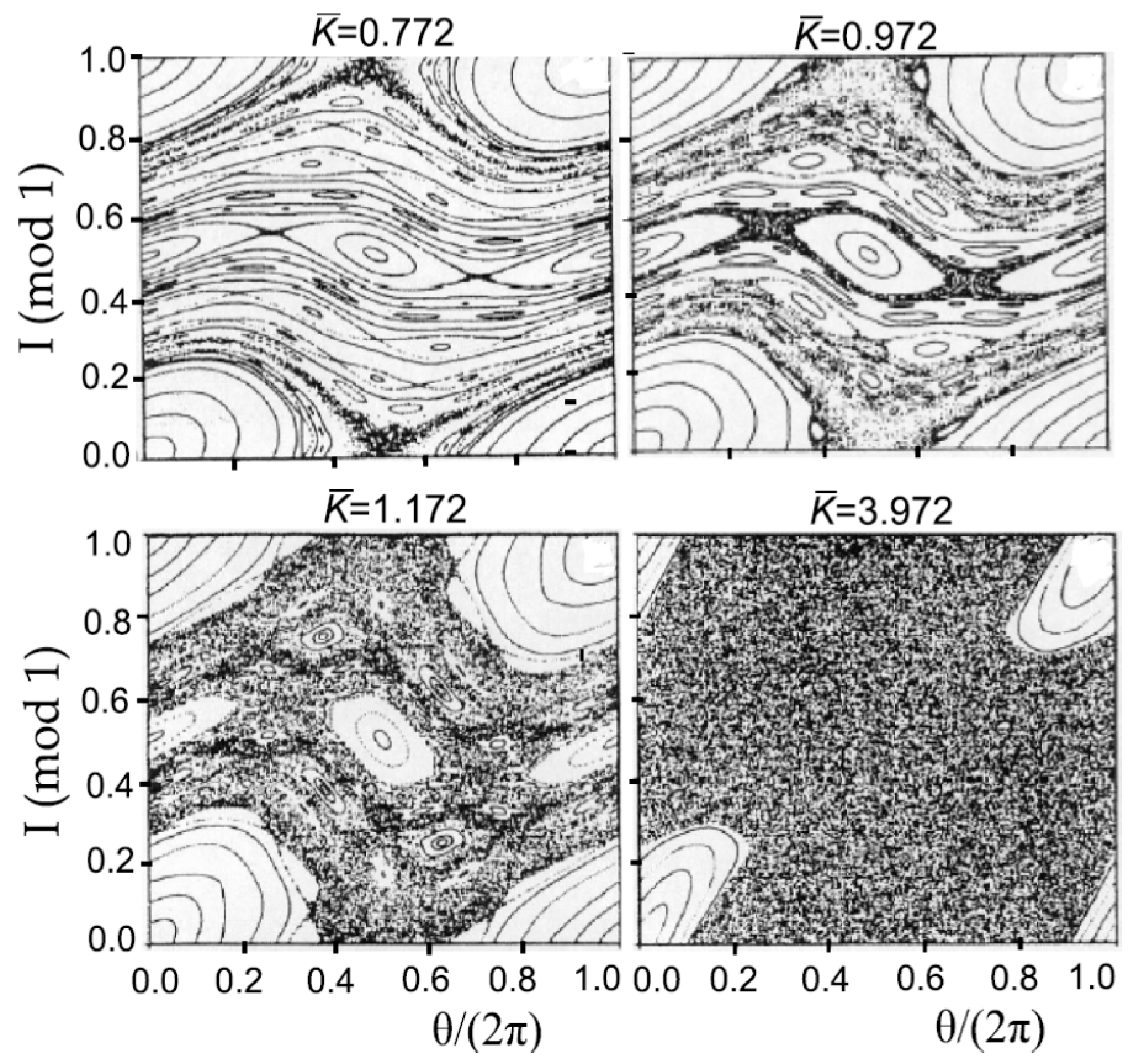
4.2. The Standard Map (SM)
4.3. Conception of Diffusional Ionization
4.4. Diffusional Ionization of Hydrogen Atom in External Field
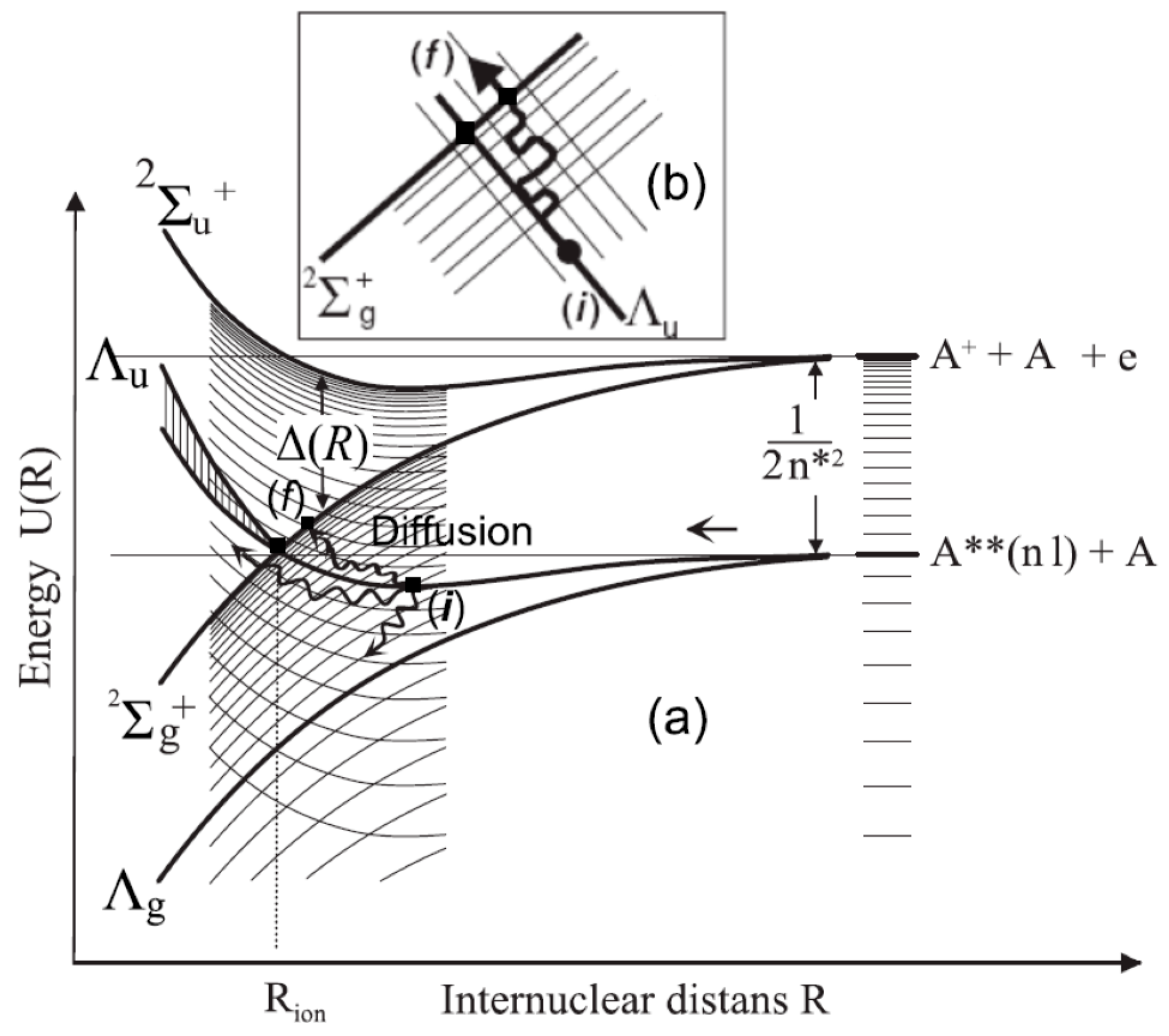
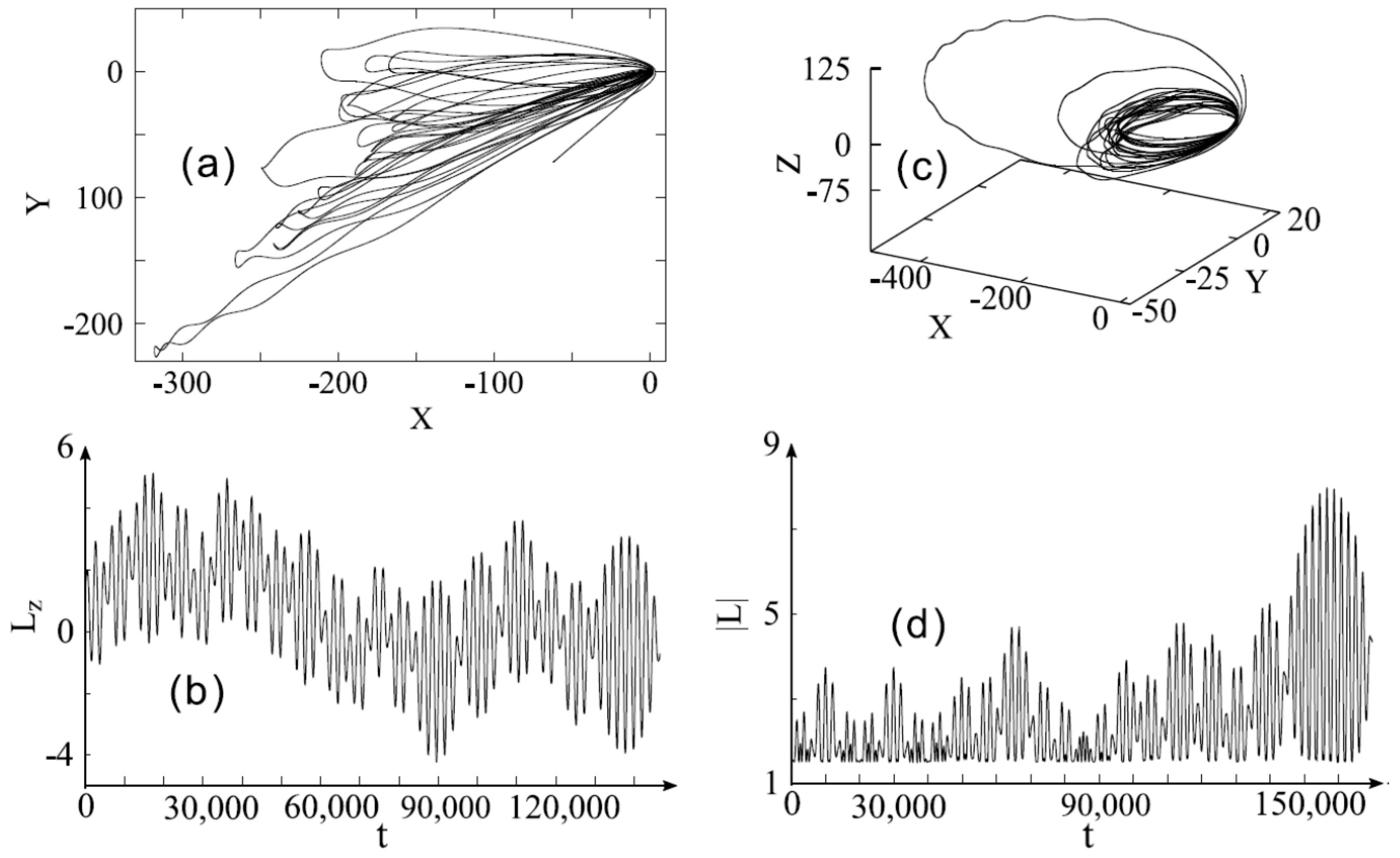
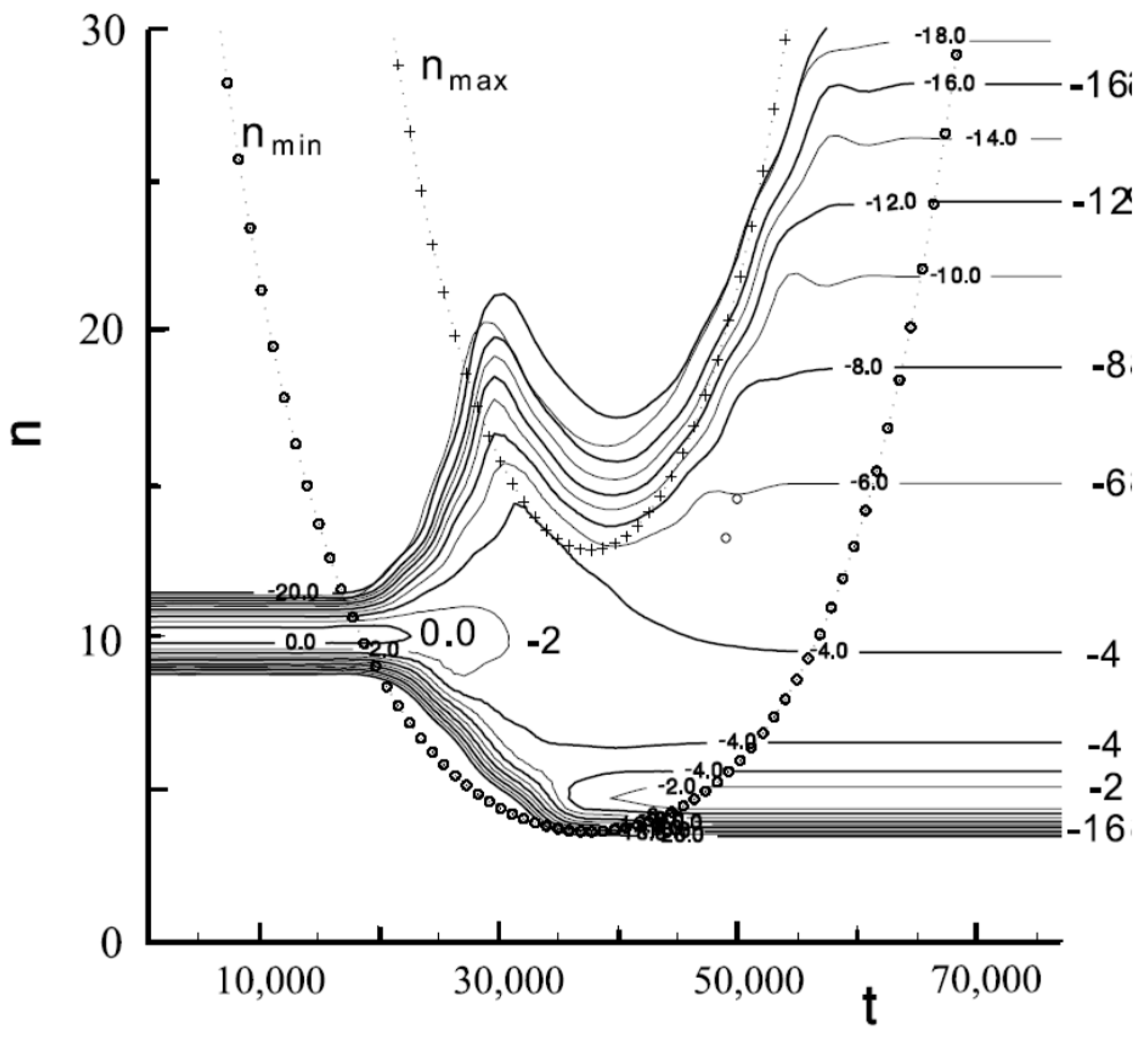
4.5. Diffusional Ionization of the Rydberg Colisional Complex
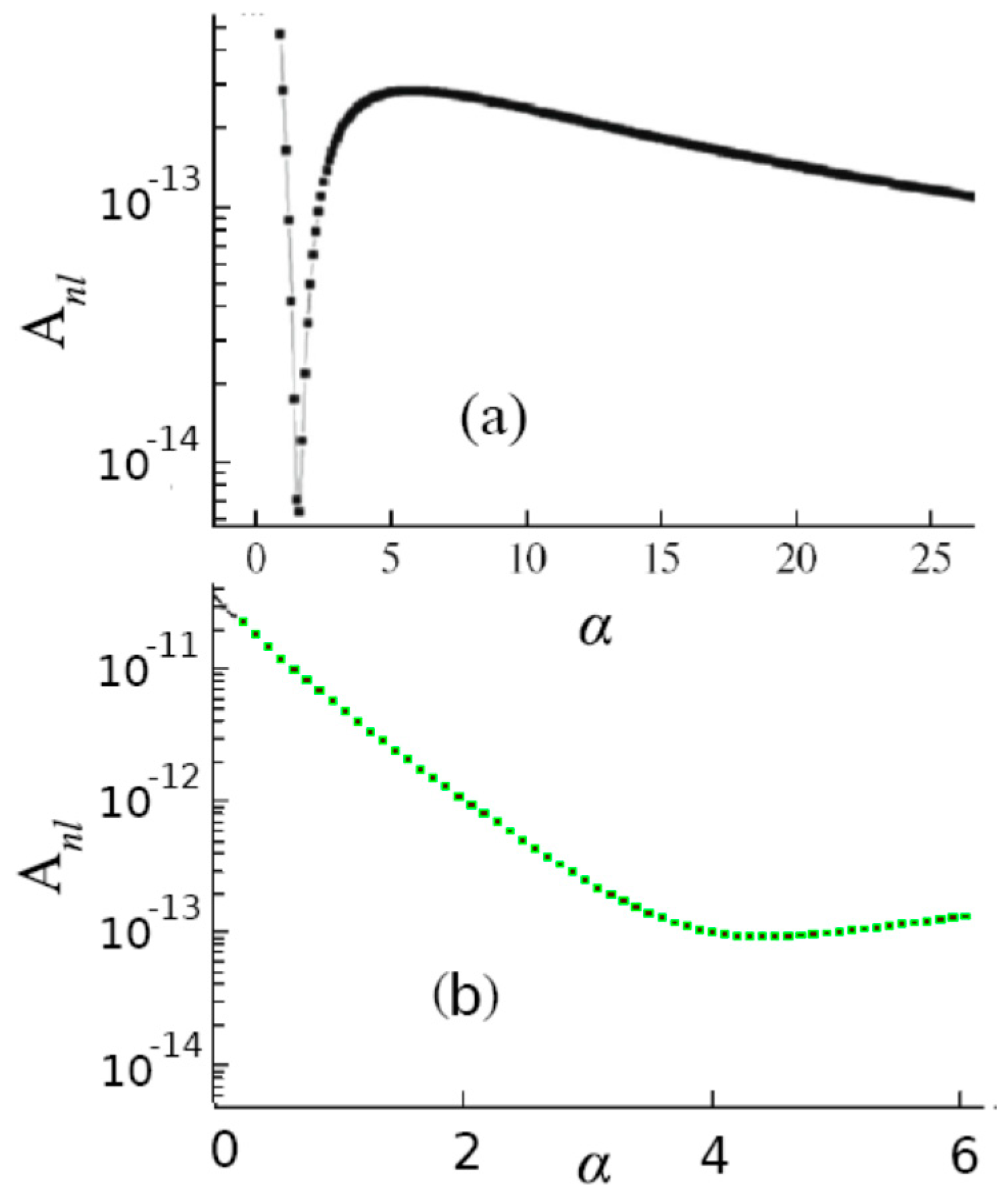
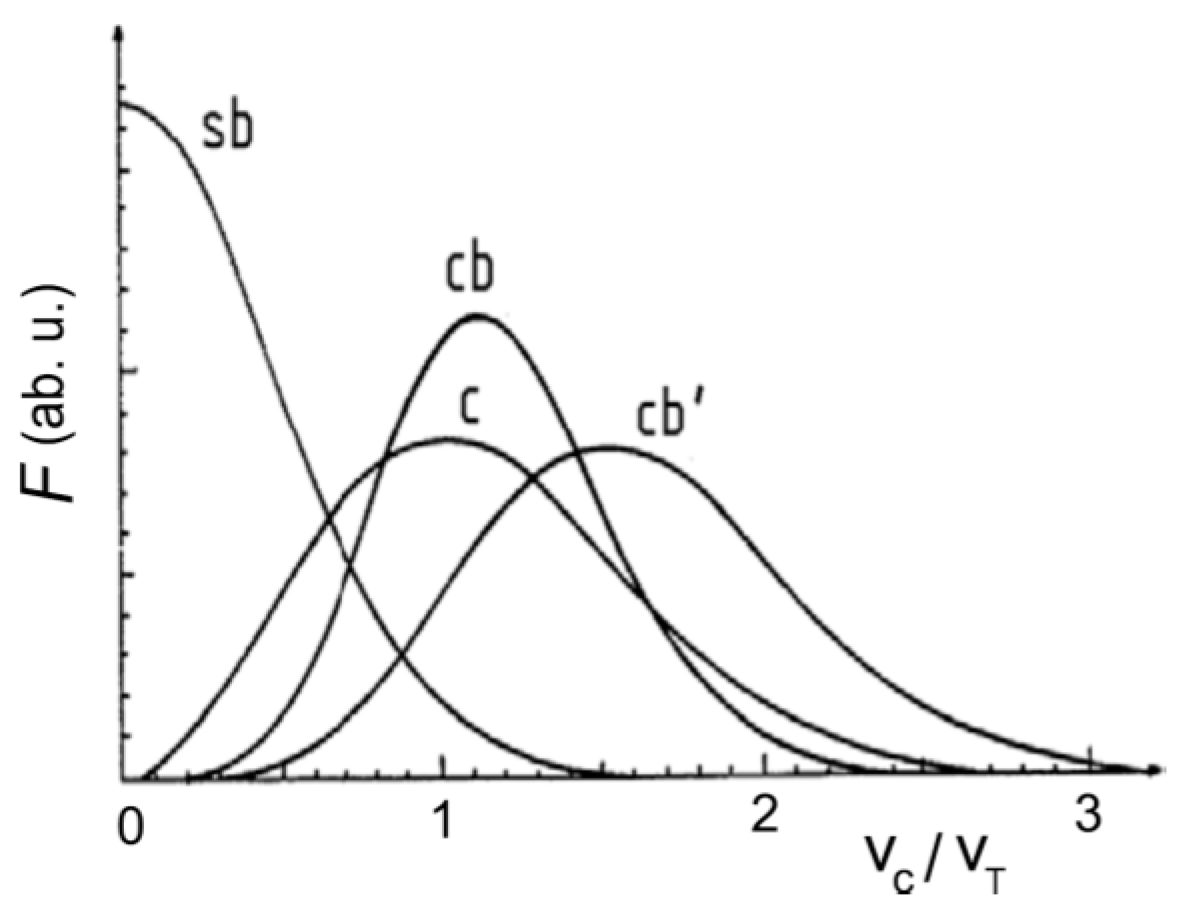
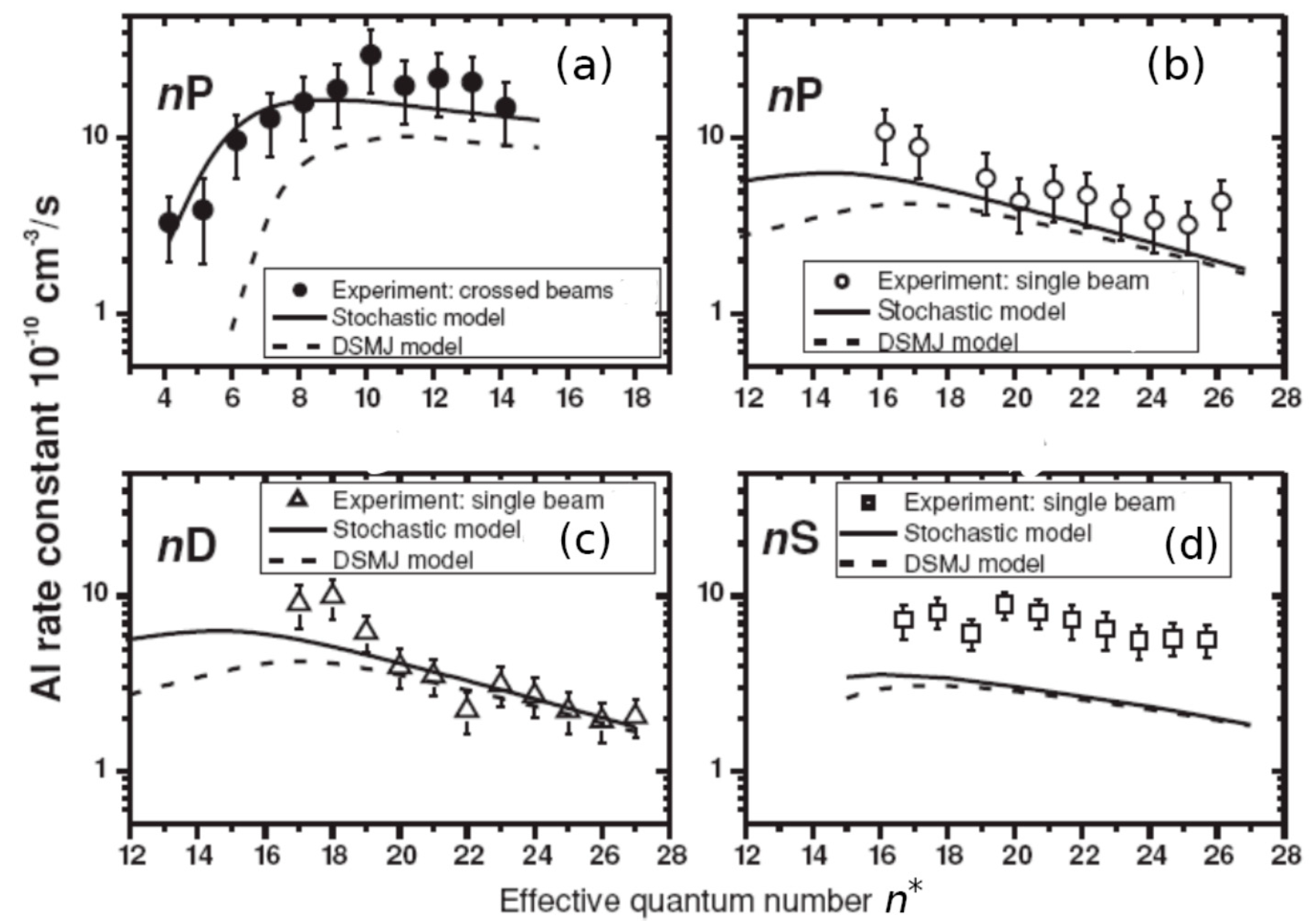
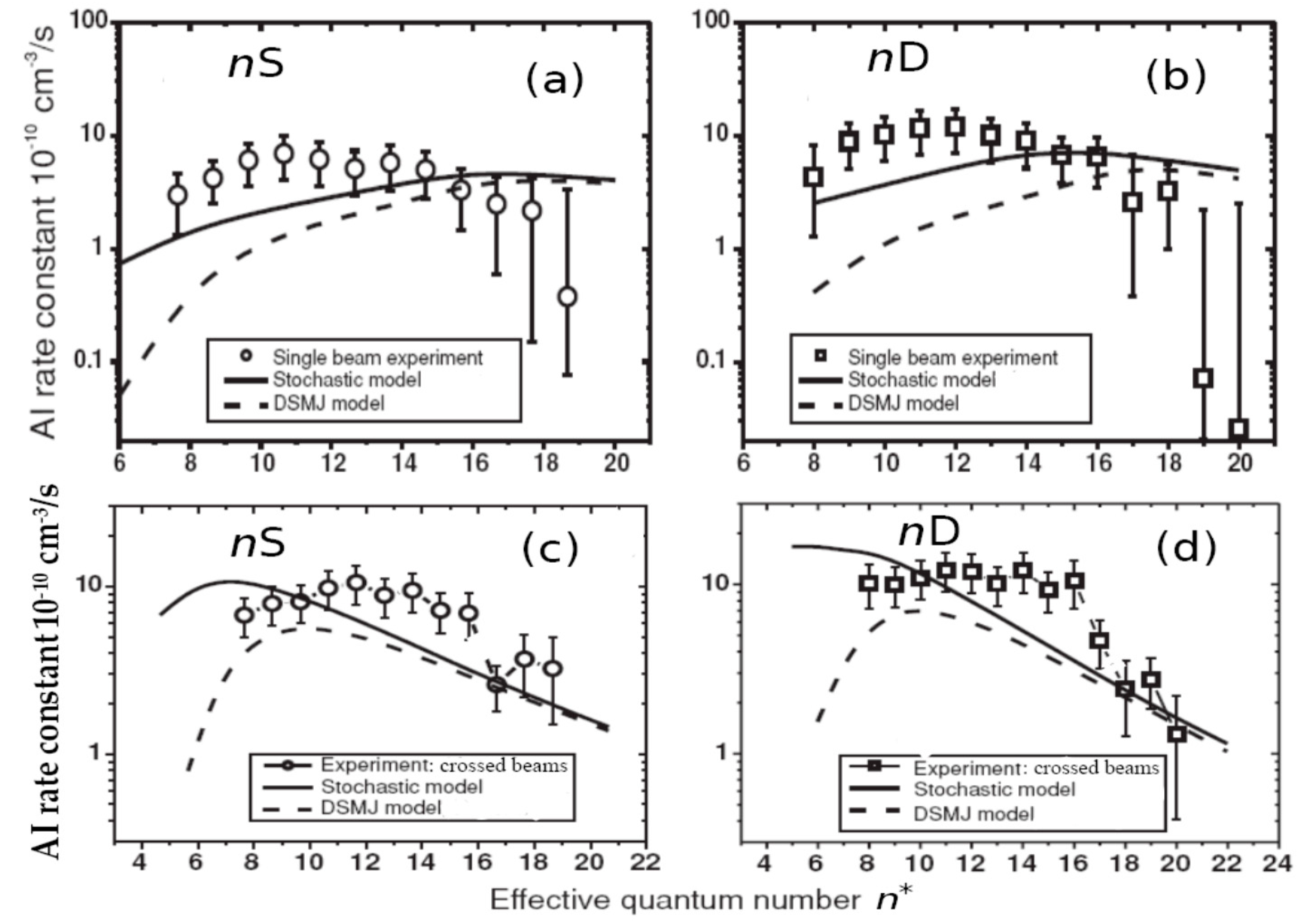
4.6. Assotiative Ionization Rate Constants
4.7. Features of Diffusional Ionization under Conditions of Förster Resonance
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stebbings, R.F.; Dunning, F.B. (Eds.) Rydberg States of Atoms and Molecules; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Gallagher, T.F. Rydberg Atoms; Cambridge Monographs on Atomic, Molecular and Chemical Physics; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Jones, M.P.A.; Marcassa, L.G.; Shaffer, J.P. Special issue on Rydberg atom physics. J. Phys. B At. Mol. Phys. 2017, 50, 060202. [Google Scholar] [CrossRef]
- Lim, J.; Lee, H.-G.; Ahn, J. Review of cold Rydberg atoms and their applications. J. Korean Phys. Soc. 2013, 63, 867–876. [Google Scholar] [CrossRef]
- Hofmann, C.S.; Günter, G.; Schempp, H.; Müller, N.L.; Faber, A.; Busche, H.; Robert-de-Saint-Vincent, M.; Weidemüller, M. An experimental approach for investigating many-body phenomena in Rydberg-interacting quantum systems. Front. Phys. 2014, 9, 571–586. [Google Scholar] [CrossRef]
- Pillet, P.; Gallagher, T.F. Rydberg atom interactions from 300 K to 300 K. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 174003. [Google Scholar] [CrossRef]
- Saffman, M.; Walker, T.G.; Mølmer, K. Quantum information with Rydberg atoms. Rev. Mod. Phys. 2010, 82, 2313. [Google Scholar] [CrossRef]
- Ryabtsev, I.I.; Beterov, I.I.; Tretyakov, D.B.; Entin, V.M.; Yakshina, E.A. Spectroscopy of cold rubidium rydberg atoms for applications in quantum information. Phys.-Uspekhi 2016, 59, 196–208. [Google Scholar] [CrossRef]
- Marcassa, L.G.; Shaffer, J.P. Interactions in Ultracold Rydberg Gases. In Advances in Atomic, Molecular, and Optical Physics; Arimondo, E., Berman, P.R., Lin, C.C., Eds.; Academic: New York, NY, USA, 2014; Volume 63, pp. 47–133. [Google Scholar]
- Shaffer, J.P.; Rittenhouse, S.T.; Sadeghpour, H.R. Ultracold Rydberg molecules. Nat. Commun. 2018, 9, 1965. [Google Scholar] [CrossRef] [PubMed]
- Schlagmüller, M.; Liebisch, T.C.; Engel, F.; Kleinbach, K.S.; Böttcher, F.; Hermann, U.; Westphal, K.M.; Gaj, A.; Löw, R.; Hofferberth, S.; et al. Ultracold Chemical Reactions of a Single Rydberg Atom in a Dense Gas. Phys. Rev. X 2016, 6, 031020. [Google Scholar] [CrossRef]
- Lyon, M.; Rolston, S.L. Ultracold neutral plasmas. Rep. Prog. Phys. 2017, 80, 017001. [Google Scholar] [CrossRef] [PubMed]
- Klyucharev, A.N.; Vujnović, V. Chemi-ionization in thermal-energy binary collisions of optically excited atoms. Phys. Rep. 1990, 185, 55–81. [Google Scholar] [CrossRef]
- Graham, W.G.; Fritsch, W.; Hahn, Y.; Tanis, J.A. Recombination of Atomic Ions; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Beterov, I.I.; Tretyakov, D.B.; Ryabtsev, I.I.; Entin, V.M.; Ekers, A.; Bezuglov, N.N. Ionization of rydberg atoms by blackbody radiation. New J. Phys. 2009, 11, 013052. [Google Scholar] [CrossRef]
- Hahn, Y. Density dependence of molecular autoionization in a cold gas. J. Phys. B At. Mol. Opt. Phys. 2000, 33, L655. [Google Scholar] [CrossRef]
- Efimov, D.K.; Miculis, K.; Bezuglov, N.N.; Ekers, A. Strong enhancement of Penning ionization for asymmetric atom pairs in cold Rydberg gases: The Tom and Jerry effect. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 125302. [Google Scholar] [CrossRef]
- Gnedin, Y.N.; Mihajlov, A.A.; Ignjatović, L.J.M.; Sakan, N.M.; Srećković, V.A.; Zakharov, M.Y.; Bezuglov, N.N.; Klycharev, A.N. Rydberg atoms in astrophysics. New Astron. Rev. 2009, 53, 259–265. [Google Scholar] [CrossRef]
- Buenker, R.J.; Golubkov, G.V.; Golubkov, M.G.; Karpov, I.; Manzheliy, M. Relativity laws for the variation of rates of clocks moving in free space and GPS positioning errors caused by space-weather events. In Global Navigation Satellite System-From Stellar Navigation; Mohamed, A.H., Ed.; In Tech: Berlin, Germany, 2013. [Google Scholar]
- Koch, P.M.; van Leeuwen, K.A.H. The importance of resonances in microwave “ionization” of excited hydrogen atoms. Phys. Rep. 1995, 255, 289–403. [Google Scholar] [CrossRef]
- Mitchell, K.A.; Handlay, J.P.; Tighe, B.; Flower, A.; Delos, J.B. Analysis of chaos-induced pulse trains in the ionization of hydrogen. Phys. Rev. A 2004, 70, 043407. [Google Scholar] [CrossRef]
- Krainov, V.P. Ionization of atoms in strong low-frequency electromagnetic field. J. Exp. Theor. Phys. 2010, 111, 171–179. [Google Scholar] [CrossRef]
- Park, H.; Shuman, E.S.; Gallagher, T.F. Ionization of Rb Rydberg atoms in the attractive ns-np dipole-dipole potential. Phys. Rev. A 2011, 84, 052708. [Google Scholar] [CrossRef]
- Dashevskaya, E.I.; Litvin, I.; Nikitin, E.E.; Oref, I.; Troe, J. Classical diffusion model of vibrational predissociation of van der Waals complexes Part III. Comparison with quantum calculations. Phys. Chem. Chem. Phys. 2002, 4, 3330–3340. [Google Scholar] [CrossRef]
- Bezuglov, N.N.; Golubkov, G.V.; Klyucharev, A.N. Ionization of Excited Atoms in Thermal Collisions; The Atmosphere and Ionosphere: Elementary Processes, Discharges and Plasmoids; Springer: New York, NY, USA; London, UK, 2013; Chapter 1; pp. 1–60. [Google Scholar]
- Reichl, L.E. The Transition to Chaos: Conservative Classical Systems and Quantum Manifestations; Springer: New York, NY, USA, 2004. [Google Scholar]
- Zaslavskii, G.M. Physics of Chaos in Hamiltonian Systems, 2nd ed; Imperial College Press: London, UK, 2007. [Google Scholar]
- Bezuglov, N.N.; Golubkov, G.V.; Klyucharev, A.N. Manifestations of “Dynamic Chaos” in Reactions with Participation of Rydberg States; St. Petersburg State University: St. Petersburg, Russia, 2017. (In Russian) [Google Scholar]
- Paris-Mandoki, A.; Gorniaczyk, H.; Tresp, C.; Mirgorodskiy, I.; Hofferberth, S. Tailoring Rydberg interactions via Förster resonances: State combinations, hopping and angular dependence. J. Phys. B 2016, 49, 164001. [Google Scholar] [CrossRef]
- Gianninas, A.; Dufour, P.; Kilic, M.; Brown, W.R.; Bergeron, P.; Hermes, J.J. Precise atmospheric parameters for the shortest-period binary white dwarfs: Gravitational waves, metals, and pulsations. Astrophys. J. 2014, 794, 35–52. [Google Scholar] [CrossRef]
- Bezuglov, N.N.; Borisov, E.N.; Verolainen, Y.F. Distribution of the radiative lifetimes over the excited states of atoms and ions. Sov. Phys. Uspekhi 1991, 34, 3–29. [Google Scholar] [CrossRef]
- Hezel, T.P.; Burkhardt, C.E.; Ciocca, M.; He, L.W.; Leventhal, J.J. Classical view of the properties of Rydberg atoms: Application of the correspondence principle. Am. J. Phys. 1992, 60, 329–335. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics; Pergamon: Oxford, UK, 1977. [Google Scholar]
- Omidvar, K. Semiclassical formula for the radiative mean lifetime of the excited state of the hydrogenlike atoms. Phys. Rev. A 1982, 26, 3053–3061. [Google Scholar] [CrossRef]
- Mack, M.; Grimmel, J.; Karlewski, F.; Sárkány, L.; Hattermann, H.; Fortágh, J. All-optical measurement of Rydberg-state lifetimes. Phys. Rev. A 2015, 92, 012517. [Google Scholar] [CrossRef]
- Tretyakov, D.B.; Beterov, I.I.; Entin, V.M.; Yakshina, E.A.; Ryabtsev, I.I.; Dyubko, S.F.; Alekseev, E.A.; Pogrebnyak, N.L.; Bezuglov, N.N.; Arimondo, E. Effect of photoions on the line shape of the Förster resonance lines and microwave transitions in cold rubidium Rydberg atoms. J. Exp. Theor. Phys. 2012, 114, 14–24. [Google Scholar] [CrossRef]
- Hund, F. The History of Quantum Theory; Barnes & Noble Books: New York, NY, USA, 1974; Chapter 11. [Google Scholar]
- Bokulich, P.; Bokulich, A. Niels Bohr’s generalization of classical mechanics. Found. Phys. 2005, 35, 347–371. [Google Scholar] [CrossRef]
- Delone, N.B.; Goreslavsky, S.P.; Krainov, V.P. Dipole matrix elements in the quasi-classical approximation. J. Phys. B 1994, 27, 4403. [Google Scholar] [CrossRef]
- Arefieff, K.N.; Miculis, N.; Bezuglov, N.N.; Dimitrijević, M.S.; Klyucharev, A.N.; Mihajlov, A.A.; Srećković, V.A. Dynamics Resonances in Atomic States of Astrophysical Relevance. J. Astrophys. Astron. 2015, 36, 613–622. [Google Scholar] [CrossRef]
- Sommerfeld, A. Atomic Structure and Spectral Lines; Methuen: London, UK, 1934. [Google Scholar]
- Grouzdev, P.F. Atomic and Ionic Spectra in X-ray and Ultraviolet Region’s; Energoatomizdat: Moscow, Russia, 1982. (In Russian) [Google Scholar]
- Zakharov, M.Y.; Bezuglov, N.N.; Klyucharev, A.N.; Matveev, A.A.; Beterov, I.I.; Dulieu, O. Specifics of the stochastic ionization of a Rydberg collision complex with Förster resonance. Russ. J. Phys. Chem. B 2011, 5, 537–545. [Google Scholar] [CrossRef]
- Fermi, E. Sopra lo spostamento per pressione delle righe elevate delle serie spettrali. Nuovo Cimento 1934, 11, 157–166. [Google Scholar] [CrossRef]
- Janev, R.K.; Mihajlov, A.A. Resonant ionization in slow-atom-Rydberg-atom collisions. Phys. Rev. A 1980, 21, 819–826. [Google Scholar] [CrossRef]
- Mihajlov, A.A.; Janev, R.K. Ionisation in atom-Rydberg atom collisions: Ejected electron energy spectra and reaction rate coefficients. J. Phys. B 1981, 14, 1639. [Google Scholar] [CrossRef]
- Duman, E.L.; Shmatov, I.P. Ionization of highly excited atoms in their own gas. Sov. Phys. JETP 1980, 51, 1061–1065. [Google Scholar]
- Srećković, V.A.; Dimitrijević, M.S.; Ignjatović, Lj.M.; Bezuglov, N.N.; Klyucharev, A. The Collisional Atomic Processes of Rydberg Hydrogen and Helium Atoms: Astrophysical Relevance. Galaxies 2018, 6, 72. [Google Scholar] [CrossRef]
- Bezuglov, N.N.; Borodin, V.M.; Kazanskiy, A.K.; Klyucharev, A.N.; Matveev, A.A.; Orlovskii, K.V. Analysis of Fokker-Planck type stochastic equations with variable boundary conditions in an elementary process of collisional ionization. Opt. Spectrosc. 2001, 91, 19–26. [Google Scholar] [CrossRef]
- Zaslavskij, G.M. Hamiltonian Chaos and Fractional Dynamics; Oxford Univ. Press: Oxford, UK, 2005. [Google Scholar]
- Delone, N.B.; Krainov, V.P.; Shepelyanskii, D.L. Highly-excited atoms in the electromagnetic field. Sov. Phys. Uspekhi 1983, 26, 551. [Google Scholar] [CrossRef]
- Bezuglov, N.N.; Borodin, V.M.; Ekers, A.; Klyucharev, A.N. A quasi-classical description of the stochastic dynamics of a Rydberg electron in a diatomic quasi-molecular complex. Opt. Spectrosc. 2002, 93, 661–669. [Google Scholar] [CrossRef]
- Ryabtsev, I.I.; Tretyakov, D.B.; Beterov, I.I.; Bezuglov, N.N.; Miculis, K.; Ekers, A. Collisional and thermal ionization of sodium Rydberg atoms: I. Experiment for nS and nD atoms with n = 8–20. J. Phys. B 2005, 38, S17–S35. [Google Scholar] [CrossRef]
- Efimov, D.K.; Bezuglov, N.N.; Klyucharev, A.N.; Gnedin, Y.N.; Miculis, K.; Ekers, A. Analysis of light-induced diffusion ionization of a three-dimensional hydrogen atom based on the Floquet technique and split-operator method. Opt. Spectrosc. 2014, 117, 8–17. [Google Scholar] [CrossRef]
- Chu, S.-I.; Telnov, D.A. Beyond the Floquet theorem: Generalized Floquet formalisms and quasienergy methods for atomic and molecular multiphoton processes in intense laser fields. Phys. Rep. 2004, 390, 1–131. [Google Scholar] [CrossRef]
- Hairer, E. Numeral Geometric Integration; Universite de Geneve: Geneve, Switzerland, 1999. [Google Scholar]
- Kazansky, A.K.; Bezuglov, N.N.; Molisch, A.F.; Fuso, F.; Allegrini, M. Direct numerical method to solve radiation trapping problems with a Doppler-broadening mechanism for partial frequency redistribution. Phys. Rev. A 2001, 64, 022719. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Mechanics Course of Theoretical Physics Mechanics; (Nauka, Moscow, 1973); English Tran.; Permagon Press: Oxford, UK; New York, NY, USA; Toronto, ON, Canada, 1976; Volume 1. [Google Scholar]
- Ramsey, N.F. Molecular Beams, 2nd ed.; Clarendon: Oxford, UK, 1989. [Google Scholar]
- Michulis, K.; Beterov, I.I.; Bezuglov, N.N.; Ryabtsev, I.I.; Tretyakov, D.B.; Ekers, A.; Klucharev, A.N. Collisional and thermal ionization of sodium Rydberg atoms: II. Theory for nS, nP and nD states with n= 5–25. J. Phys. B 2005, 38, 1811–1831. [Google Scholar] [CrossRef]
- Sydoryk, I.; Bezuglov, N.N.; Beterov, I.I.; Miculis, K.; Saks, E.; Janovs, A.; Spels, P.; Ekers, A. Broadening and intensity redistribution in the Na(3p) hyperfine excitation spectra due to optical pumping in the weak excitation limit. Phys. Rev. A 2008, 77, 042511. [Google Scholar] [CrossRef]
- Kirova, T.; Cinins, A.; Efimov, D.K.; Bruvelis, M.; Miculis, K.; Bezuglov, N.N.; Auzinsh, M.; Ryabtsev, I.I.; Ekers, A. Hyperfine interaction in the Autler-Townes effect: The formation of bright, dark, and chameleon states. Phys. Rev. A 2017, 96, 043421. [Google Scholar] [CrossRef]
- Porfido, N.; Bezuglov, N.N.; Bruvelis, M.; Shayeganrad, G.; Birindelli, S.; Tantussi, F.; Guerri, I.; Viteau, M.; Fioretti, A.; Ciampini, D.; et al. Nonlinear effects in optical pumping of a cold and slow atomic beam. Phys. Rev. A 2015, 92, 043408. [Google Scholar] [CrossRef]
- Klyucharev, A.N.; Bezuglov, N.N.; Matveev, A.A.; Mihajlov, A.A.; Ignjatović, L.M.; Dimitrijević, M.S. Rate coefficients for the chemi-ionization processes in sodium- and other alkali-metal geocosmical plasmas. New Astron. Rev. 2007, 51, 547–562. [Google Scholar] [CrossRef]
- Tantussi, F.; Mangasuli, V.; Porfido, N.; Prescimone, F.; Fuso, F.; Arimondo, E.; Allegrini, M. Towards laser-manipulated deposition for atom-scale technologies. Appl. Surf. Sci. 2009, 255, 9665–9670. [Google Scholar] [CrossRef]
- Boulmer, J.; Bonanno, R.; Weiner, J. Crossed-beam measurements of absolute rates coefficients in associative ionization collisions between Na*(np) and Na(3s) for 5 ≤ n ≤ 15. J. Phys. B 1983, 16, 3015–3024. [Google Scholar] [CrossRef]
- Weiner, J.; Boulmer, J. Associative ionization rate constants as a function of quantum numbers n and l in Na*(np) + Na(3s) collisions for 17 ≤ n ≤ 27 and l = 0, l = 1 and l ≥ 2. J. Phys. B 1986, 19, 599–609. [Google Scholar] [CrossRef]
- Beterov, I.I.; Tretyakov, D.B.; Ryabtsev, I.I.; Bezuglov, N.N.; Miculis, K.; Ekers, A.; Klucharev, A.N. Collisional and thermal ionization of sodium Rydberg atoms III. Experiment and theory for nS and nD states with n = 8–20 in crossed atomic beams. J. Phys. B 2005, 38, 4349–4361. [Google Scholar] [CrossRef]
| Li | Na | K | Rb | Cs | H | |
|---|---|---|---|---|---|---|
| s | 0.40 | 1.35 | 2.19 | 3.13 | 4.06 | 0 |
| p | 0.04 | 0.85 | 1.71 | 2.66 | 3.59 | 0 |
| 0.36 | 0.50 | 0.48 | 0.47 | 0.47 | 0 | |
| 0.69 | 0.14 | 0.51 | 0.75 | 0.61 | 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dimitrijević, M.S.; Srećković, V.A.; Zalam, A.A.; Bezuglov, N.N.; Klyucharev, A.N. Dynamic Instability of Rydberg Atomic Complexes. Atoms 2019, 7, 22. https://doi.org/10.3390/atoms7010022
Dimitrijević MS, Srećković VA, Zalam AA, Bezuglov NN, Klyucharev AN. Dynamic Instability of Rydberg Atomic Complexes. Atoms. 2019; 7(1):22. https://doi.org/10.3390/atoms7010022
Chicago/Turabian StyleDimitrijević, Milan S., Vladimir A. Srećković, Alaa Abo Zalam, Nikolai N. Bezuglov, and Andrey N. Klyucharev. 2019. "Dynamic Instability of Rydberg Atomic Complexes" Atoms 7, no. 1: 22. https://doi.org/10.3390/atoms7010022
APA StyleDimitrijević, M. S., Srećković, V. A., Zalam, A. A., Bezuglov, N. N., & Klyucharev, A. N. (2019). Dynamic Instability of Rydberg Atomic Complexes. Atoms, 7(1), 22. https://doi.org/10.3390/atoms7010022







