Eccentricity-Based Topological Invariants of Some Chemical Graphs

Abstract

Topological index is an invariant of molecular graphs which correlates the structure with different physical and chemical invariants of the compound like boiling point, chemical reactivity, stability, Kovat’s constant etc. Eccentricity-based topological indices, like eccentric connectivity index, connective eccentric index, first Zagreb eccentricity index, and second Zagreb eccentricity index were analyzed and computed for families of Dutch windmill graphs and circulant graphs.

1. Introduction

A single number which represents a chemical structure, in graph-theoretical chemistry, is called a topological descriptor (or index). A topological index is a real number which correlates the structure of chemical compound with their chemical reactivity or physical properties. Chemical graph theory is well-known branch of graph theory which concerns with mathematical modeling of molecules. It also deals with the study of development of topological indices, isomerism, and found applications in quantum chemistry and stereochemistry. Topological indices are mainly used in quantitative structure–activity relations (QSAR) as well as quantitative structure–property relations (QSPR) which describe the relation between chemical structure with the properties and reactivity of the compounds. Chemical structure is depicted as graphs with vertices representing atoms and the edges represent the chemical bonds between atoms.

Let $G\left(V,E\right)$ be a simple and connected graph with $n$ vertices and $m$ edges. Let $u\in V$ then be the eccentricity of a vertex where $u$ is a maximum distance of $u$ from other vertices of graph $G$, which is denoted by $\epsilon \left(u\right)$, i.e., $\epsilon \left(u\right)=\max \left\{d\left(u,v\right); v\in V\right\}$, where $d\left(u,v\right)$ is a distance between $u$ and $v$. The degree of a vertex $u$, denoted by $d\left(u\right)$, is number of vertices which are attached to $u$ by the edges. The eccentric connectivity index is introduced by Sharma, Goswami, and Madan [1], and defined as

$${\xi }^c={\displaystyle \sum }_{u\in V}d\left(u\right)\epsilon \left(u\right).$$

(1)

In 2000, Gupta, Singh, and Madan [2] introduced a topological descriptor termed the connective eccentricity index, which is defined as

$$C^{\xi }={\displaystyle \sum }_{u\in V}\frac{d\left(u\right)}{\epsilon \left(u\right)}.$$

(2)

The Zagreb indices were introduced more than thirty years ago by Gutman and Trinajestic [3]. They are defined as

$$\begin{gathered} M_1^{*}={\displaystyle \sum }_{u\in V}{d}^2\left(u\right), \\ {M}_2^{*}={\displaystyle \sum }_{uv\in E}d\left(u\right)d\left(v\right). \end{gathered}$$

After thirty years, new version of Zagreb indices introduced by Ghorbani and Hosseinzadeh [4] are first and second Zagreb eccentricity index, which are stated as

$$M_1\left(G\right)={\displaystyle \sum }_{z\in V\left(G\right)}{\epsilon }^2\left(z\right),$$

(3)

$$M_2\left(G\right)={\displaystyle \sum }_{yz\in E\left(G\right)}\epsilon \left(y\right)\epsilon \left(z\right).$$

(4)

Khalifeh et al. [5] calculated the Zagreb indices of arbitrary $C_4$ tube, $C_4$ torus, and q-multiwalled polyhex nanotorus. Doslic et al. [6] gave formulae of the eccentric connectivity index for armchair hexagonal belts, zigzag belts, and the corresponding open chains. Ashrafi et al. [7] found formulas for the eccentric connectivity index of $TU{C}_4{C}_8\left(S\right)$ nanotube and $T{C}_4{C}_8\left(S\right)$ nanotorus. Ghorbani [8] derived bounds of the connective eccentric index and calculated connective eccentricity index for two classes of fullerenes which are infinite. Ilić [9] presented the unicyclic graphs and extremal trees with minimum and maximum eccentric connectivity index subject to the certain graph constraints. Ilić et al. [10] derived explicit formulae for the eccentric distance sum for the Cartesian product and joining of graphs. Morgan et al. [11] showed a quite low lower bound for a tree on the eccentric connectivity index, in expressions of diameter and order. Songhori [12] computed the eccentric connectivity for an infinite class of fullerene graphs. Recently, Gao et al. provided several interesting results about topological indices and their applications in biological sciences [13] and nanoscience [14], which are quite promising and motivating for further studies in the area.

2. Results and Discussions

In this section, we will compute the connective eccentricity, eccentric connective, first Zagreb eccentricity index, and second Zagreb eccentricity indices of Dutch windmill graph and circulant graph by analyzing the eccentricities of the vertices of the graphs.

Dutch Windmill graph: A graph $D_m^n$ obtained by joining $n$ numbers of cycle graphs $C_m$ with a common vertex is known as Dutch windmill graph. The Dutch windmill graph is an undirected and planar graph.

Circulant graph: Let $a_1,a_2,a_3,\dots ,a_m$ be positive integers where $1\le a_i\le \lfloor \frac{n}{2}\rfloor$, $a_i\ne a_j\forall 1\le i,j\le m$, and $i\ne j.$ An undirected and simple graph with vertex $V=\left\{u_1,u_2,u_3,\dots ,u_n\right\}$, and the edge set is $E=\left\{u_i{u}_{i+a_j};1\le i\le n,1\le j\le m\right\}$ which is called the circulant graph and is denoted by $C_n\left(a_1,a_2,a_3,\dots ,a_m\right)$. The indices being taken modulo $n$. The numbers $a_1,a_2,a_3,\dots ,a_m$ are called generators. A circulant graph is a regular graph. Let $r$ denote the degree of vertices of the graph, then

$$r=\{\begin{array}{ll}2m-1,& if \frac{n}{2}\in \left\{a_1,a_2,a_3,\dots ,a_m\right\}\\ 2m& otherwise\end{array}.$$

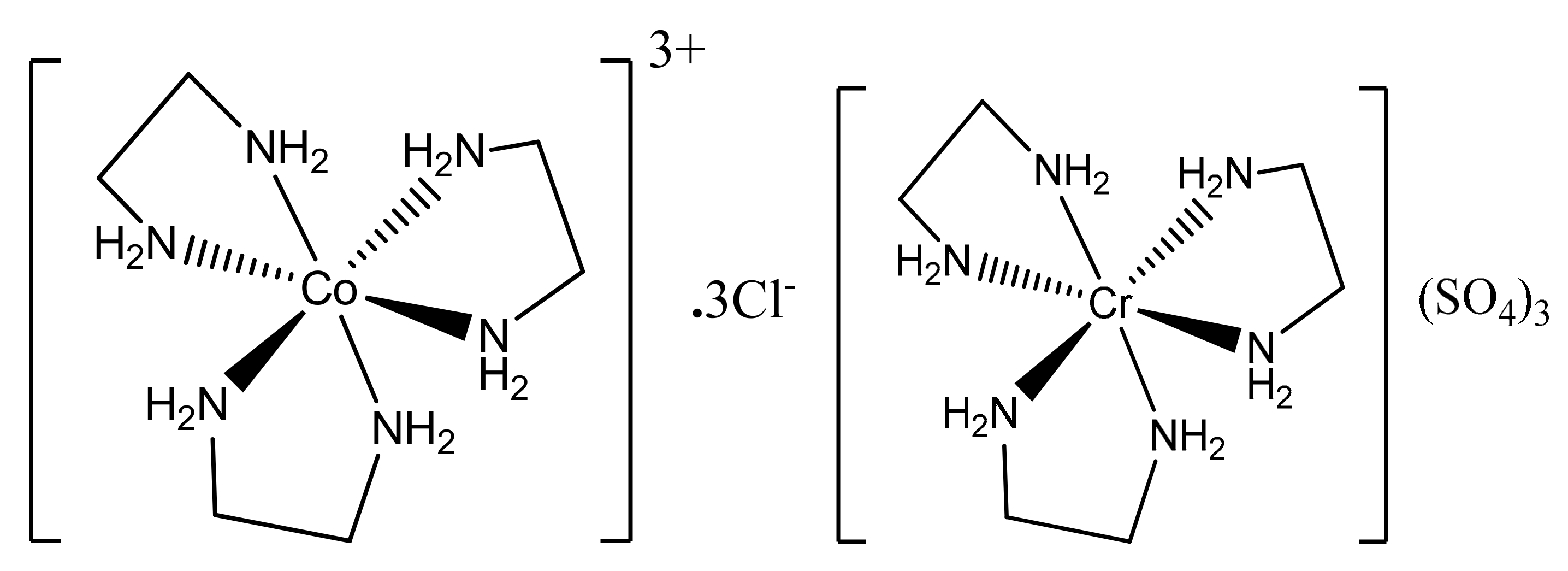
These graphs correspond to wide variety of chemical graphs. For instance, the Dutch windmill graph represents bidentate ligands, as can be seen in the Figure 1 below.

Theorem 1. 

The connective eccentricity index of Dutch windmill graph, denoted by$C^{\xi }\left(D_m^n\right)$, is given by

$$C^{\xi }\left(D_m^n\right)=\{\begin{array}{ll}\frac{2n}{\lfloor \frac{m}{2}\rfloor }+4n{{\displaystyle \sum }}_{j=1}^{\lfloor \frac{m}{2}\rfloor }\frac{1}{\left(\lfloor \frac{m}{2}\rfloor +j\right)};& if m is odd\\ \frac{6n}{m}+4n\frac{1}{{{\displaystyle \sum }}_{j=1}^{\frac{m-2}{2}}\left(\frac{m}{2}+j\right)};& if m is even\end{array},$$

and the eccentric connective index, denoted by${\xi }^c\left(D_m^n\right)$, is given by

$${\xi }^c\left(D_m^n\right)=\{\begin{array}{ll}2n\lfloor \frac{m}{2}\rfloor +4n{{\displaystyle \sum }}_{j=1}^{\lfloor \frac{m}{2}\rfloor }\left(\lfloor \frac{m}{2}\rfloor +j\right);& if m is odd\\ 3mn+4n{{\displaystyle \sum }}_{j=1}^{\frac{m-2}{2}}\left(\frac{m}{2}+j\right);& ifmiseven\end{array}.$$

Proof. 

Let $D_m^n$ be the Dutch windmill graph with $n$ copies of cycle $C_m$ having common vertex $z$ with degree $\left(z\right)=2n$. The degree of other vertices of the graph is two. □

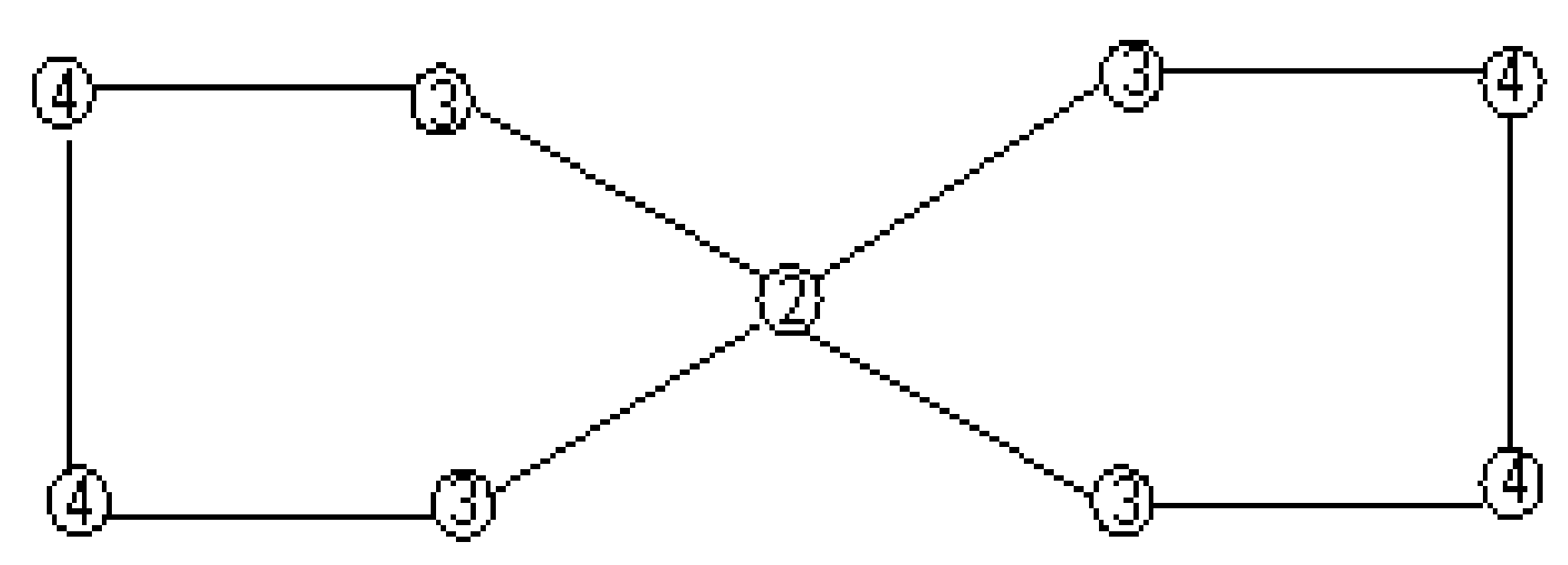
Case 1:$m$ is odd. The eccentricity of the central vertex is $\epsilon \left(z\right)=\lfloor \frac{m}{2}\rfloor$ and eccentricity of other vertices increase by one as we move away from the common vertex to the half of the cycle, as can be seen in Figure 2. When $m$ odd, the vertices other than the common vertex are even in number in each cycle. The eccentricity of the vertices, in each cycle, is pairwise equal, and are equidistant from the central vertex. Therefore, $n$ cycles of $D_m^n$ have a total $2n$ vertices of same eccentricity, which are obtained by adding $\epsilon \left(z\right)=\lfloor \frac{m}{2}\rfloor$ to their distance from the central vertex.

The connective eccentricity index of $D_m^n$, as given in Equation (1), can be written as

$$\begin{array}{ll}{\xi }^c\left(D_m^n\right)& =d\left(z\right)\epsilon \left(z\right)+2n{{\displaystyle \sum }}_{i=1}^{\lfloor \frac{m}{2}\rfloor }d\left(z_i\right)\epsilon \left(z_i\right)\\ & =\left(2n\right)\left(\lfloor \frac{m}{2}\rfloor \right)+2n\left[2\left(\lfloor \frac{m}{2}\rfloor +1\right)+2\left(\lfloor \frac{m}{2}\rfloor +2\right)+2\left(\lfloor \frac{m}{2}\rfloor +3\right)+\dots +2\left(\lfloor \frac{m}{2}\rfloor +\lfloor \frac{m}{2}\rfloor \right)\right]\hfill \\ & =\left(2n\right)\left(\lfloor \frac{m}{2}\rfloor \right)+\left(2n\right)\left(2\right)\left[\left(\lfloor \frac{m}{2}\rfloor +1\right)+\left(\lfloor \frac{m}{2}\rfloor +2\right)+\left(\lfloor \frac{m}{2}\rfloor +3\right)+\dots +\left(\lfloor \frac{m}{2}\rfloor +\lfloor \frac{m}{2}\rfloor \right)\right]\hfill \\ & =\left(2n\right)\left(\lfloor \frac{m}{2}\rfloor \right)+4n\left[\left(\lfloor \frac{m}{2}\rfloor +1\right)+\left(\lfloor \frac{m}{2}\rfloor +2\right)+\left(\lfloor \frac{m}{2}\rfloor +3\right)+\dots +\left(\lfloor \frac{m}{2}\rfloor +\lfloor \frac{m}{2}\rfloor \right)\right]\hfill \end{array}$$

$${\xi }^c\left(D_m^n\right)=\left(2n\right)\left(\lfloor \frac{m}{2}\rfloor \right)+4n{{\displaystyle \sum }}_{j=1}^{\lfloor \frac{m}{2}\rfloor }(\lfloor \frac{m}{2}\rfloor +j).$$

The eccentric connective index of $D_m^n$ , as given in Equation (2), can be expressed as

$$\begin{array}{ll}{C}^{\xi }\left(D_m^n\right)& =\frac{d\left(z\right)}{\epsilon \left(z\right)}+2n{{\displaystyle \sum }}_{i=1}^{\lfloor \frac{m}{2}\rfloor }\frac{d\left(z_i\right)}{\epsilon \left(z_i\right)}\\ & =\frac{2n}{\lfloor \frac{m}{2}\rfloor }+2n(\frac{2}{\lfloor \frac{m}{2}\rfloor +1}+\frac{2}{\lfloor \frac{m}{2}\rfloor +2}+\frac{2}{\lfloor \frac{m}{2}\rfloor +3}+\dots +\frac{2}{\lfloor \frac{m}{2}\rfloor +\lfloor \frac{m}{2}\rfloor })\\ & =\frac{2n}{\lfloor \frac{m}{2}\rfloor }+4n(\frac{1}{\lfloor \frac{m}{2}\rfloor +1}+\frac{1}{\lfloor \frac{m}{2}\rfloor +2}+\frac{1}{\lfloor \frac{m}{2}\rfloor +3}+\dots +\frac{1}{\lfloor \frac{m}{2}\rfloor +\lfloor \frac{m}{2}\rfloor })\\ & =\frac{2n}{\lfloor \frac{m}{2}\rfloor }+4n\frac{1}{{{\displaystyle \sum }}_{j=1}^{\lfloor \frac{m}{2}\rfloor }(\lfloor \frac{m}{2}\rfloor +j)}\end{array}$$

$$C^{\xi }\left(D_m^n\right)=\frac{2n}{\lfloor \frac{m}{2}\rfloor }+4n{{\displaystyle \sum }}_{j=1}^{\lfloor \frac{m}{2}\rfloor }\frac{1}{(\lfloor \frac{m}{2}\rfloor +j)}.$$

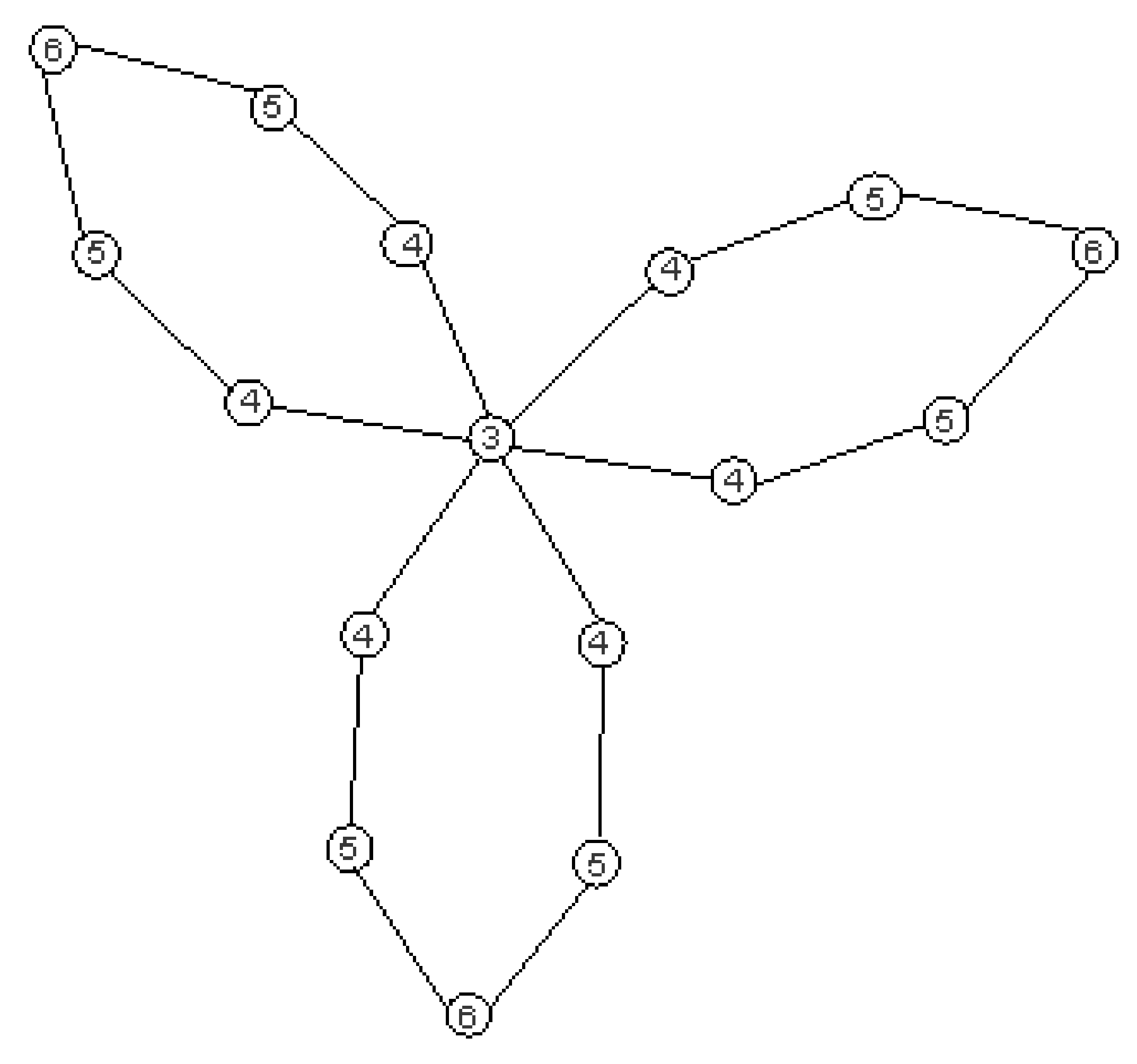
Case 2:$m$ is even. In this case, each cycle of $D_m^n$ has an odd number of vertices excluding the central vertex; among these, each pair of vertices which are equidistant from central vertex have the same eccentricity, which is equal to the eccentricity of central vertex when adding the distance from the vertex pair, which can be observed in Figure 3. The eccentricity of central vertex is $\left(z\right)=\frac{m}{2}$, and for other vertex pairs, it increases by one as we move away from central vertex.

Let $z_i$ be the vertices of graph which have, pairwise, the same eccentricity, and these are $2n$ in number in each cycle. The eccentricity of last vertex in each cycle is $m$, and these vertices are $n$ in number.

The connective eccentricity index of $D_m^n$ is

$$\begin{array}{ll}{\xi }^c\left(D_m^n\right)& =d\left(z\right)\epsilon \left(z\right)+{{\displaystyle \sum }}_{i=1}^{2n}d\left(z_i\right)\epsilon \left(z_i\right)+nd\left(v\right)\epsilon \left(v\right)\\ & =\left(2n\right)\left(\frac{m}{2}\right)+2n\left[2\left(\frac{m}{2}+1\right)+2\left(\frac{m}{2}+2\right)+2\left(\frac{m}{2}+3\right)+\dots +2\left(\frac{m}{2}+\frac{m}{2}-1\right)\right]+n\left(2\right)\left(m\right)\\ & =\left(2n\right)\left(\frac{m}{2}\right)+\left(2n\right)\left(2\right)\left[\left(\frac{m}{2}+1\right)+\left(\frac{m}{2}+2\right)+\left(\frac{m}{2}+3\right)+\dots +\left(\frac{m}{2}+\frac{m}{2}-1\right)\right]+2\left(n\right)\left(m\right)\\ & =\left(n\right)\left(m\right)+4n\left[\left(\frac{m}{2}+1\right)+\left(\frac{m}{2}+2\right)+\left(\frac{m}{2}+3\right)+\dots +\left(\frac{m}{2}+\frac{m}{2}-1\right)\right]+2\left(n\right)\left(m\right)\\ & =3\left(n\right)\left(m\right)+4n\left[\left(\frac{m}{2}+1\right)+\left(\frac{m}{2}+2\right)+\left(\frac{m}{2}+3\right)+\dots +\left(\frac{m}{2}+\frac{m}{2}-1\right)\right]\\ & =3\left(n\right)\left(m\right)+4n\left[\left(\frac{m}{2}+1\right)+\left(\frac{m}{2}+2\right)+\left(\frac{m}{2}+3\right)+\dots +\left(\frac{m}{2}+\frac{m}{2}-1\right)\right]\end{array}$$

$${\xi }^c\left(D_m^n\right)=3nm+4n{{\displaystyle \sum }}_{j=1}^{\frac{m-2}{2}}(\frac{m}{2}+j).$$

The eccentric connective index of $D_m^n$ is

$$\begin{array}{ll}{C}^{\xi }\left(D_m^n\right)& =\frac{d\left(z\right)}{\epsilon \left(z\right)}+2n{{\displaystyle \sum }}_{i=1}^{\frac{m}{2}-1}\frac{d\left(z_i\right)}{\epsilon \left(z_i\right)}+n\frac{d\left(v\right)}{\epsilon \left(v\right)}\\ & =\frac{2n}{\frac{m}{2}}+2n\left(\frac{2}{\frac{m}{2}+1}+\frac{2}{\frac{m}{2}+2}+\frac{2}{\frac{m}{2}+3}+\dots +\frac{2}{\frac{m}{2}+\frac{m}{2}-1}\right)+n\frac{2}{m}\\ & =\frac{4n}{m}+4n\left(\frac{1}{\frac{m}{2}+1}+\frac{1}{\frac{m}{2}+2}+\frac{1}{\frac{m}{2}+3}+\dots +\frac{1}{\frac{m}{2}+\frac{m}{2}-1}\right)+\frac{2n}{m}\\ & =\frac{4n}{m}+\frac{2n}{m}+4n\left(\frac{1}{\frac{m}{2}+1}+\frac{1}{\frac{m}{2}+2}+\frac{1}{\frac{m}{2}+3}+\dots +\frac{1}{\frac{m}{2}+\frac{m}{2}-1}\right)\end{array}$$

$$C^{\xi }\left(D_m^n\right)=\frac{6n}{m}+4n·\frac{1}{{{\displaystyle \sum }}_{j=1}^{\frac{m-2}{2}}(\frac{m}{2}+j)}.$$

Theorem 2. 

The first Zagreb eccentricity index and the second Zagreb eccentricity index of Dutch windmill graph$D_m^n$, denoted by$M_1\left(D_m^n\right)$and$M_2\left(D_m^n\right)$, respectively, are given as

$$M_1\left(D_m^n\right)=\{\begin{array}{ll}{\left(\lfloor \frac{m}{2}\rfloor \right)}^2+2n{{\displaystyle \sum }}_{j=1}^{\lfloor \frac{m}{2}\rfloor }{\left(\lfloor \frac{m}{2}\rfloor +j\right)}^2,& if m is odd\\ \left(4n+1\right){\left(\frac{m}{2}\right)}^2+2n{{\displaystyle \sum }}_{j=1}^{\frac{m-2}{2}}{\left(\frac{m}{2}+j\right)}^2,& if m is even\end{array},$$

$$M_2\left(D_m^n\right)=\{\begin{array}{ll}2n{{\displaystyle \sum }}_{j=0}^{\lfloor \frac{m}{2}\rfloor -1}\left[\left(\lfloor \frac{m}{2}\rfloor +j\right)\times \left(\lceil \frac{m}{2}\rceil +j\right)\right]+n{\left(m-1\right)}^2,& if m is odd\\ 2n{{\displaystyle \sum }}_{j=0}^{\frac{m-2}{2}}\left[{\left(\frac{m}{2}+j\right)}^2+\left(\frac{m}{2}+j\right)\right],& if m even\end{array}.$$

Proof. 

Let $D_m^n$ be a dutch windmill graph with $n$ copies of cycle $C_m$ with common vertex $z$ with the eccentricity $\epsilon \left(z\right)=\lfloor \frac{m}{2}\rfloor$. The eccentricity of vertex increases by one as we move away from the common vertex. □

Case 1:$m$ is odd: When $m$ is odd then the vertices other than common vertex are even in number. The behavior of eccentricity of these vertices is discussed in detail in case 1 of Theorem 1. In each cycle $C_m$, we denote the vertex pair by $z_1$, which is at a distance one apart from the central vertex, similarly, $z_i$ denotes the vertex pair which is distance $i$ apart from central vertex $z$.

The first Zagreb eccentricity index is

$$\begin{array}{ll}{M}_1\left(D_m^n\right)& ={\epsilon }^2\left(z\right)+{{\displaystyle \sum }}_{i=1}^{2n}{\epsilon }^2\left(z_i\right)\\ & ={\left(\lfloor \frac{m}{2}\rfloor \right)}^2+2n\left[{\left(\lfloor \frac{m}{2}\rfloor +1\right)}^2+{\left(\lfloor \frac{m}{2}\rfloor +2\right)}^2+\dots +{\left(\lfloor \frac{m}{2}\rfloor +\lfloor \frac{m}{2}\rfloor \right)}^2\right]\\ & ={\lfloor \frac{m}{2}\rfloor }^2+2n\left[{\left(\lfloor \frac{m}{2}\rfloor +1\right)}^2+{\left(\lfloor \frac{m}{2}\rfloor +2\right)}^2+\dots +{\left(\lfloor \frac{m}{2}\rfloor +\lfloor \frac{m}{2}\rfloor \right)}^2\right],\end{array}$$

$$M_1\left(D_m^n\right)={\lfloor \frac{m}{2}\rfloor }^2+2n{{\displaystyle \sum }}_{j=1}^{\lfloor \frac{m}{2}\rfloor }{\left(\lfloor \frac{m}{2}\rfloor +j\right)}^2.$$

The second Zagreb eccentricity index is sum of product of eccentricities of endpoints of all edges, i.e.,

$$M_2\left(D_m^n\right)={\displaystyle \sum }_{yz\in E\left(G\right)}\epsilon \left(y\right)\epsilon \left(z\right).$$

Eccentricity of adjacent vertices differ by 1 in $D_m^n$. From Figure 2, we observe that in every cycle, there must be two edges with same eccentricity of endpoint vertices, therefore, in $n$ copies of cycle there are $2n$ edges with the same eccentricity. Moreover, each cycle of odd length has an odd number of edges so, after pairing, we are left with an edge whose endpoints have the same eccentricity, which is $m-1$.

$$\begin{array}{ll}{M}_2\left(D_m^n\right)& =2n·\epsilon \left(z\right)\epsilon \left(z_1\right)+2n{{\displaystyle \sum }}_{i=1}^{\lfloor \frac{m}{2}\rfloor -1}\epsilon \left(z_i\right)\epsilon \left(z_{i+1}\right)+n·\epsilon {(z_{\lfloor \frac{m}{2}\rfloor })}^2\\ & =\left[2n\left\{\left(\lfloor \frac{m}{2}\rfloor \right)\times \left(\lceil \frac{m}{2}\rceil +1\right)\right\}+2n\left\{\left(\lfloor \frac{m}{2}\rfloor +1\right)\times \left(\lceil \frac{m}{2}\rceil +2\right)\right\}+\dots +2n\left\{\left(\lfloor \frac{m}{2}\rfloor +\lfloor \frac{m}{2}\rfloor -1\right)\times \left(\lceil \frac{m}{2}\rceil +\lfloor \frac{m}{2}\rfloor \right)\right\}\right]+n\left(m-1\right)\left(m-1\right)\\ & =2n\left[\left\{\left(\lfloor \frac{m}{2}\rfloor \right)\times \left(\lceil \frac{m}{2}\rceil +1\right)\right\}+\left\{\left(\lfloor \frac{m}{2}\rfloor +1\right)\times \left(\lceil \frac{m}{2}\rceil +2\right)\right\}+\dots +\left\{\left(\lfloor \frac{m}{2}\rfloor +\lfloor \frac{m}{2}\rfloor -1\right)\times \left(\lceil \frac{m}{2}\rceil +\lfloor \frac{m}{2}\rfloor \right)\right\}\right]+n{\left(m-1\right)}^2\end{array}$$

$$M_2\left(D_m^n\right)=2n{{\displaystyle \sum }}_{j=0}^{\lfloor \frac{m}{2}\rfloor -1}\left\{\left(\lfloor \frac{m}{2}\rfloor +j\right)\times \left(\lceil \frac{m}{2}\rceil +j+1\right)\right\}+n{\left(m-1\right)}^2$$

Case 2:$m$ is even. Let $D_m^n$ be a Dutch windmill graph with $n$ copies of cycle $C_m$ with common vertex $z$, the degree $d\left(z\right)=2n$, and the eccentricity $\epsilon \left(z\right)=\frac{m}{2}$. The degree of other vertices of graph is two, and eccentricity of vertex increases by one as we move away from the common vertex.

From the figure, the vertices of the same degree are $2n$ in number because in every cycle eccentricity of the pair of vertices same. There are $n$ number of vertices having degree $m$. Let $z_i$ be vertices of the same degree. The first Zagreb eccentricity index is

$$M_1\left(D_m^n\right)={\epsilon }^2\left(z\right)+{{\displaystyle \sum }}_{i=1}^{2n}{\epsilon }^2\left(z_i\right)$$

where $z_i$ denote the pair of vertices which have the same eccentricity. Hence,

$$\begin{array}{ll}{M}_1\left(D_m^n\right)& ={\left(\frac{m}{2}\right)}^2+2n\left[{\left(\frac{m}{2}+1\right)}^2+{\left(\frac{m}{2}+2\right)}^2+\dots +{\left(\frac{m}{2}+\frac{m}{2}-1\right)}^2\right]+n{\left(m\right)}^2\\ & ={\left(\frac{m}{2}\right)}^2+2n\left[{\left(\frac{m}{2}+1\right)}^2+{\left(\frac{m}{2}+2\right)}^2+\dots +{\left(\frac{m}{2}+\left(\frac{m}{2}-1\right)\right)}^2\right]+n\frac{4m^2}{4}\\ & ={\left(\frac{m}{2}\right)}^2+2n\left[{\left(\frac{m}{2}+1\right)}^2+{\left(\frac{m}{2}+2\right)}^2+\dots +{\left(\frac{m}{2}+\left(\frac{m}{2}-1\right)\right)}^2\right]+4n{\left(\frac{m}{2}\right)}^2\\ & =\left(4n+1\right){\left(\frac{m}{2}\right)}^2+2n\left[{\left(\frac{m}{2}+1\right)}^2+{\left(\frac{m}{2}+2\right)}^2+\dots +{\left(\frac{m}{2}+\left(\frac{m}{2}-1\right)\right)}^2\right],\end{array}$$

$$M_1\left(D_m^n\right)=\left(4n+1\right){\left(\frac{m}{2}\right)}^2+2n{{\displaystyle \sum }}_{j=1}^{\frac{m-2}{2}}{\left(\frac{m}{2}+j\right)}^2.$$

Now, we compute the second Zagreb eccentricity index of the Dutch windmill graph.

In every cycle there must be two edges with the same eccentricity, therefore, in $n$ copies of cycle, there are $2n$ edges with the same eccentricity. Since each cycle has even, $m$, number of edges, so there are a total $m/2$ pairs of edges in each cycle whose endpoint eccentricities differ by one. Let $z=z_0$.

$$\begin{array}{ll}{M}_2\left(D_m^n\right)& ={{\displaystyle \sum }}_{i=1}^{\frac{m}{2}-1}\epsilon \left(z_i\right)\epsilon \left(z_{i+1}\right)\\ & =\left[2n\left\{\left(\frac{m}{2}+0\right)\times \left(\frac{m}{2}+1\right)\right\}+2n\left\{\left(\frac{m}{2}+1\right)\times \left(\lceil \frac{m}{2}\rceil +2\right)\right\}+\dots +2n\left\{\left(\frac{m}{2}+\frac{m}{2}-1\right)\times \left(\frac{m}{2}+\frac{m}{2}\right)\right\}\right]\\ & =2n\left[\left\{\left(\frac{m}{2}+0\right)\times \left(\frac{m}{2}+1\right)\right\}+\left\{\left(\frac{m}{2}+1\right)\times \left(\lceil \frac{m}{2}\rceil +2\right)\right\}+\dots +\left\{\left(\frac{m}{2}+\frac{m}{2}-1\right)\times \left(\frac{m}{2}+\frac{m}{2}\right)\right\}\right]\\ & =2n{{\displaystyle \sum }}_{j=0}^{\frac{m}{2}-1}\left\{\left(\frac{m}{2}+j\right)\times \left(\left(\frac{m}{2}+1\right)+j\right)\right\}\\ & =2n{{\displaystyle \sum }}_{j=0}^{\frac{m}{2}-1}\left\{\left(\frac{m}{2}+j\right)\times \left(\left(\frac{m}{2}+j\right)+1\right)\right\}\end{array}$$

$$M_2\left(D_m^n\right)=2n{{\displaystyle \sum }}_{j=0}^{\frac{m-2}{2}}\left\{{\left(\frac{m}{2}+j\right)}^2+\left(\frac{m}{2}+j\right)\right\}.$$

Theorem 3. 

The connective eccentricity index of$C_n\left(a_1,a_2,\dots ,a_m\right)$is given by

$$C^{\xi }\left\{C_n\left(a_1,a_2,\dots ,a_m\right)\right\}=\{\begin{array}{ll}n\frac{2m}{\lfloor \frac{n}{2}\rfloor };& if n is odd\\ 4m;& if n is even\end{array}.$$

The eccentric connectivity index of$C_n\left(a_1,a_2,\dots ,a_m\right)$is given by

$${\xi }^c\left\{C_n\left(a_1,a_2,\dots ,a_m\right)\right\}=\{\begin{array}{ll}\left(2mn\right)\lfloor \frac{n}{2}\rfloor ;& if n is odd\\ n^{2}m;& if n is even\end{array}.$$

Proof. 

Let $C_n\left(a_1,a_2,\dots ,a_m\right)$ be a circulant graph with vertex set $\left(u_1,u_2,\dots ,u_n\right)$ and the edge set $\left\{u_i{u}_{i+a_j};1\le j\le n,1\le j\le m\right\}$. The degree and eccentricity of the vertices of circulant graph are given by $d_{C_n}=2m$. □

Case 1:$n$ is odd: Eccentricity of all the vertices of circulant graph is ${\epsilon }_{C_n}=\lfloor \frac{n}{2}\rfloor$, respectively, where $m$ is number of generators.

The connective eccentricity index of $C_n\left(a_1,a_2,\dots ,a_m\right)$ is given by using Equation (1) as

$$\begin{array}{ll}{\xi }^c\left(C_n\right)& ={{\displaystyle \sum }}_{i=1}^n{d}_{C_n}(u_i){\epsilon }_{C_n}\left(u_i\right)\\ & ={{\displaystyle \sum }}_{i=1}^{n}2m\lfloor \frac{n}{2}\rfloor \\ & =n\left(2m\right)\lfloor \frac{n}{2}\rfloor \end{array}$$

$${\xi }^c\left(C_n\right)=\left(2nm\right)\lfloor \frac{n}{2}\rfloor .$$

Now the eccentric connective index of $C_n\left(a_1,a_2,\dots ,a_m\right)$ is given by

$$\begin{array}{ll}{C}^{\xi }\left(C_n\right)& ={{\displaystyle \sum }}_{i=1}^n\frac{d_{C_n}\left(u_i\right)}{{\epsilon }_{C_n}\left(u_i\right)}\\ & ={{\displaystyle \sum }}_{i=1}^n\frac{2m}{\lfloor \frac{n}{2}\rfloor }\end{array}$$

$$C^{\xi }\left(C_n\right)=n\frac{2m}{\lfloor \frac{n}{2}\rfloor }.$$

Case 2:$n$ is even: Eccentricity of all the vertices of circulant graph is ${\epsilon }_{C_n}=\frac{n}{2}$, respectively.

The connective eccentricity index of $C_n\left(a_1,a_2,\dots ,a_m\right)$ is given by

$$\begin{array}{ll}{\xi }^c\left(C_n\right)& ={{\displaystyle \sum }}_{i=1}^n{d}_{C_n}(u_i){\epsilon }_{C_n}\left(u_i\right)\\ & ={{\displaystyle \sum }}_{i=1}^n\left(2m\right)(\frac{n}{2})\\ & =n\left(2m\right)\frac{n}{2}\end{array}$$

$${\xi }^c\left(C_n\right)=n^{2}m.$$

Now, the eccentric connective index of $C_n\left(a_1,a_2,\dots ,a_m\right)$ is given by

$$\begin{array}{ll}{C}^{\xi }\left(C_n\right)& ={{\displaystyle \sum }}_{i=1}^n\frac{d_{C_n}\left(u_i\right)}{{\epsilon }_{C_n}\left(u_i\right)}\\ & ={{\displaystyle \sum }}_{i=1}^n\frac{2m}{\frac{n}{2}}\\ & =n\frac{4m}{n}\end{array}$$

$$C^{\xi }\left(C_n\right)=4m.$$

Theorem 4. 

The first Zagreb eccentricity index of$C_n\left(a_1,a_2,\dots ,a_m\right)$is given by

$$M_1\left(C_n\right)=\{\begin{array}{ll}n{\lfloor \frac{n}{2}\rfloor }^2;& if n is odd\\ \frac{n^3}{4};& if n is even\end{array}.$$

The second Zagreb eccentricity index of$C_n\left(a_1,a_2,\dots ,a_m\right)$is given by

$$M_2\left(C_n\right)=\{\begin{array}{ll}n{\lfloor \frac{n}{2}\rfloor }^2;& if n is odd \\ \frac{n^3}{4};& if n is even\end{array}.$$

Proof. 

Let $C_n\left(a_1,a_2,\dots ,a_m\right)$ be the circulant graph with vertex set $\left\{u_1,u_2,\dots ,u_n\right\}$ and the edge set $\left\{u_i{u}_{i+a_j};1\le j\le n,1\le j\le m\right\}$. □

Case 1:$n$ is odd: The eccentricity of the vertices of circulant graph is ${\epsilon }_{C_n}=\lfloor \frac{n}{2}\rfloor$, where $m$ is the number of generators. The first Zagreb eccentricity index of $C_n\left(a_1,a_2,\dots ,a_m\right)$ is given by

$$\begin{array}{ll}{M}_1\left(C_n\right)& ={{\displaystyle \sum }}_{i=1}^n{{\epsilon }_{C_n}}^2\left(u_i\right)\\ & ={{\displaystyle \sum }}_{i=1}^n{\left(\lfloor \frac{n}{2}\rfloor \right)}^2\\ & =n{\left(\lfloor \frac{n}{2}\rfloor \right)}^2\end{array}$$

$$M_1\left(C_n\right)=n{\lfloor \frac{n}{2}\rfloor }^2.$$

The second Zagreb eccentricity index of $C_n\left(a_1,a_2,\dots ,a_n\right)$ is given as

$$\begin{array}{ll}{M}_2\left(C_n\right)& ={\displaystyle \sum }_{uv\in E\left(G\right)}\epsilon \left(u\right)\epsilon \left(v\right)\\ & ={\displaystyle \sum }_{uv\in E\left(G\right)}\left(\lfloor \frac{n}{2}\rfloor \right)\left(\lfloor \frac{n}{2}\rfloor \right)\\ & =n{\left(\lfloor \frac{n}{2}\rfloor \right)}^2\end{array}$$

$$M_2(C_n)=n{\lfloor \frac{n}{2}\rfloor }^2.$$

Case 2:$n$ is even. The eccentricity of the vertices of circulant graph is ${\epsilon }_{C_n}=\frac{n}{2}$, where $m$ is the number of generators. The first Zagreb index of $C_n\left(a_1,a_2,\dots ,a_m\right)$, as defined in Equation (3), is given as

$$\begin{array}{ll}{M}_1\left(C_n\right)& ={{\displaystyle \sum }}_{i=1}^n{{\epsilon }_{C_n}}^2\left(u_i\right)\\ & ={{\displaystyle \sum }}_{i=1}^n{\left(\frac{n}{2}\right)}^2\\ & =n{\left(\frac{n}{2}\right)}^2\end{array}$$

$$M_1\left(C_n\right)=\frac{n^3}{4}.$$

The second Zagreb eccentricity index of $C_n\left(a_1,a_2,\dots ,a_n\right)$ is given by

$$\begin{array}{ll}{M}_2\left(C_n\right)& ={\displaystyle \sum }_{uv\in E\left(G\right)}\epsilon \left(u\right)\epsilon \left(v\right)\\ & ={\displaystyle \sum }_{uv\in E\left(G\right)}\left(\frac{n}{2}\right)\left(\frac{n}{2}\right)\\ & ={{\displaystyle \sum }}_{i=1}^n{\left(\frac{n}{2}\right)}^2\\ & =n{\left(\frac{n}{2}\right)}^2\end{array}$$

$$M_2\left(C_n\right)=\frac{n^3}{4}.$$

3. Conclusions

We analyzed the topological indices of chemical graphs which are being widely used in QSAR studies. These indices are correlated to the underlying physical and chemical properties of compounds. Dutch windmill graph and circulant graph are discussed in this paper in terms of their distance and degree-based invariants. Connective eccentricity, eccentric connectivity, first Zagreb index, and second Zagreb index were computed for these graphs. These results can be greatly helpful in QSAR/QSPR studies for chemical structures corresponding to the graphs investigated in the study.