Abstract
Atoms and molecules in highly excited (Rydberg) states have a number of unique characteristics due to the strong dependence of their properties on the values of principal quantum numbers. The paper discusses the results of an investigation of collisional Rydberg complexes specific features, resulting in the development of dynamic chaos and the accompanying diffusion autoionization processes. It is shown (experiment and theory) that, in subthermal low energies, the global chaotic regime that evolved in quasimolecular systems leads to significant changes in the Rydberg gases radiation/ionization kinetics. The effect of Förster resonance on the width of the fluorescence spectra and stochastic ionization processes in Rydberg systems is also discussed.
1. Introduction
The interest in the research of physical processes involving highly excited (Rydberg) atomic systems is caused by their significance in the fundamental issues of science (due to the combination of quantum and classical properties) [1,2] and the prospects of their wide implementations in modern applied knowledge-intensive technologies (see, e.g., [3]). The main feature of Rydberg particles is their extremely big size ~n2 (where n is the principal quantum number), which results in huge dipole moments. This opens up unique opportunities for both the controlled and addressed management of quantum states by external electromagnetic fields [4], and for the creation of long-lived coherent (entangled) states in cold Rydberg media due to the long range dipole-dipole interaction between the medium particles [5,6]. Therefore, the cold Rydberg atoms are considered to be promising objects for solving the problems of quantum information. With their help, the physical carriers of quantum bits [7] can be realized with the simultaneous execution of the basic quantum operations [8].
Another class of interesting phenomena in dense gaseous media is associated with the collision and radiation kinetics of Rydberg electrons when they are scattered on cold atoms in the ground states, which can lead to the formation of exotic molecules [9,10] and specific chemical reactions [11]. Under certain conditions, cold Rydberg media quickly evolve into cold neutral plasma, which is accompanied by the formation of free electrons and the development of various phenomena, such as spontaneous plasma expansion, recombination of Rydberg atoms, plasma instabilities, and the propagation of collective waves [12]. The physics of ultra-low-temperature plasma should take into account not only traditional ionization and recombination processes involving electrons and ions [13,14], but also the formation of charged particles, which are both due to the ionization of Rydberg atoms by thermal radiation [12,15] and as a result of the Penning autoionization of Rydberg atomic pairs [16,17].
Recombination processes leading to populating highly excited states are the sources of Rydberg atoms/molecules formation in stellar atmospheres of late spectral types, interstellar nebulae, and other space objects, including our solar system (see “Rydberg atoms in astrophysics” by Dalgarno in [1,18]). Rydberg particles play a fundamental role in the Earth’s lower ionosphere, primarily affecting the propagation of satellite radio signals of the global positioning system (GPS) or radar stations [19]. Besides, they are a source of super background incoherent radiation in the decimeter and infrared ranges.
An important feature of the Rydberg systems is related to the “Coulomb” condensation of their quantum states near the energy continuum (). Due to strong Stark/Zeeman effects, interaction with electromagnetic fields can lead to multiple quasi-crossings and the mixing of Rydberg electron sublevels with different orbital (l), azimuthal (m), and principal (n) quantum numbers. This allows for the selectively excited initial state to begin a chaotic motion across a dense grid of Rydberg levels with the subsequent transition to the energy continuum. Such uncontrolled drift of a highly excited electron, leading to diffusion ionization, can be observed for single Rydberg atoms under the influence of external fields [20,21,22], as well as for an ensemble of Rydberg atoms with strong long-range dipole-dipole interaction [23]. In molecular or quasi-molecular collisional Rydberg complexes, the diffusion migration of the initial excitation causes both the dissociation of molecules [24] and the formation of molecular/atomic ions [25]. These diffusion processes, as induced by either external controlling or internal molecular fields, lead to the development of instability with the loss of initial coherence in the ensemble of Rydberg particles. The analysis of the dynamics of quantum complexes with a complex branched quasi-crossing structure of energy surfaces is extremely challenging within the framework of traditional quantum mechanical methods of calculation. The purpose of our work is to describe an alternative, semiclassical approach that is based on the concept of dynamic chaos evolution in Hamiltonian systems [26,27,28]. Another set of questions under consideration concerns the features of the radiation kinetics of Rydberg atoms in the vicinity of the Förster resonance. The latter is used as a controlling mechanism for varying the long-range interatomic interaction [29] and it has numerous applications in applied problems of Rydberg media. Noteworthy, the peculiarities of the radiative rate constants, as discussed below, are of potential interest for the interpretation of spectroscopic data, as obtained from fluorescence spectra of cold media of astrophysical relevance, such as different modifications of cold white dwarfs [30] or neutral sodium clouds near Jovian moon Io.
2. Kinetics of Radiative Transitions for Highly Excited Atoms
2.1. Spectral Parameters of an Excited Atom
We note that the atomic system of units is used, unless otherwise stated.
Knowledge of the probabilities of optical transitions lies at the basis of any analysis of processes involving excited atoms. Despite the fact that literature on this subject today has many dozens of works, the topic has not lost its actuality. As a rule, the existing theoretical methods for calculating the lifetime , or the radiation width of the quantum state of an excited atom, leads to better agreement with the experiment in comparison with the probability of an individual optical transition. According to the review work from 1991 [31], even then, the discrepancy between the experimental and theoretical values of the radiation width for excited states of alkali metal atoms did not exceed 10%. Such accuracy was sufficient to use these data in an analysis of collisional processes in optically thin gas media and low-temperature plasmas. In the framework of the semiclassical approximation of quantum mechanics [32,33], the principal quantum number n determines in the first approximation the parameters of the orbit of the valence electron of the hydrogen atom and its energy. The orbital quantum number l determines the magnitude of the orbital angular momentum (Langer’s correction [33]), and also the degree of perturbation of the valence electron in the field of the atomic residue; the field of which may differ from the Coulomb. The corresponding “perturbed” value of energy is found, introducing the concepts of a quantum defect and an effective quantum number : .
The experimental data on the lifetimes , as known today, can be described by a power law [31]:
where and are dimensionless constants for a given -series [31] and c is the speed of light. Accordingly, for example, for hydrogen and alkali atoms [31,34]. At the primary selective excitation of Rydberg atoms (with a fixed value ) and an increase of the concentration of normal atoms, the formation of a block of states with values of the quantum number l from 0 to n − 1 and with an average lifetime ~n5, becomes possible due to intense atom-atom interactions. In this case, the principal fraction of the population of excited states is from those with large l values. In the case of a complete l mixing of the Hydrogen atom Rydberg states, the expression for the probabilities of radiative decay of the block of n-states is written in the form [31,34]:
The current level of fundamental research and their engineering applications requires reliable data on the lifetimes of excited atoms. Until recently, such information for highly excited atoms in modern databases, as a rule, was absent. Importantly, Rydberg’s lifetimes are highly dependent on ambient temperatures [15], so the correct measurement of their natural widths remains a challenge [35]. Concerning this, an extrapolation scheme for estimating the lifetimes of Rydberg states, tested while using the example of alkali metal atoms, has been developed [31].
2.2. Blocking of the Spectral Transitions. Double Stark (Förster) Resonance
One should have in mind that the term “hydrogen-like” atom, which is often used in the literature for Rydberg states, does not guarantee the complete coincidence of the structure of the energy levels of the excited atom with the energy structure of the hydrogen atom. Thus, for a “hydrogen-like” alkali metal atom with a standard [L-S] bond between the moments [33], the level may be located between the and states of the excited atom (see Figure 1), which does not correspond to the case of the hydrogen atom [33]. In the case when the level is located exactly in the middle between the and states, the Stark two-photon resonance condition is realized, otherwise the Förster resonance (hereinafter FR) [29] achieved in practice by an electric field of the order of 5 Vcm−1 [36]. The criterion for the emergence of the FR is simply formulated in terms of a quantum defect of atomic series:
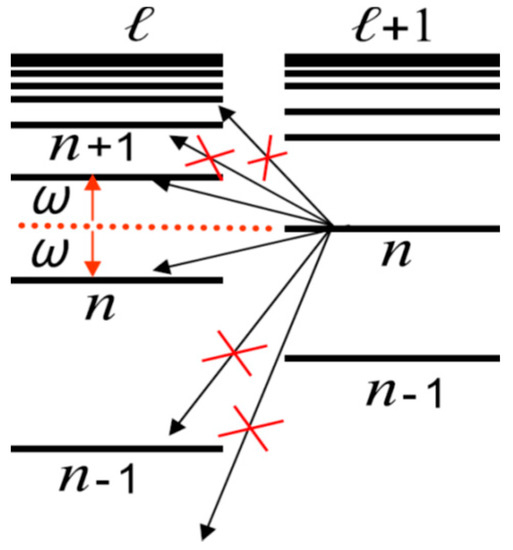
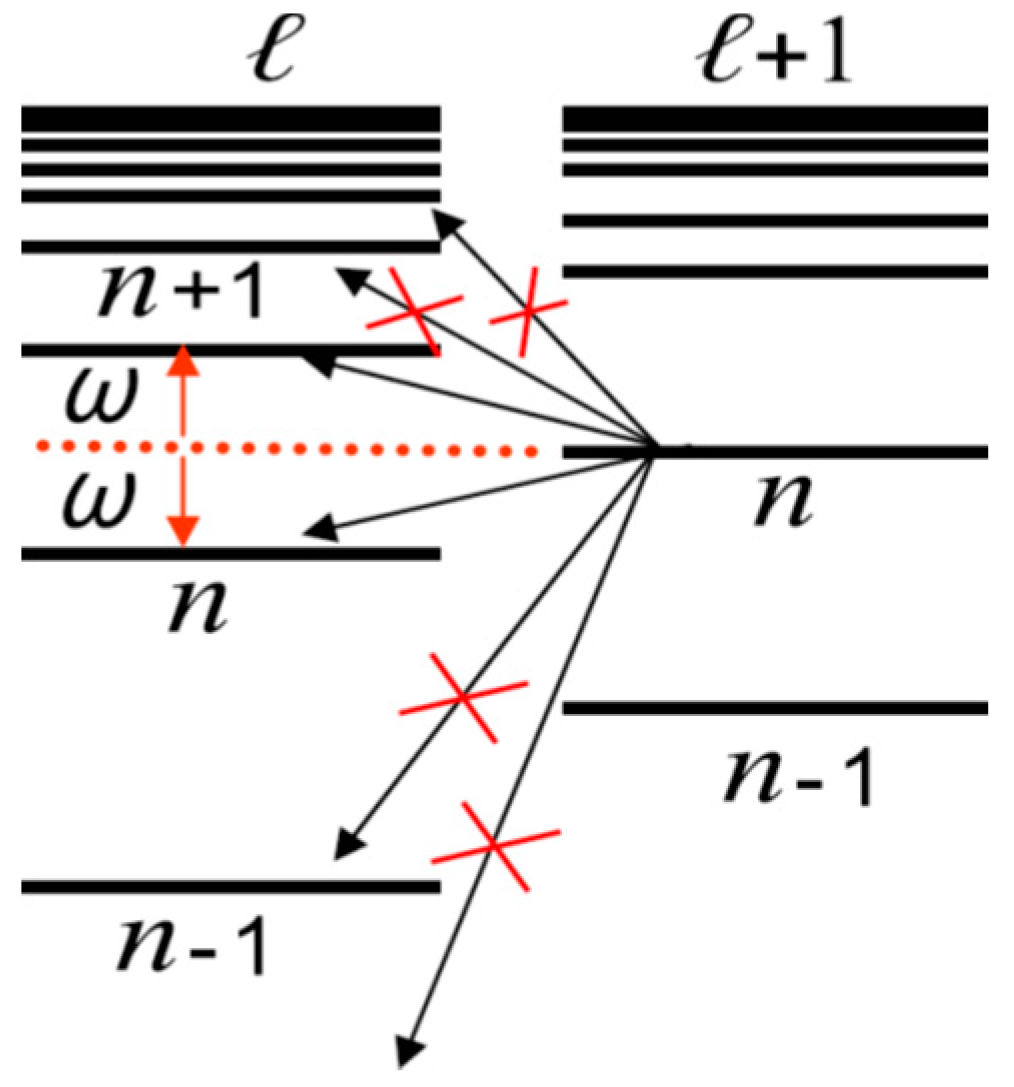
Figure 1.
Scheme of Rydberg atomic levels, illustrating the effect of the double Stark (Förster) resonance in {l + 1, l} atomic series on blocking of the “long” transitions between remote states.
The simplest example is a three-dimensional oscillator with a frequency , for which the energies of the levels [33]
for all -series satisfies FR. The unique frequency of oscillator emission is its natural frequency . Therefore, according to the Bohr-Heisenberg correspondence principle [32,37,38], the dipole matrix elements of the spectral transitions are nonzero only for “short” transitions between adjacent quantum states (see, for instance, Equations (2) and (9) in review work [39]). It means that, under conditions of FR, one should expect a significant weakening of the optical oscillator strengths for the “long” transitions (see Figure 1). This situation is most closely realized for the sodium atom for the s- and p-series (see Table 1), which causes the anomalously small radiation widths of the Rydberg states of sodium p-series, whose value is ~ 5 times smaller than the widths of the other alkali atoms (see Table 1, last row where are presented in) at the same energies of the corresponding states [31].

Table 1.
Qantum defect for s-, p-series [32] along with and the factor from Equation (1).
Thus, the Förster resonance is a unique phenomenon, in which anomalies in the spectral characteristics of excited atomic systems should be expected. Accordingly, in Ref. [36], under the conditions of the FR, the processes of blocking microwave transitions between Rydberg levels of rubidium in (A** + A) quasimolecular complex were investigated (experiment). From the academic point of view, the RF influence on the spectra of the excited atoms is considered in [40] within the framework of a model one-electron atom with the Sommerfeld potential [41]
where is the distance of the valence electron to the center of the atomic core and is a parameter of the model. Sommerfeld introduced a potential of such a type in describing relativistic corrections to the theory of a hydrogen atom. An important particularity of Sommerfeld’s potential is the possibility of an accurate analytical description of atomic parameters. For example, the energy of atomic states is given by the following expression
The quantity is called the effective orbital number and is directly connected with the quantity of the quantum defect: . The concept of an effective orbital number is widely used in calculating the probability of radiative transitions in alkali atoms [42]. It allows, in particular, for describing the FR between and atomic series [43] by selecting the parameter :
Accordingly, in the case of {p, s} series, = 2.81. For {d, p} series, = 11.8.
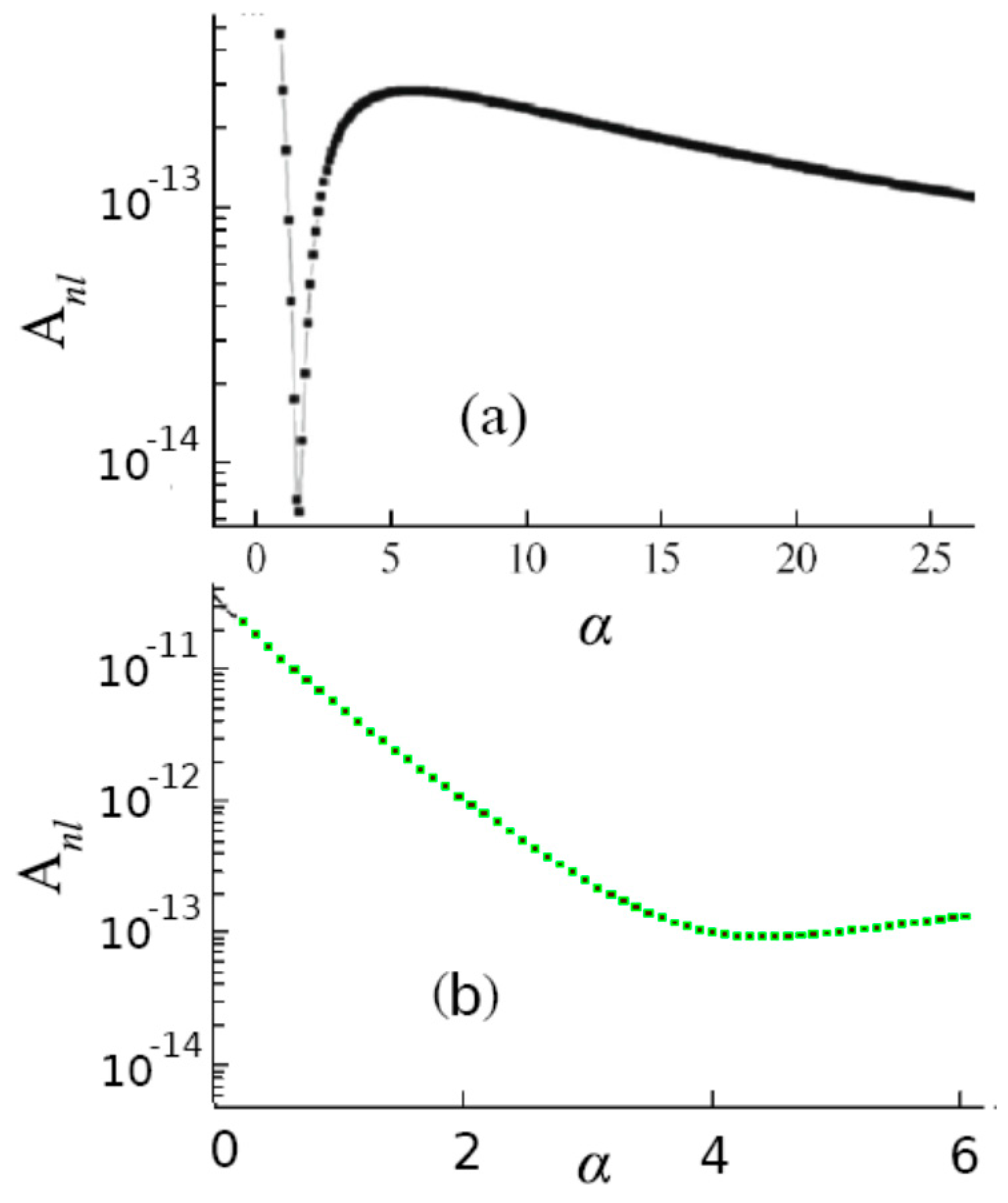
In Figure 2, the dependence of the radiative decay probability (Einstein’s coefficients) on the parameter for fixed 30s and 25p states of the model Sommerfeld atom is shown. It can be seen that, in the vicinity of the FR, the radiative lifetimes of the Rydberg states can vary significantly (by orders of magnitude). Similar effects manifest themselves, and in collision Rydberg complexes [25,43], which will be discussed in the following sections.
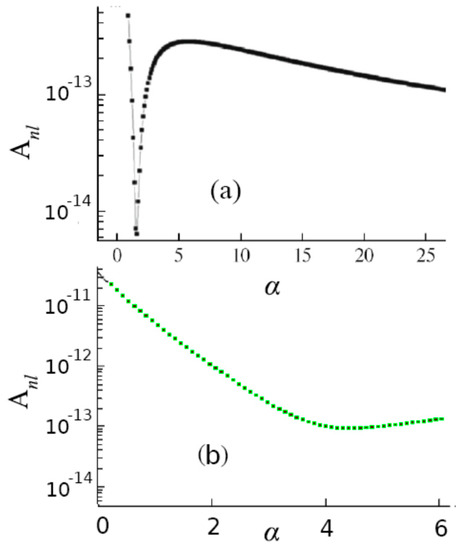
Figure 2.
(a) Natural width of Rydberg state of s-series (l = 0) with n = 30 as a function of parameter α of Sommerfeld’s atom. (b) The same for the state of p-series (l = 1) with n = 25. The Förster resonance corresponds to the value = 2.81.
3. Rydberg Quasimolecular Complex in the Framework of the Dipole Resonance Mechanism Model
A wide range of collisional processes
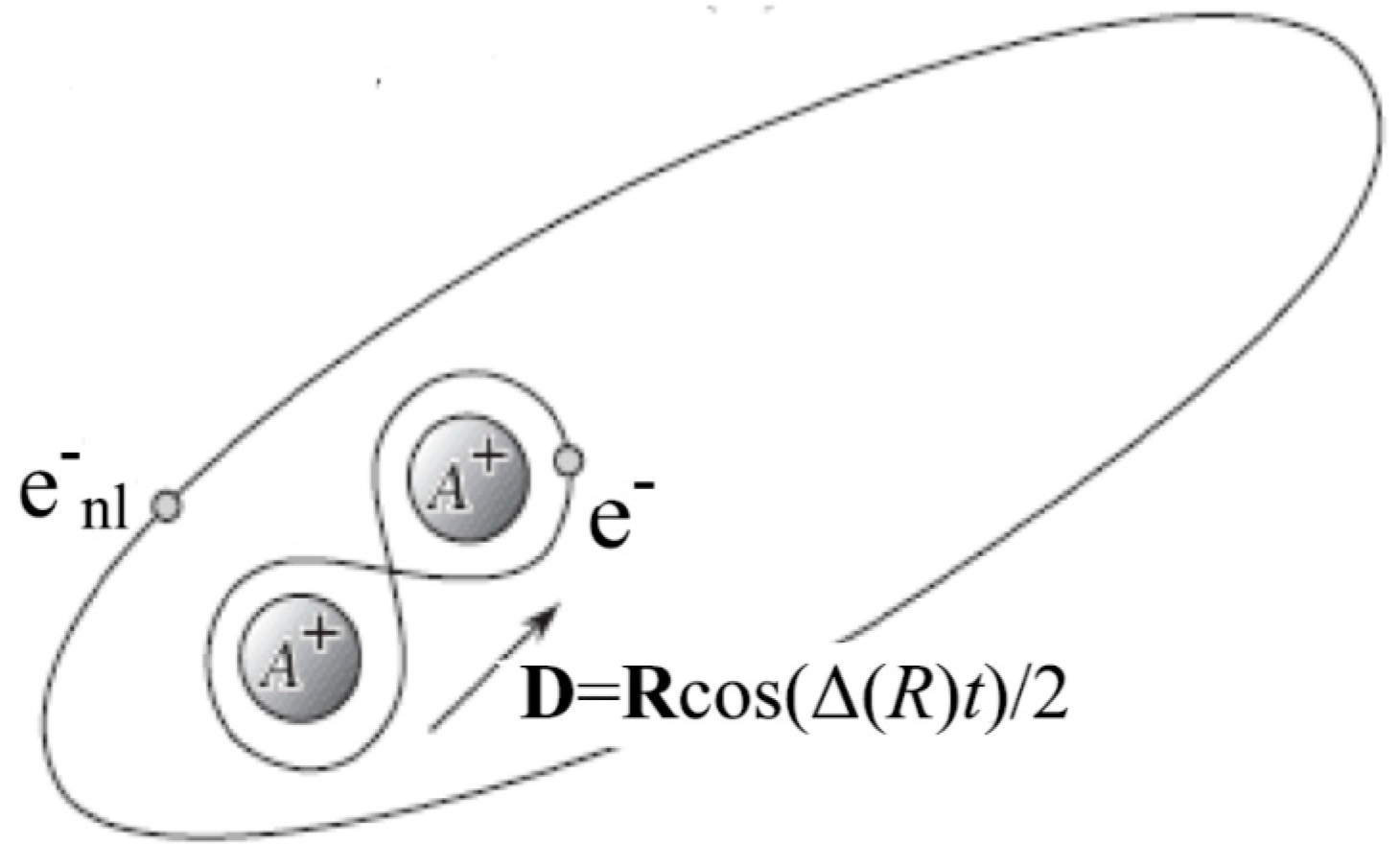
with the participation of Rydberg states pass through the phase of formation of the intermediate Rydberg complex . A fundamental contribution to “Rydberg Physics” was made by Fermi [44], who proposed considering the quasimolecular formation of as a structure that consists of two positively charged atomic cores , a quasi-free Rydberg electron (RE) in the Keplerian orbit, and the generalized valence electron (see Figure 3). The further development of the Fermi approach [45,46,47], the so-called dipole resonance ionization (DRI), has found wide application in the solution of a diverse range of problems (see, for example, the review [13]) from the broadening and shift of spectral lines to the balance of ionization processes in the solar photosphere (see, for example, [25,48]).
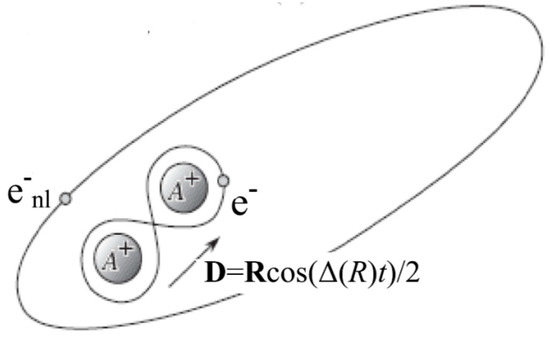
Figure 3.
Scheme of highly excited collisional complex where D—vector of the quasi-molecular ion dipole moment, R—vector of internuclear distance, —Rydberg electron, which is shared by the atomic cores of the quasi-molecular ion .
Within the framework of the DRI model, the probability of realization of various final channels for the collision (8) is determined by the internal dipole moment D of the quasimolecule . The moment D arises in the process of the charge exchange in the system (A + A+) and it induces an alternating electric field E(t), perturbing the motion of the RE on the Coulomb orbit (see Figure 3). With respect to the ionization channels for the DRI model, the following simplifying assumptions are accepted: (i) both the trajectory of the external electron and relative motion of the ion and unexcited atom A are semiclassical (ii) with the initial impact parameter ; and, (iii) ionization proceeds within a certain region with a given limiting distance between colliding atoms, which depends on the type of ion-atom residue and it is a parameter of the theory. The system is traditionally described in the adiabatic approximation using the appropriate potential curves of the Rydberg complex and the molecular ion .
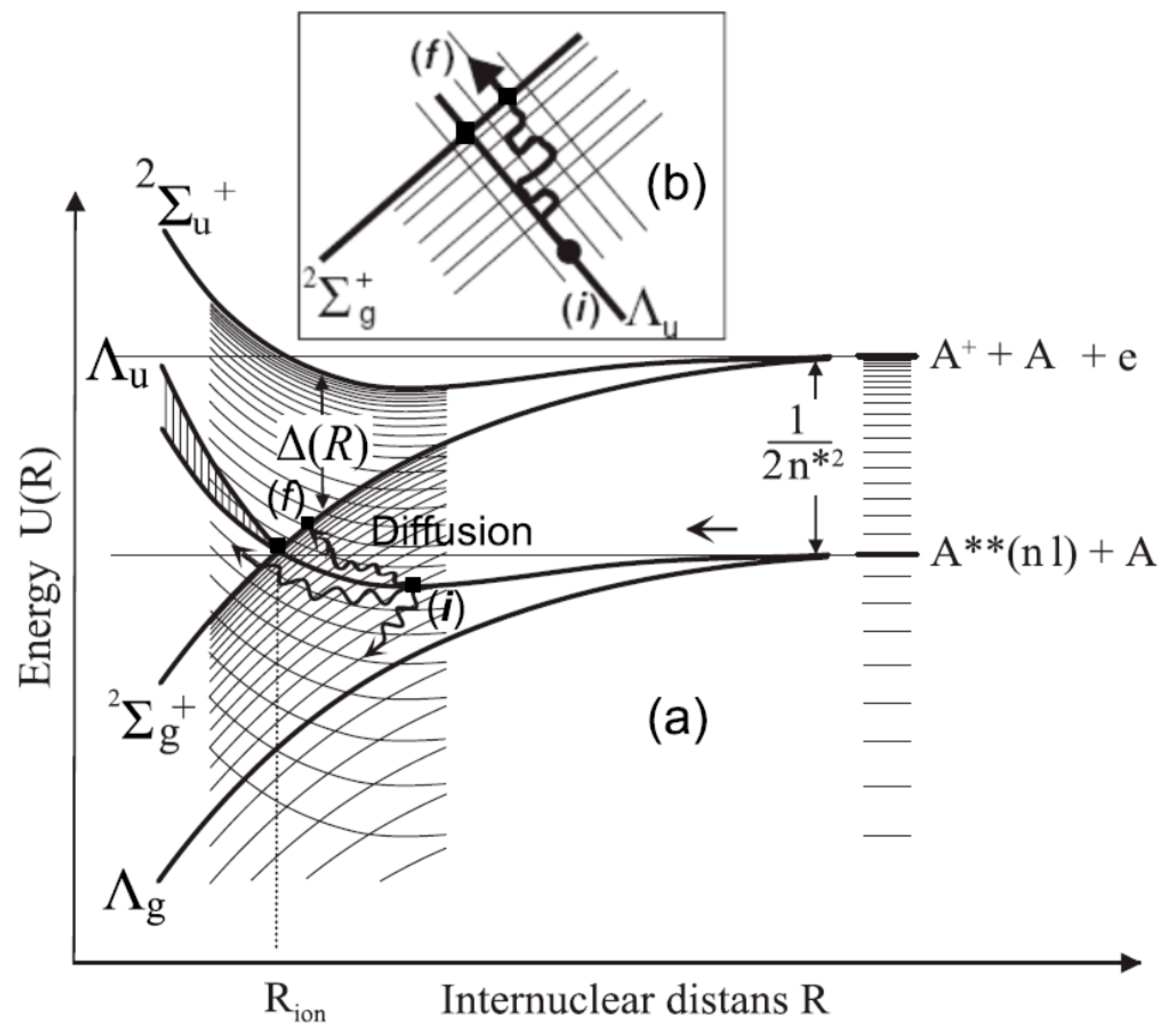
A graphical illustration of the ionization process is given in Figure 4. Under the assumptions made, the charge exchange between atomic residues A+ within the quasimolecule ion leads to the splitting (known as “exchange interaction” [45]) of its energy levels and it creates a time-dependent dipole moment D = , which oscillates with frequency , i.e., outside the complex an alternating quasimonochromatic microwave electric field E(t) is induced (see Figure 3). We note that, as shown in [49], the effect of the field E(t) on the Rydberg electron is equivalent to its perturbation by an external, spatially uniform field with the frequency , and with polarization along the interatomic axis R. Ionization occurs inside the range of distances (), where the exchange interaction ), starting from the threshold value , exceeds the binding energy of the electron and, thus, opens the autoionization channel of the quasimolecule complex . The probability of ionization per unit time, or the autoionization width of the process, is expressed in terms of the photoionization cross section .
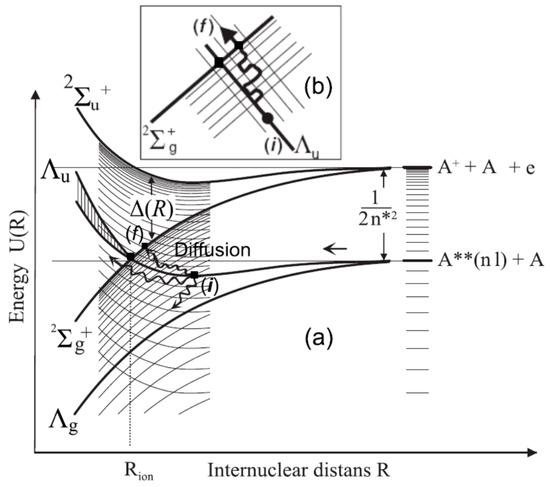
Figure 4.
Mechanism of collisional ionization involving a Rydberg atom and an atom in normal state.
The considered mechanism of dipole resonance, which played an important role in the development of the physics of thermal collisions of heavy particles, has a strictly deterministic character. However, as the main quantum number n of the Rydberg atom A**(nl) increases, when the initial energy curve (as shown in Figure 4) passes through a set of quasi-intersections with the neighboring energy curves during the collision, the trajectory instability of the Rydberg electron begins to appear in the simiclassical approximation. As a result, the random migration of excitation occurs along the grid of energy terms, which have the energy separation between them. In the framework of modern concepts of nonlinear mechanics [26], this makes it possible to introduce the idea of dynamic chaos [27], in chemi-ionization processes in thermal and subthermal collisions that involve RA.
4. Rydberg Collisional Complex in Approximation of Dynamic Chaos
At the end of the 19th century, in mathematics, Poincaré [27] introduced the notion of integrable and nonintegrable systems. In the first case, we meant a system with a “smooth” response to a small external perturbation and the conditions for the motion of individual particles are amenable to a direct description. However, in the general case, dynamical systems are not integrable, since perturbations that violate the total symmetry, as a rule, cannot be eliminated.
4.1. Nonlinear Dynamic Resonances and the Emergence of Deterministic Chaos
The main reason for the nontrivial influence of external periodic perturbations on the dynamic properties of integrable systems is associated with the appearance of nonlinear dynamic resonances [26], which, for large time intervals, leads to strong instability of the solutions obtained. In the framework of the KAM theory (Kolmogorov, Arnold, Moser) [27], it was shown that the presence of multiple resonances leads to the appearance of layers in the phase space of the considered ensembles of particles with diffusion motion that form a branched “stochastic web” [50]. To get into the element of the “stochastic web”, the excitation energy of the initial state should be as close as possible to one of the “resonant” values. For given perturbation parameters, a set of quantum states associated with initial dynamic nonlinear resonances can be indicated.
The quantitative consideration of the instability of the RE dynamics in a periodic external microwave electromagnetic field (where is the frequency) is based in the frame of the semiclassical approach on the Bohr–Heisenberg correspondence principles [32,37,38]. The largest perturbation by the field (i.e., strong mixing between populations of two levels with fixed and values of principal quantum numbers) should be expected in the case of -photon resonance (). For this, a “dynamic” coincidence of the “photon” energy with the energy distance between the levels is necessary (see Figure 5):
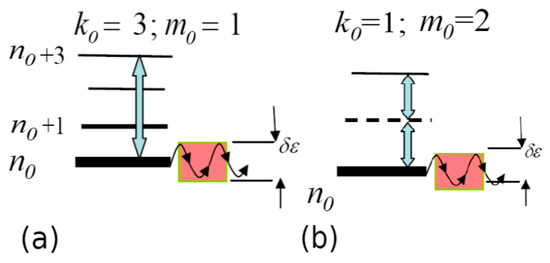
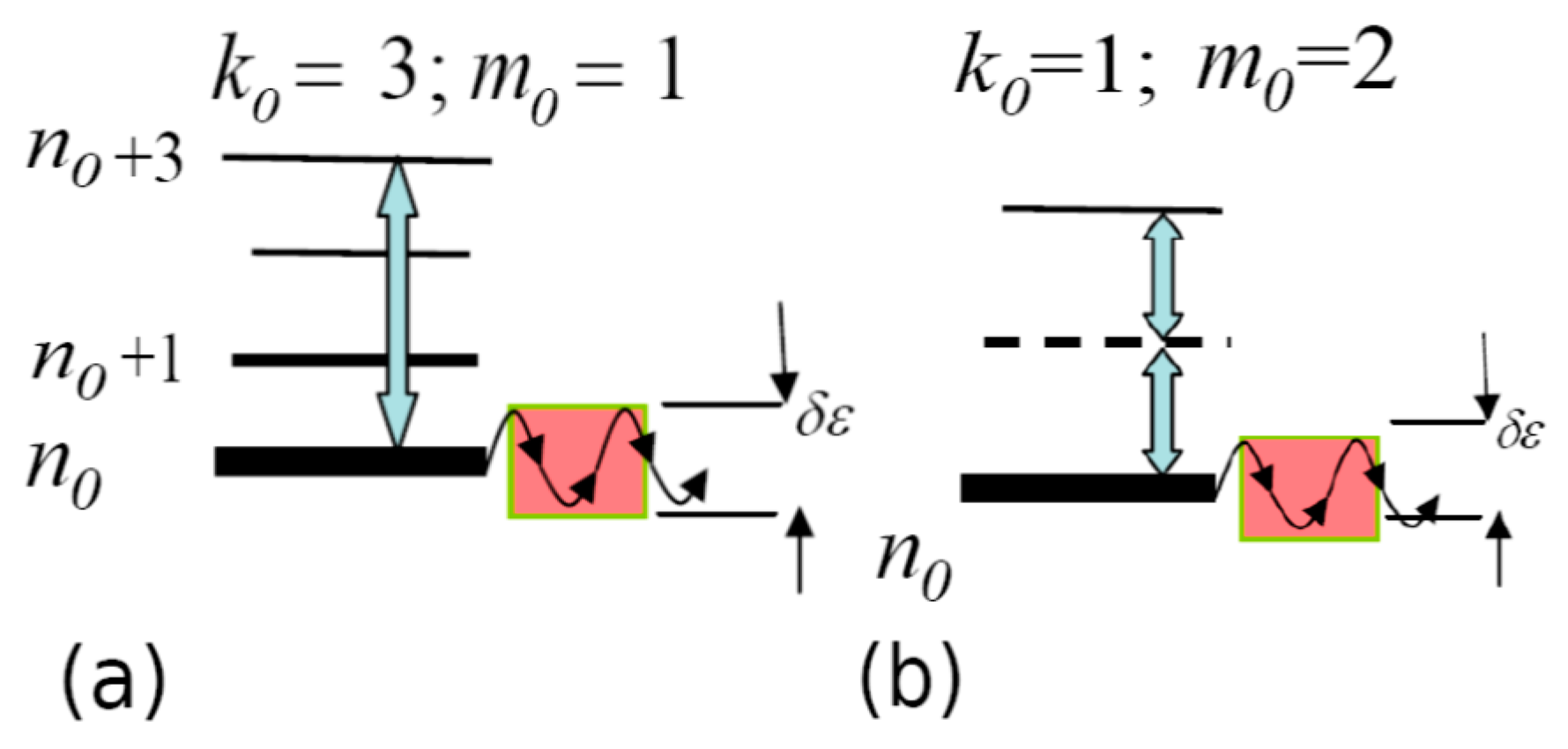
Figure 5.
Schematic of nonlinear dynamic resonances of different orders for the initial quantum state : (a) single-photon () and (b) double-photon () resonances.
Note that the energy density of the levels can be expressed through the frequency of the classical revolution of the electron along the Keplerian orbit [32]. The realization of relation (9) is termed in the literature (see, for example, [27]) as the manifestation of a dynamic nonlinear resonance of the order in the vicinity of the energy (see Figure 5). In this case, the electron energy begins to oscillate with respect to its unperturbed value with the amplitude [26,27]:
where is an amplitude of the -term at the frequency in the Fourier series of the field .
The width of the nonlinear resonance (the amplitude of the energy oscillations) is characterized by a root dependence on the amplitude of the perturbation. Out of resonance, the amplitude of the energy variations corresponds to a linear dependence on .
For linear systems , which formally lead to an arbitrarily large excitation of the electron () without transition into the stochastic regime. For a nonlinear system, the finiteness of the widths of nonlinear resonances causes the emergence of a global chaos regime according to the Chirikov criterion [27]
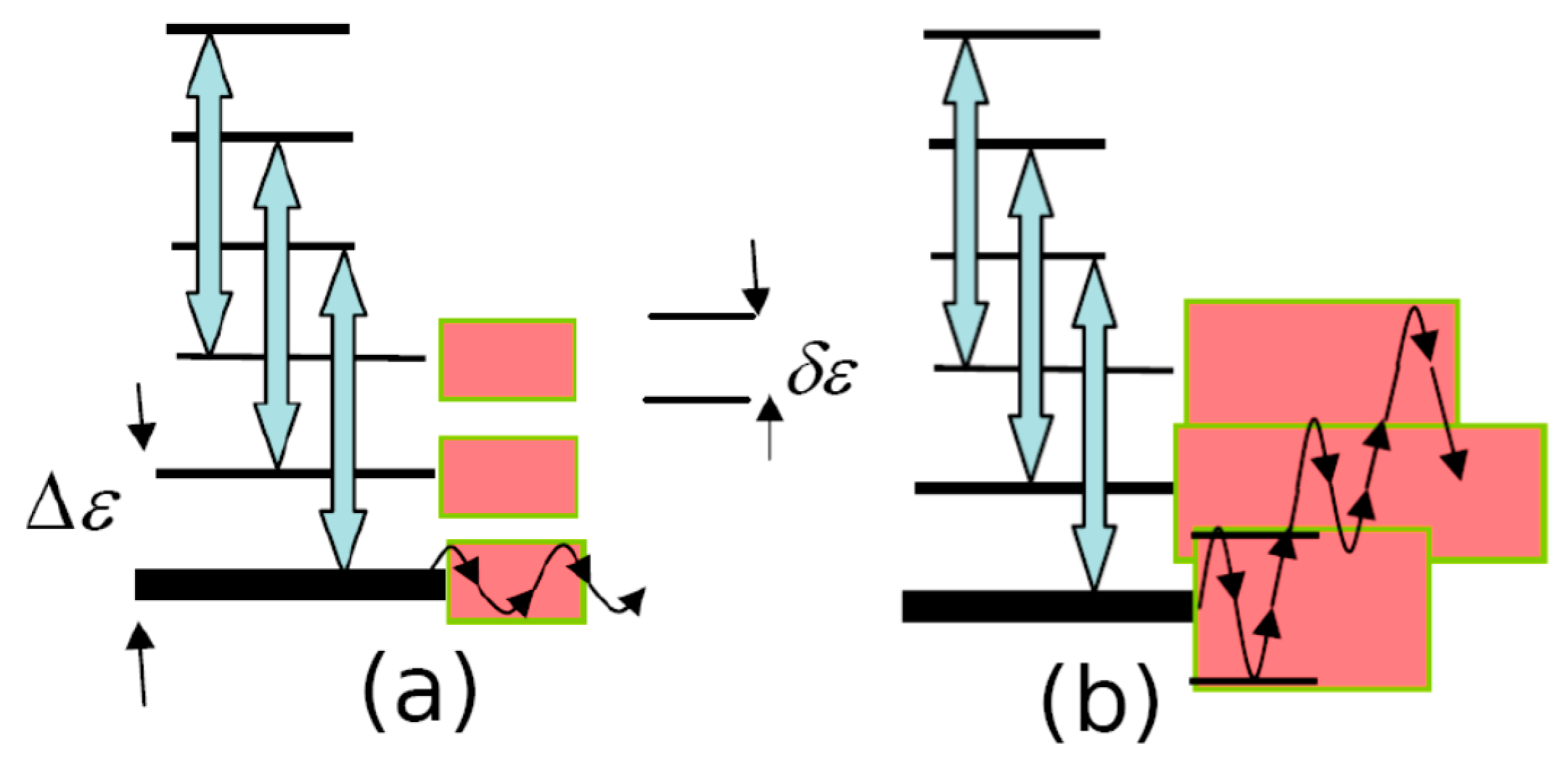
is satisfied, where is energy distance between neighboring levels. In the general case, for a particular system of quantum states of an excited atom, a whole set of quantum number values corresponding to different orders of dynamic resonances can be realized (see Figure 5). In the absence of the overlapping effect () between the widths of neighboring resonances, separate islands of instability can arise in the energy space. Figure 6a shows the dynamics of the change in the energy of the Rydberg electron for such a case. It can be seen that the “overlap” of resonances is still not enough for the onset of global chaos, and the energy of the initial level undergoes finite oscillations within the width (10). In the case of the overlapping of resonances (see Figure 6b), an electron can go far from its initial state up to the states of a continuous spectrum (ionization) during diffusion. This corresponds to the onset of a global chaos regime. Here, the essential point is the threshold of the intensity of external perturbation, leading to a global chaos regime, the criterion of which appears in the inequality (11).
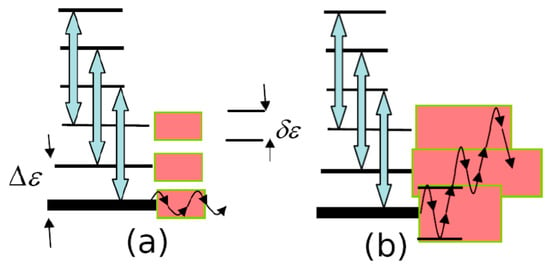
Figure 6.
(a) Occurrence of dynamic nonlinear resonances without their widths overlapping. (b) Complete overlapping of widths , corresponding to the formation of the global dynamic chaos. The initial states correspond to the lowest levels (bold lines).
4.2. The Standard Map (SM)
A nice illustration of the mechanisms that are involved in the transition to the global chaos is an example of the so-called standard mapping [26]. The standard map (SM), also known as the Chirikov–Taylor map [26], is one of the simplest models of chaos, in which the most characteristic and complex features of this problem are preserved. The corresponding model Hamiltonian, resulting in SM, has the form
and describes a rotor (an initial free atomic system with Hamiltonian ) periodically kicked by delta-impulses of some external force (a perturbation). Here, T = 2π is the corresponding period, while is a dimensionless parameter that characterizes the force amplitude. The rotor phase space variables “angle-action” (θ, I) are defined on a cylinder (−∞ < I < ∞; 0 < θ < 2π).
When considering the identity
we can rewrite the Hamiltonian (12) in the form
with . Expression (14) corresponds to the motion of the rotor in a periodic wave packet with an infinite number of harmonics. The amplitudes of the harmonics have the same magnitude, while their phases depend on the rotor angle .
To identify the range of applicability of the Chirikov criterion (11), consider the Hamiltonian equations of the perturbed rotor (14)
where is an angular frequency of the rotor having the angular momentum I. The nonlinear resonances (9) arise in the frame of the zero order of the perturbation theory when we use in (15) unperturbed temporal dependence for the angle variable: . The external force provides the strongest influence at the rotor dynamics if the series (15) contain stationary terms, i.e., the action variable I should satisfy . This relation corresponds to Equation (11) provided , which means that the nonlinear resonances under consideration have orders with and . Since , we may restrict ourselves to the case of the resonance values . In the vicinity of one of these resonances (), one may simplify series (15) by dropping all the oscillating terms. This transforms the system (15), (16) into
with and . System (17) is reduced to the nonlinear equation of the phase oscillation
Equations (17), (18) result in the oscillation of the action with the maximum amplitude ~ corresponding to the maximum distance between two separatrix branches that are generated in the phase space by Equation (7) [27]. We may assess the amplitudes of the energy oscillations of the resonance states that are depicted in Figure 6 as . The distance ΔI1,m between two adjacent resonance values I1,m is ΔI1,m = 1, which gives, for the corresponding energy separation, (see Figure 6). Chirikov criterion (11), hence, is reduced to the form
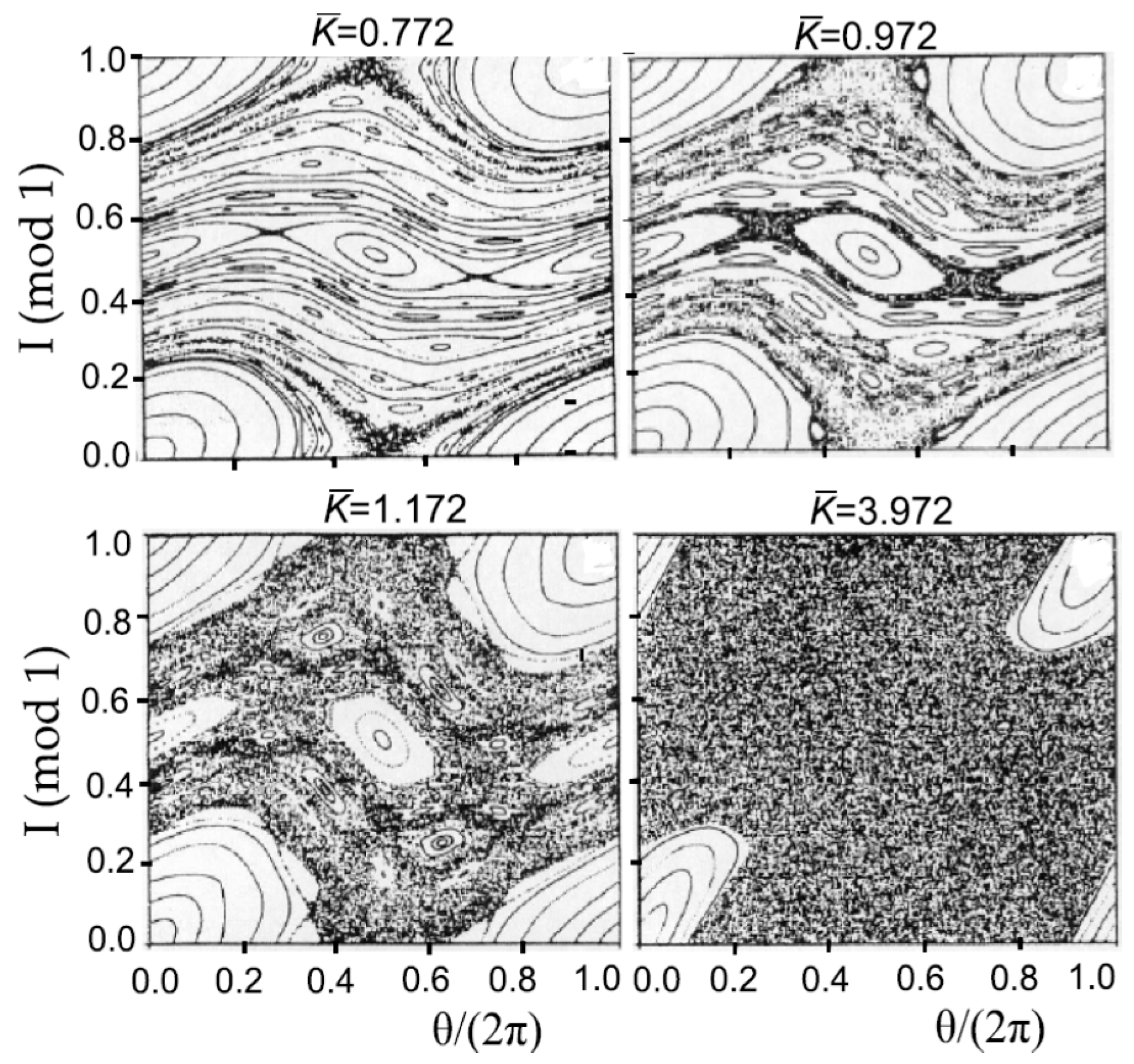
The characteristic important feature of the Hamiltonian (12) in the standard map model is the simultaneous overlapping of all resonance energies widths, as shown in Figure 6b. Figure 7 demonstrates the evolution of the rotor trajectories in the phase space for some parameter values. It is clearly seen that, initially (), small islands of instabilities (black areas) increase their size as the parameter increases, forming a “stochastic sea” for large amplitudes () of the external force.
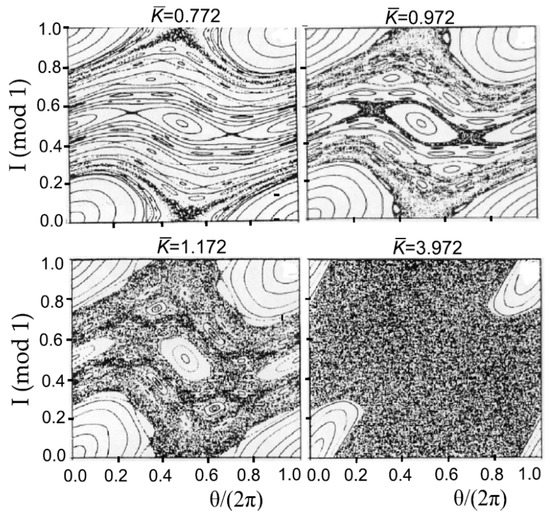
Figure 7.
Phase space trajectories of a kicked rotor with Hamiltonian (12) (adopted from [26]).
4.3. Conception of Diffusional Ionization
A significant contribution to the development of the theory of stochastization of quantized systems was made by the authors of Refs. [20,51], who considered the evolution of a bound Rydberg electron with its ionization in an external microwave field. The adaptation of the methods of work [51] in describing the development of dynamic chaos in the act of a single collision (8) is described in [49]. It is shown that, under the influence of a quasimonochromatic internal electric field E(t), nonlinear dynamic resonances can arise due to the coincidence of the overtone of the angular frequency of motion of RE on the Keplerian orbit with charge-exchange frequency of the internal electron (see Figure 3). As a result, the motion of the RE becomes unstable, and the RE evolution in the energy space takes the character of random walks along the quasi-intersecting “grid” of potential curves (see Figure 4), which opens the possibility of a kinetic description of the RE dynamics
In a series of subsequent works [22,52,53,54], data on the formation of dynamic nonlinear resonances with a transition to the stage of global chaos for isolated atoms in an external linearly polarized electric field were refined. We note that, the widths of the dynamic resonances (10), as well as the effects of stochastic dynamics, are directly related to the matrix elements of the perturbation operators. This conclusion is confirmed by the results of [52], in which the coefficients of the light-induced diffusion equation for a weakly bound electron in an external microwave field are explicitly expressed in terms of the dipole matrix elements for optical transitions. Since the implementation of the diffusion ionization requires finite time, to take into account the regime of dynamic chaos becomes important for slow collisions, which is for a range of thermal and subthermal energies. A transition to the ionization continuum due to a stochastic walk (see Figure 6b) can be described, with good accuracy, in terms of kinetic methods using the distribution function [22,27] in the bound state region of a Rydberg electron (). For calculations, it is more convenient to work with the distribution over the principal quantum number
using the relation . In this case, the time dependence of is found from the solution of a diffusion equation of the Fokker–Planck type [27]
with the initial condition that at the moment the excited electron is at the level , i.e., ( is the Dirac delta-function). To determine the evolution of , Equation (21a) must be supplemented by the following boundary conditions with respect to the quantum variable at the boundaries of the region of development of stochasticity :
where the quantity is determined from the Chirikov criterion (11), as [22]
The boundary of the continuum () is an absorbing wall for the diffusion flux where becomes zero. The amplitude of the microwave field determines the critical value of the principal quantum number below which the electron has regular motion, and the underlying states () refer to the deterministic region, since here the energy separation of the neighboring levels exceed the widths of the dynamic resonances (see Figure 6a). Thus, the values determine the position of the “reflecting wall”, on which the diffusion flux vanishes.
According to [22,51], the value of the diffusion coefficient is
From here, the average time, , required to reach the ionization limit by RE, which begins its diffusion motion with an initial binding energy , is determined as [24,49]
The distribution makes it possible to find parameters of the diffusion process, such as the average number of jumps from one level to another, experienced by the particle during its diffusion drift to the continuum of energies, the average lifetime of the excited atom, and the degree of its “survival” at a given time interval, i.e., knowledge of relatively simply makes it possible to obtain theoretical data for comparison with the values that were observed in the experiment.
4.4. Diffusional Ionization of Hydrogen Atom in External Field
More detailed information on the processes of diffusional ionization requires numerical calculations. Within the semiclassical approximation, numerical data are extracted from the study of the dynamics of motion (trajectories) of the RE. Analysis of time processes with the strong stochastization of trajectories requires the use of a stable numerical calculation scheme. The corresponding algorithm, which is based on the Floquet technique [55] and geometric integration methods [56,57], was proposed in [54] to find the parameters of atomic systems that were subjected to external periodic fields.
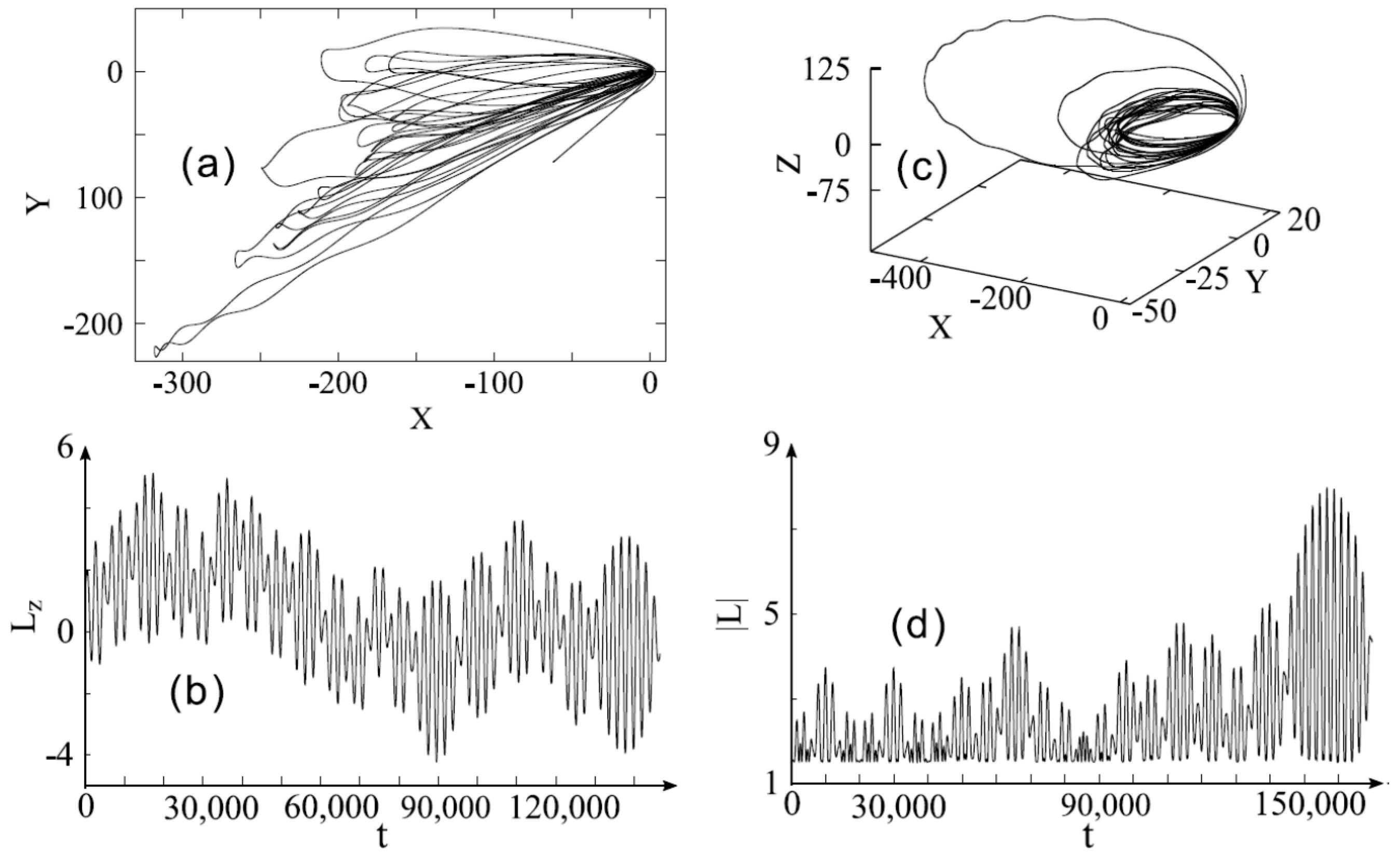
As an example, Figure 8 shows the trajectories of motion and shows the time dependence of the orbital angular momentum L in conditions of dynamic chaos development. We take the initial 10P () state of the hydrogen atom in the microwave field with frequency and amplitude , exceeding its threshold value [22]. Two characteristic initial configurations of the vector and the Runge-Lenz vector (directed along the semiaxis of the unperturbed Keplerian orbit [58]) were chosen, corresponding to the maximal changes in the modulus |L| for cases of two-dimensional () and three-dimensional () trajectories. Note that, according to the literature data, the range of values of n ≈ 10 corresponds to the range of strong interaction of the dipole field of the cluster with the Rydberg electron (see Figure 3). Also note that the results of numerical calculations in Figure 8 show a significant change of the orbital momentum L in the microwave field under the conditions of development of global chaos, which is in contrast to the main approximation of the authors [22,51], assuming the adiabatic invariance of L.
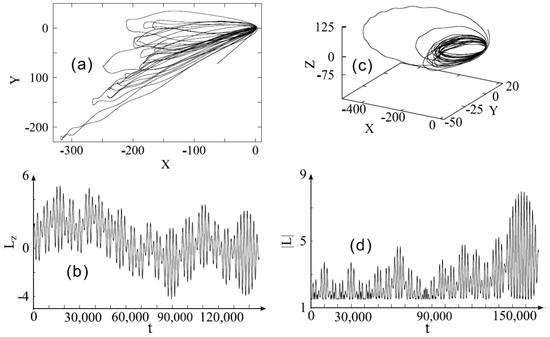
Figure 8.
Trajectories of Rydberg electron (frames a,c) and the evolution of its angular momentum L (frames b,d) for the 10P-state () of the hydrogen atom. For two-dimensional (2D) motion of an electron in the {X, Y}-plane (frame a), frame b shows the projection of the momentum L on the z-axis, orthogonal to the motion plane {X, Y}. For three-dimensional (3D) motion (frame c), frame d shows |L|.
4.5. Diffusional Ionization of the Rydberg Colisional Complex
The diffusion Equation (13) have a number of specific features with respect to the calculations of chaotic motion of RE in collisional molecular complexes due to the variation of both the amplitude and the frequency of the internal electric field as the (adiabatic) internuclear distance changes (see Figure 3 and Figure 4). At the same time, the RE ionization boundary shifts (see Figure 4), since it is determined by the potential curve . Figure 9 shows the boundaries of the stochasticity region for RE (see the discussion of Equation (21b)) in the case of collisions of hydrogen and atoms: the lower dashed curve (circles) corresponds to the lower “reflective wall” ( is found from Equation (22)), while the upper dotted curve (crosses) defines the position of the “absorbing wall” . For the Rydberg states, lying above , the exchange interaction exceeds their binding energies, so that the internal microwave field results in the fast photoionization of those states. The parameters of the problem are chosen in such a way that no ionization occurs when the RE () motion is regular (i.e., without any stochatization).
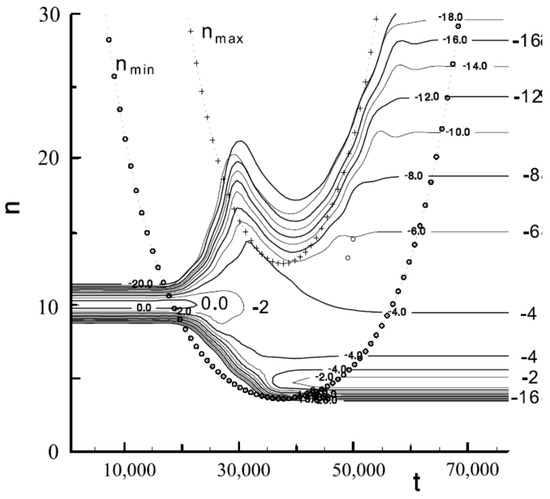
Figure 9.
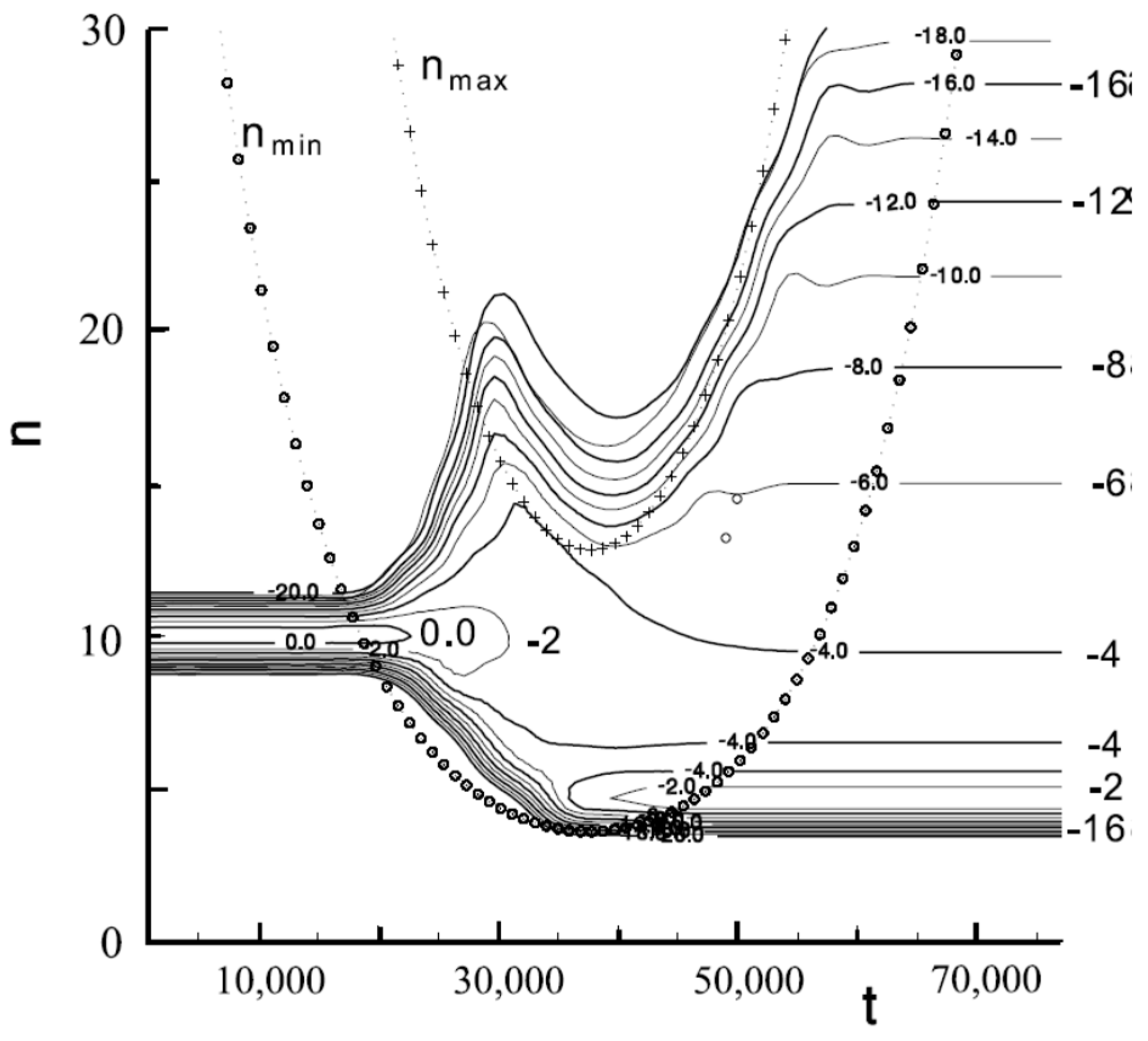
The time evolution of the distribution function of a Rydberg electron in a quasimolecular collisional complex with the impact parameter and collision energy a. u. = 600 K. The initial value .
Figure 9 also shows the results of calculating [47]; the parameters of RE diffusion evolution for a time-varying region of the phase space. The initial distribution, corresponding to the localization of the RE at the energy level with , was chosen as the narrow Gaussian distribution . The principal feature of the present is the realization of the RE diffusion along the energy levels in the act of a single collision. The solid lines in the figure give a map of levels —the values of the logarithm are plotted alongside the corresponding curves. The position of the minima of the boundary curves is determined by the turning point with the minimum approach of the nuclei. It is evident that, while the initial value is located lower than , i.e., lies in the regular motion region, there is no diffusion along the n axis. Diffusion begins to develop after the moment of entry of the initial value in the stochastic region (the region lying above the curve ). As a result of stochastic diffusion, the Rydberg electron has a finite probability of reaching the ionization boundary and passing to a continuum of energies through the photoionization channel. In this case, ionization is found as the probability of the electron leaving the region of bound states. The validity of such a model was verified on the quantitative level by the example of the chemi-ionization process involving Rydberg atoms of sodium [49].
4.6. Assotiative Ionization Rate Constants
The experimental methods existing in atomic and molecular physics make it possible to compare the ionization parameters that were calculated in the frame of stochastic dynamics with the results of direct measurements performed in atomic beams of different types [59]. Atomic/molecular beams have been widely implemented in practice as convenient sources of particles that are used for investigations in the physics of collisions [60], spectroscopy [61], and the analysis of the interaction of light and matter [62]. In recent decades, a new type of beams, known as “cold beams” [63], has been added to the two classical types of beams, i.e., diffusion [14,64] and supersonic [59] ones. Cold beams are extracted from magneto-optical traps and they have unique prospects for use in nanotechnology [65] due to their extremely narrow divergence angle.
An important parameter that characterizes the efficiency of ionization processes (8) is the rate constants . In experiments, rate constants are found from a measured number of registered charged particles. A theoretical treatment of
operates with the cross sections (v) and the distribution function f (v, T) over the relative (impact) velocity v = vc of colliding atoms of the same mass M:
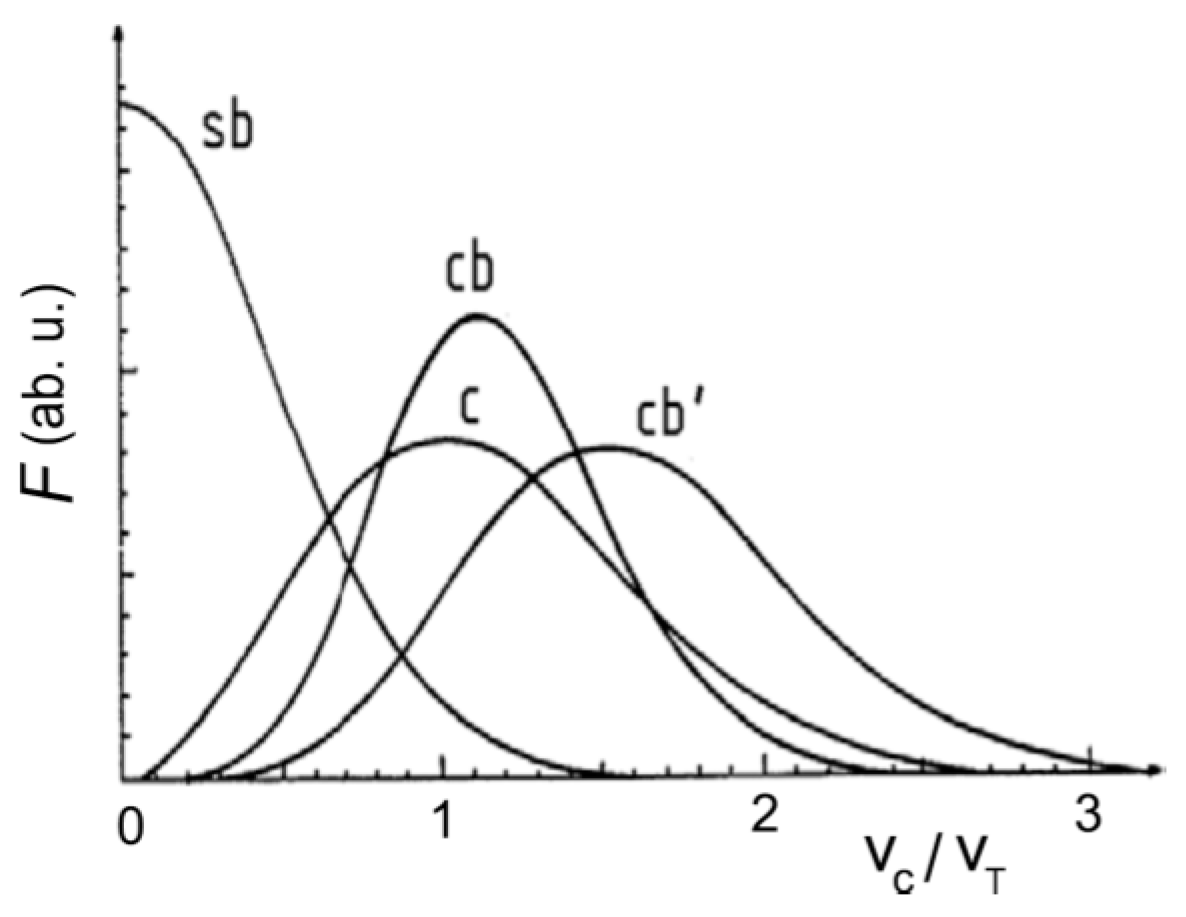
The velocity distribution dependence on the beams source temperature T may be expressed via the characteristic thermal velocity as . The function has quite different profiles in cells, single beams, and crossed beams cases, as demonstrated in Figure 10 [13,64].
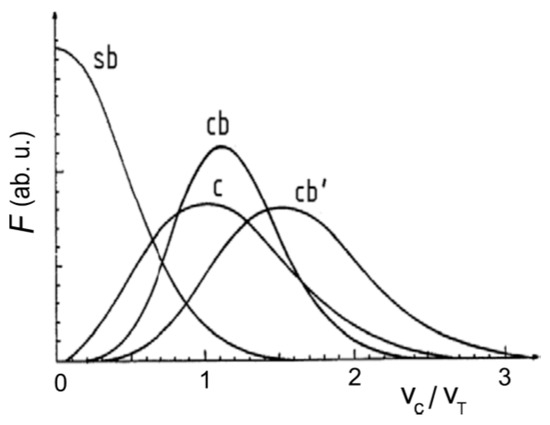
Figure 10.
Distribution function F in a single beam (sb), crossed beams (cb), counter beams (cb’), and gas cell (c).
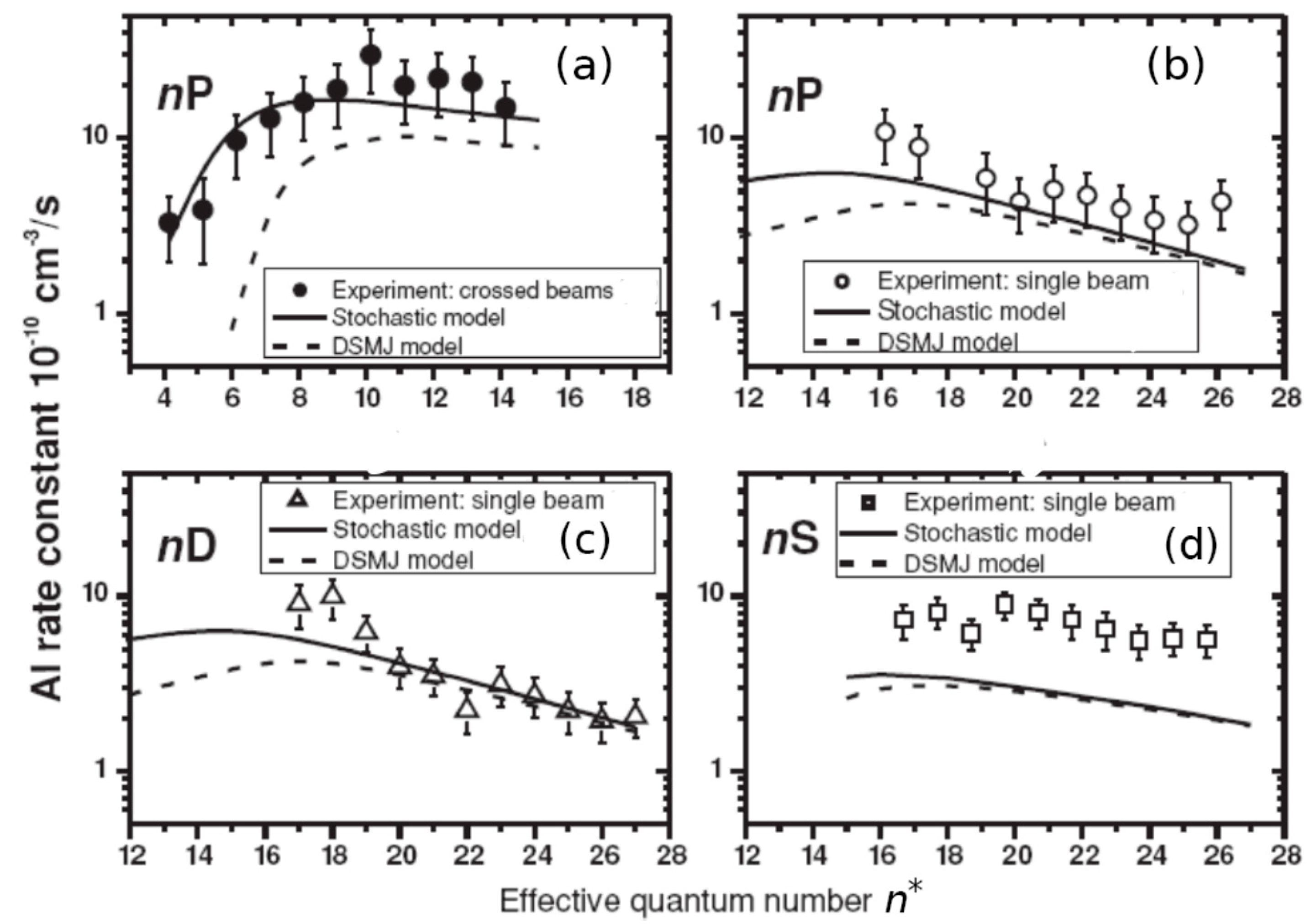
Figure 11 and Figure 12 show, following [53,60,66,67,68], the values of the associative ionization (AI) rate constants obtained under the conditions of a single and two orthogonal beams. The formation of molecular ion occurs upon the collisions of Rydberg sodium atoms excited to nS, nP, or nD states with atoms A in the ground state. Experimental data of Figure 11, frame (a) (dots, l = 1), corresponds to crossed beams conditions, T = 600 K [66]. Figure 11 data related to frame (b) (open circles, l = 1), frame (c) (open triangles, l = 2), and frame (d) (open squares, l = 2) were obtained in a single beam of Na atoms, T = 1000 K [67]. Full curves exhibit results of theory [60], accounting for stochastic diffusion effects, while dotted curves correspond to calculations in the frame of regular DSMJ model [43,44,45].
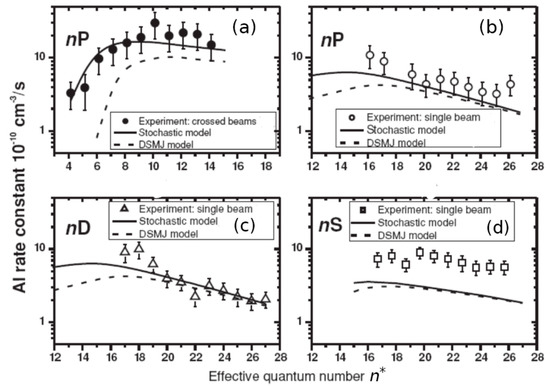
Figure 11.
Values of rate constants of associative ionization for collisions in a single beam (frames (b–d)) and in two orthogonal crossed beams (frames (a)) of sodium atoms excited in nS, nP, and nD Rydberg states [66,67].
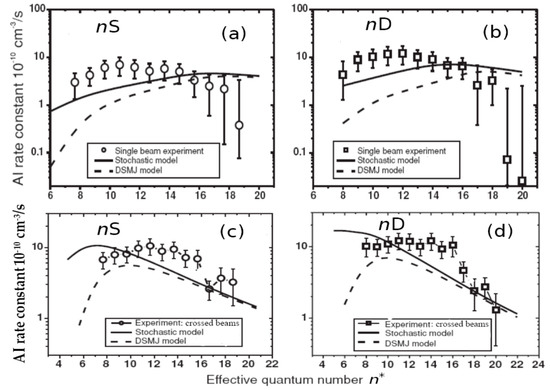
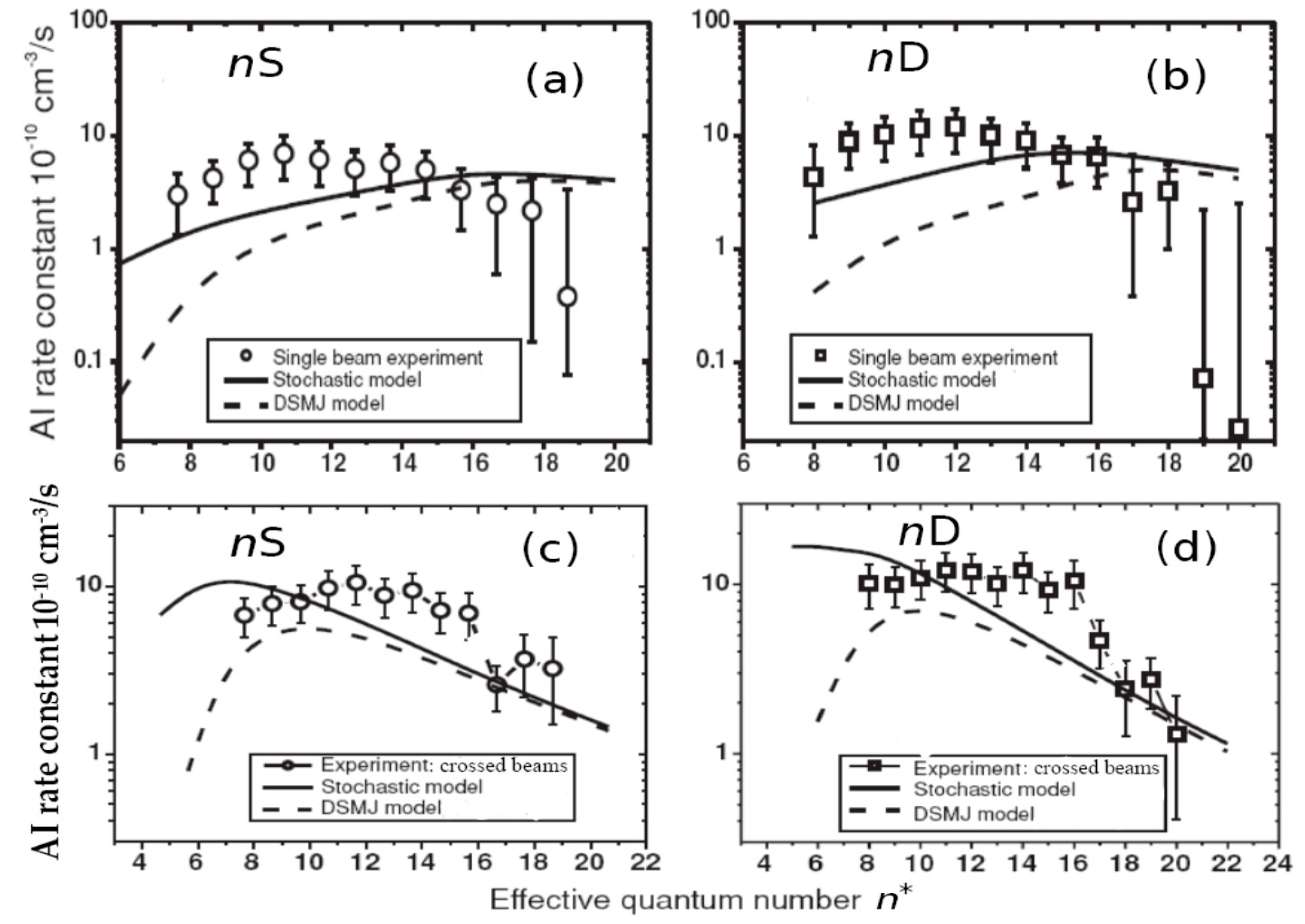
Figure 12.
Associative ionization rate constants for Na*(nl) + Na(3s) collisions in a single beam [53] (frames (a,b)) and in two orthogonal crossed beams [66] (frames (c,d)), T = 600 K.
Figure 12 shows the results of more recent experiments [53,66] on AI rate constants measurements, the authors of which took into account the effects of free electrons escaping due to atoms photoionization by black body radiation.
It can be seen that, in the range of effective quantum numbers, the data of the experiment and the stochastic theory (solid curves) agree with each other (although measurements have large error bars), whereas calculations using the traditional DSMJ model [43,44,45] (dashed curves) significantly underestimate the corresponding results, particularly for the lower values of n.
4.7. Features of Diffusional Ionization under Conditions of Förster Resonance
In Section 2.2, a significant decrease in the probabilities of Rydberg states radiative decay in Förster resonance (FR) conditions was demonstrated, which is due to the suppression of dipole matrix elements. Since the widths of the nonlinear resonances δε, as shown in [43,52], are directly related to the probabilities of microwave transitions in the excited atom, the blocking of the latter means the blocking of the development of dynamic chaos. The possibility of “controlling” the development of global chaos in the Rydberg diatomic cluster, using the double Stark resonance (or FR) mechanism, was considered in [40,43].
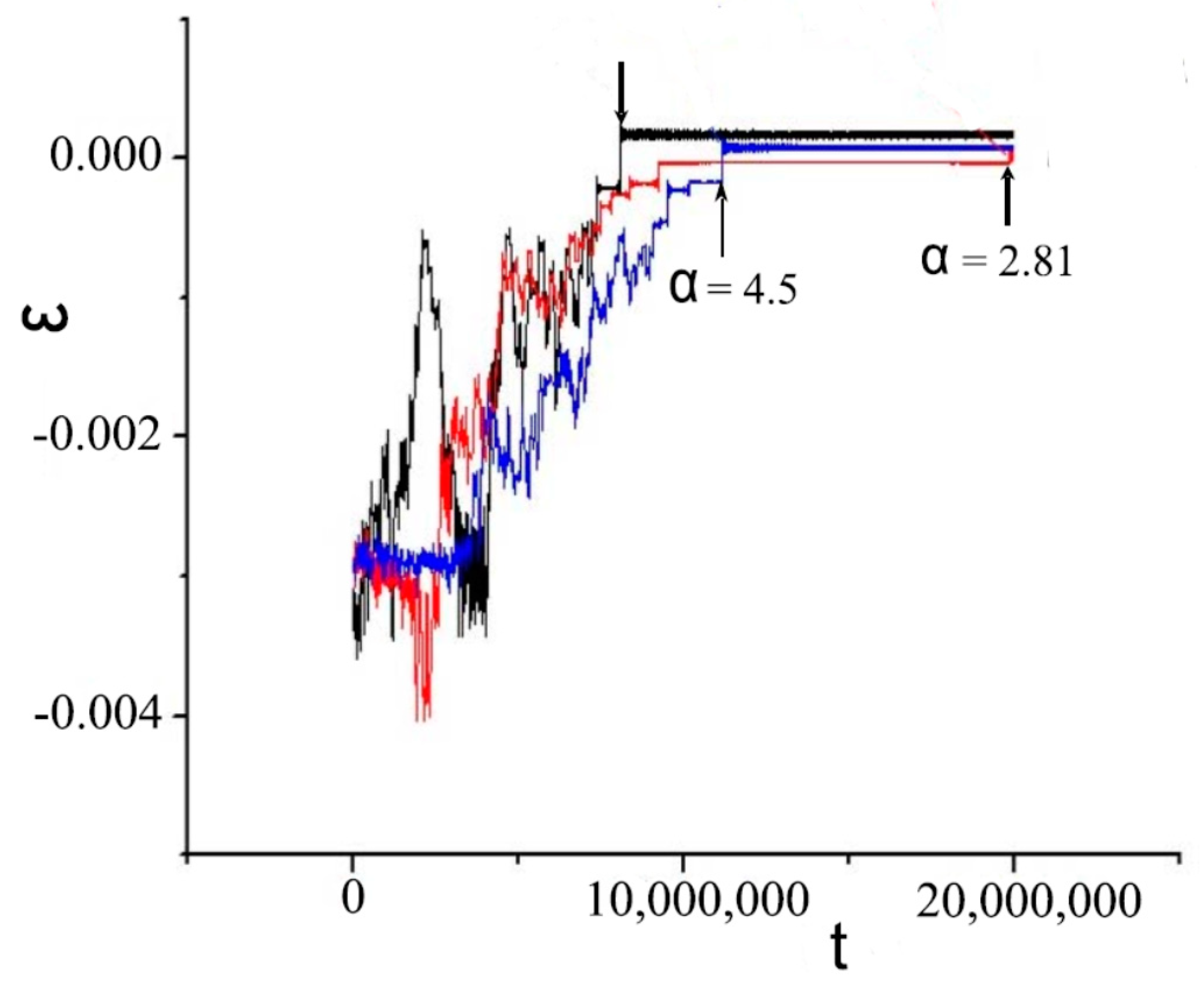
Figure 13 shows the time dependence of the RE binding energy under conditions of the development of diffusional ionization of Rydberg states of the model Sommerfeld atom, which is under the influence of an external microwave field, for different values of the Sommerfeld parameter α (see Equation (5)). It can be seen that the ionization time is significantly prolonged when the FR is realized (α = 2.81), which indicates the partial blockage of global stochatization.
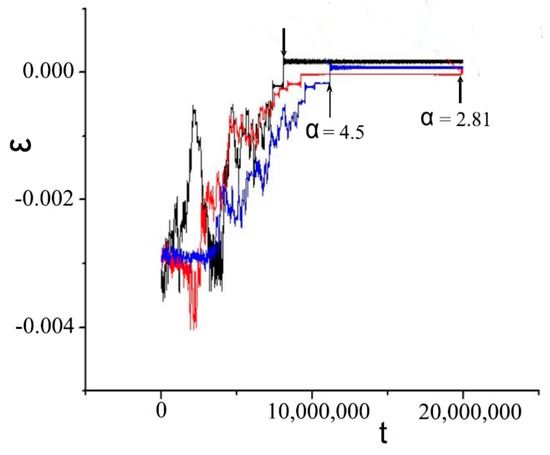
Figure 13.
Temporal evolution of binding energy ε of the 13P-state (l = 1) of the Rydberg electron in the Sommerfeld atom in an external microwave field of frequency ω = 1/133 and amplitude , which exceeds ten times the critical value . The calculations were performed for three values of Sommerfeld parameter: α = 0, 2.81, and 4.5. The arrows indicate the moments of ionization. The occurrence of Förster resonance corresponds to = 2.81.
5. Conclusions
Our work presents the results of studies (experiment and theory) of the radiative and collisional kinetics of Rydberg atoms, with their specific features arising from the closeness of highly excited bound states to the energy continuum. The model problems that are considered here reveal significant changes (by orders of magnitude) in the dipole matrix elements values of optical transitions in the vicinity of the Förster resonance, which is an important tool for creating entangled states in the system of cold Rydberg atoms. In particular, the anomalously long lifetimes of the p-series Rydberg states of the sodium atom are explained by the proximity of the Na p- and s-series energy levels structure to the Förster resonance configuration. We have considered the ionization processes of Rydberg atomic complexes in microwave electric fields. Under the multiplicity of the quasi-crossing of energy levels near the ionization continuum, the semiclassical method for taking into account the ionization instability of Rydberg states is discussed. This method is based on the formalism of nonlinear dynamic resonances and the evolution of dynamic chaos in Hamiltonian systems. The results of the numerical modeling of diffusion ionization of atomic hydrogen Rydberg states in an external microwave field are given with a demonstration of the nontrivial evolution of the orbital moment. The possibility of reducing the theoretical analysis of collisional ionization of Rydberg alkali metal atoms to the problem of the stochastic ionization of a Rydberg electron by an “internal” microwave field is shown. This field is induced by the charge exchange processes in the system “ion core of a Rydberg atom plus neutral atom-collision partner”. The comparison of the experimental and calculated data on the associative ionization rate constants in “Rydberg sodium atom-normal sodium atom” collision demonstrates the validity of describing the dynamic instability of Rydberg complexes within the framework of the dynamic chaos evolutionary theory for Hamiltonian systems.
Author Contributions
A.N.K. contributed analysis tools; A.A.Z. and V.A.S. analyzed the data with writing-original draft preparation; N.N.B., M.S.D. wrote the paper.
Funding
This research was partially funded by Ministry of Education, Science and Technological Development of the Republic of Serbia grants number III 44002 and 176002, and by the Russian Science Foundation under the grant NO 18-12-00313 in the part regarding the control of Rydberg complexes rate constants via Förster resonance.
Acknowledgments
Authors acknowledge the support of Russian Science Foundation under the grant NO 18-12-00313 in the part regarding the control of Rydberg complexes rate constants via Förster resonance.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Stebbings, R.F.; Dunning, F.B. (Eds.) Rydberg States of Atoms and Molecules; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Gallagher, T.F. Rydberg Atoms; Cambridge Monographs on Atomic, Molecular and Chemical Physics; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Jones, M.P.A.; Marcassa, L.G.; Shaffer, J.P. Special issue on Rydberg atom physics. J. Phys. B At. Mol. Phys. 2017, 50, 060202. [Google Scholar] [CrossRef]
- Lim, J.; Lee, H.-G.; Ahn, J. Review of cold Rydberg atoms and their applications. J. Korean Phys. Soc. 2013, 63, 867–876. [Google Scholar] [CrossRef]
- Hofmann, C.S.; Günter, G.; Schempp, H.; Müller, N.L.; Faber, A.; Busche, H.; Robert-de-Saint-Vincent, M.; Weidemüller, M. An experimental approach for investigating many-body phenomena in Rydberg-interacting quantum systems. Front. Phys. 2014, 9, 571–586. [Google Scholar] [CrossRef]
- Pillet, P.; Gallagher, T.F. Rydberg atom interactions from 300 K to 300 K. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 174003. [Google Scholar] [CrossRef]
- Saffman, M.; Walker, T.G.; Mølmer, K. Quantum information with Rydberg atoms. Rev. Mod. Phys. 2010, 82, 2313. [Google Scholar] [CrossRef]
- Ryabtsev, I.I.; Beterov, I.I.; Tretyakov, D.B.; Entin, V.M.; Yakshina, E.A. Spectroscopy of cold rubidium rydberg atoms for applications in quantum information. Phys.-Uspekhi 2016, 59, 196–208. [Google Scholar] [CrossRef]
- Marcassa, L.G.; Shaffer, J.P. Interactions in Ultracold Rydberg Gases. In Advances in Atomic, Molecular, and Optical Physics; Arimondo, E., Berman, P.R., Lin, C.C., Eds.; Academic: New York, NY, USA, 2014; Volume 63, pp. 47–133. [Google Scholar]
- Shaffer, J.P.; Rittenhouse, S.T.; Sadeghpour, H.R. Ultracold Rydberg molecules. Nat. Commun. 2018, 9, 1965. [Google Scholar] [CrossRef] [PubMed]
- Schlagmüller, M.; Liebisch, T.C.; Engel, F.; Kleinbach, K.S.; Böttcher, F.; Hermann, U.; Westphal, K.M.; Gaj, A.; Löw, R.; Hofferberth, S.; et al. Ultracold Chemical Reactions of a Single Rydberg Atom in a Dense Gas. Phys. Rev. X 2016, 6, 031020. [Google Scholar] [CrossRef]
- Lyon, M.; Rolston, S.L. Ultracold neutral plasmas. Rep. Prog. Phys. 2017, 80, 017001. [Google Scholar] [CrossRef] [PubMed]
- Klyucharev, A.N.; Vujnović, V. Chemi-ionization in thermal-energy binary collisions of optically excited atoms. Phys. Rep. 1990, 185, 55–81. [Google Scholar] [CrossRef]
- Graham, W.G.; Fritsch, W.; Hahn, Y.; Tanis, J.A. Recombination of Atomic Ions; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Beterov, I.I.; Tretyakov, D.B.; Ryabtsev, I.I.; Entin, V.M.; Ekers, A.; Bezuglov, N.N. Ionization of rydberg atoms by blackbody radiation. New J. Phys. 2009, 11, 013052. [Google Scholar] [CrossRef]
- Hahn, Y. Density dependence of molecular autoionization in a cold gas. J. Phys. B At. Mol. Opt. Phys. 2000, 33, L655. [Google Scholar] [CrossRef]
- Efimov, D.K.; Miculis, K.; Bezuglov, N.N.; Ekers, A. Strong enhancement of Penning ionization for asymmetric atom pairs in cold Rydberg gases: The Tom and Jerry effect. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 125302. [Google Scholar] [CrossRef]
- Gnedin, Y.N.; Mihajlov, A.A.; Ignjatović, L.J.M.; Sakan, N.M.; Srećković, V.A.; Zakharov, M.Y.; Bezuglov, N.N.; Klycharev, A.N. Rydberg atoms in astrophysics. New Astron. Rev. 2009, 53, 259–265. [Google Scholar] [CrossRef]
- Buenker, R.J.; Golubkov, G.V.; Golubkov, M.G.; Karpov, I.; Manzheliy, M. Relativity laws for the variation of rates of clocks moving in free space and GPS positioning errors caused by space-weather events. In Global Navigation Satellite System-From Stellar Navigation; Mohamed, A.H., Ed.; In Tech: Berlin, Germany, 2013. [Google Scholar]
- Koch, P.M.; van Leeuwen, K.A.H. The importance of resonances in microwave “ionization” of excited hydrogen atoms. Phys. Rep. 1995, 255, 289–403. [Google Scholar] [CrossRef]
- Mitchell, K.A.; Handlay, J.P.; Tighe, B.; Flower, A.; Delos, J.B. Analysis of chaos-induced pulse trains in the ionization of hydrogen. Phys. Rev. A 2004, 70, 043407. [Google Scholar] [CrossRef]
- Krainov, V.P. Ionization of atoms in strong low-frequency electromagnetic field. J. Exp. Theor. Phys. 2010, 111, 171–179. [Google Scholar] [CrossRef]
- Park, H.; Shuman, E.S.; Gallagher, T.F. Ionization of Rb Rydberg atoms in the attractive ns-np dipole-dipole potential. Phys. Rev. A 2011, 84, 052708. [Google Scholar] [CrossRef]
- Dashevskaya, E.I.; Litvin, I.; Nikitin, E.E.; Oref, I.; Troe, J. Classical diffusion model of vibrational predissociation of van der Waals complexes Part III. Comparison with quantum calculations. Phys. Chem. Chem. Phys. 2002, 4, 3330–3340. [Google Scholar] [CrossRef]
- Bezuglov, N.N.; Golubkov, G.V.; Klyucharev, A.N. Ionization of Excited Atoms in Thermal Collisions; The Atmosphere and Ionosphere: Elementary Processes, Discharges and Plasmoids; Springer: New York, NY, USA; London, UK, 2013; Chapter 1; pp. 1–60. [Google Scholar]
- Reichl, L.E. The Transition to Chaos: Conservative Classical Systems and Quantum Manifestations; Springer: New York, NY, USA, 2004. [Google Scholar]
- Zaslavskii, G.M. Physics of Chaos in Hamiltonian Systems, 2nd ed; Imperial College Press: London, UK, 2007. [Google Scholar]
- Bezuglov, N.N.; Golubkov, G.V.; Klyucharev, A.N. Manifestations of “Dynamic Chaos” in Reactions with Participation of Rydberg States; St. Petersburg State University: St. Petersburg, Russia, 2017. (In Russian) [Google Scholar]
- Paris-Mandoki, A.; Gorniaczyk, H.; Tresp, C.; Mirgorodskiy, I.; Hofferberth, S. Tailoring Rydberg interactions via Förster resonances: State combinations, hopping and angular dependence. J. Phys. B 2016, 49, 164001. [Google Scholar] [CrossRef]
- Gianninas, A.; Dufour, P.; Kilic, M.; Brown, W.R.; Bergeron, P.; Hermes, J.J. Precise atmospheric parameters for the shortest-period binary white dwarfs: Gravitational waves, metals, and pulsations. Astrophys. J. 2014, 794, 35–52. [Google Scholar] [CrossRef]
- Bezuglov, N.N.; Borisov, E.N.; Verolainen, Y.F. Distribution of the radiative lifetimes over the excited states of atoms and ions. Sov. Phys. Uspekhi 1991, 34, 3–29. [Google Scholar] [CrossRef]
- Hezel, T.P.; Burkhardt, C.E.; Ciocca, M.; He, L.W.; Leventhal, J.J. Classical view of the properties of Rydberg atoms: Application of the correspondence principle. Am. J. Phys. 1992, 60, 329–335. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics; Pergamon: Oxford, UK, 1977. [Google Scholar]
- Omidvar, K. Semiclassical formula for the radiative mean lifetime of the excited state of the hydrogenlike atoms. Phys. Rev. A 1982, 26, 3053–3061. [Google Scholar] [CrossRef]
- Mack, M.; Grimmel, J.; Karlewski, F.; Sárkány, L.; Hattermann, H.; Fortágh, J. All-optical measurement of Rydberg-state lifetimes. Phys. Rev. A 2015, 92, 012517. [Google Scholar] [CrossRef]
- Tretyakov, D.B.; Beterov, I.I.; Entin, V.M.; Yakshina, E.A.; Ryabtsev, I.I.; Dyubko, S.F.; Alekseev, E.A.; Pogrebnyak, N.L.; Bezuglov, N.N.; Arimondo, E. Effect of photoions on the line shape of the Förster resonance lines and microwave transitions in cold rubidium Rydberg atoms. J. Exp. Theor. Phys. 2012, 114, 14–24. [Google Scholar] [CrossRef]
- Hund, F. The History of Quantum Theory; Barnes & Noble Books: New York, NY, USA, 1974; Chapter 11. [Google Scholar]
- Bokulich, P.; Bokulich, A. Niels Bohr’s generalization of classical mechanics. Found. Phys. 2005, 35, 347–371. [Google Scholar] [CrossRef]
- Delone, N.B.; Goreslavsky, S.P.; Krainov, V.P. Dipole matrix elements in the quasi-classical approximation. J. Phys. B 1994, 27, 4403. [Google Scholar] [CrossRef]
- Arefieff, K.N.; Miculis, N.; Bezuglov, N.N.; Dimitrijević, M.S.; Klyucharev, A.N.; Mihajlov, A.A.; Srećković, V.A. Dynamics Resonances in Atomic States of Astrophysical Relevance. J. Astrophys. Astron. 2015, 36, 613–622. [Google Scholar] [CrossRef]
- Sommerfeld, A. Atomic Structure and Spectral Lines; Methuen: London, UK, 1934. [Google Scholar]
- Grouzdev, P.F. Atomic and Ionic Spectra in X-ray and Ultraviolet Region’s; Energoatomizdat: Moscow, Russia, 1982. (In Russian) [Google Scholar]
- Zakharov, M.Y.; Bezuglov, N.N.; Klyucharev, A.N.; Matveev, A.A.; Beterov, I.I.; Dulieu, O. Specifics of the stochastic ionization of a Rydberg collision complex with Förster resonance. Russ. J. Phys. Chem. B 2011, 5, 537–545. [Google Scholar] [CrossRef]
- Fermi, E. Sopra lo spostamento per pressione delle righe elevate delle serie spettrali. Nuovo Cimento 1934, 11, 157–166. [Google Scholar] [CrossRef]
- Janev, R.K.; Mihajlov, A.A. Resonant ionization in slow-atom-Rydberg-atom collisions. Phys. Rev. A 1980, 21, 819–826. [Google Scholar] [CrossRef]
- Mihajlov, A.A.; Janev, R.K. Ionisation in atom-Rydberg atom collisions: Ejected electron energy spectra and reaction rate coefficients. J. Phys. B 1981, 14, 1639. [Google Scholar] [CrossRef]
- Duman, E.L.; Shmatov, I.P. Ionization of highly excited atoms in their own gas. Sov. Phys. JETP 1980, 51, 1061–1065. [Google Scholar]
- Srećković, V.A.; Dimitrijević, M.S.; Ignjatović, Lj.M.; Bezuglov, N.N.; Klyucharev, A. The Collisional Atomic Processes of Rydberg Hydrogen and Helium Atoms: Astrophysical Relevance. Galaxies 2018, 6, 72. [Google Scholar] [CrossRef]
- Bezuglov, N.N.; Borodin, V.M.; Kazanskiy, A.K.; Klyucharev, A.N.; Matveev, A.A.; Orlovskii, K.V. Analysis of Fokker-Planck type stochastic equations with variable boundary conditions in an elementary process of collisional ionization. Opt. Spectrosc. 2001, 91, 19–26. [Google Scholar] [CrossRef]
- Zaslavskij, G.M. Hamiltonian Chaos and Fractional Dynamics; Oxford Univ. Press: Oxford, UK, 2005. [Google Scholar]
- Delone, N.B.; Krainov, V.P.; Shepelyanskii, D.L. Highly-excited atoms in the electromagnetic field. Sov. Phys. Uspekhi 1983, 26, 551. [Google Scholar] [CrossRef]
- Bezuglov, N.N.; Borodin, V.M.; Ekers, A.; Klyucharev, A.N. A quasi-classical description of the stochastic dynamics of a Rydberg electron in a diatomic quasi-molecular complex. Opt. Spectrosc. 2002, 93, 661–669. [Google Scholar] [CrossRef]
- Ryabtsev, I.I.; Tretyakov, D.B.; Beterov, I.I.; Bezuglov, N.N.; Miculis, K.; Ekers, A. Collisional and thermal ionization of sodium Rydberg atoms: I. Experiment for nS and nD atoms with n = 8–20. J. Phys. B 2005, 38, S17–S35. [Google Scholar] [CrossRef]
- Efimov, D.K.; Bezuglov, N.N.; Klyucharev, A.N.; Gnedin, Y.N.; Miculis, K.; Ekers, A. Analysis of light-induced diffusion ionization of a three-dimensional hydrogen atom based on the Floquet technique and split-operator method. Opt. Spectrosc. 2014, 117, 8–17. [Google Scholar] [CrossRef]
- Chu, S.-I.; Telnov, D.A. Beyond the Floquet theorem: Generalized Floquet formalisms and quasienergy methods for atomic and molecular multiphoton processes in intense laser fields. Phys. Rep. 2004, 390, 1–131. [Google Scholar] [CrossRef]
- Hairer, E. Numeral Geometric Integration; Universite de Geneve: Geneve, Switzerland, 1999. [Google Scholar]
- Kazansky, A.K.; Bezuglov, N.N.; Molisch, A.F.; Fuso, F.; Allegrini, M. Direct numerical method to solve radiation trapping problems with a Doppler-broadening mechanism for partial frequency redistribution. Phys. Rev. A 2001, 64, 022719. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Mechanics Course of Theoretical Physics Mechanics; (Nauka, Moscow, 1973); English Tran.; Permagon Press: Oxford, UK; New York, NY, USA; Toronto, ON, Canada, 1976; Volume 1. [Google Scholar]
- Ramsey, N.F. Molecular Beams, 2nd ed.; Clarendon: Oxford, UK, 1989. [Google Scholar]
- Michulis, K.; Beterov, I.I.; Bezuglov, N.N.; Ryabtsev, I.I.; Tretyakov, D.B.; Ekers, A.; Klucharev, A.N. Collisional and thermal ionization of sodium Rydberg atoms: II. Theory for nS, nP and nD states with n= 5–25. J. Phys. B 2005, 38, 1811–1831. [Google Scholar] [CrossRef]
- Sydoryk, I.; Bezuglov, N.N.; Beterov, I.I.; Miculis, K.; Saks, E.; Janovs, A.; Spels, P.; Ekers, A. Broadening and intensity redistribution in the Na(3p) hyperfine excitation spectra due to optical pumping in the weak excitation limit. Phys. Rev. A 2008, 77, 042511. [Google Scholar] [CrossRef]
- Kirova, T.; Cinins, A.; Efimov, D.K.; Bruvelis, M.; Miculis, K.; Bezuglov, N.N.; Auzinsh, M.; Ryabtsev, I.I.; Ekers, A. Hyperfine interaction in the Autler-Townes effect: The formation of bright, dark, and chameleon states. Phys. Rev. A 2017, 96, 043421. [Google Scholar] [CrossRef]
- Porfido, N.; Bezuglov, N.N.; Bruvelis, M.; Shayeganrad, G.; Birindelli, S.; Tantussi, F.; Guerri, I.; Viteau, M.; Fioretti, A.; Ciampini, D.; et al. Nonlinear effects in optical pumping of a cold and slow atomic beam. Phys. Rev. A 2015, 92, 043408. [Google Scholar] [CrossRef]
- Klyucharev, A.N.; Bezuglov, N.N.; Matveev, A.A.; Mihajlov, A.A.; Ignjatović, L.M.; Dimitrijević, M.S. Rate coefficients for the chemi-ionization processes in sodium- and other alkali-metal geocosmical plasmas. New Astron. Rev. 2007, 51, 547–562. [Google Scholar] [CrossRef]
- Tantussi, F.; Mangasuli, V.; Porfido, N.; Prescimone, F.; Fuso, F.; Arimondo, E.; Allegrini, M. Towards laser-manipulated deposition for atom-scale technologies. Appl. Surf. Sci. 2009, 255, 9665–9670. [Google Scholar] [CrossRef]
- Boulmer, J.; Bonanno, R.; Weiner, J. Crossed-beam measurements of absolute rates coefficients in associative ionization collisions between Na*(np) and Na(3s) for 5 ≤ n ≤ 15. J. Phys. B 1983, 16, 3015–3024. [Google Scholar] [CrossRef]
- Weiner, J.; Boulmer, J. Associative ionization rate constants as a function of quantum numbers n and l in Na*(np) + Na(3s) collisions for 17 ≤ n ≤ 27 and l = 0, l = 1 and l ≥ 2. J. Phys. B 1986, 19, 599–609. [Google Scholar] [CrossRef]
- Beterov, I.I.; Tretyakov, D.B.; Ryabtsev, I.I.; Bezuglov, N.N.; Miculis, K.; Ekers, A.; Klucharev, A.N. Collisional and thermal ionization of sodium Rydberg atoms III. Experiment and theory for nS and nD states with n = 8–20 in crossed atomic beams. J. Phys. B 2005, 38, 4349–4361. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).