Cosmological Probes of Structure Growth and Tests of Gravity
Abstract
1. Introduction
2. An Overview of the Modified Gravity Models
2.1. Conformal Coupling Models: Gravity
2.2. Derivative Coupling Models: DGP Gravity
2.3. Screening Mechanisms
2.3.1. Thin-Shell Screening
2.3.2. Kinetic Screening
2.4. Parameterised Frameworks of Gravity
2.4.1. MG Phenomenological Functions
2.4.2. Effective Field Theory of Dark Energy
- Usually, the validity of the weak equivalence principle is assumed a priori. This makes the Jordan frame, where the metric is universally coupled to the matter fields, the best-suited framework. We refer to [63] for details on the Jordan frame and the alternative formulation in the Einstein frame;
- The action is constructed within the unitary gauge [60,61]. In practice, this means that the perturbation of the extra scalar degree of freedom representing the DE–MG framework is vanishing. This corresponds to foliate the 4D spacetime in 3D hypersurfaces by breaking the time-translation symmetry and fixing a preferred time slicing;
- The chosen foliation is characterised through the unit vector perpendicular to the time slicingwhere is the Jordan frame metric. From the unit vector, we can define the extrinsic curvature as ;
- We construct the action from all the perturbed operators invariant under the residual symmetry of spatial diffeomorphisms, such as the upper time component of the metric , the Riemann tensor , the Ricci tensor and scalar , the extrinsic curvature and its trace ;
- Due to the broken time-translation symmetry, the coefficient of the operators in the action are allowed to be time-dependent functions. We call these parameters EFT functions.
2.4.3. The -Basis Parameterisation
- , dubbed as kineticity, is connected to the kinetic energy term in the Horndeski Lagrangian (see Equation (3)) and depends on the functions K, , and ;
- quantifies the braiding, i.e., the mixing between the kinetic terms of the scalar field and the metric. It depends on the , and functions;
- describes the running of the effective Planck mass and can be easily expressed in terms of Horndeski functions aswith H being the Hubble parameter and ;
- is the tensor speed excess, that quantifies the speed excess of GWs with respect to the speed of light. It depends on the Horndeski functions as
2.5. Why Do We Still Study and DGP?
2.5.1. Survivors from GWs
2.5.2. Further Parametrization
3. Observational Probes of Gravity Models
3.1. Derived Observables
3.1.1. Potential-Based Derived Observables
- (i)
- Temperature fluctuation. As the CMB photons travel between the last scattering surface and the observers, their wavelengths are altered when they travel through the time-varying gravitational potentials. The integrated Sachs–Wolfe(ISW) [88] effect measures the decay of gravitational potential due to cosmic expansion. The integrated temperature anisotropies can be expressed as8where is the average temperature of the CMB background. Here, the two potentials and are allowed to be different, with as the conformal time.
- (ii)
- Deflection of photon trajectories. In the presence of MG, the modified potential can source different inhomogeneous density distributions between the photons sources and the observer compared to the ones given by GR. The additional inhomogeneity of the density field thus deflects the trajectories of photons. When the detected photons are emitted by the last scattering surface, the derived observables are CMB lensing(see reviews [89,90]). Alternatively, when the photons are emitted from distant source galaxies, the galaxy shapes can be subtly distorted by intervening mass distribution and are hence named cosmic shear or galaxy WL (see review [91]).
3.1.2. Density-Based Derived Observables
- (i)
- Density contrast field. As can be seen from the Poisson equation, the metric perturbations directly source the density contrast field given by
3.1.3. Velocity-Based Derived Observables
- (i)
- Redshift space distortions. MG forces leave strong imprints on the matter velocity fields. On sufficiently large scales, galaxies trace matter velocity fields and there is no velocity bias between the galaxies and matter distribution. The galaxies’ peculiar velocities add an additional component to the galaxies’ redshifts and lead to an anisotropic clustering pattern, which is known as redshift space distortion (RSD). The observed density contrast field is in redshift space, thus receiving a velocity correction that is parallel to the LoS direction. In the linear regime and under the distant observer approximation, the density contrast field in redshift space is given bywith the co-moving Hubble scale , the LoS-parallel velocity , and the real and redshift space positions are related as .
- (ii)
- Temperature anisotropies in CMB Photons. As CMB photons travel through the Universe, they can be inverse Thompson scattered by hot ionized gas. The induced shifts in the photon temperature are referred to as Sunyaev–Zeldovich effects. In the case of the kinetic Sunyaev–Zeldovich (kSZ) effect [104], the shift in photon temperature is caused by the bulk motion of the ionised gas in clusters. The shift temperature can be expressed aswhere is the electron Thomson cross-section, is the mean gas density at redshift , is the mean mass per electron, is the redshift at which reionization ends, is the Thomson optical depth, is the electron ionization fraction which depends on the primordial helium abundance and the number of ionized helium electrons [105,106], and is the density-weighted peculiar velocity of the electron (bulk peculiar velocity of ionized regions or clouds). The dot product in Equation (35) implies that only the LoS-parallel component velocity contributes to the temperature anisotropies. Given that the velocity is proportional to the Fourier modes of matter density contrast (we use ∼ to denote Fourier space quantities) in linear theory, only modes parallel to the LoS can contribute to the anisotropy. However, since Fourier modes parallel to the LoS direction cancel with each other after the projection, the angular correlation at smaller scales mainly receives contributions from components perpendicular to the LoS direction .
- (iii)
- Direct peculiar velocity measurements. The radial component of the peculiar velocity of a galaxy can be directly estimated when both the redshift and redshift-independent distance estimates are available. Distance estimates can be obtained via well-known correlations of galaxy properties such as the Tully–Fisher relation for spiral galaxies [107,108] and the fundamental plane for ellipticals [109]. These relations provide distances to galaxies with 20% uncertainties for redshifts reaching . Another alternative to obtain distances is using type-Ia supernovae, which have smaller intrinsic scatters in luminosity after standardisation and can provide distances with 7% uncertainties. The statistics of the peculiar velocities and their cross-correlation with the galaxy density field can yield tighter constraints on the growth rate at , where cosmic variance limits the constraints from RSD.
3.2. Two-Point Statistics
3.2.1. Redshift Space Power Spectrum
3.2.2. Angular Power Spectrum for LoS-Integrated Observables
- (i)
- Galaxy lensing. One advantage of galaxy WL is that it can access smaller-scale information relative to galaxy-clustering analysis.10 Contemporary galaxy WL analyses measure two-point statistics of the observed shear field, which is the anisotropic distortion induced by the lensing potential introduced in Equation (31) (e.g., [131,132,133,134,135,136,137]. In photometric surveys, source galaxies are binned into tomographic redshift bins, and the correlation of the shear field within these tomographic bins, as well as their cross-correlations, are estimated with a selection of two-point statistics. Common examples of employed two-point statistics are correlation functions, (pseudo) angular power spectra, or complete orthogonal sets of E-/B-mode integrals (COSEBIs) [138]. All these statistics can be related to the angular power spectrum of the shear field through linear transformations. For first-order, the angular power spectrum of the shear field is equivalent to that of the convergence given in Equation (32) (see, e.g., Equation (6.32) in [92]. The power spectrum is the matter power spectrum at redshift today , and the kernel that enters the angular power spectrum Equation (38) can be written aswhere is the distribution of source galaxies in tomographic redshift bin i.
- (ii)
- CMB lensing. As CMB photons travel along the LoS, they are deflected by the gravitational potential gradients associated with the large-scale structure in the late-time epoch. The CMB lensing thus indirectly traces the underlying matter distribution. Although CMB lensing and galaxy lensing share common features, the broad CMB lensing kernel guarantees its sensitivity to higher redshifts. Unlike galaxy lensing, the source redshifts of CMB lensing are almost exactly known; CMB lensing is thus free from photometric redshift uncertainties.
- (iii)
- Combined probes analyses. The two-point statistics of various combinations of different fields can be combined into pt analyses. A common joint analysis consists of the combination of the two-point statistics of the lensing fields, the galaxy density fields, and their cross-correlations. These pt analyses form the backbone of current and future photometric surveys (e.g., [164,165,166]). Jointly analysing the different probes helps to break parameter degeneracies due to different sensitivities of the respective probes to both cosmological parameters, as well as astrophysical and observational parameters. For example, in the linear regime, the two-point statistics of the galaxy density field scale as , while the cross-correlation of galaxy density and lensing—called galaxy–galaxy lensing—and cosmic shear scale as and , respectively, since lensing does not depend on the galaxy bias b. This combination of probes can therefore break the degeneracy between galaxy bias and clustering amplitude. Similarly, observational systematics in lensing, such as multiplicative shear biases, affect different probe combinations to varying degrees and therefore can be handled more robustly in joint analyses than in a single-probe analysis. Combined with the high signal-to-noise of these measurements (e.g., for DES-Y3 [166]), this allows for tight parameter constraints.
- (iv)
- ISW and cross-correlation with galaxy. The ISW effect is sensitive to the time-dependent Weyl potential and can thus be used to constrain in Equation (22). During the expansion of the Universe, gravitational potential decays. At the same time, the gravity enhances structure growth below the Compton wavelength, and photons thus become colder (decrease in angular power spectrum). Therefore, the ISW effect affects the larger scales by suppressing the power for low-multipole moments. The sensitivity at larger scales also implies that the ISW effect is cosmic variance-limited due to the limited number of modes [183]. While a direct measurement of the ISW effect from the CMB spectrum is very small [184], expected to be measurable through the cross-correlation with the large-scale structure. The authors of [185] proposed the correlation of the X-ray survey and the CMB anisotropy measurements, e.g., the authors of [186] performed a combined analysis for galaxy surveys, radio survey, and hard X-ray counts and found a detection significance of the ISW signal. In the ISW–galaxy cross-correlation case, the power spectrum is given by the matter clustering , and the ISW kernel is given bywhile the galaxy kernel iswith as the galaxy bias and as a normalized galaxy selection function. Alternatively, expressing the ISW kernel in terms of the ratio between the Newtonian and curvature potential can be used to test the function (see Equation (22)). The authors of [184,186] used the ISW–galaxy cross-correlation to constrain .
- (v)
- kSZ power spectrum. The amplitude of the kSZ angular power spectrum strongly depends on the normalization of matter perturbations and is thus sensitive to the growth of structure. As mentioned in Section 3.1.3, the photon temperature is shifted by the bulk motion of the ionized gas, and thus the kSZ effect is also sensitive to the velocity field. The kSZ angular power is given by taking the expectation value of Equation (35). As discussed previously, the angular power spectrum only receives contribution components perpendicular to the LoS direction as the LoS-component averages out due to the integral at linear scales. The power spectrum P is given by the Vishniac power spectrum [197], which requires modelling the power spectrum of the density field, velocity field, as well as the cross-correlation of the density–velocity fields [198,199,200]. The kernel is given bywith dots denoting the derivative with respect to the proper time. Compared to other secondary anisotropies of the CMB, the kSZ effect is weak, with detections of the kSZ power spectrum and cross-correlations with galaxies only in the 3–5 range [201,202,203,204,205].

3.2.3. Power Spectrum of Line Intensity Mapping
3.3. Higher-Order Statistics and Morphology of the Structure
3.3.1. Galaxy NPCFs/Polyspectra
3.3.2. Convergence-Derived Quantities: Moments of Aperture Mass and Peak Counting
3.3.3. Wavelet Scattering Transforms
3.3.4. Topological Tools
3.3.5. One-Point Probability Density Distribution
3.3.6. Nearest Neighbour Distributions
3.4. Environment-Sensitive Estimators
3.4.1. Density Split Statistics
3.4.2. Galaxy Clusters
3.4.3. Properties of 2D and 3D Underdense Regions
3.4.4. Marked Correlation Function
3.5. Modelling the Observables
4. Simulations for MG
4.1. Simulations for Galaxies
4.2. Simulations for Radio Sources
4.3. Simulation-Based Inference
5. Cosmological Surveys of Our Universe
5.1. Photometric Surveys
5.2. Spectroscopic Surveys
5.3. Radio Surveys: Continuum and Intensity Mapping
5.4. Cosmic Microwave Background Surveys
5.5. Insights into MG from Current Surveys
6. Conclusions and Discussion
- Model-dependent vs. model-independent: above we mentioned the downsides of the model-specific approach. The parametrization framework is more general and can quantify broader classes of gravity models. To date, most MG studies within the parametrization framework are only suitable in the linear regime. Only recently have there been studies that generalized the approach to all scales (Section 2.4). However, extracting physical insights from the parametrized approach can be a difficult task.
- Analytic templates for observables: although the null hypothesis can be applied to quantify potential deviations from GR, a first-principle-derived template for a given observable helps to deepen the understanding of structure growth in the presence of a fifth force. However, such templates typically rely on the specifics of MG models, and computing such templates including MG effects is usually challenging. Furthermore, the templates are often motivated by PT. They are more suitable for summary statistics, while templates (even within the standard GR case) that characterize topological properties are yet to be developed.
- Cosmic degeneracies: massive neutrino and baryonic processes can both have impacts on the small-scale matter power spectrum (e.g., [577,578]). While various analytic approaches [579,580,581] have been used to study non-linear effects and baryonic processes, they typically require careful calibration upon hydrodynamical simulations. Meanwhile, the baryonic processes predicted by hydrodynamical simulations [405,582,583,584,585] are affected by resolution, calibration strategies, and the choice of sub-grid physics (see review by [142]). These variations can result in uncertainties in predicting the statistics of small-scale phenomena.
- Simulation degeneracies: many simulation-based conclusions rely on post-processing of N-body simulations. Various assumptions on the construction of observable catalogues can have non-negligible impacts on the conclusions. Typical examples are degeneracies between the HOD parameters or neglect of observational systematics.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | Quasi-static limit assumes that the time derivative of the scalar field perturbation is negligible compared to the spatial gradient of the scalar field. |
| 2 | Weak field approximation assumes that the amplitudes of the scalar field perturbations and gravitational potentials are much smaller than the speed of light squared. |
| 3 | |
| 4 | See: http://eftcamb.org/ (accessed on 13 June 2023). |
| 5 | See: http://miguelzuma.github.io/hi_class_public/ (accessed on 13 June 2023). |
| 6 | Of course one could try to force with very large . However, this would lead to exotic theories incompatible with the Universe we observe. |
| 7 | A conformal metric transformation is . At linear order it leads to . Thus, the sum of the potential is conformally invariant. |
| 8 | We approximate the optical depth and . |
| 9 | The authors of [11] worked in the unit , and we restored the c in the equation. |
| 10 | Here, we only compare to galaxy clustering focusing on BAO and RSD analysis. There is, in principle, no restriction in applying galaxy-clustering analysis to highly non-linear regimes. |
| 11 | |
| 12 | Mitigation schemes have been shown to pass various null tests. However, one should keep in mind there could still be redshift-sensitive or scale-sensitive residuals. |
| 13 | The lensing power spectrum is constructed from the angular power spectrum of the convergence , with as an effective lens distance in co-moving coordinates. |
| 14 | An animation demonstrating percolating cosmic structure: https://wwwmpa.mpa-garching.mpg.de/paper/singlestream2017/percolation.html (accessed on 13 June 2023) |
| 15 | Euler characteristic is also called genus. It is a topological invariant (a property of a topological space when transformed under a bijective and continuous function—homeomorphisms). |
| 16 | An intriguing connection between the Euler characteristic and Betti number (represents the “dimension” of a homology group) is discussed in Bobrowski and Skraba [294]. The reader can find more information about persistent homology in Wasserman [285], Edelsbrunner et al. [286] and Koplik [295] for a visualized explanation. |
| 17 | The radial distance is often normalized by voids’ radii given that the void density profiles are almost universal in terms of the void size. |
| 18 | In most of the MG simulations with the N-body algorithms, the field is discretized and solved using a finite-difference method; the relaxation method is usually applied to iteratively solve a system of differential equations. The goal of each iteration is to update the discretized field with a new value until the equality of the left- and right-hand sides of Equation (57) converges. |
| 19 | The authors of [543] found the is unconstrained in the cosmic shear analysis after marginalizing over nuisance or cosmological parameters. |
References
- Taylor, J.H.; Weisberg, J.M. A new test of general relativity—Gravitational radiation and the binary pulsar PSR 1913+16. Astrophys. J. 1982, 253, 908–920. [Google Scholar] [CrossRef]
- Holberg, J.B. Sirius B and the Measurement of the Gravitational Redshift. J. Hist. Astron. 2010, 41, 41–64. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [PubMed]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Frieman, J.A.; Turner, M.S.; Huterer, D. Dark energy and the accelerating universe. Annu. Rev. Astron. Astrophys. 2008, 46, 385–432. [Google Scholar] [CrossRef]
- Weinberg, D.H.; Mortonson, M.J.; Eisenstein, D.J.; Hirata, C.; Riess, A.G.; Rozo, E. Observational probes of cosmic acceleration. Phys. Rep. 2013, 530, 87–255. [Google Scholar] [CrossRef]
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Rubin, V.C.; Ford, W.K., Jr.; Thonnard, N. Rotational properties of 21 SC galaxies with a large range of luminosities and radii, from NGC 4605 (R=4kpc) to UGC 2885 (R=122kpc). Astrophys. J. 1980, 238, 471–487. [Google Scholar] [CrossRef]
- Joyce, A.; Lombriser, L.; Schmidt, F. Dark Energy Versus Modified Gravity. Annu. Rev. Nucl. Part. Sci. 2016, 66, 95–122. [Google Scholar] [CrossRef]
- Brans, C.; Dicke, R.H. Mach’s Principle and a Relativistic Theory of Gravitation. Phys. Rev. 1961, 124, 925–935. [Google Scholar] [CrossRef]
- Horndeski, G.W. Second-Order Scalar-Tensor Field Equations in a Four-Dimensional Space. Int. J. Theor. Phys. 1974, 10, 363–384. [Google Scholar] [CrossRef]
- Sotiriou, T.P.; Faraoni, V. f(R) Theories of Gravity. Rev. Mod. Phys. 2010, 82, 451–497. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S. f(R) theories. Living Rev. Relativ. 2010, 13, 3. [Google Scholar] [CrossRef]
- Capozziello, S.; Fang, L.Z. Curvature Quintessence. Int. J. Mod. Phys. D 2002, 11, 483–491. [Google Scholar] [CrossRef]
- Capozziello, S.; Carloni, S.; Troisi, A. Quintessence without scalar fields. arXiv 2003, arXiv:astro-ph/0303041. [Google Scholar]
- Carroll, S.M.; Duvvuri, V.; Trodden, M.; Turner, M.S. Is cosmic speed-up due to new gravitational physics? Phys. Rev. D 2004, 70, 043528. [Google Scholar] [CrossRef]
- Chiba, T. 1/R gravity and scalar-tensor gravity. Phys. Lett. B 2003, 575, 1–3. [Google Scholar] [CrossRef]
- Erickcek, A.L.; Smith, T.L.; Kamionkowski, M. Solar system tests do rule out 1/R gravity. Phys. Rev. D 2006, 74, 121501. [Google Scholar] [CrossRef]
- Hu, W.; Sawicki, I. Models of f(R) Cosmic Acceleration that Evade Solar-System Tests. Phys. Rev. D 2007, 76, 064004. [Google Scholar] [CrossRef]
- Barrow, J.D.; Cotsakis, S. Inflation and the Conformal Structure of Higher Order Gravity Theories. Phys. Lett. B 1988, 214, 515–518. [Google Scholar] [CrossRef]
- Baker, T.; Barreira, A.; Desmond, H.; Ferreira, P.; Jain, B.; Koyama, K.; Li, B.; Lombriser, L.; Nicola, A.; Sakstein, J.; et al. The Novel Probes Project—Tests of Gravity on Astrophysical Scales. arXiv 2019, arXiv:1908.03430. [Google Scholar] [CrossRef]
- Dvali, G.R.; Gabadadze, G.; Porrati, M. 4-D gravity on a brane in 5-D Minkowski space. Phys. Lett. B 2000, 485, 1–3. [Google Scholar] [CrossRef]
- Deffayet, C. Cosmology on a brane in Minkowski bulk. Phys. Lett. B 2001, 502, 199–208. [Google Scholar] [CrossRef]
- Luty, M.A.; Porrati, M.; Rattazzi, R. Strong interactions and stability in the DGP model. J. High Energy Phys. 2003, 2003, 029. [Google Scholar] [CrossRef]
- Fang, W.; Wang, S.; Hu, W.; Haiman, Z.; Hui, L.; May, M. Challenges to the DGP model from horizon-scale growth and geometry. Phys. Rev. D 2008, 78, 103509. [Google Scholar] [CrossRef]
- Sahni, V.; Shtanov, Y. Braneworld models of dark energy. J. Cosmol. Astropart. Phys. 2003, 2003, 014. [Google Scholar] [CrossRef]
- Schmidt, F. Cosmological simulations of normal-branch braneworld gravity. Phys. Rev. D 2009, 80, 123003. [Google Scholar] [CrossRef]
- Koyama, K.; Silva, F.P. Non-linear interactions in a cosmological background in the DGP braneworld. Phys. Rev. D 2007, 75, 084040. [Google Scholar] [CrossRef]
- Nicolis, A.; Rattazzi, R.; Trincherini, E. Galileon as a local modification of gravity. Phys. Rev. D 2009, 79, 064036. [Google Scholar] [CrossRef]
- Deffayet, C.; Gao, X.; Steer, D.A.; Zahariade, G. From k-essence to generalized Galileons. Phys. Rev. D 2011, 84, 064039. [Google Scholar] [CrossRef]
- Kobayashi, T.; Yamaguchi, M.; Yokoyama, J. Generalized G-Inflation: Inflation with the Most General Second-Order Field Equations. Prog. Theor. Phys. 2011, 126, 511–529. [Google Scholar] [CrossRef]
- Bertotti, B.; Iess, L.; Tortora, P. A test of general relativity using radio links with the Cassini spacecraft. Nature 2003, 425, 374–376. [Google Scholar] [CrossRef] [PubMed]
- Merkowitz, S. Tests of Gravity Using Lunar Laser Ranging. Living Rev. Relativ. 2010, 13, 1–30. [Google Scholar] [CrossRef] [PubMed]
- Murphy, T.W., Jr.; Adelberger, E.G.; Battat, J.B.R.; Hoyle, C.D.; Johnson, N.H.; McMillan, R.J.; Stubbs, C.W.; Swanson, H.E. APOLLO: Millimeter lunar laser ranging. Class. Quantum Gravity 2012, 29, 184005. [Google Scholar] [CrossRef]
- Adelberger, E.G.; Heckel, B.R.; Nelson, A.E. Tests of the Gravitational Inverse-Square Law. Annu. Rev. Nucl. Part. Sci. 2003, 53, 77–121. [Google Scholar] [CrossRef]
- Kapner, D.J.; Cook, T.S.; Adelberger, E.G.; Gundlach, J.H.; Heckel, B.R.; Hoyle, C.D.; Swanson, H.E. Tests of the Gravitational Inverse-Square Law below the Dark-Energy Length Scale. Phys. Rev. Lett. 2007, 98, 021101. [Google Scholar] [CrossRef]
- Hinterbichler, K.; Khoury, J. Symmetron Fields: Screening Long-Range Forces Through Local Symmetry Restoration. arXiv 2010, arXiv:1001.4525. [Google Scholar]
- Hinterbichler, K.; Khoury, J.; Levy, A.; Matas, A. Symmetron Cosmology. Phys. Rev. D 2011, 84, 103521. [Google Scholar] [CrossRef]
- Khoury, J.; Weltman, A. Chameleon fields: Awaiting surprises for tests of gravity in space. Phys. Rev. Lett. 2004, 93, 171104. [Google Scholar] [CrossRef] [PubMed]
- Khoury, J.; Weltman, A. Chameleon cosmology. Phys. Rev. D 2004, 69, 044026. [Google Scholar] [CrossRef]
- Mota, D.F.; Shaw, D.J. Evading Equivalence Principle Violations, Cosmological and other Experimental Constraints in Scalar Field Theories with a Strong Coupling to Matter. Phys. Rev. D 2007, 75, 063501. [Google Scholar] [CrossRef]
- Brax, P.; van de Bruck, C.; Davis, A.C.; Shaw, D.J. f(R) Gravity and Chameleon Theories. Phys. Rev. D 2008, 78, 104021. [Google Scholar] [CrossRef]
- Vainshtein, A.I. To the problem of nonvanishing gravitation mass. Phys. Lett. B 1972, 39, 393–394. [Google Scholar] [CrossRef]
- Babichev, E.; Deffayet, C.; Ziour, R. k-Mouflage gravity. Int. J. Mod. Phys. D 2009, 18, 2147–2154. [Google Scholar] [CrossRef]
- Brax, P.; Valageas, P. K-mouflage Cosmology: The Background Evolution. Phys. Rev. D 2014, 90, 023507. [Google Scholar] [CrossRef]
- Brax, P.; Valageas, P. K-mouflage Cosmology: Formation of Large-Scale Structures. Phys. Rev. D 2014, 90, 023508. [Google Scholar] [CrossRef]
- Ade, P.A.R. et al. [Planck Collaboration] Planck 2015 results. XIV. Dark energy and modified gravity. Astron. Astrophys. 2016, 594, A14. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Mukhanov, V.; Steinhardt, P.J. Dynamical Solution to the Problem of a Small Cosmological Constant and Late-Time Cosmic Acceleration. Phys. Rev. Lett. 2000, 85, 4438–4441. [Google Scholar] [CrossRef]
- Armendariz-Picon, C.; Mukhanov, V.; Steinhardt, P.J. Essentials of k-essence. Phys. Rev. D 2001, 63, 103510. [Google Scholar] [CrossRef]
- Ishak, M. Testing general relativity in cosmology. Living Rev. Relativ. 2019, 22, 1. [Google Scholar] [CrossRef] [PubMed]
- Sefusatti, E.; Vernizzi, F. Cosmological structure formation with clustering quintessence. J. Cosmol. Astropart. Phys. 2011, 2011, 047. [Google Scholar] [CrossRef]
- Hassani, F.; L’Huillier, B.; Shafieloo, A.; Kunz, M.; Adamek, J. Parametrising non-linear dark energy perturbations. J. Cosmol. Astropart. Phys. 2020, 2020, 039. [Google Scholar] [CrossRef]
- Frusciante, N.; Peirone, S.; Atayde, L.; De Felice, A. Phenomenology of the generalized cubic covariant Galileon model and cosmological bounds. Phys. Rev. D 2020, 101, 064001. [Google Scholar] [CrossRef]
- Pogosian, L.; Silvestri, A. What can cosmology tell us about gravity? Constraining Horndeski gravity with Σ and μ. Phys. Rev. D 2016, 94, 104014. [Google Scholar] [CrossRef]
- Zhao, G.B.; Pogosian, L.; Silvestri, A.; Zylberberg, J. Cosmological Tests of General Relativity with Future Tomographic Surveys. Phys. Rev. Lett. 2009, 103, 241301. [Google Scholar] [CrossRef]
- Bloomfield, J.; Flanagan, É.É.; Park, M.; Watson, S. Dark energy or modified gravity? An effective field theory approach. J. Cosmol. Astro-Part. Phys. 2013, 2013, 010. [Google Scholar] [CrossRef]
- Frusciante, N.; Perenon, L. Effective field theory of dark energy: A review. Phys. Rept. 2020, 857, 1–63. [Google Scholar] [CrossRef]
- Creminelli, P.; Luty, M.A.; Nicolis, A.; Senatore, L. Starting the Universe: Stable Violation of the Null Energy Condition and Non-standard Cosmologies. J. High Energy Phys. 2006, 12, 080. [Google Scholar] [CrossRef]
- Cheung, C.; Creminelli, P.; Fitzpatrick, A.L.; Kaplan, J.; Senatore, L. The Effective Field Theory of Inflation. J. High Energy Phys. 2008, 03, 014. [Google Scholar] [CrossRef]
- Weinberg, S. Effective Field Theory for Inflation. Phys. Rev. D 2008, 77, 123541. [Google Scholar] [CrossRef]
- Gubitosi, G.; Piazza, F.; Vernizzi, F. The Effective Field Theory of Dark Energy. J. Phys. Rev. D 2008, 77, 123541. [Google Scholar] [CrossRef]
- Hu, B.; Raveri, M.; Frusciante, N.; Silvestri, A. Effective Field Theory of Cosmic Acceleration: An implementation in CAMB. Phys. Rev. D 2014, 89, 103530. [Google Scholar] [CrossRef]
- Raveri, M.; Hu, B.; Frusciante, N.; Silvestri, A. Effective Field Theory of Cosmic Acceleration: Constraining dark energy with CMB data. J. Phys. Rev. D 2014, 90, 043513. [Google Scholar] [CrossRef]
- Bellini, E.; Sawicki, I. Maximal freedom at minimum cost: Linear large-scale structure in general modifications of gravity. J. Cosmol. Astropart. Phys. 2014, 07, 050. [Google Scholar] [CrossRef]
- Zumalacárregui, M.; Bellini, E.; Sawicki, I.; Lesgourgues, J.; Ferreira, P.G. hi_class: Horndeski in the Cosmic Linear Anisotropy Solving System. J. Cosmol. Astropart. Phys. 2017, 08, 019. [Google Scholar] [CrossRef]
- Bellini, E.; Sawicki, I.; Zumalacárregui, M. hi_class: Background Evolution, Initial Conditions and Approximation Schemes. J. Cosmol. Astropart. Phys. 2020, 02, 008. [Google Scholar] [CrossRef]
- Lombriser, L.; Taylor, A. Breaking a dark degeneracy with gravitational waves. J. Cosmol. Astropart. Phys. 2016, 2016, 031. [Google Scholar] [CrossRef]
- Lombriser, L.; Lima, N.A. Challenges to self-acceleration in modified gravity from gravitational waves and large-scale structure. Phys. Lett. B 2017, 765, 382–385. [Google Scholar] [CrossRef]
- Nunes, R.C.; Alves, M.E.S.; de Araujo, J.C.N. Primordial gravitational waves in Horndeski gravity. Phys. Rev. D 2019, 99, 084022. [Google Scholar] [CrossRef]
- Pettorino, V.; Amendola, L. Friction in gravitational waves: A test for early-time modified gravity. Phys. Lett. B 2015, 742, 353–357. [Google Scholar] [CrossRef]
- Matos, I.S.; Calvão, M.O.; Waga, I. Gravitational wave propagation in f (R ) models: New parametrizations and observational constraints. Phys. Rev. D 2021, 103, 104059. [Google Scholar] [CrossRef]
- Sathyaprakash, B.; Abernathy, M.; Acernese, F.; Ajith, P.; Allen, B.; Amaro-Seoane, P.; Andersson, N.; Aoudia, S.; Arun, K.; Astone, P.; et al. Scientific objectives of Einstein Telescope. Class. Quantum Gravity 2012, 29, 124013. [Google Scholar] [CrossRef]
- Pardo, K.; Fishbach, M.; Holz, D.E.; Spergel, D.N. Limits on the number of spacetime dimensions from GW170817. J. Cosmol. Astropart. Phys. 2018, 2018, 048. [Google Scholar] [CrossRef]
- Thomas, D.B. Cosmological gravity on all scales: Simple equations, required conditions, and a framework for modified gravity. Phys. Rev. D 2020, 101, 123517. [Google Scholar] [CrossRef]
- Hu, W.; Sawicki, I. Parametrized post-Friedmann framework for modified gravity. Phys. Rev. D 2007, 76, 104043. [Google Scholar] [CrossRef]
- Milillo, I.; Bertacca, D.; Bruni, M.; Maselli, A. Missing link: A nonlinear post-Friedmann framework for small and large scales. Phys. Rev. D 2015, 92, 023519. [Google Scholar] [CrossRef]
- Srinivasan, S.; Thomas, D.B.; Pace, F.; Battye, R. Cosmological gravity on all scales. Part II. Model independent modified gravity N-body simulations. J. Cosmol. Astropart. Phys. 2021, 06, 016. [Google Scholar] [CrossRef]
- Zhao, G.B.; Giannantonio, T.; Pogosian, L.; Silvestri, A.; Bacon, D.J.; Koyama, K.; Nichol, R.C.; Song, Y.S. Probing modifications of General Relativity using current cosmological observations. Phys. Rev. D 2010, 81, 103510. [Google Scholar] [CrossRef]
- Hojjati, A.; Zhao, G.B.; Pogosian, L.; Silvestri, A.; Crittenden, R.; Koyama, K. Cosmological tests of General Relativity: A principal component analysis. Phys. Rev. D 2012, 85, 043508. [Google Scholar] [CrossRef]
- Casas, S.; Kunz, M.; Martinelli, M.; Pettorino, V. Linear and non-linear Modified Gravity forecasts with future surveys. Phys. Dark Universe 2017, 18, 73–104. [Google Scholar] [CrossRef]
- Raveri, M. Reconstructing Gravity on Cosmological Scales. Phys. Rev. D 2020, 101, 083524. [Google Scholar] [CrossRef]
- Raveri, M.; Pogosian, L.; Martinelli, M.; Koyama, K.; Silvestri, A.; Zhao, G.B.; Li, J.; Peirone, S.; Zucca, A. Principal reconstructed modes of dark energy and gravity. arXiv 2021, arXiv:2107.12990. [Google Scholar] [CrossRef]
- Pogosian, L.; Raveri, M.; Koyama, K.; Martinelli, M.; Silvestri, A.; Zhao, G.B.; Li, J.; Peirone, S.; Zucca, A. Imprints of cosmological tensions in reconstructed gravity. Nat. Astron. 2022, 6, 1484–1490. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Yu, J.T. Primeval Adiabatic Perturbation in an Expanding Universe. Astrophys. J. 1970, 162, 815. [Google Scholar] [CrossRef]
- Sunyaev, R.A.; Zeldovich, Y.B. Small-Scale Fluctuations of Relic Radiation. Astrophys. Space Sci. 1970, 7, 3–19. [Google Scholar] [CrossRef]
- Sachs, R.K.; Wolfe, A.M. Perturbations of a Cosmological Model and Angular Variations of the Microwave Background. Astrophys. J. 1967, 147, 73. [Google Scholar] [CrossRef]
- Lewis, A.; Challinor, A. Weak gravitational lensing of the CMB. Phys. Rep. 2006, 429, 1–65. [Google Scholar] [CrossRef]
- Hanson, D.; Challinor, A.; Lewis, A. Weak lensing of the CMB. Gen. Relativ. Gravit. 2010, 42, 2197–2218. [Google Scholar] [CrossRef]
- Mandelbaum, R. Weak Lensing for Precision Cosmology. Annu. Rev. Astron. Astrophys. 2018, 56, 393–433. [Google Scholar] [CrossRef]
- Bartelmann, M. TOPICAL review Gravitational lensing. Class. Quantum Gravity 2010, 27, 233001. [Google Scholar] [CrossRef]
- Desjacques, V.; Jeong, D.; Schmidt, F. Large-scale galaxy bias. Phys. Rep. 2018, 733, 1–193. [Google Scholar] [CrossRef]
- Zivick, P.; Sutter, P.M.; Wandelt, B.D.; Li, B.; Lam, T.Y. Using cosmic voids to distinguish f(R) gravity in future galaxy surveys. Mon. Not. R. Astron. Soc. 2015, 451, 4215–4222. [Google Scholar] [CrossRef]
- Cai, Y.C.; Padilla, N.; Li, B. Testing gravity using cosmic voids. Mon. Not. R. Astron. Soc. 2015, 451, 1036–1055. [Google Scholar] [CrossRef]
- Barreira, A.; Cautun, M.; Li, B.; Baugh, C.M.; Pascoli, S. Weak lensing by voids in modified lensing potentials. J. Cosmol. Astropart. Phys. 2015, 2015, 028. [Google Scholar] [CrossRef]
- Baker, T.; Clampitt, J.; Jain, B.; Trodden, M. Void lensing as a test of gravity. Phys. Rev. D 2018, 98, 023511. [Google Scholar] [CrossRef]
- Alam, S.; Arnold, C.; Aviles, A.; Bean, R.; Cai, Y.C.; Cautun, M.; Cervantes-Cota, J.L.; Cuesta-Lazaro, C.; Devi, N.C.; Eggemeier, A.; et al. Towards testing the theory of gravity with DESI: Summary statistics, model predictions and future simulation requirements. J. Cosmol. Astropart. Phys. 2021, 2021, 050. [Google Scholar] [CrossRef]
- Padilla, N.D.; Ceccarelli, L.; Lambas, D.G. Spatial and dynamical properties of voids in a Λ cold dark matter universe. Mon. Not. R. Astron. Soc. 2005, 363, 977–990. [Google Scholar] [CrossRef]
- Platen, E.; van de Weygaert, R.; Jones, B.J.T. A cosmic watershed: The WVF void detection technique. Mon. Not. R. Astron. Soc. 2007, 380, 551–570. [Google Scholar] [CrossRef]
- Neyrinck, M.C. ZOBOV: A parameter-free void-finding algorithm. Mon. Not. R. Astron. Soc. 2008, 386, 2101–2109. [Google Scholar] [CrossRef]
- Cautun, M.; Paillas, E.; Cai, Y.C.; Bose, S.; Armijo, J.; Li, B.; Padilla, N. The Santiago-Harvard-Edinburgh-Durham void comparison—I. SHEDding light on chameleon gravity tests. Mon. Not. R. Astron. Soc. 2018, 476, 3195–3217. [Google Scholar] [CrossRef]
- Gruen, D.; Friedrich, O.; Amara, A.; Bacon, D.; Bonnett, C.; Hartley, W.; Jain, B.; Jarvis, M.; Kacprzak, T.; Krause, E.; et al. Weak lensing by galaxy troughs in DES Science Verification data. Mon. Not. R. Astron. Soc. 2016, 455, 3367–3380. [Google Scholar] [CrossRef]
- Sunyaev, R.A.; Zeldovich, I.B. Microwave background radiation as a probe of the contemporary structure and history of the universe. Annu. Rev. Astron. Astrophys. 1980, 18, 537–560. [Google Scholar] [CrossRef]
- Shaw, L.D.; Rudd, D.H.; Nagai, D. Deconstructing the Kinetic SZ Power Spectrum. Astrophys. J. 2012, 756, 15. [Google Scholar] [CrossRef]
- Ma, Y.Z.; Zhao, G.B. Dark energy imprints on the kinematic Sunyaev-Zel’dovich signal. Phys. Lett. B 2014, 735, 402–411. [Google Scholar] [CrossRef]
- Tully, R.B.; Fisher, J.R. A new method of determining distances to galaxies. Astron. Astrophys. 1977, 54, 661–673. [Google Scholar]
- McGaugh, S.S.; Schombert, J.M.; Bothun, G.D.; de Blok, W.J.G. The Baryonic Tully-Fisher Relation. Astrophys. J. Lett. 2000, 533, L99–L102. [Google Scholar] [CrossRef]
- Djorgovski, S.; Davis, M. Fundamental Properties of Elliptical Galaxies. Astrophys. J. 1987, 313, 59. [Google Scholar] [CrossRef]
- Kaiser, N. Clustering in real space and in redshift space. Mon. Not. R. Astron. Soc. 1987, 227, 1–21. [Google Scholar] [CrossRef]
- Linder, E.V. Cosmic growth history and expansion history. Phys. Rev. D 2005, 72, 043529. [Google Scholar] [CrossRef]
- Linder, E.V.; Cahn, R.N. Parameterized beyond-Einstein growth. Astropart. Phys. 2007, 28, 481–488. [Google Scholar] [CrossRef]
- Jennings, E.; Baugh, C.M.; Li, B.; Zhao, G.B.; Koyama, K. Redshift-space distortions in f(R) gravity. Mon. Not. R. Astron. Soc. 2012, 425, 2128–2143. [Google Scholar] [CrossRef]
- Barreira, A.; Sánchez, A.G.; Schmidt, F. Validating estimates of the growth rate of structure with modified gravity simulations. Phys. Rev. D 2016, 94, 084022. [Google Scholar] [CrossRef]
- Hernández-Aguayo, C.; Hou, J.; Li, B.; Baugh, C.M.; Sánchez, A.G. Large-scale redshift space distortions in modified gravity theories. Mon. Not. R. Astron. Soc. 2019, 485, 2194–2213. [Google Scholar] [CrossRef]
- Hernández-Aguayo, C.; Prada, F.; Baugh, C.M.; Klypin, A. Building a digital twin of a luminous red galaxy spectroscopic survey: Galaxy properties and clustering covariance. Mon. Not. R. Astron. Soc. 2021, 503, 2318–2339. [Google Scholar] [CrossRef]
- He, J.h.; Guzzo, L.; Li, B.; Baugh, C.M. No evidence for modifications of gravity from galaxy motions on cosmological scales. Nat. Astron. 2018, 2, 967–972. [Google Scholar] [CrossRef]
- Hui, L.; Nicolis, A.; Stubbs, C.W. Equivalence principle implications of modified gravity models. Phys. Rev. D 2009, 80, 104002. [Google Scholar] [CrossRef]
- Clampitt, J.; Cai, Y.C.; Li, B. Voids in modified gravity: Excursion set predictions. Mon. Not. R. Astron. Soc. 2013, 431, 749–766. [Google Scholar] [CrossRef]
- Lam, T.Y.; Clampitt, J.; Cai, Y.C.; Li, B. Voids in modified gravity reloaded: Eulerian void assignment. Mon. Not. R. Astron. Soc. 2015, 450, 3319–3330. [Google Scholar] [CrossRef]
- Hamaus, N.; Sutter, P.M.; Lavaux, G.; Wandelt, B.D. Probing cosmology and gravity with redshift-space distortions around voids. J. Cosmol. Astropart. Phys. 2015, 2015, 036. [Google Scholar] [CrossRef]
- Hamaus, N.; Pisani, A.; Sutter, P.M.; Lavaux, G.; Escoffier, S.; Wandelt, B.D.; Weller, J. Constraints on Cosmology and Gravity from the Dynamics of Voids. Phys. Rev. Lett. 2016, 117, 091302. [Google Scholar] [CrossRef]
- Cai, Y.C.; Taylor, A.; Peacock, J.A.; Padilla, N. Redshift-space distortions around voids. Mon. Not. R. Astron. Soc. 2016, 462, 2465–2477. [Google Scholar] [CrossRef]
- Hamaus, N.; Wandelt, B.D.; Sutter, P.M.; Lavaux, G.; Warren, M.S. Cosmology with Void-Galaxy Correlations. Phys. Rev. Lett. 2014, 112, 041304. [Google Scholar] [CrossRef]
- Hamaus, N.; Pisani, A.; Choi, J.A.; Lavaux, G.; Wandelt, B.D.; Weller, J. Precision cosmology with voids in the final BOSS data. J. Cosmol. Astropart. Phys. 2020, 2020, 023. [Google Scholar] [CrossRef]
- Hawken, A.J.; Aubert, M.; Pisani, A.; Cousinou, M.C.; Escoffier, S.; Nadathur, S.; Rossi, G.; Schneider, D.P. Constraints on the growth of structure around cosmic voids in eBOSS DR14. J. Cosmol. Astropart. Phys. 2020, 2020, 012. [Google Scholar] [CrossRef]
- Nadathur, S.; Woodfinden, A.; Percival, W.J.; Aubert, M.; Bautista, J.; Dawson, K.; Escoffier, S.; Fromenteau, S.; Gil-Marín, H.; Rich, J.; et al. The completed SDSS-IV extended baryon oscillation spectroscopic survey: Geometry and growth from the anisotropic void-galaxy correlation function in the luminous red galaxy sample. Mon. Not. R. Astron. Soc. 2020, 499, 4140–4157. [Google Scholar] [CrossRef]
- Nadathur, S.; Percival, W.J. An accurate linear model for redshift space distortions in the void-galaxy correlation function. Mon. Not. R. Astron. Soc. 2019, 483, 3472–3487. [Google Scholar] [CrossRef]
- Nadathur, S.; Carter, P.; Percival, W.J. A Zeldovich reconstruction method for measuring redshift space distortions using cosmic voids. Mon. Not. R. Astron. Soc. 2019, 482, 2459–2470. [Google Scholar] [CrossRef]
- Limber, D.N. The Analysis of Counts of the Extragalactic Nebulae in Terms of a Fluctuating Density Field. Astrophys. J. 1953, 117, 134. [Google Scholar] [CrossRef]
- Troxel, M.A.; MacCrann, N.; Zuntz, J.; Eifler, T.F.; Krause, E.; Dodelson, S.; Gruen, D.; Blazek, J.; Friedrich, O.; Samuroff, S.; et al. Dark Energy Survey Year 1 results: Cosmological constraints from cosmic shear. Phys. Rev. D 2018, 98, 043528. [Google Scholar] [CrossRef]
- Hildebrandt, H.; Köhlinger, F.; van den Busch, J.L.; Joachimi, B.; Heymans, C.; Kannawadi, A.; Wright, A.H.; Asgari, M.; Blake, C.; Hoekstra, H.; et al. KiDS+VIKING-450: Cosmic shear tomography with optical and infrared data. Astron. Astrophys. 2020, 633, A69. [Google Scholar] [CrossRef]
- Hikage, C.; Oguri, M.; Hamana, T.; More, S.; Mandelbaum, R.; Takada, M.; Köhlinger, F.; Miyatake, H.; Nishizawa, A.J.; Aihara, H.; et al. Cosmology from cosmic shear power spectra with Subaru Hyper Suprime-Cam first-year data. Publ. Astron. Soc. Jpn. 2019, 71, 43. [Google Scholar] [CrossRef]
- Hamana, T.; Shirasaki, M.; Miyazaki, S.; Hikage, C.; Oguri, M.; More, S.; Armstrong, R.; Leauthaud, A.; Mandelbaum, R.; Miyatake, H.; et al. Cosmological constraints from cosmic shear two-point correlation functions with HSC survey first-year data. Phys. Rev. D 2022, 74, 488–491. [Google Scholar] [CrossRef]
- Asgari, M.; Lin, C.A.; Joachimi, B.; Giblin, B.; Heymans, C.; Hildebrandt, H.; Kannawadi, A.; Stölzner, B.; Tröster, T.; van den Busch, J.L.; et al. KiDS-1000 cosmology: Cosmic shear constraints and comparison between two point statistics. Astron. Astrophys. 2022, 645, A104. [Google Scholar] [CrossRef]
- Amon, A.; Gruen, D.; Troxel, M.A.; MacCrann, N.; Dodelson, S.; Choi, A.; Doux, C.; Secco, L.F.; Samuroff, S.; Krause, E.; et al. Dark Energy Survey Year 3 results: Cosmology from cosmic shear and robustness to data calibration. Phys. Rev. D 2022, 105, 023514. [Google Scholar] [CrossRef]
- Secco, L.F.; Samuroff, S.; Krause, E.; Jain, B.; Blazek, J.; Raveri, M.; Campos, A.; Amon, A.; Chen, A.; Doux, C.; et al. Dark Energy Survey Year 3 results: Cosmology from cosmic shear and robustness to modeling uncertainty. Phys. Rev. D 2022, 105, 023515. [Google Scholar] [CrossRef]
- Schneider, P.; Eifler, T.; Krause, E. hlDark Energy Survey Year 3 results: Cosmology from cosmic shear and robustness to modeling uncertainty. Astron. Astrophys. 2010, 520, A116. [Google Scholar] [CrossRef]
- Li, B.; Shirasaki, M. Galaxy-galaxy weak gravitational lensing in f(R) gravity. Mon. Not. R. Astron. Soc. 2018, 474, 3599–3614. [Google Scholar] [CrossRef]
- Cataneo, M.; Lombriser, L.; Heymans, C.; Mead, A.J.; Barreira, A.; Bose, S.; Li, B. On the road to percent accuracy: Non-linear reaction of the matter power spectrum to dark energy and modified gravity. Mon. Not. R. Astron. Soc. 2019, 488, 2121–2142. [Google Scholar] [CrossRef]
- Bose, B.; Cataneo, M.; Tröster, T.; Xia, Q.; Heymans, C.; Lombriser, L. On the road to per cent accuracy IV: ReACT—Computing the non-linear power spectrum beyond ΛCDM. Mon. Not. R. Astron. Soc. 2020, 498, 4650–4662. [Google Scholar] [CrossRef]
- Chisari, N.E.; Mead, A.J.; Joudaki, S.; Ferreira, P.G.; Schneider, A.; Mohr, J.; Tröster, T.; Alonso, D.; McCarthy, I.G.; Martin-Alvarez, S.; et al. Modelling baryonic feedback for survey cosmology. Cosmol. Nongalact. Astrophys. 2019, 2, 4. [Google Scholar] [CrossRef]
- Hildebrandt, H.; van den Busch, J.L.; Wright, A.H.; Blake, C.; Joachimi, B.; Kuijken, K.; Tröster, T.; Asgari, M.; Bilicki, M.; de Jong, J.T.A.; et al. KiDS-1000 catalogue: Redshift distributions and their calibration. Astronom. Astrophys. 2020, 647, A124. [Google Scholar] [CrossRef]
- Myles, J.; Alarcon, A.; Amon, A.; Sánchez, C.; Everett, S.; DeRose, J.; McCullough, J.; Gruen, D.; Bernstein, G.M.; Troxel, M.A.; et al. Dark Energy Survey Year 3 results: Redshift calibration of the weak lensing source galaxies. Mon. Not. 2021, 647, 4249–4277. [Google Scholar] [CrossRef]
- Giblin, B.; Heymans, C.; Asgari, M.; Hildebrandt, H.; Hoekstra, H.; Joachimi, B.; Kannawadi, A.; Kuijken, K.; Lin, C.A.; Miller, L.; et al. KiDS-1000 catalogue: Weak gravitational lensing shear measurements. Astronom. Astrophys. 2021, 645, A105. [Google Scholar] [CrossRef]
- Gatti, M.; Sheldon, E.; Amon, A.; Becker, M.; Troxel, M.; Choi, A.; Doux, C.; MacCrann, N.; Navarro-Alsina, A.; Harrison, I.; et al. KiDS-1000 catalogue: Weak gravitational lensing shear measurements. Mon. Not. 2021, 504, 4312–4336. [Google Scholar] [CrossRef]
- Huterer, D. Growth of Cosmic Structure. arXiv 2022, arXiv:2212.05003. [Google Scholar]
- Aghanim, N. et al. [Planck Collaboration] Planck 2018 results. VIII. Gravitational lensing. Astron. Astrophys. 2020, 641, A8. [Google Scholar] [CrossRef]
- Sunyaev, R.A.; Zeldovich, Y.B. The Observations of Relic Radiation as a Test of the Nature of X-Ray Radiation from the Clusters of Galaxies. Comments Astrophys. Space Phys. 1972, 4, 173. [Google Scholar]
- Darwish, O.; Madhavacheril, M.S.; Sherwin, B.D.; Aiola, S.; Battaglia, N.; Beall, J.A.; Becker, D.T.; Bond, J.R.; Calabrese, E.; Choi, S.K.; et al. The Atacama Cosmology Telescope: A CMB lensing mass map over 2100 square degrees of sky and its cross-correlation with BOSS-CMASS galaxies. Mon. Not. R. Astron. Soc. 2021, 500, 2250–2263. [Google Scholar] [CrossRef]
- White, M.; Zhou, R.; DeRose, J.; Ferraro, S.; Chen, S.F.; Kokron, N.; Bailey, S.; Brooks, D.; García-Bellido, J.; Guy, J.; et al. Cosmological constraints from the tomographic cross-correlation of DESI Luminous Red Galaxies and Planck CMB lensing. J. Cosmol. Astropart. Phys. 2022, 2022, 007. [Google Scholar] [CrossRef]
- Modi, C.; White, M.; Vlah, Z. Modeling CMB lensing cross correlations with CLEFT. J. Cosmol. Astropart. Phys. 2017, 2017, 009. [Google Scholar] [CrossRef]
- Chung, E.; Foreman, S.; van Engelen, A. Baryonic effects on CMB lensing and neutrino mass constraints. Phys. Rev. D 2020, 101, 063534. [Google Scholar] [CrossRef]
- McCarthy, F.; Foreman, S.; van Engelen, A. Avoiding baryonic feedback effects on neutrino mass measurements from CMB lensing. Phys. Rev. D 2021, 103, 103538. [Google Scholar] [CrossRef]
- McCarthy, F.; Hill, J.C.; Madhavacheril, M.S. Baryonic feedback biases on fundamental physics from lensed CMB power spectra. Phys. Rev. D 2022, 105, 023517. [Google Scholar] [CrossRef]
- Bragança, D.P.L.; Lewandowski, M.; Sekera, D.; Senatore, L.; Sgier, R. Baryonic effects in the Effective Field Theory of Large-Scale Structure and an analytic recipe for lensing in CMB-S4. J. Cosmol. Astropart. Phys. 2021, 2021, 074. [Google Scholar] [CrossRef]
- Hu, W.; Okamoto, T. Mass Reconstruction with Cosmic Microwave Background Polarization. Astrophys. J. 2002, 574, 566–574. [Google Scholar] [CrossRef]
- Okamoto, T.; Hu, W. Cosmic microwave background lensing reconstruction on the full sky. Phys. Rev. D 2003, 67, 083002. [Google Scholar] [CrossRef]
- Maniyar, A.S.; Ali-Haïmoud, Y.; Carron, J.; Lewis, A.; Madhavacheril, M.S. Quadratic estimators for CMB weak lensing. Phys. Rev. D 2021, 103, 083524. [Google Scholar] [CrossRef]
- Hirata, C.M.; Seljak, U. Reconstruction of lensing from the cosmic microwave background polarization. Phys. Rev. D 2003, 68, 083002. [Google Scholar] [CrossRef]
- Millea, M.; Seljak, U. Marginal unbiased score expansion and application to CMB lensing. Phys. Rev. D 2022, 105, 103531. [Google Scholar] [CrossRef]
- Legrand, L.; Carron, J. Lensing power spectrum of the cosmic microwave background with deep polarization experiments. Phys. Rev. D 2022, 105, 123519. [Google Scholar] [CrossRef]
- Carron, J. Real-world CMB lensing quadratic estimator power spectrum response. arXiv 2022, arXiv:2210.05449. [Google Scholar] [CrossRef]
- DES collaboration; Abbott, T.M.C.; Abdalla, F.B.; Avila, S.; Banerji, M.; Baxter, E.; Bechtol, K.; Becker, M.R.; Bertin, E.; Blazek, J.; et al. Dark Energy Survey year 1 results: Constraints on extended cosmological models from galaxy clustering and weak lensing. Phys. Rev. D 2019, 99, 123505. [Google Scholar] [CrossRef]
- Heymans, C.; Tröster, T.; Asgari, M.; Blake, C.; Hildebrandt, H.; Joachimi, B.; Kuijken, K.; Lin, C.A.; Sánchez, A.G.; van den Busch, J.L.; et al. KiDS-1000 Cosmology: Multi-probe weak gravitational lensing and spectroscopic galaxy clustering constraints. Astron. Astrophys. 2021, 646, A140. [Google Scholar] [CrossRef]
- Abbott, T.M.C. et al. [DES Collaboration] Dark Energy Survey Year 3 results: Cosmological constraints from galaxy clustering and weak lensing. Phys. Rev. D 2022, 105, 023520. [Google Scholar] [CrossRef]
- Abbott, T.M.C. et al. [DES Collaboration] Joint analysis of DES Year 3 data and CMB lensing from SPT and Planck III: Combined cosmological constraints. arXiv 2022, arXiv:2206.10824. [Google Scholar]
- Singh, S.; Mandelbaum, R.; Brownstein, J.R. Cross-correlating Planck CMB lensing with SDSS: Lensing-lensing and galaxy-lensing cross-correlations. Mon. Not. R. Astron. Soc. 2017, 464, 2120–2138. [Google Scholar] [CrossRef]
- Singh, S.; Mandelbaum, R.; Seljak, U.; Rodríguez-Torres, S.; Slosar, A. Cosmological constraints from galaxy-lensing cross-correlations using BOSS galaxies with SDSS and CMB lensing. Mon. Not. R. Astron. Soc. 2020, 491, 51–68. [Google Scholar] [CrossRef]
- Omori, Y.; Giannantonio, T.; Porredon, A.; Baxter, E.J.; Chang, C.; Crocce, M.; Fosalba, P.; Alarcon, A.; Banik, N.; Blazek, J.; et al. Dark Energy Survey Year 1 Results: Tomographic cross-correlations between Dark Energy Survey galaxies and CMB lensing from South Pole Telescope +Planck. Phys. Rev. D 2019, 100, 043501. [Google Scholar] [CrossRef]
- Krolewski, A.; Ferraro, S.; White, M. Cosmological constraints from unWISE and Planck CMB lensing tomography. J. Cosmol. Astropart. Phys. 2021, 2021, 028. [Google Scholar] [CrossRef]
- Schmittfull, M.; Seljak, U. Parameter constraints from cross-correlation of CMB lensing with galaxy clustering. Phys. Rev. D 2018, 97, 123540. [Google Scholar] [CrossRef]
- Reyes, R.; Mandelbaum, R.; Seljak, U.; Baldauf, T.; Gunn, J.E.; Lombriser, L.; Smith, R.E. Confirmation of general relativity on large scales from weak lensing and galaxy velocities. Nature 2010, 464, 256–258. [Google Scholar] [CrossRef]
- Blake, C.; Joudaki, S.; Heymans, C.; Choi, A.; Erben, T.; Harnois-Deraps, J.; Hildebrandt, H.; Joachimi, B.; Nakajima, R.; van Waerbeke, L.; et al. RCSLenS: Testing gravitational physics through the cross-correlation of weak lensing and large-scale structure. Mon. Not. R. Astron. Soc. 2016, 456, 2806–2828. [Google Scholar] [CrossRef]
- de la Torre, S.; Jullo, E.; Giocoli, C.; Pezzotta, A.; Bel, J.; Granett, B.R.; Guzzo, L.; Garilli, B.; Scodeggio, M.; Bolzonella, M.; et al. The VIMOS Public Extragalactic Redshift Survey (VIPERS). Gravity test from the combination of redshift-space distortions and galaxy-galaxy lensing at 0.5 < z < 1.2. Astron. Astrophys. 2017, 608, A44. [Google Scholar] [CrossRef]
- Amon, A.; Blake, C.; Heymans, C.; Leonard, C.D.; Asgari, M.; Bilicki, M.; Choi, A.; Erben, T.; Glazebrook, K.; Harnois-Déraps, J.; et al. KiDS+2dFLenS+GAMA: Testing the cosmological model with the EG statistic. Mon. Not. R. Astron. Soc. 2018, 479, 3422–3437. [Google Scholar] [CrossRef]
- Blake, C.; Amon, A.; Asgari, M.; Bilicki, M.; Dvornik, A.; Erben, T.; Giblin, B.; Glazebrook, K.; Heymans, C.; Hildebrandt, H.; et al. Testing gravity using galaxy-galaxy lensing and clustering amplitudes in KiDS-1000, BOSS, and 2dFLenS. Astron. Astrophys. 2020, 642, A158. [Google Scholar] [CrossRef]
- Pullen, A.R.; Alam, S.; Ho, S. Probing gravity at large scales through CMB lensing. Mon. Not. R. Astron. Soc. 2015, 449, 4326–4335. [Google Scholar] [CrossRef]
- Zhang, Y.; Pullen, A.R.; Alam, S.; Singh, S.; Burtin, E.; Chuang, C.H.; Hou, J.; Lyke, B.W.; Myers, A.D.; Neveux, R.; et al. Testing general relativity on cosmological scales at redshift z ∼ 1.5 with quasar and CMB lensing. Mon. Not. R. Astron. Soc. 2021, 501, 1013–1027. [Google Scholar] [CrossRef]
- Ross, A.J.; Bautista, J.; Tojeiro, R.; Alam, S.; Bailey, S.; Burtin, E.; Comparat, J.; Dawson, K.S.; de Mattia, A.; du Mas des Bourboux, H.; et al. The Completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: Large-scale structure catalogues for cosmological analysis. Mon. Not. R. Astron. Soc. 2020, 498, 2354–2371. [Google Scholar] [CrossRef]
- Hou, J.; Sánchez, A.G.; Ross, A.J.; Smith, A.; Neveux, R.; Bautista, J.; Burtin, E.; Zhao, C.; Scoccimarro, R.; Dawson, K.S.; et al. The completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: BAO and RSD measurements from anisotropic clustering analysis of the quasar sample in configuration space between redshift 0.8 and 2.2. Mon. Not. R. Astron. Soc. 2021, 500, 1201–1221. [Google Scholar] [CrossRef]
- Aghanim, N. et al. [Planck Collaboration] Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
- Dupé, F.X.; Rassat, A.; Starck, J.L.; Fadili, M.J. Measuring the integrated Sachs-Wolfe effect. Astron. Astrophys. 2011, 534, A51. [Google Scholar] [CrossRef]
- Ferraro, S.; Sherwin, B.D.; Spergel, D.N. WISE measurement of the integrated Sachs-Wolfe effect. Phys. Rev. D 2015, 91, 083533. [Google Scholar] [CrossRef]
- Crittenden, R.G.; Turok, N. Looking for a Cosmological Constant with the Rees-Sciama Effect. Phys. Rev. Lett. 1996, 76, 575–578. [Google Scholar] [CrossRef]
- Giannantonio, T.; Scranton, R.; Crittenden, R.G.; Nichol, R.C.; Boughn, S.P.; Myers, A.D.; Richards, G.T. Combined analysis of the integrated Sachs-Wolfe effect and cosmological implications. Phys. Rev. D 2008, 77, 123520. [Google Scholar] [CrossRef]
- Lombriser, L.; Hu, W.; Fang, W.; Seljak, U. Cosmological constraints on DGP braneworld gravity with brane tension. Phys. Rev. D 2009, 80, 063536. [Google Scholar] [CrossRef]
- Song, Y.S.; Peiris, H.; Hu, W. Cosmological constraints on f(R) acceleration models. Phys. Rev. D 2007, 76, 063517. [Google Scholar] [CrossRef]
- Lombriser, L.; Slosar, A.; Seljak, U.; Hu, W. Constraints on f(R) gravity from probing the large-scale structure. Phys. Rev. D 2012, 85, 124038. [Google Scholar] [CrossRef]
- Renk, J.; Zumalacárregui, M.; Montanari, F.; Barreira, A. Galileon gravity in light of ISW, CMB, BAO and H0 data. J. Cosmol. Astropart. Phys. 2017, 2017, 020. [Google Scholar] [CrossRef]
- Krolewski, A.; Ferraro, S. The Integrated Sachs Wolfe effect: UnWISE and Planck constraints on dynamical dark energy. J. Cosmol. Astropart. Phys. 2022, 2022, 033. [Google Scholar] [CrossRef]
- Raccanelli, A.; Zhao, G.B.; Bacon, D.J.; Jarvis, M.J.; Percival, W.J.; Norris, R.P.; Röttgering, H.; Abdalla, F.B.; Cress, C.M.; Kubwimana, J.C.; et al. Cosmological measurements with forthcoming radio continuum surveys. Mon. Not. R. Astron. Soc. 2012, 424, 801–819. [Google Scholar] [CrossRef]
- Hang, Q.; Alam, S.; Peacock, J.A.; Cai, Y.C. Galaxy clustering in the DESI Legacy Survey and its imprint on the CMB. Mon. Not. R. Astron. Soc. 2021, 501, 1481–1498. [Google Scholar] [CrossRef]
- Buchert, T.; Carfora, M.; Ellis, G.F.R.; Kolb, E.W.; MacCallum, M.A.H.; Ostrowski, J.J.; Räsänen, S.; Roukema, B.F.; Andersson, L.; Coley, A.A.; et al. Is there proof that backreaction of inhomogeneities is irrelevant in cosmology? Class. Quantum Gravity 2015, 32, 215021. [Google Scholar] [CrossRef]
- Rácz, G.; Dobos, L.; Beck, R.; Szapudi, I.; Csabai, I. Concordance cosmology without dark energy. Mon. Not. R. Astron. Soc. 2017, 469, L1–L5. [Google Scholar] [CrossRef]
- Foreman, S.; Meerburg, P.D.; Meyers, J.; van Engelen, A. Cosmic variance mitigation in measurements of the integrated Sachs-Wolfe effect. Phys. Rev. D 2019, 99, 083506. [Google Scholar] [CrossRef]
- Vishniac, E.T. Reionization and Small-Scale Fluctuations in the Microwave Background. Astrophys. J. 1987, 322, 597. [Google Scholar] [CrossRef]
- Jaffe, A.H.; Kamionkowski, M. Calculation of the Ostriker-Vishniac effect in cold dark matter models. Phys. Rev. D 1998, 58, 043001. [Google Scholar] [CrossRef]
- Dodelson, S.; Jubas, J.M. Reionization and Its Imprint on the Cosmic Microwave Background. Astrophys. J. 1995, 439, 503. [Google Scholar] [CrossRef]
- Ma, C.P.; Fry, J.N. Nonlinear Kinetic Sunyaev-Zeldovich Effect. Phys. Rev. Lett. 2002, 88, 211301. [Google Scholar] [CrossRef]
- Reichardt, C.L.; Patil, S.; Ade, P.A.R.; Anderson, A.J.; Austermann, J.E.; Avva, J.S.; Baxter, E.; Beall, J.A.; Bender, A.N.; Benson, B.A.; et al. An Improved Measurement of the Secondary Cosmic Microwave Background Anisotropies from the SPT-SZ + SPTpol Surveys. Astrophys. J. 2021, 908, 199. [Google Scholar] [CrossRef]
- Gorce, A.; Douspis, M.; Salvati, L. Retrieving cosmological information from small-scale CMB foregrounds. II. The kinetic Sunyaev Zel’dovich effect. Astron. Astrophys. 2022, 662, A122. [Google Scholar] [CrossRef]
- Calafut, V.; Gallardo, P.A.; Vavagiakis, E.M.; Amodeo, S.; Aiola, S.; Austermann, J.E.; Battaglia, N.; Battistelli, E.S.; Beall, J.A.; Bean, R.; et al. The Atacama Cosmology Telescope: Detection of the pairwise kinematic Sunyaev-Zel’dovich effect with SDSS DR15 galaxies. Phys. Rev. D 2021, 104, 043502. [Google Scholar] [CrossRef]
- Tanimura, H.; Zaroubi, S.; Aghanim, N. Direct detection of the kinetic Sunyaev-Zel’dovich effect in galaxy clusters. Astron. Astrophys. 2021, 645, A112. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, P.; Yang, X.; Zheng, Y. Detection of pairwise kSZ effect with DESI galaxy clusters and Planck. Mon. Not. R. Astron. Soc. 2022, 510, 5916–5928. [Google Scholar] [CrossRef]
- Zhao, G.B.; Pogosian, L.; Silvestri, A.; Zylberberg, J. Searching for modified growth patterns with tomographic surveys. Phys. Rev. D 2009, 79, 083513. [Google Scholar] [CrossRef]
- Zhao, G.B. Modeling the Nonlinear Clustering in Modified Gravity Models. I. A Fitting Formula for the Matter Power Spectrum of f(R) Gravity. Astrophys. J. Supp. 2009, 211, 23. [Google Scholar] [CrossRef]
- Bianchini, F.; Silvestri, A. Kinetic Sunyaev-Zel’dovich effect in modified gravity. Phys. Rev. D 2016, 93, 064026. [Google Scholar] [CrossRef]
- Ho, S.; Hirata, C.; Padmanabhan, N.; Seljak, U.; Bahcall, N. Correlation of CMB with large-scale structure. I. Integrated Sachs-Wolfe tomography and cosmological implications. Phys. Rev. D 2008, 78, 043519. [Google Scholar] [CrossRef]
- Kosowsky, A.; Bhattacharya, S. A future test of gravitation using galaxy cluster velocities. Phys. Rev. D 2009, 80, 062003. [Google Scholar] [CrossRef]
- Mitchell, M.A.; Arnold, C.; Hernández-Aguayo, C.; Li, B. The impact of modified gravity on the Sunyaev-Zeldovich effect. Mon. Not. R. Astron. Soc. 2021, 501, 4565–4578. [Google Scholar] [CrossRef]
- Kovetz, E.D.; Viero, M.P.; Lidz, A.; Newburgh, L.; Rahman, M.; Switzer, E.; Kamionkowski, M.; Aguirre, J.; Alvarez, M.; Bock, J.; et al. Line-Intensity Mapping: 2017 Status Report. arXiv 2017, arXiv:1709.09066. [Google Scholar]
- Furlanetto, S.; Oh, S.P.; Briggs, F. Cosmology at Low Frequencies: The 21 cm Transition and the High-Redshift Universe. Phys. Rep. 2006, 433, 181–301. [Google Scholar] [CrossRef]
- Bernal, J.L.; Breysse, P.C.; Gil-Marín, H.; Kovetz, E.D. User’s guide to extracting cosmological information from line-intensity maps. Phys. Rev. D 2019, 100, 123522. [Google Scholar] [CrossRef]
- Pritchard, J.R.; Loeb, A. 21 cm cosmology in the 21st century. Rep. Prog. Phys. 2012, 75, 086901. [Google Scholar] [CrossRef]
- Ansari, R.; Campagne, J.E.; Colom, P.; Le Goff, J.M.; Magneville, C.; Martin, J.M.; Moniez, M.; Rich, J.; Yèche, C. 21 cm observation of large-scale structures at z ∼ 1. Instrument sensitivity and foreground subtraction. Astron. Astrophys. 2012, 540, A129. [Google Scholar] [CrossRef]
- Bull, P.; Ferreira, P.G.; Patel, P.; Santos, M.G. Late-time cosmology with 21cm intensity mapping experiments. Astrophys. J. 2015, 803, 21. [Google Scholar] [CrossRef]
- Villaescusa-Navarro, F.; Genel, S.; Castorina, E.; Obuljen, A.; Spergel, D.N.; Hernquist, L.; Nelson, D.; Carucci, I.P.; Pillepich, A.; Marinacci, F.; et al. Ingredients for 21 cm Intensity Mapping. Astrophys. J. 2018, 866, 135. [Google Scholar] [CrossRef]
- Brax, P.; Clesse, S.; Davis, A.C. Signatures of modified gravity on the 21 cm power spectrum at reionisation. Mon. Not. R. Astron. Soc. 2013, 2013, 003. [Google Scholar] [CrossRef]
- Hall, A.; Bonvin, C.; Challinor, A. Testing general relativity with 21-cm intensity mapping. Phys. Rev. D 2013, 87, 064026. [Google Scholar] [CrossRef]
- Chowdhury, A.; Kanekar, N.; Chengalur, J.N.; Sethi, S.; Dwarakanath, K.S. H I 21-centimetre emission from an ensemble of galaxies at an average redshift of one. Nature 2020, 586, 369–372. [Google Scholar] [CrossRef]
- Wang, D. Testing modified gravity with 21 cm intensity mapping, HI galaxy, cosmic microwave background, optical galaxy, weak lensing, galaxy clustering, type Ia supernovae and gravitational wave surveys. arXiv 2021, arXiv:2108.08480. [Google Scholar] [CrossRef]
- Lidz, A.; Furlanetto, S.R.; Oh, S.P.; Aguirre, J.; Chang, T.C.; Doré, O.; Pritchard, J.R. Intensity Mapping with Carbon Monoxide Emission Lines and the Redshifted 21 cm Line. Astrophys. J. 2011, 741, 70. [Google Scholar] [CrossRef]
- Breysse, P.C.; Kovetz, E.D.; Kamionkowski, M. Carbon monoxide intensity mapping at moderate redshifts. Mon. Not. R. Astron. Soc. 2014, 443, 3506–3512. [Google Scholar] [CrossRef]
- Li, T.Y.; Wechsler, R.H.; Devaraj, K.; Church, S.E. Connecting CO Intensity Mapping to Molecular Gas and Star Formation in the Epoch of Galaxy Assembly. Astrophys. J. 2016, 817, 169. [Google Scholar] [CrossRef]
- Silva, M.; Santos, M.G.; Cooray, A.; Gong, Y. Prospects for Detecting C II Emission during the Epoch of Reionization. Astrophys. J. 2015, 806, 209. [Google Scholar] [CrossRef]
- Pullen, A.R.; Serra, P.; Chang, T.C.; Doré, O.; Ho, S. Search for C II emission on cosmological scales at redshift Z ∼ 2.6. Mon. Not. R. Astron. Soc. 2018, 478, 1911–1924. [Google Scholar] [CrossRef]
- Silva, M.B.; Santos, M.G.; Gong, Y.; Cooray, A.; Bock, J. Intensity Mapping of Lyα Emission during the Epoch of Reionization. Astrophys. J. 2013, 763, 132. [Google Scholar] [CrossRef]
- Pullen, A.R.; Doré, O.; Bock, J. Intensity Mapping across Cosmic Times with the Lyα Line. Astrophys. J. 2014, 786, 111. [Google Scholar] [CrossRef]
- Gong, Y.; Cooray, A.; Silva, M.B.; Zemcov, M.; Feng, C.; Santos, M.G.; Dore, O.; Chen, X. Intensity Mapping of Hα, Hβ, [OII], and [OIII] Lines at z < 5. Astrophys. J. 2017, 835, 273. [Google Scholar] [CrossRef]
- Silva, B.M.; Zaroubi, S.; Kooistra, R.; Cooray, A. Tomographic intensity mapping versus galaxy surveys: Observing the Universe in H α emission with new generation instruments. Mon. Not. R. Astron. Soc. 2018, 475, 1587–1608. [Google Scholar] [CrossRef]
- Alonso, D.; Bull, P.; Ferreira, P.G.; Maartens, R.; Santos, M. Ultra large-scale cosmology in next-generation experiments with single tracers. Astrophys. J. 2015, 814, 145. [Google Scholar] [CrossRef]
- Wolz, L.; Tonini, C.; Blake, C.; Wyithe, J.S.B. Intensity Mapping Cross-Correlations: Connecting the Largest Scales to Galaxy Evolution. Mon. Not. R. Astron. Soc. 2016, 458, 3399–3410. [Google Scholar] [CrossRef]
- Carucci, I.P.; Irfan, M.O.; Bobin, J. Recovery of 21 cm intensity maps with sparse component separation. Mon. Not. R. Astron. Soc. 2020, 499, 304–319. [Google Scholar] [CrossRef]
- Matshawule, S.D.; Spinelli, M.; Santos, M.G.; Ngobese, S. Hi intensity mapping with MeerKAT: Primary beam effects on foreground cleaning. Mon. Not. R. Astron. Soc. 2021, 506, 5075–5092. [Google Scholar] [CrossRef]
- Irfan, M.O.; Bull, P. Cleaning foregrounds from single-dish 21 cm intensity maps with Kernel principal component analysis. Mon. Not. R. Astron. Soc. 2021, 506, 3551–3568. [Google Scholar] [CrossRef]
- Soares, P.S.; Watkinson, C.A.; Cunnington, S.; Pourtsidou, A. Gaussian Process Regression for foreground removal in H i Intensity Mapping experiments. Mon. Not. R. Astron. Soc. 2021, 504, 4312–4336. [Google Scholar] [CrossRef]
- Spinelli, M.; Carucci, I.P.; Cunnington, S.; Harper, S.E.; Irfan, M.O.; Fonseca, J.; Pourtsidou, A.; Wolz, L. SKAO H i intensity mapping: Blind foreground subtraction challenge. Mon. Not. R. Astron. Soc. 2022, 509, 2048–2074. [Google Scholar] [CrossRef]
- Pourtsidou, A. Interferometric HI intensity mapping: Perturbation theory predictions and foreground removal effects. arXiv 2022, arXiv:astro-ph.CO/2206.14727. [Google Scholar]
- Dinda, B.R.; Sen, A.A.; Choudhury, T.R. Dark energy constraints from the 21 cm intensity mapping surveys with SKA1. arXiv 2018, arXiv:1804.11137. [Google Scholar]
- Masui, K.W.; Switzer, E.R.; Banavar, N.; Bandura, K.; Blake, C.; Calin, L.M.; Chang, T.C.; Chen, X.; Li, Y.C.; Liao, Y.W.; et al. Measurement of 21 cm Brightness Fluctuations at z ~0.8 in Cross-correlation. Astrophys. J. Lett. 2013, 763, L20. [Google Scholar] [CrossRef]
- Anderson, C.J.; Luciw, N.J.; Li, Y.-C.; Kuo, C.Y.; Yadav, J.; Masui, K.W.; Chang, T.-C.; Chen, X.; Oppermann, N.; Liao, Y.-W.; et al. Low-amplitude clustering in low-redshift 21-cm intensity maps cross-correlated with 2dF galaxy densities. Mon. Not. R. Astron. Soc. 2018, 476, 3382–3392. [Google Scholar] [CrossRef]
- Croft, R.A.C.; Miralda-Escudé, J.; Zheng, Z.; Blomqvist, M.; Pieri, M. Intensity mapping with SDSS/BOSS Lyman-α emission, quasars, and their Lyman-α forest. Mon. Not. R. Astron. Soc. 2018, 481, 1320–1336. [Google Scholar] [CrossRef]
- Croft, R.A.C.; Miralda-Escudé, J.; Zheng, Z.; Bolton, A.; Dawson, K.S.; Peterson, J.B.; York, D.G.; Eisenstein, D.; Brinkmann, J.; Brownstein, J.; et al. Large-scale clustering of Lyman α emission intensity from SDSS/BOSS. Mon. Not. Roy. Astron. Soc. 2016, 457, 3541–3572. [Google Scholar] [CrossRef]
- Keating, G.K.; Marrone, D.P.; Bower, G.C.; Leitch, E.; Carlstrom, J.E.; DeBoer, D.R. COPSS II: The molecular gas content of ten million cubic megaparsecs at redshift z ∼ 3. Astrophys. J. 2016, 830, 34. [Google Scholar] [CrossRef]
- Cunnington, S.; Li, Y.; Santos, M.G.; Wang, J.; Carucci, I.P.; Irfan, M.O.; Pourtsidou, A.; Spinelli, M.L.; Wolz, M.; Soares, P.S.; et al. HI intensity mapping with MeerKAT: Power spectrum detection in cross-correlation with WiggleZ galaxies. arXiv 2022, arXiv:astro-ph.CO/2206.01579. [Google Scholar]
- Peebles, P.J.E. The Large-Scale Structure of the Universe; Princeton University Press: Princeton, NJ, USA, 1980. [Google Scholar]
- Peebles, P.J.E.; Groth, E.J. Statistical analysis of catalogs of extragalactic objects. V. Three-point correlation function for the galaxy distribution in the Zwicky catalog. Astrophys. J. 1975, 196, 1–11. [Google Scholar] [CrossRef]
- Kayo, I.; Suto, Y.; Nichol, R.C.; Pan, J.; Szapudi, I.; Connolly, A.J.; Gardner, J.; Jain, B.; Kulkarni, G.; Matsubara, T.; et al. Three-Point Correlation Functions of SDSS Galaxies in Redshift Space: Morphology, Color, and Luminosity Dependence. Publ. Astron. Soc. Jpn. 2004, 56, 415–423. [Google Scholar] [CrossRef]
- Nichol, R.C.; Sheth, R.K.; Suto, Y.; Gray, A.J.; Kayo, I.; Wechsler, R.H.; Marin, F.; Kulkarni, G.; Blanton, M.; Connolly, A.J.; et al. The effect of large-scale structure on the SDSS galaxy three-point correlation function. Mon. Not. R. Astron. Soc. 2006, 368, 1507–1514. [Google Scholar] [CrossRef]
- McBride, C.K.; Connolly, A.J.; Gardner, J.P.; Scranton, R.; Newman, J.A.; Scoccimarro, R.; Zehavi, I.; Schneider, D.P. Three-point Correlation Functions of SDSS Galaxies: Luminosity and Color Dependence in Redshift and Projected Space. Astrophys. J. 2011, 726, 13. [Google Scholar] [CrossRef]
- McBride, C.K.; Connolly, A.J.; Gardner, J.P.; Scranton, R.; Scoccimarro, R.; Berlind, A.A.; Marín, F.; Schneider, D.P. Three-point Correlation Functions of SDSS Galaxies: Constraining Galaxy-mass Bias. Astrophys. J. 2011, 739, 85. [Google Scholar] [CrossRef]
- Guo, H.; Zheng, Z.; Jing, Y.P.; Zehavi, I.; Li, C.; Weinberg, D.H.; Skibba, R.A.; Nichol, R.C.; Rossi, G.; Sabiu, C.G.; et al. Modelling the redshift-space three-point correlation function in SDSS-III. Mon. Not. R. Astron. Soc. 2015, 449, L95–L99. [Google Scholar] [CrossRef]
- Slepian, Z.; Eisenstein, D.J. Computing the three-point correlation function of galaxies in O(N ) time. Mon. Not. R. Astron. Soc. 2015, 454, 4142–4158. [Google Scholar] [CrossRef]
- Cahn, R.N.; Slepian, Z. Isotropic N-Point Basis Functions and Their Properties. arXiv 2020, arXiv:2010.14418. [Google Scholar] [CrossRef]
- Philcox, O.H.E.; Slepian, Z.; Hou, J.; Warner, C.; Cahn, R.N.; Eisenstein, D.J. ENCORE: An O (Ng2) estimator for galaxy N-point correlation functions. Mon. Not. R. Astron. Soc. 2022, 509, 2457–2481. [Google Scholar] [CrossRef]
- Slepian, Z.; Warner, C.; Hou, J.; Cahn, R.N. CADENZA: Harmonics on the GPU for N-Point Correlation Functions. in print.
- Portillo, S.K.N.; Slepian, Z.; Burkhart, B.; Kahraman, S.; Finkbeiner, D.P. Developing the 3-point Correlation Function for the Turbulent Interstellar Medium. Astrophys. J. 2018, 862, 119. [Google Scholar] [CrossRef]
- Sunseri, J.; Slepian, Z.; Portillo, S.; Hou, J.; Kahraman, S.; Finkbeiner, D.P. SARABANDE: 3/4 Point Correlation Functions with Fast Fourier Transforms. RAS Tech. Instrum. 2023, 2, 62–77. [Google Scholar] [CrossRef]
- Cahn, R.N.; Slepian, Z.; Hou, J. Test for Cosmological Parity Violation Using the 3D Distribution of Galaxies. Phys. Rev. Lett. 2021, 130, 201002. [Google Scholar] [CrossRef]
- Hou, J.; Cahn, R.N.; Slepian, Z. Measurement of parity-odd modes in the large-scale 4-point correlation function of Sloan Digital Sky Survey Baryon Oscillation Spectroscopic Survey twelfth data release CMASS and LOWZ galaxies. Mon. Not. R. Astron. Soc. 2023, 522, 5701–5739. [Google Scholar] [CrossRef]
- Philcox, O.H.E. Probing parity violation with the four-point correlation function of BOSS galaxies. Phys. Rev. D 2022, 106, 063501. [Google Scholar] [CrossRef]
- Scoccimarro, R.; Feldman, H.A.; Fry, J.N.; Frieman, J.A. The Bispectrum of IRAS Redshift Catalogs. Astrophys. J. 2001, 546, 652–664. [Google Scholar] [CrossRef]
- Feldman, H.A.; Frieman, J.A.; Fry, J.N.; Scoccimarro, R. Constraints on Galaxy Bias, Matter Density, and Primordial Non–Gaussianity from the PSCz Galaxy Redshift Survey. Phys. Rev. Lett. 2001, 86, 1434–1437. [Google Scholar] [CrossRef] [PubMed]
- Verde, L.; Heavens, A.F.; Percival, W.J.; Matarrese, S.; Baugh, C.M.; Bland-Hawthorn, J.; Bridges, T.; Cannon, R.; Cole, S.; Colless, M.; et al. The 2dF Galaxy Redshift Survey: The bias of galaxies and the density of the Universe. Mon. Not. R. Astron. Soc. 2002, 335, 432–440. [Google Scholar] [CrossRef]
- Gil-Marín, H.; Noreña, J.; Verde, L.; Percival, W.J.; Wagner, C.; Manera, M.; Schneider, D.P. The power spectrum and bispectrum of SDSS DR11 BOSS galaxies—I. Bias and gravity. Mon. Not. R. Astron. Soc. 2015, 451, 539–580. [Google Scholar] [CrossRef]
- Gil-Marín, H.; Verde, L.; Noreña, J.; Cuesta, A.J.; Samushia, L.; Percival, W.J.; Wagner, C.; Manera, M.; Schneider, D.P. The power spectrum and bispectrum of SDSS DR11 BOSS galaxies—II. Cosmological interpretation. Mon. Not. R. Astron. Soc. 2015, 452, 1914–1921. [Google Scholar] [CrossRef]
- Scoccimarro, R. Fast estimators for redshift-space clustering. Phys. Rev. D 2015, 92, 083532. [Google Scholar] [CrossRef]
- Sugiyama, N.S.; Saito, S.; Beutler, F.; Seo, H.J. A complete FFT-based decomposition formalism for the redshift-space bispectrum. Mon. Not. R. Astron. Soc. 2019, 484, 364–384. [Google Scholar] [CrossRef]
- Gil-Marín, H.; Schmidt, F.; Hu, W.; Jimenez, R.; Verde, L. The bispectrum of f(R) cosmologies. J. Cosmol. Astropart. Phys. 2011, 2011, 019. [Google Scholar] [CrossRef]
- Schneider, P. Detection of (dark) matter concentrations via weak gravitational lensing. Mon. Not. R. Astron. Soc. 1996, 283, 837–853. [Google Scholar] [CrossRef]
- Schneider, P.; van Waerbeke, L.; Jain, B.; Kruse, G. A new measure for cosmic shear. Mon. Not. R. Astron. Soc. 1998, 296, 873–892. [Google Scholar] [CrossRef]
- Giocoli, C.; Metcalf, R.B.; Baldi, M.; Meneghetti, M.; Moscardini, L.; Petkova, M. Disentangling dark sector models using weak lensing statistics. Mon. Not. R. Astron. Soc. 2015, 452, 2757–2772. [Google Scholar] [CrossRef]
- Kruse, G.; Schneider, P. Statistics of dark matter haloes expected from weak lensing surveys. Mon. Not. R. Astron. Soc. 1999, 302, 821–829. [Google Scholar] [CrossRef]
- Hagstotz, S.; Costanzi, M.; Baldi, M.; Weller, J. Joint halo-mass function for modified gravity and massive neutrinos—I. Simulations and cosmological forecasts. Mon. Not. R. Astron. Soc. 2019, 486, 3927–3941. [Google Scholar] [CrossRef]
- Peel, A.; Pettorino, V.; Giocoli, C.; Starck, J.L.; Baldi, M. Breaking degeneracies in modified gravity with higher (than 2nd) order weak-lensing statistics. Astron. Astrophys. 2018, 619, A38. [Google Scholar] [CrossRef]
- Shirasaki, M.; Nishimichi, T.; Li, B.; Higuchi, Y. The imprint of f(R) gravity on weak gravitational lensing—II. Information content in cosmic shear statistics. Mon. Not. R. Astron. Soc. 2017, 466, 2402–2417. [Google Scholar] [CrossRef]
- Hamana, T.; Colombi, S.T.; Thion, A.; Devriendt, J.E.G.T.; Mellier, Y.; Bernardeau, F. Source-lens clustering effects on the skewness of the lensing convergence. Mon. Not. R. Astron. Soc. 2002, 330, 365–377. [Google Scholar] [CrossRef]
- Cheng, S.; Ting, Y.S.; Ménard, B.; Bruna, J. A new approach to observational cosmology using the scattering transform. Mon. Not. R. Astron. Soc. 2020, 499, 5902–5914. [Google Scholar] [CrossRef]
- Cheng, S.; Ménard, B. Weak lensing scattering transform: Dark energy and neutrino mass sensitivity. Mon. Not. R. Astron. Soc. 2021, 507, 1012–1020. [Google Scholar] [CrossRef]
- Valogiannis, G.; Dvorkin, C. Towards an optimal estimation of cosmological parameters with the wavelet scattering transform. Phys. Rev. D 2022, 105. [Google Scholar] [CrossRef]
- Eickenberg, M.; Allys, E.; Moradinezhad Dizgah, A.; Lemos, P.; Massara, E.; Abidi, M.; Hahn, C.; Hassan, S.; Regaldo-Saint Blancard, B.; Ho, S.; et al. Wavelet Moments for Cosmological Parameter Estimation. arXiv 2022, arXiv:2204.07646. [Google Scholar] [CrossRef]
- Mallat, S.; Zhang, S.; Rochette, G. Phase Harmonic Correlations and Convolutional Neural Networks. arXiv 2018, arXiv:1810.12136. [Google Scholar] [CrossRef]
- Allys, E.; Marchand, T.; Cardoso, J.F.; Villaescusa-Navarro, F.; Ho, S.; Mallat, S. New interpretable statistics for large-scale structure analysis and generation. Phys. Rev. D 2020, 102, 103506. [Google Scholar] [CrossRef]
- Wasserman, L. Topological Data Analysis. arXiv 2016, arXiv:1609.08227. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Letscher, D.; Zomorodian, A. Topological Persistence and Simplification. Discret. Comput. Geom. 2002, 28, 511–533. [Google Scholar] [CrossRef]
- Ghrist, R. Barcodes: The persistent topology of data. Bull. New Ser. Am. Math. Soc. 2008, 45, 61–75. [Google Scholar] [CrossRef]
- Gott, J.; Richard, I.; Miller, J.; Thuan, T.X.; Schneider, S.E.; Weinberg, D.H.; Gammie, C.; Polk, K.; Vogeley, M.; Jeffrey, S.; et al. The Topology of Large-Scale Structure. III. Analysis of Observations. Astrophys. J. 1989, 340, 625. [Google Scholar] [CrossRef]
- Mecke, K.R.; Buchert, T.; Wagner, H. Robust morphological measures for large-scale structure in the Universe. Astron. Astrophys. 1994, 288, 697–704. [Google Scholar]
- Park, C.; Kim, Y.R. Large-scale Structure of the Universe as a Cosmic Standard Ruler. Astrophys. J. Lett. 2010, 715, L185–L188. [Google Scholar] [CrossRef]
- Wang, X.; Chen, X.; Park, C. Topology of a Large-scale Structure as a Test of Modified Gravity. Astrophys. J. 2012, 747, 48. [Google Scholar] [CrossRef]
- Fang, W.; Li, B.; Zhao, G.B. New Probe of Departures from General Relativity Using Minkowski Functionals. Phys. Rev. Lett. 2017, 118, 181301. [Google Scholar] [CrossRef] [PubMed]
- Busch, P.; Eide, M.B.; Ciardi, B.; Kakiichi, K. Opening reionization: Quantitative morphology of the epoch of reionization and its connection to the cosmic density field. Mon. Not. R. Astron. Soc. 2020, 498, 4533–4549. [Google Scholar] [CrossRef]
- Bobrowski, O.; Skraba, P. Homological percolation and the Euler characteristic. Phys. Rev. E 2020, 101, 032304. [Google Scholar] [CrossRef]
- Koplik, G. Persistent Homology: A Non-Mathy Introduction with Examples. 2019. Available online: https://towardsdatascience.com/persistent-homology-with-examples-1974d4b9c3d0 (accessed on 13 June 2023).
- Kono, K.T.; Takeuchi, T.T.; Cooray, S.; Nishizawa, A.J.; Murakami, K. A Study on the Baryon Acoustic Oscillation with Topological Data Analysis. arXiv 2020, arXiv:astro-ph.CO/2006.02905. [Google Scholar]
- Heydenreich, S.; Brück, B.; Burger, P.; Harnois-Déraps, J.; Unruh, S.; Castro, T.; Dolag, K.; Martinet, N. Persistent homology in cosmic shear. II. A tomographic analysis of DES-Y1. Astron. Astrophys. 2022, 667, A125. [Google Scholar] [CrossRef]
- Xu, X.; Cisewski-Kehe, J.; Green, S.B.; Nagai, D. Finding cosmic voids and filament loops using topological data analysis. Astron. Comput. 2019, 27, 34. [Google Scholar] [CrossRef]
- Wilding, G.; Nevenzeel, K.; van de Weygaert, R.; Vegter, G.; Pranav, P.; Jones, B.J.T.; Efstathiou, K.; Feldbrugge, J. Persistent homology of the cosmic web—I. Hierarchical topology in ΛCDM cosmologies. Mon. Not. R. Astron. Soc. 2021, 507, 2968–2990. [Google Scholar] [CrossRef]
- van de Weygaert, R.; Kreckel, K.; Platen, E.; Beygu, B.; van Gorkom, J.H.; van der Hulst, J.M.; Aragón-Calvo, M.A.; Peebles, P.J.E.; Jarrett, T.; Rhee, G.; et al. The Void Galaxy Survey. In Environment and the Formation of Galaxies: 30 Years Later: Proceedings of Symposium 2 of JENAM 2010; Springer: Berlin/Heidelberg, Germany, 2011; Volume 27, p. 17. [Google Scholar] [CrossRef]
- van de Weygaert, R.; Pranav, P.; Jones, B.J.T.; Bos, E.G.P.; Vegter, G.; Edelsbrunner, H.; Teillaud, M.; Hellwing, W.A.; Park, C.; Hidding, J.; et al. Probing Dark Energy with Alpha Shapes and Betti Numbers. arXiv 2011, arXiv:1110.5528. [Google Scholar] [CrossRef]
- Appleby, S.; Park, C.; Pranav, P.; Hong, S.E.; Hwang, H.S.; Kim, J.; Buchert, T. Minkowski Functionals of SDSS-III BOSS: Hints of Possible Anisotropy in the Density Field? Astrophys. J. 2022, 928, 108. [Google Scholar] [CrossRef]
- Uhlemann, C.; Friedrich, O.; Villaescusa-Navarro, F.; Banerjee, A.; Codis, S. Fisher for complements: Extracting cosmology and neutrino mass from the counts-in-cells PDF. Mon. Not. R. Astron. Soc. 2020, 495, 4006–4027. [Google Scholar] [CrossRef]
- Cataneo, M.; Uhlemann, C.; Arnold, C.; Gough, A.; Li, B.; Heymans, C. The matter density PDF for modified gravity and dark energy with Large Deviations Theory. Mon. Not. R. Astron. Soc. 2022, 513, 1623–1641. [Google Scholar] [CrossRef]
- Bernardeau, F.; Pichon, C.; Codis, S. Statistics of cosmic density profiles from perturbation theory. Phys. Rev. D 2014, 90, 103519. [Google Scholar] [CrossRef]
- Uhlemann, C.; Codis, S.; Pichon, C.; Bernardeau, F.; Reimberg, P. Back in the saddle: Large-deviation statistics of the cosmic log-density field. Mon. Not. R. Astron. Soc. 2016, 460, 1529–1541. [Google Scholar] [CrossRef]
- Banerjee, A.; Abel, T. Nearest neighbour distributions: New statistical measures for cosmological clustering. Mon. Not. R. Astron. Soc. 2020, 500, 5479–5499. [Google Scholar] [CrossRef]
- Banerjee, A.; Kokron, N.; Abel, T. Modelling nearest neighbour distributions of biased tracers using hybrid effective field theory. Mon. Not. R. Astron. Soc. 2022, 511, 2765–2781. [Google Scholar] [CrossRef]
- Banerjee, A.; Abel, T. Cosmological cross-correlations and nearest neighbour distributions. Mon. Not. R. Astron. Soc. 2021, 504, 2911–2923. [Google Scholar] [CrossRef]
- Friedrich, O.; Gruen, D.; DeRose, J.; Kirk, D.; Krause, E.; McClintock, T.; Rykoff, E.; Seitz, S.; Wechsler, R.; Bernstein, G.; et al. Density split statistics: Joint model of counts and lensing in cells. Phys. Rev. D 2018, 98, 023508. [Google Scholar] [CrossRef]
- Gruen, D.; Friedrich, O.; Krause, E.; DeRose, J.; Cawthon, R.; Davis, C.; Elvin-Poole, J.; Rykoff, E.; Wechsler, R.; Alarcon, A.; et al. Density split statistics: Cosmological constraints from counts and lensing in cells in DES Y1 and SDSS data. Phys. Rev. D 2018, 98, 023507. [Google Scholar] [CrossRef]
- Burger, P.A.; Friedrich, O.; Harnois-Déraps, J.; Schneider, P.; Asgari, M.; Bilicki, M.; Hildebrandt, H.; Wright, A.H.; Castro, T.; Dolag, K.; et al. KiDS-1000 cosmology: Constraints from density split statistics. Astron. Astrophys. 2023, 669, A69. [Google Scholar] [CrossRef]
- Paillas, E.; Cai, Y.C.; Padilla, N.; Sánchez, A.G. Redshift-space distortions with split densities. Mon. Not. R. Astron. Soc. 2021, 505, 5731–5752. [Google Scholar] [CrossRef]
- Paillas, E.; Cuesta-Lazaro, C.; Zarrouk, P.; Cai, Y.C.; Percival, W.J.; Nadathur, S.; Pinon, M.; de Mattia, A.; Beutler, F. Constraining νΛCDM with density-split clustering. arXiv 2022, arXiv:astro-ph.CO/2209.04310. [Google Scholar] [CrossRef]
- Allen, S.W.; Evrard, A.E.; Mantz, A.B. Cosmological Parameters from Observations of Galaxy Clusters. Annu. Rev. Astron. Astrophys. 2011, 49, 409–470. [Google Scholar] [CrossRef]
- Gunn, J.E.; Gott, J.; Richard, I. On the Infall of Matter Into Clusters of Galaxies and Some Effects on Their Evolution. Astrophys. J. 1972, 176, 1. [Google Scholar] [CrossRef]
- Cataneo, M.; Rapetti, D.; Lombriser, L.; Li, B. Cluster abundance in chameleon f(R) gravity I: Toward an accurate halo mass function prediction. J. Cosmol. Astropart. Phys. 2016, 12, 024. [Google Scholar] [CrossRef]
- Schmidt, F.; Lima, M.; Oyaizu, H.; Hu, W. Nonlinear evolution of f(R) cosmologies. III. Halo statistics. Phys. Rev. D 2009, 79, 083518. [Google Scholar] [CrossRef]
- Navarro, J.F.; Frenk, C.S.; White, S.D.M. The Structure of Cold Dark Matter Halos. Astrophys. J. 1996, 462, 563. [Google Scholar] [CrossRef]
- Mitchell, M.A.; Arnold, C.; He, J.h.; Li, B. A general framework to test gravity using galaxy clusters II: A universal model for the halo concentration in f(R) gravity. Mon. Not. R. Astron. Soc. 2019, 487, 1410–1425. [Google Scholar] [CrossRef]
- Lombriser, L.; Schmidt, F.; Baldauf, T.; Mandelbaum, R.; Seljak, U.; Smith, R.E. Cluster density profiles as a test of modified gravity. Phys. Rev. D 2012, 85, 102001. [Google Scholar] [CrossRef]
- Diemer, B.; Kravtsov, A.V. Dependence of the Outer Density Profiles of Halos on Their Mass Accretion Rate. Astrophys. J. 2014, 789, 1. [Google Scholar] [CrossRef]
- Adhikari, S.; Sakstein, J.; Jain, B.; Dalal, N.; Li, B. Splashback in galaxy clusters as a probe of cosmic expansion and gravity. J. Cosmol. Astropart. Phys. 2018, 2018, 033. [Google Scholar] [CrossRef]
- Terukina, A.; Lombriser, L.; Yamamoto, K.; Bacon, D.; Koyama, K.; Nichol, R.C. Testing chameleon gravity with the Coma cluster. J. Cosmol. Astropart. Phys. 2014, 2014, 013. [Google Scholar] [CrossRef]
- Terukina, A.; Yamamoto, K.; Okabe, N.; Matsushita, K.; Sasaki, T. Testing a generalized cubic Galileon gravity model with the Coma Cluster. J. Cosmol. Astropart. Phys. 2015, 2015, 064. [Google Scholar] [CrossRef]
- Sakstein, J.; Wilcox, H.; Bacon, D.; Koyama, K.; Nichol, R.C. Testing gravity using galaxy clusters: New constraints on beyond Horndeski theories. J. Cosmol. Astropart. Phys. 2016, 2016, 019. [Google Scholar] [CrossRef]
- Ettori, S.; Tozzi, P.; Borgani, S.; Rosati, P. Scaling laws in X-ray galaxy clusters at redshift between 0.4 and 1.3. Astron. Astrophys. 2004, 417, 13–27. [Google Scholar] [CrossRef]
- Arnaud, M.; Pointecouteau, E.; Pratt, G.W. The structural and scaling properties of nearby galaxy clusters. II. The M-T relation. Astron. Astrophys. 2005, 441, 893–903. [Google Scholar] [CrossRef]
- Vikhlinin, A.; Kravtsov, A.; Forman, W.; Jones, C.; Markevitch, M.; Murray, S.S.; Van Speybroeck, L. Chandra Sample of Nearby Relaxed Galaxy Clusters: Mass, Gas Fraction, and Mass-Temperature Relation. Astrophys. J. 2006, 640, 691–709. [Google Scholar] [CrossRef]
- Stanek, R.; Evrard, A.E.; Böhringer, H.; Schuecker, P.; Nord, B. The X-Ray Luminosity-Mass Relation for Local Clusters of Galaxies. Astrophys. J. 2006, 648, 956–968. [Google Scholar] [CrossRef]
- Salvati, L.; Douspis, M.; Aghanim, N. Impact of systematics on cosmological parameters from future galaxy cluster surveys. Astron. Astrophys. 2020, 643, A20. [Google Scholar] [CrossRef]
- Pizzuti, L.; Sartoris, B.; Borgani, S.; Biviano, A. Calibration of systematics in constraining modified gravity models with galaxy cluster mass profiles. J. Cosmol. Astropart. Phys. 2020, 2020, 024. [Google Scholar] [CrossRef]
- Sheth, R.K.; van de Weygaert, R. A Hierarchy of voids: Much ado about nothing. Mon. Not. R. Astron. Soc. 2004, 350, 517–538. [Google Scholar] [CrossRef]
- Voivodic, R.; Lima, M.; Llinares, C.; Mota, D.F. Modeling void abundance in modified gravity. Phys. Rev. D 2017, 95, 024018. [Google Scholar] [CrossRef]
- Davies, C.T.; Cautun, M.; Li, B. Cosmological test of gravity using weak lensing voids. Mon. Not. R. Astron. Soc. 2019, 490, 4907–4917. [Google Scholar] [CrossRef]
- Paillas, E.; Cautun, M.; Li, B.; Cai, Y.C.; Padilla, N.; Armijo, J.; Bose, S. The Santiago-Harvard-Edinburgh-Durham void comparison II: Unveiling the Vainshtein screening using weak lensing. Mon. Not. R. Astron. Soc. 2019, 484, 1149–1165. [Google Scholar] [CrossRef]
- Wilson, C.; Bean, R. Challenges in Constraining Gravity with Cosmic Voids. arXiv 2022, arXiv:2212.02569. [Google Scholar] [CrossRef]
- Nadathur, S.; Hotchkiss, S. The nature of voids—II. Tracing underdensities with biased galaxies. Mon. Not. R. Astron. Soc. 2015, 454, 889–901. [Google Scholar] [CrossRef]
- Davies, C.T.; Cautun, M.; Li, B. Weak lensing by voids in weak lensing maps. Mon. Not. R. Astron. Soc. 2018, 480, L101–L105. [Google Scholar] [CrossRef]
- Osato, K.; Shirasaki, M.; Yoshida, N. Impact of Baryonic Processes on Weak-lensing Cosmology: Power Spectrum, Nonlocal Statistics, and Parameter Bias. Astrophys. J. 2015, 806, 186. [Google Scholar] [CrossRef]
- Weiss, A.J.; Schneider, A.; Sgier, R.; Kacprzak, T.; Amara, A.; Refregier, A. Effects of baryons on weak lensing peak statistics. J. Cosmol. Astropart. Phys. 2019, 2019, 011. [Google Scholar] [CrossRef]
- Fong, M.; Choi, M.; Catlett, V.; Lee, B.; Peel, A.; Bowyer, R.; King, L.J.; McCarthy, I.G. The impact of baryonic physics and massive neutrinos on weak lensing peak statistics. Mon. Not. R. Astron. Soc. 2019, 488, 3340–3357. [Google Scholar] [CrossRef]
- Sheth, R.K.; Connolly, A.J.; Skibba, R. Marked correlations in galaxy formation models. arXiv 2005, arXiv:astro-ph/0511773. [Google Scholar]
- White, M. A marked correlation function for constraining modified gravity models. J. Cosmol. Astropart. Phys. 2016, 2016, 057. [Google Scholar] [CrossRef]
- Neyrinck, M.C.; Szapudi, I.; Szalay, A.S. Rejuvenating the Matter Power Spectrum: Restoring Information with a Logarithmic Density Mapping. Astrophys. J. Lett. 2009, 698, L90–L93. [Google Scholar] [CrossRef]
- Llinares, C.; McCullagh, N. Weighted density fields as improved probes of modified gravity models. Mon. Not. R. Astron. Soc. 2017, 472, L80–L84. [Google Scholar] [CrossRef]
- Hernández-Aguayo, C.; Baugh, C.M.; Li, B. Marked clustering statistics in f(R) gravity cosmologies. Mon. Not. R. Astron. Soc. 2018, 479, 4824–4835. [Google Scholar] [CrossRef]
- Aviles, A.; Koyama, K.; Cervantes-Cota, J.L.; Winther, H.A.; Li, B. Marked correlation functions in perturbation theory. J. Cosmol. Astropart. Phys. 2020, 01, 006. [Google Scholar] [CrossRef]
- Bernardeau, F.; Colombi, S.; Gaztañaga, E.; Scoccimarro, R. Large-scale structure of the Universe and cosmological perturbation theory. Phys. Rep. 2002, 367, 1–248. [Google Scholar] [CrossRef]
- Crocce, M.; Scoccimarro, R. Renormalized cosmological perturbation theory. Phys. Rev. D 2006, 73, 063519. [Google Scholar] [CrossRef]
- Crocce, M.; Scoccimarro, R. Nonlinear evolution of baryon acoustic oscillations. Phys. Rev. D 2008, 77, 023533. [Google Scholar] [CrossRef]
- Matsubara, T. Resumming cosmological perturbations via the Lagrangian picture: One-loop results in real space and in redshift space. Phys. Rev. D 2008, 77, 063530. [Google Scholar] [CrossRef]
- Bernardeau, F.; Crocce, M.; Scoccimarro, R. Multipoint propagators in cosmological gravitational instability. Phys. Rev. D 2008, 78, 103521. [Google Scholar] [CrossRef]
- Baumann, D.; Nicolis, A.; Senatore, L.; Zaldarriaga, M. Cosmological non-linearities as an effective fluid. J. Cosmol. Astropart. Phys. 2012, 2012, 051. [Google Scholar] [CrossRef]
- Carrasco, J.J.M.; Hertzberg, M.P.; Senatore, L. The effective field theory of cosmological large scale structures. J. High Energy Phys. 2012, 2012, 82. [Google Scholar] [CrossRef]
- Scoccimarro, R. Redshift-space distortions, pairwise velocities, and nonlinearities. Phys. Rev. D 2004, 70, 083007. [Google Scholar] [CrossRef]
- Matsubara, T. Nonlinear perturbation theory with halo bias and redshift-space distortions via the Lagrangian picture. Phys. Rev. D 2008, 78, 083519. [Google Scholar] [CrossRef]
- Taruya, A.; Nishimichi, T.; Saito, S. Baryon acoustic oscillations in 2D: Modeling redshift-space power spectrum from perturbation theory. Phys. Rev. D 2010, 82, 063522. [Google Scholar] [CrossRef]
- Senatore, L.; Zaldarriaga, M. Redshift Space Distortions in the Effective Field Theory of Large Scale Structures. arXiv 2014, arXiv:1409.1225. [Google Scholar]
- Lewandowski, M.; Senatore, L.; Prada, F.; Zhao, C.; Chuang, C.H. EFT of large scale structures in redshift space. Phys. Rev. D 2018, 97, 063526. [Google Scholar] [CrossRef]
- Koyama, K.; Taruya, A.; Hiramatsu, T. Nonlinear evolution of the matter power spectrum in modified theories of gravity. Phys. Rev. D 2009, 79, 123512. [Google Scholar] [CrossRef]
- Bose, B.; Koyama, K. A perturbative approach to the redshift space power spectrum: Beyond the Standard Model. J. Cosmol. Astropart. Phys. 2016, 2016, 032. [Google Scholar] [CrossRef]
- Taruya, A.; Koyama, K.; Hiramatsu, T.; Oka, A. Beyond consistency test of gravity with redshift-space distortions at quasilinear scales. Phys. Rev. D 2014, 89, 043509. [Google Scholar] [CrossRef]
- Taruya, A.; Nishimichi, T.; Bernardeau, F.; Hiramatsu, T.; Koyama, K. Regularized cosmological power spectrum and correlation function in modified gravity models. Phys. Rev. D 2014, 90, 123515. [Google Scholar] [CrossRef]
- Aviles, A.; Cervantes-Cota, J.L. Lagrangian perturbation theory for modified gravity. Phys. Rev. D 2017, 96, 123526. [Google Scholar] [CrossRef]
- Valogiannis, G.; Bean, R.; Aviles, A. An accurate perturbative approach to redshift space clustering of biased tracers in modified gravity. J. Cosmol. Astropart. Phys. 2020, 2020, 055. [Google Scholar] [CrossRef]
- Cooray, A.; Sheth, R. Halo models of large scale structure. Phys. Rep. 2002, 372, 1–129. [Google Scholar] [CrossRef]
- Bose, B.; Tsedrik, M.; Kennedy, J.; Lombriser, L.; Pourtsidou, A.; Taylor, A. Fast and accurate predictions of the nonlinear matter power spectrum for general models of Dark Energy and Modified Gravity. arXiv 2022, arXiv:2210.01094. [Google Scholar]
- Bose, B.; Taruya, A. The one-loop matter bispectrum as a probe of gravity and dark energy. J. Cosmol. Astropart. Phys. 2018, 2018, 019. [Google Scholar] [CrossRef]
- Aviles, A.; Niz, G. On the galaxy 3-point correlation function in Modified Gravity. arXiv 2023, arXiv:2301.07240. [Google Scholar] [CrossRef]
- Bose, B.; Byun, J.; Lacasa, F.; Moradinezhad Dizgah, A.; Lombriser, L. Modelling the matter bispectrum at small scales in modified gravity. J. Cosmol. Astropart. Phys. 2020, 2020, 025. [Google Scholar] [CrossRef]
- Vogelsberger, M.; Marinacci, F.; Torrey, P.; Puchwein, E. Cosmological Simulations of Galaxy Formation. Nat. Rev. Phys. 2020, 2, 42–66. [Google Scholar] [CrossRef]
- Angulo, R.E.; Hahn, O. Large-scale dark matter simulations. Living Rev. Comput. Astrophys. 2022, 8, 1. [Google Scholar] [CrossRef]
- Winther, H.A.; Schmidt, F.; Barreira, A.; Arnold, C.; Bose, S.; Llinares, C.; Baldi, M.; Falck, B.; Hellwing, W.A.; Koyama, K.; et al. Modified Gravity N-body Code Comparison Project. Mon. Not. R. Astron. Soc. 2015, 454, 4208–4234. [Google Scholar] [CrossRef]
- Brandt, A. Multi-Level Adaptive Solutions to Boundary-Value Problems. Math. Comput. 1977, 31, 333–390. [Google Scholar] [CrossRef]
- Trottenberg, U.; Oosterlee, C.; Schüller, A. Multigrid Methods: Basics, Parallelism and Adaptivity; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Li, B. Simulating Large-Scale Structure for Models of Cosmic Acceleration; IOP Publishing: Bristol, UK, 2018; p. 25143433. [Google Scholar] [CrossRef]
- Li, B.; Zhao, G.B.; Teyssier, R.; Koyama, K. ECOSMOG: An Efficient Code for Simulating Modified Gravity. J. Cosmol. Astropart. Phys. 2012, 1201, 051. [Google Scholar] [CrossRef]
- Li, B.; Zhao, G.B.; Koyama, K. Exploring Vainshtein mechanism on adaptively refined meshes. J. Cosmol. Astropart. Phys. 2013, 2013, 023. [Google Scholar] [CrossRef]
- Brax, P.; Davis, A.C.; Li, B.; Winther, H.A.; Zhao, G.B. Systematic simulations of modified gravity: Symmetron and dilaton models. J. Cosmol. Astropart. Phys. 2012, 2012, 002. [Google Scholar] [CrossRef]
- Brax, P.; Davis, A.C.; Li, B.; Winther, H.A.; Zhao, G.B. Systematic simulations of modified gravity: Chameleon models. J. Cosmol. Astropart. Phys. 2013, 2013, 029. [Google Scholar] [CrossRef]
- Llinares, C.; Mota, D.F.; Winther, H.A. ISIS: A new N-body cosmological code with scalar fields based on RAMSES. Code presentation and application to the shapes of clusters. Astron. Astrophys. 2014, 562, A78. [Google Scholar] [CrossRef]
- Teyssier, R. Cosmological hydrodynamics with adaptive mesh refinement: A new high resolution code called ramses. Astron. Astrophys. 2002, 385, 337–364. [Google Scholar] [CrossRef]
- Puchwein, E.; Baldi, M.; Springel, V. Modified-Gravity-GADGET: A new code for cosmological hydrodynamical simulations of modified gravity models. Mon. Not. R. Astron. Soc. 2013, 436, 348–360. [Google Scholar] [CrossRef]
- Arnold, C.; Leo, M.; Li, B. Realistic simulations of galaxy formation in f(R) modified gravity. Nat. Astron. 2019, 3, 945–954. [Google Scholar] [CrossRef]
- Hernández-Aguayo, C.; Arnold, C.; Li, B.; Baugh, C.M. Galaxy formation in the brane world I: Overview and first results. Mon. Not. R. Astron. Soc. 2021, 503, 3867–3885. [Google Scholar] [CrossRef]
- Springel, V. The Cosmological simulation code GADGET-2. Mon. Not. R. Astron. Soc. 2005, 364, 1105–1134. [Google Scholar] [CrossRef]
- Springel, V. E pur si muove: Galilean-invariant cosmological hydrodynamical simulations on a moving mesh. Mon. Not. R. Astron. Soc. 2010, 401, 791–851. [Google Scholar] [CrossRef]
- Hernández-Aguayo, C.; Ruan, C.Z.; Li, B.; Arnold, C.; Baugh, C.M.; Klypin, A.; Prada, F. Fast full N-body simulations of generic modified gravity: Derivative coupling models. J. Cosmol. Astropart. Phys. 2022, 01, 048. [Google Scholar] [CrossRef]
- Ruan, C.Z.; Hernández-Aguayo, C.; Li, B.; Arnold, C.; Baugh, C.M.; Klypin, A.; Prada, F. Fast full N-body simulations of generic modified gravity: Conformal coupling models. J. Cosmol. Astropart. Phys. 2022, 05, 018. [Google Scholar] [CrossRef]
- Klypin, A.; Prada, F. Dark matter statistics for large galaxy catalogues: Power spectra and covariance matrices. Mon. Not. R. Astron. Soc. 2018, 478, 4602–4621. [Google Scholar] [CrossRef]
- Barreira, A.; Bose, S.; Li, B. Speeding up N-body simulations of modified gravity: Vainshtein screening models. J. Cosmol. Astropart. Phys. 2015, 2015, 059. [Google Scholar] [CrossRef]
- Bose, S.; Li, B.; Barreira, A.; He, J.H.; Hellwing, W.A.; Koyama, K.; Llinares, C.; Zhao, G.B. Speeding up N-body simulations of modified gravity: Chameleon screening models. J. Cosmol. Astropart. Phys. 2017, 2017, 050. [Google Scholar] [CrossRef]
- Tassev, S.; Zaldarriaga, M.; Eisenstein, D.J. Solving large scale structure in ten easy steps with COLA. J. Cosmol. Astropart. Phys. 2013, 2013, 036. [Google Scholar] [CrossRef]
- Winther, H.A.; Koyama, K.; Manera, M.; Wright, B.S.; Zhao, G.B. COLA with scale-dependent growth: Applications to screened modified gravity models. J. Cosmol. Astropart. Phys. 2017, 2017, 006. [Google Scholar] [CrossRef]
- Valogiannis, G.; Bean, R. Efficient simulations of large-scale structure in modified gravity cosmologies with comoving Lagrangian acceleration. Phys. Rev. D 2017, 95, 103515. [Google Scholar] [CrossRef]
- Springel, V.; White, S.D.; Tormen, G.; Kauffmann, G. Populating a cluster of galaxies. 1. Results at z = 0. Mon. Not. R. Astron. Soc. 2001, 328, 726–750. [Google Scholar] [CrossRef]
- Behroozi, P.S.; Wechsler, R.H.; Wu, H.Y. The Rockstar Phase-Space Temporal Halo Finder and the Velocity Offsets of Cluster Cores. Astrophys. J. 2013, 762, 109. [Google Scholar] [CrossRef]
- Berlind, A.A.; Weinberg, D.H. The Halo Occupation Distribution: Toward an Empirical Determination of the Relation between Galaxies and Mass. Astrophys. J. 2002, 575, 587–616. [Google Scholar] [CrossRef]
- Conroy, C.; Wechsler, R.H.; Kravtsov, A.V. Modeling Luminosity-dependent Galaxy Clustering through Cosmic Time. Astrophys. J. 2006, 647, 201–214. [Google Scholar] [CrossRef]
- Manera, M.; Scoccimarro, R.; Percival, W.J.; Samushia, L.; McBride, C.K.; Ross, A.J.; Sheth, R.K.; White, M.; Reid, B.A.; Sánchez, A.G.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: A large sample of mock galaxy catalogues. Mon. Not. R. Astron. Soc. 2012, 428, 1036–1054. [Google Scholar] [CrossRef]
- Devi, N.C.; Rodríguez-Puebla, A.; Valenzuela, O.; Avila-Reese, V.; Hernández-Aguayo, C.; Li, B. The galaxy–halo connection in modified gravity cosmologies: Environment dependence of galaxy luminosity function. Mon. Not. R. Astron. Soc. 2019, 488, 782–802. [Google Scholar] [CrossRef]
- Dragomir, R.; Rodríguez-Puebla, A.; Primack, J.R.; Lee, C.T. Does the galaxy-halo connection vary with environment? Mon. Not. R. Astron. Soc. 2018, 476, 741–758. [Google Scholar] [CrossRef]
- Pillepich, A.; Springel, V.; Nelson, D.; Genel, S.; Naiman, J.; Pakmor, R.; Hernquist, L.; Torrey, P.; Vogelsberger, M.; Weinberger, R.; et al. Simulating galaxy formation with the IllustrisTNG model. Mon. Not. R. Astron. Soc. 2018, 473, 4077–4106. [Google Scholar] [CrossRef]
- Weinberger, R.; Springel, V.; Hernquist, L.; Pillepich, A.; Marinacci, F.; Pakmor, R.; Nelson, D.; Genel, S.; Vogelsberger, M.; Naiman, J.; et al. Simulating galaxy formation with black hole driven thermal and kinetic feedback. Mon. Not. R. Astron. Soc. 2017, 465, 3291–3308. [Google Scholar] [CrossRef]
- Leo, M.; Arnold, C.; Li, B. High-redshift test of gravity using enhanced growth of small structures probed by the neutral hydrogen distribution. Phys. Rev. D 2019, 1000, 064044. [Google Scholar] [CrossRef]
- Mitchell, M.A.; Arnold, C.; Li, B. A general framework to test gravity using galaxy clusters—VI. Realistic galaxy formation simulations to study clusters in modified gravity. arXiv 2022, arXiv:2109.01147. [Google Scholar] [CrossRef]
- Ruan, C.Z.; Cuesta-Lazaro, C.; Eggemeier, A.; Hernández-Aguayo, C.; Baugh, C.M.; Li, B.; Prada, F. Towards an accurate model of small-scale redshift-space distortions in modified gravity. Mon. Not. R. Astron. Soc. 2022, 514, 440–459. [Google Scholar] [CrossRef]
- Carucci, I.P.; Corasaniti, P.S.; Viel, M. Imprints of non-standard dark energy and dark matter models on the 21cm intensity map power spectrum. J. Cosmol. Astropart. Phys. 2017, 2017, 018. [Google Scholar] [CrossRef]
- Bagla, J.S.; Khandai, N.; Datta, K.K. HI as a probe of the large-scale structure in the post-reionization universe. Mon. Not. R. Astron. Soc. 2010, 407, 567–580. [Google Scholar] [CrossRef]
- Carucci, I.P.; Villaescusa-Navarro, F.; Viel, M.; Lapi, A. Warm dark matter signatures on the 21cm power spectrum: Intensity mapping forecasts for SKA. J. Cosmol. Astropart. Phys. 2015, 2015, 047. [Google Scholar] [CrossRef]
- Carucci, I.P.; Villaescusa-Navarro, F.; Viel, M. The cross-correlation between 21 cm intensity mapping maps and the Lyα forest in the post-reionization era. J. Cosmol. Astropart. Phys. 2017, 2017, 001. [Google Scholar] [CrossRef]
- Alimi, J.M.; Bouillot, V.; Rasera, Y.; Reverdy, V.; Corasaniti, P.S.; Balmes, I.; Requena, S.; Delaruelle, X.; Richet, J.N. DEUS Full Observable ΛCDM Universe Simulation: The numerical challenge. arXiv 2012, arXiv:1206.2838. [Google Scholar] [CrossRef]
- Corasaniti, P.S.; Agarwal, S.; Marsh, D.J.E.; Das, S. Constraints on dark matter scenarios from measurements of the galaxy luminosity function at high redshifts. Phys. Rev. D 2017, 95, 083512. [Google Scholar] [CrossRef]
- Feng, Y.; Chu, M.Y.; Seljak, U.; McDonald, P. FASTPM: A new scheme for fast simulations of dark matter and haloes. Mon. Not. R. Astron. Soc. 2016, 463, 2273–2286. [Google Scholar] [CrossRef]
- Modi, C.; Castorina, E.; Feng, Y.; White, M. Intensity mapping with neutral hydrogen and the Hidden Valley simulations. J. Cosmol. Astropart. Phys. 2019, 2019, 024. [Google Scholar] [CrossRef]
- Moradinezhad Dizgah, A.; Nikakhtar, F.; Keating, G.K.; Castorina, E. Precision tests of CO and [CII] power spectra models against simulated intensity maps. J. Cosmol. Astropart. Phys. 2022, 2022, 026. [Google Scholar] [CrossRef]
- Mesinger, A.; Furlanetto, S.; Cen, R. 21CMFAST: A fast, seminumerical simulation of the high-redshift 21-cm signal. Mon. Not. R. Astron. Soc. 2011, 411, 955–972. [Google Scholar] [CrossRef]
- Bond, J.R.; Cole, S.; Efstathiou, G.; Kaiser, N. Excursion Set Mass Functions for Hierarchical Gaussian Fluctuations. Phys. Rev. Lett. 1991, 379, 440. [Google Scholar] [CrossRef]
- Heneka, C.; Amendola, L. General modified gravity with 21cm intensity mapping: Simulations and forecast. J. Cosmol. Astropart. Phys. 2018, 2018, 004. [Google Scholar] [CrossRef]
- Wilman, R.J.; Miller, L.; Jarvis, M.J.; Mauch, T.; Levrier, F.; Abdalla, F.B.; Rawlings, S.; Klöckner, H.R.; Obreschkow, D.; Olteanu, D.; et al. A semi-empirical simulation of the extragalactic radio continuum sky for next generation radio telescopes. Mon. Not. R. Astron. Soc. 2008, 388, 1335–1348. [Google Scholar] [CrossRef]
- Bonaldi, A.; Bonato, M.; Galluzzi, V.; Harrison, I.; Massardi, M.; Kay, S.; Zotti, G.D.; Brown, M.L. The Tiered Radio Extragalactic Continuum Simulation (T-RECS). Mon. Not. R. Astron. Soc. 2018, 482, 2–19. [Google Scholar] [CrossRef]
- Magliocchetti, M. Hosts and environments: A (large-scale) radio history of AGN and star-forming galaxies. Astron. Astrophys. Rev. 2022, 30, 6. [Google Scholar] [CrossRef]
- D’Amico, G.; Donath, Y.; Lewandowski, M.; Senatore, L.; Zhang, P. The BOSS bispectrum analysis at one loop from the Effective Field Theory of Large-Scale Structure. arXiv 2022, arXiv:2206.08327. [Google Scholar]
- Philcox, O.H.E.; Ivanov, M.M. BOSS DR12 full-shape cosmology: Λ CDM constraints from the large-scale galaxy power spectrum and bispectrum monopole. Phys. Rev. D 2022, 105, 043517. [Google Scholar] [CrossRef]
- Yuan, S.; Hadzhiyska, B.; Abel, T. Full forward model of galaxy clustering statistics with simulation lightcones. arXiv 2022, arXiv:2211.02068. [Google Scholar] [CrossRef]
- Hahn, C.; Eickenberg, M.; Ho, S.; Hou, J.; Lemos, P.; Massara, E.; Modi, C.; Dizgah, A.M.; Blancard, B.R.S.; Abidi, M.M. SIMBIG: Mock Challenge for a Forward Modeling Approach to Galaxy Clustering. arXiv 2022, arXiv:2211.00660. [Google Scholar] [CrossRef]
- Zhai, Z.; Tinker, J.L.; Becker, M.R.; DeRose, J.; Mao, Y.Y.; McClintock, T.; McLaughlin, S.; Rozo, E.; Wechsler, R.H. The Aemulus Project. III. Emulation of the Galaxy Correlation Function. Astrophys. J. 2019, 874, 95. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Nishimichi, T.; Takada, M.; Takahashi, R.; Osato, K. Accurate emulator for the redshift-space power spectrum of dark matter halos and its application to galaxy power spectrum. Phys. Rev. D 2020, 102. [Google Scholar] [CrossRef]
- Arnold, C.; Li, B.; Giblin, B.; Harnois-Déraps, J.; Cai, Y.C. FORGE: The f(R)-gravity cosmic emulator project—I. Introduction and matter power spectrum emulator. Mon. Not. R. Astron. Soc. 2022, 515, 4161–4175. [Google Scholar] [CrossRef]
- Harnois-Déraps, J.; Hernandez-Aguayo, C.; Cuesta-Lazaro, C.; Arnold, C.; Li, B.; Davies, C.T.; Cai, Y.C. MGLenS: Modified gravity weak lensing simulations for emulation-based cosmological inference. arXiv 2022, arXiv:2211.05779. [Google Scholar] [CrossRef]
- Newman, J.A.; Gruen, D. Photometric Redshifts for Next-Generation Surveys. Annu. Rev. Astron. Astrophys. 2022, 60, 363–414. [Google Scholar] [CrossRef]
- Maddox, S.J.; Efstathiou, G.; Loveday, J. The APM Galaxy Survey. In Large Scale Structures of the Universe, Proceedings of the 130th Symposium of the International Astronomical Union, Dedicated to the Memory of Marc A. Aaronson (1950–1987), Balatonfured, Hungary, 15–20 June 1987; Audouze, J., Pelletan, M.C., Szalay, A., Zel’dovich, Y.B., Peebles, P.J.E., Eds.; Springer: Berlin/Heidelberg, Germany, 1988; Volume 130, p. 151. [Google Scholar]
- Collins, C.A.; Guzzo, L.; Nichol, R.C.; Lumsden, S.L. The Edinburgh-Durham Southern Galaxy Catalogue—VII. The Edinburgh-Milano cluster redshift survey. Mon. Not. R. Astron. Soc. 1995, 274, 1071–1092. [Google Scholar] [CrossRef]
- Wolf, C.; Meisenheimer, K.; Rix, H.W.; Borch, A.; Dye, S.; Kleinheinrich, M. The COMBO-17 survey: Evolution of the galaxy luminosity function from 25 000 galaxies with 0.2< z <1.2. Astron. Astrophys. 2003, 401, 73–98. [Google Scholar] [CrossRef]
- Ilbert, O.; Arnouts, S.; McCracken, H.J.; Bolzonella, M.; Bertin, E.; Le Fèvre, O.; Mellier, Y.; Zamorani, G.; Pellò, R.; Iovino, A.; et al. Accurate photometric redshifts for the CFHT legacy survey calibrated using the VIMOS VLT deep survey. Astron. Astrophys. 2006, 457, 841–856. [Google Scholar] [CrossRef]
- Rowan-Robinson, M.; Babbedge, T.; Oliver, S.; Trichas, M.; Berta, S.; Lonsdale, C.; Smith, G.; Shupe, D.; Surace, J.; Arnouts, S.; et al. Photometric redshifts in the SWIRE Survey. Mon. Not. R. Astron. Soc. 2008, 386, 697–714. [Google Scholar] [CrossRef]
- Mobasher, B.; Capak, P.; Scoville, N.Z.; Dahlen, T.; Salvato, M.; Aussel, H.; Thompson, D.J.; Feldmann, R.; Tasca, L.; Le Fevre, O.; et al. Photometric Redshifts of Galaxies in COSMOS. Astrophys. J. Supp. 2007, 172, 117–131. [Google Scholar] [CrossRef]
- Wright, E.L.; Eisenhardt, P.R.M.; Mainzer, A.K.; Ressler, M.E.; Cutri, R.M.; Jarrett, T.; Kirkpatrick, J.D.; Padgett, D.; McMillan, R.S.; Skrutskie, M.; et al. The Wide-field Infrared Survey Explorer (WISE): Mission Description and Initial On-orbit Performance. Astron. J. 2010, 140, 1868–1881. [Google Scholar] [CrossRef]
- Skrutskie, M.F.; Cutri, R.M.; Stiening, R.; Weinberg, M.D.; Schneider, S.; Carpenter, J.M.; Beichman, C.; Capps, R.; Chester, T.; Elias, J.; et al. The Two Micron All Sky Survey (2MASS). Astron. J. 2006, 131, 1163–1183. [Google Scholar] [CrossRef]
- de Jong, J.T.A.; Verdoes Kleijn, G.A.; Kuijken, K.H.; Valentijn, E.A. The Kilo-Degree Survey. Exp. Astron. 2013, 35, 25–44. [Google Scholar] [CrossRef]
- Abbott, T. et al. [Dark Energy Survey Collaboration] The Dark Energy Survey: More than dark energy—An overview. Mon. Not. R. Astron. Soc. 2016, 460, 1270–1299. [Google Scholar] [CrossRef]
- Aihara, H.; Arimoto, N.; Armstrong, R.; Arnouts, S.; Bahcall, N.A.; Bickerton, S.; Bosch, J.; Bundy, K.; Capak, P.L.; Chan, J.H.H.; et al. The Hyper Suprime-Cam SSP Survey: Overview and survey design. Publ. Astron. Soc. Jpn. 2018, 70, S4. [Google Scholar] [CrossRef]
- de Jong, J.T.A.; Verdoes Kleijn, G.A.; Erben, T.; Hildebrandt, H.; Kuijken, K.; Sikkema, G.; Brescia, M.; Bilicki, M.; Napolitano, N.R.; Amaro, V.; et al. The third data release of the Kilo-Degree Survey and associated data products. Astron. Astrophys. 2017, 604, A134. [Google Scholar] [CrossRef]
- Kuijken, K.; Heymans, C.; Dvornik, A.; Hildebrandt, H.; de Jong, J.T.A.; Wright, A.H.; Erben, T.; Bilicki, M.; Giblin, B.; Shan, H.Y.; et al. The fourth data release of the Kilo-Degree Survey: Ugri imaging and nine-band optical-IR photometry over 1000 square degrees. Astron. Astrophys. 2019, 625, A2. [Google Scholar] [CrossRef]
- Drlica-Wagner, A.; Sevilla-Noarbe, I.; Rykoff, E.S.; Gruendl, R.A.; Yanny, B.; Tucker, D.L.; Hoyle, B.; Carnero Rosell, A.; Bernstein, G.M.; Bechtol, K.; et al. Dark Energy Survey Year 1 Results: The Photometric Data Set for Cosmology. Astrophys. J. Supp. 2018, 235, 33. [Google Scholar] [CrossRef]
- Sevilla-Noarbe, I.; Bechtol, K.; Carrasco Kind, M.; Carnero Rosell, A.; Becker, M.R.; Drlica-Wagner, A.; Gruendl, R.A.; Rykoff, E.S.; Sheldon, E.; Yanny, B.; et al. Dark Energy Survey Year 3 Results: Photometric Data Set for Cosmology. Astrophys. J. Supp. 2021, 254, 24. [Google Scholar] [CrossRef]
- Abell, P.A. et al. [LSST Science Collaboration] LSST Science Book, Version 2.0. arXiv 2009, arXiv:0912.0201. [Google Scholar]
- Laureijs, R.; Gondoin, P.; Duvet, L.; Saavedra Criado, G.; Hoar, J.; Amiaux, J.; Auguères, J.L.; Cole, R.; Cropper, M.; Ealet, A.; et al. Euclid: ESA’s mission to map the geometry of the dark universe. In Space Telescopes and Instrumentation 2012: Optical, Infrared, and Millimeter Wave; Clampin, M.C., Fazio, G.G., MacEwen, H.A., Oschmann, J.M., Jr., Eds.; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; SPIE: Bellingham, WA, USA, 2012; Volume 8442, p. 84420T. [Google Scholar] [CrossRef]
- Spergel, D.; Gehrels, N.; Breckinridge, J.; Donahue, M.; Dressler, A.; Gaudi, B.S.; Greene, T.; Guyon, O.; Hirata, C.; Kalirai, J.; et al. Wide-Field InfraRed Survey Telescope-Astrophysics Focused Telescope Assets WFIRST-AFTA Final Report. arXiv 2013, arXiv:1305.5422. [Google Scholar]
- Colless, M. First results from the 2dF Galaxy Redshift Survey. Philos. Trans. R. Soc. Lond. Ser. A 1999, 357, 105. [Google Scholar] [CrossRef]
- Jones, D.H.; Saunders, W.; Colless, M.; Read, M.A.; Parker, Q.A.; Watson, F.G.; Campbell, L.A.; Burkey, D.; Mauch, T.; Moore, L.; et al. The 6dF Galaxy Survey: Samples, observational techniques and the first data release. Mon. Not. R. Astron. Soc. 2004, 355, 747–763. [Google Scholar] [CrossRef]
- Drinkwater, M.J.; Jurek, R.J.; Blake, C.; Woods, D.; Pimbblet, K.A.; Glazebrook, K.; Sharp, R.; Pracy, M.B.; Brough, S.; Colless, M.; et al. The WiggleZ Dark Energy Survey: Survey design and first data release. Mon. Not. R. Astron. Soc. 2010, 401, 1429–1452. [Google Scholar] [CrossRef]
- Guzzo, L.; Scodeggio, M.; Garilli, B.; Granett, B.R.; Fritz, A.; Abbas, U.; Adami, C.; Arnouts, S.; Bel, J.; Bolzonella, M.; et al. The VIMOS Public Extragalactic Redshift Survey (VIPERS). An unprecedented view of galaxies and large-scale structure at 0.5 < z < 1.2. Astron. Astrophys. 2014, 566, A108. [Google Scholar] [CrossRef]
- Eisenstein, D.J.; Weinberg, D.H.; Agol, E.; Aihara, H.; Allende Prieto, C.; Anderson, S.F.; Arns, J.A.; Aubourg, É.; Bailey, S.; Balbinot, E.; et al. SDSS-III: Massive Spectroscopic Surveys of the Distant Universe, the Milky Way, and Extra-Solar Planetary Systems. Astron. J. 2011, 142, 72. [Google Scholar] [CrossRef]
- Blanton, M.R.; Bershady, M.A.; Abolfathi, B.; Albareti, F.D.; Allende Prieto, C.; Almeida, A.; Alonso-García, J.; Anders, F.; Anderson, S.F.; Andrews, B.; et al. Sloan Digital Sky Survey IV: Mapping the Milky Way, Nearby Galaxies, and the Distant Universe. Astron. J. 2017, 154, 28. [Google Scholar] [CrossRef]
- Dawson, K.S.; Schlegel, D.J.; Ahn, C.P.; Anderson, S.F.; Aubourg, É.; Bailey, S.; Barkhouser, R.H.; Bautista, J.E.; Beifiori, A.; Berlind, A.A.; et al. The Baryon Oscillation Spectroscopic Survey of SDSS-III. Astron. J. 2013, 145, 10. [Google Scholar] [CrossRef]
- Dawson, K.S.; Kneib, J.P.; Percival, W.J.; Alam, S.; Albareti, F.D.; Anderson, S.F.; Armengaud, E.; Aubourg, É.; Bailey, S.; Bautista, J.E.; et al. The SDSS-IV Extended Baryon Oscillation Spectroscopic Survey: Overview and Early Data. Astron. J. 2016, 151, 44. [Google Scholar] [CrossRef]
- Aghamousa, A. et al. [DESI Collaboration] The DESI Experiment Part I: Science, Targeting, and Survey Design. arXiv 2016, arXiv:1611.00036. [Google Scholar]
- Takada, M.; Ellis, R.S.; Chiba, M.; Greene, J.E.; Aihara, H.; Arimoto, N.; Bundy, K.; Cohen, J.; Doré, O.; Graves, G.; et al. Extragalactic science, cosmology, and Galactic archaeology with the Subaru Prime Focus Spectrograph. Publ. Astron. Soc. Jpn. 2014, 66, R1. [Google Scholar] [CrossRef]
- de Jong, R.S.; Agertz, O.; Berbel, A.A.; Aird, J.; Alexander, D.A.; Amarsi, A.; Anders, F.; Andrae, R.; Ansarinejad, B.; Ansorge, W.; et al. 4MOST: Project overview and information for the First Call for Proposals. Messenger 2019, 175, 3–11. [Google Scholar] [CrossRef]
- Battye, R.A.; Browne, I.W.A.; Dickinson, C.; Heron, G.; Maffei, B.; Pourtsidou, A. HI intensity mapping: A single dish approach. Mon. Not. R. Astron. Soc. 2013, 434, 1239–1256. [Google Scholar] [CrossRef]
- Becker, R.H.; White, R.L.; Helfand, D.J. The FIRST Survey: Faint Images of the Radio Sky at Twenty Centimeters. Astrophys. J. 1995, 450, 559. [Google Scholar] [CrossRef]
- Condon, J.J.; Cotton, W.D.; Greisen, E.W.; Yin, Q.F.; Perley, R.A.; Taylor, G.B.; Broderick, J.J. The NRAO VLA Sky Survey. Astron. J. 1998, 115, 1693–1716. [Google Scholar] [CrossRef]
- Intema, H.T.; Jagannathan, P.; Mooley, K.P.; Frail, D.A. The GMRT 150 MHz all-sky radio survey. First alternative data release TGSS ADR1. Astron. Astrophys. 2017, 598, A78. [Google Scholar] [CrossRef]
- De Gasperin, F.; Williams, W.; Best, P.; Brüggen, M.; Brunetti, G.; Cuciti, V.; Dijkema, T.; Hardcastle, M.; Norden, M.; Offringa, A.; et al. The LOFAR LBA Sky Survey-I. Survey description and preliminary data release. Astron. Astrophys. 2021, 648, A104. [Google Scholar] [CrossRef]
- McConnell, D.; Hale, C.; Lenc, E.; Banfield, J.K.; Heald, G.; Hotan, A.; Leung, J.K.; Moss, V.A.; Murphy, T.; O’Brien, A.; et al. The Rapid ASKAP Continuum Survey I: Design and first results. Publ. Astron. Soc. Aust. 2020, 37, e048. [Google Scholar] [CrossRef]
- Lacy, M.; Baum, S.; Chandler, C.; Chatterjee, S.; Clarke, T.; Deustua, S.; English, J.; Farnes, J.; Gaensler, B.; Gugliucci, N.; et al. The Karl G. Jansky very large array sky survey (VLASS). Science case and survey design. Publ. Astron. Soc. Pac. 2020, 132, 035001. [Google Scholar] [CrossRef]
- Wayth, R.; Lenc, E.; Bell, M.; Callingham, J.; Dwarakanath, K.; Franzen, T.; Gaensler, B.; Hancock, P.; Hindson, L.; Hurley-Walker, N.; et al. GLEAM: The galactic and extragalactic all-sky MWA survey. Publ. Astron. Soc. Aust. 2015, 32, e025. [Google Scholar] [CrossRef] [PubMed]
- Van Haarlem, M.P.; Wise, M.W.; Gunst, A.W.; Heald, G.; McKean, J.P.; Hessels, J.W.T.; de Bruyn, A.G.; Nijboer, R.; Swinbank, J.; Fallows, R.; et al. LOFAR: The LOw-Frequency ARray. Astron. Astrophys. 2013, 556, A2. [Google Scholar] [CrossRef]
- Shimwell, T.W.; Hardcastle, M.J.; Tasse, C.; Best, P.N.; Röttgering, H.J.A.; Williams, W.L.; Botteon, A.; Drabent, A.; Mechev, A.; Shulevski, A.; et al. The LOFAR Two-metre Sky Survey. V. Second data release. Astron. Astrophys. 2022, 659, A1. [Google Scholar] [CrossRef]
- Norris, R.P.; Hopkins, A.M.; Afonso, J.; Brown, S.; Condon, J.J.; Dunne, L.; Feain, I.; Hollow, R.; Jarvis, M.; Johnston-Hollitt, M.; et al. EMU: Evolutionary Map of the Universe. Publ. Astron. Soc. Aust. 2011, 28, 215–248. [Google Scholar] [CrossRef]
- Norris, R.P.; Marvil, J.; Collier, J.D.; Kapińska, A.D.; O’Brien, A.N.; Rudnick, L.; Andernach, H.; Asorey, J.; Brown, M.J.; Brüggen, M.; et al. The Evolutionary Map of the Universe pilot survey. Publ. Astron. Soc. Aust. 2021, 38, e046. [Google Scholar] [CrossRef]
- Röttgering, H.; Afonso, J.; Barthel, P.; Batejat, F.; Best, P.; Bonafede, A.; Brüggen, M.; Brunetti, G.; Chyży, K.; Conway, J.; et al. LOFAR and APERTIF Surveys of the Radio Sky: Probing Shocks and Magnetic Fields in Galaxy Clusters. J. Astrophys. Astron. 2011, 32, 557–566. [Google Scholar] [CrossRef]
- SKA Cosmology SWG. Cosmology with Phase 1 of the Square Kilometre Array: Red Book 2018: Technical specifications and performance forecasts. Publ. Astron. Soc. Aust. 2020, 37, e007. [Google Scholar] [CrossRef]
- Bengaly, C.A.; Maartens, R.; Santos, M.G. Probing the Cosmological Principle in the counts of radio galaxies at different frequencies. J. Cosmol. Astropart. Phys. 2018, 2018, 031. [Google Scholar] [CrossRef]
- Smith, D.J.B.; Best, P.N.; Duncan, K.J.; Hatch, N.A.; Jarvis, M.J.; Röttgering, H.J.A.; Simpson, C.J.; Stott, J.P.; Cochrane, R.K.; Coppin, K.E.; et al. The WEAVE-LOFAR Survey. In Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, SF2A-2016, Lyon, France, 14–17 June 2016; pp. 271–280. [Google Scholar] [CrossRef]
- Bandura, K.; Addison, G.E.; Amiri, M.; Bond, J.R.; Campbell-Wilson, D.; Connor, L.; Cliche, J.F.; Davis, G.; Deng, M.; Denman, N.; et al. Canadian Hydrogen Intensity Mapping Experiment (CHIME) Pathfinder. In Ground-Based and Airborne Telescopes V; SPIE: Bellingham, WA, USA, 2014; Volume 9145, pp. 738–757. [Google Scholar]
- Amiri, M. et al. [CHIME Collaboration] Detection of Cosmological 21 cm Emission with the Canadian Hydrogen Intensity Mapping Experiment. arXiv 2022, arXiv:2202.01242. [Google Scholar]
- Newburgh, L.B.; Bandura, K.; Bucher, M.A.; Chang, T.C.; Chiang, H.C.; Cliche, J.F.; Davé, R.; Dobbs, M.; Clarkson, C.; Ganga, K.M.; et al. HIRAX: A Probe of Dark Energy and Radio Transients. In Ground-Based and Airborne Telescopes VI; SPIE: Bellingham, WA, USA, 2016; Volume 9906, pp. 2039–2049. [Google Scholar]
- Wolz, L.; Pourtsidou, A.; Masui, K.W.; Chang, T.C.; Bautista, J.E.; Müller, E.M.; Avila, S.; Bacon, D.; Percival, W.J.; Cunnington, S.; et al. H I constraints from the cross-correlation of eBOSS galaxies and Green Bank Telescope intensity maps. Mon. Not. R. Astron. Soc. 2022, 510, 3495–3511. [Google Scholar] [CrossRef]
- Hu, W.; Wang, X.; Wu, F.; Wang, Y.; Zhang, P.; Chen, X. Forecast for FAST: From Galaxies Survey to Intensity Mapping. Mon. Not. R. Astron. Soc. 2020, 493, 5854–5870. [Google Scholar] [CrossRef]
- Costa, A.A.; Landim, R.G.; Novaes, C.P.; Xiao, L.; Ferreira, E.G.; Abdalla, F.B.; Wang, B.; Abdalla, E.; Battye, R.A.; Marins, A.; et al. The BINGO project—VII. Cosmological forecasts from 21 cm intensity mapping. Astron. Astrophys. 2022, 664, A20. [Google Scholar] [CrossRef]
- Wuensche, C.A.; Villela, T.; Abdalla, E.; Liccardo, V.; Vieira, F.; Browne, I.; Peel, M.W.; Radcliffe, C.; Abdalla, F.B.; Marins, A.; et al. The BINGO project—II. Instrument description. Astron. Astrophys. 2022, 664, A15. [Google Scholar] [CrossRef]
- Vanderlinde, K.; Liu, A.; Gaensler, B.; Bond, D.; Hinshaw, G.; Ng, C.; Chiang, C.; Stairs, I.; Brown, J.A.; Sievers, J.; et al. The Canadian Hydrogen Observatory and Radio-transient Detector (CHORD). arXiv 2019, arXiv:1911.01777. [Google Scholar] [CrossRef]
- Wu, F.; Li, J.; Zuo, S.; Chen, X.; Das, S.; Marriner, J.P.; Oxholm, T.M.; Phan, A.; Stebbins, A.; Timbie, P.T.; et al. The Tianlai dish pathfinder array: Design, operation, and performance of a prototype transit radio interferometer. Mon. Not. R. Astron. Soc. 2021, 506, 3455–3482. [Google Scholar] [CrossRef]
- Perdereau, O.; Ansari, R.; Stebbins, A.; Timbie, P.T.; Chen, X.; Wu, F.; Li, J.; Marriner, J.P.; Tucker, G.S.; Cong, Y.; et al. The Tianlai dish array low-z surveys forecasts. Mon. Not. R. Astron. Soc. 2022, 517, 4637–4655. [Google Scholar] [CrossRef]
- Santos, M.G.; Cluver, M.; Hilton, M.; Jarvis, M.; Jozsa, G.I.; Leeuw, L.; Smirnov, O.; Taylor, R.; Abdalla, F.; Afonso, J.; et al. MeerKLASS: MeerKAT Large Area Synoptic Survey. In Proceedings of the MeerKAT Science: On the Pathway to the SKA, Stellenbosch, South Africa, 25–27 May 2016. [Google Scholar]
- Wang, J.; Santos, M.G.; Bull, P.; Grainge, K.; Cunnington, S.; Fonseca, J.; Irfan, M.O.; Li, Y.; Pourtsidou, A.; Soares, P.S.; et al. H i intensity mapping with MeerKAT: Calibration pipeline for multidish autocorrelation observations. Mon. Not. R. Astron. Soc. 2021, 505, 3698–3721. [Google Scholar] [CrossRef]
- Wyithe, S.; Loeb, A.; Geil, P. Baryonic Acoustic Oscillations in 21cm Emission: A Probe of Dark Energy out to High Redshifts. Mon. Not. R. Astron. Soc. 2008, 383, 1195–1209. [Google Scholar] [CrossRef]
- Chang, T.C.; Pen, U.L.; Peterson, J.B.; McDonald, P. Baryon Acoustic Oscillation Intensity Mapping as a Test of Dark Energy. Phys. Rev. Lett. 2008, 108, 091303. [Google Scholar] [CrossRef] [PubMed]
- Wu, P.J.; Zhang, X. Prospects for measuring dark energy with 21 cm intensity mapping experiments. J. Cosmol. Astropart. Phys. 2022, 2022, 060. [Google Scholar] [CrossRef]
- Wu, P.J.; Li, Y.; Zhang, J.F.; Zhang, X. Prospects for measuring dark energy with 21 cm intensity mapping experiments: A joint survey strategy. arXiv 2022, arXiv:astro-ph.CO/2212.07681. [Google Scholar] [CrossRef]
- Masui, K.W.; Schmidt, F.; Pen, U.L.; McDonald, P. Projected constraints on modified gravity cosmologies from 21 cm intensity mapping. Phys. Rev. D 2010, 81, 062001. [Google Scholar] [CrossRef]
- Zhao, G.; Bacon, D.; Maartens, R.; Santos, M.; Raccanelli, A. Model-independent constraints on dark energy and modified gravity with the SKA. In Proceedings of the Advancing Astrophysics with the Square Kilometre Array (AASKA14), Giardini Naxos, Italy, 9–13 June 2014; p. 165. [Google Scholar] [CrossRef]
- Berti, M.; Spinelli, M.; Haridasu, B.S.; Viel, M.; Silvestri, A. Constraining beyond ΛCDM models with 21cm intensity mapping forecasted observations combined with latest CMB data. arXiv 2021, arXiv:2109.03256. [Google Scholar] [CrossRef]
- Bull, P.; White, M.; Slosar, A. Searching for dark energy in the matter-dominated era. Mon. Not. R. Astron. Soc. 2021, 505, 2285–2299. [Google Scholar] [CrossRef]
- Ansari, R. et al. [Cosmic Visions 21 cm Collaboration] Inflation and Early Dark Energy with a Stage II Hydrogen Intensity Mapping experiment. arXiv 2018, arXiv:astro-ph.CO/1810.09572. [Google Scholar]
- Karkare, K.S.; Bird, S. Constraining the Expansion History and Early Dark Energy with Line Intensity Mapping. Phys. Rev. D 2018, 98, 043529. [Google Scholar] [CrossRef]
- Xu, X.; Ma, Y.Z.; Weltman, A. Constraining the interaction between dark sectors with future HI intensity mapping observations. Phys. Rev. D 2018, 97, 083504. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, B.; Wu, P.J.; Qi, J.Z.; Xu, Y.; Zhang, J.F.; Zhang, X. Prospects for Constraining Interacting Dark Energy Models with 21 cm Intensity Mapping Experiments. Astrophys. J. 2021, 918, 56. [Google Scholar] [CrossRef]
- Pourtsidou, A. Testing gravity at large scales with HI intensity mapping. Mon. Not. R. Astron. Soc. 2016, 461, 1457–1464. [Google Scholar] [CrossRef]
- Dash, C.B.V.; Sarkar, T.G. Constraining dark energy using the cross correlations of weak lensing with post-reionization probes of neutral hydrogen. J. Cosmol. Astropart. Phys. 2021, 02, 016. [Google Scholar] [CrossRef]
- Scelfo, G.; Berti, M.; Silvestri, A.; Viel, M. Testing gravity with gravitational waves × electromagnetic probes cross-correlations. arXiv 2022, arXiv:astro-ph.CO/2210.02460. [Google Scholar] [CrossRef]
- Casas, S.; Carucci, I.P.; Pettorino, V.; Camera, S.; Martinelli, M. Constraining gravity with synergies between radio and optical cosmological surveys. arXiv 2022, arXiv:astro-ph.CO/2210.05705. [Google Scholar] [CrossRef]
- Abidi, M.M.; Bonvin, C.; Jalilvand, M.; Kunz, M. Model-Independent Test for Gravity using Intensity Mapping and Galaxy Clustering. arXiv 2022, arXiv:astro-ph.CO/2208.10419. [Google Scholar] [CrossRef]
- Scott, B.R.; Karkare, K.S.; Bird, S. A Forecast for Large Scale Structure Constraints on Horndeski Gravity with Line Intensity Mapping. arXiv 2022, arXiv:astro-ph.CO/2209.13029. [Google Scholar] [CrossRef]
- Boggess, N.W.; Mather, J.C.; Weiss, R.; Bennett, C.L.; Cheng, E.S.; Dwek, E.; Gulkis, S.; Hauser, M.G.; Janssen, M.A.; Kelsall, T.; et al. The COBE Mission: Its Design and Performance Two Years after Launch. Astrophys. J. 1992, 397, 420. [Google Scholar] [CrossRef]
- Bennett, C.L.; Larson, D.; Weiland, J.L.; Jarosik, N.; Hinshaw, G.; Odegard, N.; Smith, K.M.; Hill, R.S.; Gold, B.; Halpern, M.; et al. Nine-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Final Maps and Results. Astrophys. J. Supp. 2013, 208, 20. [Google Scholar] [CrossRef]
- Adam, R. et al. [Planck Collaboration] Planck 2015 results. I. Overview of products and scientific results. Astron. Astrophys. 2016, 594, A1. [Google Scholar] [CrossRef]
- De Bernardis, F.; Stevens, J.R.; Hasselfield, M.; Alonso, D.; Bond, J.R.; Calabrese, E.; Choi, S.K.; Crowley, K.T.; Devlin, M.; Dunkley, J.; et al. Survey strategy optimization for the Atacama Cosmology Telescope. In Observatory Operations: Strategies, Processes, and Systems VI; Peck, A.B., Seaman, R.L., Benn, C.R., Eds.; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; SPIE: Bellingham, WA, USA, 2016; Volume 9910, p. 991014. [Google Scholar] [CrossRef]
- Louis, T.; Grace, E.; Hasselfield, M.; Lungu, M.; Maurin, L.; Addison, G.E.; Ade, P.A.R.; Aiola, S.; Allison, R.; Amiri, M.; et al. The Atacama Cosmology Telescope: Two-season ACTPol spectra and parameters. J. Cosmol. Astropart. Phys. 2017, 2017, 031. [Google Scholar] [CrossRef]
- Benson, B.A.; Ade, P.A.R.; Ahmed, Z.; Allen, S.W.; Arnold, K.; Austermann, J.E.; Bender, A.N.; Bleem, L.E.; Carlstrom, J.E.; Chang, C.L.; et al. SPT-3G: A next-generation cosmic microwave background polarization experiment on the South Pole telescope. In Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VII; Holland, W.S., Zmuidzinas, J., Eds.; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; SPIE: Bellingham, WA, USA, 2014; Volume 9153, p. 91531P. [Google Scholar] [CrossRef]
- Henning, J.W.; Sayre, J.T.; Reichardt, C.L.; Ade, P.A.R.; Anderson, A.J.; Austermann, J.E.; Beall, J.A.; Bender, A.N.; Benson, B.A.; Bleem, L.E.; et al. Measurements of the Temperature and E-mode Polarization of the CMB from 500 Square Degrees of SPTpol Data. Astrophys. J. 2018, 852, 97. [Google Scholar] [CrossRef]
- Keating, B.G.; Ade, P.A.R.; Bock, J.J.; Hivon, E.; Holzapfel, W.L.; Lange, A.E.; Nguyen, H.; Yoon, K.W. BICEP: A large angular scale CMB polarimeter. In Polarimetry in Astronomy; Fineschi, S., Ed.; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; SPIE: Belingham, WA, USA, 2003; Volume 4843, pp. 284–295. [Google Scholar] [CrossRef]
- Ogburn, R.W.; Ade, P.A.R.; Aikin, R.W.; Amiri, M.; Benton, S.J.; Bischoff, C.A.; Bock, J.J.; Bonetti, J.A.; Brevik, J.A.; Bullock, E.; et al. BICEP2 and Keck array operational overview and status of observations. In Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VI; Holland, W.S., Zmuidzinas, J., Eds.; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; SPIE: Belingham, WA, USA, 2012; Volume 8452, p. 84521A. [Google Scholar] [CrossRef]
- Grayson, J.A.; Ade, P.A.R.; Ahmed, Z.; Alexander, K.D.; Amiri, M.; Barkats, D.; Benton, S.J.; Bischoff, C.A.; Bock, J.J.; Boenish, H.; et al. BICEP3 performance overview and planned Keck Array upgrade. In Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VIII; Holland, W.S., Zmuidzinas, J., Eds.; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; SPIE: Belingham, WA, USA, 2016; Volume 9914, p. 99140S. [Google Scholar] [CrossRef]
- Essinger-Hileman, T.; Ali, A.; Amiri, M.; Appel, J.W.; Araujo, D.; Bennett, C.L.; Boone, F.; Chan, M.; Cho, H.M.; Chuss, D.T.; et al. CLASS: The cosmology large angular scale surveyor. In Millimeter, Submillimeter, and Far-Infrared Detectors and Instrumentation for Astronomy VII; Holland, W.S., Zmuidzinas, J., Eds.; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series; SPIE: Belingham, WA, USA, 2014; Volume 9153, p. 91531I. [Google Scholar] [CrossRef]
- Abazajian, K.N.; Adshead, P.; Ahmed, Z.; Allen, S.W.; Alonso, D.; Arnold, K.S.; Baccigalupi, C.; Bartlett, J.G.; Battaglia, N.; Benson, B.A.; et al. CMB-S4 Science Book, First Edition. arXiv 2016, arXiv:1610.02743. [Google Scholar]
- Ade, P.; Aguirre, J.; Ahmed, Z.; Aiola, S.; Ali, A.; Alonso, D.; Alvarez, M.A.; Arnold, K.; Ashton, P.; Austermann, J.; et al. The Simons Observatory: Science goals and forecasts. J. Cosmol. Astropart. Phys. 2019, 2019, 056. [Google Scholar] [CrossRef]
- Alam, S. et al. [BOSS Collaboration] The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological analysis of the DR12 galaxy sample. Mon. Not. R. Astron. Soc. 2017, 470, 2617–2652. [Google Scholar] [CrossRef]
- Beutler, F.; Blake, C.; Colless, M.; Jones, D.H.; Staveley-Smith, L.; Poole, G.B.; Campbell, L.; Parker, Q.; Saunders, W.; Watson, F. The 6dF Galaxy Survey: Z≈ 0 measurements of the growth rate and σ8. Mon. Not. R. Astron. Soc. 2012, 423, 3430–3444. [Google Scholar] [CrossRef]
- Blake, C.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; Davis, T.; Drinkwater, M.J.; Forster, K.; Gilbank, D.; et al. The WiggleZ Dark Energy Survey: The growth rate of cosmic structure since redshift z=0.9. Mon. Not. R. Astron. Soc. 2011, 415, 2876–2891. [Google Scholar] [CrossRef]
- Howlett, C.; Ross, A.J.; Samushia, L.; Percival, W.J.; Manera, M. The clustering of the SDSS main galaxy sample—II. Mock galaxy catalogues and a measurement of the growth of structure from redshift space distortions at z = 0.15. Mon. Not. R. Astron. Soc. 2015, 449, 848–866. [Google Scholar] [CrossRef]
- de la Torre, S.; Guzzo, L.; Peacock, J.A.; Branchini, E.; Iovino, A.; Granett, B.R.; Abbas, U.; Adami, C.; Arnouts, S.; Bel, J.; et al. The VIMOS Public Extragalactic Redshift Survey (VIPERS). Galaxy clustering and redshift-space distortions at z ≃ 0.8 in the first data release. Astron. Astrophys. 2013, 557, A54. [Google Scholar] [CrossRef]
- Bautista, J.E.; Paviot, R.; Vargas Magaña, M.; de la Torre, S.; Fromenteau, S.; Gil-Marín, H.; Ross, A.J.; Burtin, E.; Dawson, K.S.; Hou, J.; et al. The completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: Measurement of the BAO and growth rate of structure of the luminous red galaxy sample from the anisotropic correlation function between redshifts 0.6 and 1. Mon. Not. R. Astron. Soc. 2021, 500, 736–762. [Google Scholar] [CrossRef]
- Gil-Marín, H.; Bautista, J.E.; Paviot, R.; Vargas-Magaña, M.; de la Torre, S.; Fromenteau, S.; Alam, S.; Ávila, S.; Burtin, E.; Chuang, C.H.; et al. The Completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: Measurement of the BAO and growth rate of structure of the luminous red galaxy sample from the anisotropic power spectrum between redshifts 0.6 and 1.0. Mon. Not. R. Astron. Soc. 2020, 498, 2492–2531. [Google Scholar] [CrossRef]
- Tamone, A.; Raichoor, A.; Zhao, C.; de Mattia, A.; Gorgoni, C.; Burtin, E.; Ruhlmann-Kleider, V.; Ross, A.J.; Alam, S.; Percival, W.J.; et al. The completed SDSS-IV extended baryon oscillation spectroscopic survey: Growth rate of structure measurement from anisotropic clustering analysis in configuration space between redshift 0.6 and 1.1 for the emission-line galaxy sample. Mon. Not. R. Astron. Soc. 2020, 499, 5527–5546. [Google Scholar] [CrossRef]
- de Mattia, A.; Ruhlmann-Kleider, V.; Raichoor, A.; Ross, A.J.; Tamone, A.; Zhao, C.; Alam, S.; Avila, S.; Burtin, E.; Bautista, J.; et al. The completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: Measurement of the BAO and growth rate of structure of the emission line galaxy sample from the anisotropic power spectrum between redshift 0.6 and 1.1. Mon. Not. R. Astron. Soc. 2021, 501, 5616–5645. [Google Scholar] [CrossRef]
- Neveux, R.; Burtin, E.; de Mattia, A.; Smith, A.; Ross, A.J.; Hou, J.; Bautista, J.; Brinkmann, J.; Chuang, C.H.; Dawson, K.S.; et al. The completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: BAO and RSD measurements from the anisotropic power spectrum of the quasar sample between redshift 0.8 and 2.2. Mon. Not. R. Astron. Soc. 2020, 499, 210–229. [Google Scholar] [CrossRef]
- Ade, P.A.R. et al. [Planck Collaboration] Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Scolnic, D. Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics beyond ΛCDM. Astrophys. J. 2019, 876, 85. [Google Scholar] [CrossRef]
- Qu, F.J.; Sherwin, B.D.; Madhavacheril, M.S.; Han, D.; Crowley, K.T.; Abril-Cabezas, I.; Ade, P.A.R.; Aiola, S.; Alford, T.; Amiri, M.; et al. The Atacama Cosmology Telescope: A Measurement of the DR6 CMB Lensing Power Spectrum and its Implications for Structure Growth. arXiv 2023, arXiv:2304.05202. [Google Scholar] [CrossRef]
- Tröster, T.; Sánchez, A.G.; Asgari, M.; Blake, C.; Crocce, M.; Heymans, C.; Hildebrandt, H.; Joachimi, B.; Joudaki, S.; Kannawadi, A.; et al. Cosmology from large-scale structure. Constraining ΛCDM with BOSS. Astron. Astrophys. 2020, 633, L10. [Google Scholar] [CrossRef]
- Semenaite, A.; Sánchez, A.G.; Pezzotta, A.; Hou, J.; Scoccimarro, R.; Eggemeier, A.; Crocce, M.; Chuang, C.H.; Smith, A.; Zhao, C.; et al. Cosmological implications of the full shape of anisotropic clustering measurements in BOSS and eBOSS. Mon. Not. R. Astron. Soc. 2022, 512, 5657–5670. [Google Scholar] [CrossRef]
- Schellenberger, G.; Reiprich, T.H. HICOSMO: Cosmology with a complete sample of galaxy clusters—II. Cosmological results. Mon. Not. R. Astron. Soc. 2017, 471, 1370–1389. [Google Scholar] [CrossRef]
- Bocquet, S.; Dietrich, J.P.; Schrabback, T.; Bleem, L.E.; Klein, M.; Allen, S.W.; Applegate, D.E.; Ashby, M.L.N.; Bautz, M.; Bayliss, M.; et al. Cluster Cosmology Constraints from the 2500 deg2 SPT-SZ Survey: Inclusion of Weak Gravitational Lensing Data from Magellan and the Hubble Space Telescope. Astrophys. J. 2019, 878, 55. [Google Scholar] [CrossRef]
- Abbott, T.M.C.; Aguena, M.; Alarcon, A.; Allam, S.; Allen, S.; Annis, J.; Avila, S.; Bacon, D.; Bechtol, K.; Bermeo, A.; et al. Dark Energy Survey Year 1 Results: Cosmological constraints from cluster abundances and weak lensing. Phys. Rev. D 2020, 102, 023509. [Google Scholar] [CrossRef]
- Chiu, I.N.; Klein, M.; Mohr, J.; Bocquet, S. Cosmological Constraints from Galaxy Clusters and Groups in the eROSITA Final Equatorial Depth Survey. arXiv 2022, arXiv:2207.12429. [Google Scholar] [CrossRef]
- Lesci, G.F.; Nanni, L.; Marulli, F.; Moscardini, L.; Veropalumbo, A.; Maturi, M.; Sereno, M.; Radovich, M.; Bellagamba, F.; Roncarelli, M.; et al. AMICO galaxy clusters in KiDS-DR3: Constraints on cosmological parameters and on the normalisation of the mass-richness relation from clustering. Astron. Astrophys. 2022, 665, A100. [Google Scholar] [CrossRef]
- Douspis, M.; Salvati, L.; Gorce, A.; Aghanim, N. Retrieving cosmological information from small-scale CMB foregrounds. I. The thermal Sunyaev Zel’dovich effect. Astron. Astrophys. 2022, 659, A99. [Google Scholar] [CrossRef]
- Tanimura, H.; Douspis, M.; Aghanim, N.; Salvati, L. Constraining cosmology with a new all-sky Compton parameter map from the Planck PR4 data. Mon. Not. R. Astron. Soc. 2022, 509, 300–313. [Google Scholar] [CrossRef]
- Tröster, T.; Mead, A.J.; Heymans, C.; Yan, Z.; Alonso, D.; Asgari, M.; Bilicki, M.; Dvornik, A.; Hildebrandt, H.; Joachimi, B.; et al. Joint constraints on cosmology and the impact of baryon feedback: Combining KiDS-1000 lensing with the thermal Sunyaev-Zeldovich effect from Planck and ACT. Astron. Astrophys. 2022, 660, A27. [Google Scholar] [CrossRef]
- Abdalla, E.; Abellán, G.F.; Aboubrahim, A.; Agnello, A.; Akarsu, Ö.; Akrami, Y.; Alestas, G.; Aloni, D.; Amendola, L.; Anchordoqui, L.A.; et al. Cosmology intertwined: A review of the particle physics, astrophysics, and cosmology associated with the cosmological tensions and anomalies. J. High Energy Astrophys. 2022, 34, 49–211. [Google Scholar] [CrossRef]
- Di Valentino, E.; Bridle, S. Exploring the Tension between Current Cosmic Microwave Background and Cosmic Shear Data. Symmetry 2018, 10, 585. [Google Scholar] [CrossRef]
- Aghanim, N. et al. [Planck Collaboration] Planck intermediate results. XLVI. Reduction of large-scale systematic effects in HFI polarization maps and estimation of the reionization optical depth. Astron. Astrophys. 2016, 596, A107. [Google Scholar] [CrossRef]
- Aiola, S.; Calabrese, E.; Maurin, L.; Naess, S.; Schmitt, B.L.; Abitbol, M.H.; Addison, G.E.; Ade, P.A.R.; Alonso, D.; Amiri, M.; et al. The Atacama Cosmology Telescope: DR4 maps and cosmological parameters. J. Cosmol. Astropart. Phys. 2020, 2020, 047. [Google Scholar] [CrossRef]
- Ade, P.A.R. et al. [Planck Collaboration] Planck 2015 results. XV. Gravitational lensing. Astron. Astrophys. 2016, 594, A15. [Google Scholar] [CrossRef]
- Abbott, T.M.C. et al. [Dark Energy Survey, Kilo-Degree Survey Collaboration] DES Y3 + KiDS-1000: Consistent cosmology combining cosmic shear surveys. arXiv 2023, arXiv:2305.17173. [Google Scholar] [CrossRef]
- Pratt, G.W.; Arnaud, M.; Biviano, A.; Eckert, D.; Ettori, S.; Nagai, D.; Okabe, N.; Reiprich, T.H. The Galaxy Cluster Mass Scale and Its Impact on Cosmological Constraints from the Cluster Population. Space Sci. Rev. 2019, 215, 25. [Google Scholar] [CrossRef]
- Sánchez, A.G. Arguments against using h-1 Mpc units in observational cosmology. Phys. Rev. D 2020, 102, 123511. [Google Scholar] [CrossRef]
- Knox, L.; Millea, M. Hubble constant hunter’s guide. Phys. Rev. D 2020, 101, 043533. [Google Scholar] [CrossRef]
- Schöneberg, N.; Abellán, G.F.; Sánchez, A.P.; Witte, S.J.; Poulin, V.; Lesgourgues, J. The H0 Olympics: A fair ranking of proposed models. Phys. Rep. 2022, 984, 1–55. [Google Scholar] [CrossRef]
- Silverstein, E.; Westphal, A. Monodromy in the CMB: Gravity waves and string inflation. Phys. Rev. D 2008, 78, 106003. [Google Scholar] [CrossRef]
- McAllister, L.; Silverstein, E.; Westphal, A. Gravity waves and linear inflation from axion monodromy. Phys. Rev. D 2010, 82, 046003. [Google Scholar] [CrossRef]
- Meerburg, P.D. Alleviating the tension at low ℓ through axion monodromy. Phys. Rev. D 2014, 90, 063529. [Google Scholar] [CrossRef]
- Battye, R.A.; Moss, A. Evidence for Massive Neutrinos from Cosmic Microwave Background and Lensing Observations. Phys. Rev. Lett. 2014, 112, 051303. [Google Scholar] [CrossRef] [PubMed]
- Böhringer, H.; Chon, G. Constraints on neutrino masses from the study of the nearby large-scale structure and galaxy cluster counts. Mod. Phys. Lett. A 2016, 31, 1640008. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Mena, O.; Vagnozzi, S. Nonminimal dark sector physics and cosmological tensions. Phys. Rev. D 2020, 101, 063502. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Mena, O.; Vagnozzi, S. Interacting dark energy in the early 2020s: A promising solution to the H0 and cosmic shear tensions. Phys. Dark Universe 2020, 30, 100666. [Google Scholar] [CrossRef]
- Camera, S.; Martinelli, M.; Bertacca, D. Does quartessence ease cosmic tensions? Phys. Dark Universe 2019, 23, 100247. [Google Scholar] [CrossRef]
- Davari, Z.; Marra, V.; Malekjani, M. Cosmological constrains on minimally and non-minimally coupled scalar field models. Mon. Not. R. Astron. Soc. 2020, 491, 1920–1933. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Silk, J. Cosmological hints of modified gravity? Phys. Rev. D 2016, 93, 023513. [Google Scholar] [CrossRef]
- Solà Peracaula, J.; Gómez-Valent, A.; de Cruz Pérez, J.; Moreno-Pulido, C. Brans-Dicke Gravity with a Cosmological Constant Smoothes Out ΛCDM Tensions. Astrophys. J. Lett. 2019, 886, L6. [Google Scholar] [CrossRef]
- Sola, J.; Gomez-Valent, A.; de Cruz Perez, J.; Moreno-Pulido, C. Brans-Dicke cosmology with a Λ-term: A possible solution to ΛCDM tensions. arXiv 2020, arXiv:2006.04273. [Google Scholar]
- Alam, S. et al. [eBOSS Collaboration] Completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: Cosmological implications from two decades of spectroscopic surveys at the Apache Point Observatory. Phys. Rev. D 2021, 103, 083533. [Google Scholar] [CrossRef]
- Simpson, F.; Heymans, C.; Parkinson, D.; Blake, C.; Kilbinger, M.; Benjamin, J.; Erben, T.; Hildebrandt, H.; Hoekstra, H.; Kitching, T.D.; et al. CFHTLenS: Testing the laws of gravity with tomographic weak lensing and redshift-space distortions. Mon. Not. R. Astron. Soc. 2013, 429, 2249–2263. [Google Scholar] [CrossRef]
- Abbott, T.M.C. et al. [DES Collaboration] Dark Energy Survey Year 3 Results: Constraints on extensions to ΛCDM with weak lensing and galaxy clustering. arXiv 2022, arXiv:2207.05766. [Google Scholar] [CrossRef]
- Marchini, A.; Melchiorri, A.; Salvatelli, V.; Pagano, L. Constraints on modified gravity from the Atacama Cosmology Telescope and the South Pole Telescope. Phys. Rev. D 2013, 87, 083527. [Google Scholar] [CrossRef]
- Marchini, A.; Salvatelli, V. Updated constraints from the Planck experiment on modified gravity. Phys. Rev. D 2013, 88, 027502. [Google Scholar] [CrossRef]
- Hu, B.; Liguori, M.; Bartolo, N.; Matarrese, S. Parametrized modified gravity constraints after Planck. Phys. Rev. D 2013, 88, 123514. [Google Scholar] [CrossRef]
- Yamamoto, K.; Nakamura, G.; Hütsi, G.; Narikawa, T.; Sato, T. Constraint on the cosmological f(R) model from the multipole power spectrum of the SDSS luminous red galaxy sample and prospects for a future redshift survey. Phys. Rev. D 2010, 81, 103517. [Google Scholar] [CrossRef]
- Giannantonio, T.; Martinelli, M.; Silvestri, A.; Melchiorri, A. New constraints on parametrised modified gravity from correlations of the CMB with large scale structure. J. Cosmol. Astropart. Phys. 2010, 2010, 030. [Google Scholar] [CrossRef]
- Schmidt, F.; Vikhlinin, A.; Hu, W. Cluster constraints on f(R) gravity. Phys. Rev. D 2009, 80, 083505. [Google Scholar] [CrossRef]
- Ferraro, S.; Schmidt, F.; Hu, W. Cluster Abundance in f(R) Gravity Models. Phys. Rev. D 2011, 83, 063503. [Google Scholar] [CrossRef]
- Harnois-Déraps, J.; Munshi, D.; Valageas, P.; van Waerbeke, L.; Brax, P.; Coles, P.; Rizzo, L. Testing modified gravity with cosmic shear. Mon. Not. R. Astron. Soc. 2015, 454, 2722–2735. [Google Scholar] [CrossRef]
- Lesgourgues, J.; Pastor, S. Massive neutrinos and cosmology. Phys. Rep. 2006, 429, 307–379. [Google Scholar] [CrossRef]
- van Daalen, M.P.; Schaye, J.; Booth, C.M.; Dalla Vecchia, C. The effects of galaxy formation on the matter power spectrum: A challenge for precision cosmology. Mon. Not. R. Astron. Soc. 2011, 415, 3649–3665. [Google Scholar] [CrossRef]
- Mead, A.J.; Peacock, J.A.; Heymans, C.; Joudaki, S.; Heavens, A.F. An accurate halo model for fitting non-linear cosmological power spectra and baryonic feedback models. Mon. Not. R. Astron. Soc. 2015, 454, 1958–1975. [Google Scholar] [CrossRef]
- Schneider, A.; Teyssier, R. A new method to quantify the effects of baryons on the matter power spectrum. J. Cosmol. Astropart. Phys. 2015, 2015, 049. [Google Scholar] [CrossRef]
- Schneider, A.; Teyssier, R.; Stadel, J.; Chisari, N.E.; Le Brun, A.M.C.; Amara, A.; Refregier, A. Quantifying baryon effects on the matter power spectrum and the weak lensing shear correlation. J. Cosmol. Astropart. Phys. 2019, 2019, 020. [Google Scholar] [CrossRef]
- Schaye, J.; Dalla Vecchia, C.; Booth, C.M.; Wiersma, R.P.C.; Theuns, T.; Haas, M.R.; Bertone, S.; Duffy, A.R.; McCarthy, I.G.; van de Voort, F. The physics driving the cosmic star formation history. Mon. Not. R. Astron. Soc. 2010, 402, 1536–1560. [Google Scholar] [CrossRef]
- Dubois, Y.; Pichon, C.; Welker, C.; Le Borgne, D.; Devriendt, J.; Laigle, C.; Codis, S.; Pogosyan, D.; Arnouts, S.; Benabed, K.; et al. Dancing in the dark: Galactic properties trace spin swings along the cosmic web. Mon. Not. R. Astron. Soc. 2014, 444, 1453–1468. [Google Scholar] [CrossRef]
- Peirani, S.; Dubois, Y.; Volonteri, M.; Devriendt, J.; Bundy, K.; Silk, J.; Pichon, C.; Kaviraj, S.; Gavazzi, R.; Habouzit, M. Density profile of dark matter haloes and galaxies in the HORIZON-AGN simulation: The impact of AGN feedback. Mon. Not. R. Astron. Soc. 2017, 472, 2153–2169. [Google Scholar] [CrossRef]
- McCarthy, I.G.; Schaye, J.; Bird, S.; Le Brun, A.M.C. The BAHAMAS project: Calibrated hydrodynamical simulations for large-scale structure cosmology. Mon. Not. R. Astron. Soc. 2017, 465, 2936–2965. [Google Scholar] [CrossRef]
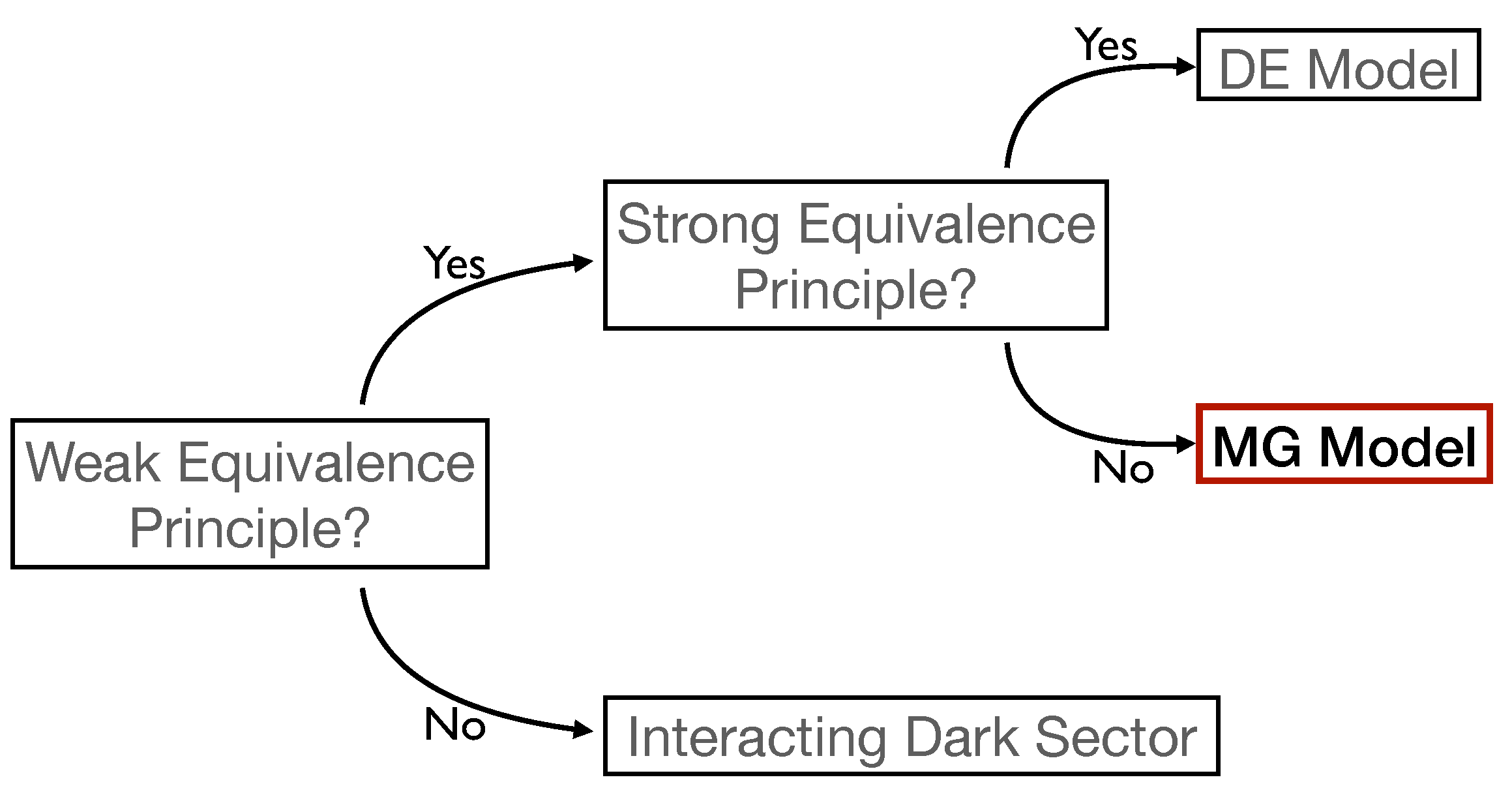
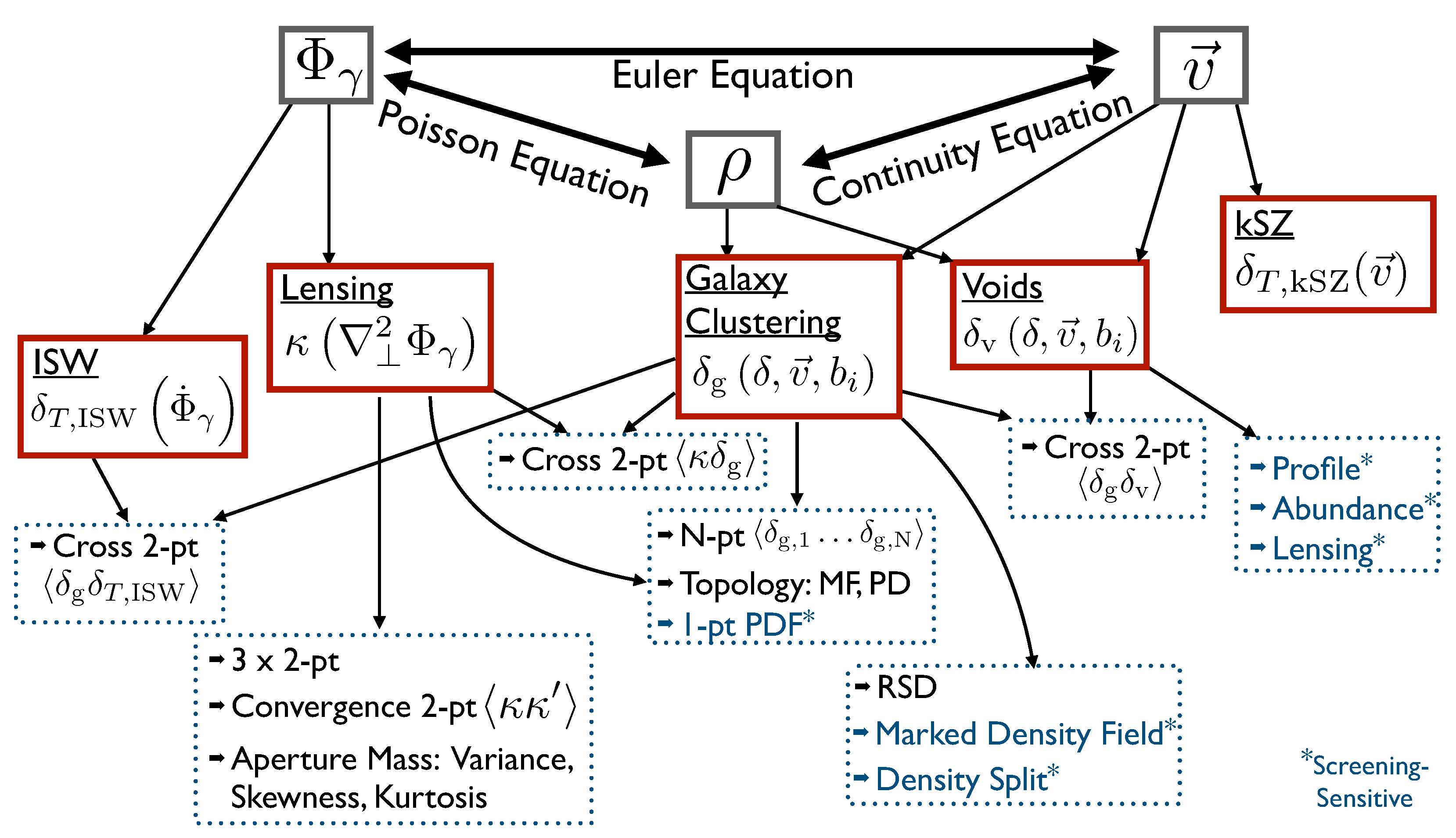


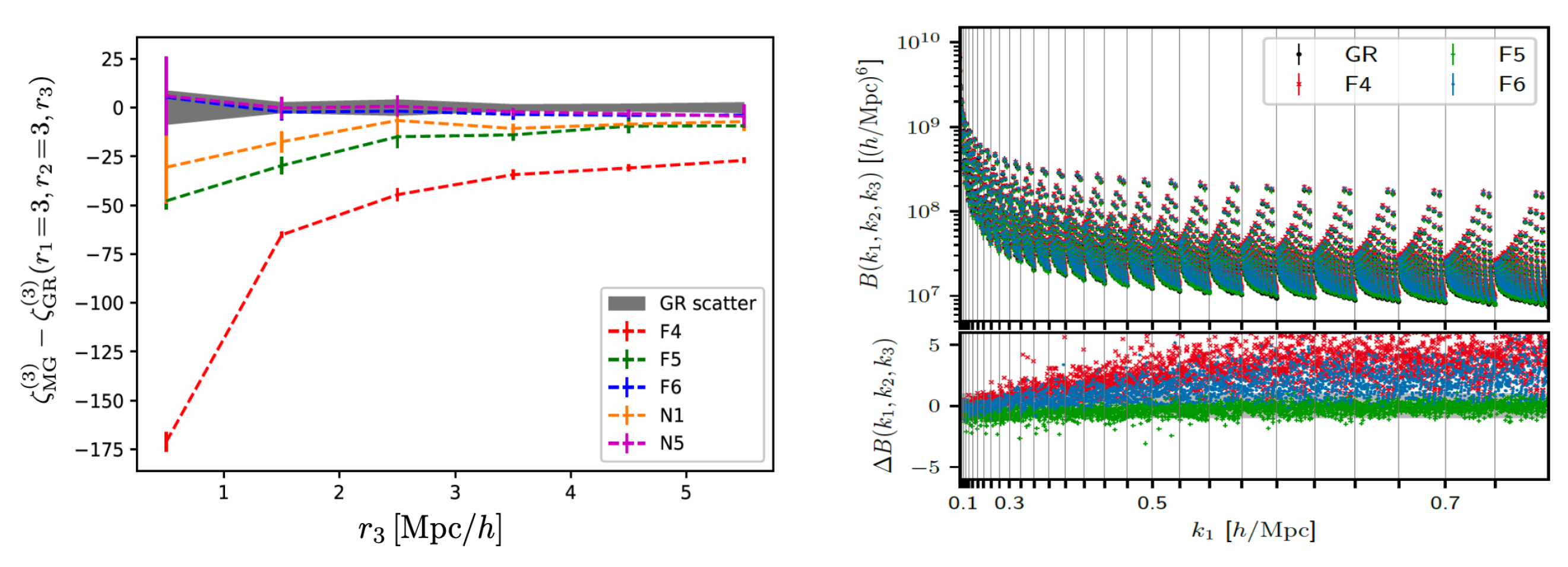

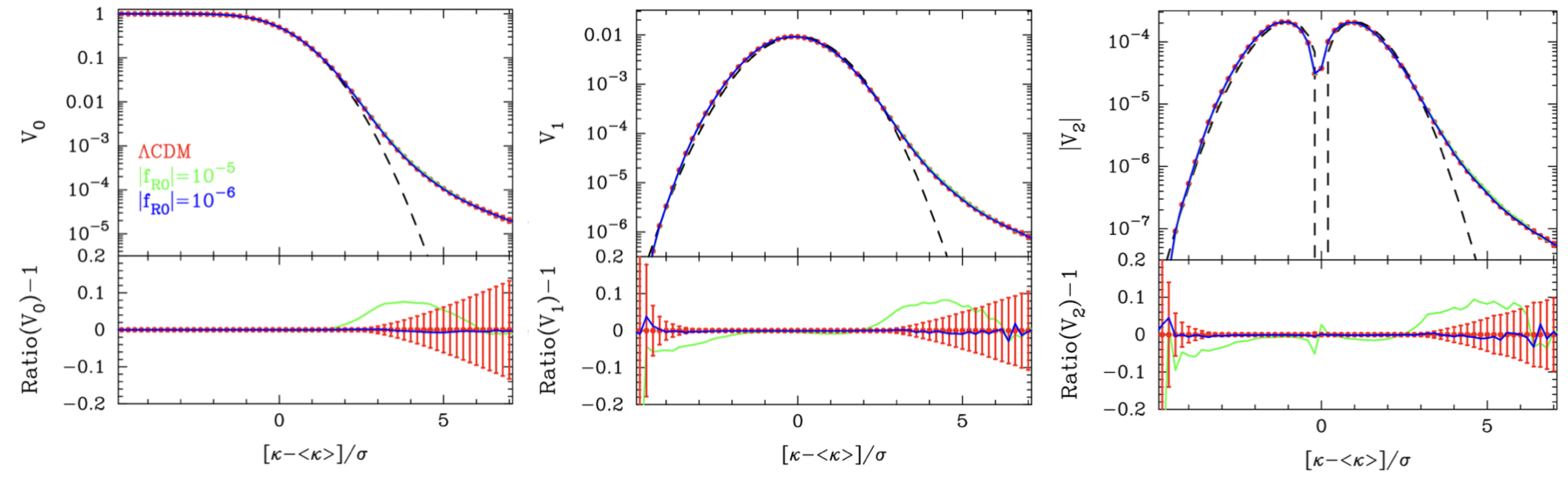

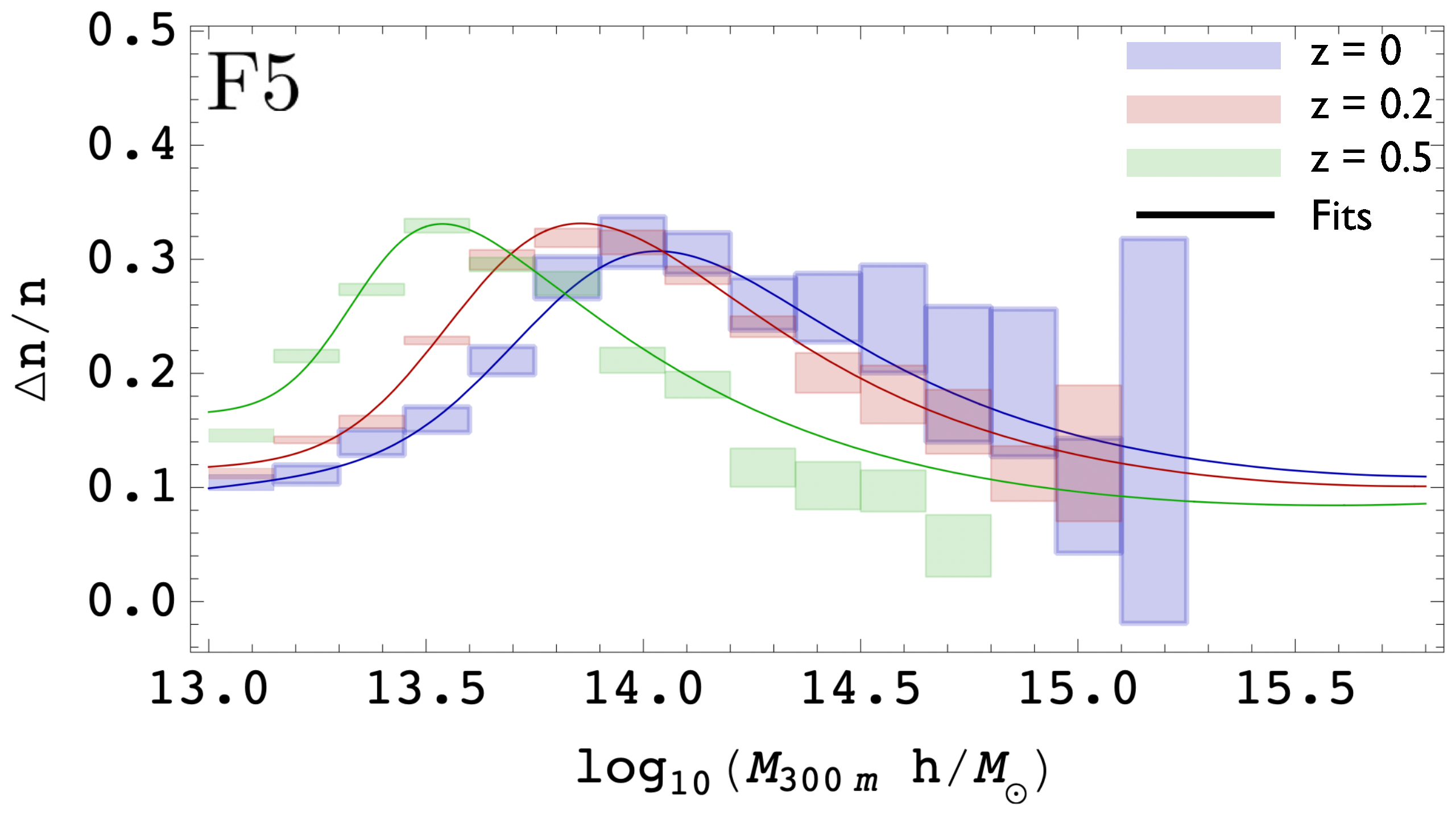
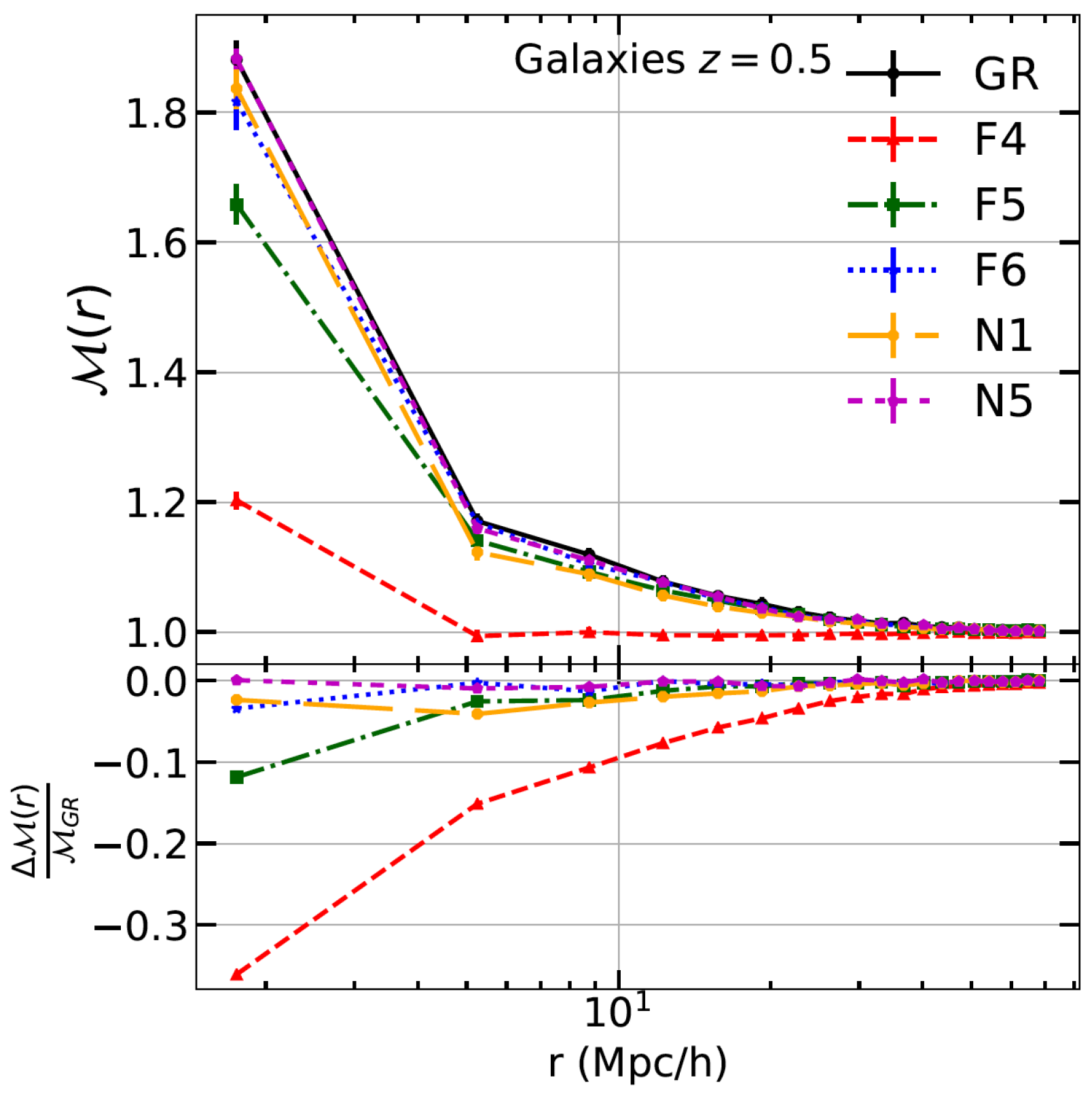


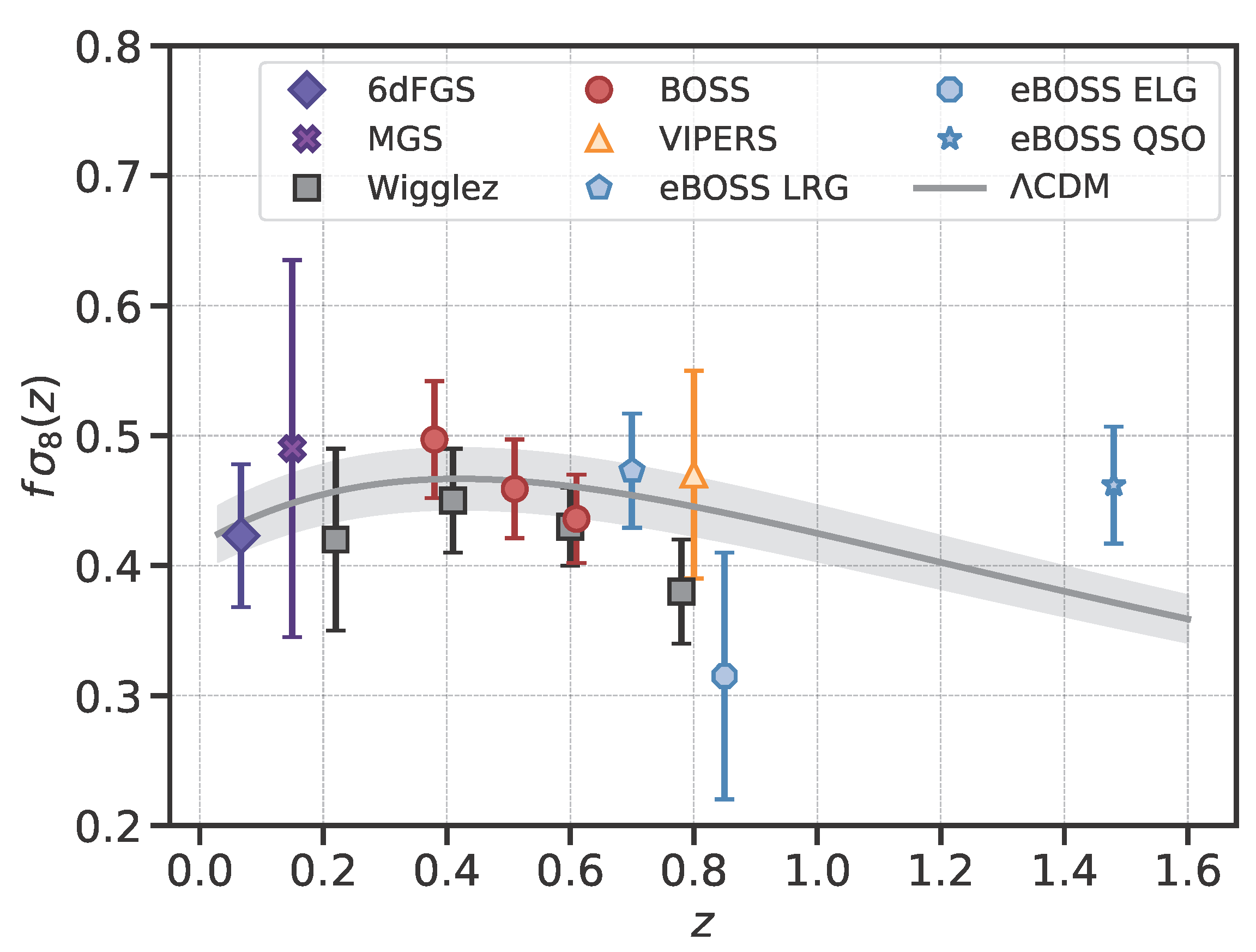
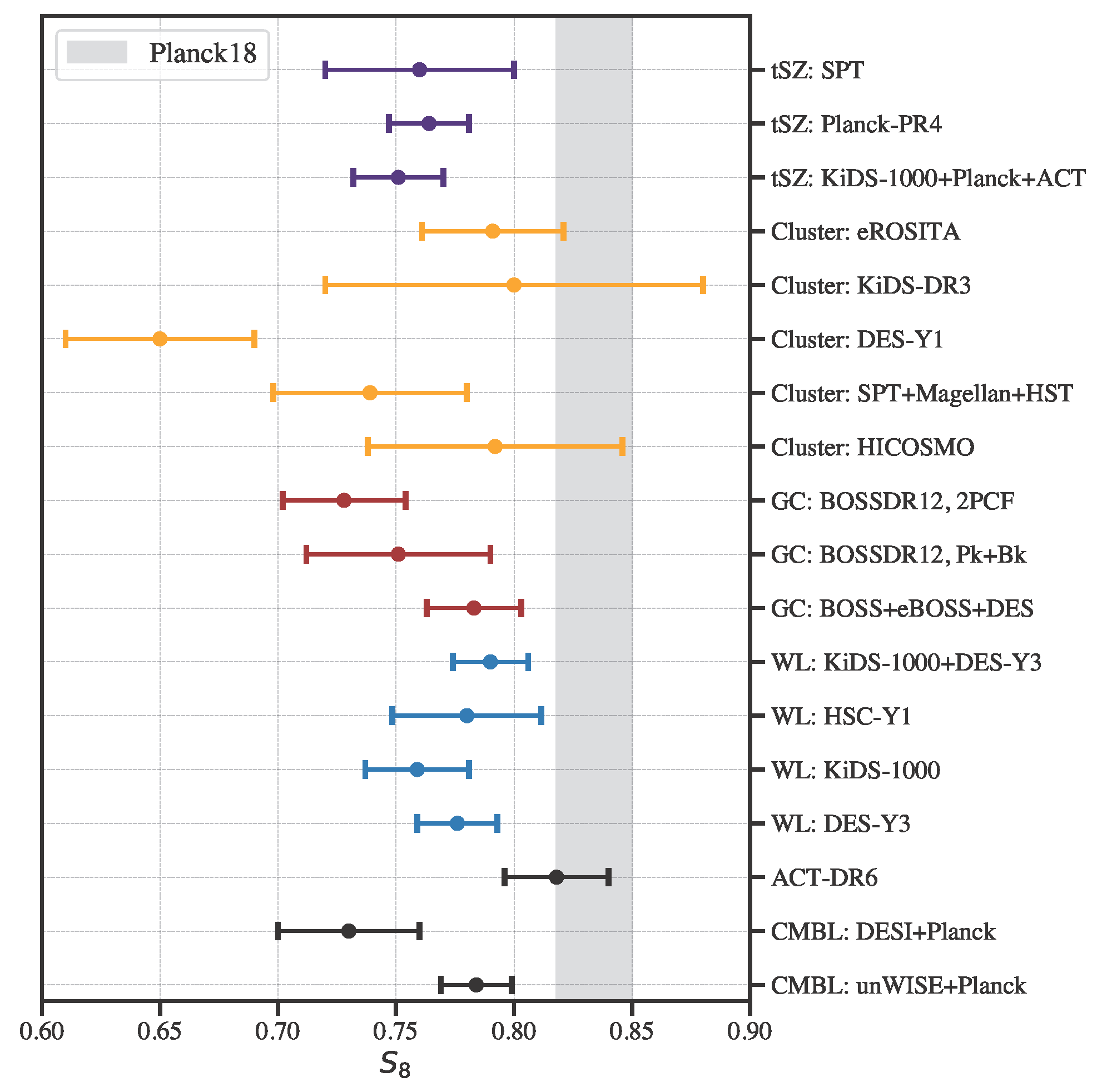

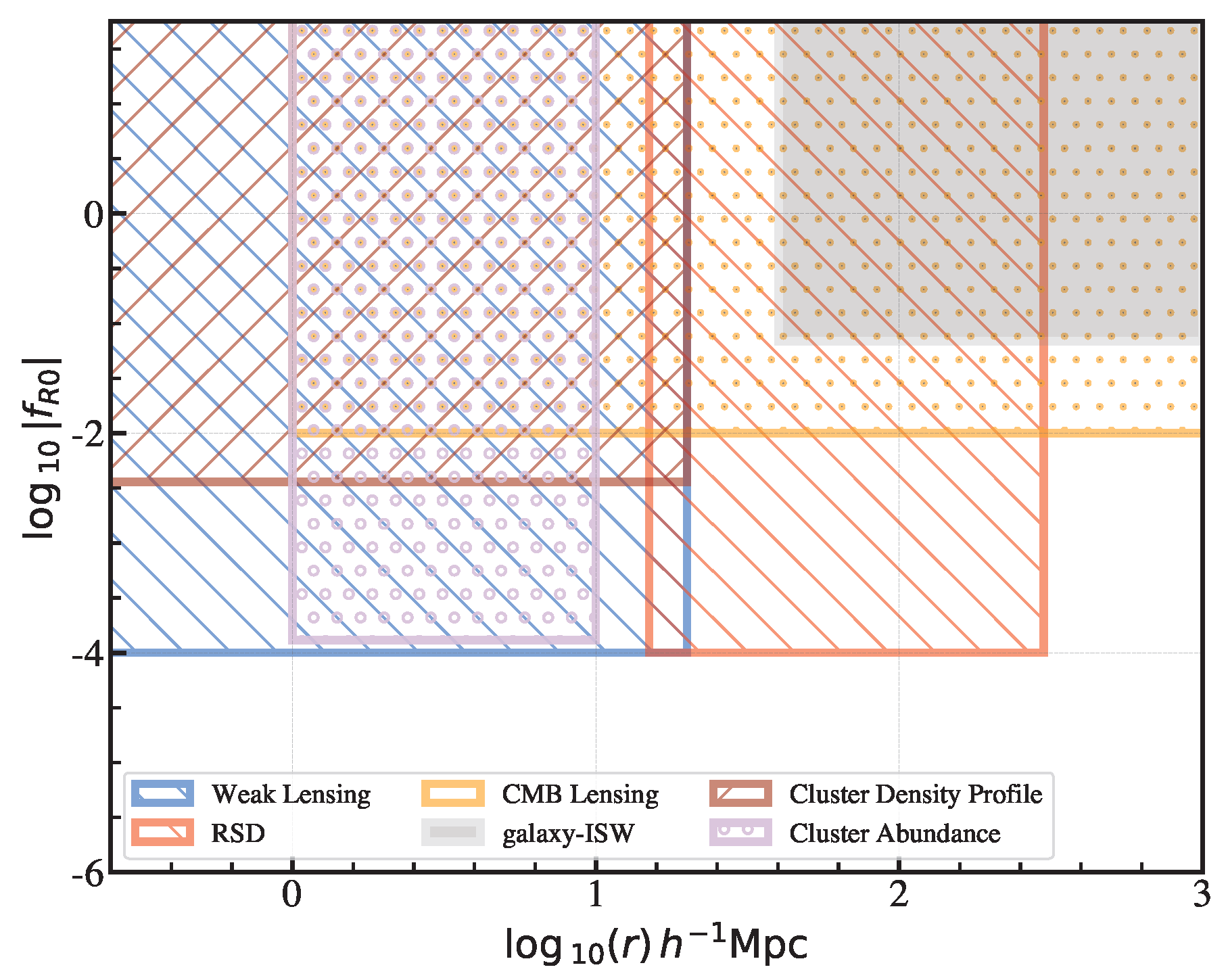
| c | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CDM | 0 | ✓ | – | – | – | – | – | – | – | 1 | 1 | 1 |
| ✓ | ✓ | – | – | – | – | – | – | – | ||||
| Brans–Dicke | ✓ | ✓ | ✓ | – | – | – | – | – | – | |||
| Quintessence | 0 | ✓ | ✓ | – | – | – | – | – | – | 1 | 1 | 1 |
| k-essence | 0 | ✓ | ✓ | ✓ | – | – | – | – | – | 1 | ||
| DGP | ✓ | ✓ | ✓ | ✓ ★ | ✓ | – | – | – | – | |||
| Horndeski | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ ★ | ✓ ★ | – | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, J.; Bautista, J.; Berti, M.; Cuesta-Lazaro, C.; Hernández-Aguayo, C.; Tröster, T.; Zheng, J. Cosmological Probes of Structure Growth and Tests of Gravity. Universe 2023, 9, 302. https://doi.org/10.3390/universe9070302
Hou J, Bautista J, Berti M, Cuesta-Lazaro C, Hernández-Aguayo C, Tröster T, Zheng J. Cosmological Probes of Structure Growth and Tests of Gravity. Universe. 2023; 9(7):302. https://doi.org/10.3390/universe9070302
Chicago/Turabian StyleHou, Jiamin, Julian Bautista, Maria Berti, Carolina Cuesta-Lazaro, César Hernández-Aguayo, Tilman Tröster, and Jinglan Zheng. 2023. "Cosmological Probes of Structure Growth and Tests of Gravity" Universe 9, no. 7: 302. https://doi.org/10.3390/universe9070302
APA StyleHou, J., Bautista, J., Berti, M., Cuesta-Lazaro, C., Hernández-Aguayo, C., Tröster, T., & Zheng, J. (2023). Cosmological Probes of Structure Growth and Tests of Gravity. Universe, 9(7), 302. https://doi.org/10.3390/universe9070302







