Abstract
We conjecture that the Higgs potential can be significantly modified when it is in close proximity to the horizon of an astrophysical black hole, leading to the destabilization of the electroweak vacuum. In this situation, the black hole should be encompassed by a shell consisting of a “bowling substance” of the nucleating new-phase bubbles. In a binary black-hole merger, just before the coalescence, the nucleated bubbles can be prevented from falling under their seeding horizons, as they are simultaneously attracted by the gravitational potential of the companion. For a short time, the unstable vacuum will be “sandwiched” between two horizons of the binary black hole, and therefore the bubbles may collide and form micro-black holes, which are rapidly evaporated by thermal emission of Hawking radiation of all Standard Model species. This evaporation, being triggered by a gravitational wave signal from the binary black-hole merger, can manifest itself in observations of gamma rays and very-high-energy neutrinos, which makes it a perfect physics case for multi-messenger astronomical observations.
1. Introduction
The discovery of the Higgs boson at the LHC [1,2] was a confirmation of the Standard Model (SM) and it provided an exciting opportunity to understand properties of the electroweak (EW) vacuum. In particular, it was demonstrated [3,4] that there is an available lower-energy vacuum state, to which the EW vacuum can eventually decay. Actually, this possibility has been known for a long time and comprehensively analyzed in [5,6,7,8,9]. It appears that the Higgs potential is sensitive to experimental inputs, particularly to the physical masses for the Higgs boson and the top quark and also to physics beyond the SM. The recent measurements of the Higgs boson and top quark masses, GeV, GeV [10], implies that our universe resides in the unstable SM vacuum state. Thus, if the SM is valid up to energies greater than about GeV, the EW vacuum is meta-stable and the transition into a lower energy state will occur in the future. The transition happens initially locally, nucleating a small bubble of the true vacuum. The bubble then starts expanding at high rate, reaching quickly almost the speed of light and converting the meta-stable vacuum to the true one everywhere.
Although the fact of our existence testifies that at the present day, the vacuum decay rate is extremely low, this was not necessarily the case in the early universe. For example, a high Hubble rate during inflation and high temperatures afterwards could potentially increase the rate significantly [11,12]. The decay rate also can be very sensitive to the presence of new physics, such as an extension of the SM via the introduction of higher-dimension operators [13,14], or the Higgs potential dependence on the space–time curvature through the direct non-minimal coupling of the Higgs field to curvature (see, for example [15]). The presence of a small black hole (BH) can catalyze vacuum decay and make it significantly faster [16,17,18,19,20,21,22]1. Thus, the fact that we still observe the universe in its EW vacuum state enables us to impose constraints on the cosmological history. This includes factors such as the reheating temperature and the scale of inflation, as well as beyond SM parameters, such as coupling constants between the Higgs field and space–time curvature or higher-dimension operators.
One could ask the question of whether there is another way, not based on the anthropic arguments, of using the meta-stability of the EW vacuum to study extreme conditions or the effects of new physics in cosmology and astrophysics. Namely, would it be possible to think of some physical conditions under which vacuum decay could occur and manifest itself as a potentially observable phenomenon, while not leading to catastrophic consequences for the existence of the universe in its present meta-stable state? In this paper, we would like to propose the idea of such a phenomenon and elaborate on its driving mechanism and observational signatures in multi-messenger astronomy.
The idea is creating physical conditions for putting the EW vacuum in a high decay rate regime within a finite spatial volume for a certain time period. The desired conditions can be realized in a close vicinity of the horizon of a BH of astrophysical origin, as a result of gravitationally induced corrections to the Higgs potential. In particular, the position and the height of the potential barrier, which “screens” the metastable minimum of the Higgs potential, can be modified so significantly that the vacuum becomes unstable already at present temperatures within a certain distance above the horizon of the BH. Since the instability implies a high nucleation rate of the Higgs new phase bubbles, a BH immersed into EW vacuum is encompassed by a thin shell consisting of a “bowling substance” represented by nucleating new phase bubbles surrounded with the SM vacuum. Although the nucleation is permanently going on within the thickness of the shell, the bubbles immediately fall under the horizon so that an external observer of a single BH always stays in the EW meta-stable state.
The situation can be different if we consider a binary black-hole (BBH) merger [24,25,26], where BHs circle their common center. In the merger, the BHs spiral inward, losing their orbital energies in the form of gravitational radiation so that their horizons get very close to each other and finally coalescence to form a single BH. Just before the coalescence, when the horizons of the components are close to each other, namely at a distance of the order of the thickness of the shells, the nucleated bubbles can be prevented from falling under their seeding horizon, being pulled out by the gravitational potential of the other component of the BBH merger. Thus, within some volume “sandwiched’’ in the gap between the approaching each other horizons, a temporal stabilization of the process of the EW vacuum conversion into a new phase can occur. Inside this volume, within the time of its existence, nucleating bubbles will expand, collide and even percolate. Some of these collisions can result in formations of microscopic black holes (BHs) via mechanisms described in [27,28]. Namely, when three bubbles collide, the surface energy in parts of their walls can be focused to the extent that its density tends to infinity, which converts the triple collision point into a BH [27]. Moreover, the collapse of a non-trivial vacuum structure left over after collisions of only two bubbles can also lead to the formation of a BH as it is argued in [28]2. The masses of such a “split off” from the merger BHs depend on the sizes of the colliding bubble and their walls tension. The sizes of the bubbles at the collisions are mostly determined by the phase transition developed in the volume of the stabilized SM vacuum decay process. The wall tension should depend on the details of modification of the position of the barrier separating the meta-stable EW vacuum from the true vacuum state and should be driven by the energy scale not essentially exceeding the EW one.
The formed BHs will start to evaporate, emitting thermal Hawking radiation [30] in all SM species. Finally, the coalescence of the merger results in the formation of a single horizon of the final BH. Thus, the conditions of vacuum instability created in the volume “sandwiched” in the gap between the horizons of the merger are broken so that the stabilized conditions for bubble nucleation are destroyed. All remnants of the new vacuum phase and still-not-evaporated small BHs should fall into the final BH. This ensures that an external observer will remain in the EW vacuum state.
The duration of the emission of Hawking radiation by the BHs cannot exceed the typical time scale of the last portion of gravitational wave signals from BBH mergers discovered by LIGO and Virgo [24,25,26,31], which is less than a second. One might expect that the energy release of Hawking radiation can be at the level of isotropic energy equivalents measured for short gamma ray bursts (SGRBs) [32]. Therefore, the electromagnetic part of the burst could be observed by space-based gamma ray burst monitors [33,34,35] and the telescope [36]. Moreover, the Hawking emission of other SM model particles and, maybe, beyond SM species can produce a neutrino signal in IceCube [37]. The very-high-energy spectral part of the electromagnetic component of the Hawking radiation also might produce a signature in very-high-energy atmospheric Cherenkov facilities [38,39,40,41,42].
The mechanism described above is akin to so-called triboluminescence [43], which refers to the phenomenon that materials can emit light when they are mechanically stimulated, such as rubbing, grinding, impact, stretching, and compression. Here, with a certain degree of analogy, the vacuum “bowling substance”, being the “material” of the shell encompassing the horizon of an astrophysical BH, is stretched between two approaching horizons in a BBH merger which finally leads to an emission of detectable Hawking radiation.
The paper is organized as follows. In Section 2, we describe heuristically general phenomenological features of the proposed mechanism of the formation and evaporation of BHs within the gap between horizons of BBH-merger components. In Section 3, we study basic features of the spectra, temporal characteristics and energy budget of the electromagnetic and neutrino messengers of the phenomenon. In Section 4, we review the Higgs field effective potential in the Standard Model; in Section 5 and Section 6, the idea of the mechanism of gravitationally induced corrections to the Higgs potential in the vicinity of the BH horizon is introduced. In Section 7, estimates of basic quantities driving the proposed mechanism are performed in the framework of a toy model. The energy budget of the Higgs-induced triboluminescence phenomenon, in the framework of the toy model, is discussed in Section 8. Finally, conclusions are presented in Section 9.
2. Formation of BHs in Unstable Vacuum “Sandwich”
To specify further the anticipated multi-messenger manifestations of the phenomenon outlined in the introduction, it is helpful to provide a heuristic sketch of the underlying mechanism of gravitational corrections to the vacuum decay process. A more detailed description of the Higgs phase transition at nucleation sites located in the vicinity of the horizon is deferred to subsequent sections.
The rate of the first-order phase transition with the Higgs field, when its nucleation site is located at the center of a BH, was investigated in [16,17,18,19,20,21]. In these studies, it was concluded that Higgs true vacuum formation rate can be increased so much that even a single BH of the smallest mass (≪1 g) that existed in the past could already destroy the current SM meta-stable vacuum state. Hence, it might happen that any primordial BH with a lifetime smaller than the age of the universe could serve as a source of such a fatal catalysis corresponding to Higgs vacuum phase transition.
Here, we conjecture that the Higgs phase transition rate also could be substantially increased in the vicinity of the horizon of a BH, while the nucleation site is located outside the BH. Some recent efforts to investigate such a possibility were made in [44,45]. Heuristically thinking, one presumes that the closer a nucleation site is to the horizon of a BH, the higher the phase transition rate and hence the higher the probability of the formation of a bubble of the true Higgs vacuum. Moreover, one might expect that a BH of any mass, even such as that one of an astrophysical origin, could create a nucleation site in the vicinity of its horizon. In this case, since the nucleation site with a bubble of the true vacuum falls quickly under the horizon, it is obvious that the fatal catalysis of the Higgs vacuum phase transition cannot take place.
The bubble formation probability is driven by , where stands for the four-dimensional Euclidean action computed along the tunneling trajectory for the spherical bubble solution [46,47,48,49]. In general, gravitational correction effects in the vicinity of a BH depend on the distance to the horizon so that can be represented as an effective action , which implies that the probability of tunneling per unit time per unit volume from a vacuum in the meta-stable state to the true vacuum is given by
where the pre-factor is of mass dimension and is the distance to the horizon measured in units of the Schwarzschild radius of the BH. For illustration, in the regime of gravitational corrections, one may model the effective action with a simple power law
where indicates the value of the action at the distance , that is to say, at one Schwarzschild radius from the horizon, and a is the power to be specified from the details of the gravitational corrections for the Higgs potential3. Therefore, the closer the location of a bubble nucleation site to the horizon, the higher the probability of tunneling from the meta-stable vacuum state at GeV to the true Higgs vacuum. If one goes away from the horizon, the exponential suppression in (1) slows down the bubble nucleation rate so that they have more time to grow up before starting to collide if they were prevented from falling down into the BH. This effect could take place in a BBH merger consisting of BHs of about LIGO-Virgo scale [24,25,26,31], just before touching each other by their horizons.
Indeed, between the horizons of the BBH components, at their close-enough mutual approach, one might expect an instant formation of a volume with effective zero gravity so that for a short time period, the unstable vacuum is kind of “sandwiched” between the horizons of the components. In these conditions, bubbles could have enough time to grow up and finally percolate, terminating their existence in wall collisions. In triple bubble collisions, the surface energy of the parts of the colliding walls can be focused in a way that they find themselves under their Schwarzschild radius leading to a formation of BHs as argued in [27]. The formation of BHs is also possible through the evolution of non-trivial vacuum configuration produced in a collision of walls of only two bubbles [28]. Either case is feasible under conditions of percolation within quite a limited volume. Being formed, the BHs is rapidly evaporated by a thermal emission of Hawking radiation [30] with the black-body spectrum at an effective temperature, which increases as the mass of the BH decreases.
In general, the masses of such “split off” BHs are defined by sizes of the bubbles at the instance of their collision and their vacuum wall tensions. The wall tension is mostly defined by parameters of the modified Higgs potential, namely by a location of the maximum of the barrier separating the meta-stable EW vacuum from the true vacuum state and the Higgs self-interaction constant , at the barrier. Both parameters for unmodified potential are quite well defined by the measurements of the Higgs boson and top masses as well as the SM physics renormalization group corrections [12].
The surface tension is estimated as
where is the Higgs field value defined by a bounce solution at the modified maximum, which, for sanity reasons, cannot substantially exceed the position of the electroweek vacuum so that
It is reasonable to assume that the mass of a BH formed in a collision contains fraction of the mass of the colliding bubbles. Thus, one can say that a BH of mass is created out of a bubble of radius
where and are the Planck length and Planck mass, respectively. The value of depends on the details of the conversion mechanism and, in general, it is expected to amount to a non-negligible (up to a percentage) fraction of the bubble mass [28].
For the sake of simplicity of the rough estimates, let us assume that the volume of the unstable vacuum “sandwich” (UVS) defined by is populated with bubbles of approximately equal sizes, which implies that all BHs in this volume are formed with equal masses. In the course of the bubble nucleation and growth, the BHs will be created in the bubbles’ double and triple collisions, as argued above. Therefore, one has to estimate the abundance of such collisions occurring within the volume .
The volume is assumed to be formed within a narrow gap between the spherical caps of the horizons of the components of the BBH just before their mutual touching as shown in Figure 1. The thickness of the UVS can be taken as , provided that the power in (2) is not very high so that the transition rate does not change dramatically across the UVS. Thus, one can represent as a body bounded between the convex surfaces of two spherical caps separated at their closest points by distance as shown in Figure 1. The volume can be calculated as
where is the cylindrical volume formed by the base circles of radius a separated by distance . This ensures that the width of the UVS, at its edges framed by the caps, does not increase more than by a factor 1.5, keeping the Euclidean action (2) increasing only within factor , which is moderate, provided that, once again, the power a is not very large. Taking into account that according to the construction of the cylinder above (see Figure 1), , the radius of the base circle is given by
which allows us to express the UVS volume as4
Evaluating (6), we consider BBH of equal mass components so that both caps have the same volume. Additionally, obtaining (8), we ignore everywhere with respect to values . Taking into account these two approximations, it would be more correct to say that (6) expresses a sort of upper estimate of the UVS volume, within which the action (2) does not vary by more than a factor of . Thus, below, for simple estimates, we use a constant value of the action (2) defined by inside the UVS.
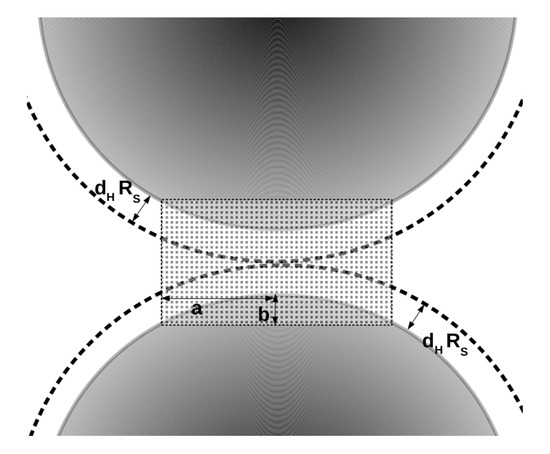
Figure 1.
A schematic representation of the UVS formed just before the horizons of the BBH components, shown by the gray gradient parts of spheres, come into contact. The dashed enveloping line represents the layer spreading outside the horizons of the BHs, which contains the unstable vacuum.
Depending of the degree of the closeness of the horizons of the BBH components in the course of their mutual approach, two different scenarios of bubble collisions leading to the formation of BHs of distinct masses are possible.
The first scenario refers to the regime when the bubble nucleation rate is significantly enhanced in comparison with the nucleation rate in the horizons free space, while it is still low in the sense of providing the percolation of the bubbles of radius within . Therefore, in this scenario, the only bubbles which nucleated in closed pairs and closed triplets would collide and form BHs. In order to estimate the number of these collisions, one can use some findings from the site percolation theory [50], where the random distribution of occupied and empty sites on a lattice is considered. The occupied sites tend to aggregate into clusters of size distribution 5, which is defined as a number of clusters containing s occupied sites per one lattice site when the fraction of occupied sites on the lattice is equal to p. The cluster numbers are calculated on the basis of lattice animals counting, and for large clusters and low occupancy (), it is given by the corresponding equation in [50]:
where C is a constant. For a three-dimensional lattice, as inferred in [51]. Similar behavior as (9) is confirmed for small clusters as well in simulations performed in [52]. In the context of the formation of BHs in bubbles collisions, we are interested in clusters of size and aggregated on a simple 3D lattice of volume with sites measured by the volume of individual bubble defined, in its turn, by the radius (5). Therefore, the number of BHs created inside out of collisions of bubbles of volume can be expressed as
where and is the probability of the formation of the BH by two [28] or three [27] bubbles. The fraction of occupied sites on this lattice can be expressed as
where is the nucleation rate averaged over , and is the time elapsed from the bubbles nucleation to their collisions. For the small clusters number, we use the result obtained in [52] for a cubic lattice, which reads
where the numerical values for and C are inferred, reading out the relevant parameters from Figure 5 of [52]. Thus, collecting together (10)–(12), the number of BHs created in the UVS can be represented as
The collision time in (13) can be evaluated as the time spent by bubbles while they were growing from the critical radius up to given in (5), which implies that
where c is the velocity of light.
It is practical to express (13) separately for and mechanisms as follows:
where km stands for the Schwarzschild radius of a solar mass object. Since dynamical effects, which might be caused by gravitational forces applied at the sites of bubbles collisions, are not taken into account, the BHs counted by (15) and (16) are assumed to be scattered uniformly across the .
The second scenario refers to the regime when one can allocate a volume, fitting within , where the nucleation rate reaches the high enough level to make the bubbles of radius percolating. This regime implies that, in fact, all bubbles participate in both double and triple collision mechanisms of BHs formation. The necessary condition for the realization of such a scenario is quite simple, namely, the probability of nucleation of a bubble of critical radius (critical volume ) within the collision time should be close to unity. The latter implies the validity of the following relation:
where the critical radius is defined by the mechanism of the correction of the Higgs potential and will be estimated in Section 7. Unlike in the first scenario, here, the number of created BHs cannot be calculated directly, but it can be normalized by the total energy output to be estimated in the next section.
It is obvious that, in reality, while the horizons of components in the BBH merger are approaching each other, one has to expect a mixture of contributions from both scenarios. However, this complication does not affect the estimate presented below so that one can postpone its discussion for later publications.
3. The Electromagnetic and Neutrino Signals
In this section, we consider possible observational signatures of the Hawking evaporation of the BHs, which is the essence of the multi-messenger nature of the phenomenon described above.
The luminosity of gravitation signal from a BBH merger is described by the quadrupole formula
where is the third time derivative of the quadrupole moment of a relevant mass distribution. For a binary system with similar mass components separated by , the quadrupole moment can be estimated as
Its third derivative is proportional to the third power of the orbital angular frequency
so that
Therefore, the luminosity (18) can be expressed as
From the other hand, the gravitational energy of such BBH to be released by a merger can be expressed as
Therefore, the time scale of the merger is defined as
At the final stage of the merger, the distance between the components constricts down to their Schwarzschild radius, , so that the time scale (24) of this stage is measured in ms. Note that a BBH composed of stellar mass BHs localized at separation distance about 10–100 times of their Schwarzschild radii would radiate out its gravitational energy within an hour time scale, while a BBH with times larger orbit will need a Hubble time scale to exhaust its energy into emission of gravitational waves.
In terms of the gravitational wave signal, the final merger stage corresponds to the gravitational wave frequency , at which the waveform has a maximal amplitude, as it is shown in Figures 1 and 2 of [24] for GW150914, as well as in Figure 10 of [25] for frequency maps and reconstructed signal waveforms for other BBH events. Using these figures, we read out the conservative low values of the maximal frequencies Hz, which indicates that the horizons of the BHs in a BBH spent about ms in the closest vicinity from each other. We treat this time scale as a rough estimate of the upper limit of the lifetime of the UVS.
We assume that during their stabilized existence period, the vacuum bubbles will be converted into BHs by the mean of the mechanisms described in Section 2, which evaporated emitting SM particles with the black body spectrum [53],
characterized by the Hawking temperature
and absorption probability . Provided that Hawking evaporation time is given by
one can conclude that BHs with mass g will be completely evaporated within the time scale of ms emitting SM species at energies above 200 TeV as it follows from (26).
Photons of energy propagating through a background of soft photons of energy will produce pairs if their energies exceed the threshold [54,55]
Soft photons with energies from 0.1 to 10 eV being produced by star formation in galaxies are abundant in the universe and known as the extragalactic background light (EBL) [56,57]. The profile of the spectral energy density of EBL contains two bumps located at the near infra-red energy eV, formed due to the direct starlight emission, and the far-infrared energies eV, produced by the scattering of starlight on dust. The energy density of the EBL is estimated to be about [58], which is a factor below the energy density of CMB. Photons with energies above 100 GeV should interact with EBL, which leads to an energy-dependent suppression of their flux from extra-galactic sources. The mean free path of such rays is given by
where is the pair production cross section [59,60]
In (30), cm is the classical electron radius, , is the electron mass, and is the squared center of mass energy. The cross section (30) has its maximum [61] at MeV leading to the most effective interactions with the EBL photons of energy .
Photons created in the vicinity of a BH should experience the gravitational red shift. The photon of energy emitted at the radius is observed at energy
by an external observer where red shift is given by (see for example the text book [62])
Thus, the energy of an exiting photon will be scaled down by factor
It implies that for a typical distance , the energy of photons detected by an external observer TeV would be about a half of the energy of the emitted photons because of the photon propagation in strong gravitational fields of the merging BHs.
According to (29) and (30), the mean free path of most of the photons with energy TeV can extend up to about 10 Mpc, if photons interact with EBL of eV, which is much less than the typical distance D to any extra galactic source, so that the source fluxes of such rays are suppressed by factor . Since the number density of the target EBL photons increases with the cosmological red shift as , expression (29) gives the overestimated upper limit of the mean free pass Mpc. More rigorous calculations (see for example [63] for details) show that Mpc for sources at red shifts between 0.5 and 0.1, respectively. We notice that about half of BBH mergers detected in the first and second observing runs (O1 and O2) of the advanced gravitational-wave detector network [25] and three quarter of BBH mergers seen in the first half of the third observing run (O3) [26] performed by advanced LIGO and Virgo detectors are over .
However, being absorbed on EBL, the very-high-energy -rays inject pairs in the inter galactic media (IGM). These highly relativistic pairs are aligned with the beam line of -rays emitted from the source, at a distance of about . Therefore, the full power of the source contained in the absorbed VHE -rays is transferred into the energy of the pairs. In their turn, electrons and positrons very effectively lose their energies via inverse Compton scattering on CMB photons. The distance of inverse Compton scattering energy attenuation of relativistic pairs of energy is given by [64]
where is the energy density of the CMB and is the Thomson cross section. The mean energy of the photons produced in the inverse Compton effect is calculated as [64]
where stands for the mean energy of the CMB photons.
Therefore, in the case of maximally efficient triboluminescence, which implies that BHs are small enough to radiate out their whole energy within the duration time of the final stage of the merger, one would have the following picture of the propagation of the electromagnetic component. The primary short duration signal of thermal VHE -rays of energies TeV emitted at the BBH merger will be converted via pair production on EBL, and their subsequent inverse Compton scattering of CMB into softer but still VHE -rays of energies TeV as it follows from (35). This conversion will occur within the main free path of 100 TeV rays, Mpc (for sources at red shifts between 0.5 and 0.1) since the Compton scattering distance of 0 TeV pairs is negligibly short (34). In its turn, the mean free path of TeV rays, which are mostly absorbed by the near infra-red part of the EBL spectrum, amounts to Mpc [63] (for sources at red shifts between 0.5 and 0.1), which implies that, for a distant source, a good fraction of them will be again converted into , whose subsequent inverse Compton scattering on CMB will produce rays of energy GeV. Additionally, still some of photons will travel a long distance without significant energy loss. Thus, the power of Hawking VHE photons tend to be converted into the secondary sub TeV -rays. For a source, at a distance larger than , the cascade will be also populated by much softer rays of energy GeV. As it seems, a substantial fraction of the power of the triboluminescence emission produced at a remote BBH merger is transmitted into the secondary -rays of the energy range from 1 GeV to 1 TeV, and, hence, to observe this phenomenon, one should rely on the Fermi-LAT [36] and very-high-energy atmospheric facilities, MAGIC [38], HESS [39], VERITAS [40], HAWC [41] and LHASSO [42].
Since the electron is massive, the arrival timing of the secondary rays should be delayed by the amount of
where the velocity of light c is introduced explicitly. Thus, for ≃ GeV secondary -rays, which are produced by ≃ TeV electrons (35) covering the Compton scattering distance (34) of about kpc, the delay (36) can be as large as s, which exceeds essentially the duration of the original signal , in the observer’s frame for a BBH at . In particular, it seems that the very short pulse of VHE -rays of Hawking radiation from sources at redshift over (at luminosity distance over 1 Gpc) will be converted into a burst of ≃ GeV to TeV -rays of s duration.
The Hawking luminosity
implies that a BH releases the energy in the amount of
within its evaporation time (27).
For further estimates, let us assume that the total energy release, for the considered effect, at least, could be comparable to the isotropic equivalent energy of SGRBs, which is of the order of erg. Thus, to emit erg of the isotropic equivalent energy, in the process of the triboluminescence, one would need to evaporate about
of BHs of mass g so that the cumulative mass of the evaporated BHs capable of providing the radiation power similar to a SGRB amounts to . The value (39) may serve as a lower estimate of the amount of BHs capable of providing an observable electromagnetic counterpart of the phenomenon. The gravitation waves energy radiated in BBH mergers discovered by LIGO and VIRGO ranges from a few to several solar masses [24,25] and is estimated with a precision of about 10% (see Table III in [25]). It is reasonable to accept as the maximal possible energy budget of the electromagnetic messenger the amount ( erg), which implies a generation of
in a BBH merger.
Along with rays, the BHs will emit the same amount of isotropic energy equivalent,
in neutrinos of the mean energy, observed by an external observer, about 100 TeV, in the process of Hawking evaporation. Therefore, one expects that the phenomenon should be manifested in the arrival of about 10 ms long high-energy neutrino signal in temporal and directional coincidence with the GWs signal from a BBH merger. The energy release in such a neutrino burst can be compared with that of the neutrino flare [65] arrived from the direction of the blazar TXS 0506 + 056 prior to the first multi-messenger event in the neutrino–photon astronomy, baptized IceCube-170922A [66]. The energy fluence of the TXS 0506 + 056 flare implies that the average isotropic neutrino luminosity delivered by the source during 158 days is [65]
This luminosity is at least two orders of magnitude lower than that which can be provided by the triboluminescence phenomenon,
The TXS 0506+056 flare mostly consists of neutrinos with energies GeV, which is an order of magnitude lower than the energy of neutrinos emitted by the BHs. Therefore, the number of neutrinos in the burst which might arrive from the BBH merger should be at least one order of magnitude higher than that one in the TXS 0506+056 flare [65]. We notice that the energy of IceCube-170922A [66] is reported to be 290 TeV, which is similar to the average neutrino energy expected from the BHs created in a BBH merger. Therefore, one may expect that IceCube will be able to detect a neutrino burst from the multi-messenger effect of the triboluminescence.
4. Standard Model Effective Potential
To fix notations, we start from an explicit renormalizable Lagrangian that leads to a vacuum expectation value for the Higgs field H
where the low energy self-coupling constant and vacuum expectation value (VEV) are
The expansion of the complex Higgs doublet,
generates a canonically normalized physical Higgs scalar h of the mass
with the potential
which has a minimum at . In this way, the Higgs doublet develops a non-zero VEV so that is broken. The VEV GeV corresponds to the EW vacuum, which is stable at the tree level. However, the Higgs potential obtains radiative corrections so that coupling constants must be running when the energy regime, or correspondingly, the field value, changes.
In quantum field theory, in Minkowski space, the standard regularization [67] appears from specific integrals, e.g., for a scalar particle of mass m [68,69],
where is a regularization scale. This implies that an observable, at energy scale , differs from its value at higher-energy scale by a logarithmic term. Therefore, when quantized, the Higgs field potential (48) becomes modified by corrections such as (49) so that
with radiative corrections term expressed in the general form as
In (51), the index i runs over particle species, counts degrees of freedom (with a minus sign for fermions), and the field-dependent mass squared of i-th specie is given by
where are coupling constants, while are some definite constants [69].
For the regularization scale , in (51), the VEV of the Higgs field can be chosen as v since this is the scale where the running SM parameters still can be associated with the experimentally observed values so that the Higgs potential is to be well approximated by its classical form. It is known that the leading terms of the one-loop corrections (corresponding to the t quark, W and Z bosons, Higgs and Goldstone bosons, respectively) are [5,6,7,8,9],
where is the Higgs potential mass constant and the t-quark Yukawa coupling and gauge bosons coupling constants have the values
The factor of 12 in the t-quark contribution in (53) (first line), corresponds to the 3 colors times 4 components of a Dirac spinor, and the minus sign reflects the Fermi statistics. The factor of 3 in the vector-boson terms (second line) comes from tracing the numerator of the gauge-boson propagator in the Landau gauge, and the additional factor of 2 in the first term of the second line appears due to the existence of 2 W-boson species.
Below, we review the behavior of for different values of h.
EW regime. For the EW regime, namely at , logarithm terms in (53) are smaller than the corresponding constants in square brackets. The largest contribution comes from the t-quark, which appears to be positive, making the entire correction to the Higgs tree level potential also positive. Therefore, at EW scales, radiative corrections do not destabilize the Higgs vacuum, which is located at .
Intermediate regime. The one-loop approximation (53) is still valid at intermediate scales, TeV. At this regime, the logarithm terms in (53) become positive and larger than constants so that the effective potential (50) is well approximated by
Due to the minus sign in front of the t-quark term, the one-loop correction becomes negative, i.e., the SM effective potential has a local minimum. However, due to the large value of the denominator, , the second term in (55) is smaller than so that the effective potential remains positive, i.e., higher than the vacuum value . Therefore, in Minkowski space, at the scales TeV, the global minimum of the Higgs system is still located at .
Large Higgs field regime. For larger values of the Higgs field 1 TeV, the effective potential (50) can be approximated [3,4,12] as
where is the running coupling. The behavior of the running coupling in the renormalization group approach is shown in Figure 2.
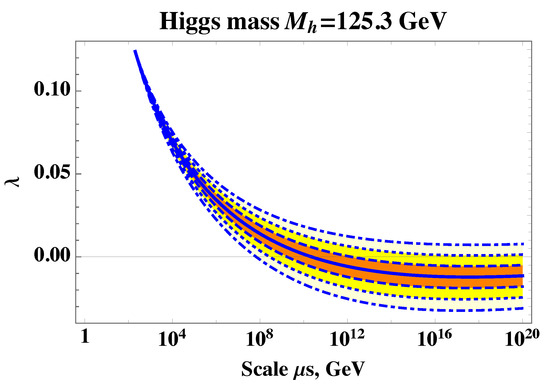
Figure 2.
Higgs self-coupling (solid line), obtained in the framework of renormalization scheme for central values GeV and GeV. Deviations for GeV (dashed lines), GeV (dotted lines), GeV (dashed-dotted lines) are shown.
The renormalization group evolution of the running coupling demonstrates that becomes negative above GeV and is very sensitive to the top quark mass [70,71]. Therefore, in general, the SM vacuum is a local minimum, and it becomes unstable at energies much higher than the EW scale.
5. Gravitational Corrections to Vacuum Decay
Although the vacuum decay rate in Minkowski space is extremely slow, this is not necessarily the case in strong gravitational fields. The full theory of quantum gravity is unknown and there only exists a simple semi-analytic approximation that captures the leading gravitational corrections [72,73]. It was found [16,17,18,19,20,21,74,75] that due to the external gravitational field, the vacuum decay can be significantly increased. This raises the question of SM vacuum stability in the external classical gravitational potential. For example, close to the horizon of a BH, the strong local spacetime curvature can enhance vacuum decay rate to a level incompatible with the age of the universe [17,18,19].
Existing calculations on gravity-mediated Higgs vacuum decay mainly consider small BHs located inside new phase bubbles and take into account only the effects of curvature on the running of the SM constants. These corrections appear after inserting the non-minimal coupling term ∼ into the action that connects the Higgs field H to the scalar curvature of gravity R.
In this paper, we want to estimate the impact of gravitational potential on the rate of the nucleation of the new phase bubble close to the horizon of a BH of astrophysical origin. Let us ask the important question: Is the SM vacuum stable in large gravitational potential? The models of quantum theory in curved spacetime is a topic of intense research [76,77], which reveal many interesting phenomena, such as the Hawking radiation, the Unruh effect, etc. Here, we will consider modifications of the dispersion relations for quantum fields in the renormalization integrals (49) in an external large static gravitational potential. Similar ideas were considered in models of quantum theory in cosmological spaces, where dispersion relation in the integrals (49) is modified by inserting the scale factor describing cosmic expansion (see the recent review [78]).
Note that the gravitational deformation of dispersion relations assumes an effective violation of the Lorentz invariance. Several models predict a departure from exact Lorentz invariance [79,80,81,82], when the free particle dispersion relation exhibits extra momentum-dependent terms, apart from the usual quadratic one occurring in the Lorentz invariant dispersion relation. Most of the studies were performed in the QED, gravity, and for some of the SM particles, where strong constraints on the Lorentz invariance violating terms were obtained [79,80,81,82]. However, not many studies were performed for the Higgs sector [83,84,85,86], especially on curved backgrounds. Higgs is very different from other fundamental fields, and one cannot exclude a possibility that the large effective Lorentz violation, close to the horizon of a BH, could be important only in the Higgs sector.
Usually, it is assumed that close to the horizon of an astrophysical BH, where gravitational invariants are negligible, a curvature has a small impact on the quantum particles. In many cases, the most useful invariant is the Kretschmann scalar [87], which is inversely proportional to the sixth power of the radius of a BH. However, the quantum vacuum is not an empty Minkowski space, and a large gravitational potential can significantly change the renormalization parameters. It is known that the density of particle states at large energy grows exponentially [88]. So, if a gravitational energy is pumped into the system, new higher mass states are produced (rather than the energy of already existing states being increased, which implies an increase in the temperature), which can amplify loop corrections in the quantum vacuum state.
In general, if quantum fluctuations in the Higgs sector create a bubble of a new phase that is large enough, it is energetically favorable for this bubble to expand due to the gain in volume energy over the energy stored in the bubble wall. On the other hand, if the bubble is small, its surface tension compresses the bubble and it disappears. The addition of an external gravitational potential, i.e., an additional energy, can change the situation dramatically. The distortion of space changes the balance between volume and surface energies, the “cost” of bubbles formation is lower, and bubbles with smaller radii can be created.
6. Quantum Vacuum at a Horizon
Let us estimate the impact of the large gravitational potential on the properties of a quantum vacuum close to the horizon of a BH of mass M. For simplicity, we write the Schwarzschild metric in isotropic coordinates,
where the metric coefficients are
Here, the radial function has the following expression in terms of the Schwarzschild radial coordinate r:
which only holds if when , and outside the event horizon, . It follows from (59) that close to the horizon , we have and and, unlike the Schwarzschild case, the isotropic metric (57) leads to a real singularity at the Schwarzschild horizon since the determinant
becomes zero at , or at .
Since and , for a distant observer, the gravitational potential effectively reduces the speed of light and increases spatial distances close to the BH horizon. This will reduce the volume of integration,
and thus will modify the Euclidean action with an external gravitational potential for the bounce solution,
So, the bounce has a smaller action and the vacuum decay process can be significantly enhanced for the large gravitational potentials () at some proper distance from the Schwarzschild horizon.
As an example, let us consider a scalar particle of mass m on the Schwarzschild background. The radial geodesic equation has the form
Note that close to the horizon , or for the relativistic case , the mass term in (63) can be neglected. It is known that the energy of a relativistic particle and hence its frequency in static gravitational potential does not depend on the distance from the gravitating body [89,90]. As the energy E does not depend on r, we immediately obtain from (63) that its momentum is dependent and in the limit
So, the closer the particle is to the horizon, the larger its momentum6. In the isotropic coordinates (57) with the constant parameters V and A, the dispersion relation (63) takes the form
and the integral (49) is modified as
One may comment that in static gravity, to preserve dispersion relations with constant energy, the momentum and mass terms should be modified. Then in Pauli–Villars regularization, for example, we have real and ghost particles, with the mass m and some fixed large mass , both affected by V,
so that the factor V does not show up in the logarithm.
Similar results can be obtained for vector particles. The definition of the fermion propagators summing is performed by tetrads instead of metrics. However, the factor containing the gravitational potential for the fermionic loop contribution, in (50), is the same as that for scalars and vectors since the trace of an odd number of Dirac -matrices is zero and we must consider an even number of fermion propagators. Then, the calculation becomes exactly the same as for the scalar and vector cases, except the important difference of an overall minus sign (due to the Fermi statistics) for the fermionic loop integral.
Thus, we conclude that close to the BH horizon, the entire radiative corrections in (50) are modified by the universal factor ,
In summary, within the considered scenario, integrals of the type presented in Equation (49) are subject to modifications as demonstrated by Equation (66). Therefore, in the vicinity of a BH horizon, the standard radiative corrections described by Equation (50) are further influenced by Equation (67). This implies that near the horizon, the one-loop corrections (53) are altered in a manner that shifts the position of the maximum of the Higgs field effective potential closer to the electroweak scale. As a result, the vacuum destabilization and the possibility of nucleating new phase bubbles become feasible at significantly lower scales.
Contrary to the seemingly natural assumption that an astrophysical BH cannot possess a large enough curvature, even at the horizon, to be able to influence the regularization discussed above, one can elaborate as follows. For the case of the Schwarzschild solution, the origin point is considered a true physical singularity, which appears in quantities that are independent of the choice of coordinates, such as the Kretschmann scalar. In contrary, the singularity at the horizon is called a coordinate singularity, which can be avoided by changing to “good” coordinates. However, the necessary ingredient of all these singular coordinates is the so-called Regge–Wheeler tortoise coordinate, which does not belong to the -class of admissible coordinate transformations. Then, the singular transformations (such as those introduced by Kruskal=-Szekeres, Eddington–Finkelstein, Lemaitre, or Gullstrand–Painleve) give delta functions in the second derivatives (see, for example [62], for details). This means that transformed metric tensors at the horizon are not differentiable, i.e., they are of unacceptable class . The Einstein equation for these metrics is altered with fictitious delta sources at the horizon7. For a sufficiently large BH, one can let the Kretschmann invariant be arbitrarily small at the horizon. This would be usually interpreted as the lack of a large curvature so that one can use Minkowski space to describe the particles. However, the conclusion on the finiteness of the Kretschmann invariant, at the horizon, is usually based on the assumption of a mutual cancellation of a delta-function source, such as divergences.The same is true for other invariants of the gravitational field. In general, metric components are independent functions, and the cancellation of their zeros at the horizon is accidental since it follows from the exact validity of the vacuum Einstein equations, implying a perfect sphericity. However, perfect spherical symmetry and true vacuums are rarely observed, if ever. Therefore, a smallness of the Kretschmann scalar does not mean that the curvature is small at the BH horizon. Indeed, the three from six non-zero independent components of the mixed Riemann tensor for Schwarzschild metric blow up at the horizon. So, we consider a model where at the BH horizon, the spacetime is not Minkowskian (see, for example [91,92,93,94]). In summary, the extension of geodesics across the Schwarzschild horizon by singular diffeomorphisms presents difficulties, even at the classical GR level. The Regge–Wheeler radial variable expression should include a Heaviside function at the Schwarzschild horizon, which corresponds to delta-like sources and leads to infinite Riemann and Ricci tensors [94]. Thus, plane-wave solutions that cross the horizon are not viable, and we must establish appropriate boundary conditions and redefine the concept of the quantum vacuum in proximity to the Schwarzschild horizon [94].
7. The Toy Model
In order to estimate a vacuum decay rate and new phase bubble parameters, let us consider a toy model presenting the effective potential (55) in the form
In (68), the k parameter is given by
where couplings are defined at scale as 0.934 and 0.127 and changes in these couplings are neglected up to a few TeV scale. It follows from (68) that in Minkowski spacetime, where , the SM vacuum at is meta-stable, but the probability of its decay is extremely low. However, in a strong gravitational field close to a BH horizon, the parameter (69) decreases, and at some distance to the horizon, the potential (68) becomes negative already at , leading to significant vacuum instability. The potential (68) is shown in Figure 3 at .
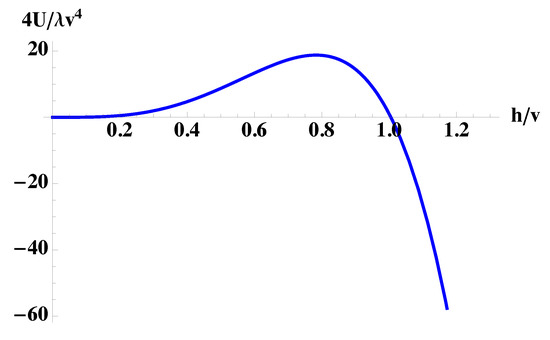
Figure 3.
The modified Higgs potential (68) at .
The probability of vacuum decay can be calculated by solving numerically the equation of bounce motion. The presence of a BH breaks the translational symmetry, and as the result, a bounce shape corresponding to the minimal action can be not spherically symmetric. However, a solution with symmetry can be used as the lower bound on the vacuum decay probability.
The bounce solution [46] is a configuration satisfying the Euclidean field equation
with the boundary condition (false vacuum) as , where is the Euclidean 4-radius
Equation (70) is not exactly solvable. We solve it numerically by using , a package [95] for finding the bounce solution for the false vacuum decay. An example of a numerical solution with obtained in an assumption that a distance to the Schwarzschild sphere is constant during nucleation and collapse of the new phase bubble presented in Figure 4. For different values of k, the bounce solution can be parameterized as
where and the critical radius of a true vacuum bubble is given by
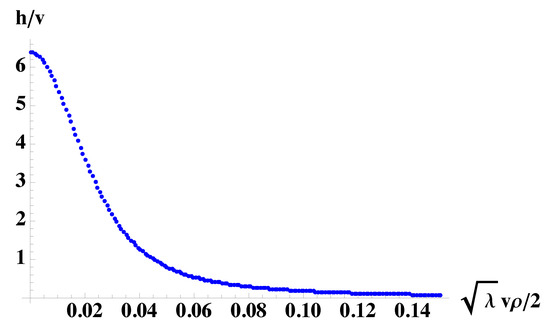
Figure 4.
The bounce solution of Equation (70) at .
At a high nucleation rate, one distinguishes expanding and contracting bubbles. In order for the bubbles to expand rather than contract, it is necessary that the gain in volume energy from the bubble interior being in the lower free energy phase overcomes the unfavorable surface tension of the bubble. This will happen if the bubble radius is larger than the critical radius , for which the two effects balance out [46,48,96].
For the bounce, the Euclidean action is given by the equation
This equation, in combination with (62), gives the action for the critical bubble in a gravitational field
8. Discussion
The toy realization, described above, implies that the modification of the Higgs vacuum decay in the vicinity of a BH corresponds to and introduced in heuristic formula (2). Besides this, as it follows from Figure 3, the Higgs potential is modified in a way that the position of its maximum is moved close to the values of the EW scale. In its turn, the bounce solution, presented in Figure 4, indicates that
in (3). Therefore, according to (5), bubbles which are capable of converting into BHs of mass g by the Higgs vacuum decay at TeV should have radius cm. This implies that the collision (percolation) time fs is negligible, compared with the merging time ms, which ensures that in the case of maximal effective triboluminescence discussed in Section 3, the BHs of required masses are formed almost immediately to have enough time to evaporate out completely and produce the detectable gamma ray and neutrino signals with characteristics elucidated in Section 3.
Notice, the temporal properties of disturbed spacetime dynamics at the merging are also defined by . Since it takes a negligible fraction of the merging time to grow the bubbles to the relevant size, any dynamical evolution of the spacetime within UVS, during the bubbles conversion into BHs, should not affect the formation of BHs. Additionally, it is assumed that the Hawking evaporation of BHs, immersed into rapidly evolving spacetime within the gap of the merger, stays intact.
One can express the total numbers of BHs (15) and (16) created by and mechanisms, in the first scenario allocated in Section 2 as follows:
These estimates are obtained for a BBH merger with components of mass . Using the numerically computed action (75) along with (1) and (2), one can express the average decay rate as follows:
Some examples of analytical and numerical calculations of the pre-factor can be found in [97,98,99,100]. In the following, will be used as a rough value in (77) and (78).
Comparing the estimates (77) and (78), with the number of BHs needed to provide the energy budget of the detectable electromagnetic counterpart, as discussed in Section 3, we arrive at the following estimate:
made for , taken from the assessment of [28]. The estimate (80) is valid for both and mechanisms.
Due to the logarithmic dependence defining the value of (80), is quite weakly sensitive to and and stays almost the same for both quantities (39) and (40)8
Finally, evaluating the condition (17) which corresponds to the second scenario, discussed in Section 2, we obtain
These results, obtained within the framework of the aforementioned toy model above, substantiate our conjecture that the nucleation of new phase bubbles may be enhanced in a region “sandwiched” between the horizons of merging BHs.
Notice that, in the second scenario, in order to produce the BHs in the amount of and , the colliding bubbles need to occupy the volumes about and , respectively. Certainly, these volumes can fit inside calculated from (8) for in the case of components of the BBH merger. In other words, the amount of the Higgs meta-stable vacuum needed to produce a planetary cumulative mass of BHs, which are capable of providing SGRB energy budget for the electromagnetic messenger, is about . A of the Higgs meta-stable vacuum is capable of emitting about 10% of in Hawking radiation.
It is expected that a combination of both scenarios, discussed in Section 2, will take place. This implies that photons and neutrinos are suppose to be emitted within the distance range , defined by (80) and (81) so that the gravitational energy reduction factor (33), . This red shift was used for the model of the electromagnetic and neutrino signals, developed in Section 3, for TeV outgoing photons and neutrinos.
It is extremely unlikely that any expanding bubble wall, escaping from the UVS, would survive in a way to be able to trigger the decay of the SM metastable vacuum everywhere. Indeed, to reach the outer space by its domain wall, an expanding bubble should ultimately fill in the entire volume of UVS, which will contain already a great multitude of small, while already overcritical, bubbles due to the conditions of high nucleation rate created inside the UVS within ms. Colliding with the multitude of bubbles, the expanding wall will be numerously perforated so that the continuous topology of the wall providing the vacuum decay conditions is destroyed, leaving only some rapidly decaying pieces of the wall escaping out of the UVS. Moreover, occupying the entire volume, a potentially escaping bubble should ultimately touch the horizons of the components of a BBH merger, which, in turn, are still covered by the ongoing process of bubble nucleation. The collisions with those at horizon bubbles, the constituents of the bowling substance, will also lead to the ultimate perforation of the escaping wall and destruction of its continuous topology. The bubble with expanding walls, if any, will fill in the entire volume of UVS and collides with the horizons provided that exceeds given by (8). This condition can be recast into constraint on the mass of the BBH component, which reads . Therefore, it is extremely unlikely that BBH mergers with parameters considered in this study could trigger the decay of the global metastable state of the SM vacuum.
Furthermore, we note that, it would be interesting exploring the application of the considered model of gravitational modifications of the Higgs potential to other classes of models with strong gravitational fields, particularly in the context of particle models in the early universe. These investigations have the potential to reveal alternative mechanisms for the cancellation of vacuum energy during inflationary epochs as presented in [101,102,103], offering valuable insights into the interplay between gravity and fundamental particle physics. By extending our understanding in this direction, we can gain a deeper comprehension of the early universe and its intriguing dynamics.
9. Conclusions
In this paper, we explored the phenomenon that may occur in the vicinity of a BH horizon due to the gravitational corrections of the Higgs potential. The gravitational corrections can provide conditions for the Higgs vacuum decay so that a BH being immersed in the EW vacuum will be encompassed by a thin shell consisting of a “bowling substance” represented by nucleating bubbles of new vacuum phase surrounded by the SM vacuum. Since the nucleating bubbles fall under the horizon, an external observer of a single BH should always stay in the EW meta-stable state. However, in the gap between the components of a BBH merger, one might expect a formation of a volume with effective zero gravity so that for a short time period, the unstable vacuum is kind of “sandwiched” between the horizons of the components. Within the time of existence of the “sandwich”, the bubbles, nucleated in its volume, will collide and convert their energy into BHs, which in their turn will be evaporated by the emission of the Hawking radiation within the final stage of the coalescence of the BBH. The energy release in this burst-like evaporation, at a BBH of LIGO-Virgo scale, may range from the isotropic energy equivalent of SGRBs up to 10% fraction of . We call this phenomenon the Higgs-induced triboluminescence as an analogy of that existing in solid-state physics when materials can emit light by being mechanically stimulated, such as rubbing, grinding, impact, stretching, and compression.
Due to the emission of very-high-energy radiation TeV of all SM particles and, maybe, beyond the SM species, the phenomenon of Higgs-induced triboluminescence in BBH mergers should have quite distinguishable multi-messenger signatures. Indeed, a gravitational wave signal from a BBH merger arriving at currently running LIGO, VIRGO and KAGRA, or to be constructed in the future, more sensitive, gravitational wave facilities, should be accompanied with a ≳100 TeV neutrino signal in IceCube detected from the same direction and with an electromagnetic counterpart to be registered by space-based gamma ray monitors [33,34,35], the high-energy gamma ray telescope [36] and/or very-high-energy atmospheric Cherenkov facilities [38,39,40,41,42]. Propagating through the universe, gamma rays of such high energy will develop electromagnetic cascades due to pair production on cosmic microwave background and extra-galactic background light, which will multiply the TeV-GeV spectral component at the cost of very-high-energy thermal Hawking emission. However, whatever the arrived spectrum of the gamma rays, we always have to expect a burst-like temporal behavior of the signal. The observation of this phenomenon involves the detection of three types of messengers, namely gravitational waves, very-high-energy neutrinos and gamma rays, which makes it a perfect physics case for the multi-messenger campaign.
In the case of the observation of the effect of Higgs-induced triboluminescence in BBH mergers, one benefits, for valuable impact, from the understanding of at least two very intriguing topics of contemporary physics, namely, the decay of the meta-stable state of the EW vacuum and the evaporation of BHs via Hawking radiation.
Author Contributions
Conceptualization, A.S.S., M.G. and R.K.; methodology, A.S.S., M.G., M.C. and R.K.; software, R.K. and A.S.S.; validation, A.S.S., M.G. and R.K.; formal analysis, A.S.S., M.G., M.C. and R.K. All authors have read and agreed to the published version of the manuscript.
Funding
The work of Mariam Chitishvili was supported by the Shota Rustaveli National Science Foundation of Georgia (SRNSFG) through the grant PHDF-19-6294. The work of Rostislav Konoplich was partially supported by the Kakos Endowed Chair in Science Fellowship.
Data Availability Statement
Not available.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BH | Black hole |
| UVS | Unstable vacuum sandwich |
| GRB | Gamma ray burst |
| BBH | Binary black hole |
| SM | Standard model |
| BH | Micro black hole |
Notes
| 1 | However, this claim has been questioned in [23]. |
| 2 | See also a recent study of the mechanism [28] presented in [29]. |
| 3 | Choosing (2), we were governed by the argument that power laws can naturally satisfy the demand that a distance dependence of the nucleation rate is invariant under arbitrary rescaling, up to normalization measured here by the Schwarzschild radius. |
| 4 | Standard textbook formulas were used to obtain this result. |
| 5 | This quantity serves a discrete analog of distribution function in statistical physics. |
| 6 | The example is considered in order to stress the point that the energy of a particle does not depend on gravitational potential , so that, in the dispersion relation (63), the momentum and the mass terms are affected by V. Additionally, at the horizon , which implies that and hence the mass term does not destroy the renormalization scheme. |
| 7 | Recall that the -differentiability assumption for metric tensors plays a key role in the singularity theorems of the general relativity. Thus, the second-order partial derivatives of the metric tensor should exist and be continuous. The initial value analysis also leads to the restriction that admissible coordinate transformations are to be of class since they should not change the Riemann tensor, which would lead to the fictitious extra source in the Einstein equations. |
| 8 | Our current ignorance of details of the mechanism of formation in bubble collisions which might be represented by a poor knowledge of the value of , say up to about 10 orders of magnitude uncertainty (), results only in about 10% variation in estimate (80). A detailed consideration of the formation of BHs in bubble collisions is in preparation. |
References
- Chatrchyan, S. et al. [CMS Collaboration] Observation of a New Boson at a Mass of 125 GeV with the CMS Experiment at the LHC. Phys. Lett. B 2012, 716, 30. [Google Scholar] [CrossRef]
- Aad, G. et al. [ATLAS Collaboration] Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 2012, 716, 1–29. [Google Scholar] [CrossRef]
- Degrassi, G.; Vita, S.D.; Elias-Miro, J.; Espinosa, J.R.; Giudice, G.F.; Isidori, G.; Strumia, A. Higgs mass and vacuum stability in the Standard Model at NNLO. J. High Energy Phys. 2012, 2012, 98. [Google Scholar] [CrossRef]
- Buttazzo, D.; Degrassi, G.; Giardino, P.P.; Giudice, G.F.; Sala, F.; Salvio, A.; Strumia, A. Investigating the near-criticality of the Higgs boson. J. High Energy Phys. 2013, 2013, 89. [Google Scholar] [CrossRef]
- Isidori, G.; Ridolfi, G.; Strumia, A. On the metastability of the standard model vacuum. Nucl. Phys. B 2001, 609, 387. [Google Scholar] [CrossRef]
- Sher, M. Precise vacuum stability bound in the standard model. Phys. Lett. B 1993, 317, 159, Addendum in Phys. Lett. B 1994, 331, 448. https://doi.org/10.1016/0370-2693(93)91586-C. [Google Scholar] [CrossRef]
- Ellis, J.; Espinosa, J.R.; Giudice, G.F.; Hoecker, A.; Riotto, A. The Probable Fate of the Standard Model. Phys. Lett. B 2009, 679, 369. [Google Scholar] [CrossRef]
- Casas, J.A.; Espinosa, J.R.; Quiros, M. Standard model stability bounds for new physics within LHC reach. Phys. Lett. B 1996, 382, 374. [Google Scholar] [CrossRef]
- Elias-Miro, J.; Espinosa, J.R.; Giudice, G.F.; Isidori, G.; Riotto, A.; Strumia, A. Higgs mass implications on the stability of the electroweak vacuum. Phys. Lett. B 2012, 709, 222. [Google Scholar] [CrossRef]
- Zyla, P.A. Particle Data Group. Prog. Theor. Exp. Phys. 2020, 083C01, 32. [Google Scholar]
- Espinosa, J.R.; Giudice, G.F.; Riotto, A. Cosmological implications of the Higgs mass measurement. J. Cosmol. Astropart. Phys. 2008, 805, 2. [Google Scholar] [CrossRef]
- Espinosa, J.R.; Giudice, G.F.; Morgante, E.; Riotto, A.; Senatore, L.; Strumia, A.; Tetradis, N. The cosmological Higgstory of the vacuum instability. J. High Energy Phys. 2015, 1509, 174. [Google Scholar] [CrossRef]
- Branchina, V.; Messina, E. Stability, Higgs Boson Mass and New Physics. Phys. Rev. Lett. 2013, 111, 241801. [Google Scholar] [CrossRef] [PubMed]
- Luzio, L.D.; Isidori, G.; Ridolfi, G. Stability of the electroweak ground state in the Standard Model and its extensions. Phys. Lett. B 2016, 753, 150. [Google Scholar] [CrossRef]
- Markkanen, T.; Nurmi, S.; Rajantie, A.; Stopyra, S. The 1-loop effective potential for the Standard Model in curved spacetime. J. High Energy Phys. 2018, 1806, 40. [Google Scholar] [CrossRef]
- Gregory, R.; Moss, I.G.; Withers, B. Black holes as bubble nucleation sites. J. High Energy Phys. 2014, 1403, 81. [Google Scholar] [CrossRef]
- Burda, P.; Gregory, R.; Moss, I. Gravity and the stability of the Higgs vacuum. Phys. Rev. Lett. 2015, 115, 071303. [Google Scholar] [CrossRef]
- Burda, P.; Gregory, R.; Moss, I. Vacuum metastability with black holes. J. High Energy Phys. 2015, 1508, 114. [Google Scholar] [CrossRef]
- Burda, P.; Gregory, R.; Moss, I. The fate of the Higgs vacuum. J. High Energy Phys. 2016, 1606, 025. [Google Scholar] [CrossRef]
- Tetradis, N. Black Holes and Higgs Stability. J. Cosmol. Astropart. Phys. 2016, 1609, 36. [Google Scholar] [CrossRef]
- Canko, D.; Gialamas, I.; Jelic-Cizmek, G.; Riotto, A.; Tetradis, N. On the Catalysis of the Electroweak Vacuum Decay by Black Holes at High Temperature. Eur. Phys. J. C 2018, 78, 328. [Google Scholar] [CrossRef]
- Mukaida, K.; Yamada, M. False Vacuum Decay Catalyzed by Black Holes. Phys. Rev. D 2017, 96, 103514. [Google Scholar] [CrossRef]
- Strumia, A. Black holes don’t source fast Higgs vacuum decay. J. High Energy Phys. 2023, 2023, 39. [Google Scholar] [CrossRef]
- Abbott, B.P. et al. [LIGO Scientific and Virgo Collaborations] Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P. et al. [LIGO Scientific and Virgo Collaborations] GWTC-1: A Gravitational-Wave Transient Catalog of Compact Binary Mergers Observed by LIGO and Virgo during the First and Second Observing Runs. Phys. Rev. X 2019, 9, 031040. [Google Scholar] [CrossRef]
- Abbott, R. et al. [LIGO Scientific and Virgo] GWTC-2: Compact Binary Coalescences Observed by LIGO and Virgo During the First Half of the Third Observing Run. Phys. Rev. X 2021, 11, 021053. [Google Scholar] [CrossRef]
- Moss, I.G. Singularity formation from colliding bubbles. Phys. Rev. D 1994, 50, 676. [Google Scholar] [CrossRef]
- Konoplich, R.V.; Rubin, S.G.; Sakharov, A.S.; Khlopov, M.Y. Formation of black holes in first-order phase transitions as a cosmological test of symmetry-breaking mechanisms. Phys. Atom. Nucl. 1999, 62, 1593–1600. [Google Scholar]
- Jung, T.H.; Okui, T. Primordial black holes from bubble collisions during a first-order phase transition. arXiv 2021, arXiv:2110.04271. [Google Scholar]
- Hawking, S.W. Black hole explosions. Nature 1974, 248, 30. [Google Scholar] [CrossRef]
- Abbott, R. et al. [LIGO Scientific, VIRGO and KAGRA] GWTC-3: Compact Binary Coalescences Observed by LIGO and Virgo During the Second Part of the Third Observing Run. arXiv 2021, arXiv:2111.03606. [Google Scholar]
- Berger, E. Short-Duration Gamma-Ray Bursts. Ann. Rev. Astron. Astrophys. 2014, 52, 43. [Google Scholar] [CrossRef]
- Gehrels, N. et al. [Swift Science Collaboration] The Swift Gamma-Ray Burst Mission. Astrophys. J. 2004, 611, 1005, Erratum in Astrophys. J. 2005, 621, 558. https://doi.org/10.1086/422091. [Google Scholar] [CrossRef]
- Courvoisier, T.L.; Walter, R.; Beckmann, V.; Dean, A.J.; Dubath, P.E.; Hudec, R.; Kretschmar, P.; Mereghetti, S.; Montmerle, T.; Mowlavi, N.; et al. The INTEGRAL Science Data Centre (ISDC). Astron. Astrophys. 2003, 411, L53. [Google Scholar] [CrossRef]
- Meegan, C.; Lichti, G.; Bhat, P.N.; Bissaldi, E.; Briggs, M.S.; Connaughton, V.; Diehl, R.; Fishman, G.; Greiner, J.; Hoover, A.S.; et al. The Fermi Gamma-Ray Burst Monitor. Astrophys. J. 2009, 702, 791. [Google Scholar] [CrossRef]
- Atwood, W.B. et al. [Fermi-LAT Collaboration] The Large Area Telescope on the Fermi Gamma-ray Space Telescope Mission. Astrophys. J. 2009, 697, 1071. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [IceCube] The IceCube Neutrino Observatory: Instrumentation and Online Systems. J. Instrum. 2017, 12, P03012. [Google Scholar] [CrossRef]
- Aleksić, J. et al. [MAGIC] The major upgrade of the MAGIC telescopes, Part II: A performance study using observations of the Crab Nebula. Astropart. Phys. 2016, 72, 76–94. [Google Scholar] [CrossRef]
- Hinton, J.A. [H.E.S.S.]. The Status of the H.E.S.S. project. New Astron. Rev. 2004, 48, 331–337. [Google Scholar] [CrossRef]
- Weekes, T.C.; Badran, H.; Biller, S.D.; Bond, I.; Bradbury, S.; Buckley, J.; Carter-Lewis, D.; Catanese, M.; Criswell, S.; Cui, W.; et al. VERITAS: The Very energetic radiation imaging telescope array system. Astropart. Phys. 2002, 17, 221–243. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Albert, A.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Arceo, R.; Arteaga-Velázquez, J.C.; Solares, H.A.A.; Barber, A.S.; Bautista-Elivar, N.; et al. Observation of the Crab Nebula with the HAWC Gamma-Ray Observatory. Astrophys. J. 2017, 843, 39. [Google Scholar] [CrossRef]
- Bai, X.; Bi, B.Y.; Bi, X.J.; Cao, Z.; Chen, S.Z.; Chen, Y.; Chiavassa, A.; Cui, X.H.; Dai, Z.G.; della Volpe, D.; et al. The Large High Altitude Air Shower Observatory (LHAASO) Science White Paper. arXiv 2019, arXiv:1905.02773. [Google Scholar]
- Olawale, D.O.; Okoli, O.O.I.; Fontenot, R.S.; Hollerman, W.A. (Eds.) Triboluminescence Theory, Synthesis, and Application; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Miyachi, T.; Soda, J. False vacuum decay in a two-dimensional black hole spacetime. Phys. Rev. D 2021, 103, 085009. [Google Scholar] [CrossRef]
- Shkerin, A.; Sibiryakov, S. Black hole induced false vacuum decay from first principles. J. High Energy Phys. 2021, 11, 197. [Google Scholar] [CrossRef]
- Coleman, S.R. The Fate of the False Vacuum. 1. Semiclassical Theory. Phys. Rev. D 1977, 15, 2929, Erratum in Phys. Rev. D 1977, 16, 1248. https://doi.org/10.1103/PhysRevD.16.1248. [Google Scholar] [CrossRef]
- Callan, C.G.; Coleman, S.R. The Fate of the False Vacuum. 2. First Quantum Corrections. Phys. Rev. D 1977, 16, 1762. [Google Scholar] [CrossRef]
- Kobzarev, I.Y.; Okun, L.B.; Voloshin, M.B. Bubbles in Metastable Vacuum. Yad. Fiz. 1974, 20, 1229. [Google Scholar]
- Coleman, S.R.; Luccia, F.D. Gravitational Effects on and of Vacuum Decay. Phys. Rev. D 1980, 21, 3305. [Google Scholar] [CrossRef]
- Stauffer, D.; Aharony, A. Introduction To Percolation Theory; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Parisi, G.; Sourlas, N. Critical Behavior of Branched Polymers and the Lee-Yang Edge Singularity. Phys. Rev. Lett. 1981, 46, 871. [Google Scholar] [CrossRef]
- Ding, B.; Li, C.; Zhang, M.; Lu, G.; Ji, F. Numerical analysis of percolation cluster size distribution in two-dimensional and three-dimensional lattices. Eur. Phys. J. B 2014, 87, 179. [Google Scholar] [CrossRef]
- MacGibbon, J.H.; Webber, B.R. Quark and gluon jet emission from primordial black holes: The instantaneous spectra. Phys. Rev. D 1990, 41, 3052. [Google Scholar] [CrossRef] [PubMed]
- Nikishov, A.I. Absorption of High-Energy Photons in the Universe. J. Exp. Theor. Phys. 1962, 14, 393. [Google Scholar]
- Gould, R.; Schréder, G. Opacity of the Universe to High-Energy Photons. Phys. Rev. Lett. 1966, 16, 252. [Google Scholar] [CrossRef]
- Madau, P.; Pozzetti, L. Deep galaxy counts, extragalactic background light, and the stellar baryon budget. Mon. Not. R. Astron. Soc. 2000, 312, L9. [Google Scholar] [CrossRef]
- Dwek, E.; Krennrich, F. The Extragalactic Background Light and the Gamma-ray Opacity of the Universe. Astropart. Phys. 2013, 43, 112. [Google Scholar] [CrossRef]
- Abramowski, A. et al. [H.E.S.S.] Measurement of the extragalactic background light imprint on the spectra of the brightest blazars observed with H.E.S.S. Astron. Astrophys. 2013, 550, A4. [Google Scholar] [CrossRef]
- Akhiezer, A.I.; Berestetsky, V.B. Quantum Electrodynamics, 4th ed.; Nauka: Moscow, Russia, 1981. [Google Scholar]
- Greiner, W.; Reinhardt, J. Quantum Electrodynamics, 4th ed.; Springer: Berlin, Germany, 2009. [Google Scholar]
- Aharonian, F.A. Very High Energy Cosmic Gamma Radiation: A Crucial Window on the Extreme Universe; World Scientific: Singapore; Hong Kong, China, 2004. [Google Scholar]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W. H. Freeman: San Francisco, CA, USA, 1973; ISBN 978-0-7167-0344-0. [Google Scholar]
- Fitoussi, T.; Belmont, R.; Malzac, J.; Marcowith, A.; Cohen-Tanugi, J.; Jean, P. Physics of cosmological cascades and observable properties. Mon. Not. R. Astron. Soc. 2017, 466, 3472–3487. [Google Scholar] [CrossRef]
- Blumenthal, G.R.; Gould, R.J. Bremsstrahlung, synchrotron radiation, and compton scattering of high-energy electrons traversing dilute gases. Rev. Mod. Phys. 1970, 42, 237. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [IceCube Collaboration] Neutrino emission from the direction of the blazar TXS 0506+056 prior to the IceCube-170922A alert. Science 2018, 361, 147. [Google Scholar] [CrossRef]
- Aartsen, M.G. et al. [IceCube and Fermi-LAT and MAGIC and AGILE and ASAS-SN and HAWC and H.E.S.S. and INTEGRAL and Kanata and Kiso and Kapteyn and Liverpool Telescope and Subaru and Swift NuSTAR and VERITAS and VLA/17B-403 Collaborations] Multimessenger observations of a flaring blazar coincident with high-energy neutrino IceCube-170922A. Science 2018, 361, eaat1378. [Google Scholar] [CrossRef]
- Coleman, S.R.; Weinberg, E.J. Radiative Corrections as the Origin of Spontaneous Symmetry Breaking. Phys. Rev. D 1973, 7, 1888. [Google Scholar] [CrossRef]
- Peskin, M.E.; Schroeder, D.V. An Introduction to Quantum Field Theory; Perseus Books Publishing, L.L.C.: New York, NY, USA, 1995. [Google Scholar]
- Schwartz, M.D. Quantum Field Theory and the Standard Model; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Bezrukov, F.; Shaposhnikov, M. Why should we care about the top quark Yukawa coupling? J. Theor. Exp. Phys. 2015, 120, 335. [Google Scholar] [CrossRef]
- Grobov, A.V.; Konoplich, R.V.; Rubin, S.G. Cosmological implications of Higgs field fluctuations during inflation. Ann. Phys. 2015, 528, 187–192. [Google Scholar] [CrossRef]
- Isidori, G.; Rychkov, V.S.; Strumia, A.; Tetradis, N. Gravitational Corrections to Standard Model Vacuum Decay. Phys. Rev. D 2008, 77, 025034. [Google Scholar] [CrossRef]
- Salvio, A.; Strumia, A.; Tetradis, N.; Urbano, A. On Gravitational and Thermal Corrections to Vacuum Decay. J. High Energy Phys. 2016, 1609, 54. [Google Scholar] [CrossRef]
- Hiscock, W.A. Can Black Holes Nucleate Vacuum Phase Transitions? Phys. Rev. D 1987, 35, 1161. [Google Scholar] [CrossRef] [PubMed]
- Berezin, V.A.; Kuzmin, V.A.; Tkachev, I.I. Black Holes Initiate False Vacuum Decay. Phys. Rev. D 1991, 43, 3112. [Google Scholar] [CrossRef] [PubMed]
- Birrell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Wald, R.M. Quantum Field Theory in Curved Spacetime and Black Hole Thermodynamics; The University of Chicago Press: Chicago, IL, USA, 1994. [Google Scholar]
- Markkanen, T.; Rajantie, A.; Stopyra, S. Cosmological Aspects of Higgs Vacuum Metastability. Front. Astron. Space Sci. 2018, 5, 40. [Google Scholar] [CrossRef]
- Mattingly, D. Modern tests of Lorentz invariance. Living Rev. Relativ. 2005, 8, 5. [Google Scholar] [CrossRef] [PubMed]
- Bluhm, R. Overview of the SME: Implications and phenomenology of Lorentz violation. Lect. Notes Phys. 2006, 702, 191. [Google Scholar] [CrossRef]
- Kostelecky, V.A.; Russell, N. Data Tables for Lorentz and CPT Violation. Rev. Mod. Phys. 2011, 83, 11. [Google Scholar] [CrossRef]
- Costa, H.A.S.; Carvalho, P.R.S.; da Paz, I.G. Parameter estimation for a Lorentz invariance violation. Int. J. Mod. Phys. D 2018, 28, 1950028. [Google Scholar] [CrossRef]
- Anderson, D.L.; Sher, M.; Turan, I. Lorentz and CPT Violation in the Higgs Sector. Phys. Rev. D 2004, 70, 016001. [Google Scholar] [CrossRef]
- Lehnert, R. Constraining Lorentz Violation in Electroweak Physics. J. Phys. Conf. Ser. 2018, 952, 012008. [Google Scholar] [CrossRef]
- Aghababaei, S.; Haghighat, M.; Kheirandish, A. Lorentz Violation in the Higgs Sector and Noncommutative Standard Model. Phys. Rev. D 2013, 87, 047703. [Google Scholar] [CrossRef]
- Altschul, B. Lorentz Violation and the Higgs Mechanism. Phys. Rev. D 2012, 86, 045008. [Google Scholar] [CrossRef]
- Henry, R.C. Kretschmann scalar for a kerr-newman black hole. Astrophys. J. 2000, 535, 350. [Google Scholar] [CrossRef]
- Hagedorn, R. Statistical thermodynamics of strong interactions at high-energies. Nuovo C. Suppl. 1965, 3, 147. [Google Scholar]
- Okun, L.B. Photons and static gravity. Mod. Phys. Lett. A 2000, 15, 1941. [Google Scholar] [CrossRef]
- Okun, L.B. Photons, clocks, gravity and the concept of mass. Nucl. Phys. Proc. Suppl. 2002, 110, 151. [Google Scholar] [CrossRef]
- Gogberashvili, M.; Pantskhava, L. Black Hole Information Problem and Wave Bursts. Int. J. Theor. Phys. 2018, 57, 1763–1773. [Google Scholar] [CrossRef]
- Gogberashvili, M. Can Quantum Particles Cross a Horizon? Int. J. Theor. Phys. 2019, 58, 3711–3725. [Google Scholar] [CrossRef]
- Beradze, R.; Gogberashvili, M.; Pantskhava, L. Reflective black holes. Mod. Phys. Lett. A 2021, 36, 2150200. [Google Scholar] [CrossRef]
- Gogberashvili, M. Einstein’s hole argument and Schwarzschild singularities. Ann. Phys. 2023, 452, 169274. [Google Scholar] [CrossRef]
- Sato, R. Simple Gradient Flow Equation for the Bounce Solution. Phys. Rev. D 2020, 101, 016012. [Google Scholar] [CrossRef]
- Gleiser, M.; Kolb, E.W.; Watkins, R. Phase transitions with subcritical bubbles. Nucl. Phys. B 1991, 364, 411. [Google Scholar] [CrossRef]
- Konoplich, R.V. Calculation of quantum corrections to nontrivial classical solutions by means of the zeta function. Theor. Math. Phys. 1987, 73, 1286–1295. [Google Scholar] [CrossRef]
- Amendola, L.; Baccigalupi, C.; Konoplich, R.; Occhionero, F.; Rubin, S. Reconstruction of the bubble nucleating potential. Phys. Rev. D 1996, 54, 7199. [Google Scholar] [CrossRef] [PubMed]
- Dunne, G.V.; Min, H. Beyond the thin-wall approximation: Precise numerical computation of prefactors in false vacuum decay. Phys. Rev. D 2005, 72, 125004. [Google Scholar] [CrossRef]
- Guada, V.; Nemevšek, M. Exact one-loop false vacuum decay rate. Phys. Rev. D 2020, 102, 125017. [Google Scholar] [CrossRef]
- Luongo, O.; Muccino, M. Speeding up the universe using dust with pressure. Phys. Rev. D 2018, 98, 103520. [Google Scholar] [CrossRef]
- D’Agostino, R.; Luongo, O.; Muccino, M. Healing the cosmological constant problem during inflation through a unified quasi-quintessence matter field. Class. Quant. Grav. 2022, 39, 195014. [Google Scholar] [CrossRef]
- Belfiglio, A.; Giambò, R.; Luongo, O. Alleviating the cosmological constant problem from particle production. Class. Quant. Grav. 2023, 40, 105004. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).