Sensorless Fractional Order Control of PMSM Based on Synergetic and Sliding Mode Controllers
Abstract
1. Introduction
2. Fractional Order Calculus
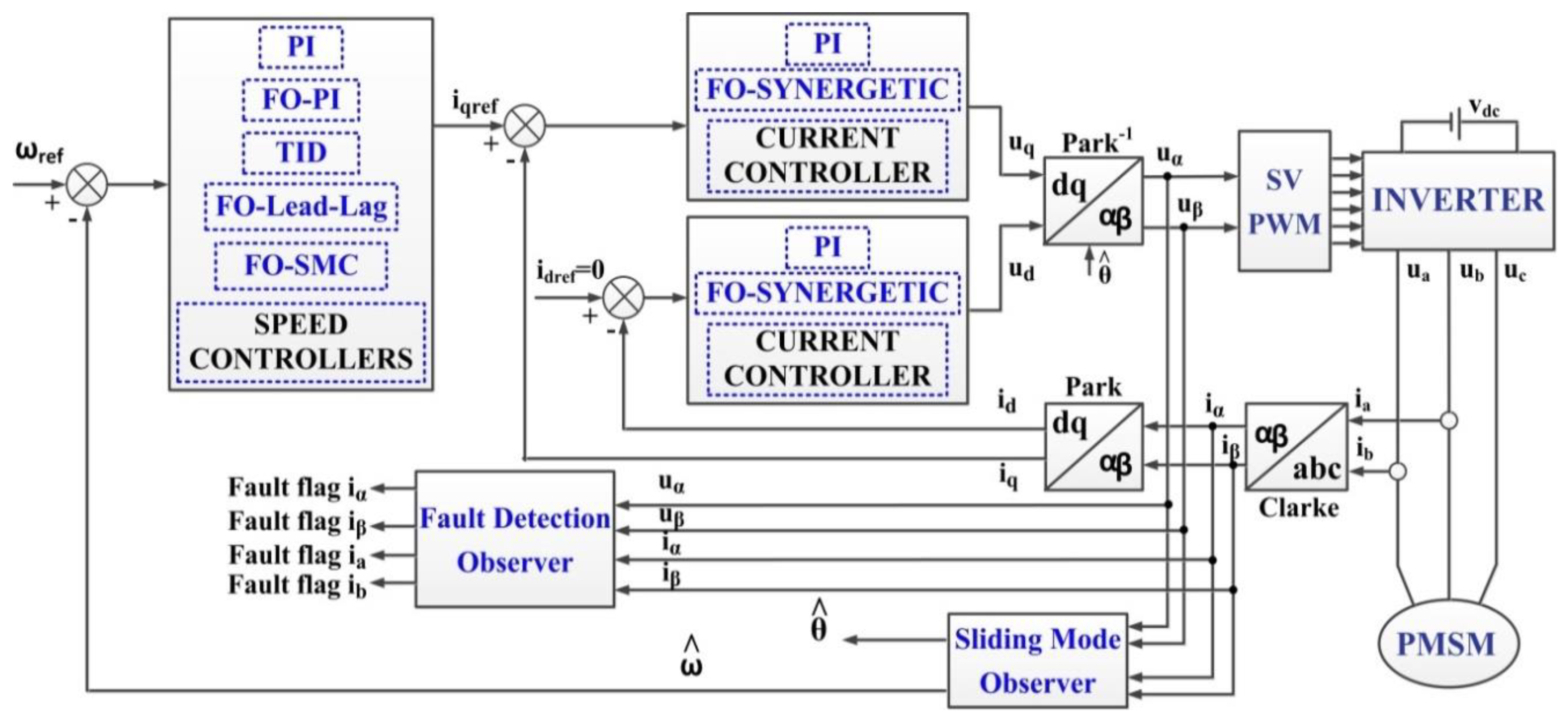
3. Mathematical Model of PMSM. Transfer Function Representation. FOC Strategy of PMSM
4. Fractional Order Speed Controllers for PMSM
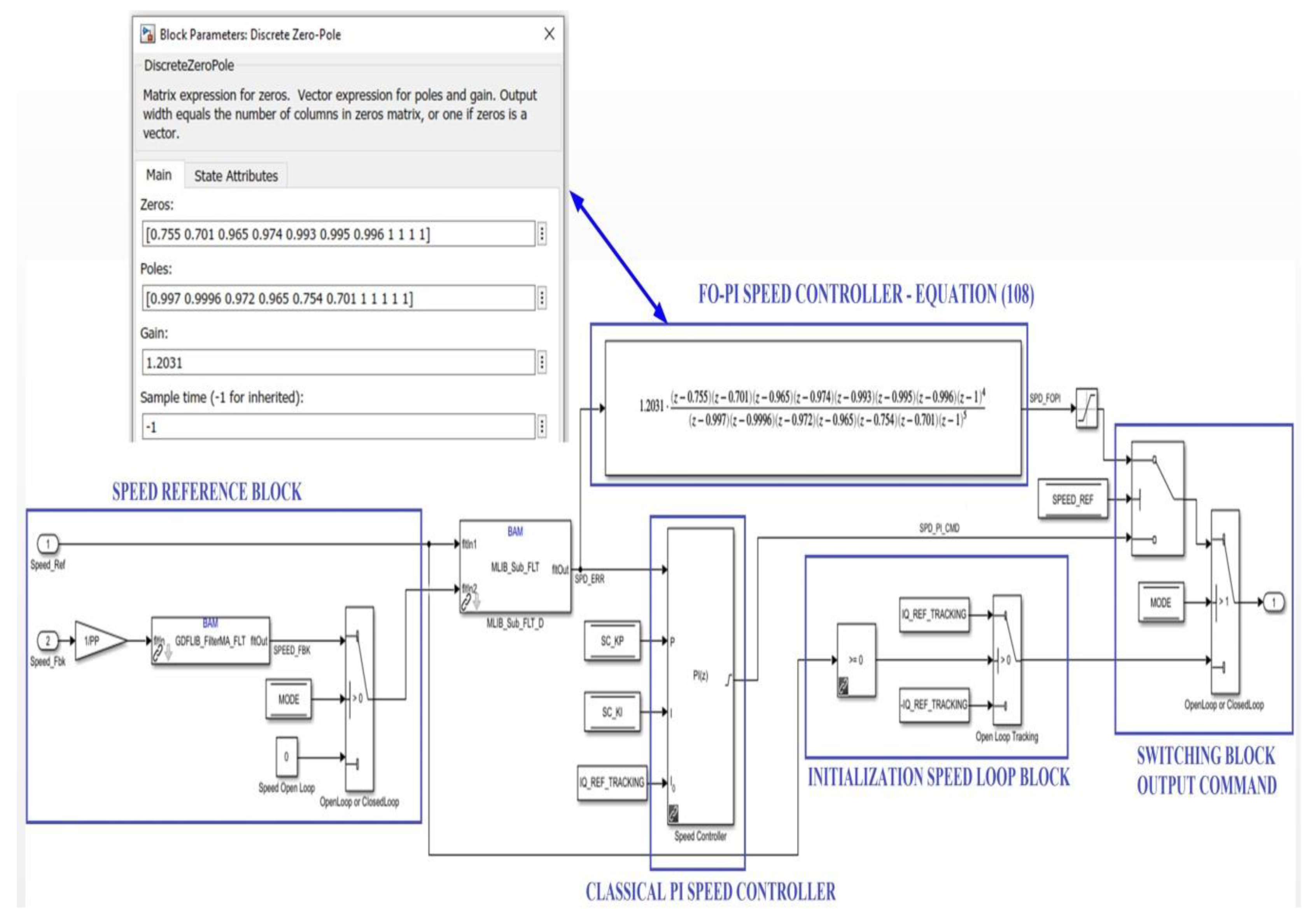
4.1. FO-PI Speed Controller
4.2. TID Speed Controller
4.3. Lead-Lag Speed Controller
4.4. FO-SMC Speed Controller
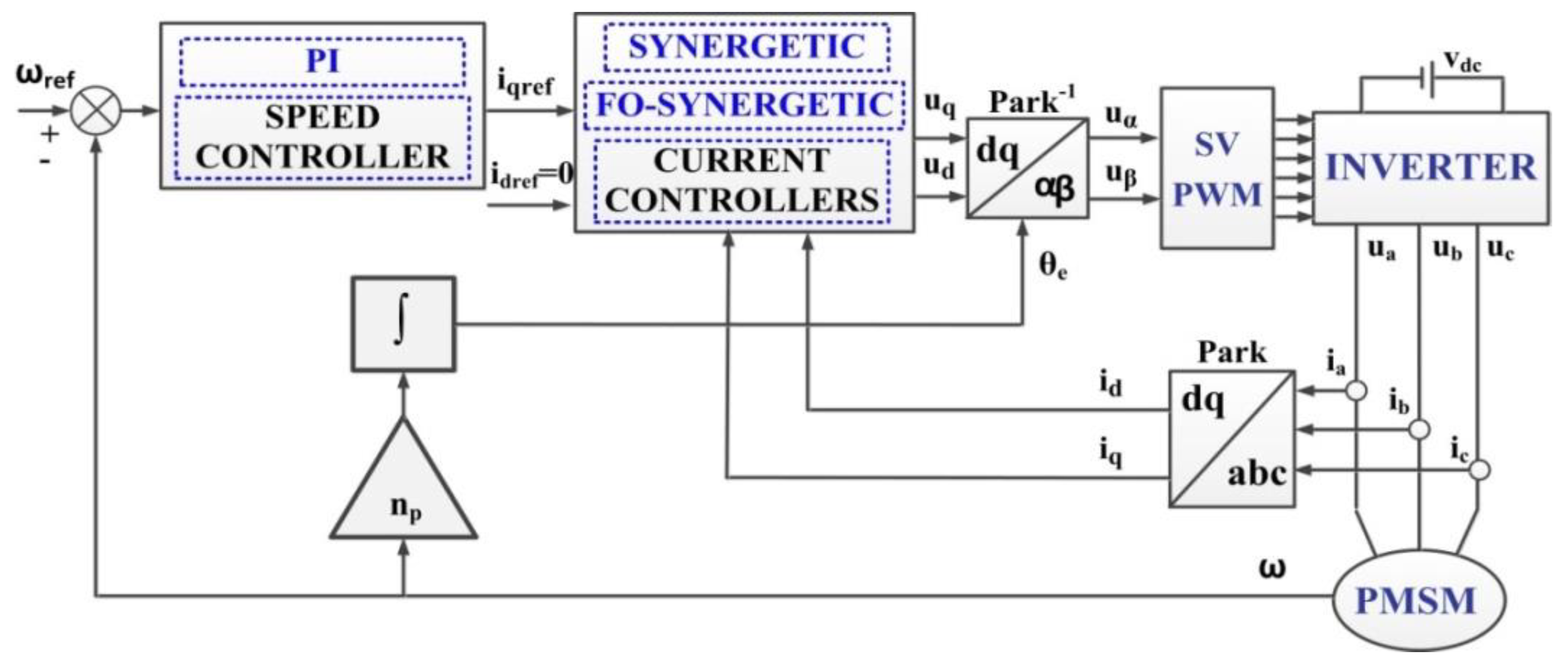
5. Fractional Order Synergetic Current Controllers for PMSM
6. Rotor Speed Estimation and Fault Detection
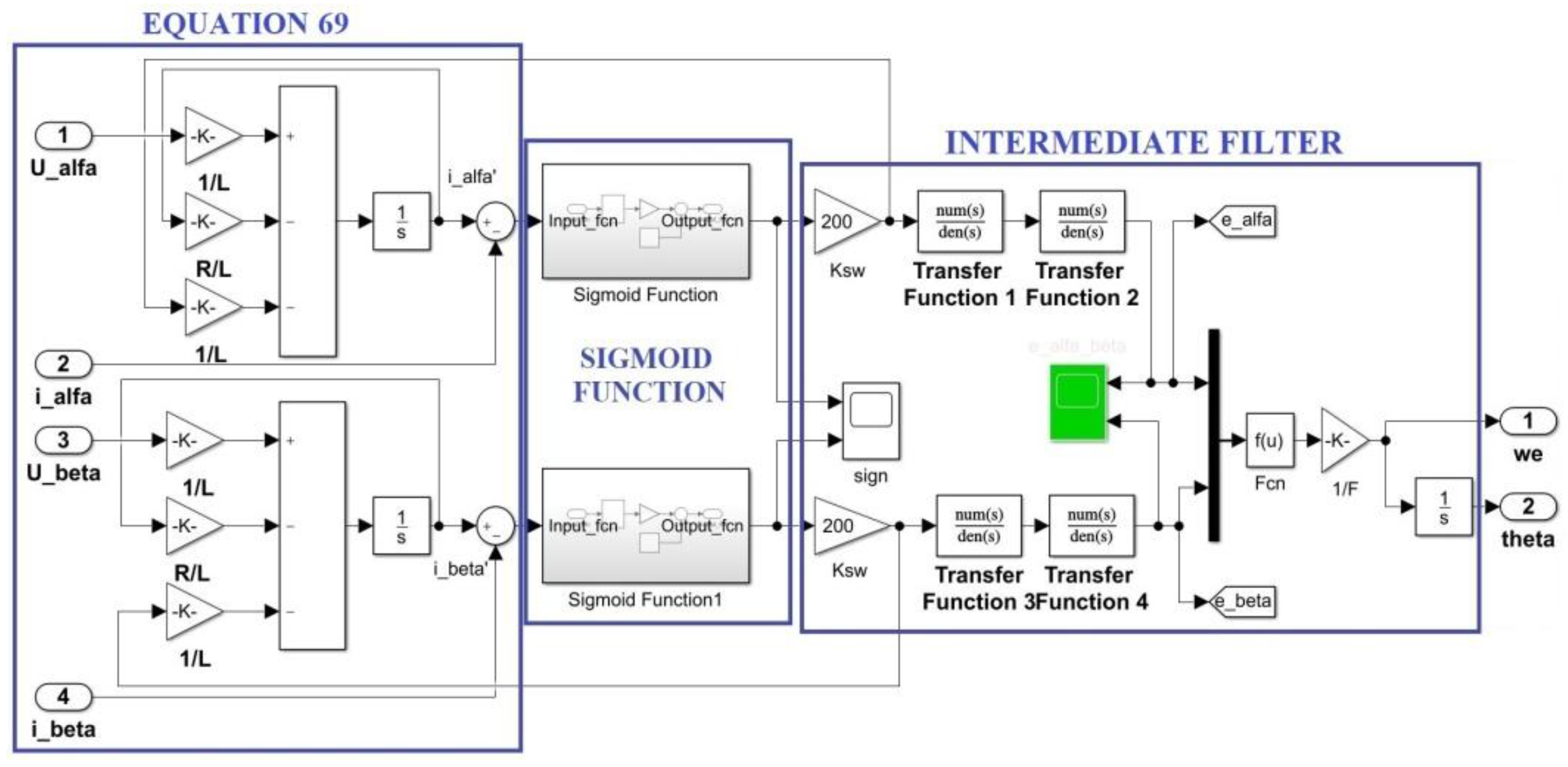
6.1. Rotor Speed and Position Estimations Based on SMO-Type Observer
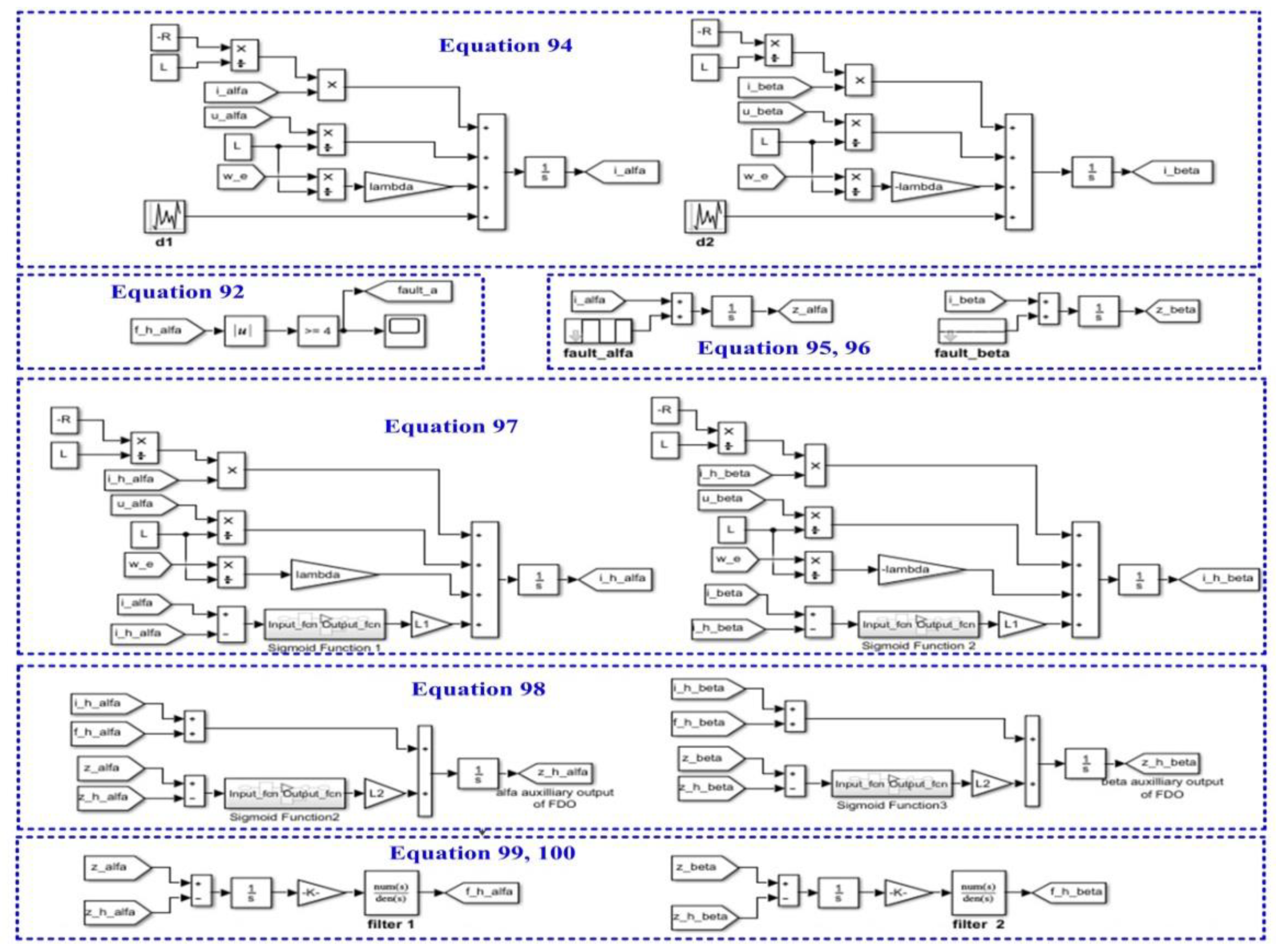
6.2. Fault Detection Based on FDO-Type Observer
7. Numerical Simulations
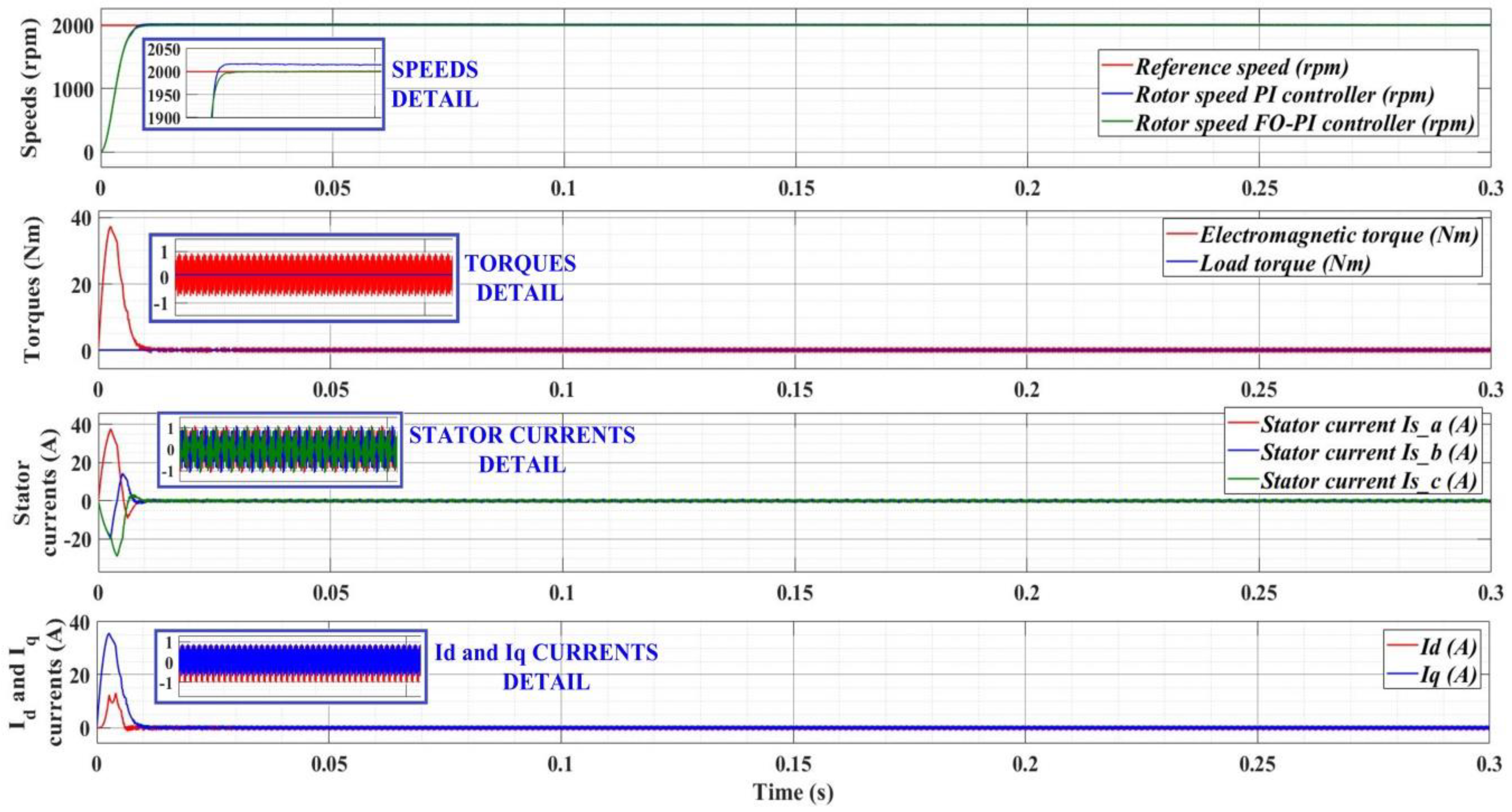
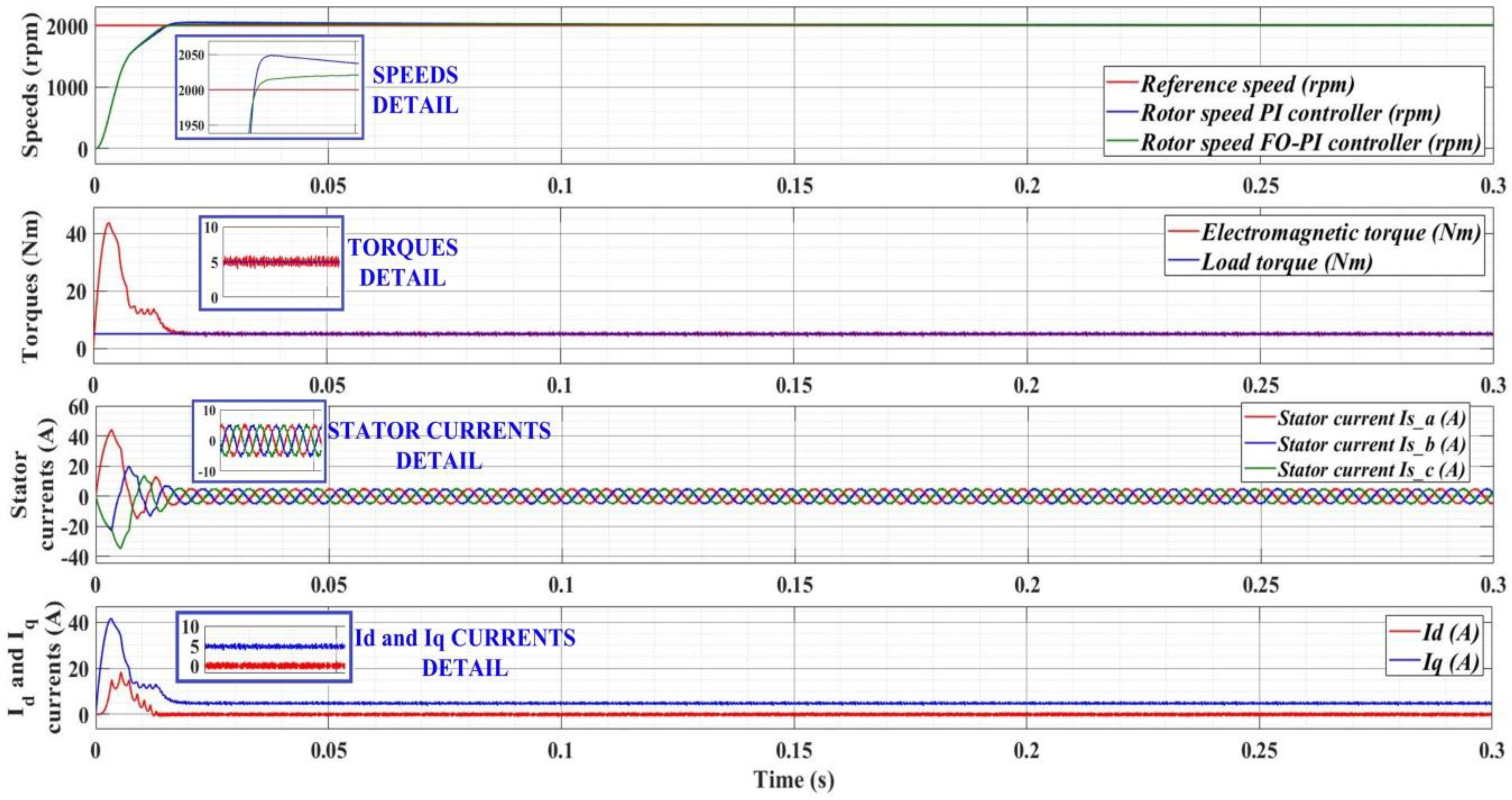
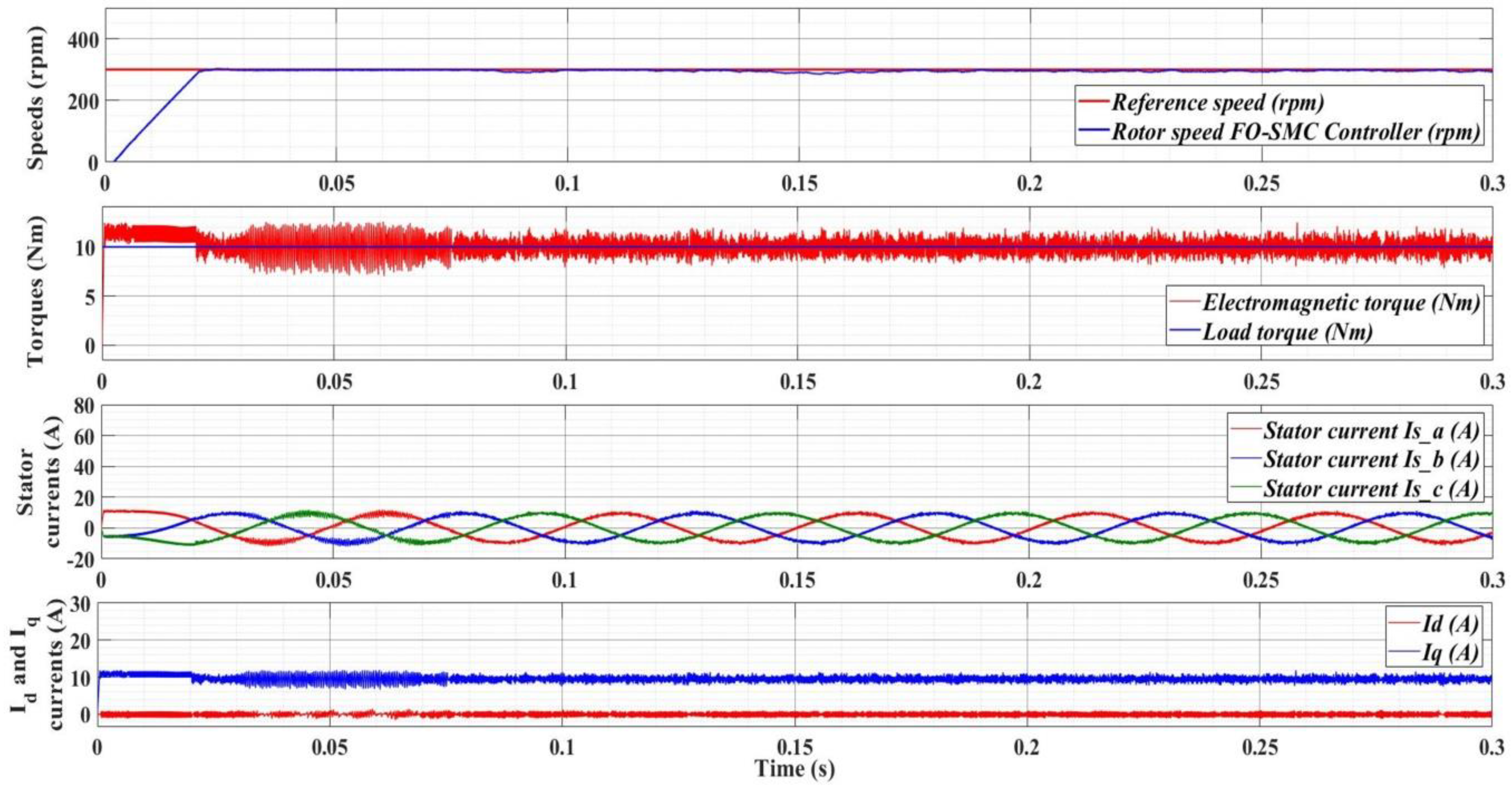
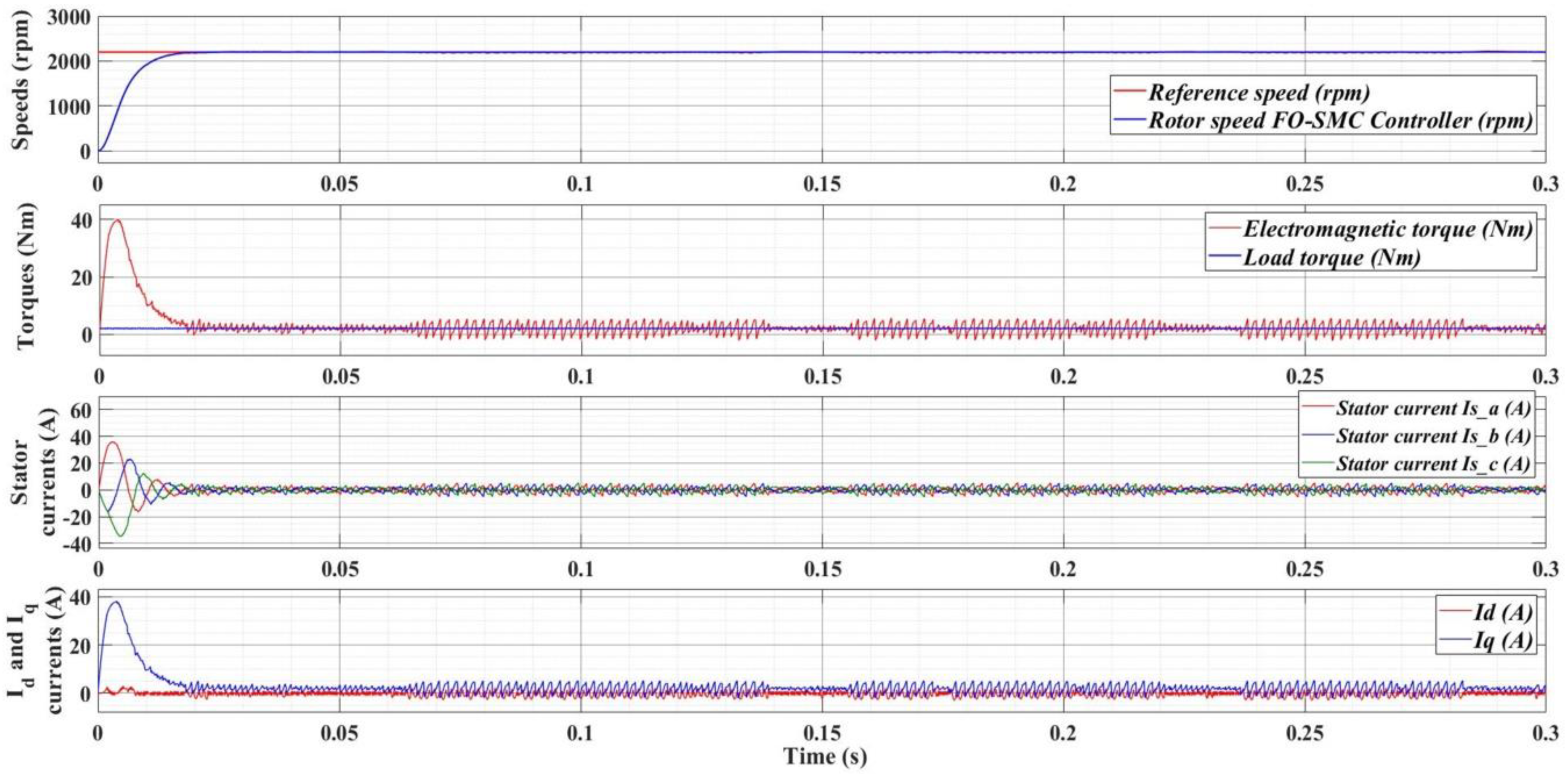
7.1. Numerical Simulations—Fractional Order Speed Controllers for PMSM
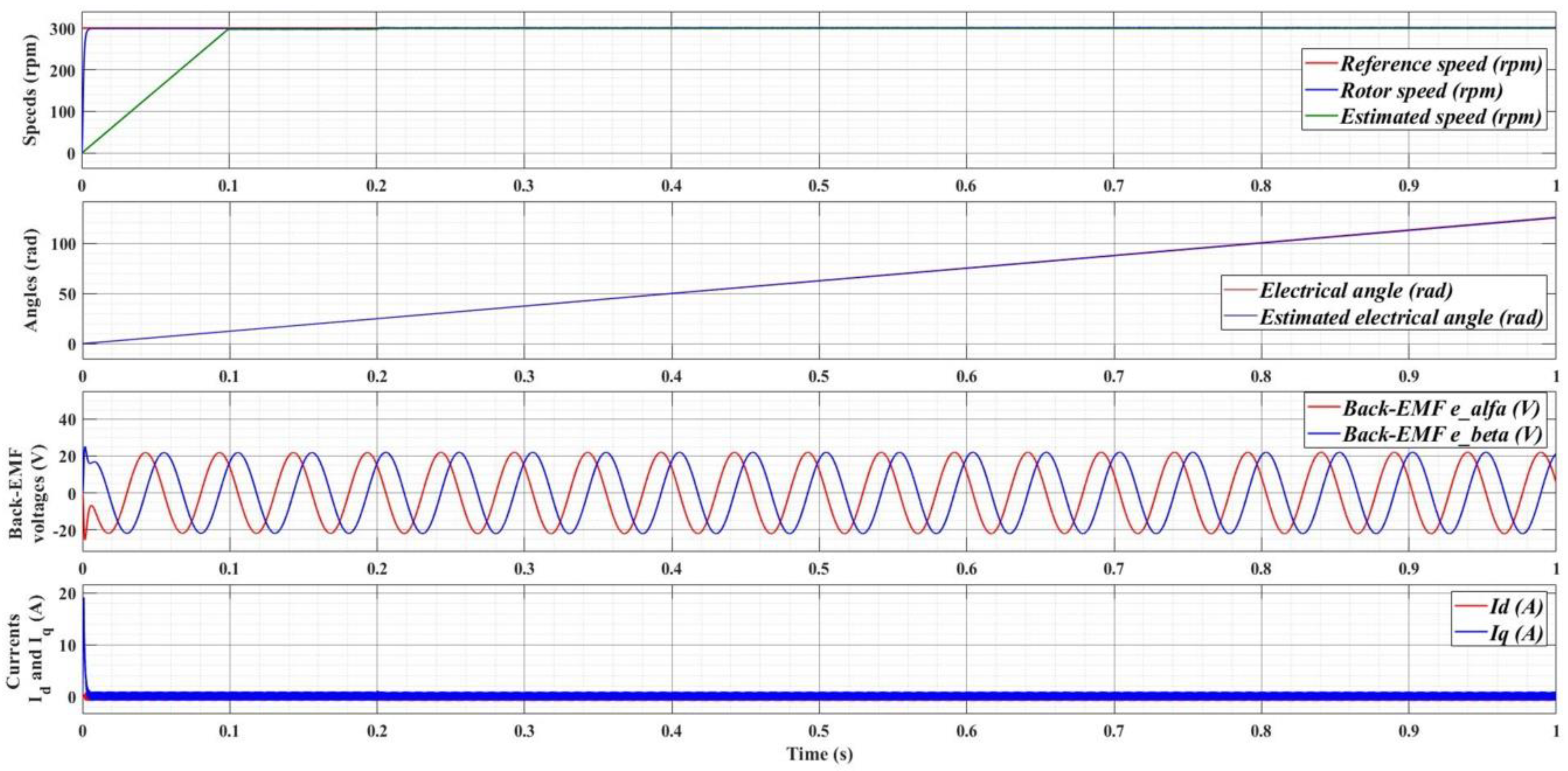
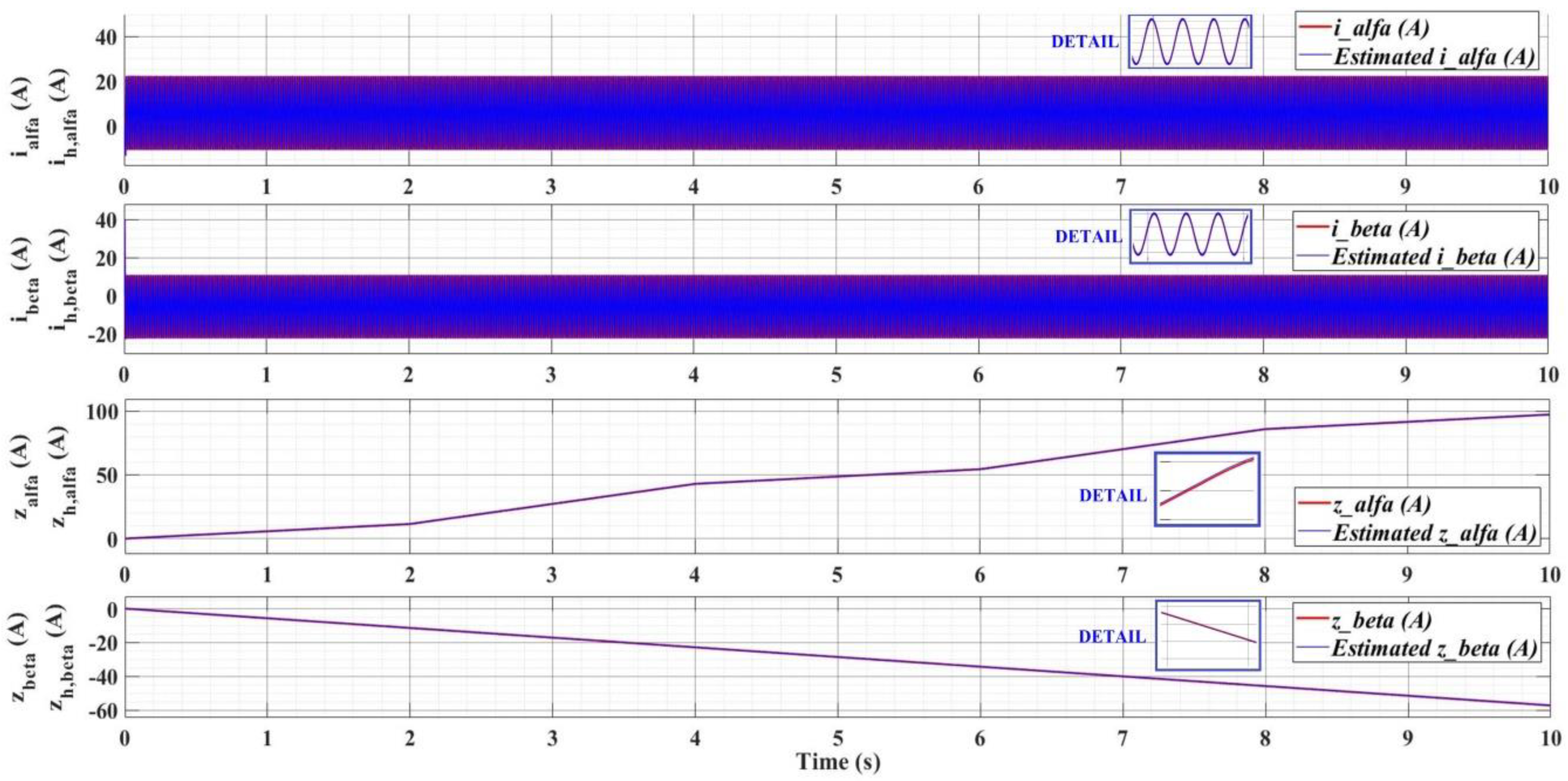
7.2. Numerical Simulations for Rotor Speed Estimation and Fault Detection
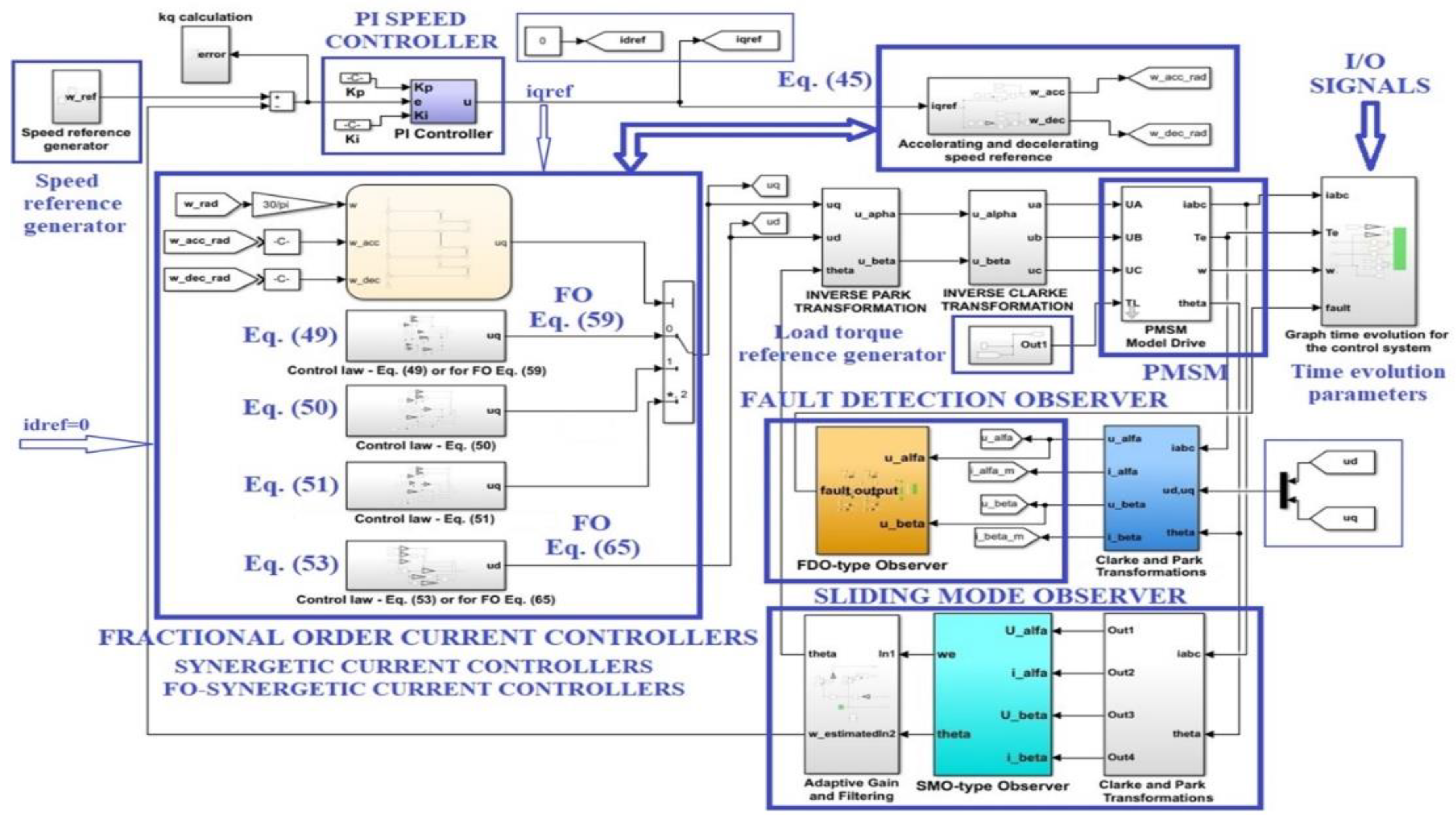
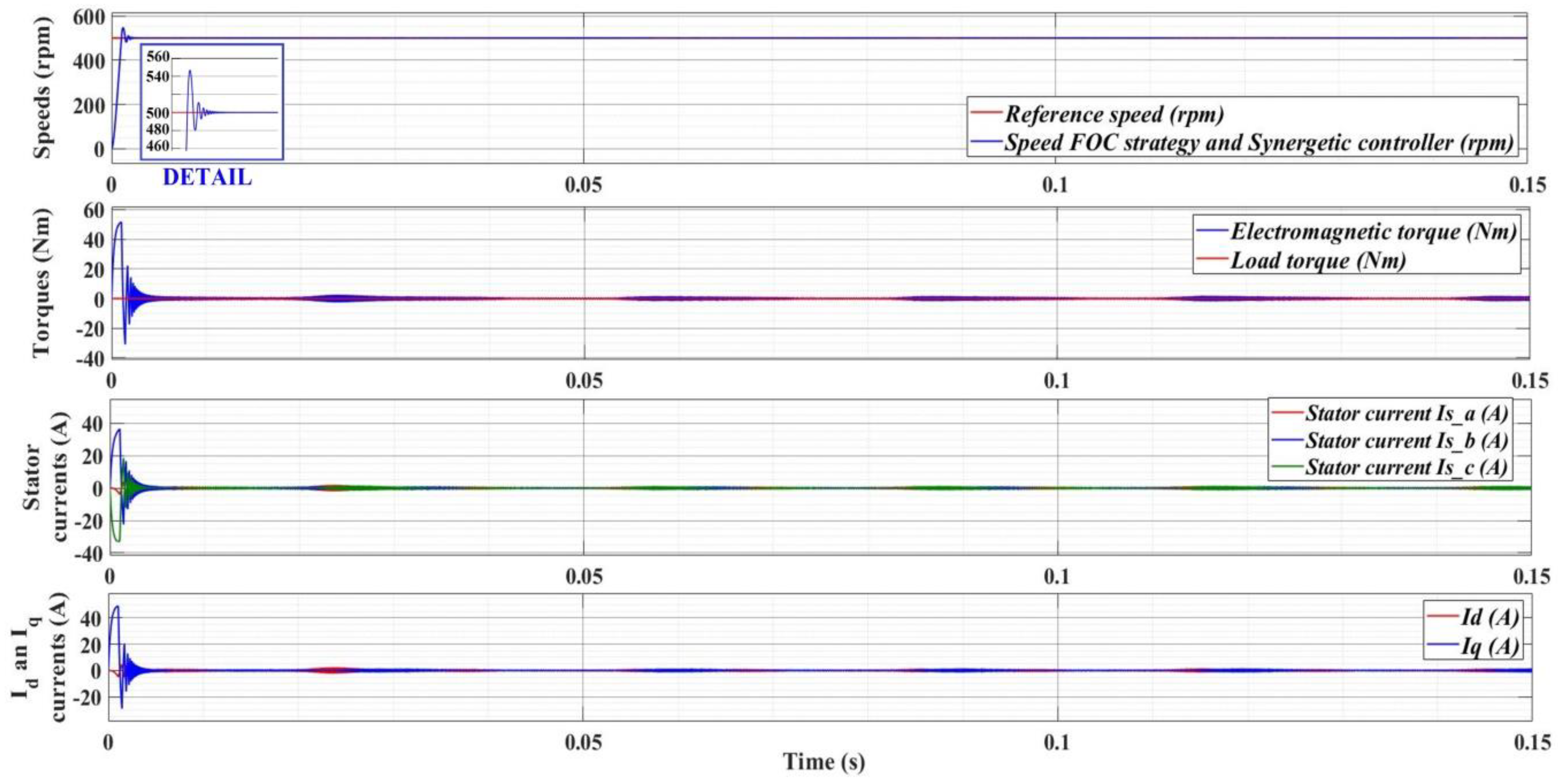
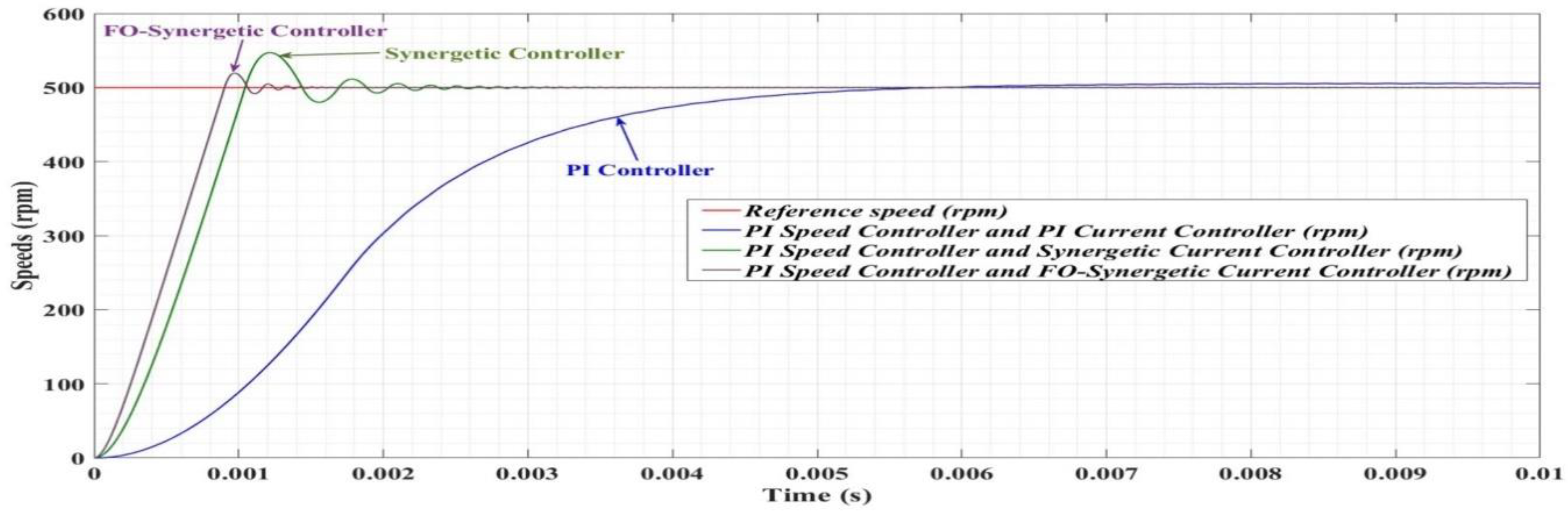
7.3. Numerical Simulations—Fractional Order Synergetic Current Controllers and PI Speed Controller for PMSM
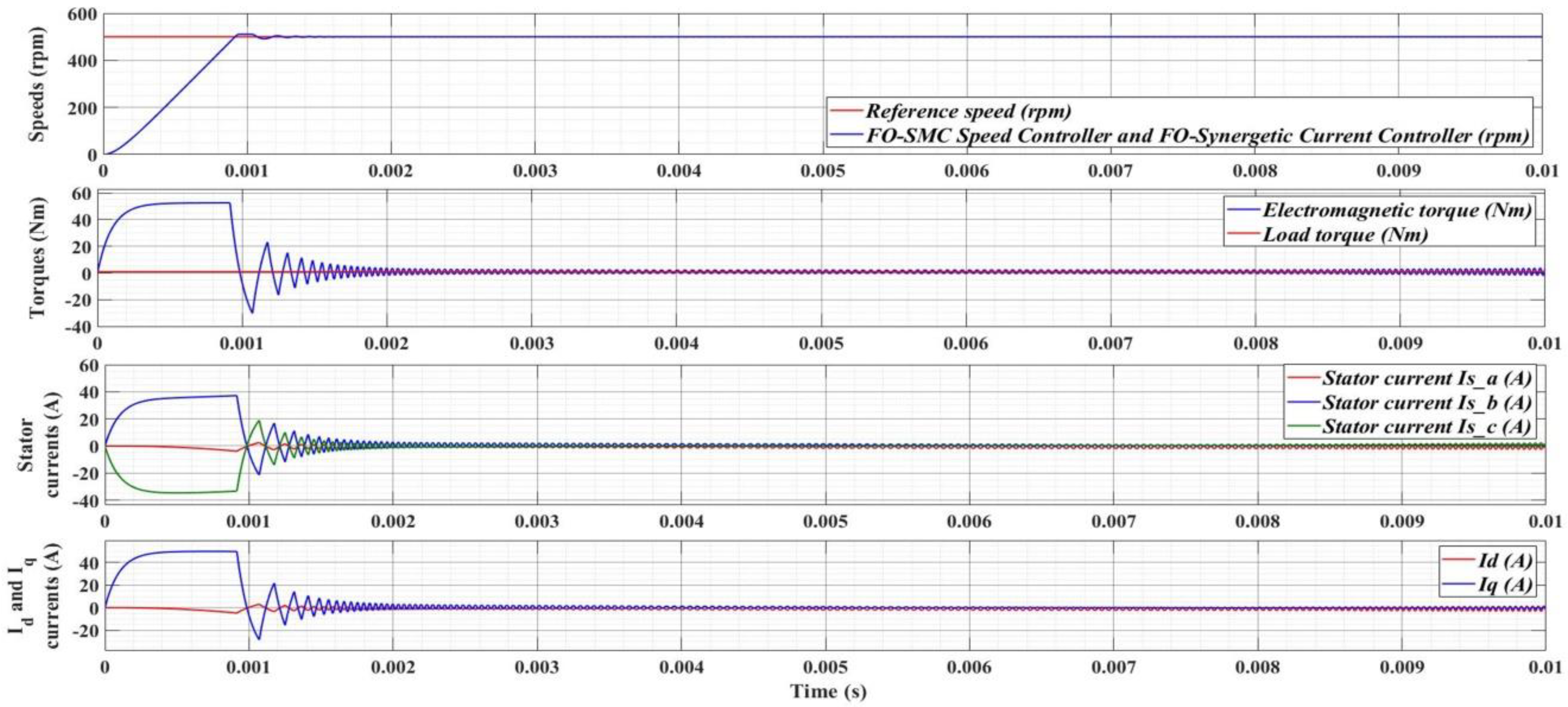
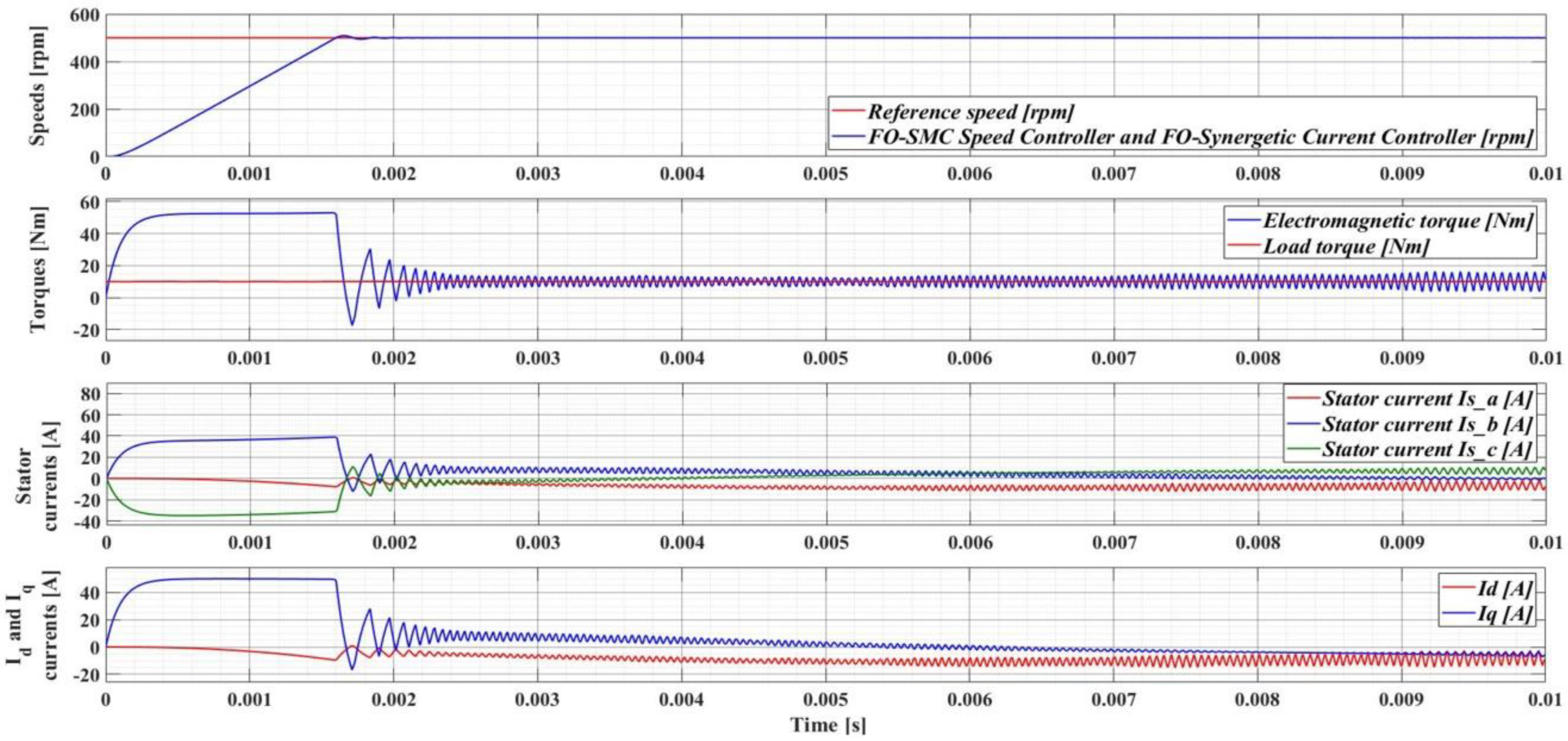
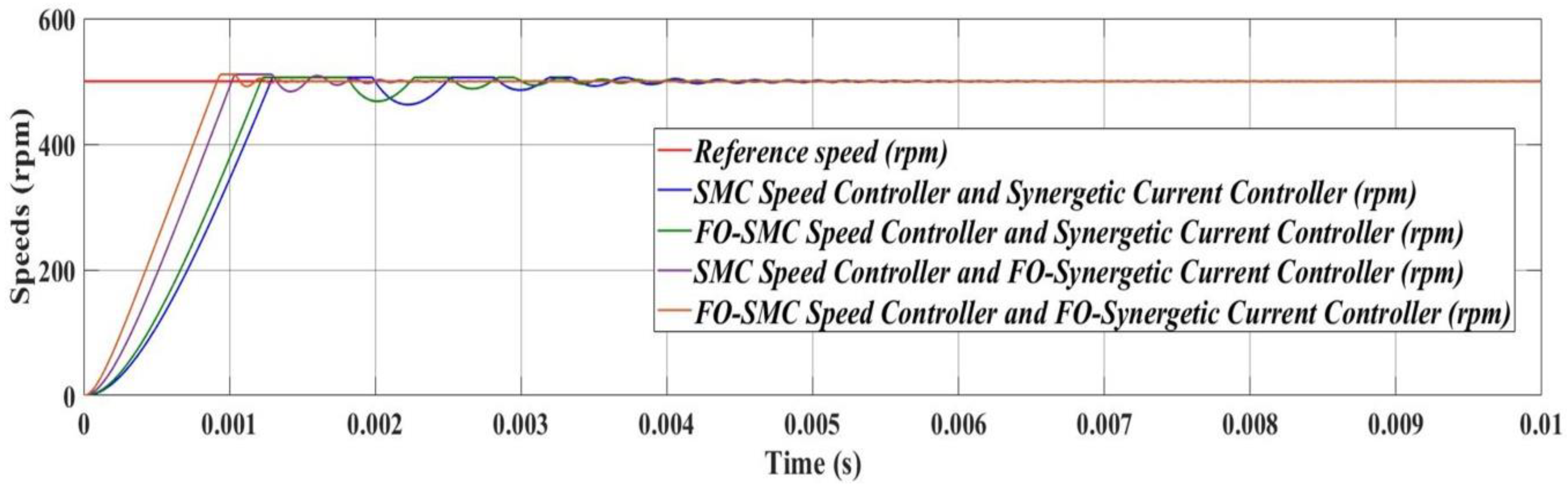
7.4. Numerical Simulations—Fractional Order Speed Controllers and Fractional Order Synergetic Current Controller for PMSM
8. Experimental Results
9. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Utkin, V.; Guldner, J.; Shi, J. Automation and Control Engineering. In Sliding Mode Control in Electromechanical Systems, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2009; pp. 223–271. [Google Scholar]
- Bose, B.K. Modern Power Electronics and AC Drives; Prentice Hall: Upper Saddle River, NJ, USA, 2002; pp. 439–534. [Google Scholar]
- Alkorta, P.; Barambones, O.; Cortajarena, J.A.; Martija, I.; Maseda, F.J. Effective Position Control for a Three-Phase Motor. Electronics 2020, 9, 241. [Google Scholar] [CrossRef]
- Yuan, T.; Wang, D. Performance Improvement for PMSM DTC System through Composite Active Vectors Modulation. Electronics 2018, 7, 263. [Google Scholar] [CrossRef]
- Wang, H.; Leng, J. Summary on development of permanent magnet synchronous motor. In Proceedings of the Chinese Control and Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 689–693. [Google Scholar]
- Bao, G.; Qi, W.; He, T. Direct Torque Control of PMSM with Modified Finite Set Model Predictive Control. Energies 2020, 13, 234. [Google Scholar] [CrossRef]
- Wu, Z.; Gu, W.; Zhu, Y.; Lu, K. Current Control Methods for an Asymmetric Six-Phase Permanent Magnet Synchronous Motor. Electronics 2020, 9, 172. [Google Scholar] [CrossRef]
- Wang, W.; Tan, F.; Wu, J.; Ge, H.; Wei, H.; Zhang, Y. Adaptive Integral Backstepping Controller for PMSM with AWPSO Parameters Optimization. Energies 2019, 12, 2596. [Google Scholar] [CrossRef]
- Wang, J. Fuzzy Adaptive Repetitive Control for Periodic Disturbance with Its Application to High Performance Permanent Magnet Synchronous Motor Speed Servo Systems. Entropy 2016, 18, 261. [Google Scholar] [CrossRef]
- Lu, S.; Tang, X.; Song, B. Adaptive PIF Control for Permanent Magnet Synchronous Motors Based on GPC. Sensors 2013, 13, 175–192. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, X.; Zhang, Q. Predictive Speed-Control Algorithm Based on a Novel Extended-State Observer for PMSM Drives. Appl. Sci. 2019, 9, 2575. [Google Scholar] [CrossRef]
- Tang, M.; Zhuang, S. On Speed Control of a Permanent Magnet Synchronous Motor with Current Predictive Compensation. Energies 2019, 12, 65. [Google Scholar] [CrossRef]
- Zhang, G.; Chen, C.; Gu, X.; Wang, Z.; Li, X. An Improved Model Predictive Torque Control for a Two-Level Inverter Fed Interior Permanent Magnet Synchronous Motor. Electronics 2019, 8, 769. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Q. Robust Current Predictive Control-Based Equivalent Input Disturbance Approach for PMSM Drive. Electronics 2019, 8, 1034. [Google Scholar] [CrossRef]
- Ma, Y.; Li, Y. Active Disturbance Compensation Based Robust Control for Speed Regulation System of Permanent Magnet Synchronous Motor. Appl. Sci. 2020, 10, 709. [Google Scholar] [CrossRef]
- Larbaoui, A.; Belabbes, B.; Meroufel, A.; Tahour, A.; Bouguenna, D. Backstepping Control with Integral Action of PMSM Integrated According to the MRAS Observer. IOSR J. Electr. Electron. Eng. 2014, 9, 59–68. [Google Scholar] [CrossRef]
- Merabet, A. Cascade Second Order Sliding Mode Control for Permanent Magnet Synchronous Motor Drive. Electronics 2019, 8, 1508. [Google Scholar] [CrossRef]
- Qian, J.; Ji, C.; Pan, N.; Wu, J. Improved Sliding Mode Control for Permanent Magnet Synchronous Motor Speed Regulation System. Appl. Sci. 2018, 8, 2491. [Google Scholar] [CrossRef]
- Bounasla, N.; Hemsas, K.E.; Mellah, H. Synergetic and sliding mode controls of a PMSM: A comparative study. J. Electr. Electron. Eng. 2015, 3, 22–26. [Google Scholar] [CrossRef]
- Bogani, T.; Lidozzi, A.; Solero, L.; Di Napoli, A. Synergetic Control of PMSM Drives for High Dynamic Applications. In Proceedings of the IEEE International Conference on Electric Machines and Drives, San Antonio, TX, USA, 15 May 2005; pp. 710–717. [Google Scholar]
- Khettab, K.; Ladaci, S.; Bensafia, Y. Fuzzy adaptive control of fractional order chaotic systems with unknown control gain sign using a fractional order Nussbaum gain. IEEE/CAA J. Autom. Sin. 2019, 6, 816–823. [Google Scholar] [CrossRef]
- Wang, M.-S.; Hsieh, M.-F.; Lin, H.-Y. Operational Improvement of Interior Permanent Magnet Synchronous Motor Using Fuzzy Field-Weakening Control. Electronics 2018, 7, 452. [Google Scholar] [CrossRef]
- Nicola, M.; Nicola, C.-I.; Duţă, M. Sensorless Control of PMSM using FOC Strategy Based on Multiple ANN and Load Torque Observer. In Proceedings of the 2020 International Conference on Development and Application Systems (DAS), Suceava, Romania, 21–23 May 2020; pp. 32–37. [Google Scholar]
- Hoai, H.-K.; Chen, S.-C.; Than, H. Realization of the Sensorless Permanent Magnet Synchronous Motor Drive Control System with an Intelligent Controller. Electronics 2020, 9, 365. [Google Scholar] [CrossRef]
- Wang, M.-S.; Tsai, T.-M. Sliding Mode and Neural Network Control of Sensorless PMSM Controlled System for Power Consumption and Performance Improvement. Energies 2017, 10, 1780. [Google Scholar] [CrossRef]
- Liu, X.; Du, J.; Liang, D. Analysis and Speed Ripple Mitigation of a Space Vector Pulse Width Modulation-Based Permanent Magnet Synchronous Motor with a Particle Swarm Optimization Algorithm. Energies 2019, 9, 923. [Google Scholar] [CrossRef]
- Zhu, Y.; Tao, B.; Xiao, M.; Yang, G.; Zhang, X.; Lu, K. Luenberger Position Observer Based on Deadbeat-Current Predictive Control for Sensorless PMSM. Electronics 2020, 9, 1325. [Google Scholar] [CrossRef]
- Nicola, M.; Nicola, C.-I.; Sacerdotianu, D. Sensorless Control of PMSM using DTC Strategy Based on PI-ILC Law and MRAS Observer. In Proceedings of the 2020 International Conference on Development and Application Systems (DAS), Suceava, Romania, 21–23 May 2020; pp. 38–43. [Google Scholar]
- Ye, M.; Shi, T.; Wang, H.; Li, X.; Xiai, C. Sensorless-MTPA Control of Permanent Magnet Synchronous Motor Based on an Adaptive Sliding Mode Observer. Energies 2019, 12, 3773. [Google Scholar] [CrossRef]
- Urbanski, K.; Janiszewski, D. Sensorless Control of the Permanent Magnet Synchronous Motor. Sensors 2019, 19, 3546. [Google Scholar] [CrossRef]
- Kamel, T.; Abdelkader, D.; Said, B.; Padmanaban, S.; Iqbal, A. Extended Kalman Filter Based Sliding Mode Control of Parallel-Connected Two Five-Phase PMSM Drive System. Electronics 2018, 7, 14. [Google Scholar] [CrossRef]
- Tepljakov, A. Fractional-Order Calculus Based Identification and Control of Linear Dynamic Systems. Master’s Thesis, Tallinn University of Technology—Department of Computer Control, Tallinn, Estonia, 2011. [Google Scholar]
- Tepljakov, A.; Petlenkov, E.; Belikov, J. FOMCON: Fractional-order modeling and control toolbox for MATLAB. In Proceedings of the 18th International Conference Mixed Design of Integrated Circuits and Systems—MIXDES, Gliwice, Poland, 16–18 June 2011; pp. 684–689. [Google Scholar]
- Mohd Zaihidee, F.; Mekhilef, S.; Mubin, M. Robust Speed Control of PMSM Using Sliding Mode Control (SMC)—A Review. Energies 2019, 12, 1669. [Google Scholar] [CrossRef]
- Wang, D.; Song, B.; Kang, C.; Xu, J. Design of Fractional Order PI Controller for Permanent Magnet Synchronous Motor. In Proceedings of the 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi’an, China, 25–27 May 2018; pp. 780–784. [Google Scholar]
- Nicola, M.; Sacerdotianu, D.; Nicola, C.-I.; Hurezeanu, A. Simulation and Implementation of Sensorless Control in Multi-Motors Electric Drives with High Dynamics. Adv. Sci. Technol. Eng. Syst. J. 2017, 2, 59–67. [Google Scholar] [CrossRef]
- Nicola, M.; Nicola, C.-I.; Vintila, A. Sensorless Control of Multi-Motors PMSM using Back-EMF Sliding Mode Observer. In Proceedings of the Electric Vehicles International Conference (EV2019), Bucharest, Romania, 3–4 October 2019; pp. 1–6. [Google Scholar]
- Nicola, M.; Velea, F. Automatic Control of a Hidropower Dam Spillway. Ann. Univ. Craiova Electr. Eng. Ser. 2010, 34, 1–4. [Google Scholar]
- Nicola, M.; Nicola, C.I.; Duţă, M. Delay Compensation in the PMSM Control by using a Smith Predictor. In Proceedings of the 2019 8th International Conference on Modern Power Systems (MPS), Cluj Napoca, Romania, 21–23 May 2019; pp. 1–6. [Google Scholar]
- Huang, G.; Luo, Y.-P.; Zhang, C.-F.; He, J.; Huang, Y.-S. Current Sensor Fault Reconstruction for PMSM Drives. Sensors 2016, 16, 178. [Google Scholar] [CrossRef]
- Biris, I.; Muresan, C.; Nascu, I.; Ionescu, C. A Survey of Recent Advances in Fractional Order Control for Time Delay Systems. IEEE Access 2019, 7, 30951–30965. [Google Scholar] [CrossRef]
- Hwang, J.-C.; Wei, H.-T. The Current Harmonics Elimination Control Strategy for Six-Leg Three-Phase Permanent Magnet Synchronous Motor Drives. IEEE Trans. Power Electron. 2015, 6, 3032–3040. [Google Scholar] [CrossRef]
- Ponce, P.; Molina, A.; Mata, O.; Ibarra, L.; MacCleery, B. Power System Fundamentals; CRC Press: Boca Raton, FL, USA, 2018; pp. 55–120. [Google Scholar]




















| Motor Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Stator resistance | Rs | 2.875 | Ω |
| d axes inductance | Ld | 0.0085 | H |
| q axes inductance | Lq | 0.0085 | H |
| Combined inertia of rotor and load | J | 0.0008 | kg·m2 |
| Combined viscous friction of rotor and load | B | 0.005 | N·m·s/rad |
| Flux induced by permanent magnets of rotor in stator phases | λ0 | 0.175 | Wb |
| Pole pairs number | np | 4 | - |
| Performance Indices | PI Speed Controller | FO-PI Speed Controller | TID Speed Controller | FO-Lead-Lag Speed Controller | FO-SMC Speed Controller |
|---|---|---|---|---|---|
| Overshoot (%) nominal J | 0 | 0 | 0 | 0 | 0 |
| Overshoot (%) double J | 0 | 0 | 0 | 0 | 0 |
| Settling time (ms) nominal J | 300 | 240 | 220 | 180 | 16 |
| Settling time (ms) double J | 450 | 300 | 280 | 220 | 40 |
| Steady state error (%) nominal J | 0.11 | 0.11 | 0.1 | 0.1 | 0.09 |
| Steady state error (%) double J | 0.12 | 0.12 | 0.11 | 0.1 | 0.09 |
| Speed ripple (rpm) nominal J | 121.78 | 81.14 | 142.24 | 112.94 | 102.81 |
| Speed ripple (rpm) double J | 289.28 | 192.35 | 216.14 | 204.91 | 131.15 |
| Torque ripple (Nm) nominal J | 13.68 | 17.16 | 10.08 | 9.23 | 18.91 |
| Torque ripple (Nm) double J | 11.8 | 15.45 | 12.91 | 12.1 | 16.01 |
| Performance Indices | PI Current Controller | Synergetic Current Controller | FO-Synergetic Current Controller |
|---|---|---|---|
| Overshoot (%) nominal J | 0 | 8 | 2 |
| Overshoot (%) double J | 0 | 14 | 3.5 |
| Settling time (ms) nominal J | 6 | 1.2 | 1 |
| Settling time (ms) double J | 11 | 1.8 | 1.6 |
| Steady state error (%) nominal J | 0.1 | 0.08 | 0.07 |
| Steady state error (%) double J | 0.1 | 0.08 | 0.07 |
| Speed ripple (rpm) nominal J | 182.16 | 112.91 | 102.45 |
| Speed ripple (rpm) double J | 214.91 | 129.54 | 107.63 |
| Torque ripple (Nm) nominal J | 15.21 | 17.95 | 15.82 |
| Torque ripple (Nm) double J | 19.44 | 21.02 | 18.73 |
| Performance Indices | SMC Speed Controller and Synergetic Currents Controller | FO-SMC Speed Controller and Synergetic Currents Controller | SMC Speed Controller and FO-Synergetic Currents Controller | FO-SMC Speed Controller and FO-Synergetic Currents Controller |
|---|---|---|---|---|
| Overshoot (%) nominal J | 1.15 | 1.15 | 1.18 | 1.15 |
| Overshoot (%) double J | 1.18 | 1.9 | 1.8 | 1.2 |
| Settling time (ms) nominal J | 1.4 | 1.3 | 1 | 0.92 |
| Settling time (ms) double J | 1.5 | 1.7 | 1.22 | 1.8 |
| Steady state error (%) nominal J | 0.07 | 0.07 | 0.06 | 0.06 |
| Steady state error (%) double J | 0.08 | 0.07 | 0.06 | 0.06 |
| Speed ripple (rpm) nominal J | 123.03 | 118.73 | 104.50 | 95.34 |
| Speed ripple (rpm) double J | 149.25 | 148.16 | 120.85 | 83.09 |
| Torque ripple (Nm) nominal J | 14.92 | 14.74 | 126.29 | 14.71 |
| Torque ripple (Nm) double J | 20.96 | 20.82 | 112.13 | 14.33 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nicola, M.; Nicola, C.-I. Sensorless Fractional Order Control of PMSM Based on Synergetic and Sliding Mode Controllers. Electronics 2020, 9, 1494. https://doi.org/10.3390/electronics9091494
Nicola M, Nicola C-I. Sensorless Fractional Order Control of PMSM Based on Synergetic and Sliding Mode Controllers. Electronics. 2020; 9(9):1494. https://doi.org/10.3390/electronics9091494
Chicago/Turabian StyleNicola, Marcel, and Claudiu-Ionel Nicola. 2020. "Sensorless Fractional Order Control of PMSM Based on Synergetic and Sliding Mode Controllers" Electronics 9, no. 9: 1494. https://doi.org/10.3390/electronics9091494
APA StyleNicola, M., & Nicola, C.-I. (2020). Sensorless Fractional Order Control of PMSM Based on Synergetic and Sliding Mode Controllers. Electronics, 9(9), 1494. https://doi.org/10.3390/electronics9091494






