1. Introduction
Since the concept of a multiple-input multiple-output (MIMO) radar [
1] was proposed in 2004, it has attracted large amounts of attention of researchers. As in MIMO communication systems, multiple transmitting antennas and multiple receiving antennas are arranged in an MIMO array system to improve the accuracy of angular measurement [
2,
3]. Benefitting from the equivalent virtual array principle [
4], an MIMO radar has the ability to identify more targets and to get a higher azimuth resolution than traditional phased array radars. Because that the frequency-modulated continuous wave (FMCW) signals have the ranging ability and low power consumption [
5], they are widely used in MIMO radar systems. As a method that is relatively easier to implement than frequency division multiplexing structure [
6], the time division multiplexing (TDM) structure [
7] is widely used in MIMO radar systems. This structure realizes the orthogonality of the waveform by switching the transmitting and receiving channels at different times.
With a large number of theoretical results [
8,
9,
10] in MIMO radars, some MIMO radar systems [
11,
12,
13,
14,
15] have been implemented for the experimental verification of related technologies. In reference [
11], a through-wall MIMO imaging radar system that generated the real-time imaging of a target at a frame rate of 0.5 Hz and that operated at a stand-off range of 6 m or more was proposed. The 44 virtual antennas with half-wavelength element-to-element spacing in uniform linear array (ULA) were formed by using a time division multiplexing technique with eight real receive elements and 13 transmit elements that could produce 2D (range vs. cross-range) image. A demonstration of an MIMO over-the-horizon radar was presented in [
12]. This system created the beamforming of the transmitter signal on a multi-element array and used a trans-horizon radar receiver to receive the target echo. After using space-time signal processing, the results showed that the ability of the MIMO radar to suppress spatial clutter was improved by 35 dB, a result that verified the superior performance of the MIMO system. These radars are relatively large and have high power consumption. On the other hand, some small MIMO radars have been designed [
6,
13,
14]. In [
6], a prototype automotive radar system was able to simultaneously generate multiple transmit beams. The system was based on a four-channel 77 GHz FMCW radar sensor, and the measured beam pattern of multiple, simultaneously generated beams were in good accordance with simulations. Similarly, a 77 GHz FMCW MIMO radar was implemented for 2D target localization by using an SiGe single-chip transceiver in [
13]. Radar measurements were performed by using the digital-beamforming method with a 10 GHz modulation bandwidth to show the applicability of a highly miniaturized two-channel radar in [
14]. However, the monolithic microwave-integrated circuits (MMIC) MIMO radar is limited in size and can only obtain fewer virtual array elements.
In terms of MIMO radar positioning algorithms, most practical radars use conventional beamforming (CBF) to estimate the distance and angle of targets. This approach is easy to implement, but its resolution is limited by the Rayleigh criterion [
15], and the bandwidth [
16] of the radar system is not satisfactory. In reference [
17], a 2D multiple signal classification (MUSIC) algorithm for the joint estimation of the angle and distance was presented. The algorithm was analyzed with respect to its application to coherent MIMO arrays, and it was able to achieve a good performance on the experimental data scenarios. However, there are many estimation algorithms [
18,
19,
20,
21,
22,
23,
24] with excellent performances that are only based on the simulation data, and there is no experimental system to verify them. For example, a signal model of a monostatic MIMO sparse frequency FMCW radar was established in [
21], and a modified 2D iterative adaptive approach (IAA) algorithm for range-azimuth processing was presented and verified with simulated data. A sparse spectrum fitting (SpSF) algorithm for the estimation of direction of arrivals (DOAs) of multiple sources was introduced in [
23], and the method of signal power estimation was proposed in [
24]. Simulation examples were presented to illustrate several performance characteristics of the technique in the context of low signal-to-noise ratios (SNRs) and small snapshots.
In order to achieve a feasible MIMO radar system for performing the range and angular estimation algorithm, the contribution of this paper can be summarized as follows:
A small engineering FMCW MIMO radar system is implemented with four transmitter and four receiver antennas by using the time division multiplexing (TDM) technique.
Based on experiment and real data, a sparse spectrum fitting (SpSF) algorithm is designed for estimating the distance and angle of a target via the use of the the sparsity of signals, which verify not only the effectiveness of the designed MIMO radar system but also the superior performance of the algorithm.
The paper is organized as follows:
Section 2 describes the signal model of the FMCW MIMO radar, the implemented FMCW MIMO radar system is described in
Section 3, the SpSF algorithm is described in
Section 4, the simulation and experimental results are presented in
Section 5; and
Section 6 draws the conclusions.
2. FMCW MIMO Signal Model
When the FMCW signal is used for the transmission signal of a radar system, its expression for a sweep period can be written as:
where
and
represent the amplitude and the start frequency of the chirp sweeping, respectively;
, where
denotes the transmitted bandwidth and
is the sweep duration; and
is the initial phase of the signal.
In the case of ignoring the addition of noise while assuming that a far-field target scatters the signal, the echo signal received by the receiving elements is expressed as:
where
is the sum of the receiving element gains and the propagation loss of the signal, and
is the time delay of the signal scattering from the transmitting element to the target and then back to the receiving element, which contains the range and angle information of the target.
Under the assumption of a narrowband far-field signal source, there is an approximate relationship such that:
Then, the received echo is mixed with the transmitting signal like
, and it can be filtered out of the high frequency component; then, the intermediate frequency (IF) signal can be obtained and expressed as:
where
is the amplitude of the IF signal. According to the definition of
, it has the following relationship
. Then, there is an approximate relationship, which is shown as:
Then, the IF signal is discretely sampled, and the sampling frequency is assumed to be
. The sampled discrete signal can be expressed as:
where
is the sampling time and
is the total number of sampling points.
In an MIMO radar system model, it is assumed that there are
far-field targets and
equivalent receiving array elements, and these array elements are generally arranged into a uniform linear array with equal intervals. Assuming that the gain of each array element is the same, the echo signal received by the
array element (after mixing and sampling) can be expressed as:
where
is the discrete noise and
is the sum of
target echoes.
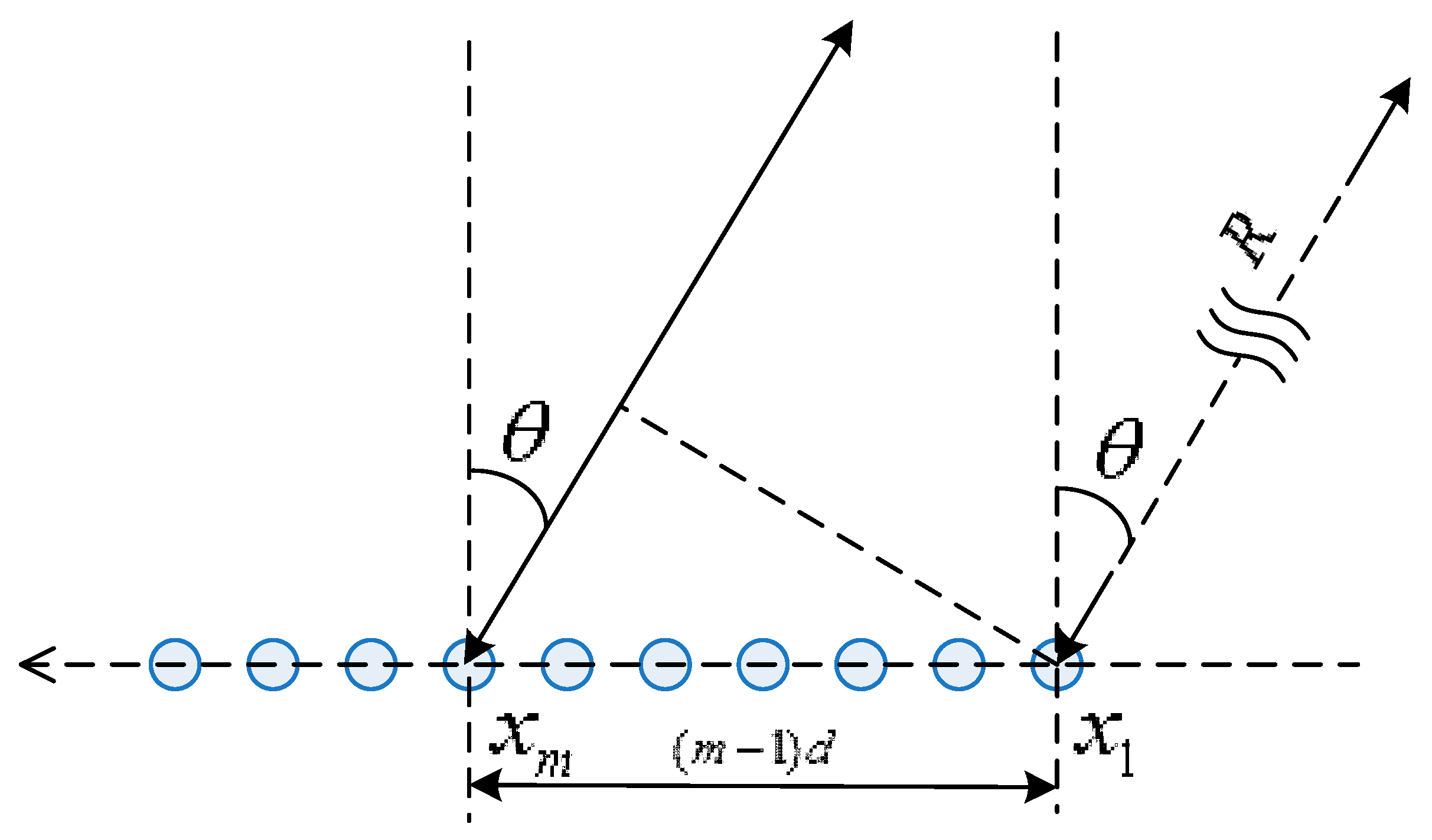
Then, the definition of
is discussed. By assuming that the first element on the right of the equivalent virtual array in the MIMO system is the reference element, denoted by
and the distance between adjacent elements is
, then, the position of the
elements relative to the reference element is
, which is shown in
Figure 1. Then, the two-way delay
from the
element to the target can be expressed as:
where
is the range from target to reference element and
is the angle of arrival relative to normal.
By combining Equations (7) and (8), the IF signal can be expressed as:
After performing the signal Hilbert transform on the
IF signal, an analytic signal matrix can be obtained as:
It can be rewritten as:
where
is the received signal matrix,
is the noise matrix,
is the signal matrix containing the position information of targets, matrix
contains the angle information of the target, and matrix
contains the distance information.
3. MIMO Radar System Implementation
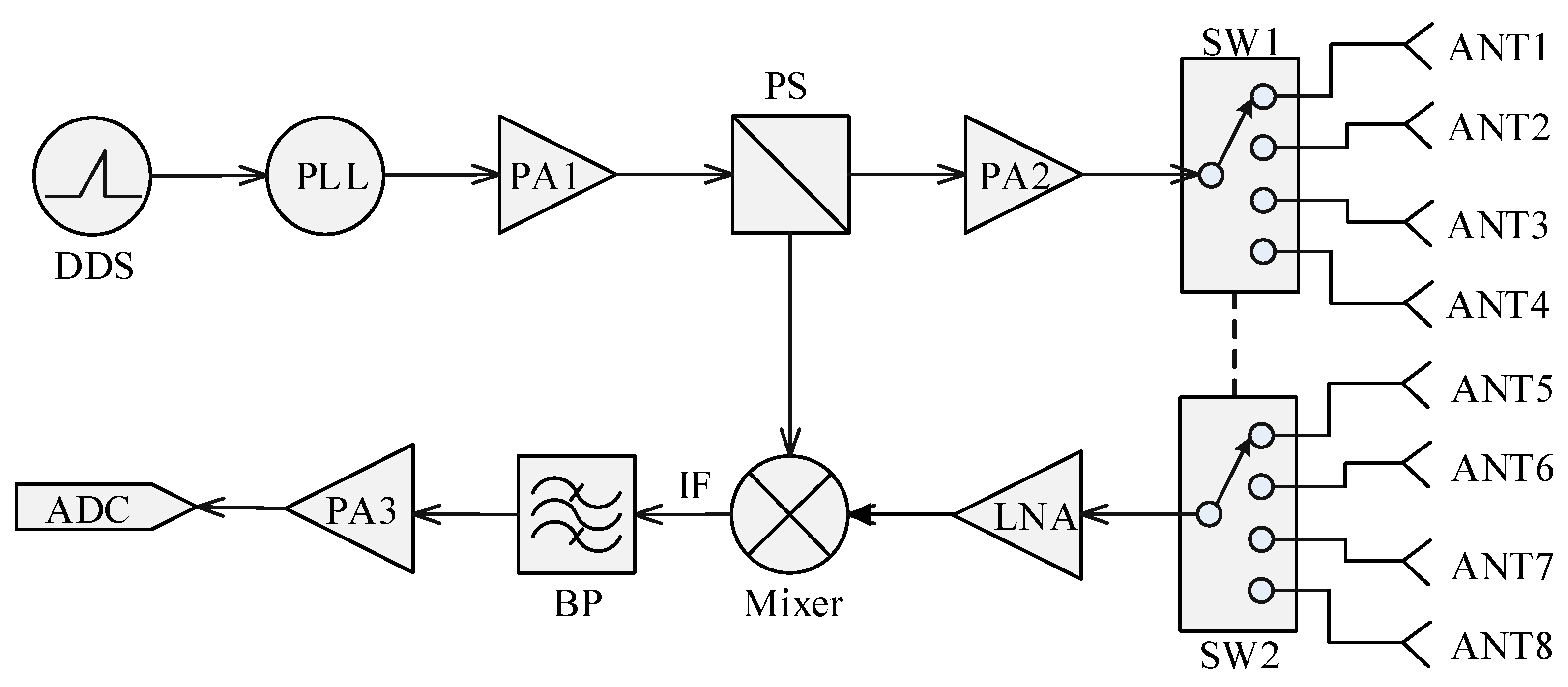
For this paper, a small FMCW MIMO radar system working in the S-band was implemented. The block diagram is shown in
Figure 2.
Table 1 shows the main parameters of the proposed MIMO radar system. This radar system can be divided into four parts: the signal generator, the RF front-end, the antenna array, and the IF signal preprocessing circuit. A detailed description of the system block diagram follows.
3.1. FMCW Signal Generator
As the core of this system, a hybrid direct digital synthesizer (DDS) and phase locked loop (PLL) structure was applied to generate the required FMCW signal [
25,
26]. Compared with the traditional mixing method, this method does not produce the image frequencies, so it can generate high quality FMCW signals. Accordingly, no additional filter was required at the signal generator. This specific method uses a DDS with digital-to-analog converter (DAC) function to generate an analog signal whose frequency changes linearly with time, whose phase is controllable, and whose amplitude is adjustable. The start frequency of the chirp signal is 49.2 MHz. The bandwidth is 1.6 MHz, and the sweep time of one chirp is 20.6 ms. Then, the chirp signal that is generated by the DDS is sent to the PLL. The PLL chip that was used in this system has excellent performance characteristics, such as a high phase detection frequency, short frequency lock time, and extremely low phase noise. Thus, the frequency of the DDS output could be multiplied by 50 times to 2.46–2.54 GHz, and the bandwidth becomes 80 MHz, which is also the frequency and bandwidth of the transmitted signal.
3.2. The RF Front End
The signal from the PLL passes through a power amplifier (PA1) to increase the gain from the original −4 to 12 dBm. Thereafter, the signal is passed through a power splitter (PS), where it can be split into two paths: One is amplified and sent to the transmitter, and the other is entered into the mixer as a local oscillator signal. The transmitting signal passes through an adjustable power amplifier (PA2), and the gain parameter is set according to the transmission power requirement. On the other side, the reflected signal from the receiving antenna is mixed with the local oscillator signal after passing through a low noise amplifier (LNA) by the mixer (Mixer). The noise figure of PA1 and LNA is 0.8 dB. In order to reduce the instability of the system, some RF front end components (PA1, PS, LNA and Mixer) are integrated modules that are produced by Mini-Circuits.
The orthogonal transmission waveform of the MIMO radar is achieved by a RF coaxial switch (SW1). This switch turns on the transmitting signal to the four transmitting antennas at different times, and the receiving antennas achieve the echo signals in this way by another RF coaxial switch (SW2). In each time period, only one transmitting antenna and one receiving antenna can be connected, so that 16 transmit–receive channels can be formed in one complete cycle. This TDM technique is a relatively simple and general method for implementing an MIMO radar that can greatly reduce the complexity of system design.
Figure 3 shows the RF front end.
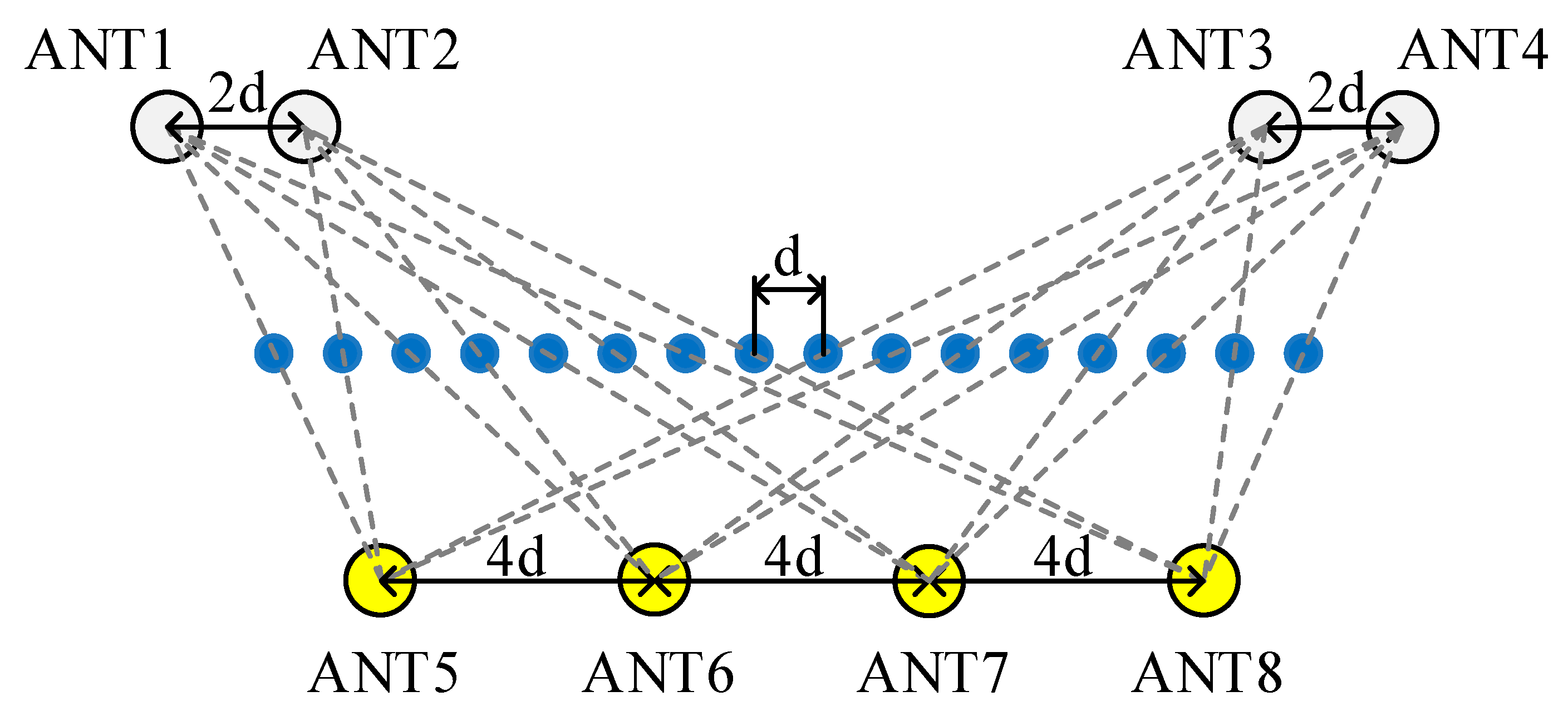
3.3. The MIMO Antenna Array
The independent transmitting and receiving antenna elements are used to minimize transmit-to-receive coupling in the MIMO radar system, the schematic of which is shown in
Figure 4. The transmitting antenna array on the top row of the diagram is composed of four antennas with unequal spacing (ANT1-4). The receiving antennas are on the bottom row and are composed of four elements with equal spacing (ANT5-8). At any moment, the transmitter and receiver are routed to only one antenna pair. Each pair of transmitting and receiving elements can be independently equivalent to a monostatic element. This equivalent element is marked as the midpoint of the transmit–receive element connection. In this way, 16 effective virtual elements can be obtained and shown in the middle row. The antenna that was used in the system is a flat directional antenna with 4 dipoles that can provide a high RF gain, shown in
Figure 5.
3.4. IF Signal Preprocessing Circuit
After using the RF switch (SW2) and LNA, the echo signal is mixed with the local oscillator signal to obtain the IF signal. The IF signal needs to be filtered and amplified before discrete sampling. This specific operation was used to design a band-pass filter with an adjustable cut-off frequency. The cut-off frequency of the band-pass filter chip can be changed in order to adjust the input drive frequency so that only the target echo within the desired observation range is passed. The drive frequency of the adjustable filter is provided by an FPGA control board, shown in
Figure 6. After the filter, an adjustable gain amplifier (PA3) is used to accommodate the high dynamic range of the radar cross section (RCS). The desired gain amplification can be achieved by adjusting a resistance on the circuit board [
27].
Due to the small sweep slope of the transmitted signal, an analog-to-digital converter (ADC) chip with a low sampling rate was selected to sample the IF signal. For example, if the detected maximum target distance is 500 m, the IF signal frequency that is obtained after mixing is 13000 Hz. Considering the maximum detection range, the actual sampling frequency was set as 40 kHz.
The MIMO radar prototype is shown in
Figure 7. A complete scan cycle of a radar contains 16 chirps. The time of each chirp is 20.6 ms. During this time, only one set of transmitter–receiving antennas is locked by the switch. When a chirp is over, the switch immediately switches to the next transmit–receive channel. When counting the switching time, a complete scan cycle is about 0.6 s.
4. Sparse spectrum fitting Description
The basic principle of sparse recovery for angle estimation is that the angles of the incident signals have sparsity in the whole space domain. For a ULA, the space domain for angle estimation is [−90 degrees, 90 degrees]. If the appropriate step size is set and the mesh is divided, an over-complete set of angles will be obtained. In this way, the angle estimation problem of the incident signal is transformed into a problem of selecting K atoms from the angle set and optimizing the corresponding signal amplitude. Similarly, this method also suitable for ranging.
4.1. Sparse Spectrum Fitting for Angle Estimation
The covariance of the received data is defined as:
where
is the covariance matrix of the signal,
is the variance of the noise, and
is the identity matrix. Considering the actual received data matrix with finite snapshots, the maximum likelihood estimation of the covariance matrix is:
Assuming the targets are uncorrelated, there is a vectorized covariance matrix:
where
is the number of grids divided by the angle of the expected estimate, and:
When the number of snapshots is large enough, there is a convex optimization, which has the following form:
where
is the optimal vector and
is the regularization parameter, which can be determined by the chi-square distribution and noise power. When the number of snapshots tends to infinity,
tends to
.
4.2. Sparse Spectrum Fitting for Range Estimation
It can be seen from Equation (10) that vector contains the distance information of the target, so one must use the SpSF method to estimate the distance required for the space sequence matrix as the body of the signal.
In Equation (11), the transpose of the received signal matrix is shown as:
Its covariance is:
The maximum likelihood estimate of the covariance matrix is:
Then, the desired range of the estimated distance is set to a suitable step size and meshed, and an ultra-complete range set is obtained. The estimation method is similar to that of angle estimation and is thus not repeated here.
5. Simulated and Experimental Results
For this section, the SpSF algorithm was used to test the simulation data and real data achieved by the designed FMCW MIMO radar, and the performance of the algorithm is compared with the MUSIC algorithm and the Capon algorithm.
5.1. Simulated Results
In order to more intuitively compare the algorithm performance, the MIMO radar parameters in the simulation were the same as those introduced in
Section 3. With a sampling frequency of 40 kHz, 824 discrete data could be sampled in a chirp duration. Suppose that are there are three targets in the scenario. The specific parameters are shown in the
Table 2 below. Gaussian white noise was added to the simulation data.
Firstly, the angle of the target was estimated, and the results are shown in
Figure 8:
Figure 8a,c are the estimated angles of targets when using all the sampling points (824 points) of a chirp cycle, while
Figure 8b,d are estimated angles of the targets when using the first 100 sampling points of a chirp cycle. The SNR of
Figure 8a,b is 0 dB, and that of
Figure 8c,d is −10 dB.
Compared with the Capon and MUSIC algorithms, it can be seen that in the case of a high SNR and large snapshots, these three algorithms could accurately estimate the angles of the three targets. However, with the decrease of the SNR, the performance of the Capon and MUSIC algorithms declined under different conditions. Especially in the case of a small number of snapshots, the performance significantly deteriorated and the angles of different targets could be hardly distinguished. However, the SpSF algorithm had an excellent estimation performance, even in the case of a low SNR and small snapshots.
Next, the distance of the targets based on simulated data was estimated. Since the estimation of distance is obtained by transposing a received matrix, when the number of snapshots is too large, the calculation amount explodes, which is not desirable to practical application. Thus, simulated data with 100 snapshots were used to estimate the distance.
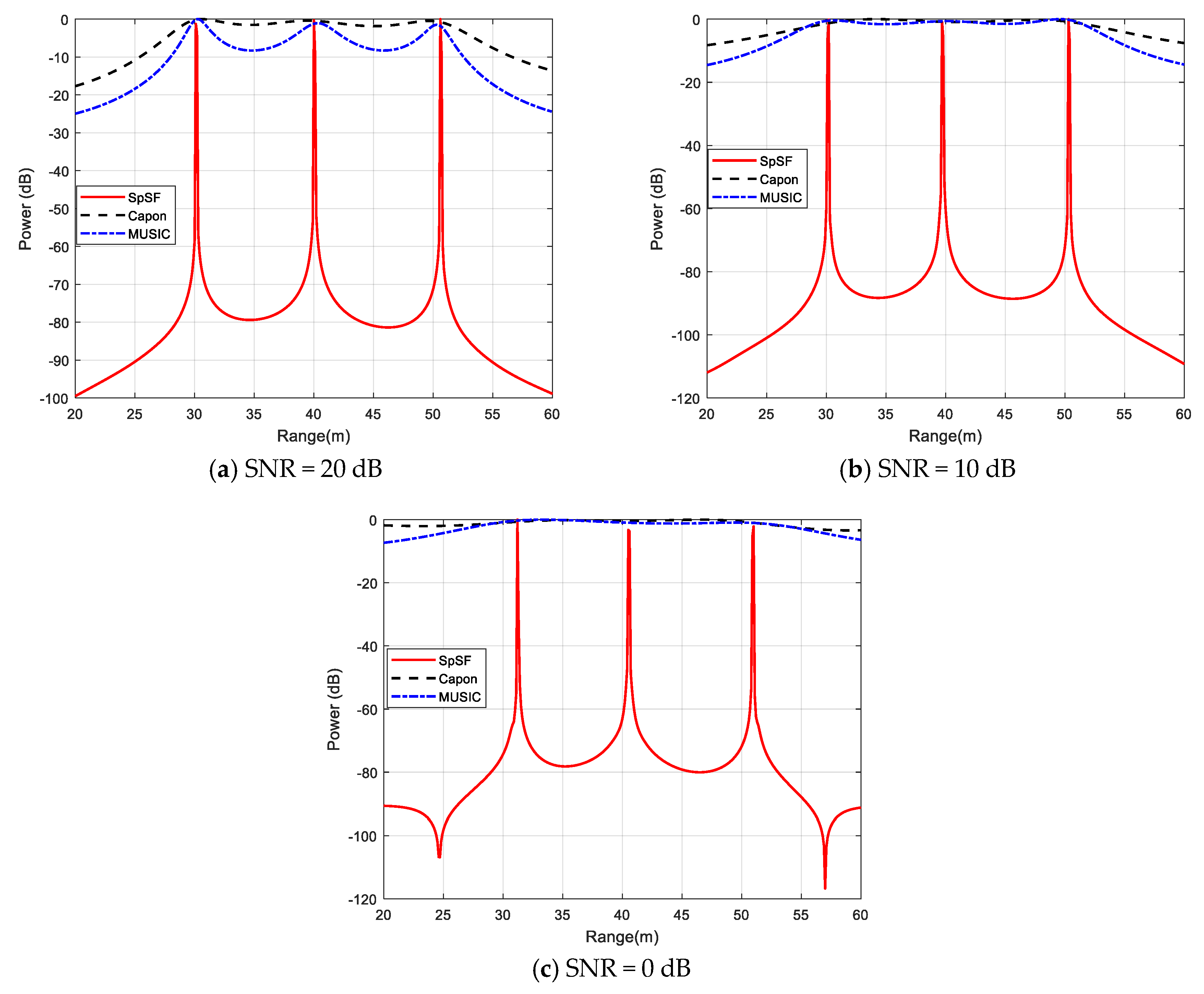
Figure 9 shows the estimated results when the SNR was 20, 10, and 0 dB, respectively.
It can be seen from the simulation results that when the number of snapshots was constant, the estimation performance of the Capon and MUSIC algorithms significantly deteriorated with the decrease of the SNR. When the SNR was 0 dB, the MUSIC and Capon algorithms could no longer distinguish the distance of the targets, while the SpSF algorithm still maintained an excellent estimation performance.
5.2. Field Experimental Results
The experimental data were obtained by the FMCW MIMO radar system that was introduced in
Section 3. The experimental site was an empty field with three highlight metal reflectors whose location is shown in
Figure 10. The distance from the target to the antennas was measured by using a tape, and the angle was calculated by triangle conversion. The specific parameters are shown in
Table 3 below.
In the experiment, the maximum angle of the target relative to the center of the antenna array was 12.4 degrees, so the estimated range was selected as [−20 degrees, 20 degrees], and the step size was set to 0.1 degrees. For the distance, the distance between the target and the antenna should not exceed 50 m. Thus, the estimated range was chosen to be [20 m, 60 m], and the step size was set to 0.1 m. The echo signals outside the desired detection range were filtered out by the IF preprocessing circuit in the radar system before ADC sampling so that the reflected interference of distant buildings and trees was avoided.
Figure 11 shows the angle estimation results of the received data when the number of snapshots was 824 and 100. All three algorithms could estimate the angle of targets well in the case of large snapshots. Through the detailed comparison of the spectral peaks that were estimated by the three algorithms, the error could be seen as being within 0.1 degrees. In the case of the small snapshots, the performance of the three methods decreased to different degrees, among which the comparison method could not normally distinguish the angles of the three targets, while the SpSF algorithm could estimate the angles and have good performance.
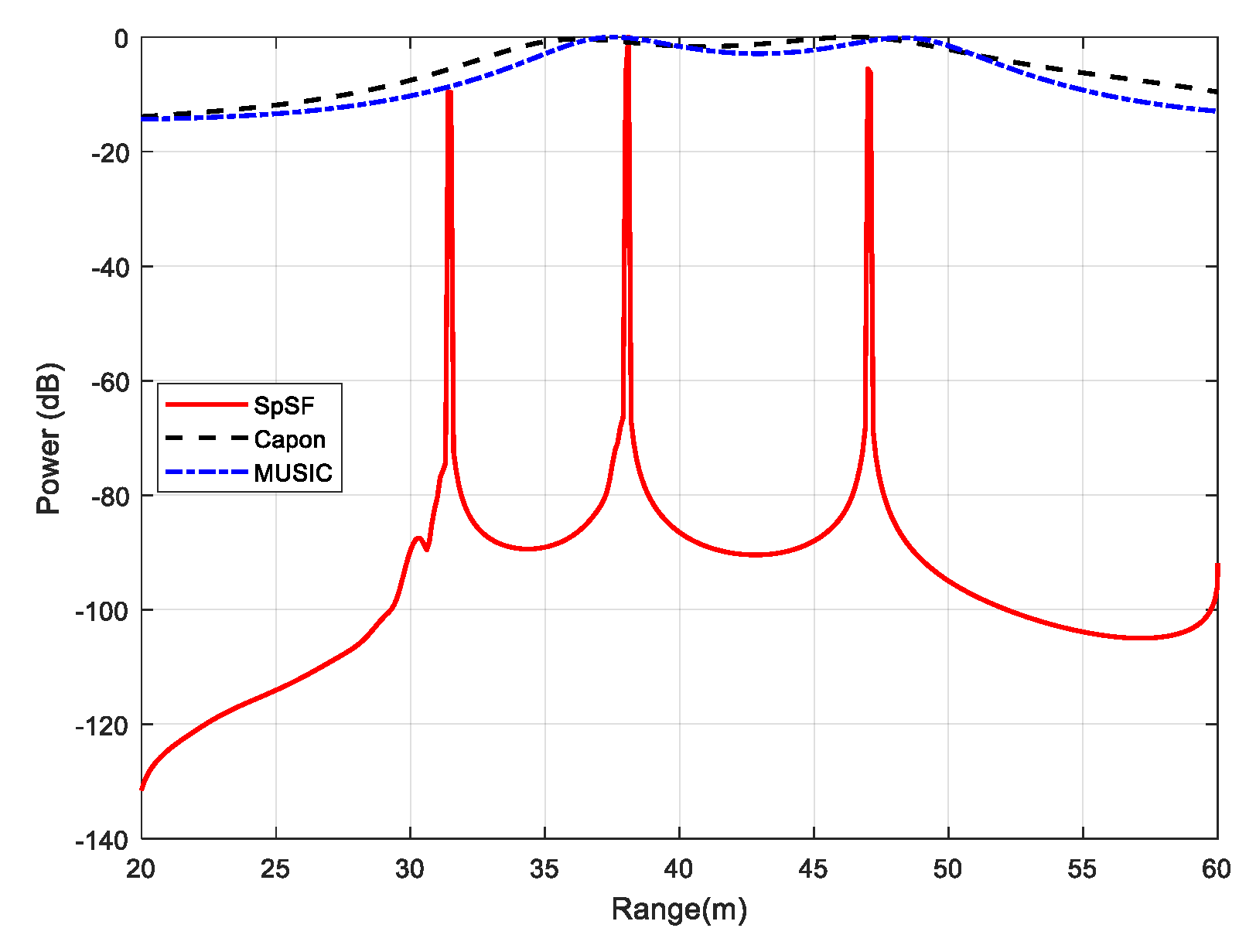
One hundred snapshots were selected to estimate the distance of the target. As can be seen from the results in
Figure 12, in the case of the MUSIC and Capon algorithms, only two slightly larger spectral peaks could be seen, which indicates that they failed to work. However, the SpSF algorithm could accurately estimate the three target distances with an error range of 0.5 m.
The experimental scenario that was used to perform the experimental results of the two targets is shown in
Figure 13, and the experimental results are shown in
Figure 14.
The distance and the angle of target1 (T1) were 34.4 m and 0.3 degrees, respectively; the distance and the angle of target2 (T2) were 41.8 m and −7.9 degrees, respectively. It can be seen from the experimental results that the SpSF algorithm had a superior performance, whether for the angle estimation or distance estimation of the targets, as shown in
Figure 14.