Simple Setup for Measuring the Response to Differential Mode Noise of Common Mode Chokes
Abstract
1. Introduction
2. Analysis
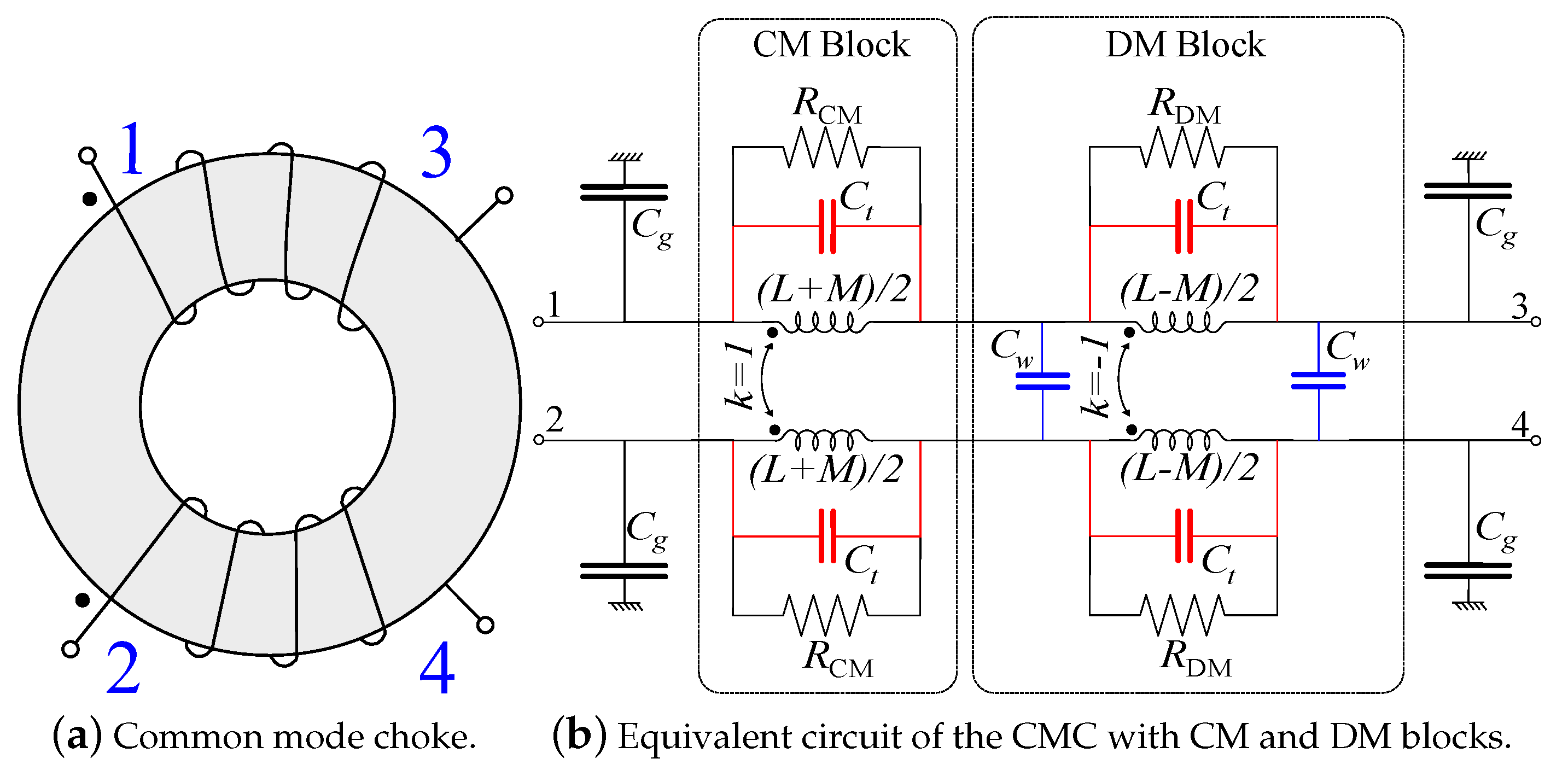
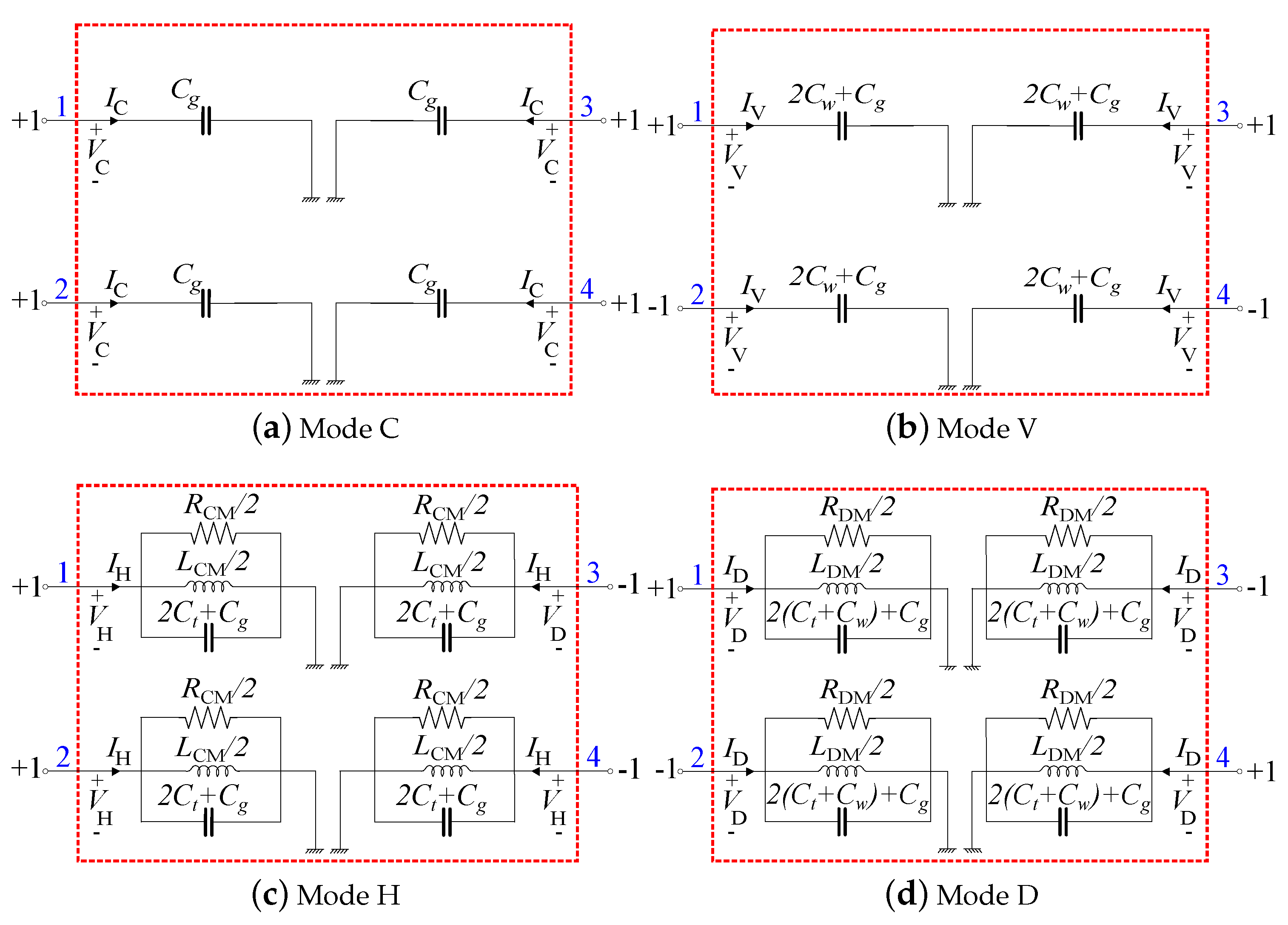
2.1. Modal Analysis of the CMC
2.2. Effect of Electric Coupling to Metallic Surfaces
2.3. Effect of Magnetic Coupling to Metallic Surfaces
3. Results
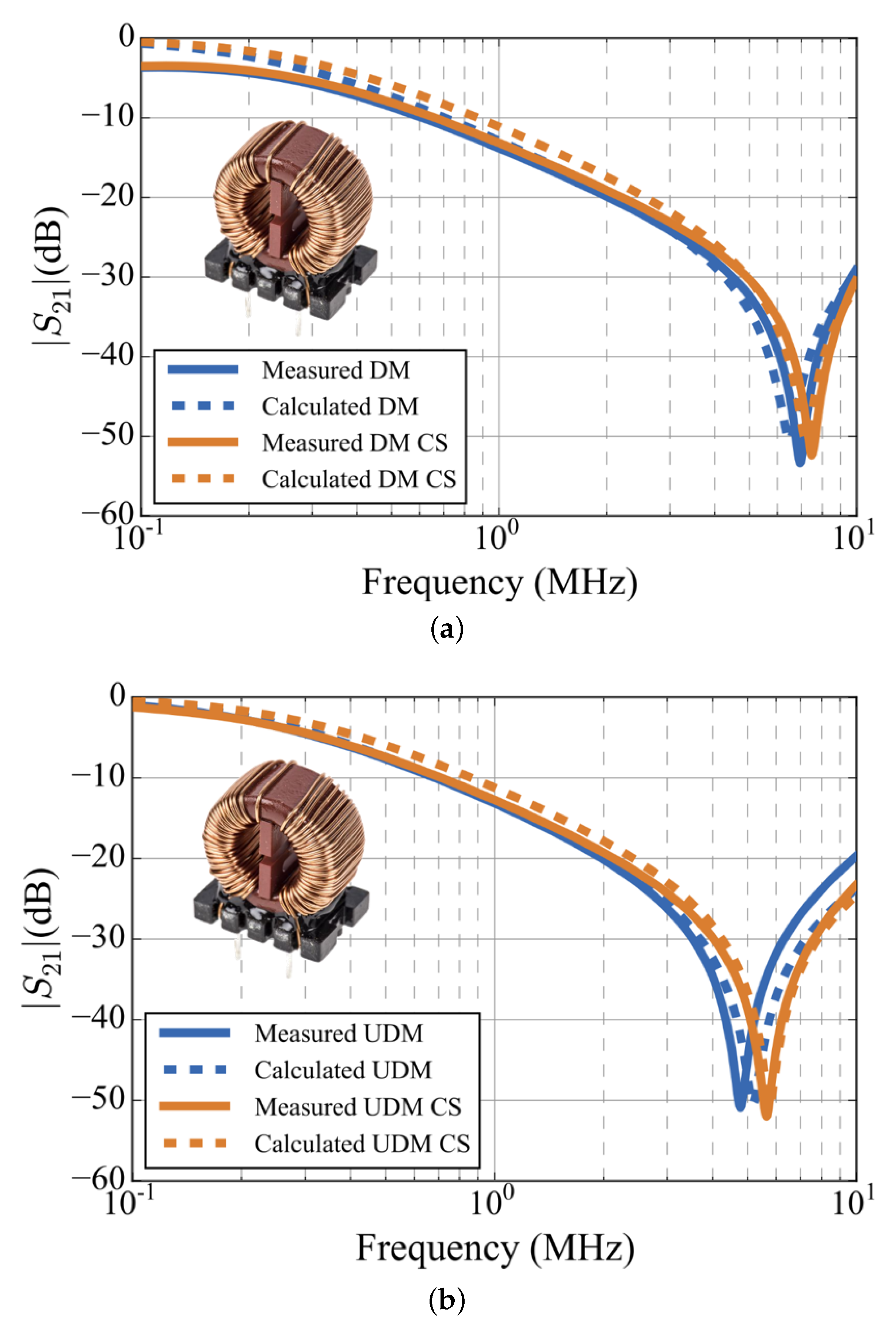
3.1. Analysis of the Response of a Standalone CMC
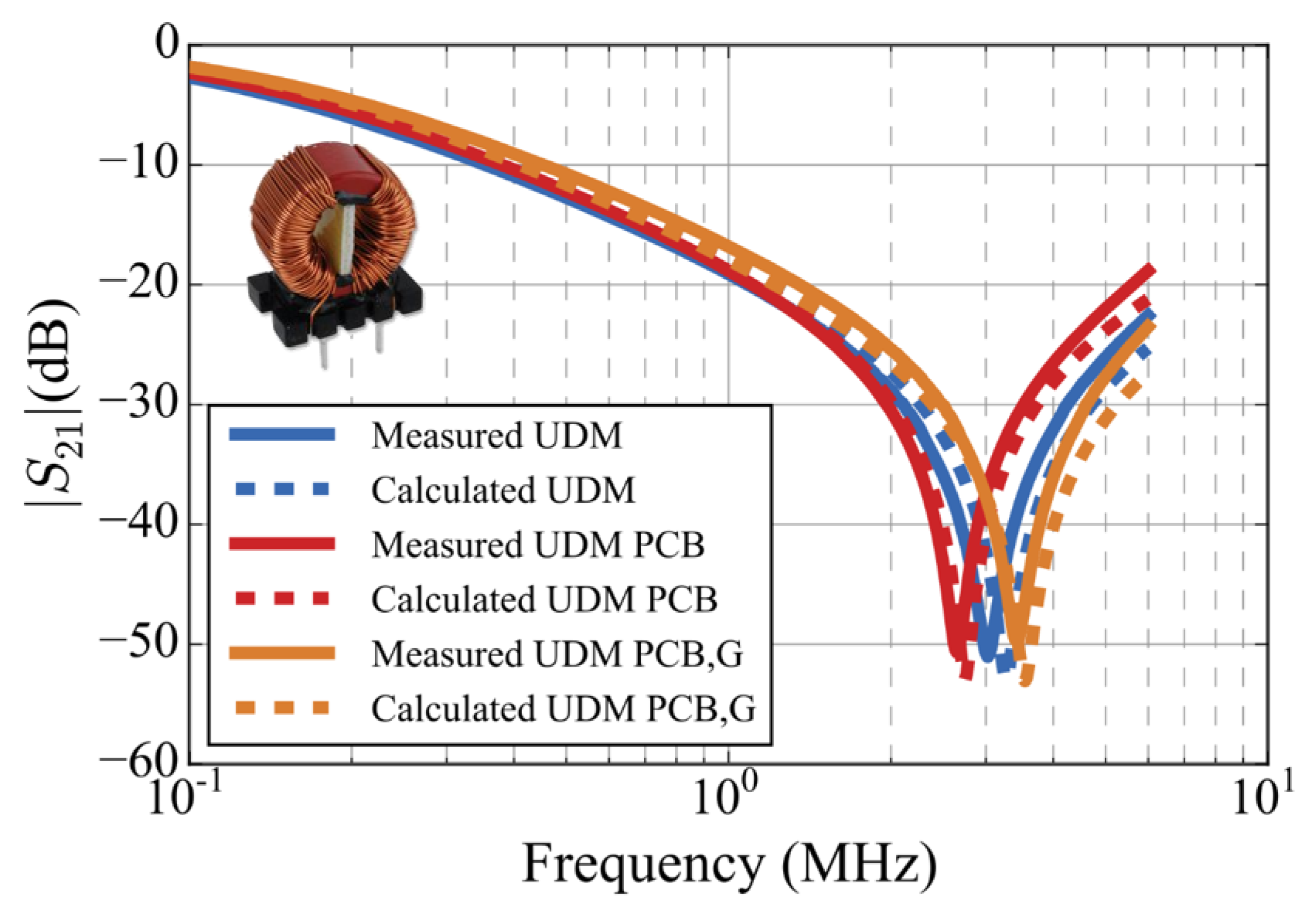
3.2. Effect of Capacitive Couplings in a PCB
3.3. Effect of Magnetic Coupling to Nearby Conducting Surfaces
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kovacevic, I.F.; Friedli, T.; Muesing, A.M.; Kolar, J.W. 3-D electromagnetic modeling of EMI input filters. IEEE Trans. Ind. Electron. 2014, 61, 231–242. [Google Scholar] [CrossRef]
- Paul, C.R. Introduction to Electromagnetic Compatibility; John Wiley and Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Wang, S.; Lee, F.; Chen, D.; Odendaal, W. Effects of parasitic parameters on EMI filter performance. IEEE Trans. Power Electron. 2004, 19, 869–877. [Google Scholar] [CrossRef]
- Wang, S.; Chen, R.; Van Wyk, J.D.; Lee, F.C.; Odendaal, W.G. Developing parasitic cancellation technologies to improve EMI filter performance for switching mode power supplies. IEEE Trans. Electromagn. Compat. 2005, 47, 921–929. [Google Scholar] [CrossRef]
- Chiu, H.J.; Pan, T.F.; Yao, C.J.; Lo, Y.K. Automatic EMI measurement and filter design system for telecom power supplies. IEEE Trans. Instrum. Meas. 2007, 56, 2254–2261. [Google Scholar] [CrossRef]
- Kotny, J.L.; Margueron, X.; Idir, N. High-frequency model of the coupled inductors used in EMI filters. IEEE Trans. Power Electron. 2012, 27, 2805–2812. [Google Scholar] [CrossRef]
- Baccigalupi, A.; Daponte, P.; Grimaldi, D. On a circuit theory approach to evaluate the stray capacitances of two coupled inductors. IEEE Trans. Instrum. Meas. 1994, 43, 774–776. [Google Scholar] [CrossRef]
- Cogitore, B.; Keradec, J.; Barbaroux, J. The two-winding transformer: An experimental method to obtain a wide frequency range equivalent circuit. IEEE Trans. Instrum. Meas. 1994, 43, 364–371. [Google Scholar] [CrossRef]
- Schellmanns, A.; Berrouche, K.; Keradec, J.P. Multiwinding transformers: A successive refinement method to characterize a general equivalent circuit. IEEE Trans. Instrum. Meas. 1998, 47, 1316–1321. [Google Scholar] [CrossRef]
- Margueron, X.; Keradec, J.P. Identifying the magnetic part of the equivalent circuit of n-winding transformers. IEEE Trans. Instrum. Meas. 2007, 56, 146–152. [Google Scholar] [CrossRef]
- Besri, A.; Chazal, H.; Keradec, J.P. Capacitive behavior of HF power transformers: global approach to draw robust equivalent circuits and experimental characterization. In Proceedings of the 2009 IEEE Instrumentation and Measurement Technology Conference, Singapore, 5–7 May 2009; pp. 1262–1267. [Google Scholar]
- Roc’h, A.; Bergsma, H.; Zhao, D.; Ferreira, B.; Leferink, F. A new behavioural model for performance evaluation of common mode chokes. In Proceedings of the 2007 18th International Zurich Symposium on Electromagnetic Compatibility, Munich, Germany, 24–28 September 2007; pp. 501–504. [Google Scholar]
- Stevanovic, I.; Skibin, S.; Masti, M.; Laitinen, M. Behavioral modeling of chokes for EMI simulations in power electronics. IEEE Trans. Power Electron. 2013, 28, 695–705. [Google Scholar] [CrossRef]
- CISPR 17:2011. Methods of Measurement of the Suppression Characteristics of Passive EMC Filtering Devices; IEC: Geneve, Switezerland, 2011. [Google Scholar]
- Kyyrä, J.; Kostov, K. Insertion loss in terms of four-port network parameters. IET Sci. Meas. Technol. 2009, 3, 208–216. [Google Scholar]
- Dominguez-Palacios, C.; Bernal-Méndez, J.; Martin Prats, M.A. Characterization of common mode chokes at high frequencies with simple measurements. IEEE Trans. Power Electron. 2018, 33, 3975–3987. [Google Scholar] [CrossRef]
- Den Bossche, A.V.; Valchev, V.C. Inductors and Transformers for Power Electronics; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Bockelman, D.E.; Eisenstadt, W.R. Combined differential and common-mode scattering parameters: Theory and simulation. IEEE Trans. Microw. Theory Technol. 1995, 43, 1530–1539. [Google Scholar] [CrossRef]
- Bernal-Méndez, J.; Freire, M.J.; Martin Prats, M.A. Overcoming the effect of test fixtures on the measurement of parasitics of capacitors and inductors. IEEE Trans. Power Electron. 2020, 35, 15–19. [Google Scholar] [CrossRef]
- Pozar, D. Microwave Engineering; Wiley&Son: Hoboken, NJ, USA, 2011. [Google Scholar]
- Nave, M. Power Line Filter Design for Switched-Mode Power Supplies; Van Nostrand Reinhold: New York, NY, USA, 1991. [Google Scholar]
- Dominguez Palacios, C.; Gonzalez Vizuete, P.; Martin Prats, M.A.; Bernal, J. Smart shielding techniques for common mode chokes in EMI filters. IEEE Trans. Electromagn. Compat. 2019, 61, 1329–1336. [Google Scholar] [CrossRef]
- Bernal-Méndez, J.; Freire, M.J. On-site, quick and cost-effective techniques for improving the performance of EMI filters by using conducting bands. In Proceedings of the 2016 IEEE International Symposium on Electromagnetic Compatibility, Ottawa, ON, Canada, 25–29 July 2016; pp. 390–395. [Google Scholar]
- Weile, D.; Michielssen, E. Genetic algorithm optimization applied to electromagnetics: A review. IEEE Trans. Antennas Propag. 1997, 45, 343–353. [Google Scholar] [CrossRef]
- EN55011:2011/CISPR 11. Industrial, Scientific, and Medical Equipment—Radio-Frequency Disturbance Characteristics—Limits and Methods of Measurement; Beuth Verlag: Berlin, Germany, 2009. [Google Scholar]
- EN55022:2011/CISPR 22. Information Technology Equipment—Radio disturbance characteristics—Limits and methods of measurement; Beuth Verlag: Berlin, Germany, 2008. [Google Scholar]
- FCC Part 15. The FCC 47 CFR Part 15 from the Federal Communications Commission: Rules and Regulations for EMC; Federal Communications Commission: Washington, DC, USA, 2020.
- Available online: https://www.coilcraft.com/wbt.cfm (accessed on 15 March 2012).
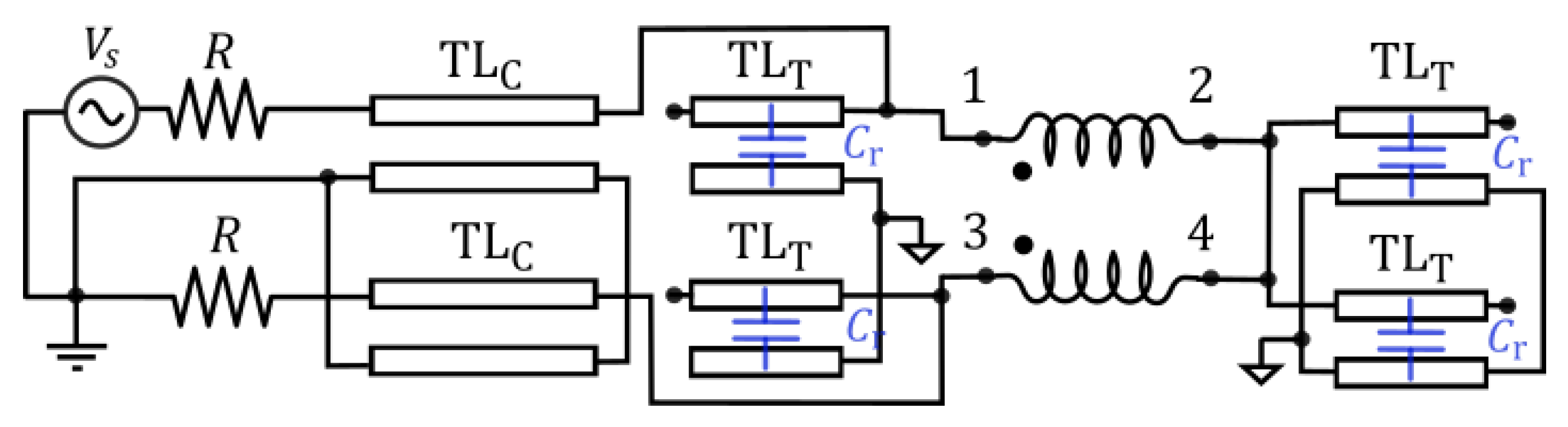

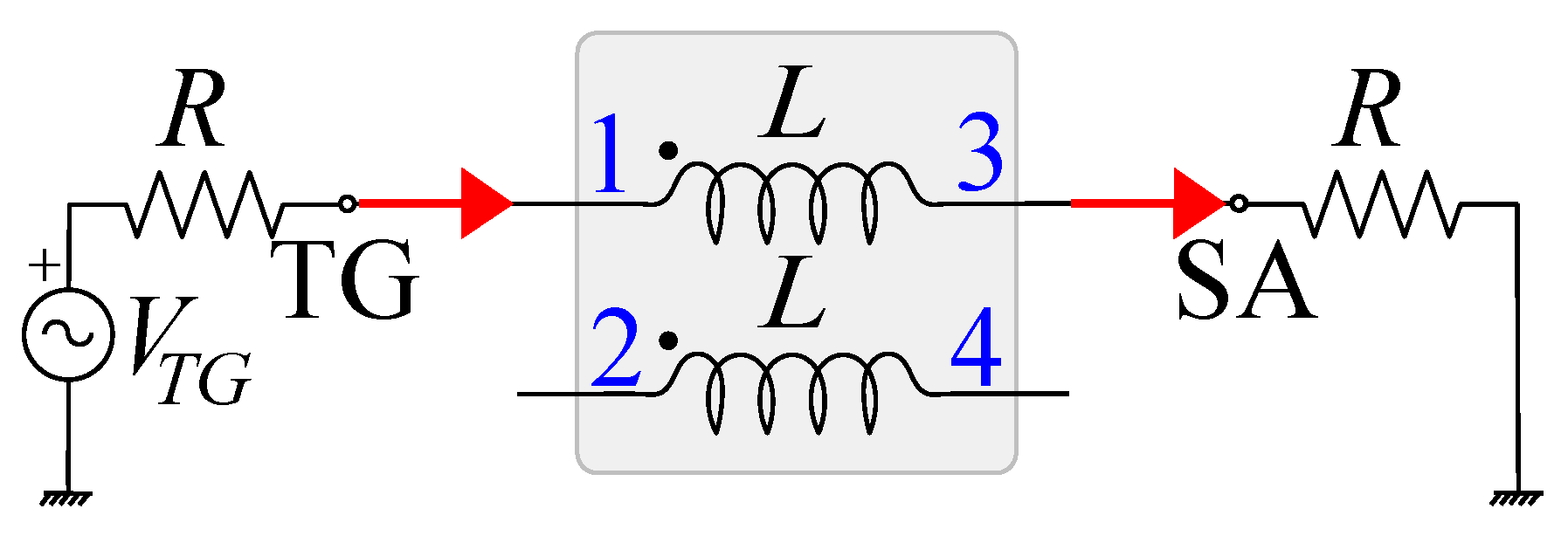
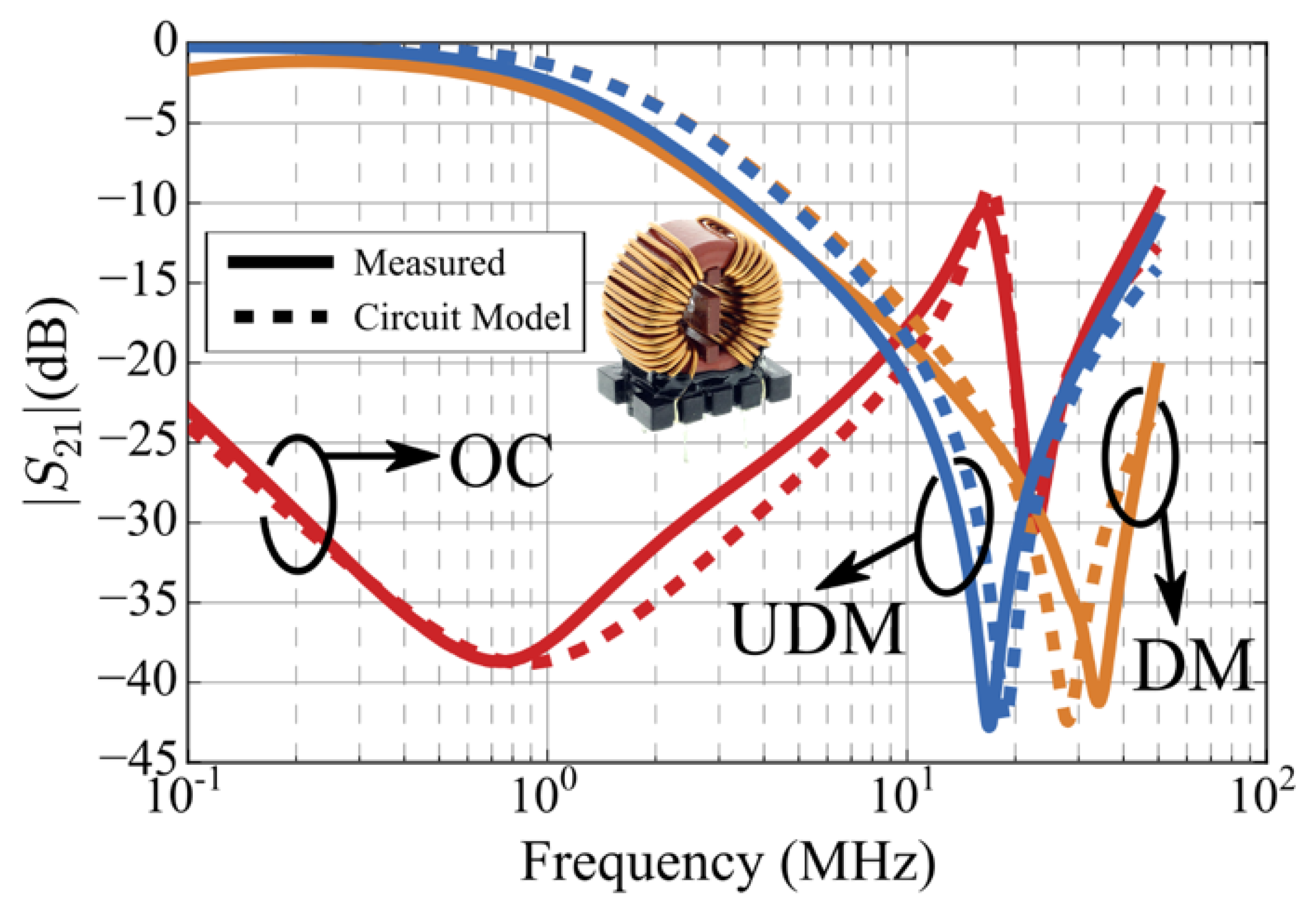
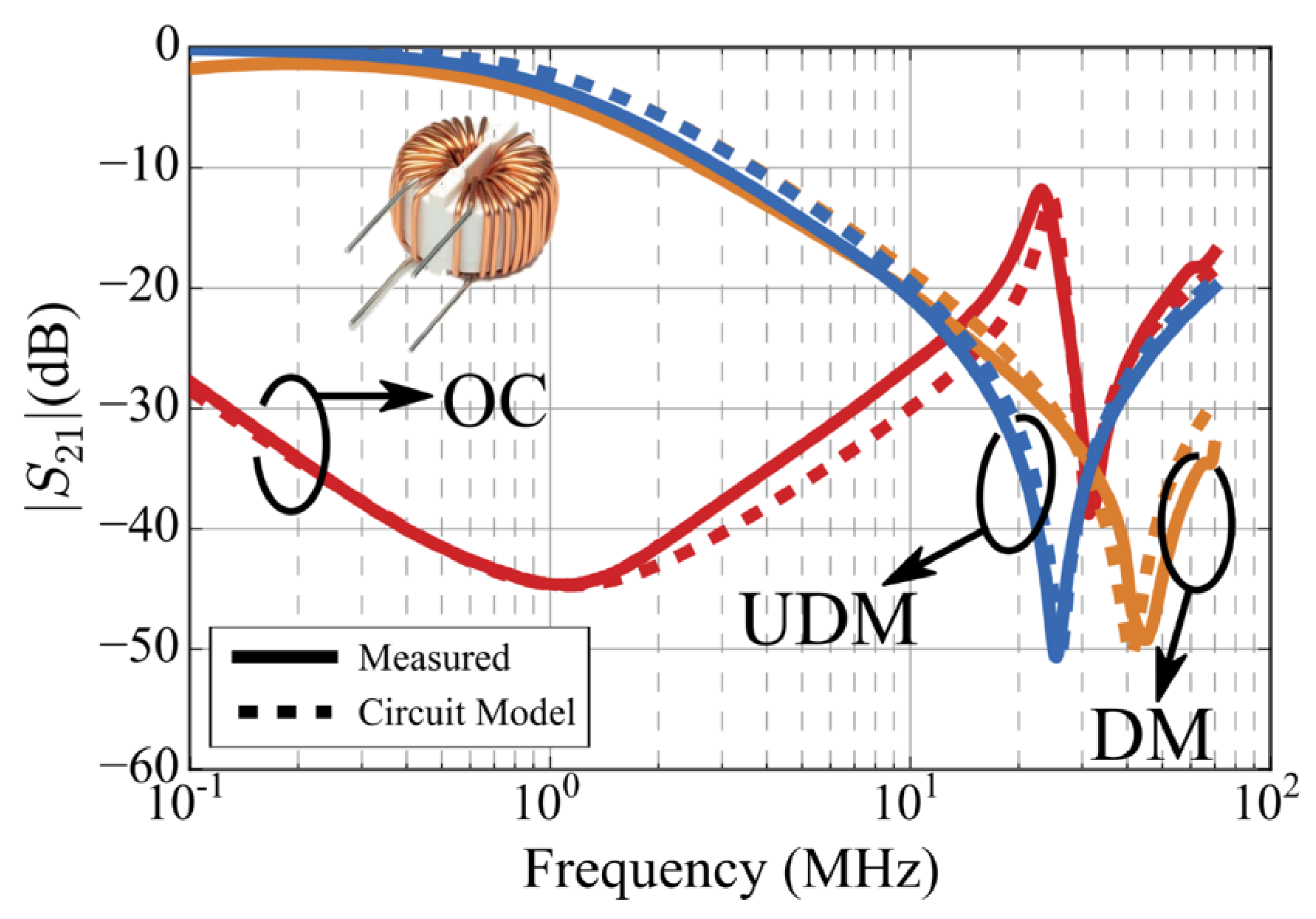

| Setup | Transmission Coefficient | Frequencies of Resonance |
|---|---|---|
| DM | ||
| UDM | ||
| OC |
| Manufacturer and Part Number | L (mH) | (mH) | (uH) | (pF) | (pF) | (k) | (k) |
|---|---|---|---|---|---|---|---|
| WÜRTH ELEKT. 744824622 | 2.2 | 4.94 | 4.7 | 4.2 | 6.8 | 17.2 | 6.5 |
| WÜRTH ELEKT. 744824310 | 10 | 26.7 | 33.6 | 4.7 | 18.3 | 118 | 16.6 |
| WÜRTH ELEKT. 744824220 | 20 | 54.1 | 57.6 | 10.7 | 20.2 | 203 | 22.2 |
| WÜRTH ELEKT. 7448011008 | 8.0 | 6.90 | 6.5 | 0.86 | 2.7 | 22.1 | 8.1 |
| MURATA PLA10AN2230R4D2B | 22 | 71.3 | 173 | 1.8 | 2.9 | 73.9 | 33.0 |
| KEMET SC-02-30G | 3.0 | 7.40 | 5.8 | 1.4 | 2.8 | 34.3 | 16.7 |
| KEMET SCF20-05-1100 | 11 | 13.4 | 5.1 | 8.6 | 7.2 | 15.4 | 7.9 |
| (MHz) | |||
|---|---|---|---|
| CMC Isolated | CMC on Ungrounded PCB | ||
| CMC Part Number | Measured | Measured | Calculated |
| WE 744824622 | 16.9 | 13.6 | 12.8 |
| WE 744824310 | 4.77 | 4.30 | 4.07 |
| WE 744824220 | 3.02 | 2.65 | 2.74 |
| (MHz) | |||
|---|---|---|---|
| CMC Isolated | CMC on Grounded PCB | ||
| CMC Part Number | Measured | Measured | Calculated |
| WE 744824622 | 16.9 | 21.7 | 22.8 |
| WE 744824310 | 4.77 | 5.63 | 5.64 |
| WE 744824220 | 3.02 | 3.40 | 3.72 |
| CMC Part Number | (H) | (H) |
|---|---|---|
| WE 744824622 | 4.73 | 3.38 |
| WE 744824310 | 33.6 | 27.0 |
| WE 744824220 | 58.2 | 44.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Vizuete, P.; Domínguez-Palacios, C.; Bernal-Méndez, J.; Martín-Prats, M.A. Simple Setup for Measuring the Response to Differential Mode Noise of Common Mode Chokes. Electronics 2020, 9, 381. https://doi.org/10.3390/electronics9030381
González-Vizuete P, Domínguez-Palacios C, Bernal-Méndez J, Martín-Prats MA. Simple Setup for Measuring the Response to Differential Mode Noise of Common Mode Chokes. Electronics. 2020; 9(3):381. https://doi.org/10.3390/electronics9030381
Chicago/Turabian StyleGonzález-Vizuete, Pablo, Carlos Domínguez-Palacios, Joaquín Bernal-Méndez, and María A. Martín-Prats. 2020. "Simple Setup for Measuring the Response to Differential Mode Noise of Common Mode Chokes" Electronics 9, no. 3: 381. https://doi.org/10.3390/electronics9030381
APA StyleGonzález-Vizuete, P., Domínguez-Palacios, C., Bernal-Méndez, J., & Martín-Prats, M. A. (2020). Simple Setup for Measuring the Response to Differential Mode Noise of Common Mode Chokes. Electronics, 9(3), 381. https://doi.org/10.3390/electronics9030381





