1. Introduction
The modern scenario for power electronics is of one of ever increasing complexity with radical paradigm shifts in many sectors. On the power distribution side, the advent of renewable energies has brought forward a set of challenges [
1] that can be solved by moving from a traditional transformer-based, unidirectional power distribution network to smart grids. In this context, static power converters can more easily allow for bidirectional power flow while helping to maintain overall grid stability, by employing a wide array of control techniques [
2]. The pervasive electrification of the transportation sector is also driving up power electronics complexity, for both cars [
3] with the introduction of hybrid and electric vehicles, and aircraft [
4]. In fact, the More Electric Aircraft (MEA) [
5] framework aims to replace the mechanical, hydraulic, and pneumatic systems with electromechanical ones. This will lead to an increase in overall efficiency through the use of a more effective, bleedless turbofan main engine, and to weight reduction due to the elimination of ducting, valving, and other power transmission components. In these types of systems, fault tolerance is one of the most important design aspects. This goal can be achieved again through modularization, adopting segmented motors, and drives [
6].
Traditional architecture for power converters and machine drives relies on a single inverter driving a three-phase electrical machine, as shown in
Figure 1a. In segmented drives, conversely, the electrical machine is designed with multi three-phase windings, each of them driven by a separated power electronics module (inverter). The different power modules jointly contribute to drive the electrical machines in a distributed way, making the system intrinsically more reliable and resilient. A single centralized controller (master controller,
Figure 1b) can still be employed for both control loop execution and direct gate signal generation for the power modules. However, the high number of power devices used in modular power conversion setups, makes this impractical. In addition, the reliability of direct gate signal distribution, in the increasingly distributed system, is also lower as the electromagnetic noise, inherently generated by the switching action, can cause an unwanted device commutation with catastrophic consequences. A different approach that could solve this issues is a different architecture, moving from a classical to a networked control system, where each sub-module generates the gate signals locally, as shown in
Figure 1c. This transition is made more complex by the lack of a communication protocol specifically designed for these tasks, thus forcing designers of power converters to use industrial automation targeted ones. Few efforts have been made to introduce more modern communication techniques to power electronics [
7]. In [
8], a custom UDP (User Datagram Protocol) implementation on top of a 100BASE-TX ethernet link is proposed, however the reliance on standard protocol for the first and second OSI layers, leads to a very large transmission delay that makes the system unsuitable for state-of-the-art high frequency power electronic converters. Another approach is presented in [
9], where the authors use a commercial off-the-shelf transceiver integrated circuit (now discontinued), originally meant for server and backplane applications, based on an optical fiber link in order to achieve better performance. The downside of what is presented here is a complete reliance on the availability of this circuit, which is problematic, not only because it limits the flexibility of the resulting system, but also because it poses long term availability issues.
In this scenario, the adoption of a communication method that is at the same time robust and has a low and predictable latency is of the utmost importance in order to support the required system dynamics [
10]. Along with the latency, the jitter introduced in the system by the network layer is particularly problematic. In fact, it is inherent to the protocol that uses error detection and subsequent re-transmission to ensure the correctness of the received messages, that will thus be delayed by an amount of time that is dependent on both protocol and channel conditions. Forward Error Correction (FEC) techniques can instead be used in order to ensure the absence of errors on the link, even when the channel conditions are not ideal, without the need to request and wait for a full message re-transmission by the master controller. Several well-established techniques [
11,
12], already used in other networking settings, can be re-purposed as long as performance in terms of payload integrity, low latency, and low jitter can match the peculiar requirements of this application.
The application of FEC techniques to power electronics has been recently studied, especially in the context of smart grids [
13,
14], where the low operating frequencies and large impedance of the network do not require large control system bandwidth, as in the field of machine drives. The core problem that has slowed the widespread adoption of FEC techniques is the large latency associated with Microcontroller or DSP (Digital Signal Processor) implementation. Even when using state-of-the-art algorithms on modern hardware [
15], the calculations still require several hundreds of microseconds, which is too much when targeting system sampling frequencies in the tens of kHz, as is typical for these applications. Only recently, the availability of low cost, high density Field Programmable Gate Arrays (FPGA) has also allowed the use of these techniques in the filed of machine drives. In [
16], a communication protocol for optical fibers-based distributed power electronic systems is developed. However, in [
13,
14,
16] a comprehensive evaluation of the impact of the introduction of digital communication to the control of distributed drive applications is still not fully examined. In particular, how FEC techniques can reduce the vulnerability of a control system to network-related jitter is still an open issue. The aim of this paper, is hence to investigate the impact of FEC techniques in power electronics systems and their control, considering the particular requirements of very low jitter and small payload sizes encountered in this specific field.
The paper is organized as follows. In
Section 2, used communication protocol and FEC techniques are introduced. In
Section 3, implementations are detailed, whereas in
Section 4, the effects of latency in a distributed drive control loop are discussed. In
Section 5, experimental results are discussed and finally, in
Section 6 conclusions are drawn.
2. Communication Protocol
The aim of the designed communication protocol is to enable the exchange of control information from a master controller to one or more nodes, with as little latency or jitter as possible. The overall structure of the communication protocol implementation can be found in
Figure 2.
2.1. Synchronization
The primary problem to solve when designing distributed networks of any kind is the need for synchronization, in order to enable the various nodes composing the system to act in a coherent way. Several techniques [
17] can be used for this purpose, for example, clock distribution networks, preamble synchronization, clock embedding, and scrambling-based clock recovery with periodic transmissions.
The first solution is very attractive, making the implementation of the communication protocol much easier as the synchronization is guaranteed by the physical distribution of clock signals throughout the system. Despite its simplicity, this solution is rarely used in practice as it shifts the complexity and reliability issued on a physical level, requiring extra conductors and more elaborate and expensive connectors. With preamble synchronization these problems are addressed by shifting the clock signal in band. In this case, an alternating bit pattern is transmitted at the start of each message, enabling the receiver to lock the internal oscillator to it. Following this solution, the extra clock distribution hardware is removed and thus reduces system complexity. The downside of this is a less efficient use of the channel bandwidth as extra information has to be transmitted.
Similarly, the second technique includes a synchronization signal in band, but instead of transmitting it before the message, it is embedded in the signal itself by the use of a suitable line encoding (e.g., Manchester encoding, 8 b/10 b, etc.). The first field of application of this method is for messages with small payloads where it can have a lower impact with respect to the addition of a preamble, whose size is determined only by the characteristics of the receiver clocking system.
The last technique to be taken into consideration is based on the periodic transmission of scrambled data. This, while requiring additional complexity, can guarantee clock synchronization at no additional costs in terms of packet size. This technique has been adopted in this paper as the receiver employs a phase locked loop to synchronize the system clock with the incoming signal edges. In order to guarantee a sufficient amount of signal transitions, a multiplicative, self-synchronizing [
18] scrambler is used, along with a minimum packet transmission frequency.
2.2. Error Handling
The next problem that the protocol needs to solve is the protection against errors in order to ensure communication reliability. The simplest error handling technique that can be used is error detection and re-transmission. Thanks to appropriate algorithms, the receiver can evaluate the integrity of the received data [
19]. The downside of this approach are the large latency spikes on the communication channel when a re-transmission is required. FEC, by contrast, focuses on trying to add just enough redundancy to enable the correction of errors most likely to occur. The main advantage is the ability to significantly reduce latency variance by avoiding re-transmissions. This comes at the cost of higher complexity and a limited number of correctable errors, depending on the chosen type of coding. In order to guarantee an error free communication, a balance must be determined between FEC technique strength and the physical channel minimum Signal to Noise Ratio (SNR). The SNR strongly depends on the chosen physical channel and/or transceiver, that differ in each application. Depending on the application, it will be necessary to estimate the desired minimum SNR and choose the better FEC technique, considering the best compromise between its strength and its complexity. For this reason, in this paper three cases with increasing error correction capacity will be compared: The uncoded modulation, a Hamming, and a Reed–Solomon (RS) coding.
2.3. Compared Algorithms Details
In this work, two different FEC methods have been compared, Hamming and RS coding. An unprotected communication stream is also evaluated serving as a baseline. In the studied application the minimal practical payload length is of 40 bits, chosen as a compromise between bandwidth efficiency and transmission delay.
The first considered algorithm is a shortened SECDED (Single-Error Correcting and Double-Error Detecting) Hamming code that can detect two bit errors, by transmitting along with the payload (up to
bits) a number of different “parity” bits (this number, denoted with
, is usually equal to 6). The first step in order to construct this code is the choice of a perfect Hamming code [
20], that can encode enough information to fit the entire message. The redundant information bits are then removed, in an operation called shortening. The last step is to apply a standard checksum, increasing the Hamming distance of the resulting code, enabling the double error detection. A second class of studied algorithms are RS codes, a class of q-ary block codes operating over the
q (
) elements of the Galois Field
GF(q) [
21]. A RS code is defined by the following parameters:
m is the number of bits per symbol,
k is the number of data symbols,
is the number of parity symbols, and
n is the total length of the coded word (
). A RS code with these parameters is able to correct up to
t errors in the received word. Since RS code theory is based on Galois Field (GF) mathematics, to perform encoding and decoding two polynomials have to be defined: The primitive (or field generator) polynomial, from which all elements in a GF can be generated, and the code generator polynomial, the roots of which are consecutive elements in the GF. Their choice is of particular importance as it can greatly simplify the decoder architecture. The values for all the parameters used in this study are shown in
Table 1 and
Table 2.
3. Implementation
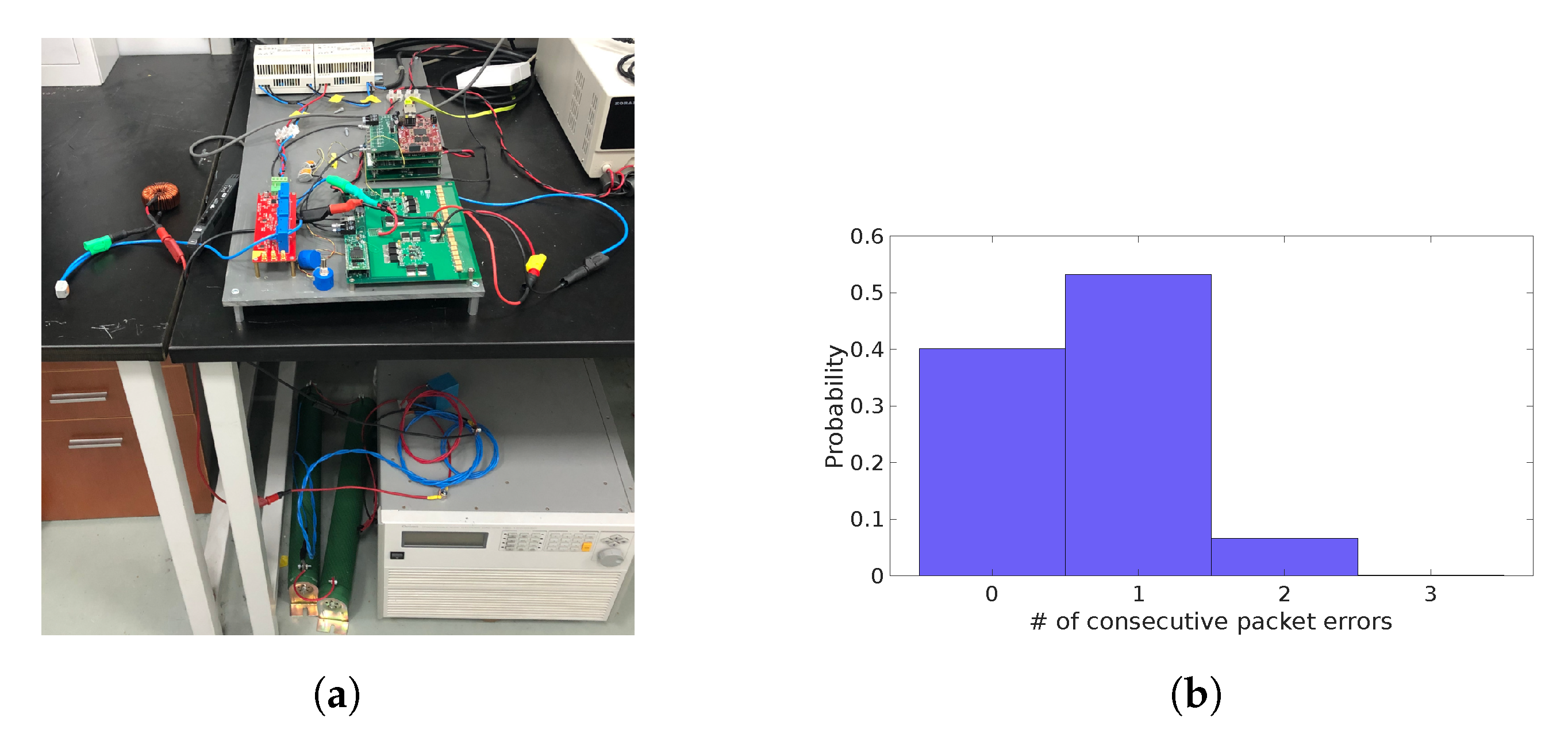
Several different factors have steered the choice of the device for the implementation of the designed protocol and the studied error correction. The use of a traditional Microcontroller or DSP-based system has been discarded as the lack of flexibility of such devices would have either meant the use of a standard protocol like SPI or UART, or forced the use of a feature specific to a single manufacturer or even to a single product line, resulting in highly sub-optimal performances or the loss of generality. By contrast, a FPGA structure is much better suited for the implementation of custom serial communication protocols, providing high performance I/O resources capable of managing high frequency bit streams. Another advantage of this class of devices is their highly parallel nature, helping to achieve the lowest possible latency. The essential role of the FPGA in addressing power electronics communication protocol processing in time-critical operations is highlighted in [
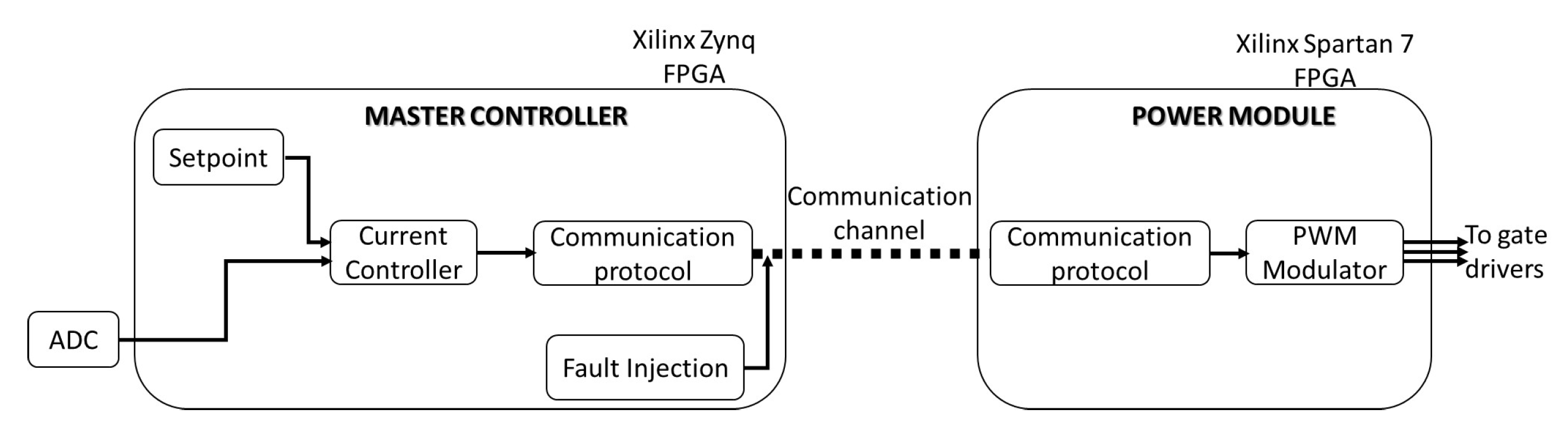
9]. The following paragraphs outline the technical choice that were made for the implementation on a FPGA. From a high level perspective, the system is composed of two parts: A master controller and one (or more) power module, as shown in
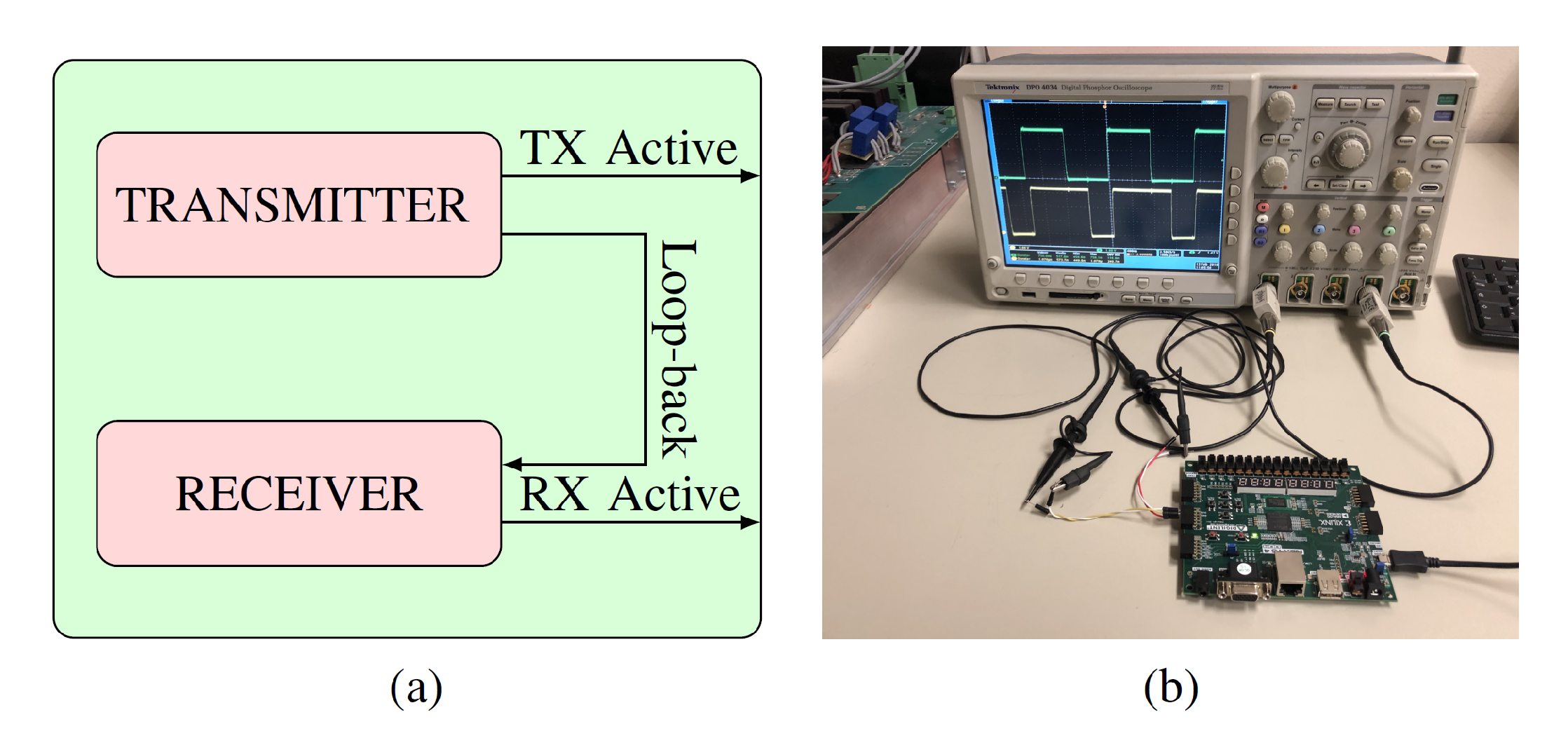
Figure 3. Both the master controller and power module are implemented on FPGA. The master controller exploits a Xilinx Zynq FPGA and is responsible for main control loop operations. It computes the control variables and send them to the power modules for its correct operation. Moreover, it measures the actual output current through an external ADC (Analog to Digital Converter) and compute the relevant duty cycles to be transmitted to the power module. For testing purposes, a fault injection module has been added to the implementation of the master controller. Before the communication signal is transmitted, some network errors are added in order to simulate the not ideal situation repeatably. The power module is implemented on a Xilinx Spartan 7 FPGA. In addition to the communication device needed to receive the appropriate instructions from the main controller, it generates the relevant PWM (Pulse Width Modulation) signals to control an external traditional buck converter. The communication blocks embedded on master and power modules follow the protocol described in
Section 2. To evaluate the impact of different FEC techniques, two versions of the coder-decoder have been implemented and tested. In the following paragraph, the two solutions, based on the Hamming and RS algorithm respectively, are detailed.
3.1. Hamming Code
The designed Hamming encoder has to calculate the parity bits along with the global message checksum. To do this the payload needs to be modulo-2 multiplied by the generator matrix (often denoted with G). This matrix, when well chosen, will be fairly sparse, leading to a relatively simple set of multiple input exclusive or gates, whose implementation poses very few timing and area consumption problems. On the other hand, the global message checksum calculation, requiring very low computational power, results in gates with a large fan-in that can have a significant negative impact on timing. It is thus beneficial to split this operation into several smaller steps. The optimal partitioning choice is highly dependent on the underlying hardware architecture, however a simple two-stage pipeline is selected, as a balanced trade-off between area utilization and timing margins.
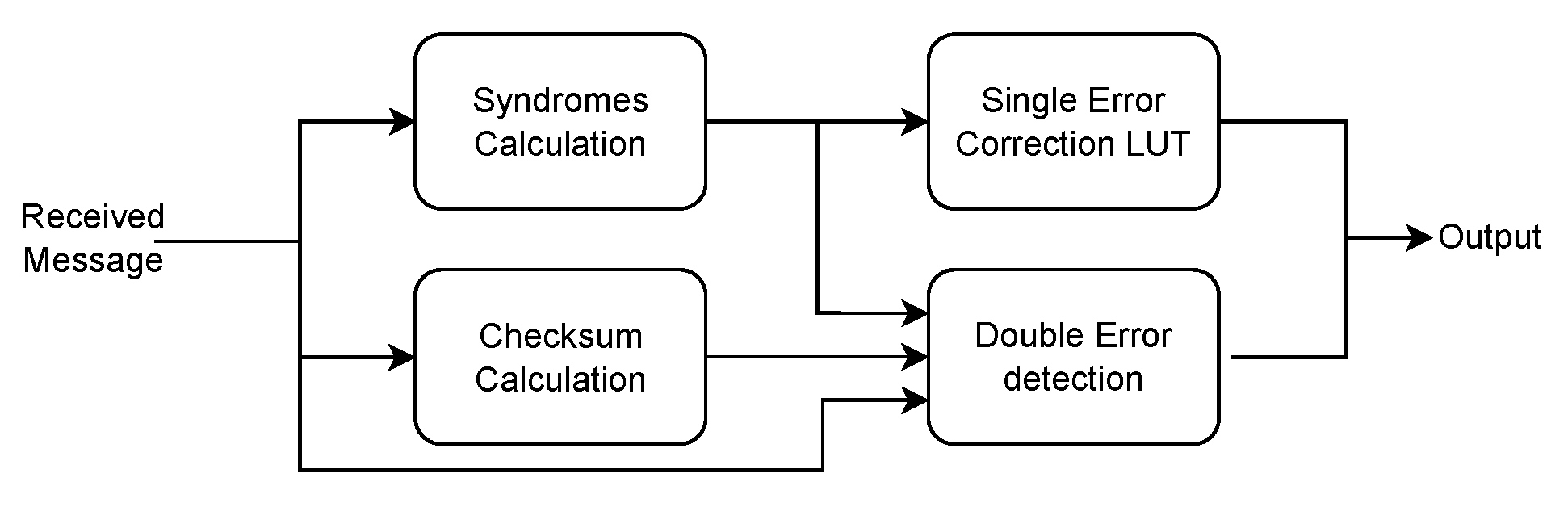
The traditional algorithm employed with Hamming encoded data is based on the principle of syndrome decoding. The
bits “syndrome” is calculated, by multiplying (modulo-2) the received code-word by the parity check matrix (usually denoted with
H, obtained by calculating the inverse of the parity columns in the
G matrix). The value of the syndrome is only dependent on the position of the wrong bit. The core of this decoder’s implementation, whose structure is shown in
Figure 4, organized in a two-stage pipeline. In the first step the syndrome of the received message, and the overall checksum are calculated. In the next clock cycle, single errors are corrected by locating the incorrect bit using a RAM-based Look Up Table (LUT), addressed by the calculated syndrome. At the same time, checksums are compared to detect whether a two bit error has occurred. Depending on the output of these two blocks, the correct message is sent to the outputs or, in case of a double bit error, a flag is raised, allowing the controller to discard the message.
3.2. Reed-Solomon
The architecture of a RS encoder is based on a Linear Feedback Shift Register [
22]. It consists of four GF multipliers and adders, and four 4-bit registers.
The general RS decoder architecture is depicted in
Figure 5a. The syndrome block consists of 2t basic cell to compute syndromes symbols [
23]. Since in a single cell the data is multiplied by a constant that represents a root of the generator polynomial, to limit the area occupation and speed up the operations, the Galois multiplier of the single cell has been replaced by a LUT. Moreover, thanks to the chosen generator polynomial the cell corresponding to the zero root of the polynomial does not need any multiplier. To compute Error Locator Polynomials the Euclidean algorithm is exploited [
24]. The architecture for the Galois divider is shown in
Figure 5b.
At the beginning, the registers T0-T4 are loaded with the divisor, while the dividend is stored in registers D3-D0. As the division proceed, the quotient and remainder of the division will be available in the T0-T4 registers. Depending on the degrees of the divisor polynomials and dividend, the remainder and quotient could have different degrees and therefore a different symbols number. A designed control logic deals with recognizing which of the T4-T0 symbols actually belong to the quotient or to the remainder. The designed divider is also able to handle the special case in which the most significant symbol of the syndrome is zero. Errors positions and values evaluation has been carried out with well-established Chien [
25] and Forney [
15,
26] methods respectively. The whole designed architecture is, also in this case, pipe-lined.
3.3. Resource Usage
All the studied solutions have been implemented on a Xilinx XC7A100T Artix 7 family, with the Xilinx provided toolchain and common default settings and the resource usage relative to each design is consequently shown in
Table 3. It is worth mentioning that these figures are highly dependent not only on the logic design but also on the underlying hardware architecture, toolchain used, optimization steps executed, and related parameter choice. The given figures should thus be examined in relation to each other. As already seen in the previous sections, there is high asymmetry between the encoder and decoder complexity. When comparing Hamming with the RS error correction algorithm, it is clear that the latter has a much higher complexity than the former. If these figures are normalized to the number of correctable errors, the cost for each correctable bit is much lower, making the RS Error Correction Code (ECC) very promising for application in this field. Lastly, when comparing the logic usages with respect to the capabilities of the FPGA’s in the Artix family, it is clear that the overall cost of even high performance error correction is quite low with a worst case usage of roughly
(for the XC7A12T device).
6. Conclusions
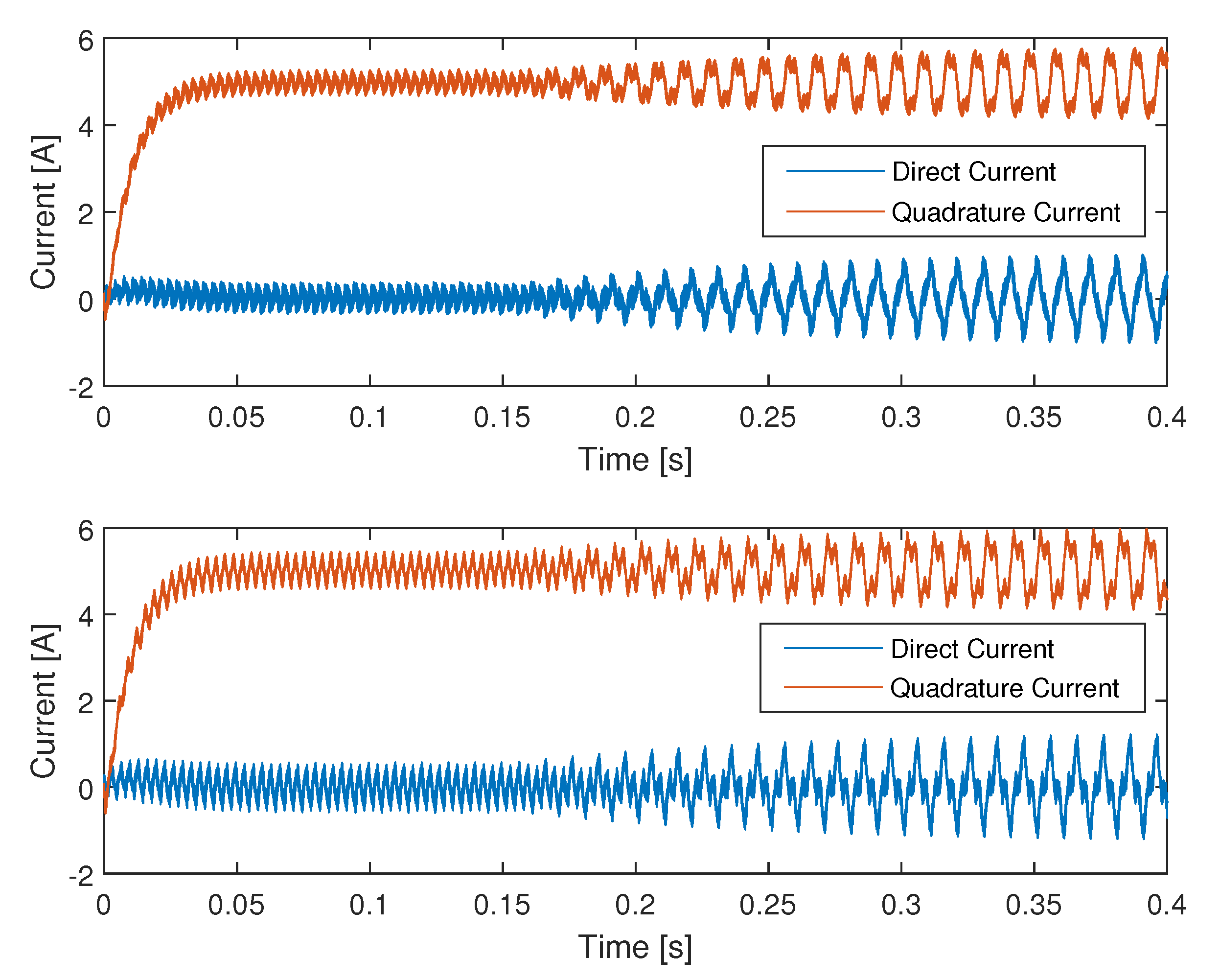
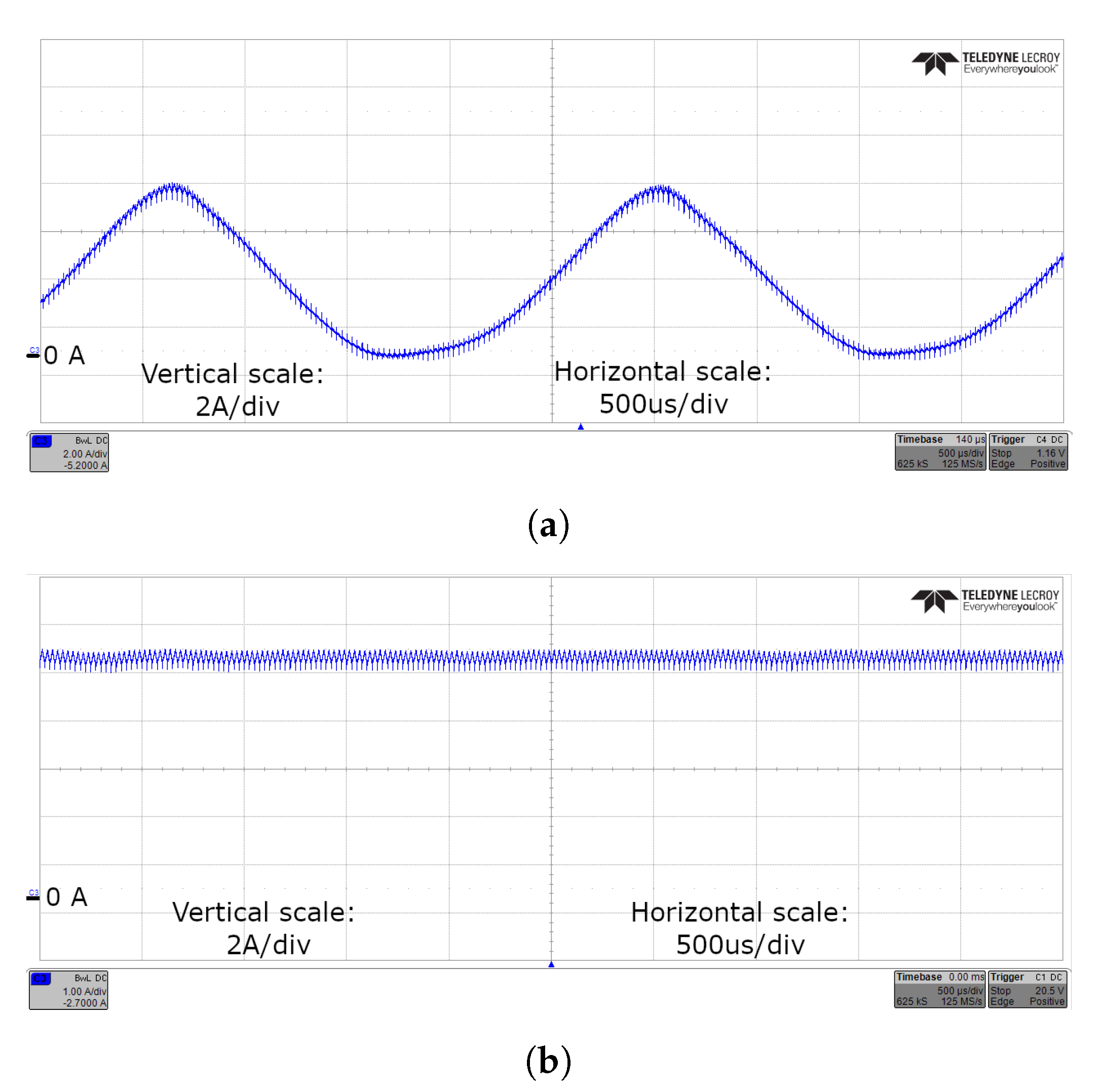
This paper showed how the performance and viability of distributed power electronics controls is highly dependent on the network performance. In particular, in non-ideal channel conditions, when reception errors are possible, the common detect and re-transmit strategy, while ensuring correctness of the data stream, could introduce jitter in the control loop, ultimately leading to instability. In fact, this constituted a time varying delay placed in the direct path of the control loop and it worsened the overall phase margin, potentially leading to oscillation. This phenomenon was proven by the simulations and then confirmed through experimental validations.
The introduction of FEC techniques to the communication between the master controller and the slave power modules, on the other hand, could still ensure an error-free data stream, while avoiding the introduction of any random jitter in the communication, thus proving to be the ideal method for distributed power electronics systems. The complementary switching transistor pairs were connected only to the PWM generator, whose duty-cycle was controlled by the rest of the system. Hence, the hardware of the slave power modules was affected only in an indirect way by the introduction of FEC. Two different FEC coding were evaluated and the performance of the proposed communication strategy was experimentally validated. A latency of 910 ns and of 200 ns were measured in the case of RS and Hamming code techniques, respectively. Both these results were comparable or even better than those presented in the state-of-the-art [
16]. It is worth noting that the RS solution had better performances in terms of BER regardless of the channel conditions. However, the choice of which technique should be preferred must be made considering the characteristics of the specific application and installation (e.g., physical layout of the system, EMC immunity of the communication physical layer, dynamics of the overall system including load and power supply, etc.). Independently, on the specific application, it was proven that both RS and Hamming code improved the power control, deleting the oscillations that were visible in case of simple re-transmission requests when errors occurred in the communication.