Switch Elements with S-Shaped Current-Voltage Characteristic in Models of Neural Oscillators
Abstract
1. Introduction
2. Materials and Methods
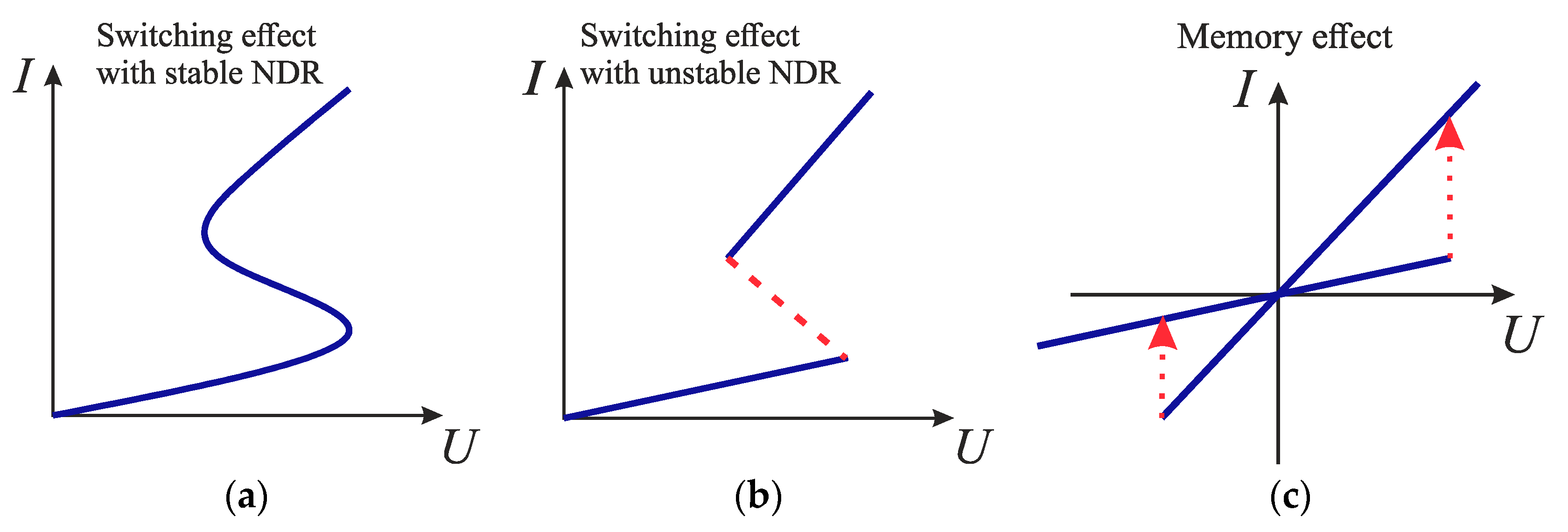
2.1. S-Type Switch Models Controlled by Current and Voltage
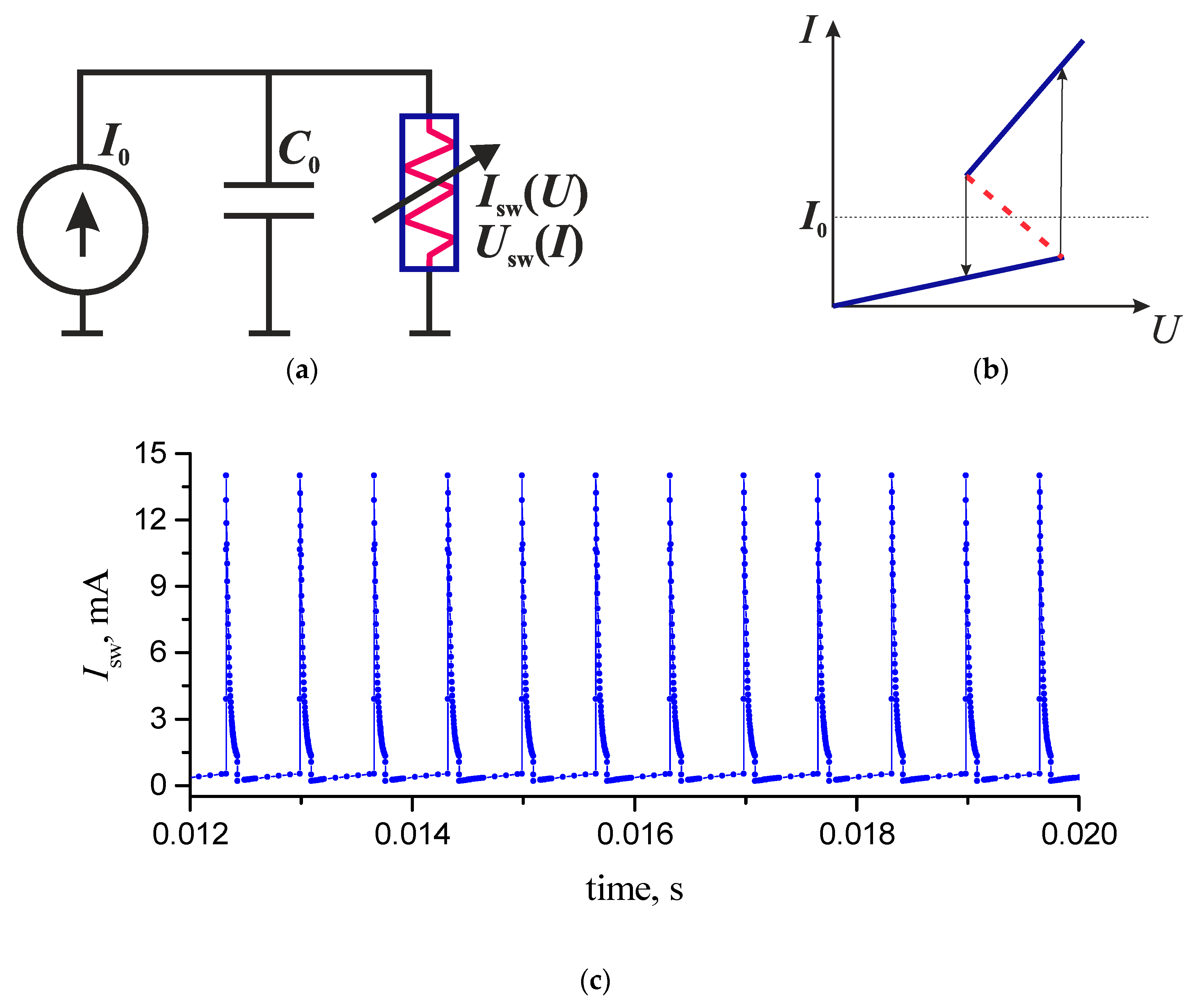
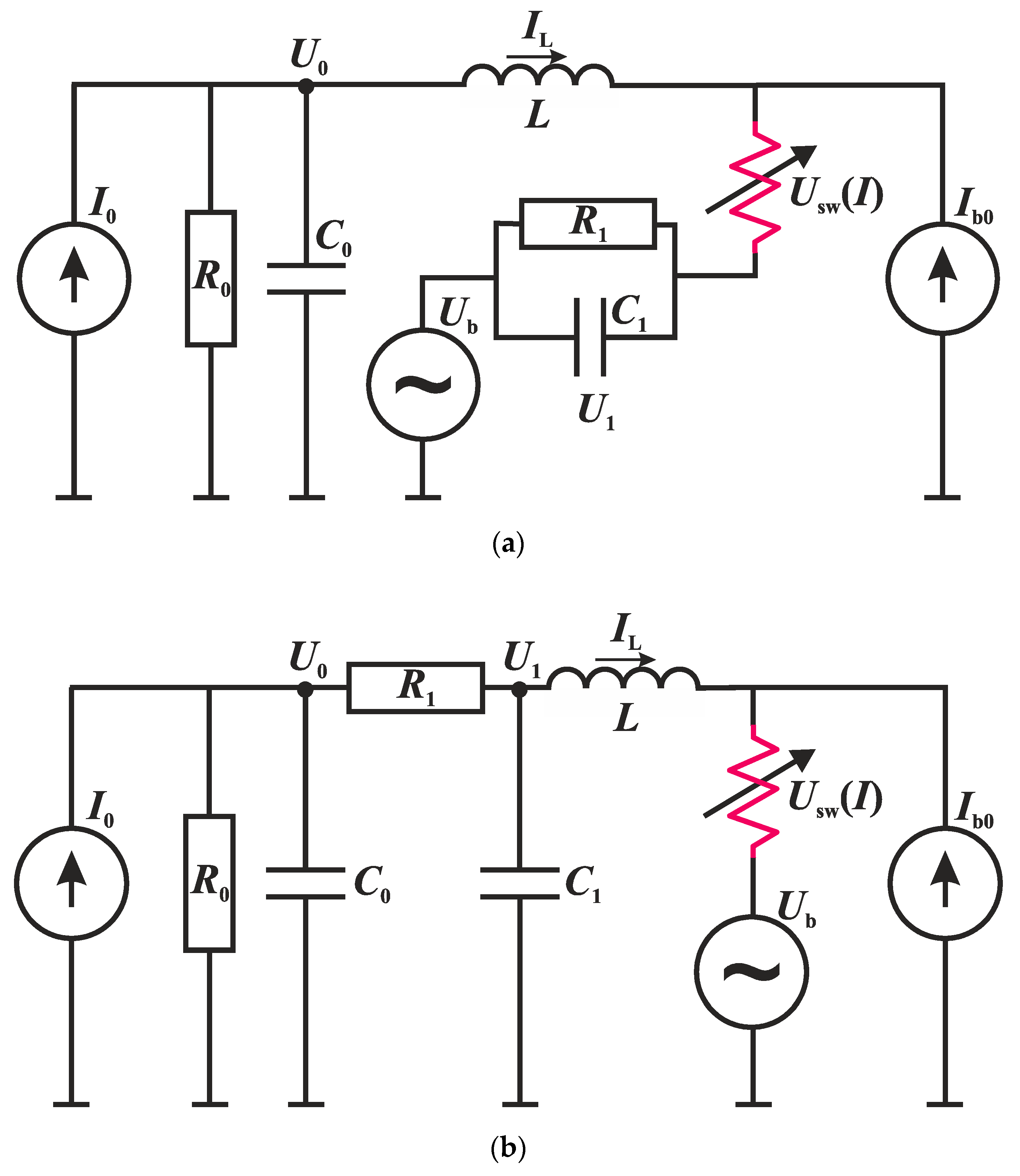
2.2. Relaxation Oscillator
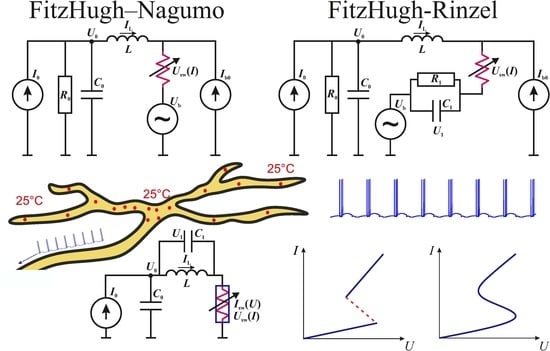
2.3. FitzHugh–Nagumo and FitzHugh–Rinzel Models
3. Results
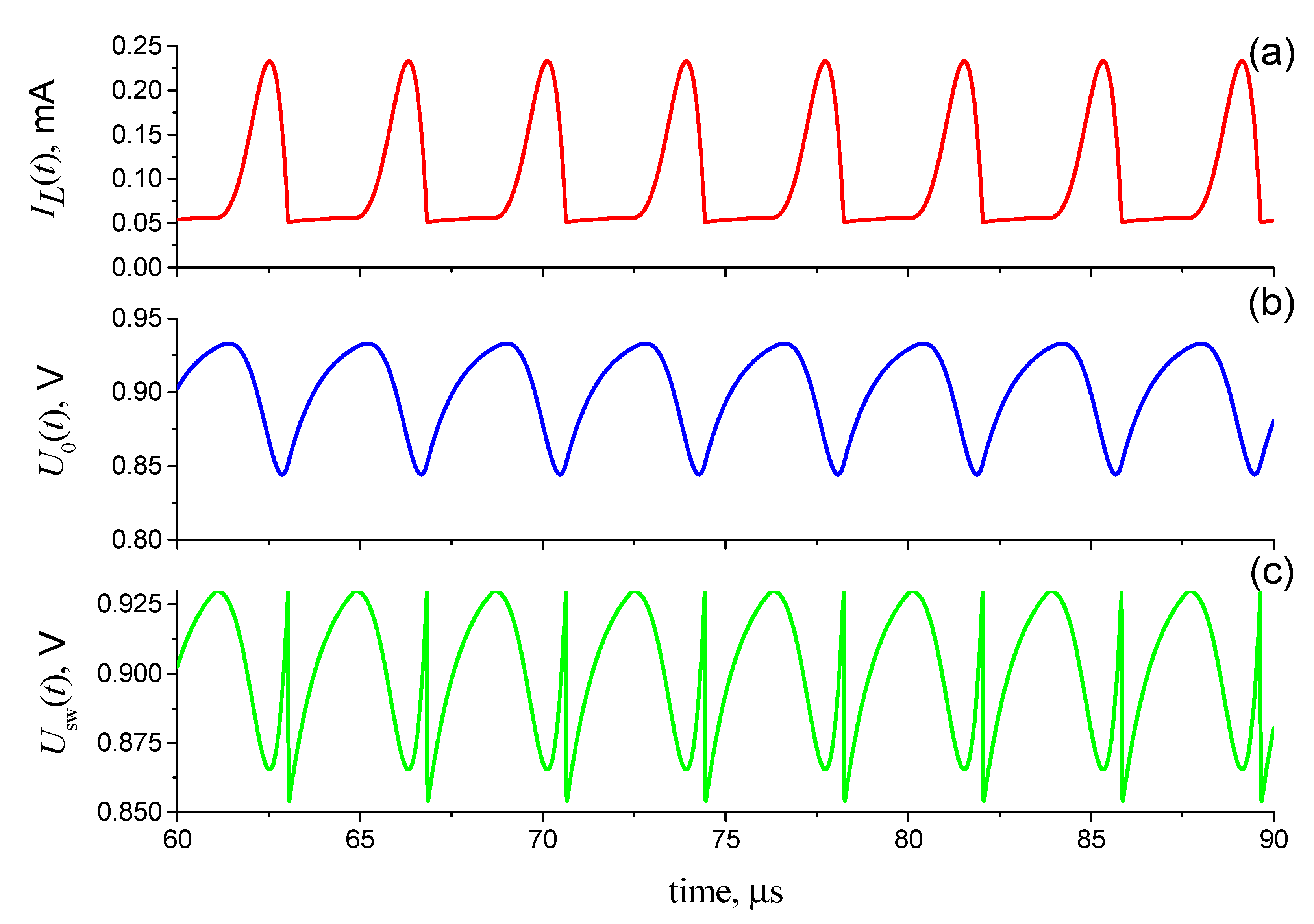
3.1. FitzHugh–Nagumo Model Based on a Current-Controlled Switching S-Element
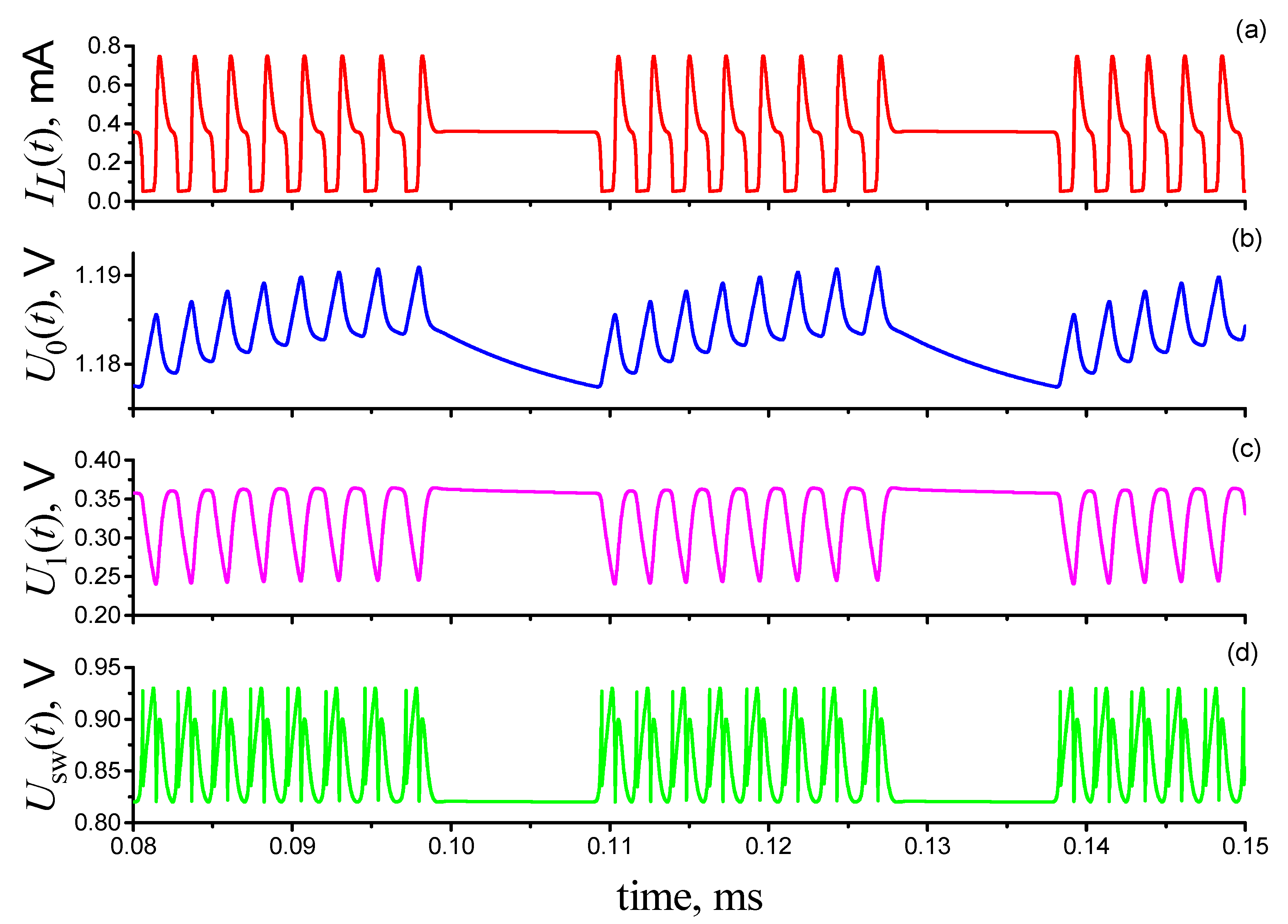
3.2. FitzHugh–Rinzel Model Based on a Current-Controlled Switching S-Element
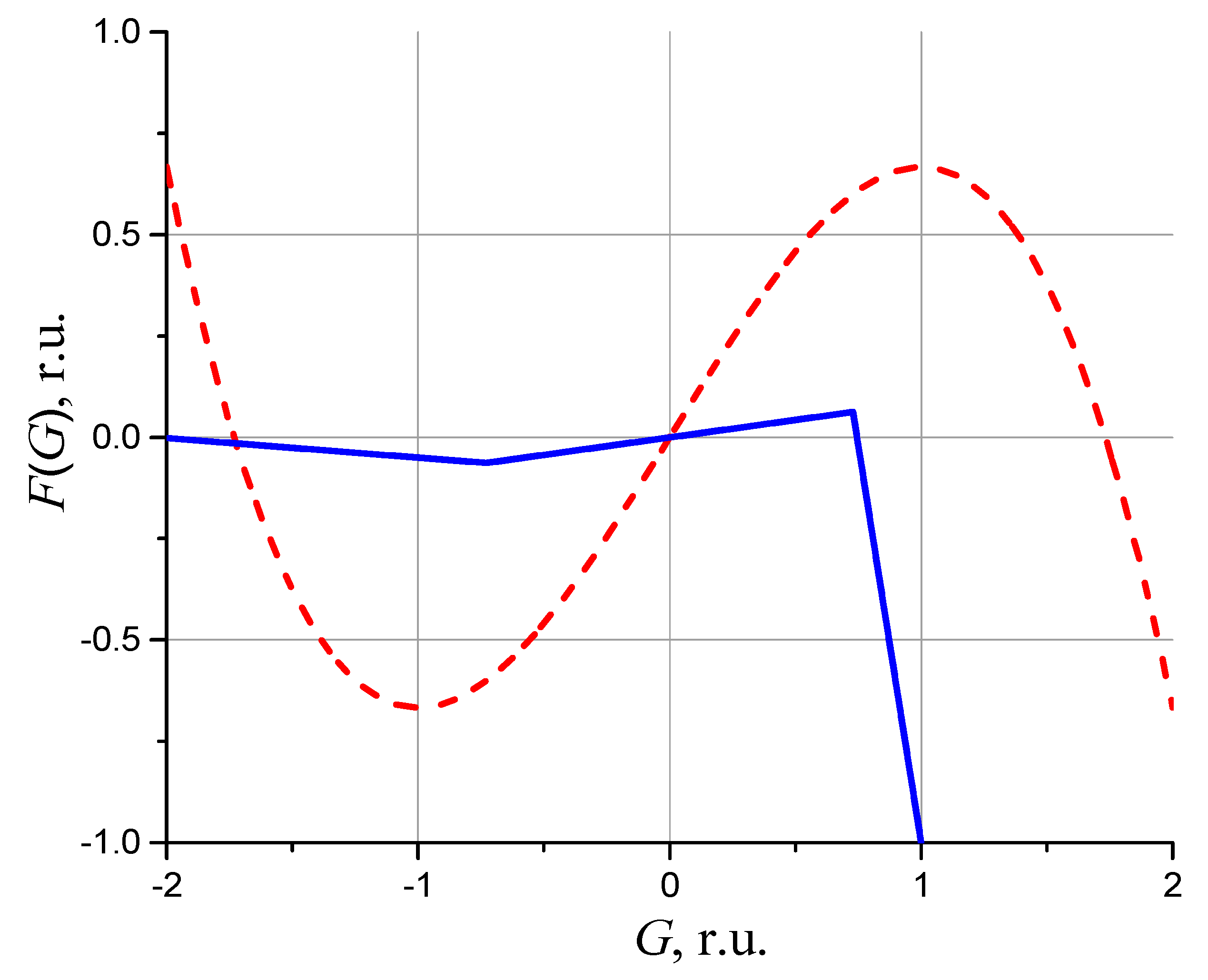
3.3. Alternative Neural-Like Circuits Based on a Switching S-Element
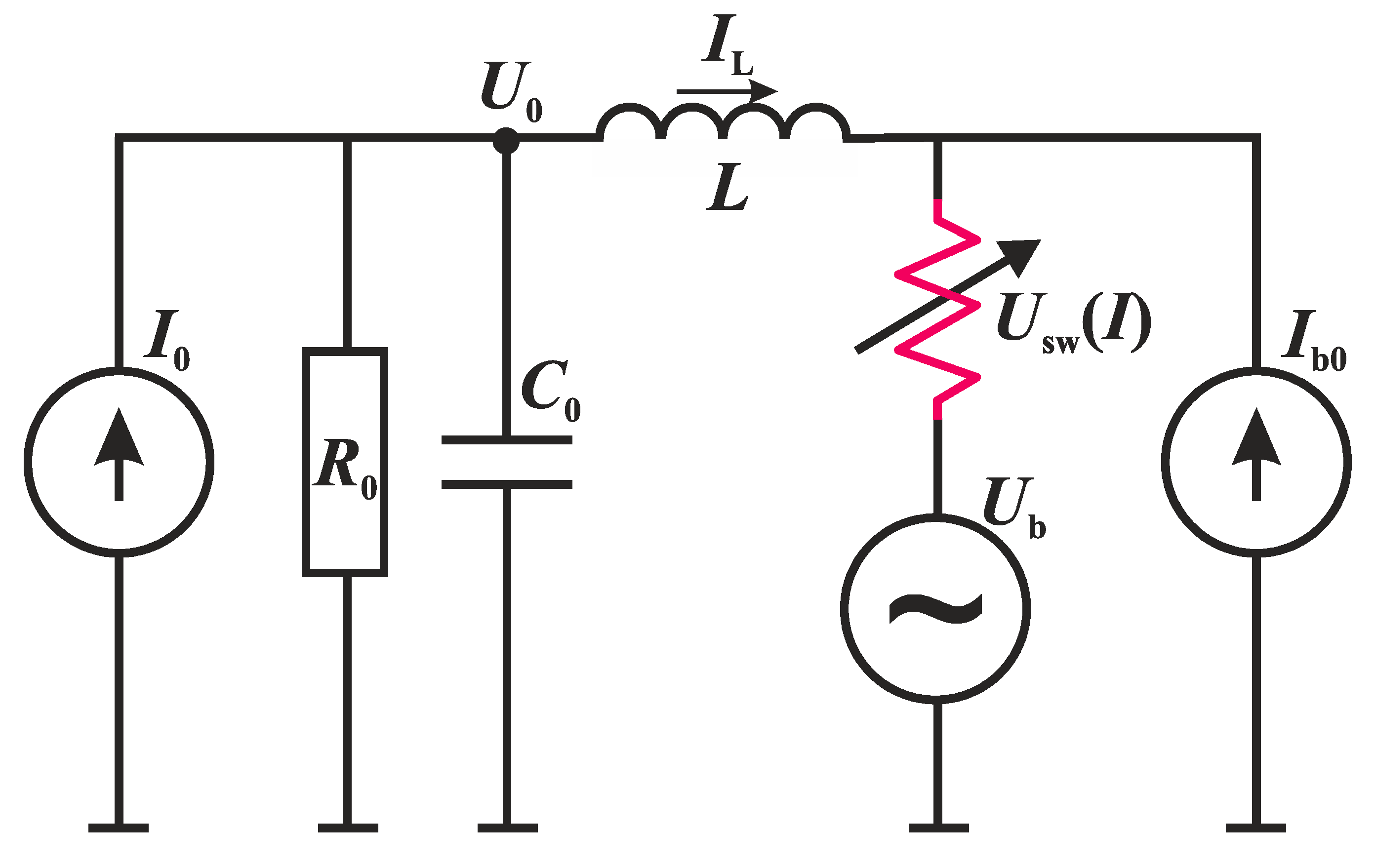
3.4. The Auto-Relaxation Oscillator as an Integrate-And-Fire Neuron Based on a Switching S-Element
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Keener, J.P. Analog circuitry for the van der Pol and FitzHugh-Nagumo equations. IEEE Trans. Syst. Man Cybern. 1983, SMC-13, 1010–1014. [Google Scholar] [CrossRef]
- Zhang, J.; Liao, X. Synchronization and chaos in coupled memristor-based FitzHugh-Nagumo circuits with memristor synapse. AEU Int. J. Electron. Commun. 2017, 75, 82–90. [Google Scholar] [CrossRef]
- Sherwood, W.E. FitzHugh–Nagumo Model. In Encyclopedia of Computational Neuroscience; Springer: New York, NY, USA, 2014; pp. 1–11. [Google Scholar]
- Ji, Y.; Zhang, X.; Liang, M.; Hua, T.; Wang, Y. Dynamical analysis of periodic bursting in piece-wise linear planar neuron model. Cognit. Neurodyn. 2015, 9, 573–579. [Google Scholar] [CrossRef] [PubMed]
- Rotstein, H.G.; Coombes, S.; Gheorghe, A.M. Canard-Like Explosion of Limit Cycles in Two-Dimensional Piecewise-Linear Models of FitzHugh–Nagumo Type. SIAM J. Appl. Dyn. Syst. 2012, 11, 135–180. [Google Scholar] [CrossRef]
- Koppelaar, H.; Kordestani Moghadam, P.; Khan, K.; Kouhkani, S.; Segers, G.; van Warmerdam, M. Reaction Time Improvements by Neural Bistability. Behav. Sci. 2019, 9, 28. [Google Scholar] [CrossRef] [PubMed]
- Zhen, B.; Li, Z.; Song, Z.; Zhen, B.; Li, Z.; Song, Z. Influence of Time Delay in Signal Transmission on Synchronization between Two Coupled FitzHugh-Nagumo Neurons. Appl. Sci. 2019, 9, 2159. [Google Scholar] [CrossRef]
- Rinzel, J. A Formal Classification of Bursting Mechanisms in Excitable Systems; Springer: Berlin/Heidelberg, Germany, 1987; pp. 267–281. [Google Scholar]
- Yi, W.; Tsang, K.K.; Lam, S.K.; Bai, X.; Crowell, J.A.; Flores, E.A. Biological plausibility and stochasticity in scalable VO2 active memristor neurons. Nat. Commun. 2018, 9, 4661. [Google Scholar] [CrossRef] [PubMed]
- Sejnowski, T.J. Neural Pulse Coding. In Pulsed Neural Networks; MIT Press: Cambridge, MA, USA, 1999; p. 377. ISBN 9780262133500. [Google Scholar]
- Bachiller-Burgos, P.; Manso, L.J.; Bustos, P. A Spiking Neural Model of HT3D for Corner Detection. Front. Comput. Neurosci. 2018, 12, 37. [Google Scholar] [CrossRef] [PubMed]
- Velichko, A.; Belyaev, M.; Boriskov, P. A Model of an Oscillatory Neural Network with Multilevel Neurons for Pattern Recognition and Computing. Electronics 2019, 8, 75. [Google Scholar] [CrossRef]
- Itoh, M.; Chua, L.O. Star cellular neural networks for associative and dynamic memories. Int. J. Bifurc. Chaos 2004, 14, 1725–1772. [Google Scholar] [CrossRef]
- Roska, T.; Chua, L.O. The CNN universal machine: An analogic array computer. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 1993, 40, 163–173. [Google Scholar] [CrossRef]
- Romera, M.; Talatchian, P.; Tsunegi, S.; Abreu Araujo, F.; Cros, V.; Bortolotti, P.; Trastoy, J.; Yakushiji, K.; Fukushima, A.; Kubota, H.; et al. Vowel recognition with four coupled spin-torque nano-oscillators. Nature 2018, 563, 230–234. [Google Scholar] [CrossRef] [PubMed]
- Velichko, A. A Method for Evaluating Chimeric Synchronization of Coupled Oscillators and Its Application for Creating a Neural Network Information Converter. Electronics 2019, 8, 756. [Google Scholar] [CrossRef]
- Indiveri, G.; Linares-Barranco, B.; Hamilton, T.J.; Van Schaik, A.; Etienne-Cummings, R.; Delbruck, T.; Liu, S.-C.; Dudek, P.; Häfliger, P.; Renaud, S.; et al. Neuromorphic Silicon Neuron Circuits. Front. Neurosci. 2011, 5, 73. [Google Scholar] [CrossRef] [PubMed]
- Edwards, R.T.; Cauwenberghs, G. Synthesis of Log-Domain Filters from First-Order Building Blocks. Analog Integr. Circuits Signal Process. 2000, 22, 177–186. [Google Scholar] [CrossRef]
- Mead, C. Carver Analog VLSI and Neural Systems; Addison-Wesley: Boston, MA, USA, 1989; ISBN 0201059924. [Google Scholar]
- Izhikevich, E.M. Simple model of spiking neurons. IEEE Trans. Neural Netw. 2003, 14, 1569–1572. [Google Scholar] [CrossRef] [PubMed]
- Bogoslovskiy, N.A.; Tsendin, K.D. Physics of switching and memory effects in chalcogenide glassy semiconductors. Semiconductors 2012, 46, 559–590. [Google Scholar] [CrossRef]
- Chudnovskii, F.A.; Odynets, L.L.; Pergament, A.L.; Stefanovich, G.B. Electroforming and Switching in Oxides of Transition Metals: The Role of Metal–Insulator Transition in the Switching Mechanism. J. Solid State Chem. 1996, 122, 95–99. [Google Scholar] [CrossRef]
- Wehmeyer, G.; Yabuki, T.; Monachon, C.; Wu, J.; Dames, C. Thermal diodes, regulators, and switches: Physical mechanisms and potential applications. Appl. Phys. Rev. 2017, 4, 041304. [Google Scholar] [CrossRef]
- Pergament, A.; Stefanovich, G.; Malinenko, V.; Velichko, A. Electrical Switching in Thin Film Structures Based on Transition Metal Oxides. Adv. Condens. Matter Phys. 2015, 2015, 654840. [Google Scholar] [CrossRef]
- Sze, S.M.; Ng, K.K. Physics of Semiconductor Devices; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; ISBN 9780470068328. [Google Scholar]
- Solovyov, V.F.; Li, Q. Fast high-temperature superconductor switch for high current applications. Appl. Phys. Lett. 2013, 103, 032603. [Google Scholar] [CrossRef]
- Volkov, N.V.; Eremin, E.V.; Tsikalov, V.S.; Patrin, G.S.; Kim, P.D.; Seong-Cho, Y.; Kim, D.-H.; Chau, N. Current-driven channel switching and colossal positive magnetoresistance in the manganite-based structure. J. Phys. D Appl. Phys. 2009, 42, 065005. [Google Scholar] [CrossRef][Green Version]
- Lu, W.; Wang, D.; Chen, L. Near-Static Dielectric Polarization of Individual Carbon Nanotubes. Nano Lett. 2007, 7, 2729–2733. [Google Scholar] [CrossRef] [PubMed]
- Ageev, O.A.; Blinov, Y.F.; Il’in, O.I.; Konoplev, B.G.; Rubashkina, M.V.; Smirnov, V.A.; Fedotov, A.A. Study of the resistive switching of vertically aligned carbon nanotubes by scanning tunneling microscopy. Phys. Solid State 2015, 57, 825–831. [Google Scholar] [CrossRef]
- Belyaev, M.A.; Boriskov, P.P.; Velichko, A.A.; Pergament, A.L.; Putrolainen, V.V.; Ryabokon’, D.V.; Stefanovich, G.B.; Sysun, V.I.; Khanin, S.D. Switching Channel Development Dynamics in Planar Structures on the Basis of Vanadium Dioxide. Phys. Solid State 2018, 60, 447–456. [Google Scholar] [CrossRef]
- Kumar, S.; Strachan, J.P.; Williams, R.S. Chaotic dynamics in nanoscale NbO2 Mott memristors for analogue computing. Nature 2017, 548, 318–321. [Google Scholar] [CrossRef] [PubMed]
- Chua, L.O.; Wu, C.W.; Huang, A.; Zhong, G.Q. A universal circuit for studying and generating chaos. I. Routes to chaos. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1993, 40, 732–744. [Google Scholar] [CrossRef]
- Pearson, S.O.; Anson, H.S.G. Demonstration of Some Electrical Properties of Neon-filled Lamps. Proc. Phys. Soc. Lond. 1921, 34, 175–176. [Google Scholar] [CrossRef][Green Version]
- Koch, C. Biophysics of Computation: Information Processing in Single Neurons; Stryker, M., Ed.; Oxford University Press: Oxford, UK, 1999; Volume 428, ISBN 0195181999. [Google Scholar]
- Morris, C.; Lecar, H. Voltage oscillations in the barnacle giant muscle fiber. Biophys. J. 1981, 35, 193–213. [Google Scholar] [CrossRef]
- Rowat, P.F.; Selverston, A.I. Modeling the gastric mill central pattern generator of the lobster with a relaxation-oscillator network. J. Neurophysiol. 1993, 70, 1030–1053. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Hybrid spiking models. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 368, 5061–5070. [Google Scholar] [CrossRef] [PubMed]
- Fitzhugh, R. Impulses and Physiological States in Theoretical Models of Nerve Membrane. Biophys. J. 1961, 1, 445–466. [Google Scholar] [CrossRef]
- Hindmarsh, J.L.; Rose, R.M. A model of the nerve impulse using two first-order differential equations. Nature 1982, 296, 162–164. [Google Scholar] [CrossRef] [PubMed]
- Izhikevich, E.M. Which model to use for cortical spiking neurons? IEEE Trans. Neural Netw. 2004, 15, 1063–1070. [Google Scholar] [CrossRef] [PubMed]
- Izhikevich, E.M. Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting; The MIT Press: Cambridge, MA, USA, 2007; ISBN 9780262090438. [Google Scholar]
- Reinagel, P.; Godwin, D.; Sherman, S.M.; Koch, C. Encoding of visual information by LGN bursts. J. Neurophysiol. 1999, 81, 2558–2569. [Google Scholar] [CrossRef] [PubMed]
- Rabinovich, M.; Varona, P.; Selverston, A.; Abarbanel, H. Dynamical principles in neuroscience. Rev. Mod. Phys. 2006, 78, 1213–1265. [Google Scholar] [CrossRef]
- Binczak, S.; Jacquir, S.; Bilbault, J.-M.; Kazantsev, V.B.; Nekorkin, V.I. Experimental study of electrical FitzHugh-Nagumo neurons with modified excitability. Neural Netw. 2006, 19, 684–693. [Google Scholar] [CrossRef] [PubMed]
- Belykh, V.N.; Pankratova, E.V. Chaotic synchronization in ensembles of coupled neurons modeled by the FitzHugh-Rinzel system. Radiophys. Quantum Electron. 2006, 49, 910–921. [Google Scholar] [CrossRef]
- Vitale, W.A.; Moldovan, C.F.; Tamagnone, M.; Paone, A.; Schuler, A.; Ionescu, A.M. Steep-Slope Metal–Insulator-Transition VO 2 Switches with Temperature-Stable High Ion. IEEE Electron. Device Lett. 2015, 36, 972–974. [Google Scholar] [CrossRef]
- Schäfer, K.; Braun, H.A.; Rempe, L. Classification of a calcium conductance in cold receptors. Prog. Brain Res. 1988, 74, 29–36. [Google Scholar]
- Velichko, A.; Belyaev, M.; Putrolaynen, V.; Perminov, V.; Pergament, A. Modeling of thermal coupling in VO2-based oscillatory neural networks. Solid State Electron. 2018, 139, 8–14. [Google Scholar] [CrossRef]
- Velichko, A.; Belyaev, M.; Putrolaynen, V.; Perminov, V.; Pergament, A. Thermal coupling and effect of subharmonic synchronization in a system of two VO2 based oscillators. Solid State Electron. 2018, 141, 40–49. [Google Scholar] [CrossRef]
- Darby, S.A.; Frysztak, R.J. Neuroanatomy of the Spinal Cord. In Clinical Anatomy of the Spine, Spinal, Cord and Ans, 3rd ed.; Elsevier: Amsterdam, the Netherlands, 2014; pp. 341–412. [Google Scholar]
- Ignatov, M.; Ziegler, M.; Hansen, M.; Petraru, A.; Kohlstedt, H. A memristive spiking neuron with firing rate coding. Front. Neurosci. 2015, 9, 376. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Guha, S.; Ramanathan, S. Vanadium Dioxide Circuits Emulate Neurological Disorders. Front. Neurosci. 2018, 12, 856. [Google Scholar] [CrossRef] [PubMed]
- Jerry, M.; Tsai, W.; Xie, B.; Li, X.; Narayanan, V.; Raychowdhury, A.; Datta, S. Phase transition oxide neuron for spiking neural networks. In Proceedings of the 2016 74th Annual Device Research Conference (DRC), Newark, DE, USA, 19–22 June 2016; pp. 1–2. [Google Scholar]
- Zerov, V.Y.; Kulikov, Y.V.; Leonov, V.N.; Malyarov, V.G.; Khrebtov, I.A.; Shaganov, I.I. Features of the operation of a bolometer based on a vanadium dioxide film in a temperature interval that includes a phase transition. J. Opt. Technol. 1999, 66, 387. [Google Scholar] [CrossRef]
- Verkelis, J.; Bliznikas, Z.; Breivé, K.; Dikinis, V.; Šarmaitis, R. Vanadium oxides thin films and fixed-temperature heat sensor with memory. Sens. Actuators A Phys. 1998, 68, 338–343. [Google Scholar] [CrossRef]
- Pergament, A.; Velichko, A.; Belyaev, M.; Putrolaynen, V. Electrical switching and oscillations in vanadium dioxide. Phys. B Condens. Matter 2018, 536, 239–248. [Google Scholar] [CrossRef]
- Mishchenko, M.A.; Gerasimova, S.A.; Lebedeva, A.V.; Lepekhina, L.S.; Pisarchik, A.N.; Kazantsev, V.B. Optoelectronic system for brain neuronal network stimulation. PLoS ONE 2018, 13, e0198396. [Google Scholar] [CrossRef]
- Iqbal, M.; Rehan, M.; Hong, K.-S. Robust Adaptive Synchronization of Ring Configured Uncertain Chaotic FitzHugh–Nagumo Neurons under Direction-Dependent Coupling. Front. Neurorobot. 2018, 12, 6. [Google Scholar] [CrossRef]
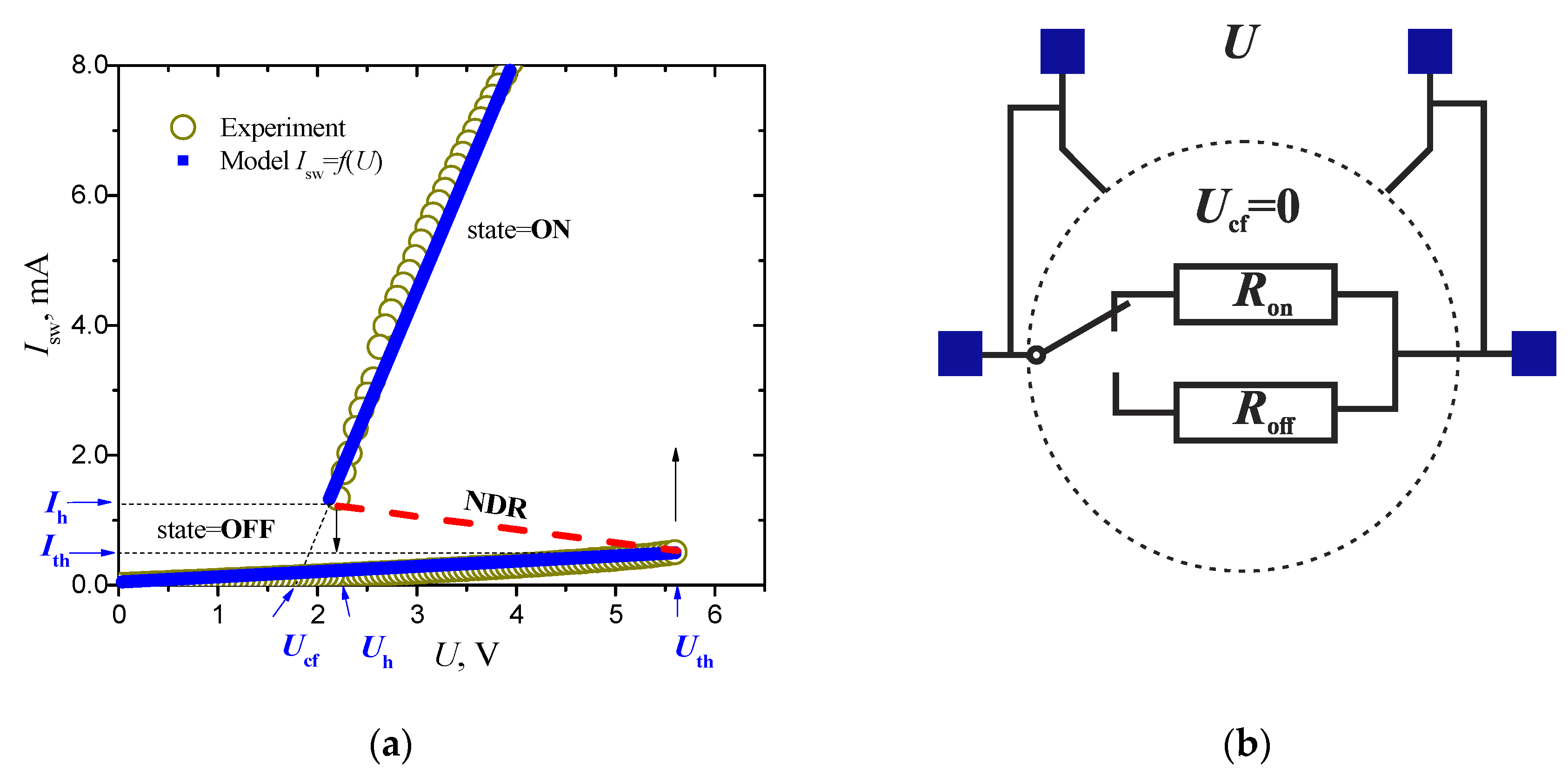
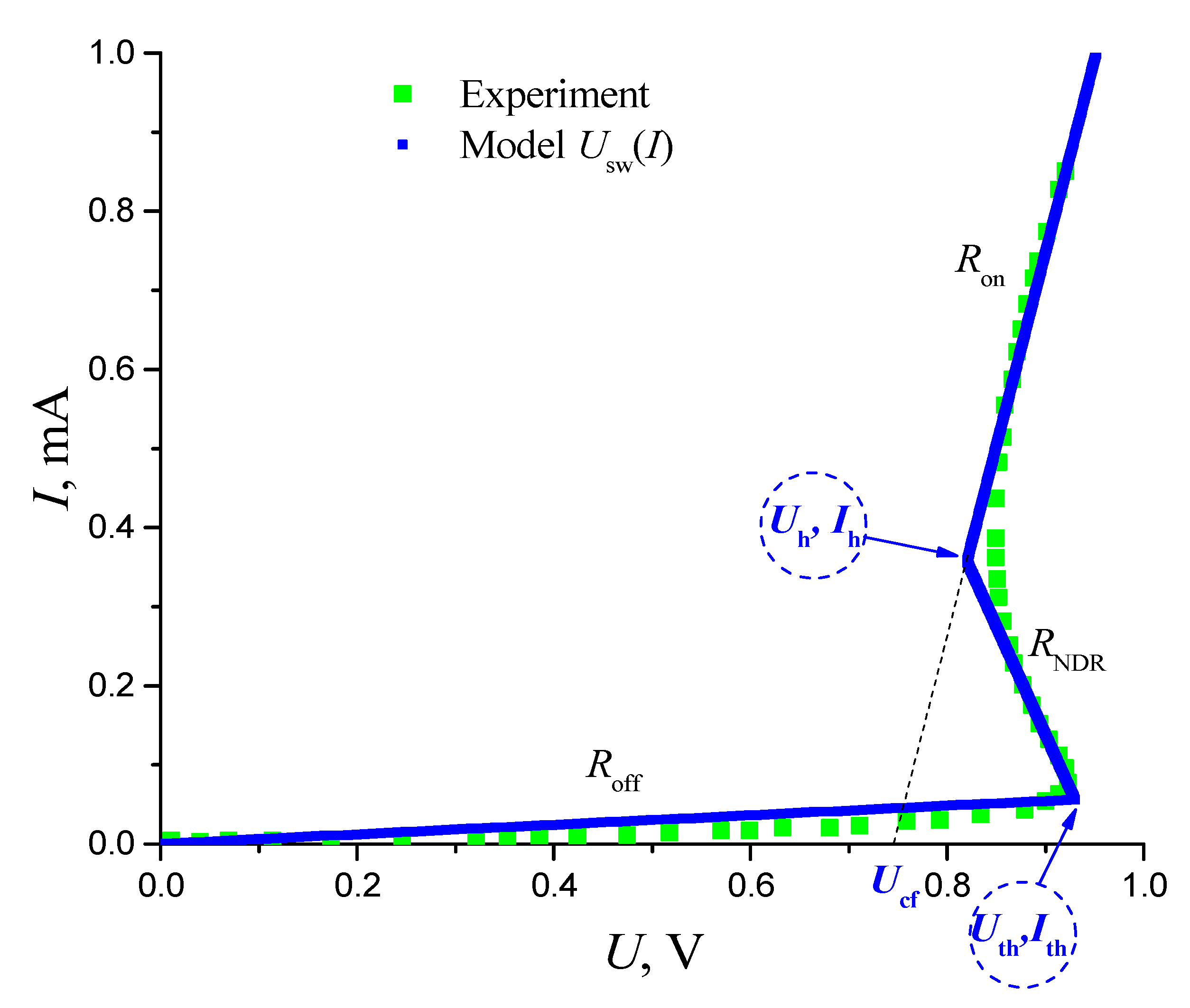
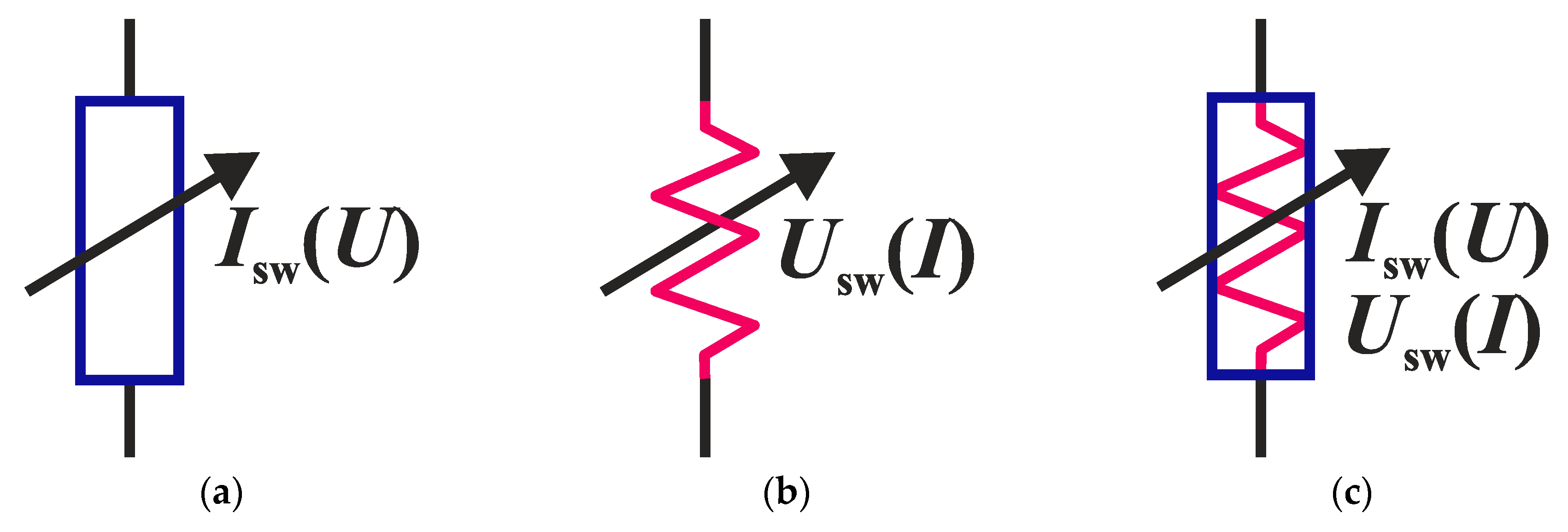
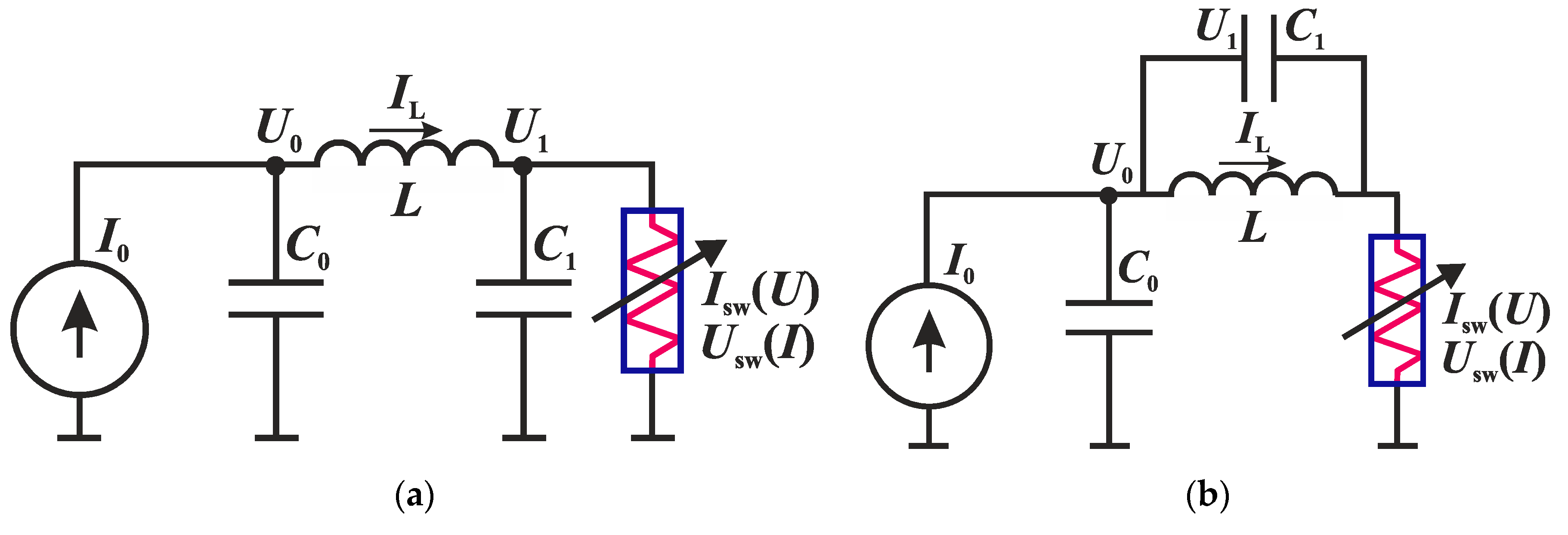
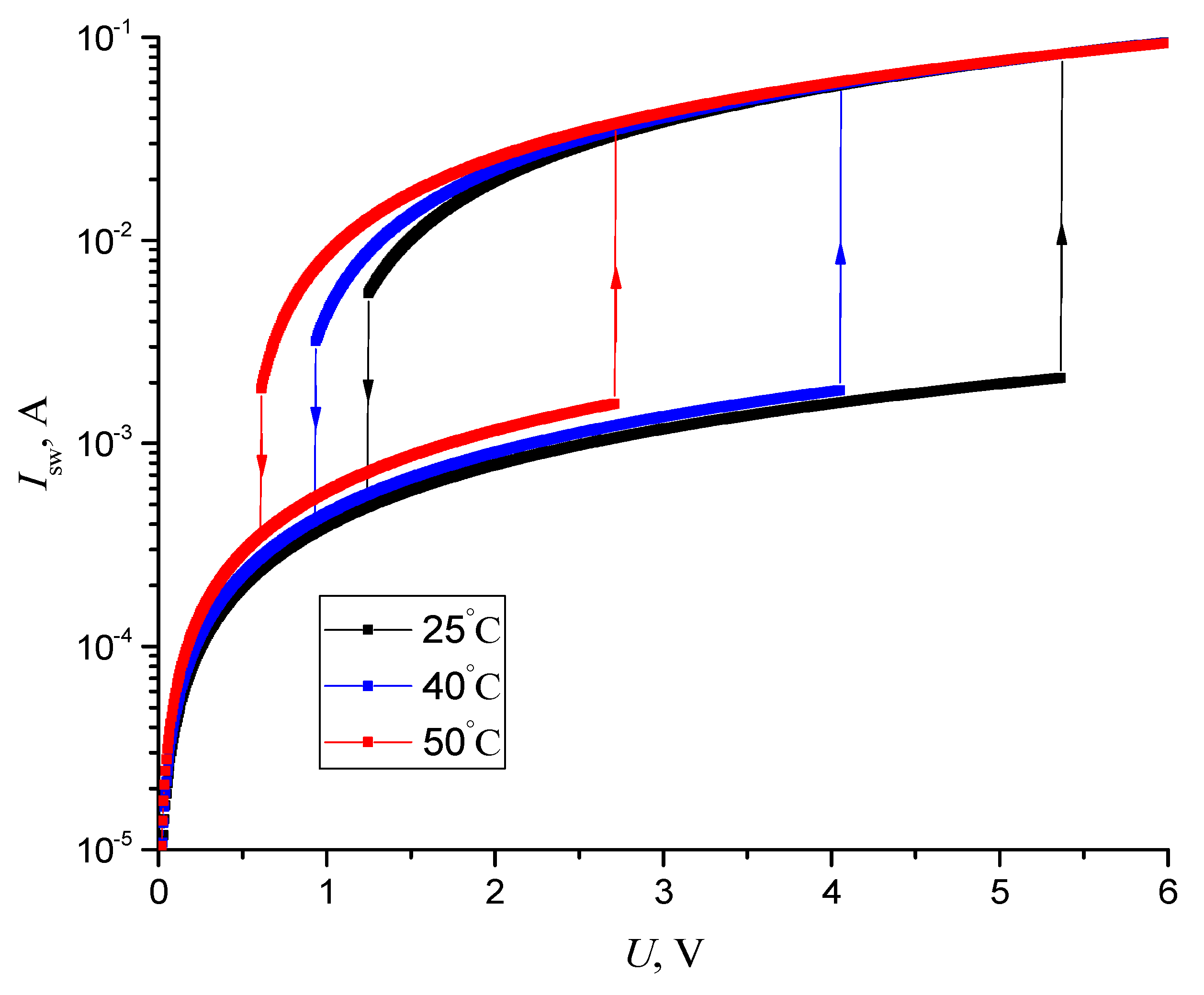
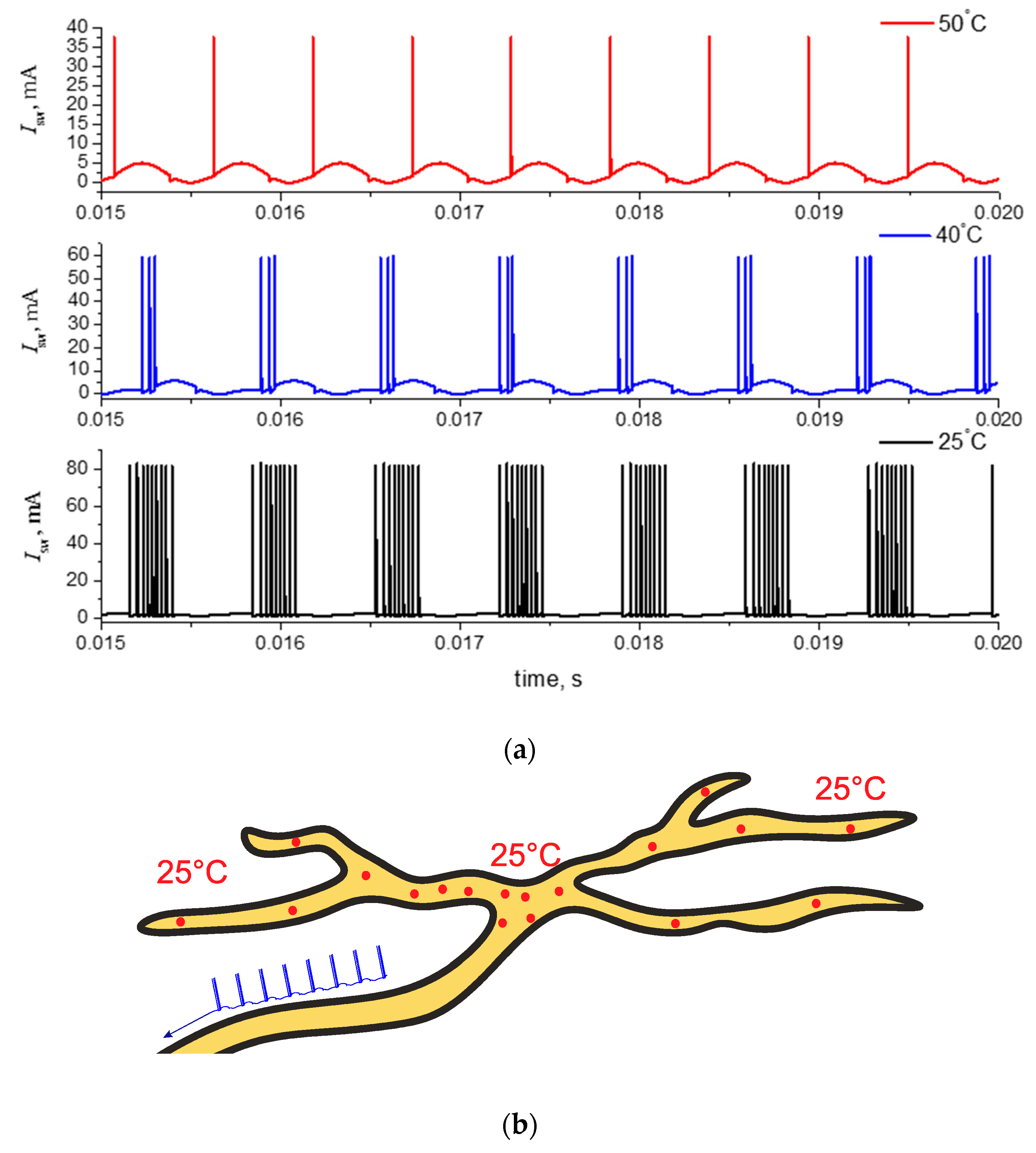
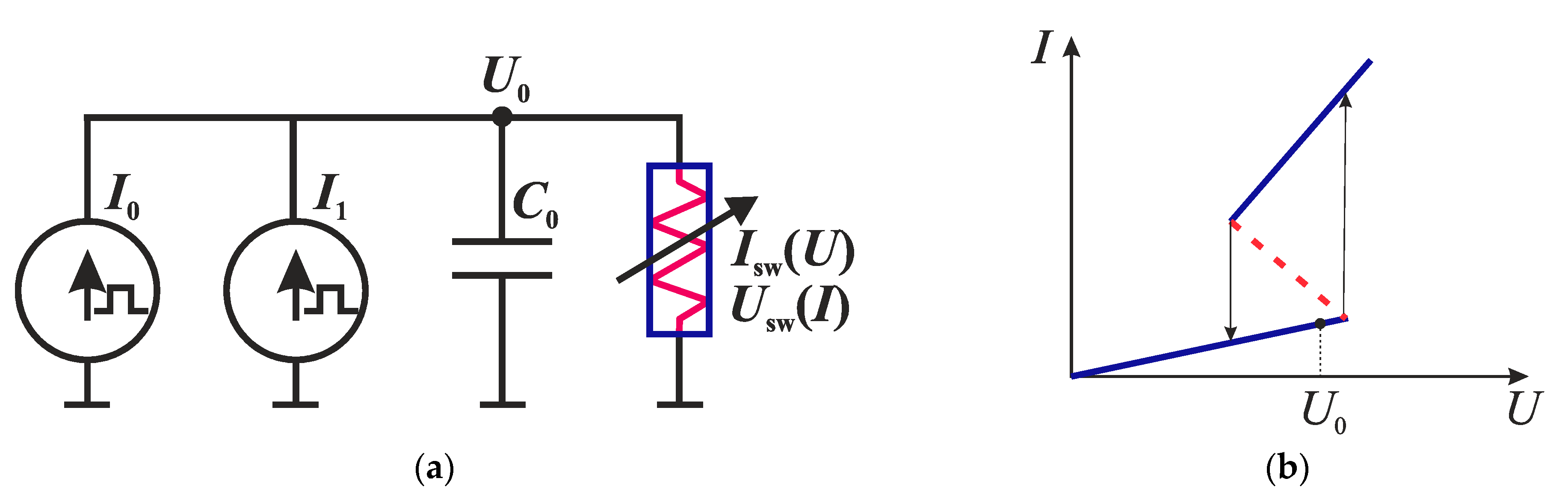
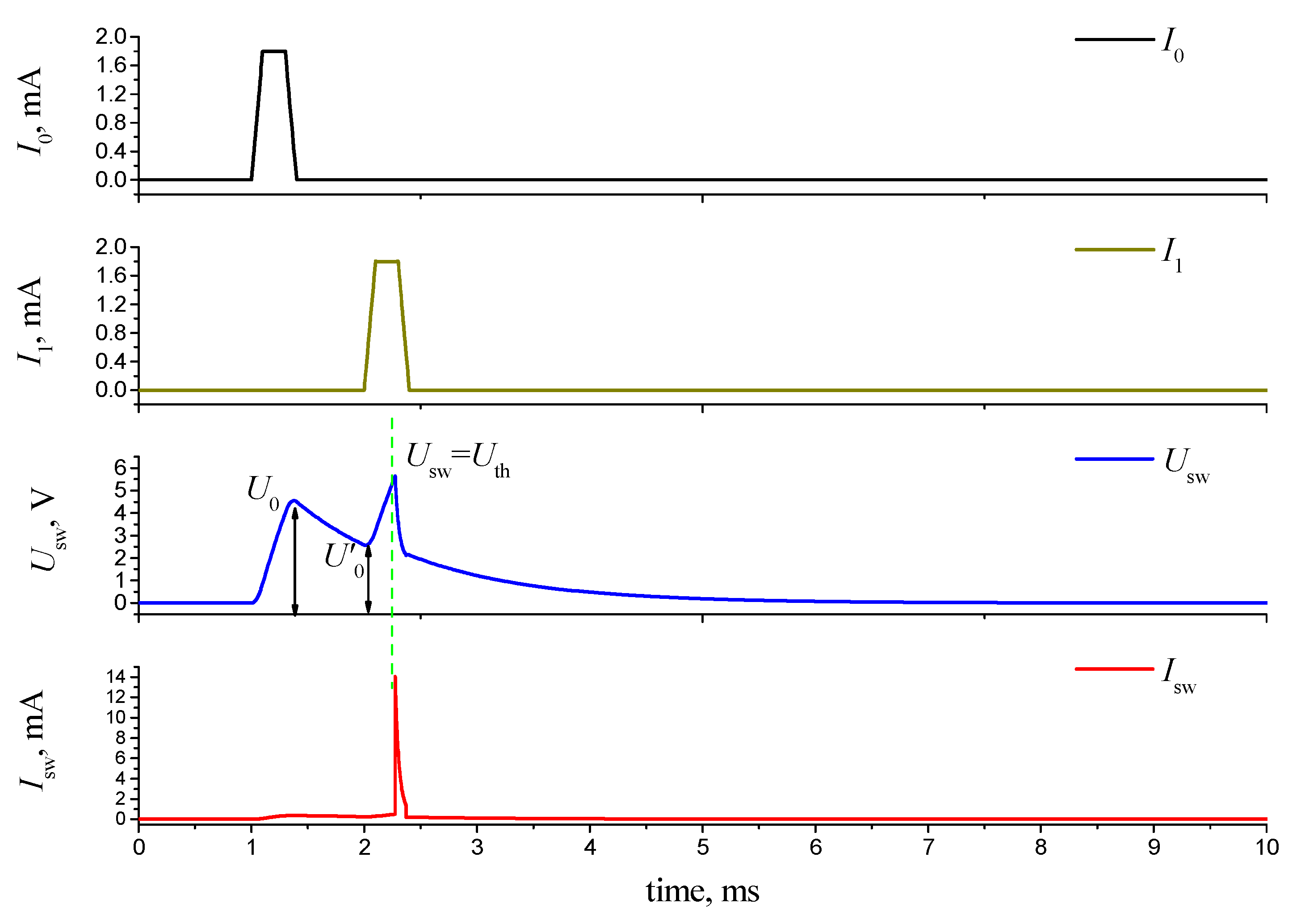
| Temperature, °C | Uth, V | Uh, V | Ron, Ω | Roff, Ω | Ucf, V |
|---|---|---|---|---|---|
| 25 | 5.36 | 1.247 | 53 | 2550 | 0.955 |
| 40 | 4.052 | 0.93 | 55 | 2216 | 0.758 |
| 50 | 2.714 | 0.607 | 58 | 1726 | 0.502 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boriskov, P.; Velichko, A. Switch Elements with S-Shaped Current-Voltage Characteristic in Models of Neural Oscillators. Electronics 2019, 8, 922. https://doi.org/10.3390/electronics8090922
Boriskov P, Velichko A. Switch Elements with S-Shaped Current-Voltage Characteristic in Models of Neural Oscillators. Electronics. 2019; 8(9):922. https://doi.org/10.3390/electronics8090922
Chicago/Turabian StyleBoriskov, Petr, and Andrei Velichko. 2019. "Switch Elements with S-Shaped Current-Voltage Characteristic in Models of Neural Oscillators" Electronics 8, no. 9: 922. https://doi.org/10.3390/electronics8090922
APA StyleBoriskov, P., & Velichko, A. (2019). Switch Elements with S-Shaped Current-Voltage Characteristic in Models of Neural Oscillators. Electronics, 8(9), 922. https://doi.org/10.3390/electronics8090922