Rollover-Free Path Planning for Off-Road Autonomous Driving
Abstract
1. Introduction
- To the best of our knowledge, this paper is the first time the vehicle rollover model has been introduced into path planning for off-road autonomous driving to enhance its safety.
- A path generation method is developed to generate a set of 3D path candidates following the off-road baseline.
- For each path candidate, a cost function to measure its driving comfortability is proposed with the consideration of road unevenness and path curvature.
- A cascaded path selection algorithm is developed in this paper to select the optimal path candidate in terms of rollover-free and collision-free safety and comfortability.
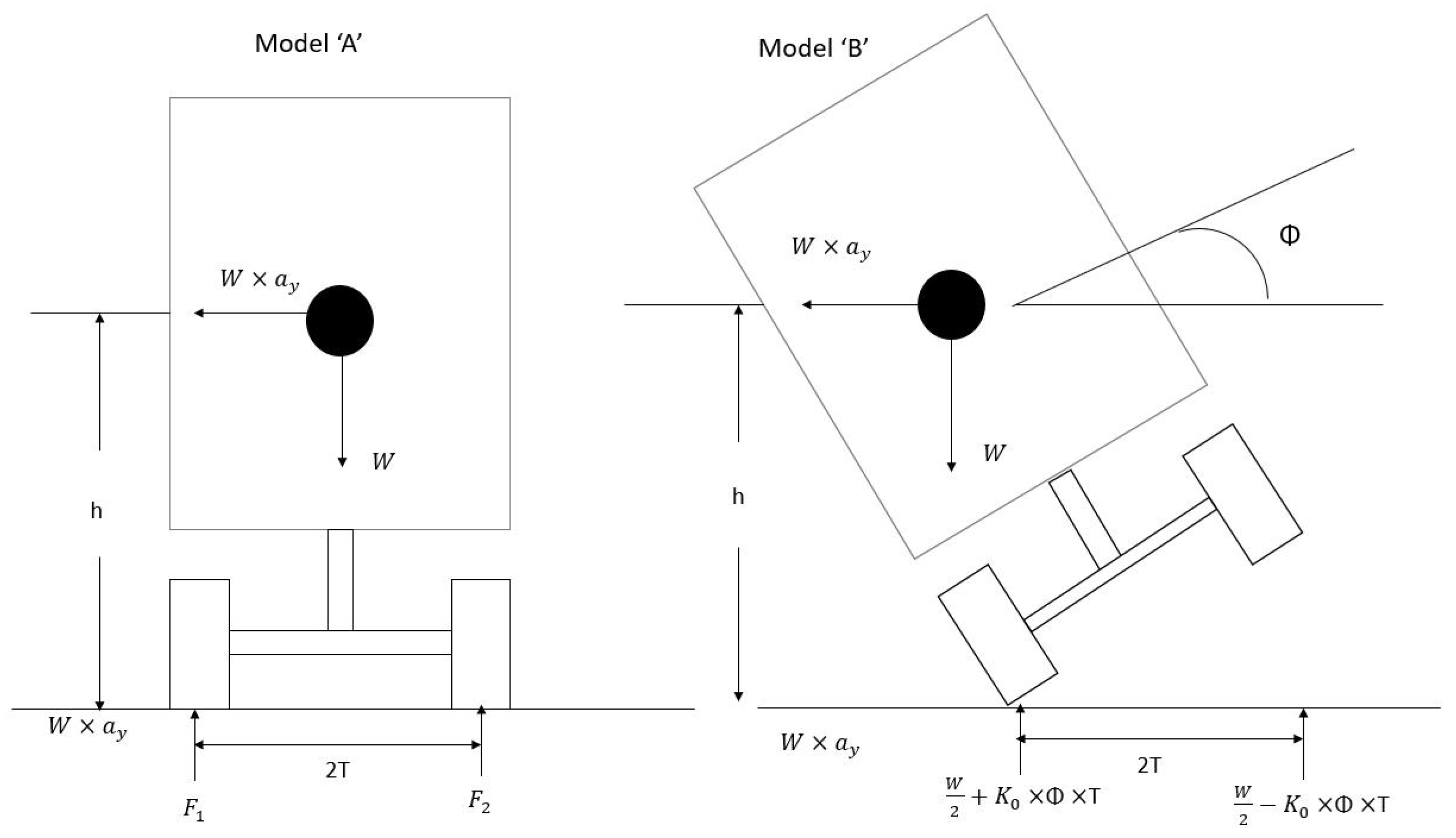
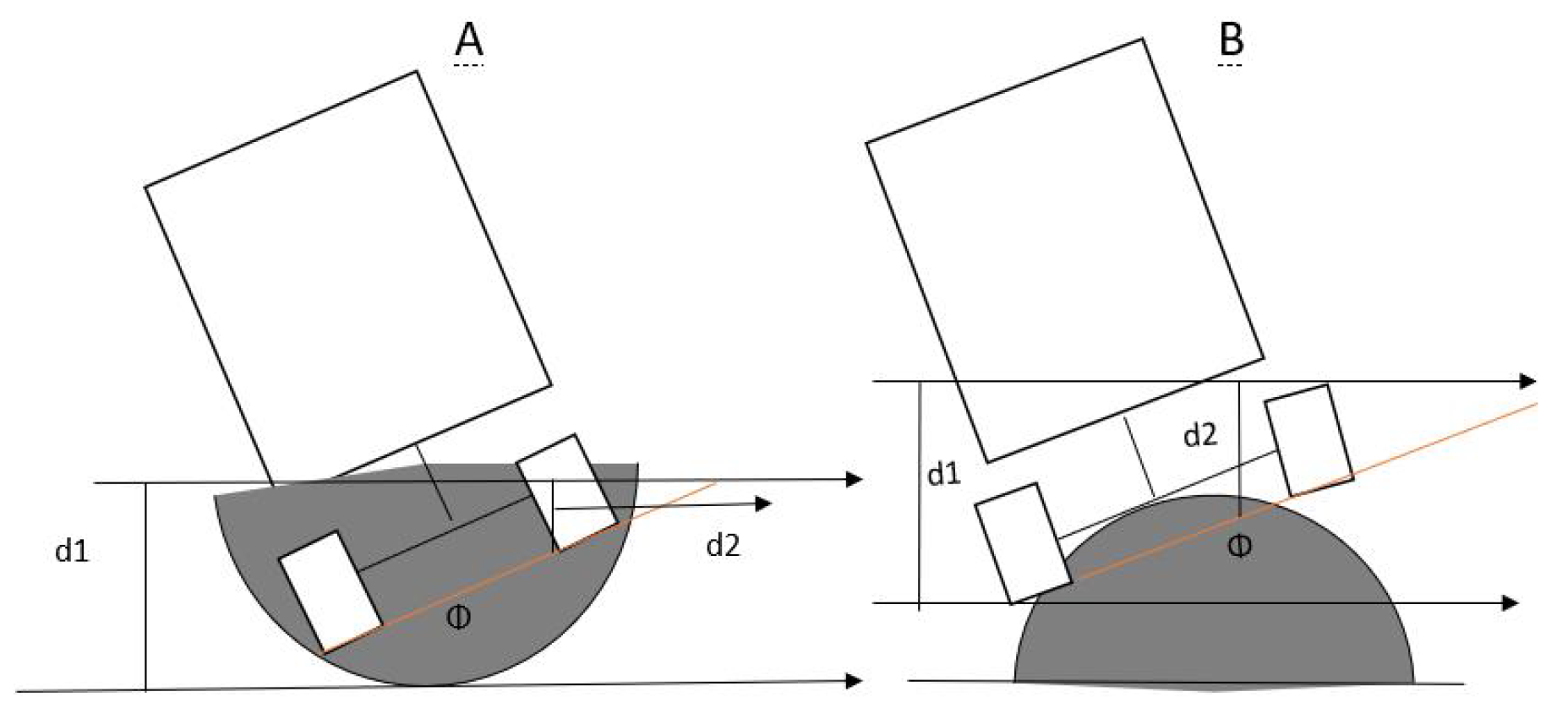
2. Time-to-Rollover Model
2.1. Introduction to the Time-To-Rollover Model
2.2. Rollover Model
3. Rollover-Free Local Path Planning
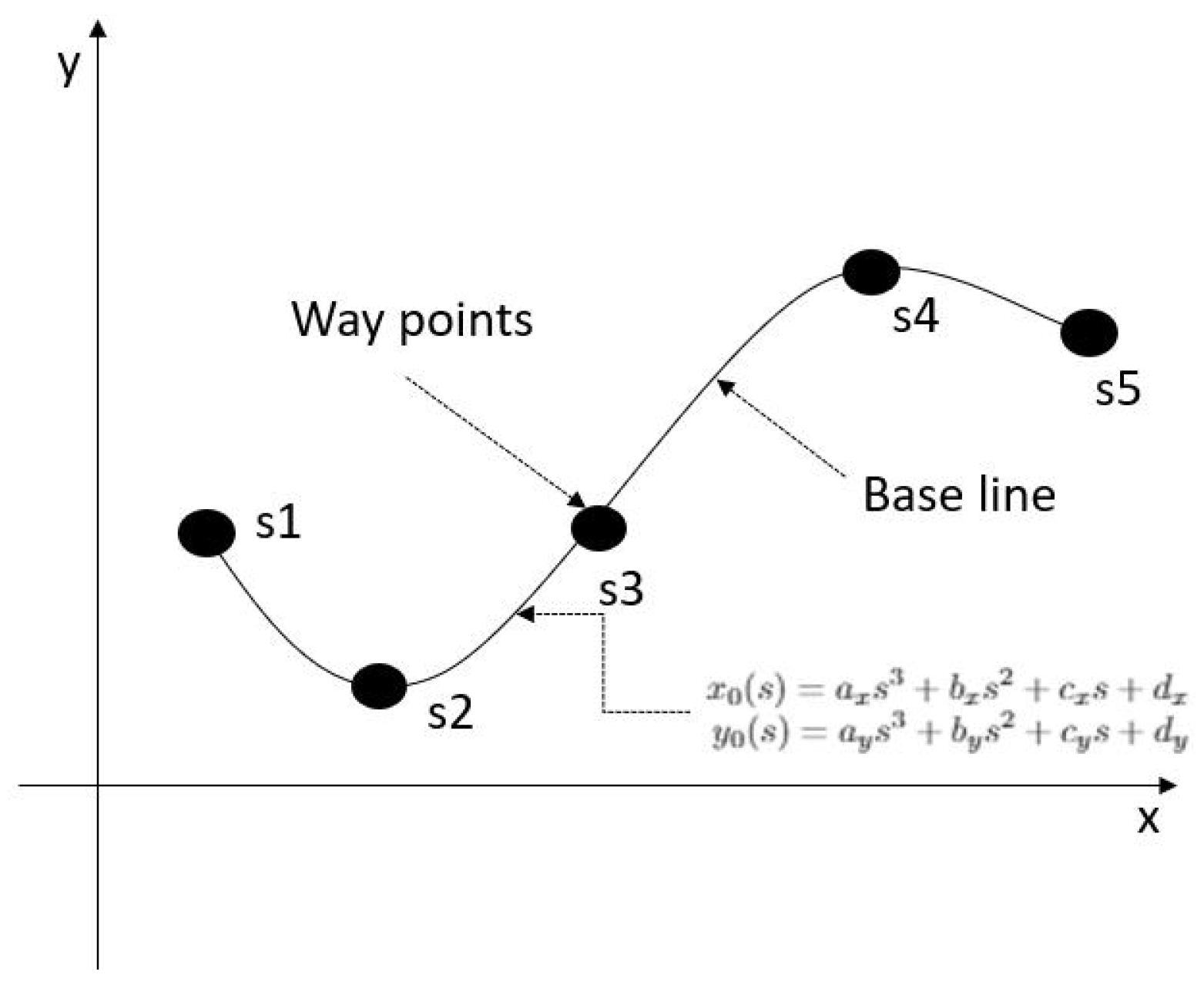
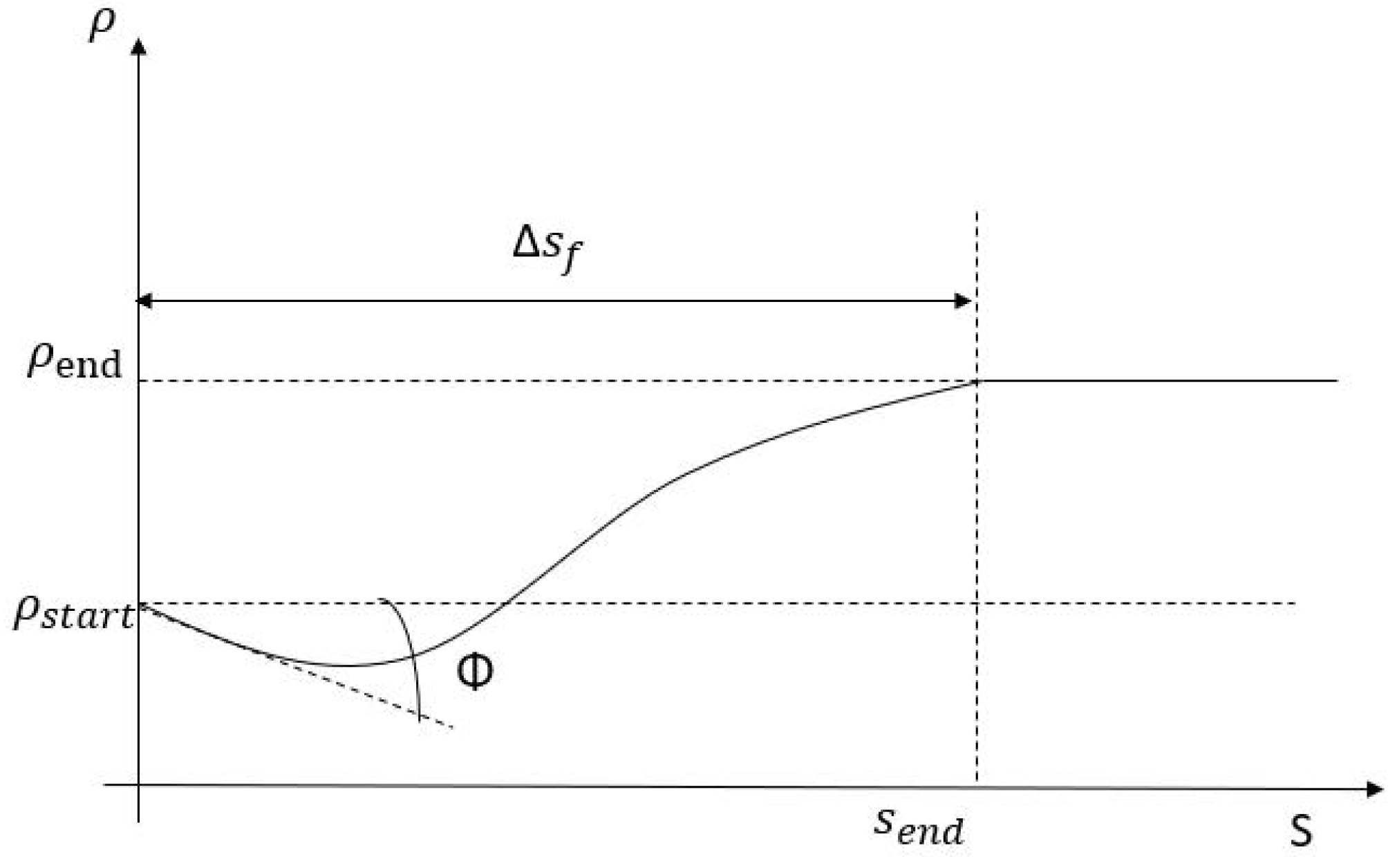
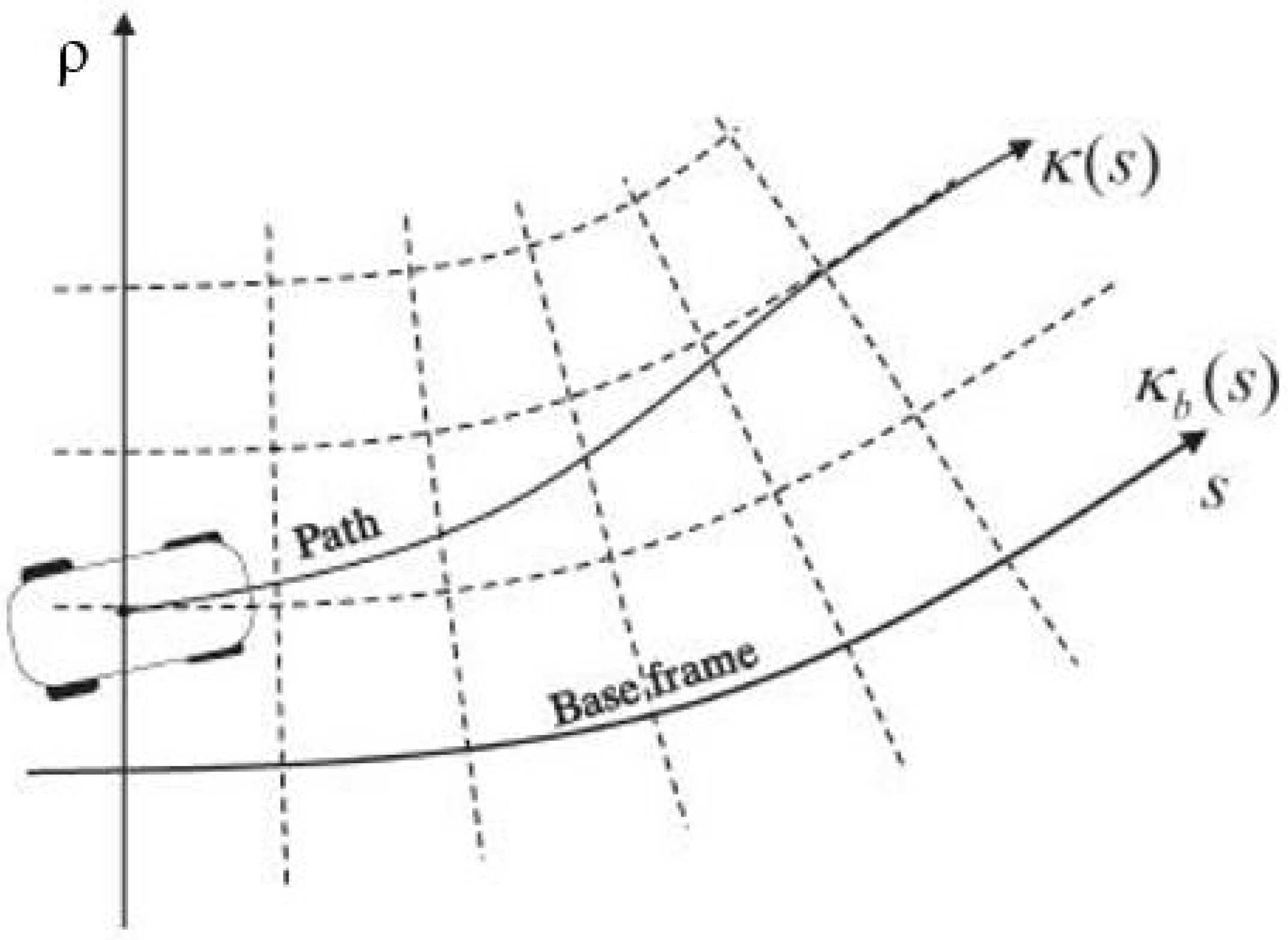
3.1. Off-Road Baseline Construction
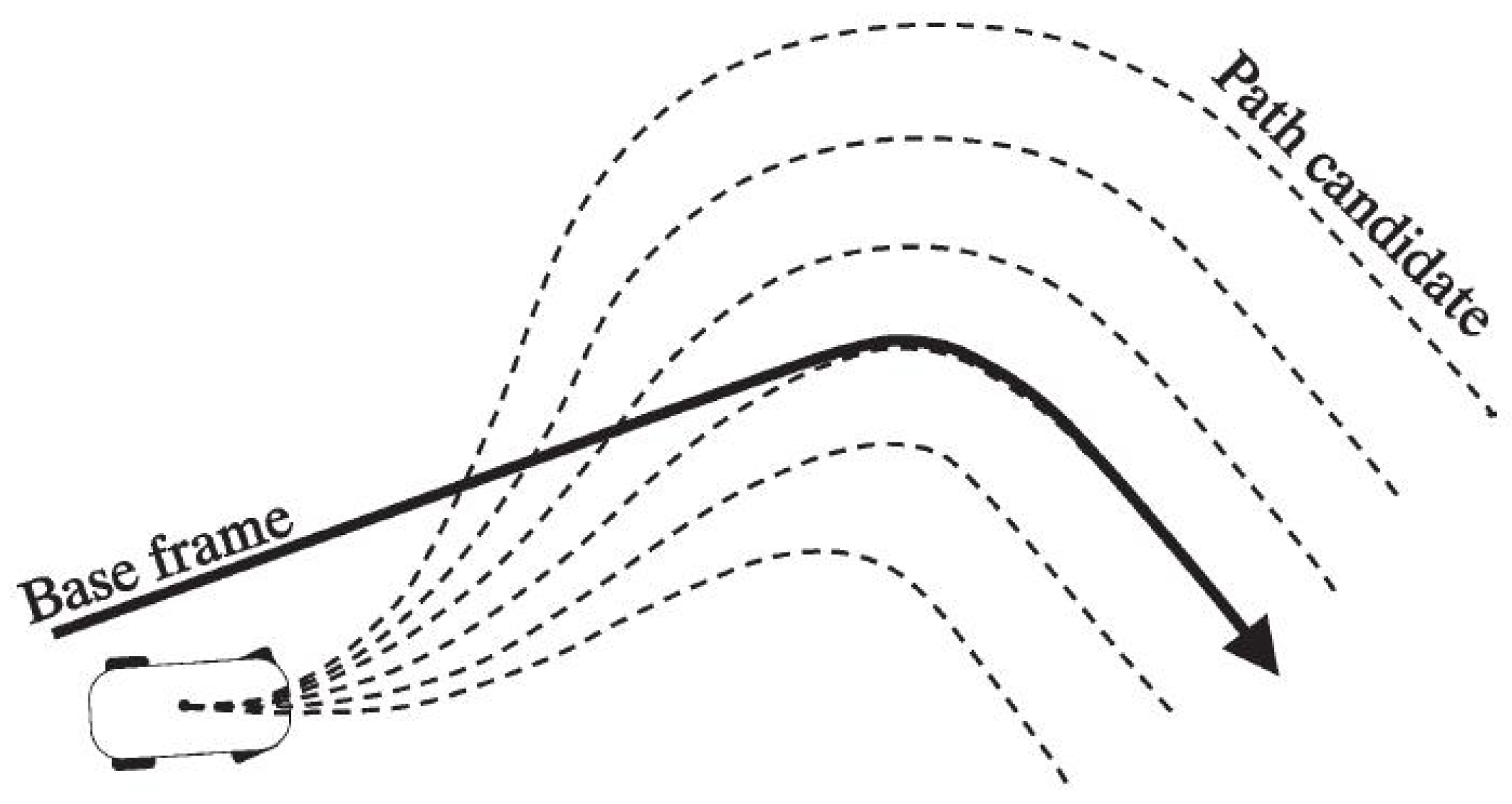
3.2. Path Candidates’ Generation
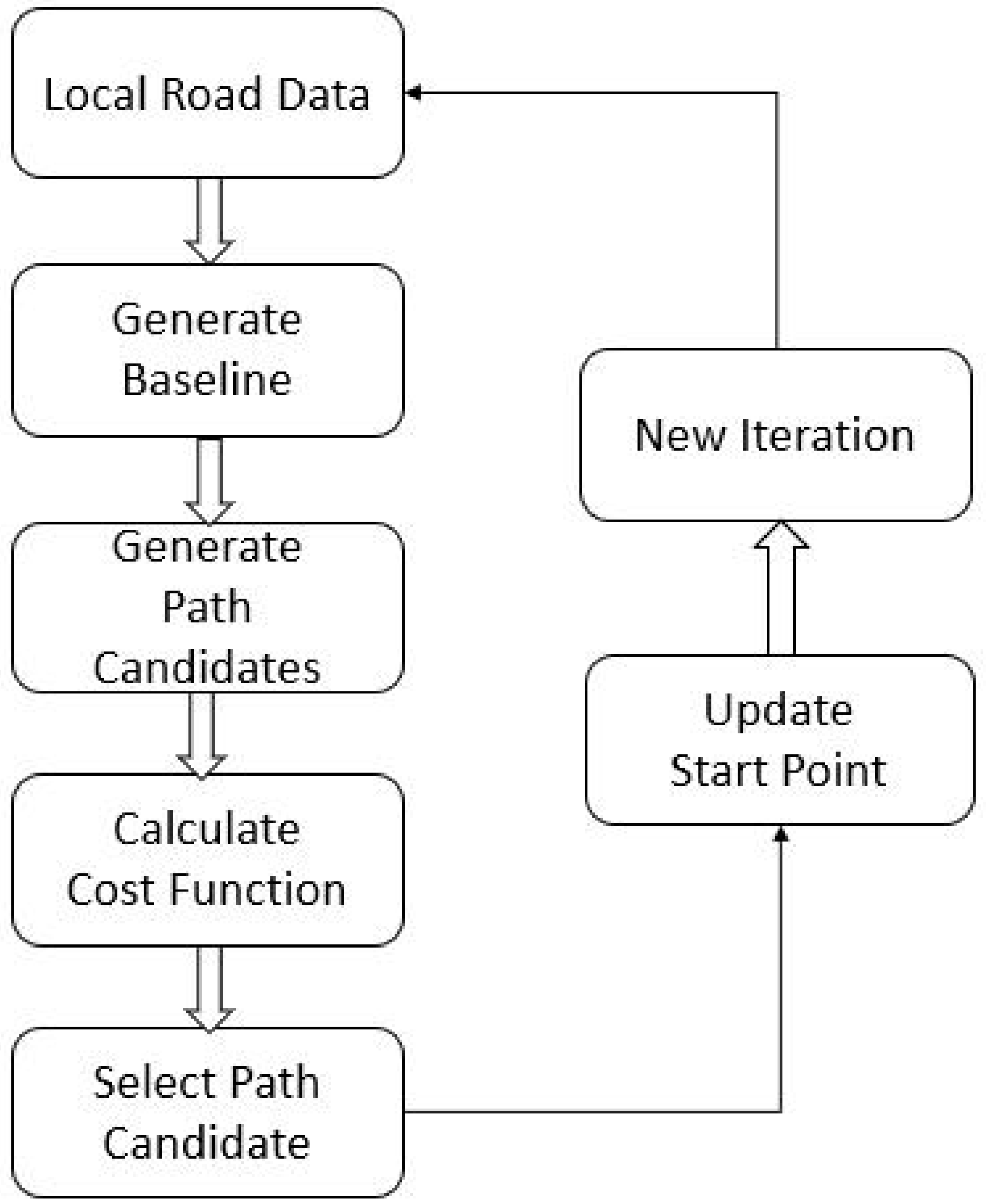
3.3. Path Selection Algorithm
3.3.1. Cost Function for Driving Safety
3.3.2. Cost Function for Comfortability
| Algorithm 1 Path candidate selection algorithm for off-road autonomous driving. |
| Require: The set of path candidates: , and 3D local map |
|
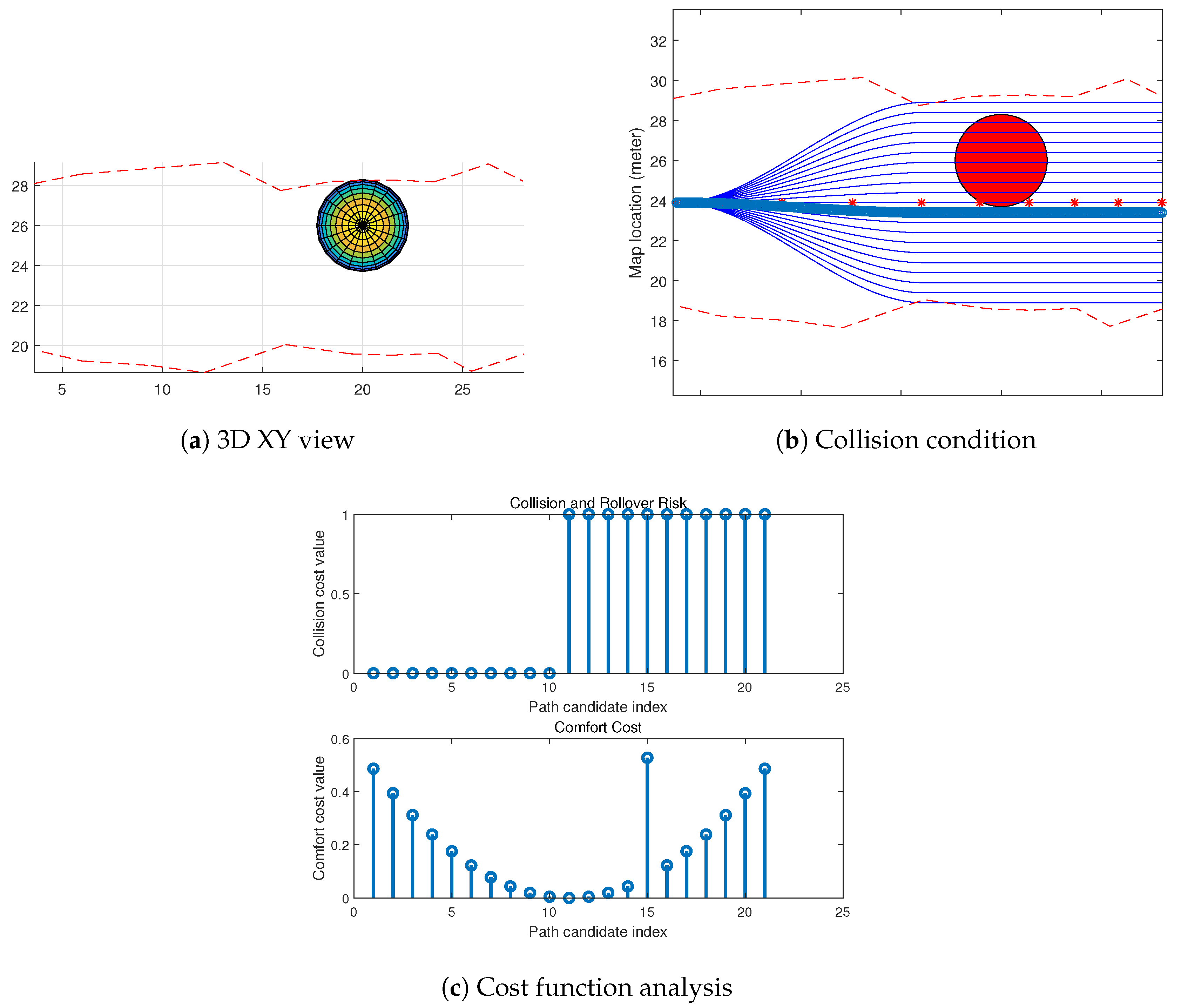
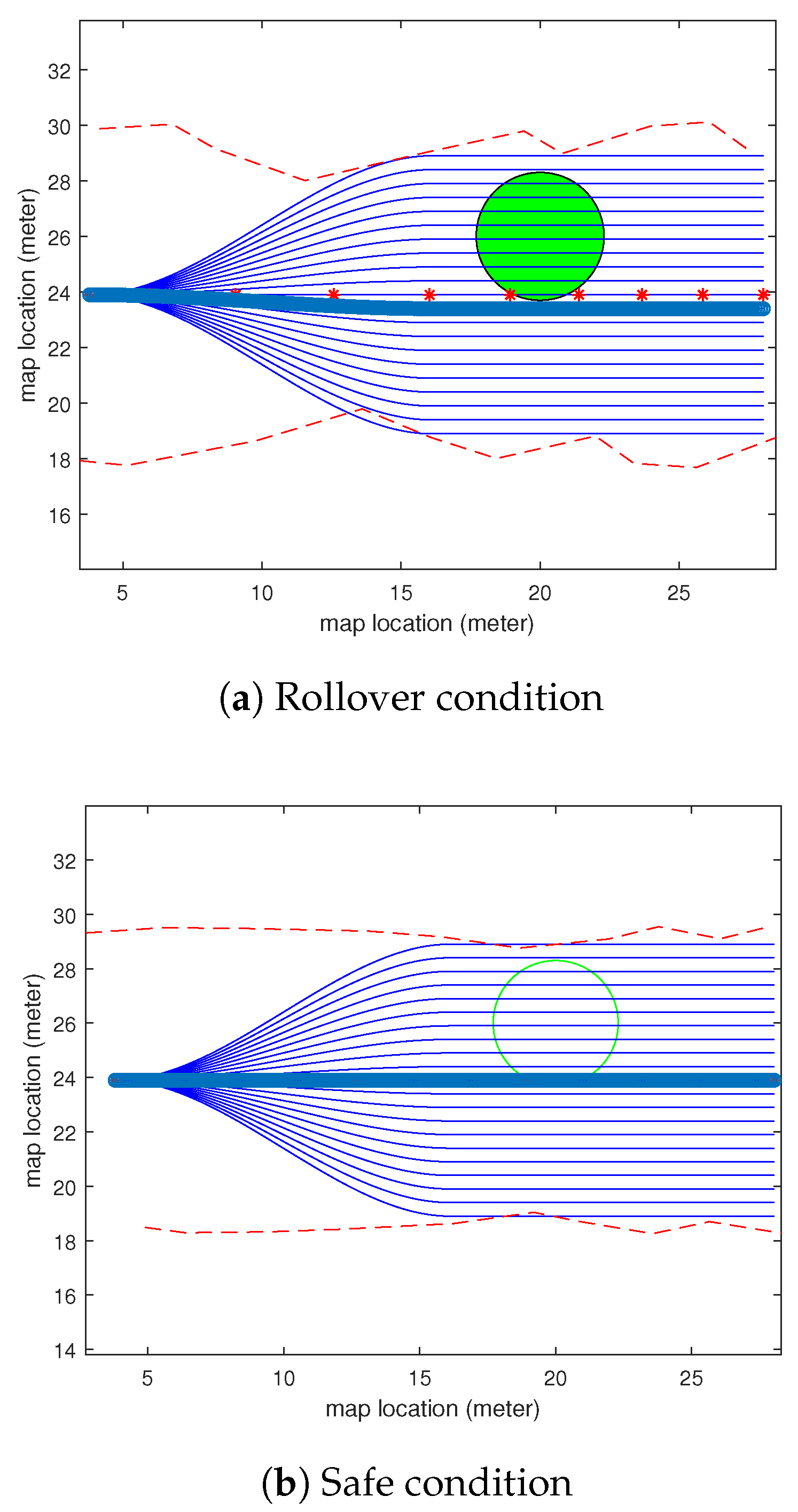
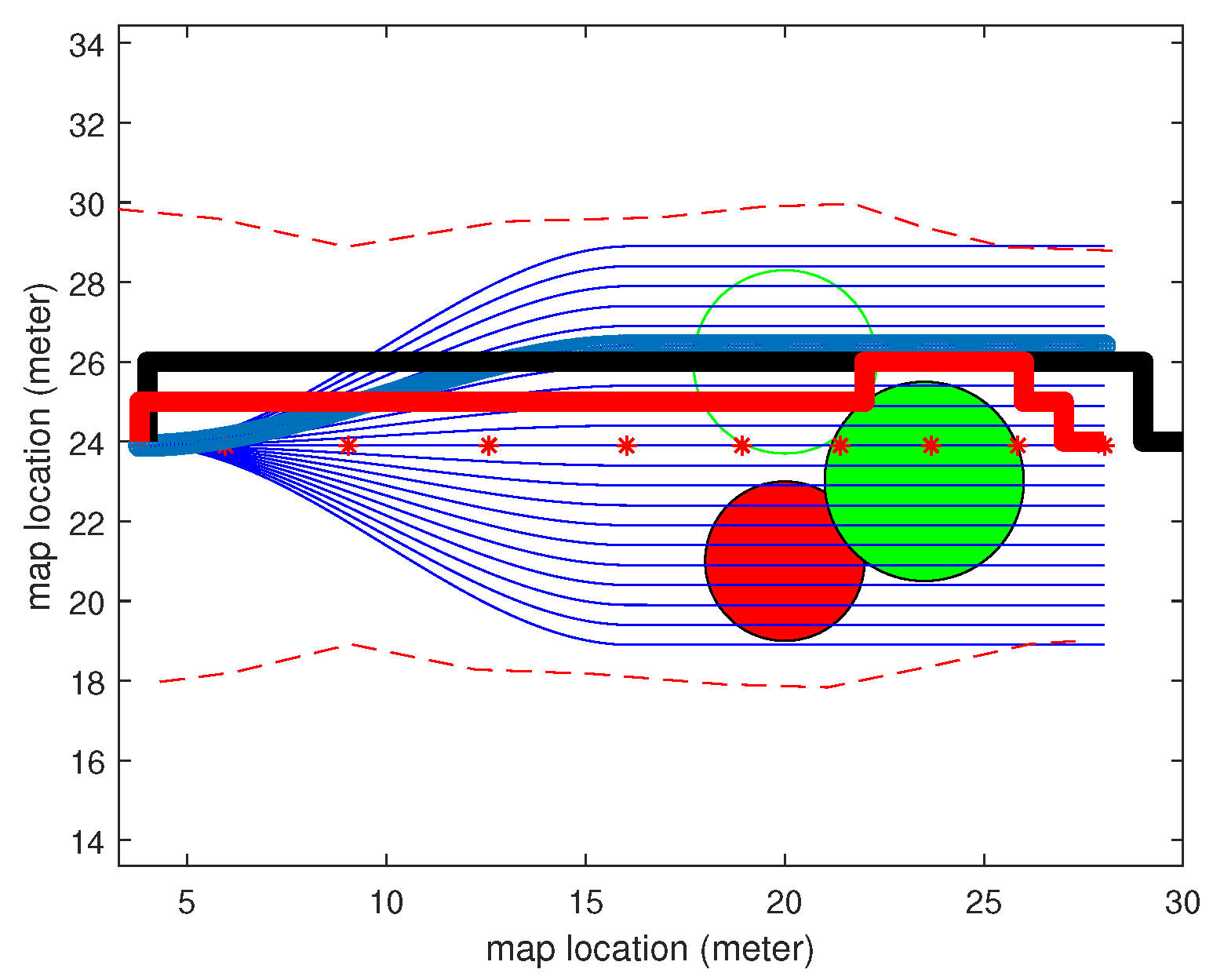
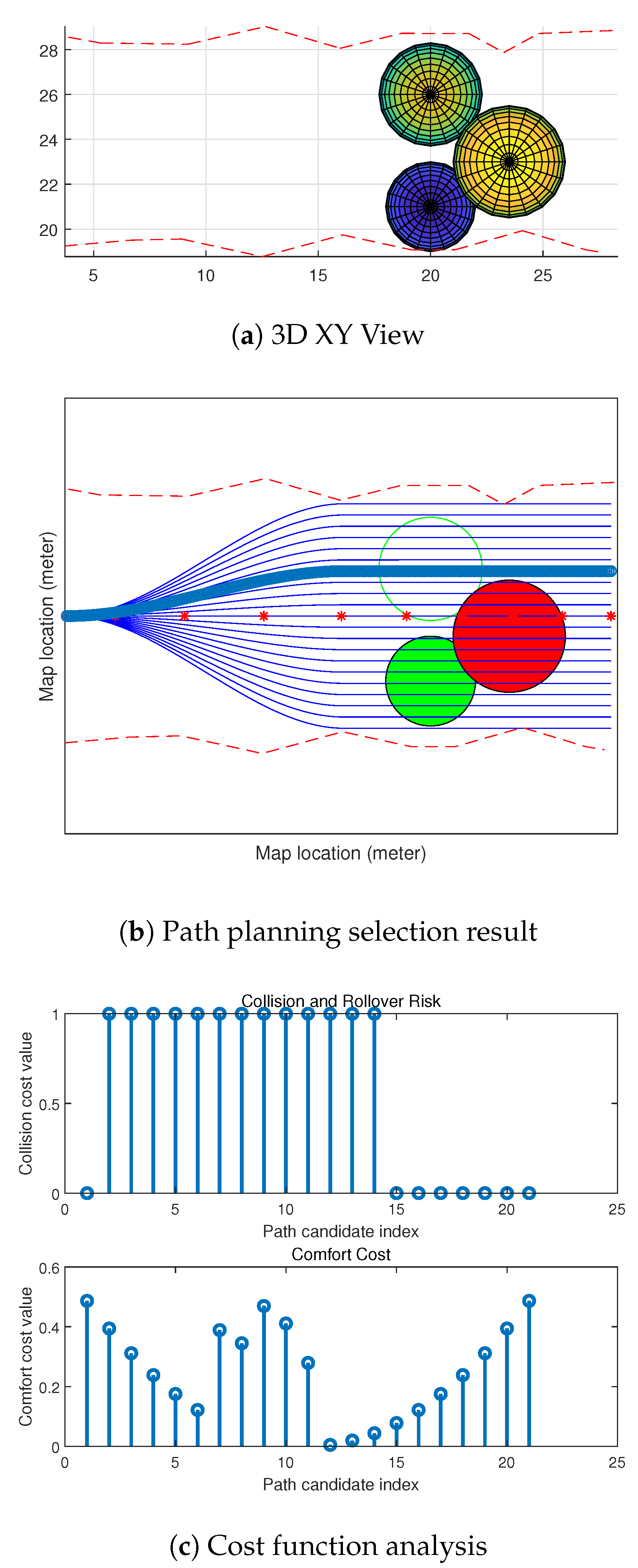
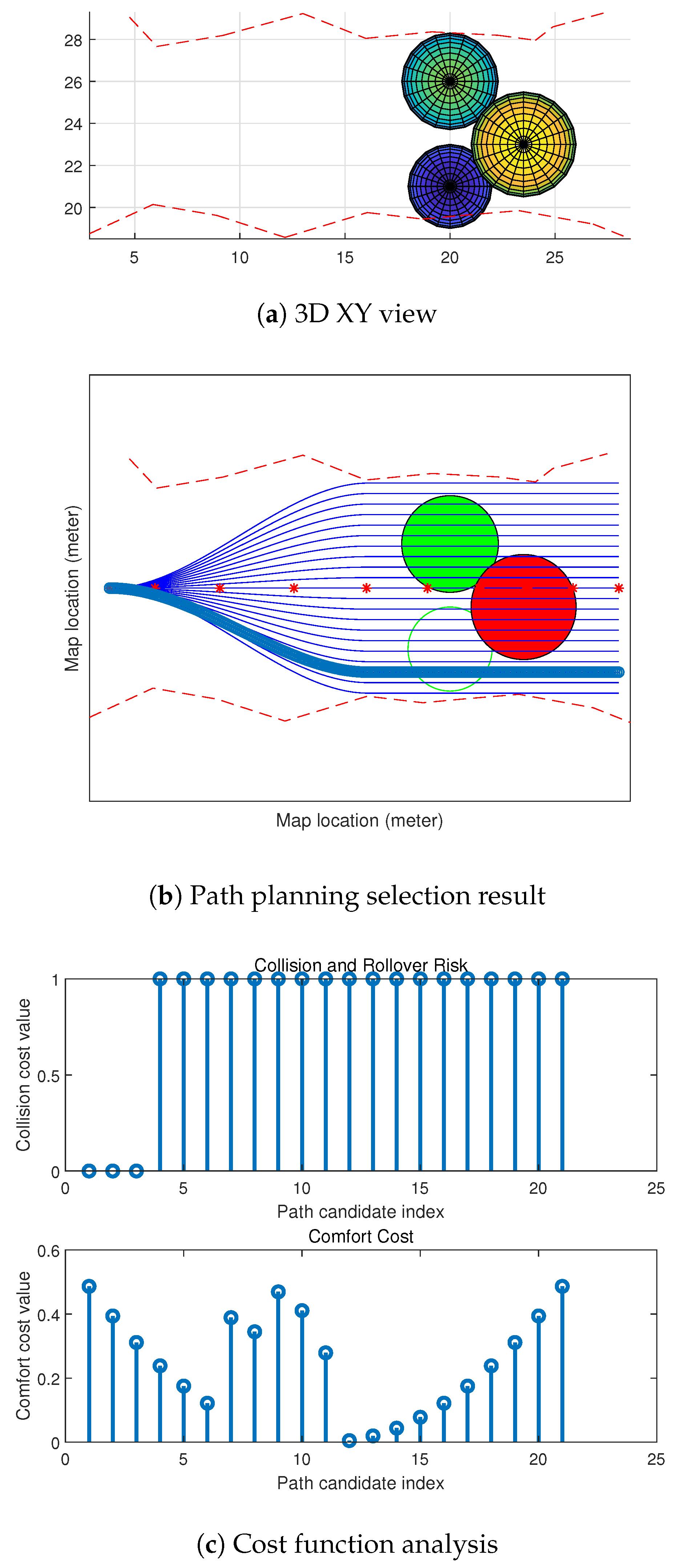
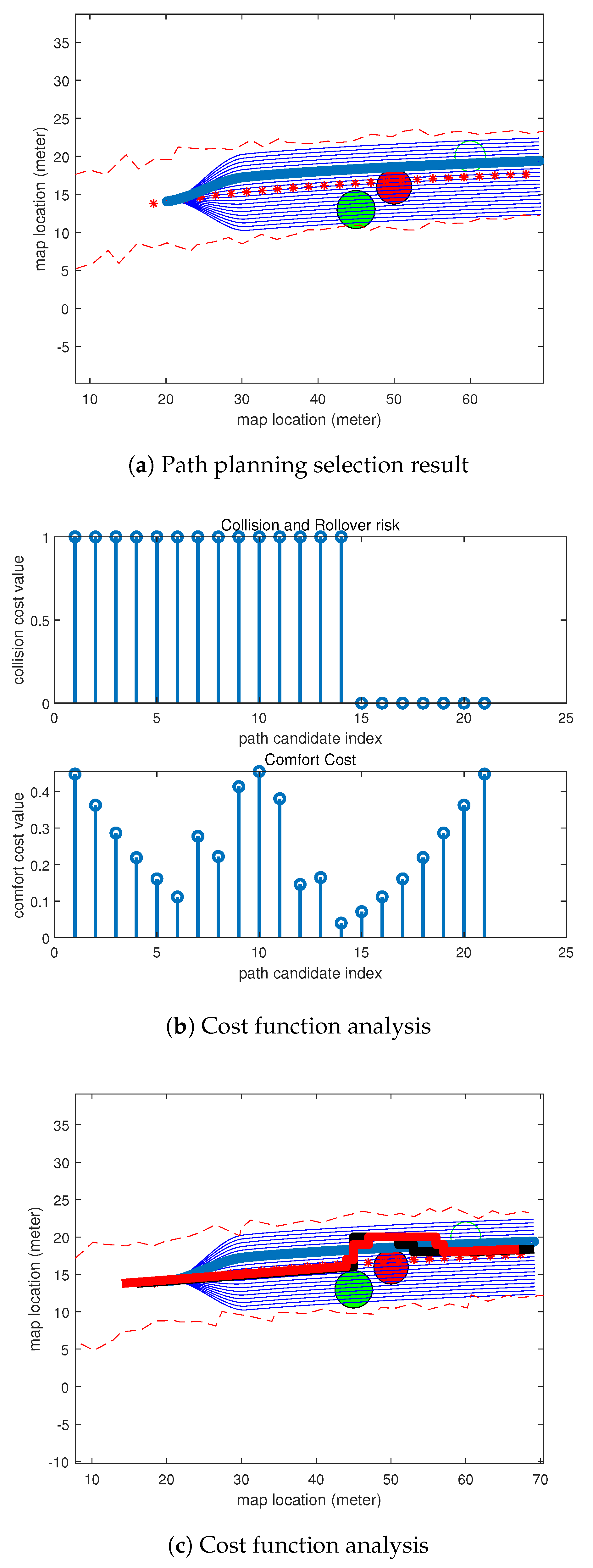
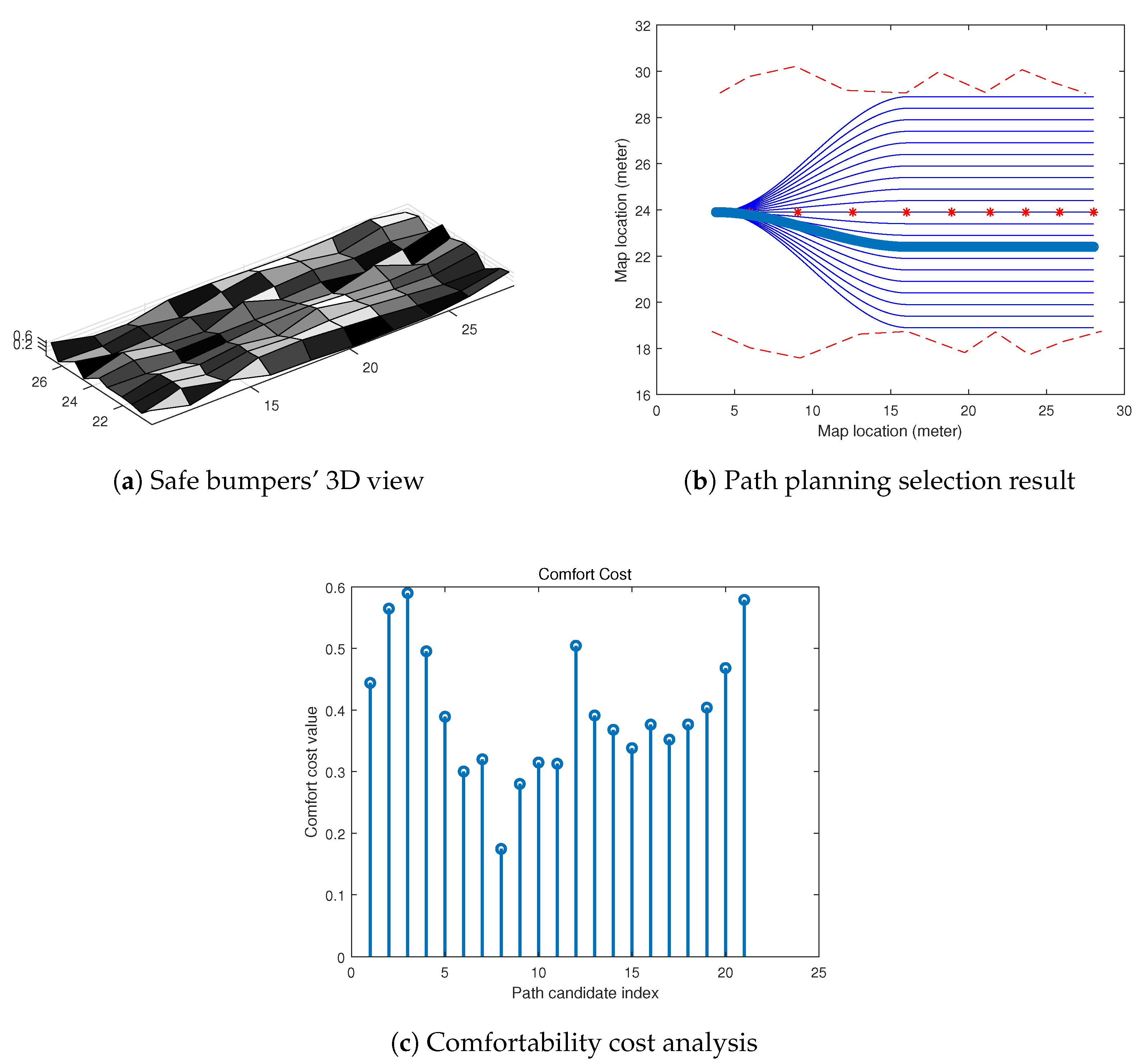
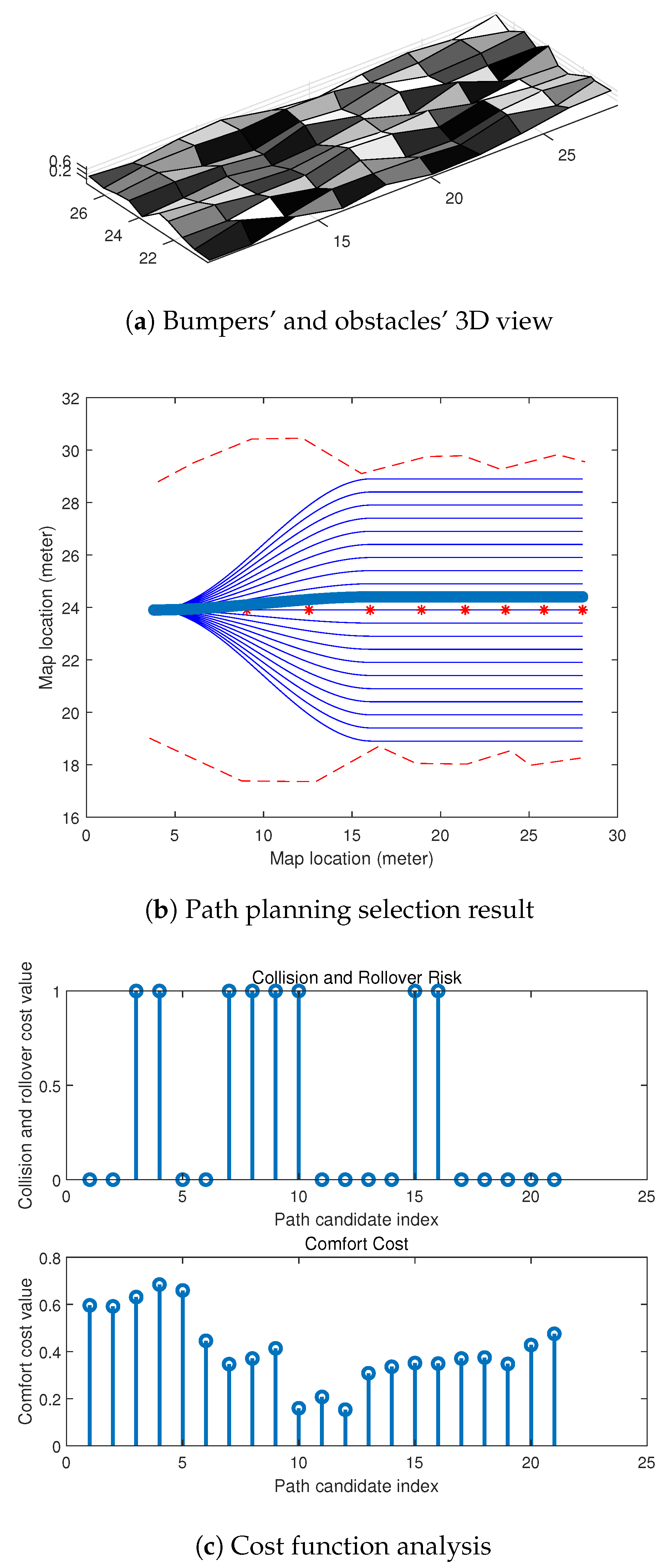
4. Experimental Results and Analysis
- Firstly, compared to the method, the path candidates generated by our method were able to follow the curvature of the baseline using the coordinate. This makes the generated paths have less turns on the map, which means it will be more comfortable for passengers in our autonomous vehicles.
- Secondly, the method was less efficient at determining the heuristic value when an obstacle was safe to pass, but needed more calculations on the vertical comfortability comparison. However, in our method, we built a good path selection model to find the best path candidate in a local map.
5. Discussions
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Glaser, S.; Vanholme, B.; Mammar, S.; Gruyer, D.; Nouveliere, L. Maneuver-based trajectory planning for highly autonomous vehicles on real road with traffic and driver interaction. IEEE Trans. Intell. Transp. Syst. 2010, 11, 589–606. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, J. Active steering actuator fault detection for an automatically-steered electric ground vehicle. IEEE Trans. Veh. Technol. 2017, 66, 3685–3702. [Google Scholar] [CrossRef]
- Hwang, J.; Lee, D.; Huh, K.; Na, H.; Kang, H. Development of a path planning system using mean shift algorithm for driver assistance. Int. J. Autom. Technol. 2011, 12, 119–124. [Google Scholar] [CrossRef]
- Yang, S.; Cao, Y.; Peng, Z.; Wen, G.; Guo, K. Distributed formation control of nonholonomic autonomous vehicle via RBF neural network. Mech. Syst. Signal Proces. 2017, 87, 81–95. [Google Scholar] [CrossRef]
- Zhu, M.; Chen, H.; Xiong, G. A model predictive speed tracking control approach for autonomous ground vehicles. Mech. Syst. Signal Proces. 2017, 87, 138–152. [Google Scholar] [CrossRef]
- Urmson, C.; Anhalt, J.; Bagnell, D.; Baker, C.; Bittner, R.; Clark, M.N.; Dolan, J.; Duggins, D.; Galatali, T.; Geyer, C.; et al. Autonomous driving in urban environments: Boss and the urban challenge. J. Field Robot. 2008, 25, 425–466. [Google Scholar] [CrossRef]
- Lee, H.-Y.; Shin, H.; Chae, J. Path Planning for Mobile Agents Using a Genetic Algorithm with a Direction Guided Factor. Electronics 2018, 7, 212. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. RRT-connect: An efficient approach to single-query path planning. In Proceedings of the IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 24–28 April 2000. [Google Scholar]
- Barraquand, J.; Langlois, B.; Latombe, J.-C. Numerical potential field techniques for robot path planning. IEEE Trans. Syst. Man Cybern. 1992, 22, 224–241. [Google Scholar] [CrossRef]
- Tang, W.; Sanville, E.; Henkelman, G. A grid-based Bader analysis algorithm without lattice bias. J. Phys. Condens. Matter 2009, 21, 84–204. [Google Scholar] [CrossRef]
- Pardalos, P.M.; Prokopyev, O.A.; Busygin, S. Continuous approaches to discrete optimization problems. Nonlinear Optim. Appl. 1996, 313–325. [Google Scholar]
- Hadsell, R.; Sermanet, P.; Ben, J.; Erkan, A.; Scoffier, M.; Kavukcuoglu, K.; Muller, U.; LeCun, Y. Learning long-range vision for autonomous off-road driving. J. Field Robot. 2009, 26, 120–144. [Google Scholar] [CrossRef]
- Hussein, A.; Marín-Plaza, P.; Martín, D.; de la Escalera, A.; Armingol, J.M. Autonomous off-road navigation using stereo-vision and laser-rangefinder fusion for outdoor obstacles detection. In Proceedings of the 2016 IEEE Intelligent Vehicles Symposium (IV), Gothenburg, Sweden, 19–22 June 2016; pp. 104–109. [Google Scholar]
- Raibert, M.; Blankespoor, K.; Nelson, G.; Playter, R. Bigdog, the rough-terrain quadruped robot. IFAC Proc. Vol. 2008, 41, 10822–10825. [Google Scholar] [CrossRef]
- Semini, C.; Tsagarakis, N.G.; Guglielmino, E.; Focchi, M.; Cannella, F.; Caldwell, D.G. Design of HyQ—A hydraulically and electrically actuated quadruped robot. J. Syst. Control Eng. 2011, 225, 831–849. [Google Scholar] [CrossRef]
- Wang, L.; Shu, C.; Jin, J.; Zhang, J. A novel traveling wave piezoelectric actuated tracked mobile robot utilizing friction effect. Smart Mater. Struct. 2017, 26, 035003. [Google Scholar] [CrossRef]
- Zhu, B.; Piao, Q.; Zhao, J.; Guo, L. Integrated chassis control for vehicle rollover prevention with neural network time-to-rollover warning metrics. Adv. Mech. Eng. 2016, 8. [Google Scholar] [CrossRef]
- Wang, H.; Lyu, W.; Yao, P.; Liang, X.; Liu, C. Three-dimensional path planning for unmanned aerial vehicle based on interfered fluid dynamical system. Chin. J. Aeronaut. 2015, 28, 229–339. [Google Scholar] [CrossRef]
- Maile, M.; Chen, Q.; Brown, G.; Delgrossi, L. Intersection collision avoidance: From driver alerts to vehicle control. In Proceedings of the 2015 IEEE 81st Vehicular Technology Conference (VTC Spring), Glasgow, UK, 11–14 May 2015; pp. 1–5. [Google Scholar]
- Cabodi, G.; Camurati, P.; Garbo, A.; Giorelli, M.; Quer, S.; Savarese, F. A Smart Many-Core Implementation of a Motion Planning Framework along a Reference Path for Autonomous Cars. Electronics 2019, 8, 177. [Google Scholar] [CrossRef]
- National Center for Statistics and Analysis. 2015 Motor Vehicle Crashes: Overview. In Traffic Safety Facts Research Note; National Highway Traffic Safety Administration: Washington, DC, USA, 2016; Volume 2016, pp. 1–9. [Google Scholar]
- Zhang, D.; Gordon, T.; Gao, Y.; Zong, C.; Lidberg, M. A novel control mediation approach to active rollover prevention. In Proceedings of the 13th International Symposium on Advanced Vehicle Control (AVEC’16), Munich, Germany, 13–16 September 2016; CRC Press: Boca Raton, FL, USA, 2016; p. 203. [Google Scholar]
- Jiménez, F.; Clavijo, M.; Naranjo, J.E.; Gómez, Ó. Improving the lane reference detection for autonomous road vehicle control. J. Sens. 2016, 2016, 9497524. [Google Scholar] [CrossRef]
- Chen, B.-C. Warning and Control for Vehicle Rollover Prevention. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2001. [Google Scholar]
- Goodin, C.; Doude, M.; Hudson, C.; Carruth, D. Enabling off-road autonomous navigation-simulation of LIDAR in dense vegetation. Electronics 2018, 7, 154. [Google Scholar] [CrossRef]
- Hudson, C.R.; Goodin, C.; Doude, M.; Carruth, D.W. Analysis of Dual LIDAR Placement for Off-Road Autonomy Using MAVS. In Proceedings of the IEEE 2018 World Symposium on Digital Intelligence for Systems and Machines (DISA), Kosice, Slovakia, 23–25 August 2018; pp. 137–142. [Google Scholar]
- Goodin, C.; Carruth, D.; Doude, M.; Hudson, C. Predicting the Influence of Rain on LIDAR in ADAS. Electronics 2018, 8, 89. [Google Scholar] [CrossRef]
- Goodin, C.; Sharma, S.; Doude, M.; Carruth, D.; Dabbiru, L.; Hudson, C. Training of Neural Networks with Automated Labeling of Simulated Sensor Data; SAE Technical Paper; SAE: Detroit, MI, USA, 2019. [Google Scholar]
- Choset, H.M.; Hutchinson, S.; Lynch, K.M.; Kantor, G.; Burgard, W.; Kavraki, L.E.; Thrun, S. Principles of Robot Motion: Theory, Algorithms, and Implementation; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Ahlberg, J.H.; Nilson, E.N.; Walsh, J.L. The Theory of Splines and Their Applications: Mathematics in Science and Engineering: A Series of Monographs and Textbooks; Elsevier: New York, NY, USA; London, UK, 1967; Volume 38. [Google Scholar]
- Guenter, B.; Parent, R. Computing the arc length of parametric curves. IEEE Comput. Graph. Appl. 1990, 10, 72–78. [Google Scholar] [CrossRef]
- Wang, H.; Kearney, J.; Atkinson, K. Arc-length parameterized spline curves for real-time simulation. In Proceedings of the 5th International Conference on Curves and Surfaces, Saint-Malo, France, 27 June–3 July 2002; pp. 387–396. [Google Scholar]
- Wang, H.; Kearney, J.; Atkinson, K. Robust and efficient computation of the closest point on a spline curve. In Proceedings of the 5th International Conference on Curves and Surfaces, Saint-Malo, France, 27 June–3 July 2002; pp. 397–406. [Google Scholar]
- Barfoot, T.D.; Clark, C.M. Motion planning for formations of mobile robots. Robot. Auton. Syst. 2004, 46, 365–378. [Google Scholar] [CrossRef]
- Chu, K.; Lee, M.; Sunwoo, M. Local path planning for off-road autonomous driving with avoidance of static obstacles. IEEE Trans. Intell. Trans. Syst. 2012, 13, 1599–1616. [Google Scholar] [CrossRef]
- Duchoň, F.; Babinec, A.; Kajan, M.; Beňo, P.; Florek, M.; Fico, T.; Jurišica, L. Path planning with modified a star algorithm for a mobile robot. Procedia Eng. 2014, 96, 59–69. [Google Scholar] [CrossRef]
- Aslam, J.A.; Pelekhov, E.; Rus, D. The star clustering algorithm for static and dynamic information organization. J. Graph Algorithms Appl. 2004, 8, 95–129. [Google Scholar] [CrossRef]
- Gil-García, R.; Pons-Porrata, A. Dynamic hierarchical algorithms for document clustering. Pattern Recognit. Lett. 2010, 31, 469–477. [Google Scholar] [CrossRef]
- Castaño, F.; Beruvides, G.; Haber, R.; Artuñedo, A. Obstacle recognition based on machine learning for on-chip LiDAR sensors in a cyber-physical system. Sensors 2017, 17, 2109. [Google Scholar] [CrossRef] [PubMed]
- Spagnol, S.; Saitis, C.; Bujacz, M.; Jóhannesson, O.I.; Kalimeri, K.; Moldoveanu, A.; Kristjánsson, A.; Unnthorsson, R. Model-based obstacle sonification for the navigation of visually impaired persons. In Proceedings of the 19th International Conference Digital Audio Effects (DAFx-16), Brno, Czech Republic, 5–9 September 2016; pp. 309–316. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Tang, B.; Ball, J.; Doude, M.; Carruth, D.W. Rollover-Free Path Planning for Off-Road Autonomous Driving. Electronics 2019, 8, 614. https://doi.org/10.3390/electronics8060614
Li X, Tang B, Ball J, Doude M, Carruth DW. Rollover-Free Path Planning for Off-Road Autonomous Driving. Electronics. 2019; 8(6):614. https://doi.org/10.3390/electronics8060614
Chicago/Turabian StyleLi, Xingyu, Bo Tang, John Ball, Matthew Doude, and Daniel W. Carruth. 2019. "Rollover-Free Path Planning for Off-Road Autonomous Driving" Electronics 8, no. 6: 614. https://doi.org/10.3390/electronics8060614
APA StyleLi, X., Tang, B., Ball, J., Doude, M., & Carruth, D. W. (2019). Rollover-Free Path Planning for Off-Road Autonomous Driving. Electronics, 8(6), 614. https://doi.org/10.3390/electronics8060614







