A Novel MFDFA Algorithm and Its Application to Analysis of Harmonic Multifractal Features
Abstract
1. Introduction
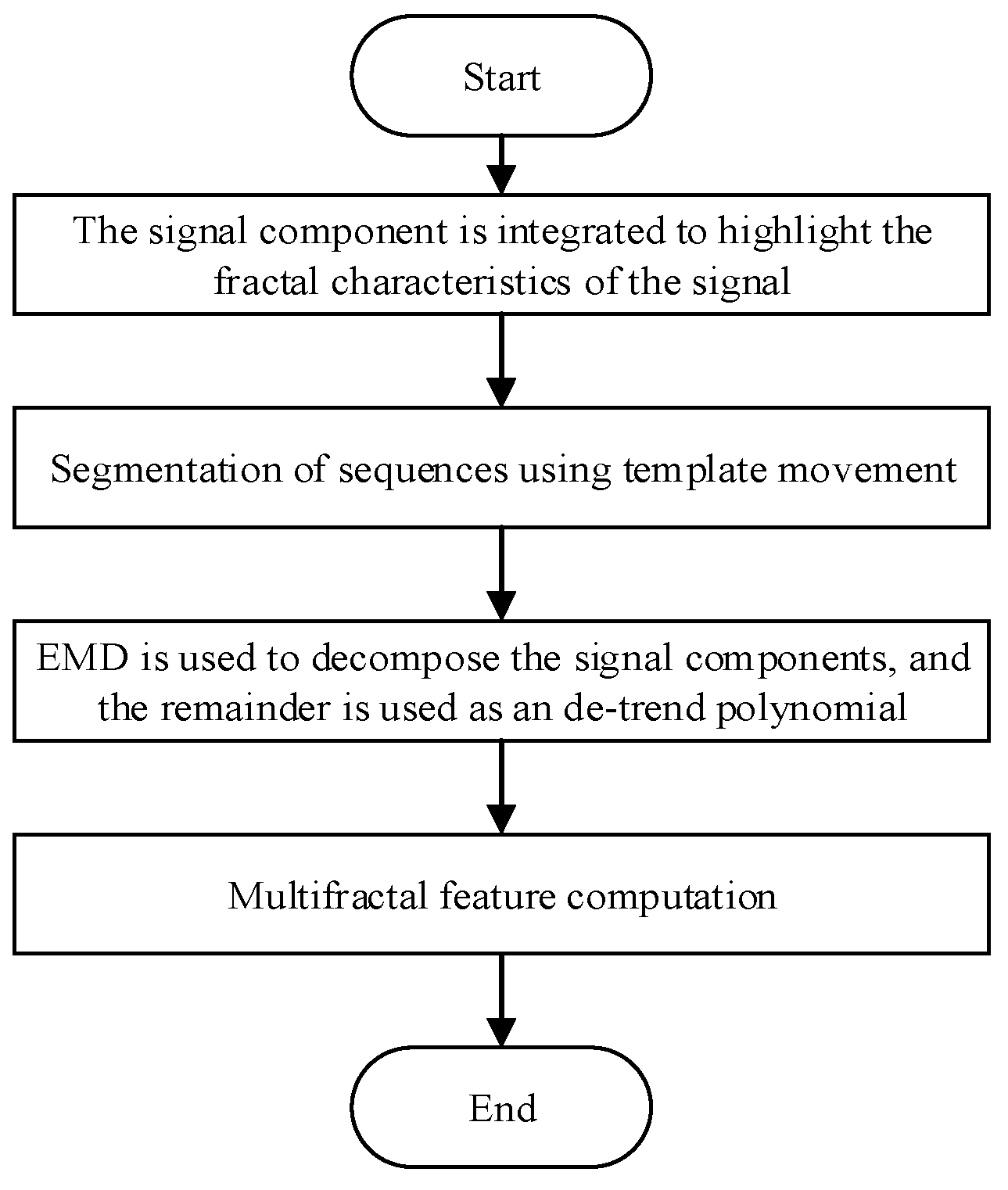
2. MFDFA Algorithm Based on Empirical Modality and Template Movement
2.1. Empirical Mode Decomposition Algorithm
- Find all local extreme points in signal and connect the extreme points smoothly through the cubic spline function to get the upper envelope , lower envelope and the average envelope of the original signal;
- Find the difference function ;
- Determine whether meets intrinsic mode function’s (IMF) conditions or not. If it is not satisfied, repeat the above steps. If it is satisfied, is the first IMF and is recorded as ;
- Finally, is decomposed by EMD into n frequencies from high to low and a remainder . Essentially, .
2.2. Proposed Novel MFDFA Algorithm
- Judging by and :
- If is not related to , the signal is monofractal.
- If is related to , the signal is multifractal.
- Judging by and :
- If is a straight line, the signal is monofractal.
- If and are nonlinear, the signal is multifractal.
- Judging by and :
- If is a constant, the signal is monofractal.
- If the curve of and has a single-peak bell shape, the signal is multifractal.
2.3. MFDFA Feature Extraction Parameters
3. Signal Acquisition and Analysis
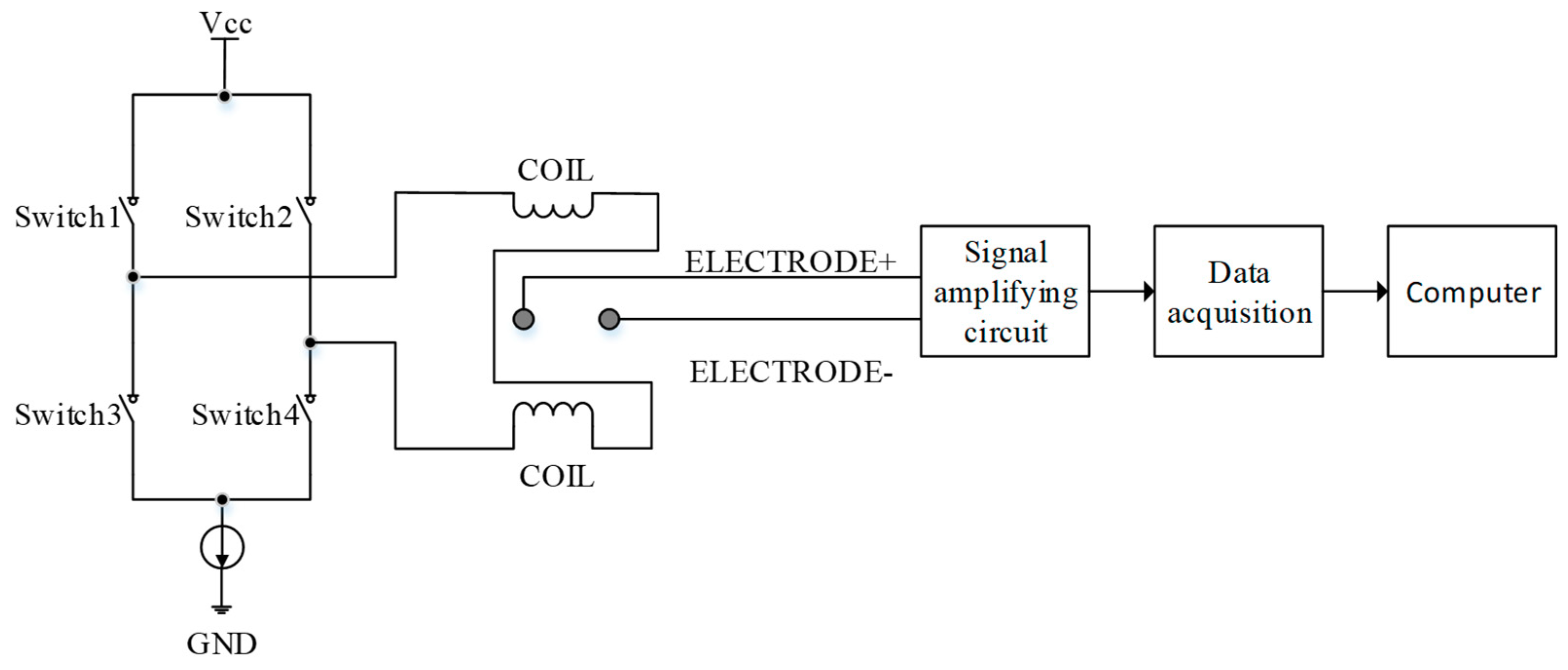
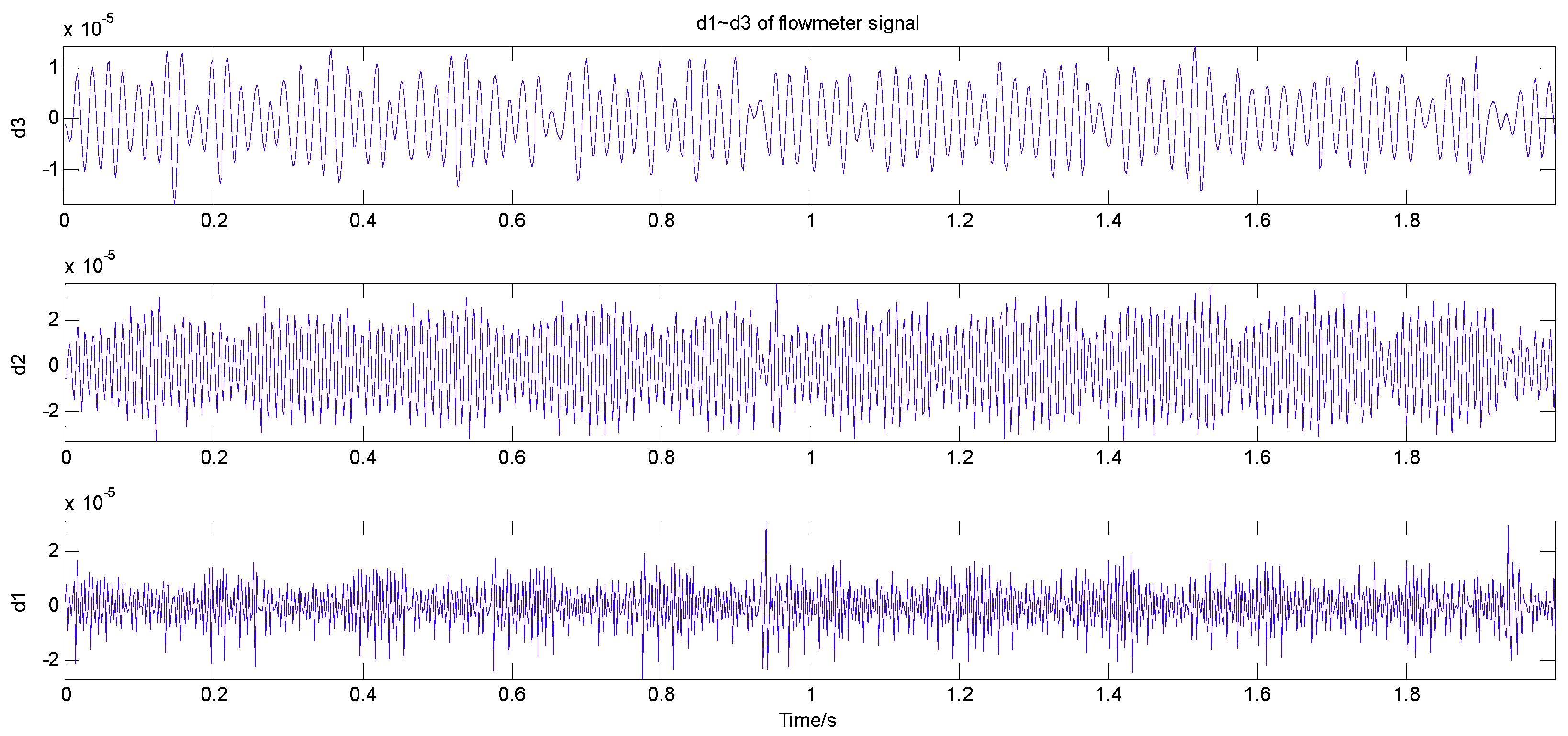
3.1. Signal Acquisition
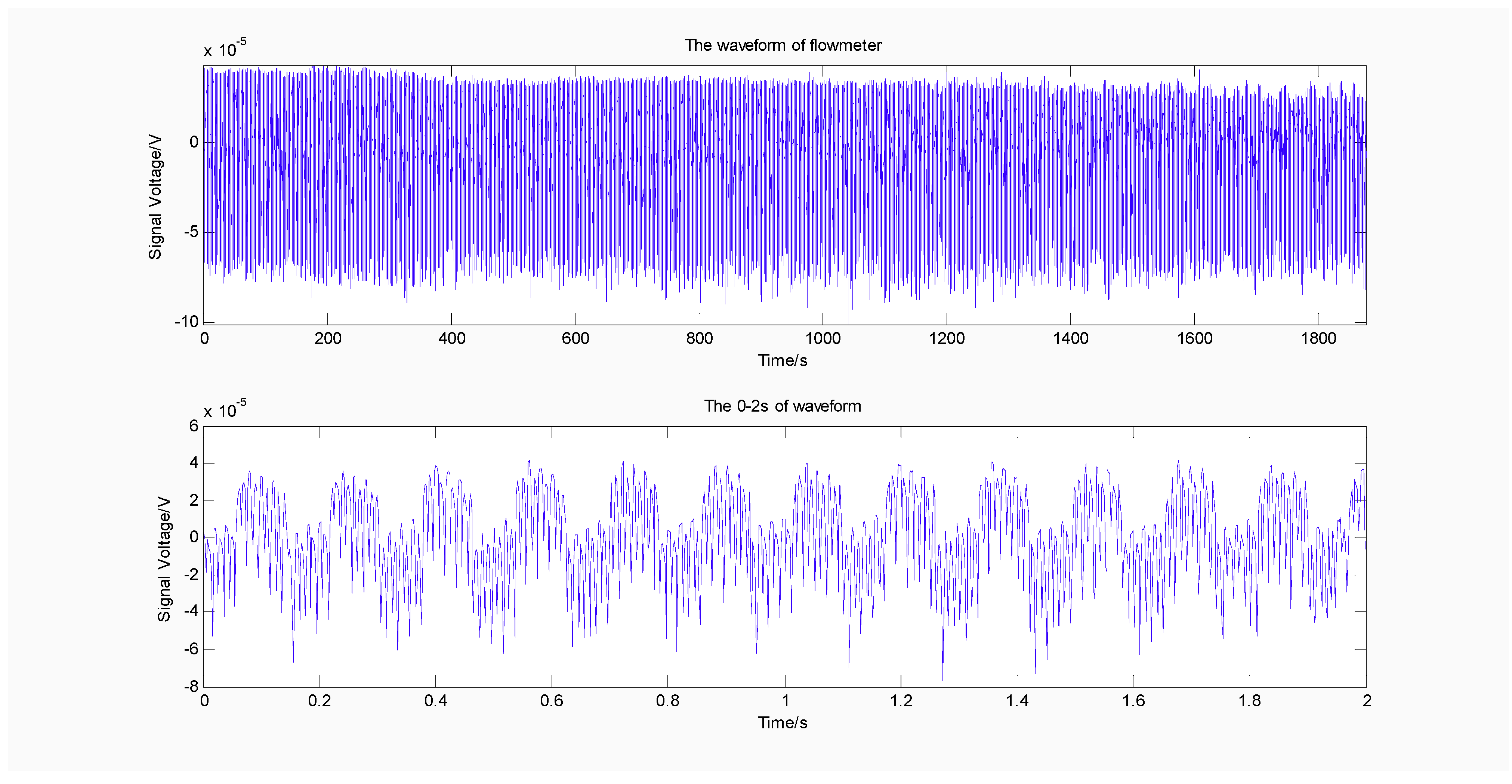
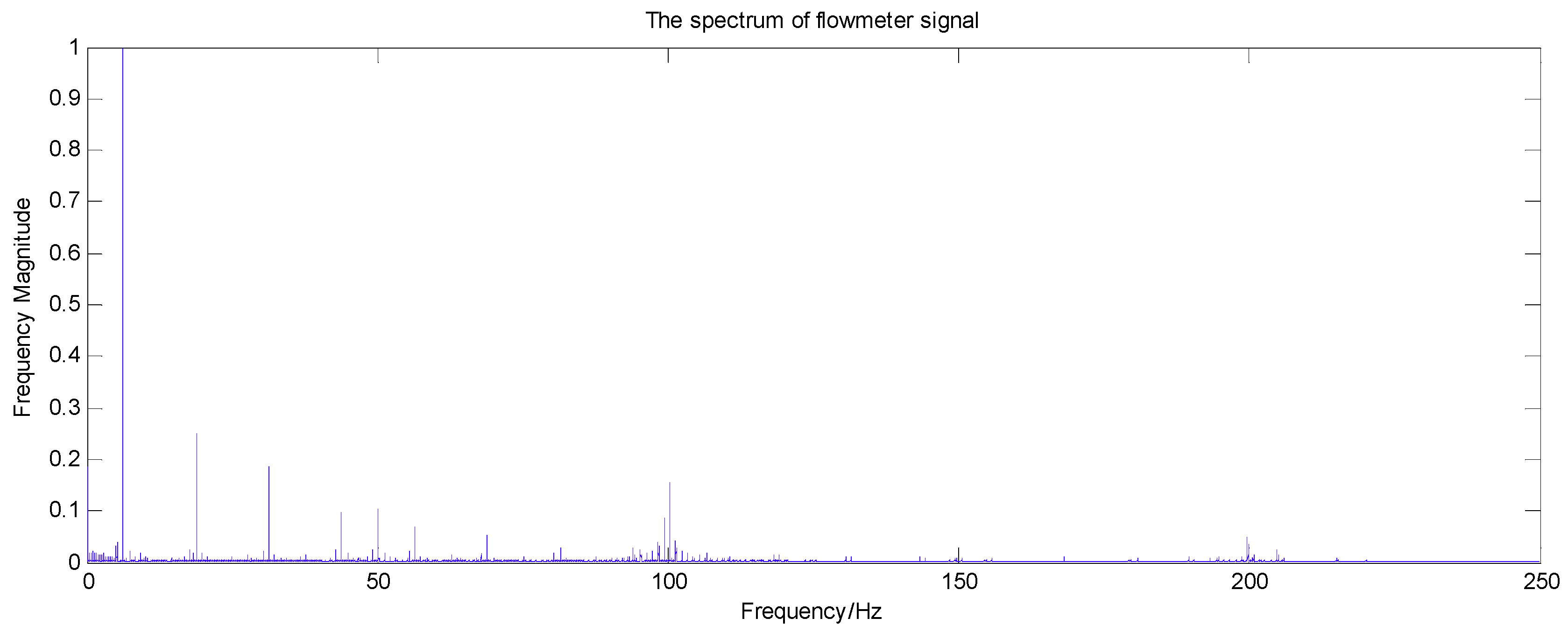
3.2. Signal Analysis
4. Conclusions
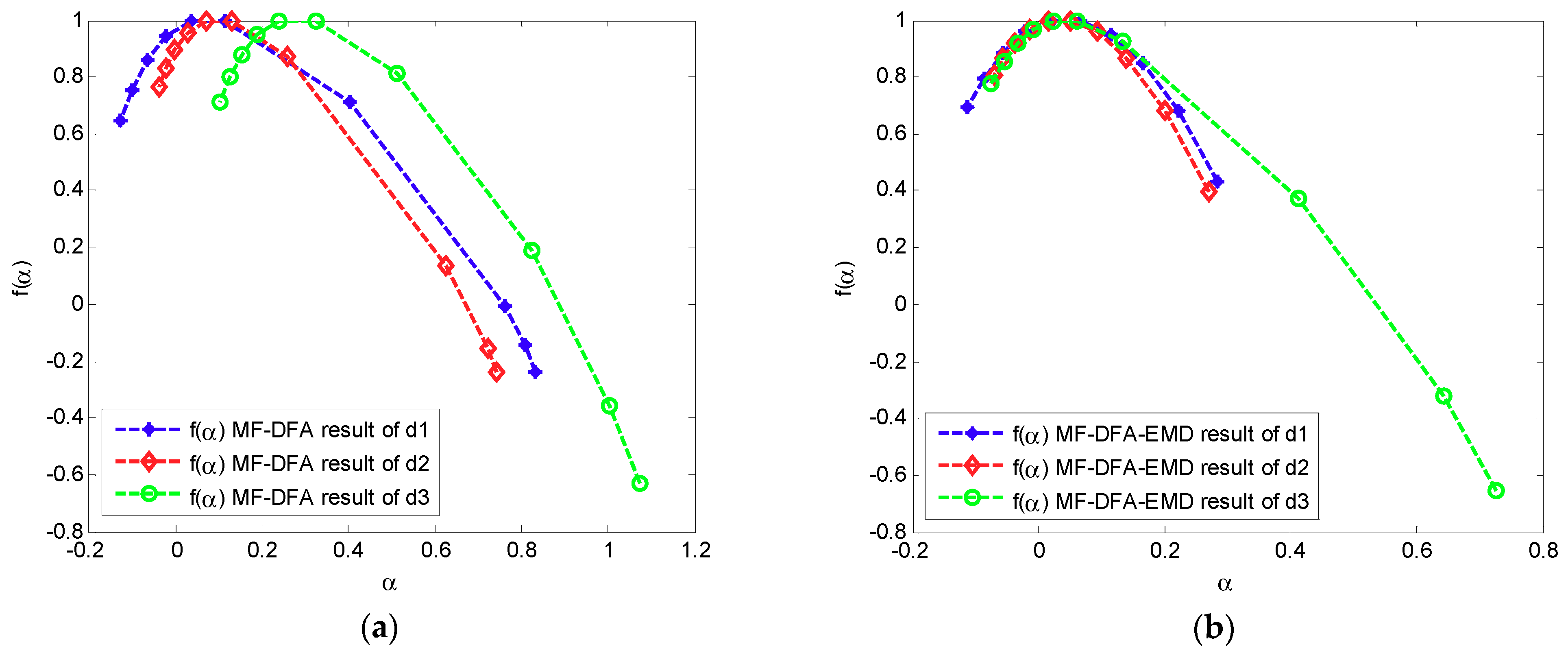
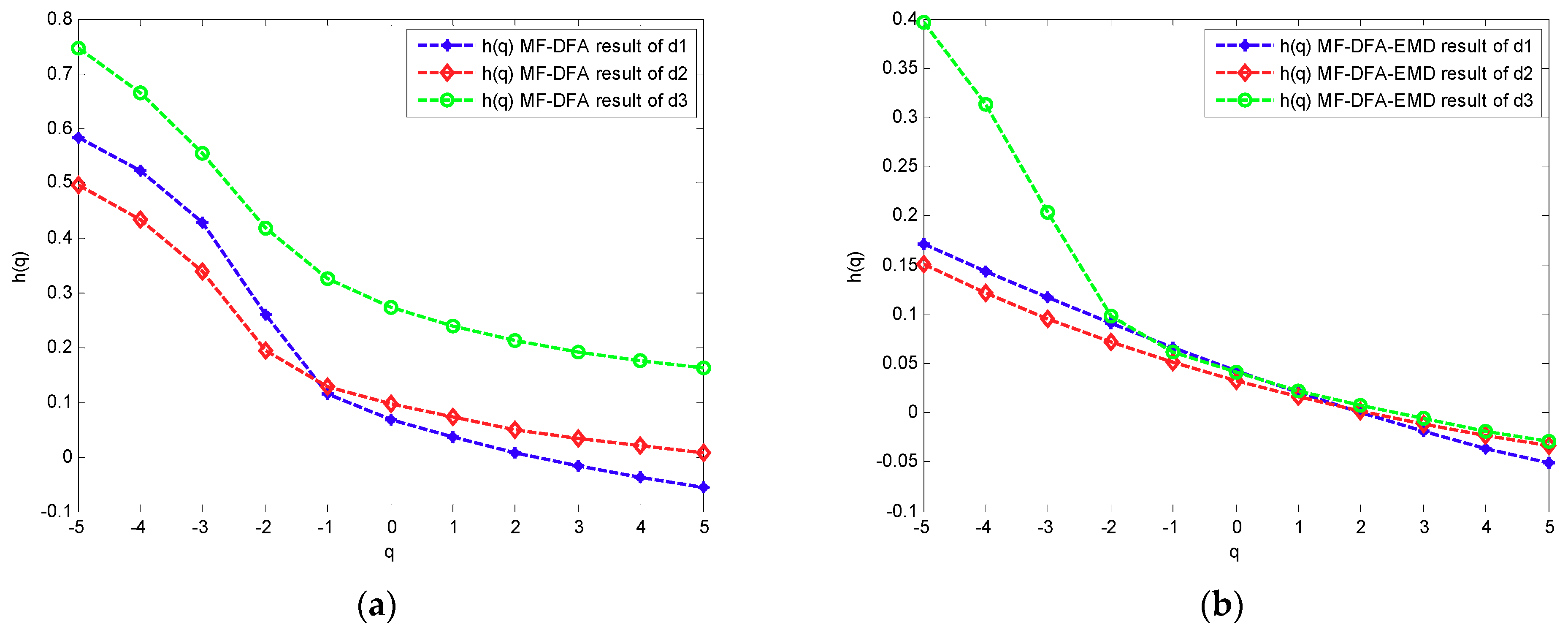
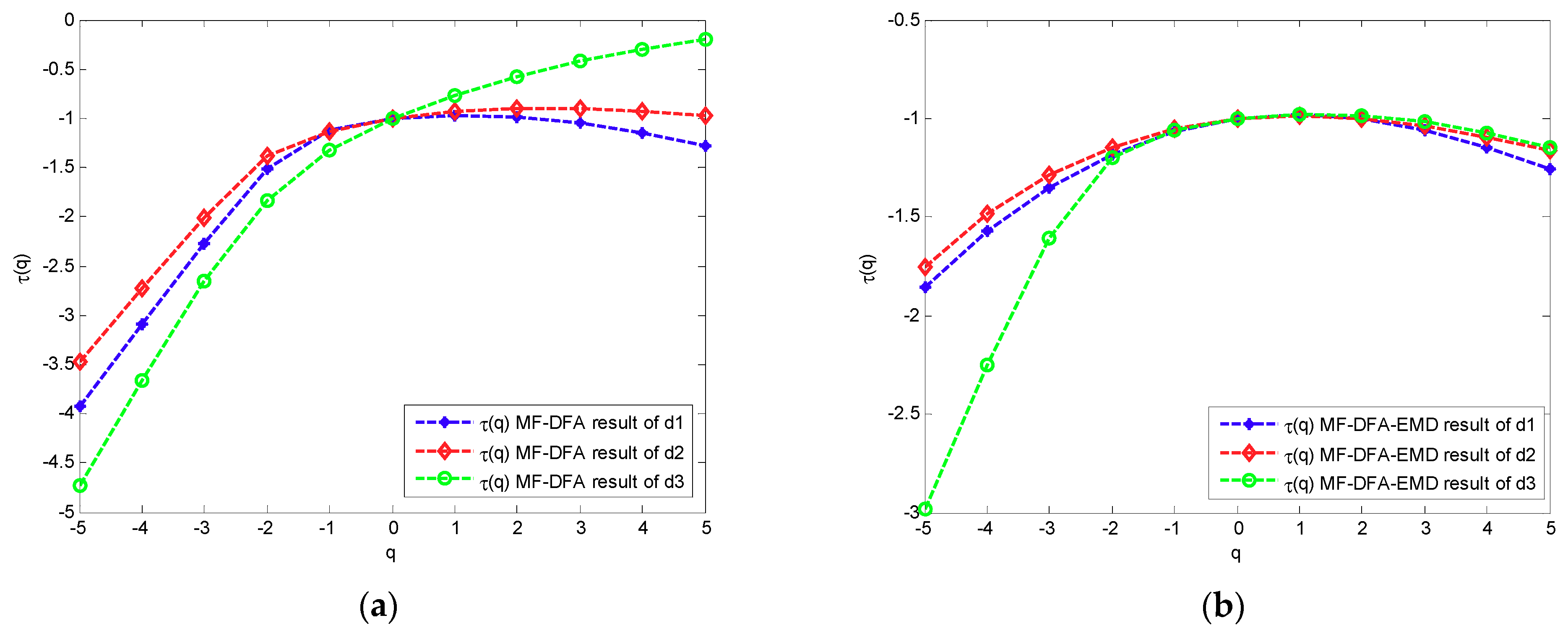
- The power grid harmonic signals in the flow meter signal exhibit multifractal characteristics. Furthermore, the multifractal intensity of the fundamental signal is the largest and the multifractal intensity of the higher-order harmonic is larger than that of the lower harmonic.
- Compared with the traditional MFDFA algorithm, the new algorithm can effectively reduce the pseudofluctuation error caused by the discontinuity of the traditional algorithm, making the fitting curve more stable and more accurately revealing the multifractal characteristics of harmonic signals.
- , , and can provide theoretical and algorithmic support for grid harmonic management.
- Although the algorithm shows good performance in the multifractal-characteristics analysis of harmonic signals, the new algorithm is mainly for integer subharmonics. Using the algorithm for analyzing noninteger harmonics still remains an interesting issue that needs to be studied.
Author Contributions
Funding
Conflicts of Interest
References
- Kumar, D.; Zare, F. Harmonic Analysis of Grid Connected Power Electronic Systems in Low Voltage Distribution Networks. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 70–79. [Google Scholar] [CrossRef]
- Cheng, X.; Lin, X.; Zhu, C.; Chen, Q.; Cao, M. Hierarchy Fault Diagnosis Method for Power System Based on Weight Fuzzy Petri Net. J. Shandong Univ. Sci. Technol. (Nat. Sci.) 2017, 36, 86–93. [Google Scholar]
- Peng, X.; Zou, Q.; Cao, X. A high precision combinational optimization algorithm of power grid harmonic/inter-harmonic signal detection. Power Sys. Prot. Control. 2014, 42, 95–101. [Google Scholar]
- Zou, P.; Huang, C.; Jiang, H.; Zou, D. Harmonics and Interharmonics Measurement Based on All-Phase Spectrum Zoomand Correction. Power Sys. Technol. 2016, 40, 2496–2502. [Google Scholar]
- Xu, L.; Cao, M.; Song, B.; Zhang, J.; Liu, Y.; Alsaadi, F.E. Open-circuit fault diagnosis of power rectifier using sparse auto encoder based deep neural network. Neurocompting 2018, 311, 1–10. [Google Scholar] [CrossRef]
- Ding, L.; Han, Q.; Zhang, X. Distributed Secondary Control for Active Power Sharing and Frequency Regulation in Islanded Microgrids Using an Event-triggered Communication Mechanism. IEEE Trans. Ind. Inf. 2018. [Google Scholar] [CrossRef]
- Xiao, J.; Li, S.; Wu, K.; He, Y. A Novel Approach of Harmonic Detection in Power System Based on Neural Network. Trans. China Electrotech. Soc. 2013, 28, 345–348. [Google Scholar]
- Liu, W.; Wang, Z.; Liu, X.; Zeng, N.; Liu, Y.; Alsaadi, F.E. A survey of deep neural network architectures and their applications. Neurocomputing 2017, 234, 11–26. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, Z.; Zou, L.; Liu, H. Finite-Horizon H∞ State Estimation for Artificial Neural Networks with Component-Based Distributed Delays and Stochastic Protocol. Neurocomputing 2018, 321, 169–177. [Google Scholar] [CrossRef]
- Murugan, A.S.S.; Kumar, V.S. Determining true harmonic contributions of sources using neural network. Neurocomputing 2016, 173, 72–80. [Google Scholar] [CrossRef]
- Yang, R.; Tan, K.K.; Tay, A.; Huang, S.; Fuh, J.; Wong, Y.S.; Teo, C.S.; Wang, Z. An RBF neural network approach to geometric error compensation with displacement measurements only. Neural Comput. Appl. 2017, 28, 1235–1248. [Google Scholar] [CrossRef]
- Yang, R.; Er, P.V.; Dong, Z.; Tan, K.K. An RBF Neural Network Approach Towards Precision Motion System with Selective Sensor Fusion. Neurocomputing. 2016, 199, 31–39. [Google Scholar] [CrossRef]
- Huang, X.; Zhao, Z.; Li, Y. Chaos and Hyperchaos in Fractional-Order Cellular Neural Networks. Neurocomputing. 2012, 94, 13–21. [Google Scholar] [CrossRef]
- Geng, C.; Wang, F.; Huang, R.; Zhang, J.; Zhang, X.; Feng, L. Harmonic detection of electrified railway based on improved Hilbert-Huang transform method. J. Shanghai Jiaotong Univ. 2014, 48, 1225–1230. [Google Scholar]
- Sahani, M.; Dash, P.K. Variational mode decomposition and weighted online sequential extreme learning machine for power quality event patterns Recognition. Neurocompting 2018, 310, 10–27. [Google Scholar] [CrossRef]
- Wang, X.; Du, C. Instantaneous Reactive Power Theory and the Measurement Methods for Detecting Harmonics. Electr. Eng. 2014, 4, 38–41. [Google Scholar]
- Chen, H.; He, Y.; Xiao, J.; Liu, X.; Wang, D. Harmonics detection based on a combination of continuous wavelet transform and discrete wavelet transform. Power Syst. Prot. Control. 2015, 43, 71–75. [Google Scholar]
- Dick, O.E.; Svyatogor, I.A. Potentialities of the wavelet and multifractal techniques to evaluate changes in the functional state of the human brain. Neurocompting 2012, 82, 207–215. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, K.; Wang, L.; Chen, W. A rapid algorithm for harmonic analysis based on four-spectrum-line interpolation FFT. Power Syst. Prot. Control. 2017, 45, 139–145. [Google Scholar]
- Jia, F.; Wu, B.; Xiong, X.; Xiong, S. Intelligent diagnosis of bearing based on EMD and multifractal detrended fluctuation analysis. J. Central South. Univ. (Sci. Technol.) 2015, 46, 491–497. [Google Scholar]
- Chu, Q.; Xiao, H.; Lv, Y.; Yang, Z. Gear fault diagnosis based on multifractal theory and neural network. J. Vibr. Shock 2015, 34, 15–18. [Google Scholar]
- Maity, A.K.; Pratihar, R.; Mitra, A.; Dey, S.; Agrawal, V.; Sanyal, S.; Banerjee, A.; Sengupta, R.; Ghosh, D. Multifractal Detrended Fluctuation Analysis of alpha and theta EEG rhythms with musical stimuli. Chaos Solitons Fractals 2015, 81, 52–67. [Google Scholar] [CrossRef]
- Dick, O.E.; Svyatogor, I.A. Wavelet and multifractal estimation of the intermittent photic stimulation response in the electroencephalogram of patients with dyscirculatory encephalopathy. Neurocomputing 2015, 165, 361–374. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Mutifractal detrended fluctuation analysis of nonstationary time series. Phys. A 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, J.; Cheng, H. Multifractal features of metal futures market based on multifractal detrended cross-correlation analysis. Kybernetes 2012, 41, 1509–1525. [Google Scholar] [CrossRef]
- Kalamaras, N.; Philippopoulos, K.; Deligiorgi, D.; Tzanis, C.G.; Karvounis, G. Multifractal scaling properties of daily air temperature time series. Chaos Solitons Fractals 2017, 98, 38–43. [Google Scholar] [CrossRef]
- Fan, X.; Lin, M. Multiscale multifractal detrended fluctuation analysis of earthquake magnitude series of Southern California. Phys. A 2017, 479, 225–235. [Google Scholar] [CrossRef]
- Lu, S.; Wang, J.; Xue, Y. Study on multifractal fault diagnosis based on EMD fusion in hydraulic engineering. Appl. Therm. Eng. 2016, 103, 798–806. [Google Scholar] [CrossRef]
- Wang, F.; Fan, Q.; Stanley, H.E. Multiscale multifractal detrended-fluctuation analysis of two-dimensional surfaces. Phys. Rev. E 2016, 93. [Google Scholar] [CrossRef]
- Zhao, H.; He, S. Analysis of speech signals’ characteristics based on MFDFA with moving overlapping windows. Phys. A 2016, 442, 343–349. [Google Scholar] [CrossRef]
- Kracík, J.; Lavička, H. Fluctuation analysis of high frequency electric power load in the Czech Republic. Phys. A 2016, 462, 951–961. [Google Scholar] [CrossRef]
- Li, C.; Li, Q.; Wang, Q.; Song, Y. Research on Electric Power Load Risk Warning Threshold Based on SMF-DFA. Power Syst. Technol. 2016, 40, 1437–1441. [Google Scholar]
- Zhu, N.; Bai, X.; Dong, W. Harmonic Detection Method Based on EEMD. Proc. CSEE 2013, 33, 92–98. [Google Scholar]
- Lin, H.; Chen, L. Denoising Method of Power System Perturbed. Electr. Eng. 2014, 8, 11–13. [Google Scholar]
- Bustos, A.; Rubio, H.; Castejón, C.; Carlos, J. García-Prada EMD-Based Methodology for the Identification of a High-Speed Train Running in a Gear Operating State. Sensors 2018, 18, 793. [Google Scholar] [CrossRef] [PubMed]
- Ihlen, E.F. Introduction to multifractal detrended fluctuation analysis in matlab. Front. Physiol. 2012, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Mensi, W.; Tiwar, A.K.; Yoon, S.M. Global financial crisis and weak-form efficiency of Islamic sectoral stock markets: An MF-DFA analysi. Phys. A 2016, 471, 135–146. [Google Scholar] [CrossRef]
- Xi, C.; Zhang, S.; Xiong, G.; Zhao, C. A comparative study of multifractal detrended fluctuation analysis and multifractal detrended moving average algorithm to estimate the multifractal spectrum. Acta Phys. Chim. Sin. 2015, 13, 335–348. [Google Scholar]
- Tian, Z.; Li, H.; Sun, J.; Lin, B. Degradation state identification method of hydraulic pump based on improved MF-DFA and SSM-FCM. Chin. J. Sciebtific Instrum. 2016, 37, 1851–1860. [Google Scholar]
- Lin, J.; Chen, Q. Applications of multifractal detrended fluctuation analysis to severity Identification of rolling bearing damages. Chin. Mech. Eng. 2014, 25, 1760–1765. [Google Scholar]
- Lei, R.; Hao, Z. A harmonic detection for power network based on wavelet transform Mallat algorithm. Ind. Mine Autom. 2014, 42, 65–69. [Google Scholar]
- Zou, X.; Ye, Y. Multi-fault diagnosis method on Mallat pyramidal algorithmwavelet analysis. Control. Decis. 2004, 19, 592–594. [Google Scholar]
- Zhang, B.; Sun, J. A power quality analysis method based on mallat algorithm and fast fourier transform. Power Sys. Technol. 2007, 31, 35–40. [Google Scholar]
- Ihlen, E.A.F. Introduction to multifractal detrended fluctuation analysis in Matlab. Front. Physiol. Fractal Physiol. 2012, 3, 1–18. [Google Scholar] [CrossRef] [PubMed]
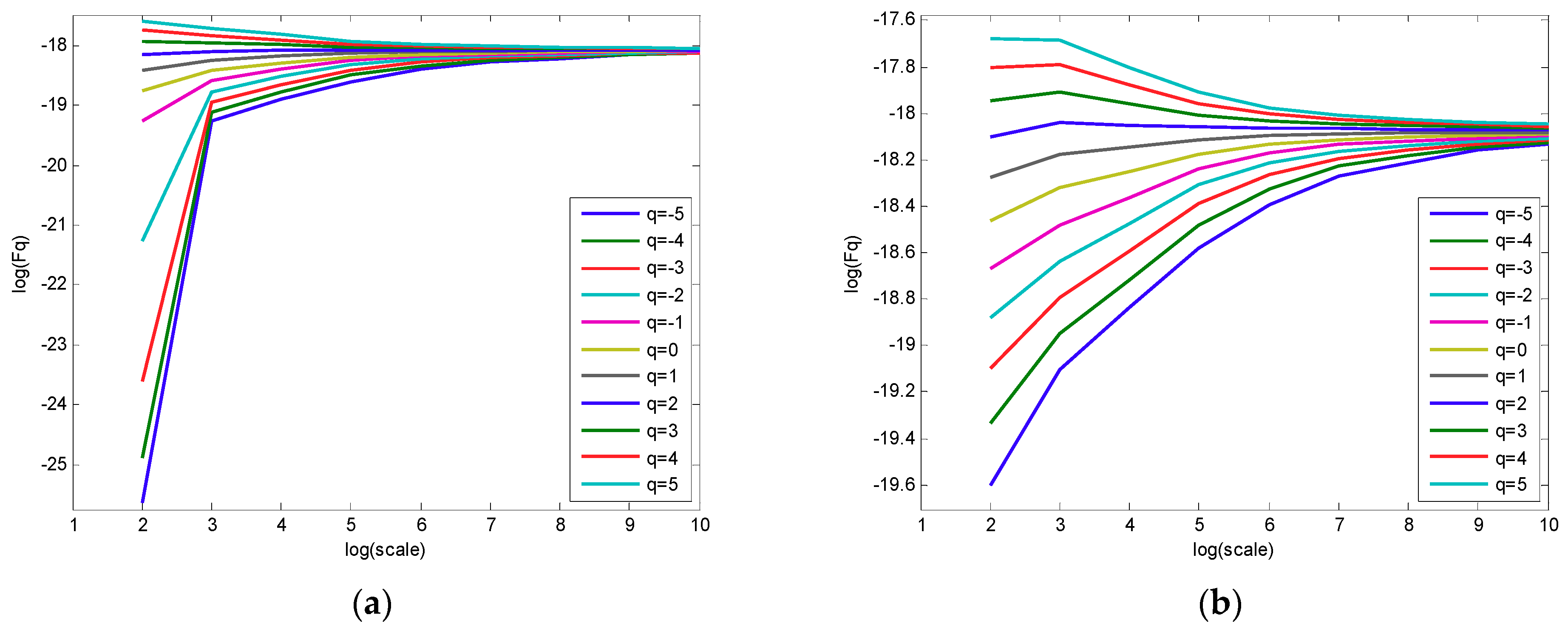
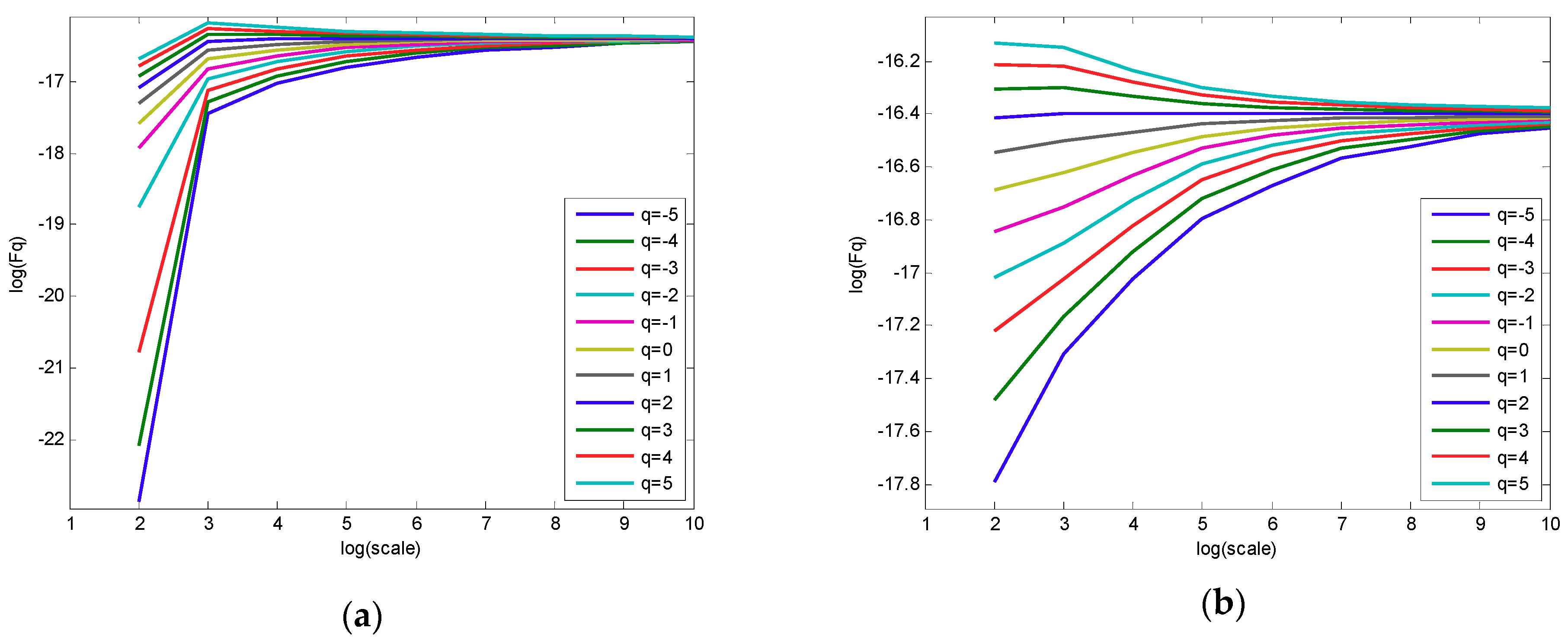
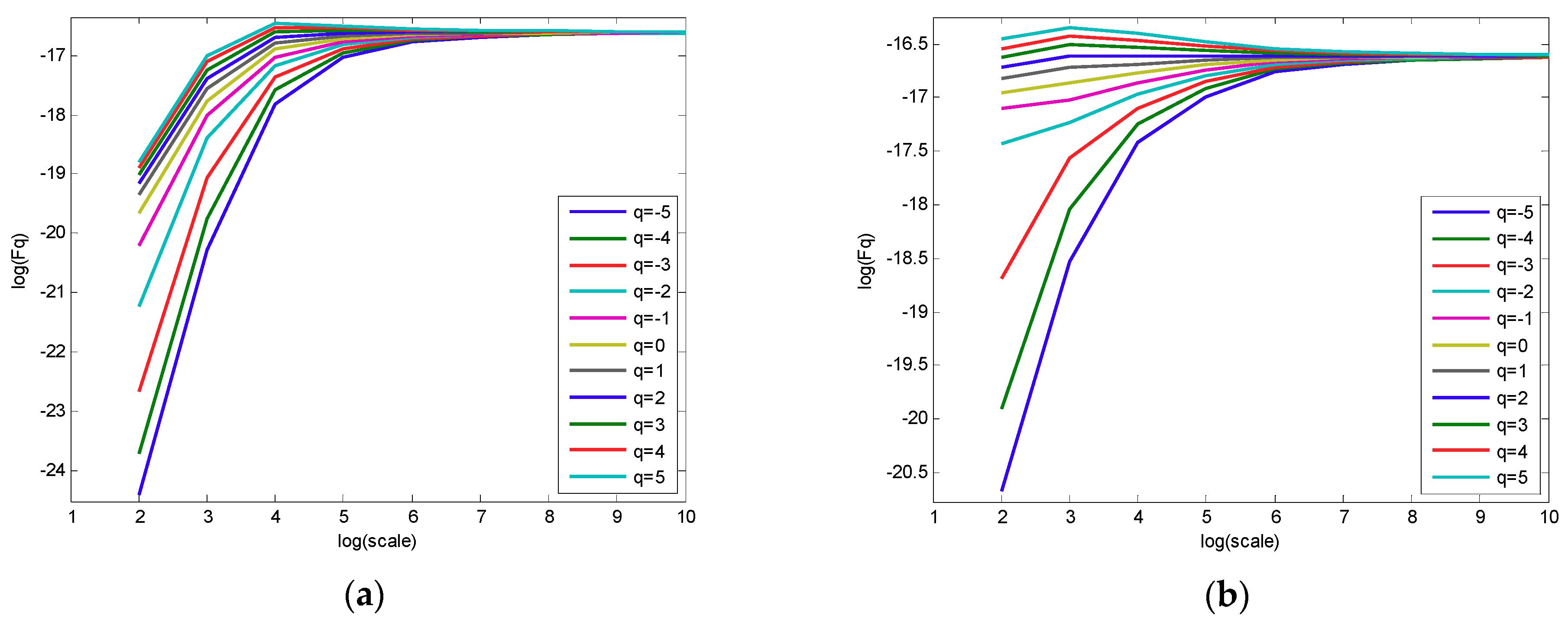
| Layer | Frequency Band |
|---|---|
| a5 | 0–7.8125 Hz |
| a4 | 0–15.625 Hz |
| a3 | 0–31.25 Hz |
| a2 | 0–62.5 Hz |
| a1 | 0–125 Hz |
| d5 | 7.8125–15.625 Hz |
| d4 | 15.625–31.25 Hz |
| d3 | 31.25–62.5 Hz |
| d2 | 62.5–125 Hz |
| d1 | 125–250 Hz |
| Harmonic Component | Traditional MFDFA | New MFDFA | ||||
|---|---|---|---|---|---|---|
| d1 | 0.957 | 0.113 | −0.126 | 0.397 | 0.066 | −0.122 |
| d2 | 0.782 | 0.128 | −0.039 | 0.342 | 0.051 | −0.071 |
| d3 | 0.969 | 0.324 | 0.103 | 0.800 | 0.061 | −0.074 |
| Traditional MFDFA | New MFDFA | |||||
|---|---|---|---|---|---|---|
| d1 | d2 | d3 | d1 | d2 | d3 | |
| −5 | 0.583 | 0.495 | 0.747 | 0.171 | 0.151 | 0.395 |
| −4 | 0.521 | 0.433 | 0.666 | 0.142 | 0.121 | 0.313 |
| −3 | 0.426 | 0.336 | 0.553 | 0.116 | 0.094 | 0.202 |
| −2 | 0.258 | 0.192 | 0.418 | 0.091 | 0.072 | 0.098 |
| −1 | 0.113 | 0.128 | 0.324 | 0.066 | 0.051 | 0.061 |
| 0 | 0.067 | 0.097 | 0.272 | 0.042 | 0.033 | 0.041 |
| 1 | 0.034 | 0.071 | 0.238 | 0.02 | 0.016 | 0.022 |
| 2 | 0.006 | 0.049 | 0.212 | 0 | 0.001 | 0.007 |
| 3 | −0.017 | 0.032 | 0.192 | −0.019 | −0.012 | −0.006 |
| 4 | −0.037 | 0.018 | 0.175 | −0.036 | −0.023 | −0.018 |
| 5 | −0.055 | 0.006 | 0.160 | −0.051 | −0.032 | −0.029 |
| 0.638 | 0.489 | 0.587 | 0.222 | 0.183 | 0.4244 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Ma, X.; Zhao, M.; Cheng, X. A Novel MFDFA Algorithm and Its Application to Analysis of Harmonic Multifractal Features. Electronics 2019, 8, 209. https://doi.org/10.3390/electronics8020209
Li J, Ma X, Zhao M, Cheng X. A Novel MFDFA Algorithm and Its Application to Analysis of Harmonic Multifractal Features. Electronics. 2019; 8(2):209. https://doi.org/10.3390/electronics8020209
Chicago/Turabian StyleLi, Jiming, Xinyan Ma, Meng Zhao, and Xuezhen Cheng. 2019. "A Novel MFDFA Algorithm and Its Application to Analysis of Harmonic Multifractal Features" Electronics 8, no. 2: 209. https://doi.org/10.3390/electronics8020209
APA StyleLi, J., Ma, X., Zhao, M., & Cheng, X. (2019). A Novel MFDFA Algorithm and Its Application to Analysis of Harmonic Multifractal Features. Electronics, 8(2), 209. https://doi.org/10.3390/electronics8020209





