Tri-polarized Sparse Array Design for Mutual Coupling Reduction in Direction Finding and Polarization Estimation
Abstract
1. Introduction
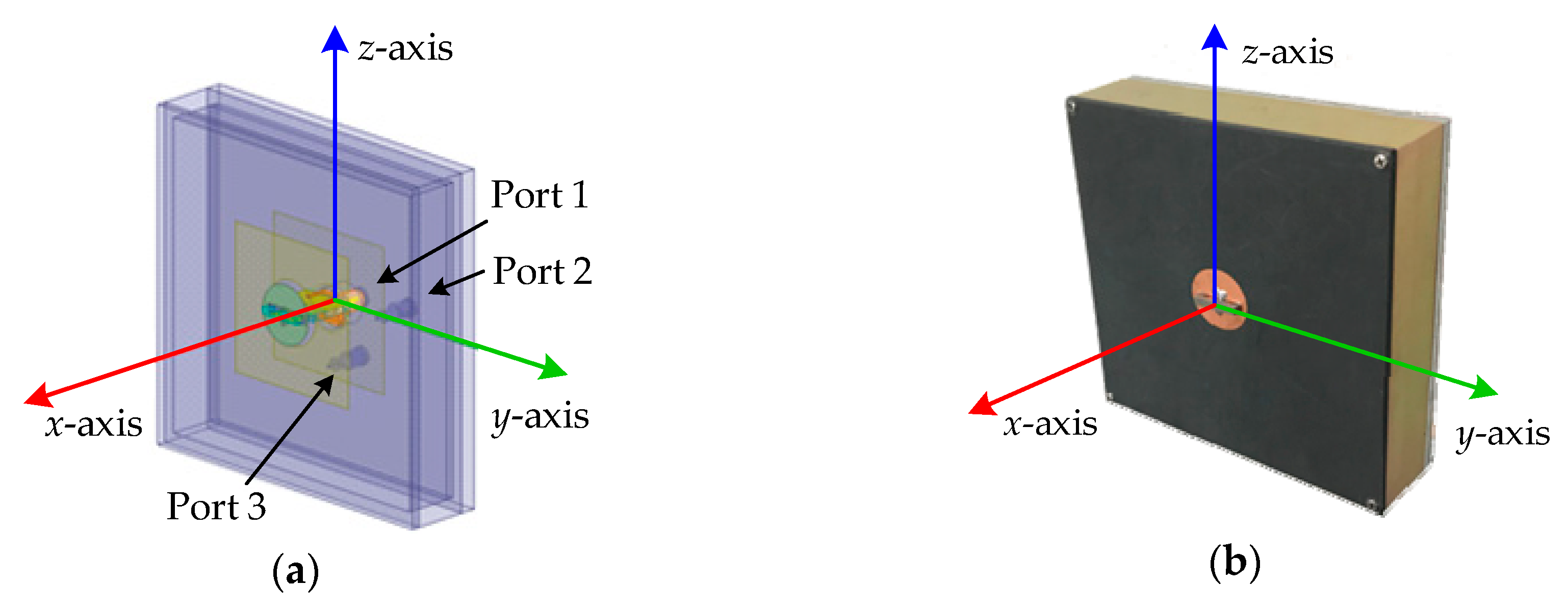
2. Tri-polarized Antenna Array Signal Model
3. Inter-VA Spacing-Constrained Sparse Array
| Algorithm 1 Scrunch recursive algorithm for an ISC array |
| Input: the number of VAs the array aperture Output: the ISC array configuration the position of the rightmost VA in the consecutive virtual array Procedure:
|
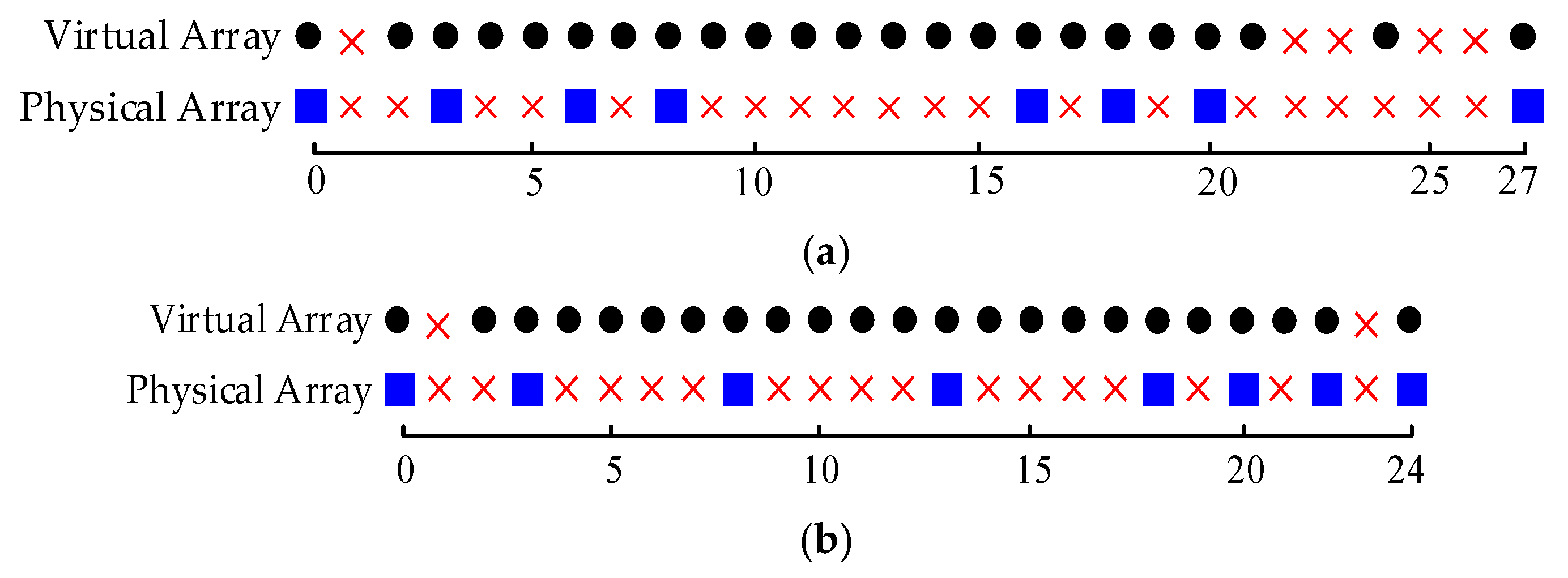
- Given , the aperture parameter is important for the design of the ISC array ( is required). If , there exists a certain set of aperture parameters achieving (i.e., ). The obtained “fully augmentable” ISC arrays involve different redundancies. Concerning aperture extension, the ISC array with “minimum redundancy” (where is minimal or even zero) is of interest. For example, if , the use of any belonging to the set will lead to a fully augmentable ISC array. The ISC array with is of minimal redundancy and the virtual aperture is larger than others. For different values of , some minimum-redundancy ISC array configurations are listed in Table A1 of Appendix A.
- For the same setting of , the virtual aperture of the ISC array can be further increased by using a larger . The obtained ISC arrays now are “partially augmentable” (). A partially augmentable ISC array is said to be “maximum contiguous” if the synthesized virtual ULA has the largest aperture. For example, if , () for the maximum-contiguous ISC array (), while () for the minimum-redundancy ISC array ().
- A degenerate case is , under which . Note also that when . So, if aperture extension and mutual coupling reduction are desired, should be no less than 4.
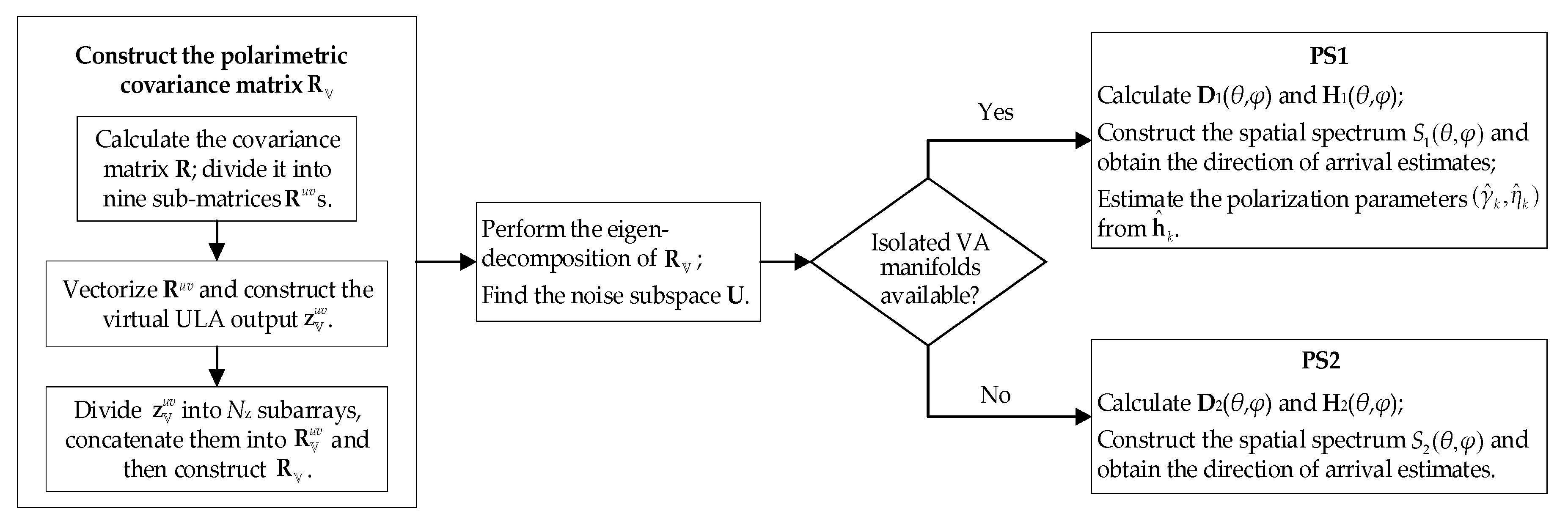
4. ISC-Based DOA–Polarization Parameter Estimation
4.1. Using the Nominal Isolated VA Manifold Vectors
4.2. Without Using the Nominal Isolated VA Manifold Vectors
4.3. Analysis of Intra-VA MC Alleviation in PS1 and PS2
5. Simulation and Experimental Results
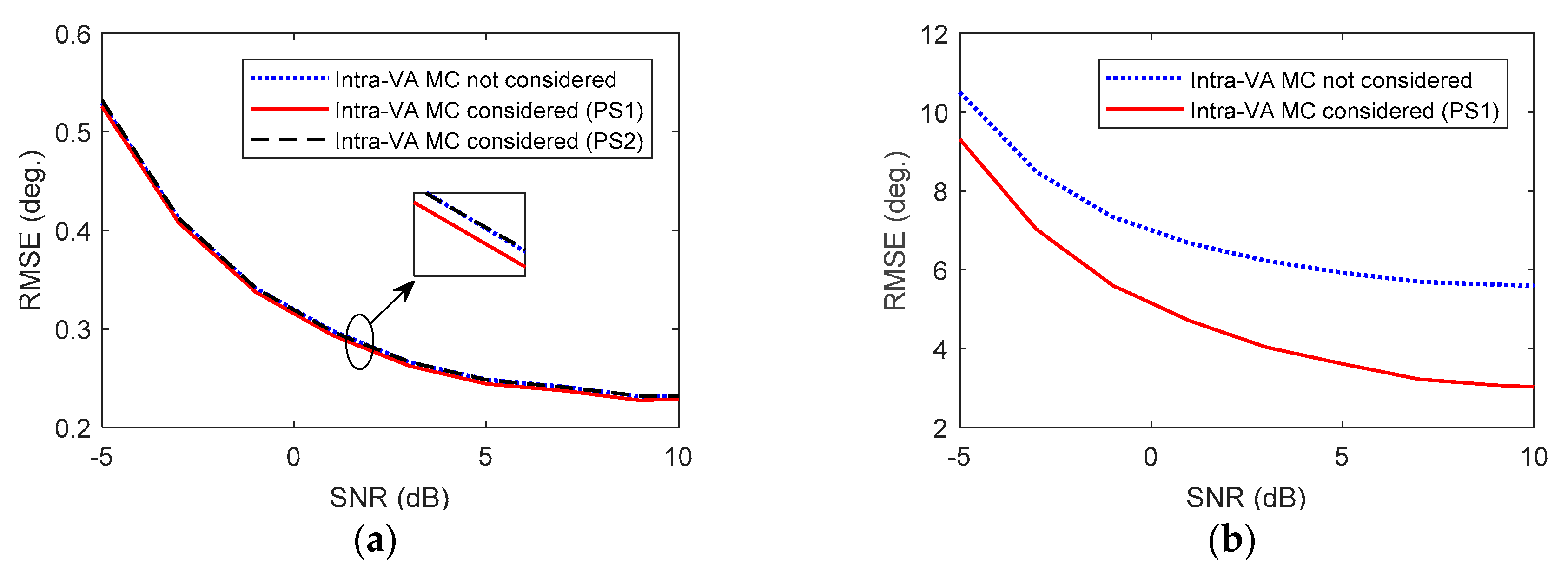
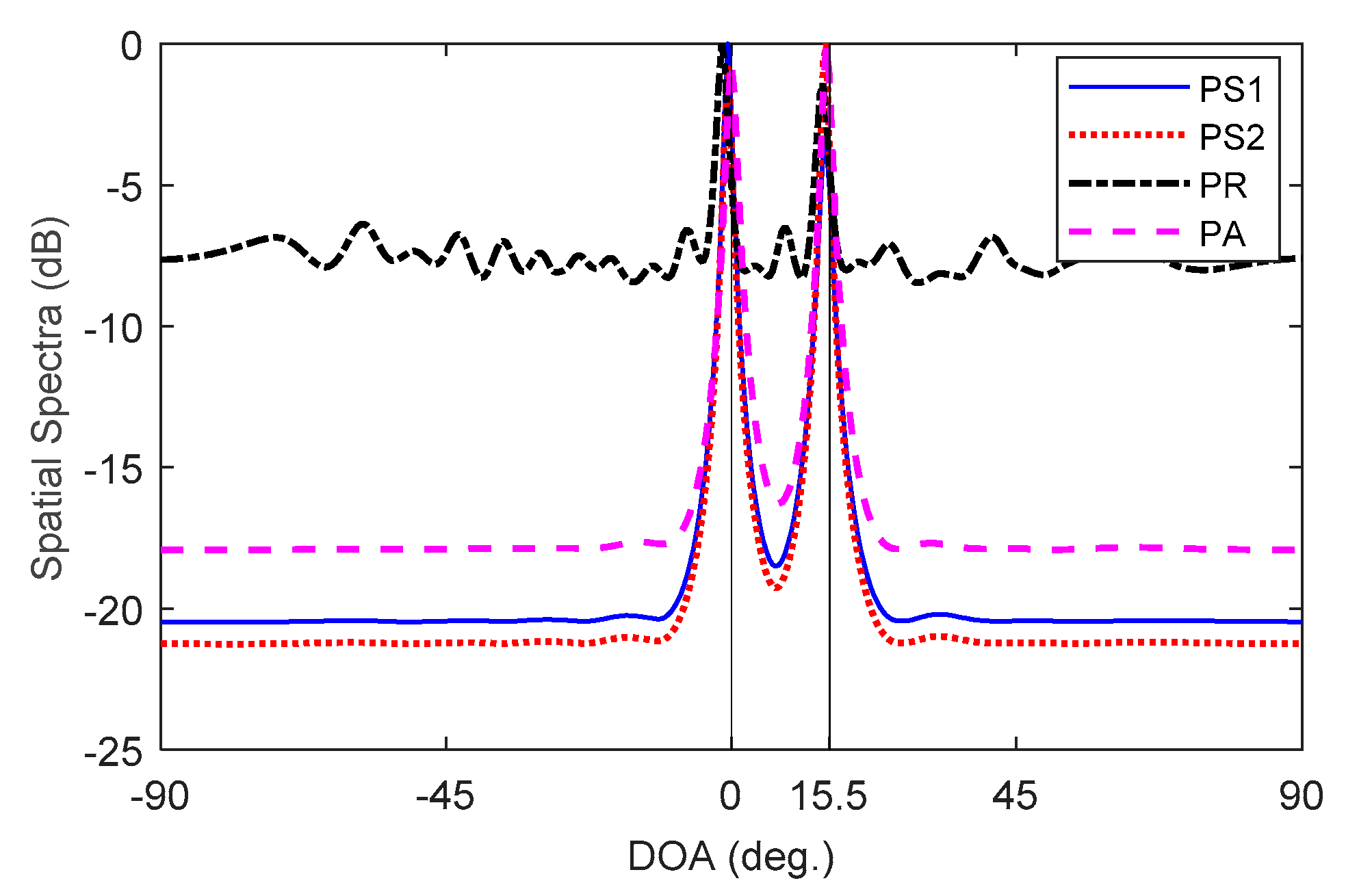
5.1. Capability of Intra-VA MC Alleviation
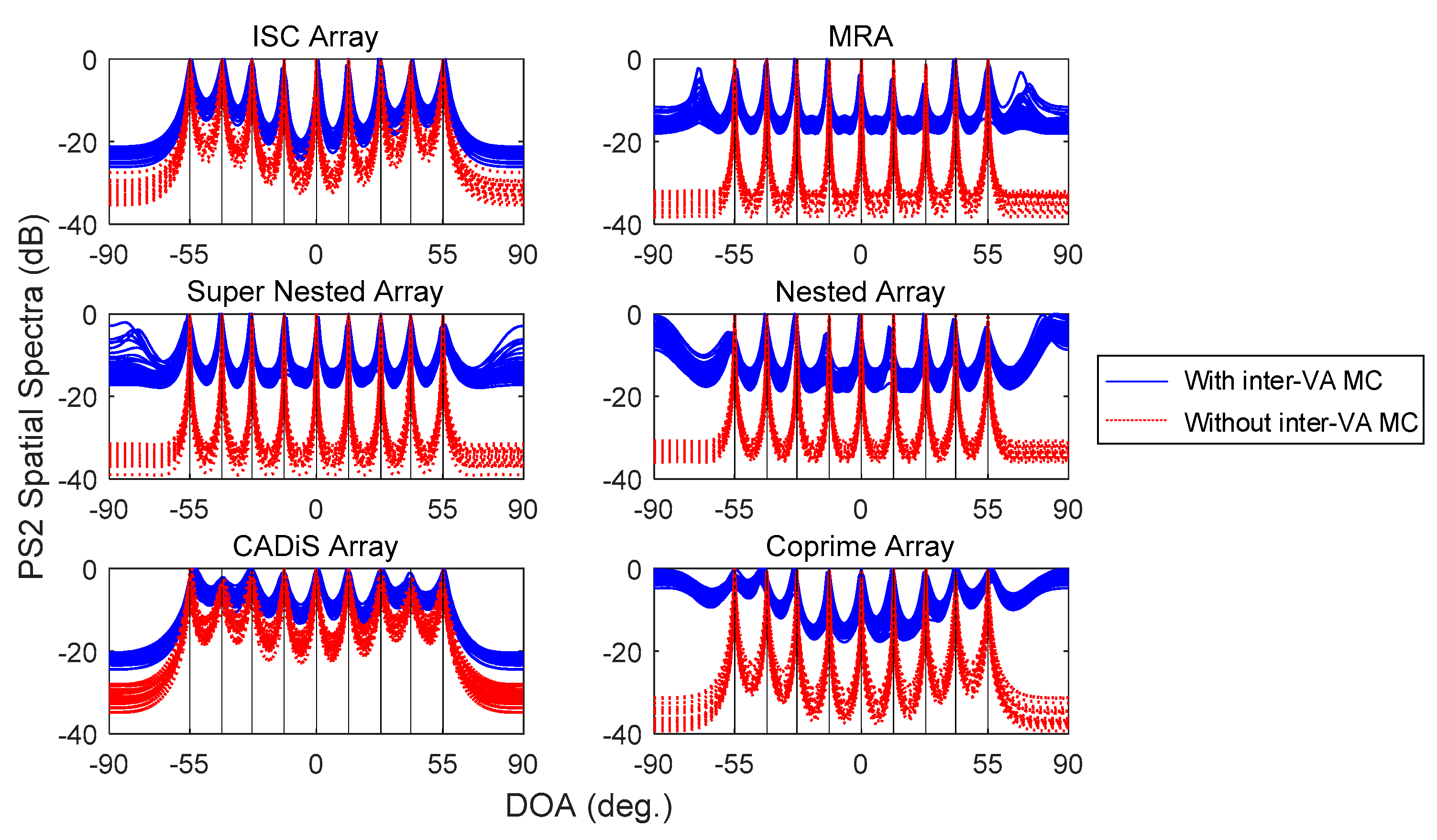
5.2. Capability of Inter-VA MC Reduction
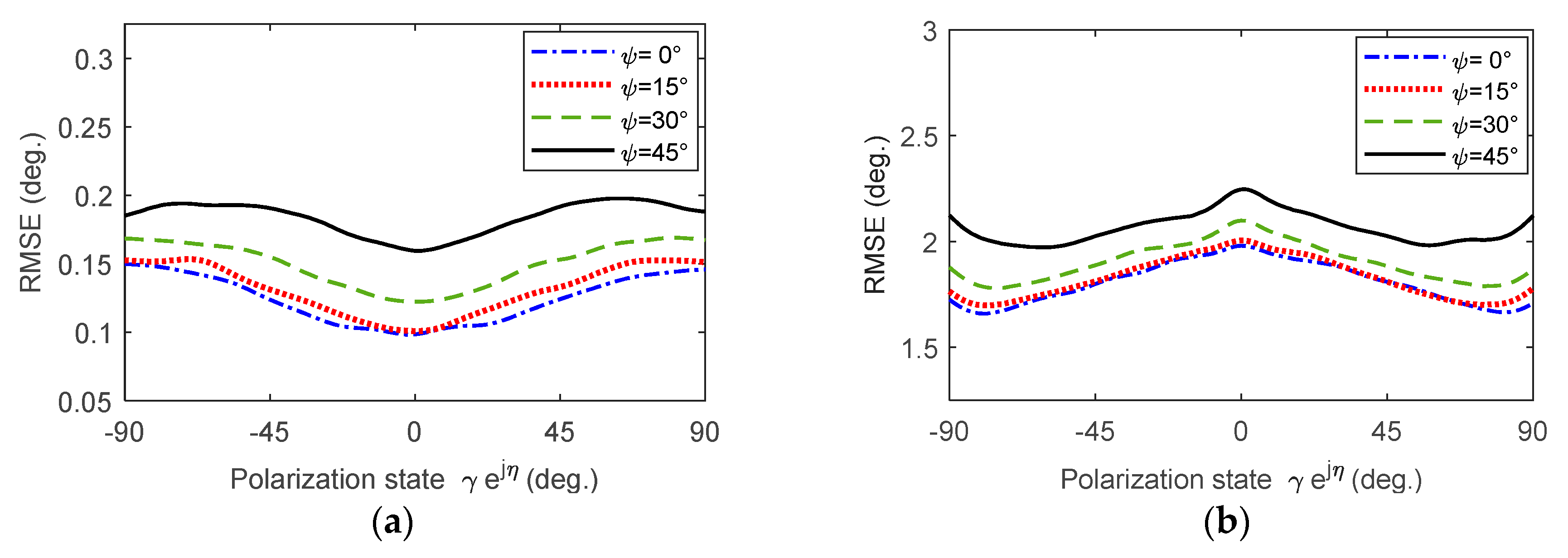
5.3. Robustness Against VA Misalignment
5.4. Parameter Estimation Using Real-World Data
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| N | N0 | VA Locations |
|---|---|---|
| 3 | 3 | 0 2 5 |
| 4 | 5 | 0 2 4 7 |
| 5 | 8 | 0 2 4 7 10 |
| 6 | 13 | 0 2 4 9 12 15 |
| 7 | 18 | 0 2 4 9 14 17 20 |
| 8 | 23 | 0 2 4 9 14 19 22 25 |
| 9 | 28 | 0 2 4 9 14 19 24 27 30 |
| 10 | 33 | 0 2 4 6 8 13 20 25 32 35 |
| 11 | 40 | 0 2 4 6 13 20 27 34 37 39 42 |
| 12 | 48 | 0 2 4 6 8 10 19 24 35 40 47 50 |
| 13 | 55 | 0 2 4 6 8 10 19 24 31 42 47 54 57 |
| 14 | 64 | 0 2 4 6 8 17 22 35 40 47 56 59 63 66 |
| 15 | 72 | 0 2 4 6 8 36 39 43 48 53 58 63 68 71 74 |
| 16 | 83 | 0 2 4 6 8 10 17 24 44 49 54 59 70 73 82 85 |
| 17 | 93 | 0 2 4 8 15 22 26 33 38 43 70 80 83 86 89 92 95 |
| 18 | 103 | 0 2 4 6 8 10 43 52 54 63 68 75 80 87 92 99 102 105 |
| 19 | 116 | 0 2 4 6 8 10 53 60 63 69 74 81 86 93 98 105 108 115 118 |
| 20 | 129 | 0 2 4 6 8 10 61 68 75 79 82 91 94 103 106 115 118 123 128 131 |
References
- Compton, R.T., Jr. The tripole antenna: An adaptive array with full polarization flexibility. IEEE Trans. Antennas Propag. 1981, 29, 944–952. [Google Scholar] [CrossRef]
- Weiss, A.J.; Friedlander, B. Performance analysis of diversely polarized antenna arrays. IEEE Trans. Signal Process. 1991, 39, 1589–1603. [Google Scholar] [CrossRef]
- Nehorai, A.; Ho, K.C.; Tan, B.T.G. Minimum-noise-variance beamformer with an electromagnetic vector sensor. IEEE Trans. Signal Process. 1999, 47, 601–618. [Google Scholar] [CrossRef]
- Ferrara, E.R., Jr.; Parks, T.M. Direction finding with an array of antennas having diverse polarizations. IEEE Trans. Antennas Propag. 1983, 31, 231–236. [Google Scholar] [CrossRef]
- Li, J.; Compton, R.T., Jr. Angle and polarization estimation using ESPRIT with a polarization sensitive array. IEEE Trans. Antennas Propag. 1991, 39, 1376–1383. [Google Scholar] [CrossRef]
- Nehorai, A.; Paldi, E. Vector-sensor array processing for electromagnetic source localization. IEEE Trans. Signal Process. 1994, 42, 376–398. [Google Scholar] [CrossRef]
- Li, J.; Stoica, P.; Zheng, D. Efficient direction and polarization estimation with a COLD array. IEEE Trans. Antennas Propag. 1996, 44, 539–547. [Google Scholar] [CrossRef]
- Han, K.; Nehorai, A. Nested vector-sensor array processing via tensor modeling. IEEE Trans. Signal Process. 2014, 62, 2542–2553. [Google Scholar] [CrossRef]
- He, J.; Zhang, Z.; Shu, T.; Yu, W. Direction finding of multiple partially polarized signals with a nested cross-dipole array. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 1679–1682. [Google Scholar] [CrossRef]
- Wong, K.T.; Yuan, X. “Vector cross-product direction-finding” with an electromagnetic vector-sensor of six orthogonally oriented but spatially noncollocating dipoles/loops. IEEE Trans. Signal Process. 2011, 59, 160–171. [Google Scholar] [CrossRef]
- Wong, K.T.; Song, Y.; Fulton, C.J.; Khan, S.; Tam, W. Electrically “long” dipoles in a collocated/orthogonal triad—for direction finding and polarization estimation. IEEE Trans. Antennas Propag. 2017, 65, 6057–6067. [Google Scholar] [CrossRef]
- Rao, S.; Chepuri, S.P.; Leus, G. DOA estimation using sparse vector sensor arrays. In Proceedings of the IEEE 6th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing, Cancun, Mexico, 13–16 December 2015; pp. 333–336. [Google Scholar] [CrossRef]
- Shen, L.; Liu, Z.; Xu, Y. Parameter estimation using partly calibrated vector antennas. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 860–863. [Google Scholar] [CrossRef]
- Elnour, B.; Erricolo, D. A novel colocated cross-polarized two-loop PCB antenna in the ISM 2.4-GHz band. IEEE Antennas Wirel. Propag. Lett. 2010, 9, 1237–1240. [Google Scholar] [CrossRef]
- Costa, M.; Richter, A.; Koivunen, V. DoA and polarization estimation for arbitrary array configurations. IEEE Trans. Signal Process. 2012, 60, 2330–2343. [Google Scholar] [CrossRef]
- Slater, M.J.; Schmitz, C.D.; Anderson, M.D.; Jones, D.L.; Bernhard, J.T. Demonstration of an electrically small antenna array for UHF direction-of-arrival estimation. IEEE Trans. Antennas Propag. 2013, 61, 1371–1377. [Google Scholar] [CrossRef]
- Lominé, J.; Morlaas, C.; Aubert, H. Novel vector sensors design with three co-located or distributed elements for the 3D DoA estimation. Prog. Electromagn. Res. B 2014, 57, 207–220. [Google Scholar] [CrossRef]
- Lominé, J.; Morlaas, C.; Imbert, C.; Aubert, H. Dual-band vector sensor for direction of arrival estimation of incoming electromagnetic waves. IEEE Trans. Antennas Propag. 2015, 63, 3662–3671. [Google Scholar] [CrossRef][Green Version]
- Duplouy, J.; Morlaas, C.; Aubert, H.; Potier, P.; Pouliguen, P.; Djoma, C. Reconfigurable grounded vector antenna for 3-D electromagnetic direction-finding applications. IEEE Antennas Wireless Propag. Lett. 2018, 17, 197–200. [Google Scholar] [CrossRef]
- Liu, Z.; Li, R.; Li, B.; Liu, Y.; Lv, X. A wideband tri-polarized antenna at 2.4 GHz for array application. In Proceedings of the IEEE 6th Asia-Pacific Conference on Antennas and Propagation, Xi’an, China, 16–19 October 2017. [Google Scholar] [CrossRef]
- Friedlander, B. Antenna array manifolds for high-resolution direction finding. IEEE Trans. Signal Process. 2018, 66, 923–932. [Google Scholar] [CrossRef]
- Friedlander, B. Polarization sensitivity of antenna arrays. IEEE Trans. Signal Process. 2019, 67, 234–244. [Google Scholar] [CrossRef]
- Balanis, C.A. Antenna Theory, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016; pp. 448–473. [Google Scholar]
- Moffet, A. Minimum-redundancy linear arrays. IEEE Trans. Antennas Propag. 1968, 16, 172–175. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P.; Pal, P. Sparse sensing with co-prime samplers and arrays. IEEE Trans. Signal Process. 2011, 59, 573–586. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P. Nested arrays: A novel approach to array processing with enhanced degrees of freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef]
- Liu, C.; Vaidyanathan, P.P. Super nested arrays: Linear sparse arrays with reduced mutual coupling Part I: Fundamentals. IEEE Trans. Signal Process. 2016, 64, 3997–4012. [Google Scholar] [CrossRef]
- Qin, S.; Zhang, Y.D.; Amin, M.G. Generalized coprime array configurations for direction-of-arrival estimation. IEEE Trans. Signal Process. 2015, 63, 1377–1390. [Google Scholar] [CrossRef]
- Wang, J.; Xu, H.; Leus, G.J.T.; Vandenbosch, G.A.E. Experimental assessment of the coarray concept for DoA estimation in wireless communications. IEEE Trans. Antennas Propag. 2018, 66, 3064–3075. [Google Scholar] [CrossRef]
- Robison, A.D. Parallel Computation of Sparse Rulers. Available online: https://software.intel.com/en-us/articles/parallel-computation-of-sparse-rulers (accessed on 10 April 2019).
- Ruf, C.S. Numerical annealing of low-redundancy linear arrays. IEEE Trans. Antennas Propag. 1993, 41, 85–90. [Google Scholar] [CrossRef]
- Dong, J.; Li, Q.; Jin, R.; Zhu, Y.; Huang, Q.; Gui, L. A method for seeking low-redundancy large linear arrays in aperture synthesis microwave radiometers. IEEE Trans. Antennas Propag. 2010, 58, 1913–1921. [Google Scholar] [CrossRef]
- Abramovich, Y.I.; Spencer, N.K.; Gorokhov, A.Y. Positive-definite Toeplitz completion in DOA estimation for nonuniform linear antenna arrays. II. Partially augmentable arrays. IEEE Trans. Signal Process. 1999, 47, 1502–1521. [Google Scholar] [CrossRef]



| L | N0 | VA Locations |
|---|---|---|
| 22 | 20 | 0 2 4 6 11 14 19 22 |
| 23 | 21 | 0 2 4 6 8 13 20 23 |
| 24 | 22 | 0 2 4 6 11 16 21 24 |
| 25 1 | 23 | 0 2 4 9 14 19 22 25 |
| 26 | 21 | 0 3 6 9 17 19 21 26 |
| 27 | 21 | 0 3 6 8 16 18 20 27 |
| 28 | 21 | 0 2 8 10 16 19 23 28 |
| 29 | 22 | 0 3 8 16 18 20 22 29 |
| 30 | 23 | 0 5 7 9 19 22 25 30 |
| 31 2 | 24 | 0 3 8 18 20 22 24 31 |
| 32 | 22 | 0 2 4 11 16 19 22 32 |
| 33 | 22 | 0 2 5 12 14 18 22 33 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, S.; Xu, Y.; Zhuang, J.; Zhao, K.; Huang, Y.; Liu, Z. Tri-polarized Sparse Array Design for Mutual Coupling Reduction in Direction Finding and Polarization Estimation. Electronics 2019, 8, 1557. https://doi.org/10.3390/electronics8121557
Shi S, Xu Y, Zhuang J, Zhao K, Huang Y, Liu Z. Tri-polarized Sparse Array Design for Mutual Coupling Reduction in Direction Finding and Polarization Estimation. Electronics. 2019; 8(12):1557. https://doi.org/10.3390/electronics8121557
Chicago/Turabian StyleShi, Shuli, Yougen Xu, Junpeng Zhuang, Kang Zhao, Yulin Huang, and Zhiwen Liu. 2019. "Tri-polarized Sparse Array Design for Mutual Coupling Reduction in Direction Finding and Polarization Estimation" Electronics 8, no. 12: 1557. https://doi.org/10.3390/electronics8121557
APA StyleShi, S., Xu, Y., Zhuang, J., Zhao, K., Huang, Y., & Liu, Z. (2019). Tri-polarized Sparse Array Design for Mutual Coupling Reduction in Direction Finding and Polarization Estimation. Electronics, 8(12), 1557. https://doi.org/10.3390/electronics8121557





