High Performance Graphene-Based Electrochemical Double Layer Capacitors Using 1-Butyl-1-methylpyrrolidinium tris (pentafluoroethyl) trifluorophosphate Ionic Liquid as an Electrolyte
Abstract
1. Introduction
2. Materials and Methods
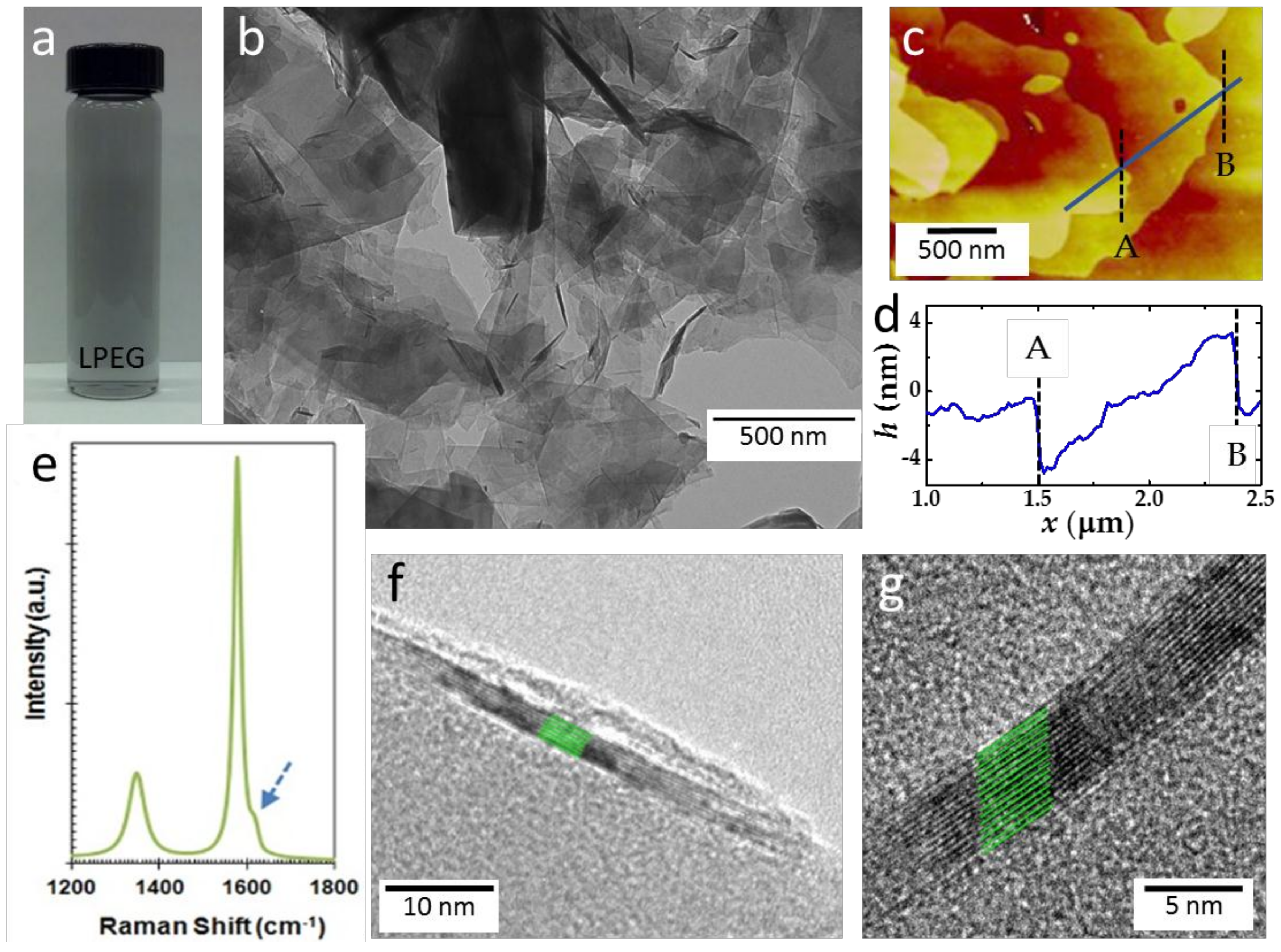
2.1. Structural Characterizations
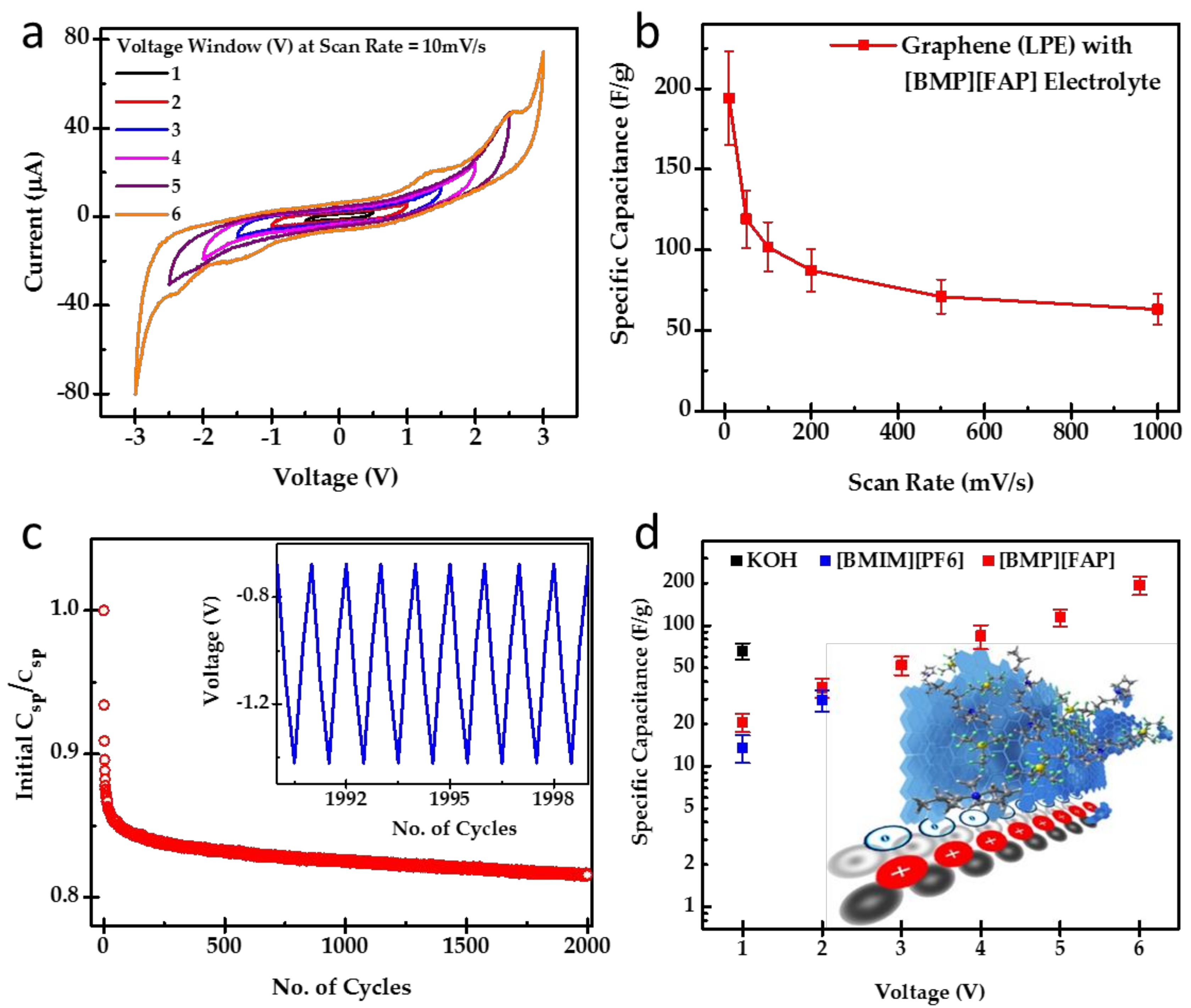
2.2. Electrochemical Characterizations
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods: Fundamentals and Applications, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Conway, B.E. Electrochemical Supercapacitors: Scientific Fundamentals and Technological Applications; Kluwer Acad.: New York, NY, USA, 2009; ISBN 978-1-4757-3058-6. [Google Scholar]
- Goodenough, J.B.; Abruna, H.D.; Buchanan, M.V. Basic Research Needs for Electrical Energy Storage; Technical Report of the basic energy sciences workshop on electrical energy storage; DOESC (USDOE Office of Science (SC)): Washington, DC, USA, 2–4 April 2007. [Google Scholar] [CrossRef]
- Rufer, A.; Barrade, P. A supercapacitor-based energy-storage system for elevators with soft commutated interface. IEEE Trans. Ind. Appl. 2002, 38, 1151–1159. [Google Scholar] [CrossRef]
- Christen, T.; Carlen, M.W. Theory of ragone plots. J. Power Sources 2000, 91, 210–216. [Google Scholar] [CrossRef]
- Borenstein, A.; Hanna, O.; Attias, R.; Luski, S.; Brousse, T.; Aurbach, D. Carbon-based composite materials for supercapacitor electrodes: A review. J. Mater. Chem. A 2017, 5, 12653–12672. [Google Scholar] [CrossRef]
- Khan, A.H.; Ghosh, S.; Pradhan, B.; Dalui, A.; Shrestha, L.K.; Acharya, S.; Ariga, K. Two-dimensional (2d) nanomaterials towards electrochemical nanoarchitectonics in energy-related applications. Bull. Chem. Soc. Jpn. 2017, 90, 627–648. [Google Scholar] [CrossRef]
- Wang, Y.; Mayorga-Martinez, C.C.; Pumera, M. Polyaniline/mosx supercapacitor by electrodeposition. Bull. Chem. Soc. Jpn. 2017, 90, 847–853. [Google Scholar] [CrossRef]
- Sheberla, D.; Bachman, J.C.; Elias, J.S.; Sun, C.-J.; Shao-Horn, Y.; Dincă, M. Conductive mof electrodes for stable supercapacitors with high areal capacitance. Nat. Mater. 2016, 16, 220. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Kim, J.H.; Ariga, K. Redox-active polymers for energy storage nanoarchitectonics. Joule 2017, 1, 739–768. [Google Scholar] [CrossRef]
- Frackowiak, E.; Béguin, F. Electrochemical storage of energy in carbon nanotubes and nanostructured carbons. Carbon 2002, 40, 1775–1787. [Google Scholar] [CrossRef]
- Hu, S.; Rajamani, R.; Yu, X. Flexible solid-state paper based carbon nanotube supercapacitor. Appl. Phys. Lett. 2012, 100, 104103. [Google Scholar] [CrossRef]
- Pandey, S.; Maiti, U.N.; Palanisamy, K.; Nikolaev, P.; Arepalli, S. Ultrasonicated double wall carbon nanotubes for enhanced electric double layer capacitance. Appl. Phys. Lett. 2014, 104, 233902. [Google Scholar] [CrossRef]
- Rakesh, S.; Xianfeng, Z.; Saikat, T. Electrochemical double layer capacitor electrodes using aligned carbon nanotubes grown directly on metals. Nanotechnology 2009, 20, 395202. [Google Scholar]
- Gao, Y.; Zhou, Y.S.; Xiong, W.; Jiang, L.J.; Mahjouri-samani, M.; Thirugnanam, P.; Huang, X.; Wang, M.M.; Jiang, L.; Lu, Y.F. Transparent, flexible, and solid-state supercapacitors based on graphene electrodes. APL Mater. 2013, 1, 012101. [Google Scholar] [CrossRef]
- Mishra, A.K.; Ramaprabhu, S. Ultrahigh arsenic sorption using iron oxide-graphene nanocomposite supercapacitor assembly. J. Appl. Phys. 2012, 112, 104315. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, Z.; Huang, Y.; Ma, Y.; Wang, C.; Chen, M.; Chen, Y. Supercapacitor devices based on graphene materials. J. Phys. Chem. C 2009, 113, 13103–13107. [Google Scholar] [CrossRef]
- Wu, Q.; Xu, Y.; Yao, Z.; Liu, A.; Shi, G. Supercapacitors based on flexible graphene/polyaniline nanofiber composite films. ACS Nano 2010, 4, 1963–1970. [Google Scholar] [CrossRef] [PubMed]
- Yu, A.; Roes, I.; Davies, A.; Chen, Z. Ultrathin, transparent, and flexible graphene films for supercapacitor application. Appl. Phys. Lett. 2010, 96, 253105. [Google Scholar] [CrossRef]
- Zang, X.; Li, P.; Chen, Q.; Wang, K.; Wei, J.; Wu, D.; Zhu, H. Evaluation of layer-by-layer graphene structures as supercapacitor electrode materials. J. Appl. Phys. 2014, 115, 024305. [Google Scholar] [CrossRef]
- Zhang, L.L.; Zhou, R.; Zhao, X.S. Graphene-based materials as supercapacitor electrodes. J. Mater. Chem. 2010, 20, 5983–5992. [Google Scholar] [CrossRef]
- Prabaharan, S.R.S.; Vimala, R.; Zainal, Z. Nanostructured mesoporous carbon as electrodes for supercapacitors. J. Power Sources 2006, 161, 730–736. [Google Scholar] [CrossRef]
- Al-Asadi, A.S.; Henley, L.A.; Wasala, M.; Muchharla, B.; Perea-Lopez, N.; Carozo, V.; Lin, Z.; Terrones, M.; Mondal, K.; Kordas, K.; et al. Aligned carbon nanotube/zinc oxide nanowire hybrids as high performance electrodes for supercapacitor applications. J. Appl. Phys. 2017, 121, 124303. [Google Scholar] [CrossRef]
- Gong, W.; Fugetsu, B.; Wang, Z.; Sakata, I.; Su, L.; Zhang, X.; Ogata, H.; Li, M.; Wang, C.; Li, J.; et al. Carbon nanotubes and manganese oxide hybrid nanostructures as high performance fiber supercapacitors. Commun. Chem. 2018, 1, 16. [Google Scholar] [CrossRef]
- Cakici, M.; Kakarla, R.R.; Alonso-Marroquin, F. Advanced electrochemical energy storage supercapacitors based on the flexible carbon fiber fabric-coated with uniform coral-like mno2 structured electrodes. Chem. Eng. J. 2017, 309, 151–158. [Google Scholar] [CrossRef]
- Fletcher, S.I.; Sillars, F.B.; Hudson, N.E.; Hall, P.J. Physical properties of selected ionic liquids for use as electrolytes and other industrial applications. J.Chem. Eng. Data 2010, 55, 778–782. [Google Scholar] [CrossRef]
- Ignat’ev, N.V.; Welz-Biermann, U.; Kucheryna, A.; Bissky, G.; Willner, H. New ionic liquids with tris(perfluoroalkyl)trifluorophosphate (fap) anions. J. Fluorine Chem. 2005, 126, 1150–1159. [Google Scholar] [CrossRef]
- Aboutalebi, S.H.; Jalili, R.; Esrafilzadeh, D.; Salari, M.; Gholamvand, Z.; Aminorroaya Yamini, S.; Konstantinov, K.; Shepherd, R.L.; Chen, J.; Moulton, S.E.; et al. High-performance multifunctional graphene yarns: Toward wearable all-carbon energy storage textiles. ACS Nano 2014, 8, 2456–2466. [Google Scholar] [CrossRef] [PubMed]
- Sahu, V.; Shekhar, S.; Sharma, R.K.; Singh, G. Ultrahigh performance supercapacitor from lacey reduced graphene oxide nanoribbons. ACS Appl. Mater. Interfaces 2015, 7, 3110–3116. [Google Scholar] [CrossRef] [PubMed]
- Albrektsen, O.; Eriksen, R.L.; Novikov, S.M.; Schall, D.; Karl, M.; Bozhevolnyi, S.I.; Simonsen, A.C. High resolution imaging of few-layer graphene. J. Appl. Phys. 2012, 111, 064305. [Google Scholar] [CrossRef]
- Wu, J.X.; Xu, H.; Zhang, J. Raman spectroscopy of graphene. Acta Chim. Sin. 2014, 72, 301–318. [Google Scholar] [CrossRef]
- Pensado, A.S.; Malberg, F.; Gomes, M.F.C.; Pádua, A.A.H.; Fernández, J.; Kirchner, B. Interactions and structure of ionic liquids on graphene and carbon nanotubes surfaces. RSC Adv. 2014, 4, 18017–18024. [Google Scholar] [CrossRef]
- Jorcin, J.-B.; Orazem, M.E.; Pébère, N.; Tribollet, B. Cpe analysis by local electrochemical impedance spectroscopy. Electrochim. Acta. 2006, 51, 1473–1479. [Google Scholar] [CrossRef]
- Kötz, R.; Hahn, M.; Gallay, R. Temperature behavior and impedance fundamentals of supercapacitors. J. Power Sources 2006, 154, 550–555. [Google Scholar] [CrossRef]
- Macdonald, J.R. Impedance spectroscopy. Ann. Biomed. Eng. 1992, 20, 289–305. [Google Scholar] [CrossRef] [PubMed]
- Qu, L.; Zhao, Y.; Khan, A.M.; Han, C.; Hercule, K.M.; Yan, M.; Liu, X.; Chen, W.; Wang, D.; Cai, Z.; et al. Interwoven three-dimensional architecture of cobalt oxide nanobrush-graphene@nixco2x(oh)6x for high-performance supercapacitors. Nano Lett. 2015, 15, 2037–2044. [Google Scholar] [CrossRef] [PubMed]
- Cho, S.; Kim, M.; Jang, J. Screen-printable and flexible ruo2 nanoparticle-decorated pedot:Pss/graphene nanocomposite with enhanced electrical and electrochemical performances for high-capacity supercapacitor. ACS Appl. Mater. Interfaces 2015, 7, 10213–10227. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.; Wang, Q.; Wei, T.; Jiang, L.; Zhang, M.; Jing, X.; Fan, Z. Template-assisted low temperature synthesis of functionalized graphene for ultrahigh volumetric performance supercapacitors. ACS Nano 2014, 8, 4720–4729. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S.; An, X.; Shah, R.; Rawat, D.; Dave, B.; Kar, S.; Talapatra, S. Effect of 1- pyrene carboxylic-acid functionalization of graphene on its capacitive energy storage. J. Phys. Chem. C 2012, 116, 20688–20693. [Google Scholar] [CrossRef]
- Ghosh, D.; Das, C.K. Hydrothermal growth of hierarchical ni3s2 and co3s4 on a reduced graphene oxide hydrogel@ni foam: A high-energy-density aqueous asymmetric supercapacitor. ACS Appl. Mater. Interfaces 2015, 7, 1122–1131. [Google Scholar] [CrossRef] [PubMed]
- Podolyan, Y.; Leszczynski, J. Mask: A visualization tool for teaching and research in computational chemistry. Int. J. Quantum Chem. 2009, 109, 8–16. [Google Scholar] [CrossRef]


| Parameters | Value |
|---|---|
| Pseudo-capacitance (C1)/F | 1.5959 × 10−6 |
| Pseudo-capacitance (C2)/F | 9.5812 × 10−6 |
| Equivalent series resistance (ESR) (R1)/Ω | 25.605 |
| Faradaic resistance (R2)/Ω | 155.17 |
| Warburg component (W) | 3029 |
| Constant phase element (CPE) factor (Y0) | 2.7059 × 10−5 |
| CPE exponent (n) | 0.70632 |
| ESR (experimental)/Ω | 25.57 |
| Double layer capacitance (at lowest frequency)/F | 3.273 × 10−5 |
| Total device capacitance/F (from the model) | 4.391 × 10−5 |
| Total device capacitance/F/g | 3.0699 |
| Experimental capacitance (1000 mV/s)/F/g | 4.13 |
| Source | Method | Measurement | Electrolyte | ED (Wh/kg) | PD (kW/kg) |
|---|---|---|---|---|---|
| [36] | CNG@NCH | Three-electrode | Aqueous (1 M LiOH) | 78.8 | 8.4 |
| [37] | RuO2/PEDOT-G30 | Three-electrode | Aqueous (0.5 M H2SO4) | 73 | 1.1 |
| [38] | Graphene w/Mg(OH)2 template | Three-electrode & Two-electrode | Aqueous (6 M KOH) | ≈27 | ≈17 |
| [28] | Graphene Yarns | Two-electrode | Aqueous (1 M H2SO4) | 14 | 25 |
| [40] | NI3S2 & Co3S4 on RGO Hydrogel @Ni Foam | Asymmetrical Two-electrode | Aqueous (6 M KOH) | 55.2 | 13 |
| [29] | LRGONR | Two-electrode | Aqueous (2 M H2SO4) | 15.1 | ≈10 |
| IL ([TEA][BF4]) | 90 | 2.0 a | |||
| IL ([BMIM][BF4]) | 181.5 | 2.3 a | |||
| This work | LPEG | Two-electrode | IL ([BMP][FAP]) | 24.9 | 47.5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huffstutler, J.D.; Wasala, M.; Richie, J.; Barron, J.; Winchester, A.; Ghosh, S.; Yang, C.; Xu, W.; Song, L.; Kar, S.; et al. High Performance Graphene-Based Electrochemical Double Layer Capacitors Using 1-Butyl-1-methylpyrrolidinium tris (pentafluoroethyl) trifluorophosphate Ionic Liquid as an Electrolyte. Electronics 2018, 7, 229. https://doi.org/10.3390/electronics7100229
Huffstutler JD, Wasala M, Richie J, Barron J, Winchester A, Ghosh S, Yang C, Xu W, Song L, Kar S, et al. High Performance Graphene-Based Electrochemical Double Layer Capacitors Using 1-Butyl-1-methylpyrrolidinium tris (pentafluoroethyl) trifluorophosphate Ionic Liquid as an Electrolyte. Electronics. 2018; 7(10):229. https://doi.org/10.3390/electronics7100229
Chicago/Turabian StyleHuffstutler, Jacob D., Milinda Wasala, Julianna Richie, John Barron, Andrew Winchester, Sujoy Ghosh, Chao Yang, Weiyu Xu, Li Song, Swastik Kar, and et al. 2018. "High Performance Graphene-Based Electrochemical Double Layer Capacitors Using 1-Butyl-1-methylpyrrolidinium tris (pentafluoroethyl) trifluorophosphate Ionic Liquid as an Electrolyte" Electronics 7, no. 10: 229. https://doi.org/10.3390/electronics7100229
APA StyleHuffstutler, J. D., Wasala, M., Richie, J., Barron, J., Winchester, A., Ghosh, S., Yang, C., Xu, W., Song, L., Kar, S., & Talapatra, S. (2018). High Performance Graphene-Based Electrochemical Double Layer Capacitors Using 1-Butyl-1-methylpyrrolidinium tris (pentafluoroethyl) trifluorophosphate Ionic Liquid as an Electrolyte. Electronics, 7(10), 229. https://doi.org/10.3390/electronics7100229





