Hybrid Energy Storage System for Regenerative Braking Utilization and Peak Power Decrease in 3 kV DC Railway Electrification System
Abstract
1. Introduction
2. The Procedure of Energy Storage Parameters Optimization
- (a)
- carrying out the measurements of the 15-min substation traction power for one year (the historical data of 15-min average power, hence? the values are registered according to the agreement with the DNO),
- (b)
- conducting the simulation of the railway line based on the timetable of the trains’ operation in order to obtain the instantaneous values of the traction power for 24-h cycle, including the available regeneration power. Regeneration power is available as the result of the limited overhead catenary receptivity. The 24-h cycle of instantaneous power profile is needed to carry out the evaluation of the annual regenerative energy,
- (c)
- comparing the 15-min power obtained from the simulation in point (b) above with the average 15-min power measured in the real substation in order to validate the correctness of the simulation model. This point is not necessary for the sizing procedure but provides the validation of the simulation model with the real model.
- (d)
- conducting the second simulation of 24-h operation of the traction substation with the traffic concentration near the analyzed substation, which will give the comparable value to the maximum 15-min power during 1-year measurements. This process requires the modification of the train timetable such a way as to obtain the peak power demand close to the value obtained in the measurements as the sizing process requires the time profile of substation power for 24 h cycle containing available regenerative power (negative values) and peak power obtained due to ? traffic concentration,
- (e)
- sizing the parameters of supercapacitor module (energy capacity and nominal power of DC/DC converter) based on the criterion of payback period value [12],
- (f)
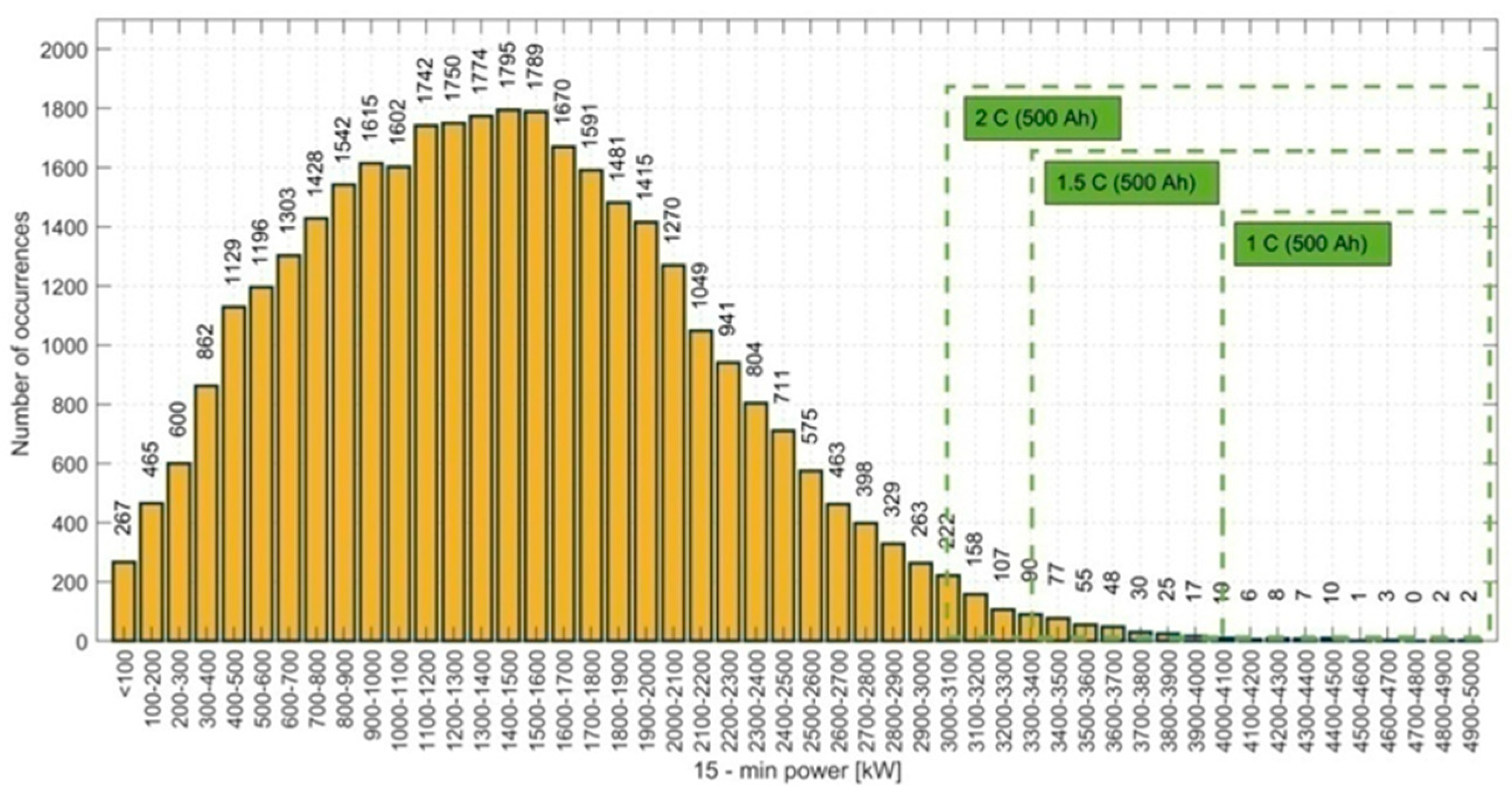
- sizing the parameters of the battery module of the energy storage based on the histogram of the 15-min power measurements and the simulation of the energy storage model with the 24-h values with the traffic concentration.
3. The Validation of Simulation Model of DC Electrification System with Limited Receptivity
- -
- including normal train operation according to the standard timetable
- -
- including train operation according to the timetable with the train traffic concentration near the traction substation with energy storage.
- -
- the model contains 160 trains of different types operating during 24-h cycle,
- -
- the trains of type 1 and 3 are equipped with regenerative braking.
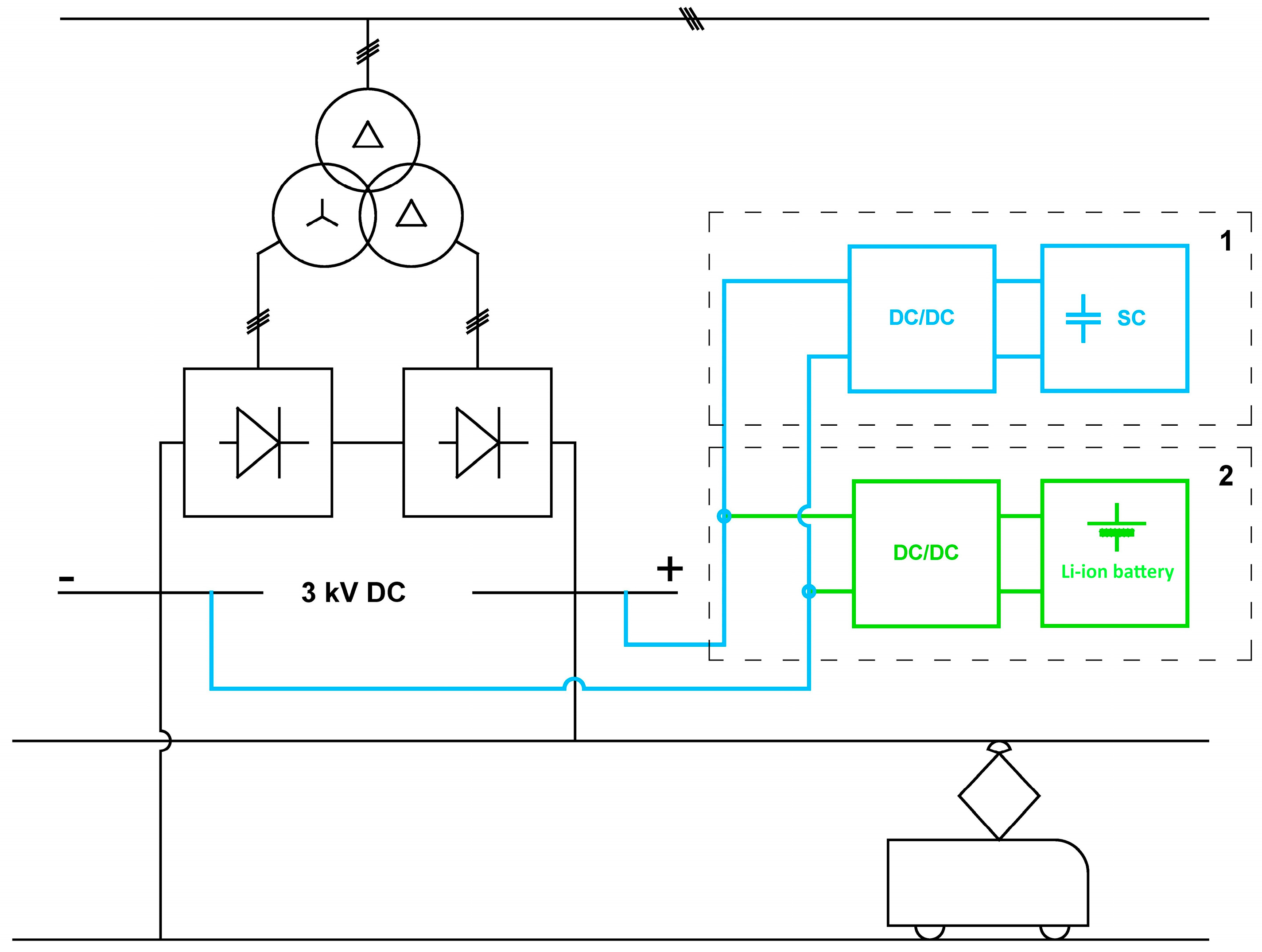
4. The Algorithm of ESS Operation
- -
- maximum/maximizing the use of available excessive regenerative energy of the braking trains,
- -
- maximum decrease of peak power and ensuring that the peak power is below the new limit,
- -
- maximizing the live cycle of the lithium-ion battery.
- -
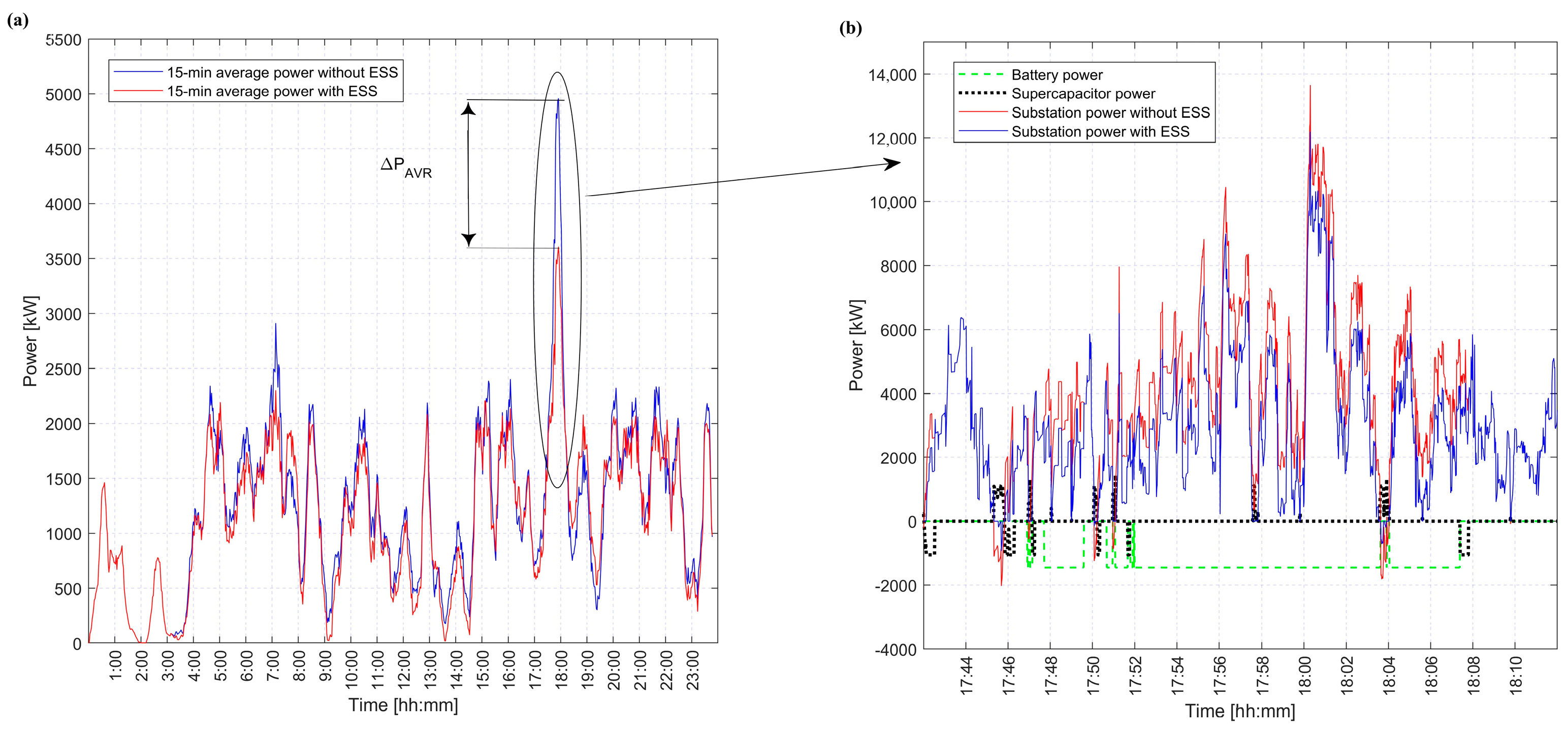
- active energy saved by use of regenerative power (E24reg),
- -
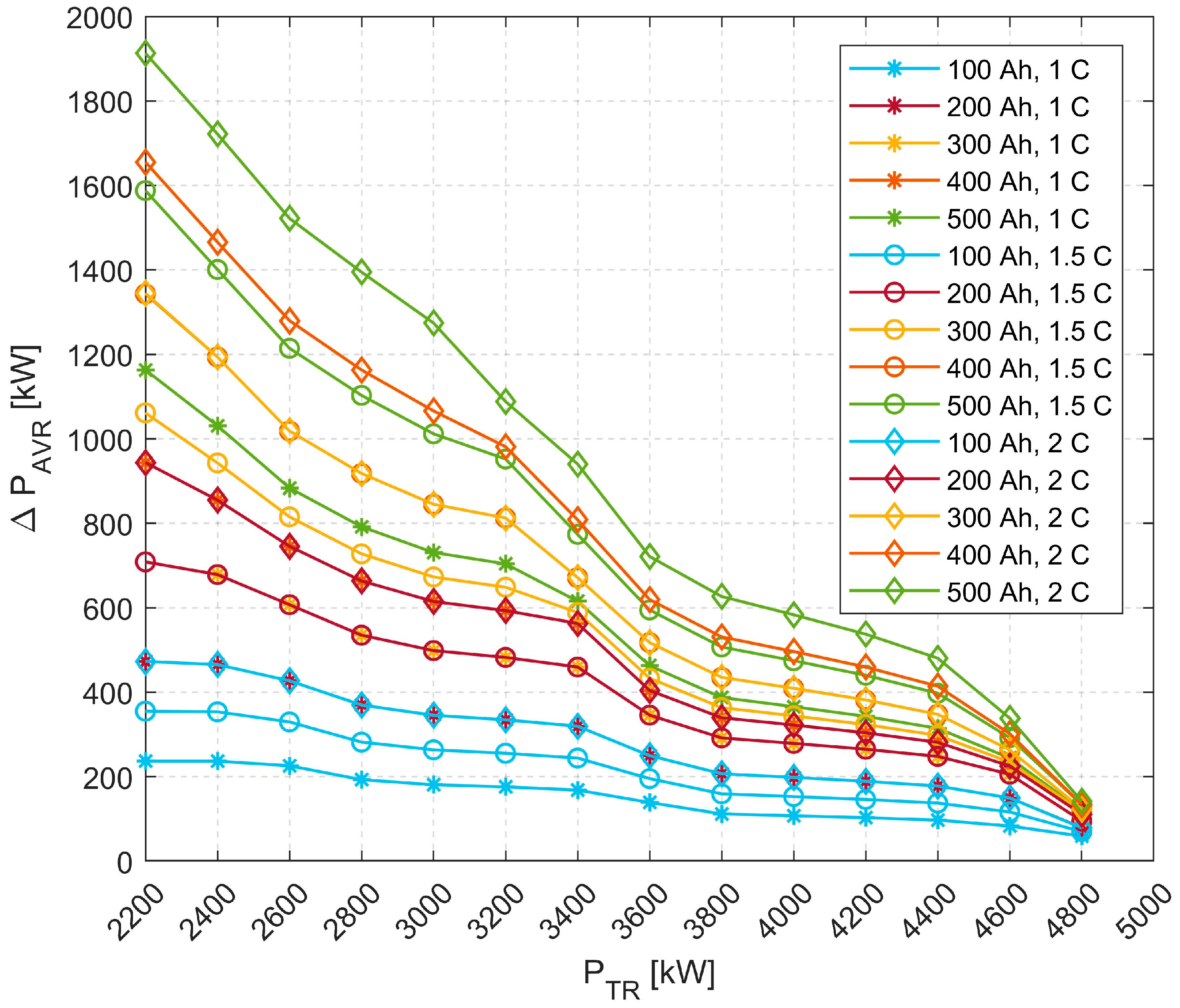
- reduction of maximum 15-min power resulting from ESS operation (ΔPAVR).
5. Results and Discussion
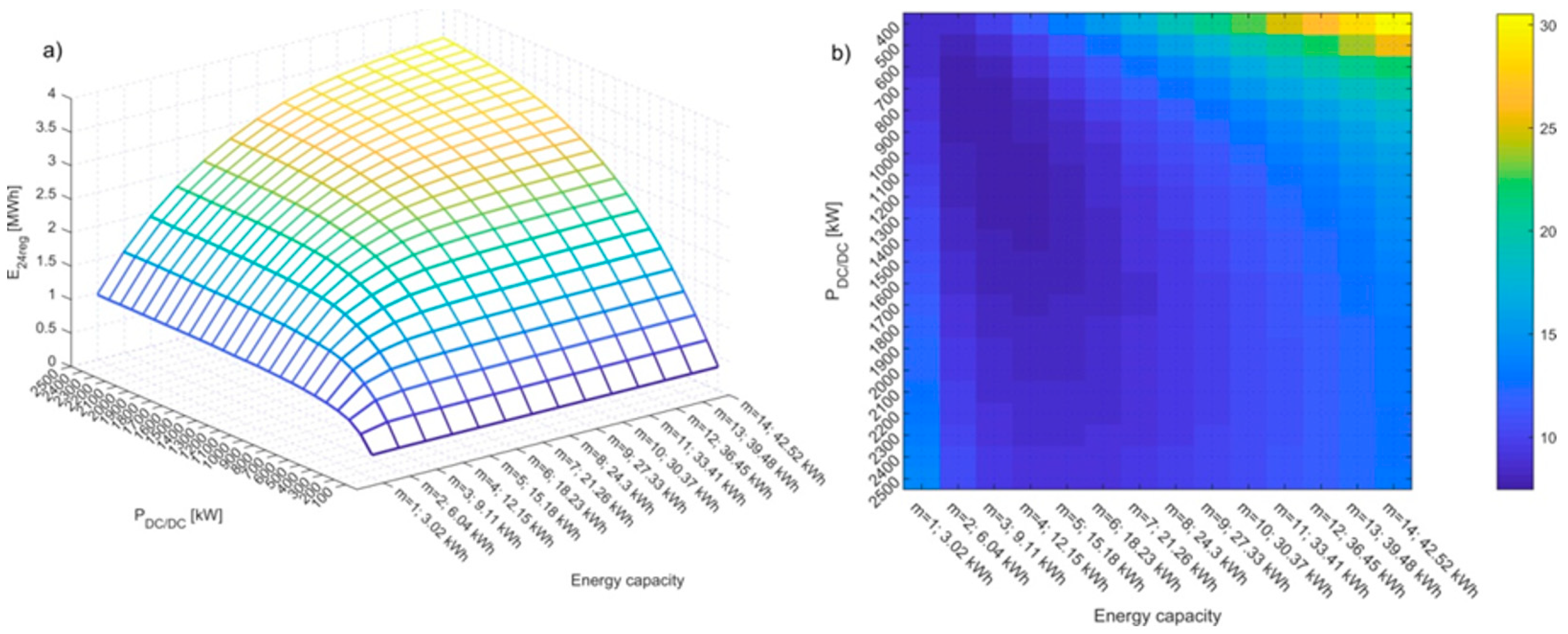
5.1. Supercapacitor Module
5.2. Li-Ion Battery Module
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Ah | total charge flowing through the battery (Ah) |
| B | pre-exponential factor |
| C | rate of battery discharge |
| CDC/DC | constant cost of DC/DC converter manufacturing and installation ($) |
| cDC/DC | unit cost of DC/DC converter manufacturing and installation ($/kW) |
| Cel | unit price of active electric energy ($/MWh) |
| CFA | annual savings resulting from regenerative energy use by supercapacitor module of ESS ($) |
| CLFP | cost of LFP battery pack ($) |
| cLFP | price of single LFP battery cell |
| COP | annual operation cost of LFP module ($) |
| cpower | unit price of demand power ($/MW·year) |
| CSC | cost of supercapacitor module installation ($) |
| cSC | price of single supercapacitor cell |
| CΔP | annual savings resulting from peak power reduction ($) |
| DoD | depth of discharge |
| E24reg | energy returned by SC module during 24-h operation (MWh) |
| EMS | average 24-h energy consumption during the preceding year (MWh) |
| i | number of 15-min period during 24-h cycle ({1:96}) |
| mLFP | number of LFP battery cells connected in parallel |
| mSC | number of supercapacitors cells connected in parallel |
| n | number of 24-h periods during the preceding year ({1:365}) |
| nLFP | number of LFP battery cells connected in series |
| npeak | number of 15-min power measured values during 1-year registration |
| nSC | number of supercapacitors cells connected in series |
| p | instantaneous power (W) |
| P15 | 15-min measured power (W) |
| P15MS | 15-min measured power for the15-min period in 24-h cycle as an average of the measured values in ti 15-min periods during the preceding year (W) |
| P15Sim | 15-min power obtained by the simulation (W) |
| PAVR | average 15-min power calculated as an rolling average (W) |
| PLFP | instantaneous power of LFP battery part of the ESS in connection to 3 kV DC (W) |
| PLFPmax | maximum power of PLFP assumed in EMS of ESS(W) |
| PPSC | payback period of supercapacitor module installation (years) |
| PSC | instantaneous power of supercapacitor part of the ESS in connection to 3 kV DC (W) |
| PSCmax | maximum power of PSC assumed in EMS of ESS (W) |
| PTR | threshold value of the average rolling power (W) |
| PTS | power on a busbar of a traction substation (W) |
| Qcell | LFP battery single cell charge during single discharge (Ah) |
| Qloss | loss of battery capacity (%) |
| R | gas constant |
| SoC | state of charge |
| T | temperature |
| tLFP | duration in time of LFP battery life cycle |
| TSS | traction substation |
| USC | state of charge of supercapacitor pack (V) |
| USCtr | threshold state of charge of supercapacitor pack assumed in EMS of ESS (V) |
| α | profitability index of the battery module installation |
| ΔPAVR | difference of peak 15-min power of traction substation between the cases with and without ESS |
| DNO | Distribution Grid Operator |
| DoD | Depth of Discharge |
| EMS | Energy Management Strategy |
| ESS | Energy Storage System |
| LFP | LiFePO4 battery |
| SC | Supercapacitor |
| SoC | State of Charge |
| TE | Tractive Effort |
References
- Van Daalen, K.R.; Tonne, C.; Semenza, J.C.; Rocklöv, J.; Markandya, A.; Dasandi, N.; Jankin, S.; Achebak, H.; Ballester, J.; Bechara, H.; et al. The 2024 Europe report of the Lancet Countdown on health and climate change: Unprecedented warming demands unprecedented action. Lancet Public Health 2024, 9, e495–e522. [Google Scholar] [CrossRef]
- Douglas, H.; Roberts, C.; Hillmansen, S.; Schmid, F. An assessment of available measures to reduce traction energy use in railway networks. Energy Convers. Manag. 2015, 106, 1149–1165. [Google Scholar] [CrossRef]
- Yuan, J.; Peng, L.; Zhou, H.; Gan, D.; Qu, K. Recent research progress and application of energy storage system in electrified railway. Electr. Power Syst. Res. 2024, 226, 109893. [Google Scholar] [CrossRef]
- Domínguez, M.; Fernández-Cardador, A.; Fernández-Rodríguez, A.; Cucala, A.; Pecharromán, R.; Sánchez, P.U.; Cortázar, I.V. Review on the use of energy storage systems in railway applications. Renew. Sustain. Energy Rev. 2024, 207, 114904. [Google Scholar] [CrossRef]
- Suzuki, T. DC power-supply system with inverting substations for traction systems using regenerative brakes. IEE Proc. B Electr. Power Appl. 1982, 129, 18–26. [Google Scholar] [CrossRef]
- Aneke, M.; Wang, M. Energy storage technologies and real life applications—A state of the art review. Appl. Energy 2016, 179, 350–377. [Google Scholar] [CrossRef]
- Uddin, M.; Romlie, M.F.; Abdullah, M.F.; Halim, S.A.; Kwang, T.C. A review on peak load shaving strategies. Renew. Sustain. Energy Rev. 2018, 82, 3323–3332. [Google Scholar] [CrossRef]
- Jefimowski, W.; Nikitenko, A. Case study of stationary energy storage device in a 3 kV DC traction system. In Proceedings of the 13th International Conference Modern Electrified Transport—MET, Warsaw, Poland, 5–7 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Iannuzzi, D.; Ciccarelli, F.; Lauria, D. Stationary ultracapacitors storage device for improving energy saving and voltage profile of light transportation networks. Transp. Res. Part C Emerg. Technol. 2012, 21, 321–337. [Google Scholar] [CrossRef]
- Barrero, R.; Tackoen, X.; Van Mierlo, J. Analysis and configuration of supercapacitor based energy storage system on-board light rail vehicles. In Proceedings of the 13th International Power Electronics and Motion Control Conference, Poznan, Poland, 1–3 September 2008; pp. 1512–1517. [Google Scholar]
- Kashani, S.J.; Farjah, E. Applying Neural Network and Genetic Algorithm for Optimal Placement of Ultra-Capacitors in Metro Systems. In Proceedings of the 2011 IEEE Electrical Power and Energy Conference, Winnipeg, MB, Canada, 3–5 October 2011; pp. 35–40. [Google Scholar]
- Sirmelis, U.; Zakis, J.; Grigans, L. Optimal supercapacitor energy storage system sizing for traction substations. In Proceedings of the 2015 IEEE 5th International Conference on Power Engineering, Energy and Electrical Drives (POWERENG), Riga, Latvia 11–13 May 2015; pp. 592–595. [Google Scholar]
- Chua, K.H.; Lim, Y.S.; Morris, S. A novel fuzzy control algorithm for reducing the peak demands using energy storage system. Energy 2017, 122, 265–273. [Google Scholar] [CrossRef]
- Fossati, J.P.; Galarza, A.; Martín-Villate, A.; Fontán, L. A method for optimal sizing energy storage systems for microgrids. Renew. Energy 2015, 77, 539–549. [Google Scholar] [CrossRef]
- Jarnut, M.; Kaniewski, J.; Protasiuk, V. Energy Storage System for Peak Power Reduction of Traction Substation. In Proceedings of the 2018 Innovative Materials and Technologies in Electrical Engineering (i-MITEL), Sulecin, Poland, 18–20 April 2018; pp. 1–5. [Google Scholar]
- Ovalle, A.; Pouget, J.; Bacha, S.; Gerbaud, L.; Vinot, E.; Sonier, B. Energy storage sizing methodology for mass-transit direct-current wayside support: Application to French railway company case study. Appl. Energy 2018, 230, 1673–1684. [Google Scholar] [CrossRef]
- Graber, G.; Calderaro, V.; Galdi, V.; Piccolo, A.; Lamedica, R.; Ruvio, A. Techno-economic sizing of auxiliary-battery-based substations in DC railway systems. IEEE Trans. Transp. Electrif. 2018, 4, 616–625. [Google Scholar] [CrossRef]
- Pankovits, P.; Pouget, J.; Robyns, B.; Delhaye, F.; Brisset, S. Towards railway-smartgrid: Energy management optimization for hybrid railway power substations. In Proceedings of the 2014 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Istanbul, Turkey, 12–15 October 2014; pp. 1–6. [Google Scholar]
- Ciccarelli, F.; Iannuzzi, D.; Lauria, D.; Natale, P. Optimal Control of Stationary Lithium-Ion Capacitor-Based Storage Device for Light Electrical Transportation Network. IEEE Trans. Transp. Electrif. 2017, 3, 618–631. [Google Scholar] [CrossRef]
- Zheng, C.; Wei, S.; Wang, Z.; Liu, S.; Yuan, Y. Research and implementation on hybrid energy storage system experimental platform of rail transit. Energy Procedia 2017, 105, 3603–3608. [Google Scholar] [CrossRef]
- Li, G.; Or, S.W. Multi-agent deep reinforcement learning-based multi-time scale energy management of urban rail traction networks with distributed photovoltaic–regenerative braking hybrid energy storage systems. J. Clean. Prod. 2024, 466, 142842. [Google Scholar] [CrossRef]
- Wieczorek, M.; Lewandowski, M. A mathematical representation of an energy management strategy for hybrid energy storage system in electric vehicle and real time optimization using a genetic algorithm. Appl. Energy 2017, 192, 222–233. [Google Scholar] [CrossRef]
- Zheng, S.; Teh, J.; Alharbi, B.; Lai, C.-M. A review of equivalent-circuit model, degradation characteristics and economics of Li-ion battery energy storage system for grid applications. J. Energy Storage 2024, 101, 113908. [Google Scholar] [CrossRef]
- Grimaldi, A.; Minuto, F.D.; Perol, A.; Casagrande, S.; Lanzini, A. Ageing and energy performance analysis of a utility-scale lithium-ion battery for power grid applications through a data-driven empirical modelling approach. J. Energy Storage 2023, 65, 107232. [Google Scholar] [CrossRef]
- Koltermann, L.; Cortés, M.C.; Figgener, J.; Zurmühlen, S.; Sauer, D.U. Improved rule-based power distribution algorithm for hybrid battery storage systems and real-world validation. J. Energy Storage 2024, 86, 111360. [Google Scholar] [CrossRef]
- Jefimowski, W.; Szeląg, A. The multi-criteria optimization method for implementation of a regenerative inverter in a 3 kV DC traction system. Electr. Power Syst. Res. 2018, 161, 61–73. [Google Scholar] [CrossRef]
- Jefimowski, W.; Nikitenko, A.; Drążek, Z.; Wieczorek, M. Stationary supercapacitor energy storage operation algorithm based on neural network learning system. Bull. Pol. Acad. Sci. Technol. Sci. 2020, 68, 733–738. [Google Scholar] [CrossRef]
- Wang, J.; Liu, P.; Hicks-Garner, J.; Sherman, E.; Soukiazian, S.; Verbrugge, M.; Tataria, H.; Musser, J.; Finamore, P. Cycle-life model for graphite-LiFePO4 cells. J. Power Sources 2011, 196, 3942–3948. [Google Scholar] [CrossRef]
- The Boston Consulting Group Inc. Focus Batteries for Electric Cars: Challenges, Opportunities, and the Outlook to 2020. 2010. Available online: https://gerpisa.org/en/system/files/file36615.pdf (accessed on 27 December 2024).
- Regulation of The Minister of Climate and Environment of 26 October 2023 on the greenhouse gas emission factor for electricity in 2024. J. Laws Repub. Pol. 2370 2023. Available online: https://eli.gov.pl/eli/DU/2023/2370/ogl (accessed on 27 December 2024).
- Available online: https://www.statista.com/statistics/1322214/carbon-prices-european-union-emission-trading-scheme/ (accessed on 17 December 2024).


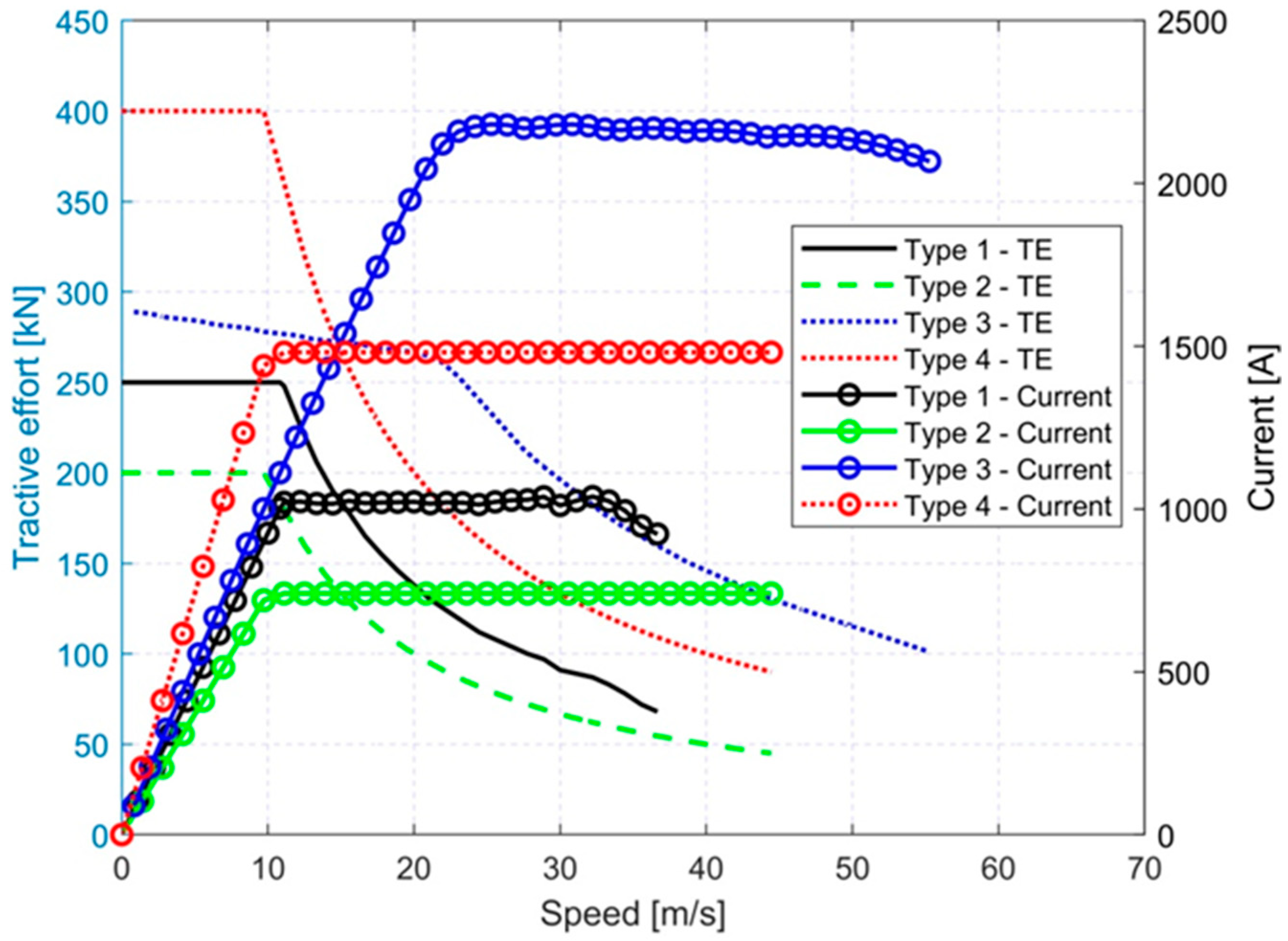






| Type 1 (Electric Multiple Unit) | Type 2 (Passenger Carriage Train 1) | Type 3 (Passenger Carriage Train 2) | Type 3 (Freight Train) | |
|---|---|---|---|---|
| Mass (t) | 280 | 330 | 430 | 1300 |
| Auxiliary power (kW) | 2 × 76 | 150 | 160 | 30 |
| a0, a1, a2—coefficients in Davis equation of rolling resistance | ||||
| a0 | 3.92 | 4.56 | 3.56 | 17.21 |
| a1 | 0 | 0.251 | 0.25 | 1.1 |
| a2 | 0.01 | 0.00446 | 0.0016 | 0.026 |
| Efficiency | 90% | 90% | 90% | 90% |
| Parameter | Value |
|---|---|
| CDC/DC | 102,000 ($) |
| cDC/DC | 102 ($/kW) |
| cSC | 55 ($) |
| Cel | 87.4 ($/MWh) |
| Parameter | Value |
|---|---|
| cpower | 38,273 ($/year) |
| cLFP | 110 ($) |
| Cel | 87.4 ($/MWh) |
| Cost of SC ($) | Cost of LFP ($) | Saving Resulting from SC Operation ($/Year) | Saving Resulting from LFP Operation ($/Year) |
|---|---|---|---|
| 425,364 | 357,818 | 59,970 | 36,124 |
| Payback period of SC (years) | Payback period of LFP (years) | ||
| 7.46 | 9.9 | ||
| Total payback period (years) | |||
| 8.41 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szeląg, A.; Jefimowski, W.; Maciołek, T.; Nikitenko, A.; Wieczorek, M.; Lewandowski, M. Hybrid Energy Storage System for Regenerative Braking Utilization and Peak Power Decrease in 3 kV DC Railway Electrification System. Electronics 2025, 14, 1752. https://doi.org/10.3390/electronics14091752
Szeląg A, Jefimowski W, Maciołek T, Nikitenko A, Wieczorek M, Lewandowski M. Hybrid Energy Storage System for Regenerative Braking Utilization and Peak Power Decrease in 3 kV DC Railway Electrification System. Electronics. 2025; 14(9):1752. https://doi.org/10.3390/electronics14091752
Chicago/Turabian StyleSzeląg, Adam, Włodzimierz Jefimowski, Tadeusz Maciołek, Anatolii Nikitenko, Maciej Wieczorek, and Mirosław Lewandowski. 2025. "Hybrid Energy Storage System for Regenerative Braking Utilization and Peak Power Decrease in 3 kV DC Railway Electrification System" Electronics 14, no. 9: 1752. https://doi.org/10.3390/electronics14091752
APA StyleSzeląg, A., Jefimowski, W., Maciołek, T., Nikitenko, A., Wieczorek, M., & Lewandowski, M. (2025). Hybrid Energy Storage System for Regenerative Braking Utilization and Peak Power Decrease in 3 kV DC Railway Electrification System. Electronics, 14(9), 1752. https://doi.org/10.3390/electronics14091752








