Lifetime Prediction of SiC MOSFET by LSTM Based on IGWO Algorithm
Abstract
1. Introduction
- (1)
- A Tent chaotic mapping was introduced to enhance the uniformity of initial population distribution.
- (2)
- A nonlinear control strategy was adopted to enable smooth and continuous transitions in the search mechanism.
- (3)
- The particle swarm optimization (PSO) principle was incorporated to strengthen global search capability.
2. The Failure Mechanism of SiC MOSFET
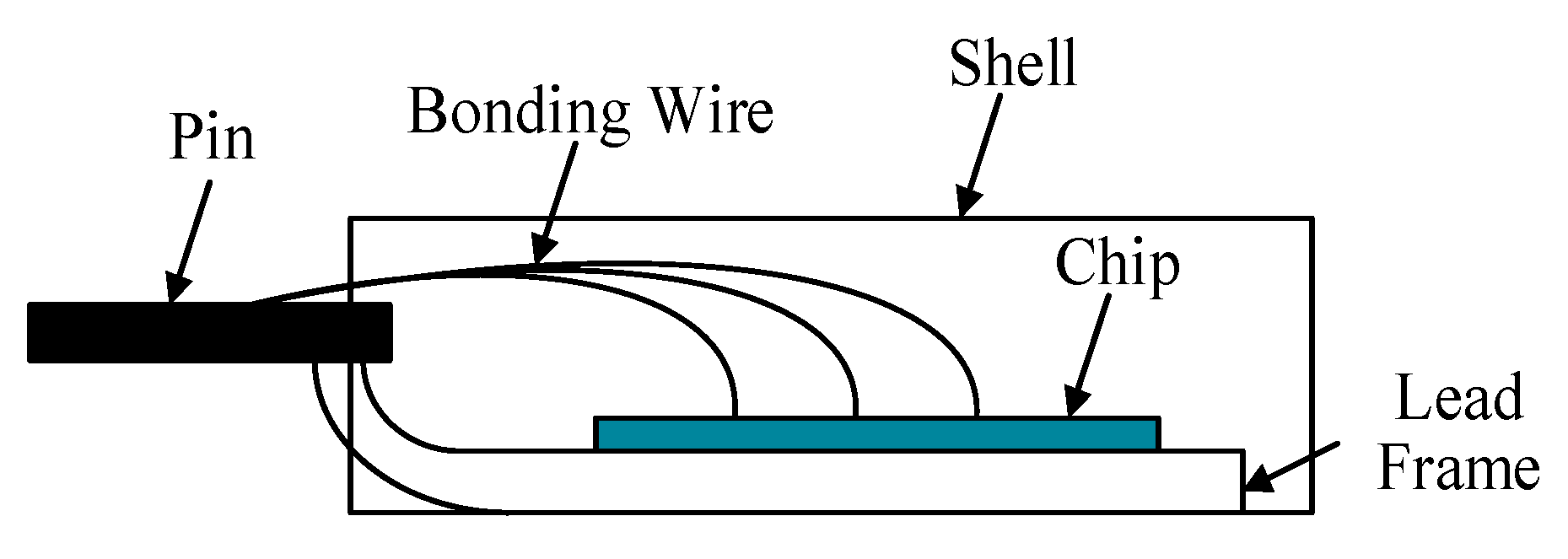
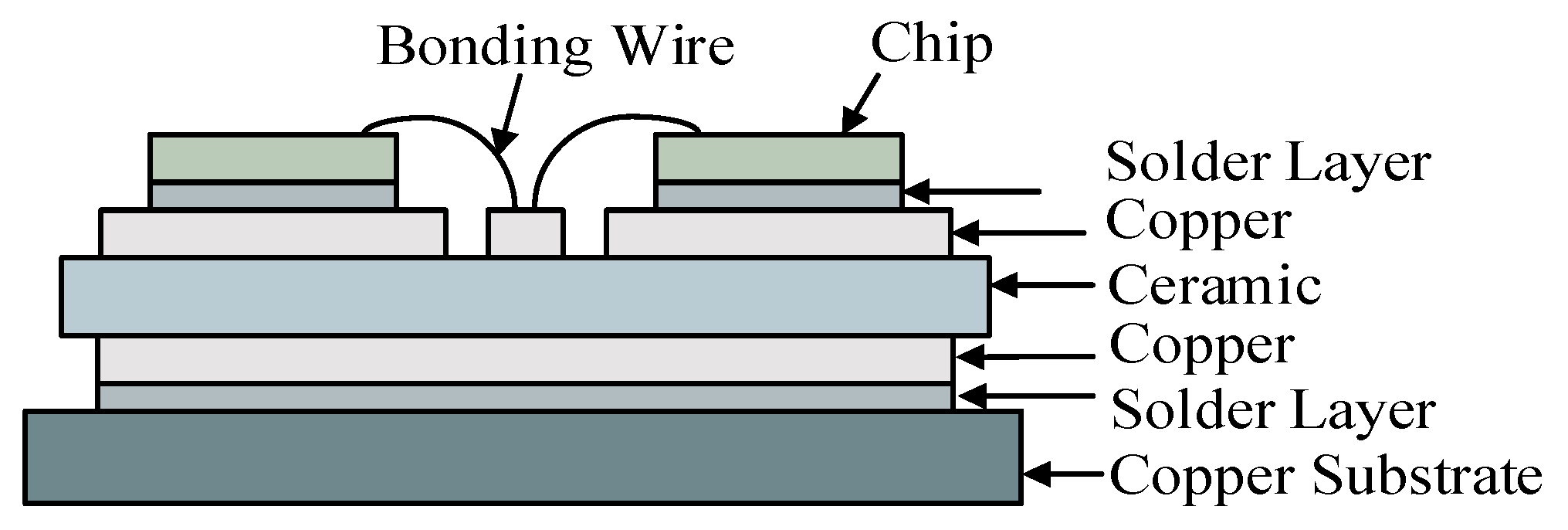
2.1. The SiC MOSFET Packaging Structure
2.1.1. Discrete Packaging
2.1.2. Modular Packaging
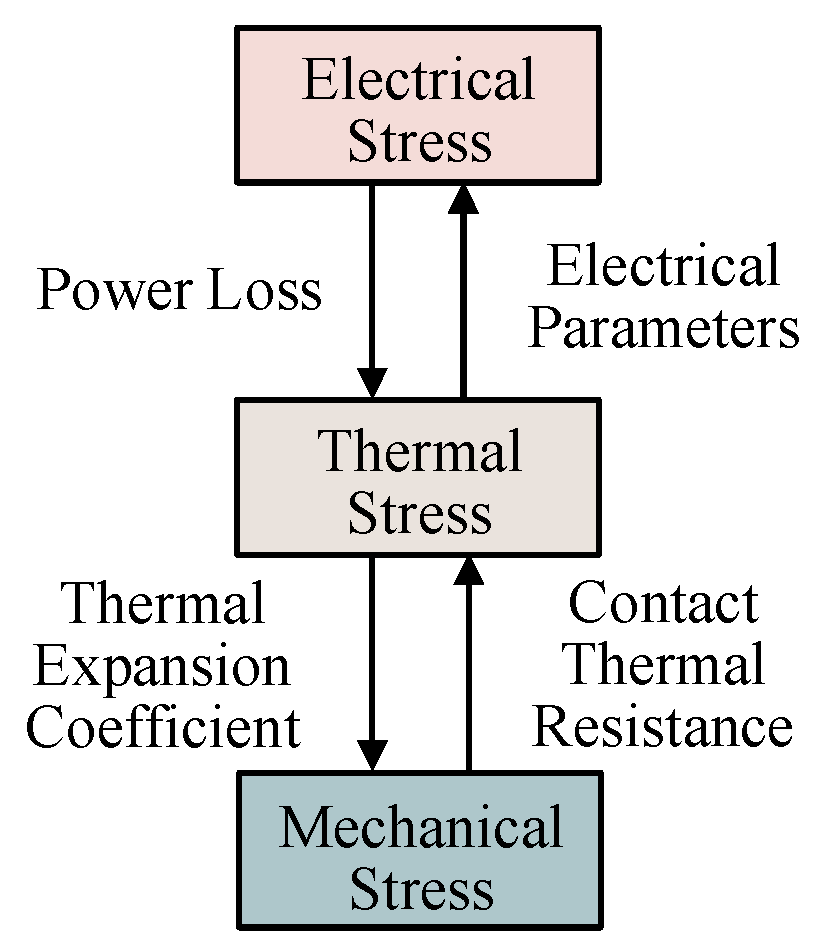
2.2. Analysis of SiC MOSFET Failure Mechanism
2.3. Selection of SiC MOSFET Characteristic Parameters
3. Establishment and Analysis of Models
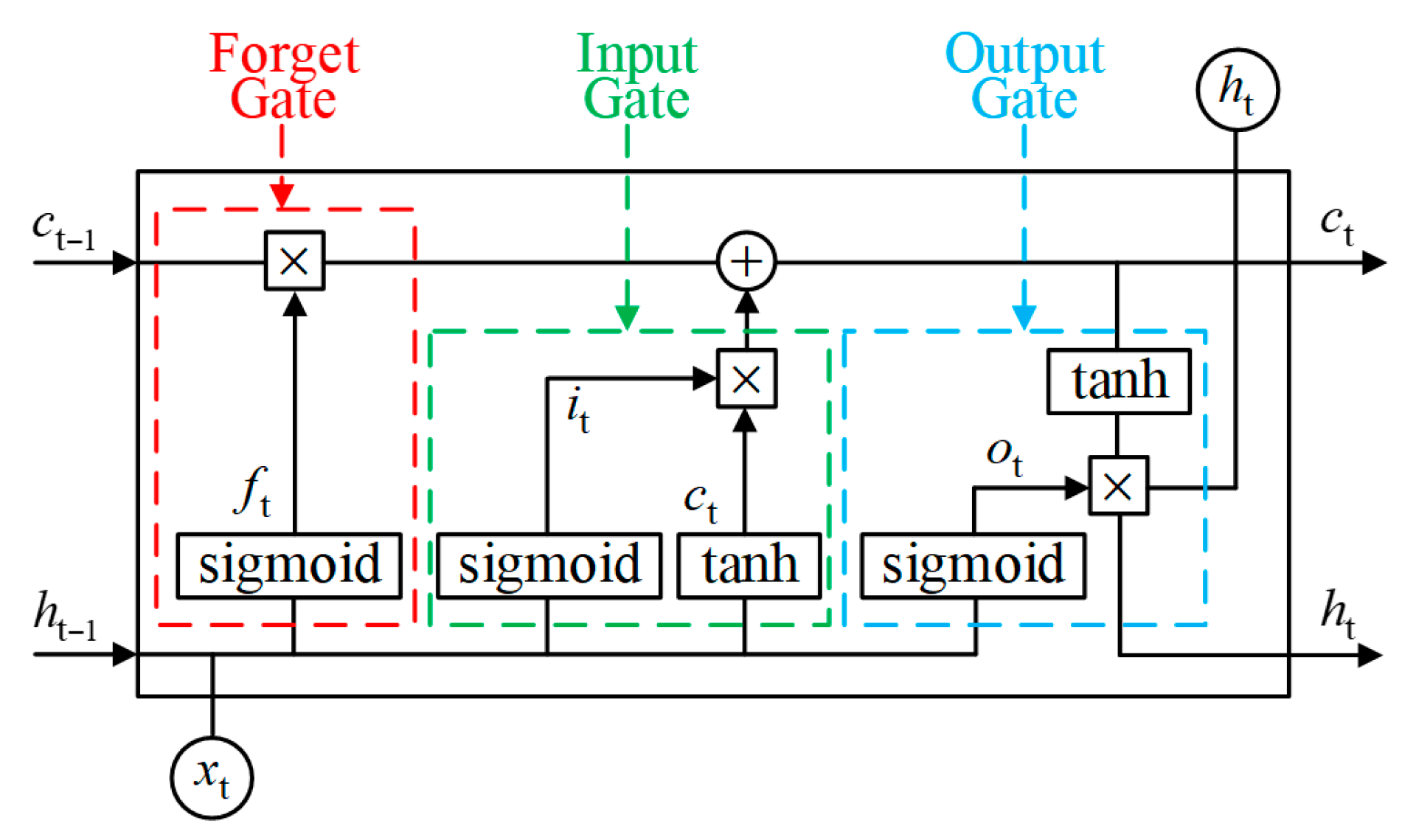
3.1. The Conventional LSTM Prediction Model
3.2. The Grey Wolf Optimization Algorithm
3.2.1. Social Hierarchy Stratification
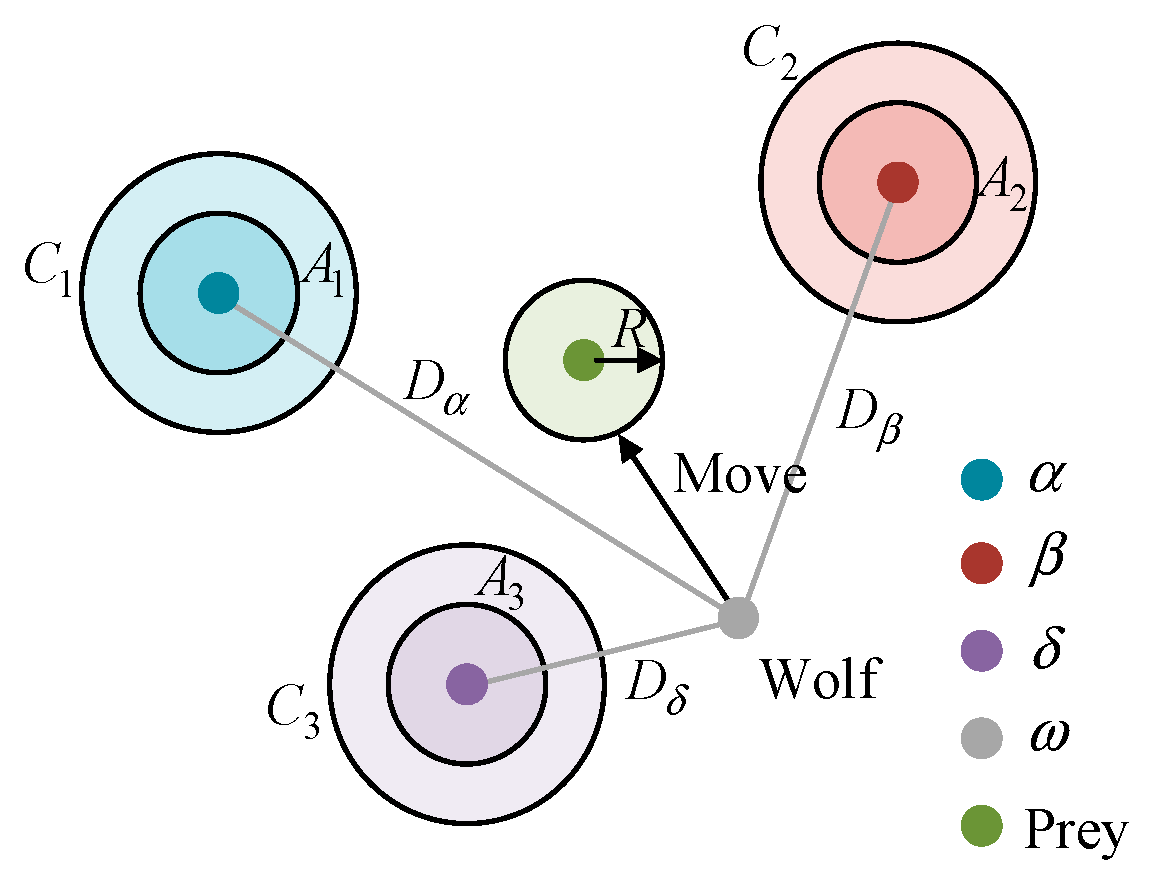
3.2.2. Encircling the Prey
3.2.3. Pursuing the Prey
3.2.4. Attacking the Prey
3.3. Improved Grey Wolf Optimization Algorithm
3.3.1. Initialization with a Tent Chaotic Mapping
3.3.2. The Nonlinear Control Parameters Strategy
3.3.3. The Concept of PSO
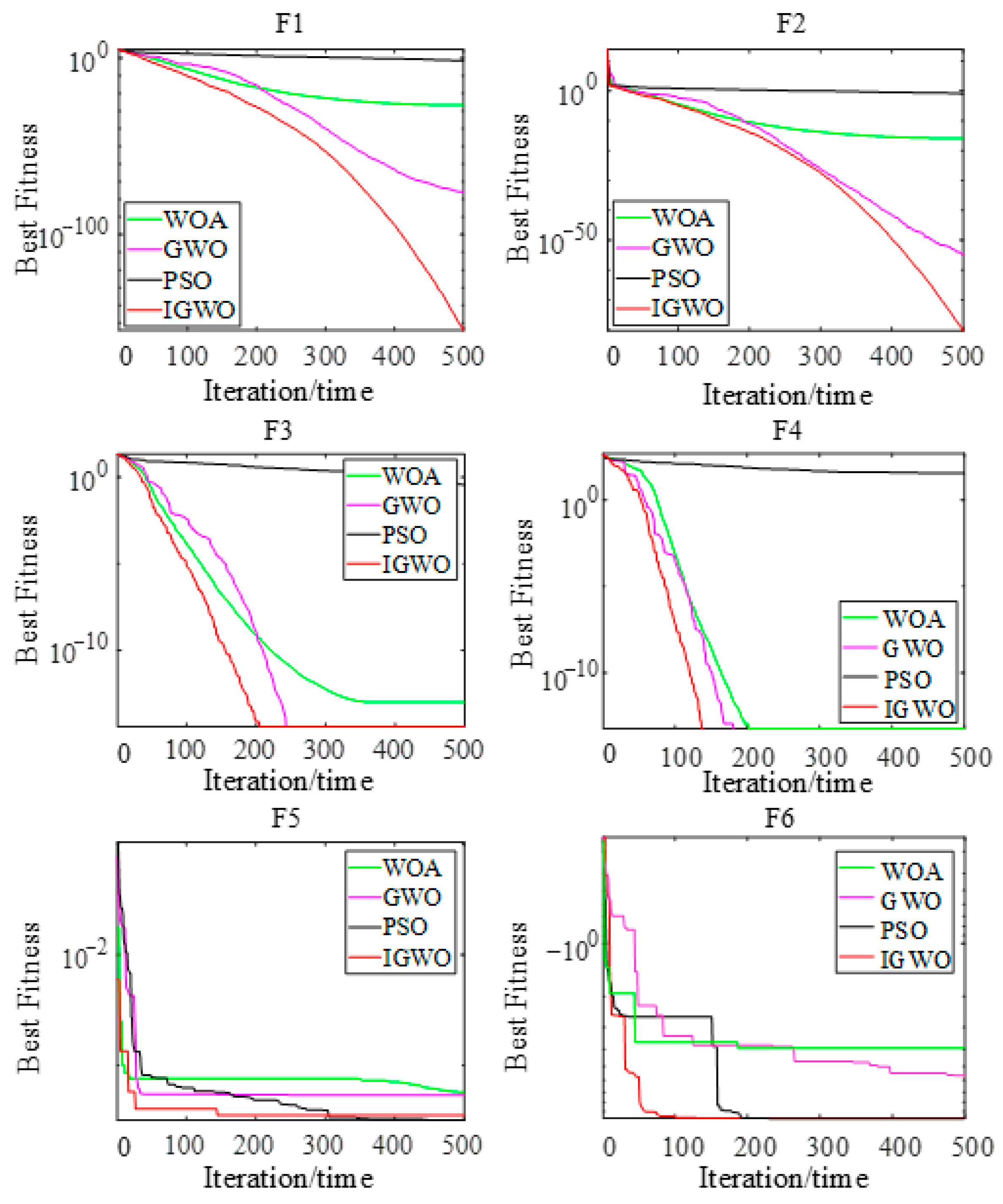
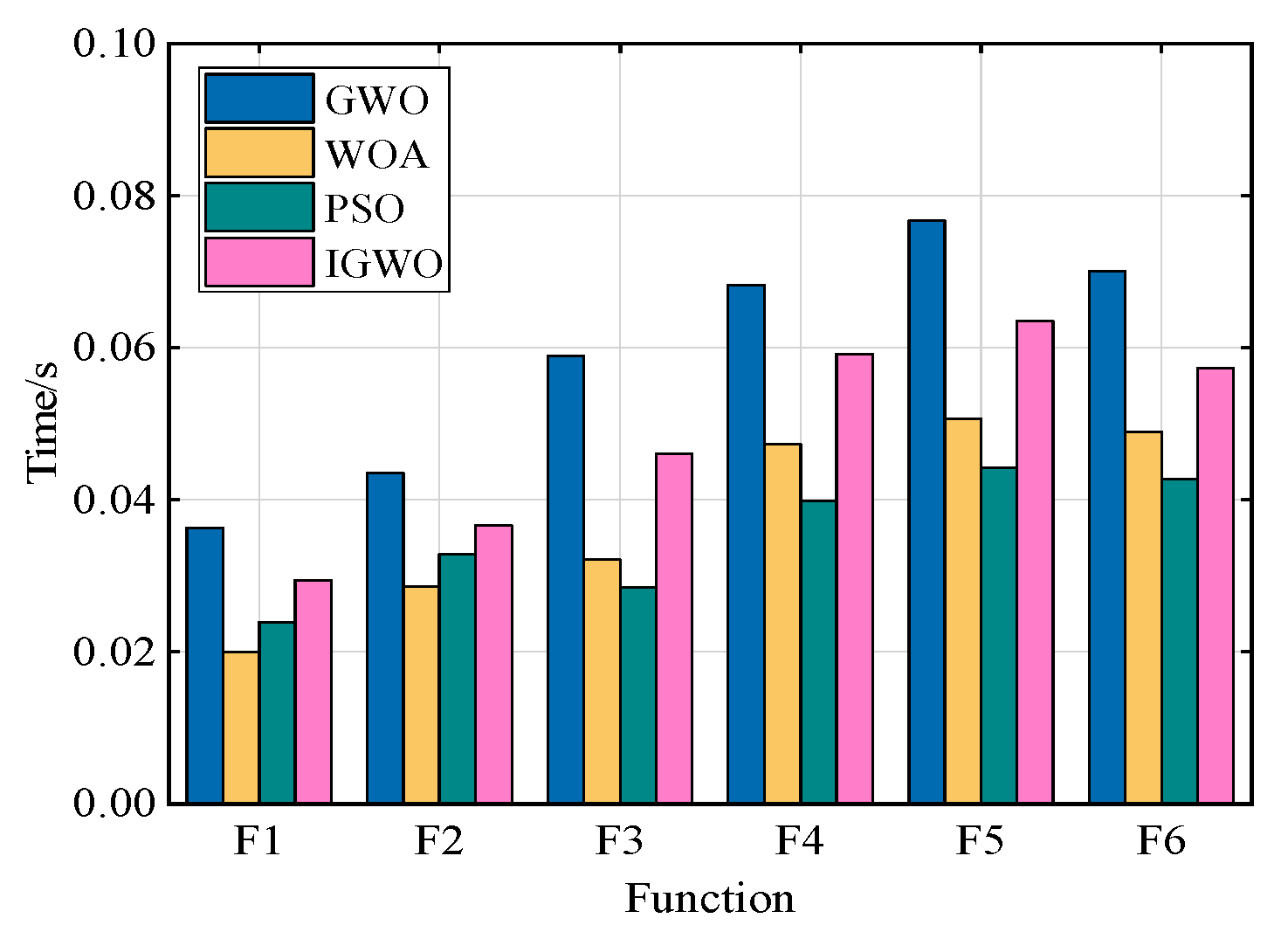
3.4. The Testing Performance of IGWO
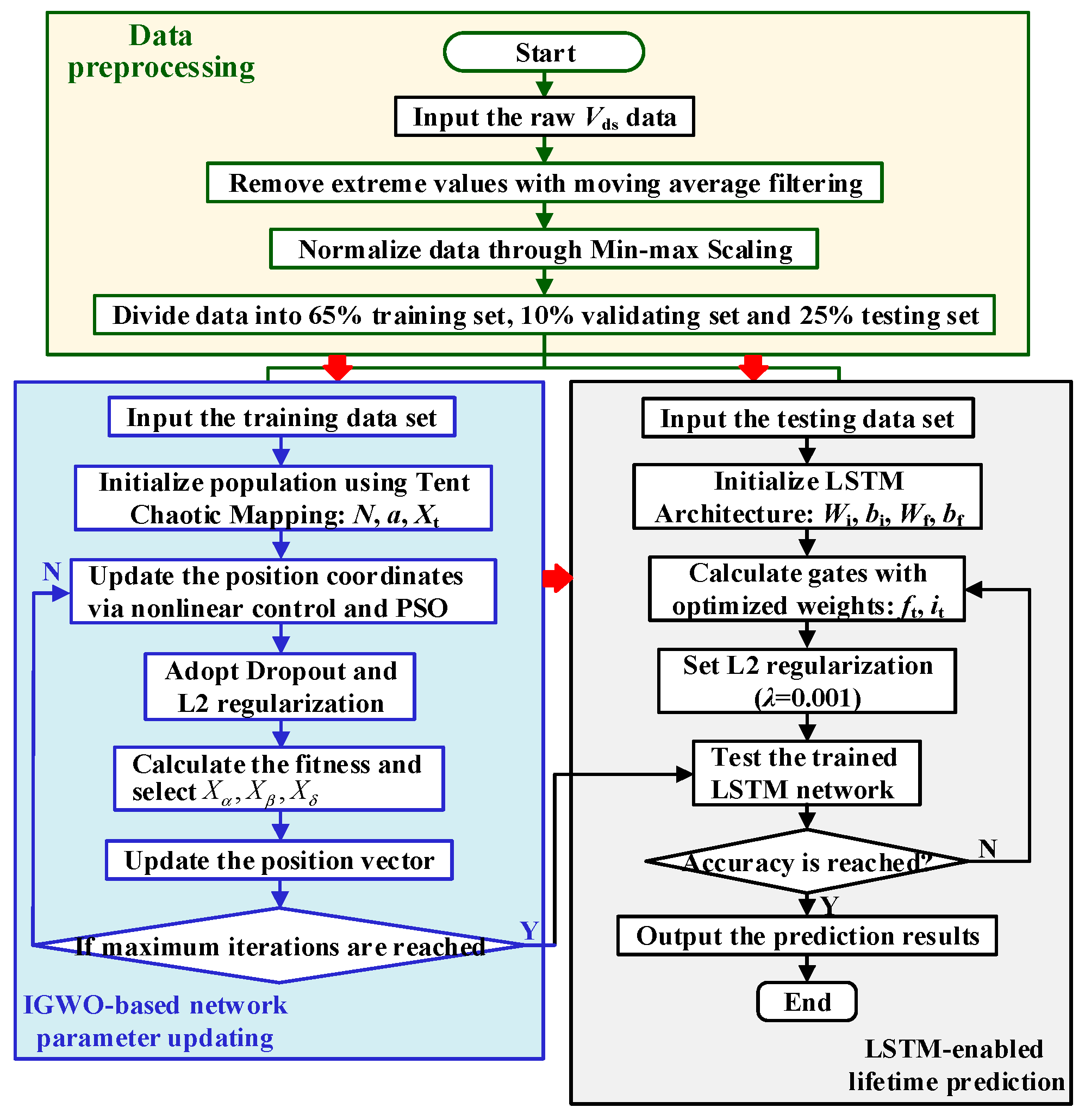
3.5. A SiC MOSFET Lifetime Prediction Model Based on IGWO-LSTM
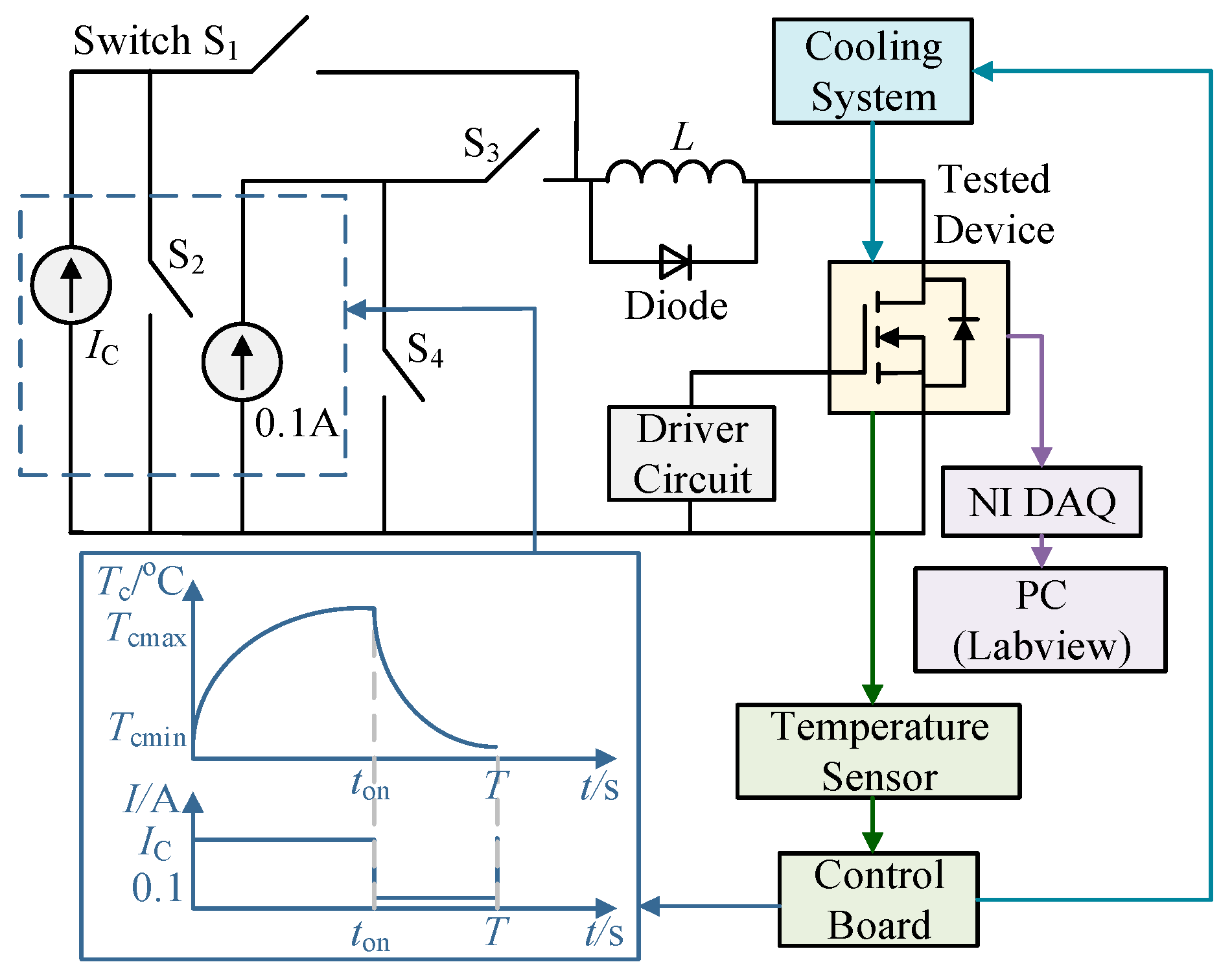
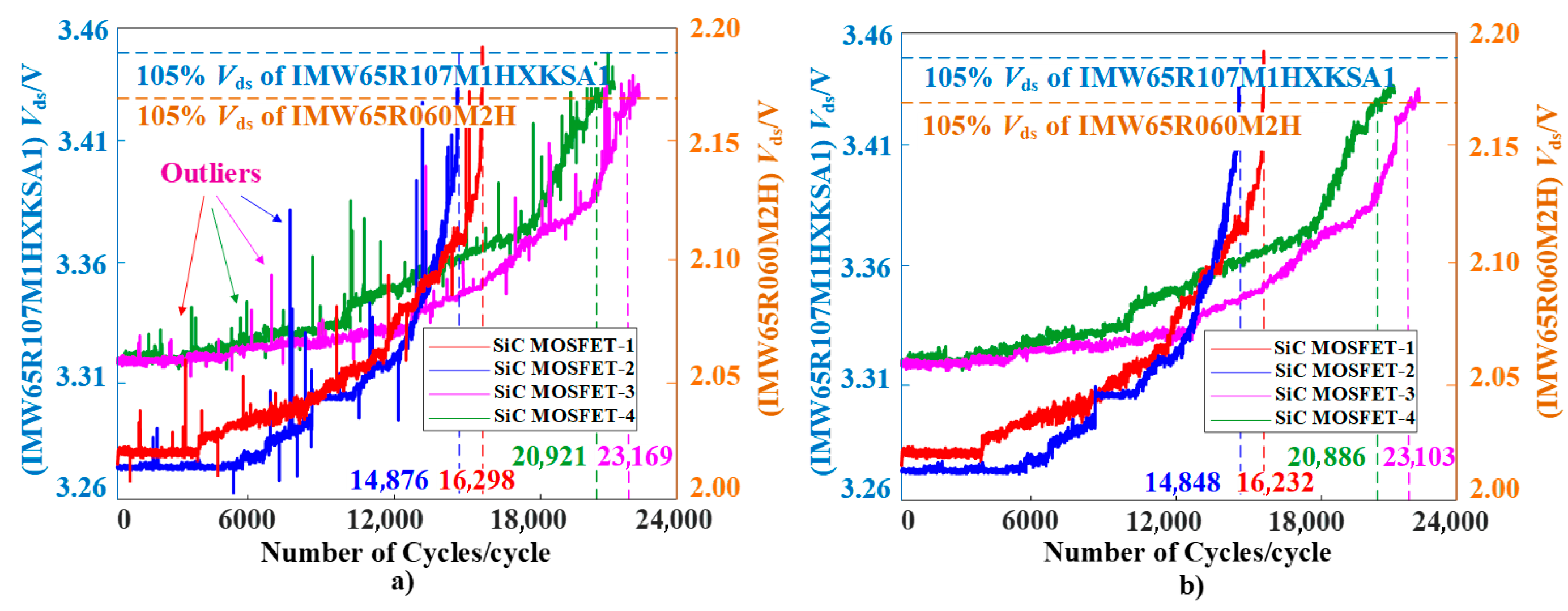
4. The Accelerated Ageing Test of SiC MOSFET
5. Analysis of Prediction Results
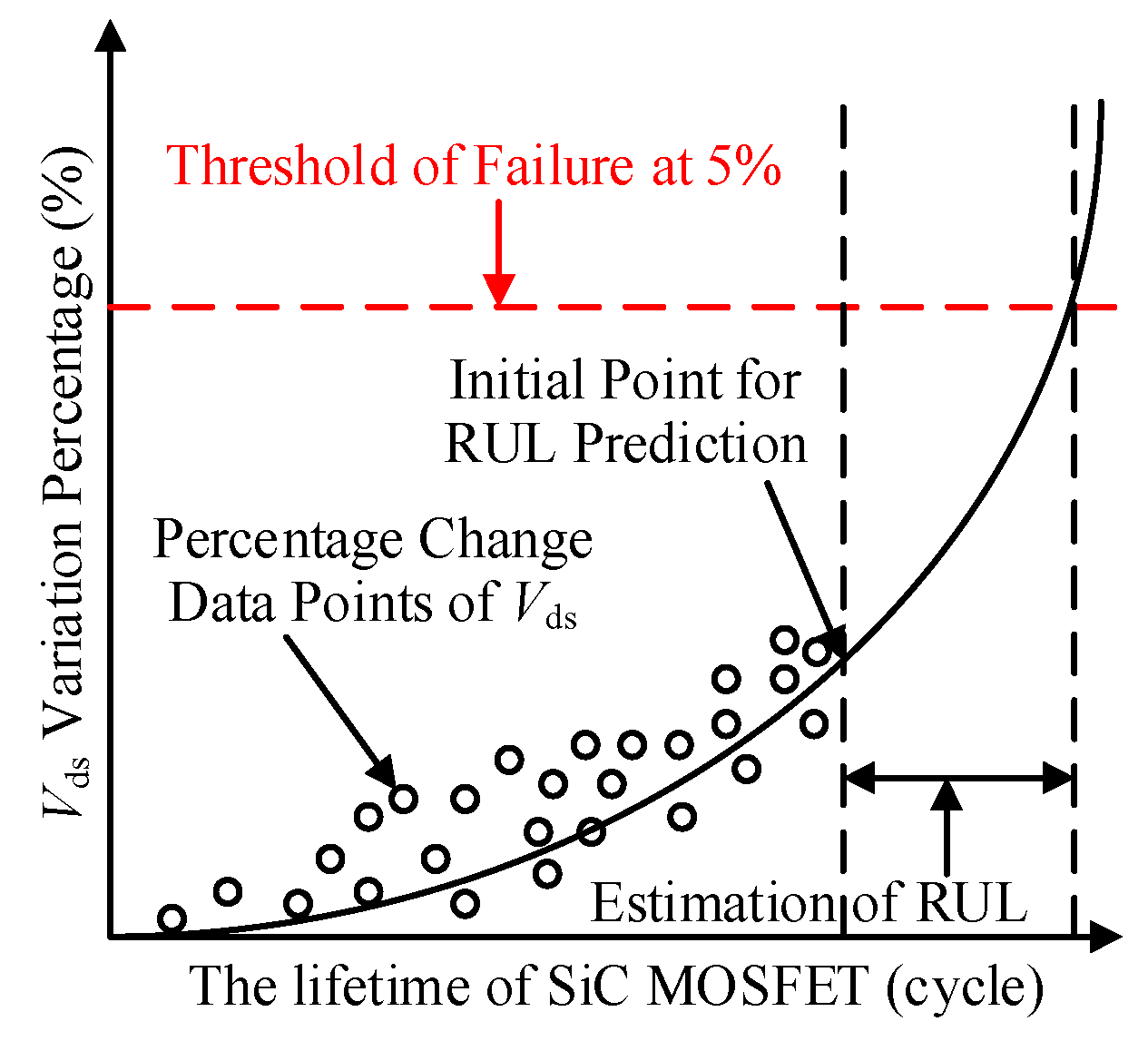
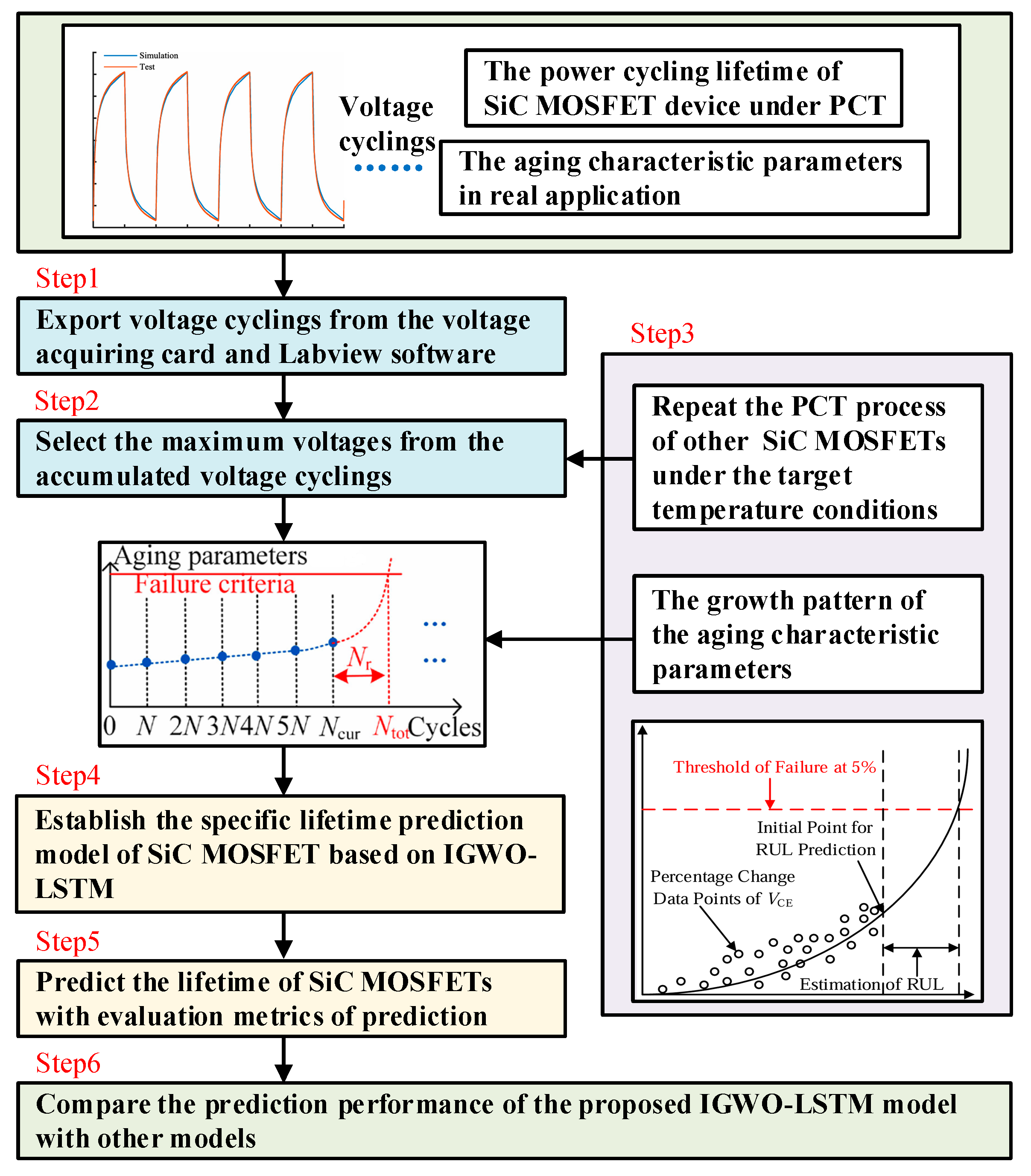
5.1. Health Assessment Model of SiC MOSFET
5.2. The Process of Data Processing
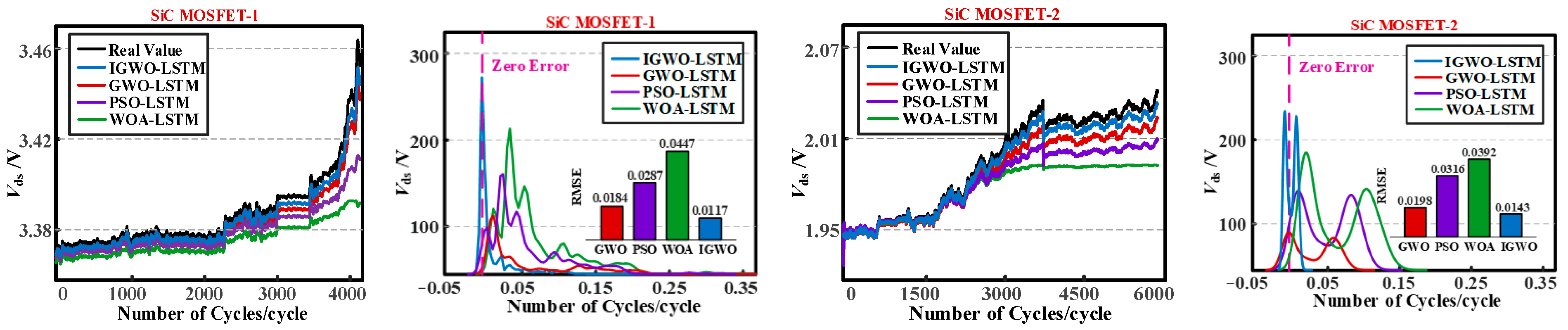
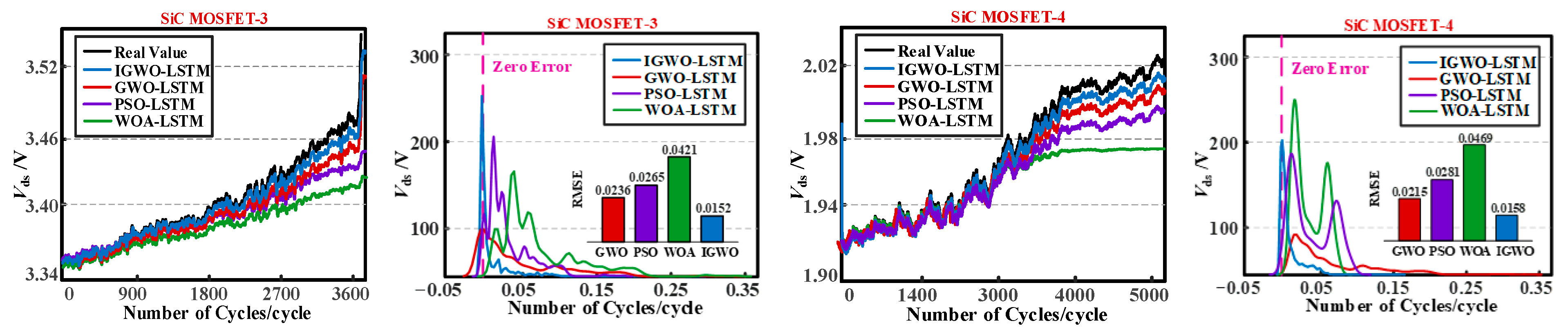
5.3. The Analysis of Life Prediction Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ni, Z.; Lyu, X.; Yadav, O.P.; Singh, B.N.; Zheng, S.; Cao, D. Overview of Real-Time Lifetime Prediction and Extension for SiC Power Converters. IEEE Trans. Power Electron. 2020, 35, 7765–7794. [Google Scholar] [CrossRef]
- Cheng, H.-C.; Syu, J.-Y.; Wang, H.-H.; Liu, Y.-C.; Kao, K.-S.; Chang, T.-C. Power Cycling Modeling and Lifetime Evaluation of SiC Power MOSFET Module Using a Modified Physical Lifetime Model. IEEE Trans. Device Mater. Reliab. 2024, 24, 142–153. [Google Scholar] [CrossRef]
- Ceccarelli, L.; Kotecha, R.M.; Bahman, A.S.; Iannuzzo, F.; Mantooth, H.A. Mission-profile-based lifetime prediction for a SiC MOSFET power module using a multi-step condition-mapping simulation strategy. IEEE Trans. Power Electron. 2019, 34, 9698–9708. [Google Scholar] [CrossRef]
- Hanif, A.; Yu, Y.; DeVoto, D.; Khan, F. A Comprehensive Review Toward the State-of-the-Art in Failure and Lifetime Predictions of Power Electronic Devices. IEEE Trans. Power Electron. 2019, 34, 4729–4746. [Google Scholar] [CrossRef]
- Dusmez, S.; Duran, H.; Akin, B. Remaining useful lifetime estimation for thermally stressed power MOSFETs based on on-state resistance variation. IEEE Trans. Ind. Appl. 2016, 52, 2554–2563. [Google Scholar] [CrossRef]
- Shu, X.; Li, G.; Zhang, Y.; Shen, S.; Chen, Z.; Liu, Y. Stage of Charge Estimation of Lithium-Ion Battery Packs Based on Improved Cubature Kalman Filter With Long Short-Term Memory Model. IEEE Trans. Transp. Electrif. 2021, 7, 1271–1284. [Google Scholar] [CrossRef]
- Nguyen, B.V.; Jeon, J.W. Enhancing Particle Filter Performance for High Accuracy State Estimation and RUL Prediction. IEEE Trans. Instrum. Meas. 2025, 74, 3537112. [Google Scholar] [CrossRef]
- Martínez, A.L.H.; Khursheed, S.; Alnuayri, T.; Rossi, D. Online Remaining Useful Lifetime Prediction Using Support Vector Regression. IEEE Trans. Emerg. Top. Comput. 2022, 10, 1546–1557. [Google Scholar] [CrossRef]
- Qian, Y.; Hou, F.; Fan, J.; Lv, Q.; Fan, X.; Zhang, G. Design of a Fan-Out Panel-Level SiC MOSFET Power Module Using Ant Colony Optimization-Back Propagation Neural Network. IEEE Trans. Electron Devices 2021, 68, 3460–3467. [Google Scholar] [CrossRef]
- Wang, L.; Littler, T.; Liu, X. Dynamic Incipient Fault Forecasting for Power Transformers Using an LSTM Model. IEEE Trans. Dielectr. Electr. Insul. 2023, 30, 1353–1361. [Google Scholar] [CrossRef]
- Miao, Y.; Bai, X.; Cao, Y.; Liu, Y.; Dai, F.; Wang, F.; Qi, L.; Dou, W. A Novel Short-Term Traffic Prediction Model Based on SVD and ARIMA With Blockchain in Industrial Internet of Things. IEEE Internet Things J. 2023, 10, 21217–21226. [Google Scholar] [CrossRef]
- Shi, J.; Wang, Y.; Zhou, Y.; Ma, Y.; Gao, J.; Wang, S.; Fu, Z. Bayesian Optimization—LSTM Modeling and Time Frequency Correlation Mapping Based Probabilistic Forecasting of Ultra-short-term Photovoltaic Power Outputs. IEEE Trans. Ind. Appl. 2024, 60, 2422–2430. [Google Scholar] [CrossRef]
- Yu, Y.; Jiang, Y.; Li, C. Remaining Life Prediction Method for Mechano-Thermal Aged Insulating Paper Based on Whale Optimization Algorithm-Long Short-Term Memory Network Model. Trans. China Electrotech. Soc. 2022, 37, 3162–3171. [Google Scholar]
- Liu, Q. Failure Modeling and Prediction of Low-Power IGBT. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2022. [Google Scholar]
- Xu, H.; Xu, Q.; Duanmu, F.; Shen, J.; Jin, L.; Gou, B.; Wu, F.; Zhang, W. State-of-Charge Estimation of Lithium-Ion Batteries Based on EKF Integrated With PSO-LSTM for Electric Vehicles. IEEE Trans. Transp. Electrif. 2025, 11, 2311–2321. [Google Scholar] [CrossRef]
- Pan, J.; Jing, B.; Jiao, X.; Wang, S. Analysis and Application of Grey Wolf Optimizer-Long Short-Term Memory. IEEE Access 2020, 8, 121460–121468. [Google Scholar] [CrossRef]
- Zhu, N.; Mantooth, H.A.; Xu, D.; Chen, M.; Glover, M.D. A Solution to Press-Pack Packaging of SiC MOSFETS. IEEE Trans. Ind. Electron. 2017, 64, 8224–8234. [Google Scholar] [CrossRef]
- Chen, W.; Jiang, J.; Meda, A.H.; Ibrahim, M.S.; Zhang, G.; Fan, J. A Thin and Low-Inductance 1200 V SiC MOSFET Fan-Out Panel-Level Packaging With Thermal Cycling Reliability Evaluation. IEEE Trans. Electron Devices 2023, 70, 2268–2275. [Google Scholar] [CrossRef]
- Lee, H.; Smet, V.; Tummala, R. A Review of SiC Power Module Packaging Technologies: Challenges, Advances, and Emerging Issues. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 239–255. [Google Scholar] [CrossRef]
- DiMarino, C.; Mouawad, B.; Johnson, C.M.; Wang, M.; Tan, Y.-S.; Lu, G.-Q.; Boroyevich, D.; Burgos, R. Design and Experimental Validation of a Wire-Bond-Less 10-kV SiC MOSFET Power Module. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 381–394. [Google Scholar] [CrossRef]
- Li, Q.; Li, Y.-B.; Fu, H.-D.; Tu, C.-M.; Xiao, B.; Xiao, F.; Zhai, D.-Y.; Lu, J.-W. Review of the Failure Mechanism and Methodologies of IGBT Bonding Wire. IEEE Trans. Compon. Packag. Manuf. Technol. 2023, 13, 1045–1057. [Google Scholar] [CrossRef]
- Chen, J.; Deng, E.; Liu, P.; Yang, S.; Huang, Y. The Influence and Application of Bond Wires Failure on Electrothermal Characteristics of IGBT Module. IEEE Trans. Compon. Packag. Manuf. Technol. 2021, 11, 1426–1434. [Google Scholar] [CrossRef]
- Yang, X.; Ye, J.; Wu, X.; Heng, K.; He, Y.; Liu, G. Lifetime Prediction for Lift-off of Bond Wires in IGBTs Using Paris Law With Analytical Calculation of Crack Length. IEEE Trans. Power Electron. 2023, 38, 13099–13110. [Google Scholar] [CrossRef]
- Vemulapati, U.R.; Bianda, E.; Torresin, D.; Arnold, M.; Agostini, F. A Method to Extract the Accurate Junction Temperature of an IGCT During Conduction Using Gate–Cathode Voltage. IEEE Trans. Power Electron. 2016, 31, 5900–5905. [Google Scholar] [CrossRef]
- Yi, J.; Ma, C.; Wang, H. A Data-Driven Remaining Useful Life Prediction Method for Power MOSFETs Considering Nonlinear Dynamical Behaviors. IEEE Trans. Electron Devices 2025, 72, 1885–1892. [Google Scholar] [CrossRef]
- Yang, L.; Agyakwa, P.A.; Johnson, C.M. Physics-of-failure lifetime prediction models for wire bond interconnects in power electronic modules. IEEE Trans. Device Mater. Reliab. 2012, 13, 9–17. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, X.; Zhao, Y.; Jia, Y.; Hu, D.; Wu, Y.; Zhang, L.; Chen, Z.; Huang, A.Q. Gate Bias Dependence of VTH Degradation in Planar and Trench SiC MOSFETs Under Repetitive Short Circuit Tests. IEEE Trans. Electron Devices 2022, 69, 2521–2527. [Google Scholar] [CrossRef]
- Smirnov, V.; Gavrikov, A.; Neichev, V. Measuring Specificities of Thermal Resistance of IGBT Power Modules. IEEE Trans. Compon. Packag. Manuf. Technol. 2024, 14, 2348–2354. [Google Scholar] [CrossRef]
- Zhang, Z.; Dyer, J.; Wu, X.; Wang, F.; Costinett, D.; Tolbert, L.M.; Blalock, B.J. Online junction temperature monitoring using intelligent gate drive for SiC power devices. IEEE Trans. Power Electron. 2019, 34, 7922–7932. [Google Scholar] [CrossRef]
- Karki, U.; Peng, F.Z. Effect of gate oxide degradation on electrical parameters of power MOSFETs. IEEE Trans. Power Electron. 2018, 33, 10764–10773. [Google Scholar] [CrossRef]
- AQG 324; Qualification of Power Modules for Use in Power Electronics Converter Units (PCUs) in Motor Vehicles. ECPE: Nuremberg, Germany, 2021.
- GSO IEC 60749-34:2014; Semiconductor Devices—Mechanical and Climatic Test Methods—Part 34: Power Cycling. Gulf Standardization Organization (GSO): Riyadh, Saudi Arabia, 2014.
- JEDEC JESD22-A122A; Power Cycling. JEDEC Solid State Technology Association: Arlington, VA, USA, 2016.
- Qin, Y.; Xiang, S.; Chai, Y.; Chen, H. Macroscopic–Microscopic Attention in LSTM Networks Based on Fusion Features for Gear Remaining Life Prediction. IEEE Trans. Ind. Electron. 2020, 67, 10865–10875. [Google Scholar] [CrossRef]
- Xu, L.; Wang, H.; Lin, W.; Gulliver, T.A.; Le, K.N. GWO-BP Neural Network Based OP Performance Prediction for Mobile Multiuser Communication Networks. IEEE Access 2019, 7, 152690–152700. [Google Scholar] [CrossRef]
- Hou, K.; Guo, M.; Li, X.; Zhang, H. Research on Optimization of GWO-BP Model for Cloud Server Load Prediction. IEEE Access 2021, 9, 162581–162589. [Google Scholar] [CrossRef]
- Deng, W.; Feng, J.; Zhao, H. Autonomous Path Planning via Sand Cat Swarm Optimization With Multistrategy Mechanism for Unmanned Aerial Vehicles in Dynamic Environment. IEEE Internet Things J. 2025, 12, 26003–26013. [Google Scholar] [CrossRef]
- Duan, B.; Ma, Y.; Liu, J.; Jin, Y. A Nonlinear Grey Wolf Optimizer Based on Chaotic Mapping and Opposition-Based Learning Mechanism. Softw. Eng. 2023, 26, 36–40. [Google Scholar]
- Teng, Z.; Lv, J.; Guo, L.; Xu, Y. An Improved Hybrid Grey Wolf Optimization Algorithm Based on Tent Mapping. J. Harbin Inst. Technol. 2018, 50, 40–49. [Google Scholar]
- Liu, J.; Li, L.; Chen, G.; Liu, Y. High Precision IGBT Health Evaluation Method: Extreme Learning Machine Optimized by Improved Krill Herd Algorithm. IEEE Trans. Device Mater. Reliab. 2023, 23, 37–50. [Google Scholar] [CrossRef]
- Zhu, H.; Liu, T. Rotor Displacement Self-Sensing Modeling of Six-Pole Radial Hybrid Magnetic Bearing Using Improved Particle Swarm Optimization Support Vector Machine. IEEE Trans. Power Electron. 2020, 35, 12296–12306. [Google Scholar] [CrossRef]
- Pu, S.; Yang, F.; Vankayalapati, B.T.; Akin, B. Aging Mechanisms and Accelerated Lifetime Tests for SiC MOSFETs: An Overview. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 1232–1254. [Google Scholar] [CrossRef]
- Wang, B.; Cai, J.; Du, X.; Zhou, L. Review of power semiconductor device reliability for power converters. CPSS Trans. Power Electron. Appl. 2017, 2, 101–117. [Google Scholar] [CrossRef]
- Ren, H.; Yu, Y.; Du, X.; Liu, J.; Zhou, J. A Lifetime Prediction Model for IGBT Based on Optimized Long Short-Term Memory Neural Network. Trans. China Electrotech. Soc. 2024, 39, 1074–1086. [Google Scholar]
- Ma, X.; Wang, J.; Wei, Z.; Ding, L. Online Prediction Method for the Remaining Useful Life of Power Devices Based on Composite Indicator. IEEE Trans. Power Electron. 2024, 39, 10326–10338. [Google Scholar] [CrossRef]



| Function | Lower | Upper | Dim | Optimum |
|---|---|---|---|---|
| F1 | −100 | 100 | 30 | 0 |
| F2 | −10 | 10 | 30 | 0 |
| F3 | −32 | 32 | 30 | 0 |
| F4 | −5.12 | 5.12 | 30 | 0 |
| F5 | −5 | 5 | 4 | 0.1484 |
| F6 | 0 | 10 | 4 | −1 |
| Function | WOA | GWO | PSO | IGWO | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
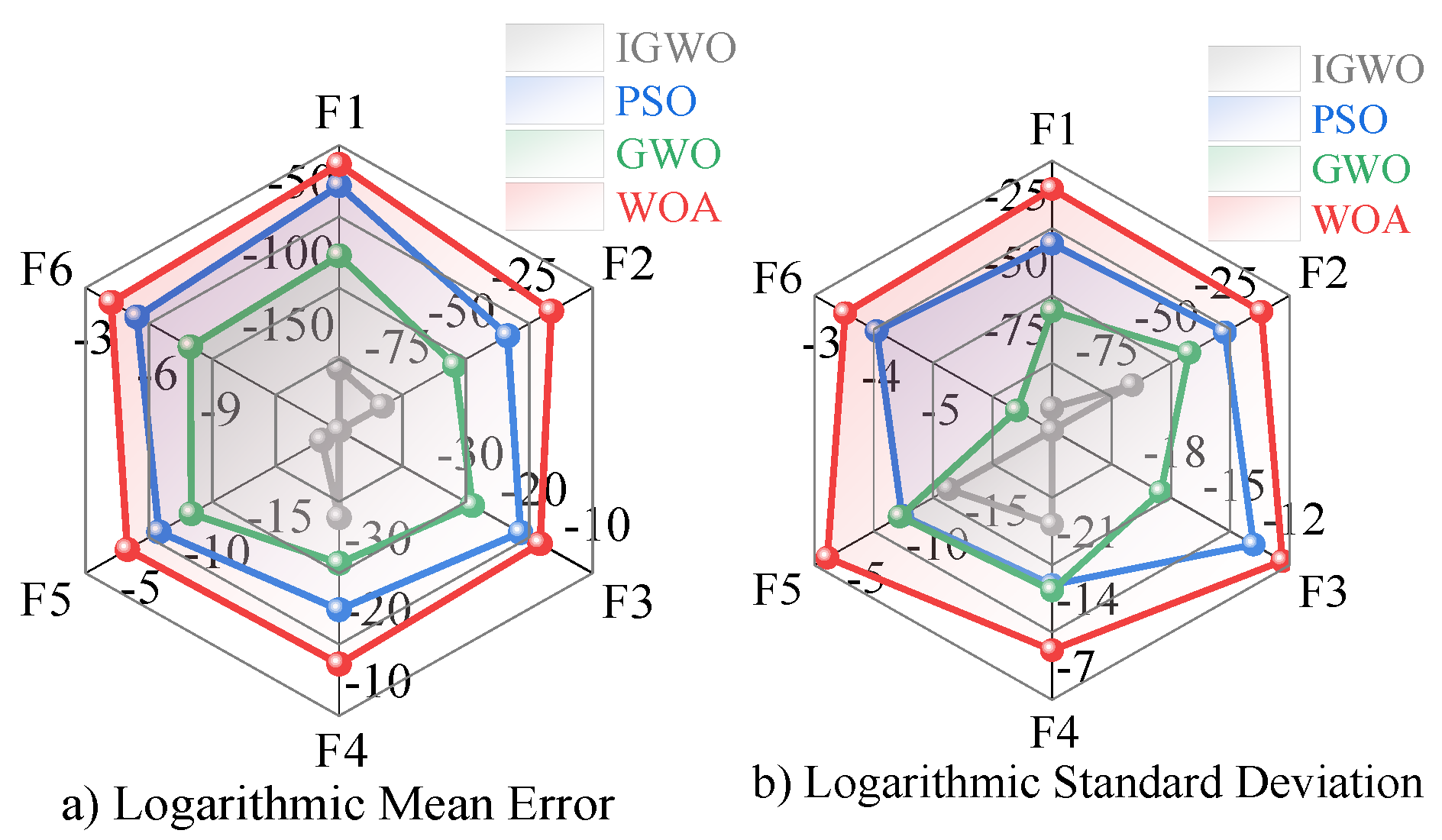
| F1 | 3.49 × 10−14 | 3.59 × 10−11 | 3.23 × 10−78 | 1.87 × 10−56 | 3.66 × 10−29 | 1.65 × 10−31 | 3.06 × 10−157 | 1.94 × 10−92 |
| F2 | 5.05 × 10−17 | 1.08 × 10−12 | 4.68 × 10−55 | 5.34 × 10−43 | 2.81 × 10−34 | 4.92 × 10−28 | 1.18 × 10−83 | 4.11 × 10−67 |
| F3 | 5.11 × 10−9 | 4.23 × 10−10 | 1.03 × 10−19 | 3.11 × 10−16 | 4.29 × 10−12 | 1.48 × 10−11 | 0 | 0 |
| F4 | 5.68 × 10−8 | 7.16 × 10−6 | 4.12 × 10−22 | 4.30 × 10−12 | 1.31 × 10−15 | 1.12 × 10−12 | 1.62 × 10−28 | 6.11 × 10−19 |
| F5 | 4.89 × 10−4 | 8.03 × 10−2 | 4.46 × 10−9 | 6.27 × 10−8 | 1.63 × 10−6 | 4.18 × 10−8 | 2.34 × 10−19 | 5.14 × 10−12 |
| F6 | −5.99 × 10−2 | 3.01 × 10−3 | −1.09 × 10−5 | 3.91 × 10−6 | −3.65 × 10−3 | 8.87 × 10−4 | 0 | 0 |
| SiC MOSFET | Vgs | Rds | Tcmax | Tcmin | Ta | Ic | ton | Cooling | Sampling Rate |
|---|---|---|---|---|---|---|---|---|---|
| IMW65R107M1HXKSA1 | 15 V | 142 mΩ | 155 °C | 50 °C | 25 °C | 20 A | 5 s | Air Cooling | 10 Hz |
| IMW65R060M2H | 15 V | 73 mΩ | 155 °C | 50 °C | 25 °C | 23 A | 8 s | Air Cooling | 10 Hz |
| Sample | Model | R2 | RMSE | MAE | MAPE |
|---|---|---|---|---|---|
| 1 | WOA-LSTM | 77.5% | 0.0447 | 0.0358 | 4.35% |
| PSO-LSTM | 85.9% | 0.0287 | 0.0225 | 2.78% | |
| GWO-LSTM | 92.7% | 0.0184 | 0.0143 | 1.80% | |
| IGWO-LSTM | 96.2% | 0.0117 | 0.0089 | 1.15% | |
| 2 | WOA-LSTM | 80.6% | 0.0392 | 0.0308 | 3.85% |
| PSO-LSTM | 84.2% | 0.0316 | 0.0247 | 3.05% | |
| GWO-LSTM | 91.3% | 0.0198 | 0.0154 | 1.92% | |
| IGWO-LSTM | 94.8% | 0.0143 | 0.0110 | 1.40% | |
| 3 | WOA-LSTM | 78.4% | 0.0421 | 0.0332 | 4.15% |
| PSO-LSTM | 87.7% | 0.0265 | 0.0205 | 2.55% | |
| GWO-LSTM | 89.2% | 0.0236 | 0.0183 | 2.25% | |
| IGWO-LSTM | 94.1% | 0.0152 | 0.0116 | 1.48% | |
| 4 | WOA-LSTM | 75.8% | 0.0469 | 0.0372 | 4.70% |
| PSO-LSTM | 86.1% | 0.0281 | 0.0218 | 2.72% | |
| GWO-LSTM | 90.3% | 0.0215 | 0.0166 | 2.08% | |
| IGWO-LSTM | 93.9% | 0.0158 | 0.0121 | 1.55% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, P.; Bao, J.; Gong, Z.; Gao, M.; Xu, Q. Lifetime Prediction of SiC MOSFET by LSTM Based on IGWO Algorithm. Electronics 2025, 14, 4486. https://doi.org/10.3390/electronics14224486
Dai P, Bao J, Gong Z, Gao M, Xu Q. Lifetime Prediction of SiC MOSFET by LSTM Based on IGWO Algorithm. Electronics. 2025; 14(22):4486. https://doi.org/10.3390/electronics14224486
Chicago/Turabian StyleDai, Peng, Junyi Bao, Zheng Gong, Mingchang Gao, and Qing Xu. 2025. "Lifetime Prediction of SiC MOSFET by LSTM Based on IGWO Algorithm" Electronics 14, no. 22: 4486. https://doi.org/10.3390/electronics14224486
APA StyleDai, P., Bao, J., Gong, Z., Gao, M., & Xu, Q. (2025). Lifetime Prediction of SiC MOSFET by LSTM Based on IGWO Algorithm. Electronics, 14(22), 4486. https://doi.org/10.3390/electronics14224486







