Abstract
Accurate 3D hand pose estimation remains a key challenge due to the scarcity of annotated training data. While 2D studies have shown that incorporating additional modalities like language can mitigate data limitations, leveraging such strategies in the 3D domain remains underexplored. Inspired by the success of CLIP in vision-language tasks, we propose TriPose, a tri-modal framework that integrates image, text, and point cloud data for robust 3D hand pose estimation. Recognizing that CLIP is not optimized for spatial localization, we design structured textual representations for hand poses and employ CLIP visual encoder to extract global semantic features. To address CLIP’s spatial limitations, we introduce a spatial-awareness module tailored to ViT’s architecture. The model is pre-trained on image–text–point cloud triplets, enabling precise pose localization through multi-modal alignment. Experiments on MSRA, ICVL, and NYU datasets show that TriPose consistently outperforms state-of-the-art methods, especially on the low-resource ICVL dataset, demonstrating the effectiveness of our structured language supervision and tri-modal fusion strategy in enhancing 3D hand pose understanding.
1. Introduction
Three-dimensional Hand Pose Estimation (HPE) is a critical research topic in computer vision and artificial intelligence, aiming to accurately capture the spatial coordinates of hand joints in three-dimensional space for a deeper understanding and analysis of human hand movements. This technology holds significant potential across a range of applications, including human–computer interaction (HCI), robotic control, virtual reality (VR), augmented reality (AR), and interactive gaming, by enabling more natural and intuitive interfaces. With the rapid advancement of deep learning techniques and the widespread availability of low-cost depth sensors, research in 3D HPE has entered a stage of accelerated development. Existing approaches for 3D hand pose estimations [1,2,3,4,5,6,7,8,9,10,11,12] are primarily categorized into two paradigm: regression-based and detection-based methods. While these traditional methods have achieved promising performance in terms of accuracy and computational efficiency, they still face considerable challenges in real-world scenarios, especially under complex poses and occlusions. Self-occlusion and hand object occlusion often lead to missing or ambiguous visual information, making it difficult for single-modality approaches (e.g., image-only or point cloud-only) to produce reliable results. Moreover, the limited scale and diversity of current hand pose datasets further hinder the generalization capability of unimodal models. Integrating multi-modal information not only enriches spatial structural representations but also helps alleviate training difficulties caused by insufficient data, offering a more robust foundation for accurate 3D hand pose estimation. To address the aforementioned challenges, we propose TriPose, a unified framework that integrates a spatially aware structural module with a tri-modal fusion strategy to enhance the model’s ability to perceive and represent fine-grained spatial details of hand gestures. Specifically, we extend the general-purpose language encoding capability of the CLIP model [13] to a structured spatial relationship modeling mechanism, where the spatial configuration of hand keypoints is represented in a structured textual format. The textual modality then serves as semantic guidance for both image and point cloud feature representations. In the image modality, we retain the frozen CLIP visual encoder (ViT) [13] and augment it with an additional spatial-aware Transformer module to improve its ability to capture local geometric details. In the point cloud modality, we employ a lightweight architecture composed of MiniPointNet and stacked Transformers [14] to jointly extract local geometric features and global contextual information. We choose point clouds, 2D images, and structured text for their complementarity, availability on MSRA/ICVL/NYU, and fair comparability with prior work. Point clouds provide metric 3D geometry, images add appearance and global semantics, and structured text injects axis-ordered anatomical priors that reduce ambiguity under occlusion; all three are obtainable without extra sensors (depth → points; RGB/depth → image; synthesized prompts), whereas adding IMUs, multi-view video, or wearables would break compatibility and fairness. At inference, prompts are fixed and cached, so the text branch contributes priors without runtime overhead.
These three modalities, image, text, and point cloud, are integrated through a triplet-based cross-modal contrastive learning framework, aligning their representations in a shared feature space. This strategy enables deep fusion of semantic and geometric cues, substantially improving the model’s robustness and accuracy in 3D hand pose estimation, especially in challenging scenarios involving complex poses, occlusions, or limited data resources. We conducted comprehensive evaluations of TriPose on three widely used 3D hand pose estimation benchmarks: MSRA [15], ICVL [16], and NYU [17]. The results demonstrate that TriPose consistently achieves state-of-the-art performance across all datasets. Specifically, it attains a mean joint error of 6.98 mm on MSRA, 5.68 mm on ICVL, and 7.43 mm on NYU, clearly validating the effectiveness of the proposed tri-modal fusion strategy. Beyond alleviating data scarcity, TriPose’s tri-modal fusion explicitly targets higher accuracy and robustness rather than lower computational complexity. The advantage stems from a multi-view co-regularization effect—our symmetric contrastive alignment enforces consistent evidence across image, point-cloud, and structured-text views—and fromstructured priors encoded by axis-ordered textual prompts, which constrain anatomically plausible poses and reduce ambiguity under occlusion.
Our main contributions are summarized as follows:
- Introducing structured language descriptions to assist 3D hand pose estimation: We incorporate structured textual representations as a third modality in the estimation framework. By leveraging CLIP’s text encoder, spatial cues embedded in language are aligned with visual and geometric features, compensating for the limitations of point clouds and images in handling complex poses and occlusions. This opens a new direction for multi-modal fusion in 3D hand pose estimation.
- Designing a unified image–text–point cloud alignment mechanism with spatial-awareness modules: We propose a tri-modal dual-alignment strategy based on contrastive learning, and introduce a spatial-aware Transformer in the image modality to enhance the ViT’s capacity for modeling local spatial structures. In the point cloud modality, we design a locality-sensitive Transformer encoder that efficiently captures the geometric configuration of hand shapes, enabling deep fusion of semantic and structural information.
- Tri-modal fusion strategy: We formalize a Tri-modal Symmetric Contrastive Learning (TSCL) objective that aligns image–point and text–point pairs (optionally image–text) in a shared feature space while keeping the CLIP encoders frozen. This fusion design narrows modality gaps and supports a single shared representation for downstream pose regression; its effect is isolated via ablations in Section 4.4.
- Proposing a stable and efficient two-stage training paradigm for robust estimation: Instead of end-to-end training, we adopt an “alignment-to-regression” two-stage optimization scheme that significantly improves training stability and the quality of cross-modal alignment. Combined with a multi-scale point cloud augmentation strategy, TriPose achieves strong generalization even on low-resource datasets like ICVL, demonstrating its robustness under data-scarce scenarios.
2. Related Work
2.1. 3D Hand Pose Estimation
Three-dimensional hand pose estimation has received significant attention due to its importance in gesture recognition. Existing methods are generally categorized into three paradigms: generative methods, discriminative methods, and hybrid methods. Generative approaches [18,19,20,21,22,23,24] reconstruct a 3D hand model that best matches the input data, while discriminative approaches [3,9,15,16,25,26,27,28,29,30] directly predict joint positions. Hybrid methods [17,31,32,33,34,35] combine the advantages of both, leveraging generative priors to guide discriminative predictions. Despite their success, these methods still face challenges in accuracy and robustness, especially under occlusion.
Traditional 2D convolutional neural networks (CNNs) [3,36] generate 2D heatmaps from depth images, which are used to infer 3D joint positions. However, these methods are limited by their inability to model 3D structures effectively due to viewpoint dependency.
To overcome these limitations, some researchers have proposed voxel-based 3D CNNs that operate directly on volumetric representations [27,37]. While more expressive, these methods are computationally intensive and may lose fine-grained geometric details due to voxelization.
More recently, point cloud-based approaches [4,7,8] have emerged as a promising direction. By reconstructing hand surfaces from depth maps and operating directly on 3D points, these methods better preserve the geometric structure of hands. Nevertheless, they often struggle with sparse or noisy input and are highly dependent on large annotated datasets. To address these issues, we propose TriPose, a multi-modal framework that integrates structured language, images, and point clouds. CLIP-based text embeddings guide spatial reasoning, while a spatial-aware Transformer captures fine-grained details. Compared to unimodal methods, TriPose improves robustness and generalization through cross-modal learning.
Concurrently, two recent surveys complement our depth/point-cloud focus from different angles. Xiao and Liu (2024) provide a survey of RGB-image-based 3D hand pose estimation, summarizing architectures and evaluation protocols mainly on recent RGB/RGB-D benchmarks such as FreiHAND, HO3D, InterHand2.6M, and RHD, rather than the classic depth-centric MSRA/ICVL/NYU used in this work [38]. Żywanowski et al. (2025) present an AR-oriented evaluation on HoloLens 2 in an industrial setting (Computers in Industry, 171:104328), emphasizing device-side tracking and usability on HMD platforms instead of reporting accuracy on academic benchmarks like MSRA/ICVL/NYU [39]. These perspectives are complementary to our setting; although their datasets and metrics differ from ours, the modeling principles they highlight (representation learning, robustness, and cross-modal cues) align with our motivation and help position TriPose within the broader landscape of multimodal hand pose research.
2.2. Multi-Modal Learning for 3D Hand Pose Estimation
With advances in sensor technologies and computer vision, multi-modal learning has become a key trend in 3D hand pose estimation. Instead of relying on a single input modality, recent methods leverage combinations of RGB images, depth maps, point clouds, skeletal data, and sensor signals to enhance robustness and accuracy. Multi-modal fusion can be categorized into early, late, and intermediate strategies. Early fusion concatenates raw inputs from all modalities; late fusion combines decision outputs from separate pipelines; intermediate fusion merges features at network midpoints, balancing interaction and independence. Transformer-based attention mechanisms have been widely adopted to model cross-modal dependencies. Additionally, techniques like modality dropout improve robustness to missing modalities during inference. Several works demonstrate the benefits of multi-modal fusion. Neverova [40] combined RGB, depth, and skeleton data in a multi-stream CNN and achieved top results on ChaLearn. Molchanov [41] used a 3D CNN-LSTM hybrid on RGB-D-infrared streams for dynamic gesture recognition. Recent works like GestFormer [42] explore cross-modal attention using Transformer architectures. Furthermore, combining point cloud data with structured language has shown strong results. Text descriptions provide semantic guidance, helping models focus on relevant regions. This synergy improves generalization, especially when labeled 3D data is limited. In summary, multi-modal learning enhances spatial understanding and robustness in 3D hand pose estimation, offering a promising foundation for real-world gesture recognition systems.
3. Method
3.1. Overall Architecture of TriPose
TriPose is a multi-modal learning framework for 3D hand pose estimation that integrates complementary information from three modalities: images, point clouds, and structured language descriptions. The framework is inspired by the ULIP model for unified cross-modal representation learning, and adopts a pretraining strategy based on cross-modal contrastive learning to align the three modalities within a shared semantic space. The overall architecture of TriPose is depicted in Figure 1, comprising three main stages: multi-modal feature encoding, tri-modal alignment and fusion, and pose regression.
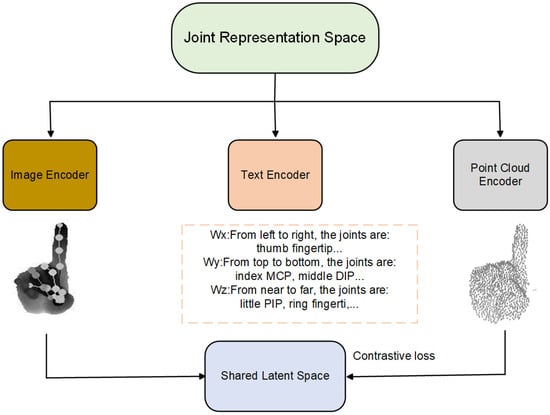
Figure 1.
Tri-modal representation alignment framework. We project the representations from the image encoder, structured text encoder, and point cloud encoder into a joint semantic space. The contrastive objective is applied among all three modalities to encourage semantic consistency, leveraging the complementary strengths of visual, linguistic, and geometric information.
In the feature encoding stage, TriPose independently extracts representations from the image, text, and point cloud modalities. For the image modality, a frozen CLIP Vision Transformer (ViT) [14] is employed to obtain global semantic features from hand images. To address ViT’s limited ability in modeling local structures, a spatial-aware Transformer module is introduced. This module incorporates positional encoding and multi-head self-attention to enhance the extraction of fine-grained geometric features from the input images.
For the text modality, we design structured language prompts tailored for 3D hand gestures. These prompts explicitly encode the relative spatial order of hand keypoints along the three coordinate axes (, , and ). The resulting textual embeddings provide both semantic and structural information, serving as guidance for aligning representations across modalities in the shared feature space.
For the point cloud modality, the input 3D hand point cloud is partitioned into local regions (tokens). Each region is processed through a shared multilayer perceptron (MLP) to generate initial embeddings. These embeddings are then fed into a series of Transformer encoder blocks to aggregate local and global spatial context via self-attention. In contrast to ULIP [42], which optimizes only the point cloud encoder, TriPose freezes the image and text encoders and trains only the point cloud branch to align its output with the semantic space defined by the pretrained CLIP model.
In the alignment and fusion stage, TriPose applies a symmetric contrastive learning strategy to align the representations from all three modality pairs: image–text, image–point cloud, and text–point cloud. An InfoNCE-style contrastive loss [43] is used to encourage semantically consistent representations across modalities. This alignment facilitates implicit cross-modal knowledge transfer and enhances the model’s robustness in multi-modal understanding.
Finally, the aligned multi-modal embeddings are input to a multilayer perceptron (MLP) regression module that captures the nonlinear relationships among modalities and predicts the 3D coordinates of hand keypoints.
By leveraging the complementary strengths of visual, geometric, and linguistic modalities, TriPose significantly improves the performance of 3D hand pose estimation. Extensive evaluations on multiple public datasets demonstrate the effectiveness and generalization ability of the proposed tri-modal fusion framework.
3.1.1. Image Encoder
The image encoder in TriPose is designed to extract both global semantic and local spatial information from input images. To achieve this, we adopt the Vision Transformer (ViT) from the CLIP framework [14] as the backbone visual encoder. ViT effectively captures high-level semantics through self-attention across image patches. However, its ability to represent fine-grained spatial structures is limited, which is critical in 3D hand pose estimation tasks. To address this limitation, a spatial-aware Transformer module is introduced to enhance local feature representation.
As shown in Figure 2, given an input image , ViT first partitions it into N non-overlapping patches of size , where . Each patch is flattened and projected into an embedding space using a learnable projection matrix . Positional embeddings are added to retain spatial location information. The input sequence to the Transformer is thus initialized as:
The encoded sequence is processed through L layers of standard Transformer blocks, each comprising a multi-head self-attention (MSA) mechanism and a feed-forward multilayer perceptron (MLP), formulated as:
where denotes layer normalization.
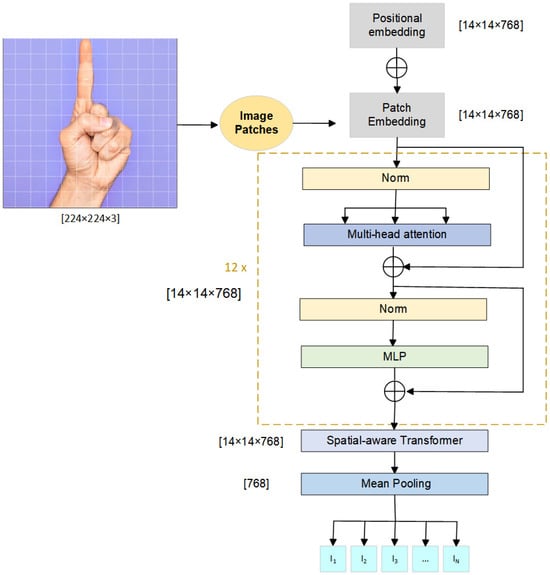
Figure 2.
The architecture of the image encoder. The input image is divided into fixed-size patches, which are linearly projected and embedded with positional information. The patch embeddings are passed through a CLIP-based ViT to extract global semantic features. A spatial-aware Transformer is then appended to capture local geometric relationships among patches, producing the final image feature representation.
To enhance the representation of local spatial patterns, a spatial-aware Transformer module is appended after ViT. This module introduces a learnable spatial embedding to the final ViT output:
The spatial-aware module consists of S customized Transformer layers with Spatial-MSA, focusing on the geometric relationships between patches:
Finally, the output of the spatial-aware Transformer is aggregated using mean pooling to obtain the final image representation:
This two-stage encoding scheme enables the image encoder to capture both global contextual semantics and localized structural features, offering a rich and spatially aware visual representation that supports the downstream multi-modal alignment and 3D pose estimation tasks.
3.1.2. Text Encoder
To enhance the spatial representation capability of the language modality in 3D hand pose estimation, a structured textual encoding strategy is proposed. Inspired by 3D-HandCLIP [44], and unlike conventional approaches that utilize generic labels or free-form language descriptions, our method encodes the relative spatial positions of hand joints along three orthogonal axes: (left-to-right), (top-to-bottom), and (near-to-far). These axis-aligned structured prompts enrich textual features with explicit spatial topology, thereby facilitating more effective alignment with image and point cloud modalities.
As illustrated in Figure 3, we first analyze the 3D coordinates of hand joints to generate three directional textual prompts. Each prompt describes the ordered sequence of joints along one axis, for example:
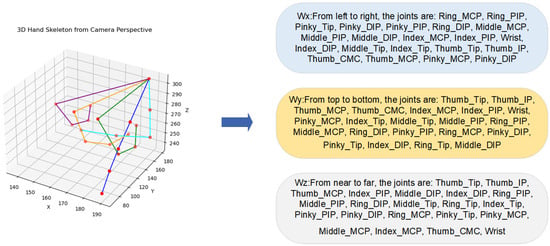
Figure 3.
Generation of structured textual prompts from 3D joint coordinates.Each directional description captures the topological order of joints along a specific axis: left-to-right (), top-to-bottom (), and near-to-far (). Different colored lines represent different finger joint chains, with each color corresponding to the sequential joints of one finger. These prompts provide explicit spatial constraints to guide text encoding.
- : “From left to right, the joints are: …”
- : “From top to bottom, the joints are: …”
- : “From near to far, the joints are: …”
These prompts are then independently embedded using the frozen CLIP text encoder :
where N is the number of joints and D is the feature dimension.
To obtain a unified representation, mean pooling is applied to each directional embedding:
An attention-based fusion mechanism is further employed to adaptively combine these directional features:
where are trainable attention weights learned during training.
This structured text encoder like in Figure 4 enables the model to capture both semantic and spatial information, significantly enhancing tri-modal feature alignment for robust 3D hand pose estimation.
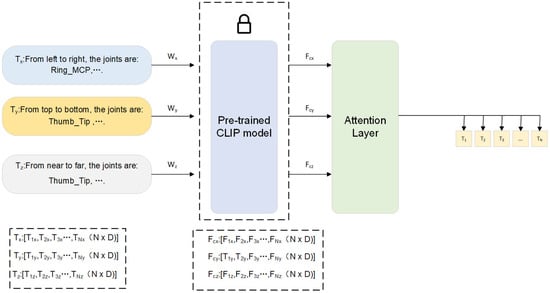
Figure 4.
Architecture of the structured text encoding module. Directional spatial descriptions , , and are independently encoded by a frozen CLIP text encoder. Their representations are aggregated via attention to generate the unified textual feature .
3.1.3. Point Cloud Encoder
To model the 3D geometric structure of the hand, the point cloud modality in TriPose is encoded using a lightweight Transformer-based architecture. This design enables efficient extraction of both local geometric features and global contextual information from sparse 3D hand point clouds.
As illustrated in Figure 5, given a sampled point cloud representing N 3D points, the input is partitioned into non-overlapping local regions via spatial clustering. Each region is normalized and fed into a shared Mini-PointNet module to extract localized geometric embeddings:
where denotes the feature embedding of the i-th point cluster, and d is the feature dimension.
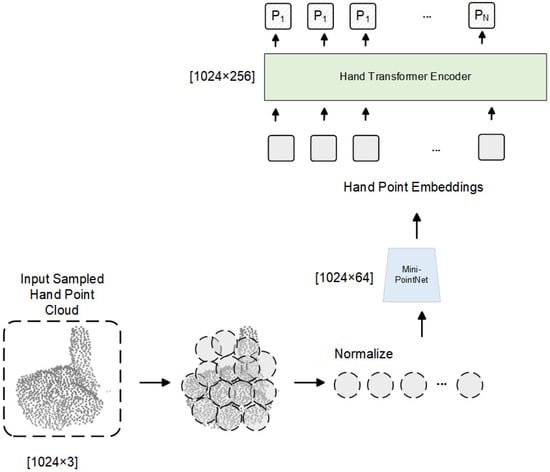
Figure 5.
Architecture of the point cloud encoder. The input 3D hand point cloud is divided into spatial clusters, each processed by a shared Mini-PointNet [45] to extract local features. A Transformer-based encoder further contextualizes these features, and mean pooling is applied to generate the global point cloud embedding .
The resulting embeddings are processed by a stacked Transformer-based encoder [14], referred to as the Hand Transformer Encoder. Each layer consists of a Multi-Head Self-Attention (MSA) module and a Feedforward Network (FFN), integrated with residual connections and layer normalization. The update process in the l-th layer is defined as:
with initial input for all and denoting the number of Transformer layers.
To obtain the final point cloud representation, the outputs from the last Transformer layer are aggregated by mean pooling:
The resulting feature encodes both fine-grained local geometry and global hand structure, enabling robust alignment with image and text modalities for downstream 3D pose regression.
3.2. Tri-Modal Fusion and Alignment Strategy
To project image, text, and point cloud features into a unified semantic space, we propose a Tri-modal Symmetric Contrastive Learning: (TSCL) strategy. This strategy is inspired by the alignment mechanisms in CLIP and ULIP, and introduces structured text prompts and 3D geometry to bridge modality gaps and facilitate semantic fusion.
As shown in Figure 6, each training instance is represented as a triplet , where is the image feature, the text feature, and the point cloud feature. A similarity matrix is constructed by computing pairwise cosine similarities between modalities. Diagonal elements represent positive pairs (i.e., features from the same sample), while off-diagonal elements are treated as negative samples.
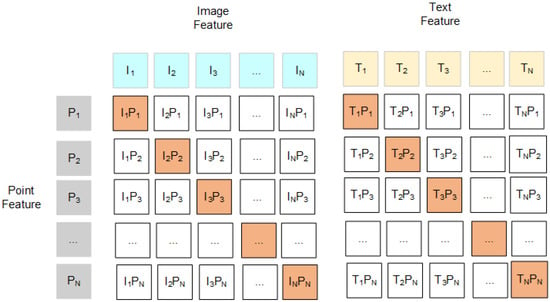
Figure 6.
Tri-modal contrastive alignment. Each row corresponds to a point cloud sample, and each column to an image or text sample. Diagonal entries represent positive pairs. Contrastive loss is computed across all three modality pairs.
To enforce semantic alignment, we apply a symmetric InfoNCE-based contrastive loss [43] for each modality pair: image–point, text–point, and (optionally) image–text. Taking the image–point pair as an example, the loss is formulated as:
where denotes cosine similarity and is a learnable temperature parameter.
The total contrastive loss combines all modality pairs:
In practice, we set and to focus on aligning point cloud with both image and text features. The image and text encoders (, ) are frozen from the pretrained CLIP model to preserve learned semantics, while the point cloud encoder is optimized to align with this shared feature space.
Data Formats and Alignment
Image (2D). We use RGB (or depth-to-RGB visualization) crops resized to , float 32, channel-first (C × H × W), normalized by CLIP mean/std. The CLIP ViT produces a 768-D token feature which we project to a 512-D vector and L2-normalize.
Point cloud (3D). Each sample provides points in meters, float32. We center by the hand centroid and scale to a fixed radius. MiniPointNet + Transformer yields a 256-D global feature, linearly mapped to a 512-D vector and L2-normalized.
Text (structured). We form three axis-ordered prompts describing the ordinal order of named joints from left → right, top → bottom, and near → far (e.g., “From left to right: wrist → thumb_MCP ”). Each prompt is encoded by CLIP text; we mean-pool per-axis phrases and fuse them with learned attention to obtain a 512-D vector , then L2-normalize.
Shared space and TSCL All three vectors lie in a shared 512-D space with cosine similarity. For a batch of B triplets , we minimize symmetric InfoNCE over pairs and :
with learnable temperature . This pulls image/point and text/point positives together while pushing negatives apart, yielding well-aligned features for pose regression.
Example triplet (for Figure 1). Image: crop of the hand. Point cloud: points after centering/scaling. Text:
: “From left to right: wrist, thumb_MCP, thumb_IP, index_MCP, …, pinky_TIP.”
: “From top to bottom: pinky_TIP, ring_TIP, …, wrist.”
: “From near to far: thumb_TIP, index_TIP, …, wrist.”
After encoding and projection, are L2-normalized and compared by cosine similarity within the batch.
3.3. Pose Regression Module
The final goal of TriPose is to accurately regress the 3D coordinates of hand keypoints. To achieve this, we employ a compact yet expressive Multi-Layer Perceptron (MLP) regression module that maps the fused tri-modal representation to the final pose output.
Let denote the aligned tri-modal embedding, which encodes complementary information from image, text, and point cloud modalities. This feature is passed through an MLP comprising fully connected layers with ReLU activations and dropout regularization, producing the predicted 3D positions of K hand joints:
where each row in corresponds to the coordinates of a keypoint.
As illustrated in Figure 7, the regression head consists of three linear layers with intermediate hidden dimensions of 512 and 256, each followed by a ReLU and dropout layer:
- Input: ;
- Linear(512) → ReLU → Dropout;
- Linear(256) → ReLU → Dropout;
- Linear() → Reshape to .
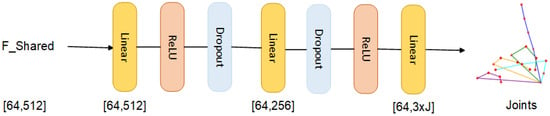
Figure 7.
Architecture of the MLP-based pose regression module. The fused tri-modal feature is passed through stacked Linear–ReLU–Dropout blocks and mapped to a -dimensional output, representing 3D coordinates of K hand joints. Different colored lines represent different finger joint chains, with each color corresponding to the sequential joints of one finger.
To enhance generalization and prevent overfitting, we adopt a two-stage training paradigm. In the first stage, the tri-modal encoders are pretrained and frozen, ensuring stable and consistent feature alignment. In the second stage, the regression module is trained independently using the fixed embeddings, leading to more stable optimization and better convergence in low-data regimes.
3.4. Loss Function
To achieve unified feature representation across image, text, and point cloud modalities while enabling accurate 3D hand pose prediction, TriPose jointly optimizes two types of loss functions: cross-modal contrastive loss and 3D pose regression loss. The former promotes semantic alignment among modalities, while the latter directly supervises spatial prediction of hand joint coordinates.
3.4.1. Cross-Modal Contrastive Loss
A symmetric InfoNCE-based contrastive learning strategy is adopted to enforce explicit alignment among the three modalities. Let , , and denote the encoded features from the image, text, and point cloud modalities, respectively. The total contrastive loss is defined as:
where , , and control the relative importance of each modality pair.
Each modality-pair loss follows a symmetric InfoNCE formulation:
where the directional loss is given by:
where denotes cosine similarity and is a learnable temperature parameter.
3.4.2. Pose Regression Loss
To ensure accurate 3D hand joint localization, we adopt a mean squared error (MSE) loss. Let be the predicted joint coordinates and the corresponding ground truth. The MSE loss is computed as:
3.4.3. Total Loss
The overall training objective combines both contrastive and regression losses, forming a joint optimization target:
where is a balancing hyperparameter that controls the trade-off between cross-modal alignment and pose prediction accuracy.
4. Experiments
We evaluate the effectiveness of TriPose for 3D hand pose estimation through extensive experiments on three widely used public datasets: NYU, MSRA, and ICVL. All experiments are implemented using PyTorch 1.13 and conducted on a workstation equipped with an Intel Core i9-13900KF CPU, 64 GB RAM, and an NVIDIA RTX 3090 GPU.
4.1. Training Protocol
TriPose is trained using a two-stage strategy. In the first stage, the CLIP image and text encoders are frozen, and only the point cloud encoder is updated. The objective is to align the point cloud representations with the pretrained CLIP embedding space through contrastive learning.
The frozen Vision Transformer (ViT) serves as the global image feature extractor, while a trainable spatial-aware Transformer module is appended to enhance the modeling of local geometric structures. This module leverages positional encoding and multi-head self-attention to extract fine-grained features that complement the global semantics provided by ViT.
4.2. Data Augmentation for Robustness
To improve generalization and robustness, we employ a diverse set of data augmentation techniques, especially for the point cloud modality. Inspired by ModelNet-C [46], we introduce seven types of corruptions, including local jittering, global point dropping, non-uniform scaling, and surface perturbations.
The augmentations used are visualized in Figure 8 and summarized as follows:
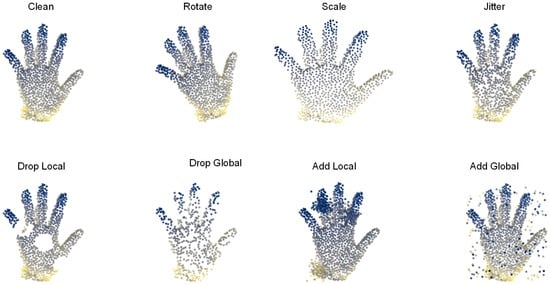
Figure 8.
Visualization of point cloud corruption types used for data augmentation. These augmentations simulate realistic distortions to improve model robustness.
- Clean: original point cloud without distortion;
- Rotate: random 3D rotation;
- Scale: isotropic scaling transformations;
- Jitter: additive Gaussian noise;
- Drop Local: randomly remove points in local regions;
- Drop Global: uniformly drop points across the global surface;
- Add Local: add noisy points within localized areas;
- Add Global: inject global outliers to simulate sensor artifacts.
Additionally, we incorporate PointWOLF and RSMix augmentations to simulate local deformation and rigid-body part mixing, enhancing the model’s ability to generalize to occlusions, spatial variance, and imperfect sensor data.
4.3. Datasets
MSRA Dataset [15]: This dataset contains approximately 76,000 depth frames from 9 subjects, each performing 17 predefined gestures. Each frame is annotated with 21 hand joints. We follow the standard leave-one-subject-out (LOSO) protocol: for each fold, models are trained on 8 subjects and evaluated on the held-out subject, and we report the average over all 9 folds. Within each fold, we further hold out 10% of the frames from the raining subjects (stratified per subject) as a validation subset for early stopping and hyperparameter selection; the held-out test subject is never used for tuning. ICVL Dataset [16]: ICVL provides 22,000 training and 1600 testing depth frames with 16 annotated joints per frame, and is known for relatively clean depth and limited occlusions. We use the official train/test split and create a validation subset by holding out 10% of the training frames (stratified by gesture category). All hyperparameters and early-stopping criteria are selected on this validation subset only. NYU Dataset [17]: Captured from three camera views, NYU includes 72,000 training and 8000 testing frames. Following common practice, we use a single camera view and select 14 key joints (out of 36) for training and evaluation. We adopt the official train/test split, and we derive a validation subset by holding out 10% of the training frames (stratified per camera view and sampled temporally to avoid leakage).
4.3.1. Validation Protocol and Fairness
Unless otherwise stated, all optimizer settings, regularization terms (e.g., weight decay, dropout), and contrastive temperatures are tuned on the aforementioned validation subsets only; no test frames are used for model selection. This prevents optimistic bias and ensures comparability across datasets and folds.
4.3.2. Dataset Characteristics and Complementarity
MSRA [15] is depth-only with 9 subjects and 17 gestures (21 joints; ∼76k frames), containing frequent self-occlusion and articulation diversity, and—under the LOSO protocol—primarily probes cross-subject generalization. ICVL [16] (22k train/1.6k test; 16 joints) features relatively clean depth and fewer occlusions but a smaller scale and fewer subjects, forming a low-resource regime to test whether our structured-language guidance and tri-modal fusion improve accuracy with limited data. NYU [17] (single-view setting with 14 key joints; 72k train/8k test) is RGB-D with noisier depth and more severe occlusions, offering a challenging setting for robustness to sensing noise and occlusion. Taken together, these benchmarks evaluate complementary aspects of 3D HPE—MSRA (cross-subject generalization in depth), ICVL (generalization under data scarcity), and NYU (robustness to noise/occlusion)—providing a comprehensive assessment of TriPose.
4.4. Comparison with State-of-the-Art Methods
To comprehensively assess the performance of TriPose, we conduct systematic comparisons with a variety of representative methods on the MSRA, ICVL, and NYU datasets. The compared baselines span both 2D depth-image-based approaches and 3D point cloud or voxel-based models, including early classical frameworks and recent deep learning architectures.
Two-dimensional input-based methods include model-fitting-based DeepModel, shape-prior-based DeepPrior and DeepPrior++, matrix-completion-based DeepHand, local surface normal-based LSN, and the multi-view method Multi-view CNN.
Three-dimensional input-based methods include voxel-based 3DCNN, spatial-structure modeling SHPR-Net, point cloud-based HandPointNet, geometric-structure-enhanced HandFoldingNet, voxel regression-based V2V-PoseNet, and more recent deep models such as CrossInfoNet, IPNet, and the generative diffusion-based HandDiff.
Figure 9 presents the overall performance comparison on the MSRA (left), ICVL (middle), and NYU (right) benchmarks in terms of mean joint error and percentage of correct keypoints (PCK). TriPose achieves superior or comparable results across all datasets. Notably, on ICVL, it achieves a mean joint error of 5.68 mm, outperforming most prior works by a significant margin.
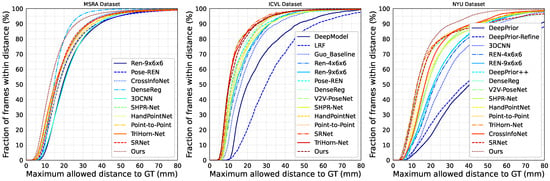
Figure 9.
Comparison with state-of-the-art methods on MSRA (left), ICVL (middle), and NYU (right) datasets. Results are shown in terms of percentage of correct keypoints (PCK) and mean 3D joint error (mm).
To further analyze the per-joint prediction performance, Figure 10 illustrates the joint-wise average errors. TriPose exhibits lower errors for relatively stable joints (e.g., wrist, MCPs), and it maintains strong accuracy on highly dynamic fingertip regions, indicating robust spatial modeling capabilities.
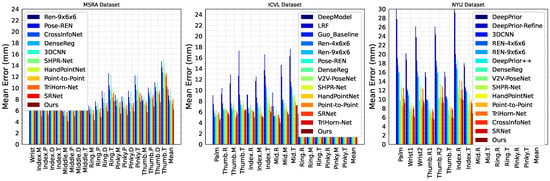
Figure 10.
Joint-wise error analysis across the MSRA (left), ICVL (middle), and NYU (right) datasets. Bars represent average errors for each joint. R: root joint; T: fingertip.
Qualitative results are shown in Figure 11, where predicted and ground-truth joints are visualized on point cloud inputs. Red dots denote predictions by TriPose, and black dots indicate ground-truth locations. The model demonstrates high structural consistency and spatial precision, even under challenging conditions such as occlusion, extreme articulation, and varied orientations.

Figure 11.
Qualitative results on MSRA (left), ICVL (middle), and NYU (right). The model outputs (red) are overlaid on the point cloud inputs; ground-truth joints are shown in blue.
Table 1 summarizes the quantitative results, reporting mean 3D joint errors across all datasets. TriPose achieves the best or second-best results in each case. On the ICVL dataset known for its limited training data, TriPose achieves a mean error of 5.68 mm, demonstrating its robustness in low-data regimes.

Table 1.
Comparison of mean 3D joint errors (in mm) on MSRA, ICVL, and NYU datasets. Lower is better.
The results clearly demonstrate that TriPose effectively integrates semantic information from language and visual modalities to compensate for challenges in point cloud data, particularly under occlusion and data scarcity. The tri-modal fusion enables richer representation learning and mitigates overfitting, contributing to more robust and accurate hand pose estimation in real-world scenarios.
4.5. Ablation Study
To better understand the contributions of individual components in the TriPose framework, we conduct ablation experiments on the MSRA, ICVL, and NYU datasets. We systematically disable key modules or modify training strategies to analyze the impact of each design choice, including modality configurations, spatial modeling, data augmentation, and optimization procedures. Table 2 reports the average 3D joint errors (in mm) for various architectural variants.

Table 2.
Ablation study on MSRA, ICVL, and NYU datasets. Average 3D joint errors (mm). Lower is better (↓).
Text Modality: Removing the structured language input (w/o Text) results in increased error across all datasets, e.g., from 5.68 mm to 6.47 mm on ICVL and a 0.8 mm increase on NYU, demonstrating that structured language provides valuable spatial priors, especially in data-scarce settings.
Image Transformer: Disabling the spatial-aware Transformer in the image branch (w/o Image Transformer) degrades performance on all datasets. For instance, the NYU error rises from 7.43 mm to 7.92 mm, confirming the importance of local geometry modeling.
Point Cloud Augmentation: Excluding all point cloud augmentations (w/o Point Augmentations) leads to notable performance drops under occlusion and noise, with ICVL error increasing to 6.59 mm. This validates the role of augmentation in improving robustness. To further investigate the impact of individual augmentation techniques, we conducted a fine-grained ablation study focusing on the seven types of point cloud corruptions introduced in the data augmentation phase (see Figure 8 for details). These corruptions—Add Global, Add Local, Drop Global, Drop Local, Jitter, Rotate, and Scale—are visualized in Figure 8, where each type simulates realistic distortions such as sensor noise, occlusions, or geometric transformations. Additionally, Figure 12 provides a direct comparison of hand point clouds with and without data augmentation, where the top row (blue) represents augmented point clouds and the bottom row (red) represents the original state, highlighting the introduced distortions. We evaluated the model by excluding each augmentation type individually while keeping the others active. The results, summarized in Table 3, show that removing any single augmentation type leads to a performance drop, with the most significant degradation observed when excluding Jitter (ICVL error increases to 6.32 mm) and Drop Local (NYU error increases to 7.88 mm). This suggests that Jitter helps the model generalize to noisy sensor data, while Drop Local is critical for handling partial occlusions. The combination of all augmentation types in the full TriPose model yields the best performance, underscoring the importance of diverse data augmentation for robust 3D hand pose estimation.

Figure 12.
Visualization of hand point clouds with and without data augmentation. The top row (blue) shows the point clouds after applying our data augmentation methods, including seven types of corruptions: Add Global, Add Local, Drop Global, Drop Local, Jitter, Rotate, and Scale. The bottom row (red) shows the point clouds without any data augmentation, preserving their original state. The comparison highlights how data augmentation introduces realistic distortions to enhance model robustness for 3D hand pose estimation.

Table 3.
Fine-grained ablation study on the impact of individual point cloud augmentation types. Average 3D joint errors (mm) on MSRA, ICVL, and NYU datasets. Lower is better (↓).
Modality Combinations: Using only the point cloud (Point Only) yields the worst performance, while combining it with image data (Two-modal) significantly improves accuracy. The full TriPose configuration achieves the best results, highlighting the effectiveness of tri-modal fusion.
Training Strategy: Compared to our two-stage training, a fully end-to-end strategy (Three-modal + End-to-End) shows slightly inferior performance (e.g., 7.12 mm vs. 6.98 mm on MSRA), indicating that staged optimization helps in stabilizing multi-modal alignment and regression.
4.6. Runtime and Model Size
4.6.1. Protocol
To ensure a transparent comparison, we report runtime under a unified protocol: batch size ; image input ; point cloud size ; PyTorch eval() with fixed structured-text prompts whose embeddings are cached at inference (the text encoder incurs no online cost). Each latency number is the median over 1000 timed iterations after 200 warm-up iterations; GPU timings are synchronized with torch.cuda.synchronize. We distinguish preprocessing (e.g., depth-to-point cloud, normalization) and network time when applicable.
4.6.2. Positioning
Unlike PointNet-style lightweight backbones, TriPose combines a CLIP ViT image encoder, a point-cloud Transformer, and a spatial-aware module to maximize accuracy on MSRA/ICVL/NYU. Consequently, our model is not the smallest nor the fastest among point-cloud methods; instead, it targets a better accuracy–efficiency trade-off. Table 4 lists representative 3D-input baselines with the numbers as reported in their original papers (measured on heterogeneous GPUs), together with our measurements under the unified protocol.

Table 4.
Comparison of model size and inference time for 3D-input methods. Baseline figures are copied from original papers (hardware and timing definitions vary). Our numbers follow the unified protocol (batch = 1, , , cached text embeddings) on RTX 3090.
4.6.3. Discussion
As shown in Table 4, TriPose has a larger parameter count than PointNet-style models, reflecting its stronger visual–geometric capacity. In exchange for higher accuracy on MSRA/ICVL/NYU within our setting, the full model exhibits a moderate runtime overhead, with a practical single-image latency of about ms (preprocess ms + network ms) on an RTX 3090, i.e., ∼40 FPS. We further note that (i) caching the structured-text embeddings eliminates text-branch cost at inference, and (ii) reducing point tokens () and/or pruning the spatial-aware block can substantially lower latency with modest accuracy impact (see Ablation). For completeness, the on-disk model size of TriPose is approximately 360 MB for our final trained checkpoint.
5. Conclusions
This paper presents TriPose, a novel tri-modal framework for 3D hand pose estimation that jointly leverages image, point cloud, and structured language modalities. By aligning multi-modal representations in a shared semantic space via cross-modal contrastive learning, TriPose achieves robust and accurate pose estimation across diverse hand configurations.
To enhance spatial reasoning, a spatial-aware Transformer module is introduced to model local geometry within the image modality, and a lightweight Transformer-based encoder is designed for point cloud feature extraction. The final 3D joint coordinates are regressed via a multi-layer perceptron (MLP) using the fused representation.
Extensive experiments on three public benchmarks, MSRA, ICVL, and NYU, demonstrate that TriPose consistently outperforms state-of-the-art methods. In particular, it shows strong generalization on the ICVL dataset, which is characterized by limited training samples. Ablation studies further verify the contributions of the structured language cues, spatial modeling, and augmentation strategies.
Future work will explore (1) more efficient mechanisms for vision–language–geometry interaction to boost inference speed; (2) extensions to dynamic gesture recognition and continuous motion tracking; and (3) the integration of fine-grained linguistic supervision such as task-oriented instructions to facilitate natural human–computer interaction.
Author Contributions
Conceptualization, L.S.; methodology, L.S.; software, X.G.; validation, H.S. and H.L.; writing—original draft, X.G.; writing—review and editing, X.G., H.S. and H.L.; visualization, X.G. and H.L.; supervision, L.S. and H.S.; project administration, L.S.; funding acquisition, L.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Fundamental Research Funds for the Universities of the Liaoning Provincial Department of Education, China (Project No. LJKZ0011), and the Liaoning Provincial Science Initiative, China (Grant No. 2021JH1/1040011).
Data Availability Statement
The data that support the findings of this study are openly available from third-party sources. The NYU 3D Hand Pose Dataset can be found at https://jonathantompson.github.io/NYU_Hand_Pose_Dataset.htm, accessed on 13 November 2025. The ICVL Hand Dataset is available at https://labicvl.github.io/hand.html, accessed on 13 November 2025. The MSRA Hand Pose Dataset is available at https://jimmysuen.github.io/, accessed on 13 November 2025.
Conflicts of Interest
The authors declare no conflict of interest.
Glossary
| Abbreviation | Definition |
| 3D HPE | 3D Hand Pose Estimation |
| CLIP | Contrastive Language–Image Pre-training |
| ViT | Vision Transformer |
| MSA | Multi-Head Self-Attention |
| MLP | Multi-Layer Perceptron |
| PCK | Percentage of Correct Keypoints |
| MSE | Mean Squared Error |
| TSCL | Tri-modal Symmetric Contrastive Learning |
| ULIP | Unified Language-Image Pre-training |
| NYU | New York University 3D Hand Pose Dataset |
| ICVL | Intel Collaborative Visualization Laboratory Hand Dataset |
| MSRA | Microsoft Research Asia Hand Pose Dataset |
References
- Cheng, W.; Tang, H.; Van Gool, L.; Ko, J.H. HandDiff: 3D Hand Pose Estimation with Diffusion on Image-Point Cloud. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 2274–2284. [Google Scholar]
- Chen, X.; Wang, G.; Zhang, C.; Kim, T.K.; Ji, X. Shpr-net: Deep semantic hand pose regression from point clouds. IEEE Access 2018, 6, 43425–43439. [Google Scholar] [CrossRef]
- Chen, X.; Wang, G.; Guo, H.; Zhang, C. Pose guided structured region ensemble network for cascaded hand pose estimation. Neurocomputing 2020, 395, 138–149. [Google Scholar] [CrossRef]
- Cheng, W.; Park, J.H.; Ko, J.H. Handfoldingnet: A 3d hand pose estimation network using multiscale-feature guided folding of a 2D hand skeleton. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11–17 October 2021; pp. 11260–11269. [Google Scholar]
- Du, K.; Lin, X.; Sun, Y.; Ma, X. Crossinfonet: Multi-task information sharing based hand pose estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 9896–9905. [Google Scholar]
- Fang, L.; Liu, X.; Liu, L.; Xu, H.; Kang, W. Jgr-p2o: Joint graph reasoning based pixel-to-offset prediction network for 3d hand pose estimation from a single depth image. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part VI 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 120–137. [Google Scholar]
- Ge, L.; Cai, Y.; Weng, J.; Yuan, J. Hand pointnet: 3d hand pose estimation using point sets. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 8417–8426. [Google Scholar]
- Ge, L.; Ren, Z.; Yuan, J. Point-to-point regression pointnet for 3d hand pose estimation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 475–491. [Google Scholar]
- Guo, H.; Wang, G.; Chen, X.; Zhang, C.; Qiao, F.; Yang, H. Region ensemble network: Improving convolutional network for hand pose estimation. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 4512–4516. [Google Scholar]
- Li, S.; Lee, D. Point-to-pose voting based hand pose estimation using residual permutation equivariant layer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 11927–11936. [Google Scholar]
- Ren, P.; Sun, H.; Qi, Q.; Wang, J.; Huang, W. SRN: Stacked regression network for real-time 3D hand pose estimation. In Proceedings of the BMVC, Cardiff, UK, 9–12 September 2019; Volume 112. [Google Scholar]
- Ren, P.; Chen, Y.; Hao, J.; Sun, H.; Qi, Q.; Wang, J.; Liao, J. Two heads are better than one: Image-point cloud network for depth-based 3D hand pose estimation. In Proceedings of the AAAI Conference on Artificial Intelligence, Koriyama, Japan, 8–13 July 2023; Volume 37, pp. 2163–2171. [Google Scholar]
- Radford, A.; Kim, J.W.; Hallacy, C.; Ramesh, A.; Goh, G.; Agarwal, S.; Sastry, G.; Askell, A.; Mishkin, P.; Clark, J.; et al. Learning transferable visual models from natural language supervision. In Proceedings of the International Conference on Machine Learning. PmLR, Virtual, 18–24 July 2021; pp. 8748–8763. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Sun, X.; Wei, Y.; Liang, S.; Tang, X.; Sun, J. Cascaded hand pose regression. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 824–832. [Google Scholar]
- Tang, D.; Jin Chang, H.; Tejani, A.; Kim, T.K. Latent regression forest: Structured estimation of 3d articulated hand posture. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3786–3793. [Google Scholar]
- Tompson, J.; Stein, M.; Lecun, Y.; Perlin, K. Real-time continuous pose recovery of human hands using convolutional networks. ACM Trans. Graph. (ToG) 2014, 33, 1–10. [Google Scholar] [CrossRef]
- Oikonomidis, I.; Kyriazis, N.; Argyros, A.A. Efficient model-based 3D tracking of hand articulations using Kinect. In Proceedings of the BMVC, Dundee, UK, 29 August–2 September 2011; Volume 1, p. 3. [Google Scholar]
- Ballan, L.; Taneja, A.; Gall, J.; Van Gool, L.; Pollefeys, M. Motion capture of hands in action using discriminative salient points. In Proceedings of the Computer Vision–ECCV 2012: 12th European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; Proceedings, Part VI 12. Springer: Berlin/Heidelberg, Germany, 2012; pp. 640–653. [Google Scholar]
- Tzionas, D.; Ballan, L.; Srikantha, A.; Aponte, P.; Pollefeys, M.; Gall, J. Capturing hands in action using discriminative salient points and physics simulation. Int. J. Comput. Vis. 2016, 118, 172–193. [Google Scholar] [CrossRef]
- Khamis, S.; Taylor, J.; Shotton, J.; Keskin, C.; Izadi, S.; Fitzgibbon, A. Learning an efficient model of hand shape variation from depth images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 2540–2548. [Google Scholar]
- Romero, J.; Tzionas, D.; Black, M.J. Embodied hands: Modeling and capturing hands and bodies together. arXiv 2022, arXiv:2201.02610. [Google Scholar] [CrossRef]
- Tkach, A.; Tagliasacchi, A.; Remelli, E.; Pauly, M.; Fitzgibbon, A. Online generative model personalization for hand tracking. ACM Trans. Graph. (ToG) 2017, 36, 1–11. [Google Scholar] [CrossRef]
- Remelli, E.; Tkach, A.; Tagliasacchi, A.; Pauly, M. Low-dimensionality calibration through local anisotropic scaling for robust hand model personalization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2535–2543. [Google Scholar]
- Keskin, C.; Kıraç, F.; Kara, Y.E.; Akarun, L. Hand pose estimation and hand shape classification using multi-layered randomized decision forests. In Proceedings of the Computer Vision–ECCV 2012: 12th European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; Proceedings, Part VI 12. Springer: Berlin/Heidelberg, Germany, 2012; pp. 852–863. [Google Scholar]
- Xu, C.; Cheng, L. Efficient hand pose estimation from a single depth image. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 3456–3462. [Google Scholar]
- Ge, L.; Liang, H.; Yuan, J.; Thalmann, D. 3d convolutional neural networks for efficient and robust hand pose estimation from single depth images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 June 2017; pp. 1991–2000. [Google Scholar]
- Ge, L.; Liang, H.; Yuan, J.; Thalmann, D. Robust 3d hand pose estimation in single depth images: From single-view cnn to multi-view cnns. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 3593–3601. [Google Scholar]
- Oberweger, M.; Lepetit, V. Deepprior++: Improving fast and accurate 3d hand pose estimation. In Proceedings of the IEEE International Conference on Computer Vision Workshops, Venice, Italy, 22–29 October 2017; pp. 585–594. [Google Scholar]
- Choi, C.; Kim, S.; Ramani, K. Learning hand articulations by hallucinating heat distribution. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 3104–3113. [Google Scholar]
- Taylor, J.; Bordeaux, L.; Cashman, T.; Corish, B.; Keskin, C.; Sharp, T.; Soto, E.; Sweeney, D.; Valentin, J.; Luff, B.; et al. Efficient and precise interactive hand tracking through joint, continuous optimization of pose and correspondences. ACM Trans. Graph. (ToG) 2016, 35, 1–12. [Google Scholar] [CrossRef]
- Wan, C.; Probst, T.; Van Gool, L.; Yao, A. Crossing nets: Dual generative models with a shared latent space for hand pose estimation. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 June 2017; Volume 7. [Google Scholar]
- Oberweger, M.; Wohlhart, P.; Lepetit, V. Training a feedback loop for hand pose estimation. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 3316–3324. [Google Scholar]
- Ye, Q.; Yuan, S.; Kim, T.K. Spatial attention deep net with partial pso for hierarchical hybrid hand pose estimation. In Proceedings of the Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, 11–14 October 2016; Proceedings, Part VIII 14. Springer: Berlin/Heidelberg, Germany, 2016; pp. 346–361. [Google Scholar]
- Tang, D.; Taylor, J.; Kohli, P.; Keskin, C.; Kim, T.K.; Shotton, J. Opening the black box: Hierarchical sampling optimization for estimating human hand pose. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 3325–3333. [Google Scholar]
- Zheng, Z.; Xie, S.; Dai, H.; Chen, X.; Wang, H. An overview of blockchain technology: Architecture, consensus, and future trends. In Proceedings of the 2017 IEEE International Congress on Big Data (BigData Congress), Boston, MA, USA, 11–14 December 2017; pp. 557–564. [Google Scholar]
- Moon, G.; Chang, J.Y.; Lee, K.M. V2v-posenet: Voxel-to-voxel prediction network for accurate 3d hand and human pose estimation from a single depth map. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5079–5088. [Google Scholar]
- Xiao, Y.; Liu, Y. Review on 3D Hand Pose Estimation Based on a RGB Image. J. Comput. Aided Des. Comput. Graph. 2024, 36, 161–172. [Google Scholar]
- Żywanowski, K.; Łysakowski, M.; Nowicki, M.R.; Jacques, J.T.; Tadeja, S.K.; Bohné, T.; Skrzypczyński, P. Vision-based hand pose estimation methods for Augmented Reality in industry: Crowdsourced evaluation on HoloLens 2. Comput. Ind. 2025, 171, 104328. [Google Scholar] [CrossRef]
- Neverova, N.; Wolf, C.; Taylor, G.W.; Nebout, F. Multi-scale deep learning for gesture detection and localization. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; Springer: Berlin/Heidelberg, Germany; pp. 474–490. [Google Scholar]
- Molchanov, P.; Yang, X.; Gupta, P.; Kim, K.; Tyree, S.; Kautz, J. Online detection and classification of dynamic hand gestures with recurrent 3d convolutional neural networks. In Proceedings of the CVPR Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; Volume 1, p. 3. [Google Scholar]
- Garg, M.; Ghosh, D.; Pradhan, P.M. Gestformer: Multiscale wavelet pooling transformer network for dynamic hand gesture recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 2473–2483. [Google Scholar]
- Oord, A.v.d.; Li, Y.; Vinyals, O. Representation learning with contrastive predictive coding. arXiv 2018, arXiv:1807.03748. [Google Scholar]
- Guo, S.; Cai, Q.; Qi, L.; Dong, J. Clip-hand3D: Exploiting 3D hand pose estimation via context-aware prompting. In Proceedings of the 31st ACM International Conference on Multimedia, Ottawa, ON, Canada, 29 October–3 November 2023; pp. 4896–4907. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 June 2017; pp. 652–660. [Google Scholar]
- Ren, J.; Pan, L.; Liu, Z. Benchmarking and analyzing point cloud classification under corruptions. In Proceedings of the International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022; pp. 18559–18575. [Google Scholar]
- Zhou, X.; Wan, Q.; Zhang, W.; Xue, X.; Wei, Y. Model-based deep hand pose estimation. arXiv 2016, arXiv:1606.06854. [Google Scholar] [CrossRef]
- Oberweger, M.; Wohlhart, P.; Lepetit, V. Hands deep in deep learning for hand pose estimation. arXiv 2015, arXiv:1502.06807. [Google Scholar]
- Guo, H.; Wang, G.; Chen, X.; Zhang, C. Towards good practices for deep 3d hand pose estimation. arXiv 2017, arXiv:1707.07248. [Google Scholar] [CrossRef]
- Wan, C.; Probst, T.; Van Gool, L.; Yao, A. Dense 3d regression for hand pose estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5147–5156. [Google Scholar]
- Cheng, W.; Ko, J.H. Handr2n2: Iterative 3d hand pose estimation using a residual recurrent neural network. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 20904–20913. [Google Scholar]
- Rezaei, M.; Rastgoo, R.; Athitsos, V. TriHorn-net: A model for accurate depth-based 3D hand pose estimation. Expert Syst. Appl. 2023, 223, 119922. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).