Optimized Space-Filling Curve-Driven Forward-Secure Range Query on Location-Related Data for Unmanned Aerial Vehicle Networks
Abstract
1. Introduction
- The performance of four classic space-filling curves, namely, row-wise, Z-order, Gray, and Hilbert curves, is investigated. We constructed spatial indices on plaintext datasets using encoding algorithms specifically designed for each curve. Subsequently, we conducted query experiments on real-world geographic information datasets, focusing on two classic query types, range queries and kNN queries. Finally, by leveraging the unique properties of each space-filling curve, we performed both theoretical and experimental analyses to identify the optimal curves for different query scenarios.
- A forward-secure range query scheme is presented. We first partition the original dataset into subsets using the corresponding optimal curves. We then apply a greedy merging algorithm and a dummy-point insertion algorithm to balance the number of data points within each subset, resulting in greedy subsets. Each greedy subset is encrypted with a distinct key, and a key mapping table is generated accordingly. We construct a secure index based on these encrypted subsets and upload it to the cloud server along with the ciphertext dataset. Finally, a concrete forward-secure range query scheme is proposed.
- We implemented the proposed scheme and conducted extensive experiments on both real-world and synthetic datasets containing 100 million to 1 billion objects. The experimental results demonstrate that our scheme significantly outperforms existing schemes in terms of query time and accuracy. In particular, the accuracy of our scheme is improved by 20% to 30%, and the query time is reduced by 8% to 15% compared to the state-of-the-art schemes.
2. Related Works
3. System Overview and Preliminaries
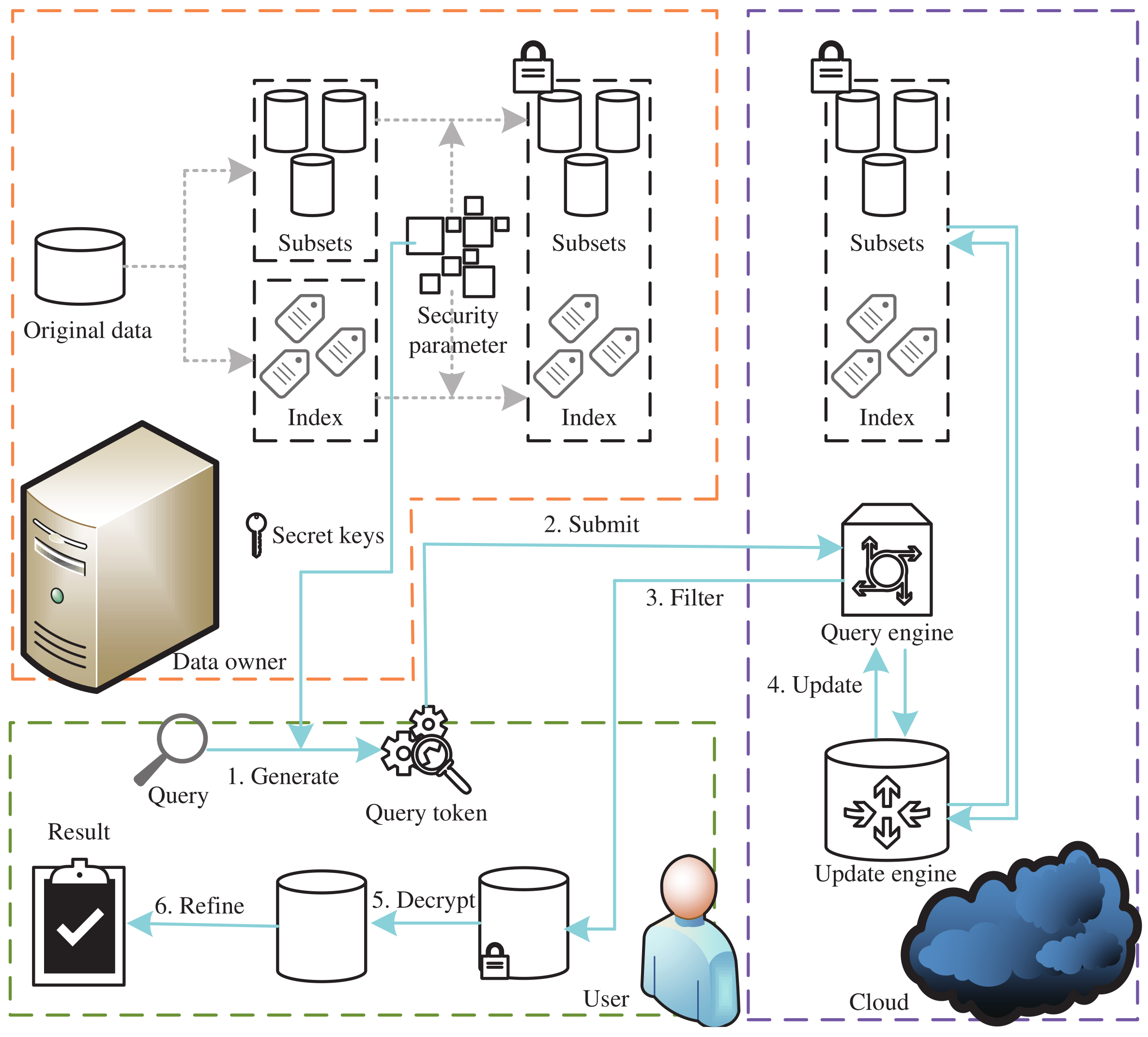
3.1. System Overview
- The data owner is assumed to be fully honest and trustworthy and will not perform any malicious operations on users’ spatial data, such as privately replacing data, altering outputs, or selling data. The data owner is responsible for managing the security parameters and the related keys generated based on these parameters. The data owner also handles all tasks required to preprocess the original dataset, including partitioning data subsets, encrypting original data points, and constructing secure indices. After completing preprocessing, the encrypted dataset and the secure index are uploaded to the cloud server.
- The cloud is assumed to be semi-honest. This means that it follows the protocol and does not perform malicious attacks on the data, such as modifying the data or altering the results of inputs and outputs. However, it remains highly curious about the data it stores, for example, by recording intermediate results and inferring additional information based on them. After the data owner completes data preprocessing, the cloud server receives and stores the uploaded encrypted dataset and secure index. During the query process, the cloud server retrieves the ciphertext labels of the candidate structure set by matching the received query token with the secure index. Finally, it completes the query based on the ciphertext and returns the candidate result set to the user.
- The user initiates a query request by specifying the query range and generating a query token locally using the security parameters. The query token is then sent to the cloud. Upon receiving the encrypted candidate result set from the cloud, the user decrypts it and performs a secondary fine-grained query to obtain the final query result set.
3.2. Security Model
3.3. Preliminaries
3.3.1. Inverted and Forward Indices
3.3.2. Pseudo-Random Function
- Efficiency: For any input , the function can be computed in polynomial time.
- Pseudo-randomness: For any probabilistic polynomial-time adversary , the probability that can distinguish between F and a truly random function is negligible.
3.3.3. Proxy Re-Encryption
- Correctness: For any ciphertext c encrypted with the data owner’s public key , if the proxy generates a re-encryption key , then the ciphertext obtained by re-encrypting c using must be decryptable using the data owner’s secret key .
- Security: For any probabilistic polynomial-time adversary , the probability that can distinguish between a ciphertext c encrypted with the data owner’s public key and a ciphertext obtained by re-encrypting c using generated by the proxy is negligible.
4. Analyses of Space-Filling Curves for Spatial Data
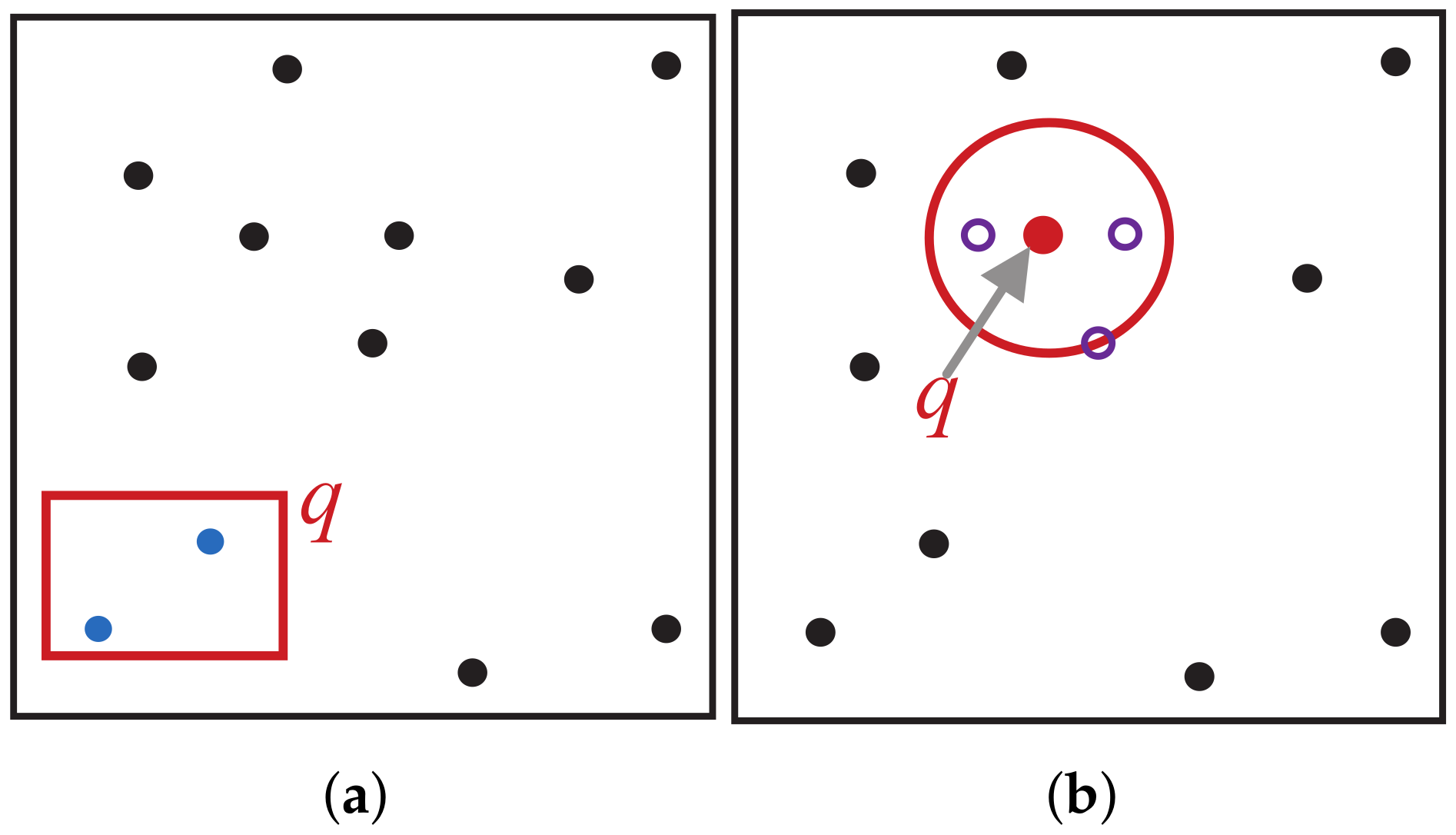
4.1. Spatial Query Framework
- Data partitioning: The space containing the original spatial data is divided into grids, thereby partitioning the original data into subsets corresponding to each grid. When constructing indices using space-filling curves, each grid is traversed non-repetitively according to the rules of the specific curve, and a unique, incrementally assigned identifier is allocated to each traversed grid. This process reduces unordered two-dimensional or higher-dimensional spatial data from a multidimensional space to a one-dimensional space, resulting in a linear sequence.
- Filtering: The input query conditions (query point or query range) are processed to obtain a query identifier using the same rules as those for the original data points. The corresponding number of candidate sets is returned based on the specific query conditions.
- Refining: An exact query is conducted within the candidate set obtained in step (2), significantly reducing the number of query points and thereby shortening the query time.
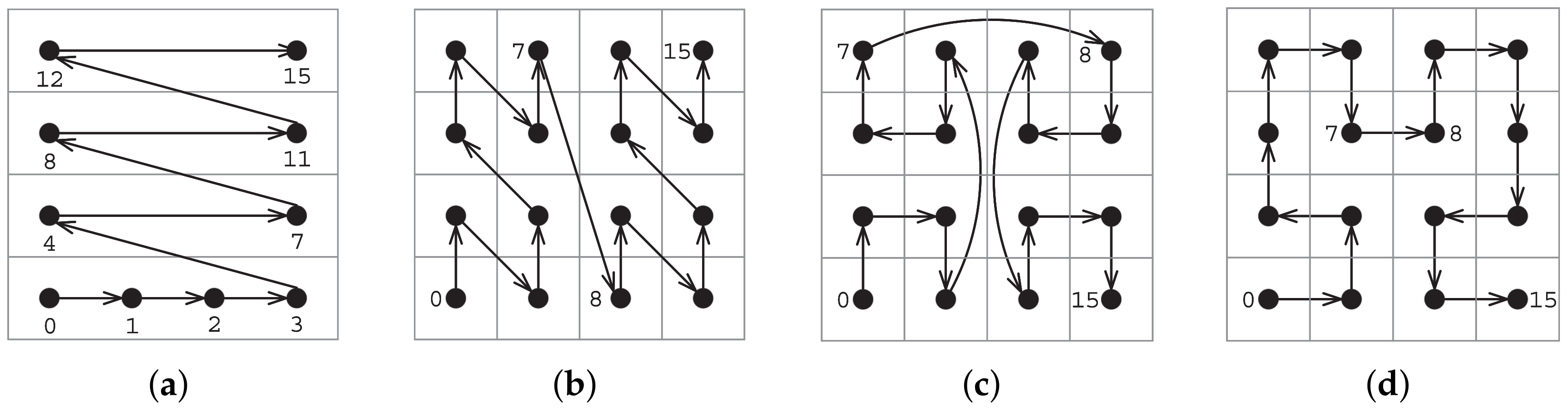
4.2. Encoding Algorithms for Space-Filling Curves
| Algorithm 1 Encoding algorithm for row-wise curve |
|
| Algorithm 2 Encoding algorithm for Z-order curve |
|
| Algorithm 3 Encoding algorithm |
|
| Algorithm 4 Encoding algorithm for Hilbert curve |
|
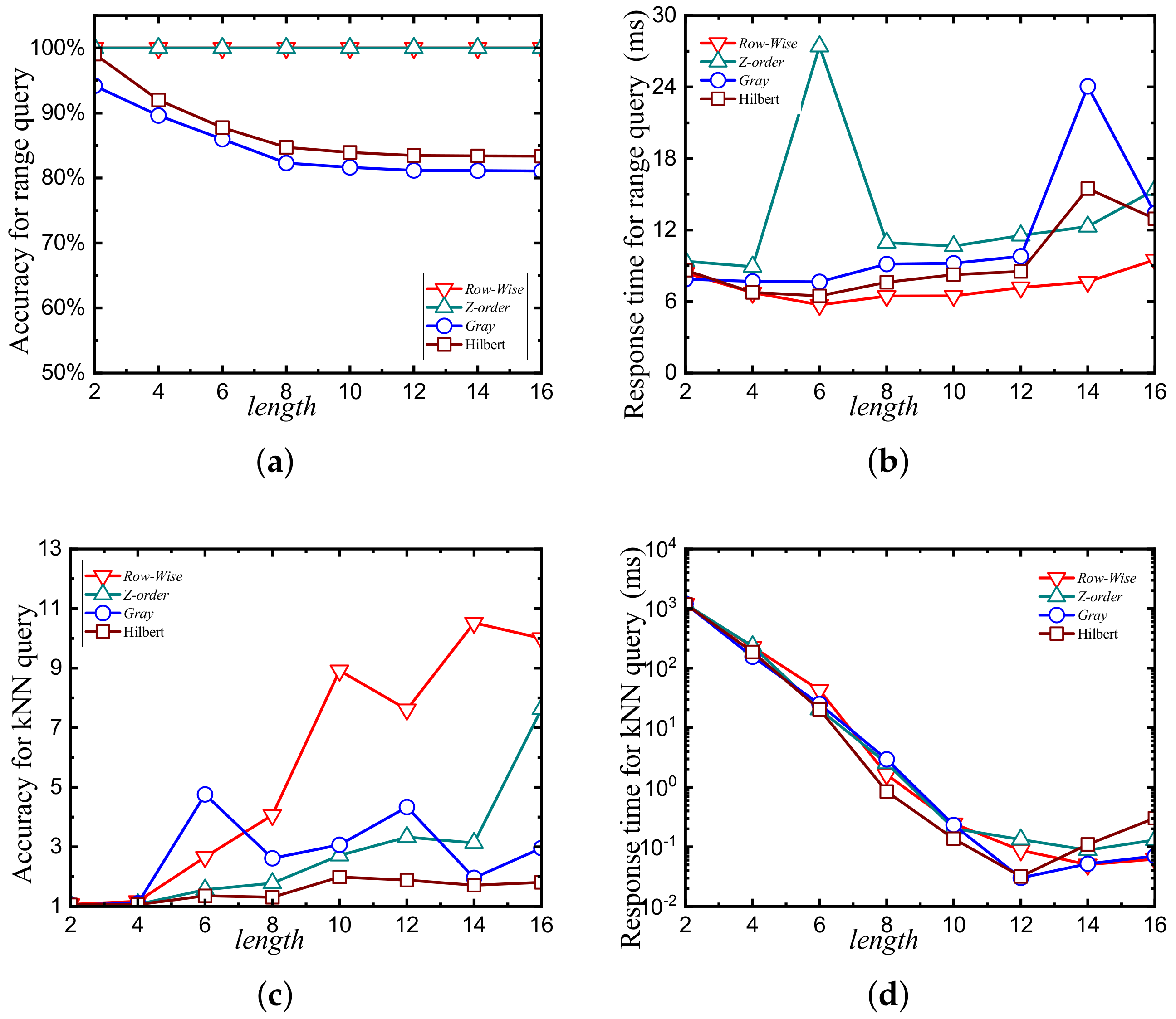
4.3. Experimental Analysis of Space-Filling Curves
5. Construction of OSFC-FSQ
5.1. Secure Index Construction
5.2. Query Mechanism
| Algorithm 5 Trapdoor generation algorithm |
|
| Algorithm 6 Query algorithm in the cloud |
|
| Algorithm 7 Query algorithm on the user side |
|
6. Theoretical Analysis
6.1. Security Analysis
6.2. Complexity Analysis
7. Experimental Evaluation
7.1. Compared Schemes
7.2. Experimental Settings
- The NE dataset contains 123,593 data points, each representing real location information in the northeastern United States.
- The HK dataset contains 1,384,420 data points, each representing real location information in the Hong Kong region.
- The UN dataset is a synthetic dataset with 1,000,000 data points uniformly distributed in a two-dimensional space.
- The GA dataset is also a synthetic dataset with 1,000,000 data points following a Gaussian distribution in a two-dimensional space.
7.3. Effect of
7.4. Preprocessing Performance
7.5. Storage Performance
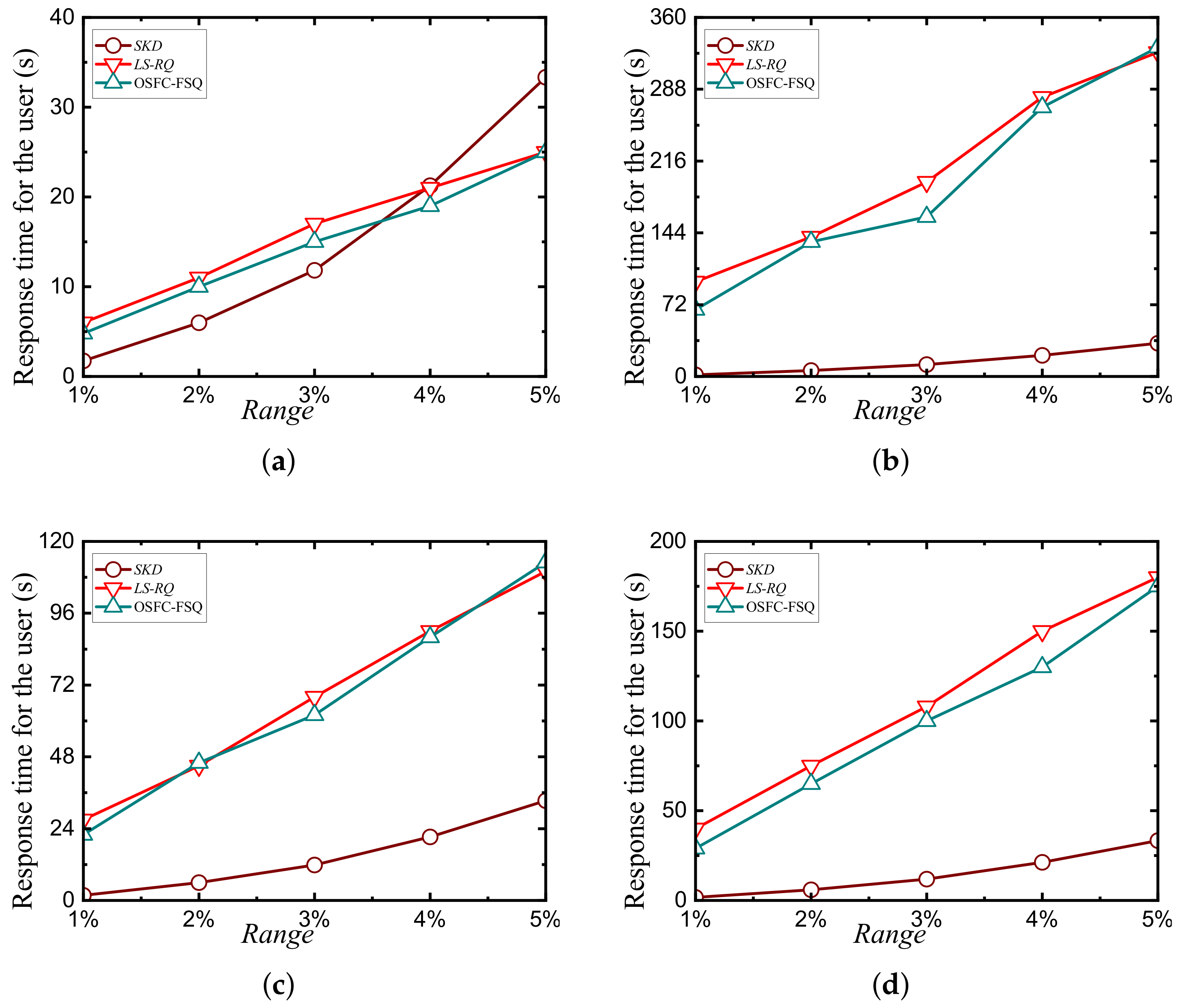
7.6. Query Performance and Comparison
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ART | Average response time |
| kNN | k-nearest neighbor |
| IND-CPA | Indistinguishability under chosen-plaintext attack |
| LSH | Locality-sensitive hashing |
| PRF | Pseudo-random function |
| PRE | Proxy re-encryption |
| UAV | Unmanned aerial vehicle |
| UAVN | Unmanned aerial vehicle network |
References
- Hu, Z.; Zhou, D.; Shen, C.; Wang, T.; Liu, L. Task Offloading Strategy for UAV-Assisted Mobile Edge Computing with Covert Transmission. Electronics 2025, 14, 446. [Google Scholar] [CrossRef]
- Singh, S.; Jeong, Y.S.; Park, J.H. A survey on cloud computing security: Issues, threats, and solutions. J. Netw. Comput. Appl. 2016, 75, 200–222. [Google Scholar] [CrossRef]
- Zolfaghari, B.; Abbasmollaei, M.; Hajizadeh, F.; Yanai, N.; Bibak, K. Secure UAV (Drone) and the Great Promise of AI. ACM Comput. Surv. 2024, 56, 1–37. [Google Scholar] [CrossRef]
- He, Y.; Huang, F.; Wang, D.; Chen, B.; Li, T.; Zhang, R. Performance Analysis and Optimization Design of AAV-Assisted Vehicle Platooning in NOMA-Enhanced Internet of Vehicles. IEEE Trans. Intell. Transp. Syst. 2025, 1–10. [Google Scholar] [CrossRef]
- Karmakar, R.; Kaddoum, G.; Akhrif, O. IntSHU: A Security-Enabled Intelligent Soft Handover Approach for UAV-Aided 5G and Beyond. IEEE Trans. Cogn. Commun. Netw. 2025, 1. [Google Scholar] [CrossRef]
- Wu, W.; Shi, H. Pairing-Free Searchable Encryption for Enhancing Security Against Frequency Analysis Attacks. Electronics 2025, 14, 552. [Google Scholar] [CrossRef]
- Song, D.X.; Wagner, D.; Perrig, A. Practical techniques for searches on encrypted data. In Proceedings of the 2000 IEEE Symposium on Security and Privacy, S&P 2000, Berkeley, CA, USA, 14–17 May 2000; pp. 44–55. [Google Scholar] [CrossRef]
- Khoshgozaran, A.; Shahabi, C. Blind Evaluation of Nearest Neighbor Queries Using Space Transformation to Preserve Location Privacy. In Proceedings of the Advances in Spatial and Temporal Databases; Papadias, D., Zhang, D., Kollios, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 239–257. [Google Scholar] [CrossRef]
- Peng, Y.; Wang, L.; Cui, J.; Liu, X.; Li, H.; Ma, J. LS-RQ: A lightweight and forward-secure range query on geographically encrypted data. IEEE Trans. Dependable Secur. Comput. 2022, 9, 388–401. [Google Scholar] [CrossRef]
- Gaede, V.; Günther, O. Multidimensional access methods. ACM Comput. Surv. 1998, 30, 170–231. [Google Scholar] [CrossRef]
- Boneh, D.; Waters, B. Conjunctive, Subset, and Range Queries on Encrypted Data. In Proceedings of the Theory of Cryptography; Vadhan, S.P., Ed.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 535–554. [Google Scholar] [CrossRef]
- Gay, R.; Méaux, P.; Wee, H. Predicate Encryption for Multi-dimensional Range Queries from Lattices. In Proceedings of the Public-Key Cryptography–PKC 2015; Katz, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 752–776. [Google Scholar] [CrossRef]
- Yang, W.; Xu, Y.; Nie, Y.; Shen, Y.; Huang, L. TRQED: Secure and Fast Tree-Based Private Range Queries over Encrypted Cloud. In Proceedings of the Database Systems for Advanced Applications; Pei, J., Manolopoulos, Y., Sadiq, S., Li, J., Eds.; Springer: Cham, Switzerland, 2018; pp. 130–146. [Google Scholar] [CrossRef]
- Bösch, C.; Hartel, P.; Jonker, W.; Peter, A. A Survey of Provably Secure Searchable Encryption. ACM Comput. Surv. 2014, 47, 18:1–18:51. [Google Scholar] [CrossRef]
- Yiu, M.L.; Ghinita, G.; Jensen, C.S.; Kalnis, P. Outsourcing Search Services on Private Spatial Data. In Proceedings of the 2009 IEEE 25th International Conference on Data Engineering, Shanghai, China, 29 March–2 April 2009; pp. 1140–1143. [Google Scholar] [CrossRef]
- Demertzis, I.; Papadopoulos, S.; Papapetrou, O.; Deligiannakis, A.; Garofalakis, M. Practical Private Range Search Revisited. In Proceedings of the 2016 International Conference on Management of Data, SIGMOD ’16, New York, NY, USA, 20–22 June 2016; pp. 185–198. [Google Scholar] [CrossRef]
- Cui, N.; Yang, X.; Wang, B.; Geng, J.; Li, J. Secure range query over encrypted data in outsourced environments. World Wide Web 2020, 23, 491–517. [Google Scholar] [CrossRef]
- Bost, R.; Minaud, B.; Ohrimenko, O. Forward and Backward Private Searchable Encryption from Constrained Cryptographic Primitives. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, CCS ’17, New York, NY, USA, 30 October–3 November 2017; pp. 1465–1482. [Google Scholar] [CrossRef]
- Sun, S.F.; Yuan, X.; Liu, J.K.; Steinfeld, R.; Sakzad, A.; Vo, V.; Nepal, S. Practical Backward-Secure Searchable Encryption from Symmetric Puncturable Encryption. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, CCS ’18, New York, NY, USA, 15–19 October 2018; pp. 763–780. [Google Scholar] [CrossRef]
- Goldreich, O.; Goldwasser, S.; Micali, S. How to construct random functions. J. ACM 1986, 33, 792–807. [Google Scholar] [CrossRef]
- Qin, Z.; Xiong, H.; Wu, S.; Batamuliza, J. A Survey of Proxy Re-Encryption for Secure Data Sharing in Cloud Computing. IEEE Trans. Serv. Comput. 2016, 1. [Google Scholar] [CrossRef]
- Tao, Y.; Yi, K.; Sheng, C.; Kalnis, P. Quality and efficiency in high dimensional nearest neighbor search. In Proceedings of the 2009 ACM SIGMOD International Conference on Management of Data, SIGMOD ’09, New York, NY, USA, 29 June–2 July 2009; pp. 563–576. [Google Scholar] [CrossRef]
- Liu, Y.; Cui, J.; Huang, Z.; Li, H.; Shen, H.T. SK-LSH: An efficient index structure for approximate nearest neighbor search. Proc. VLDB Endow. 2014, 7, 745–756. [Google Scholar] [CrossRef]
- Huang, Y.; Lu, F.; Sang, X.; Hu, B.; Tao, J. Precise Epidemic Control based on GeoHash. In Proceedings of the 2022 9th International Conference on Dependable Systems and Their Applications (DSA), Wulumuqi, China, 4–5 August 2022; pp. 1040–1048. [Google Scholar] [CrossRef]
- Jiang, B.; Zhou, W.; Han, H. Storage and Management of Ship Position Based on Geographic Grid Coding and Its Efficiency Analysis in Neighborhood Search—A Case Study of Shipwreck Rescue and Google S2. Appl. Sci. 2024, 14, 1115. [Google Scholar] [CrossRef]
- Kim, K.S.; Kim, M.; Lee, D.; Park, J.H.; Kim, W.H. Forward Secure Dynamic Searchable Symmetric Encryption with Efficient Updates. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, CCS ’17, New York, NY, USA, 30 October–3 November 2017; pp. 1449–1463. [Google Scholar] [CrossRef]
- Ghareh Chamani, J.; Papadopoulos, D.; Papamanthou, C.; Jalili, R. New Constructions for Forward and Backward Private Symmetric Searchable Encryption. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, CCS ’18, New York, NY, USA, 15–19 October 2018; pp. 1038–1055. [Google Scholar] [CrossRef]
- Amjad, G.; Kamara, S.; Moataz, T. Forward and Backward Private Searchable Encryption with SGX. In Proceedings of the 12th European Workshop on Systems Security, EuroSec ’19, New York, NY, USA, 25–28 March 2019. [Google Scholar] [CrossRef]
- Grubbs, P.; Lacharite, M.S.; Minaud, B.; Paterson, K.G. Pump up the Volume: Practical Database Reconstruction from Volume Leakage on Range Queries. In Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, CCS ’18, New York, NY, USA, 15–19 October 2018; pp. 315–331. [Google Scholar] [CrossRef]
- Grubbs, P.; Lacharité, M.S.; Minaud, B.; Paterson, K.G. Learning to Reconstruct: Statistical Learning Theory and Encrypted Database Attacks. In Proceedings of the 2019 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 20–22 May 2019; pp. 1067–1083. [Google Scholar] [CrossRef]
- Yiu, M.L.; Ghinita, G.; Jensen, C.S.; Kalnis, P. Enabling search services on outsourced private spatial data. VLDB J. 2010, 19, 363–384. [Google Scholar] [CrossRef]
- Furukawa, J. Request-Based Comparable Encryption. In European Symposium on Research in Computer Security (ESORICS); Springer: Berlin/Heidelberg, Germany, 2013; pp. 129–146. [Google Scholar] [CrossRef]
- Nuñez, D.; Agudo, I.; Lopez, J. NTRUReEncrypt: An Efficient Proxy Re-Encryption Scheme Based on NTRU. In Proceedings of the 10th ACM Symposium on Information, Computer and Communications Security, ASIA CCS ’15, New York, NY, USA, 14–17 April 2015; pp. 179–189. [Google Scholar] [CrossRef]


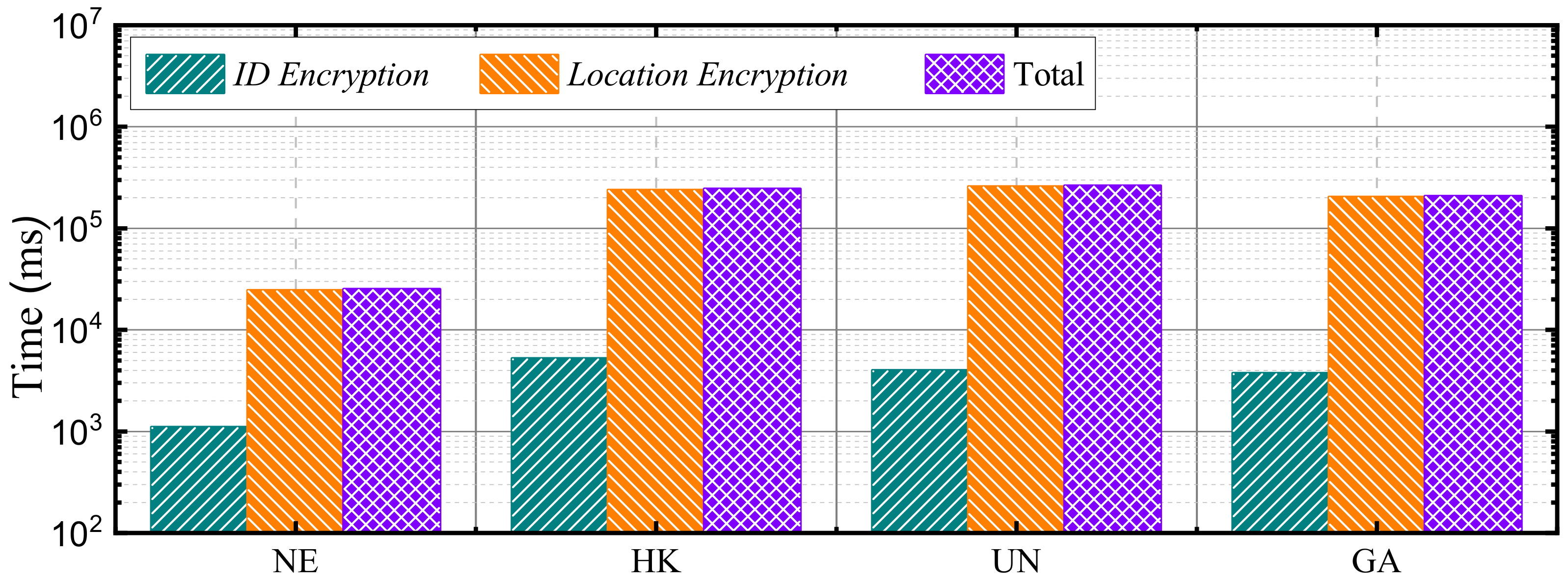


| Parameter | Meaning | Value |
|---|---|---|
| The number of bits in the space-filling curve encoding for each data point | 12 | |
| The security parameter | 160 bits | |
| The size of public and private keys in PRE | 256 bits |
| Dataset | No. of Locations | No. of Fake Locations | No. of Encrypted Locations | Storage Overhead (GB) |
|---|---|---|---|---|
| NE | 123,593 | 13,687 | 137,283 | 0.605 |
| HK | 1,384,420 | 208,084 | 1,592,504 | 7.018 |
| GA | 1,000,000 | 249,638 | 1,249,638 | 5.507 |
| UN | 1,000,000 | 642,496 | 1,642,496 | 7.239 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, Z.; Li, X.; Peng, Y.; Huang, J. Optimized Space-Filling Curve-Driven Forward-Secure Range Query on Location-Related Data for Unmanned Aerial Vehicle Networks. Electronics 2025, 14, 1978. https://doi.org/10.3390/electronics14101978
Lv Z, Li X, Peng Y, Huang J. Optimized Space-Filling Curve-Driven Forward-Secure Range Query on Location-Related Data for Unmanned Aerial Vehicle Networks. Electronics. 2025; 14(10):1978. https://doi.org/10.3390/electronics14101978
Chicago/Turabian StyleLv, Zhen, Xin Li, Yanguo Peng, and Jin Huang. 2025. "Optimized Space-Filling Curve-Driven Forward-Secure Range Query on Location-Related Data for Unmanned Aerial Vehicle Networks" Electronics 14, no. 10: 1978. https://doi.org/10.3390/electronics14101978
APA StyleLv, Z., Li, X., Peng, Y., & Huang, J. (2025). Optimized Space-Filling Curve-Driven Forward-Secure Range Query on Location-Related Data for Unmanned Aerial Vehicle Networks. Electronics, 14(10), 1978. https://doi.org/10.3390/electronics14101978






