T3OMVP: A Transformer-Based Time and Team Reinforcement Learning Scheme for Observation-Constrained Multi-Vehicle Pursuit in Urban Area
Abstract
:1. Introduction
- The MVP game in the urban environment is defined as the observation-constrained multi-vehicle pursuit (OMVP) problem with the occlusion of buildings to each pursuing vehicle.
- The OMVP scheme is proposed to address the OMVP problem using Dec-POMDPs and reinforcement learning. The OMVP introduces the transformer block to deal with the observation sequences to realize the multi-vehicle cooperation without a policy decoupling strategy.
- A novel low-cost and light-weight MVP simulation environment is constructed to verify the performance of the OMVP scheme. Compared with large-scale game environments, this simulation environment can improve the training speed of reinforcement learning. All source codes are provided on GitHub (https://github.com/its-ant-bupt/T3OMVP) (last accessed on 27 February 2022).
2. Multi-Vehicle Pursuit
2.1. Problem Statement
2.2. Dec-POMDP
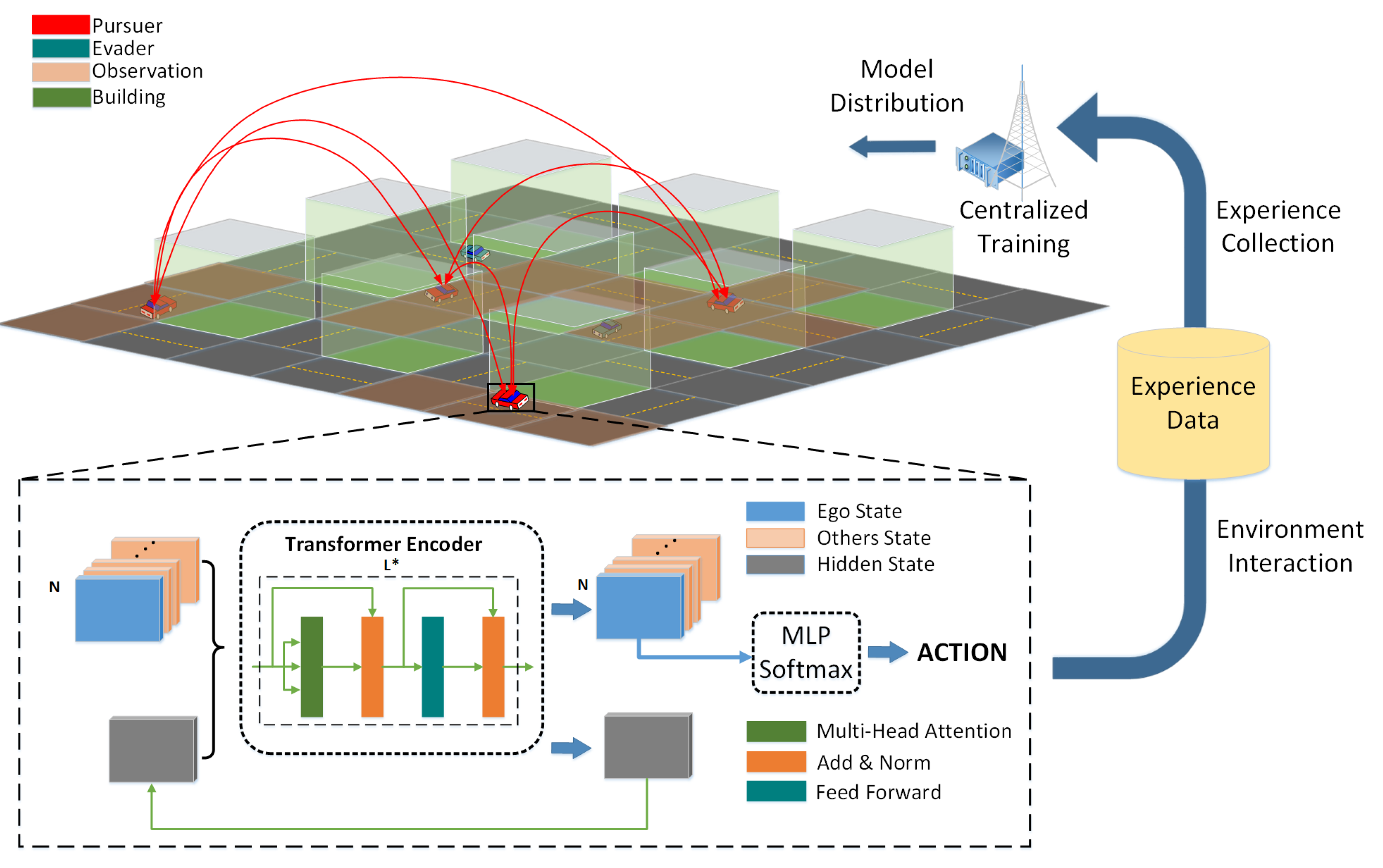
3. OMVP Scheme
3.1. State, Action, and Reward
3.2. Centralized Training with Decentralized Execution
3.3. Observation-Constrained Multi-Vehicle Pursuit
3.3.1. Monotonic Value Function Factorization
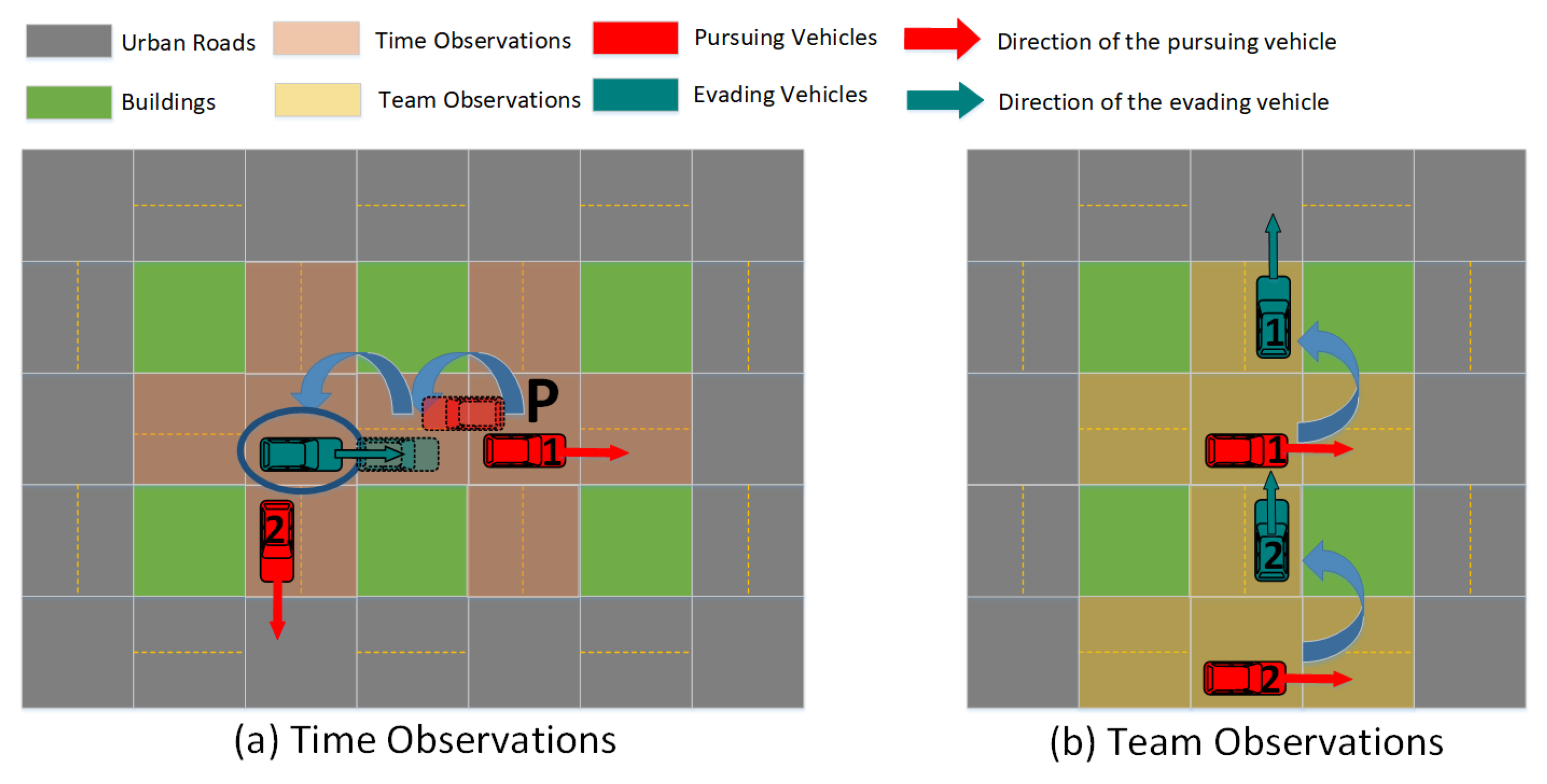
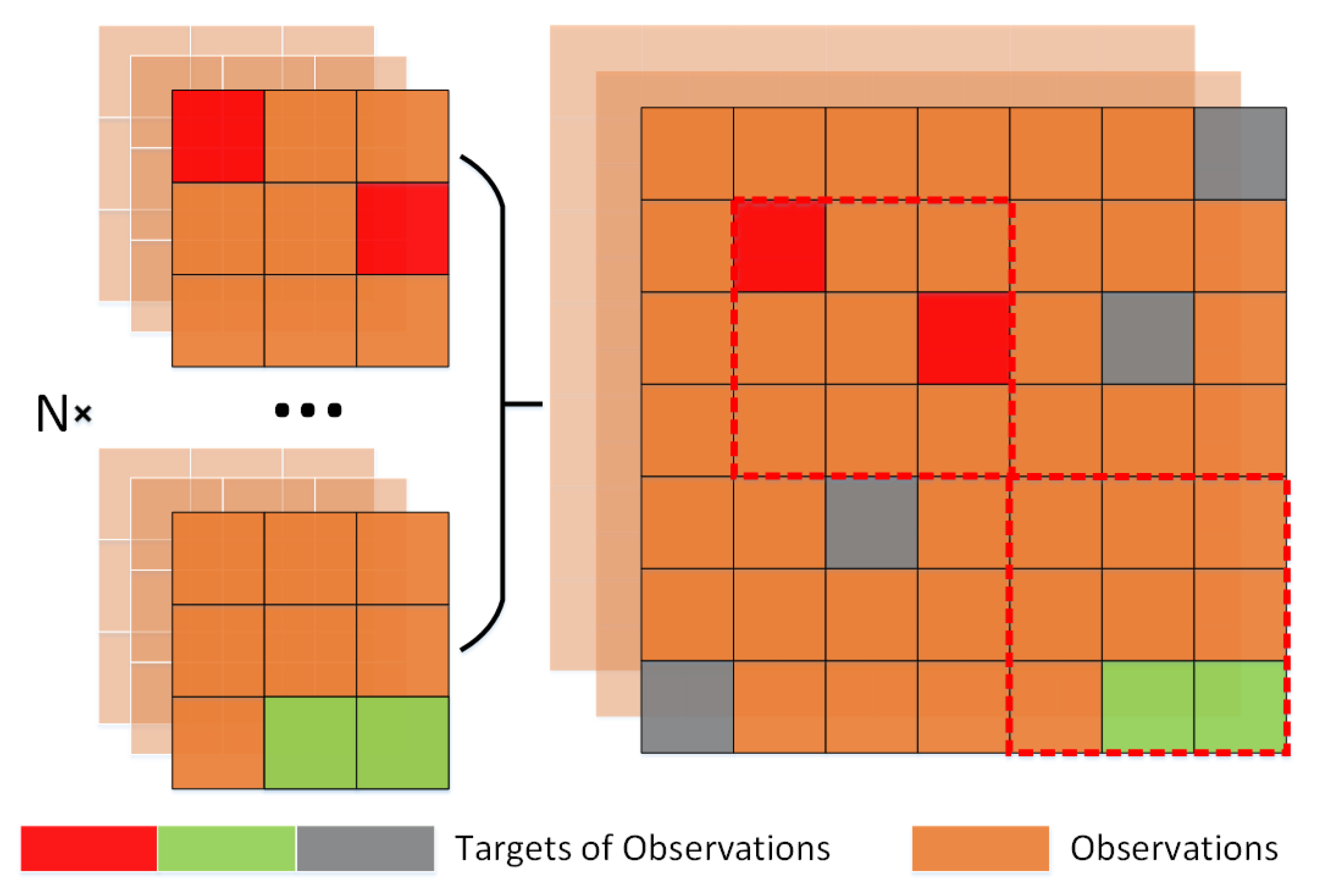
3.3.2. Observations Sequence
Time Observations
Team Observations
-
3.3.3. Transformer-Based -
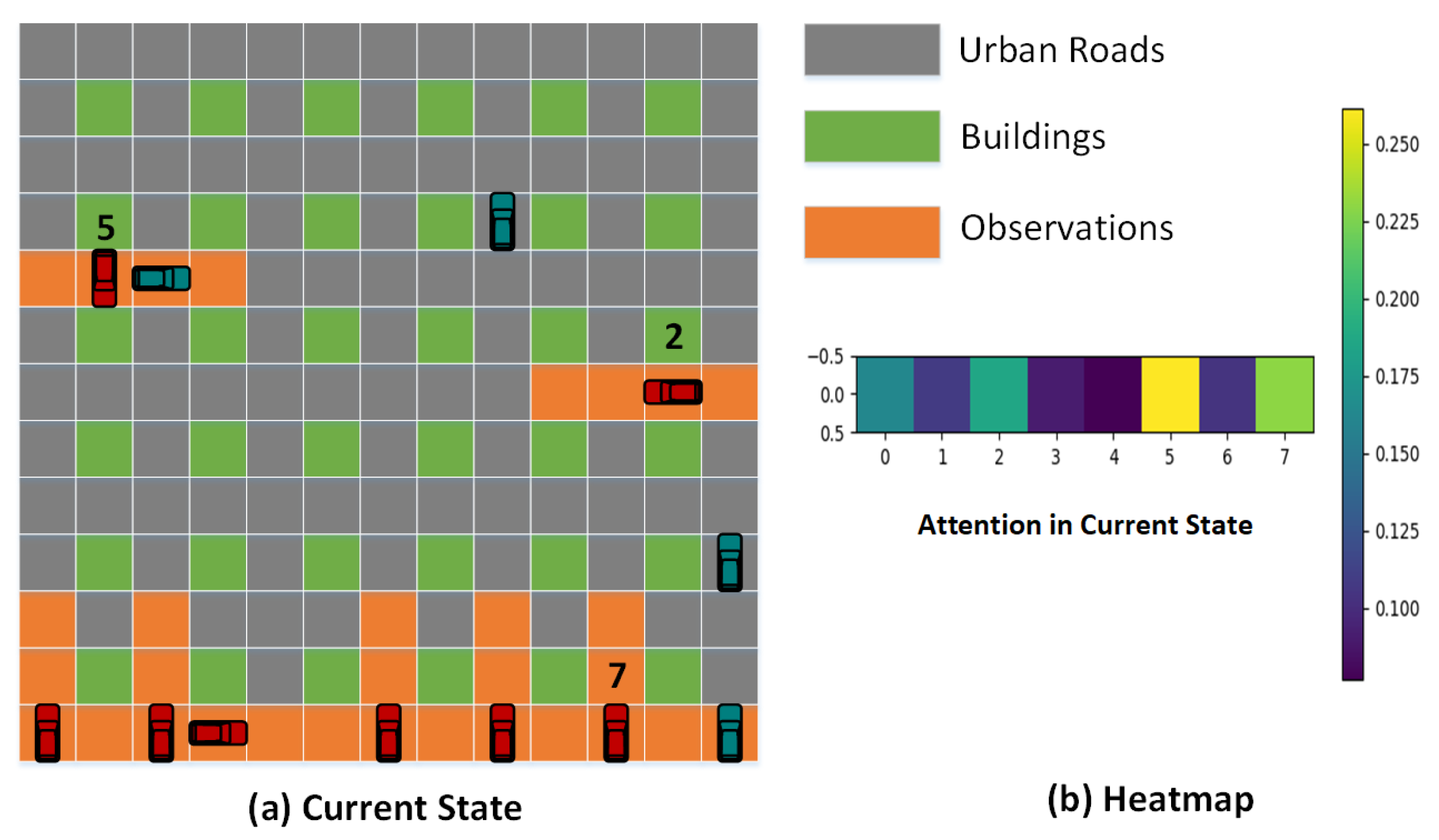
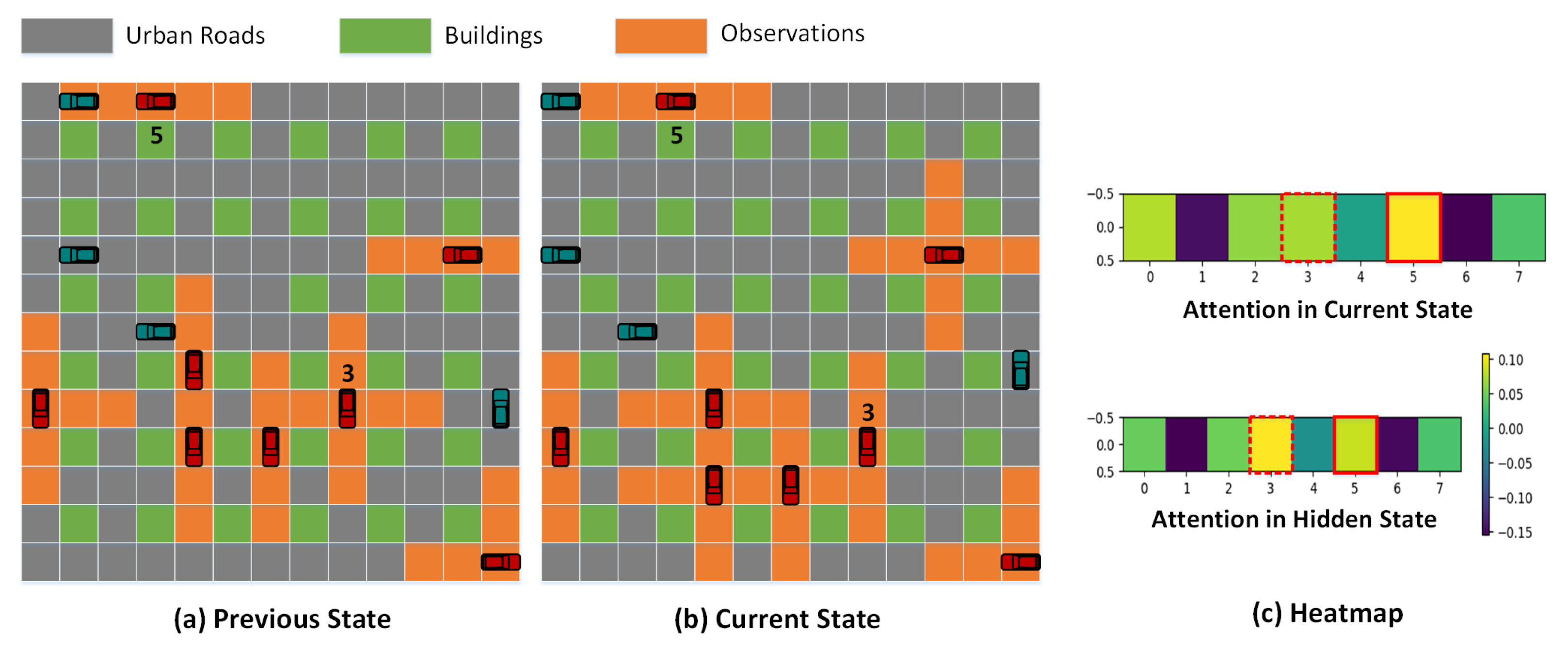
Self-Attention Mechanism
Transformer in Time and Team Observations
Decision-Making and Training Process
| Algorithm 1:OMVP On-line training |
 |
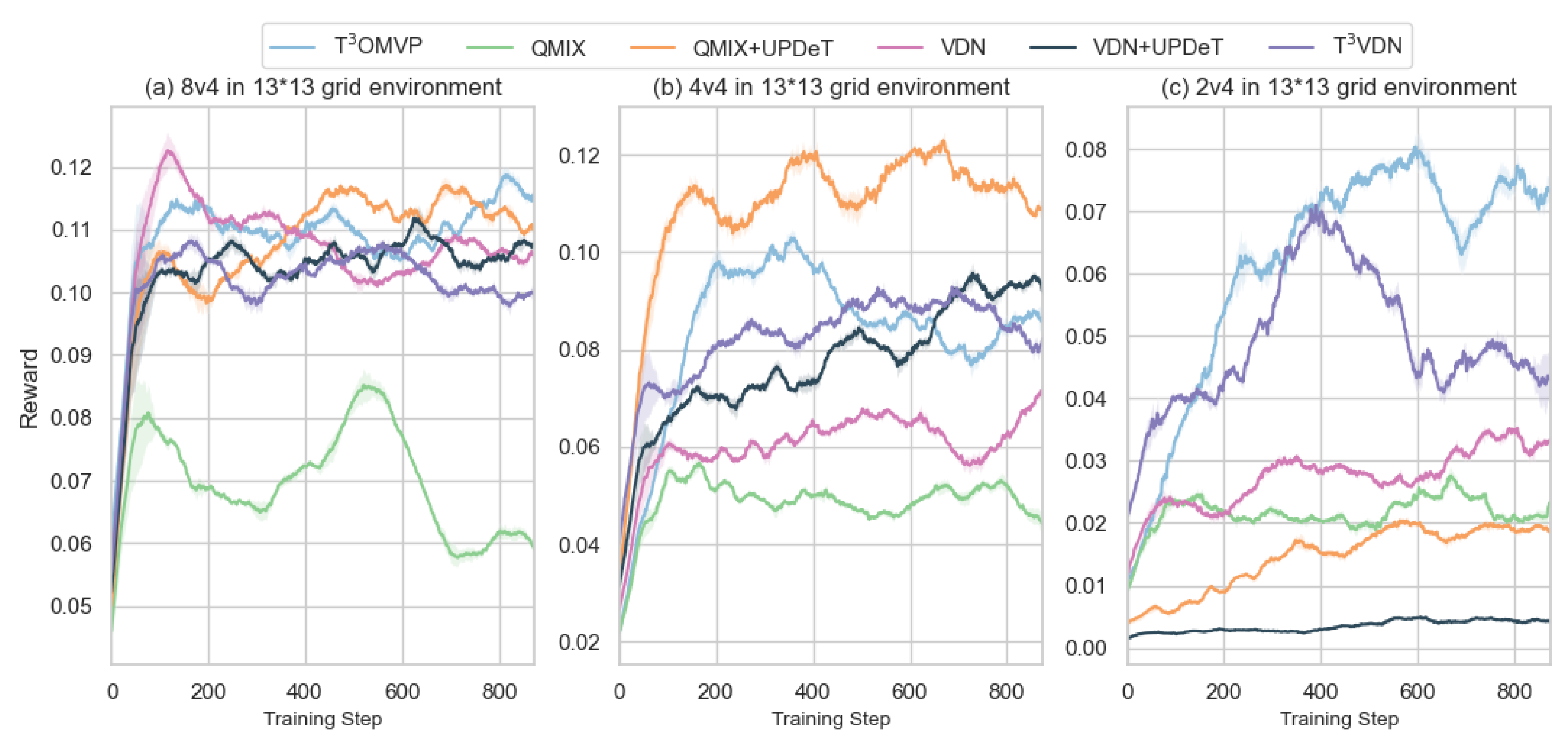
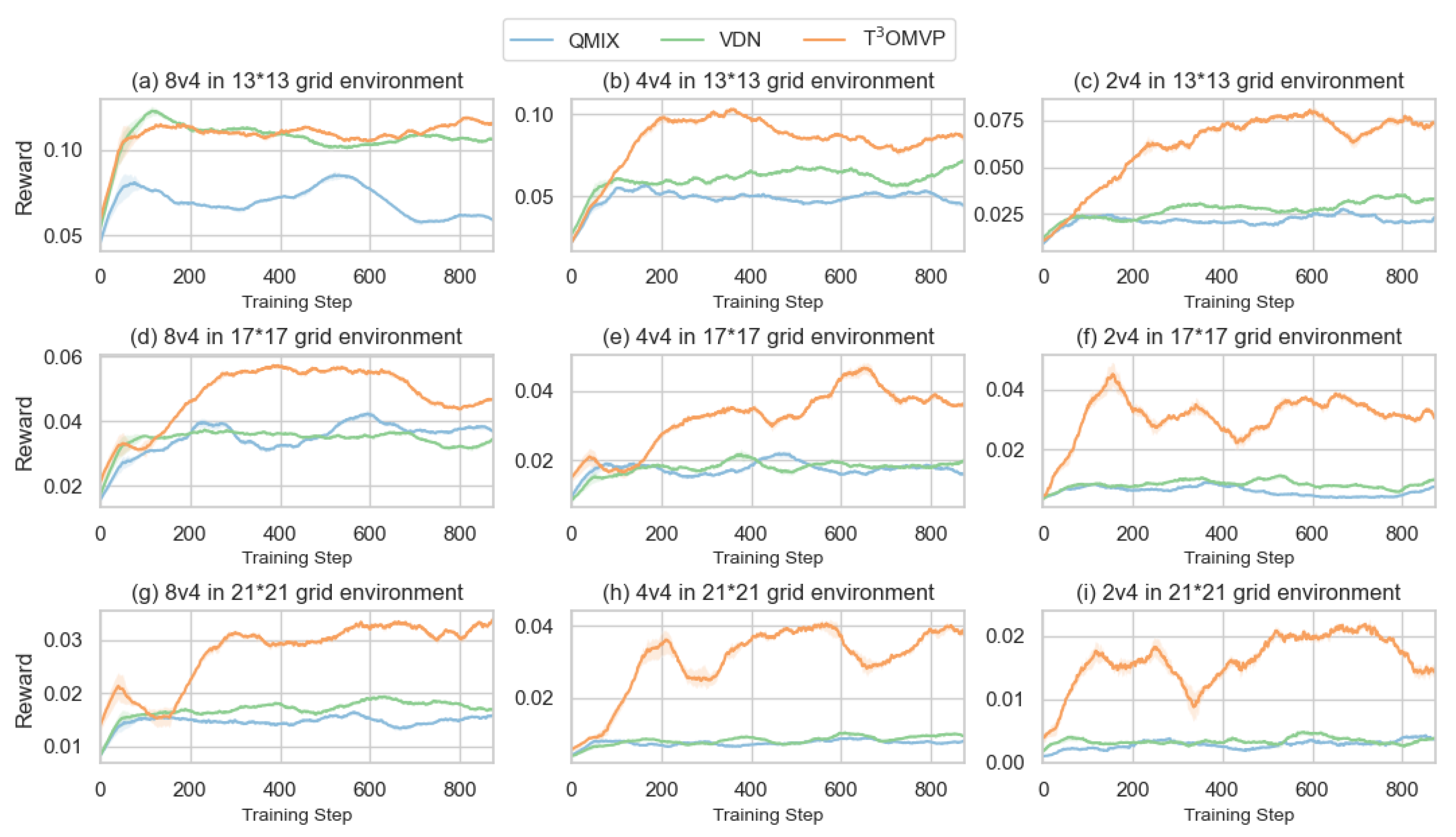
4. Results
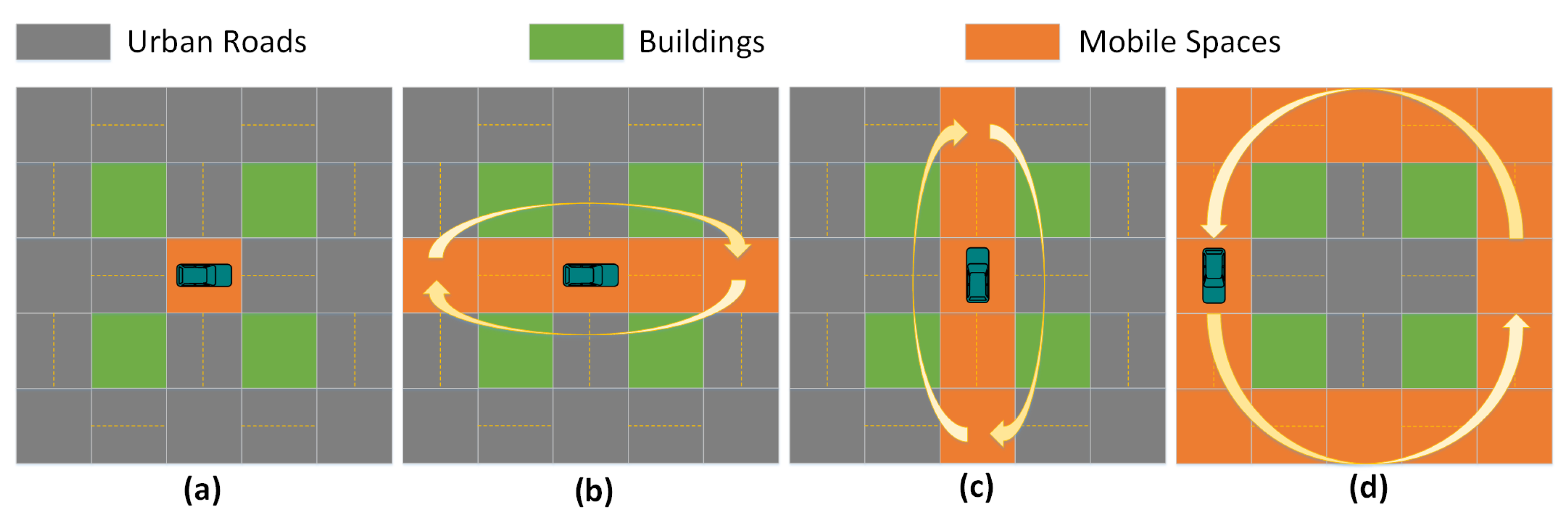
4.1. Evader Strategy
4.2. -Greedy
4.3. Simulation Settings
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| IoVs | Internet of Vehicles |
| MDP | Markov Decision Processes |
| MVP | Multi-Vehicle Pursuit |
| MARL | Multi-agent Reinforcement Learning |
| CTDE | Centralized Training with Decentralized Execution |
| OMVP | Observation-constrained Multi-Vehicle Pursuit |
| OMVP | Transformer-based Time and Team Reinforcement Learning Scheme for OMVP |
| Dec-POMDP | Decentralized Partially Observed Markov Decision Processes |
References
- Bagga, P.; Das, A.K.; Wazid, M.; Rodrigues, J.J.P.C.; Choo, K.K.R.; Park, Y. On the Design of Mutual Authentication and Key Agreement Protocol in Internet of Vehicles-Enabled Intelligent Transportation System. IEEE Trans. Veh. Technol. 2021, 70, 1736–1751. [Google Scholar] [CrossRef]
- Contreras-Castillo, J.; Zeadally, S.; Guerrero-Ibañez, J.A. Internet of Vehicles: Architecture, Protocols, and Security. IEEE Internet Things J. 2018, 5, 3701–3709. [Google Scholar] [CrossRef]
- Wu, T.; Jiang, M.; Han, Y.; Yuan, Z.; Li, X.; Zhang, L. A traffic-aware federated imitation learning framework for motion control at unsignalized intersections with internet of vehicles. Electronics 2021, 10, 3050. [Google Scholar] [CrossRef]
- Feng, S.; Xi, J.; Gong, C.; Gong, J.; Hu, S.; Ma, Y. A collaborative decision making approach for multi-unmanned combat vehicles based on the behaviour tree. In Proceedings of the 2020 3rd International Conference on Unmanned Systems (ICUS), Harbin, China, 27–28 November 2020; pp. 395–400. [Google Scholar]
- Wu, T.; Jiang, M.; Zhang, L. Cooperative multiagent deep deterministic policy gradient (comaddpg) for intelligent connected transportation with unsignalized intersection. Math. Probl. Eng. 2020, 2020, 1820527. [Google Scholar] [CrossRef]
- Haydari, A.; Yılmaz, Y. Deep Reinforcement Learning for Intelligent Transportation Systems: A Survey. IEEE Trans. Intell. Transp. Syst. 2022, 23, 11–32. [Google Scholar] [CrossRef]
- Yuan, Y.; Zheng, G.; Wong, K.K.; Letaief, K.B. Meta-Reinforcement Learning Based Resource Allocation for Dynamic V2X Communications. IEEE Trans. Veh. Technol. 2021, 70, 8964–8977. [Google Scholar] [CrossRef]
- Cui, Y.; Du, L.; Wang, H.; Wu, D.; Wang, R. Reinforcement Learning for Joint Optimization of Communication and Computation in Vehicular Networks. IEEE Trans. Veh. Technol. 2021, 70, 13062–13072. [Google Scholar] [CrossRef]
- New York City Police Department. Patrol Guide. Section: Tactical Operations. Procedure No: 221-15. 2016. Available online: https://www1.nyc.gov/assets/ccrb/downloads/pdf/investigations_pdf/pg221-15-vehicle-pursuits.pdf (accessed on 27 February 2022).
- Garcia, E.; Casbeer, D.W.; Moll, A.V.; Pachter, M. Multiple pursuer multiple evader differential games. IEEE Trans. Autom. Control 2020, 66, 2345–2350. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, W.; Ding, J.; Stipanović, D.M.; Tomlin, C.J. Guaranteed decentralized pursuit-evasion in the plane with multiple pursuers. In Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 4835–4840. [Google Scholar]
- Zhu, Z.-Y.; Liu, C.-L. A novel method combining leader-following control and reinforcement learning for pursuit evasion games of multi-agent systems. In Proceedings of the 2020 16th International Conference on Control, Automation, Robotics and Vision (ICARCV), Shenzhen, China, 13–15 December 2020; pp. 166–171. [Google Scholar]
- Qu, S.; Abouheaf, M.; Gueaieb, W.; Spinello, D. An adaptive fuzzy reinforcement learning cooperative approach for the autonomous control of flock systems. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 8927–8933. [Google Scholar]
- de Souza, C.; Newbury, R.; Cosgun, A.; Castillo, P.; Vidolov, B.; Kulić, D. Decentralized multi-agent pursuit using deep reinforcement learning. IEEE Robot. Autom. Lett. 2021, 6, 4552–4559. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Phan, T.; Belzner, L.; Gabor, T.; Sedlmeier, A.; Ritz, F.; Linnhoff-Popien, C. Resilient multi-agent reinforcement learning with adversarial value decomposition. Proc. Aaai Conf. Artif. Intell. 2021, 35, 11308–11316. [Google Scholar]
- Jiang, M.; Wu, T.; Wang, Z.; Gong, Y.; Zhang, L.; Liu, R.P. A multi-intersection vehicular cooperative control based on end-edge-cloud computing. arXiv 2020, arXiv:2012.00500. [Google Scholar] [CrossRef]
- Peng, Z.; Hui, K.M.; Liu, C.; Zhou, B. Learning to simulate self-driven particles system with coordinated policy optimization. In Proceedings of the Advances in Neural Information Processing Systems, New Orleans, LA, USA, 6–14 December 2021; Volume 34, pp. 10784–10797. [Google Scholar]
- Hu, S.; Zhu, F.; Chang, X.; Liang, X. Updet: Universal multi-agent reinforcement learning via policy decoupling with transformers. arXiv 2021, arXiv:2101.08001. [Google Scholar]
- Rashid, T.; Samvelyan, M.; Schroeder, C.; Farquhar, G.; Foerster, J.; Whiteson, S. Qmix: Monotonic value function factorisation for deep multi-agent reinforcement learning. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 4295–4304. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. arXiv 2017, arXiv:1706.03762v5. [Google Scholar]
- Clevert, D.-A.; Unterthiner, T.; Hochreiter, S. Fast and accurate deep network learning by exponential linear units (elus). arXiv 2015, arXiv:1511.07289. [Google Scholar]
| Parameters | Value |
|---|---|
| Number of episodes E | 40,000 |
| Time step T | 50 |
| Grid space width W | |
| Intersection interval | 1 |
| Number of intersections | |
| Distance of vehicle moves each time | 1 |
| Size of the observation space of the pursuing vehicle | |
| Size of the joint observation space of the pursuing vehicle | |
| Number of evading vehicles | 4 |
| Historical observation length | 5 |
| Hyperparameters | Value |
|---|---|
| Batch size | 32 |
| Memory capacity M | 20,000 |
| Learning rate | |
| Optimizer | Adam |
| Discounted factor | |
| decay | |
| min | |
| Period of update I | 4000 |
| QMIX | |
| Hypernetwork w #1 | |
| Hypernetwork w #final | |
| Hypernetwork b #1 | |
| Output | |
| Transformer Encoder | |
| Transformer depth | 2 |
| Embedding vector length | 250 |
| Number of heads | 5 |
| Sum of Rewards | Grid Space Width | 13 | 17 | 21 |
|---|---|---|---|---|
| QMIX | 3.88 | 1.1775 | 0.76 | |
| 8v4 scenario | OMVP | 4.255 | 1.5175 | 0.9175 |
| Improvement | 9.66% | 28.87% | 20.72% | |
| QMIX | 1.345 | 0.455 | 0.345 | |
| 4v4 scenario | OMVP | 2.115 | 0.88 | 0.475 |
| Improvement | 57.24% | 93.40% | 37.68% | |
| QMIX | 0.51 | 0.16 | 0.09 | |
| 2v4 scenario | OMVP | 0.86 | 0.33 | 0.18 |
| Improvement | 68.62% | 106.25% | 100% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Z.; Wu, T.; Wang, Q.; Yang, Y.; Li, L.; Zhang, L. T3OMVP: A Transformer-Based Time and Team Reinforcement Learning Scheme for Observation-Constrained Multi-Vehicle Pursuit in Urban Area. Electronics 2022, 11, 1339. https://doi.org/10.3390/electronics11091339
Yuan Z, Wu T, Wang Q, Yang Y, Li L, Zhang L. T3OMVP: A Transformer-Based Time and Team Reinforcement Learning Scheme for Observation-Constrained Multi-Vehicle Pursuit in Urban Area. Electronics. 2022; 11(9):1339. https://doi.org/10.3390/electronics11091339
Chicago/Turabian StyleYuan, Zheng, Tianhao Wu, Qinwen Wang, Yiying Yang, Lei Li, and Lin Zhang. 2022. "T3OMVP: A Transformer-Based Time and Team Reinforcement Learning Scheme for Observation-Constrained Multi-Vehicle Pursuit in Urban Area" Electronics 11, no. 9: 1339. https://doi.org/10.3390/electronics11091339
APA StyleYuan, Z., Wu, T., Wang, Q., Yang, Y., Li, L., & Zhang, L. (2022). T3OMVP: A Transformer-Based Time and Team Reinforcement Learning Scheme for Observation-Constrained Multi-Vehicle Pursuit in Urban Area. Electronics, 11(9), 1339. https://doi.org/10.3390/electronics11091339






