Application of Fractional-Order PI Controllers and Neuro-Fuzzy PWM Technique to Multi-Rotor Wind Turbine Systems
Abstract
:1. Introduction
- Numerical simulation results are presented to validate the advantages of the proposed DVC method.
- The PI controller is among the most important and most widely applied controllers in the field of control of electric generators. However, for this kind of controller, several defects can be improved or eliminated by using artificial intelligence or fractional calculus. It emerges that the proposed fractional-order PI controller is more convenient than the classic PI controller.
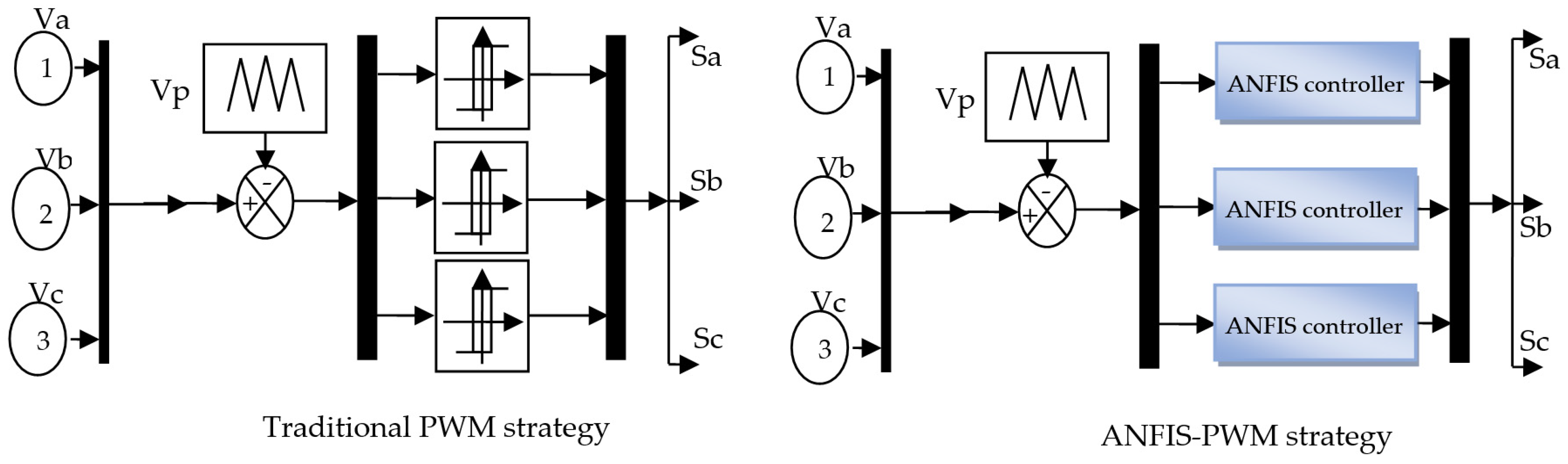
- The IPWM technique is proposed as a better solution than the classical PWM method to control the inverter to obtain a signal at its output with a fixed frequency.
- The proposed DVC method is a development of [40] because it gives a new design and optimum solution to control an asynchronous generator using the method based on the new FOPI controller, whereas the classic DVC method is based on the PI controller, which makes the current quality lower. For the same reason, the proposed DVC method has a higher probability of obtaining a higher quality of electric current and active power than the previous solution.
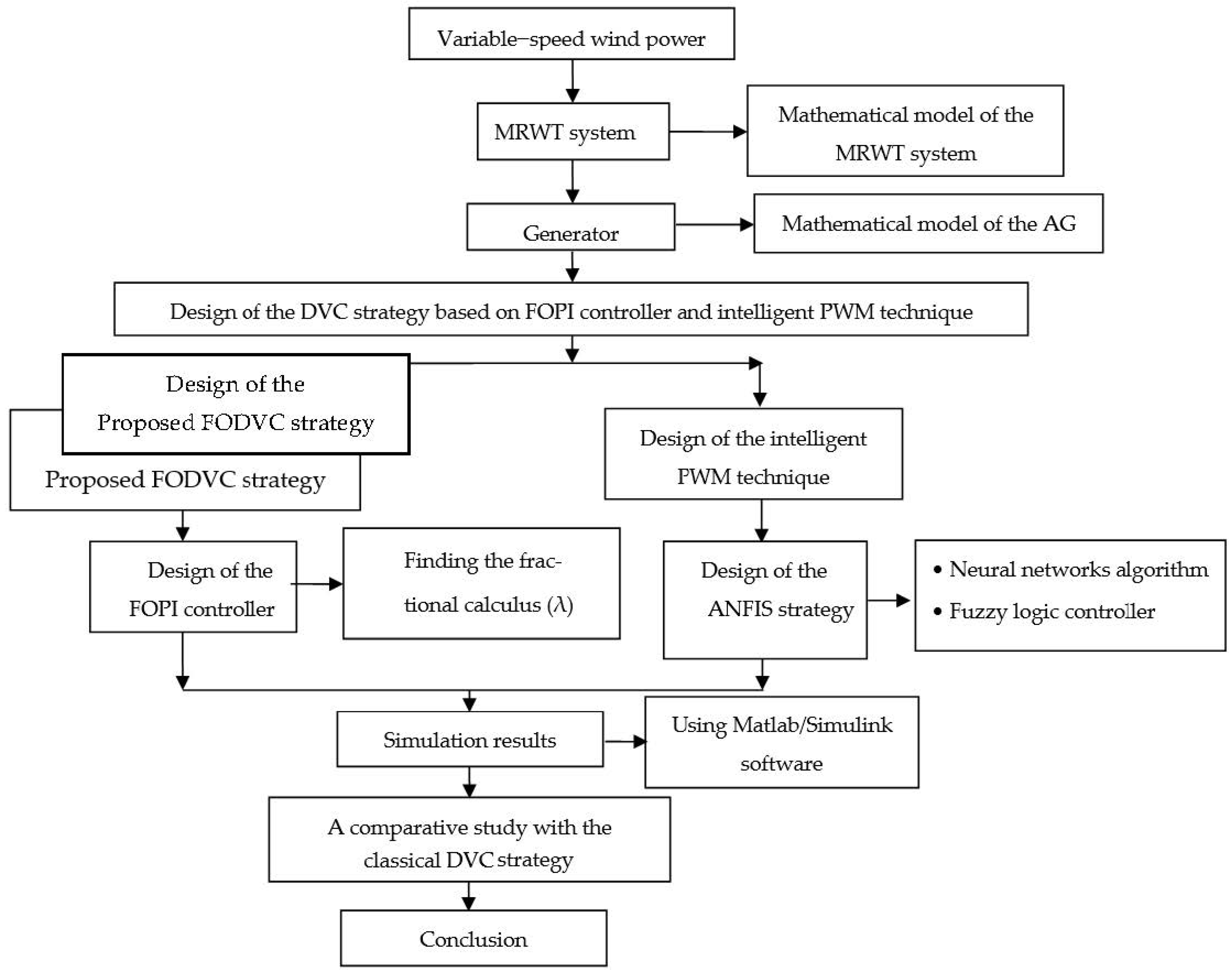
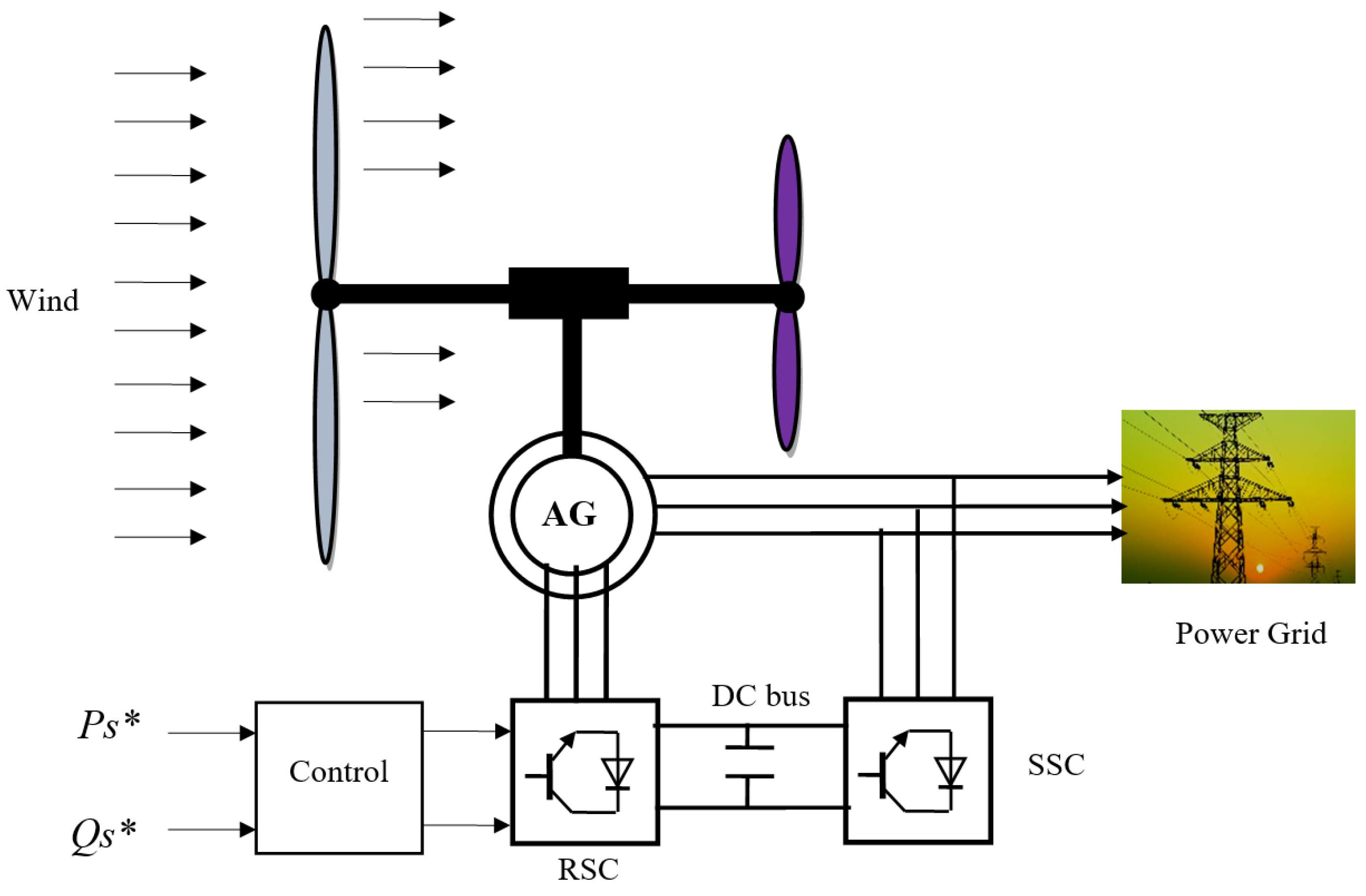
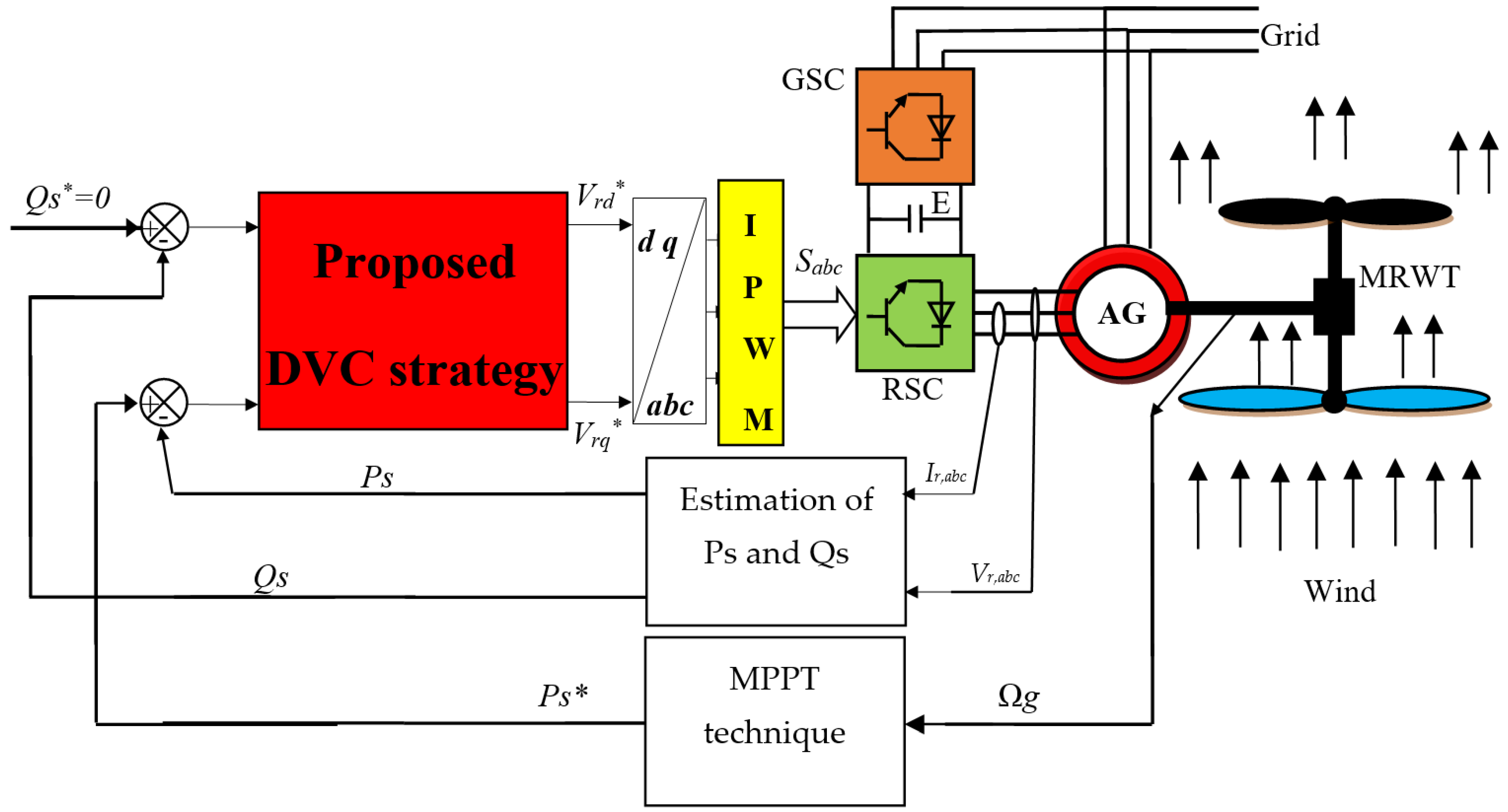
2. Multi-Rotor Wind Turbine System
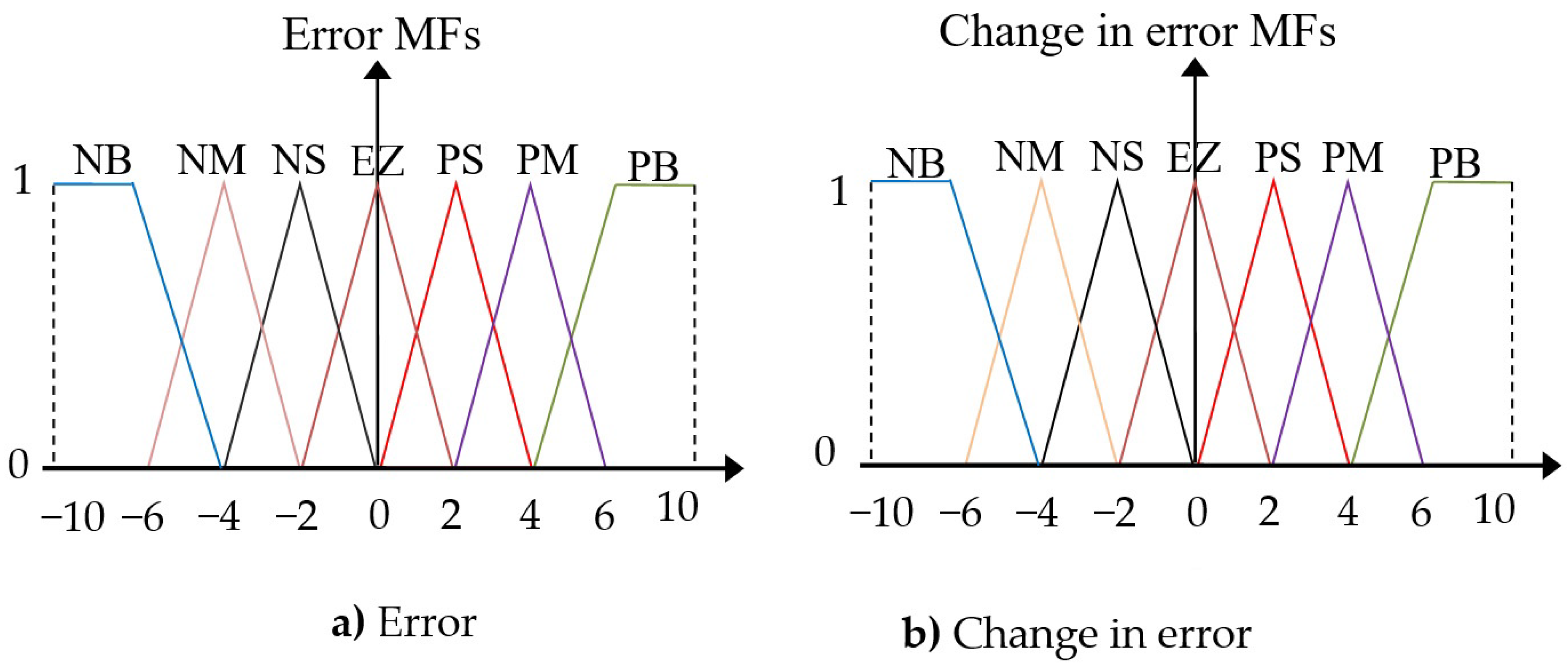
3. Proposed IPWM Technique
4. Proposed Fractional-Order PI Controller
5. Direct Vector Control
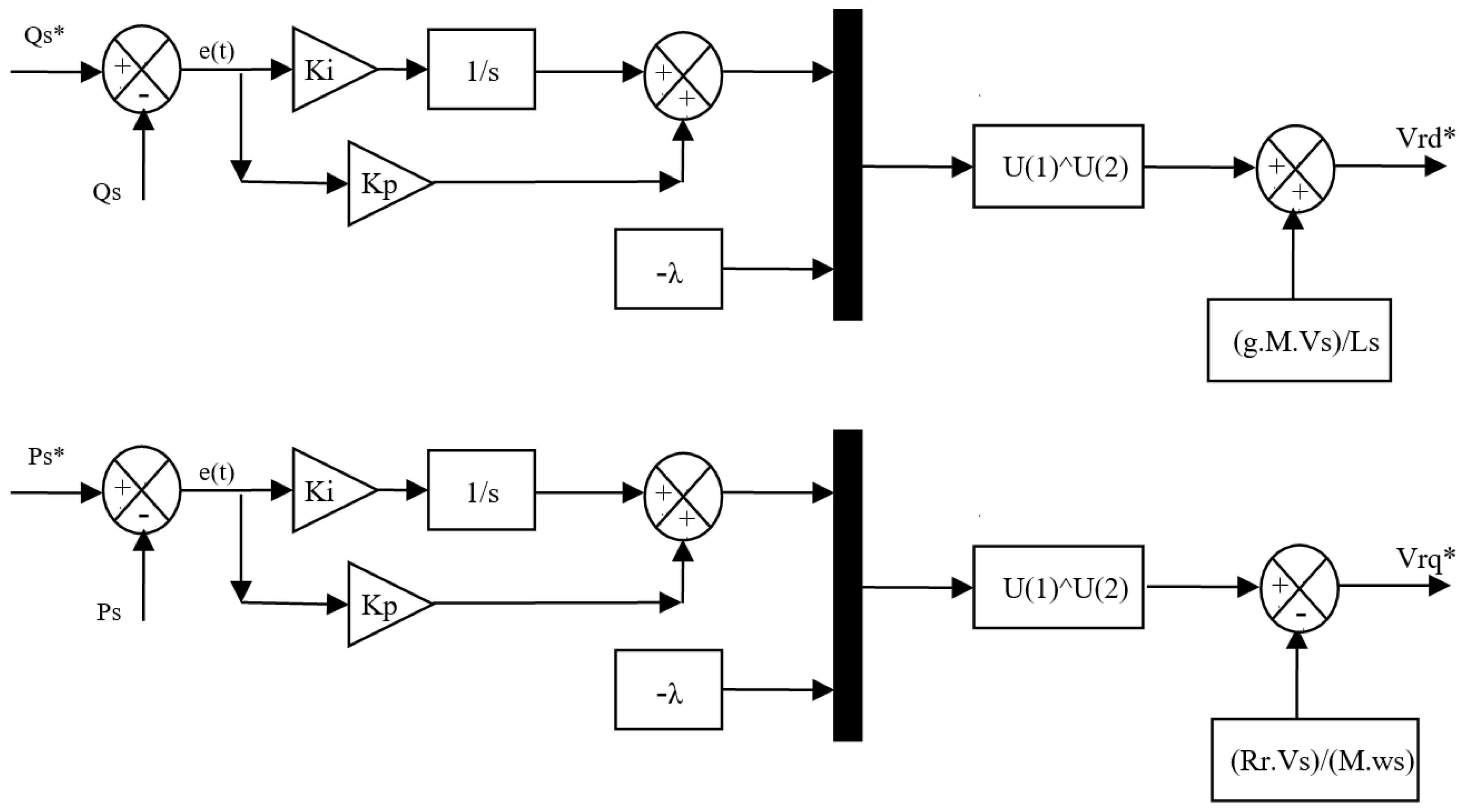
6. Proposed DVC Strategy
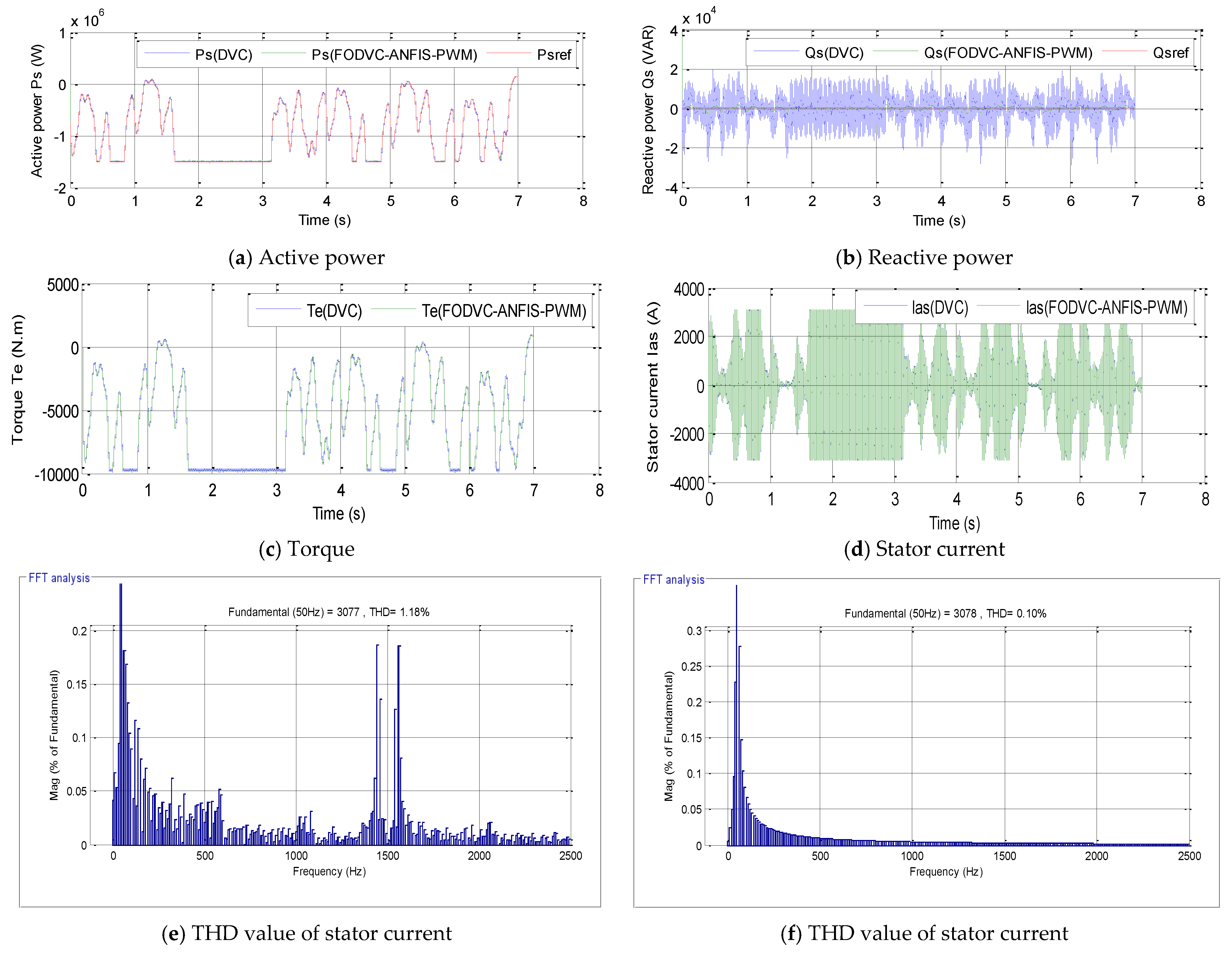
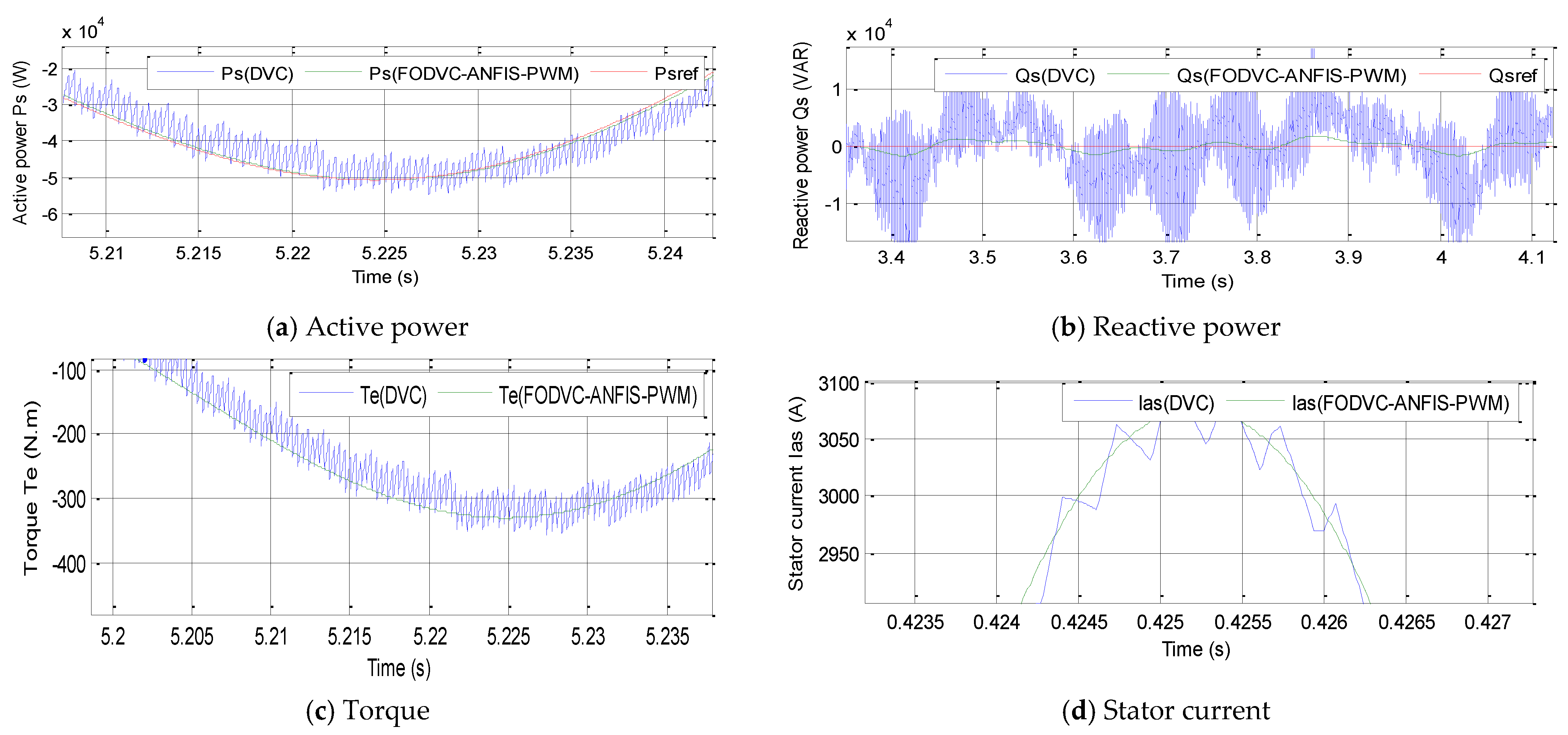
7. Numerical Results
- First test
- B.
- Robustness test
8. Conclusions
- A new fractional-order PI controller is presented and applied to the DVC strategy.
- A novel PWM strategy based on an ANFIS algorithm was presented to control the inverter of the generator to reduce torque, active power, current, and reactive power ripples.
- A robust strategy is proposed that reduces the THD value of the current.
- A new robust control strategy is proposed and presented.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Abdelrahem, M.; Hackl, C.M.; Kennel, R. Limited-Position Set Model-Reference Adaptive Observer for Control of DFIGs without Mechanical Sensors. Machines 2020, 8, 72. [Google Scholar] [CrossRef]
- Nnem, L.M.; Lonla, B.M.; Sonfack, G.B.; Mbih, J. Review of a Multipurpose Duty-Cycle Modulation Technology in Electrical and Electronics Engineering. J. Electr. Eng. Electron. Control. Comput. Sci. 2018, 4, 9–18. Available online: https://jeeeccs.net/index.php/journal/article/view/101 (accessed on 19 April 2022).
- Alhato, M.M.; Ibrahim, M.N.; Rezk, H.; Bouallègue, S. An Enhanced DC-Link Voltage Response for Wind-Driven Doubly Fed Induction Generator Using Adaptive Fuzzy Extended State Observer and Sliding Mode Control. Mathematics 2021, 9, 963. [Google Scholar] [CrossRef]
- Habib, B.; Boudjema, Z.; Belaidi, A. Higher control scheme using neural second order sliding mode and ANFIS-SVM strategy for a DFIG-based wind turbine. Int. J. Adv. Telecommun. Electrotech. Signals Syst. 2019, 8, 17–28. [Google Scholar]
- Giaourakis, D.G.; Safacas, A.N. Effect of Short-Circuit Faults in the Back-to-Back Power Electronic Converter and Rotor Terminals on the Operational Behavior of the Doubly-Fed Induction Generator Wind Energy Conversion System. Machines 2015, 3, 2–26. [Google Scholar] [CrossRef] [Green Version]
- Mohan Kumar, P.; Sivalingam, K.; Lim, T.-C.; Ramakrishna, S.; Wei, H. Strategies for Enhancing the Low Wind Speed Performance of H-Darrieus Wind Turbine-Part 1. Clean Technol. 2019, 1, 185–204. [Google Scholar] [CrossRef] [Green Version]
- Benbouhenni, H.; Bizon, N. Improved Rotor Flux and Torque Control Based on the Third-Order Sliding Mode Scheme Applied to the Asynchronous Generator for the Single-Rotor Wind Turbine. Mathematics 2021, 9, 2297. [Google Scholar] [CrossRef]
- Ullah, W.; Khan, F.; Hussain, S. A Novel Dual Rotor Permanent Magnet Flux Switching Generator for Counter Rotating Wind Turbine Applications. IEEE Access 2022, 10, 16456–16467. [Google Scholar] [CrossRef]
- Yahdou, A.; Djilali, A.B.; Boudjema, Z.; Mehedi, F. Improved Vector Control of a Counter-Rotating Wind Turbine System Using Adaptive Backstepping Sliding Mode. J. Eur. Systèmes Autom. 2020, 53, 645–651. [Google Scholar] [CrossRef]
- Luo, X.; Niu, S. A Novel Contra-Rotating Power Split Transmission System for Wind Power Generation and Its Dual MPPT Control Strategy. IEEE Trans. Power Electron. 2017, 32, 6924–6935. [Google Scholar] [CrossRef]
- Onyishi, D.U.; Ofualagba, G. Analysis of the Electricity Distribution Supply in Eastern Nigeria: Current Challenges and Possible Solutions. J. Electr. Eng. Electron. Control. Comput. Sci. 2021, 7, 1–8. Available online: https://jeeeccs.net/index.php/journal/article/view/209 (accessed on 19 April 2022).
- Shahzad, U. Application of Machine Learning for Optimal Wind Farm Location. J. Electr. Eng. Electron. Control. Comput. Sci. 2022, 8, 1–8. Available online: https://jeeeccs.net/index.php/journal/article/view/276 (accessed on 19 April 2022).
- Zhao, W.; Lipo, T.A.; Kwon, B.-I. A novel dual-rotor axial field fault-tolerant flux-switching permanent magnet machine with high-torque performance. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- No, T.S.; Kim, J.-K.; Moon, J.H.; Kim, S.J. Modeling control and simulation of dual rotor wind turbine generator system. Renew. Energy 2009, 34, 2124–2132. [Google Scholar] [CrossRef]
- Kumar, P.S.; Abraham, A.; Bensingh, R.J.; Ilangovan, S. Computational and experimental analysis of a counter-rotating wind turbine system. J. Sci. Ind. Res. 2013, 72, 300–306. [Google Scholar]
- Giger, U.; Kleinhansl, S.; Schulte, H. Design Study of Multi-Rotor and Multi-Generator Wind Turbine with Lattice Tower—A Mechatronic Approach. Appl. Sci. 2021, 11, 11043. [Google Scholar] [CrossRef]
- Salic, T.; Charpentier, J.F.; Benbouzid, M.; Le Boulluec, M. Control Strategies for Floating Offshore Wind Turbine: Challenges and Trends. Electronics 2019, 8, 1185. [Google Scholar] [CrossRef] [Green Version]
- Velpula, S.; Thirumalaivasan, R.; Janaki, M. Stability Analysis on Torsional Interactions of Turbine-Generator Connected with DFIG-WECS Using Admittance Model. IEEE Trans. Power Syst. 2020, 35, 4745–4755. [Google Scholar] [CrossRef]
- Benbouhenni, H.; Bizon, N. Terminal Synergetic Control for Direct Active and Reactive Powers in Asynchronous Generator-Based Dual-Rotor Wind Power Systems. Electronics 2021, 10, 1880. [Google Scholar] [CrossRef]
- Benbouhenni, H.; Bizon, N. Third-Order Sliding Mode Applied to the Direct Field-Oriented Control of the Asynchronous Generator for Variable-Speed Contra-Rotating Wind Turbine Generation Systems. Energies 2021, 14, 5877. [Google Scholar] [CrossRef]
- Habib, B. Amelioration effectiveness of torque and rotor flux control applied to the asynchronous generator (AG) for dual-rotor wind turbine using neural third-order sliding mode approaches. Int. J. Eng. Trans. C Asp. 2022, 35, 517–530. [Google Scholar]
- Yahdou, A.; Hemici, B.; Boudjema, Z. Second order sliding mode control of a dual-rotor wind turbine system by employing a matrix converter. J. Electr. Eng. 2016, 16, 1–11. [Google Scholar]
- Benbouhenni, H.; Bizon, N. A Synergetic Sliding Mode Controller Applied to Direct Field-Oriented Control of Induction Generator-Based Variable Speed Dual-Rotor Wind Turbines. Energies 2021, 14, 4437. [Google Scholar] [CrossRef]
- Habib, B. Synergetic control theory scheme for asynchronous generator based dual-rotor wind power. J. Electr. Eng. Electron. Control Comput. Sci. 2021, 7, 19–28. Available online: https://jeeeccs.net/index.php/journal/article/view/215 (accessed on 9 April 2022).
- Sami, I.; Ullah, S.; Ali, Z.; Ullah, N.; Ro, J.-S. A Super Twisting Fractional Order Terminal Sliding Mode Control for DFIG-Based Wind Energy Conversion System. Energies 2020, 13, 2158. [Google Scholar] [CrossRef]
- Almakki, A.N.J.; Andrey, A.M. Application of fractional-order second-order continuous sliding mode controller in direct flux and torque control system of doubly-fed induction generator integrated to wind turbine: Simulation studies. Vestn. Gos. Univ. Morskogo I Rechn. Flot. Im. Admirala S. O. Makarova 2021, 13, 887–907. [Google Scholar] [CrossRef]
- Heydari, E.E.; Rafiee, M.; Pichan, M. Fuzzy-Genetic Algorithm-Based Direct Power Control Strategy for DFIG. Iran. J. Electr. Electron. Eng. 2018, 14, 353–361. [Google Scholar] [CrossRef]
- Xu, S.; Sun, H.; Zhang, Z.; Guo, Q.; Zhao, B.; Bi, J.; Zhang, B. MAS-Based Decentralized Coordinated Control Strategy in a Micro-Grid with Multiple Microsources. Energies 2020, 13, 2141. [Google Scholar] [CrossRef]
- Mehdi, H.; Farzad, R.S. Analysis and detection of a wind system failure in a micro-grid. J. Renew. Sustain. Energy 2016, 8, 043302. [Google Scholar] [CrossRef]
- Chen, H.; Chen, X.; Xie, W. Fractional-Order PI Controller for DFIG-Based Marine Tidal Current Applications. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Zhibin, Z.; Hao, C.; Wei, X.; Xiyang, C.; Jingang, H.; Nadia, A.; Tianhao, T.; Mohamed, B. Fractional-Order PI Control of DFIG-Based Tidal Stream Turbine. J. Mar. Sci. Eng. 2020, 8, 309. [Google Scholar] [CrossRef]
- Mosaad, M.I.; Abu-Siada, A.; El-Naggar, M.F. Application of Superconductors to Improve the Performance of DFIG-Based WECS. IEEE Access 2019, 7, 103760–103769. [Google Scholar] [CrossRef]
- Hossein, M.; Seyed, A.T.; Mohsen, R.; Mohammad, S. DFIG performance improvement in grid connected mode by using fractional order [PI] controller. Int. J. Electr. Power Energy Syst. 2018, 96, 398–411. [Google Scholar] [CrossRef]
- Beik, O.; Al-Adsani, A.S. Active and Passive Control of a Dual Rotor Wind Turbine Generator for DC Grids. IEEE Access 2021, 9, 1987–1995. [Google Scholar] [CrossRef]
- Wang, B.; Wang, S.; Peng, Y.; Pi, Y.; Luo, Y. Design and High-Order Precision Numerical Implementation of Fractional-Order PI Controller for PMSM Speed System Based on FPGA. Fractal Fract. 2022, 6, 218. [Google Scholar] [CrossRef]
- Zheng, J.; Jiang, X.; Ren, G.; Xie, X.; Fan, D. High-Precision Anti-Interference Control of Direct Drive Components. Actuators 2022, 11, 95. [Google Scholar] [CrossRef]
- Li, G.; Li, Y.; Chen, H.; Deng, W. Fractional-Order Controller for Course-Keeping of Under actuated Surface Vessels Based on Frequency Domain Specification and Improved Particle Swarm Optimization Algorithm. Appl. Sci. 2022, 12, 3139. [Google Scholar] [CrossRef]
- Vu, T.N.L.; Chuong, V.L.; Truong, N.T.N.; Jung, J.H. Analytical Design of Fractional-Order PI Controller for Parallel Cascade Control Systems. Appl. Sci. 2022, 12, 2222. [Google Scholar] [CrossRef]
- Nikkhah Kashani, H.; Rouhi Ardeshiri, R.; Gheisarnejad, M.; Khooban, M.-H. Optimal Cascade Non-Integer Controller for Shunt Active Power Filter: Real-Time Implementation. Designs 2022, 6, 32. [Google Scholar] [CrossRef]
- Rostami, M.; Madani, S.M.; Ademi, S. Sensorless Closed-Loop Voltage and Frequency Control of Stand-Alone DFIGs Introducing Direct Flux-Vector Control. IEEE Trans. Ind. Electron. 2020, 67, 6078–6088. [Google Scholar] [CrossRef]
- Erturk, E.; Sivrioglu, S.; Bolat, F.C. Analysis Model of a Small Scale Counter-Rotating Dual Rotor Wind Turbine with Double Rotational Generator Armature. Int. J. Renew. Energy Res. 2018, 8, 1849–1858. [Google Scholar]
- Fukami, T.; Momiyama, M.; Shima, K.; Hanaoka, R.; Takata, S. Steady-State Analysis of a Dual-Winding Reluctance Generator with a Multiple-Barrier Rotor. IEEE Trans. Energy Convers. 2008, 23, 492–498. [Google Scholar] [CrossRef]
- Tejado, I.; Vinagre, B.M.; Traver, J.E.; Prieto-Arranz, J.; Nuevo-Gallardo, C. Back to Basics: Meaning of the Parameters of Fractional Order PID Controllers. Mathematics 2019, 7, 530. [Google Scholar] [CrossRef] [Green Version]
- Muresan, C.I.; Birs, I.R.; Dulf, E.H. Event-Based Implementation of Fractional Order IMC Controllers for Simple FOPDT Processes. Mathematics 2020, 8, 1378. [Google Scholar] [CrossRef]
- Mohamed Ahmed, S.A.; Montaser Abd El Sattar, M.A. Dynamic Performance and Effectiveness of Voltage Disturbances on the Improvement of Power Quality for Grid-Connected DFIG System Based Wind Farm. J. Electr. Eng. Electron. Control. Comput. Sci. 2020, 5, 25–30. Available online: https://jeeeccs.net/index.php/journal/article/view/126 (accessed on 19 April 2022).
- Yingjie, W.; Hui, Z.; Hao, L.; Bowei, P. Dynamic Analysis of Grid-Connected DFIG with Fractional-Order PI Control. In Proceedings of the 2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019; pp. 1690–1693. [Google Scholar] [CrossRef]
- Meraj, M.; Rahman, S.; Iqbal, A.; Al Emadi, N. Novel Level Shifted PWM Technique for Unequal and Equal Power Sharing in Quasi Z-Source Cascaded Multilevel Inverter for PV Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 937–948. [Google Scholar] [CrossRef]
- Lee, S.S.; Siwakoti, Y.P.; Lim, C.S.; Lee, K.-B. An Improved PWM Technique to Achieve Continuous Input Current in Common-Ground Transformer less Boost Inverter. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 3133–3136. [Google Scholar] [CrossRef]
- Bogaraj, T.; Kanakaraj, J. A Novel Energy Management Scheme using ANFIS for Independent Microgrid. Int. J. Renew. Energy Res. 2016, 6, 735–746. [Google Scholar]
- Fekry, H.M.; Eldesouky, A.A.; Kassem, A.M.; Abdelaziz, A.Y. Power Management Strategy Based on Adaptive Neuro Fuzzy Inference System for AC Microgrid. IEEE Access 2020, 8, 192087–192100. [Google Scholar] [CrossRef]
- Nicola, M.; Nicola, C.-I. Sensorless Fractional Order Control of PMSM Based on Synergetic and Sliding Mode Controllers. Electronics 2020, 9, 1494. [Google Scholar] [CrossRef]
- Bauer, W.; Baranowski, J. Fractional PIλD Controller Design for a Magnetic Levitation System. Electronics 2020, 9, 2135. [Google Scholar] [CrossRef]
- Alam, M.S.; Al-Ismail, F.S.; Abido, M.A. PV/Wind-Integrated Low-Inertia System Frequency Control: PSO-Optimized Fractional-Order PI-Based SMES Approach. Sustainability 2021, 13, 7622. [Google Scholar] [CrossRef]
- Reddy, C.R.; Goud, B.S.; Aymen, F.; Rao, G.S.; Bortoni, E.C. Power Quality Improvement in HRES Grid Connected System with FOPID Based Atom Search Optimization Technique. Energies 2021, 14, 5812. [Google Scholar] [CrossRef]
- Azab, M.; Serrano-Fontova, A. Optimal Tuning of Fractional Order Controllers for Dual Active Bridge-Based DC Microgrid Including Voltage Stability Assessment. Electronics 2021, 10, 1109. [Google Scholar] [CrossRef]
- Ding, J.; Jiao, X. A Novel Control Method of Clutch During Mode Transition of Single-Shaft Parallel Hybrid Electric Vehicles. Electronics 2020, 9, 54. [Google Scholar] [CrossRef] [Green Version]
- Benbouhenni, H.; Bizon, N. Advanced Direct Vector Control Method for Optimizing the Operation of a Double-Powered Induction Generator-Based Dual-Rotor Wind Turbine System. Mathematics 2021, 9, 2403. [Google Scholar] [CrossRef]
- Boudjema, Z.; Taleb, R.; Djerriri, Y.; Yahdou, A. A novel direct torque control using second order continuous sliding mode of a doubly fed induction generator for a wind energy conversion system. Turk. J. Electr. Eng. Comput. Sci. 2017, 25, 965–975. [Google Scholar] [CrossRef] [Green Version]
- Moreira, A.B.; Barros, T.A.D.S.; Teixeira, V.S.D.C.; Souza, R.R.D.; Paula, M.V.D.; Filho, E.R. Control of Powers for Wind Power Generation and Grid Current Harmonics Filtering from Doubly Fed Induction Generator: Comparison of Two Strategies. IEEE Access 2019, 7, 32703–32713. [Google Scholar] [CrossRef]
- Amrane, F.; Chaiba, A.; Babas, B.E.; Mekhilef, S. Design and implementation of high performance field oriented control for grid-connected doubly fed induction generator via hysteresis rotor current controller. Rev. Sci. Techni.-Electrotechn. Energ. 2016, 61, 319–324. [Google Scholar]
- Ayrira, W.; Ourahoua, M.; El Hassounia, B.; Haddib, A. Direct torque control improvement of a variable speed DFIG based on a fuzzy inference system. Math. Comput. Simul. 2020, 167, 308–324. [Google Scholar] [CrossRef]
- Fayssal, A.; Bruno, F.; Azeddine, C. Experimental investigation of efficient and simple wind-turbine based on DFIG-direct power control using LCL-filter for stand-alone mode. ISA Trans. 2021; 1–34, in press. [Google Scholar] [CrossRef]
- Sara, M.; Ahmed, E.; Issam, M.; Tamou, N.; Badre, B.I.; Ben Tarla, L. Performance of a vector control for DFIG driven by wind turbine: Real time simulation using DS1104 controller board. Int. J. Power Electron. Drive Syst. 2019, 10, 1003–1013. [Google Scholar] [CrossRef]
- Yusoff, N.A.; Razali, A.M.; Karim, K.A.; Sutikno, T.; Jidin, A. A concept of virtual-flux direct power control of three-phase AC-DC converter. Int. J. Power Electron. Drive Syst. 2017, 8, 1776–1784. [Google Scholar] [CrossRef]
- Boudjema, Z.; Meroufel, A.; Djerriri, Y.; Bounadja, E. Fuzzy sliding mode control of a doubly fed induction generator for energy conversion. Carpathian J. Electron. Comput. Eng. 2013, 6, 7–14. [Google Scholar]
- Said, M.; Derouich, A.; El Ouanjli, N.; El Mahfoud, M. Enhancement of the Direct Torque Control by using Artificial Neuron Network for a Doubly Fed Induction Motor. Intell. Syst. Appl. 2022, 13, 200060. [Google Scholar] [CrossRef]
- Alhato, M.M.; Bouallègue, S. Direct Power Control Optimization for Doubly Fed Induction Generator Based Wind Turbine Systems. Math. Comput. Appl. 2019, 24, 77. [Google Scholar] [CrossRef] [Green Version]
- Yaichi, I.; Semmah, A.; Wira, P.; Djeriri, Y. Super-twisting sliding mode control of a doubly-fed induction generator based on the SVM strategy. Period. Polytech. Electr. Eng. Comput. Sci. 2019, 63, 178–190. [Google Scholar] [CrossRef]
- Quan, Y.; Hang, L.; He, Y.; Zhang, Y. Multi-Resonant-Based Sliding Mode Control of DFIG-Based Wind System under Unbalanced and Harmonic Network Conditions. Appl. Sci. 2019, 9, 1124. [Google Scholar] [CrossRef] [Green Version]
- El Ouanjli, N.; Aziz, D.; El Ghzizal, A.; Mohammed, T.; Youness, E.; Khalid, M.; Badre, B. Direct torque control of doubly fed induction motor using three-level NPC inverter. Prot. Control. Mod. Power Syst. 2019, 4, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Kamarzarrin, M.; Refan, M.H.; Amiri, P.; Dameshghi, A. Fault Diagnosis of Wind Turbine Double-Fed Induction Generator Based on Multi-Level Fusion and Measurement of Back-to-Back Converter Current Signal. Iran. J. Electr. Electron. Eng. 2022, 18, 2074. Available online: http://ijeee.iust.ac.ir/article-1-2074-en.html (accessed on 19 April 2022).



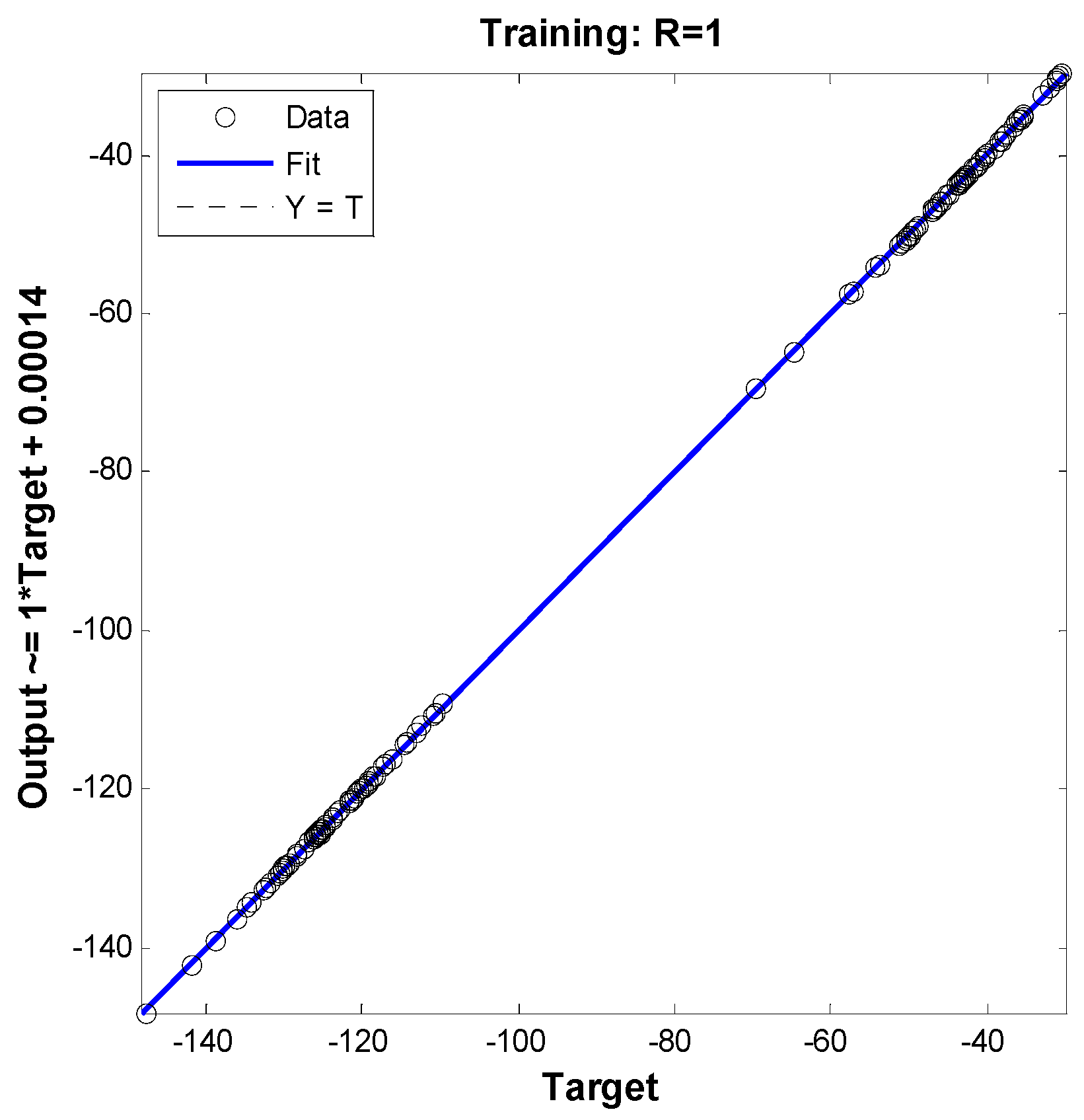

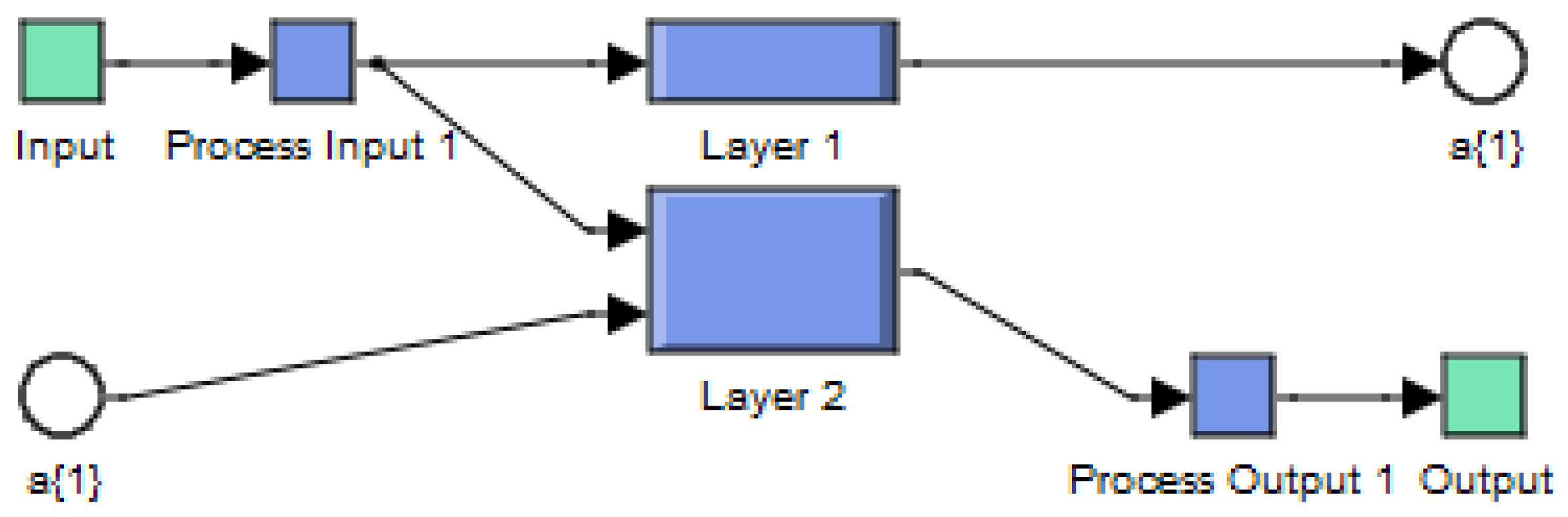
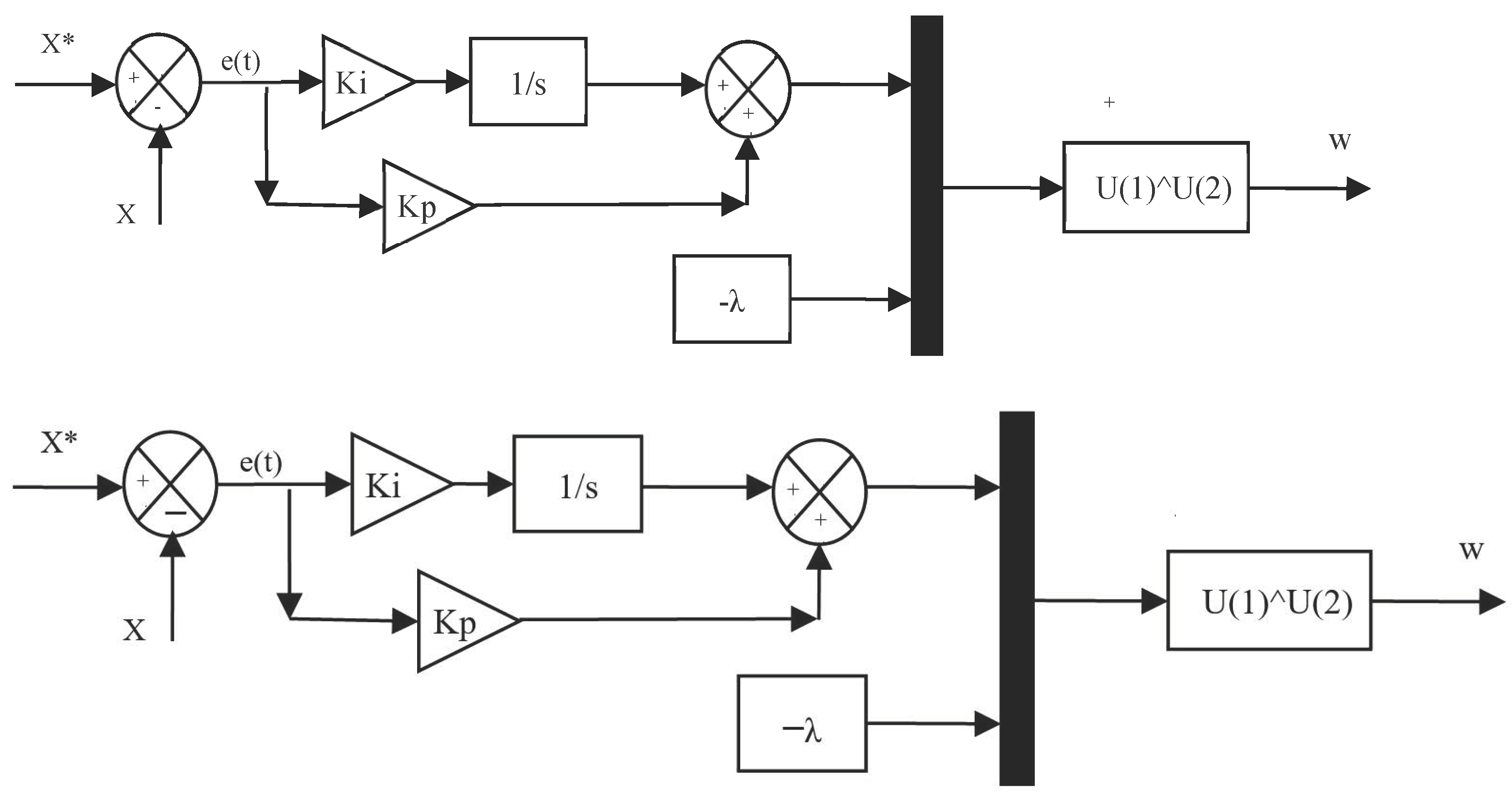
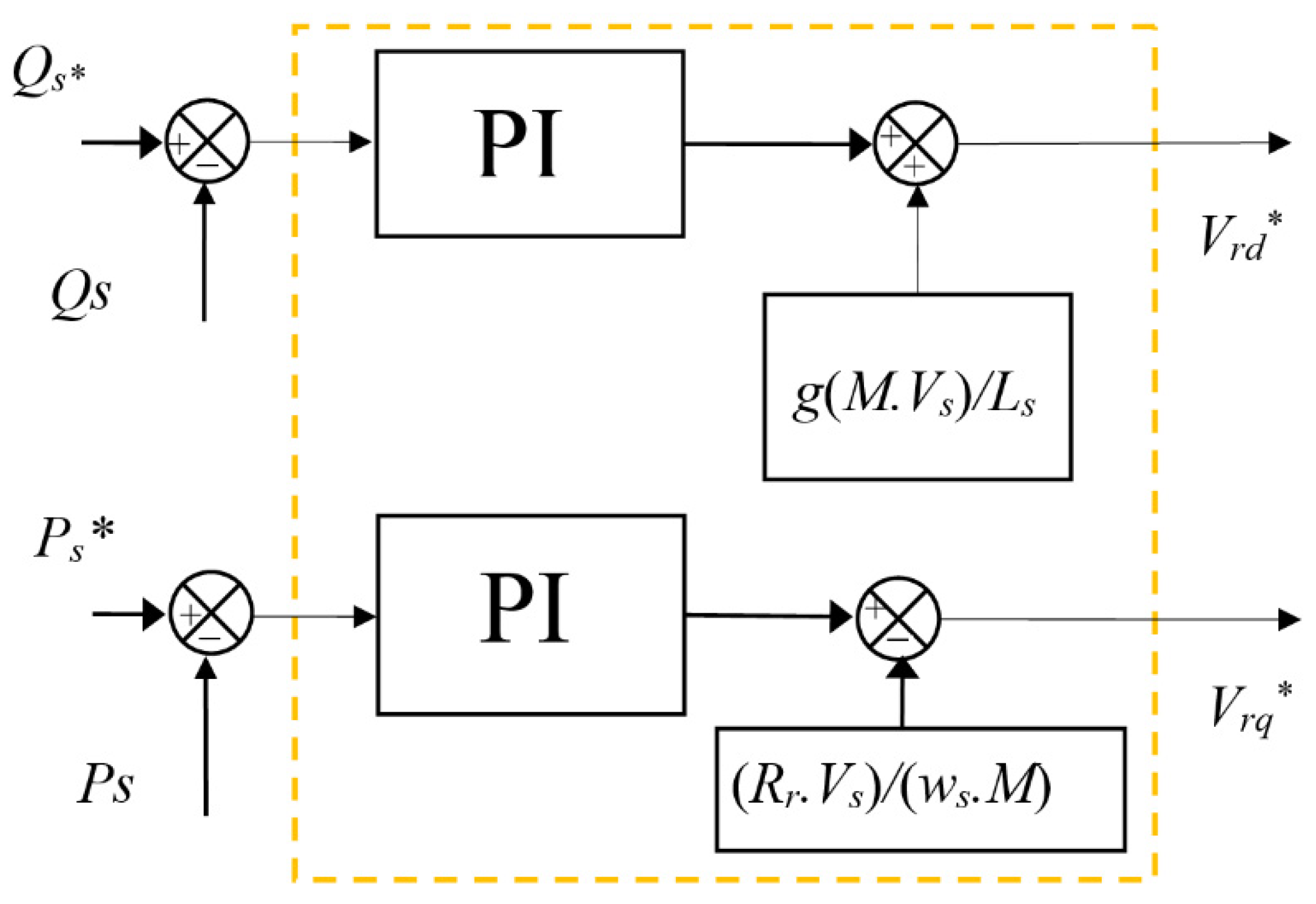

| Parameters | Values |
|---|---|
| Training | Conjugate gradient with Beale–Powell restarts |
| Train Param.eposh | 100 |
| Coeff. of acceleration of convergence(mc) | 0.9 |
| Number of neurons in hidden layer | 50 |
| Performances | Mean Squared Error (mse) |
| Train Param.mu | 0.8 |
| Functions of activation | Tansig, purelin, traincgb |
| Number of neurons in layer 1 | 2 |
| Train Param.goal | 0 |
| Train Param.show | 50 |
| Train Param.Lr | 0.05 |
| Number of neurons in layer 2 | 1 |
| Conventional DVC Strategy | Proposed DVC Strategy | |
|---|---|---|
| Type modulation used | PWM | Intelligent PWM |
| Type controller used | PI controller | FOPI controller |
| Robustness | Low | High |
| Rise time | High | Low |
| Response dynamic | Slow | Quick |
| Degree of complexity | Low | Low |
| Ease | Low | Medium |
| Simplicity of implementation | Low | Low |
| Power ripple | High | Low |
| THD | High | Low |
| Quality of current | Low | High |
| Reactive Power (VAR) | Torque (Nm) | Current (A) | Active Power (W) | ||
|---|---|---|---|---|---|
| DVC strategy | First test | 60,000 | 150 | 100 | 30,000 |
| Second test | 309,000 | 800 | 200 | 100,000 | |
| FODVC-ANFIS-PWM strategy | First test | 40 | 10 | 15 | 10 |
| Second test | 80 | 20 | 20 | 40 | |
| Ratios | First test | 99.93% | 93.33% | 85% | 99.99% |
| Second test | 99.97% | 97.50% | 90% | 99.96% | |
| Techniques | THD (%) | ||
|---|---|---|---|
| Ref. [58] | Direct torque control | 2.57 | |
| Ref. [59] | Power control | Strategy 1 | 5.6817 |
| Strategy 2 | 3.1873 | ||
| Ref. [60] | Field-oriented control | 3.7 | |
| Ref. [61] | Classical direct torque control | 6.70 | |
| Fuzzy direct torque control | 2.40 | ||
| Ref. [62] | Direct power control with IP controllers | 0.43 | |
| Ref. [63] | Indirect field-oriented control | 6.5 | |
| Ref. [64] | 12 sectors direct power control | 0.40 | |
| Ref. [65] | Fuzzy sliding mode control | 1.15 | |
| Ref. [66] | Direct torque control | 7.83 | |
| Neural direct torque control | 3.26 | ||
| Ref. [22] | Second-order sliding mode control | 3.13 | |
| Ref. [67] | DTC technique using L-filter | 10.79 | |
| DPC strategy using LCL-filter | 4.05 | ||
| Ref. [68] | DPC strategy with STA controller | 1.66 | |
| Ref. [23] | DVC with synergetic sliding mode controller | 0.50 | |
| Ref. [69] | Integral sliding mode control | 9.71 | |
| Multi-resonant-based sliding mode controller | 3.14 | ||
| Ref. [70] | Two-level direct torque control | 8.75 | |
| Three-level direct torque control | 1.57 | ||
| Ref. [71] | Genetic Algorithm Least Squares Wavelet Support Vector Machines (GA-LS-WSVM) method | 3.39 | |
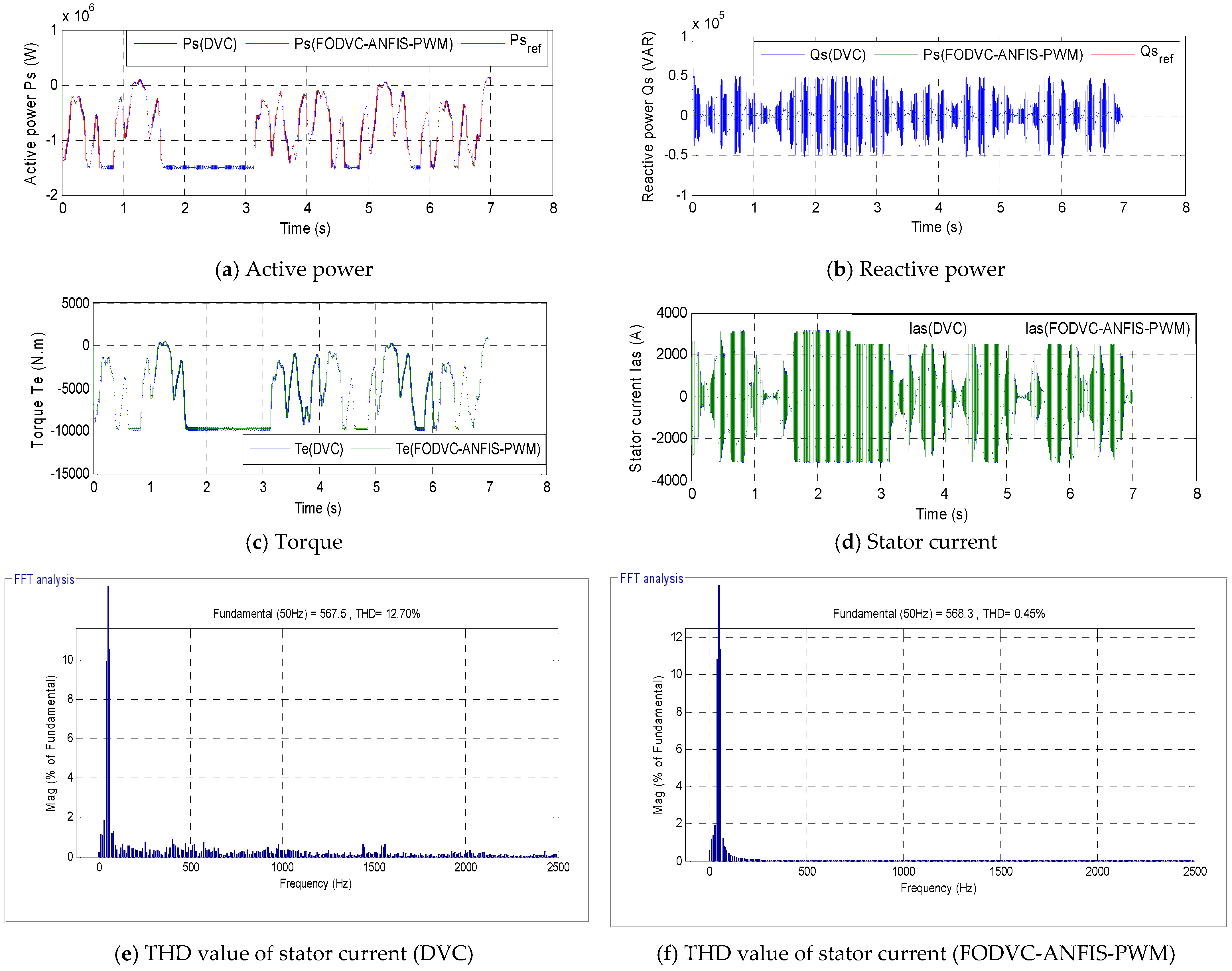
| Designed FODVC-ANFIS-PWM technique | First test | 0.10 | |
| Second test | 0.45 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benbouhenni, H.; Bizon, N.; Colak, I.; Thounthong, P.; Takorabet, N. Application of Fractional-Order PI Controllers and Neuro-Fuzzy PWM Technique to Multi-Rotor Wind Turbine Systems. Electronics 2022, 11, 1340. https://doi.org/10.3390/electronics11091340
Benbouhenni H, Bizon N, Colak I, Thounthong P, Takorabet N. Application of Fractional-Order PI Controllers and Neuro-Fuzzy PWM Technique to Multi-Rotor Wind Turbine Systems. Electronics. 2022; 11(9):1340. https://doi.org/10.3390/electronics11091340
Chicago/Turabian StyleBenbouhenni, Habib, Nicu Bizon, Ilhami Colak, Phatiphat Thounthong, and Noureddine Takorabet. 2022. "Application of Fractional-Order PI Controllers and Neuro-Fuzzy PWM Technique to Multi-Rotor Wind Turbine Systems" Electronics 11, no. 9: 1340. https://doi.org/10.3390/electronics11091340
APA StyleBenbouhenni, H., Bizon, N., Colak, I., Thounthong, P., & Takorabet, N. (2022). Application of Fractional-Order PI Controllers and Neuro-Fuzzy PWM Technique to Multi-Rotor Wind Turbine Systems. Electronics, 11(9), 1340. https://doi.org/10.3390/electronics11091340









