A PSO-Based Approach for Optimal Allocation and Sizing of Resistive-Type SFCLs to Enhance the Transient Stability of Power Systems
Abstract
1. Introduction
- (1)
- The optimization problem is solved for two cases, considering three and five RSFCLs due to a trade-off between technical and economic issues. Results are compared based on a detailed analysis.
- (2)
- Two main criteria are considered for the assessment of transient stability enhancement including the critical fault clearing time (CCT) as well as the generators’ maximum rotor angle deviations. Comprehensive simulations and investigations are performed for both criteria.
- (3)
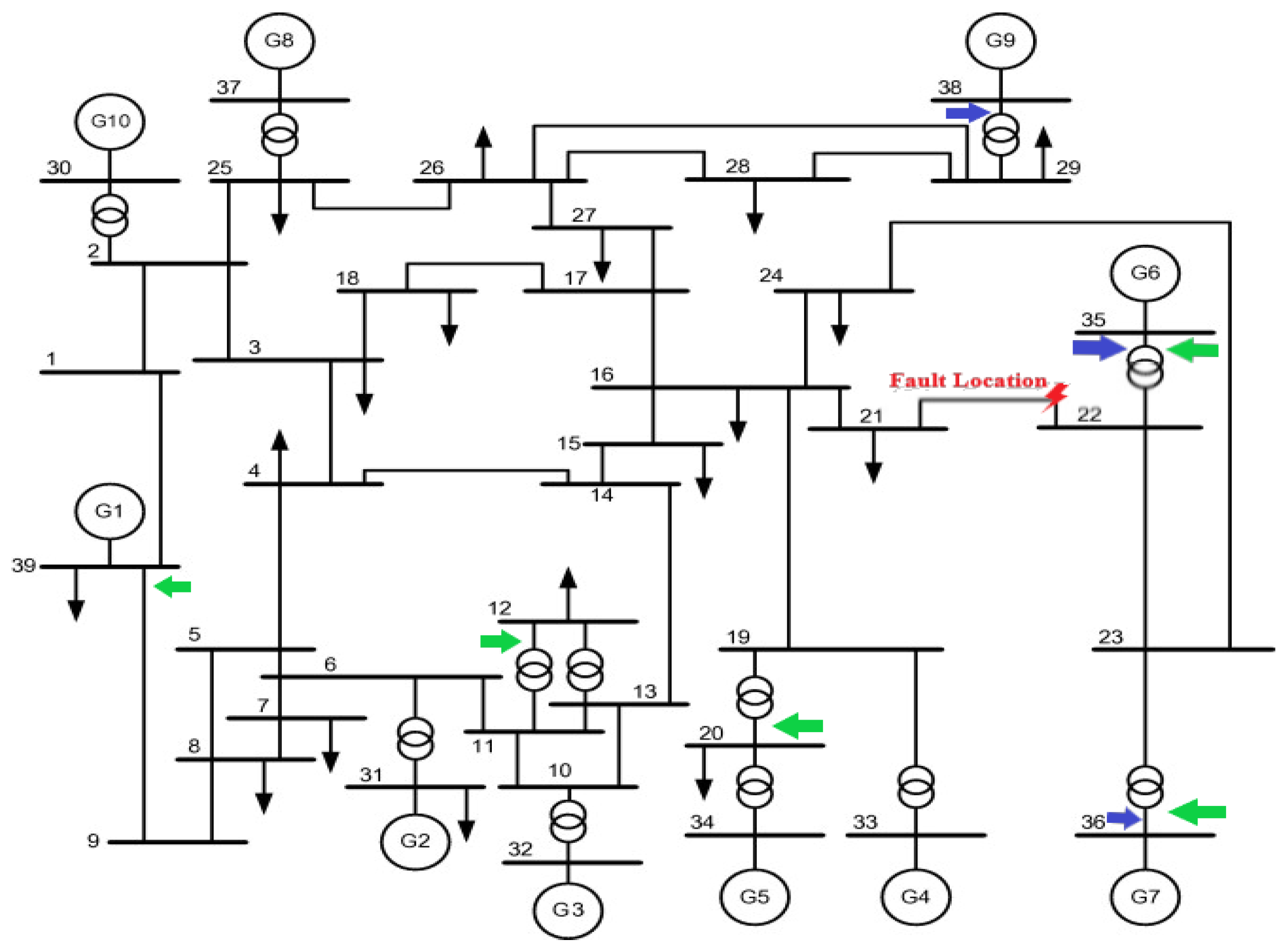
- The three-phase short-circuit fault location is carefully selected regarding the maximum normal condition power flow of the selected transmission line, which will result in a larger power swing in the event of its short-circuit fault occurrence, leading to more serious transient instability issues.
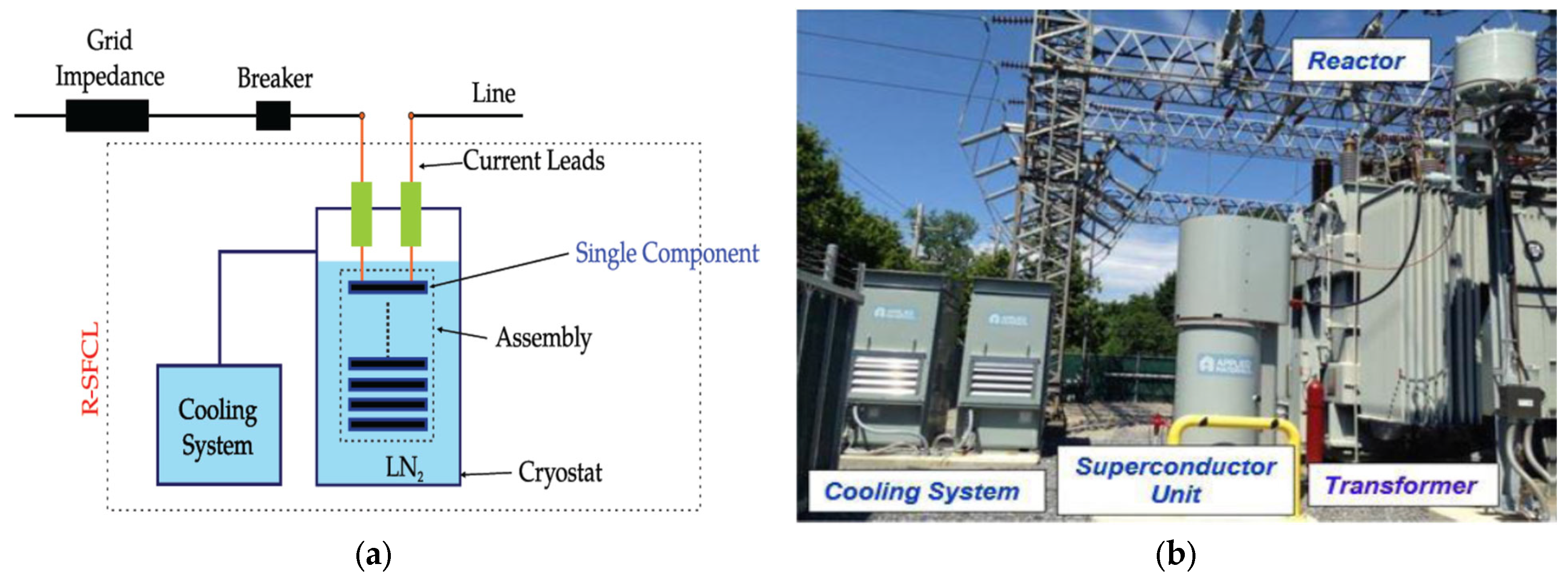
2. Resistive Superconducting Fault Current Limiters
3. Problem Formulation
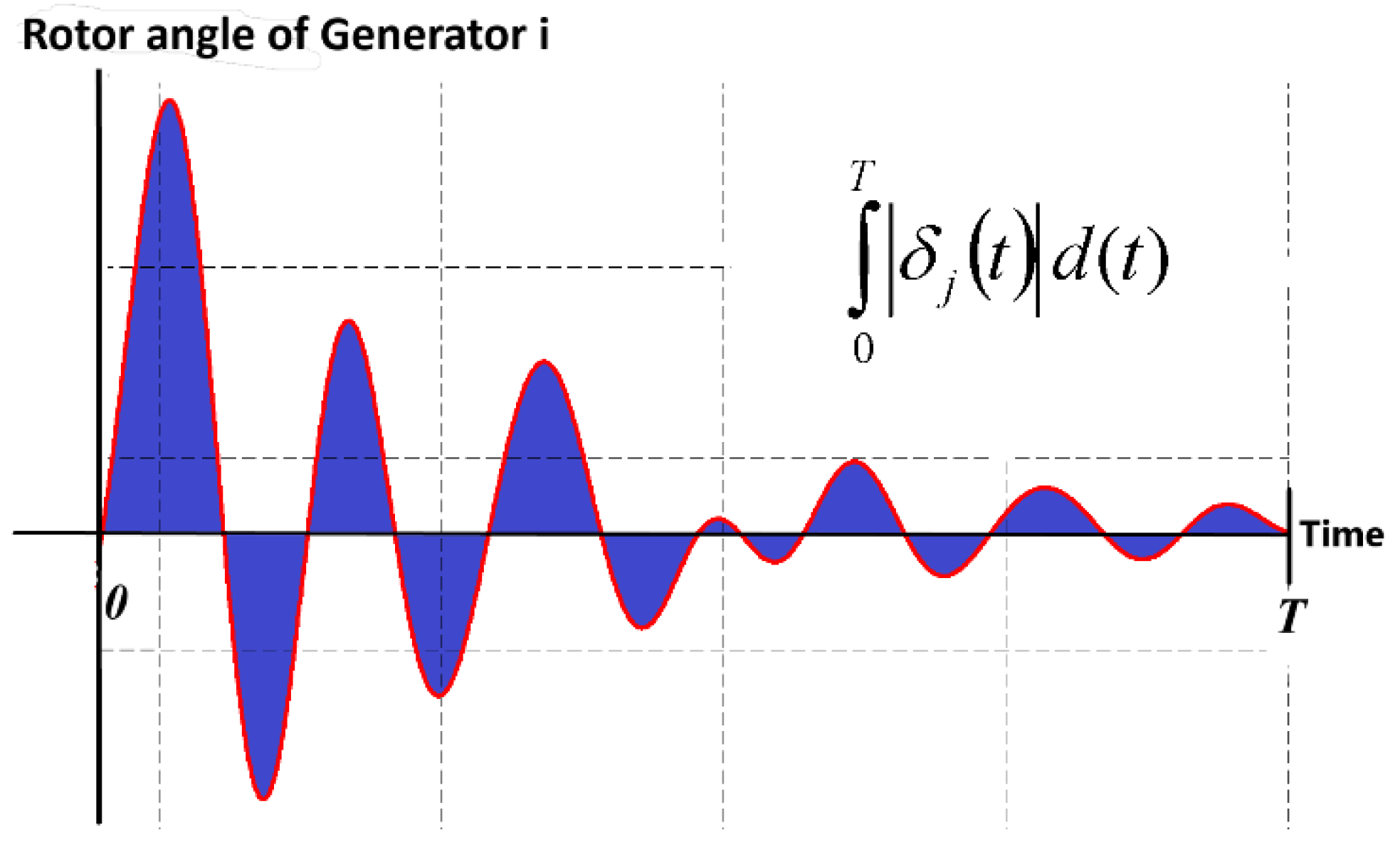
3.1. Objective Function
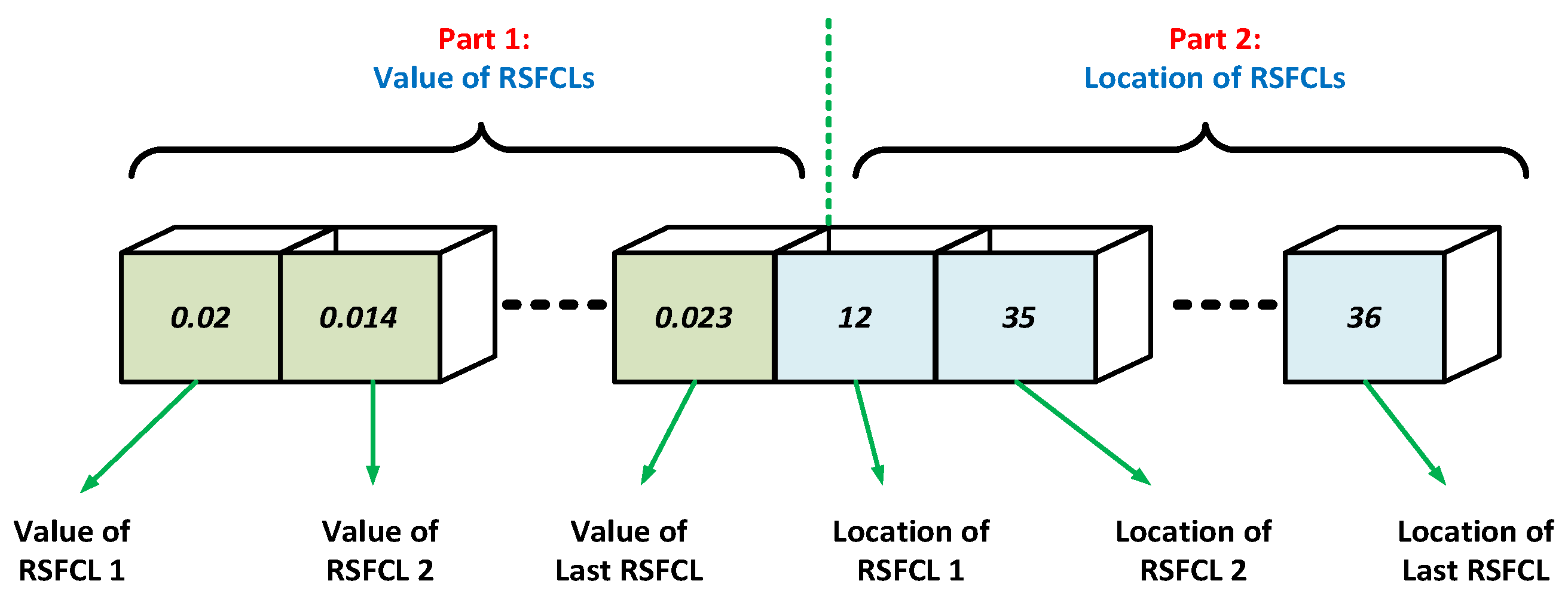
3.2. Decision Variables
3.3. Constraints
4. Problem Solution
4.1. Particle Swarm Optimization
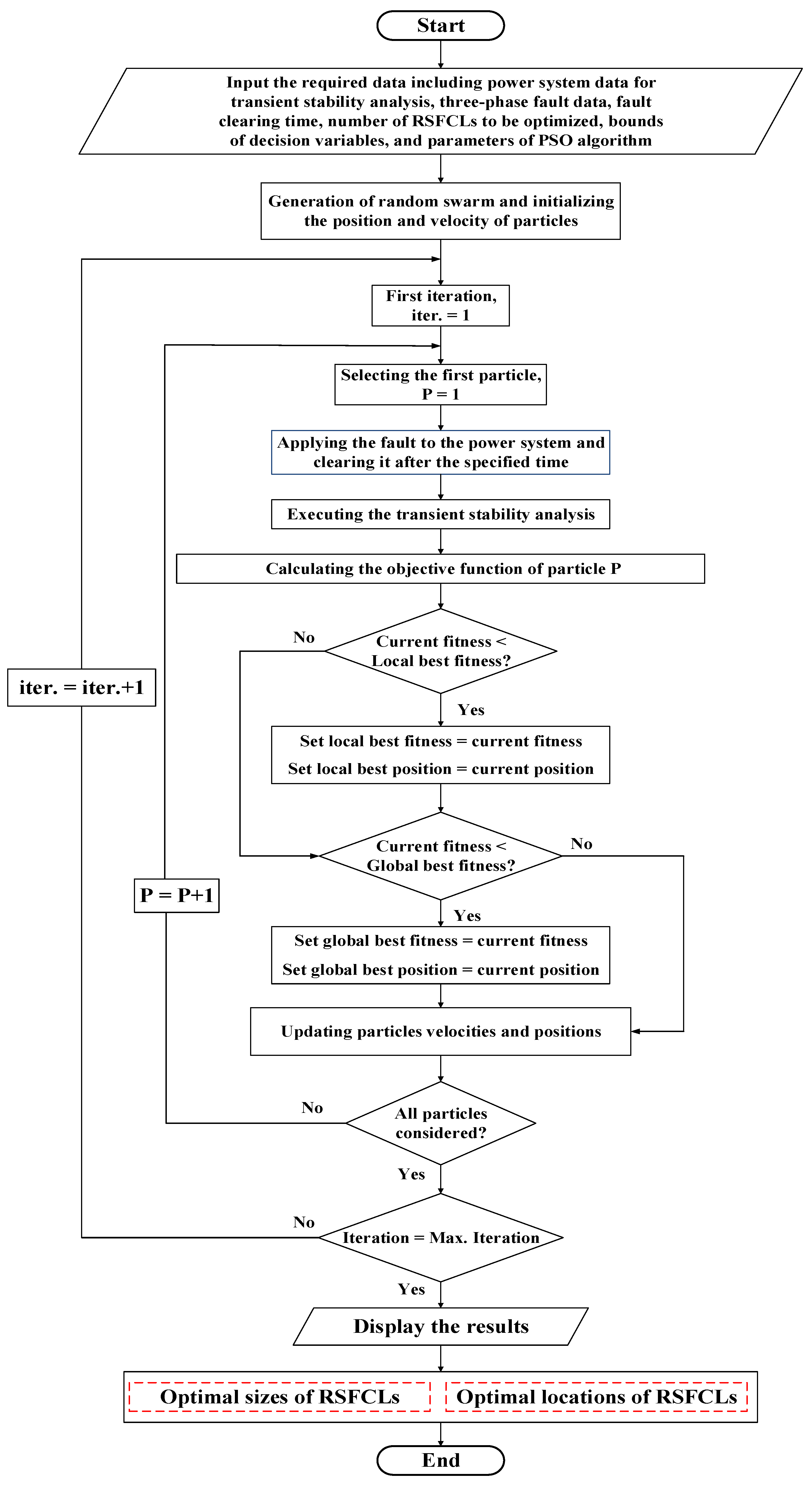
4.2. The Proposed PSO-Based Optimization Algorithm
5. Numerical Studies
6. Simulation Results and Discussion
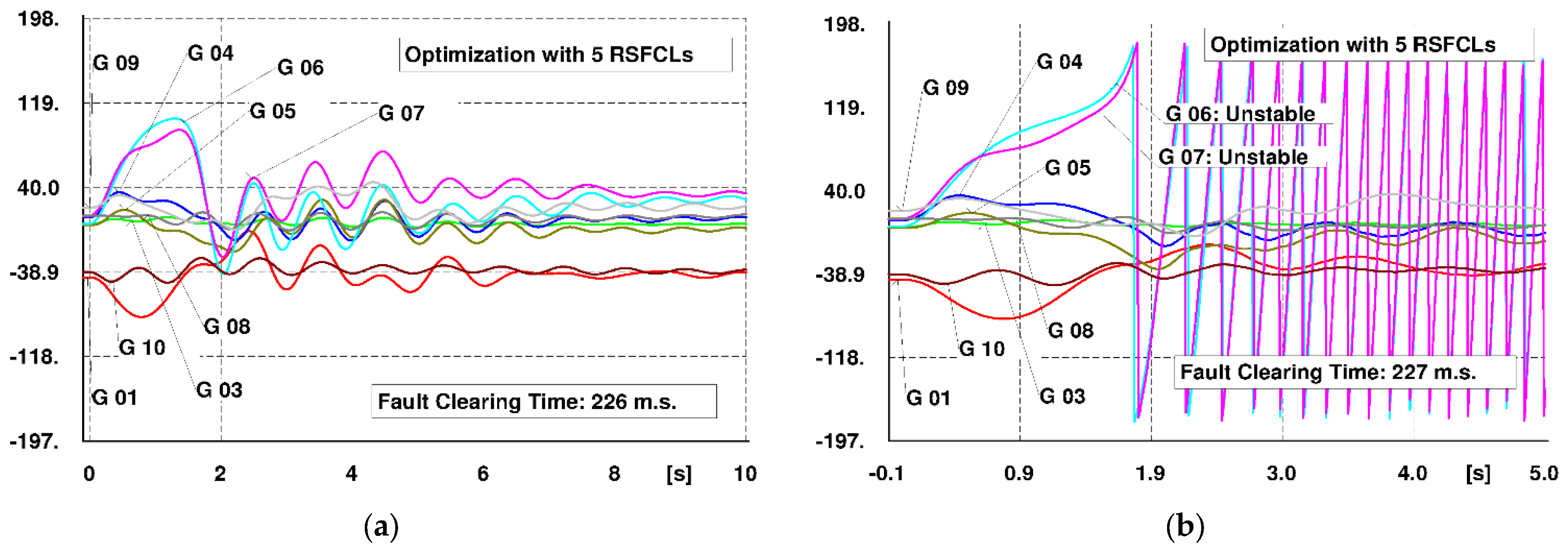
6.1. CCT Enhancement
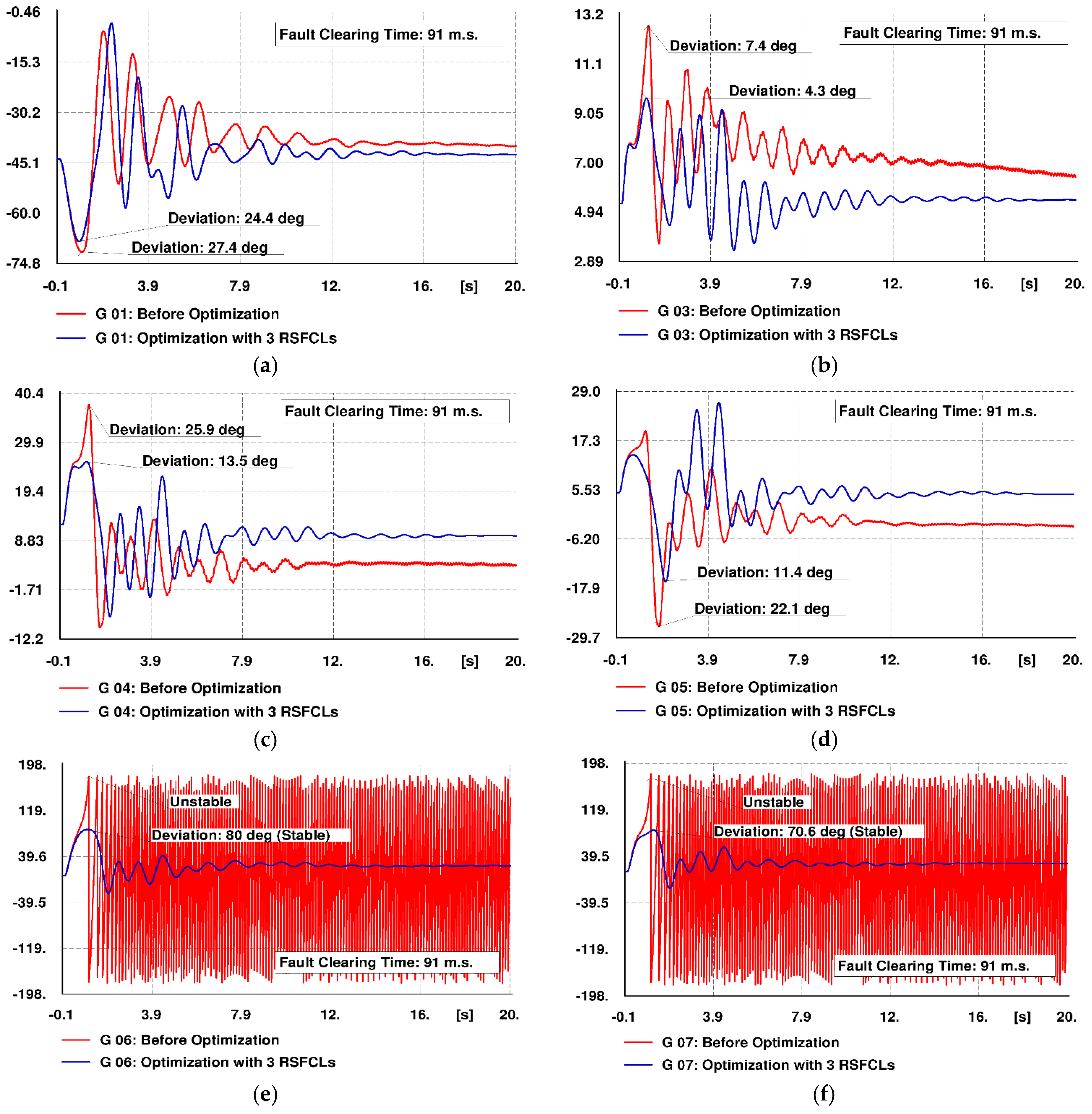
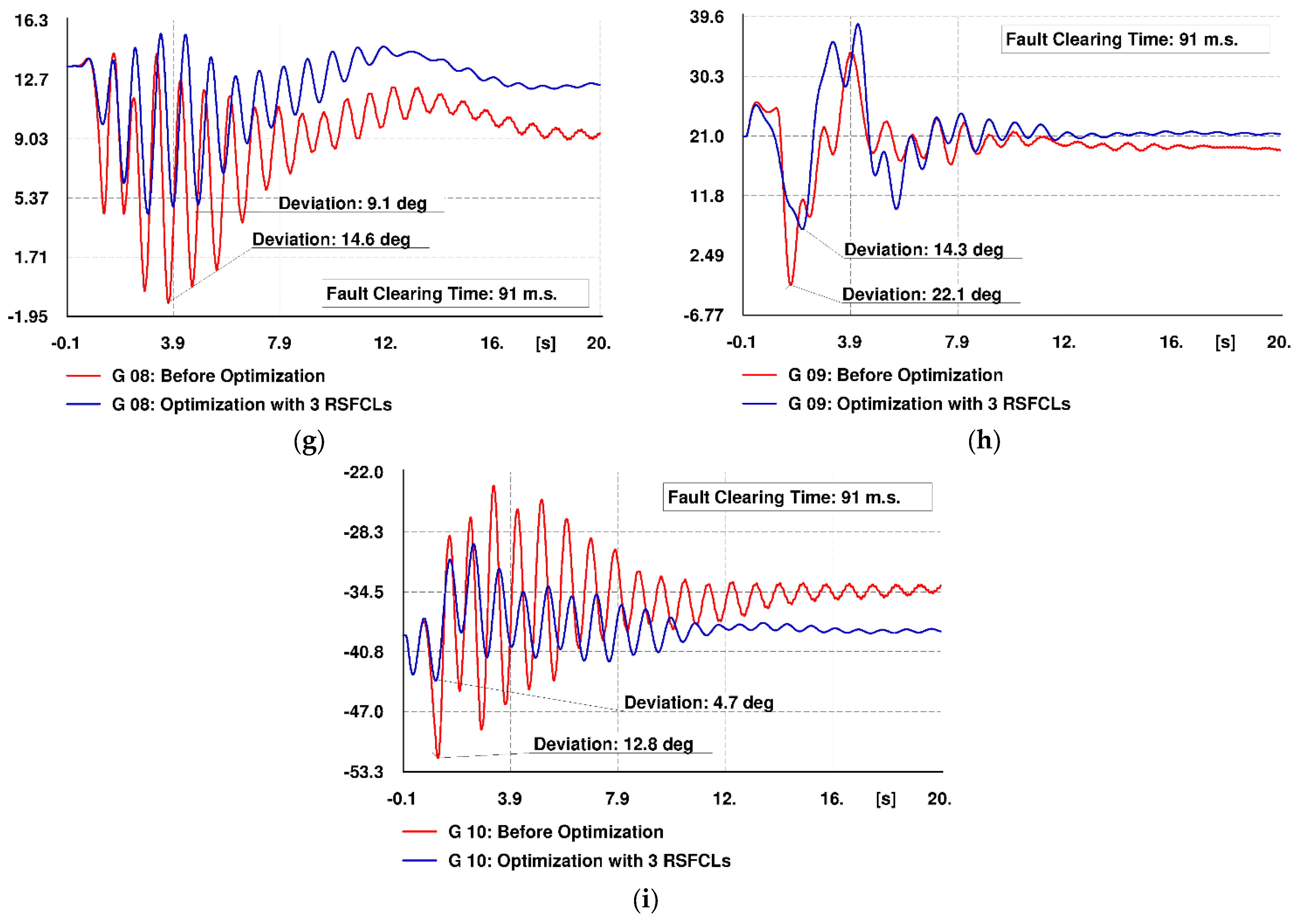
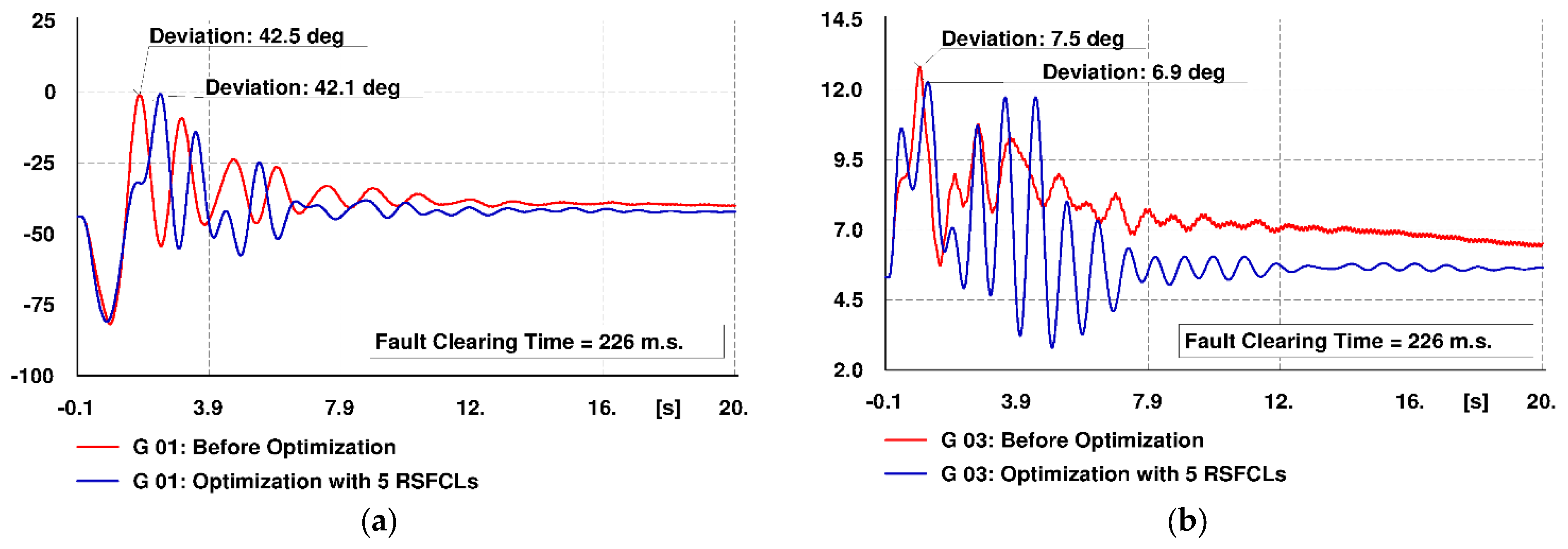
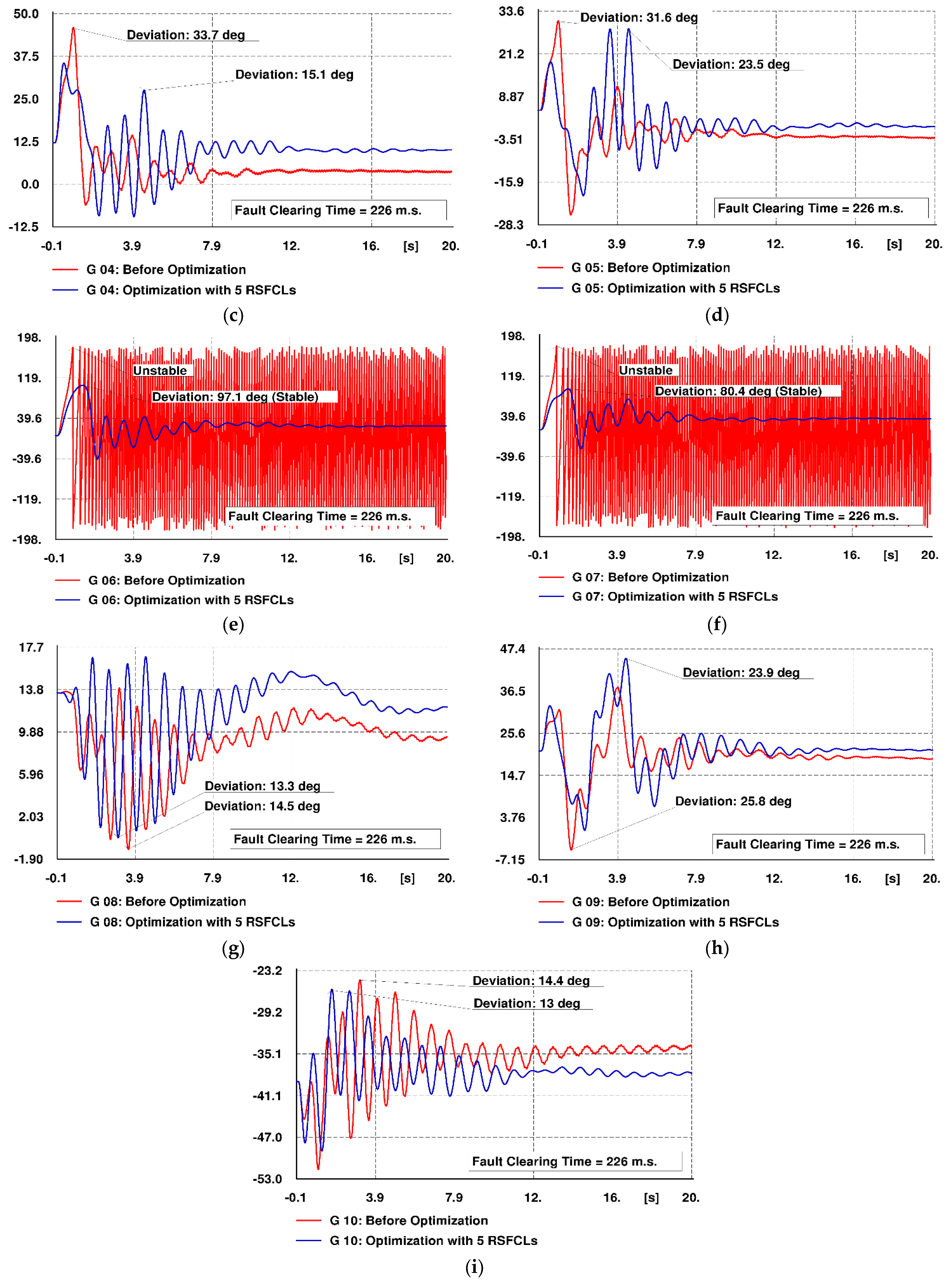
6.2. Improvement of Rotor Angle Deviations
6.2.1. Scenario 1: Optimization of Three Candidate RSFCLs
6.2.2. Optimization of 5 Candidate RSFCLs
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
- Abbreviations
| FCL | Fault current limiter |
| SFCL | Superconducting fault current limiter |
| RSFCL | Resistive-type superconducting fault current limiter |
| CCT | Critical fault clearing time |
| PSO | Particle swarm optimization |
| FCT | Fault clearing time |
| p.u. | Per unit |
- B.
- Indices and sets
| NG | Set of generation buses |
| NB | Set of power system buses |
| NL | Set of power system loads |
| NCR | Set of candidate RSFCLs |
| Set of locations for candidate RSFCLs | |
| Set of size decision variables (continuous variables) | |
| Set of location decision variables (integers) | |
| Nnsg | Set of non-slack generators |
| j | Index of non-slack generators |
| X | Set of decision variables, |
| i | Index of buses |
- C.
- Parameters and variables
| δ | Rotor angle of generator in electrical radians |
| Pm | Mechanical power input of generator in p.u. |
| Pe | Electrical power output of generator in p.u. |
| H | Inertia constant of generator in MW-s/MVA |
| ω0 | Nominal speed of generator in electrical radian/s |
| OF | Objective function |
| δj(t) | Rotor angle magnitude of the jth generator at time t with reference to the slack generator |
| n | Number of generators in the power system |
| GSL | Slack bus generator (reference machine) |
| CR | Number of candidate RSFCLs to be optimized |
| Generated active power (MW) and reactive power (MVAR) at bus i | |
| Active (MW) and reactive (MVAR) loads at bus i | |
| Minimum active power (MW) and reactive power (MVAR) of generator i | |
| Maximum active power (MW) and reactive power (MVAR) of generator i | |
| Voltage magnitude (p.u.) and angle (degree) of bus i | |
| Voltage magnitude (p.u.) and angle (degree) of bus j | |
| Voltage angle (degree) of the reference bus | |
| Admittance Amplitude (p.u.) and angle (degree) of line between buses i and j | |
| Value of candidate RSFCLs (p.u.) | |
| Maximum value of candidate RSFCL (p.u.) | |
| Location of the candidate RSFCLs | |
| Inertia weight in the PSO | |
| r1 | Cognitive factor |
| r2 | Social factor |
| C | Constriction factor |
| C1, C2 | Acceleration constants |
| Current velocity of the ith particle | |
| Next velocity of the ith particle | |
| Current position of the ith particle | |
| Next position of the ith particle | |
| Rm | The maximum resistance that the RSFCL can inject into the power system (p.u.) |
| TSc | The time of transition from the superconducting state to the normal state in the RSFCL |
References
- Hussain, A.; Kim, C.-H.; Mehdi, A. A Comprehensive Review of Intelligent Islanding Schemes and Feature Selection Techniques for Distributed Generation System. IEEE Access 2021, 9, 146603–146624. [Google Scholar] [CrossRef]
- Mehdi, A.; Kim, C.-H.; Hussain, A.; Kim, J.-S.; Jarjees Ul Hassan, S. A comprehensive review of auto-reclosing schemes in AC, DC, and hybrid (AC/DC) transmission lines. IEEE Access 2021, 9, 74325–74342. [Google Scholar] [CrossRef]
- Safaei, A.; Zolfaghari, M.; Gilvanejad, M.; Gharehpetian, G.B. A survey on fault current limiters: Development and technical aspects. Int. J. Electr. Power Energy Syst. 2020, 118, 105729. [Google Scholar] [CrossRef]
- Superconducting Fault Current Limiters: Technology Watch; EPRI: Palo Alto, CA, USA, 2009.
- Schmitt, H. Fault current limiters report on the activities of CIGRE WG A3.16. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006. [Google Scholar] [CrossRef]
- Hussain, A.; Kim, C.-H.; Admasie, S. An intelligent islanding detection of distribution networks with synchronous machine DG using ensemble learning and canonical methods. IET Gener. Transm. Distrib. 2021, 23, 3242–3255. [Google Scholar] [CrossRef]
- Hooshyar, H.; Heydari, H.; Savaghebi, M.; Sharifi, R.; Shahbazi, B. An investigation on optimum volume of superconducting element of RSFCL considering harmonic generation. In Proceedings of the 2008 3rd IEEE Conference on Industrial Electronics and Applications, Singapore, 3–5 June 2008. [Google Scholar] [CrossRef][Green Version]
- Haider, W.; Hassan, S.J.U.; Mehdi, A.; Hussain, A.; Adjayeng, G.O.M.; Kim, C.-H. Voltage Profile Enhancement and Loss Minimization Using Optimal Placement and Sizing of Distributed Generation in Reconfigured Network. Machines 2021, 9, 20. [Google Scholar] [CrossRef]
- Hooshyar, H.; Savaghebi, M. RSFCL optimum shunt resistance determination to enhance power system transient stability. In Proceedings of the 2008 43rd International Universities Power Engineering Conference, Padua, Italy, 1–4 September 2008. [Google Scholar] [CrossRef]
- Hongesombut, K.; Mitani, Y.; Tsuji, K. Optimal location assignment and design of superconducting fault current limiters applied to loop power systems. IEEE Trans. Appl. Supercond. 2003, 13, 1828–1831. [Google Scholar] [CrossRef]
- Sung, B.C.; Park, J.-W. Study on a series resistive SFCL to improve power system transient stability: Modelig, Simulation, and Experimental verification. IEEE Trans. Ind. Electron. 2009, 56, 2412–2419. [Google Scholar] [CrossRef]
- Yagami, M.; Shibata, S.; Murata, T.; Tamura, J. Improvement of power system transient stability by superconducting fault current limiter. In Proceedings of the IEEE/PES Transmission and Distribution Conference and Exhibition, Yokohama, Japan, 6–10 October 2002; Volume 1, pp. 359–364. [Google Scholar] [CrossRef]
- Tsuda, M.; Mitani, Y.; Tsuji, K.; Kakihana, K. Application of resistor based superconducting fault current limiter to enhancement of power system transient stability. IEEE Trans. Appl. Supercond. 2001, 11, 2122–2125. [Google Scholar] [CrossRef]
- Emhemed, A.S.; Tumilty, R.M.; Singh, N.K.; Burt, G.M.; McDonald, J.R. Analysis of Transient Stability Enhancement of LV-Connected Induction Microgenerators by Using Resistive-Type Fault Current Limiters. IEEE Trans. Power Syst. 2010, 25, 885–893. [Google Scholar] [CrossRef]
- Sadi, M.A.H.; Ali, M.H. Combined operation of SFCL and optimal reclosing of circuit breakers for power system transient stability enhancement. In Proceedings of the 2013 Proceedings of IEEE Southeastcon, Jacksonville, FL, USA, 4–7 April 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Tephiruk, N.; Hongesombut, K.; Kerdphol, T. Robust control of combined optimized resistive FCL and ECS for power system transient stability improvement. In Proceedings of the 2014 International Electrical Engineering Congress (iEECON), Chonburi, Thailand, 19–21 March 2014. [Google Scholar] [CrossRef]
- Rao, M.U.M.; Rosalina, K.M. Improvement of transient stability in micro grids using RSFCL with series active power filter. SN Appl. Sci. 2019, 1, 1633. [Google Scholar] [CrossRef]
- Tariverdi, F.; Doroudi, A. Selection of Resistive and Inductive Superconductor Fault Current Limiters Location Considering System Transient Stability. J. Electr. Power Energy Convers. Syst. (JEPECS) 2016, 1, 72–78. [Google Scholar]
- Didier, G.; Bonnard, C.; Lubin, T.; Lévêque, J. Comparison between inductive and resistive SFCL in terms of current limitation and power system transient stability. Electr. Power Syst. Res. 2015, 125, 150–158. [Google Scholar] [CrossRef]
- Didier, G.; Lévêque, J.; Rezzoug, A. A novel approach to determine the optimal location of SFCL in electric power grid to improve power system stability. IEEE Trans. Power Syst. 2013, 28, 978–984. [Google Scholar] [CrossRef]
- Khatibi, M.; Bigdeli, M. Transient Stability Improvement of Power Systems by Optimal Sizing and Allocation of Resistive Superconducting Fault Current Limiters Using Particle Swarm Optimization. Adv. Energy Int. J. 2014, 1, 11–27. [Google Scholar]
- Saadat, H. Power System Analysis, 3rd ed.PSA publishing LLC: Alexandria, VA, USA, 2011. [Google Scholar]
- DIgSILENT GmbH, Heinrich-Hertz-Str. 9, 72810 Gomaringen, Germany. Available online: www.digsilent.de (accessed on 23 March 2021).
- Arman Safaei, M.Z.; Gilvanejad, M. A Strategic Plan for Implementation of Fault Current Limiters in Iran’s Power Grid; Niroo Research Institute: Tehran, Iran, 2018. [Google Scholar]
- Noe, M.; Steurer, M. High-temperature superconductor fault current limiters: Concepts, applications, and development status. Supercond. Sci. Technol. 2007, 20, R15. [Google Scholar] [CrossRef]
- Kalinov, A.V.; Voloshin, I.F.; Fisher, L.M. SPICE model of high-temperature superconducting tape: Application to resistive fault-current limiter. Supercond. Sci. Technol. 2017, 30, 054002. [Google Scholar] [CrossRef]
- Zhang, X. Resistive-Type Superconducting Fault Current Limiter (RSFCL) and Its Application in Power Systems. Ph.D. Thesis, Churchill College University of Cambridge, Cambridge, UK, 2017. [Google Scholar]
- Ruiz, H.S.; Zhang, X.; Coombs, T.A. Resistive-Type Superconducting Fault Current Limiters: Concepts, Materials, and Numerical Modeling. IEEE Trans. Appl. Supercond. 2015, 25, 1–5. [Google Scholar] [CrossRef]
- Mafra, G.R.F.Q.; Sotelo, G.G.; Fortes, M.Z.; de Sousa, W.T.B. Application of resistive superconducting fault current limiters in offshore oil production platforms. Electr. Power Syst. Res. 2016, 144, 107–114. [Google Scholar] [CrossRef]
- Okakwu, P.; Orukpe, E.; Ogujor, E.A. Apolication of Superconducting Fault Current Limiter (SFCL) in Power Systems: A review. EJERS Eur. J. Eng. Res. Sci. 2018, 3, 28–32. [Google Scholar] [CrossRef]
- Hooshyar, H.; Heydari, H.; Savaghebi, M.; Sharifi, R. Resistor Type Superconducting Fault Current Limiter: Optimum Shunt Resistance Determination to Enhance Power System Transient Stability. IEEJ Trans. Power Energy 2009, 129, 299–308. [Google Scholar] [CrossRef]
- Morandi, A. State of the art of superconducting fault current limiters and their application to the electric power system. Phys. C Supercond. 2013, 484, 242–247. [Google Scholar] [CrossRef]
- Kalsi, S.S.; Malozemoff, A. HTS Fault Current Limiter Concept. IEEE Trans. Appl. Supercond. 2004, 2, 1426–1430. [Google Scholar]
- Mandic, M.; Juric-Grgic, I.; Grulovic-Plavljanic, N. Improving time integration scheme for FET analysis of power system angle stability. Electron. Energetics 2020, 33, 119–131. [Google Scholar] [CrossRef]
- Radan, M.; Dinan, A.T. Power System Transient Stability Analysis Based on the Development and Evaluation Methods. Int. J. Smart Electr. Eng. 2016, 5, 169–173. [Google Scholar]
- Odun-Ayo, T.; Crow, M.L. An analysis of power system transient stability using stochastic energy functions. Int. Trans. Electr. Energy Syst. 2013, 23, 151–165. [Google Scholar] [CrossRef]
- Ferraro, R.M. Method of Modeling the Swing Equation Using Time Synchronized. Master’s Thesis, Portland State University, Portland, OR, USA, 2021. Paper 5729. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; McGraw Hill: New York, NY, USA, 1994. [Google Scholar]
- Messalti, S.; Belkhiat, S. Comparative Study of Resistive and Inductive Superconducting Fault Current Limiters SFCL for Power System Transient Stability Improvement. J. Supercond. Nov. Magn. 2013, 26, 3009–3015. [Google Scholar] [CrossRef]
- Sengupta, S.; Basak, S.; Peters, R.A. Particle Swarm Optimization: A Survey of Historical and Recent Developments with Hybridization Perspectives. Mach. Learn. Knowl. Extr. 2018, 1, 157–191. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November—1 December 1995; pp. 1942–1948. [Google Scholar]
- Hu, X.; Eberhart, R. Solving Constrained Nonlinear Optimization Problem with Particle Swarm Optimization; Purdue University: West Lafayette, IN, USA, 2002. [Google Scholar]
- Clerc, M. Particle Swarm Optimization; Antony Rowe Ltd Publication: Chippenham, UK, 2006. [Google Scholar]
- Pai, M.A. Energy Function Analysis for Power System Stability; Kluwer Academic Publishers: Boston, MA, USA, 1989; pp. 223–227. [Google Scholar]
- Priyadi, A.; Sari, T.P.; Dwi S., W.; Yorino, N.; Purnomo, M.H. Determining Critical Clearing Time Based on Critical Trajectory Method using Unbalance Fault. In Proceedings of the 2019 International Seminar on Intelligent Technology and Its Applications (ISITIA), Surabaya, Indonesia, 28–29 August 2019. [Google Scholar] [CrossRef]
- Determining Generator Fault Clearing Time for the Synchronous Zone of Continental Europe; RG-CE System Protection & Dynamics Sub Group: Brussels, Belgium, 2017; Available online: www.entsoe.eu (accessed on 29 June 2020).
- Kastinen, P.; Fuengwarodsakul, N.; Wangdee, W. Investigation of Critical Fault Clearing Time by Applying Different Excitation System Models. In Proceedings of the 2019 Research, Invention, and Innovation Congress (RI2C), Bangkok, Thailand, 11–13 December 2019. [Google Scholar] [CrossRef]
- Sharma, S.; Pushpak, S.; Chinde, V.; Dobson, I. Sensitivity of Transient Stability Critical Clearing Time. IEEE Trans. Power Syst. 2018, 33, 6476–6486. [Google Scholar] [CrossRef]
- Ghani, A.M. Improving Stability by Enhancing Critical Fault Clearing Time. Master’s Thesis, University of South Florida, Tampa, FL, USA, 2019. Available online: https://scholarcommons.usf.edu/etd/7793 (accessed on 28 April 2021).






| Item | Number of Iterations: | Swarm Size: | PSO Setting Parameters: | Bounds of Variables | |||
|---|---|---|---|---|---|---|---|
| C1 | C2 | C | Location | Size | |||
| Value | 1000 | 40 | 2.05 | 2.05 | 0.85 | (1–46) | (0–0.025) |
| Item | Value |
|---|---|
| Fault type | Symmetrical three-phase |
| Fault location | Line (21–22), close to bus 22 |
| Fault clearing time: | 300 (m.s.) |
| Scenario | RSFCL Location (bus i–bus i’) | RSFCL Size (p.u.) | Objective Function Value |
|---|---|---|---|
| Scenario 1: (3 RSFCLs) | (35–22) | 0.013885 | 1939.500 |
| (36–23) | 0.021661 | ||
| (38–29) | 0.006964 | ||
| Scenario 2: (5 RSFCLs) | (35–22) | 0.014138 | 1793.600 |
| (36–23) | 0.023494 | ||
| (20–19) | 0.024524 | ||
| (12–11) | 0.021002 | ||
| (39–9) | 0.005074 |
| Scenario | Without Employing RSFCLs | Scenario 1 (3 RSFCLs) | Scenario 2 (5 RSFCLs) |
|---|---|---|---|
| CCT (m.s.) | 80 | 91 | 226 |
| Maximum Rotor Angle Deviation (Degrees) | ||||
|---|---|---|---|---|
| Scenario 1 (3 RSFCLs) | Scenario 2 (5 RSFCLs) | |||
| Generator No. | Without RSFCLs | With RSFCLs | Without RSFCLs | With RSFCLs |
| G1 | 27.4 | 24.4 | 42.5 | 42.1 |
| G3 | 7.4 | 4.3 | 7.5 | 6.9 |
| G4 | 25.9 | 13.5 | 33.7 | 15.1 |
| G5 | 22.1 | 11.4 | 31.6 | 23.5 |
| G6 | Unstable | 80 | Unstable | 97.1 |
| G7 | Unstable | 70.6 | Unstable | 80.4 |
| G8 | 14.6 | 9.1 | 14.5 | 13.3 |
| G9 | 22.1 | 14.3 | 25.6 | 23.9 |
| G10 | 12.8 | 4.7 | 14.4 | 13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khatibi, M.; Jalilzadeh, S.; Hussain, A.; Haider, W. A PSO-Based Approach for Optimal Allocation and Sizing of Resistive-Type SFCLs to Enhance the Transient Stability of Power Systems. Electronics 2022, 11, 3980. https://doi.org/10.3390/electronics11233980
Khatibi M, Jalilzadeh S, Hussain A, Haider W. A PSO-Based Approach for Optimal Allocation and Sizing of Resistive-Type SFCLs to Enhance the Transient Stability of Power Systems. Electronics. 2022; 11(23):3980. https://doi.org/10.3390/electronics11233980
Chicago/Turabian StyleKhatibi, Masoud, Saeid Jalilzadeh, Arif Hussain, and Waseem Haider. 2022. "A PSO-Based Approach for Optimal Allocation and Sizing of Resistive-Type SFCLs to Enhance the Transient Stability of Power Systems" Electronics 11, no. 23: 3980. https://doi.org/10.3390/electronics11233980
APA StyleKhatibi, M., Jalilzadeh, S., Hussain, A., & Haider, W. (2022). A PSO-Based Approach for Optimal Allocation and Sizing of Resistive-Type SFCLs to Enhance the Transient Stability of Power Systems. Electronics, 11(23), 3980. https://doi.org/10.3390/electronics11233980