Assessment and Improvement of the Pattern Recognition Performance of Memdiode-Based Cross-Point Arrays with Randomly Distributed Stuck-at-Faults
Abstract
1. Introduction
2. Previous Related Works
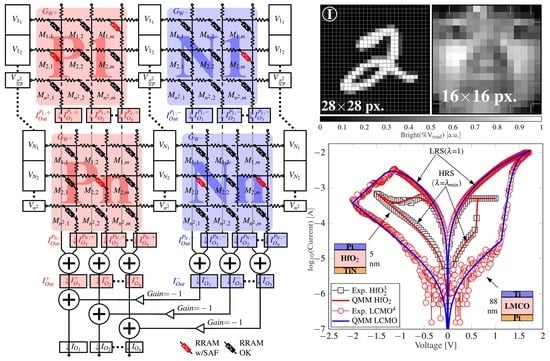
2.1. CPA Modelling
2.2. Simulation Platform
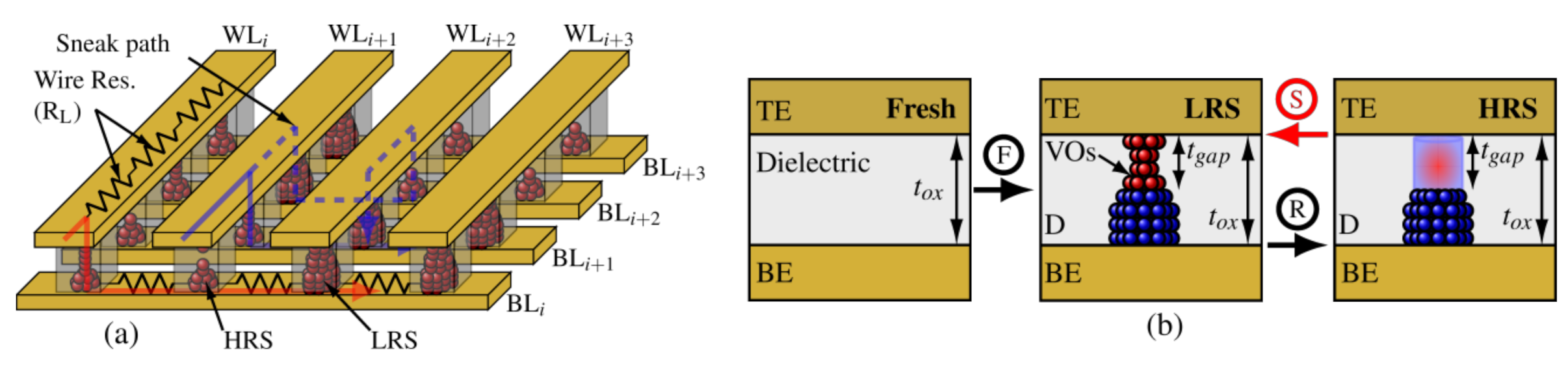
2.3. RRAM Models
2.4. Alternative RRAM Integration Structures
2.5. Costs Associated with the Mitigation of SAF Effects
3. Materials and Methods
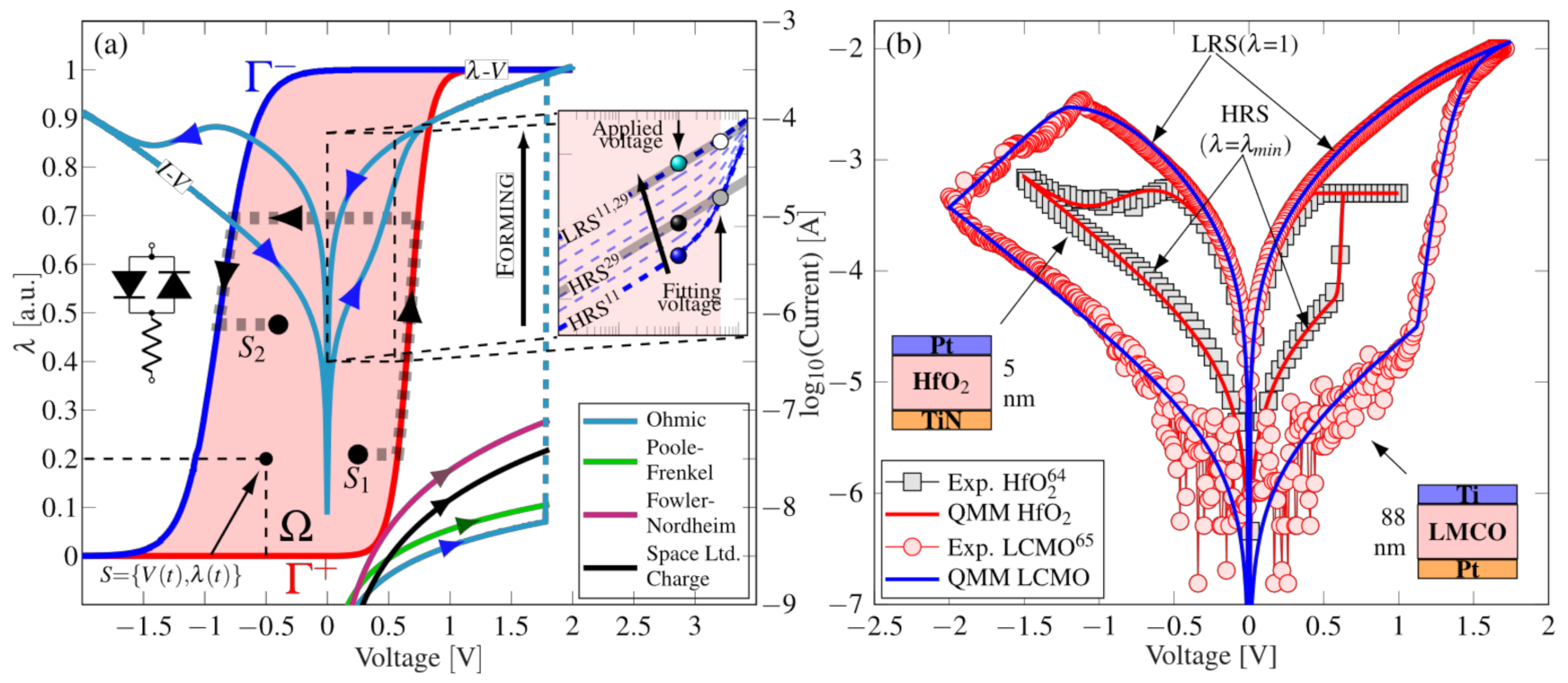
3.1. Quasi-Static Memdiode Model
3.2. Procedure for SPICE CPA Creation, Training, and Simulation
4. Results and Discussion
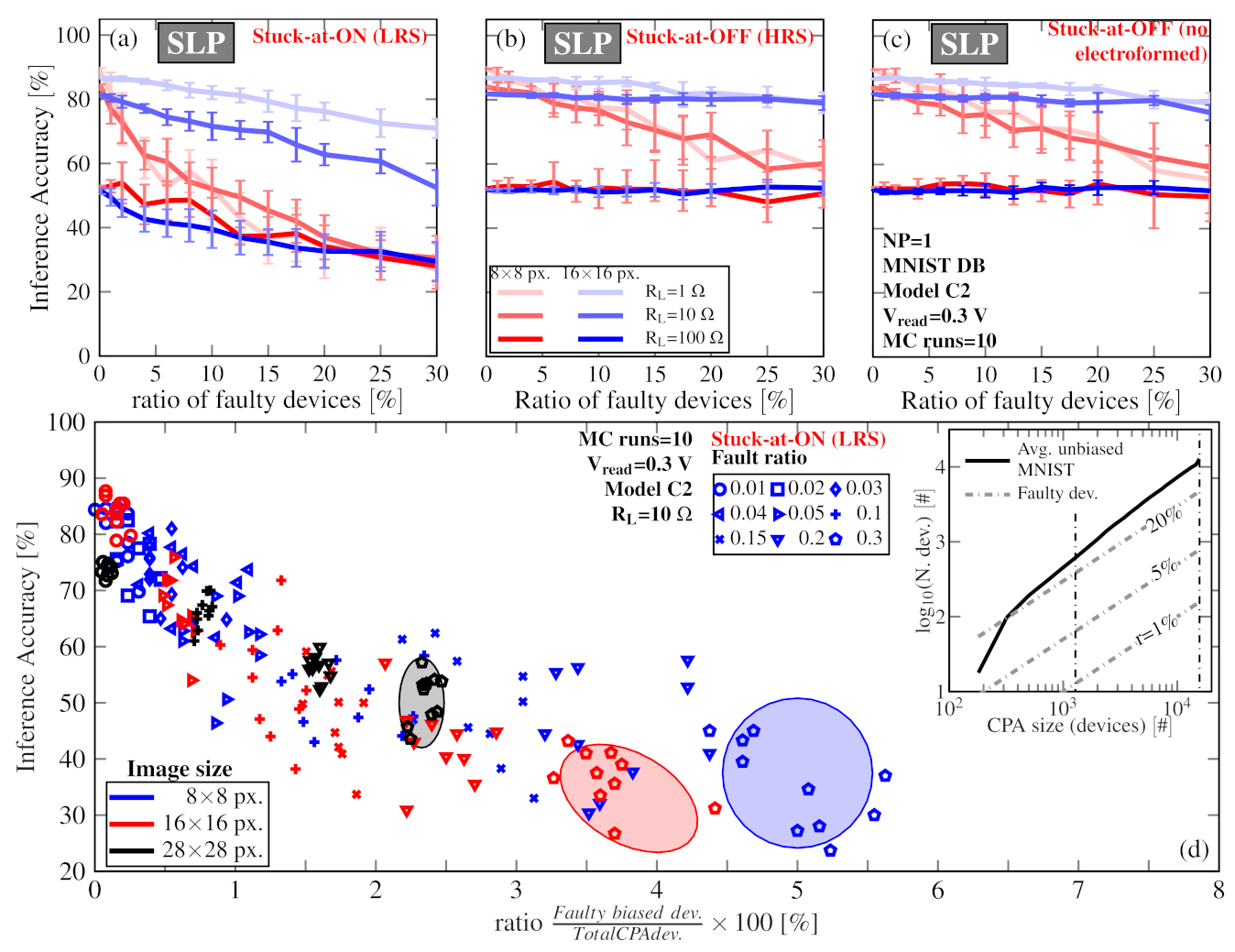
4.1. Impact of the CPA Parasitics on the Recognition Accuracy
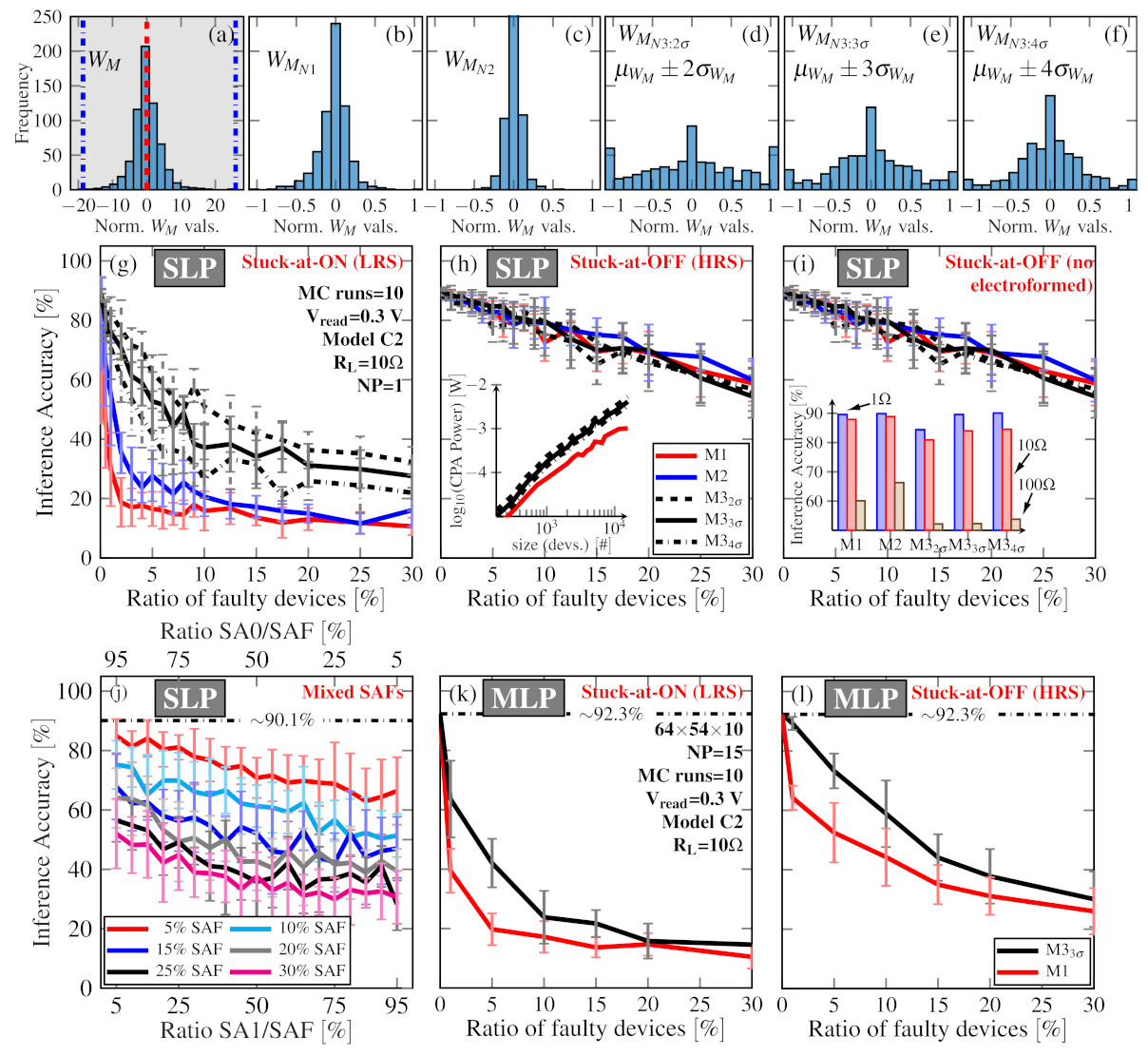
4.2. Impact of the Fault Ratio on the Inference Accuracy
4.2.1. Impact of the Normalisation Method (NM)
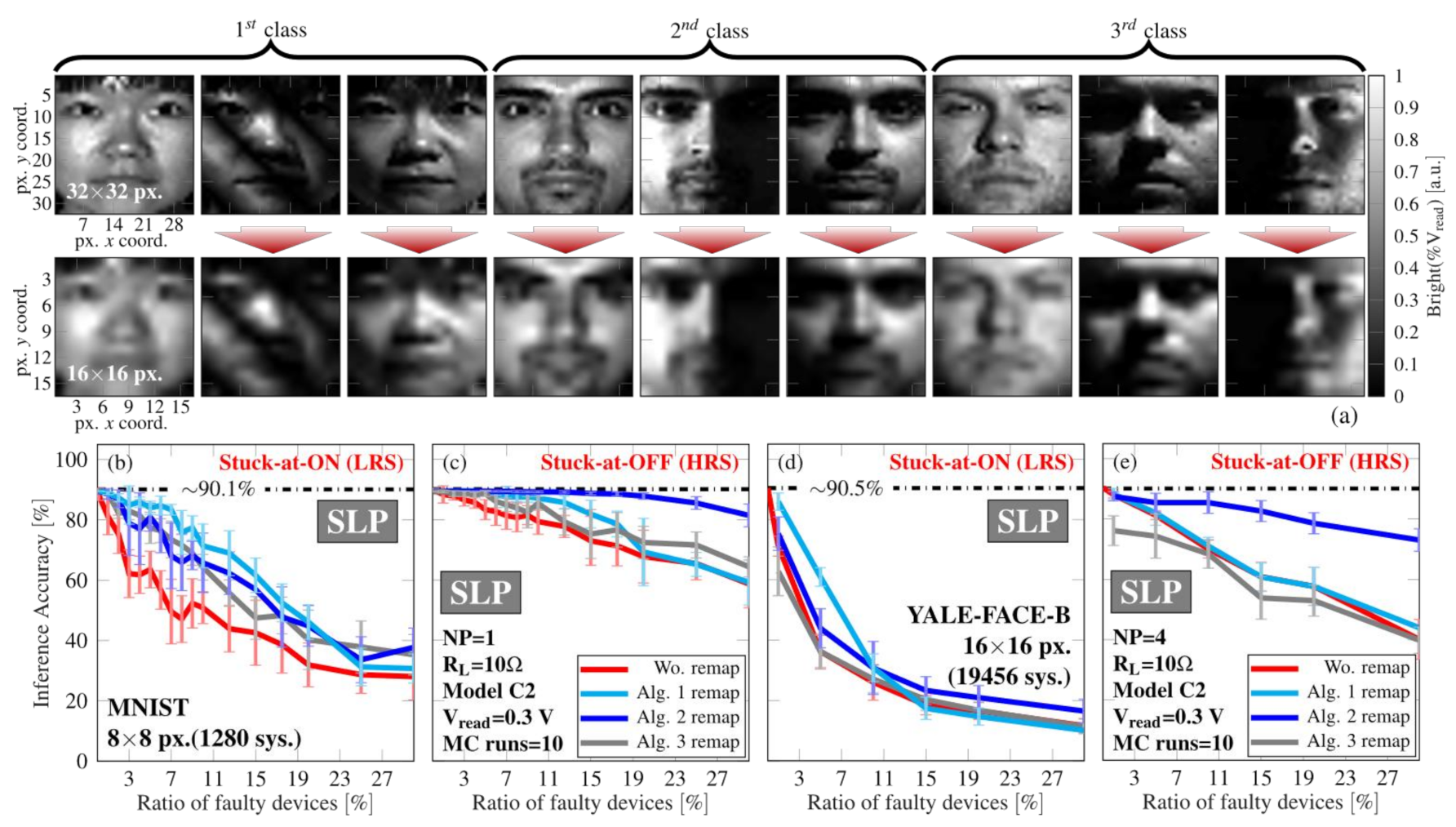
4.2.2. Influence of the Line Resistance (RL) and Image Size (n × n)
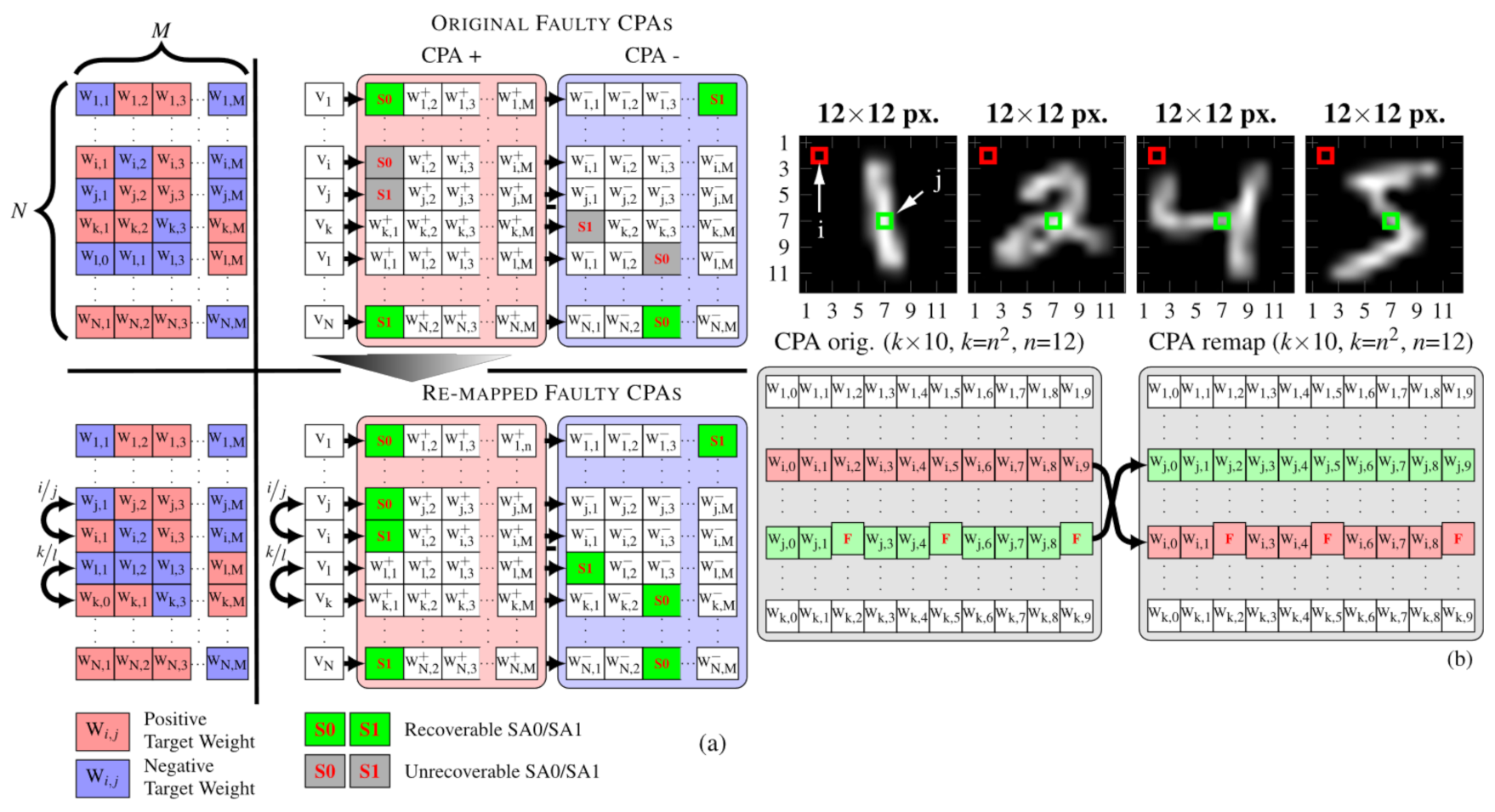
5. CPA Remapping Procedures
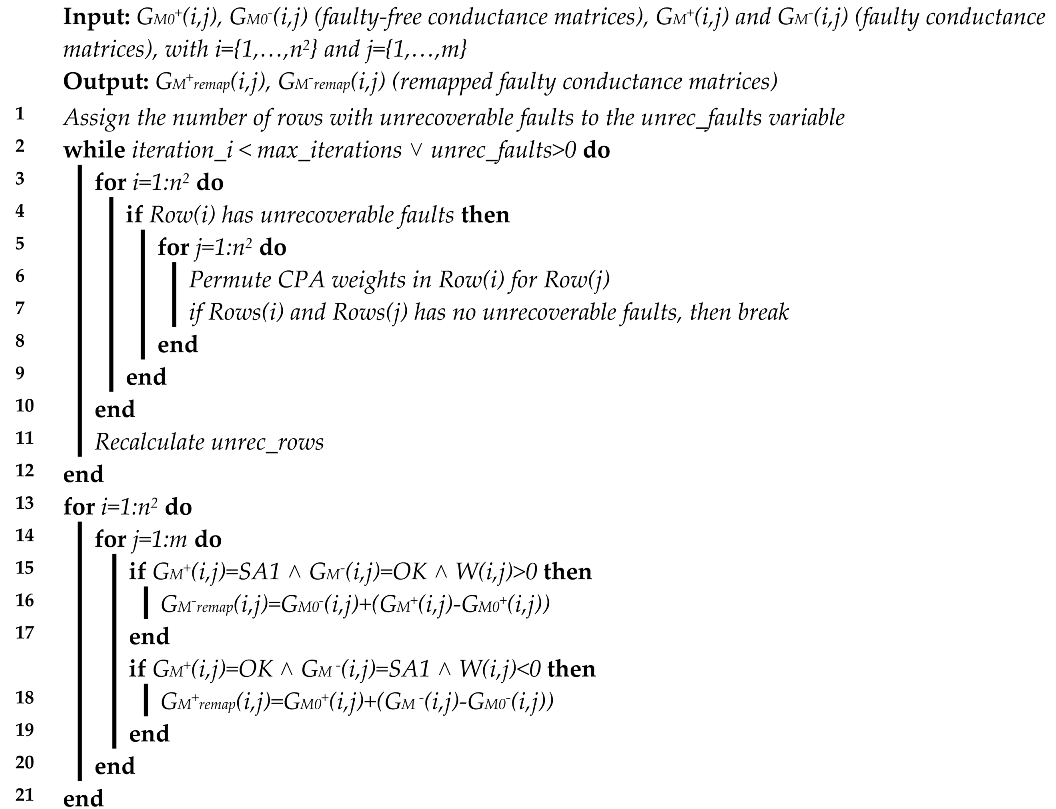
5.1. Algorithm 1: Fault-Tolerant Adaptative Mapping
| Algorithm 1: Fault-tolerant adaptive mapping |
 |
5.2. Algorithm 2: SWV-Minimisation-Based Row Permutation
| Algorithm 2: SWV-minimisation-based row permutation |
 |
5.3. Algorithm 3: Mean-Bias-Dependent Mapping
| Algorithm 3: Mean-bias-dependent mapping |
 |
5.4. Performance of the CPA-Remapping Algorithms
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- International Technology Roadmap for Semiconductors (ITRS). Edition 2.0. 2015. Available online: https://www.semiconductors.org/wp-content/uploads/2018/06/0_2015-ITRS-2.0-Executive-Report-1.pdf (accessed on 1 June 2021).
- Hu, M.; Li, H.; Chen, Y.; Wu, Q.; Rose, G.S.; Linderman, R.W. Memristor crossbar-based neuromorphic computing system: A case study. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 1864–1878. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.; Gao, B.; Fang, Z.; Yu, H.; Kang, J.; Wong, H.-S.P. A Low Energy Oxide-Based Electronic Synaptic Device for Neuromorphic Visual Systems with Tolerance to Device Variation. Adv. Mater. 2013, 25, 1774–1779. [Google Scholar] [CrossRef] [PubMed]
- Freitas, R.F.; Wilcke, W.W. Storage-class memory: The next storage system technology. IBM J. Res. Dev. 2008, 52, 439–447. [Google Scholar] [CrossRef]
- Upadhyay, N.K.; Joshi, S.; Yang, J.J. Synaptic electronics and neuromorphic computing. Sci. China Inf. Sci. 2016, 59, 061404. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, T.; Xia, L.; Li, B.; Gu, P.; Li, H.; Xie, Y.; Yang, H. Energy efficient RRAM spiking neural network for real time classification. In Proceedings of the ACM Great Lakes Symposium on VLSI, GLSVLSI, Pittsburgh, PA, USA, 20–22 May 2015; Association for Computing Machinery: New York, NY, USA, 2015; pp. 189–194. [Google Scholar]
- Sasago, Y.; Kinoshita, M.; Morikawa, T.; Kurotsuchi, K.; Hanzawa, S.; Mine, T.; Shima, A.; Fujisaki, Y.; Kume, H.; Moriya, H.; et al. Cross-point phase change memory with 4F2 cell size driven by low-contact-resistivity poly-Si diode. In Proceedings of the Symposium on VLSI Technology, Kyoto, Japan, 15–17 June 2009; pp. 24–25. [Google Scholar]
- Ielmini, D. Resistive switching memories based on metal oxides: Mechanisms, reliability and scaling. Semicond. Sci. Technol. 2016, 31, 063002. [Google Scholar] [CrossRef]
- Aguirre, F.L.; Rodriguez-Fernandez, A.; Pazos, S.M.; Sune, J.; Miranda, E.; Palumbo, F. Study on the Connection Between the Set Transient in RRAMs and the Progressive Breakdown of Thin Oxides. IEEE Trans. Electron Devices 2019, 66, 1–7. [Google Scholar] [CrossRef]
- Miranda, E. Compact Model for the Major and Minor Hysteretic I-V Loops in Nonlinear Memristive Devices. IEEE Trans. Nanotechnol. 2015, 14, 787–789. [Google Scholar] [CrossRef]
- Patterson, G.A.; Sune, J.; Miranda, E. Voltage-Driven Hysteresis Model for Resistive Switching: SPICE Modeling and Circuit Applications. IEEE Trans. Comput. Des. Integr. Circuits Syst. 2017, 36, 2044–2051. [Google Scholar] [CrossRef]
- Truong, S.N.; Min, K.S. New memristor-based crossbar array architecture with 50-% area reduction and 48-% power saving for matrix-vector multiplication of analog neuromorphic computing. J. Semicond. Technol. Sci. 2014, 14, 356–363. [Google Scholar] [CrossRef]
- Truong, S.N.; Shin, S.H.; Byeon, S.D.; Song, J.S.; Min, K.S. New Twin Crossbar Architecture of Binary Memristors for Low-Power Image Recognition with Discrete Cosine Transform. IEEE Trans. Nanotechnol. 2015, 14, 1104–1111. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef]
- Gu, P.; Li, B.; Tang, T.; Yu, S.; Cao, Y.; Wang, Y.; Yang, H. Technological exploration of RRAM crossbar array for matrix-vector multiplication. In Proceedings of the 20th Asia and South Pacific Design Automation Conference, Chiba, Japan, 19–22 January 2015. [Google Scholar]
- Li, B.; Wang, Y.; Chen, Y.; Li, H.H.; Yang, H. ICE: Inline Calibration for Memristor Crossbar-Based Computing Engine. In Proceedings of the 2014 Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 24–28 March 2014. [Google Scholar]
- Liu, C.; Hu, M.; Strachan, J.P.; Li, H.H. Rescuing Memristor-based Neuromorphic Design with High Defects. In Proceedings of the 2017 54th ACM/EDAC/IEEE Design Automation Conference (DAC), Austin, TX, USA, 18–22 June 2017. [Google Scholar]
- Degraeve, R.; Fantini, A.; Raghavan, N.; Goux, L.; Clima, S.; Govoreanu, B.; Belmonte, A.; Linten, D.; Jurczak, M. Causes and consequences of the stochastic aspect of filamentary RRAM. Microelectron. Eng. 2015, 147, 171–175. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Degraeve, R.; Clima, S.; Govoreanu, B.; Goux, L.; Fantini, A.; Kar, G.S.; Pourtois, G.; Groeseneken, G.; Wouters, D.J.; et al. Understanding of the endurance failure in scaled HfO2-based 1T1R RRAM through vacancy mobility degradation. In Proceedings of the 2012 International Electron Devices Meeting, San Francisco, CA, USA, 10–13 December 2012. [Google Scholar]
- Chen, C.Y.; Shih, H.C.; Wu, C.W.; Lin, C.H.; Chiu, P.F.; Sheu, S.S.; Chen, F.T. RRAM defect modeling and failure analysis based on march test and a novel squeeze-search scheme. IEEE Trans. Comput. 2015, 64, 180–190. [Google Scholar] [CrossRef]
- Xia, L.; Huangfu, W.; Tang, T.; Yin, X.; Chakrabarty, K.; Xie, Y.; Wang, Y.; Yang, H. Stuck-at Fault Tolerance in RRAM Computing Systems. IEEE J. Emerg. Sel. Top. Circuits Syst. 2018, 8, 102–115. [Google Scholar] [CrossRef]
- Li, C.; Roth, R.M.; Graves, C.; Sheng, X.; Strachan, J.P. Analog error correcting codes for defect tolerant matrix multiplication in crossbars. In Proceedings of the 2020 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 12–18 December 2020. [Google Scholar]
- Liu, B.; Li, H.; Chen, Y.; Li, X.; Wu, Q.; Huang, T. Vortex: Variation-aware training for memristor X-bar. In Proceedings of the 2015 52nd ACM/EDAC/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 8–12 June 2015. [Google Scholar]
- Ham, S.J.; Mo, H.S.; Min, K.S. Low-Power VDD/3 write scheme with inversion coding circuit for complementary memristor array. IEEE Trans. Nanotechnol. 2013, 12, 851–857. [Google Scholar] [CrossRef]
- Xia, L.; Liu, M.; Ning, X.; Chakrabarty, K.; Wang, Y. Fault-Tolerant Training with On-Line Fault Detection for RRAM-Based Neural Computing Systems. In Proceedings of the 2017 54th ACM/EDAC/IEEE Design Automation Conference (DAC), Austin, TX, USA, 18–22 June 2017. [Google Scholar]
- Liang, J.; Yeh, S.; Simon Wong, S.; Philip Wong, H.S. Effect of wordline/bitline scaling on the performance, energy consumption, and reliability of cross-point memory array. ACM J. Emerg. Technol. Comput. Syst. 2013, 9, 1–14. [Google Scholar] [CrossRef]
- Aguirre, F.L.; Pazos, S.M.; Palumbo, F.; Suñé, J.; Miranda, E. Application of the Quasi-Static Memdiode Model in Cross-Point Arrays for Large Dataset Pattern Recognition. IEEE Access 2020, 8, 1. [Google Scholar] [CrossRef]
- Chen, A. A comprehensive crossbar array model with solutions for line resistance and nonlinear device characteristics. IEEE Trans. Electron Devices 2013, 60, 1318–1326. [Google Scholar] [CrossRef]
- Park, S.; Kim, H.; Choo, M.; Noh, J.; Sheri, A.; Jung, S.; Seo, K.; Park, J.; Kim, S.; Lee, W.; et al. RRAM-based synapse for neuromorphic system with pattern recognition function. In Proceedings of the 2012 International Electron Devices Meeting, San Francisco, CA, USA, 10–13 October 2012. [Google Scholar]
- Liu, B.; Li, H.; Chen, Y.; Li, X.; Huang, T.; Wu, Q.; Barnell, M. Reduction and IR-drop compensations techniques for reliable neuromorphic computing systems. In Proceedings of the 2014 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), San Jose, CA, USA, 2–6 November 2014. [Google Scholar]
- Truong, S.; Ham, S.-J.; Min, K.-S. Neuromorphic crossbar circuit with nanoscale filamentary-switching binary memristors for speech recognition. Nanoscale Res. Lett. 2014, 9, 629. [Google Scholar] [CrossRef]
- Yakopcic, C.; Hasan, R.; Taha, T.M.; McLean, M.R.; Palmer, D. Efficacy of memristive crossbars for neuromorphic processors. Proc. Int. Jt. Conf. Neural Netw. 2014, 15–20. [Google Scholar] [CrossRef]
- Panda, D.; Sahu, P.P.; Tseng, T.Y. A Collective Study on Modeling and Simulation of Resistive Random Access Memory. Nanoscale Res. Lett. 2018, 13. [Google Scholar] [CrossRef]
- Prodromakis, T.; Peh, B.P.; Papavassiliou, C.; Toumazou, C. A versatile memristor model with nonlinear dopant kinetics. IEEE Trans. Electron Devices 2011, 58, 3099–3105. [Google Scholar] [CrossRef]
- Merrikh Bayat, F.; Hoskins, B.; Strukov, D.B. Phenomenological modeling of memristive devices. Appl. Phys. A Mater. Sci. Process. 2015, 118, 779–786. [Google Scholar] [CrossRef][Green Version]
- Yakopcic, C.; Taha, T.M.; Subramanyam, G.; Pino, R.E. Generalized memristive device SPICE model and its application in circuit design. IEEE Trans. Comput. Des. Integr. Circuits Syst. 2013, 32, 1201–1214. [Google Scholar] [CrossRef]
- Kvatinsky, S.; Friedman, E.G.; Kolodny, A.; Weiser, U.C. TEAM: Threshold adaptive memristor model. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 211–221. [Google Scholar] [CrossRef]
- Kvatinsky, S.; Ramadan, M.; Friedman, E.G.; Kolodny, A. VTEAM: A General Model for Voltage-Controlled Memristors. IEEE Trans. Circuits Syst. II Express Briefs 2015, 62, 786–790. [Google Scholar] [CrossRef]
- Eshraghian, K.; Kavehei, O.; Cho, K.R.; Chappell, J.M.; Iqbal, A.; Al-Sarawi, S.F.; Abbott, D. Memristive device fundamentals and modeling: Applications to circuits and systems simulation. Proc. IEEE 2012, 100, 1991–2007. [Google Scholar] [CrossRef]
- Biolek, D.; Biolek, Z.; Biolkova, V.; Kolka, Z. Reliable modeling of ideal generic memristors via state-space transformation. Radioengineering 2015, 24, 393–407. [Google Scholar] [CrossRef]
- Aguirre, F.L.; Gomez, N.M.; Pazos, S.M.; Palumbo, F.; Suñé, J.; Miranda, E. Minimization of the Line Resistance Impact on Memdiode-Based Simulations of Multilayer Perceptron Arrays Applied to Pattern Recognition. J. Low Power Electron Appl. 2021, 11, 9. [Google Scholar] [CrossRef]
- Milo, V.; Zambelli, C.; Olivo, P.; Pérez, E.; Mahadevaiah, K.M.; Ossorio, G.O.; Wenger, C.; Ielmini, D. Multilevel HfO2-based RRAM devices for low-power neuromorphic networks. APL Mater. 2019, 7. [Google Scholar] [CrossRef]
- Burr, G.W.; Shelby, R.M.; Sidler, S.; Di Nolfo, C.; Jang, J.; Boybat, I.; Shenoy, R.S.; Narayanan, P.; Virwani, K.; Giacometti, E.U.; et al. Experimental Demonstration and Tolerancing of a Large-Scale Neural Network (165,000 Synapses) Using Phase-Change Memory as the Synaptic Weight Element. IEEE Trans. Electron Devices 2015, 62, 3498–3507. [Google Scholar] [CrossRef]
- Li, C.; Belkin, D.; Li, Y.; Yan, P.; Hu, M.; Ge, N.; Jiang, H.; Montgomery, E.; Lin, P.; Wang, Z.; et al. Efficient and self-adaptive in-situ learning in multilayer memristor neural networks. Nat. Commun. 2018, 9, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Dong, Z.; Zhou, Z.; Li, Z.; Liu, C.; Huang, P.; Liu, L.; Liu, X.; Kang, J. Convolutional Neural Networks Based on RRAM Devices for Image Recognition and Online Learning Tasks. IEEE Trans. Electron Devices 2019, 66, 793–801. [Google Scholar] [CrossRef]
- Querlioz, D.; Bichler, O.; Dollfus, P.; Gamrat, C. Immunity to device variations in a spiking neural network with memristive nanodevices. IEEE Trans. Nanotechnol. 2013, 12, 288–295. [Google Scholar] [CrossRef]
- LeCun, Y.; Cortes, C.; Burges, C.J.C. The MNIST handwritten digit database of handwritten digits. Available online: http://yann.lecun.com/exdb/mnist/ (accessed on 21 November 2019).
- Georghiades, A.S.; Belhumeur, P.N.; Kriegman, D.J. From Few to Many: Illumination Cone Models for Face Recognition under Variable Lighting and Pose. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 643–660. [Google Scholar] [CrossRef]
- Josell, D.; Brongersma, S.H.; Tőkei, Z. Size-Dependent Resistivity in Nanoscale Interconnects. Annu. Rev. Mater. Res. 2009, 39, 231–254. [Google Scholar] [CrossRef]
- Rossnagel, S.M.; Kuan, T.S. Alteration of Cu conductivity in the size effect regime. J. Vac. Sci. Technol. B Microelectron. Nanomet. Struct. 2004, 22, 240–247. [Google Scholar] [CrossRef]
- Steinhögl, W.; Schindler, G.; Steinlesberger, G.; Traving, M.; Engelhardt, M. Comprehensive study of the resistivity of copper wires with lateral dimensions of 100 nm and smaller. J. Appl. Phys. 2005, 97, 023706. [Google Scholar] [CrossRef]
- Mehonic, A.; Joksas, D.; Ng, W.H.; Buckwell, M.; Kenyon, A.J. Simulation of inference accuracy using realistic rram devices. Front. Neurosci. 2019, 13, 1–15. [Google Scholar] [CrossRef]
- Dias, C.; Guerra, L.M.; Ventura, J.; Aguiar, P. Memristor-based Willshaw network: Capacity and robustness to noise in the presence of defects. Appl. Phys. Lett. 2015, 106. [Google Scholar] [CrossRef]
- Zhang, B.; Uysal, N.; Fan, D.; Ewetz, R. Handling Stuck-at-faults in Memristor Crossbar Arrays using Matrix Transformations. In Proceedings of the Asia and South Pacific Design Automation Conference, Tokyo, Japan, 21–24 January 2019. [Google Scholar]
- Zhang, B.; Uysal, N.; Fan, D.; Ewetz, R. Handling Stuck-at-fault Defects using Matrix Transformation for Robust Inference of DNNs. IEEE Trans. Comput. Des. Integr. Circuits Syst. 2019, 2448–2460. [Google Scholar] [CrossRef]
- Woo, J.; Van Nguyen, T.; Kim, J.H.; Im, J.P.; Im, S.; Kim, Y.; Min, K.S.; Moon, S.E. Exploiting defective RRAM array as synapses of HTM spatial pooler with boost-factor adjustment scheme for defect-tolerant neuromorphic systems. Sci. Rep. 2020, 10, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Diao, J.; Nie, H.; Wang, W.; Li, Z.; Li, Q.; Liu, H. Memristor Based Binary Convolutional Neural Network Architecture with Configurable Neurons. Front. Neurosci. 2021, 15, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Yeo, I.; Chu, M.; Gi, S.G.; Hwang, H.; Lee, B.G. Stuck-at-Fault Tolerant Schemes for Memristor Crossbar Array-Based Neural Networks. IEEE Trans. Electron Devices 2019, 66, 2937–2945. [Google Scholar] [CrossRef]
- Van Pham, K.; Van Nguyen, T.; Min, K.S. Partial-gated memristor crossbar for fast and power-efficient defect-tolerant training. Micromachines 2019, 10, 245. [Google Scholar] [CrossRef]
- Chen, L.; Li, J.; Chen, Y.; Deng, Q.; Shen, J.; Liang, X.; Jiang, L. Accelerator-friendly neural-network training: Learning variations and defects in RRAM crossbar. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition (DATE), Lausanne, Switzerland, 27–31 March 2017. [Google Scholar]
- Cristiano, G.; Giordano, M.; Ambrogio, S.; Romero, L.P.; Cheng, C.; Narayanan, P.; Tsai, H.; Shelby, R.M.; Burr, G.W. Perspective on training fully connected networks with resistive memories: Device requirements for multiple conductances of varying significance. J. Appl. Phys. 2018, 124. [Google Scholar] [CrossRef]
- Romero, L.P.; Ambrogio, S.; Giordano, M.; Cristiano, G.; Bodini, M.; Narayanan, P.; Tsai, H.; Shelby, R.M.; Burr, G.W. Training fully connected networks with resistive memories: Impact of device failures. Faraday Discuss. 2019, 213, 371–391. [Google Scholar] [CrossRef]
- Blasco, J.; Jančovič, P.; Fröhlich, K.; Suñé, J.; Miranda, E. Modeling of the switching I-V characteristics in ultrathin (5 nm) atomic layer deposited HfO 2 films using the logistic hysteron. J. Vac. Sci. Technol. B, Nanotechnol. Microelectron. Mater. Process. Meas. Phenom. 2015, 33, 01A102. [Google Scholar] [CrossRef]
- Miranda, E.; Román Acevedo, W.; Rubi, D.; Lüders, U.; Granell, P.; Suñé, J.; Levy, P. Modeling of the multilevel conduction characteristics and fatigue profile of Ag/La1/3Ca2/3MnO3/Pt structures using a compact memristive approach. J. Appl. Phys. 2017, 121, 205302. [Google Scholar] [CrossRef]
- Li, C.; Hu, M.; Li, Y.; Jiang, H.; Ge, N.; Montgomery, E.; Zhang, J.; Song, W.; Dávila, N.; Graves, C.E.; et al. Analogue signal and image processing with large memristor crossbars. Nat. Electron 2018, 1, 52–59. [Google Scholar] [CrossRef]
- Shi, Y.; Nguyen, L.; Oh, S.; Liu, X.; Koushan, F.; Jameson, J.R.; Kuzum, D. Neuroinspired unsupervised learning and pruning with subquantum CBRAM arrays. Nat. Commun. 2018, 9, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Fouda, M.E.; Lee, S.; Lee, J.; Eltawil, A.; Kurdahi, F. Mask Technique for Fast and Efficient Training of Binary Resistive Crossbar Arrays. IEEE Trans. Nanotechnol. 2019, 18, 704–716. [Google Scholar] [CrossRef]
- Wang, J.; Dong, X.; Xie, Y.; Jouppi, N.P. I2WAP: Improving non-volatile cache lifetime by reducing inter- and intra-set write variations. In Proceedings of the 2013 IEEE 19th International Symposium on High Performance Computer Architecture (HPCA), Shenzhen, China, 23–27 February 2013. [Google Scholar]
- Hu, M.; Strachan, J.P.; Li, Z.; Grafals, E.M.; Davila, N.; Graves, C.; Lam, S.; Ge, N.; Yang, J.J.; Williams, R.S. Dot-product engine for neuromorphic computing. In Proceedings of the 2016 53nd ACM/EDAC/IEEE Design Automation Conference (DAC), Austin, TX, USA, 5–9 June 2016. [Google Scholar]
- Montgomery, D.C.; Runger, G.C. Applied Statistics and Probability for Engineers; John Wiley & Sons: Hoboken, NJ, USA, 2010; ISBN 0470053046. [Google Scholar]
- Miranda, E.; Morell, A.; Muñoz-Gorriz, J.; Suñé, J. Simple method for monitoring the switching activity in memristive cross-point arrays with line resistance effects. Microelectron. Reliab. 2019, 100–101. [Google Scholar] [CrossRef]
- Prezioso, M.; Merrikh-Bayat, F.; Hoskins, B.D.; Adam, G.C.; Likharev, K.K.; Strukov, D.B. Training and operation of an integrated neuromorphic network based on metal-oxide memristors. Nature 2015, 521, 61–64. [Google Scholar]
| 8 × 8 px. MNIST (64 × 10 SLP) | 16 × 16 px. MNIST (256 × 10 SLP) | |||||
|---|---|---|---|---|---|---|
| RL = 1 Ω | RL = 10 Ω | RL = 100 Ω | RL = 1 Ω | RL = 10 Ω | RL = 100 Ω | |
| SA1: RMemd = RON (10 kΩ) | ~0.99 | ~0.96 | ~0.72 | ~0.99 | ~0.90 | ~0.49 |
| SA0: RMemd = ROFF (1 MΩ) | ~1 | ~0.99 | ~0.99 | ~1 | ~0.99 | ~0.98 |
| Target (Wi,j) | RRAM Cell State in Positive CPA | RRAM Cell State in Negative CPA | Recoverable? |
|---|---|---|---|
| Positive | Stuck-at-ON | Fault-Free | YES |
| Positive | Stuck-at-OFF | Fault-Free | NO |
| Positive | Fault-Free | Stuck-at-ON | NO |
| Positive | Fault-Free | Stuck-at-OFF | YES * |
| Negative | Stuck-at-ON | Fault-Free | NO |
| Negative | Stuck-at-OFF | Fault-Free | YES * |
| Negative | Fault-Free | Stuck-at-ON | YES |
| Negative | Fault-Free | Stuck-at-OFF | NO |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguirre, F.L.; Pazos, S.M.; Palumbo, F.; Morell, A.; Suñé, J.; Miranda, E. Assessment and Improvement of the Pattern Recognition Performance of Memdiode-Based Cross-Point Arrays with Randomly Distributed Stuck-at-Faults. Electronics 2021, 10, 2427. https://doi.org/10.3390/electronics10192427
Aguirre FL, Pazos SM, Palumbo F, Morell A, Suñé J, Miranda E. Assessment and Improvement of the Pattern Recognition Performance of Memdiode-Based Cross-Point Arrays with Randomly Distributed Stuck-at-Faults. Electronics. 2021; 10(19):2427. https://doi.org/10.3390/electronics10192427
Chicago/Turabian StyleAguirre, Fernando L., Sebastián M. Pazos, Félix Palumbo, Antoni Morell, Jordi Suñé, and Enrique Miranda. 2021. "Assessment and Improvement of the Pattern Recognition Performance of Memdiode-Based Cross-Point Arrays with Randomly Distributed Stuck-at-Faults" Electronics 10, no. 19: 2427. https://doi.org/10.3390/electronics10192427
APA StyleAguirre, F. L., Pazos, S. M., Palumbo, F., Morell, A., Suñé, J., & Miranda, E. (2021). Assessment and Improvement of the Pattern Recognition Performance of Memdiode-Based Cross-Point Arrays with Randomly Distributed Stuck-at-Faults. Electronics, 10(19), 2427. https://doi.org/10.3390/electronics10192427