Review of Analog-To-Digital Conversion Characteristics and Design Considerations for the Creation of Power-Efficient Hybrid Data Converters
Abstract
:1. Introduction
2. Conventional Nyquist-Rate ADC Architectures
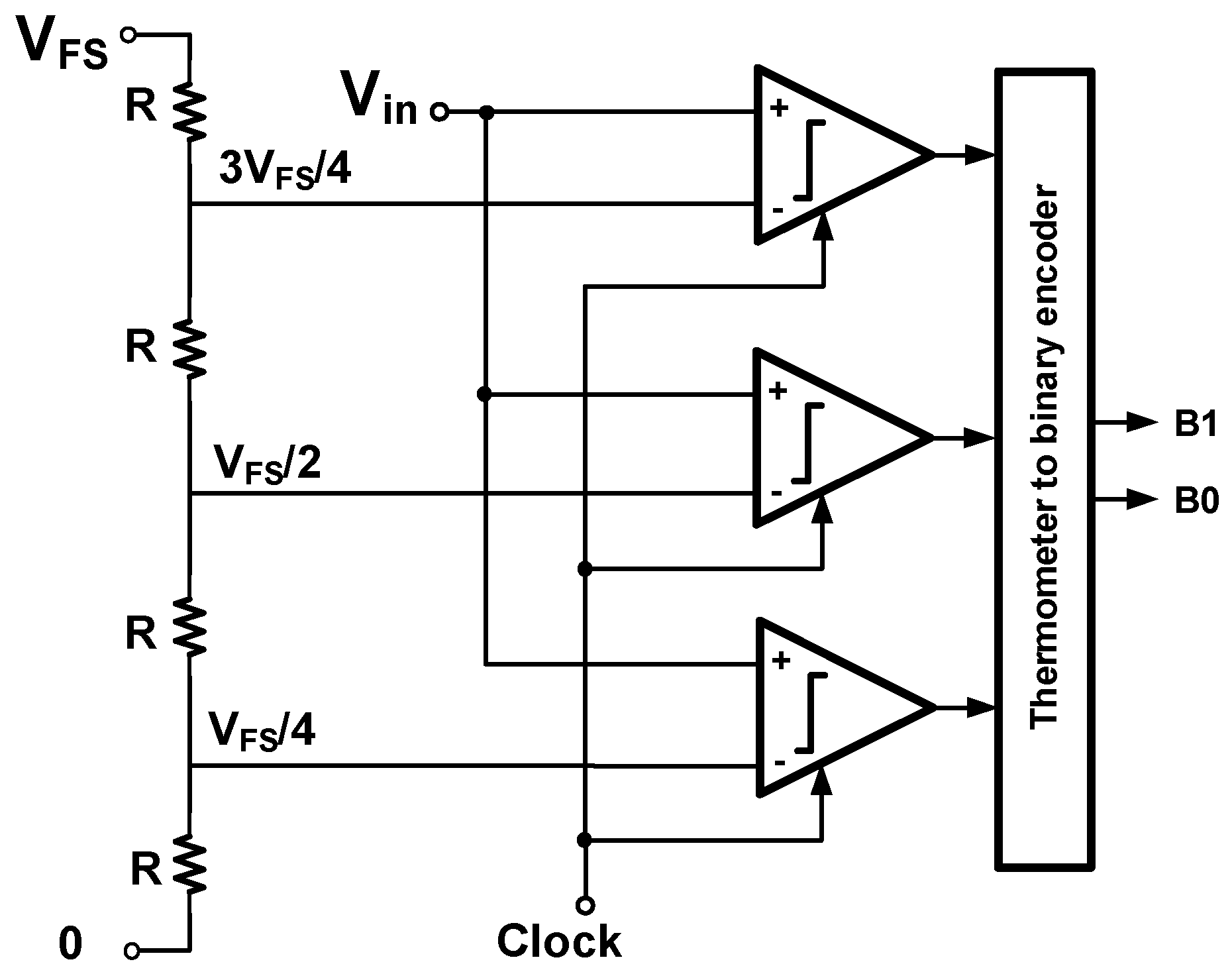
2.1. Flash ADCs
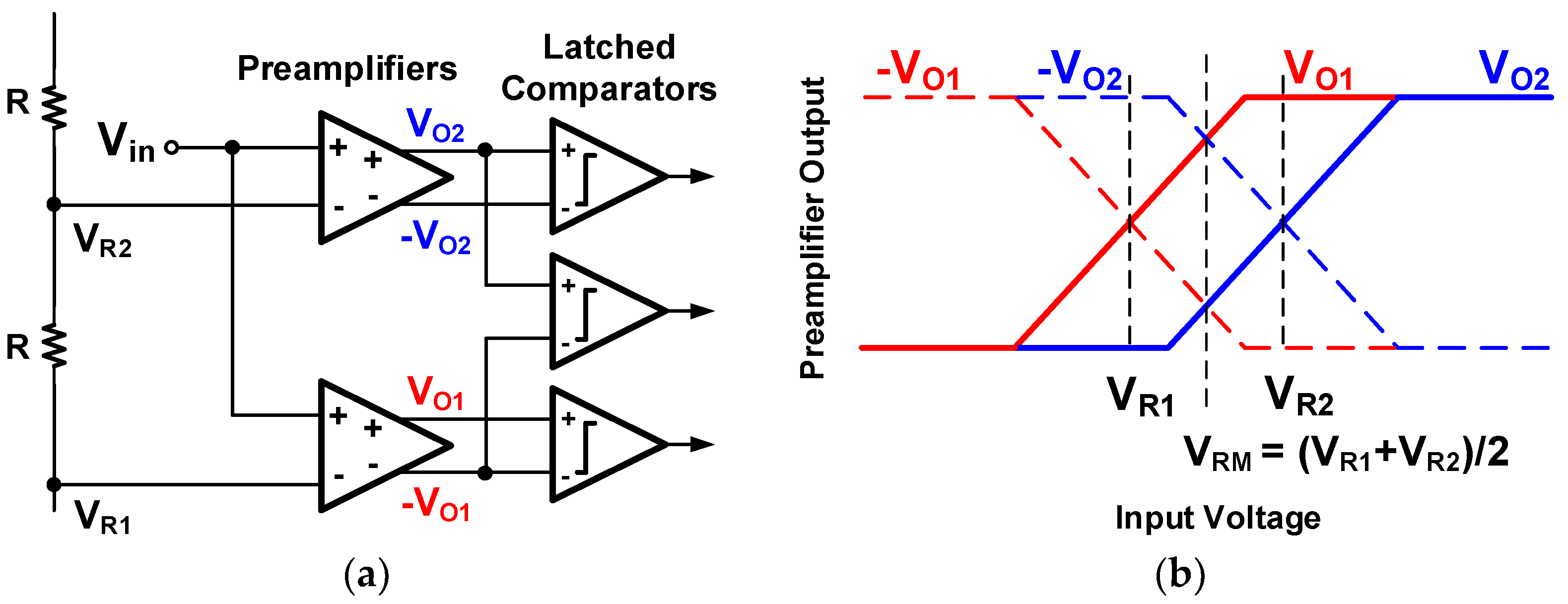
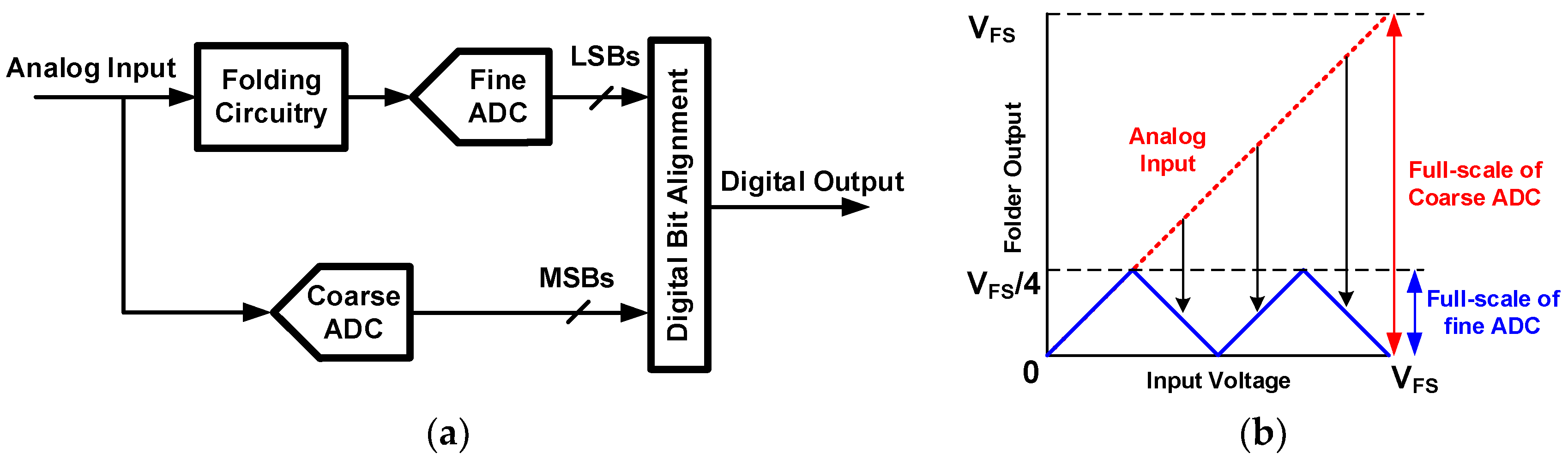
2.2. Interpolating and Folding ADCs
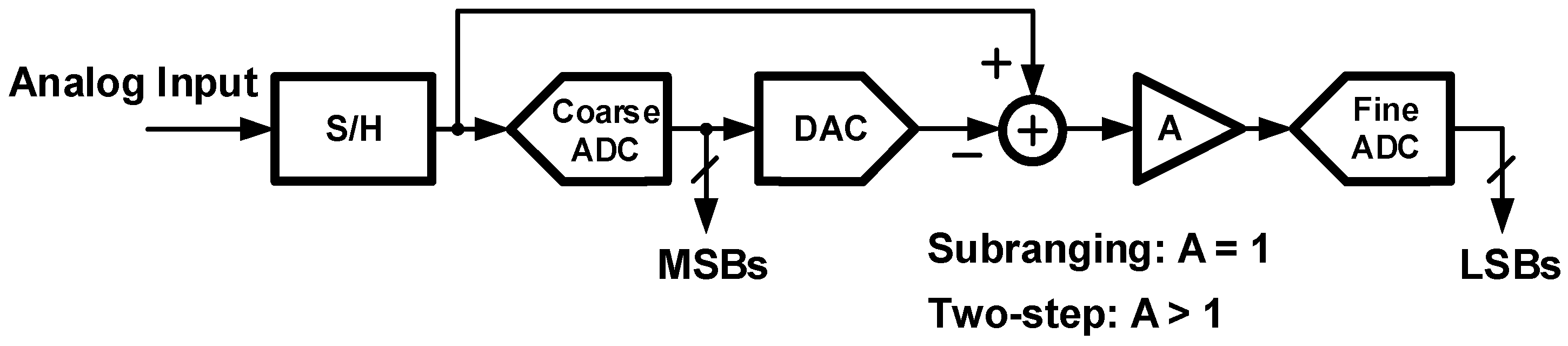
2.3. Subranging and Two-Step ADCs
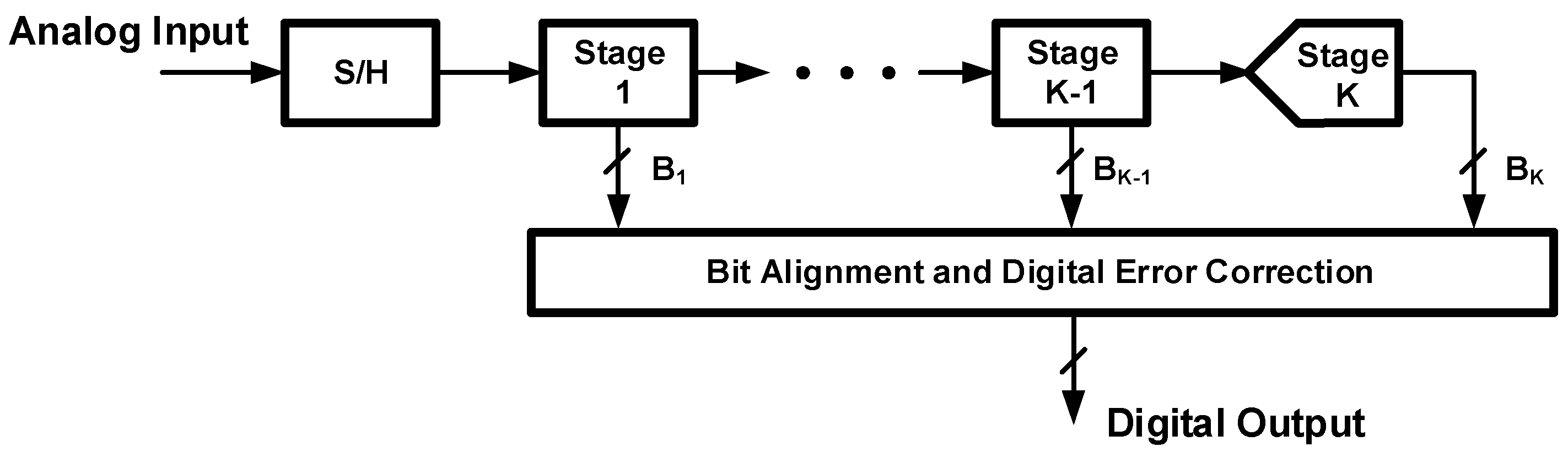
2.4. Pipelined ADCs
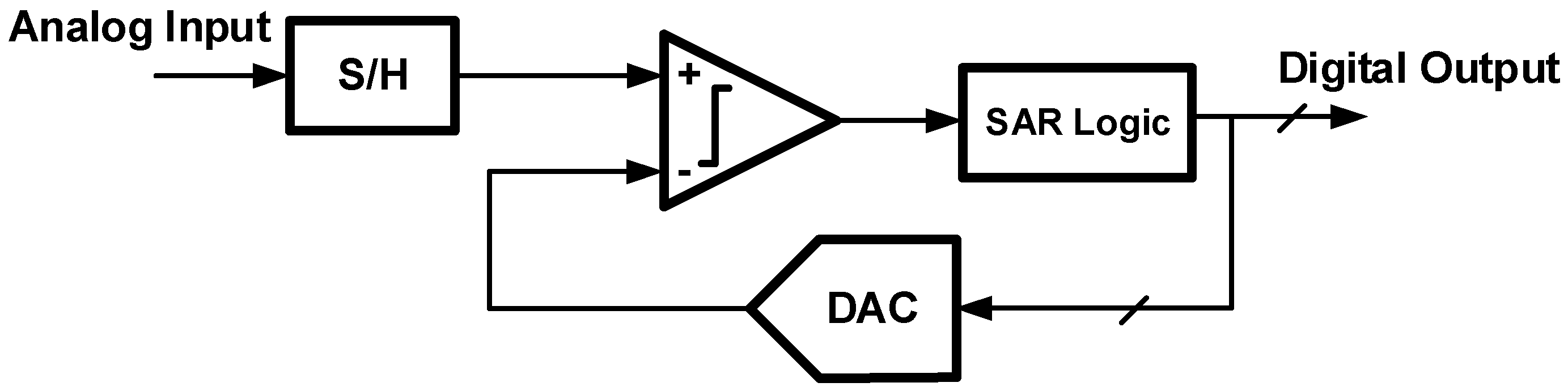
2.5. Successive Approximation Register ADCs
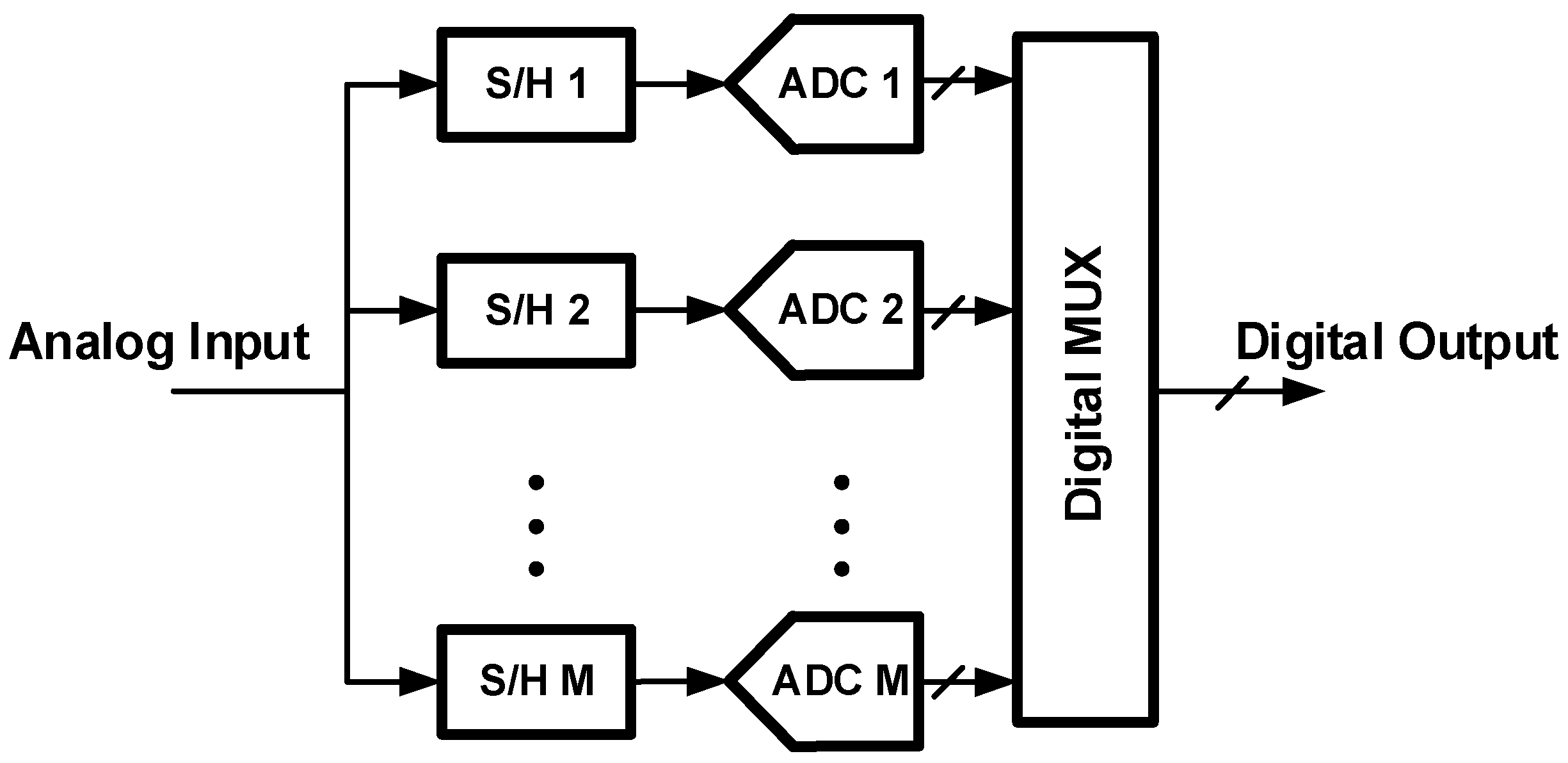
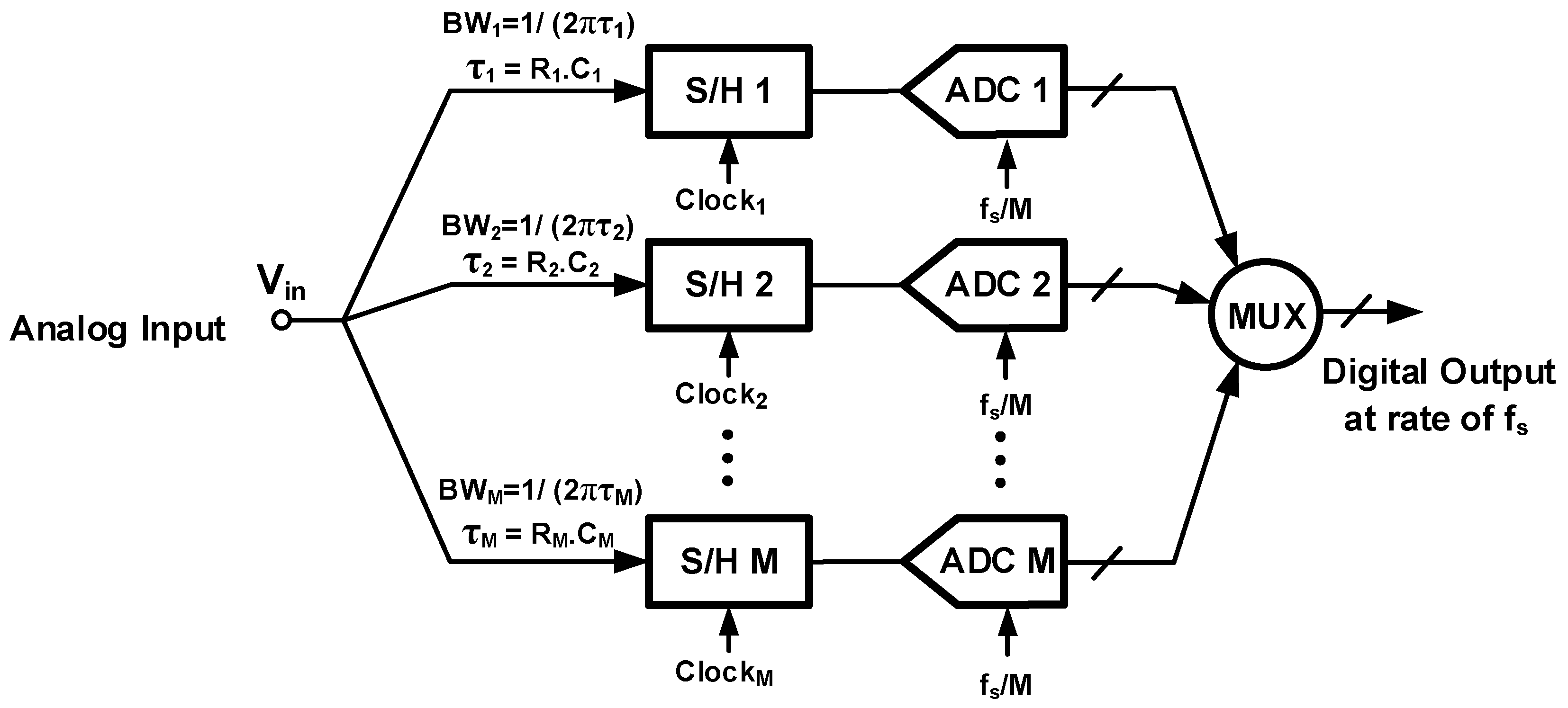
2.6. Time-Interleaved ADCs
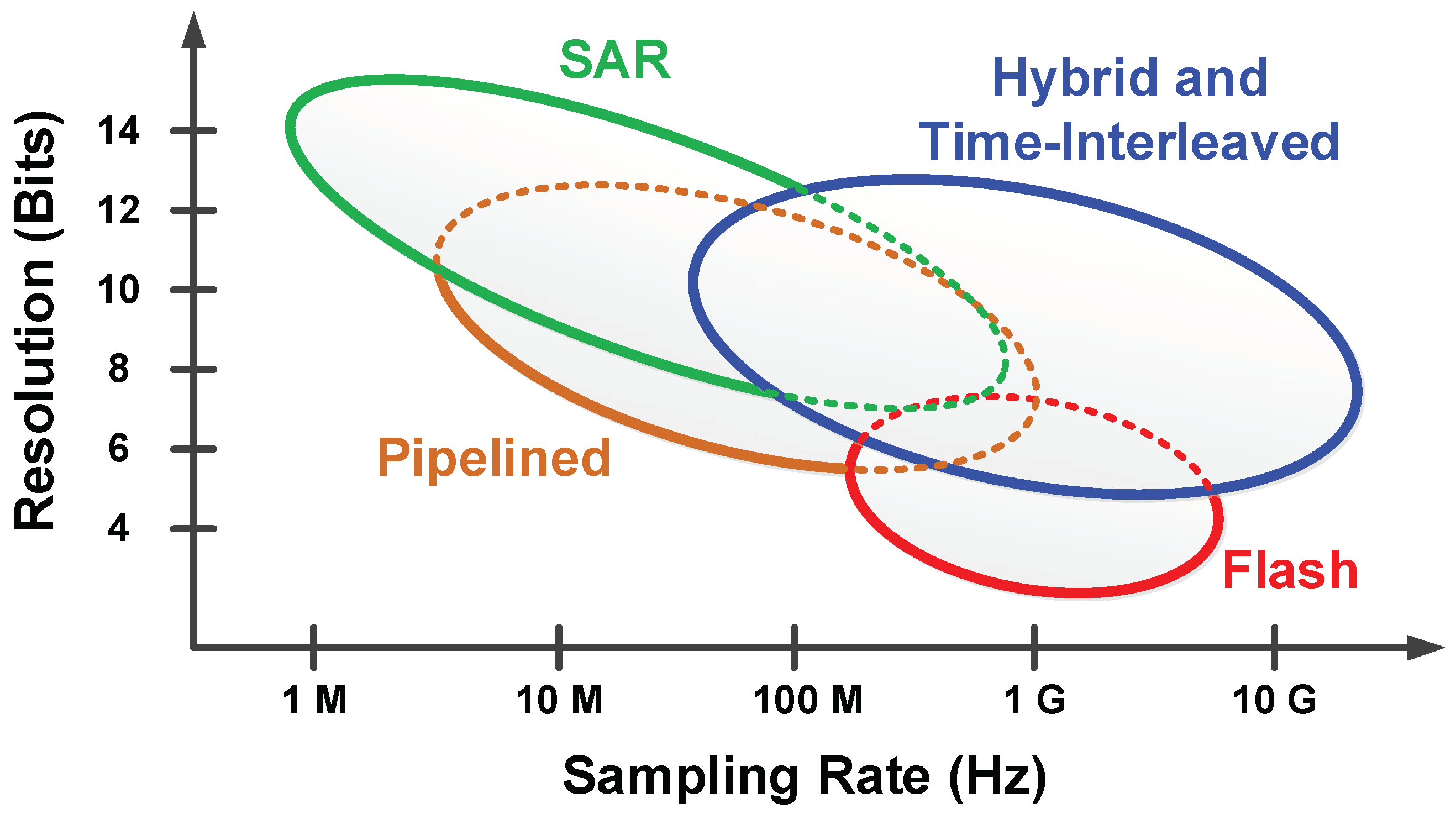
2.7. Summary
3. Design Considerations for Time-Interleaving and SAR ADCs within Hybrid Architectures
3.1. Channel Offset Mismatch
3.2. Channel Gain Mismatch
3.3. Channel Timing Mismatch (Timing Skews)
3.4. Channel Bandwidth Mismatch
3.5. Sub-ADC Architectures in Time-Interleaved ADCs
3.6. Suitability of SAR ADCs for Low-Power Hybrid ADC Architectures
3.7. Comparator-Based Asynchronous Binary Search (CABS) ADC
4. Low-Power Hybrid ADC Design
4.1. Power-Efficient High-Speed Medium-Resolution ADCs
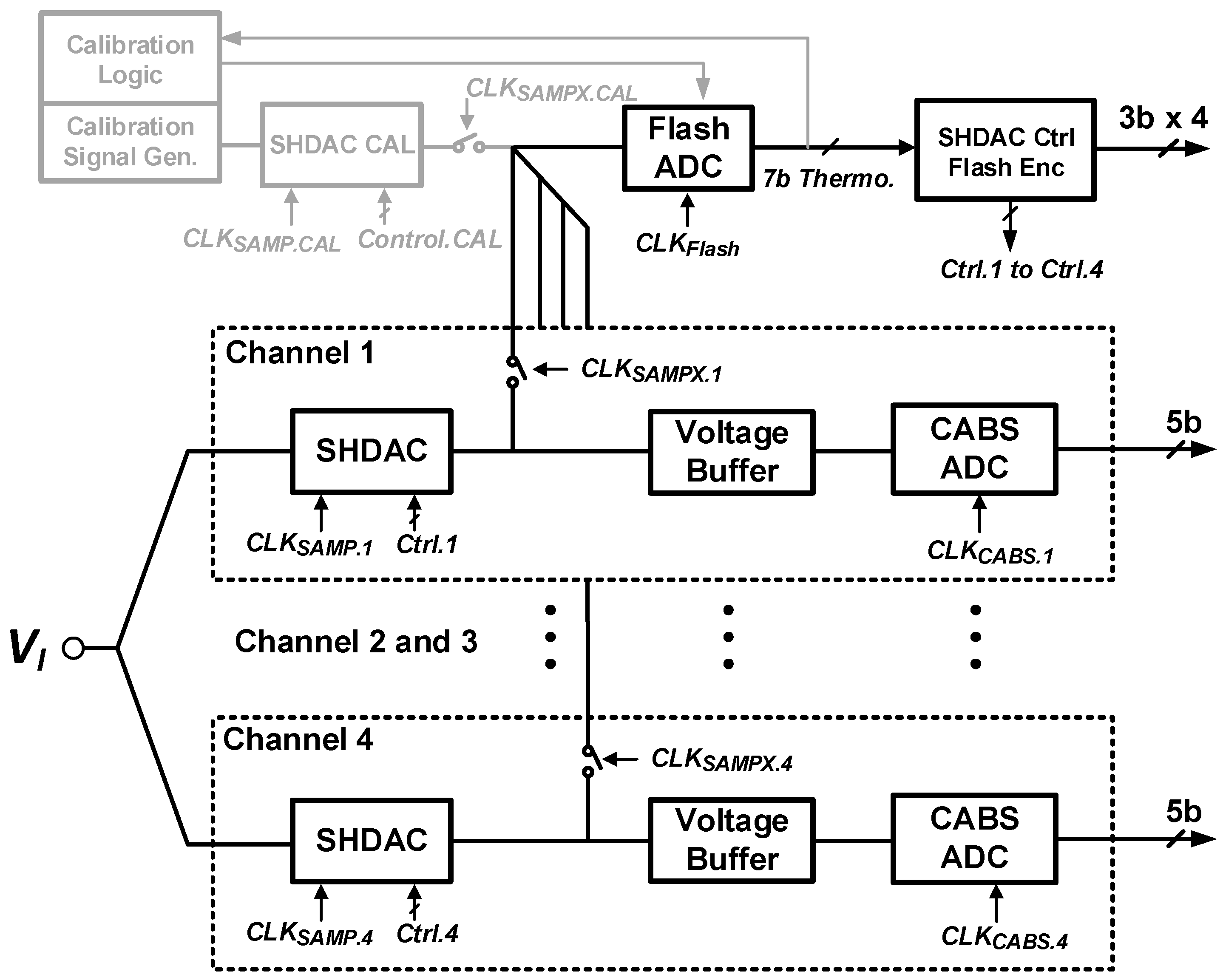
4.2. Architecture Case Study
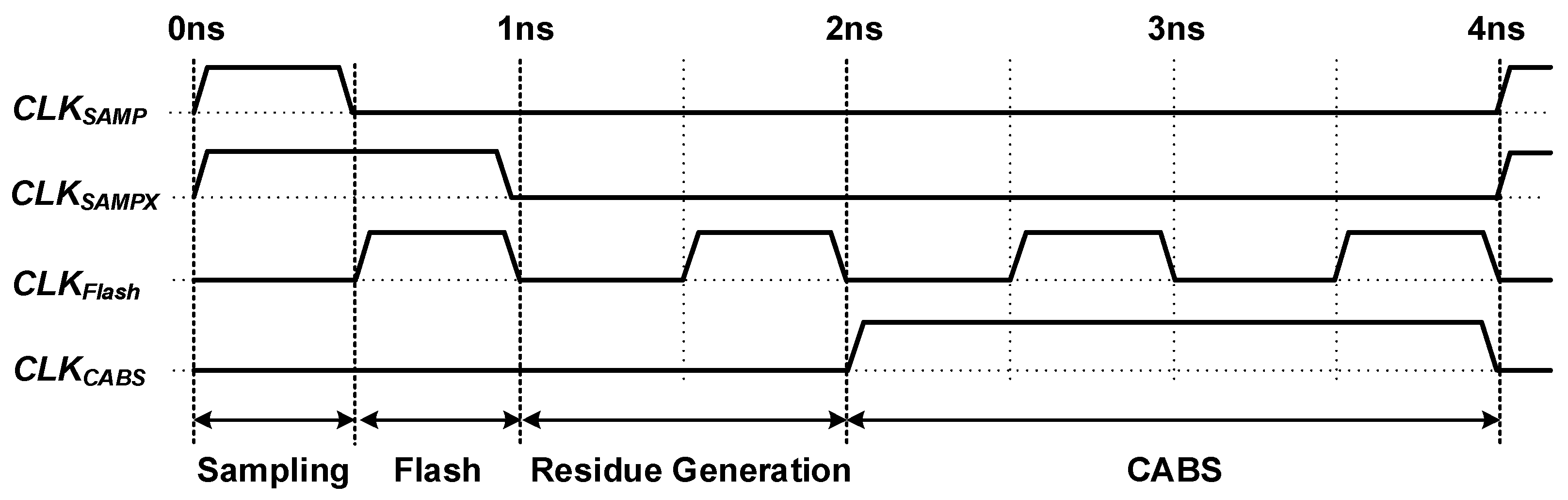
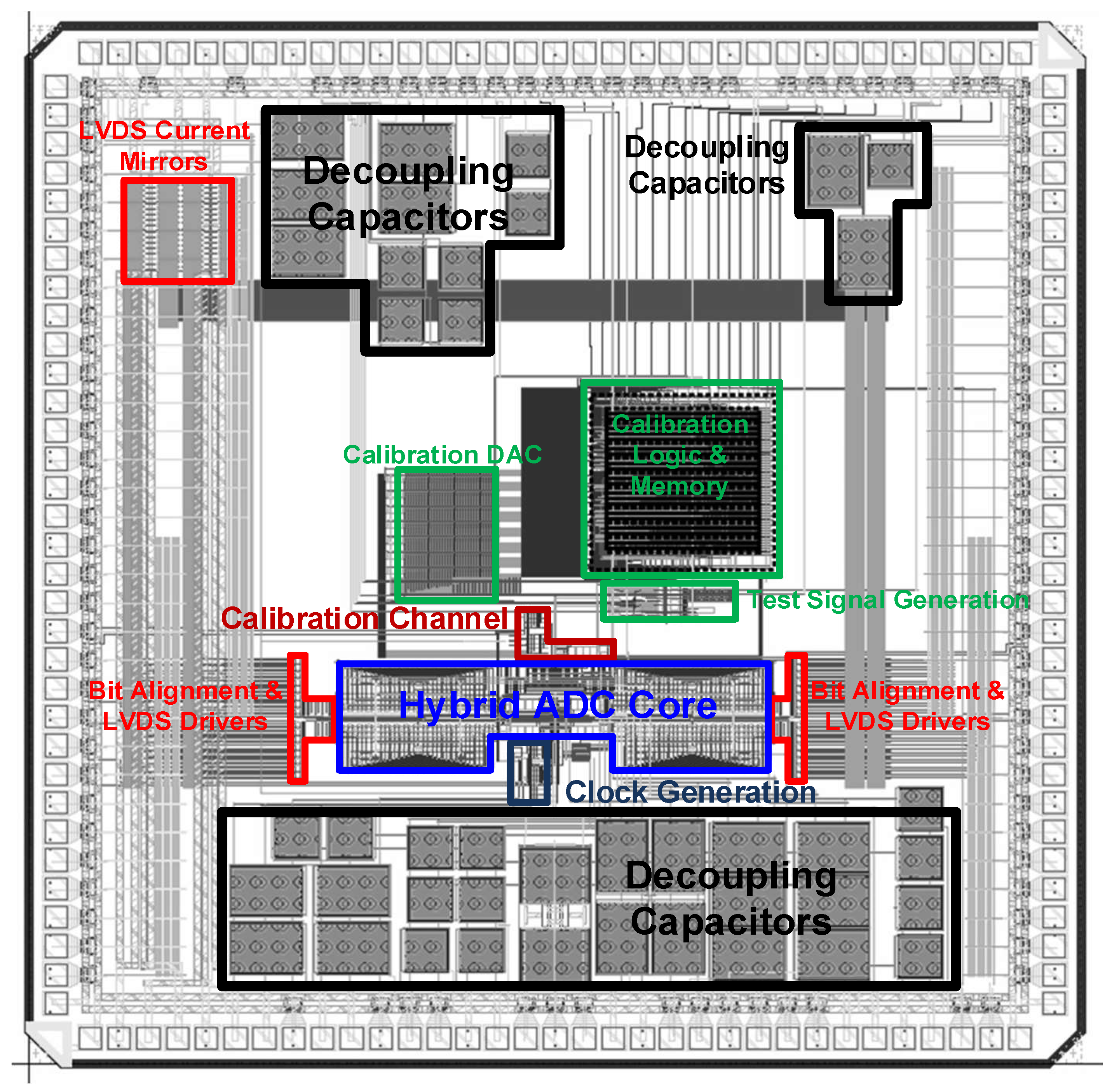
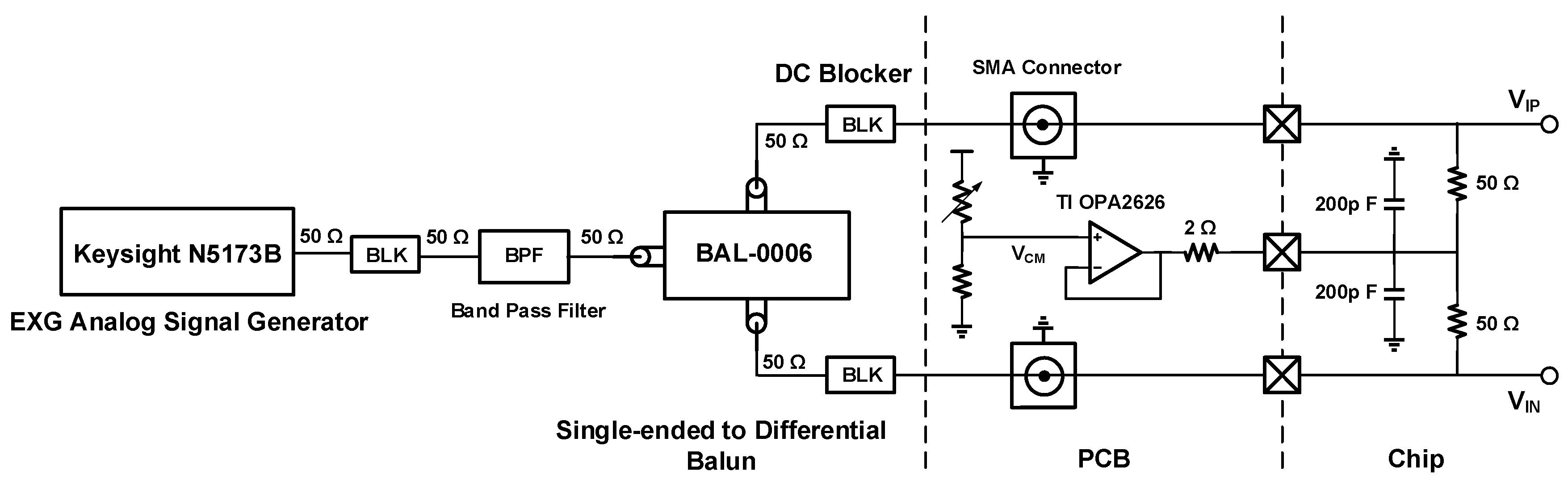
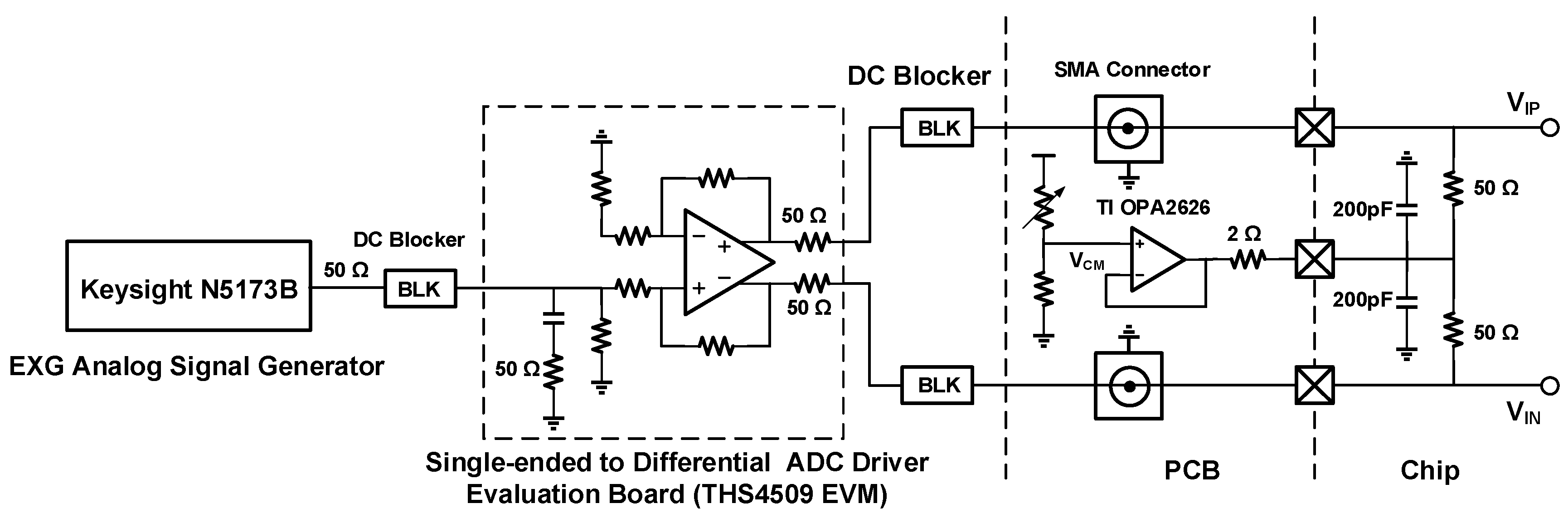
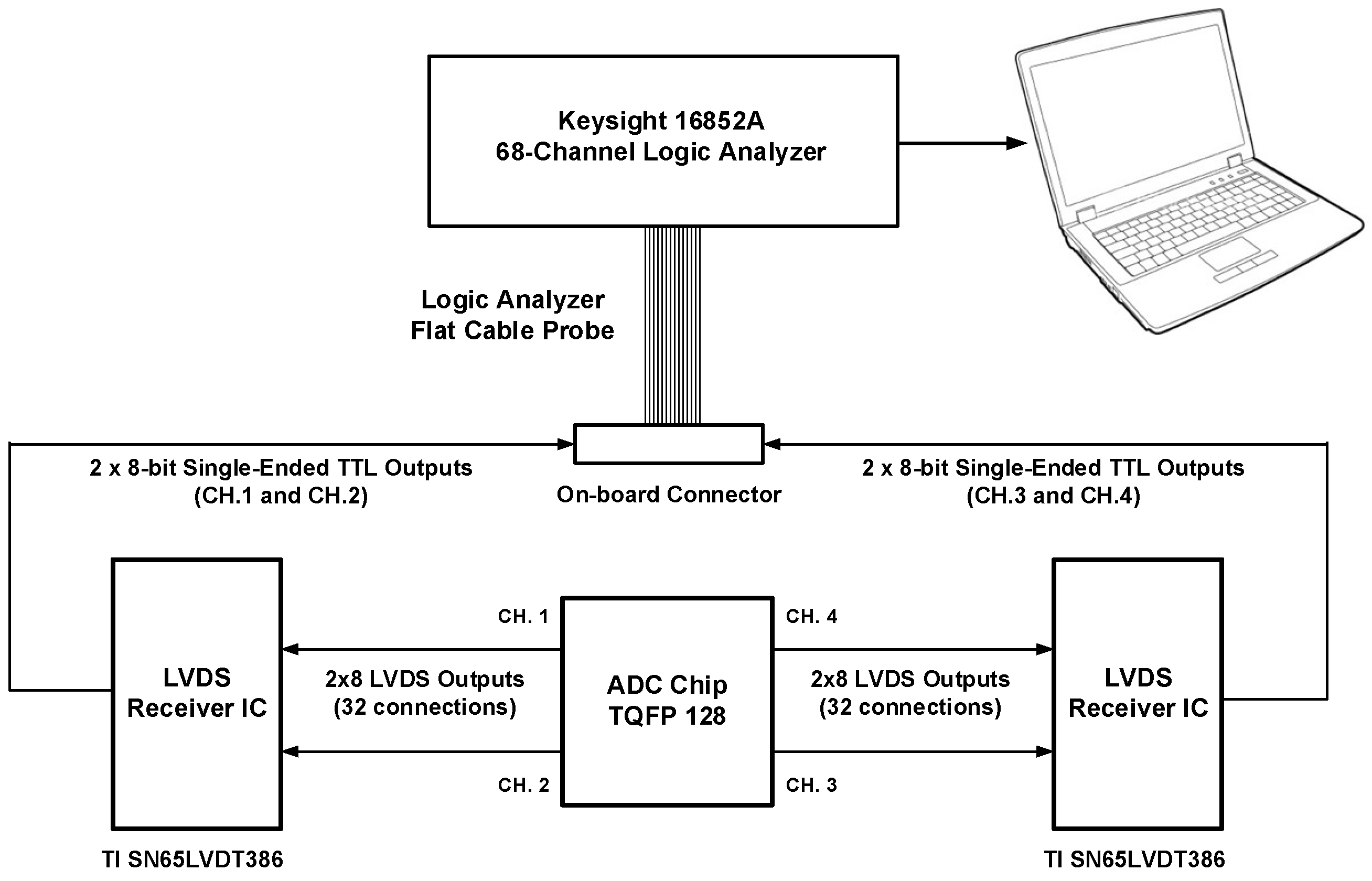
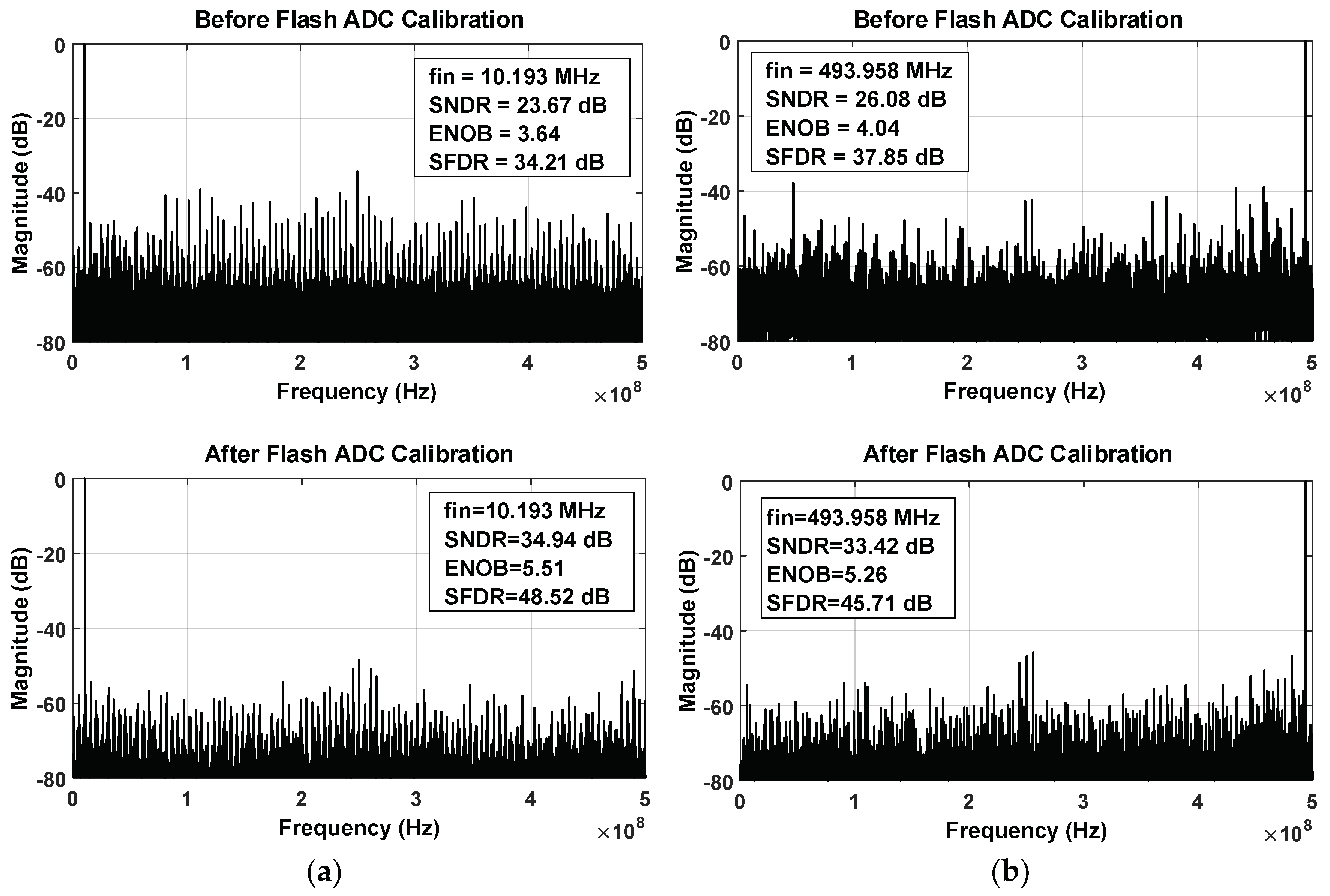
4.3. Prototype Chip Layout and Testing Considerations
4.4. Summary of Measurement Results
5. Conclusions
Conflicts of Interest
References
- Chung, Y.-H.; Wu, J.-T. A 16-mW 8-Bit 1-GS/s digital-subranging ADC in 55-nm CMOS. IEEE Trans. Very Large Scale Integr. Syst. 2015, 23, 557–566. [Google Scholar] [CrossRef]
- Ku, I.-N.; Xu, Z.; Kuan, Y.-C.; Wang, Y.-H.; Chang, M.-C.F. A 40-mW 7-bit 2.2-GS/s time-interleaved subranging CMOS ADC for low-power gigabit wireless communications. IEEE J. Solid-State Circuits 2012, 47, 1854–1865. [Google Scholar] [CrossRef]
- Cao, Z.; Yan, S.; Li, Y. A 32 mW 1.25 GS/s 6b 2b/step SAR ADC in 0.13 μm CMOS. IEEE J. Solid-State Circuits 2009, 44, 862–873. [Google Scholar] [CrossRef]
- Stepanovic, D.; Nikolic, B. A 2.8 GS/s 44.6 mW time-interleaved ADC achieving 50.9 dB SNDR and 3 dB effective resolution bandwidth of 1.5 GHz in 65 nm CMOS. IEEE J. Solid-State Circuits 2013, 48, 971–982. [Google Scholar] [CrossRef]
- Alpman, E.; Lakdawala, H.; Carley, L.R.; Soumyanath, K. A 1.1 V 50 mW 2.5 GS/s 7b time-interleaved C-2C SAR ADC in 45 nm LP digital CMOS. In Proceedings of the IEEE International Solid-State Circuits Conference, Digest of Technical Papers, San Francisco, CA, USA, 8–12 February 2009; pp. 76–78. [Google Scholar]
- Jiang, T.; Liu, W.; Zhong, F.Y.; Zhong, C.; Chiang, P.Y. Single-channel, 1.25-GS/s, 6-bit, loop-unrolled asynchronous SAR-ADC in 40nm-CMOS. In Proceedings of the IEEE Custom Integrated Circuits Conference, San Jose, CA, USA, 19–22 September 2010. [Google Scholar]
- Tseng, C.-J.; Lai, C.-F.; Chen, H.-S. A 6-Bit 1 GS/s pipeline ADC using incomplete settling with background sampling-point calibration. IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 2805–2815. [Google Scholar] [CrossRef]
- Tabasy, E.Z.; Shafik, A.; Huang, S.; Yang, N.H.W.; Hoyos, S.; Palermo, S. A 6-b 1.6-GS/s ADC with redundant cycle one-tap embedded DFE in 90-nm CMOS. IEEE J. Solid-State Circuits 2013, 48, 1885–1897. [Google Scholar] [CrossRef]
- Ismail, A.; Elmasry, M. A 6-Bit 1.6-GS/s low-power wideband flash ADC converter in 0.13-μm CMOS technology. IEEE J. Solid-State Circuits 2008, 43, 1982–1990. [Google Scholar] [CrossRef]
- Chen, H.-W.; Chen, I.-C.; Tseng, H.-C.; Chen, H.-S. A 1-GS/s 6-Bit two-channel two-step ADC in 0.13um CMOS. IEEE J. Solid-State Circuits 2009, 44, 3051–3059. [Google Scholar] [CrossRef]
- Jiang, X.; Chang, M.C.F. A 1-GHz signal bandwidth 6-bit CMOS ADC with power-efficient averaging. IEEE J. Solid-State Circuits 2005, 40, 532–535. [Google Scholar] [CrossRef]
- Mehr, I.; Dalton, D. A 500-MSample/s, 6-bit Nyquist-rate ADC for disk-drive read-channel applications. IEEE J. Solid-State Circuits 1999, 34, 912–920. [Google Scholar] [CrossRef]
- Pernillo, J.; Flynn, M.P. A 1.5-GS/s flash ADC with 57.7-dB SFDR and 6.4-bit ENOB in 90 nm digital CMOS. IEEE Trans. Circuits Syst. II Express Briefs 2011, 58, 837–841. [Google Scholar] [CrossRef]
- Chahardori, M.; Sharifkhani, M.; Sadughi, S. A 4-Bit, 1.6 GS/s low power flash ADC, based on offset calibration and segmentation. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 2285–2297. [Google Scholar] [CrossRef]
- Park, C.-J.; Onabajo, M.; Geddada, H.M.; Karsilayan, A.I.; Silva-Martinez, J. Efficient broadband current-mode adder-quantizer design for continuous-time sigma-delta modulators. IEEE Trans. Very Large Scale Integr. Syst. 2015, 23, 1920–1930. [Google Scholar] [CrossRef]
- le Dortz, N.; Blanc, J.-P.; Simon, T.; Verhaeren, S.; Rouat, E.; Urard, P.; le Tual, S.; Goguet, D.; Lelandais-Perrault, C.; Benabes, P. A 1.62GS/s time-interleaved SAR ADC with digital background mismatch calibration achieving interleaving spurs below 70dBFS. In Proceedings of the IEEE International Solid-State Circuits Conference (ISSCC), Digest of Technical Papers, San Francisco, CA, USA, 9–13 February 2014; pp. 386–388. [Google Scholar]
- Lin, C.; Wei, Y.; Lee, T. A 10b 2.6GS/s time-interleaved SAR ADC with background timing-skew calibration. In Proceedings of the IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 31 January–4 February 2016; pp. 468–469. [Google Scholar]
- Kurosawa, N.; Kobayashi, H.; Maruyama, K.; Sugawara, H.; Kobayashi, K. Explicit analysis of channel mismatch effects in time-interleaved ADC systems. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2001, 48, 261–271. [Google Scholar] [CrossRef]
- Wang, Y.; Johansson, H.; Xu, H.; Sun, Z. Joint blind calibration for mixed mismatches in two-channel time-interleaved ADCs. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 1508–1517. [Google Scholar] [CrossRef]
- Rahman, M.; Sanyal, A.; Sun, N. A novel hybrid radix-3/radix-2 SAR ADC with fast convergence and low hardware complexity. IEEE Trans. Circuits Syst. II Express Briefs 2015, 62, 426–430. [Google Scholar] [CrossRef]
- Zhang, Y.; Bonizzoni, E.; Maloberti, F. A 10-b 200-kS/s 250-nA self-clocked coarse-fine SAR ADC. IEEE Trans. Circuits Syst. II Express Briefs 2016, 63, 924–928. [Google Scholar] [CrossRef]
- Lin, Y.Z.; Liu, C.C.; Huang, G.Y.; Shyu, Y.T.; Liu, Y.T.; Chang, S.J. A 9-bit 150-MS/s subrange ADC based on SAR architecture in 90-nm CMOS. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 570–581. [Google Scholar] [CrossRef]
- Lien, Y.-C. A 4.5-mW 8-b 750-MS/s 2-b/step asynchronous subranged SAR ADC in 28-nm CMOS technology. In Proceedings of the IEEE Symposium on VLSI Circuits (VLSIC), Digest of Technical Papers, Honolulu, HI, USA, 13–15 June 2012; pp. 88–89. [Google Scholar]
- Chan, C.-H.; Zhu, Y.; Sin, S.-W.; U, S.-P.; Martins, R.P. A 3.8mW 8b 1GS/s 2b/cycle interleaving SAR ADC with compact DAC structure. In Proceedings of the IEEE Symposium on VLSI Circuits (VLSIC), Digest of Technical Papers, Honolulu, HI, USA, 13–15 June 2012; pp. 86–87. [Google Scholar]
- Wei, H.; Chan, C.-H.; Chio, U.-F.; Sin, S.-W.; U, S.-P.; Martins, R.P.; Maloberti, F. An 8-b 400-MS/s 2-b-per-cycle SAR ADC with resistive DAC. IEEE J. Solid-State Circuits 2012, 47, 2763–2772. [Google Scholar]
- van der Plas, G.; Verbruggen, B. A 150 MS/s 133uW 7 bit ADC in 90 nm digital CMOS. IEEE J. Solid-State Circuits 2008, 43, 2631–2640. [Google Scholar] [CrossRef]
- Lin, Y.Z.; Chang, S.J.; Liu, Y.T.; Liu, C.C.; Huang, G.Y. An asynchronous binary-search ADC architecture with a reduced comparator count. IEEE Trans. Circuits Syst. I Regul. Pap. 2010, 57, 1829–1837. [Google Scholar]
- Lu, C.-Y.; Onabajo, M.; Gadde, V.; Lo, Y.-C.; Chen, H.-P.; Periasamy, V.; Silva-Martinez, J. A 25 MHz bandwidth 5th-order continuous-time low-pass sigma-delta modulator with 67.7 dB SNDR using time-domain quantization and feedback. IEEE J. Solid-State Circuits 2010, 45, 1795–1808. [Google Scholar] [CrossRef]
- Lee, S.; Chandrakasan, A.P.; Lee, H.-S. A 1 GS/s 10b 18.9 mW time-interleaved SAR ADC with background timing skew calibration. IEEE J. Solid-State Circuits 2014, 49, 2846–2856. [Google Scholar] [CrossRef]
- Sung, B.-R.-S.; Jo, D.-S.; Jang, I.-H.; Lee, D.-S.; You, Y.-S.; Lee, Y.-H.; Park, H.-J.; Ryu, S.-T. A 21fJ/conv-step 9 ENOB 1.6GS/S 2x time-interleaved FATI SAR ADC with background offset and timing-skew calibration in 45nm CMOS. In Proceedings of the IEEE International Solid-State Circuits Conference (ISSCC), Digest of Technical Papers, San Francisco, CA, USA, 22–26 February 2015; pp. 464–465. [Google Scholar]
- Zahrai, S.A.; Onabajo, M. A low-power hybrid ADC architecture for high-speed medium-resolution applications. In Proceedings of the 58th IEEE International Midwest Symposium on Circuits and Systems (MWSCAS), Fort Collins, CO, USA, 2–5 August 2015. [Google Scholar]
- Zahrai, S.A.; Zlochisti, M.; le Dortz, N.; Onabajo, M. A low-power high-speed hybrid ADC with merged sample-and-hold and DAC functions for efficient subranging time-interleaved operation. IEEE Trans. Very Large Scale Integr. Syst. 2017, 25, 3193–3206. [Google Scholar] [CrossRef]
- Zahrai, S.A.; Zlochisti, M.; le Dortz, N.; Onabajo, M. Design considerations and experimental verification of a 10.5mW 1GS/s hybrid ADC for portable wireless devices. In Proceedings of the IEEE International Symposium on Circuits & Systems (ISCAS), Florence, Italy, 27–30 May 2018. [Google Scholar]
- Razavi, B. Principles of Data Conversion System Design; IEEE Press: Piscataway, NJ, USA, 1995. [Google Scholar]
- Nuzzo, P.; Nani, C.; Armiento, C.; Sangiovanni-Vincentelli, A.; Craninckx, J.; van der Plas, G. A 6-Bit 50-MS/s threshold configuring SAR ADC in 90-nm digital CMOS. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 59, 80–92. [Google Scholar] [CrossRef]
- Chan, C.-H.; Zhu, Y.; Chio, U.-F.; Sin, S.-W.; Seng-Pan, U.; Martins, R.P. A reconfigurable low-noise dynamic comparator with offset calibration in 90nm CMOS. In Proceedings of the IEEE Asian Solid-State Circuits Conference, Jeju, Korea, 14–16 November 2011; pp. 233–236. [Google Scholar]
- van de Grift, R.; Rutten, I.W.J.M.; van der Veen, M. An 8-bit video ADC incorporating folding and interpolation techniques. IEEE J. Solid-State Circuits 1987, 22, 944–953. [Google Scholar] [CrossRef]
- Kimura, H.; Matsuzawa, A.; Nakamura, T.; Sawada, S. A 10-b 300-MHz interpolated-parallel A/D converter. IEEE J. Solid-State Circuits 1993, 28, 438–446. [Google Scholar] [CrossRef]
- Maloberti, F. Data Converters; Springer: Berlin, Germany, 2007. [Google Scholar]
- Taft, R.C.; Menkus, C.A.; Tursi, M.R.; Hidri, O.; Pons, V. A 1.8-V 1.6-G sample/s 8-b self-calibrating folding ADC with 7.26 ENOB at Nyquist frequency. IEEE J. Solid-State Circuits 2004, 39, 2107–2115. [Google Scholar] [CrossRef]
- Taft, R.C.; Francese, P.A.; Tursi, M.R.; Hidri, O.; MacKenzie, A.; Hoehn, T.; Schmitz, P.; Werker, H.; Glenny, A. A 1.8V 1.0GS/s 10b self-calibrating unified-folding-interpolating ADC with 9.1 ENOB at Nyquist frequency. In Proceedings of the IEEE International Solid-State Circuits Conference (ISSCC), Digest of Technical Papers, San Francisco, CA, USA, 8–12 February 2009; pp. 78–79. [Google Scholar]
- Doernberg, J.; Gray, P.R.; Hodges, D.A. A 10-bit 5-Msample/s CMOS two-step flash ADC. IEEE J. Solid-State Circuits 1989, 24, 241–249. [Google Scholar] [CrossRef]
- Ahmed, I. Pipelined ADC Design and Enhancement Techniques Consulting; Springer: Berlin, Germany, 2010. [Google Scholar]
- Lee, S.; Chandrakasan, A.P.; Lee, H.S. A 1GS/s 10b 18.9mW time-interleaved SAR ADC with background timing-skew calibration. In Proceedings of the IEEE International Solid-State Circuits Conference (ISSCC), Digest of Technical Papers, San Francisco, CA, USA, 9–13 February 2014; pp. 384–385. [Google Scholar]
- Pelgrom, M.J.M. Analog-to-Digital Conversion, 2nd ed.; Springer: Berlin, Germany, 2013. [Google Scholar]
- Zahrai, S.A.; Azhari, S.J. A 12b 100MS/s Highly Power Efficient Pipelined ADC for Communication Applications. Cyber J. J. Sel. Areas Microelectron. 2011, 2, 1–7. [Google Scholar]
- Waltari, M. Circuit Techniques for Low-Voltage and High-Speed A/D Converters; Helsinki University of Technology: Espoo, Finland, 2002. [Google Scholar]
- Sumanen, L. Pipeline Analog-to-Digital Converters for Wide-Band Wireless Communications; Helsinki University of Technology: Espoo, Finland, 2002. [Google Scholar]
- Abo, A.M.; Gray, P.R. A 1.5-V, 10-bit, 14.3-MS/s CMOS pipeline analog-to-digital converter. IEEE J. Solid-State Circuits 1999, 34, 599–606. [Google Scholar] [CrossRef]
- Cho, T.B.; Gray, P.R. A 10 b, 20 Msample/s, 35 mW pipeline A/D converter. IEEE J. Solid-State Circuits 1995, 30, 166–172. [Google Scholar] [CrossRef]
- Nagaraj, K.; Fetterman, H.S.; Anidjar, J.; Lewis, S.H.; Renninger, R.G. A 250-mW, 8-b, 52-Msamples/s parallel-pipelined A/D converter with reduced number of amplifiers. IEEE J. Solid-State Circuits 1997, 32, 312–320. [Google Scholar] [CrossRef]
- Chang, D.Y.; Moon, U.K. A 1.4-V 10-bit 25-MS/s pipelined ADC using opamp-reset switching technique. IEEE J. Solid-State Circuits 2003, 38, 1401–1404. [Google Scholar] [CrossRef]
- Fiorenza, J.K.; Sepke, T.; Holloway, P.; Sodini, C.G.; Lee, H.S. Comparator-based switched-capacitor circuits for scaled CMOS technologies. IEEE J. Solid-State Circuits 2006, 41, 2658–2668. [Google Scholar] [CrossRef]
- Ahmed, I.; Mulder, J.; Johns, D.A. A low-power capacitive charge pump based pipelined ADC. IEEE J. Solid-State Circuits 2010, 45, 1016–1027. [Google Scholar] [CrossRef]
- Zhang, D.; Bhide, A.; Alvandpour, A. A 53-nW 9.1-ENOB 1-kS/s SAR ADC in 0.13um CMOS for medical implant devices. IEEE J. Solid-State Circuits 2012, 47, 1585–1593. [Google Scholar] [CrossRef]
- Zhu, Z.; Liang, Y. A 0.6-V 38-nW 9.4-ENOB 20-kS/s SAR ADC in 0.18-μm CMOS for Medical Implant Devices. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 2167–2176. [Google Scholar] [CrossRef]
- Kull, L.; Toifl, T.; Schmatz, M.; Francese, P.A.; Menolfi, C.; Brändli, M.; Kossel, M.; Morf, T.; Andersen, T.M.; Leblebici, Y.; et al. A 3.1mW 8b 1.2GS/s single-channel asynchronous SAR ADC with alternate comparators for enhanced speed in 32nm digital SOI CMOS. In Proceedings of the IEEE International Solid-State Circuits Conference (ISSCC), Digest of Technical Papers, San Francisco, CA, USA, 17–21 February 2013; pp. 468–469. [Google Scholar]
- Thirunakkarasu, S.; Bakkaloglu, B. Built-in self-calibration and digital-trim technique for 14-bit SAR ADCs achieving ±1 LSB INL. IEEE Trans. Very Large Scale Integr. Syst. 2015, 23, 916–925. [Google Scholar] [CrossRef]
- Louwsma, S.M.; van Tuijl, A.J.M.; Vertregt, M.; Nauta, B. A 1.35 GS/s, 10 b, 175 mW time-interleaved AD converter in 0.13 um CMOS. IEEE J. Solid-State Circuits 2008, 43, 778–786. [Google Scholar] [CrossRef]
- Razavi, B. Design considerations for interleaved ADCs. IEEE J. Solid-State Circuits 2013, 48, 1806–1817. [Google Scholar] [CrossRef]
- Alpman, E. A 7-Bit 2.5GS/sec Time-Interleaved C-2C SAR ADC for 60GHz Multi-Band OFDM-Based Receivers. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 2009. [Google Scholar]
- El-Chammas, M. Background calibration of timing skew in time-interleaved A/D converters. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2010. [Google Scholar]
- Louwsma, S.; van Tuijl, E.; Nauta, B. Time-interleaved Analog-to-Digital Converters; Springer: Dordrecht, The Netherlands, 2011. [Google Scholar]
- Pelgrom, M.J.M.; Duinmaijer, A.C.J.; Welbers, A.P.G. Matching properties of MOS transistors. IEEE J. Solid-State Circuits 1989, 24, 1433–1439. [Google Scholar] [CrossRef]
- Zahrai, S.A.; le Dortz, N.; Onabajo, M. Design of clock generation circuitry for high-speed subranging time-interleaved ADCs. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Baltimore, MD, USA, 28–31 May 2017. [Google Scholar]
- El-Chammas, M.; Murmann, B. General analysis on the impact of phase-skew in time-interleaved ADCs. IEEE Trans. Circuits Syst. I Regul. Pap. 2009, 56, 902–910. [Google Scholar] [CrossRef]
- El-Chammas, M.; Murmann, B. A 12-GS/s 81-mW 5-bit time-interleaved flash ADC with background timing skew calibration. IEEE J. Solid-State Circuits 2011, 46, 838–847. [Google Scholar] [CrossRef]
- Park, Y.; Kim, J.; Kim, C. A scalable bandwidth mismatch calibration technique for time-interleaved ADCs. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 1889–1897. [Google Scholar] [CrossRef]
- Kundu, S.; Alpman, E.; Lu, J.H.; Lakdawala, H.; Paramesh, J.; Jung, B.; Zur, S.; Gordon, E. A 1.2 V 2.64 GS/s 8 bit 39 mW skew-tolerant time-interleaved SAR ADC in 40 nm digital LP CMOS for 60 GHz WLAN. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 1929–1939. [Google Scholar] [CrossRef]
- Chan, C.; Zhu, Y.; Sin, S.; U, S.B.; Martins, R.P. A 6 b 5 GS/s 4 interleaved 3 b/cycle SAR ADC. IEEE J. Solid-State Circuits 2015, 51, 1–13. [Google Scholar]
- Hsu, C.-C.; Huang, C.-C.; Lin, Y.-H.; Lee, C.-C.; Soe, Z.; Aytur, T.; Yan, R.-H. A 7b 1.1GS/s reconfigurable time-interleaved ADC in 90nm CMOS. In Proceedings of the IEEE Symposium on VLSI Circuits, Digest of Technical Papers, Kyoto, Japan, 14–16 June 2007; pp. 66–67. [Google Scholar]
- Um, J.-Y.; Kim, Y.-J.; Song, E.-W.; Sim, J.-Y.; Park, H.-J. A digital-domain calibration of split-capacitor DAC for a differential SAR ADC without additional analog circuits. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 2845–2856. [Google Scholar] [CrossRef]
- Sedighi, B.; Huynh, A.T.; Skafidas, E.; Micusik, D. Design of hybrid resistive-capacitive DAC for SAR A/D converters. In Proceedings of the IEEE International Conference on Electronics, Circuits, and Systems (ICECS), Seville, Spain, 9–12 December 2012; pp. 508–511. [Google Scholar]
- Chen, S.-W.M.; Brodersen, R.W. A 6-bit 600-MS/s 5.3-mW asynchronous ADC in 0.13-um CMOS. IEEE J. Solid-State Circuits 2006, 41, 2669–2680. [Google Scholar] [CrossRef]
- Liu, C.; Chang, S.; Huang, G.; Lin, Y. A 10-bit 50-MS/s SAR ADC with a monotonic capacitor switching procedure. IEEE J. Solid-State Circuits 2010, 45, 731–740. [Google Scholar] [CrossRef]
- Craninckx, J.; van der Plas, G. A 65fJ/conversion-step 0-to-50MS/s 0-to-0.7mW 9b charge-sharing SAR ADC in 90nm digital CMOS. In Proceedings of the IEEE International Solid-State Circuits Conference (ISSCC), Digest of Technical Papers, San Francisco, CA, USA, 11–15 February 2007; pp. 246–600. [Google Scholar]
- Yu, H.; Chang, M.-C.F. A 1-V 1.25-GS/S 8-bit self-calibrated flash ADC in 90-nm digital CMOS. IEEE Trans. Circuits Syst. II Express Briefs 2008, 55, 668–672. [Google Scholar]
- Makigawa, K.; Ono, K.; Ohkawa, T.; Matsuura, K.; Segami, M. A 7bit 800Msps 120mW folding and interpolation ADC using a mixed-averaging scheme. In Proceedings of the IEEE Symposium on VLSI Circuits, Digest of Technical Papers, Honolulu, HI, USA, 15–17 June 2006; pp. 138–139. [Google Scholar]
- Sahoo, B.D.; Razavi, B. A 10-b 1-GHz 33-mW CMOS ADC. IEEE J. Solid-State Circuits 2013, 48, 1442–1452. [Google Scholar] [CrossRef]
- Figueiredo, P.M.; Cardoso, P.; Lopes, A.; Fachada, C.; Hamanishi, N.; Tanabe, K.; Vital, J. A 90nm CMOS 1.2V 6b 1GS/s two-step subranging ADC. In Proceedings of the IEEE International Solid-State Circuits Conference (ISSCC), Digest of Technical Papers, San Francisco, CA, USA, 6–9 February 2006; pp. 2320–2329. [Google Scholar]
- Zlochisti, M.; Zahrai, S.A.; Onabajo, M. Digitally programmable offset compensation of comparators in flash ADCs for hybrid ADC architectures. In Proceedings of the 2015 58th IEEE International Midwest Symposium on Circuits and Systems (MWSCAS), Fort Collins, CO, USA, 2–5 August 2015. [Google Scholar]
- Maxim Integrated. Tutorial 2085—Histogram Testing Determines DNL and INL Errors. Available online: https://www.maximintegrated.com/en/app-notes/index.mvp/id/2085 (accessed on 28 April 2018).
- Nakajima, Y.; Kato, N.; Sakaguchi, A.; Ohkido, T.; Miki, T. A 7-bit, 1.4 GS/s ADC with offset drift suppression techniques for one-time calibration. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 1979–1990. [Google Scholar] [CrossRef]
- Danjo, T.; Yoshioka, M.; Isogai, M.; Hoshino, M.; Tsukamoto, S. A 6-bit, 1-GS/s, 9.9-mW, interpolated subranging ADC in 65-nm CMOS. IEEE J. Solid-State Circuits 2014, 49, 673–682. [Google Scholar] [CrossRef]
- Huang, H.; Du, L.; Chiu, Y. A 1.2-GS/s 8-bit two-step SAR ADC in 65-nm CMOS with passive residue transfer. IEEE J. Solid-State Circuits 2017, 52, 1551–1562. [Google Scholar] [CrossRef]
- Hassanpourghadi, M.; Sharma, P.K.; Chen, M.S. A 6-b, 800-MS/s, 3.62-mW Nyquist rate ac-coupled VCO-based ADC in 65-nm CMOS. IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 64, 1354–1367. [Google Scholar] [CrossRef]
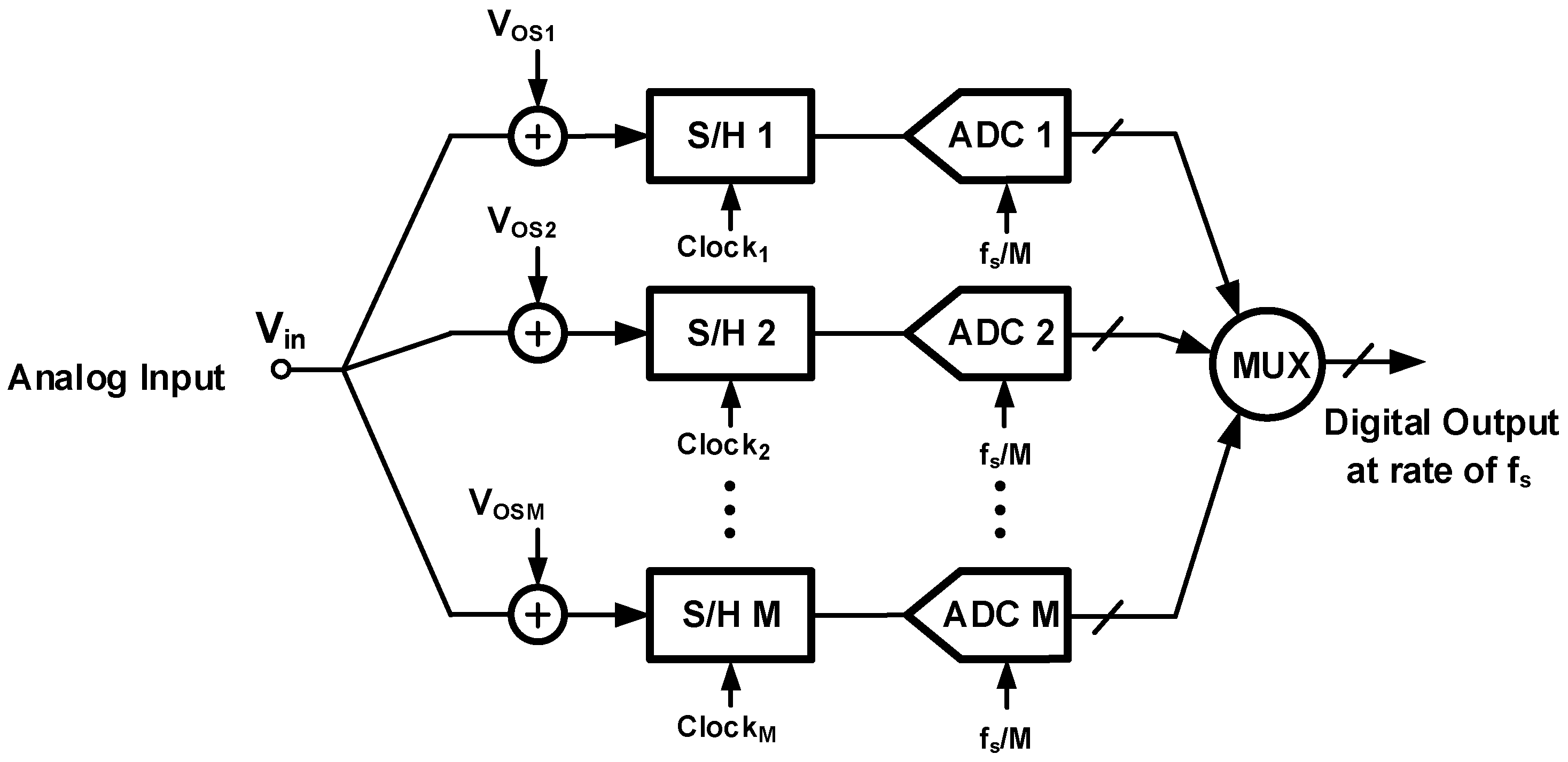
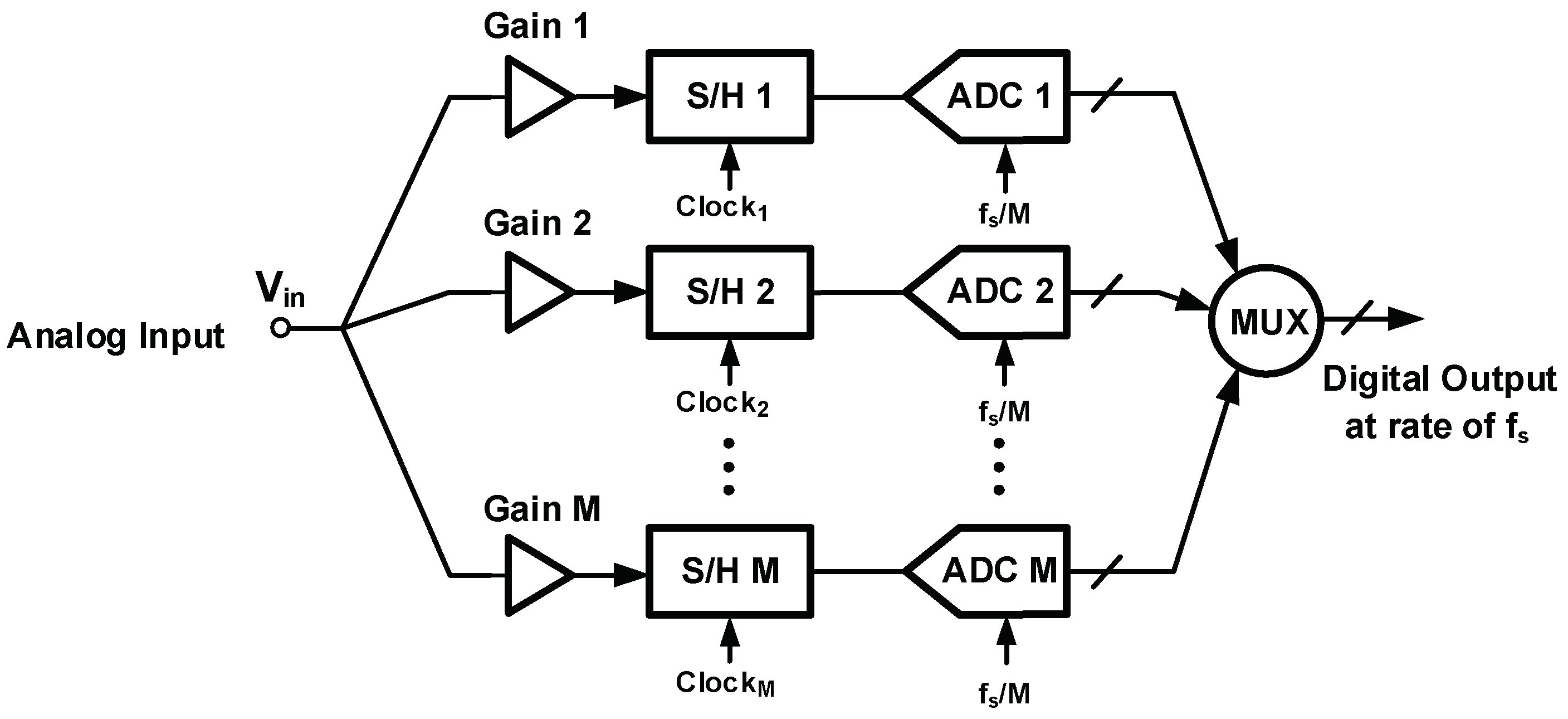
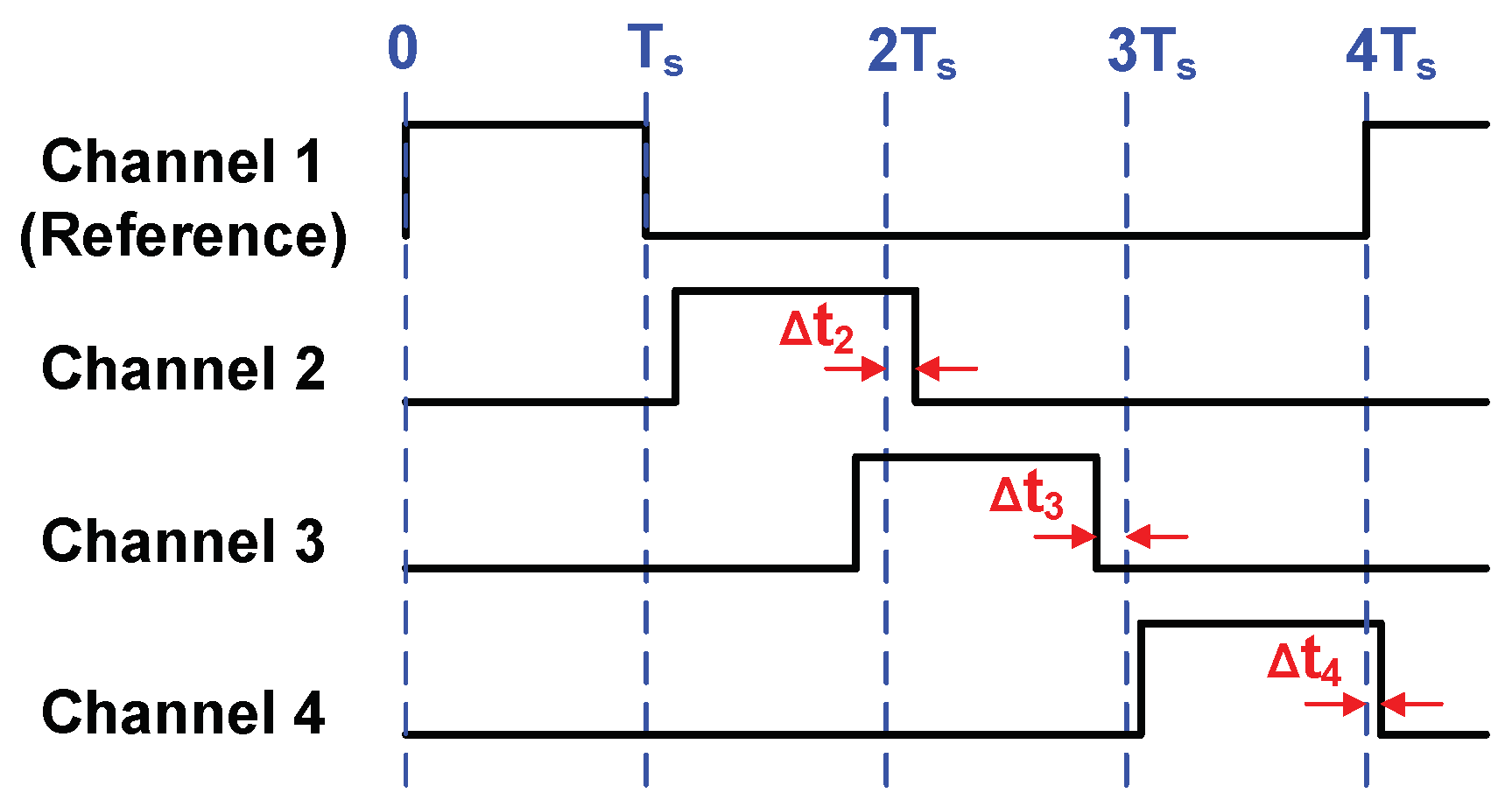
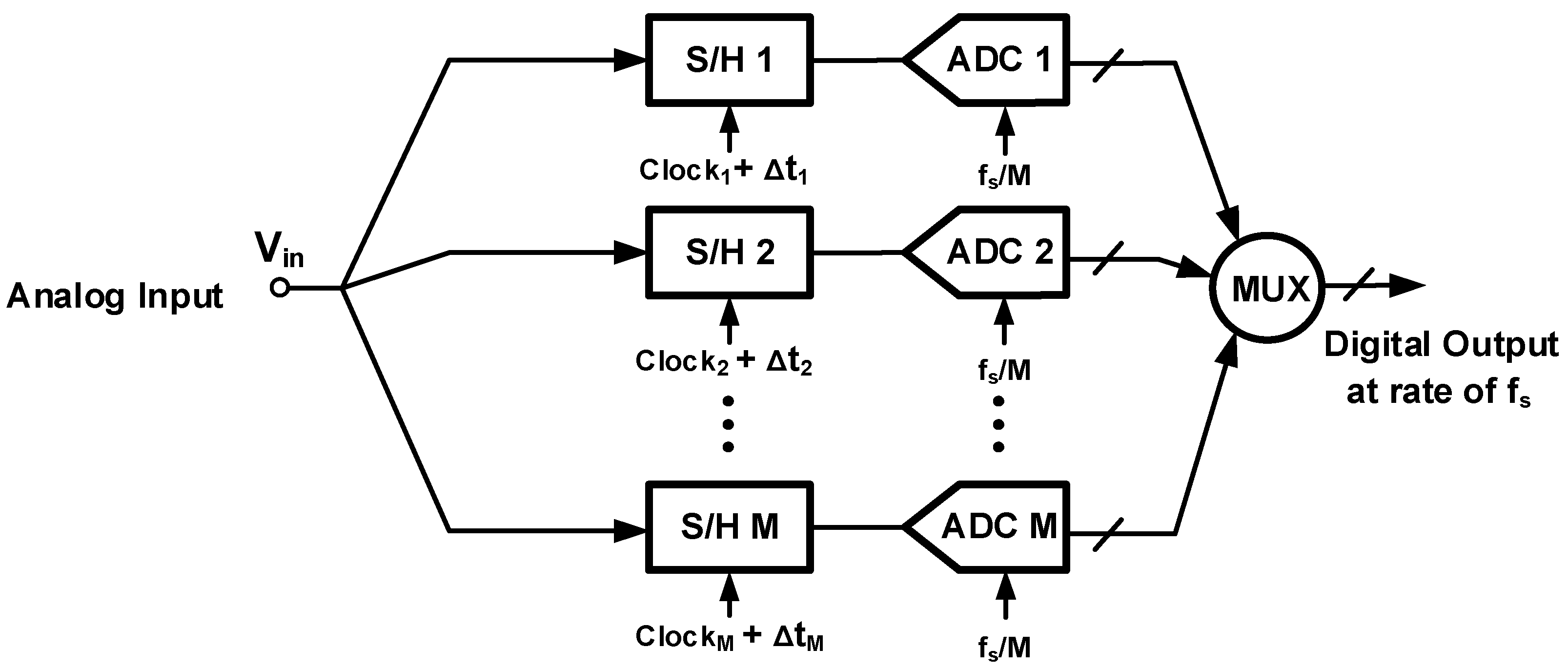
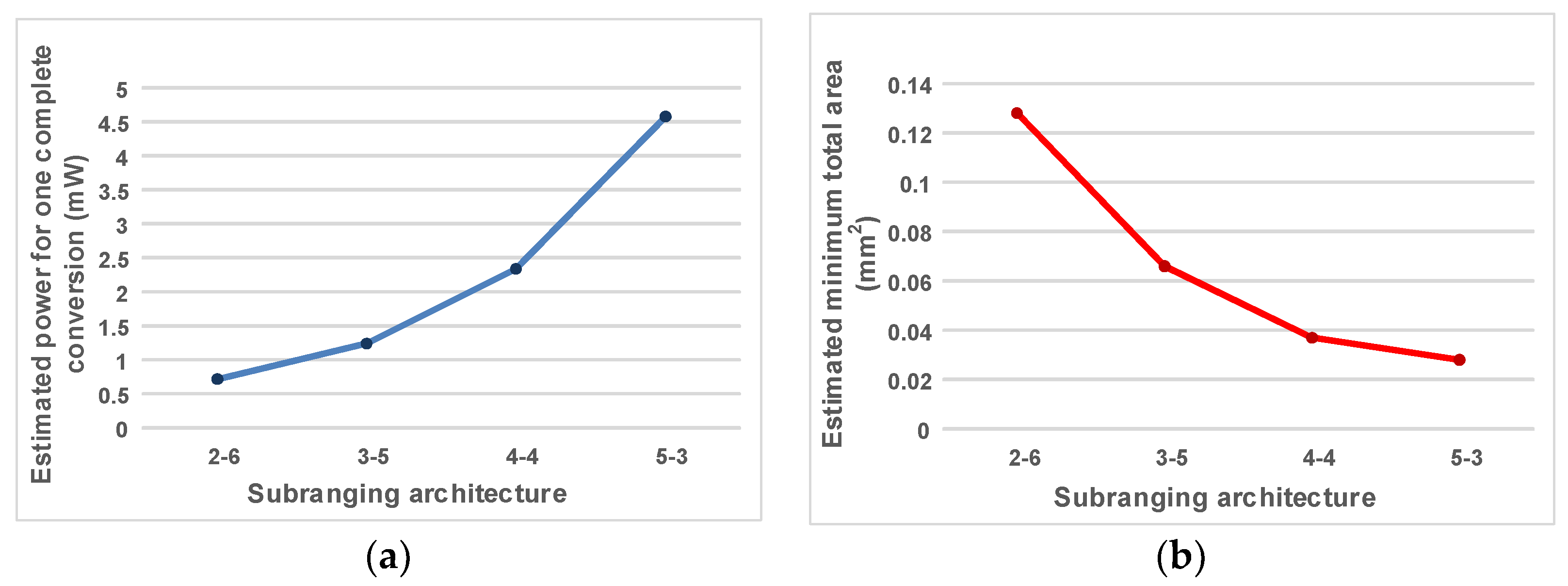


| Subranging Choice * | No. of Comp. in Flash ADC | No. of Comp. in CABS ADC | No. of Activated Comparators during Each 8-bit Conversion | Est. Power of the Flash and CABS for Each 8-bit Conversion (mW) | Est. Total Minimum Area for One Flash and Four CABS ADCs (mm2) |
|---|---|---|---|---|---|
| L–M | 2L − 1 | 2M − 1 | (2L − 1) + M | (2L − 1) ∙ Pflash.comp + M ∙ PCABS.comp | (2L − 1) ∙ Aflash.comp + 4 ∙ (2M − 1) ∙ ACABS.comp |
| 2–6 | 3 | 63 | 3 + 6 | 0.717 | 0.128 |
| 3–5 | 7 | 31 | 7 + 5 | 1.241 | 0.066 |
| 4–4 | 15 | 15 | 15 + 4 | 2.337 | 0.037 |
| 5–3 | 31 | 7 | 31 + 3 | 4.577 | 0.028 |
| Spec. | This Example | [1] | [3] | [7] | [8] | [13] | [74] | [83] | [84] | [85] | [86] | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sampling Rate (GS/s) | 1 | 1 | 1 | 1.25 | 1 | 1.6 | 1.5 | 0.6 | 1.4 | 1 | 1.2 | 0.8 |
| Resolution (bit) | 6 | 8 | 8 | 6 | 6 | 6 | 7 | 6 | 7 | 6 | 8 | 6 |
| CMOS Techn. (nm) | 130 | 130 | 55 | 130 | 65 | 90 | 90 | 130 | 45 | 65 | 65 | 65 |
| Architect. | Subr.-TI | Subr.-TI | Subr. | TI-SAR | Pipe-line | TI-SAR | Flash | Async. SAR | Flash | Interp.-Subr. | Two-Step SAR | VCO-based |
| ENOB@NQ | 5.26 | 5.48 | 6.19 | 5.0 | 5.25 | 4.44 | 6.05 | 5.02 | 6.17 | 5.16 | 6.97 | 4.8 |
| SNDR@NQ (dB) | 33.42 | 34.74 | 39 | 32 | 33.4 | 28.5 | 38.2 | 32 | 38.9 | 32.8 | 43.7 | 30.6 |
| SFDR@NQ (dB) | 45.71 | 46.03 | 53 | 35 | 41.03 | 35.5 | 46.6 | 46 | NA | 44 | 58.1 | 36.2 |
| Supply Voltage (V) | 1.2 | 1.2 | 1.2 | 1.2 | 1 | 1.3 | 1.2 | 1.2 | 1.15 | 1.1 | 1.3 | 1 |
| Power (mW) | 10.5, 8.7 2 | 11 | 16 | 32 | 62 | 20.1 | 204 | 5.3 | 33.24 | 9.9 | 5 | 3.62 |
| Area (mm2) | <0.72 3, <1.4 4 | 0.72 3, 1.4 4 | 0.2 | 0.09 | 0.3 | 0.24 | 1.2 | 0.12 | 0.085 | 0.044 | 0.013 | 0.012 |
| FoM 1@NQ (fJ/conv. step) | 274, 227 5 | 246 | 219 | 800 | 1629 | 579 | 2053 | 272 | 330 | 278 | 35 | 162 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zahrai, S.A.; Onabajo, M. Review of Analog-To-Digital Conversion Characteristics and Design Considerations for the Creation of Power-Efficient Hybrid Data Converters. J. Low Power Electron. Appl. 2018, 8, 12. https://doi.org/10.3390/jlpea8020012
Zahrai SA, Onabajo M. Review of Analog-To-Digital Conversion Characteristics and Design Considerations for the Creation of Power-Efficient Hybrid Data Converters. Journal of Low Power Electronics and Applications. 2018; 8(2):12. https://doi.org/10.3390/jlpea8020012
Chicago/Turabian StyleZahrai, Seyed Alireza, and Marvin Onabajo. 2018. "Review of Analog-To-Digital Conversion Characteristics and Design Considerations for the Creation of Power-Efficient Hybrid Data Converters" Journal of Low Power Electronics and Applications 8, no. 2: 12. https://doi.org/10.3390/jlpea8020012
APA StyleZahrai, S. A., & Onabajo, M. (2018). Review of Analog-To-Digital Conversion Characteristics and Design Considerations for the Creation of Power-Efficient Hybrid Data Converters. Journal of Low Power Electronics and Applications, 8(2), 12. https://doi.org/10.3390/jlpea8020012





