Two-Layer Error Control Codes Combining Rectangular and Hamming Product Codes for Cache Error
Abstract
:1. Introduction
- The cache error rate increases for large volume and high density cache in many-core systems, and can compromise overall system reliability if not well-protected. Meanwhile, future many-core systems place a strict budget on fault-tolerant mechanisms in terms of latency, power and area overhead. Therefore, high reliability but low cost fault-tolerant mechanisms are required;
- The encoding and decoding of rectangular codes, which simply consists of several exclusive or (XOR) gates, can be very fast compared to other error control code, such as Hamming and BCH codes. In contrast, Hamming product codes can provide high error correction capability at the cost of extra check bits overhead;
- Much of cache lines in systems are clean, which means there is another copy in next-level memory. Therefore, it is enough to detect error in clean cache lines, and only correct error in dirty cache lines [5].
2. Related Works
2.1. Soft Error Management Techniques
2.2. Hard Error Management Techniques
2.3. Reliable Circuits and Device Design for Cache
3. Two-Layer Error Control Codes Combining Rectangular and Hamming Product Codes
3.1. Rectangular Codes
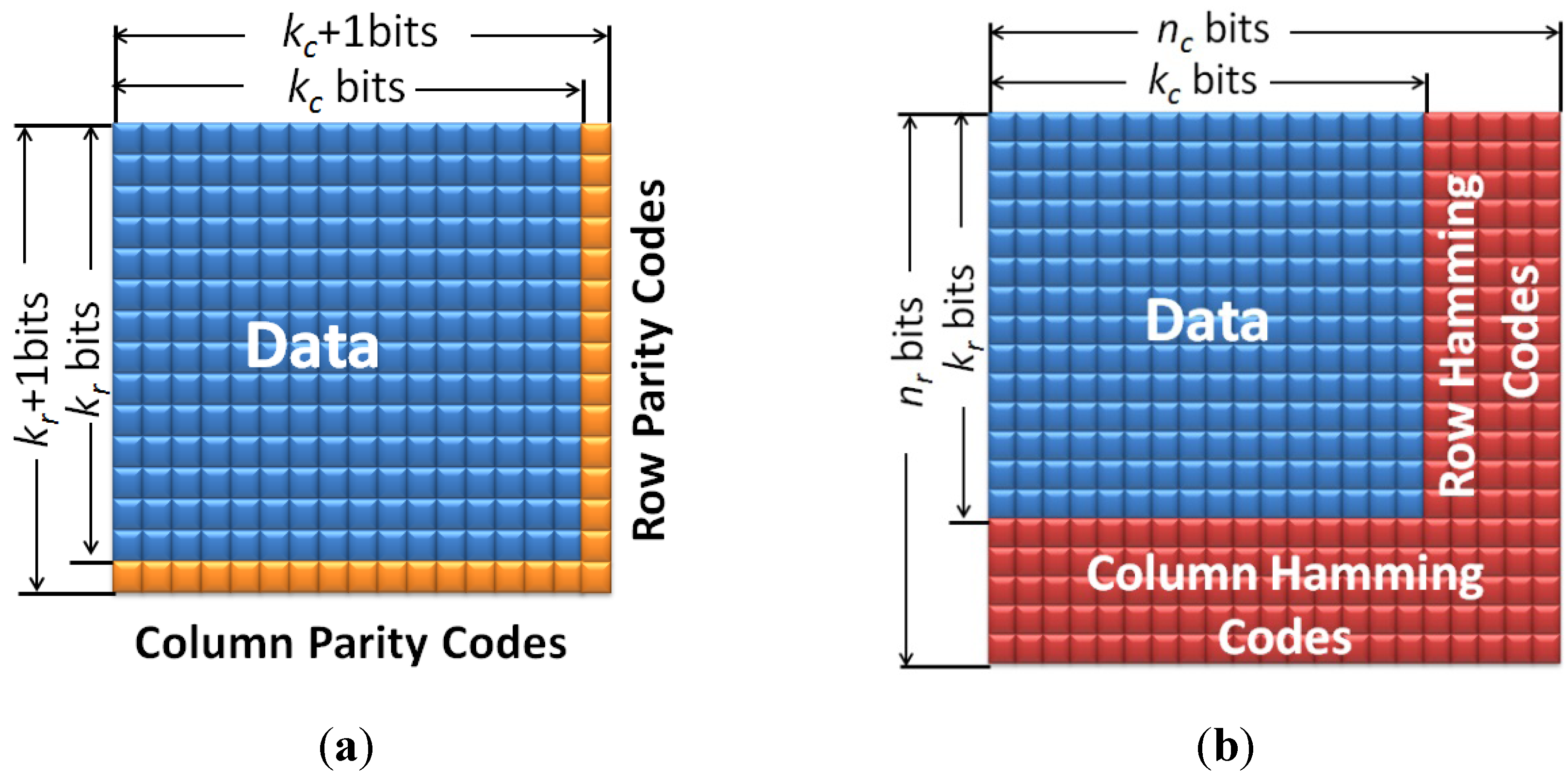
3.2. Hamming Product Codes
| Cache Line Size | nc | nr | Rectangular Check Bits | Rectangular Code Rate | HPC Check Bits | HPC Code Rate |
|---|---|---|---|---|---|---|
| 1024-bit cache line | 32 | 32 | 64 | 94.1% | 384 | 72.8% |
| 512-bit cache line | 32 | 16 | 48 | 91.4% | 256 | 66.7% |
| 256-bit cache line | 16 | 16 | 32 | 88.9% | 160 | 61.5%% |
3.3. Two-Layer ECC Combining Rectangular and Hamming Product Codes
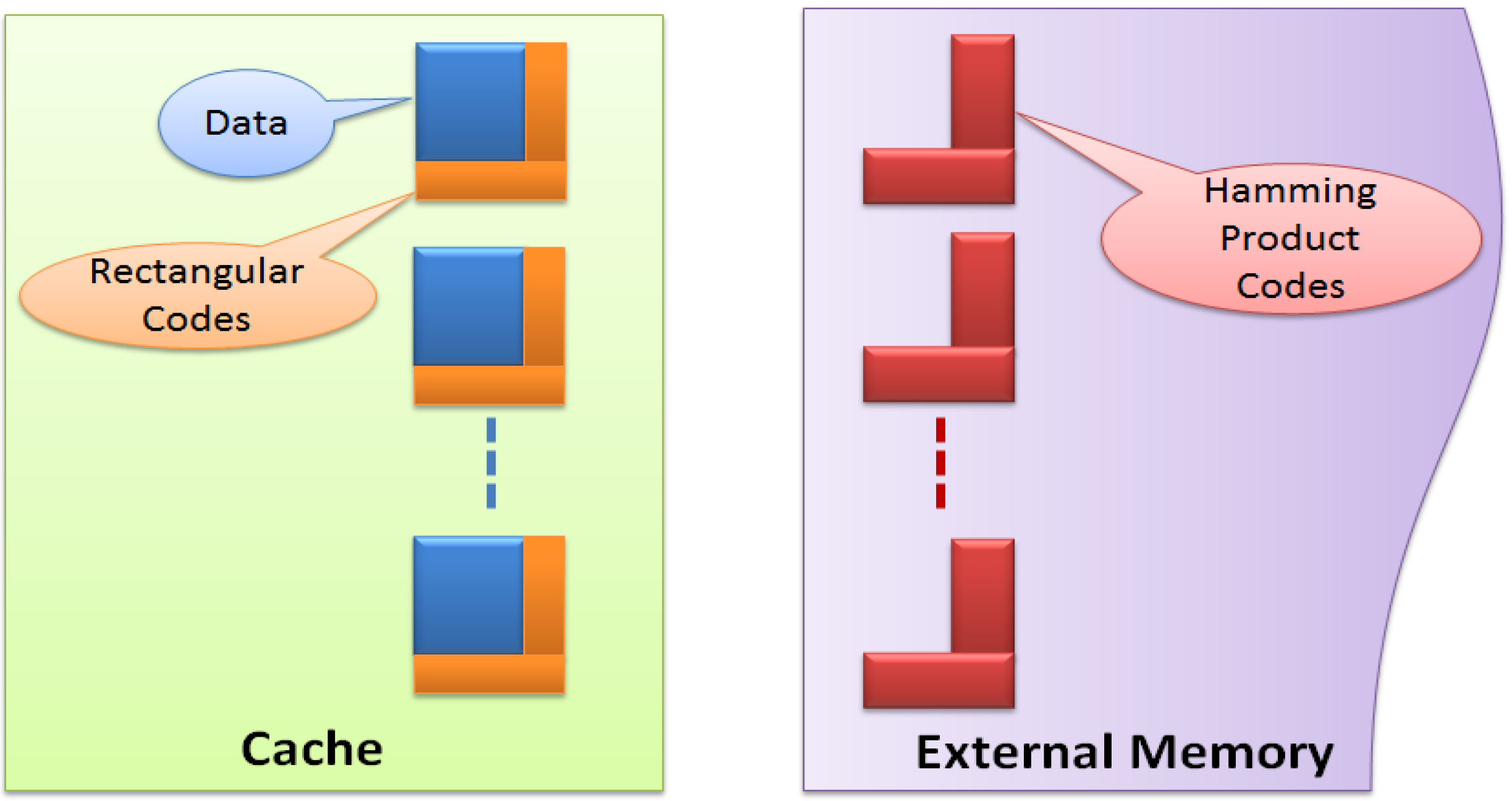
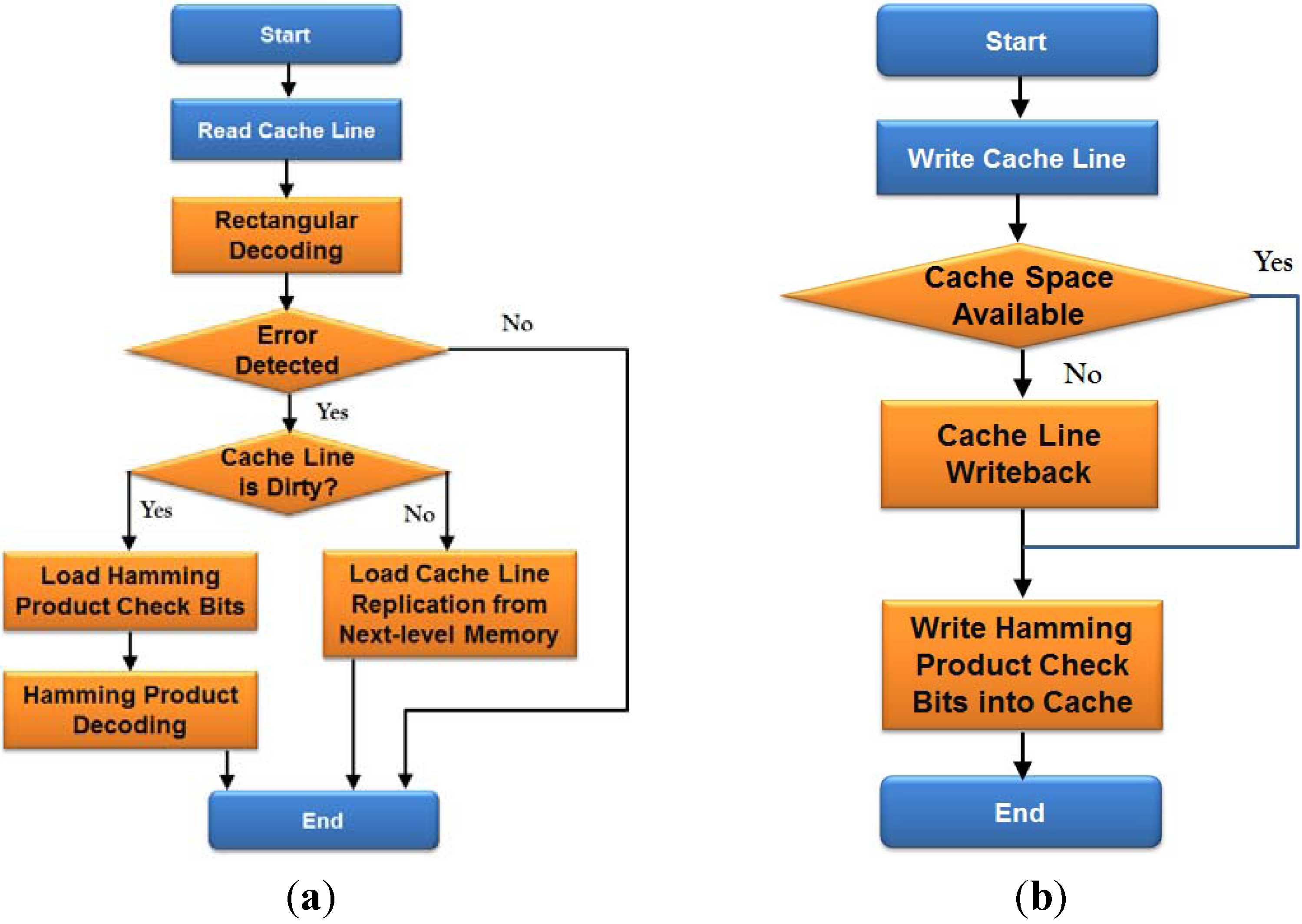
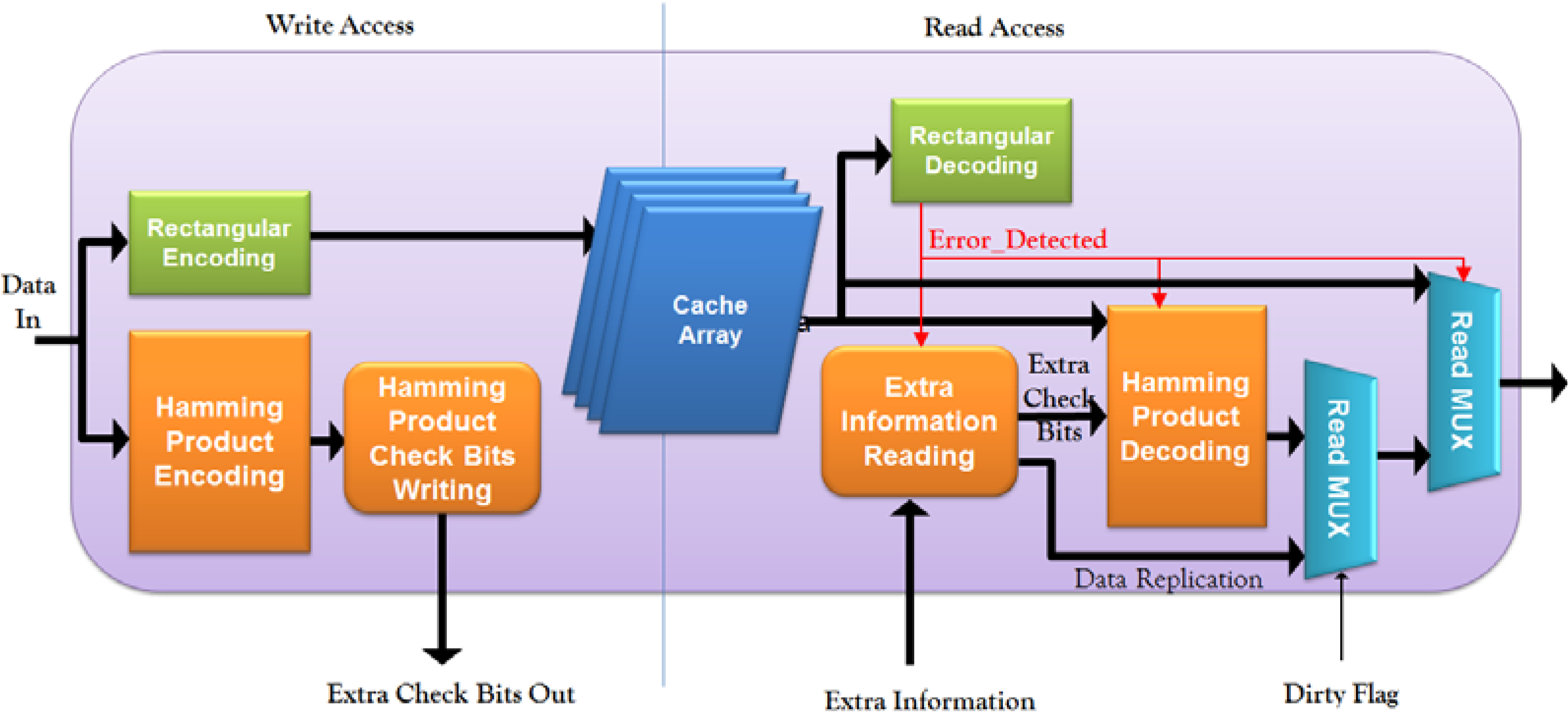
4. Analysis and Experimental Results
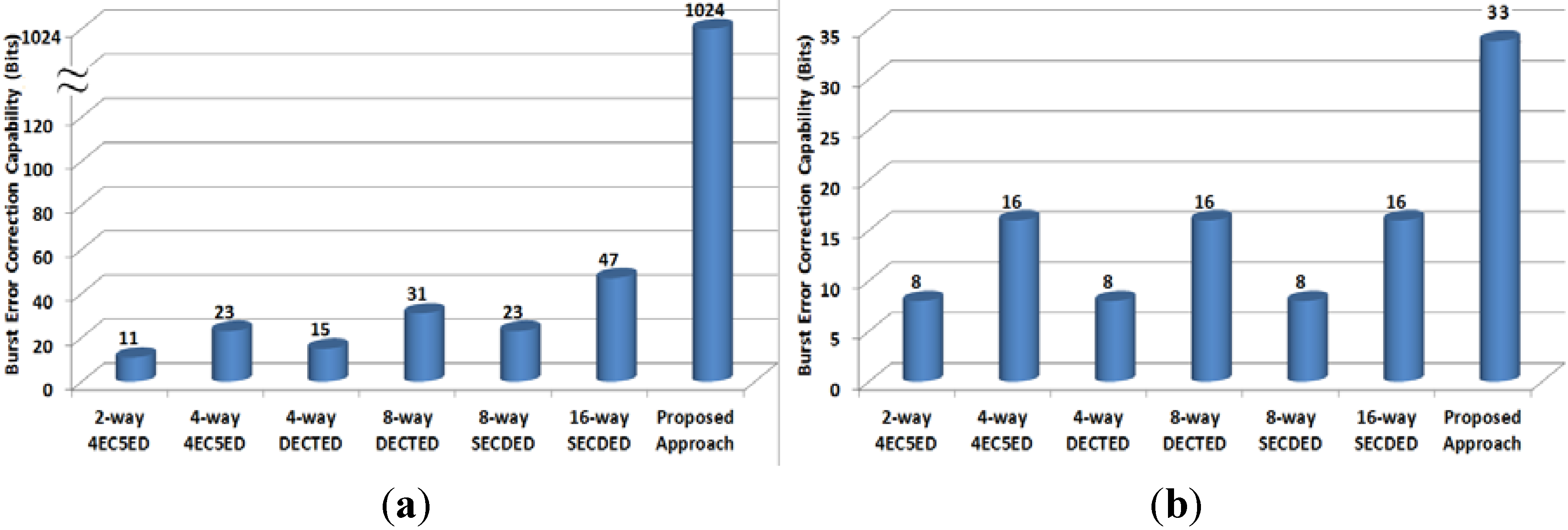
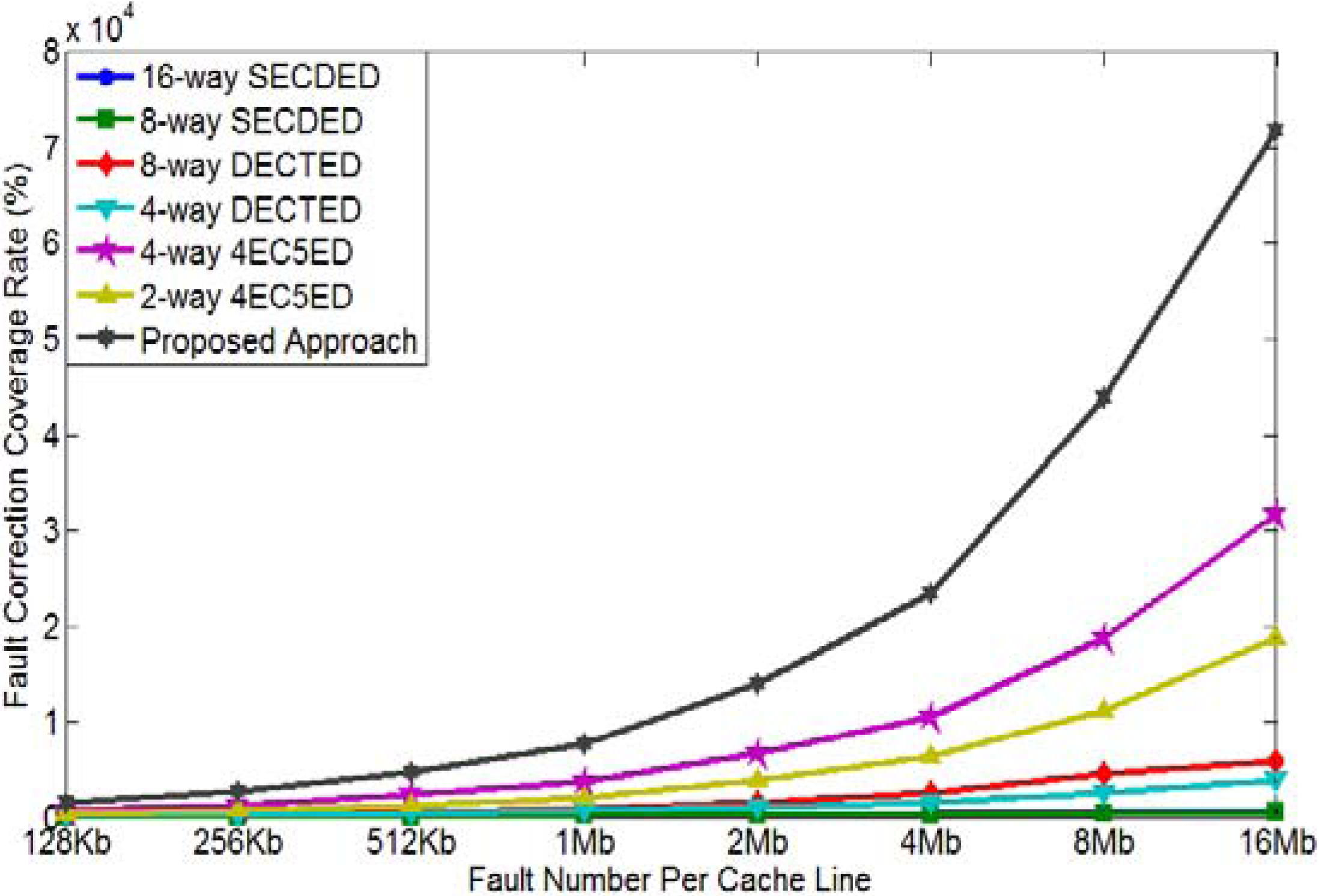
- 16-way SECDED: 16 interleaved SECDED codes are applied for every cache line;
- 8-way SECDED: 8 interleaved SECDED codes are applied for every cache line;
- 8-way DECTED: 8 interleaved DECTED codes are applied for every cache line;
- 4-way DECTED: 4 interleaved DECTED codes are applied for every cache line;
- 4-way 4EC5ED: 4 interleaved 4EC5ED codes are applied for every cache line;
- 2-way 4EC5ED: 2 interleaved 4EC5ED codes are applied for every cache line.
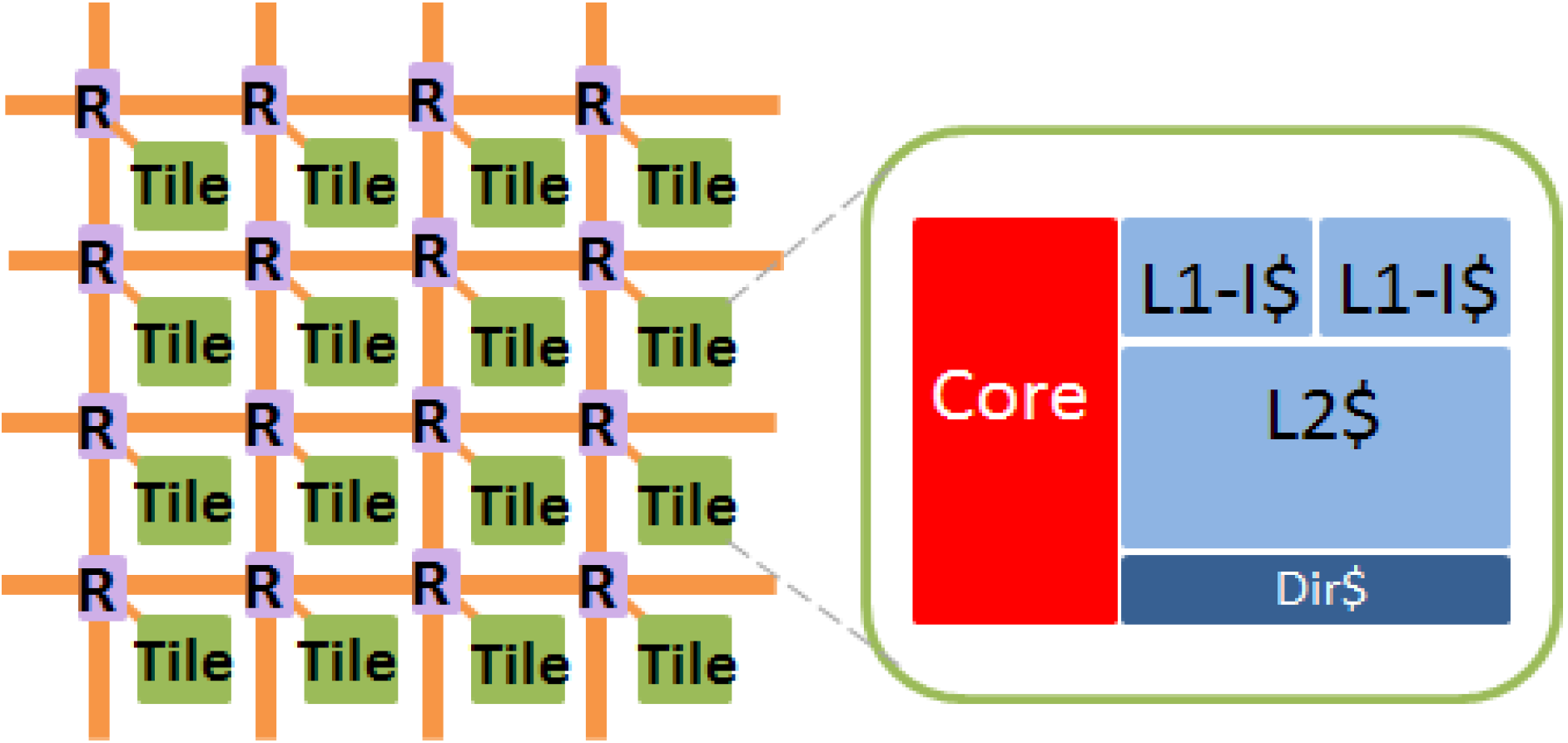
4.1. Experimental Setup
| Parameters | Value | |
|---|---|---|
| Tile Number | 1024 | |
| Core Type | 64 bits single-issue | |
| L1-I/L1-D Cache, Private | ||
| Cache Size | 32 kb | |
| Associativity | 4 | |
| Replacement Policy | LRU | |
| Tag Access Time | 1 cycle | |
| Data Access Time | 1 cycle | |
| L2 Cache, Private | ||
| Cache Size | 256 kb | |
| Associativity | 8 | |
| Replacement Policy | LRU | |
| Tag Access Time | 3 cycles | |
| Data Access Time | 8 cycles | |
| External Memory | ||
| Memory Access Time | 100 cycles | |
4.2. Burst Error Control Capability
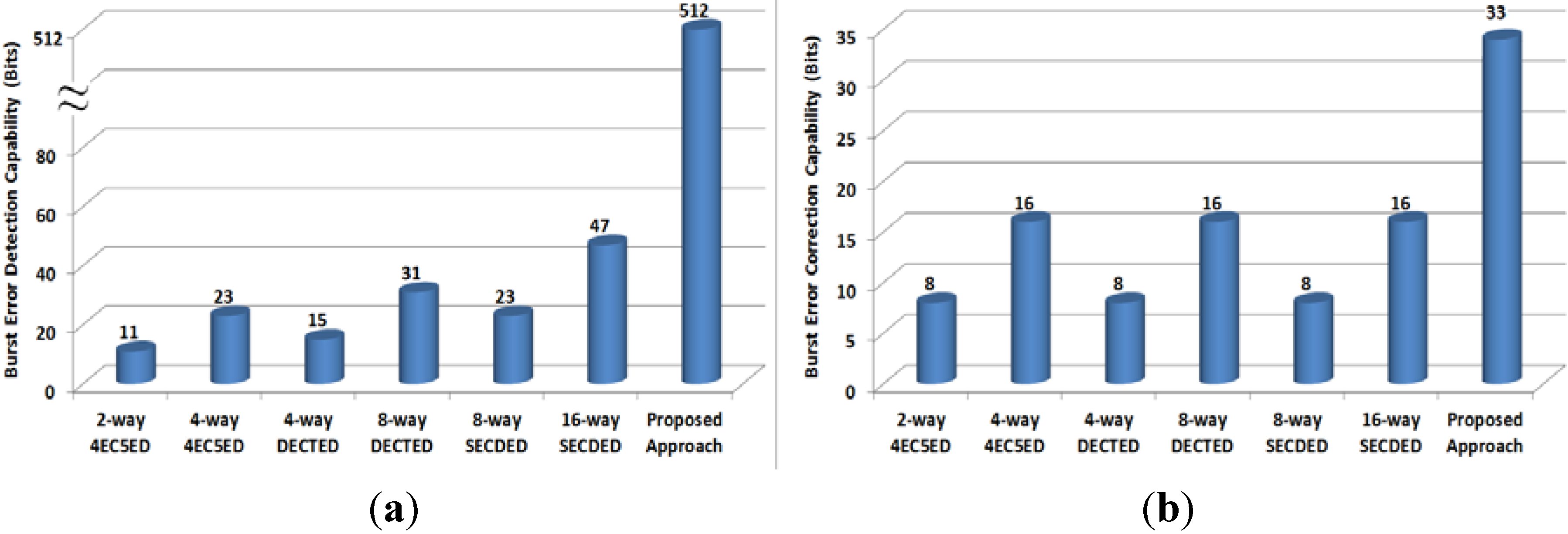
4.3. Mean-Error-to-Failure Evaluation

4.4. Mean-Time-to-Failure Evaluation

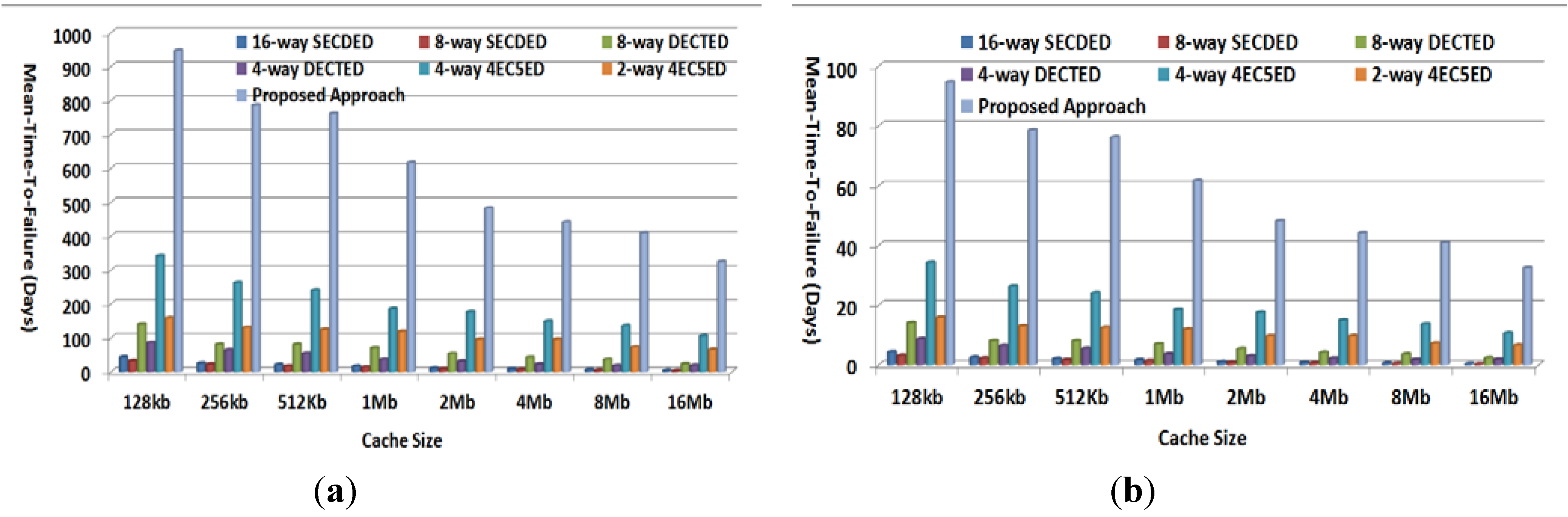
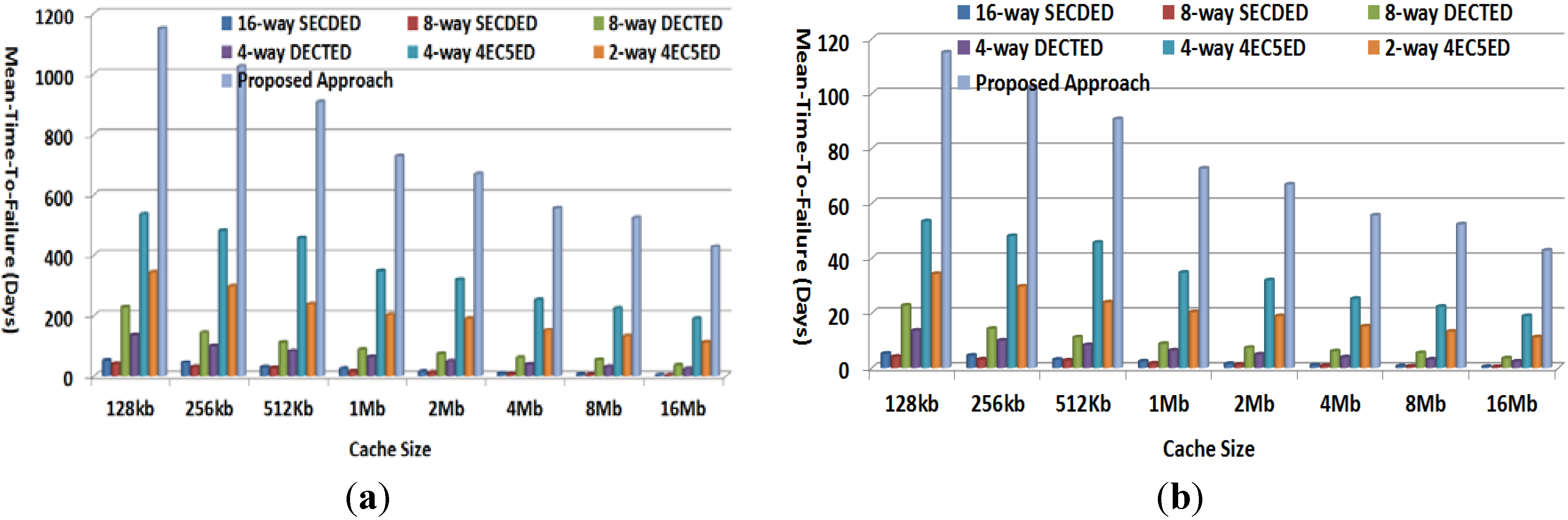
4.5. Overhead Evaluation
| (a) | Data/ Way | Check bits/Way | #Way | #Total bits | (b) | Data/ Way | Check bits/Way | #Way | #Total bits |
|---|---|---|---|---|---|---|---|---|---|
| 16-way SECDED | 64 | 8 | 16 | 128 | 16-way SECDED | 32 | 7 | 16 | 112 |
| 8-way SECDED | 128 | 9 | 8 | 72 | 8-way SECDED | 64 | 8 | 8 | 4 |
| 8-way DECTED | 128 | 17 | 8 | 136 | 8-way DECTED | 64 | 15 | 8 | 120 |
| 4-way DECTED | 256 | 19 | 4 | 76 | 4-way DECTED | 128 | 17 | 4 | 68 |
| 4-way 4EC5ED | 256 | 37 | 4 | 148 | 4-way 4EC5ED | 128 | 33 | 4 | 132 |
| 2-way 4EC5ED | 512 | 41 | 2 | 84 | 2-way 4EC5ED | 256 | 37 | 2 | 74 |
| Proposed | * | * | * | 64 | Proposed | * | * | * | 48 |
4.6. Performance Degradation
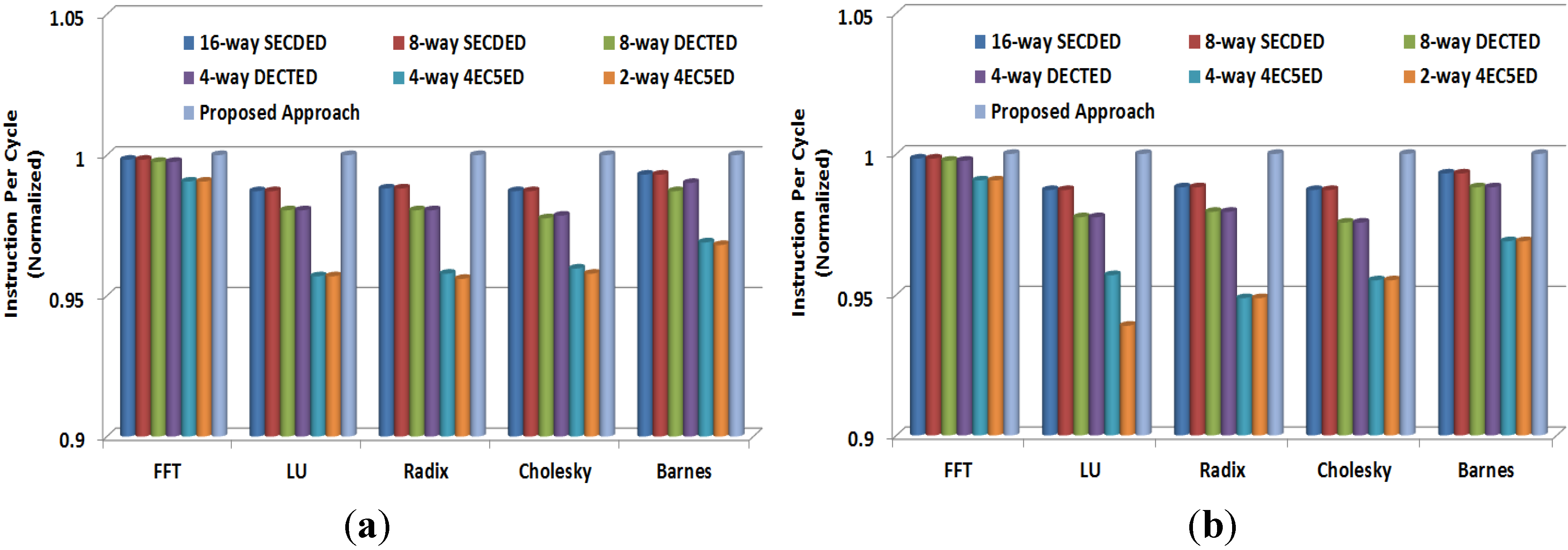
5. Conclusions
References
- Agostinelli, M.; Hicks, J.; Xu, J.; Woolery, B.; Mistry, K.; Zhang, K.; Jacobs, S.; Jopling, J.; Yang, W.; Lee, B.; et al. Erratic Fluctuations of SRAM Cache Vmin at the 90 nm Process Technology Node. In Proceedings of the IEEE International Electron Devices Meeting, IEDM Technical Digest, Washington, DC, USA, 5–7 December 2005.
- Borkar, S. Designing reliable systems from unreliable components: The challenges of transistor variability and degradation. IEEE Micro 2005, 25, 10–17. [Google Scholar] [CrossRef]
- Ruckerbauer, F.X.; Georgakos, X. Soft Error Rates in 65 nm SRAMs—Analysis of New Phenomena. In Proceedings of the IEEE International On-Line Testing Symposium (IOLTS), Crete, Greece, 8–11 July 2007; pp. 203–204.
- Zhang, M.; Ampadu, P. Variation-Tolerant Cache by Two-Layer Error Control Codes. In Proceedings of the 2013 IEEE International Symposium on Defect and Fault Tolerance in VLSI and Nanotechnology Systems (DFT), New York, NY, USA, 2–4 October 2013; pp. 161–166.
- Yoon, D.H.; Erez, M. Memory Mapped ECC: Low-Cost Error Protection for Last Level Caches. In Proceedings of the 36th International Symposium on Computer Architecture (ISCA-36), Austin, TX, USA, 20–24 June 2009; pp. 116–127.
- Reick, K.; Sanda, P.N.; Swaney, S.; Kellington, J.W.; Mack, M.J.; Floyd, M.S.; Henderson, D. Fault-Tolerant Design of the IBM Power6 Microprocessor. IEEE Micro 2008, 28, 30–38. [Google Scholar] [CrossRef]
- Chishti, Z.; Alameldeen, A.R.; Wilkerson, C.; Wu, W.; Lu, S.-L. Improving Cache Lifetime Reliability at Ultra-Low Voltages. In Proceedings of the International Symposium on Microarchitecture, New York, NY, USA, 12–16 December 2009; pp. 89–99.
- Wilkerson, C.; Alameldeen, A.R.; Chishti, Z.; Wu, W.; Somasekhar, D.; Lu, S.-L. Reducing Cache Power with Low-Cost, Multi-bit Error-Correcting Codes. In Proceedings of the International Symposium on Computer Architecture (ISCA), Saint-Malo, France, 19–23 June 2010.
- Radaelli, D.; Puchner, H.; Wong, S.; Daniel, S. Investigation of multi-bit upsets in a 150 nm technology SRAM device. IEEE Trans. Nucl. Sci. 2005, 52, 2433–2437. [Google Scholar] [CrossRef]
- Baeg, S.; Wen, S.; Wong, R. SRAM Interleaving distance selection with a soft error failure model. IEEE Trans. Nucl. Sci. 2009, 56, 2111–2118. [Google Scholar] [CrossRef]
- Kim, J.; Hardavellas, N.; Mai, K.; Falsafi, B.; Hoe, J.C. Multi-bit Error Tolerant Caches Using Two-Dimensional Error Coding. In Proceedings of the 40th International Symposium on Micro-architecture (Micro-40), Chicago, IL, USA, 1–5 December 2007.
- Argyrides, C.; Pradhan, D.K.; Kocak, T. Matrix codes for reliable and cost efficient memory chips. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2011, 19, 420–428. [Google Scholar] [CrossRef]
- Wang, S.; Hu, J.; Ziavras, S.G. Replicating tag entries for reliability enhancement in cache tag arrays. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2012, 20, 634–654. [Google Scholar]
- Kim, J.; Kim, S.; Lee, Y. SimTag: Exploiting Tag Bits Similarity to Improve the Reliability of the Data Caches. In Proceedings of the Conference on DesignAutomationand Test in Europe (DATE’10), Dresden, Germany, 8–12 March 2010; pp. 941–944.
- Wang, S. Characterizing System-Level Vulnerability for Instruction Caches against Soft Errors. In Proceedings of 2011 IEEE International Symposium on Defect and Fault Tolerance in VLSI and Nanotechnology Systems (DFT’11), Vancouver, Canada, 3–5 October2011; pp. 356–363.
- Schuster, S. Multiple word/bit line redundancy for semiconductor memories. IEEE J. Solid-State Circuits 1978, 13, 698–703. [Google Scholar] [CrossRef]
- Horiguchi, M. Redundancy Techniques for High-Density DRAMS. In Proceedings of the 2nd Annual IEEE International Conference Innovative Systems Silicon, Austin, TX, USA, 8–10 October 1997; pp. 22–29.
- Agarwal, A.; Paul, B.C.; Mahmoodi, H.; Datta, A.; Roy, K. A process-tolerant cache architecture for improved yield in nanoscale technologies. IEEE Trans. Very Large Scale Integr. (VLSI) Syst 2005, 13, 27–38. [Google Scholar] [CrossRef]
- Lee, H.; Cho, S.; Childers, B.R. Performance of Graceful Degradation for Cache faults. In Proceedings of the IEEE Computer Society Annual Symposium on VLSI (ISVLSI ’07), Porto Alegre, Brazil, 9–11 March 2007.
- Abella, J.;Carretero, J.; Chaparro, P.; Vera, X.; Gonzalez, A. Low Vccmin Fault-Tolerant Cache with Highly Predictable Performance. In Proceedings of the 42nd Annual IEEE/ACM International Symposium on Microarchitecture (MICRO’09), New York, NY, USA, 12–16 December 2009.
- Wilkerson, C.; Gao, H.; Alameldeen, A.R.; Chishti, Z.; Khellah, M.; Lu, S.-L. Trading off Cache Capacity for Reliability to Enable Low Voltage Operation. In Proceedings of the 35th International Symposium on Computer Architecture (ISCA’08), Beijing, China, 21–25 June 2008; pp. 203–214.
- Lu, S.-L.; Alameldeen, A.; Bowman, K.; Chishti, Z.; Wilkerson, C.; Wei, W. Architectural-Level Error-Tolerant Techniques for Low Supply Voltage Cache Operation. In Proceedings of the IEEE International Conference on IC Design & Technology (ICICDT’11), Kaohsiung, Taiwan, 2–4 May 2011.
- Aladmeldeen, A.; Wagner, I.; Chishti, Z.; Wu, W.; Wilkerson, C.; Lu, S.-L. Energy-Efficient Cache Design Using Variable-Strength Error-Correcting Codes. In Proceedings of the 38th International Symposium on Computer Architecture, San Jose, CA, USA, 4–8 June 2011.
- Zhang, M.; Stojanovic, V.M.; Ampadu, P. Reliable ultra-low-voltage cache design for many-core systems. IEEE Trans. Circuits Syst. II 2012, 59, 858–862. [Google Scholar] [CrossRef]
- Ampadu, P.; Zhang, M.; Stojanovic, V. Breaking the Energy Barrier in Fault-Tolerant Caches for Multicore Systems. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition, Grenoble, France, 18–22 March 2013; pp. 731–736.
- Li, C.; Zhang, M.; Ampadu, P. Reliable Ultra-Low Voltage Cache with Variation-Tolerance. In Proceedings of the IEEE 56th International Midwest Symposium on Circuits and Systems (MWSCAS), Columbus, OH, USA, 4–7 August 2013; pp. 121–124.
- Chang, L.; Fried, D.; Hergenrother, J.; Sleight, J.; Dennard, R.; Montoye, R.R.; Sekaric, L.; McNab, S.; Topol, W.; Adams, C.; et al. Stable SRAM Cell Design for the 32 nm Node and Beyond. In Proceedings of the 2005 Symposium on VLSI Technology, Digest of Technical Papers, Kyoto, Japan, 14–16 June 2005; pp. 128–129.
- Calhoun, B.H.; Chandrakasan, A. A 256 kb sub-threshold SRAM in 65 nm CMOS. IEEE J. Solid State Circuits 2007, 42, 680–688. [Google Scholar] [CrossRef]
- Fu, B.; Ampadu, P. On hamming product codes with type-II hybrid ARQ for on-chip interconnects. IEEE Trans. Circuits Syst. I 2009, 56, 2042–2054. [Google Scholar] [CrossRef]
- Kurian, G.; Chen, S.; Chen, C.-H.O.; Miller, J.E.; Michel, J.; Wei, L.; Antoniadis, D.A.; Peh, L.S.; Kimerling, L.; Stojanovic, V.; Agarwal, A. Cross-Layer Energy and Performance Evaluation of a Nanophotonic Manycore Processor System using Real Application Workloads. In Proceedings of the IEEE 26th International Parallel & Distributed Processing Symposium (IPDPS), Shanghai, China, 21–25 May 2012.
- Miller, J.; Kasture, H.; Kurian, G.; Gruenwald, C.; Beckmann, N.; Celio, C.; Eastep, J.; Agarwal, A. Graphite: A Distributed Parallel Simulator for Multicores. In Proceedings of the IEEE International Symposium on High Performance Computer Architecture (HPCA), Bangalore, India, 9–14 January 2009.
- Thoziyoor, S.; Ahn, J.; Monchiero, M.; Brockman, J.; Jouppi, N. A Comprehensive Memory Modeling Tool and its Application to the Design and Analysis of Future Memory Hierarchies. In Proceedings of the 35th International Symposium on Computer Architecture (ISCA), Beijing, China, 21–25 June 2008.
- Naseer, R.; Draper, J. Parallel Double Error Correcting Code Design to Mitigate Multi-Bit Upsets in SRAMs. In Proceedings of the 34th European Solid-State Circuits Conference (ESSCIRC), Edinburgh, UK, 15–19 September 2008; pp. 222–225.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhang, M.; Ampadu, P. Two-Layer Error Control Codes Combining Rectangular and Hamming Product Codes for Cache Error. J. Low Power Electron. Appl. 2014, 4, 44-62. https://doi.org/10.3390/jlpea4010044
Zhang M, Ampadu P. Two-Layer Error Control Codes Combining Rectangular and Hamming Product Codes for Cache Error. Journal of Low Power Electronics and Applications. 2014; 4(1):44-62. https://doi.org/10.3390/jlpea4010044
Chicago/Turabian StyleZhang, Meilin, and Paul Ampadu. 2014. "Two-Layer Error Control Codes Combining Rectangular and Hamming Product Codes for Cache Error" Journal of Low Power Electronics and Applications 4, no. 1: 44-62. https://doi.org/10.3390/jlpea4010044
APA StyleZhang, M., & Ampadu, P. (2014). Two-Layer Error Control Codes Combining Rectangular and Hamming Product Codes for Cache Error. Journal of Low Power Electronics and Applications, 4(1), 44-62. https://doi.org/10.3390/jlpea4010044




