Gate-Level Hardware Priority Resolvers for Embedded Systems
Abstract
1. Introduction
2. Priority Resolvers—Direct and Modular Design Approaches
2.1. Direct Design of Priority Resolvers
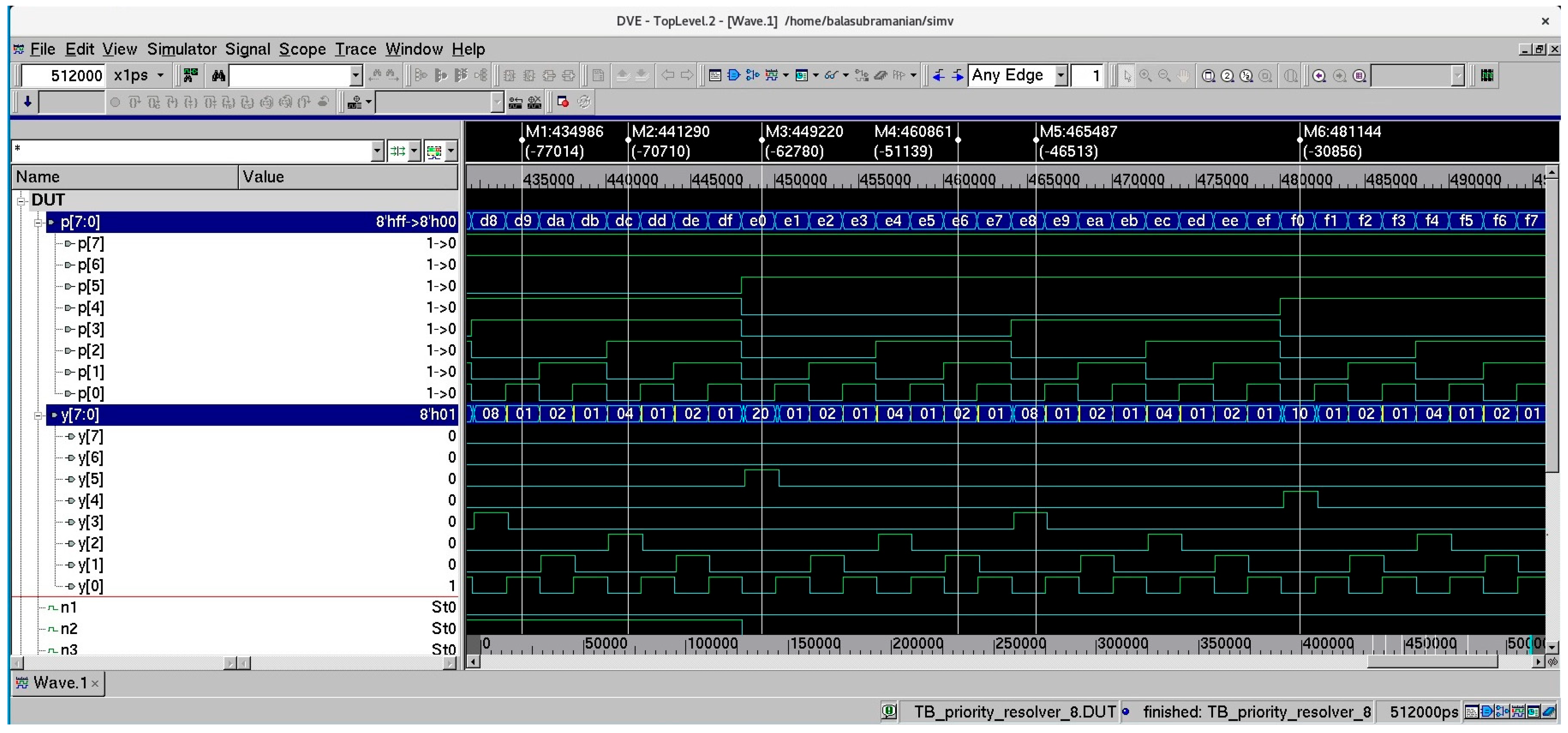
- Marker M1: primary inputs p[7], p[6], p[4], p[3], and p[0] are activated; primary output y[0] alone is high;
- Marker M2: primary inputs p[7], p[6], p[4], p[3], and p[2] are activated; primary output y[2] alone is high;
- Marker M3: primary inputs p[7], p[6], and p[5] are activated; primary output y[5] alone is high;
- Marker M4: primary inputs p[7], p[6], p[5], p[2], and p[1] are activated; primary output y[1] alone is high;
- Marker M5: primary inputs p[7], p[6], p[5], and p[3] are activated; primary output y[3] alone is high;
- Marker M6: primary inputs p[7], p[6], p[5], and p[4] are activated; primary output y[4] alone is high.
2.2. Proposed Modular Design of Priority Resolvers
3. Physical Implementation and Design Metrics
- Compared to the directly implemented 8-bit priority resolver, a 4_8 modular priority resolver had a 29.3% reduced delay;
- Compared to the directly implemented 16-bit priority resolver, the 4_16 and 8_16 modular priority resolvers achieved reductions in delay of 31.5% and 38.4%, respectively;
- Compared to the directly implemented 32-bit priority resolver, the 4_32, 8_32, and 16_32 modular priority resolvers achieved similar reductions in delay of 40.2%, 41.7%, and 39.4%, respectively;
- Compared to the directly implemented 64-bit priority resolver, among the different modular priority resolvers, the 16_64 modular priority resolver achieved a maximum reduction in delay of 68.2%;
- Compared to the directly implemented 128-bit priority resolver, the 16_128 modular priority resolver achieved a maximum reduction in delay of 71.8%, and the 32_128 modular priority resolver achieved a similar delay reduction of 70.4%.
- Compared to the directly implemented 8-bit priority resolver, a 4_8 modular 8-bit priority resolver had a 14% reduction in PDP;
- Compared to the directly implemented 16-bit priority resolver, the 4_16 and 8_16 modular 16-bit priority resolvers achieved reductions in PDP of 19% and 23%, respectively;
- Compared to the directly implemented 32-bit priority resolver, the 4_32, 8_32, and 16_32 modular 32-bit priority resolvers achieved similar reductions in PDP of 24.8%, 24.2%, and 23.1%, respectively;
- Compared to the directly implemented 64-bit priority resolver, among the different modular priority resolvers, the 16_64 modular 64-bit priority resolver achieved a maximum reduction in PDP of 56.8%;
- Compared to the directly implemented 128-bit priority resolver, among the different modular priority resolvers, the 16_128 and 32_128 modular 128-bit priority resolvers achieved similar reductions in PDP of 61.4% and 60.4%, respectively.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Adamides, E.D.; Iliades, P.; Argyrakis, I.; Tsalides, P.; Thanailakis, A. Cellular logic bus arbitration. IEE Proc. E Comput. Digit. Tech. 1993, 140, 289–296. [Google Scholar] [CrossRef]
- Huang, C.-H.; Wang, J.-S. High-performance and power-efficient CMOS comparators. IEEE J. Solid-State Circuits 2003, 38, 254–262. [Google Scholar] [CrossRef]
- Hennessy, J.L.; Patterson, D.A. Computer Architecture: A Quantitative Approach, 3rd ed.; Morgan Kaufmann Publishers: New York, NY, USA, 2002. [Google Scholar]
- Summerville, D.H.; Delgado-Frias, J.G.; Vassiliadis, S. A flexible bit-pattern associate router for interconnection networks. IEEE Trans. Parallel Distrib. Syst. 1996, 7, 477–485. [Google Scholar] [CrossRef]
- Huang, C.-H.; Wang, J.-S.; Huang, Y.-C. Design of high-performance CMOS priority encoders and incrementer/decrementers using multilevel lookahead and multilevel folding techniques. IEEE J. Solid-State Circuits 2002, 37, 63–76. [Google Scholar] [CrossRef]
- Mohan, N.; Fung, W.; Sachdev, M. Low-power priority encoder and multiple match detection circuit for ternary content addressable memory. In Proceedings of the IEEE International SOC Conference, Austin, TX, USA, 24–27 September 2006. [Google Scholar]
- Hashemian, R. A high speed compact priority encoder. In Proceedings of the 32nd Midwest Symposium on Circuits and Systems, Champaign, IL, USA, 14–16 August 1989. [Google Scholar]
- Delgado-Frias, J.G.; Nyathi, J. A VLSI high-performance encoder with priority lookahead. In Proceedings of the 8th Great Lakes Symposium on VLSI, Lafayette, LA, USA, 19–21 February 1998. [Google Scholar]
- Wang, J.-S.; Huang, C.-H. High-speed and low-power CMOS priority encoders. IEEE J. Solid-State Circuits 2000, 35, 1511–1514. [Google Scholar] [CrossRef]
- Kun, C.; Quan, S.; Mason, A. A power-optimized 64-bit priority encoder utilizing parallel priority look-ahead. In Proceedings of the IEEE International Symposium on Circuits and Systems, Vancouver, BC, Canada, 23–26 May 2004. [Google Scholar]
- Mohanraj, J.; Balasubramanian, P.; Prasad, K. Power, delay and area optimized 8-bit CMOS priority encoder for embedded applications. In Proceeding of the 10th International Conference on Embedded Systems and Applications, Las Vegas, NV, USA, 16–19 July 2012. [Google Scholar]
- Balobas, D.; Konofaos, N. Low-power, high-performance 64-bit CMOS priority encoder using static-dynamic parallel architecture. In Proceedings of the 5th International Conference on Modern Circuits and Systems, Thessaloniki, Greece, 12–14 May 2016. [Google Scholar]
- Balobas, D.; Konofaos, N. Ultra-low-power and compact 8-bit CMOS priority encoder. Int. J. Electron. Lett. 2017, 5, 272–278. [Google Scholar] [CrossRef]
- Balobas, D.; Konofaos, N. High-performance and energy-efficient 256-bit CMOS priority encoder. In Proceedings of the IEEE Computer Society Annual Symposium on VLSI, Bochum, Germany, 3–5 July 2017. [Google Scholar]
- Maurya, S.K.; Clark, L.T. Fast and scalable priority encoding using static CMOS. In Proceedings of the IEEE International Symposium on Circuits and Systems, Paris, France, 30 May–2 June 2010. [Google Scholar]
- Huang, S.-W.; Chang, Y.-J. A full parallel priority encoder design used in comparator. In Proceedings of the 53rd IEEE International Midwest Symposium on Circuits and Systems, Seattle, WA, USA, 1–4 August 2010. [Google Scholar]
- Panchal, P.; Vinitha, C.; Srivastava, R.; Balasubramanian, P.; Mastorakis, N.E. Design of 8-bit dynamic CMOS priority resolvers based on active-high and active-low logic. In Proceedings of the International Conference on Electronics and Communication Systems, Rhodes Island, Greece, 16–19 July 2013. [Google Scholar]
- Wang, X.; Feng, Y. Analysis and Design of 8-bit CMOS Priority Encoders. arXiv 2018, arXiv:1806.01443. [Google Scholar]
- Synopsys SAED_EDK32/28_CORE Databook, Revision 1.0.0. January 2012. Available online: https://www.synopsys.com/academic-research/university.html (accessed on 7 September 2023).
- Rabaey, J.M.; Chandrakasan, A.; Nikolic, B. Digital Integrated Circuits: A Design Perspective, 2nd ed.; Pearson Education: London, UK, 2003; ISBN 978-0130909961. [Google Scholar]
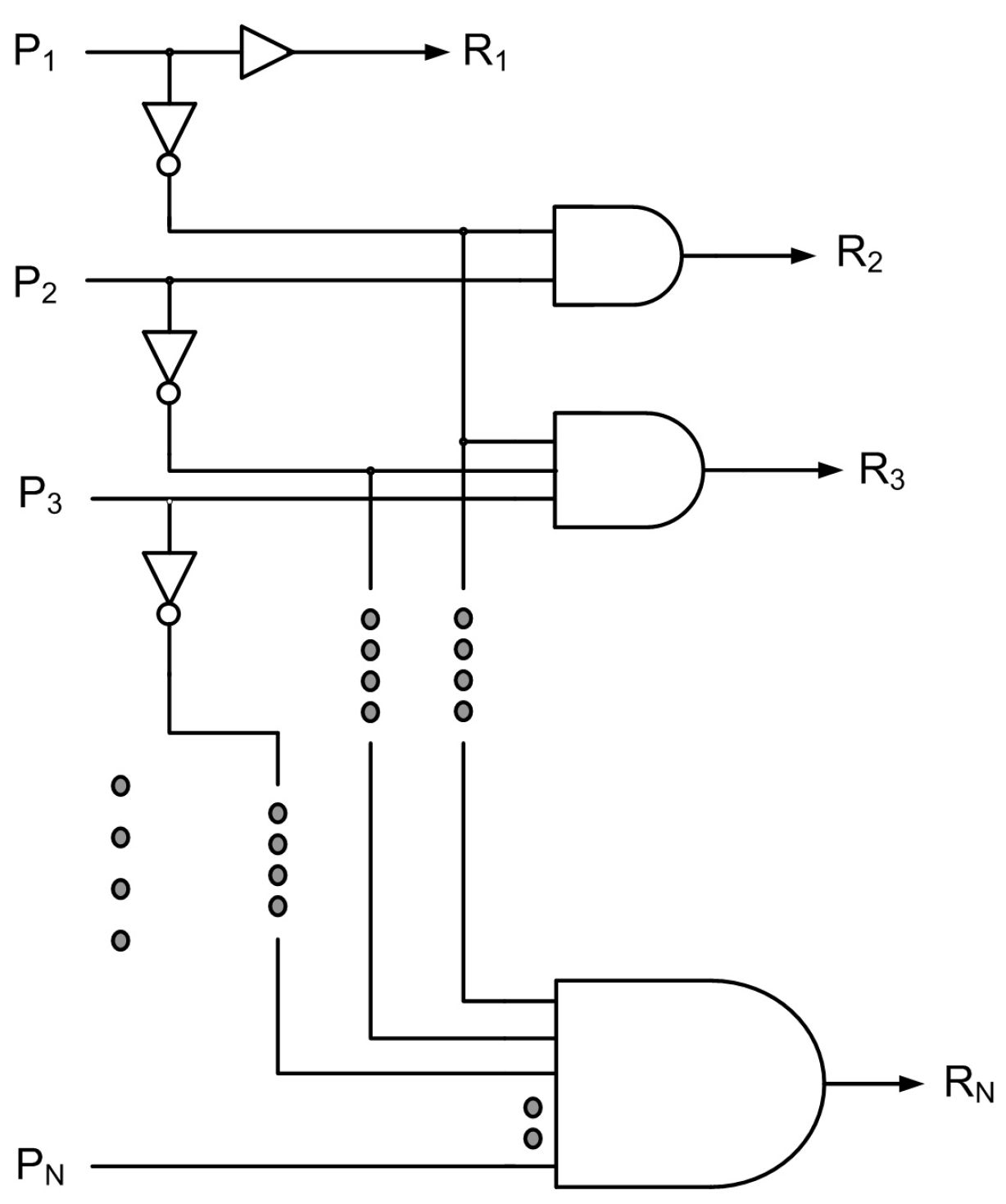

| Primary Inputs | Primary Outputs | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | R1 | R2 | R3 | R4 | R5 | R6 | R7 | R8 |
| 1 | d | d | d | d | d | d | d | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | d | d | d | d | d | d | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | d | d | d | d | d | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | d | d | d | d | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | d | d | d | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | d | d | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | d | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Priority Resolver Size | Area (µm2) | Critical Path Delay (ns) | Total Power Dissipation (µW) | ||
|---|---|---|---|---|---|
| Cells | Interconnect | Total | |||
| 4 bits | 16.77 | 1.70 | 18.47 | 0.25 | 2.86 |
| 8 bits | 41.93 | 4.04 | 45.97 | 0.41 | 4.20 |
| 16 bits | 94.80 | 9.08 | 103.88 | 0.73 | 11.40 |
| 32 bits | 200.52 | 32.93 | 233.45 | 1.27 | 16.92 |
| 64 bits | 411.97 | 67.60 | 479.57 | 2.45 | 32.62 |
| 128 bits | 834.86 | 136.96 | 971.82 | 4.79 | 51.51 |
| Priority Resolver Size | Area (µm2) | Critical Path Delay (ns) | Total Power Dissipation (µW) | ||
|---|---|---|---|---|---|
| Cells | Interconnect | Total | |||
| 4-bit priority resolver module used as the building block | |||||
| 8 bits (4_8) | 48.80 | 4.72 | 53.52 | 0.29 | 5.10 |
| 16 bits (4_16) | 114.87 | 11.17 | 126.04 | 0.50 | 13.47 |
| 32 bits (4_32) | 246.01 | 38.32 | 284.33 | 0.76 | 21.27 |
| 64 bits (4_64) | 508.29 | 79.56 | 587.85 | 1.33 | 41.60 |
| 128 bits (4_128) | 1032.84 | 162.03 | 1194.87 | 2.45 | 63.60 |
| 8-bit priority resolver module used as the building block | |||||
| 16 bits (8_16) | 112.33 | 10.89 | 123.22 | 0.45 | 14.25 |
| 32 bits (8_32) | 254.65 | 39.75 | 294.40 | 0.74 | 22.03 |
| 64 bits (8_64) | 544.38 | 85.44 | 629.82 | 1.60 | 44.42 |
| 128 bits (8_128) | 1123.88 | 176.82 | 1300.65 | 3.30 | 72.30 |
| 16-bit priority resolver module used as the building block | |||||
| 32 bits (16_32) | 240.93 | 38.16 | 279.07 | 0.77 | 21.47 |
| 64 bits (16_64) | 534.72 | 89.20 | 623.92 | 0.78 | 44.23 |
| 128 bits (16_128) | 1122.30 | 191.28 | 1313.58 | 1.35 | 70.57 |
| 32-bit priority resolver module used as the building block | |||||
| 64 bits (32_64) | 505.24 | 76.26 | 581.50 | 1.42 | 40.94 |
| 128 bits (32_128) | 1114.68 | 175.16 | 1289.84 | 1.42 | 68.77 |
| 64-bit priority resolver module used as the building block | |||||
| 128 bits (64_128) | 1028.27 | 179.97 | 1208.24 | 2.48 | 62.79 |
| Priority Resolver Size | Direct Implementation | Modular Implementation |
|---|---|---|
| 4 bits | 0.72 | – |
| 8 bits | 1.72 | 1.48 (4_8) |
| 16 bits | 8.32 | 6.74 (4_16) |
| 6.41 (8_16) | ||
| 32 bits | 21.49 | 16.17 (4_32) |
| 16.30 (8_32) | ||
| 16.53 (16_32) | ||
| 64 bits | 79.92 | 55.33 (4_64) |
| 71.07 (8_64) | ||
| 34.50 (16_64) | ||
| 58.13 (32_64) | ||
| 128 bits | 246.73 | 155.82 (4_128) |
| 238.59 (8_128) | ||
| 95.27 (16_128) | ||
| 97.65 (32_128) | ||
| 155.72 (64_128) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balasubramanian, P.; Maskell, D.L. Gate-Level Hardware Priority Resolvers for Embedded Systems. J. Low Power Electron. Appl. 2024, 14, 25. https://doi.org/10.3390/jlpea14020025
Balasubramanian P, Maskell DL. Gate-Level Hardware Priority Resolvers for Embedded Systems. Journal of Low Power Electronics and Applications. 2024; 14(2):25. https://doi.org/10.3390/jlpea14020025
Chicago/Turabian StyleBalasubramanian, Padmanabhan, and Douglas L. Maskell. 2024. "Gate-Level Hardware Priority Resolvers for Embedded Systems" Journal of Low Power Electronics and Applications 14, no. 2: 25. https://doi.org/10.3390/jlpea14020025
APA StyleBalasubramanian, P., & Maskell, D. L. (2024). Gate-Level Hardware Priority Resolvers for Embedded Systems. Journal of Low Power Electronics and Applications, 14(2), 25. https://doi.org/10.3390/jlpea14020025








