Multibeam Wideband Transmit Beamforming Using 2D Sparse FIR Trapezoidal Filters
Abstract
1. Introduction
1.1. Multibeam Multichannel Access Points
1.2. Wideband vs. Narrowband Systems in Modern Applications
1.2.1. Beam Sharpness vs. Degrees of Freedom
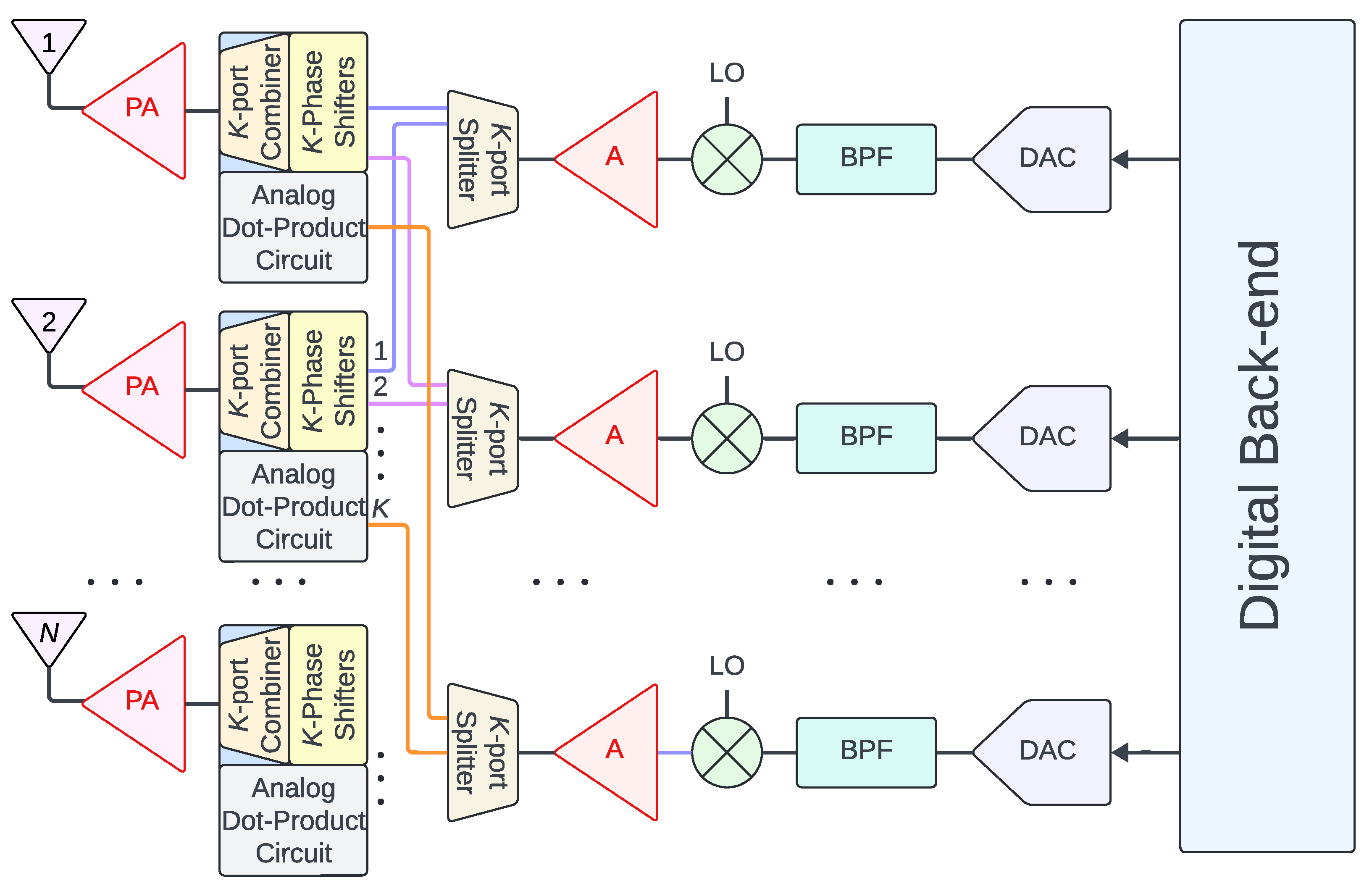
1.2.2. RF–Analog Phasing vs. Fully Digital Schemes
1.3. Advantages of an All-Digital Approach
1.4. Circuit Complexity vs. Flexibility
1.5. Fully Digital Wideband FIR Beamformers
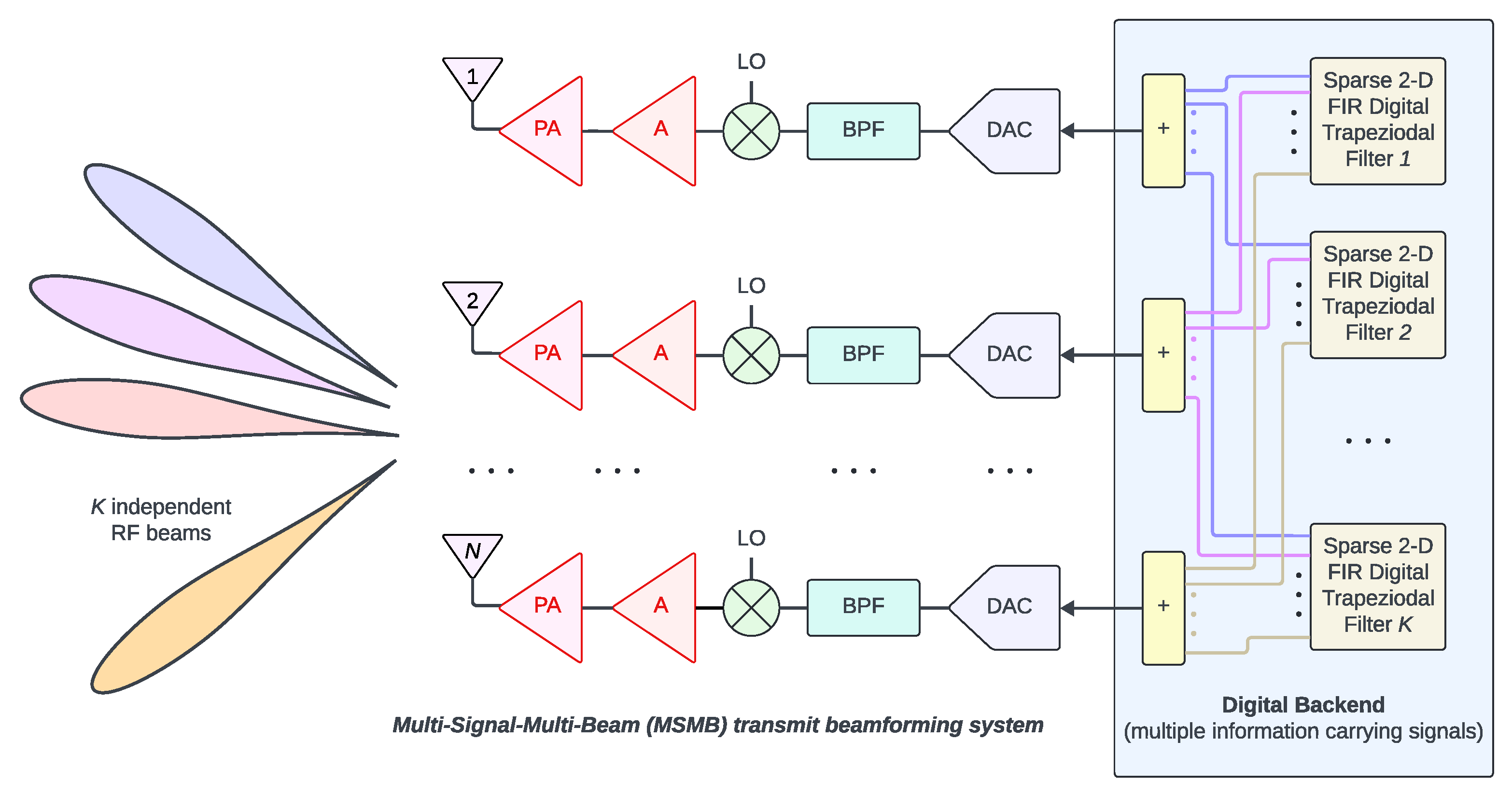
1.6. Proposed 2-D FIR Transmit Beamformer
2. Review of Spectra of 2D Plane Waves Received by Uniform Linear Arrays
3. Proposed Low-Complexity Multibeam Wideband Transmit Beamformer
3.1. Proposed Sparse 2D FIR Multibeam Beamformer
3.2. Two-Dimensional Sparse FIR Trapezoidal Filter
3.3. Minimax Design of the 2D Sparse FIR Filter
3.3.1. Step 1
3.3.2. Step 2
3.4. Analysis and Selection of Parameters
4. Full-Wave Electromagnetic Simulation Results
4.1. Multibeam Beamforming
4.1.1. Two Independent Signals Transmission in Two DODs
4.1.2. Three Independent Signals Transmission in Three DODs
4.1.3. Same Signal Transmission in Two DODs
4.1.4. Same Signal Transmission in Three DODs
4.2. Single-Beam Beamforming
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Marzetta, T.L.; Larsson, E.G.; Yang, H.; Ngo, H.Q. Fundamentals of Massive MIMO; Cambridge University Press: New York, NY, USA, 2016. [Google Scholar]
- Rappaport, T.S.; Xing, Y.; Kanhere, O.; Ju, S.; Madanayake, A.; Mandal, S.; Alkhateeb, A.; Trichopoulos, G.C. Wireless communications and applications above 100 GHz: Opportunities and challenges for 6G and beyond. IEEE Access 2019, 7, 78729–78757. [Google Scholar] [CrossRef]
- Björnson, E.; Chae, C.B.; Heath, R.W., Jr.; Marzetta, T.L.; Mezghani, A.; Sanguinetti, L.; Rusek, F.; Castellanos, M.R.; Jun, D.; Demir, Ö.T. Towards 6G MIMO: Massive Spatial Multiplexing, Dense Arrays, and Interplay Between Electromagnetics and Processing. arXiv 2024, arXiv:2401.02844. [Google Scholar]
- Liu, Y.; Ouyang, C.; Ding, Z.; Schober, R. The Road to Next-Generation Multiple Access: A 50-Year Tutorial Review. arXiv 2024, arXiv:2403.00189. [Google Scholar]
- Haykin, S. Array Signal Processing; Prentice-Hall: Englewood Cliffs, NJ, USA, 1985. [Google Scholar]
- Van Trees, H.L. Optimum Array Processing; John Wiley & Sons: New York, NY, USA, 2004. [Google Scholar]
- Benesty, J.; Chen, J.; Huang, Y. Microphone Array Signal Processing; Springer: Berlin, Germany, 2008. [Google Scholar]
- Liu, W.; Weiss, S. Wideband Beamforming: Concepts and Techniques; John Wiley & Sons: Chichester, UK, 2010. [Google Scholar]
- Friedlander, B. On Transmit Beamforming for MIMO Radar. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 3376–3388. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Xing, Y.; MacCartney, G.R.; Molisch, A.F.; Mellios, E.; Zhang, J. Overview of Millimeter Wave Communications for Fifth-Generation (5G) Wireless Networks-With a Focus on Propagation Models. IEEE Trans. Antennas Propag. 2017, 65, 6213–6230. [Google Scholar] [CrossRef]
- Boccardi, F.; Heath, R.W.; Lozano, A.; Marzetta, T.L.; Popovski, P. Five disruptive technology directions for 5G. IEEE Commun. Mag. 2014, 52, 74–80. [Google Scholar] [CrossRef]
- Qamar, F.; Siddiqui, M.U.A.; Hindia, M.N.; Hassan, R.; Nguyen, Q.N. Issues, challenges, and research trends in spectrum management: A comprehensive overview and new vision for designing 6G networks. Electronics 2020, 9, 1416. [Google Scholar] [CrossRef]
- Wang, W.; Gao, L.; Ding, R.; Lei, J.; You, L.; Chan, C.A.; Gao, X. Resource efficiency optimization for robust beamforming in multi-beam satellite communications. IEEE Trans. Veh. Technol. 2021, 70, 6958–6968. [Google Scholar] [CrossRef]
- Gao, L.; Ma, J.; You, L.; Pan, C.; Wang, W.; Gao, X. Robust energy-efficient multigroup multicast beamforming for multi-beam satellite communications. In Proceedings of the ICC 2020-2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar]
- Zhang, X.; Wang, J.; Jiang, C.; Yan, C.; Ren, Y.; Hanzo, L. Robust beamforming for multibeam satellite communication in the face of phase perturbations. IEEE Trans. Veh. Technol. 2019, 68, 3043–3047. [Google Scholar] [CrossRef]
- Yu, L.; Wan, J.; Zhang, K.; Teng, F.; Lei, L.; Liu, Y. Spaceborne Multibeam Phased Array Antennas for Satellite Communications. IEEE Aerosp. Electron. Syst. Mag. 2023, 38, 28–47. [Google Scholar] [CrossRef]
- Lin, Z.; An, K.; Niu, H.; Hu, Y.; Chatzinotas, S.; Zheng, G.; Wang, J. SLNR-Based Secure Energy Efficient Beamforming in Multibeam Satellite Systems. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 2085–2088. [Google Scholar] [CrossRef]
- Xv, H.; Sun, Y.; Zhao, Y.; Peng, M.; Zhang, S. Joint Beam Scheduling and Beamforming Design for Cooperative Positioning in Multi-beam LEO Satellite Networks. IEEE Trans. Veh. Technol. 2023, 73, 5276–5287. [Google Scholar] [CrossRef]
- Marzetta, T.; Yang, H. Massive MIMO in Line-of-Sight Propagation. In Proceedings of the 2017 IEEE 85th Vehicular Technology Conference (VTC Spring), Sydney, Australia, 4–7 June 2017. [Google Scholar]
- Rappaport, T.S.; Sun, S.; Mayzus, R.; Zhao, H.; Azar, Y.; Wang, K.; Wong, G.N.; Schulz, J.K.; Samimi, M.; Gutierrez, F. Millimeter Wave Mobile Communications for 5G Cellular: It Will Work! IEEE Access 2013, 1, 335–349. [Google Scholar] [CrossRef]
- Gong, S.; Lu, X.; Hoang, D.T.; Niyato, D.; Shu, L.; Kim, D.I.; Liang, Y.C. Toward Smart Wireless Communications via Intelligent Reflecting Surfaces: A Contemporary Survey. IEEE Commun. Surv. Tutorials 2020, 22, 2283–2314. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Mu, X.; Hou, T.; Xu, J.; Di Renzo, M.; Al-Dhahir, N. Reconfigurable intelligent surfaces: Principles and opportunities. IEEE Commun. Surv. Tutorials 2021, 23, 1546–1577. [Google Scholar] [CrossRef]
- Yu, H.; Li, P.; Su, J.; Li, Z.; Xu, S.; Yang, F. Reconfigurable Bidirectional Beam-Steering Aperture With Transmitarray, Reflectarray, and Transmit-Reflect-Array Modes Switching. IEEE Trans. Antennas Propag. 2023, 71, 581–595. [Google Scholar] [CrossRef]
- Han, S.; Chih-Lin, I.; Xu, Z.; Rowell, C. Large-scale antenna systems with hybrid analog and digital beamforming for millimeter wave 5G. IEEE Commun. Mag. 2015, 53, 186–194. [Google Scholar] [CrossRef]
- Ioushua, S.S.; Eldar, Y.C. A family of hybrid analog–digital beamforming methods for massive MIMO systems. IEEE Trans. Signal Process. 2019, 67, 3243–3257. [Google Scholar] [CrossRef]
- Slezak, C.; Dhananjay, A.; Rangan, S. 60 GHz blockage study using phased arrays. In Proceedings of the 2017 51st Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 29 October–1 November 2017; pp. 1655–1659. [Google Scholar] [CrossRef]
- Dutta, S.; Barati, C.N.; Ramirez, D.; Dhananjay, A.; Buckwalter, J.F.; Rangan, S. A Case for Digital Beamforming at mmWave. IEEE Trans. Wirel. Commun. 2020, 19, 756–770. [Google Scholar] [CrossRef]
- Dutta, S.; Barati, C.N.; Dhananjay, A.; Rangan, S. 5G millimeter wave cellular system capacity with fully digital beamforming. In Proceedings of the 2017 51st Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 29 October–1 November 2017; pp. 1224–1228. [Google Scholar] [CrossRef]
- Madanayake, A.; Ariyarathna, V.; Madishetty, S.; Pulipati, S.; Cintra, R.J.; Coelho, D.; Oliviera, R.; Bayer, F.M.; Belostotski, L.; Mandal, S.; et al. Towards a Low-SWaP 1024-Beam Digital Array: A 32-Beam Subsystem at 5.8 GHz. IEEE Trans. Antennas Propag. 2020, 68, 900–912. [Google Scholar] [CrossRef]
- Madanayake, A.; Cintra, R.J.; Akram, N.; Ariyarathna, V.; Mandal, S.; Coutinho, V.A.; Bayer, F.M.; Coelho, D.; Rappaport, T.S. Fast Radix-32 Approximate DFTs for 1024-Beam Digital RF Beamforming. IEEE Access 2020, 8, 96613–96627. [Google Scholar] [CrossRef]
- Qi, Z.; Yunhao, L.; Ying, X.; Bin, T. Transmit Multi-beamforming of Wideband Signals Based on the Focusing Transform. In Proceedings of the 2014 IEEE 17th International Conference on Computational Science and Engineering, Chengdu, China, 19–21 December 2014; pp. 1043–1046. [Google Scholar]
- Edussooriya, C.U.; Wijenayake, C.; Pulipati, S.; Madanayake, A.; Bruton, L.T. Low-Complexity Wideband Transmit Array using Variable-Precision 2-D Sparse FIR Digital Filters. In Proceedings of the 2019 IEEE International Symposium on Circuits and Systems (ISCAS), Sapporo, Japan, 26–29 May 2019; pp. 1–5. [Google Scholar]
- Ba, H.C.; Shirai, H.; Ngoc, C.D. Analysis and design of antipodal Vivaldi antenna for UWB applications. In Proceedings of the 2014 IEEE Fifth International Conference on Communications and Electronics (ICCE), Danang, Vietnam, 30 July–1 August 2014; pp. 391–394. [Google Scholar] [CrossRef]
- Neinhus, M.; Solbach, K. Finite impulse response-filter-based RF-beamforming network for wideband and ultra-wideband antenna arrays. IET Microw. Antennas Propag. 2011, 5, 844–851. [Google Scholar] [CrossRef]
- Gao, Y.; Jiang, D.; Liu, M. Wideband transmit beamforming using integer-time-delayed and phase-shifted waveforms. Electron. Lett. 2017, 53, 376–378. [Google Scholar] [CrossRef]
- Uysal, F.; Dunn, Z. Application of waveform weighting for a frequency- invariant transmit beampattern. IEEE Aerosp. Electron. Syst. Mag. 2016, 31, 4–12. [Google Scholar] [CrossRef]
- Sekiguchi, T.; Karasawa, Y. Wideband beamspace adaptive array utilizing FIR fan filters for multibeam forming. IEEE Trans. Signal Process. 2000, 48, 277–284. [Google Scholar] [CrossRef]
- Nishikawa, K. Wideband multi-beam forming method using delayed array sensors and two-dimensional digital filter. Electron. Commun. Jpn. Part 3 2005, 88, 1–12. [Google Scholar] [CrossRef]
- Gunaratne, T.K.; Bruton, L.T. Broadband beamforming of bandpass plane waves using 2D FIR trapezoidal filters at baseband. In Proceedings of the APCCAS 2006-2006 IEEE Asia Pacific Conference on Circuits and Systems, Singapore, 4–7 December 2006; pp. 546–549. [Google Scholar]
- Gunaratne, T.K.; Bruton, L.T. Beamforming of Broad-Band Bandpass Plane Waves Using Polyphase 2-D FIR Trapezoidal Filters. IEEE Trans. Circuits Syst. I 2008, 55, 838–850. [Google Scholar] [CrossRef]
- Pulipati, S.; Ariyarathna, V.; Jayaweera, A.L.; Edussooriya, C.U.S.; Wijenayake, C.; Belostotski, L.; Madanayake, A. FPGA-Based 2-D FIR Frost Beamformers with Digital Mutual Coupling Compensation. In Proceedings of the 2020 IEEE/MTT-S International Microwave Symposium (IMS), Los Angeles, CA, USA, 4–6 August 2020; pp. 1077–1080. [Google Scholar]
- Pulipati, S.; Ariyarathna, V.; Madanayake, A.; Wijesekara, R.T.; Edussooriya, C.U.; Bruton, L.T. A 16-Element 2.4-GHz Multi-Beam Array Receiver using 2-D Spatially-Bandpass Digital Filters. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 3029–3038. [Google Scholar] [CrossRef]
- Hong, W.; Jiang, Z.H.; Yu, C.; Zhou, J.; Chen, P.; Yu, Z.; Zhang, H.; Yang, B.; Pang, X.; Jiang, M.; et al. Multibeam Antenna Technologies for 5G Wireless Communications. IEEE Trans. Antennas Propag. 2017, 65, 6231–6249. [Google Scholar] [CrossRef]
- Shen, D.; Dai, L.; Su, X.; Suo, S. Multi-Beam Design for Near-Field Extremely Large-Scale RIS-Aided Wireless Communications. IEEE Trans. Green Commun. Netw. 2023, 7, 1542–1553. [Google Scholar] [CrossRef]
- Yan, J.; Liu, H.; Jiu, B.; Chen, B.; Liu, Z.; Bao, Z. Simultaneous Multibeam Resource Allocation Scheme for Multiple Target Tracking. IEEE Trans. Signal Process. 2015, 63, 3110–3122. [Google Scholar] [CrossRef]
- Zhang, J.A.; Huang, X.; Guo, Y.J.; Yuan, J.; Heath, R.W. Multibeam for Joint Communication and Radar Sensing Using Steerable Analog Antenna Arrays. IEEE Trans. Veh. Technol. 2019, 68, 671–685. [Google Scholar] [CrossRef]
- Sahin, C.; McCormick, P.M.; Metcalf, J.G.; Blunt, S.D. Power-Efficient Multi-Beam Phase-Attached Radar/Communications. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Monteys, X.; Harris, P.; Caloca, S.; Cahalane, C. Spatial prediction of coastal bathymetry based on multispectral satellite imagery and multibeam data. Remote Sens. 2015, 7, 13782–13806. [Google Scholar] [CrossRef]
- Iupikov, O.A.; Ivashina, M.V.; Skou, N.; Cappellin, C.; Pontoppidan, K.; van’t Klooster, C.G.M. Multibeam Focal Plane Arrays With Digital Beamforming for High Precision Space-Borne Ocean Remote Sensing. IEEE Trans. Antennas Propag. 2018, 66, 737–748. [Google Scholar] [CrossRef]
- Bruton, L.; Bartley, N. Three-dimensional image processing using the concept of network resonance. IEEE Trans. Circuits Syst. 1985, 32, 664–672. [Google Scholar] [CrossRef]
- Madanayake, A.; Wijenayake, C.; Dansereau, D.G.; Gunaratne, T.K.; Bruton, L.T.; Williams, S.B. Multidimensional (MD) circuits and systems for emerging applications including cognitive radio, radio astronomy, robot vision and imaging. IEEE Circuits Syst. Mag. 2013, 13, 10–43. [Google Scholar] [CrossRef]
- Lu, W.S.; Hinamoto, T. Two-dimensional digital filters with sparse coefficients. Multidimens. Syst. Signal Process. 2011, 22, 173–189. [Google Scholar] [CrossRef]
- Dudgeon, D.E. Multidimensional Digital Signal Processing; Prentice-Hall: Engewood Cliffs, NJ, USA, 1983. [Google Scholar]
- Jayaweera, S.S.; Edussooriya, C.U.S.; Wijenayake, C.; Agathoklis, P.; Bruton, L. Multi-Volumetric Refocusing of Light Fields. IEEE Signal Process. Lett. 2021, 28, 31–35. [Google Scholar] [CrossRef]
- Antoniou, A. Digital Signal Processing: Signals, Systems, and Filters; McGraw-Hill: New York, NY, USA, 2006. [Google Scholar]







| Case | DOD (Nonsparse FIR) | DOD (Sparse FIR) | DOD (Nonsparse FIR) | DOD (Sparse FIR) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| DOD (degrees) | ||||||||||
| Average | −28.2 | 26.0 | −27.3 | 25.9 | −45.0 | 0.0 | 44.9 | −45.6 | 0.0 | 45.6 |
| Standard deviation | 1.32 | 1.01 | 0.99 | 0.94 | 3.06 | 0.00 | 3.04 | 2.52 | 0.12 | 2.52 |
| Gain (dB) | ||||||||||
| Average | 10.44 | 10.56 | 10.28 | 10.47 | 8.25 | 8.52 | 8.29 | 7.77 | 8.37 | 7.99 |
| Side-lobe level † (dB) | ||||||||||
| Peak | −17.18 | −13.83 | −17.76 | −16.54 | ||||||
| Average | −26.11 | −23.86 | −22.28 | −23.11 | ||||||
| Filter passband ripple (dB) | ||||||||||
| Along main beam directions | 2.25 | 2.07 | 2.34 | 2.84 | 3.32 | 3.10 | 3.32 | 4.00 | 3.61 | 4.54 |
| In the defined passband | 3.16 | 4.75 | 4.89 | 6.34 | ||||||
| Filter stopband attenuation (dB) | ||||||||||
| Average in the defined stopbands | −28.86 | −24.66 | −25.80 | −23.36 | ||||||
| DSP complexity | ||||||||||
| ADDs | 974 + 974 = 1948 | 148 + 138 = 286 | 974 + 974 + 974 = 2922 | 120 + 164 + 120 = 404 | ||||||
| MULs | 488 + 488 = 976 | 75 + 70 = 145 | 488 + 488 + 488 = 1464 | 61 + 83 + 61 = 205 | ||||||
| Case | DOD (Nonsparse FIR) | DOD (Sparse FIR) | DOD (Nonsparse FIR) | DOD (Sparse FIR) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| DOD (degrees) | ||||||||||
| Average | −28.8 | 26.4 | −27.9 | 26.4 | −44.9 | 0.0 | 44.9 | −45.5 | 0.0 | 45.4 |
| Standard deviation | 1.17 | 1.03 | 1.23 | 1.46 | 2.28 | 0.00 | 2.24 | 2.22 | 0.00 | 2.21 |
| Gain (dB) | ||||||||||
| Average | 10.57 | 10.43 | 10.48 | 10.36 | 8.40 | 8.24 | 8.44 | 8.18 | 8.28 | 8.22 |
| Side-lobe level † (dB) | ||||||||||
| Peak | −17.67 | −15.14 | −21.31 | −18.39 | ||||||
| Average | −23.76 | −22.25 | −27.68 | −25.11 | ||||||
| Filter passband ripple (dB) | ||||||||||
| Along main beam directions | 1.84 | 2.98 | 2.64 | 2.61 | 1.23 | 2.21 | 1.23 | 1.90 | 2.81 | 1.90 |
| In the defined passband | 4.00 | 3.87 | 3.39 | 4.04 | ||||||
| Filter stopband attenuation (dB) | ||||||||||
| Average in the defined stopband | −25.57 | −24.17 | −48.64 | −24.42 | ||||||
| DSP complexity | ||||||||||
| ADDs | 974 | 160 | 974 | 160 | ||||||
| MULs | 488 | 81 | 488 | 81 | ||||||
| Case | Windowing Method (Nonsparse FIR) [39,40] | Optimization (Nonsparse FIR) [41] | Windowing Method (Sparse FIR) [32] | Proposed (Sparse FIR) |
|---|---|---|---|---|
| DOD (degrees) | ||||
| Average | 30.1 | 30.1 | 30.1 | 30.0 |
| Standard deviation | 0.33 | 0.87 | 0.39 | 0.85 |
| Gain (dB) | ||||
| Average | 13.43 | 13.43 | 13.67 | 13.30 |
| Side-lobe level † (dB) | ||||
| Peak | −11.47 | −20.75 | −13.63 | −17.96 |
| Average | −17.02 | −27.93 | −19.76 | −27.07 |
| Filter passband ripple (dB) | ||||
| Along main beam directions | 11.53 | 2.24 | 11.08 | 2.56 |
| In the defined passband | 12.81 | 2.87 | 11.81 | 3.28 |
| Filter stopband attenuation (dB) | ||||
| Average in the defined stopband | −27.82 | −28.94 | -27.04 | −27.32 |
| DSP complexity | ||||
| ADDs | 974 | 974 | 142 | 142 |
| MULs | 488 | 488 | 72 | 72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dissanayake, N.; Edussooriya, C.U.S.; Wijenayake, C.; Madanayake, A. Multibeam Wideband Transmit Beamforming Using 2D Sparse FIR Trapezoidal Filters. J. Low Power Electron. Appl. 2024, 14, 26. https://doi.org/10.3390/jlpea14020026
Dissanayake N, Edussooriya CUS, Wijenayake C, Madanayake A. Multibeam Wideband Transmit Beamforming Using 2D Sparse FIR Trapezoidal Filters. Journal of Low Power Electronics and Applications. 2024; 14(2):26. https://doi.org/10.3390/jlpea14020026
Chicago/Turabian StyleDissanayake, Nadeeshan, Chamira U. S. Edussooriya, Chamith Wijenayake, and Arjuna Madanayake. 2024. "Multibeam Wideband Transmit Beamforming Using 2D Sparse FIR Trapezoidal Filters" Journal of Low Power Electronics and Applications 14, no. 2: 26. https://doi.org/10.3390/jlpea14020026
APA StyleDissanayake, N., Edussooriya, C. U. S., Wijenayake, C., & Madanayake, A. (2024). Multibeam Wideband Transmit Beamforming Using 2D Sparse FIR Trapezoidal Filters. Journal of Low Power Electronics and Applications, 14(2), 26. https://doi.org/10.3390/jlpea14020026








