Efficient Addition Circuits Using Three-Gate Reconfigurable Field Effect Transistors

Abstract

Reconfigurable FETs (RFETs) are widely recognized as a promising way to overcome conventional CMOS architectures. This paper presents novel addition circuit intentionally designed to exploit the ability of RFETs to operate efficiently on demand as n- or p-type FETs. First, a novel Full Adder (FA) is proposed and characterized. A comparison with other designs shows that the proposed FA achieves a worst-case delay and a dynamic power consumption of up to 43.5% and 79% lower. As a drawback, in terms of the estimated area, it is up to 32% larger than the competitors. Then, the new FA is used to implement Ripple-Carry Adders (RCAs). A 32-bit adder designed as proposed herein reaches an energy–delay product (EDP) ~25.7× and ~141× lower than its CMOS and the RFET-based counterparts.

1. Introduction

With the phenomenal development of intelligent systems, the demand for innovative and efficient technological supports is rapidly increasing, but CMOS technology is quickly approaching its limits [1,2]. Among the alternative technologies that emerged to address “Beyond CMOS”-era challenges, special attention has been focused on RFETs [3,4,5,6,7,8,9,10,11]. They can be reversibly reconfigured at runtime to operate as n- or p-type transistors. Moreover, since RFETs are fully compatible with traditional CMOS fabrication processes, they enable new design paradigms and allow for the extension of the usage of microelectronic systems and architectures to applications domains which are currently not affordable.

It is well known that logic and arithmetic circuits are crucial to satisfying design specifications at the system level, especially in terms of energy efficiency. Therefore, several attempts have been made to utilize RFETs to either design multifunctional circuits or to implement static functionalities with reduced complexities. The first approach leads to circuits that can be dynamically reconfigured to switch during runtime between different functionalities. On the contrary, the second approach reduces the number of devices utilized. In both cases, RFET-based designs exhibit reduced power consumption and/or computational delay [11,12,13,14,15,16,17,18,19,20,21,22] with respect to their conventional counterparts.

This paper first presents and characterizes a novel Full Adder (FA). It exploits a new implementation of the Majority Gate (MG) function that improves computational delay, static and dynamic power consumption, and area occupancy with respect to the RFET-based FA presented in [11] and the conventional mirror FA [23].

Then, Ripple-Carry Adders (RCAs) are designed at a bit-width ranging from 4 to 32 bits. The obtained results clearly show that the New RCAs (NRCAs) proposed here offer several advantages. As an example, the 32-bit NRCA uses 418 RFETs, achieves a worst-case delay of 622.7 ps, and, when performing the most time-critical addition, consumes a dynamic energy of only 0.24 fJ. On the contrary, the conventional CMOS 32-bit RCA utilizes 896 transistors, exhibits a worst-case delay of 254.7 ps, and consumes ~15 fJ to perform the most time-critical operation. Finally, the RCA employing the FA presented in [11] uses 448 RFETs and consumes ~5.75 fJ to perform the worst-case delay addition that is executed within 3.67 ns.

2. Background and Related Designs

An RFET device basically consists of an intrinsic semiconductor nanowire surrounded by two or more independent gate electrodes able to electrostatically control the type and concentration of carriers in the nanowire channel [5]. At least one of these electrodes acts as Polarity or Program Gate (PG), while the others, called Control Gates (CGs), operate as gate electrodes as in traditional FETs.

Figure 1 illustrates the functionalities of recently proposed RFETs. The Dual-Gate (DG) RFET [3,5] is based on an axial silicon nanowire heterostructure (metal/intrinsic silicon/metal) that uses Schottky junctions as independent gates. The three-gate (TG) RFET [12] exploits a monolithic Al-Ge-Al heterostructure and relies on two omega-shaped top gates surrounding the Source/Drain channel junctions to alter the device’s operation between p- and n-type. Three-Independent-Gate (TIG) RFETs and a Multiple-Independent-Gates (MIG) RFET have been also investigated and demonstrated by simulation [6].

In these devices, the voltage applied to the PG induces an additional energy barrier in the channel that blocks the undesired charge carrier type, thus favoring p- or n-type behavior. This allows for the selection of p- or n-type operation of the RFET. More specifically, a negative potential on the PG prevents electron injection from the drain electrode. Furthermore, hole injection into the active region, stimulated by the upward band bending below the PG, enables unipolar p-type operation. The opposite PG polarization favors electron injection and blocks hole injection into the Ge channel, thus switching to n-type operation.

As demonstrated in [15,16,20,21,22], the above RFETs can be exploited in more or less complex arithmetic circuits to overcome conventional CMOS designs in terms of energy dissipation. However, the results achieved clearly show that this advantage is often obtained at the expense of a remarkable increase in computational delay. This research work aims to significantly reduce such a delay penalty without notably impacting energy savings, thus improving the energy–delay trade-off. The circuits and results presented in the following sections refer to the TG-RFET device recently demonstrated physically in [12] and its 0.8V 14nm predictive Verilog-A model [11].

2.1. The Predictive Model Referenced

The predictive germanium nanowire model proposed in [11] is structurally compliant with the 14 nm FinFET process of the Intel [24] nanowire. Indeed, it is characterized by a channel thickness of 8 nm; a contacted poly pitch (CPP) of 70 nm; a fin pitch of 42 nm; an equivalent oxide thickness (EOT) of 0.8 nm; and a via size compliant with a metal 0 pitch of 56 nm. The structural features of the referenced model are those shown in Figure 1 for the TG-RFET device.

As further simulation parameters, the effective tunneling masses of electrons and holes were assumed to be me = 0.08 × m0 and mh = 0.044 × m0. The work functions of the source and drain regions (WSD = 4.34 eV) as well as the work function of all gates (WG = 4.33 eV) guarantee a symmetric static drain current behavior for the n- and the p-configurations of the RFET at VDD = 0.8 V.

Dependence of the currents, capacities, and charges on the three potentials (VD/S, VPG, and VCG) were observed, assuming that the two program gates are short-circuited at the same potential VPG. The applied voltages VD, VPG, and VCG were swept from −1.3 V to +1.3 V at intervals of 50 mV, 50 mV, and 20 mV respectively. Ranges wider than the targeted power supply voltage of VDD = 0.8 V were referenced to account for over- and undershoots in circuit simulations.

The resulting simple SPICE Verilog-A model proposed in [11] is represented by a quasi-static voltage-controlled current source between the source and drain and the coupling between each gate, the channel, and its adjacent gates. The charge distribution inside the channel is estimated as the voltage-dependent sum of the charges distributed between the various terminals (QD/S, QPG1, QCG, QPG2, and QD/S).

The voltage-dependent charges Q (V) at each terminal are taken assuming quasi-static coupling, which is modeled using a simple coefficient matrix. Such a matrix approach allows for the evaluation of the current toward a node, as given in (1). There, [I] is the vector of the current flowing into each terminal, and [Q] is the charge at each terminal as a function of the applied voltages. Finally, [S] is the coefficient matrix reported in (2), with the generic coefficient s_ij representing the coupling between the terminals i and j divided by the overall capacitance of j.

$$\left[I\right]=\left[S\right]·\frac{\partial }{\partial t}\left[Q\right]$$

(1)

$$\left[S\right]=\left(\begin{array}{ccccc}{S}_{GND,D}& S_{GND,PG1}& S_{GND,CG}& S_{GND,PG2}& S_{GND,S}\\ S_{D,D}& S_{D,PG1}& S_{D,CG}& S_{D,PG2}& S_{D,S}\\ S_{PG1,D}& S_{PG1,PG1}& S_{PG1,CG}& S_{PG1,PG2}& S_{PG1,S}\\ S_{CG,D}& S_{CG,PG1}& S_{CG,CG}& S_{CG,PG2}& S_{CG,S}\\ S_{PG2,D}& S_{PG2,PG1}& S_{PG2,CG}& S_{PG2,PG2}& S_{PG2,S}\\ S_{S,D}& S_{S,PG1}& S_{S,CG}& S_{S,PG2}& S_{S,S}\end{array}\right)=\left(\begin{array}{ccccc}0.1621& 0.1332& 0.1260& 0.1332& 0.1621\\ 0& 0.2717& 0.1799& 0.1332& 0.1135\\ 0.3308& 0& 0.2571& 0.1902& 0.1621\\ 0.2316& 0.2717& 0& 0.2717& 0.2316\\ 0.1621& 0.1902& 0.2571& 0& 0.3308\\ 0.1135& 0.1332& 0.1799& 0.2717& 0\end{array}\right)$$

(2)

The matrix model approach presented in [11] yields good agreement with TCAD simulations, achieving a mean square deviation of 0.055 on the drain current estimation. However, as a limitation, in its current form, this model is recommended only for the development of digital designs.

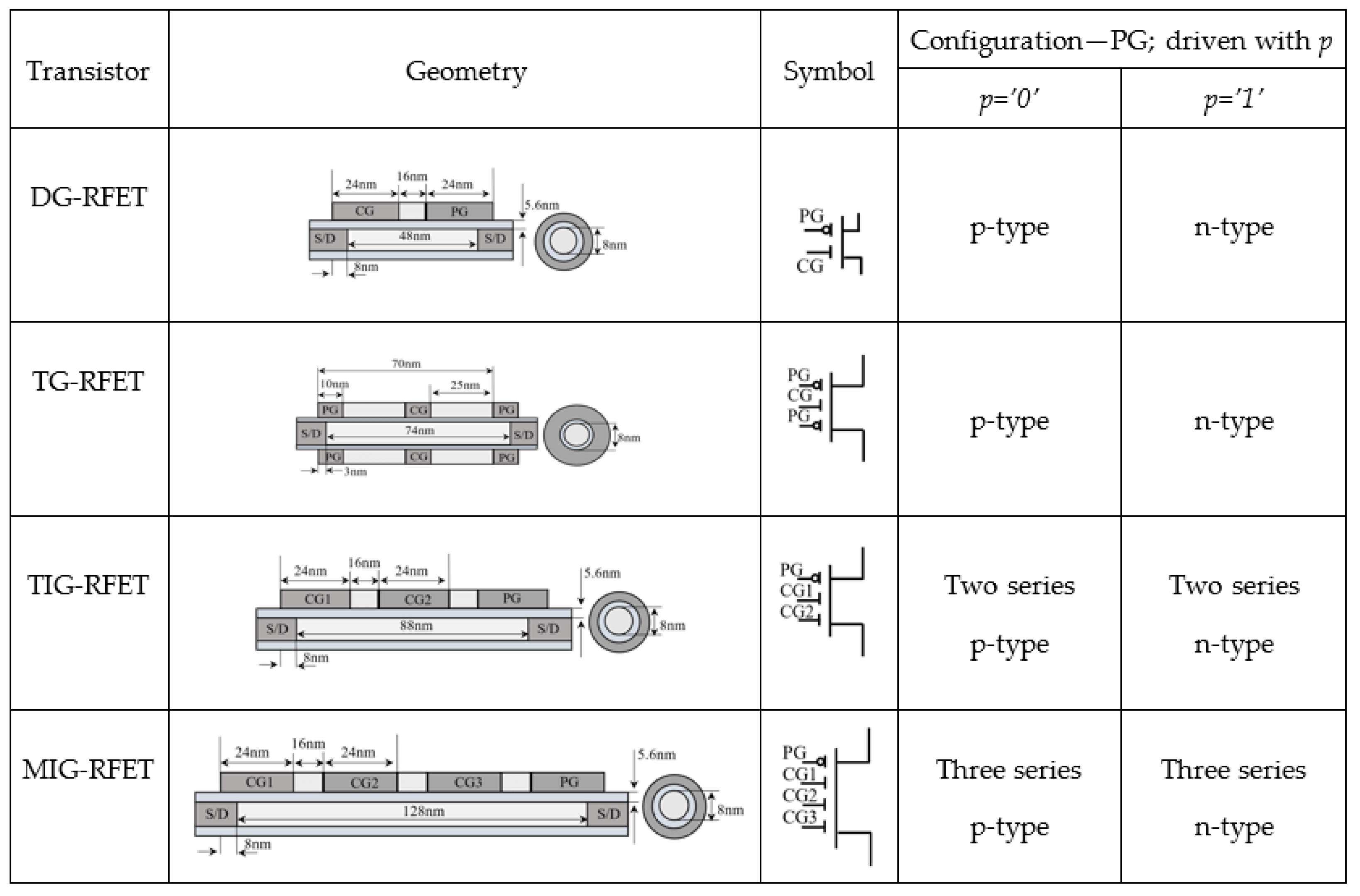
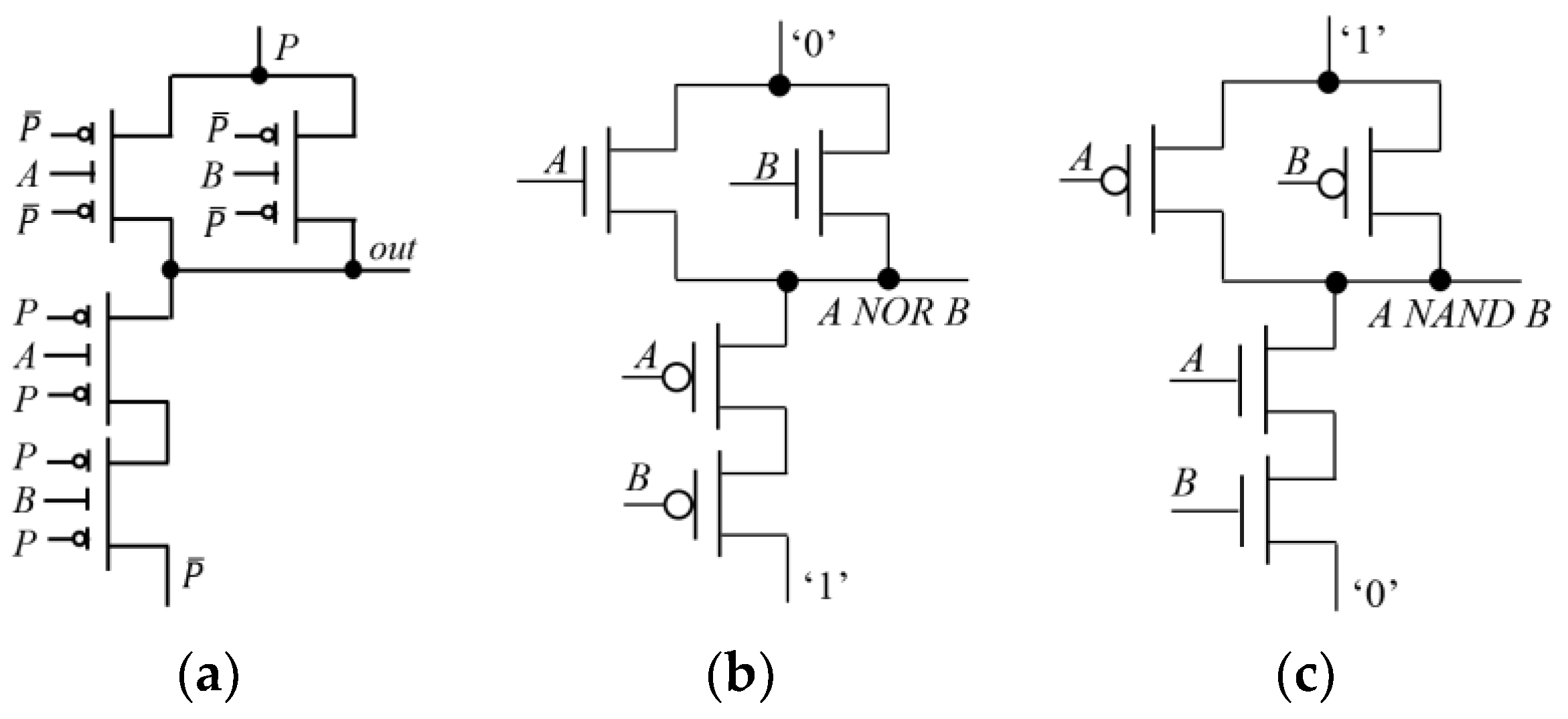
2.2. Sample RFET-Based Digital Circuits

The flexibility provided by RFETs at the transistor level enables the design of dynamically reconfigurable circuits, such as the NAND/NOR gate depicted in Figure 2a. It can be easily verified that with the signal P = ‘0’, the circuit of Figure 2a is configured as reported in Figure 2b, and it behaves like a two-input NOR gate. Conversely, with P = ‘1’, the circuit is configured as shown in Figure 2c, and it implements a two-input NAND gate.

In Figure 3a, the reconfigurability of the RFETs is exploited to design a static, compact MG. In this case, the logic function does not change, but the circuit adapts itself to comply with different combinations of the inputs. Figure 3b,c illustrate the equivalent circuits and their behavior for A = ‘0’ and A = ‘1’. It is important to note that when A ≠ B, the output signal of the MG is fed by Cin through the S/D terminals of one of the upper TG-RFETs, which therefore acts as a pass transistor. As a consequence, when multiple MGs are cascaded, as in the RCA illustrated in Figure 4, series-connected pass transistor RFETs negatively affect the computational time. The same is true for the conventional RFET-based multiplexer scheme. Therefore, when several multiplexers are cascaded, a detrimental effect on the propagation delay is observable. As shown in the following, the new MG presented here avoids such a detrimental effect, thus improving the global speed performance of the realized RCA.

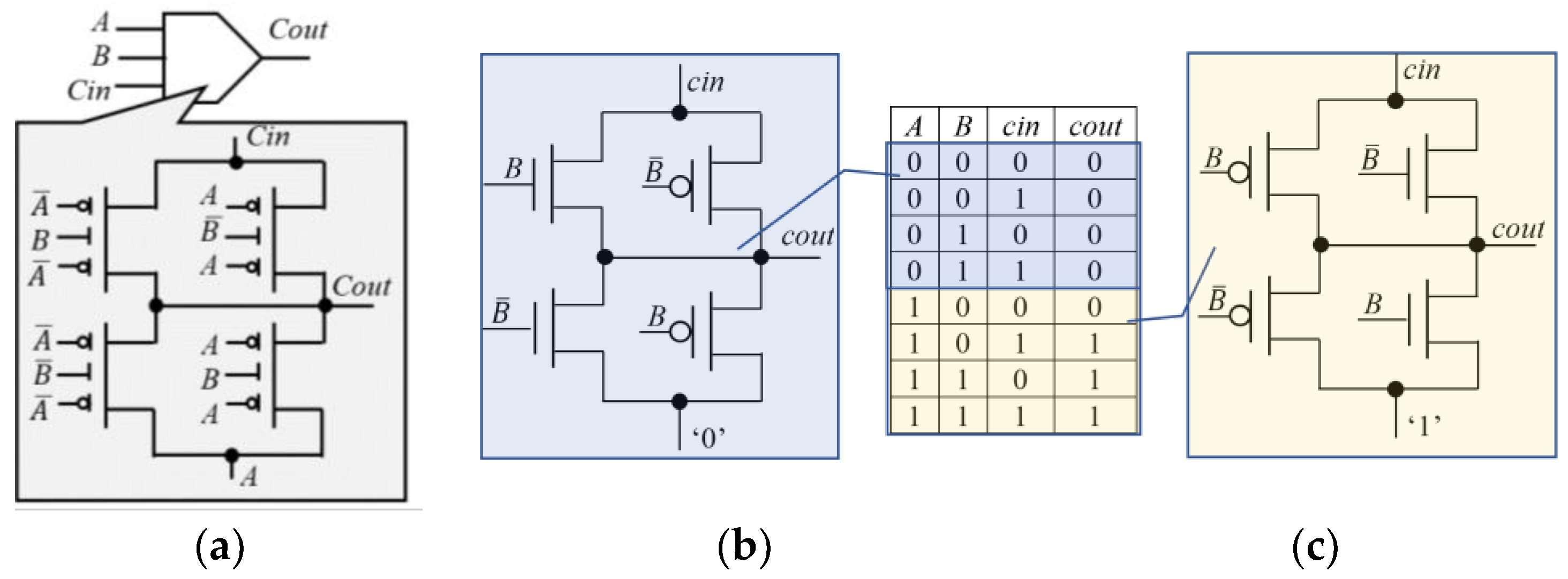
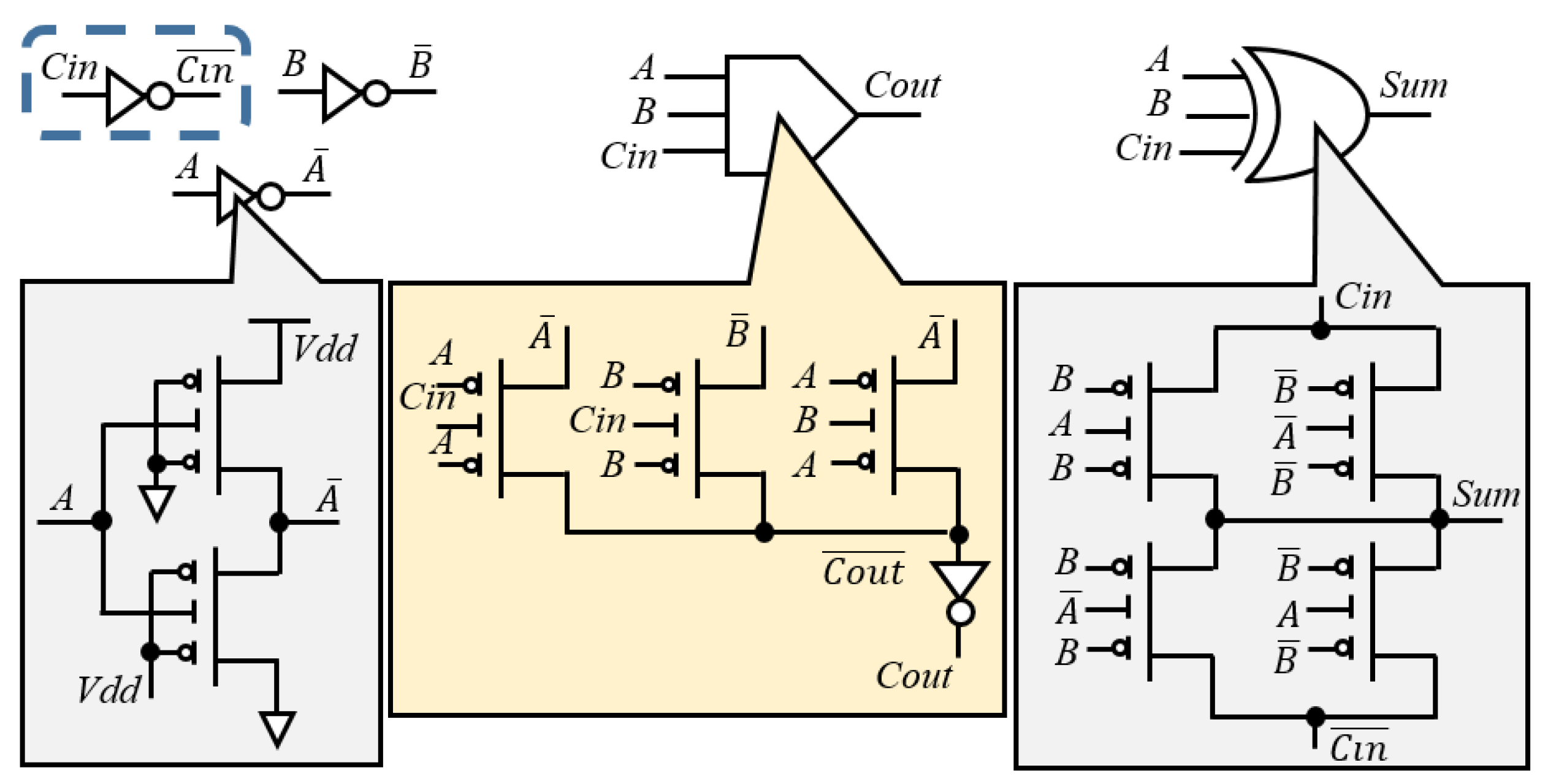
3. The Proposed Designs

Figure 4 depicts a simple n-bit RCA. With each FA using one MG and one XOR gate [7,11,13,20], the critical computational path goes through n cascaded MGs, i.e., n FAs. Figure 5 illustrates the 15-T TG-RFET-based FA proposed here. Obviously, when used at the non-LSB (NLSB) positions of the n-bit RCA, the FA receives both Cin and ($\overline{Cin}$) from the previous FA, and the inverter in the dashed box is not necessary. It must be noted that the Cin entering the MG is connected to the CG terminals of the TG-RFETs. Differently, in the scheme used in [11], it is fed through the S/D terminals of the TG-RFETs, which therefore act as pass transistors. Consequently, the carry propagation path consists of n series-connected RFETs which cause detrimental effects on the overall addition time.

The computational delay and average static and dynamic power consumption of the proposed FA were evaluated through exhaustive simulations performed @10 GHz using inverters and an FA as driving and loading gates, respectively. The same setup was also used to analyze the RFET-based FA presented in [11] and a conventional CMOS mirror FA [24] designed using an 0.8 V 14 nm FinFET model [25]. All the circuits were designed, simulated, and analyzed using the design platform Cadence Virtuoso IC6.1.8.

Table 1. Results obtained for FAs.

FA	#FETs	Estimated Area [nm2]	PStatic [W]	Pdyn [W]	Delay [ps]
					Sum-AB	Cout-AB	Sum-Cin	Cout-Cin
Mirror CMOS	28	11,760	1.65 × 10−6	6.25 × 10−6	10.8	8.3	10.7	8
TG-FET [11]	14	14,504	1.23 × 10−9	1.55 × 10−6	7.5	40.7	11	28.5
New LSB	15	15,540	1.42 × 10−9	1.69 × 10−6	7.7	36.6	11.7	17.1
New NLSB	13	13,468	0.84 × 10−9	1.29 × 10−6	7.7	36.6	10.2	16.1

summarizes the comparison results, also reporting the number of FETs used and the estimated area occupancy.

The conventional TG-FET FA [11] shows the worst carry propagation delay (Cout-Cin). Apart from the advantages intrinsically offered by TG-FETs in terms of power consumption and transistor utilization over the CMOS baseline, the new FAs exhibit a carry propagation delay (Cout-Cin) up to 43.5% lower than in [11]. As a drawback, in comparison with the CMOS design and the design in [11], the new FAs occupy 32% and 7% more area, respectively.

n-bit RCAs were then designed and characterized. To consider realistic operating conditions, in the adopted simulation setup, inverters were used as driving and loading gates.

The results obtained for the compared RCAs at various operands’ word lengths are collected in

Table 2. Results obtained for n-bit RCAs.

Adder	Tech.	n	#FETs	Estimated Area [nm2]	PStatic [μW]	Edyn [fJ]	Worst-Case Delay [ps]		EDP [J × ps]
							Sn−1-C0	Cn-C0
CMOS *	FinFet	4	112	47,040	6.32	2.1	44	33	92.4 × 10−15
RCA * [11]	TG-FET	4	56	58,016	4.08 × 10−3	0.51	102.2	106.5	54.3 × 10−15
NRCA*	TG-FET	4	54	55,944	3.84 × 10−3	0.32	75.1	85.2	27.3 × 10−15
CMOS	FinFet	8	224	94,080	14.09	1023 × 10−3	67.7	64.03	6.93 × 10−14
RCA [11]	TG-FET	8	112	116,032	7.79 × 10−3	50.86 × 10−3	302	314.5	1.60 × 10−14
NRCA	TG-FET	8	106	109,816	6.9 × 10−3	15.28 × 10−3	143.1	152.9	2.34 × 10−15
CMOS	FinFet	16	448	188,160	29.52	3.9	130	126.4	5.07 × 10−13
RCA [11]	TG-FET	16	224	232,064	18.24 × 10−3	0.57	1000	1030	5.87 × 10−13
NRCA	TG-FET	16	210	217,560	15.52 × 10−3	0.063	299.2	309.4	1.95 × 10−14
CMOS	FinFet	32	896	376,320	55.52	15.03	254.7	251	3.83 × 10−12
RCA [11]	TG-FET	32	448	464,128	36.76 × 10−3	5.76	3500	3670	2.11 × 10−11
NRCA	TG-FET	32	418	433,048	30.72 × 10−3	0.24	612.2	622.7	1.49 × 10−13

* for the 4-bit RCA, Edyn is evaluated referring to all the operand combinations. For n > 4, Edyn is related to the input combination causing the worst-case delay; with A = 0…0 and B = 1…1, C₀ switches from 1 to 0.

. The latter shows that, apart from the net remarkable advantages achieved in terms of static and dynamic power consumption, power/energy savings and the reduction in the number of transistors exhibited by the new adder increase with n. In comparison with the TG-FET (CMOS) counterpart, with n varying from 4 to 32, the dynamic energy is 1.6× (6.6×), 3.3× (66.9×), 9.1× (61.9×), and 24× (62.6×) lower, whereas the number of transistors is reduced by 3.5% (27.7%), 5.4% (29%), 6.25% (29.7%), and 6.7% (30%), respectively. As a drawback, with n varying from 4 to 32, the area occupancy of the NRCA increases over the CMOS baseline by 18.9%, 16.7%, 15.6%, and 15%, respectively.

Table 2 shows that with n doubling, the worst addition time (i.e., C_n-C₀) of the CMOS and the new RCA almost doubles, whereas the C_n-C₀ delay of the TG-FET RCA [11] more than triples, thus leading to a more rapid performance decay versus the operand’s bit-width. As expected, this is due to the carry propagation involving n cascaded pass-transistor RFETs. When performing the critical 32-bit addition, the internal carry signals, the sum bits, and the carry-out of the compared adders switch, as plotted in Figure 6.

The EDP values reported in Table 2 summarize the above considerations. Indeed, the new adder achieves an energy–delay tradeoff of up to 29× and 141× higher than its CMOS and TG_FET counterparts.

4. Conclusions

This paper presents new adders that utilize RFETs to reach a notably reduced energy dissipation compared with conventional designs with a limited delay penalty, thus also achieving a significantly better energy–delay product. The strategy proposed here allows for the chain of series RFETs acting as pass transistors in a ripple-carry adder to be avoided. This significant result is achieved by adopting a simple modification in the conventional scheme of the Majority Gate function. Such a technique can be easily exploited in more complex arithmetic circuits, like parallel prefix adders and multipliers. A 32-bit adder designed as described here shows a worst-case delay of ~622 ps, which is ~6 times lower than that achieved by the conventional scheme, also showing a dynamic energy dissipation value reduced by ~95%.