1. Introduction
Inspired by the observation that exact (or precise) computations are not always necessary in most modern applications, approximate computing is nowadays a widely used paradigm for designing error-resilient circuits that can trade accuracy for energy [
1,
2].
The topic of several papers [
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26] is the design of energy-efficient approximate arithmetic circuits realized either by using Application Specific Integrated Circuits (ASICs) or Field Programmable Gate Arrays (FPGAs). Among them, in particular, approximate integer multipliers received a great deal of attention [
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19]. Despite the generality of the adopted approximation logic, implementing such circuits into either ASIC or FPGA technologies may lead to quite different energy, timing, and area behavior due to the different utilization of available resources. For example, the simplest approximation strategy often adopted in ASIC designs is bit-truncation [
3,
4,
5,
6]. When applied statically [
3,
6], it allows the pruning of the hardware resources used to compute a pre-established number of least significant bits (LSBs) of the product. Conversely, dynamic truncation techniques [
4,
5] allow the energy saving to be tuned on a time-varying quality target. As an efficient alternative, the static approach proposed very recently in [
7] exploits a small inner multiplier to process
m-bit segments of the operands and adopts a correction technique to improve the error performance. On the contrary, the approximation approaches presented in [
8,
9] accumulate the partial products (PPs) with approximate circuits that save energy, introducing a reasonable accuracy loss.
Unfortunately, the approaches conceived for ASIC designs are often not effective when adopted for FPGA implementations. Indeed, in most cases, they lead to energy consumptions higher than the accurate multipliers. For this reason, alternative strategies specific to FPGA designs are proposed in [
10,
11,
12,
13,
14,
15,
16,
17,
18,
19]. Most of them exploit Booth’s algorithm, which is simplified by either truncating specific bits of the PPs [
14] or approximating the encoding logic [
15]. Others are based on modular approaches [
12,
16,
17,
18,
19] that allow high-order multipliers to be implemented involving approximate low-order sub-multipliers. However, these methods are based on platform-specific optimizations that allow approximate operations to be efficiently mapped within Look-Up-Tables (LUTs), and, as a consequence, they do not perform as well when implemented in ASIC.
The above overview of the state-of-the-art counterparts discloses that none of the above papers’ proposed design methods have either been demonstrated on both ASICs and FPGAs or shown the potentiality of being competitive on both platforms. Indeed, although they are described using the Very High-Speed Integrated Circuits Hardware Description Language (VHDL), the above designs can be synthesized and implemented onto both FPGAs and ASIC, and they can achieve energy-delay trade-offs quite far from that reached by counterparts natively optimized for a specific platform. Therefore, they do not appear to be good candidates for the platform-independent design approach that we want to propose.
With the aim of introducing a platform-independent approximate multiplication strategy, this paper presents a new technique that allows modular energy-efficient approximate multipliers to be designed. In contrast to existing approaches [
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19], the proposed multiplier provides inexact results by using unconventional accurate sub-multipliers on approximated input operands, instead of performing approximate computations. Thanks to this strategy, the novel multiplier can be coded at the VHDL level, avoiding any specific platform-dependent primitives. Therefore, it is suitable to be processed by any synthesis tool and for any hardware platform without requiring specific modifications concerning the target technology. It is worth underlining that the approaches discussed in previously published papers [
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19] significantly differ from the method presented here.
To demonstrate the effectiveness of the proposed strategy, experiments were performed in both the ASIC and FPGA domains. In the former case, we achieve an energy saving over the accurate baseline of up to more than 80%, which, at a comparable number of effective bits (NoEB), is quite better than that obtained by the approximate multiplier recently presented in [
7]. A significant advantage in terms of energy reduction with higher NoEB is achieved with respect to the architectures described in [
8,
9]. The results obtained in comparison with the competitors [
15,
16,
17,
18,
19] also show that, among FPGA-based implementations, the proposed strategy reaches the best energy-accuracy trade-off.
Similar to previous works, novel multipliers were included in the design of approximate 2D image filters and edge detectors. In the former application, the proposed design consumes ~82% less energy than the accurate baseline, without introducing any Structural Similarity index (SSIM) [
26] degradation, thus overcoming achievements in [
8]. Conversely, the edge detection tests demonstrate that the proposed multiplier allows a higher edge-detected percentage to be reached with an energy saving only 0.88% lower than [
14].
2. Background and Related Works
In this section, the behavior of conventional
n ×
m integer multipliers and some representative static approximation strategies are briefly described. In order to do this, let us assume, without loss of generality, that the
n-bit multiplicand
A[n−1:0] =
an−1, …,
a0 and the
m-bit multiplier
B[n−1:0] =
bn−1, …,
b0 are 2′s complement numbers represented as given in (1). As it is well known, the basic multiplication algorithm first computes the bitwise ANDs between the operand
A and the bits of
B. Then, in order to obtain the generic partial product
PPj, with
j = 0, …,
m−1, the
j-th result produced by the AND operation related to the bit
bj, is left shifted by
j bit positions and sign extended to (
n +
m) bits. Finally, as shown by (2), the exact product
Pe[n+m−1:0] is calculated by accumulating the
m computed PPs. It is important to highlight that the simpler behavior of a multiplier processing unsigned operands can be easily derived from (1) and (2) by just removing the initial minus sign.
When the radix-2
r Booth’s algorithm is adopted, the
m bits of the signed multiplier
B are split into
(
r + 1)-bit groups, with 1-bit overlaps. An encoded digit is extracted from each group and used to generate the partial product
PPi (with
i = 0, …,
) as a multiple of
A. As an example, with
r = 2 the generic encoded digit can assume the values 0, ±1 and ±2, whereas with
r = 3, it can be equal to 0, ±1, ±2, ±3, and ±4. Each
PPi is sign extended and left shifted by
r ×
i bit positions to be aligned to the other partial products for the accumulation that furnishes the exact product
Pe[n+m−1:0] as given in (3). In this case, in order to treat unsigned inputs correctly,
A and
B must be zero extended to (
n + 1)- and (
m + 1)-bit, respectively.
Both the above multiplication algorithms are suitable for the modular approach that can be applied, as an example, by splitting the operands
A and
B into two sub-words, namely,
,
,
and
. In this case, the product
Pe is calculated as shown in (4), where
,
,
, and
.
It is worth noting that, in the case of signed operands, while the sub-words
AM and
BM still represent 2′s complement numbers, the sub-words
AL and
BL are unsigned numbers. This makes the management of signs information necessary to compute the sub-products
PML, PLM, and
PLL much simpler than what is required for calculating
PMM. Obviously, the overall computation is even easier when unsigned operands are processed. Furthermore, it is easy to understand that, independent of the adopted algorithm, the modular approach could be applied recursively to compute the sub-products, as shown, for example, in [
27].
The above formulations suggest that several strategies are viable to design efficient approximate multipliers. For example, the ASIC implementations presented in [
8,
9] compute the PPs conventionally as the bitwise AND between
A and
B, and then accumulate them by means of approximate compressors. Depending on the approximation level adopted and the chosen truncation, four approximate multipliers (named 1StepFull, 1StepTrunc, 2StepFull, and 2StepTrunc) are presented in [
8], each providing a different trade-off between speed, power, and accuracy. Conversely, the two approximate multipliers (called C-N and C-FULL) described in [
9] differ from each other in the way they use approximate 4-2 compressors. While the architecture C-N exploits the approximate 4-2 compressors only to process the LSBs of the PPs, thus limiting the errors introduced with respect to the exact product, the design C-FULL uses the approximate 4-2 compressors on the entire PPs, thus saving more energy, but sacrificing the accuracy.
The approaches known for FPGA-based designs make use of quite different approximation logics. The architectures (called AxBM1 and AxBM2) proposed in [
14] approximate the radix-8 Booth’s multiplier by exploiting new encoders on purpose designed to compute inexact PPs and to be efficiently mapped within LUT primitives. A different method is applied in [
15] to design a radix-4 Booth’s approximate multiplier (called BA) by taking advantage also of a LUT-level optimization strategy. In such a case, the logic operations performed by the LUTs responsible for computing the two LSBs of the PPs are removed or approximated, thus saving energy consumption and hardware resources. Alternative ways to exploit efficiently LUT-optimized implementations are presented in [
16,
17,
18,
19]. In [
16], a 4 × 2 approximate multiplier is used as the basic block to design higher-order multipliers. In such a basic block, the PPs are computed by performing the bitwise AND between the multiplicand
A and the bits of
B, then they are grouped two by two and added by means of the fast carry chains available in modern FPGAs [
28,
29]. The modular
w ×
w multiplier, designed as described in [
16], performs the generic computation by summing four
w/2 ×
w/2 approximate sub-products using either an accurate or an approximate ternary adder, thus leading to two architectures, named CA and CC, respectively. In a similar way, the modular designs proposed in [
17,
18] exploit 4 × 4 and 2 × 2 sub-multipliers to implement higher order multipliers. Finally, the open-source library presented in [
19] collects several 8-bit approximate circuits, including 471 8 × 8 multipliers designed using conventional multiplication structures.
3. The Novel Approximation Strategy
The architecture of the proposed multiplier is illustrated in
Figure 1. It relies on a double-stage encoding logic to simplify the multiplication by minimizing the number of non-zero bits involved in the accumulation of partial products. During the first stage, the inputs
and
are split into the sub-words
,
,
and
, with
ka and
kb being chosen at design time. Then, the least significant sub-words
and
are partitioned into non-overlapping 3-bit groups and encoded through an on-purpose conceived method based on a backward propagation action. The encoded digits CDx are properly aligned and OR-ed in overlapped positions, thus obtaining the approximate versions of the least significant sub-words
and
, corresponding to the closest power-of-two. In the second stage, four sub-products are calculated by multiplying the sub-words
,
,
and
. While the most significant term
is computed through a conventional multiplier, the others are obtained by using the new radix-4 encoding logic (NR4EL) here indicated with the operator Θ, which performs an accurate multiplication on approximated input operands, having at most one non-zero partial product. That is,
,
and
. Both encoding logics above mentioned will be detailed later. Finally, the sub-products
,
,
and
are aligned, sign-extended, and accumulated to compute the final approximate product
Pa, as given in (5).
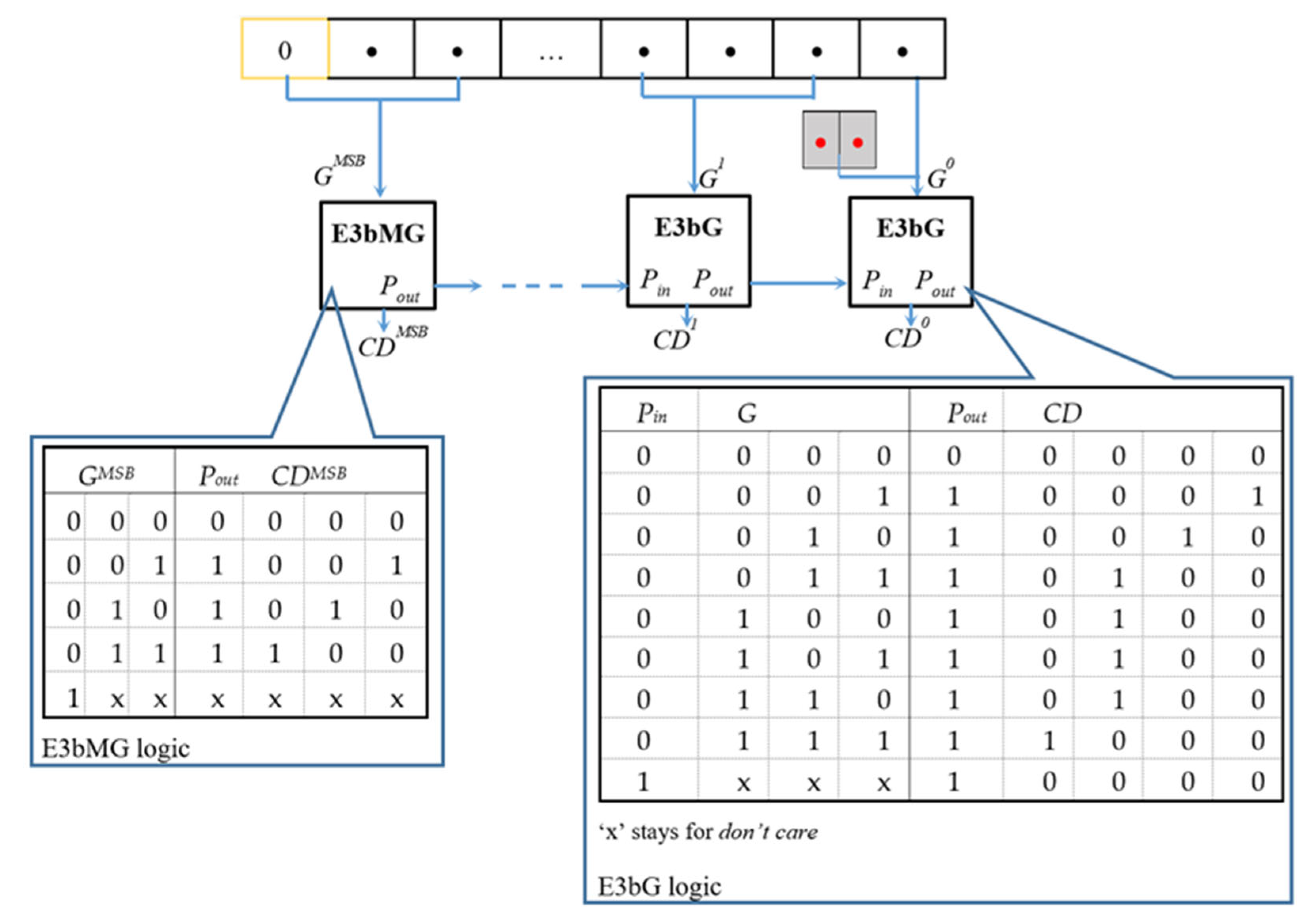
3.1. The New 3-Bit Encoding Logic for Least Significant Sub-Words
As illustrated in
Figure 2, before being encoded with the proposed method, the unsigned sub-words
and
are zero extended to be treated as positive numbers. Furthermore, additional zeros are put beside the least significant positions (as schematized with the red dots in
Figure 2) if needed to obtain an integer number of non-overlapping 3-bit groups. The most significant group is encoded by using the novel logic E3bMG, whereas for the less significant bit positions, the encoding rules E3bG are applied. As visible in
Figure 2, such an encoding logic is based on a back-propagation action sustained by the signals
Pin and
Pout. As shown in the following, coded digits
CDx are then aligned and OR-ed to finally furnish
and
.
It is worth noting that the above encoding strategy introduces an approximation to the closest power of two. As detailed in the following, this property allows simplifying the logic required to compute the accurate sub-products , and . In addition, it must be pointed out that, in this context, the novel E3bMG and E3bG logic perform much better than the conventional leading one detection. To understand this, as an example, let us consider the 8-bit numbers 127 and 65. While the proposed encoding provides the approximate values 128 and 64, thus leading to an absolute error equal to 1 in both the cases, the conventional technique approximates both the values to 64, thus causing an absolute error equal to 63 and 1, respectively.
3.2. The NR4EL Multiplication
Starting from the observation that the approximate sub-words
and
are represented as power-of-two, containing at most one non-zero bit, a further original encoding step is here proposed to exploit this property in computing the sub-products
,
and
. That is:
and
are split into 3-bit groups, with 1-bit overlaps, and zero extended if needed to complete the most significant group. The NR4EL summarized in
Figure 3 is applied to each 3-bit group
GL to obtain the corresponding partial product
PP. Since the approximate sub-words contain at most one non-zero bit, the NR4EL can output just three possible values: 0,
MD, and 2 ×
MD, with
MD being the multiplicand (i.e.,
or
or
). Moreover, the computations of the sub-products
and
involve at most one non-zero partial product, whereas at most just one bit is asserted among all the partial products computed to calculate
. Due to this, partial products are then accumulated by simple logic ORs rather than addition circuits, thus ensuring that a quite significant energy reduction is expected with respect to conventional approaches.
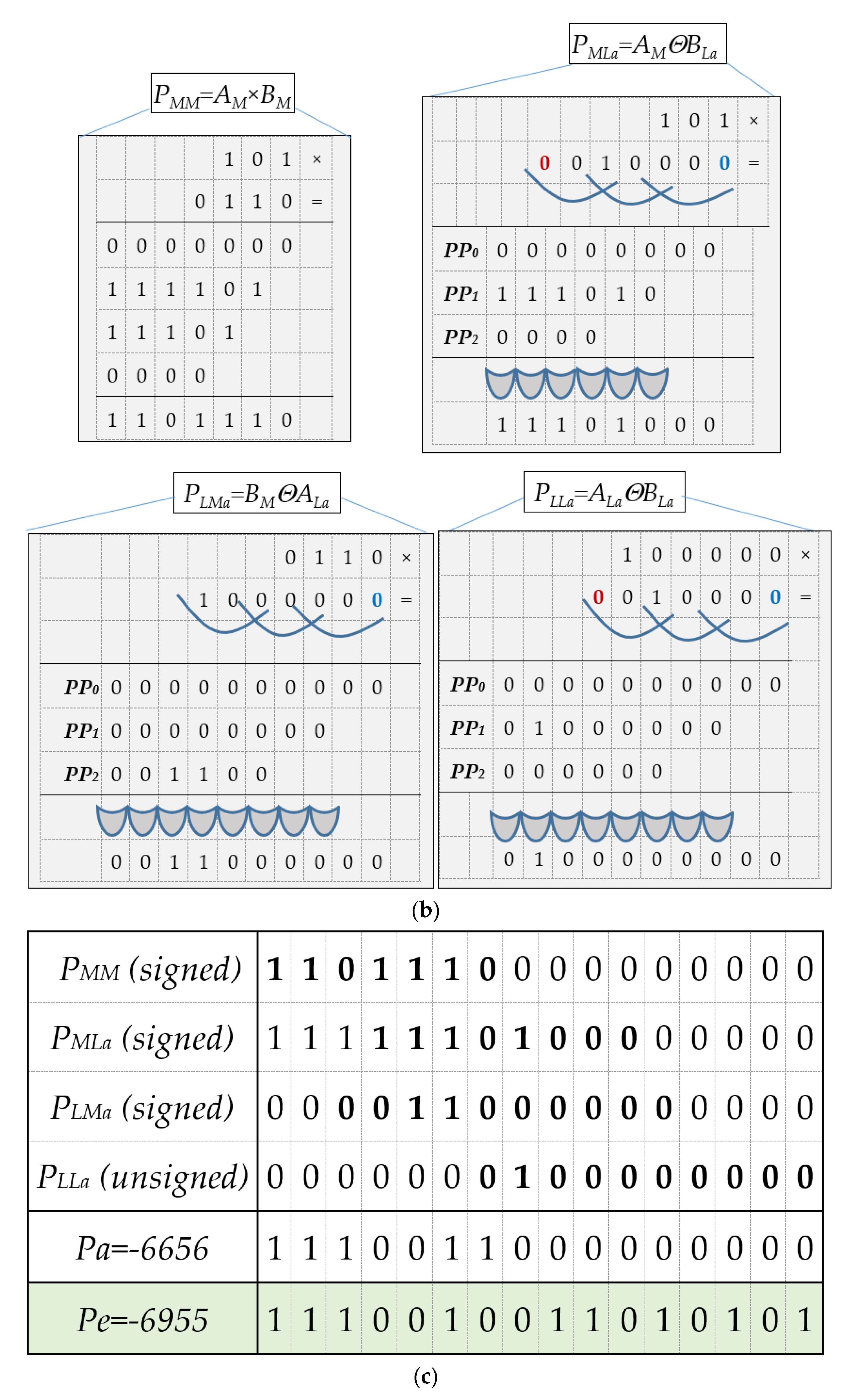
It is worth noting that, due to the approximation made on the least significant bits of the input operands, the proposed NR4EL logic leads to hardware requirements quite different from that of a conventional radix-4 Booth multiplier. Just as a comparison, let us refer to the example illustrated in
Figure 4, where
n =
m = 8 and the configuration
ka = 5 and
kb = 4 is used to perform the multiplication by the novel approximate strategy. The input operands
A and
B are firstly partitioned into the most significant (
) and least significant (
,
) parts. The latter are zero-extended and encoded through the 3-bit logic shown in
Section 3.1. Coded digits are aligned taking into account that their significance is dictated by the bit positions involved in the 3-bit groups from which they are calculated. The approximate values
and
are then obtained by simply ORing their overlapped bits. As discussed above (see
Figure 1),
is computed by a full precision conventional multiplier, whereas
,
and
exploit the NR4EL multiplication logic. In contrast to the Booth multiplier, the proposed one, thanks to its coding strategy, allows any additional circuit for the computation of
,
and
to be avoided, as illustrated in
Figure 4b. The sub-products obtained in this way are aligned, sign extended, and summed to finally furnish the approximate product
Pa, as shown in the last step of
Figure 4, which also reports the exact product
.
4. Accuracy and Implementation Results
To prove the effectiveness and the high flexibility of the proposed method, several signed
n ×
m approximate multipliers were implemented using both ASIC and FPGA realization platforms. In the following, New
ka_kb indicates a multiplier designed as described here that approximates
ka LSBs of
A and
kb LSBs of
B. This section presents results obtained for both symmetric and asymmetric designs. Performances achieved by our proposal are discussed and compared with competitors. All quality measures, in terms of average error (AE), error rate (ER), normalized mean error distance (NMED), mean relative error distance (MRED), defined as reported [
30], and number of effective bits (NoEB), introduced in [
8], have been obtained through exhaustive C++ simulations. It is worth noting that accuracy tests for multipliers with operands word lengths greater than 16-bit are excessively time consuming. Therefore, as in all the previous works [
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19] for such cases, only the hardware characteristics are provided.
4.1. Design Space Exploration
It is important to note that the possibility of differently setting
ka and
kb represents a further degree of freedom that can be exploited to finely tune the energy and accuracy of the multiplier to the requirements of a given specific application. This property leads to a design space wider than that bounded by using
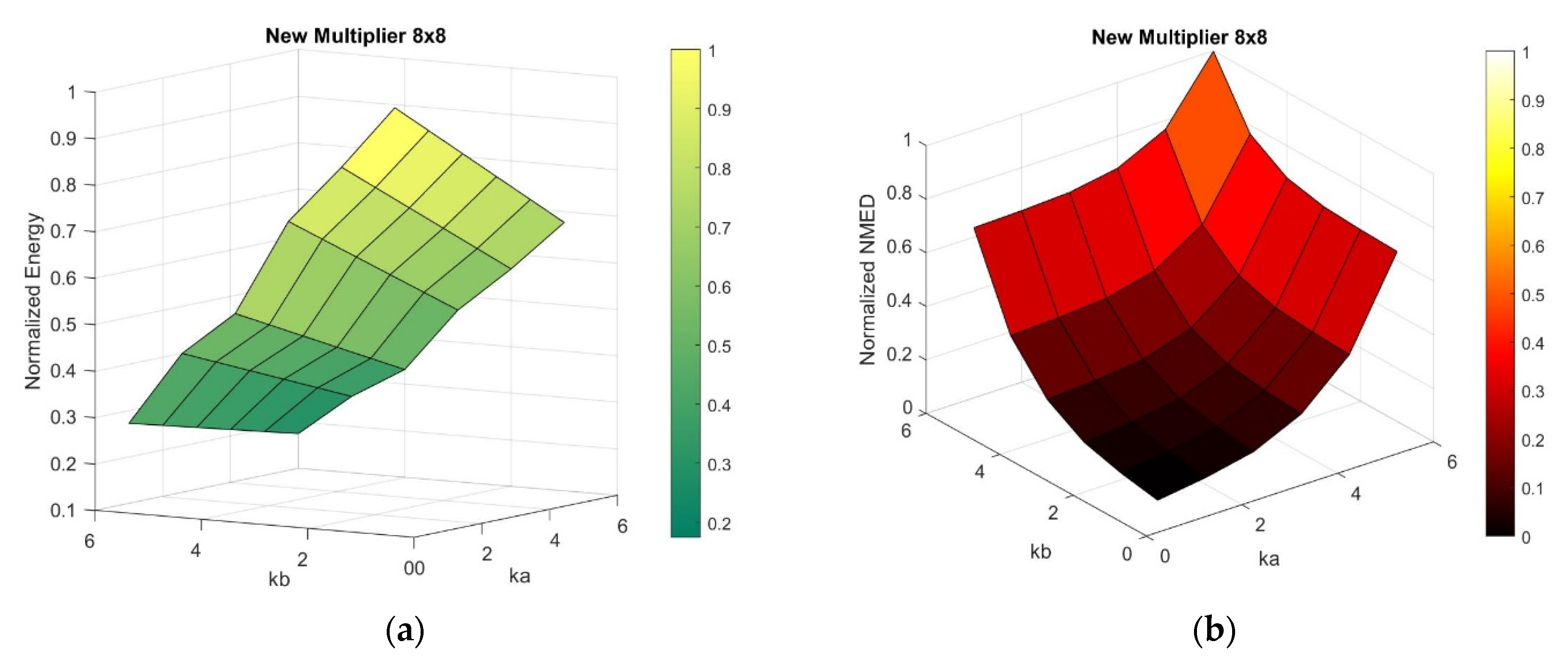
ka = kb and it cannot always be obtained by other techniques, such as those based on approximate compressors. In
Figure 5, the normalized energy-NMED design space for the 8 × 8 multiplier is illustrated for
ka and
kb varying in the range 1–6.
Just as an example, with respect to the symmetric
ka = kb = 4 scenario, approximating one more bit on one operand (e.g.,
ka = 4 and
kb = 5) leads to a 7% higher energy gain with an NMED increased by only ~0.005. On the contrary, the
ka = 3 and
kb = 4 configuration reduces the NMED by ~0.002 and the energy gain with respect to the precise architecture by ~3.5%. Such an analysis can be useful to optimize the parameters
ka and
kb for a given scenario. As an example, for the image processing applications referred to in
Section 5, the configuration with
ka = 2 and
kb = 6 is particularly efficient, given the significantly different nature of the operands to be multiplied. However, the optimizations of
ka and
kb and the realization of a design framework are beyond the scope of this paper.
4.2. ASIC Implementations
For purposes of a fair comparison with state-of-the-art counterparts, 8 × 8 and 16 × 16 signed multipliers were implemented using the TSMC40 nm CMOS 1.1 V and the ST28 nm UTBB-FDSOI 1 V technologies. They were synthesized with the Cadence Genus™ tool version 19.11 at the minimum delay constraint inserting registers as the driving and the loading logic, with the output flip-flops having 0.1 pF load capacitances. The energy consumption was analyzed using the Value Change Dump (VCD) files extracted for 100,000 random vectors.
Table 1 and
Table 2 collect results obtained in terms of delay (D), silicon area (A), energy (E), average error (AE), error rate (ER), and number of effective bits (NoEB). The behavior of each approximate multiplier is clearly appreciable in comparison with the precise baseline versions realized with the same technology process.
The New
2_6 signed design achieves an energy saving higher than 80%, with a negligible impact on the speed performances. The 2StepTrunc signed architecture [
8] shows an energy saving with respect to its baseline of ~76%, and, even though it reaches an interesting delay reduction, the achieved quality level is quite lower than the New
2_6. On the other side, while the C-Full circuit [
9] dissipates the same energy as the proposed one, it shows a much lower gain with respect to the baseline and achieves a NoEB lower than the New
2_6. Furthermore, it must be considered that the architectures in [
9] operate only on unsigned operands. The above analysis confirms the effectiveness of the proposed approach in reducing the number of non-zero bits within the tree of partial products in favor of energy efficiency. Indeed, the strategies proposed in [
8,
9], being, respectively, based on LSB truncation and approximate compressors, just partially simplify the adder circuits responsible for the accumulation of the partial products.
The energy gain obtained over the baseline generally deteriorates with the operands word length. From
Table 2, it can be observed that the New
8_8 16 × 16 signed multiplier saves ~75% of the energy, whereas [
8] saves at most ~63%. Surprisingly, [
9] shows a ~8% improvement in this figure. However, the quality level of the 16 × 16 New
8_8 multiplier still overcomes the competitors. On the other hand, [
8,
9] achieve area and delay reductions remarkably higher than the new designs.
In order to evaluate how the ASIC designs trade-off energy saving (
EnSv), accuracy, area, and delay, the figure of merit defined in (6) and the comprehensive cost function given in (7) are introduced.
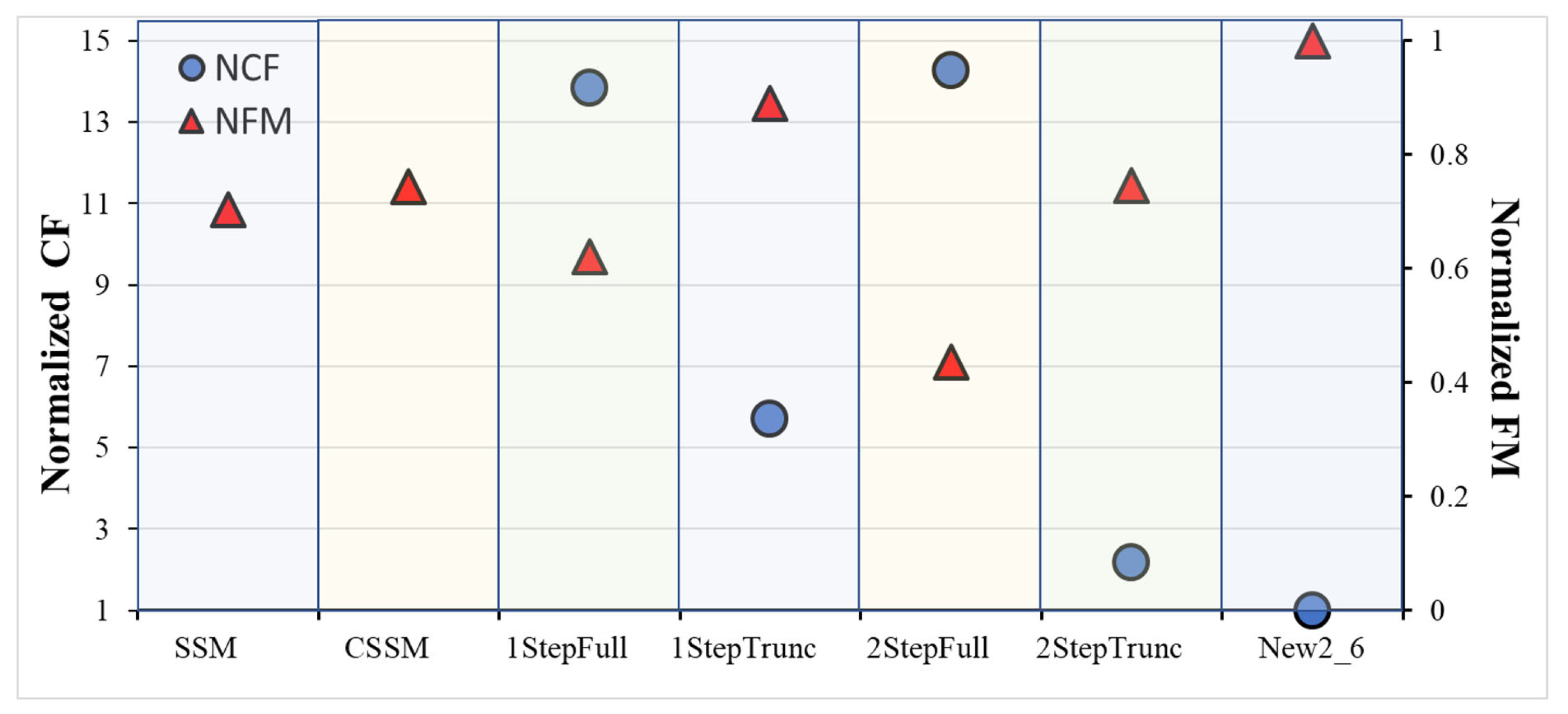
Figure 6 plots the normalized values of
FMASIC (NFM) and
CFASIC (NCF) and shows that the
FMASIC achieved by the New
2_6 circuit is 12% and 34% higher than 1StepTrunc [
8] and CSSM [
7], respectively. Indeed, at a comparable NoEB, the signed 8 × 8 architectures demonstrated in [
7] reach a power saving ~20% lower. The graceful behavior of the proposed multiplier is confirmed by the
CFASIC, which is up to 13 times lower than that of the competitors.
The
FMASIC also reveals that, among the 16 × 16 designs, 1StepTrunc [
8] reaches the best trade-off. However, the
FMASIC of the proposed New
8_8 signed multiplier is only 5% lower and up to 2.6 times higher than other competitors referenced in
Table 2.
4.3. FPGA Implementations
Table 3 and
Table 4 collect hardware characteristics of 8 × 8 and 16 × 16 approximate multipliers implemented on a Xilinx XC7VX330T FPGA device. Data related to competitors are extracted from the original papers.
Table 3 shows that the circuits BA and Trunc [
15] achieve the lowest resource requirements and energy dissipation, respectively. Conversely, CC [
16] reaches the highest speed performance. However, the above architectures are characterized by MRED values quite higher than those achieved by the multipliers designed using the strategy here proposed. Indeed, the circuit New
4_4 achieves the lowest MRED. Results in
Table 3 show that New
4_4 and New
2_6 architectures achieve the best energy-quality-delay trade-off, significantly overcoming their counterparts.
Table 4 compares a 16 × 16 architecture based on the proposed approach to the competitors AxBM1 and AxBM2 [
14], and it reports the MRED, the MED, and the NMED because those metrics are used in [
14]. It can be noted that the multipliers AxBM1 and AxBM2 achieve better energy-quality-delay trade-offs. However, such a result is obtained by adopting specific and strictly platform-dependent LUT-level optimizations, which prevent exploiting the AxBM1 and AxBM2 within ASIC designs as efficiently. Even without exploiting any specific optimization, the New
11_11 architecture is ~12% faster than [
14] and reaches a more than acceptable energy-quality behavior. As a final remark, it is worth noting that none of the competitors evaluated in
Table 1,
Table 2,
Table 3 and
Table 4 have the ability to perform well by using both ASIC and FPGA platforms.
In order to show how the operands word length and the adopted configuration affect the behavior of the novel multipliers, further implementations have been characterized. All the obtained results are summarized in
Table 5 and
Table 6, where the results presented in
Table 3 and
Table 4 are also reported, to provide a clearer picture. The former collects the achieved accuracy, whereas the latter reports the hardware characteristics in comparison with the competitors [
15,
16,
17,
18] and the accurate IP cores.
From
Table 6, it is pretty evident that the LUT-optimized approximate design BA [
15] is the cheapest one and often dissipates less energy than competitors. Conversely, at least one of the configurations examined for the new multiplier performs better than S1 [
17], S2 [
15], and S3 [
18]. In fact, the amounts of LUTs required by the newly proposed 8 × 8, 12 × 12, 16 × 16, and 24 × 24 implementations are up to ~38%, ~22%, ~54%, and ~37% lower, respectively. It is also worth noting that the designs S1, S2, and S3 always utilize more LUTs than the accurate design. Furthermore, it can be seen that the amount of LUTs required by the designs CA and CC [
16] rapidly grows with the operands bit-width, thus becoming higher than the novel multipliers starting from 16 × 16 implementations.
Table 6 also shows that CC implementation always leads to the lowest energy consumption. However, it must be taken into account that both the architectures CA and CC operate on unsigned inputs [
16]. The energy improvement achieved by the proposed approximation strategy over the accurate counterpart increases with the operands bit-width: the ~34% energy saving reached in the case of 8 × 8 multipliers, grows to ~43%, ~56%, ~63%, and ~70% for the 12 × 12, 16 × 16, 24 × 24, and 32 × 32 implementations, respectively. The novel designs also exhibit an appreciable energy savings ranging from ~20% to 72%, with respect to the competitors S1, S2, S3, BA, and CA. Conversely, their energy consumption is comparable to AxBM1 and AxBM2 [
14] (see also
Table 4).
5. Case Study: Image Processing Applications
As an example of applications, the proposed approximate multipliers have been exploited in the realization of two image processing sub-systems, commonly adopted as benchmarks in similar works [
7,
8,
9,
10,
11,
12,
13,
14,
15,
17]: the 2D filtering and the edge detector. While the former convolves the input image with a single kernel, the latter performs convolutions with two kernels that compute horizontal and vertical gradients of the input image. Both the sub-systems are based on the 8 × 8 New
2_6 multiplier and receive the kerne values as external inputs. Therefore, they can support different edge detectors and filters. However, for purposes of comparison with previous works, the Sobel operator and the 2D Gaussian smoothing filters have been referenced. The energy consumption of complete systems was analyzed with 100,000 random vectors at the maximum toggle rates. Whereas, the accuracy was examined using images from the USC-SIPI dataset [
31] as test benches. Accuracy results discussed in the following are calculated by averaging those obtained for all the 256 × 256 and 512 × 512 images available in [
31]. Sample images reported in
Figure 7 show that the new approximate multipliers work well in both the referred image processing applications.
It is worth pointing out that, in order to analyze the behavior of the designed sub-systems on different FPGA devices, they have been implemented within Xilinx VIRTEX 7 XC7VX485 and Altera CYCLONE 006YE144A7G chips.
Table 7 summarizes the hardware characteristics of the implemented sub-systems at different filter sizes. Moreover, it reports the accuracy achieved when the 2D Gaussian Smoothing Filtering is performed and averaged over the processed testbench images. The Peak Signal Noise to Ratio (PSNR) and the Structural Similarity (SSIM) [
26] quality metrics have been selected for purposes of comparison with the approximate filters presented in [
15].
To provide a complete overview, the behavior of LUT-optimized accurate filters, referenced as the baselines and employing the 8 × 8 accurate IP core multiplier, is also shown. It is worth pointing out that, in terms of SSIM, the approximate filters based on the novel multipliers achieve the same behavior as the accurate implementations. Moreover, when compared to the filter based on the BA multiplier presented in [
15], in terms of PSNR, the novel design exhibits an improvement ranging from ~4.8% to ~16%, achieved for the 3 × 3 and the 7 × 7 filter size, respectively. Xilinx VIRTEX 7 implementations exhibit an energy reduction with respect to the baseline that, depending on the filter size, varies between ~25% and ~32%, with an energy improvement up to ~8.5% achieved in comparison with [
15]. The Altera CYCLONE implementation achieves a ~56% energy reduction over the baseline.
Table 7 also shows that the approximate filters designed as proposed here are up to ~21% and ~22% faster than the baselines and the counterparts characterized in [
15], respectively. Finally, it must be noted that, since the architectures proposed in [
15] exploit FPGA-specific optimizations, they achieve appreciable reductions in terms of utilized logic resources, with respect to the accurate IP-based implementations.
Table 8 compares several 3 × 3 Sobel edge detectors based on 8 × 8 approximate multipliers. The energy gains and the edge detection accuracies achieved with respect to the precise baselines are reported. While AxBM2 [
14] achieves the highest energy gain and the architecture in [
10] obtains the best accuracy level, the proposed strategy leads to an appreciable trade-off, even though it does not exploit any specific and strictly platform-dependent LUT-level optimization. On the other hand, this is the reason for which, in contrast to the competitors, the approximation approach proposed here can be efficiently employed also in ASIC designs, as clearly visible in
Table 9. The latter reports percentage gains in terms of area, delay, and energy, achieved over the accurate baselines, and SSIM degradations attainable by several approximation techniques in Gaussian smoothing filtering. It can be observed that the proposed method significantly outperforms the competitors. It is worth highlighting that the approximation strategy presented here maintains the same accuracy achieved by the accurate baseline. Conversely, the approach exploited in [
8] reduces the SSIM by up to 8%.
Additional tests demonstrated that the approximate multipliers designed as proposed here work well also when employed in 5 × 5 and 7 × 7 Gaussian smoothing filters. In fact, energy gains close to 25% and 80% are still achieved by FPGA and ASIC designs, respectively, with PSNR higher than 50 dB and without causing SSIM degradation.
6. Conclusions
This paper presented a novel approach to designing energy-efficient platform-independent approximate multipliers. In fact, even without exploiting specific low-level optimizations, the proposed approximate approach leads to efficient designs in both ASIC and FPGAs. This is a quite remarkable advantage over existing counterparts, given that, even though any design described using VHDL can be synthesized and implemented onto any realization platform, the energy-delay trade-off achieved is typically quite far from that reached by counterparts natively optimized for a specific platform.
The novel strategy directly approximates the operands received as inputs. In order to do this in a smart way, thus limiting the overall accuracy loss, an innovative encoding logic has been introduced. The approximation method here proposed has been applied to several signed multipliers with different operands word lengths. A thorough analysis performed in terms of accuracy metrics and hardware characteristics demonstrated that the novel approximation strategy achieves remarkable energy savings in both FPGA-based and ASIC implementations. The ASIC designs have shown that the novel approximation technique achieves the best energy improvement over the accurate baseline and overcomes several competitors in terms of NoEB.
The proposed technique has been applied to design approximate 2D filters and edge detectors. When implemented onto FPGA devices, the novel approximate filters exhibit an energy consumption up to ~32% lower than the optimized baselines. Moreover, the achieved energy-delay product is more than 24% lower than its state-of-the-art counterparts [
15]. Even better behaviors have been observed for the ASIC designs that consume more than 80% less energy than the baselines without affecting the accuracy achieved in terms of SSIM.