Intra- and Inter-Server Smart Task Scheduling for Profit and Energy Optimization of HPC Data Centers
Abstract
1. Introduction
2. Related Work
3. System and Problem Definition for Scheduling Problem
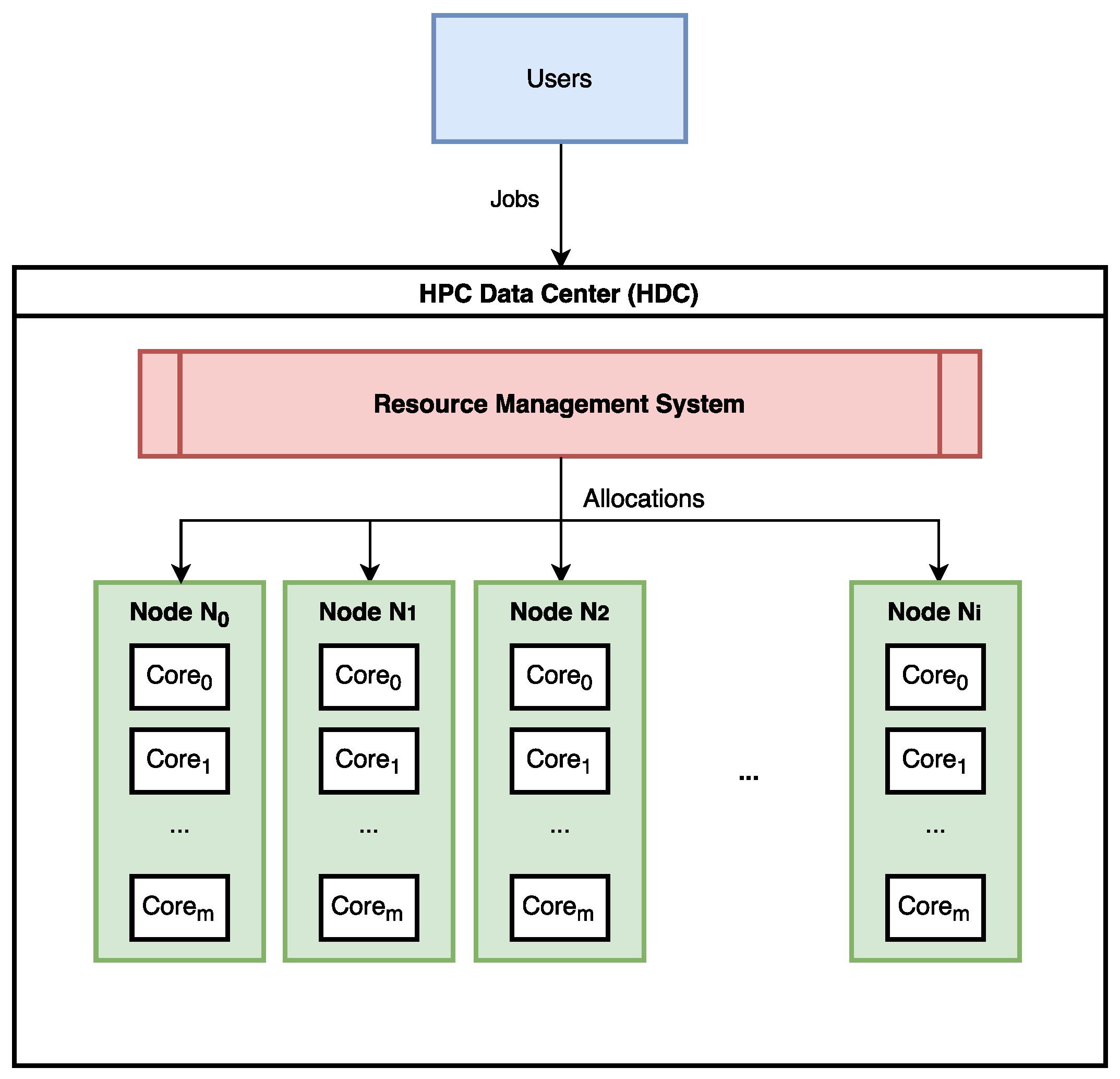
3.1. HPC System
3.2. Jobs and Value Curves
3.3. Problem Definition
- Input: Job queue (), Value curve for each job , Nodes within the HPC data center ().
- Constraints: Restricted available cores on the nodes in .
- Objective: Jointly optimize overall value and energy consumption , by maximizing the quotient .
3.4. Proposed Approach Based on Reinforcement Learning
3.4.1. Adapted Multi-Armed Bandit Model
3.4.2. Upper Confidence Bound Algorithm
3.4.3. Proposed Algorithm for Confidence-Based Approach
| Algorithm 1: CBA Resource Allocation. |
 |
4. System and Problem Definition for Network Aware Server Consolidation
4.1. Network Aware Server Consolidation
4.2. Traffic Pattern Model
4.3. The Network-Aware Consolidation Algorithm
| Algorithm 2: Algorithm for Bandwidth-Constrained Consolidation (BCC). |
 |
| Algorithm 3: Migration Function. |
 |
4.4. Complexity Analysis
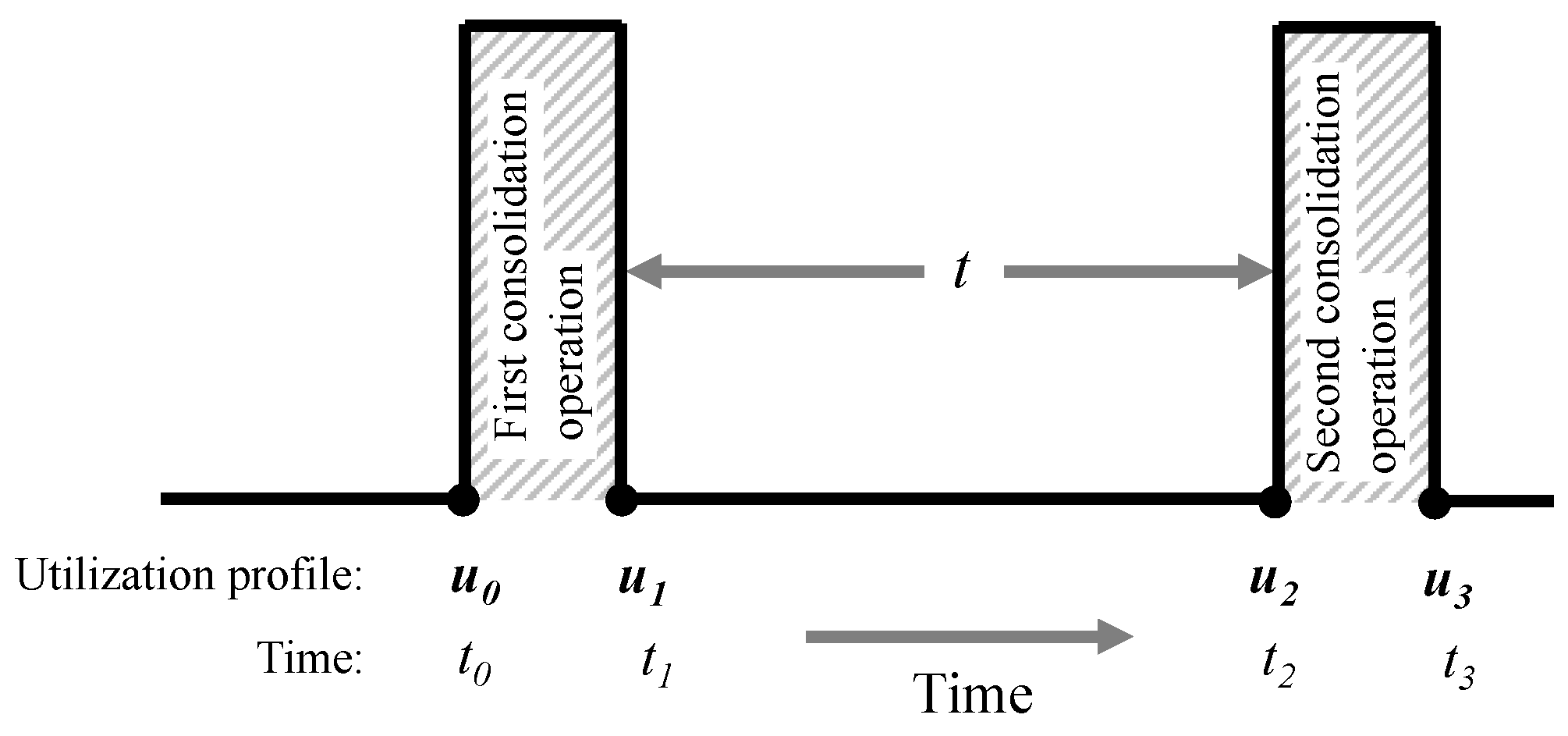
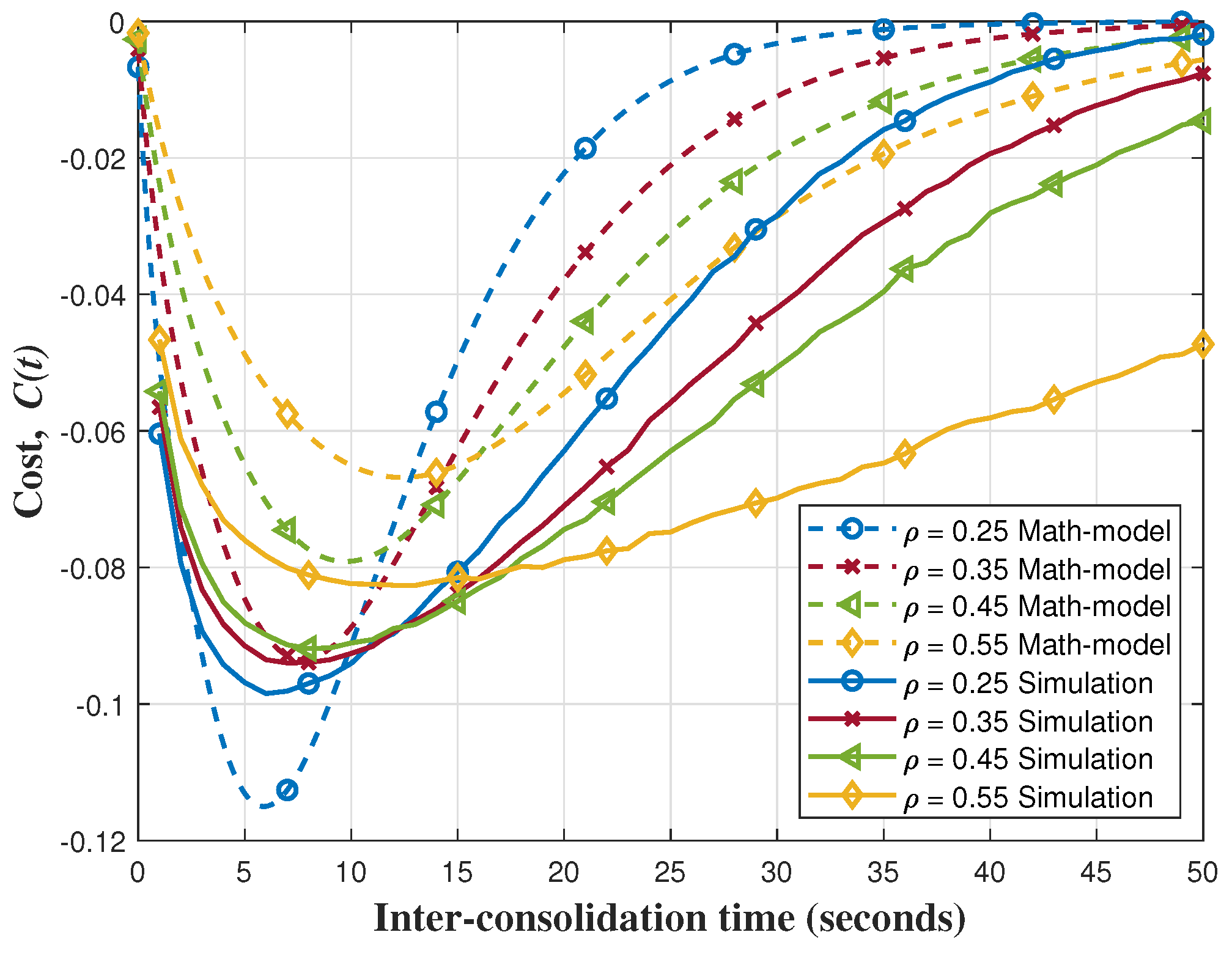
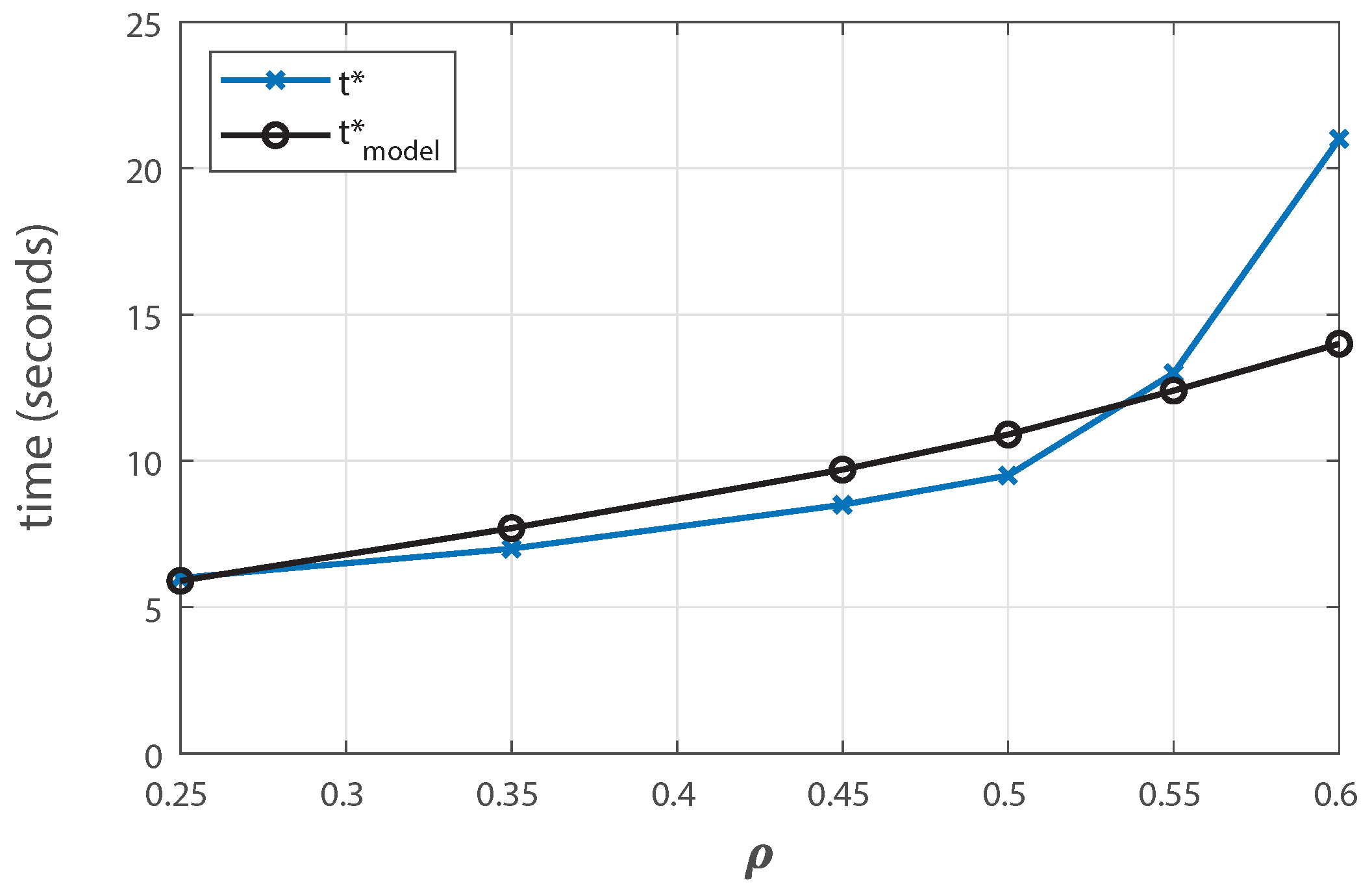
4.5. Optimizing the Inter-Consolidation Time
5. Experimental Results
5.1. Experimental Results for CBA Algorithm
5.1.1. Experimental Baselines
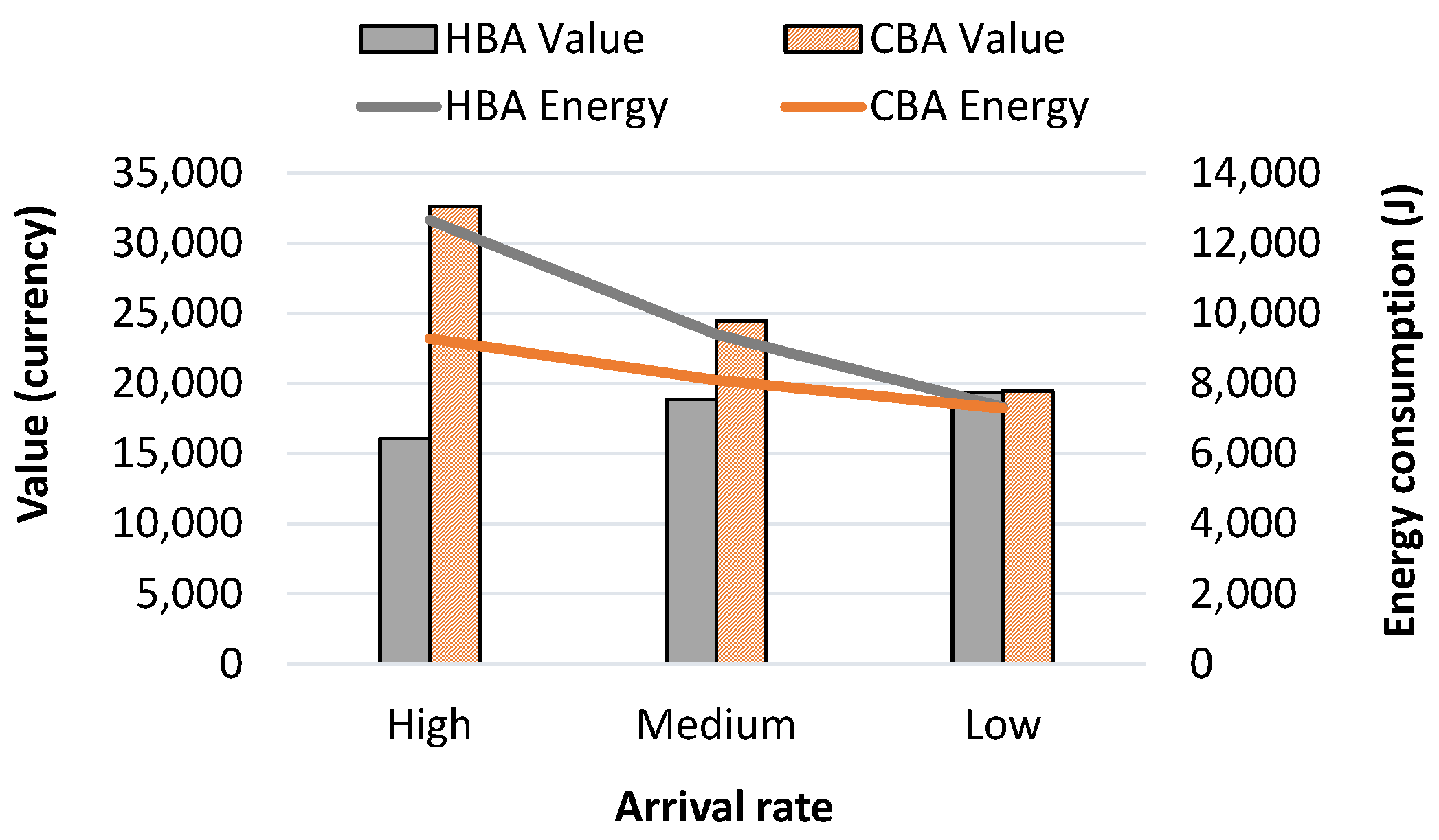
5.1.2. Profit and Energy Consumption Results at Varied Arrival Rates
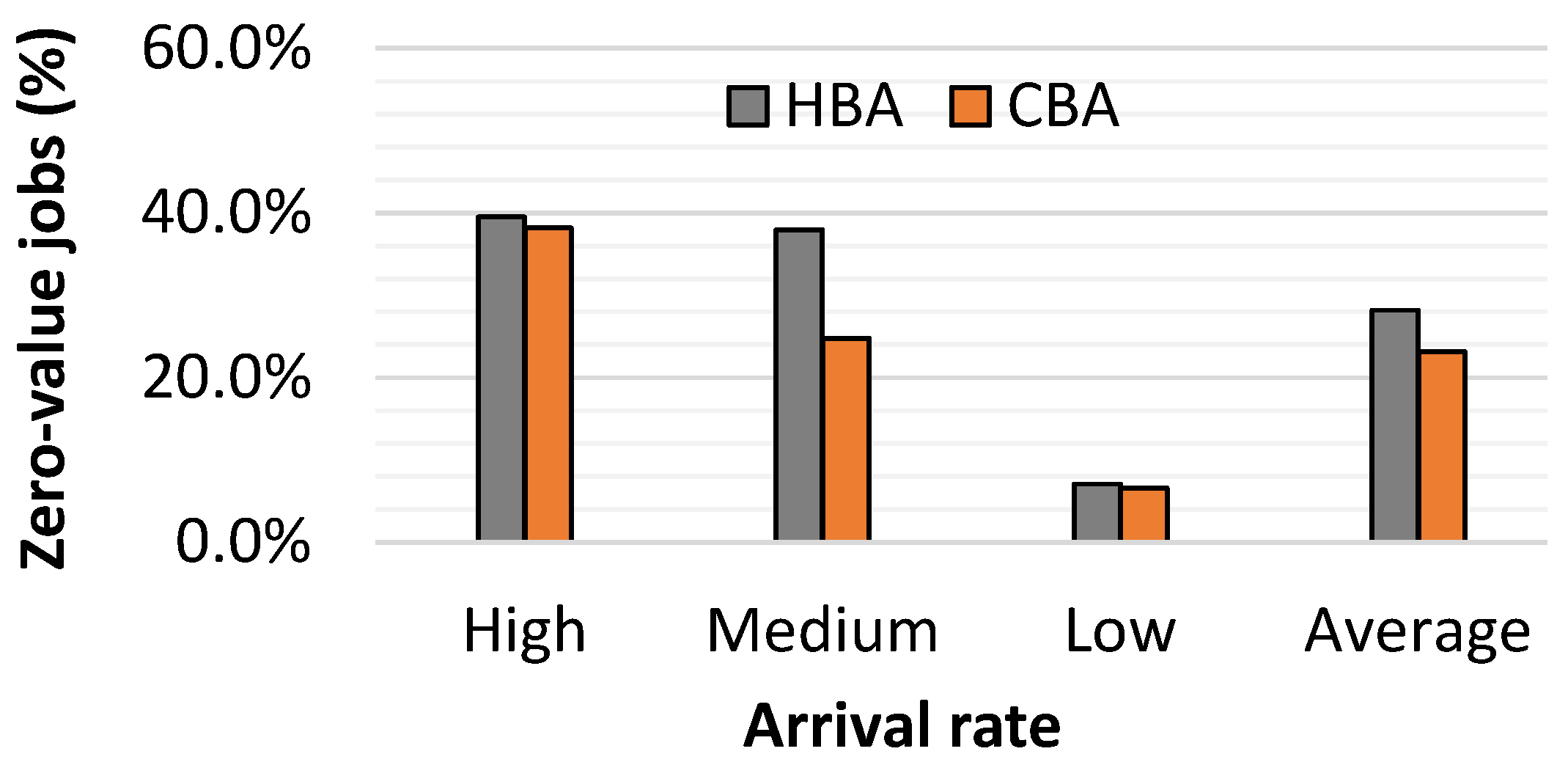
5.1.3. Percentage of Zero-Value Jobs
5.1.4. Overhead Analysis
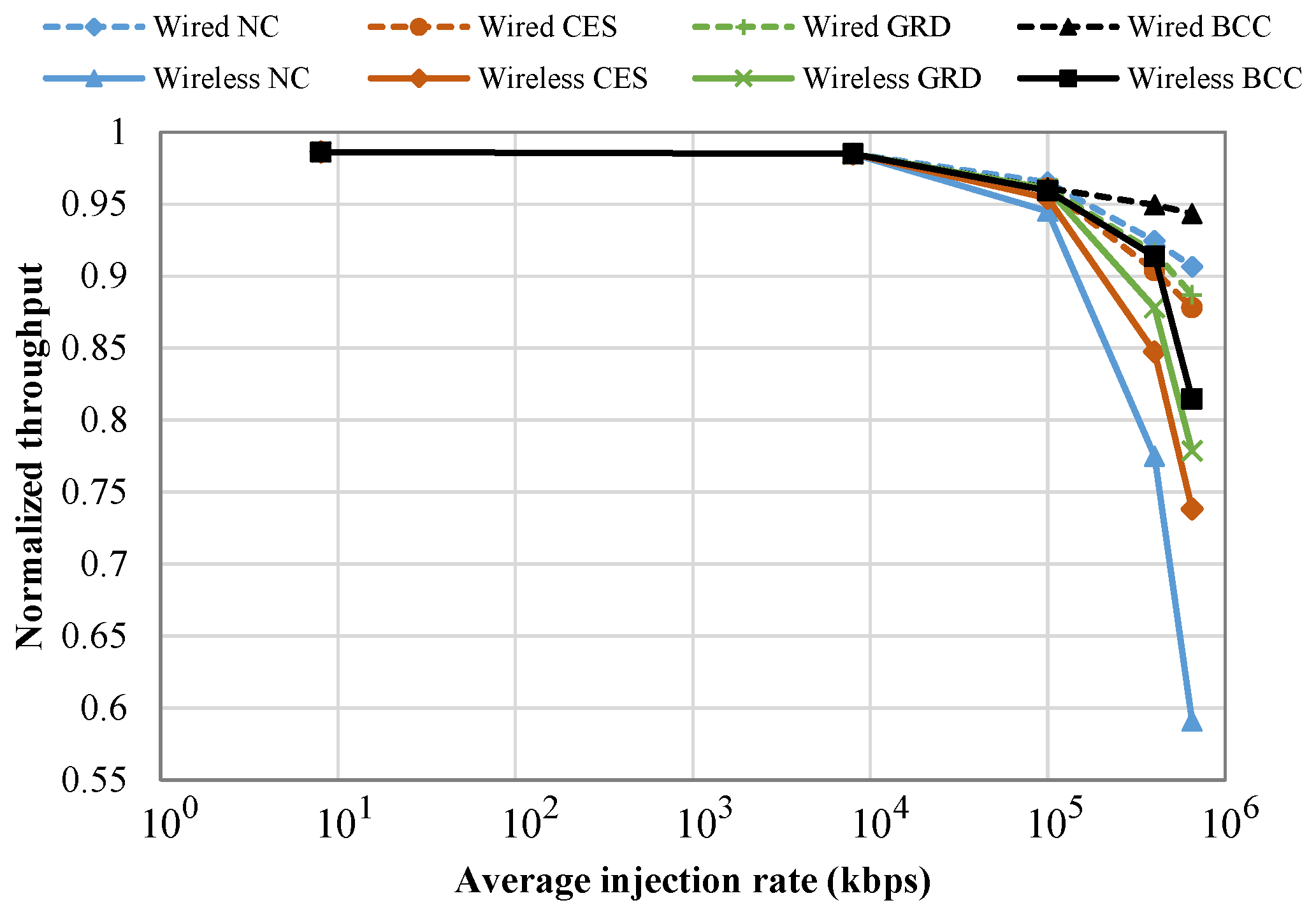
5.2. Experimental Results for BCC Algorithm
5.2.1. Traffic Generation and Simulation Platform for BCC
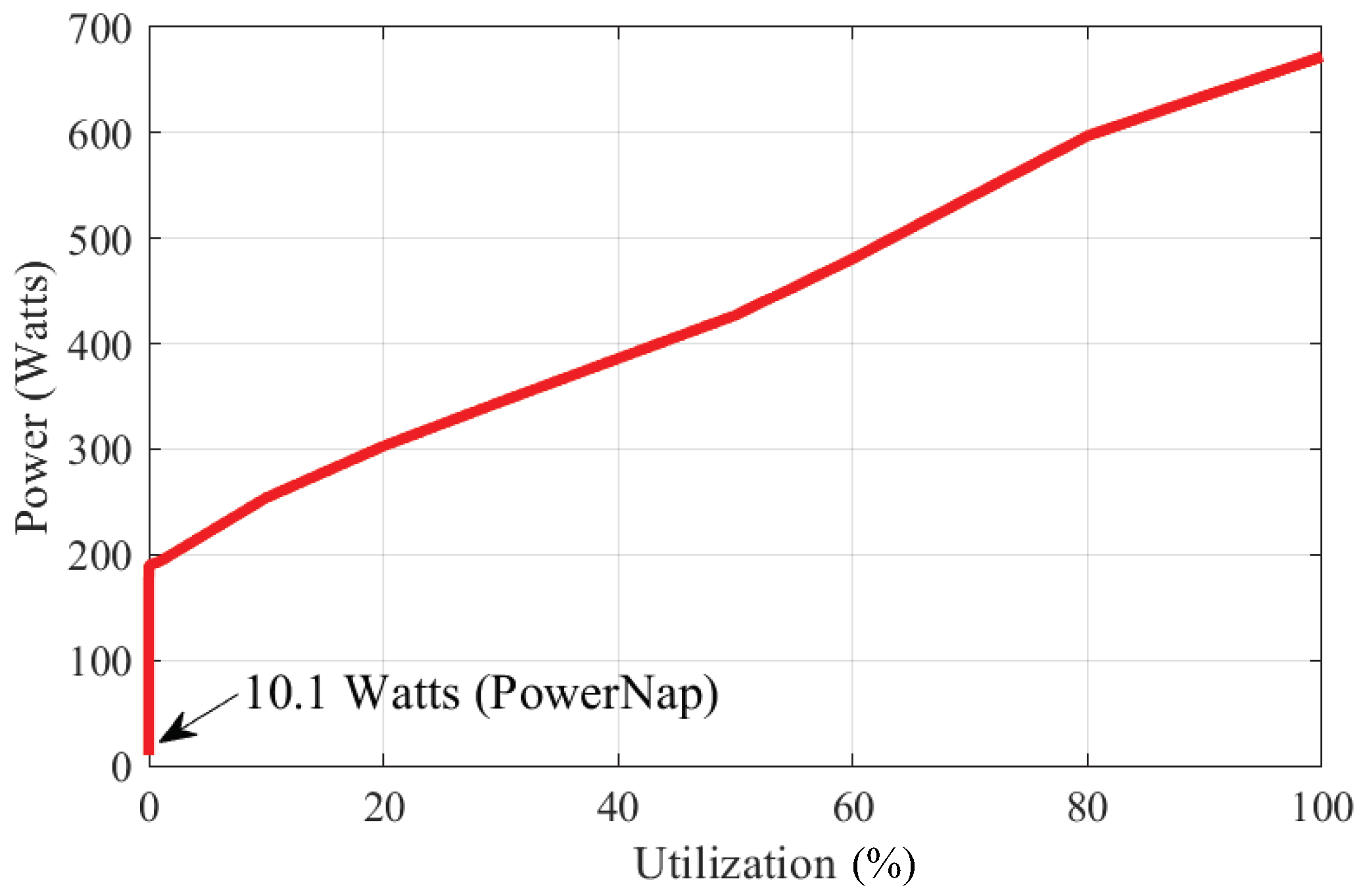
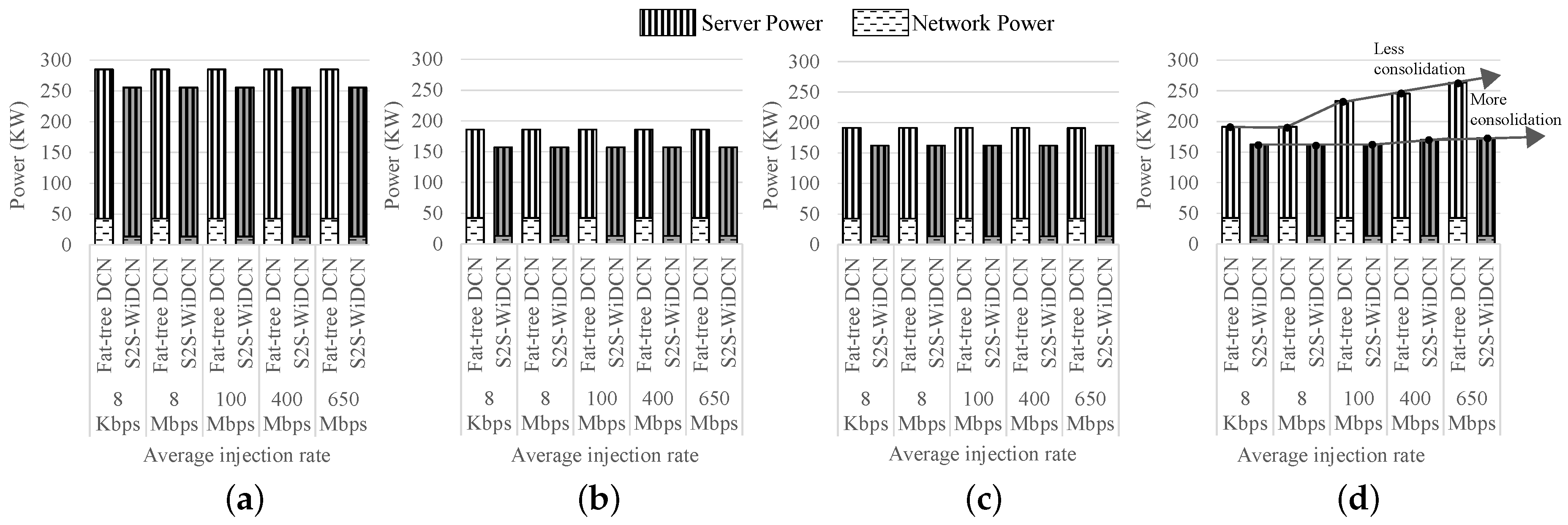
5.2.2. Power Consumption Analysis of BCC
5.2.3. Performance Analysis of BCC
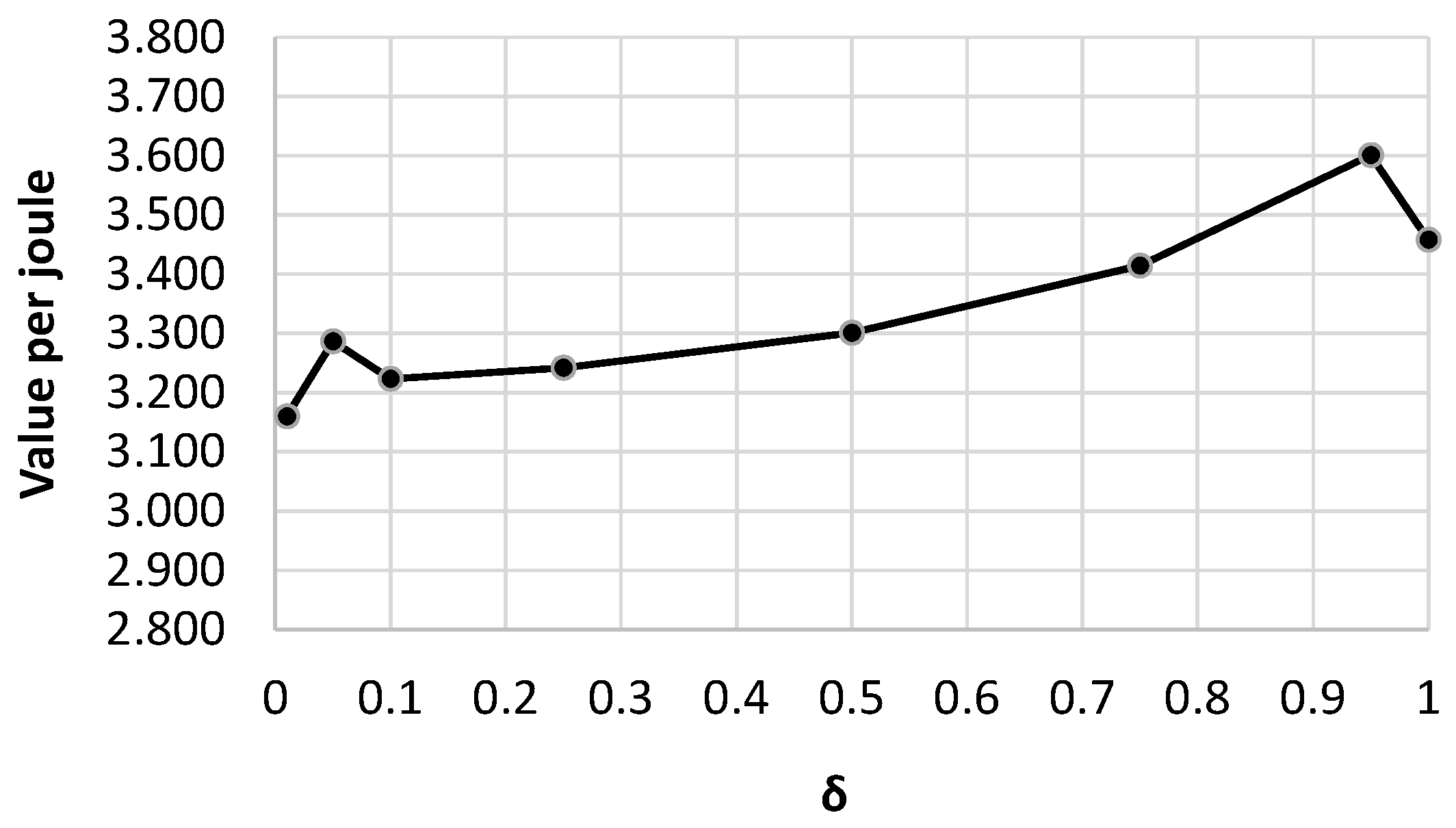
5.2.4. Accuracy of Inter-Consolidation Time Modeling
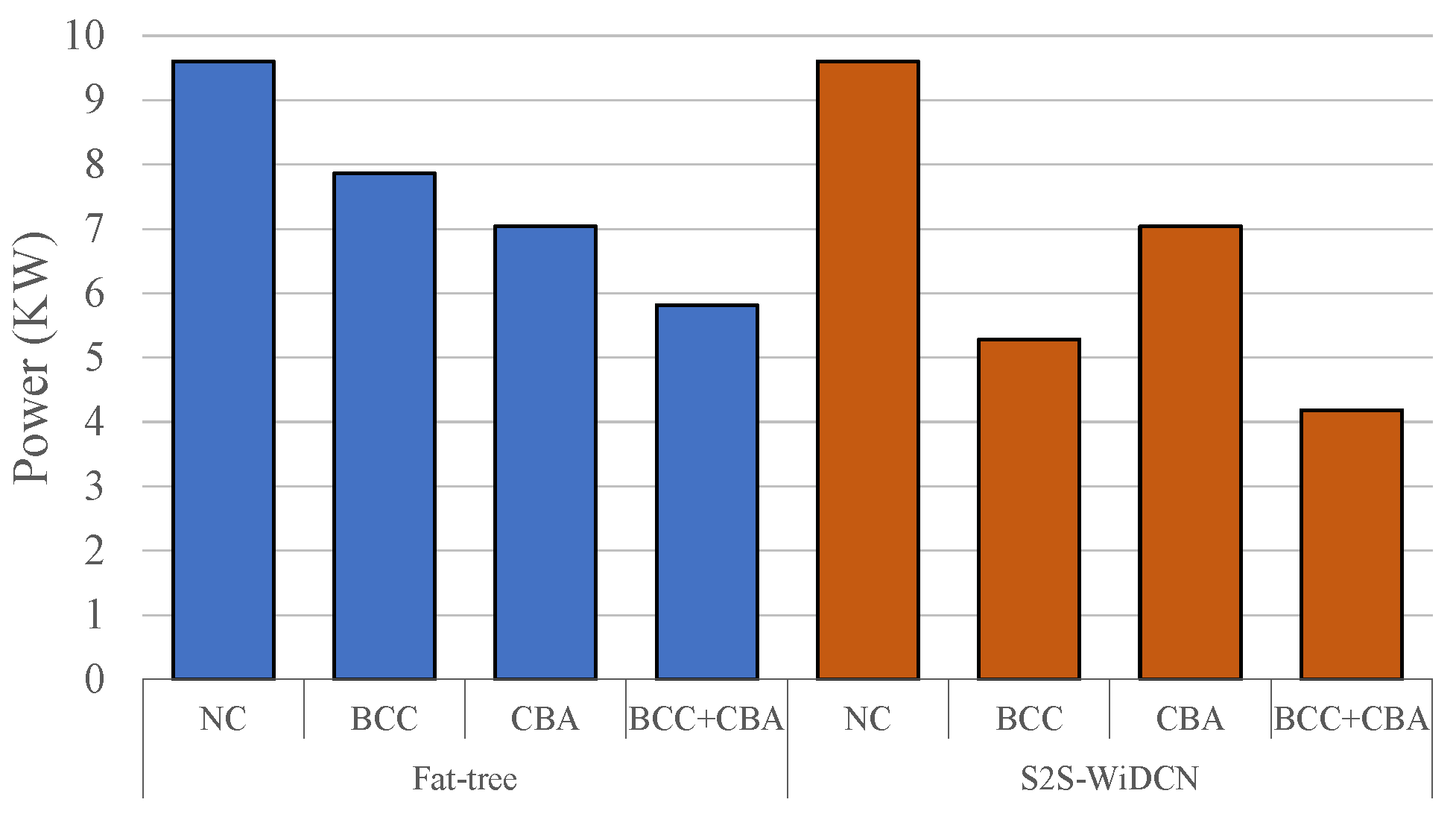
5.3. Overall Power Saving with a Combination of BCC and CBA
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rodero, I.; Jaramillo, J.; Quiroz, A.; Parashar, M.; Guim, F.; Poole, S. Energy-efficient application-aware online provisioning for virtualized clouds and data centers. In Proceedings of the International Green Computing Conference (IGCC), Chicago, IL, USA, 15–18 August 2010; pp. 31–45. [Google Scholar] [CrossRef]
- Benini, L.; Micheli, G.d. System-level power optimization: Techniques and tools. ACM Trans. Des. Autom. Electron. Syst. (Todaes) 2000, 5, 115–192. [Google Scholar] [CrossRef]
- Aksanli, B.; Rosing, T. Providing regulation services and managing data center peak power budgets. In Proceedings of the 2014 Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 24–28 March 2014; pp. 143–147. [Google Scholar]
- Bogdan, P.; Garg, S.; Ogras, U.Y. Energy-efficient computing from systems-on-chip to micro-server and data centers. In Proceedings of the 2015 Sixth International Green Computing Conference and Sustainable Computing Conference (IGSC), Las Vegas, NV, USA, 14–16 December 2015; pp. 1–6. [Google Scholar]
- Koomey, J. Growth in data center electricity use 2005 to 2010. In A Report by Analytical Press, Completed at the Request of The New York Times; Analytics Press: Burlingame, CA, USA, 2011. [Google Scholar]
- Verma, A.; Ahuja, P.; Neogi, A. pMapper: Power and migration cost aware application placement in virtualized systems. In Proceedings of the 9th ACM/IFIP/USENIX International Conference on Middleware, Leuven, Belgium, 1–5 December 2008; pp. 243–264. [Google Scholar]
- Jung, G.; Hiltunen, M.A.; Joshi, K.R.; Schlichting, R.D.; Pu, C. Mistral: Dynamically managing power, performance, and adaptation cost in cloud infrastructures. In Proceedings of the 2010 IEEE 30th International Conference on Distributed Computing Systems, Genova, Italy, 21–25 June 2010; pp. 62–73. [Google Scholar]
- Zu, Y.; Huang, T.; Zhu, Y. An efficient power-aware resource scheduling strategy in virtualized datacenters. In Proceedings of the IEEE 2013 International Conference on Parallel and Distributed Systems, Seoul, Korea, 15–18 December 2013; pp. 110–117. [Google Scholar]
- Mann, V.; Kumar, A.; Dutta, P.; Kalyanaraman, S. VMFlow: Leveraging VM mobility to reduce network power costs in data centers. In International Conference on Research in Networking; Springer: New York, NY, USA, 2011; pp. 198–211. [Google Scholar]
- Huang, D.; Yang, D.; Zhang, H.; Wu, L. Energy-aware virtual machine placement in data centers. In Proceedings of the 2012 IEEE Global Communications Conference (GLOBECOM), Anaheim, CA, USA, 3–7 December 2012; pp. 3243–3249. [Google Scholar]
- Cao, B.; Gao, X.; Chen, G.; Jin, Y. NICE: Network-aware VM consolidation scheme for energy conservation in data centers. In Proceedings of the 2014 20th IEEE International Conference on Parallel and Distributed Systems (ICPADS), Hsinchu, Taiwan, 16–19 December 2014; pp. 166–173. [Google Scholar]
- Ferreto, T.C.; Netto, M.A.; Calheiros, R.N.; De Rose, C.A. Server consolidation with migration control for virtualized data centers. Future Gener. Comput. Syst. 2011, 27, 1027–1034. [Google Scholar] [CrossRef]
- Sun, G.; Liao, D.; Zhao, D.; Xu, Z.; Yu, H. Live migration for multiple correlated virtual machines in cloud-based data centers. IEEE Trans. Serv. Comput. 2015, 11, 279–291. [Google Scholar] [CrossRef]
- Kliazovich, D.; Bouvry, P.; Khan, S.U. DENS: Data center energy-efficient network-aware scheduling. Clust. Comput. 2013, 16, 65–75. [Google Scholar] [CrossRef]
- Khemka, B.; Friese, R.; Pasricha, S.; Maciejewski, A.A.; Siegel, H.J.; Koenig, G.A.; Powers, S.; Hilton, M.; Rambharos, R.; Poole, S. Utility maximizing dynamic resource management in an oversubscribed energy-constrained heterogeneous computing system. Sustain. Comput. Inform. Syst. 2015, 5, 14–30. [Google Scholar] [CrossRef]
- Kim, S.; Kim, Y. Application-specific cloud provisioning model using job profiles analysis. In Proceedings of the 2012 IEEE 14th International Conference on High Performance Computing and Communication & 2012 IEEE 9th International Conference on Embedded Software and Systems (HPCC-ICESS), Liverpool, UK, 25–27 June 2012; pp. 360–366. [Google Scholar]
- Singh, A.K.; Dziurzanski, P.; Indrusiak, L.S. Value and energy optimizing dynamic resource allocation in many-core HPC systems. In Proceedings of the 2015 IEEE 7th International Conference on Cloud Computing Technology and Science (CloudCom), Vancouver, BC, Canada, 30 November–3 December 2015; pp. 180–185. [Google Scholar]
- Baccour, E.; Foufou, S.; Hamila, R.; Hamdi, M. A survey of wireless data center networks. In Proceedings of the 2015 49th Annual Conference on Information Sciences and Systems (CISS), Vancouver, BC, Canada, 30 November–3 December 2015; pp. 1–6. [Google Scholar]
- Vardhan, H.; Ryu, S.R.; Banerjee, B.; Prakash, R. 60 GHz wireless links in data center networks. Comput. Netw. 2014, 58, 192–205. [Google Scholar] [CrossRef]
- Halperin, D.; Kandula, S.; Padhye, J.; Bahl, P.; Wetherall, D. Augmenting data center networks with multi-gigabit wireless links. ACM Sigcomm Comput. Commun. Rev. 2011, 41, 38–49. [Google Scholar] [CrossRef]
- Zaaimia, M.; Touhami, R.; Fono, V.; Talbi, L.; Nedil, M. 60 GHz wireless data center channel measurements: Initial results. In Proceedings of the 2014 IEEE International Conference on Ultra-WideBand (ICUWB), Paris, France, 1–3 September 2014; pp. 57–61. [Google Scholar]
- Mamun, S.A.; Umamaheswaran, S.G.; Chandrasekaran, S.S.; Shamim, M.S.; Ganguly, A.; Kwon, M. An Energy-Efficient, Wireless Top-of-Rack to Top-of-Rack Datacenter Network Using 60 GHz Links. In Proceedings of the 2017 IEEE Green Computing and Communications (GreenCom), Exeter, UK, 21–23 June 2017; pp. 458–465. [Google Scholar]
- Cheng, C.L.; Zajić, A. Characterization of 300 GHz Wireless Channels for Rack-to-Rack Communications in Data Centers. In Proceedings of the 2018 IEEE 29th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Bologna, Italy, 9–12 September 2018; pp. 194–198. [Google Scholar]
- Shin, J.Y.; Kirovski, D.; Harper, D.T., III. Data Center Using Wireless Communication. U.S. Patent 9,391,716, 12 July 2016. [Google Scholar]
- Mamun, S.A.; Umamaheswaran, S.G.; Ganguly, A.; Kwon, M.; Kwasinski, A. Performance Evaluation of a Power-Efficient and Robust 60 GHz Wireless Server-to-Server Datacenter Network. IEEE Trans. Green Commun. Netw. 2018, 2, 1174–1185. [Google Scholar] [CrossRef]
- Auer, P. Using confidence bounds for exploitation-exploration trade-offs. J. Mach. Learn. Res. 2002, 3, 397–422. [Google Scholar]
- Yeo, C.S.; Buyya, R. A Taxonomy of Market-based Resource Management Systems for Utility-driven Cluster Computing. Softw. Pract. Exp. 2006, 36, 1381–1419. [Google Scholar] [CrossRef]
- Theocharides, T.; Michael, M.K.; Polycarpou, M.; Dingankar, A. Hardware-enabled Dynamic Resource Allocation for Manycore Systems Using Bidding-based System Feedback. EURASIP J. Embed. Syst. 2010, 2010, 261434. [Google Scholar] [CrossRef]
- Locke, C.D. Best-Effort Decision-Making for Real-Time Scheduling. Ph.D. Thesis, Carnegie Mellon University, Pittsburgh, PA, USA, 1986. [Google Scholar]
- Aldarmi, S.; Burns, A. Dynamic value-density for scheduling real-time systems. In Proceedings of the Euromicro Conference on Real-Time Systems, York, UK, 9–11 June 1999; pp. 270–277. [Google Scholar]
- Bansal, N.; Pruhs, K.R. Server Scheduling to Balance Priorities, Fairness, and Average Quality of Service. SIAM J. Comput. 2010, 39, 3311–3335. [Google Scholar] [CrossRef]
- Hussin, M.; Lee, Y.C.; Zomaya, A.Y. Efficient energy management using adaptive reinforcement learning-based scheduling in large-scale distributed systems. In Proceedings of the 2011 International Conference on Parallel Processing, Taipei, Taiwan, 13–16 September 2011; pp. 385–393. [Google Scholar]
- Lin, X.; Wang, Y.; Pedram, M. A reinforcement learning-based power management framework for green computing data centers. In Proceedings of the 2016 IEEE International Conference on Cloud Engineering (IC2E), Berlin, Germany, 4–8 April 2016; pp. 135–138. [Google Scholar]
- Singh, A.K.; Dziurzanski, P.; Indrusiak, L.S. Value and energy aware adaptive resource allocation of soft real-time jobs on many-core HPC data centers. In Proceedings of the 2016 IEEE 19th International Symposium on Real-Time Distributed Computing (ISORC), York, UK, 17–20 May 2016; pp. 190–197. [Google Scholar]
- Sun, X.; Ansari, N.; Wang, R. Optimizing resource utilization of a data center. IEEE Commun. Surv. Tutor. 2016, 18, 2822–2846. [Google Scholar] [CrossRef]
- Ray, M.; Sondur, S.; Biswas, J.; Pal, A.; Kant, K. Opportunistic power savings with coordinated control in data center networks. In Proceedings of the 19th International Conference on Distributed Computing and Networking, Varanasi, India, 4–7 January 2018; p. 48. [Google Scholar]
- Farrington, N.; Porter, G.; Radhakrishnan, S.; Bazzaz, H.H.; Subramanya, V.; Fainman, Y.; Papen, G.; Vahdat, A. Helios: A hybrid electrical/optical switch architecture for modular data centers. ACM SIGCOMM Comput. Commun. Rev. 2011, 41, 339–350. [Google Scholar]
- Calheiros, R.N.; Buyya, R. Energy-Efficient Scheduling of Urgent Bag-of-Tasks Applications in Clouds Through DVFS. In Proceedings of the IEEE International Conference on Cloud Computing Technology and Science (CLOUDCOM), Singapore, 15–18 December 2014; pp. 342–349. [Google Scholar]
- Irwin, D.E.; Grit, L.E.; Chase, J.S. Balancing Risk and Reward in a Market-Based Task Service. In Proceedings of the IEEE International Symposium on High Performance Distributed Computing (HPDC), Honolulu, HI, USA, 4–6 June 2004; pp. 160–169. [Google Scholar]
- Bubeck, S.; Cesa-Bianchi, N. Regret analysis of stochastic and nonstochastic multi-armed bandit problems. Found. Trends Mach. Learn. 2012, 5, 1–122. [Google Scholar] [CrossRef]
- Carpentier, A.; Lazaric, A.; Ghavamzadeh, M.; Munos, R.; Auer, P. Upper-confidence-bound algorithms for active learning in multi-armed bandits. In International Conference on Algorithmic Learning Theory; Springer: New York, NY, USA, 2011; pp. 189–203. [Google Scholar]
- Han, Y.; Yoo, J.H.; Hong, J.W.K. Poisson shot-noise process based flow-level traffic matrix generation for data center networks. In Proceedings of the 2015 IFIP/IEEE International Symposium on Integrated Network Management (IM), Ottawa, ON, Canada, 11–15 May 2015; pp. 450–457. [Google Scholar]
- Benson, T.; Akella, A.; Maltz, D.A. Network traffic characteristics of data centers in the wild. In Proceedings of the 10th ACM SIGCOMM Conference on Internet Measurement, Melbourne, Australia, 1–3 November 2010; pp. 267–280. [Google Scholar]
- Dutt, S. New faster kernighan-lin-type graph-partitioning algorithms. In Proceedings of the 1993 International Conference on Computer Aided Design (ICCAD), Santa Clara, CA, USA, 7–11 November 1993; pp. 370–377. [Google Scholar]
- Meisner, D.; Gold, B.T.; Wenisch, T.F. PowerNap: Eliminating server idle power. ACM SIGARCH Comput. Archit. News 2009, 44, 205–216. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, F.R.; Wang, S.; Huang, T.; Liu, Z.; Liu, Y. Load Balancing in Data Center Networks: A Survey. IEEE Commun. Surv. Tutor. 2018, 20, 2324–2352. [Google Scholar] [CrossRef]
- Davidson, A.; Tarjan, D.; Garland, M.; Owens, J.D. Efficient parallel merge sort for fixed and variable length keys. In Proceedings of the 2012 Innovative Parallel Computing (InPar), San Jose, CA, USA, 13–14 May 2012; pp. 1–9. [Google Scholar]
- Kleinrock, L. Queueing Systems, Volume 2: Computer Applications; Wiley: New York, NY, USA, 1976. [Google Scholar]
- ns-3 Network Simuilator. Available online: https://www.nsnam.org/ (accessed on 4 July 2019).
- Shehabi, A.; Smith, S.J.; Sartor, D.A.; Brown, R.E.; Herrlin, M.; Koomey, J.G.; Masanet, E.R.; Horner, N.; Azevedo, I.L.; Lintner, W. United States Data Center Energy Usage Report; Technical Report LBNL-1005775; LBNL: Berkeley, CA, USA, 2016.
- Pelley, S.; Meisner, D.; Wenisch, T.F.; VanGilder, J.W. Understanding and abstracting total data center power. In Proceedings of the 2009 Workshop on Energy Efficient Design (WEED), Ann Arbor, MI, USA, 20 June 2009. [Google Scholar]
- SPECpower_ssj2008. Results for Dell Inc. PowerEdge C5220. Available online: https://www.spec.org/power_ssj2008/results/res2013q2/power_ssj2008-20130402-00601.html (accessed on 4 July 2019).
- Heller, B.; Seetharaman, S.; Mahadevan, P.; Yiakoumis, Y.; Sharma, P.; Banerjee, S.; McKeown, N. Elastictree: Saving Energy in Data Center Networks. In Proceedings of the 7th USENIX Conference on Networked Systems Design and Implementation (NSDI), San Jose, CA, USA, 28–30 April 2010; pp. 249–264. [Google Scholar]
- Cisco. Cisco Data Center Switches. Available online: https://www.cisco.com/c/en/us/products/switches/data-center-switches/index.html (accessed on 4 July 2019).
- Silicom. Silicom PE2G2I35 Datasheet. Available online: http://www.silicom-usa.com/wp-content/uploads/2016/08/PE2G2I35-1G-Server-Adapter.pdf (accessed on 4 July 2019).
- Analog Devices. Analog Devices HMC6300 and HMC6301 60 GHz Millimeter Wave Transmitter and Receiver Datasheet. Available online: http://www.analog.com/media/en/technical-documentation/data-sheets/HMC6300.pdf (accessed on 4 July 2019).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
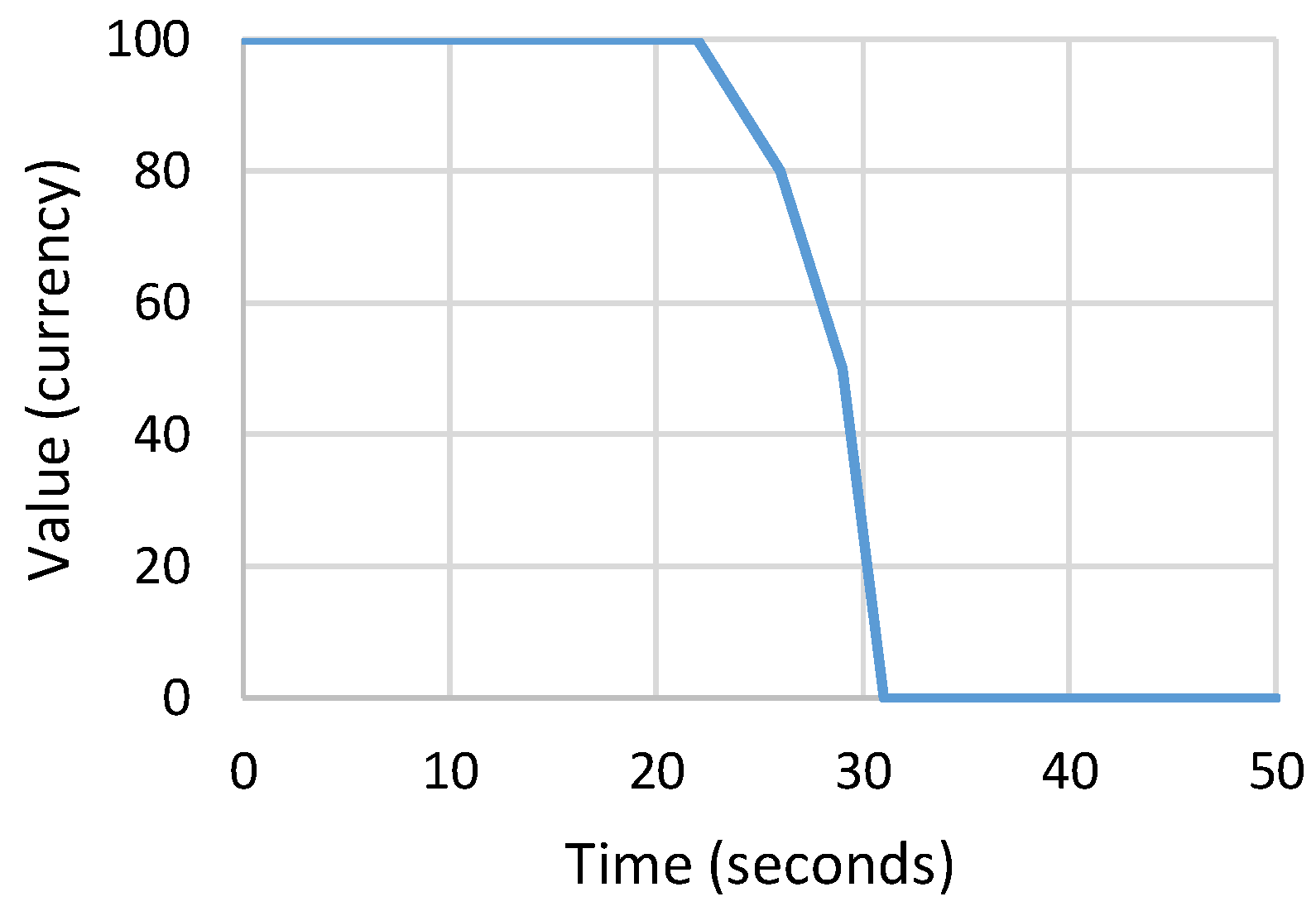
| Application | Execution Time (s) | Value (Currency) | ||||||
|---|---|---|---|---|---|---|---|---|
| blackscholes | 4 | 6 | 9 | 12 | 100 | 80 | 50 | 0 |
| bodytrack | 6 | 8 | 11 | 14 | 100 | 80 | 50 | 0 |
| dedup | 5 | 7 | 9 | 12 | 100 | 80 | 50 | 0 |
| facesim | 8 | 15 | 18 | 22 | 100 | 80 | 50 | 0 |
| ferret | 22 | 26 | 29 | 31 | 100 | 80 | 50 | 0 |
| fluidanimate | 7 | 9 | 11 | 14 | 100 | 80 | 50 | 0 |
| freqmine | 9 | 15 | 17 | 20 | 100 | 80 | 50 | 0 |
| streamcluster | 22 | 28 | 35 | 42 | 100 | 80 | 50 | 0 |
| vips | 9 | 11 | 13 | 16 | 100 | 80 | 50 | 0 |
| Device | Model | Used in | Power (W) |
|---|---|---|---|
| Access Layer Switch | Cisco 9372 | Fat-Tree | 210.0 |
| Aggregate Layer Switch | Cisco 9508 | Fat-Tree | 2527.0 |
| Core Layer Switch | Cisco 7702 | Fat-Tree, S2S-WiDCN | 837.0 |
| Network Interface Card | Silicom PE2G2I35 | Fat-Tree, S2S-WiDCN | 2.64 |
| 60 GHz Transceiver | Analog Device HMC 6300/6301 | S2S-WiDCN | 1.70 |
| IEEE802.11 2.4/5 GHz Adapter | D-link DWA-171 | S2S-WiDCN | 0.22 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mamun, S.A.; Gilday, A.; Singh, A.K.; Ganguly, A.; Merrett, G.V.; Wang, X.; Al-Hashimi, B.M. Intra- and Inter-Server Smart Task Scheduling for Profit and Energy Optimization of HPC Data Centers. J. Low Power Electron. Appl. 2020, 10, 32. https://doi.org/10.3390/jlpea10040032
Mamun SA, Gilday A, Singh AK, Ganguly A, Merrett GV, Wang X, Al-Hashimi BM. Intra- and Inter-Server Smart Task Scheduling for Profit and Energy Optimization of HPC Data Centers. Journal of Low Power Electronics and Applications. 2020; 10(4):32. https://doi.org/10.3390/jlpea10040032
Chicago/Turabian StyleMamun, Sayed Ashraf, Alexander Gilday, Amit Kumar Singh, Amlan Ganguly, Geoff V. Merrett, Xiaohang Wang, and Bashir M. Al-Hashimi. 2020. "Intra- and Inter-Server Smart Task Scheduling for Profit and Energy Optimization of HPC Data Centers" Journal of Low Power Electronics and Applications 10, no. 4: 32. https://doi.org/10.3390/jlpea10040032
APA StyleMamun, S. A., Gilday, A., Singh, A. K., Ganguly, A., Merrett, G. V., Wang, X., & Al-Hashimi, B. M. (2020). Intra- and Inter-Server Smart Task Scheduling for Profit and Energy Optimization of HPC Data Centers. Journal of Low Power Electronics and Applications, 10(4), 32. https://doi.org/10.3390/jlpea10040032








