Abstract
AI evolution is accelerating and Deep Neural Network (DNN) inference accelerators are at the forefront of ad hoc architectures that are evolving to support the immense throughput required for AI computation. However, much more energy efficient design paradigms are inevitable to realize the complete potential of AI evolution and curtail energy consumption. The Near-Threshold Computing (NTC) design paradigm can serve as the best candidate for providing the required energy efficiency. However, NTC operation is plagued with ample performance and reliability concerns arising from the timing errors. In this paper, we dive deep into DNN architecture to uncover some unique challenges and opportunities for operation in the NTC paradigm. By performing rigorous simulations in TPU systolic array, we reveal the severity of timing errors and its impact on inference accuracy at NTC. We analyze various attributes—such as data–delay relationship, delay disparity within arithmetic units, utilization pattern, hardware homogeneity, workload characteristics—and uncover unique localized and global techniques to deal with the timing errors in NTC.
1. Introduction
The proliferation of artificial intelligence (AI) is predicted to contribute up to $15.7 trillion to the global economy by 2030 [1]. To accommodate the AI evolution, the computing industry has already shifted gears to the use of specialized domain-specific AI accelerators along with major improvements in cost, energy and performance. Conventional CPUs and GPUs are no longer able to match up the required throughput and they incur wasteful power consumption through their Von-Neumann bottlenecks [2,3,4,5,6]. However, the upsurge in AI is bound to cater to a huge rise in energy consumption to facilitate power requirements throughout the wide spectrum of AI processing in the cloud data centers to smart edge devices. Andrae et al. have projected that 3–13% of global electricity in 2030 will be used by datacenters [7]. We need to develop energy efficient solutions to drag down this global consumption as low as possible to facilitate the rapid rise in AI compute infrastructure. Moreover, the AI services are propagating deeper into the edge and Internet of Things (IoT) paradigms. Edge AI architectures have several advantages, such as low latency, high privacy, more robustness and efficient use of network bandwidth, which can be useful in diverse applications, such as robotics, mobile devices, smart transportation, healthcare service, wearables, smart speakers, biometric security and so on. The penetration towards the edge will, however, be hit by walls of energy efficiency, as the availability of power from the grid will be replaced by limited power from smaller batteries. In addition, the collective power consumption from the edge and IoT devices will increase drastically. Hence, ultra low power paradigms for AI compute infrastructure, both at server and edge, are inevitable for realizing the complete potential of AI evolution.
Near-threshold computing (NTC) has been a promising roadmap for quadratic energy savings in computing architectures, where the device is operated close to threshold voltage of transistors. Researchers have explored the application of NTC to the conventional CPU/GPU architectures [8,9,10,11,12,13,14,15,16]. One of the prominent use cases of NTC systems has been to improve the energy efficiency of the computing systems by quadratically reducing the energy consumption per functional unit and increasing the number of functional units (cores). The limit of the general purpose applications to be paralleled [17,18] in this use case has hindered the potential of NTC in CPU/GPU platforms. Deep Neural Network (DNN) accelerators are the representative inference architectures for AI compute infrastructure, which have larger and scalable basic functional units, such as Multiply and Accumulate (MAC) units, which can operate in parallel. Coupled with the highly parallel nature of the DNN workloads to operate on, DNN accelerators serve as excellent candidates for energy efficiency optimization through NTC operation. Substantial energy efficiency can be rendered to inference accelerators in the datacenters. Towards edge, the quadratic reduction in the energy consumption carries the potential to curtail the collective energy demands of the edge devices and makes many compute intensive AI services feasible and practical. Secure and accurate on-device DNN computations can be enabled for AI services, such as face/voice recognition, biometric scanning, object detection, patient monitoring, short term weather prediction and so on at the closest proximity of hardware, physical sensors and body area networks. Entire new classes of edge AI applications delve further into the edge, which are limited by the power consumption from being battery operated and can be enabled by adaptation of NTC.
NTC operation in DNN accelerators is also plagued with almost all the reliability and performance issues as experienced by the conventional architectures. NTC operation is prone to a very high sensitivity to process and environmental variations, resulting in excessive increase in delay and delay variation [14]. This slows down the performance and induces high rate of timing errors in the DNN accelerator. The prevalence, detection and handling of timing error, and its manifestation on the inference accuracy are very challenging for DNN accelerators in comparison to conventional architectures. The unique challenges come from the unique nature of DNN algorithms operating in the complex interleaving among its very large number of dataflow pipelines. Amidst these challenges, the homogeneous repetition of the basic functional units throughout the architecture also bestows unique opportunities to deal with the timing errors. Innovation in the timing properties of a single MAC unit is scalable towards providing a system-wide timing resilience. We observe that very few input combinations to an MAC unit sensitize the delays close to the maximum delay. This provides us with the predictive opportunity where we can predict the bad input combinations and deal with them differently. We also establish the statistical disparity in the timing properties of the multiplier and accumulator inside a MAC unit and uncover unique opportunities to correct a timing error in a timing window derived from the disparity. Through the study of the utilization pattern of MAC units, we present opportunities for fine tuning the timing resilience approaches.
We introduce the basic architecture of DNN in Section 2 with the help of Google’s DNN accelerator, Tensor Processing Unit (TPU). We uncover the challenges of NTC DNN accelerators around the performance and timing errors in Section 3. We propose the opportunities in NTC DNN accelerators to deal with the timing errors in Section 4, by delving deep into the architectural attributes, such as utilization pattern, hardware homogeneity, sensitization delay profile and DNN workload characteristics. The quantitative illustrations of the challenges and opportunities are done using the methodology described in Section 5. Section 6 surveys the notable works in the literature close to the domain of NTC DNN accelerators. Finally, Section 7 concludes the paper.
2. Background
DNN inference involves repeated matrix multiplication operation with its input (activation) data and pre-trained weights. Conventional general purpose architectures have a limited number of processing elements (cores) to handle the unconventionally large stream of data. Additionally, the Von-Neumann design paradigm forces to have repeated sluggish and power-hungry memory accesses. DNN accelerators aim for better performance in terms of cost, energy and throughput with respect to conventional computing. DNN workload, although very large, can be highly parallel which opens up possibilities for increasing throughput by feeding data parallel to an array of simple Processing Elements (PE). The memory bottlenecks are relaxed by mixture of different techniques, such as keeping the memory close to the PEs, computing in-memory, architecting dataflow for bulk memory access, using advanced memory, data quantization and so on. DNN accelerators utilize the deterministic algorithmic properties of the DNN workload and embrace maximum reuse of the data through a combination of different dataflow schemes, such as Weight Stationary (WS), Output Stationary (OS), No Local Reuse (NLR), and Row Stationary (RS) [6].
WS dataflow is adapted in most of the DNN accelerators to minimize the memory accesses to the main memory by adding a memory element near/on PEs for storing the weights [19,20,21,22]. OS dataflow minimizes the reading and writing of the partial sums to/from main memory, by streaming the activation inputs from neighboring PEs, such as in Shidiannao [22,23]. DianNao [24] follows NLR dataflow, which reads input activations and weights from a global buffer, and processes them through PEs with custom adder trees that can complete the accumulation in a single cycle, and the resulting partial sums or output activations are then put back into the global buffer. Eyeriss [19] embraces an RS dataflow, which maximizes the reuse for all types of data, such as activation, weight and partial sums. Advanced memory wise, DianNao uses advanced eDRAM, which provides higher bandwidth and access speed than DRAMs. TPU [22] uses about 28MiB of on-chip SRAM. There are DNN accelerators which bring computation in the memory. The authors in [25] map the MAC operation to SRAM cells directly. ISAAC [26] PRIME [27], and Pipelayer [28] compute dot product operation using an array of memristors. Several architectures ranging from digital to analog and mixed signal implementations are being commercially deployed in the industry to support the upsurging AI-based economy [22,29,30,31]. Next, we take an example architecture of the leading edge DNN Accelerator, Tensor Processing Unit (TPU) by Google to better understand the internals of a DNN accelerator compute engine. TPU architecture, already being a successful industrial scale accelerator, has also put its prevalence at the edge through edge TPU [32,33]. We will use this architecture to methodologically explore different challenges and opportunities in an NTC DNN accelerator.
The usage of the systolic array of MAC units, has been recognized as a promising direction to accelerate matrix multiplication operation. TPU employs a 256 × 256 systolic array of specialized Multiply and Accumulate (MAC) units, as shown in Figure 1 [22]. These MACs, in unison with parallel operation, multiply the 8-bit integer precision weight matrix with the activation (also referred to as input) matrix. Rather than storing to and fetching from the memory for each step of matrix multiplication, the activations stream from a fast SRAM-based activation memory, reaching each column at successive clock cycles. Weights are pre-loaded into the MACs from the weight FIFO ensuring their reuse over a matrix multiplication lifecycle. The partial sums from the rows of MACs move downstream to end up at output accumulator as the result of the matrix multiplication. As a consequence, the Von-Neumann bottlenecks related to memory access are cut down. The ability of the addition of hardware elements to compute the repeating operations not only enables higher data parallelism, but also enables the scaling of the architecture from server to edge applications. This architectural configuration allows TPU to achieve 15–30 X throughput improvement and 30–80 X energy efficiency improvement over the conventional CPU/GPU implementations.
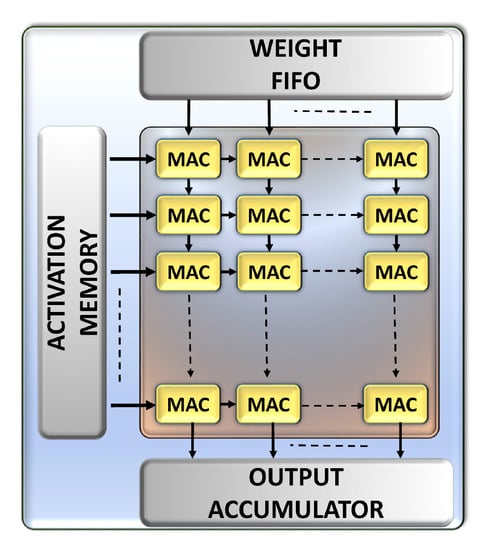
Figure 1.
TPU Systolic Array.
3. Challenges for NTC DNN Accelerators
This Section uncovers different challenges in the NTC operation of DNN accelerators. Section 3.1 demonstrates the occurrence of timing errors and their manifestations on the inference accuracy. Section 3.2 presents the challenges in the detection and handling of timing errors in high performance environment essential for a high throughput NTC system.
3.1. Unique Performance Challenge
Even though NTC circuits give a quadratic decrease in energy consumption, they are plagued with severe loss in performance. The loss is general to all the computing architectures as it fundamentally comes from delay experienced by transistors and basic gates. As shown in Figure 2a, basic gates, such as Inverter, Nand and Nor, can experience a delay more than 10×, when operating at near threshold voltages. The gates are simulated in HSPICE for a constant temperature of 25 C, for more than 10,000 Monte-Carlo iterations. On top of the increase in base delay, the extreme sensitivity of NTC circuits with temperature and circuit noise results in a delay variation of up to 5× [14]. This level of delay increase and delay variability forces the computing architectures to operate in a very relaxed frequency, to ensure the correctness in computation. An attempt to upscale the frequency introduces timing errors. To add to it, the behavior of timing errors is more challenging in DNN accelerators, than conventional CPU/GPU architectures.
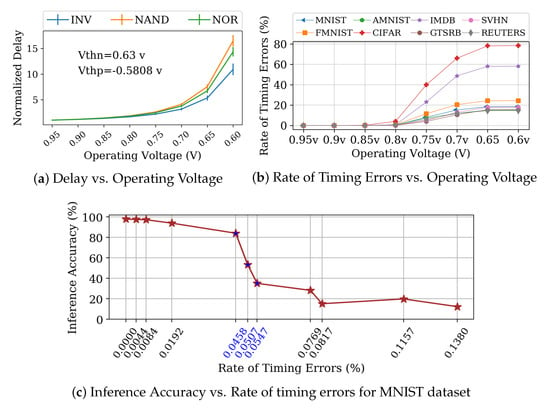
Figure 2.
(a) shows the increase in base delay with the decrease in operating voltage, (b) demonstrates the increase in the rate of timing errors with the decrease in operating voltage and (c) shows the effect of timing errors in inference accuracy. (Detailed methodology in Section 5).
In Figure 2b, we plot the rate of timing errors in the inference computations in a TPU of eight DNN datasets using the methodology described in Section 5. As there can be computations happening in all the MAC units in parallel, crossing a delay threshold brings a huge number of timing errors at once. The rate of the timing errors is different for different datasets due to its dependence on the number of actual operations which actually sensitize the delays. As DNN workload consists of several clusters of identical values, (usually zero [2]), DNN workloads tend to decrease the overall sensitization of hardware delays. The curves tend to flatten towards the end as almost all delay sensitizing operations are saturated as timing errors at prior voltages.
Inference Accuracy is the measure of the quality of the DNN applications. In Figure 2c, we show the drop in inference accuracy of MNIST dataset from 98%. We conservatively model the consequence of timing error as the flip of the correct bit with 50% probability in the MAC unit’s output. DNN workloads have an inherent algorithmic tolerance to error until a threshold [34,35]. In line with the tolerance, we see that the accuracy variation is maintained under 5% until the rate of timing errors is 0.02%. However, after the error tolerance exceeds this, the accuracy falls very rapidly with a landslide effect. By virtue of the complex interconnected pipelining of the operations, the timing error induced incorrect computations add up rapidly as errant partial sums spread over most parts of the array, towards a bad accuracy. After about 0.045% of timing errors, the accuracy rapidly drops from 84% to a totally unusable inference accuracy of 35% on the timing error difference window of just 0.009% (highlighted in blue color).
This points to a completely impotent DNN accelerator at only a timing error rate of less than 0.06%. This treacherous response of timing errors to inference accuracy in DNN accelerators is magnified at NTC. It further compels the NTC operation to consider all the process, aging and environmental extremes just to prevent a minuscule (<<0.1%), yet catastrophic rate of timing errors, resulting in extremely sluggish accelerators. This creates further distancing in the adaptation of NTC systems into mainstream server/edge applications. Hence, innovative and dynamic techniques to reliably identify and control timing errors are inevitable for NTC DNN accelerators.
3.2. Timing Error Detection and Handling
DNN accelerators have been introduced to offer a throughput, which is difficult to extract from conventional architectures for DNN workload. However, the substantial performance lag at NTC operation hinders the usefulness of NTC DNN accelerators in general. So, in order to embrace NTC design paradigm, the DNN accelerators have to be operated at very tight frequencies, with an expectation and detection of timing errors, followed by their appropriate handling. In this Section, we explore the challenges in the timing error detection and handling for NTC DNN accelerators in these high performance points through the lens of techniques available for conventional architectures.
Razor [36] is one of the most popular timing error detection mechanisms. It detects a timing error by augmenting a shadow flip-flop driven by a delayed clock, to each flip-flop in the design driven by a main clock. Figure 3 shows Razor’s mechanism through timing diagrams. A delayed clock can be obtained by a simple inversion of the main clock. Figure 3a depicts the efficient working conditions of a Razor flip-flop. Delayed transitioning of data2 results in data1 (erroneous data) being latched onto the output. However, shadow flip-flop detects a detained change in the computational output and alerts the system via an error signal, generated by the comparison of prompt and delayed output. The frequency scaling for very high performances decreases the clock period thereby, diminishing the timing error detection window or speculation window. Shrinking the speculation window, prevents detection of delayed transitions in the computational output and leads to a huge number of timing errors going undiscovered. Figure 3b depicts the late transition in the Razor Input during the second half of the Cycle 1. Since the transition occurs after the rising edge of delayed clock, the data manifestation goes undetected by the shadow flip-flop resulting in an undiscoverable timing error. Rapid transition from data2 to data3, and in-time sampling of data3 at the positive edge of clock during Cycle 2, ushers the complete withdrawal of data2 during Cycle 1 from the respective MAC computation. Hence, the undiscoverable timing error leads to the usage of data1 (erroneous data) during Cycle 1, in place of the data2 (authentic data). Figure 3c demonstrates a delayed transition from data2 to data3, causing data3 to miss the sampling point (positive edge of the clock in Cycle 2). Shadow flip-flop appropriately procures the delayed data (i.e., data3), spawning an architectural replay and delivering data3 to Razor output during the next operational clock cycle (i.e., Cycle 3). However, authentic data (i.e., data2) to be used for MAC computation during Cycle 1, is again ceded from the appropriate MAC’s computation. Erroneous values (i.e., data1) used during Cycle 1, render to an erroneous input being used in MAC calculations, generating faulty output. Hence, the undiscoverable timing error again leads to an erroneous computation.
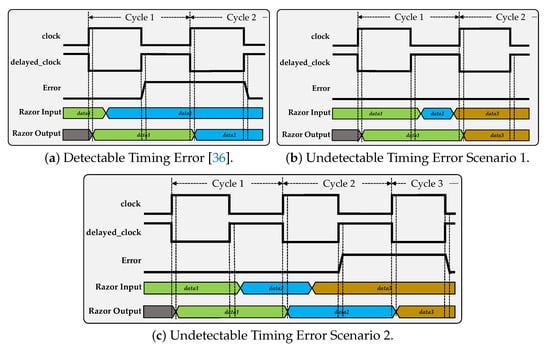
Figure 3.
(a) depicts Razor’s timing error handling effectiveness in a TPU Systolic Array during a standard detectable timing error occurrence scenario. (b,c) demonstrate the Razor’s limitations in handling undetectable timing errors arising at high performance scaling. In (c), even though data2 is sampled at Cycle 2, architectural replay invoked due to late transition and detection of data3 ensues the relinquishing of data2, entirely.
Figure 4 depicts the undiscoverable timing errors as a percentage composition of the total timing errors at various performance scaling, for different datasets. The composition of undiscoverable timing errors rises linearly until 1.7× the baseline performance. However, with the further increase in performance, the percentage of undiscoverable timing errors grows exponentially, following along with the landslide effect contributed by a large number of parallel operating MACs. This exponential composition of the undetectable timing errors points towards a hard wall of impracticality for razor-based timing error detection approaches.
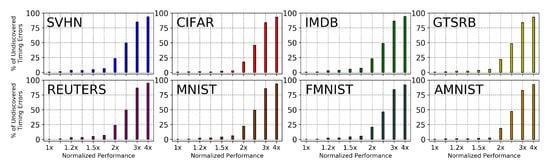
Figure 4.
Rate of undiscovered timing errors vs. Performance Scaling.
For handling of timing errors, the architectural replay of the errant computation has been a feasible and preferred way in the conventional general purpose architectures by virtue of their handful of computation pipelines [36,37]. However, the DNN accelerator involves hundreds of parallel computation pipelines and complex and coordinated interleaved dependencies among each other, which in the worst case, forces the sacrifice of computation in all the MACs for correcting just one timing error. For instance, a timing error rate of just 0.02% (starting point of accuracy fall in Figure 2c) for the matrix multiplication of a 256 × 256 activation and weight matrices in a 256 × 256 (N = 256) TPU systolic array, introduce ~3355 timing errors. Distributing the errors to the multiplication life cycle of 766 (3N-2) clock cycles creates approximately four errors per clock cycle. Even with a conservative estimate with a global sacrifice of only one relaxed clock cycle for all the errors per cycle, we get a throughput loss of more than 100%. Scaling to the inflated hardware size at the NTC design paradigm, the throughput coming from a DNN accelerator will be severely undermined by holistic stalling sacrifice of the MAC computations.
Fine tuned distributed techniques with pipelined error detection and handling [37,38] also incur larger overheads than conventional razor-based detecting and handling [35]. A technique designed exclusively for DNN accelerators, TE-Drop [35], skips an errant computation rather than replaying it by exploiting the inherent error resilience of DNN workload. However, the skipping is only triggered by a razor-based detection mechanism and thus can work for razor detectable errors only. With this comprehensive impracticality of the conventional detection and handling of timing errors for NTC performance needs, it calls for further research around the scalable solutions which can provide timing error resilience at vast magnitudes encompassing the entirety of functional units.
4. Opportunities for NTC DNN Accelerators
This Section reveals the unique opportunities for dealing with the timing errors in NTC DNN accelerators. Section 4.1 does an extensive analysis of the delay profile of the accelerators pointing towards predictive opportunities. Section 4.2 presents a novel opportunity of handling a timing error without performance loss. Section 4.3 uncovers the opportunity of an added layer of design intelligence derived from the utilization pattern of MACs in the DNN accelerators.
4.1. Predictive Opportunities
The DNN accelerator’s compute unit is comprised of homogeneously repeated simple functional units, such as MAC. In the case of TPU, the multiplier of the MAC unit operates on 8-bit activation and 8-bit weight. Delay is sensitized as a function of the change in these inputs to the multiplier. Weight is stagnant for a computation life cycle and the activations can be changed after each clock cycle. We create an exhaustive set of a 8-bit activation changed to another 8-bit activation for all possible 8-bit weights, leading to 256 × 256 × 256 = 16,777,216 unique combinations. Injecting these entries to our in-house Static Timing Analysis (STA) tool, we plot the exhaustive delay profile of the multiplier in Figure 5 as a histogram. We consider the maximum delay as one clock cycle period, to ensure an error free assessment. The histogram is divided into ten bars, each representing the percentage of the combinations falling into the ranges of clock cycles in the x-axis. We see that more than 95% of the sensitized delays fall in the range of 20–60% of the clock cycle and only about 3% of the exhaustive input sequences incur a delay of more than 60% of the clock period. As these limited sequences are the leading candidates to cause timing error in the NTC DNN accelerator, we see a huge opportunity for providing immense timing error resilience by massively curtailing the potential timing errors through their efficient prediction beforehand.
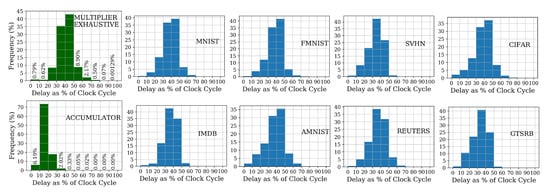
Figure 5.
Delay Profiles of multiplier, accumulator and different datasets.
As opposed to exhaustive prediction, the amount of prediction required for achieving timing error resilience is drastically reduced, while operating on real DNN workloads. Real DNN workloads will only have a subset of the exhaustive input combinations. Additionally, real DNN workloads consist of a large share of clustered, non-useful data in the computation, which can be skipped for computation. For instance, test images of MNIST and FMNIST datasets in Figure 6a,b visually show the abundant wasteful black regions in their 28 × 28 pixels of data, which can be quantized to zero. As the result of multiplication with zero is zero, we can skip the computation altogether by directly passing zero to the output. This technique has been well recognized by researchers to improve the energy efficiency of DNN accelerators, as Zero-Skip [2,19,39]. Figure 6c shows the percentage of the ZS computations in eight DNN datasets that can be transformed to have a close-to-zero sensitization delay. We see that, on average, the DNN datasets can have about ~75% of the ZS computations.
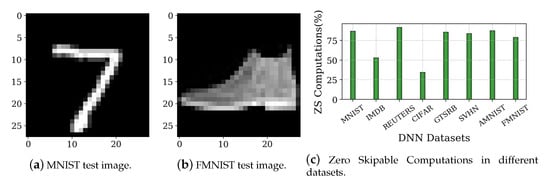
Figure 6.
Demonstration of the share of computations which can be safely skipped. The black region pixels in the MNIST and FMNIST test images can be quantized to zero and all the computations involving those pixels can be “zero skipped”.
This points to an opportunity of cutting down timing error, causing input combinations that have to be correctly predicted by ~75% in the best case. We plot the delay profile of the datasets for all the input sequences remaining after the massive reduction via ZS in Figure 5. It is evident that there is an ample delay variation across the datasets and the sensitization delays are clustered below 50% of the clock cycle. This further curtails the number of predictions required.
Hence, given that even a very small rate of timing error (<<0.1%) can cause a devastation in the inference accuracy (Section 2), the absolute feasibility of predictive approach to capture and deal with limited number of timing error causing input sequences in real DNN workloads serves as a boon. Moreover, prediction, along with ZS, provides unique opportunity for performance overscaling of NTC DNN accelerators to match STC performance. Even assuming that all the computations will incur a timing error at such environments, we would only have to predict only ~25% of the computations. We can employ NTC timing error resilience techniques, such as voltage boosting, for only the predicted bad input sequences and then scale it to larger TPU sizes. We have exploited this predictive opportunity and voltage boosting, to enable high performing NTC TPU in [40] with around less than 5% area and power overheads. Prediction can also be used in conjunction or on top of other timing error resilience schemes, such as TE-Drop [35], MATIC [41], FATE [42] and ARES [43], to yield better results. Extended research on the possibility of decreasing the amount of predictions on high performance scaling can be done with inspirations from algorithmic domains, layer wise delay analysis, and so on, to truly boost the adaptation of NTC DNN accelerators.
4.2. Opportunities from Novel Timing Error Handling
In this section, we discuss the opportunities in the handling of timing errors, bestowed by the unique architectural intricacies inside the MAC unit. We start by comparing the delay profiles of the arithmetic units, multiplier and accumulator, inside of the MAC unit. We prepare an exhaustive delay profile for multiplier as described in Section 4.1. As an exhaustive delay profile of accumulator is not feasible with its much larger input bit width (state space), we prepare its delay profile by using the outputs from multiplier fed with exhaustive inputs. From the delay histograms of the multiplier and accumulator in Figure 5, we see that accumulator operation statistically takes much less computation time than the multiplier. Over 97% of the accumulator sensitized delays fall within 30% of the clock cycle. Hence, an MAC operation temporally boils down as an expensive multiplier operation (Section 4.1) followed by a minuscule accumulator operation. This disparate timing characteristic in MAC’s arithmetic units, clubbed with the fixed order of operation, opens up a distinct timing error correction window to correct timing violations in a MAC unit, without any performance overhead.
Figure 7 shows a column-wise flow of computation using two MAC units. When MAC 1 encounters a timing error, the accumulator output (MAC 1 Out) provided by MAC 1 and the accumulator input (MAC 2 In) received by MAC 2 after data synchronization, will be an erroneous value. Although MAC 2 multiplier operation is unaffected by the faulty accumulator input, MAC 2 accumulator output (MAC 2 Out), will be corrupted due to the faulty input (MAC 2 In). While the MAC 2 accumulator is waiting for the completion of MAC 2 multiplier’s operation, the faulty input (MAC 2 In) can hypothetically use this extra time window to correct itself. Since the accumulator requires a statistically smaller computation period, the accumulation process with the corrected input can be completed within a given clock period, thereby preserving the throughput of the DNN accelerator. Next, we discuss a simple way of performing this time stealing in hardware through the intelligent remodeling of razor.
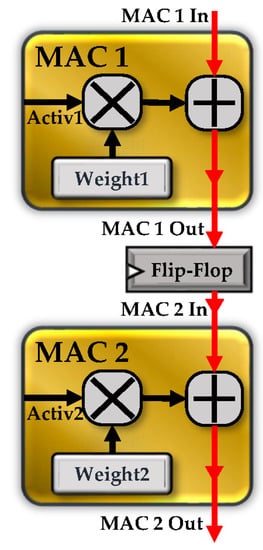
Figure 7.
Column-Wise MAC Operation.
Typical use of Razor in a Systolic Array incurs a huge performance overhead due to architectural replay when a timing error is detected (Section 3.2). However, a minimal modification in the Razor design aids in the exploitation of timing error correction window during Systolic Array operation. Figure 8a depicts the change employed in the razor which replays the errant computation [36] to ReModeled razor, which can propagate the authentic value to the downstream MAC without replaying or skipping the computation.
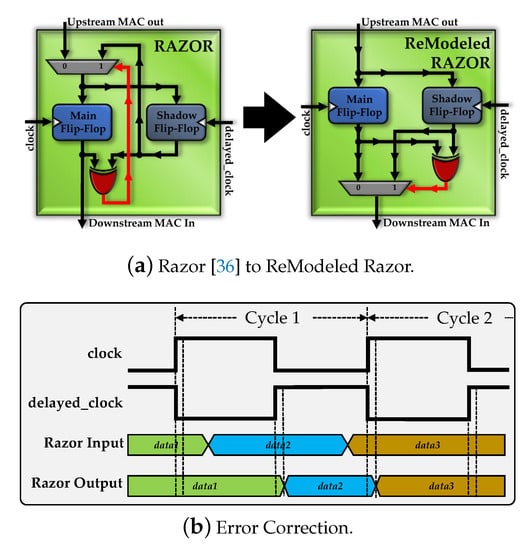
Figure 8.
(a) depicts the modifications employed in Razor to exploit the timing error correction window. (b) demonstrates the error correction process using Remodeled Razor scheme. The error is detected and corrected in the same clock cycle of operation.
Figure 8b depicts the error mitigation procedure using ReModeled Razor. In ReModeled razor, the timing error manifests as a different (correct) value from a shadow flip-flop, which overrides and propagates over the previous erroneous value passed through the main flip-flop. Since accumulation operation statistically requires much less than 50% of the clock cycle (Figure 5), the accumulator in the downstream MAC can quickly recompute with the correct value. The presence of ZS computations (Figure 6c) further aids the timing error correction window, as the skippable multiplier operations leave the accumulator to sensitize only to the upstream MAC’s output. Figure 9 demonstrates the RTL simulations for Razor/Remodeled Razor in the absence and presence of a timing error. Figure 9a depicts the standard waveform for a timing error free operation. Figure 9b shows an occurrence of a timing error due to a minor delay in the Razor input and the stretching of operational cycle to procure the correct value for the re-computation process. Figure 9c elaborates the detection and correction of the timing error, within the same clock cycle. Although, Razor adds buffers on short paths to avoid hold time violations, Zhang et al. [44] have modeled the additional buffers in timing simulations and determined that in a MAC unit only 14 out of 40 flip-flops requires a protection by Razor, which only adds a power penalty of 3.34%. The addition of ReModeled Razor into the Systolic Array adds an area overhead of only 5% into the TPU. In light of these findings, it is evident that we can extract novel opportunities to handle the timing errors at NTC by additional research on fine-tuning the combinational delays among the various arithmetic blocks inside the DNN accelerator. We have exploited this opportunistic timing error mitigation strategy in [45] to provide timing error resilience in a DNN systolic array.

Figure 9.
Timing simulations for error-free and error-handling scenarios.
4.3. Opportunities from Hardware Utilization Trend
Although DNN accelerators host very high number of functional units, not all of them are computationally active through out the computation lifecycle. We can leverage the hardware utilization pattern of the DNN accelerators to fine tune our architectural optimization strategies at NTC. In a TPU systolic array, activation is streamed to each row of MACs from left to right with a delay of one clock cycle per row. As the MACs can only operate on the presence of an activation input, a unique utilization pattern of the MAC units is formed. Visual illustration of the computation activity for a scaled down 3 × 3 systolic array during the multiplication of 3 × 3 activation and weight matrices is presented in Figure 10. Computationally active and idle MACs are represented by red and green, respectively. Figure 11a plots the computationally active MACs in every clock cycle as a fraction of the total MACs in the systolic array for the actual 256 × 256 array, for the multiplication of 256 × 256 weight and activation matrices, corresponding to a batch size of 256. The batch size dictates the amount of data available for continuous streaming, which consequently decides the computation cycles (width of the curve) and maximum usage (maximum height of the curve). Batch sizes are dependent and limited by the hardware resources to hold the activations and AI latency requirements. Regardless of the batch size, the utilization curve follows a static pattern where the activity peaks at the middle of the computation life cycle with a symmetrical rise and fall.

Figure 10.
Cycle accurate utilization pattern of the MAC units during the multiplication of 3 × 3 activation and weight matrices in a 3 × 3 systolic array.
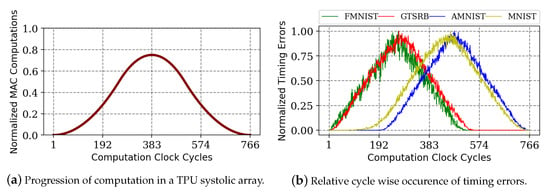
Figure 11.
The progression of number of MACs involved in computation guides the trend of timing error over the clock cycles for different datasets.
Timing errors are only encountered when the MACs are actively involved in the computation. This means that the intensity of timing errors in any clock cycle are always capped by the number of computationally active cycles in that cycle and the rate of occurrence of timing errors follow the trend of computation activity. We plot the cycle wise trend of timing errors in Figure 11b for four datasets. It is evident that the progression of timing errors is guided by the trend of compute activity. Any timing error handling schemes used for general purpose NTC paradigm can be further optimized for adaptation to DNN accelerators by leveraging this architectural behavior of timing errors. For instance, aggressive voltage boosting can be implemented at only the windows of maximum timing errors. Additionally, the timing error control schemes can be relaxed temporally at the windows of low probabilities of timing errors. In addition, predictive schemes can be tailored by adjusting the prediction windows according to these static timing error probabilities guided by hardware utilization pattern.
5. Methodology
In this Section, we explain our extensive cross-layer methodology, as depicted in Figure 12, to explore different challenges and opportunities of NTC DNN accelerators.
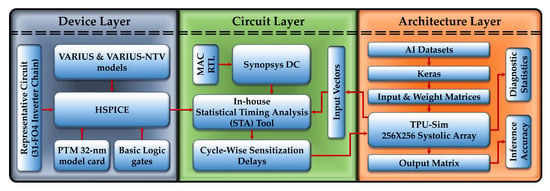
Figure 12.
Cross Layer Methodology.
5.1. Device Layer
We simulated basic logic gates (viz., Nand, Nor and Inverter) in HSPICE using basic CMOS 32-nm Predictive Technology Model libraries [46], across the spectrum of supply voltages. We used the 31-stage FO4 inverter chain as a representative of various combinational logics in a TPU for accurate estimation. We incorporated the impact of the PV at NTC using the VARIUS-NTV [47] model. The characteristics of the basic gates were mapped to the circuit layer (Section 5.2), to ascertain the sensitized path delays in a MAC at different voltages.
5.2. Circuit Layer
We developed the Verilog RTL description of MAC unit as the functional element of the systolic array. Our in-house Statistical Timing Analysis (STA) tool takes the synthesized netlist, input vectors for the netlist, and the timing properties of the logic gates. We synthesized the MAC RTL using the Synopsys Design Compiler and Synopsys’s generic 32 nm standard cell library, to get the synthesized netlist. The input vectors for the MAC units were the activation, weight and partial sum input, which came from the cycle accurate simulation described in Section 5.3. The changes in timing properties of the logic gates on different operating conditions came from the HSPICE simulation, described in Section 5.1. The STA tool propagated the path in the netlist which was sensitized by the given input vectors and calculated the delay coming from the logic gates in the path by mapping them to the delays from HSPICE. Hence, we got an accurate estimation of delay sensitized by any input change for a range of operating conditions. Our baseline NTC operating voltage and frequency were 0.45 v and 67 MHz.
5.3. Architecture Layer
Based on the architectural description detailed in [22], we developed a cycle-accurate TPU systolic array simulator—TPU-Sim—in C++, to represent a DNN accelerator. We integrated the STA tool (Section 5.2) with TPU-Sim, to accurately model timing errors in the MACs, based on real data-driven sensitized path delays. We created a real TPU-based inference eco-system by conjoining TPU-Sim with Keras [48] on Tensorflow backend. First, we train several DNN applications (viz., MNIST [49], Reuters [50], CIFAR-10 [51], IMDB [52], SVHN [53], GTSRB [54], FMNIST [55], FSDD [56]). Then, we extracted each layer’s activation as input matrices. We extract the trained model weights using Keras built-in functions. As the Keras trained model is at high floating point precision, we processed the inputs and weights into multiple 256 × 256 8-bit-integer matrices as TPU operates at 8-bit integer precision on a 256 × 256 systolic array. TPU-Sim is invoked with each pair of these TPU-quantized input and weight matrices. Each MAC operation in the TPU is mapped to a dedicated MAC unit in the TPU-Sim. The delay engine was invoked with each input vector arriving at the MAC to get the assessment of a timing error. The output matrices from the TPU-Sim were combined and compared with the original test output to evaluate the inference accuracy. We paralleled our framework for handling large amounts of test data using Python Multiprocessing.
6. Related Works
Several schemes have been proposed to increase the reliability and efficiency of neural network accelerators. Section 6.1, Section 6.2 and Section 6.3 provide brief accounts of enhancement methodologies which are categorized based on the emphasis on the architectural/design components.
6.1. Enhancements around Memory
In this Section, we enlist methodologies which target memory to provide improved performance. Kim et al. [57] demonstrate that a significant accuracy loss is caused by certain bits during faulty DNN operations and using this fault analysis proposed a fault tolerant reliability improvement scheme—DRIS-3—to mitigate the faults during DNN operations. Chandramoorthy et al. [58] present a technique which dynamically boosts the supply voltage of the embedded SRAMs to achieve superior energy savings. Yin et al. [59] evaluate thermal issues in an NN accelerator 3D memory and propose a “3D + 2.5D” integration processor named Parana which integrates 3D memory and the NPU. Parana tackles the thermal problem by lowering the amount of memory access and changing the memory access patterns. Nguyen et al. [60] propose a new memory architecture to adaptively control the DRAM cell refresh rate to store possible errors leading to a reduction in power consumption. Salami et al. [61], based on a thorough analysis of the NN accelerator components devise a strategy to appropriately mask the MSBs, to recover the corrupted bits, thereby enhancing the efficiency by mitigating the faults.
6.2. Enhancements around Architecture
This Section focuses on techniques which have provided enhancements around the architectural flow/components of the DNN Accelerator. Li et al. [62] demonstrate that, by providing appropriate precision and numeric range to values in each layer, reduces the failure rate by 200×. In each layer of DNN, this technique uses a ”symptom based fault detection” scheme to identify the range of values and adds a 10% guard-band. Libano et al. [63] propose a scheme to design and apply triple modular redundancy selectively to the vulnerable NN layers to effectively mask the faults. Zhang et al. [35] propose a technique, TE-Drop, to tackle timing errors arising due to aggressive voltage scaling. The occurrence of a timing error is detected using Razor flip-flop [36]. The MAC encountering timing error steals a clock cycle from the downstream MAC to recompute the correct output and bypasses the downstream MAC’s output with its output. Choi et al. [64] demonstrate a methodology to enhance the resilience of the DNN accelerator based on the sensitivity variations of neurons. The technique detects an error in the multiplier unit by augmenting each MAC unit with a Razor Flip-Flop [36] between multiplier and accumulator unit. Occurrence of a timing error will be lead to the upstream partial sum to be bypassed on to the downstream MAC unit. Zhang et al. [65] address the reliability concerns due to permanent faults arising from MAC units by mapping and pruning the weights of faulty MAC units.
6.3. Enhancements around Analog/Mixed-Signal Domain
Analog and mixed-signal DNN accelerators are also making a mark in the Neural Network computing realm. Analog and mixed-signal accelerators use enhanced Analog-to-Digital converter (ADC), Digital-to-Analog converter (DAC) for encoding/decoding and Non-Volatile Memories, such as ReRAM’s in DNN-based computations. Eshraghian et al. [66] utilize the frequency dependence of v-i place hysteresis to relieve the limitation on the single-bit-per-device and allocating the kernel information to the device conductance and partially to the frequency of the time-varying input. Ghodrati et al. [67] propose a technique BIHIWE, to address the issues in mixed-signal circuitry due to restricted scope of information encoding, noise susceptibility and overheads due to Analog to Digital conversions. BIHIWE, bit-partitions vector dot-product into clusters of low-bitwidth operations executing in parallel and embedding across multiple vector elements. Shafiee et al. [26] demonstrate a scheme ISAAC, by implementing a pipelined architecture with each neural network layer being dedicated specific crossbars and heaping up the data between pipe stages using eDRAM buffers. ISAAC also proposes a novel data encoding technique to reduce the analog-to-digital conversion overheads and performs a design space inspection to obtain a balance between memristor storage/compute, buffers and ADCs on the chip. Mackin et al. [68] propose the usage of crossbar arrays of NVMs to implement MAC operations at the data location and demonstrates simultaneous programming of weights at optimal hardware conditions and exploring its effectiveness under significant NVM variability. These recent developments in Analog and Mixed-signal DNN accelerators envision employing ADC, DAC and ReRAM’s in NTC DNN accelerators to yield better energy efficiency. Successive Approximation Register ADCs can be efficiently utilized at NTC owing to their simple architecture and low power usage [69,70,71,72,73]. In addition, the efficacy of ReRAM [74,75,76,77,78,79] in a low power computing environment provides a promising direction in DNN accelerators venturing into the NTC realm.
7. Conclusions
The NTC design paradigm, being a stronger direction towards energy efficiency, is plagued by timing errors for DNN applications. In this paper, we illustrate the unique challenges coming from the DNN workload and attributes of the occurrence and impact of timing errors. We discover that NTC DNN accelerators are challenged by landslide increases in the rate timing errors and the inherent algorithmic tolerance of DNNs to timing errors is quickly surpassed with a sharp decline in the inference accuracy. We explore the data–delay relationship with the practical DNN datasets to uncover an opportunity of providing bulk timing error resilience through prediction of a small group of high delay input sequences. We explore the timing disparities in the multiplier and accumulator to propose opportunities for providing an elegant timing error correction without performance loss. We correlate the hardware utilization pattern to outshine the broad control strategies for timing error resilience techniques. The application of NTC in the domain of DNN accelerators is a relatively newer domain and this article serves to present concrete possible directions towards timing error resilience, which remains to be a big hurdle for NTC systems. Energy efficient AI evolution is the need of the hour and further research with promising domains, such as NTC is required.
Author Contributions
Conceptualization, P.P. and N.D.G.; methodology, P.P., N.D.G., P.B. and T.S.; software, P.B., P.P., N.D.G. and T.S.; validation, P.P. and N.D.G.; formal analysis, P.P. and N.D.G.; investigation, P.P., N.D.G., P.B., T.S. and M.C.P.; resources, P.P., N.D.G., P.B., T.S., K.C. and S.R.; data curation, P.P.; writing—original draft preparation, P.P. and N.D.G.; writing—review and editing, P.P., N.D.G., K.C. and S.R.; visualization, P.P. and N.D.G.; supervision, K.C. and S.R.; project administration, P.P.; funding acquisition, K.C. and S.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by National Science Foundation under grant numbers CAREER-1253024 and CNS-1421022.
Conflicts of Interest
The authors declare no conflict of interest.
References
- AI Will Add 15 Trillion to the World Economy by 2030. Available online: https://www.forbes.com/sites/greatspeculations/2019/02/25/ai-will-add-15-trillion-to-the-world-economy-by-2030/ (accessed on 20 September 2020).
- Reagen, B.; Whatmough, P.; Adolf, R.; Rama, S.; Lee, H.; Lee, S.K.; Hernández-Lobato, J.M.; Wei, G.Y.; Brooks, D. Minerva: Enabling low-power, highly-accurate deep neural network accelerators. In ACM SIGARCH Computer Architecture News; IEEE Press: Piscataway, NJ, USA, 2016; Volume 44, pp. 267–278. [Google Scholar]
- Chen, Y.H.; Emer, J.; Sze, V. Using dataflow to optimize energy efficiency of deep neural network accelerators. IEEE Micro 2017, 37, 12–21. [Google Scholar] [CrossRef]
- Kim, S.; Howe, P.; Moreau, T.; Alaghi, A.; Ceze, L.; Sathe, V.S. Energy-Efficient Neural Network Acceleration in the Presence of Bit-Level Memory Errors. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 4285–4298. [Google Scholar] [CrossRef]
- Gokhale, V.; Zaidy, A.; Chang, A.X.M.; Culurciello, E. Snowflake: An efficient hardware accelerator for convolutional neural networks. In Proceedings of the 2017 IEEE International Symposium on Circuits and Systems (ISCAS), Baltimore, MD, USA, 28–31 May 2017; pp. 1–4. [Google Scholar]
- Sze, V.; Chen, Y.H.; Yang, T.J.; Emer, J.S. Efficient processing of deep neural networks: A tutorial and survey. Proc. IEEE 2017, 105, 2295–2329. [Google Scholar] [CrossRef]
- Andrae, A.S.; Edler, T. On global electricity usage of communication technology: Trends to 2030. Challenges 2015, 6, 117–157. [Google Scholar] [CrossRef]
- Seok, M.; Jeon, D.; Chakrabarti, C.; Blaauw, D.; Sylvester, D. Pipeline Strategy for Improving Optimal Energy Efficiency in Ultra-Low Voltage Design. In Proceedings of the 48th Design Automation Conference, San Diego, CA, USA, 5–10 June 2011; pp. 990–995. [Google Scholar]
- Chen, H.; Manzi, D.; Roy, S.; Chakraborty, K. Opportunistic turbo execution in NTC: Exploiting the paradigm shift in performance bottlenecks. In Proceedings of the 2015 52nd ACM/EDAC/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 8–12 June 2015; pp. 63:1–63:6. [Google Scholar]
- Mugisha, D.M.; Chen, H.; Roy, S.; Chakraborty, K. Resilient Cache Design for Mobile Processors in the Near-Threshold Regime. J. Low Power Electron. 2015, 11, 112–120. [Google Scholar] [CrossRef]
- Basu, P.; Chen, H.; Saha, S.; Chakraborty, K.; Roy, S. SwiftGPU: Fostering Energy Efficiency in a Near-Threshold GPU Through a Tactical Performance Boost. In Proceedings of the 2016 53nd ACM/EDAC/IEEE Design Automation Conference (DAC), Austin, TX, USA, 5–9 June 2016. [Google Scholar]
- Pinckney, N.; Blaauw, D.; Sylvester, D. Low-power near-threshold design: Techniques to improve energy efficiency energy-efficient near-threshold design has been proposed to increase energy efficiency across a wid. IEEE Solid State Circuits Mag. 2015, 7, 49–57. [Google Scholar] [CrossRef]
- Pinckney, N.R.; Sewell, K.; Dreslinski, R.G.; Fick, D.; Mudge, T.N.; Sylvester, D.; Blaauw, D. Assessing the performance limits of parallelized near-threshold computing. In Proceedings of the 49th Annual Design Automation Conference, San Francisco, CA, USA, 3–7 June 2012; pp. 1147–1152. [Google Scholar]
- Dreslinski, R.G.; Wieckowski, M.; Blaauw, D.; Sylvester, D.; Mudge, T.N. Near-Threshold Computing: Reclaiming Moore’s Law Through Energy Efficient Integrated Circuits. Proc. IEEE 2010, 98, 253–266. [Google Scholar] [CrossRef]
- Shabanian, T.; Bal, A.; Basu, P.; Chakraborty, K.; Roy, S. ACE-GPU: Tackling Choke Point Induced Performance Bottlenecks in a Near-Threshold Computing GPU. In Proceedings of the International Symposium on Low Power Electronics and Design (ISLPED ’18), Bellevue, WA, USA, 23–25 July 2018. [Google Scholar]
- Trapani Possignolo, R.; Ebrahimi, E.; Ardestani, E.K.; Sankaranarayanan, A.; Briz, J.L.; Renau, J. GPU NTC Process Variation Compensation With Voltage Stacking. IEEE Trans. Very Large Scale Integr. Syst. 2018, 26, 1713–1726. [Google Scholar] [CrossRef]
- Esmaeilzadeh, H.; Blem, E.; Amant, R.S.; Sankaralingam, K.; Burger, D. Dark silicon and the end of multicore scaling. In Proceedings of the 2011 38th Annual International Symposium on Computer Architecture (ISCA), San Jose, CA, USA, 4–8 June 2011. [Google Scholar]
- Silvano, C.; Palermo, G.; Xydis, S.; Stamelakos, I.S. Voltage island management in near threshold manycore architectures to mitigate dark silicon. In Proceedings of the 2014 Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 24–28 March 2014; pp. 1–6. [Google Scholar]
- Chen, Y.H.; Krishna, T.; Emer, J.S.; Sze, V. Eyeriss: An energy-efficient reconfigurable accelerator for deep convolutional neural networks. IEEE J. Solid State Circuits 2016, 52, 127–138. [Google Scholar] [CrossRef]
- Yoo, H.J.; Park, S.; Bong, K.; Shin, D.; Lee, J.; Choi, S. A 1.93 tops/w scalable deep learning/inference processor with tetra-parallel mimd architecture for big data applications. In Proceedings of the IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 22–26 February 2015; pp. 80–81. [Google Scholar]
- Cavigelli, L.; Gschwend, D.; Mayer, C.; Willi, S.; Muheim, B.; Benini, L. Origami: A convolutional network accelerator. In Proceedings of the 25th Edition on Great Lakes Symposium on VLSI, Pittsburgh, PA, USA, 20–22 May 2015; pp. 199–204. [Google Scholar]
- Jouppi, N.P.; Young, C.; Patil, N.; Patterson, D.; Agrawal, G.; Bajwa, R.; Bates, S.; Bhatia, S.; Boden, N.; Borchers, A.; et al. In-datacenter performance analysis of a tensor processing unit. In Proceedings of the 2017 ACM/IEEE 44th Annual International Symposium on Computer Architecture (ISCA), Toronto, ON, Canada, 24–28 June 2017; pp. 1–12. [Google Scholar]
- Du, Z.; Fasthuber, R.; Chen, T.; Ienne, P.; Li, L.; Luo, T.; Feng, X.; Chen, Y.; Temam, O. ShiDianNao: Shifting vision processing closer to the sensor. In Proceedings of the 2015 ACM/IEEE 42nd Annual International Symposium on Computer Architecture (ISCA), Portland, OR, USA, 13–17 June 2015; pp. 92–104. [Google Scholar] [CrossRef]
- Chen, T.; Du, Z.; Sun, N.; Wang, J.; Wu, C.; Chen, Y.; Temam, O. Diannao: A small-footprint high-throughput accelerator for ubiquitous machine-learning. ACM Sigarch Comput. Archit. News 2014, 42, 269–284. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Verma, N. A machine-learning classifier implemented in a standard 6T SRAM array. In Proceedings of the 2016 IEEE Symposium on VLSI Circuits (VLSI-Circuits), Honolulu, HI, USA, 15–17 June 2016; pp. 1–2. [Google Scholar]
- Shafiee, A.; Nag, A.; Muralimanohar, N.; Balasubramonian, R.; Strachan, J.P.; Hu, M.; Williams, R.S.; Srikumar, V. ISAAC: A convolutional neural network accelerator with in-situ analog arithmetic in crossbars. ACM Sigarch Comput. Archit. News 2016, 44, 14–26. [Google Scholar] [CrossRef]
- Chi, P.; Li, S.; Xu, C.; Zhang, T.; Zhao, J.; Liu, Y.; Wang, Y.; Xie, Y. Prime: A novel processing-in-memory architecture for neural network computation in reram-based main memory. In Proceedings of the 43rd International Symposium on Computer Architecture, Seoul, Korea, 18–22 June 2016. [Google Scholar]
- Song, L.; Qian, X.; Li, H.; Chen, Y. Pipelayer: A pipelined reram-based accelerator for deep learning. In Proceedings of the 2017 IEEE International Symposium on High Performance Computer Architecture (HPCA), Austin, TX, USA, 4–8 February 2017; pp. 541–552. [Google Scholar]
- Mythic Technology: An Architecture Built from the Ground up for AI. Available online: https://www.mythic-ai.com/technology/ (accessed on 20 September 2020).
- Graphcore IPU: Designed for Machine Intelligence. Available online: https://www.graphcore.ai/products/ipu (accessed on 20 September 2020).
- Perceive Ergo: A Complete Solution for High Accuracy, Low Power Intelligence to Consumer Products. Available online: https://perceive.io/product/ (accessed on 20 September 2020).
- Edge TPU: Google’s Purpose-Built ASIC Designed to Run Inference at the Edge. Available online: https://cloud.google.com/edge-tpu (accessed on 20 September 2020).
- Google Coral Edge TPU Explained in Depth. Available online: https://qengineering.eu/google-corals-tpu-explained.html (accessed on 20 September 2020).
- Jiao, X.; Luo, M.; Lin, J.H.; Gupta, R.K. An assessment of vulnerability of hardware neural networks to dynamic voltage and temperature variations. In Proceedings of the 36th International Conference on Computer-Aided Design, Irvine, CA, USA, 13–16 November 2017; pp. 945–950. [Google Scholar]
- Zhang, J.; Rangineni, K.; Ghodsi, Z.; Garg, S. ThUnderVolt: Enabling Aggressive Voltage Underscaling and Timing Error Resilience for Energy Efficient Deep Neural Network Accelerators. arXiv 2018, arXiv:1802.03806. [Google Scholar]
- Ernst, D.; Kim, N.S.; Das, S.; Pant, S.; Rao, R.R.; Pham, T.; Ziesler, C.H.; Blaauw, D.; Austin, T.M.; Flautner, K.; et al. Razor: A Low-Power Pipeline Based on Circuit-Level Timing Speculation. In Proceedings of the 36th Annual IEEE/ACM International Symposium on Microarchitecture (MICRO-36), San Diego, CA, USA, 5 December 2003; pp. 7–18. [Google Scholar]
- Das, S.; Tokunaga, C.; Pant, S.; Ma, W.H.; Kalaiselvan, S.; Lai, K.; Bull, D.; Blaauw, D. RazorII: In Situ Error Detection and Correction for PVT and SER Tolerance. J. Solid State Circ. 2009, 44, 32–48. [Google Scholar] [CrossRef]
- Fojtik, M.; Fick, D.; Kim, Y.; Pinckney, N.; Harris, D.; Blaauw, D.; Sylvester, D. Bubble Razor: An architecture-independent approach to timing-error detection and correction. In Proceedings of the 2012 IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 19–23 February 2012; pp. 488–490. [Google Scholar]
- Albericio, J.; Judd, P.; Hetherington, T.; Aamodt, T.; Jerger, N.E.; Moshovos, A. Cnvlutin: Ineffectual -Neuron-Free Deep Neural Network Computing. In Proceedings of the 2016 ACM/IEEE 43rd Annual International Symposium on Computer Architecture (ISCA), Seoul, Korea, 18–22 June 2016; pp. 1–13. [Google Scholar] [CrossRef]
- Pandey, P.; Basu, P.; Chakraborty, K.; Roy, S. GreenTPU: Improving Timing Error Resilience of a Near-Threshold Tensor Processing Unit. In Proceedings of the 2019 56th ACM/IEEE Design Automation Conference (DAC), Las Vegas, NV, USA, 2–6 June 2019; pp. 173:1–173:6. [Google Scholar]
- Kim, S.; Howe, P.; Moreau, T.; Alaghi, A.; Ceze, L.; Sathe, V. MATIC: Learning around errors for efficient low-voltage neural network accelerators. In Proceedings of the 2018 Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 19–23 March 2018; pp. 1–6. [Google Scholar]
- Zhang, J.J.; Garg, S. FATE: Fast and accurate timing error prediction framework for low power DNN accelerator design. In Proceedings of the 2018 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), San Diego, CA, USA, 5–8 November 2018; pp. 1–8. [Google Scholar]
- Reagen, B.; Gupta, U.; Pentecost, L.; Whatmough, P.; Lee, S.K.; Mulholland, N.; Brooks, D.; Wei, G.Y. Ares: A framework for quantifying the resilience of deep neural networks. In Proceedings of the 2018 55th ACM/ESDA/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 24–28 June 2018; pp. 1–6. [Google Scholar]
- Zhang, J.; Ghodsi, Z.; Rangineni, K.; Garg, S. Enabling Timing Error Resilience for Low-Power Systolic-Array Based Deep Learning Accelerators. IEEE Des. Test 2019, 37, 93–102. [Google Scholar] [CrossRef]
- Gundi, N.D.; Shabanian, T.; Basu, P.; Pandey, P.; Roy, S.; Chakraborty, K.; Zhang, Z. EFFORT: Enhancing Energy Efficiency and Error Resilience of a Near-Threshold Tensor Processing Unit. In Proceedings of the 2020 25th Asia and South Pacific Design Automation Conference (ASP-DAC), Beijing, China, 13–16 January 2020; pp. 241–246. [Google Scholar]
- Zhao, W.; Cao, Y. New Generation of Predictive Technology Model for sub-45nm Early Design Exploration. Electron. Devices 2006, 53, 2816–2823. [Google Scholar] [CrossRef]
- Karpuzcu, U.R.; Kolluru, K.B.; Kim, N.S.; Torrellas, J. VARIUS-NTV: A microarchitectural model to capture the increased sensitivity of manycores to process variations at near-threshold voltages. In Proceedings of the IEEE/IFIP International Conference on Dependable Systems and Networks (DSN 2012), Boston, MA, USA, 25–28 June 2012; pp. 1–11. [Google Scholar]
- Keras. Available online: https://keras.io (accessed on 20 September 2020).
- LeCun, Y.; Cortes, C. MNIST Handwritten Digit Database. Available online: http://yann.lecun.com/exdb/mnist/ (accessed on 20 September 2020).
- Reuters-21578 Dataset. Available online: http://kdd.ics.uci.edu/databases/reuters21578/reuters21578.html (accessed on 20 September 2020).
- Krizhevsky, A. Learning Multiple Layers of Features from Tiny Images. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.222.9220&rep=rep1&type=pdf (accessed on 20 September 2020).
- Maas, A.L.; Daly, R.E.; Pham, P.T.; Huang, D.; Ng, A.Y.; Potts, C. Learning Word Vectors for Sentiment Analysis. Available online: https://www.aclweb.org/anthology/P11-1015.pdf (accessed on 20 September 2020).
- Netzer, Y.; Wang, T.; Coates, A.; Bissacco, A.; Wu, B.; Ng, A.Y. Reading Digits in Natural Images with Unsupervised Feature Learning. In Proceedings of the NIPS Workshop on Deep Learning and Unsupervised Feature Learning, Granada, Spain, 12–17 December 2011. [Google Scholar]
- Stallkamp, J.; Schlipsing, M.; Salmen, J.; Igel, C. Man vs. computer: Benchmarking machine learning algorithms for traffic sign recognition. Neural Netw. 2012, 32, 323–332. [Google Scholar] [CrossRef]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-MNIST: A Novel Image Dataset for Benchmarking Machine Learning Algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- Free Spoken Digit Dataset (FSDD). Available online: https://github.com/Jakobovski/free-spoken-digit-dataset (accessed on 20 September 2020).
- Kim, J.S.; Yang, J.S. DRIS-3: Deep Neural Network Reliability Improvement Scheme in 3D Die-Stacked Memory based on Fault Analysis. In Proceedings of the 2019 56th ACM/IEEE Design Automation Conference (DAC), Las Vegas, NV, USA, 2–6 June 2019; pp. 1–6. [Google Scholar]
- Chandramoorthy, N.; Swaminathan, K.; Cochet, M.; Paidimarri, A.; Eldridge, S.; Joshi, R.; Ziegler, M.; Buyuktosunoglu, A.; Bose, P. Resilient Low Voltage Accelerators for High Energy Efficiency. In Proceedings of the 2019 IEEE International Symposium on High Performance Computer Architecture (HPCA), Washington, DC, USA, 16–20 February 2019; pp. 147–158. [Google Scholar] [CrossRef]
- Yin, S.; Tang, S.; Lin, X.; Ouyang, P.; Tu, F.; Zhao, J.; Xu, C.; Li, S.; Xie, Y.; Wei, S.; et al. Parana: A parallel neural architecture considering thermal problem of 3d stacked memory. IEEE Trans. Parallel Distrib. Syst. 2018, 30, 146–160. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Kim, H.; Lee, H.J.; Chang, I.J. An approximate memory architecture for a reduction of refresh power consumption in deep learning applications. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018; pp. 1–5. [Google Scholar]
- Salami, B.; Unsal, O.S.; Kestelman, A.C. On the resilience of rtl nn accelerators: Fault characterization and mitigation. In Proceedings of the 2018 30th International Symposium on Computer Architecture and High Performance Computing (SBAC-PAD), Lyon, France, 24–27 September 2018; pp. 322–329. [Google Scholar]
- Li, G.; Hari, S.K.S.; Sullivan, M.; Tsai, T.; Pattabiraman, K.; Emer, J.; Keckler, S.W. Understanding error propagation in deep learning neural network (DNN) accelerators and applications. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, Denver, CO, USA, 12–17 November 2017; pp. 1–12. [Google Scholar]
- Libano, F.; Wilson, B.; Anderson, J.; Wirthlin, M.; Cazzaniga, C.; Frost, C.; Rech, P. Selective hardening for neural networks in fpgas. IEEE Trans. Nucl. Sci. 2018, 66, 216–222. [Google Scholar] [CrossRef]
- Choi, W.; Shin, D.; Park, J.; Ghosh, S. Sensitivity Based Error Resilient Techniques for Energy Efficient Deep Neural Network Accelerators. In Proceedings of the 56th Annual Design Automation Conference 2019, DAC ’19, Las Vegas, NV, USA, 2–6 June 2019; pp. 204:1–204:6. [Google Scholar] [CrossRef]
- Zhang, J.J.; Gu, T.; Basu, K.; Garg, S. Analyzing and mitigating the impact of permanent faults on a systolic array based neural network accelerator. In Proceedings of the 2018 IEEE 36th VLSI Test Symposium (VTS), San Francisco, CA, USA, 22–25 April 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Eshraghian, J.K.; Kang, S.M.; Baek, S.; Orchard, G.; Iu, H.H.C.; Lei, W. Analog weights in ReRAM DNN accelerators. In Proceedings of the 2019 IEEE International Conference on Artificial Intelligence Circuits and Systems (AICAS), Hsinchu, Taiwan, 18–20 March 2019; pp. 267–271. [Google Scholar]
- Ghodrati, S.; Sharma, H.; Kinzer, S.; Yazdanbakhsh, A.; Samadi, K.; Kim, N.S.; Burger, D.; Esmaeilzadeh, H. Mixed-Signal Charge-Domain Acceleration of Deep Neural networks through Interleaved Bit-Partitioned Arithmetic. arXiv 2019, arXiv:1906.11915. [Google Scholar]
- Mackin, C.; Tsai, H.; Ambrogio, S.; Narayanan, P.; Chen, A.; Burr, G.W. Weight Programming in DNN Analog Hardware Accelerators in the Presence of NVM Variability. Adv. Electron. Mater. 2019, 5, 1900026. [Google Scholar] [CrossRef]
- Shikata, A.; Sekimoto, R.; Kuroda, T.; Ishikuro, H. A 0.5 V 1.1 MS/sec 6.3 fJ/conversion-step SAR-ADC with tri-level comparator in 40 nm CMOS. IEEE J. Solid-State Circuits 2012, 47, 1022–1030. [Google Scholar] [CrossRef]
- Lin, K.T.; Cheng, Y.W.; Tang, K.T. A 0.5 V 1.28-MS/s 4.68-fJ/conversion-step SAR ADC with energy-efficient DAC and trilevel switching scheme. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2016, 24, 1441–1449. [Google Scholar] [CrossRef]
- Liu, C.C.; Chang, S.J.; Huang, G.Y.; Lin, Y.Z. A 10-bit 50-MS/s SAR ADC with a monotonic capacitor switching procedure. IEEE J. Solid State Circuits 2010, 45, 731–740. [Google Scholar] [CrossRef]
- Song, J.; Jun, J.; Kim, C. A 0.5 V 10-bit 3 MS/s SAR ADC With Adaptive-Reset Switching Scheme and Near-Threshold Voltage-Optimized Design Technique. IEEE Trans. Circuits Syst. II Express Briefs 2020, 67, 1184–1188. [Google Scholar] [CrossRef]
- Hong, H.C.; Lin, L.Y.; Chiu, Y. Design of a 0.20–0.25-V, sub-nW, rail-to-rail, 10-bit SAR ADC for self-sustainable IoT applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 1840–1852. [Google Scholar] [CrossRef]
- Sheu, S.S.; Chang, M.F.; Lin, K.F.; Wu, C.W.; Chen, Y.S.; Chiu, P.F.; Kuo, C.C.; Yang, Y.S.; Chiang, P.C.; Lin, W.P.; et al. A 4Mb embedded SLC resistive-RAM macro with 7.2 ns read-write random-access time and 160 ns MLC-access capability. In Proceedings of the 2011 IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 20–24 February 2011; pp. 200–202. [Google Scholar]
- Niu, D.; Xu, C.; Muralimanohar, N.; Jouppi, N.P.; Xie, Y. Design trade-offs for high density cross-point resistive memory. In Proceedings of the 2012 ACM/IEEE International Symposium on LOW Power Electronics and Design, Redondo Beach, CA, USA, 30 July–1 August 2012; pp. 209–214. [Google Scholar]
- Chang, M.F.; Wu, J.J.; Chien, T.F.; Liu, Y.C.; Yang, T.C.; Shen, W.C.; King, Y.C.; Lin, C.J.; Lin, K.F.; Chih, Y.D.; et al. 19.4 embedded 1Mb ReRAM in 28 nm CMOS with 0.27-to-1V read using swing-sample-and-couple sense amplifier and self-boost-write-termination scheme. In Proceedings of the 2014 IEEE International Solid-State Circuits Conference Digest of Technical Papers (ISSCC), San Francisco, CA, USA, 9–13 February 2014. [Google Scholar]
- Chang, M.F.; Wu, C.W.; Hung, J.Y.; King, Y.C.; Lin, C.J.; Ho, M.S.; Kuo, C.C.; Sheu, S.S. A low-power subthreshold-to-superthreshold level-shifter for sub-0.5 V embedded resistive RAM (ReRAM) macro in ultra low-voltage chips. In Proceedings of the 2014 IEEE Asia Pacific Conference on Circuits and Systems (APCCAS), Ishigaki, Japan, 17–20 November 2014. [Google Scholar]
- Chang, M.F.; Wu, C.W.; Kuo, C.C.; Shen, S.J.; Lin, K.F.; Yang, S.M.; King, Y.C.; Lin, C.J.; Chih, Y.D. A 0.5 V 4 Mb logic-process compatible embedded resistive RAM (ReRAM) in 65nm CMOS using low-voltage current-mode sensing scheme with 45ns random read time. In Proceedings of the 2012 IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 19–23 February 2012. [Google Scholar]
- Ishii, T.; Ning, S.; Tanaka, M.; Tsurumi, K.; Takeuchi, K. Adaptive comparator bias-current control of 0.6 V input boost converter for ReRAM program voltages in low power embedded applications. IEEE J. Solid State Circuits 2016, 51, 2389–2397. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).