Abstract
Multiple multi-threaded tasks constitute a modern many-core application. An accompanying generic Directed Acyclic Graph (DAG) represents the execution precedence relationship between the tasks. The application comes with a hard deadline and high peak power consumption. Parallel execution of multiple tasks on multiple cores results in a quicker execution, but higher peak power. Peak power single-handedly determines the involved cooling costs in many-cores, while its violations could induce performance-crippling execution uncertainties. Less task parallelization, on the other hand, results in lower peak power, but a more prolonged deadline violating execution. The problem of peak power minimization in many-cores is to determine task-to-core mapping configuration in the spatio-temporal domain that minimizes the peak power consumption of an application, but ensures application still meets the deadline. All previous works on peak power minimization for many-core applications (with or without DAG) assume only single-threaded tasks. We are the first to propose a framework, called PkMin, which minimizes the peak power of many-core applications with DAG that have multi-threaded tasks. PkMin leverages the inherent convexity in the execution characteristics of multi-threaded tasks to find a configuration that satisfies the deadline, as well as minimizes peak power. Evaluation on hundreds of applications shows PkMin on average results in 49.2% lower peak power than a similar state-of-the-art framework.
1. Introduction
A many-core application is made up of tens of tasks. All of the tasks are inherently multi-threaded. An accompanying generic Directed Acyclic Graph (DAG) models the execution dependency between the tasks and therefore determines the precedence order for execution [1]. The application must complete execution within a given hard deadline. One way to meet the deadline is to execute as many tasks as possible in parallel. Executing them with the maximum parallelization permitted under the DAG with all available cores results in a short execution time, but also results in high peak power.
The highest power consumption observed during the task’s execution defines its peak power. Rated peak power consumption predominantly determines the cost (and weight) of cooling infrastructure that accompanies the many-core. Higher peak power also results in higher on-chip temperatures, which leads to reliability issues [2,3,4]. Higher temperatures can also trigger performance crippling thermal-throttling, which makes execution unpredictable [5]. We can minimize peak power by executing all of the tasks sequentially on a single core, but such an execution will violate the deadline.
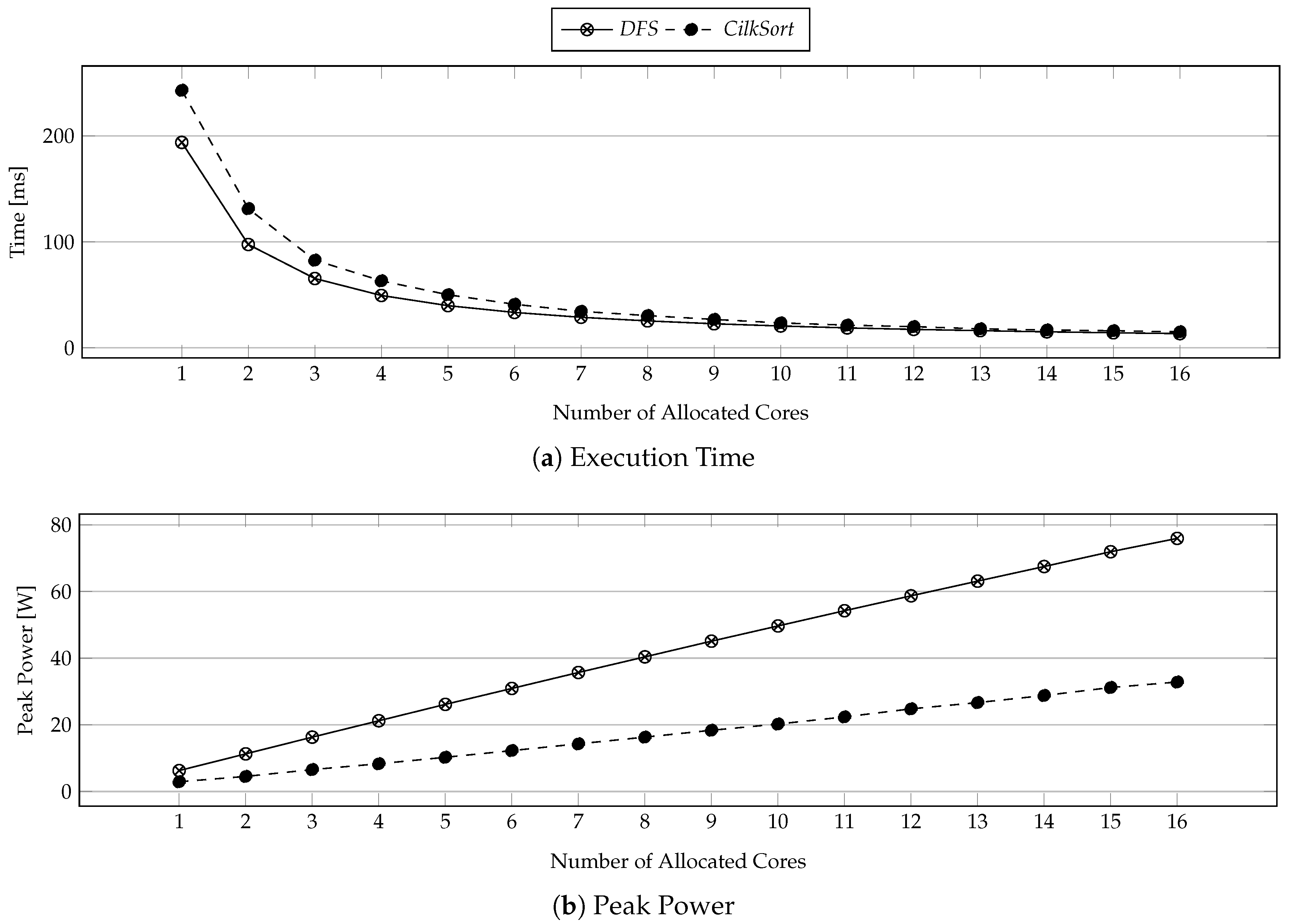
The problem of peak power minimization [6,7] in many-cores is to determine a spatio-temporal task-to-core mapping (configuration) that still meets the application deadline, but minimizes the peak power. We make use of two well-known observations in the execution of multi-threaded tasks in order to efficiently solve the problem. First, Figure 1a shows that the execution time of tasks in a many-core application is discretely convex with increasing core allocation [8,9,10,11]. Second, Figure 1b shows that the peak power of tasks is discretely linear with increasing core allocation. These two observations open up the possibility of employing convex optimization in order to solve this problem.
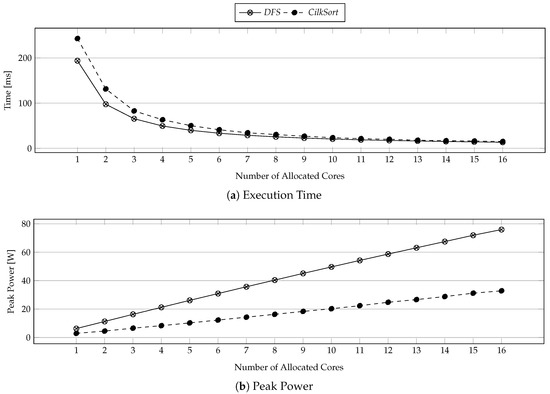
Figure 1.
Execution characteristics of different tasks with different core allocations.
Most works on peak power minimization for many-core applications only assume single-threaded tasks. Therefore, they have no hope for the exploitation of execution characteristics that are shown in Figure 1, which are specific to multi-threaded tasks. In this work, we propose a framework called PkMin that minimizes the peak power of multi-threaded many-core applications with DAG under deadline constraint by exploiting the observations made in Figure 1. We evaluate PkMin against a similar state-of-the-art framework [12] while using hundreds of applications for a thorough evaluation. Empirical evaluations show that PkMin results in on average 48% lower peak power than the state-of-the-art.
2. Motivational Example
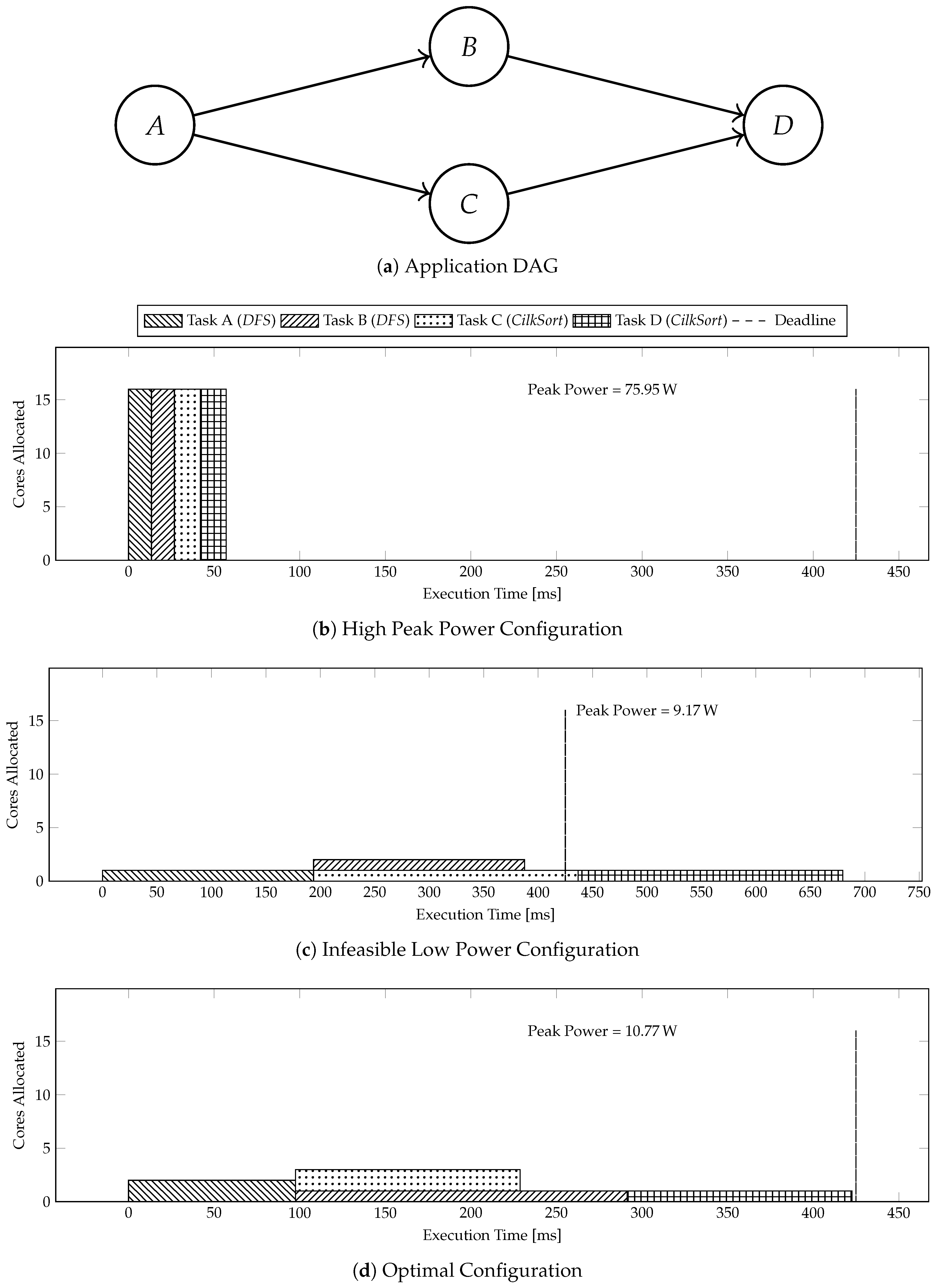
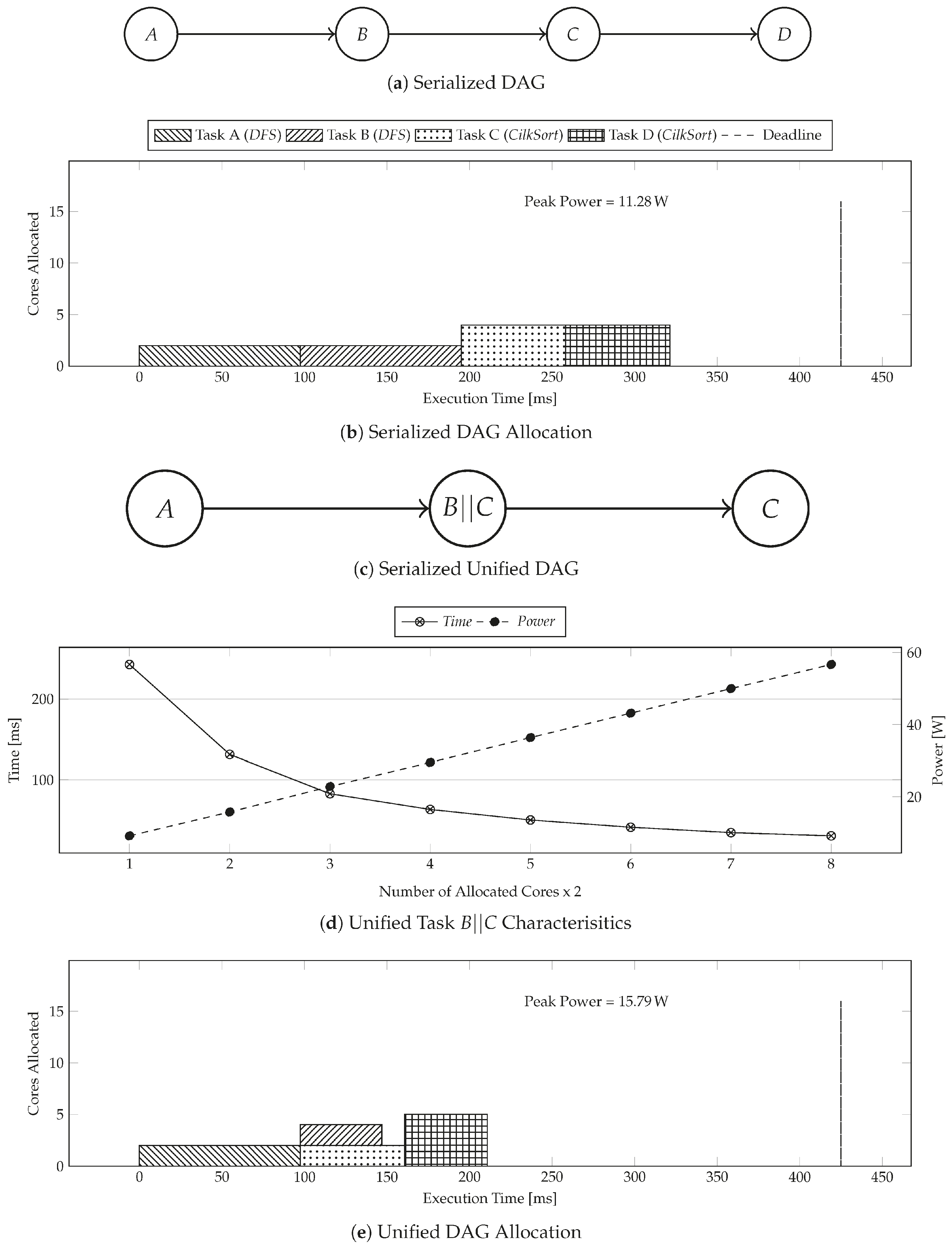
Figure 2 shows a motivational example of the problem of peak power minimization in many-cores. We use Sniper [13] multicore x86 simulator to execute the binaries that are associated with the task. Sniper directly reports the execution time values (in clock cycles) for the binaries and also generates traces that is then used by downstream tools, like McPAT [14], to estimate the power consumed by various per core components like L1 (I/D) caches, instruction fetch units, L2 caches, etc., as well uncore components, like memory controllers and DRAM subsystem. This methodology avoids the insertion of costly instrumentation hooks within the program. We account for the power consumption only on the “active” cores, i.e., those that are directly reponsible for execution of the application. Figure 2a gives a DAG for an application composed of four tasks that we need to execute on many-core within 425 ms. Tasks A and B are composed of DFS. Tasks C and D are composed of CilkSort.
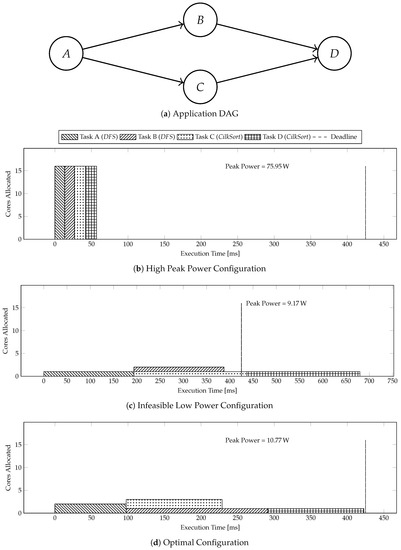
Figure 2.
Motivational example for peak power minimization of multi-threaded many-core applications with Directed Acyclic Graph (DAG) under a deadline constraints.
Figure 2b shows the execution time of the benchmark in a configuration that executes the tasks serially with all available cores. The execution in Figure 2b meets the deadline, but leads to a high peak power of 75.95 W. Figure 2c shows the execution time of the application in a configuration that parallelizes the execution, but does not use multi-threading in tasks. Execution in Figure 2c leads to low peak power, but it violates the deadline. Figure 2d shows the execution time of the application in an optimal configuration generated by PkMin that allocates just enough cores to tasks, such that both precedence and deadline constraints are met, but with a minimal peak power of 10.77 W. Figure 2d results in 85.82% lower and only 17.45% higher peak power than the configuration in Figure 2b,c, respectively.
3. Related Work
Peak power minimization in the context of multi-/many-core scheduling is an active subject of research [15]. The problem is important in both embedded [16,17,18] as well as super-computing domain [19,20]. The authors in [21] propose an algorithm to minimize peak power for an application with a task graph without a deadline. The authors of [22] were the first to study the problem of peak power minimization in the context of task graph-based many-core applications with a deadline. They propose an optimal algorithm that schedules a set of independent tasks from the application on a many-core to minimize application’s peak power while meeting its deadline. The authors of [23] work on the same problem, but proposed an alternative light-weight heuristic algorithm. Most recently, the authors in [24] proposed an algorithm to minimize peak power for many-core applications with DAG under reliability constraints. All of the works that target the peak power minimization problem directly assume the tasks with DAG within the many-core application to be single-threaded and thereby individually schedulable only on a single core. On the contrary, we focus on tasks that are all individually multi-threaded, wherein the level of multi-threading in each of them is an independently configurable design knob for solving the peak power minimization problem.
4. Convex Optimization Sub-Routine for Solving Serialized DAG
This section provides the details of the convex optimization sub-routine that is at the heart of PkMin. This sub-routine solves the problem of peak power minimization for a many-core application with a serial DAG optimally in the continuous domain and near-optimally in the discrete domain, as the problem is NP-Hard in the discrete domain. PkMin uses this sub-routine to perform peak power minimization of any generic DAG in Section 5.
System Model: we need to execute an application with multi-threaded tasks indexed while using i on a many-core with cores. Tasks execute serially in an order ordained by the serialized DAG. is the maximum number of cores that can be allocated to the task i. Each task i is executed with number of cores with the domain constraint . The number of cores allocated to the task i in practice needs to be discrete. However, we, at first, assume it to be a non-negative real value greater than equal to 1 and less than equal to for tractability.
Based on the observations made in Figure 1a, we assume execution time of task i with cores allocated to be a univariate convex function of the number of allocated cores. In the domain allocated cores, the execution time is a monotonically decreasing convex function of the number of allocated cores . Based on observations made in Figure 1b, we assume the power of a task i with cores allocated to be a univariate linear function of the number of allocated cores.
Execution Model: the execution time of the application in totality with configuration (core allocation vector) is the sum of the execution time of the individual tasks.
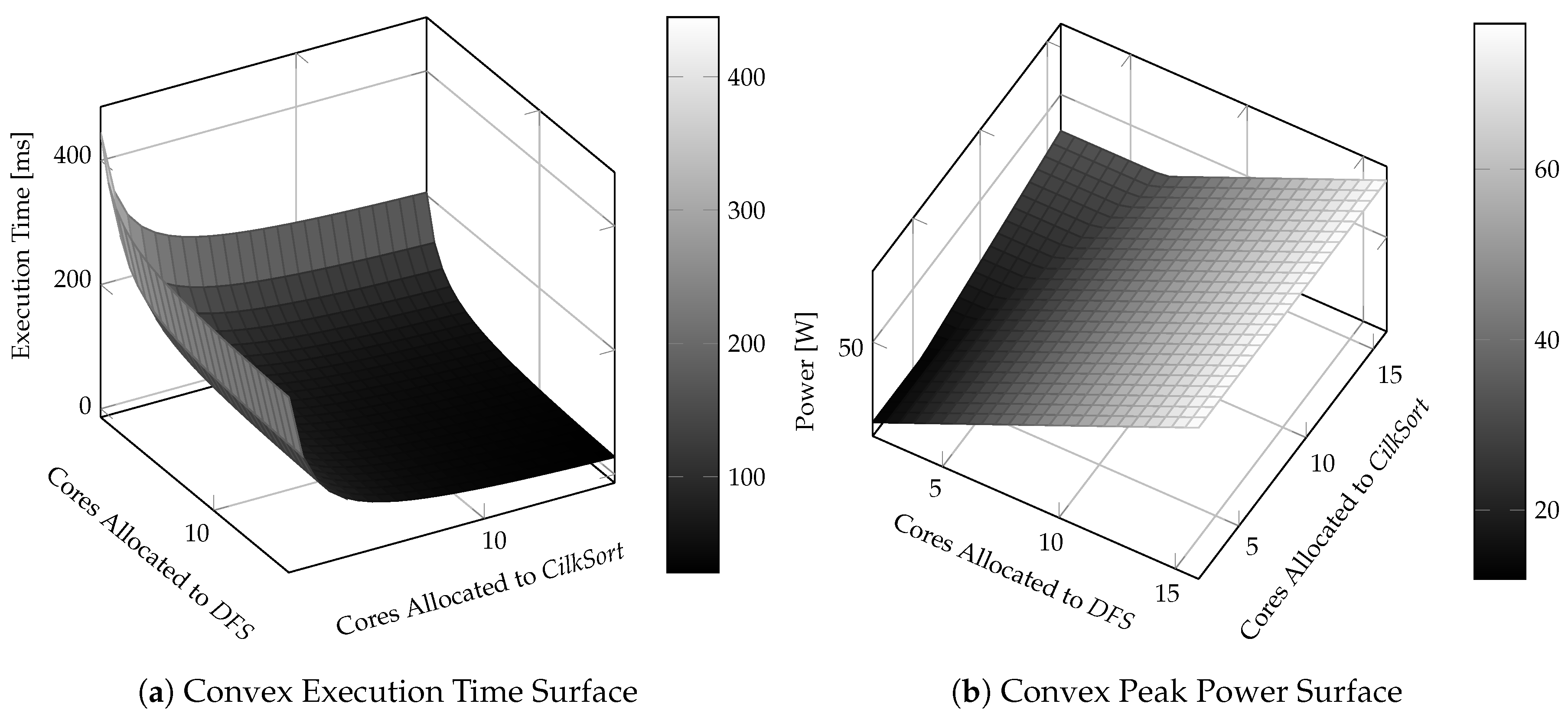
Because the execution time of each task is individually convex and the sum of convex functions is a convex function, then the application’s execution time is a multivariate convex function of configuration . Figure 3a shows the non-negative convex execution time surface of a two-task application.
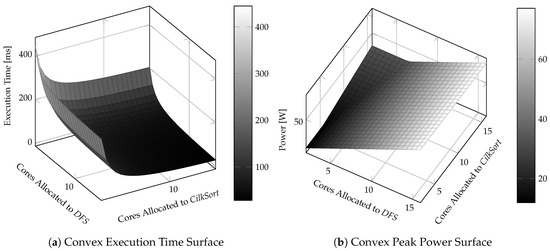
Figure 3.
Characteristics for a two-task application (with a serialized DAG) with different core allocations for each task in the continuous domain.
Peak Power Model: peak power of the application with configuration is given by task with the maximum power amongst all of the tasks.
The application’s peak power is a multivariate convex function of configuration , as the peak power of each task is individually linear and the max of linear functions is a convex function. Figure 3b shows the non-negative convex peak power surface of a two-task application.
Deadline Model: the peak power function attains its lowest value when all of the tasks execute with bare minimum cores (), but this is only permitted when there is no constraint on the execution time. The application’s hard deadline of put a constraint on its execution time. The deadline divides the domain for minimization of peak power function into feasible and infeasible regions.
Given a deadline, we are required to minimize the peak power over the feasible region . We now prove the feasible region F to be a convex set. Let be two feasible configurations. By feasibility definition
Because is a convex function,
Using Equation (3), we obtain
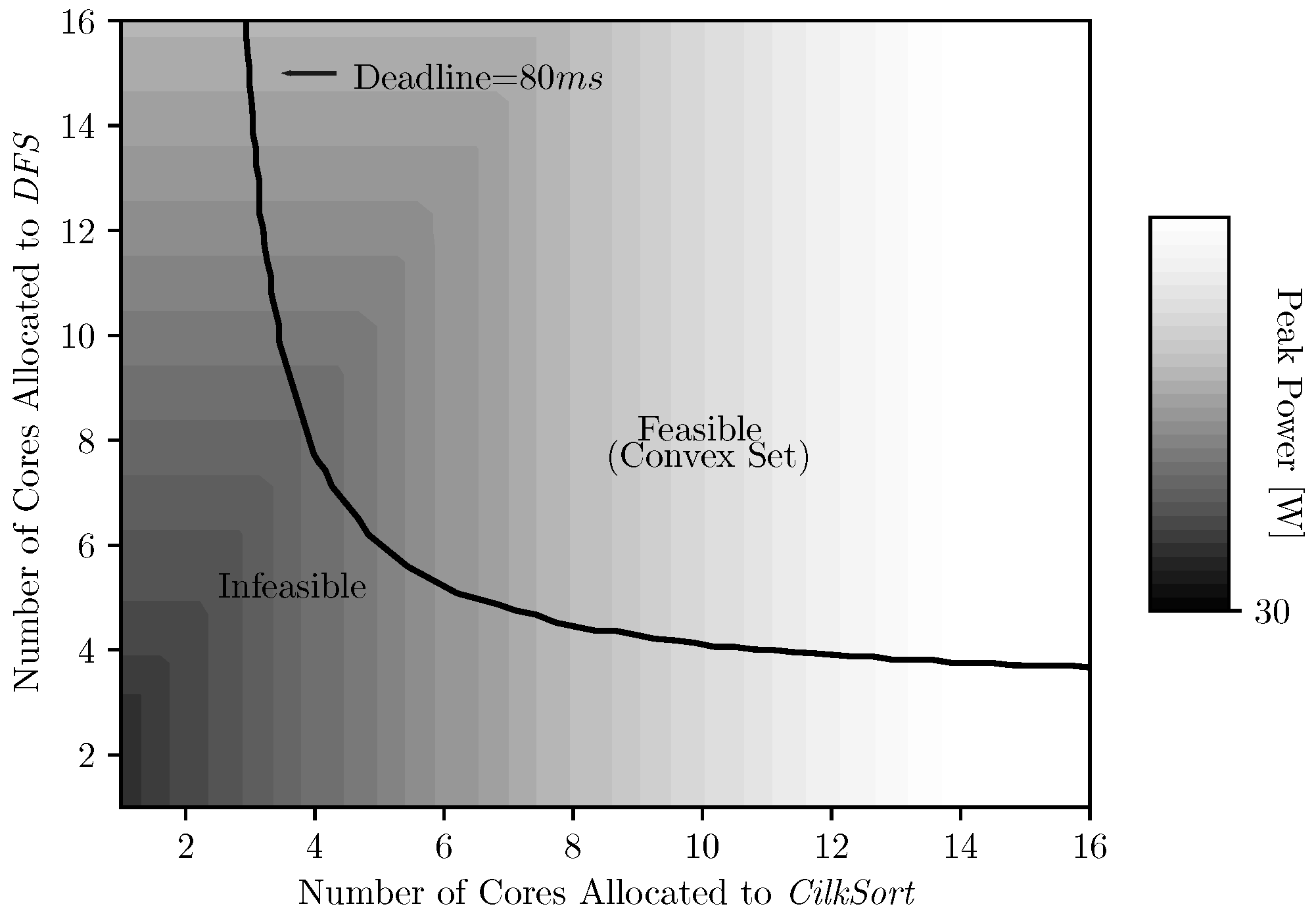
Therefore, F is a convex set, since, for any and any , we have . Figure 4 shows the feasible region F for an application with two tasks with a given hard deadline.
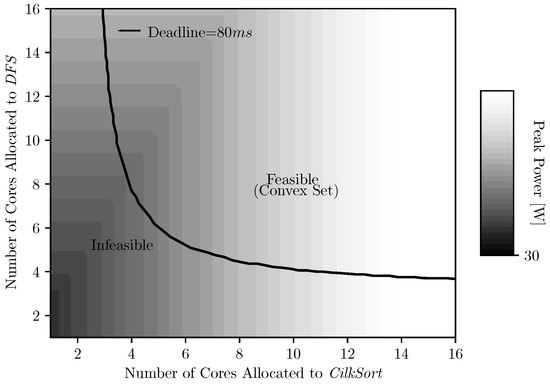
Figure 4.
Feasible region for a two-task application (with a serialized DAG) with different number of cores allocated to each task given a hard deadline.
Solution: our problem reduces to minimizing a convex peak power function over the feasible convex set F as its domain. Formally, it can also be summarized, as follows
We solve the above convex optimization problem in the continuous domain using NLOpt [25] tool that internally solves the problem whlileusing the Method of Moving Asymptotes (MMA) [26] algorithm. The problem-solving time is insignificant, even with an extremely large number of tasks.
Solution Discretization: when we modify the constraint in Equation (4) to force cores allocated to the task to be integers i.e., in the domain instead of real-numbers, the problem becomes an NP-Hard Convex Mixed Integer Non-Linear Programming (CMINLP) problem [27]. Still, we can expect local optima in the discrete domain to be close to the discrete global optimum, because the optimization is tractable using convex programming in its relaxed continuous domain, unlike an arbitrary optimization problem [28].
We first solve Equation (4) to obtain the optimal real-valued configuration in the continuous domain. We then round up all of the individual real-valued core allocations to the nearest integer. The rounding up/down decision is tricky, because there are possibilities, all of which cannot be exhaustively tested for optimality. Two choices are immediately obvious, i.e., to round-down all the allocations or round-up all of them. Because the execution time is non-increasing with increasing core allocation for any task (Figure 1a), rounding down can make the allocation infeasible while rounding up will preserve the feasibility, although it not guaranteed to be optimal in the discrete domain. For example, if the optimal configuration in a continuous domain for a three task application is found to be , then we round up to discrete configuration .
5. Peak Power Minimization with PkMin
The problem of peak power minimization for many-core applications with precedence and deadline constraints is inherently a multi-dimensional bin-packing problem, which is well-known to be NP-Hard [29]. We introduce a framework, called PkMin, which solves the problem near-optimally by exploiting the observations in Figure 1. At the heart of PkMin is a convex optimization sub-routine that can solve the problem optimally for a serialized DAG in a continuous domain. Section 4 provides the details of the sub-routine. The problem is NP-Hard, even with a serialized DAG, in the discrete domain [27]. Therefore, the sub-routine extrapolates the real-valued solution to the discrete domain.
In general, an application DAG allows for the possibility of multiple tasks to be run in parallel. For a given deadline, parallel execution allows for tasks to individually stretch out further along in the time domain more than a serialized execution. Therefore, we can execute tasks with a fewer number of cores being allocated to them individually and still meet the deadline. Tasks execute with a lower peak power (Figure 1b) with a smaller number of cores. However, parallel execution is not guaranteed to lower the peak power of the application, because the peak power of tasks that execute in parallel adds up.
Figure 5 shows the functioning of PkMin with the help of a flowchart. PkMin begins by serializing the DAG for an application by applying a topological sorting procedure [30]. It then passes the DAG to a convex optimization sub-routine (Section 4) that computes an allocation for the serialized DAG. PkMin then enumerates all of the task pairs that can be executed in parallel by computing the transitive closure [31] of the DAG that exposes the pairwise independent tasks. A pair of independent tasks is then “stacked” together to form a single unified task.

Figure 5.
Execution Flow for PkMin.
All of the sub-tasks in the unified task always execute with the same number of cores. The execution time and peak power of the unified task is the max and sum of the execution times and peak powers of the sub-tasks, respectively. The sum operator preserves the linearity of power characteristics, while the maximum operator preserves the convexity of execution time characteristics. The new unified task has characteristics that are similar to its constituent tasks. If there are multiple task pairs to choose from, PkMin chooses the task pair that gives the greatest reduction in execution time on unification.
The unified task replaces its sub-tasks in the original DAG. PkMin then serializes the modified DAG and passes it to the convex optimization sub-routine again in order to obtain a new feasible configuration. It repeats the process of DAG modification, followed by convex optimization iteratively until an exit condition is encountered in one of the following ways.
- The new configuration yields a higher peak power than the previous configuration, i.e., a local minimum is reached.
- There are no more candidate task pairs that can be parallelized.
PkMin reports the configuration from the previous iteration as the final solution configuration.
Working Example
This section explains the functioning of PkMin with the help of a working example. Figure 6 visualizes the steps that were taken by PkMin to solve the motivational example shown in Figure 2. PkMin begins with the original DAG that is shown in Figure 2a. It then serializes the DAG, as shown in Figure 6a. It then runs the convex optimization module from Section 4 in order to obtain the core allocation for the serialized DAG, as shown in Figure 6b. It then tries to stack Task B and Task C together by combining them into a new Task and create a new DAG, as shown in Figure 6c.
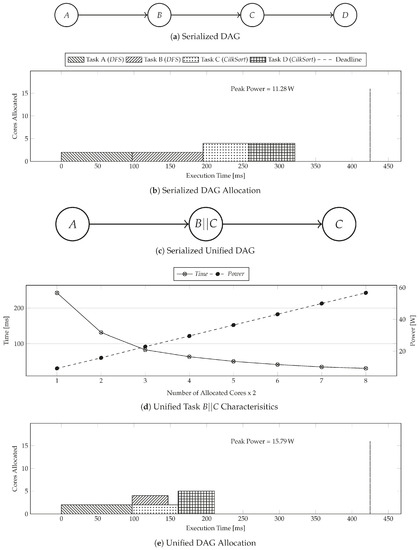
Figure 6.
Working example for peak power minimization of the motivational example that is shown in Figure 2 using PkMin.
Figure 6d gives the characteristics of unified Task , which inherits the convexity properties of the parent tasks under equal core distribution. Because the DAG in Figure 6c is already serialized, then PkMin can directly operate on it. PkMin runs convex optimization sub-routine again on the unified DAG to obtain a new core allocation as shown in Figure 6e. However, allocation in Figure 6e has worse peak power than the allocation in Figure 6b, and, therefore, the algorithm terminates with allocation in Figure 6b as the reported solution.
6. Experimental Evaluation
Experimental Setup: we use Sniper simulator [32] to simulate the execution of multi-threaded many-core applications. The simulated multi-core is composed of eight tiles—with two cores each—arranged in a 4 × 2 grid connected while using a Network on Chip (NoC) with hop latency of four cycles and link bandwidth of 256 bits. Two cores within the tile share a 1 MB L2 cache. Cores implement Intel x86 Instruction Set Architecture (ISA) and run at a frequency of 4 GHz with each core holding a 32 KB private L1 data and instruction caches. Many-core’s power consumption is provided by the integrated McPat [14] assuming a 22 nm technology node fabrication.
Application Task Graphs: we use a set of five benchmarks—CilkSort, DFS, Fibonacci, Pi, and Queens—from Lace benchmark suite [33] to create our tasks. In order to generate random DAGs of size N, we first sample with replacement N tasks from the benchmark set, thereafter with a probability p, we add an edge between select pair of nodes, such that the acyclic property of the resulting directed graph is preserved. The setup allows for us to thoroughly evaluate PkMin with an arbitrarily large number of tasks while simultaneously generating a large number of randomized applications for a given number of tasks.
Application Deadline: setting up arbitrarily short deadlines will render application execution infeasible. In order to set up a feasible deadline, we first note the minimum execution time that is achievable by all of the benchmarks, as, for example, illustrated in Figure 1a for DFS and CilkSort. Let B be the benchmark execution time that is worst among all of the benchmarks considered. We then set the deadline to for an application task graph with N tasks. This ensures the existence of a feasible solution. This is also a fairly tight deadline, as all of the tasks are forced to execute with maximum available cores, if they choose to execute one after the other in a serial fashion. If the application deadline is relaxed further, then other execution configurations with much lower cores (and hence peak power) may become feasible.
Baseline: we are unaware of any work that also solves the problem of peak power minimization for multi-threaded many-cores applications with DAG under deadline constraints. The authors of [12] propose a framework, called D&C, which uses a divide and conquer algorithm to minimize execution time for multi-threaded many-core applications with DAG under a peak power constraint. Therefore, D&C solves dual of the problem solved by PkMin. We modify D&C to DCPace that solves the same problem as PkMin by replacing the constraint from peak power to deadline and replacing the objective function from minimizing executing time to minimizing peak power. Modification keeps the underlying algorithm’s ethos intact. DCPace thus acts as a suitable baseline for PkMin.
DCPace begins by allocating cores to tasks, to run them in their most energy-efficient configuration, i.e., the one with minimum energy consumed. It then generates an intermediate schedule by scheduling the tasks at the earliest possible time permitted under precedence constraints. It then identifies the midpoint of the schedule along the time axis. All of the tasks that are actively executing at the midpoint must be independent. DCPace divides the task into three bins beg, mid, and end. All three bins are assigned a sub-deadline that is equal to the third of the original deadline. All independent tasks in mid are greedily scheduled, such that the bin’s peak power is minimized under the available core and sub-deadline constraints. This is done using a strip packing heuristic, like Next-Fit Decreasing Height (NFDH) [34]. In a strip-packing problem, a collection of rectangles of different height and width are to be packed on a rectangular bin, with a fixed width and unbounded height, such that no two rectangles overlap. This problem is NP-complete. NFDH begins by sorting the rectangles in decreasing order of their heights. After that, it packs the rectangle in a left-justified fashion until the next rectangle can no longer fit in the remaining space to the right. A new level is defined as the packing restarts from the remaining rectangles. DCPace continues to divide recursively mid and end using their midpoint. Recursion breaks when a bin becomes a singleton with only one task.
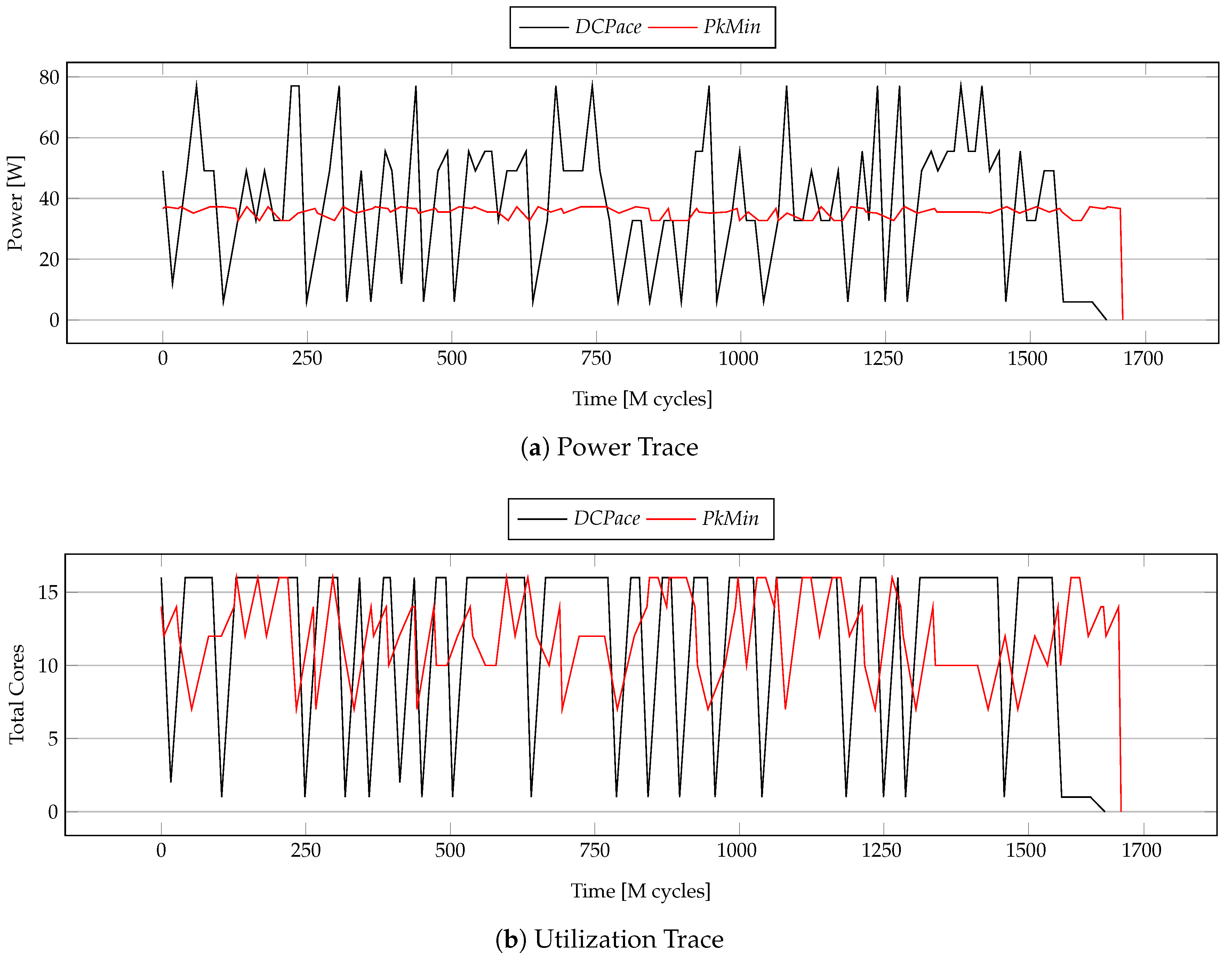
Power and Energy Consumption Analyses:Figure 7 illustrates the working of DCPace and PkMin algorithms. In this experiment, we use tasks graph with 100 tasks and set the deadline to 1700 million clock cycles or 425 ms. DCPace chooses the most energy-efficient core allocation to execute each task, which is not changed thereafter. Given the task execution time and task peak power characteristics, as shown in Figure 1, the minimum energy allocation can only occur either when all of the cores are allocated, or a minimum number of core is allocated to each task. Figure 7b, shows the variation in the total cores allocated as the application execution proceeds in time. Both DCPace and PkMin show considerable variations in the total-cores allocated, although the former exclusively varies between the maximum and the minimum possible allocations. Because the goal of PkMin is to reduce peak power exclusively, its allocations amongst tasks under PkMin are such that any two different non-overlapping tasks have almost similar peak power consumption when compared to DCPace. PkMin exploits the convexity properties of the task characteristics in order to achieve this “equivalent power” allocations. The power trace of application execution in Figure 7a under PkMin has almost no peaks and troughs as compared to DCPace.
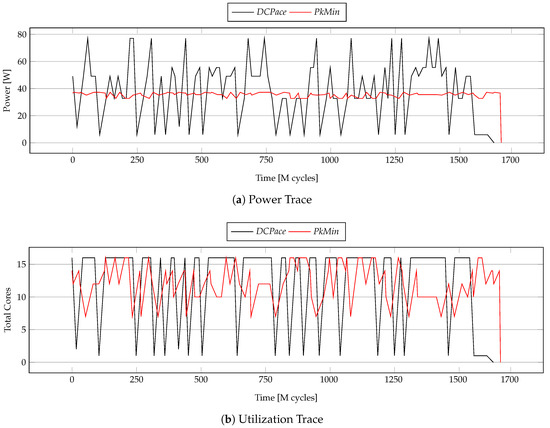
Figure 7.
Power consumption and core utilization trace.
Performance Evaluation: we evaluate the efficacy of PkMin in minimizing peak power for applications with an increasing number of tasks. We also evaluate the same applications using DCPace to put the performance of PkMin in context.
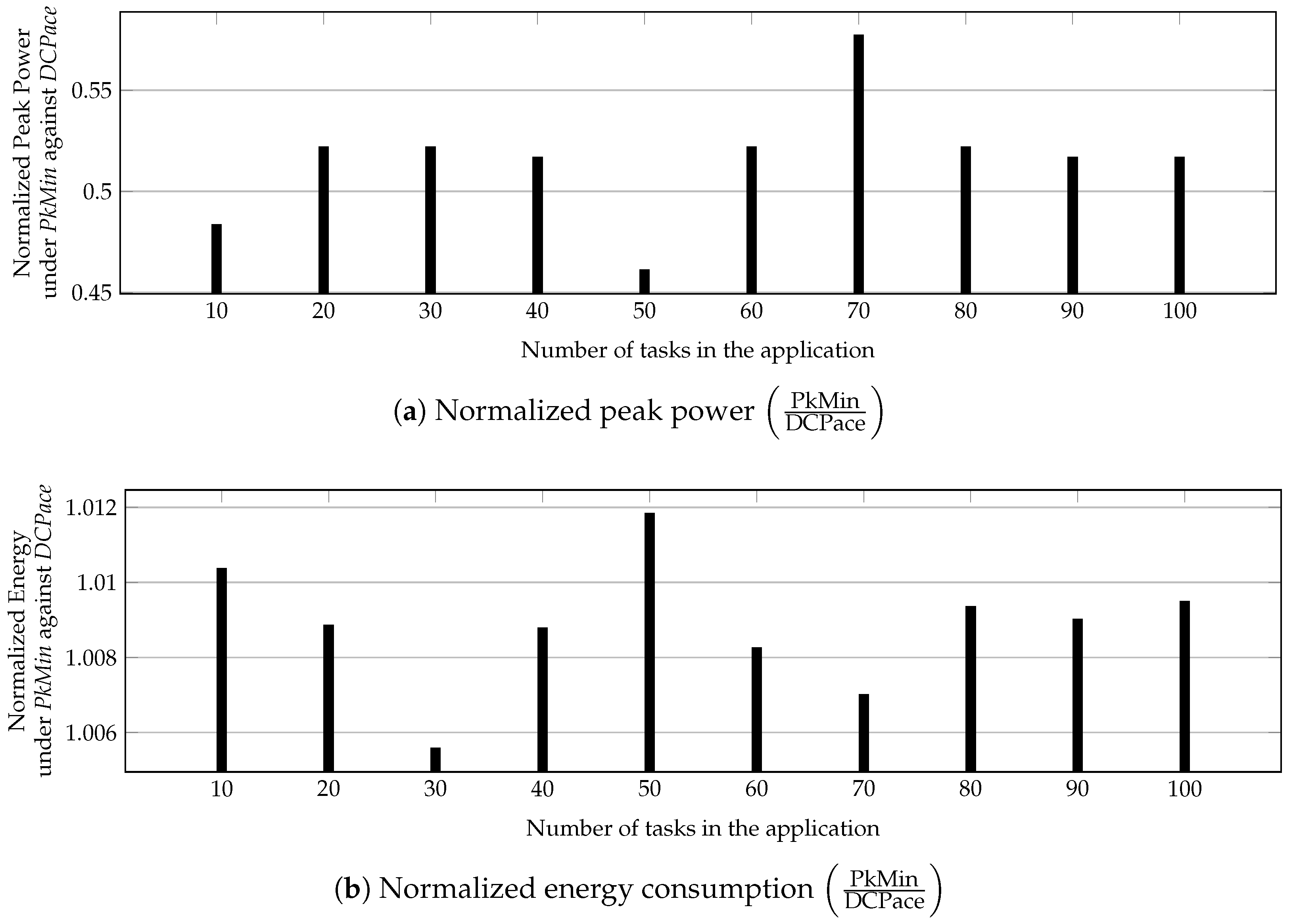
First, we show the peak power savings for application task graph of sizes varying from 10 to 100. We set the deadline to million clock cycles, where the best possible execution time of each task is 17 million clock cycles and N is the number of tasks in the application. Figure 8a shows that PkMin has, on average, 48% lower peak power when compared to the DCPace. The energy consumption of PkMin is, however, around higher than the DCPace, as illustrated in Figure 8b.
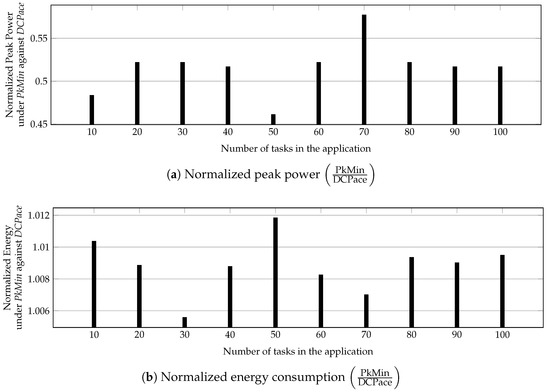
Figure 8.
Application performance under PkMin normalized with respect to DCPace. Application size varies from 10 tasks to 100 tasks.
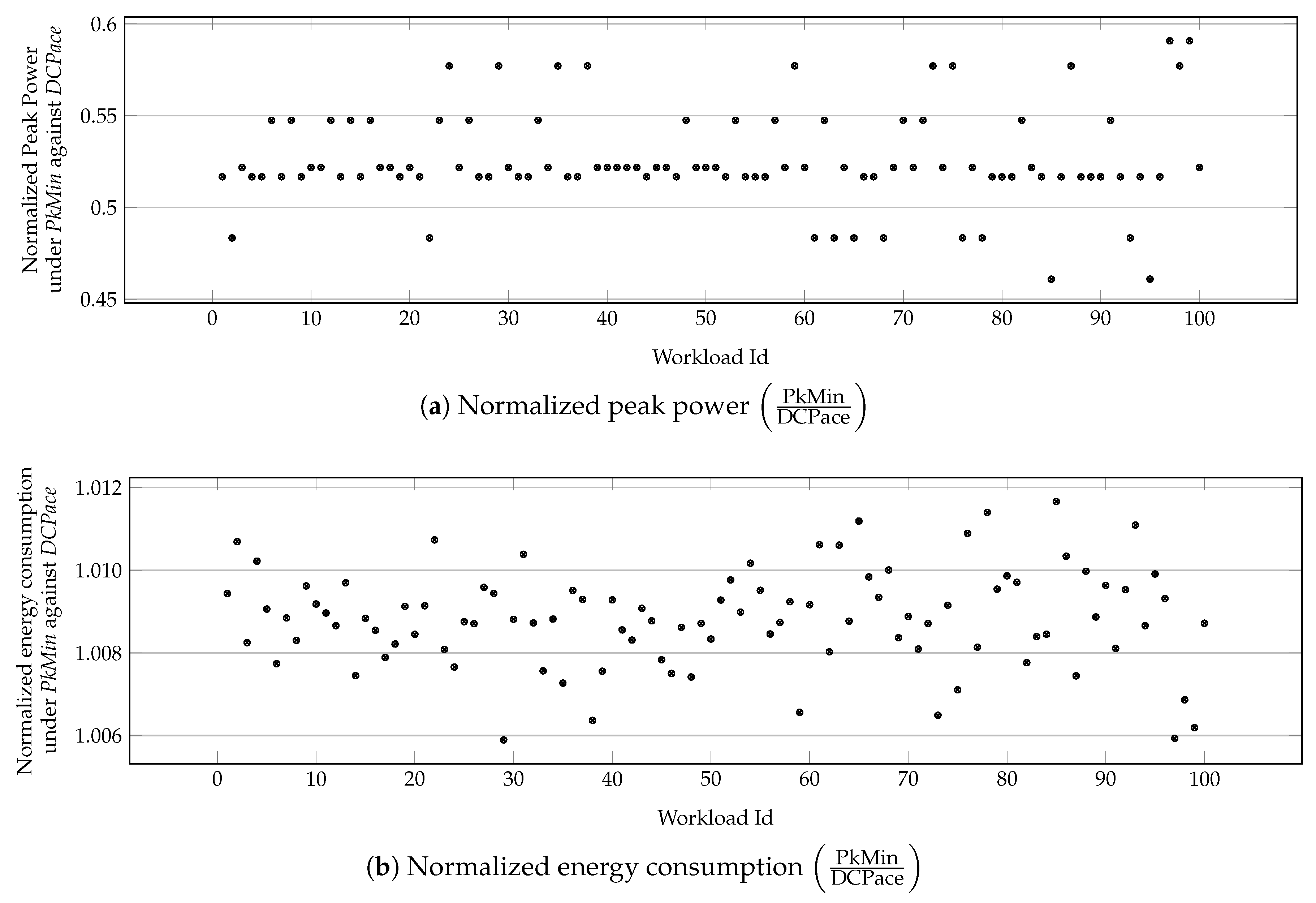
Figure 9 orthogonally shows the efficacy of PkMin in minimizing the peak power of hundred random applications, each with 100 tasks. The deadline is similarly set to . PkMin results in lower peak power than DCPace, with only additional energy overhead.
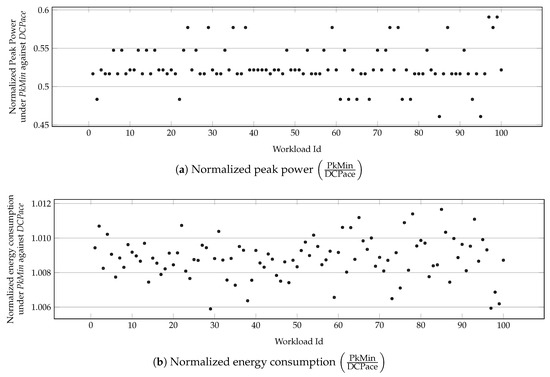
Figure 9.
Application performance under PkMin with 100 task applications normalized against their performance under DCPace.
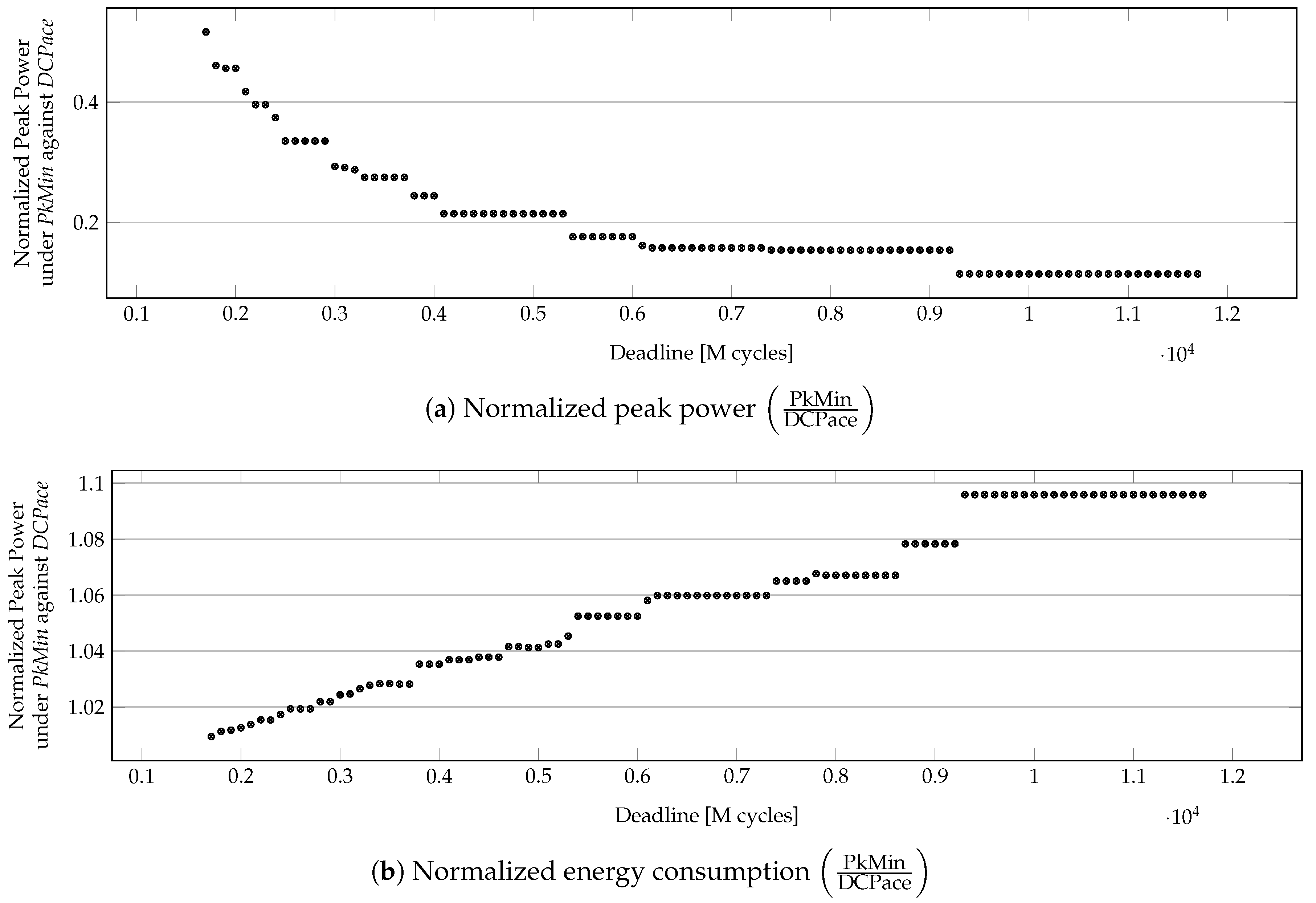
Figure 10 shows the efficacy of PkMin in minimizing peak power in a random application (with 100 tasks) as its deadline is relaxed. In this case, the improvement of peak power for PkMin over DCPace comes at the cost of worsening energy consumption. However, a significant reduction in the peak power of approximately is possible with less than increase in energy consumed.
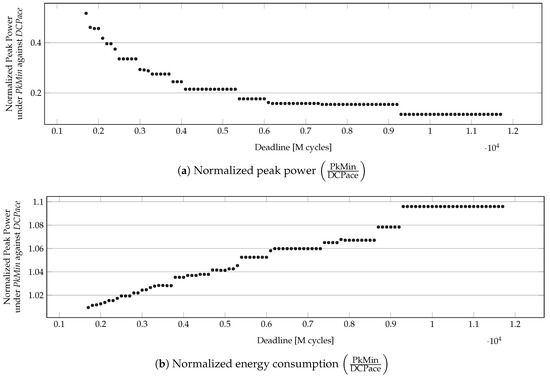
Figure 10.
Peak power under PkMin for a 100-task application with different deadlines that are normalized against its peak power under DCPace.
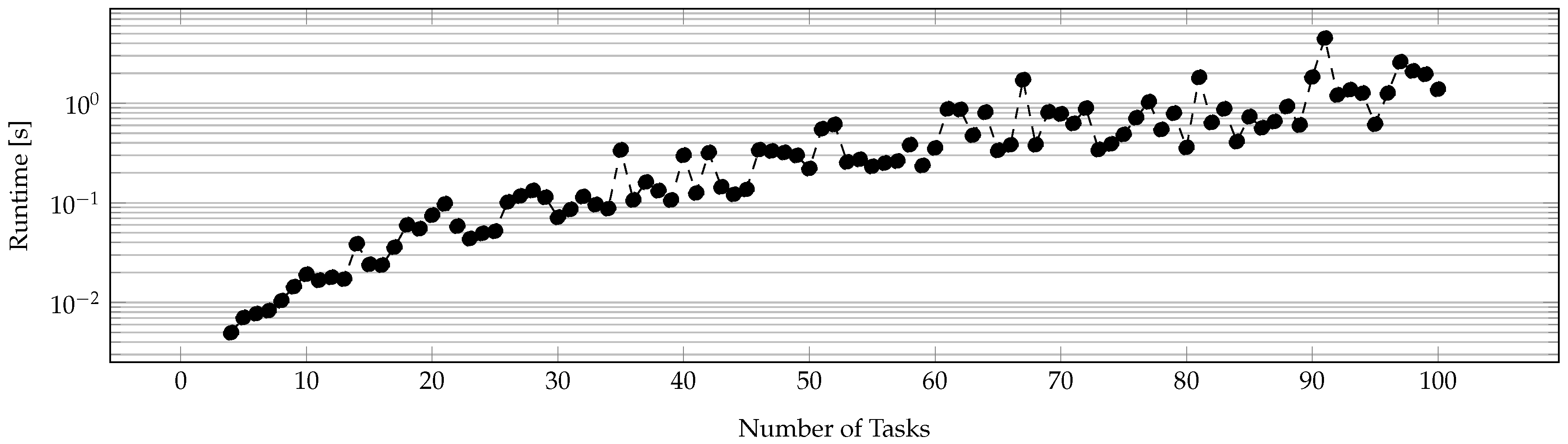
Scalability:PkMin uses NLOpt internally, which has a low polynomial-time computational complexity. It invokes NLOpt at the max number of tasks times, keeping the computational complexity still polynomial. PkMin also uses topological sort and transitive closure graph algorithms that also have a worst-case polynomial computational complexity of and , respectively. This low polynomial-time computational complexity makes PkMin highly scalable. Figure 11 shows the increase in worst-case problem-solving time that is required under PkMin with an increase in the number of tasks in applications. For a 100-task application, PkMin requires s to compute the near-optimal configuration.
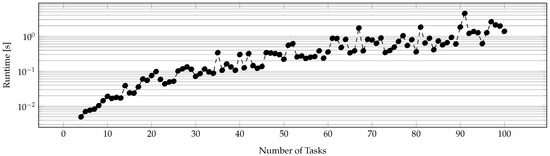
Figure 11.
Runtime of PkMin for applications with different number of tasks.
7. Conclusions
We introduced a framework, called PkMin, in this work that solves the problem of peak power minimization for a multi-thread many-core application with DAG under a deadline. PkMin exploits the execution characteristics of multi-threaded tasks in many-core applications to optimally solve the problem for a serialized DAG in the continuous domain while using convex optimization. It then uses the convex optimization sub-routine to solve the problem near-optimally for any generic DAG.
Empirical evaluations on hundreds of applications show configurations obtained under PkMin have, on average, up to 48% lower peak power than similar state-of-the-art with less than additional total energy. The peak power savings can be further increased to 88% with less than energy overheads whenever the deadline is relaxed. PkMin has polynomial-time computation complexity with negligible problem-solving overheads, which makes it suitable for use at both run-time and design-time.
Author Contributions
Conceptualization, A.M., A.P. and T.M.; methodology, A.M., A.P. and T.M.; software, A.M.; validation, A.M.; formal analysis, A.P. and A.M.; resources, T.M.; writing–original draft preparation, A.P. and A.M.; writing–review and editing, A.M., A.P. and T.M.; supervision, T.M.; project administration, T.M.; funding acquisition, T.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Research Foundation, Prime Minister’s Office, Singapore under its IndustryIHL Partnership Grant NRF2015-IIP003.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Singh, A.K.; Jigang, W.; Kumar, A.; Srikanthan, T. Run-time Mapping of Multiple Communicating Tasks on MPSoC Platforms. Procedia Comput. Sci. 2010, 1, 1019–1026. [Google Scholar] [CrossRef][Green Version]
- Kriebel, F.; Shafique, M.; Rehman, S.; Henkel, J.; Garg, S. Variability and Reliability Awareness in the Age of Dark Silicon. IEEE Des. Test 2015, 33, 59–67. [Google Scholar] [CrossRef]
- Salehi, M.; Shafique, M.; Kriebel, F.; Rehman, S.; Tavana, M.K.; Ejlali, A.; Henkel, J. dsReliM: Power-constrained Reliability Management in Dark-Silicon Many-Core Chips under Process Variations. In Proceedings of the 2015 International Conference on Hardware/Software Codesign and System Synthesis (CODES+ISSS), Amsterdam, The Netherlands, 4–9 October 2015. [Google Scholar]
- Ma, Y.; Chantem, T.; Dick, R.P.; Hu, X.S. Improving System-Level Lifetime Reliability of Multicore Soft Real-Time Systems. IEEE Trans. Very Large Scale Integr. Syst. 2017, 25, 1895–1905. [Google Scholar] [CrossRef]
- Pagani, S.; Bauer, L.; Chen, Q.; Glocker, E.; Hannig, F.; Herkersdorf, A.; Khdr, H.; Pathania, A.; Schlichtmann, U.; Schmitt-Landsiedel, D.; et al. Dark Silicon Management: An Integrated and Coordinated Cross-Layer Approach. Inf. Technol. 2016, 58. [Google Scholar] [CrossRef]
- Pathania, A.; Khdr, H.; Shafique, M.; Mitra, T.; Henkel, J. QoS-Aware Stochastic Power Management for Many-Cores. In Proceedings of the 2018 55th ACM/ESDA/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 24–28 June 2018. [Google Scholar]
- Pathania, A.; Khdr, H.; Shafique, M.; Mitra, T.; Henkel, J. Scalable Probabilistic Power Budgeting for Many-Cores. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition (DATE), Lausanne, Switzerland, 27–31 March 2017. [Google Scholar]
- Pathania, A.; Venkataramani, V.; Shafique, M.; Mitra, T.; Henkel, J. Distributed Scheduling for Many-Cores Using Cooperative Game Theory. In Proceedings of the 2016 53nd ACM/EDAC/IEEE Design Automation Conference (DAC), Austin, TX, USA, 5–9 June 2016. [Google Scholar]
- Pathania, A.; Venkataramani, V.; Shafique, M.; Mitra, T.; Henkel, J. Distributed Fair Scheduling for Many-Cores. In Proceedings of the 2016 Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 14–18 March 2016. [Google Scholar]
- Pathania, A.; Venkatramani, V.; Shafique, M.; Mitra, T.; Henkel, J. Optimal Greedy Algorithm for Many-Core Scheduling. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2017, 36, 1054–1058. [Google Scholar] [CrossRef]
- Venkataramani, V.; Pathania, A.; Shafique, M.; Mitra, T.; Henkel, J. Scalable Dynamic Task Scheduling on Adaptive Many-Core. In Proceedings of the 2018 IEEE 12th International Symposium on Embedded Multicore/Many-Core Systems-on-Chip (MCSoC), Hanoi, Vietnam, 12–14 September 2018. [Google Scholar]
- Demirci, G.; Marincic, I.; Hoffmann, H. A Divide and Conquer Algorithm for DAG Scheduling Under Power Constraints. In Proceedings of the International Conference for High Performance Computing, Networking, Storage, and Analysis, Dallas, TX, USA, 11–16 November 2018. [Google Scholar]
- Carlson, T.E.; Heirman, W.; Eeckhout, L. Sniper: Exploring the Level of Abstraction for Scalable and Accurate Parallel Multi-Core Simulation. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis (SC), Seatle, WA, USA, 12–18 November 2011. [Google Scholar]
- Li, S.; Ahn, J.H.; Strong, R.D.; Brockman, J.B.; Tullsen, D.M.; Jouppi, N.P. McPAT: An Integrated Power, Area, and Timing Modeling Framework for Multicore and Manycore Architectures. In Proceedings of the 2009 42nd Annual IEEE/ACM International Symposium on Microarchitecture (MICRO), New York, NY, USA, 12–16 December 2009. [Google Scholar]
- Singh, A.K.; Shafique, M.; Kumar, A.; Henkel, J. Mapping on multi/many-core systems: Survey of current and emerging trends. In Proceedings of the 2013 50th ACM/EDAC/IEEE Design Automation Conference (DAC), Austin, TX, USA, 29 May–7 June 2013. [Google Scholar]
- Rapp, M.; Pathania, A.; Henkel, J. Pareto-optimal power-and cache-aware task mapping for many-cores with distributed shared last-level cache. In Proceedings of the International Symposium on Low Power Electronics and Design (ISLPED), Seattle, WA, USA, 23–25 July 2018. [Google Scholar]
- Rapp, M.; Pathania, A.; Mitra, T.; Henkel, J. Prediction-Based Task Migration on S-NUCA Many-Cores. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition (DATE), Florence, Italy, 25–29 March 2019. [Google Scholar]
- Rapp, M.; Sagi, M.; Pathania, A.; Herkersdorf, A.; Henkel, J. Power-and Cache-Aware Task Mapping with Dynamic Power Budgeting for Many-Cores. IEEE Trans. Comput. 2019, 69, 1–13. [Google Scholar] [CrossRef]
- Bartolini, A.; Borghesi, A.; Libri, A.; Beneventi, F.; Gregori, D.; Tinti, S.; Gianfreda, C.; Altoè, P. The DAVIDE Big-Data-Powered Fine-Grain Power and Performance Monitoring Support. In Proceedings of the 15th ACM International Conference on Computing Frontiers, Ischia, Italy, 8–10 May 2018. [Google Scholar]
- Oleynik, Y.; Gerndt, M.; Schuchart, J.; Kjeldsberg, P.G.; Nagel, W.E. Run-Time Exploitation of Application Dynamism for Energy-Efficient Exascale Computing (READEX). In Proceedings of the 2015 IEEE 18th International Conference on Computational Science and Engineering, Porto, Portugal, 21–23 October 2015. [Google Scholar]
- Lee, B.; Kim, J.; Jeung, Y.; Chong, J. Peak Power Reduction Methodology for Multi-Core Systems. In Proceedings of the International SoC Design Conference (ISOCC), Seoul, Korea, 22–23 November 2010. [Google Scholar]
- Lee, J.; Yun, B.; Shin, K.G. Reducing Peak Power Consumption in Multi-Core Systems without Violating Real-Time Constraints. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 1024–1033. [Google Scholar]
- Munawar, W.; Khdr, H.; Pagani, S.; Shafique, M.; Chen, J.J.; Henkel, J. Peak Power Management for Scheduling Real-Time Tasks on Heterogeneous Many-Core Systems. In Proceedings of the 20th IEEE International Conference on Parallel and Distributed Systems (ICPADS), Hsinchu, Taiwan, 16–19 December 2014. [Google Scholar]
- Ansari, M.; Yeganeh-Khaksar, A.; Safari, S.; Ejlali, A. Peak-Power-Aware Energy Management for Periodic Real-Time Applications. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2019, 39, 779–788. [Google Scholar] [CrossRef]
- Johnson, S.G. The NLopt Nonlinear-Optimization Package. Available online: https://github.com/stevengj/nlopt (accessed on 25 September 2020).
- Svanberg, K. A Class of Globally Convergent Optimization Methods Based on Conservative Convex Separable Approximations. SIAM J. Optim. 2002, 12, 555–573. [Google Scholar] [CrossRef]
- Bonami, P.; Kilinç, M.; Linderoth, J. Algorithms and Software for Convex Mixed Integer Nonlinear Programs. In Mixed Integer Nonlinear Programming; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Moriguchi, S.; Tsuchimura, N. Discrete L-Convex Function Minimization Based on Continuous Relaxation. Pac. J. Optim. 2009, 5, 227–236. [Google Scholar]
- Chekuri, C.; Khanna, S. On Multidimensional Packing Problems. J. Comput. 2004, 33, 837–851. [Google Scholar] [CrossRef]
- Pearce, D.J.; Kelly, P.H. A Dynamic Topological Sort Algorithm for Directed Acyclic Graphs. J. Exp. Algorithmics 2007. [Google Scholar] [CrossRef]
- Ioannidis, Y.E.; Ramakrishnan, R. Efficient Transitive Closure Algorithms. In Proceedings of the 1988 VLDB Conference: 14th International Conference on Very Large Data Bases, Los Angeles, CA, USA, 29 August–1 September 1988. [Google Scholar]
- Pathania, A.; Henkel, J. HotSniper: Sniper-based toolchain for many-core thermal simulations in open systems. IEEE Embed. Syst. Lett. 2018, 11, 54–57. [Google Scholar] [CrossRef]
- Van Dijk, T.; van de Pol, J.C. Lace: Non-Blocking Split Deque for Work-Stealing. In European Conference on Parallel Processing (Euro-Par); Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Coffman, E.G., Jr.; Garey, M.R.; Johnson, D.S.; Tarjan, R.E. Performance Bounds for Level-Oriented Two-Dimensional Packing Algorithms. SIAM J. Comput. 1980, 9, 808–826. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).