An Interpretable Hybrid System Using Temporal Convolutional Network and Informer Model for Carbon Price Prediction

Abstract

Scientific, accurate, and interpretable carbon price forecasts provide critical support for addressing climate change, achieving low-carbon goals, and informing policy-making and corporate decision-making in energy and environmental markets. However, the existing studies mainly focus on deterministic forecasting, with obvious limitations in data feature diversity, model interpretability, and uncertainty quantification. To fill these gaps, this study constructs an interpretable hybrid system for carbon market price prediction by combining feature screening algorithms, deep learning models, and interpretable explanatory analysis methods. Specifically, this study first screens important variables from twenty-one multi-source structured and unstructured influencing factor datasets on five dimensions affecting carbon price using the Boruta algorithm. Immediately after that, this study proposes a hybrid architecture of bidirectional temporal convolutional network and Informer models, where a bidirectional temporal convolutional network is used to extract local spatio-temporal dependent features, while Informer captures long sequences of global features through the connectivity mechanism, thus realizing staged feature extraction. Then, to improve the interpretability of the model and quantify the uncertainty, this study introduces Shapley additive explanations to analyze the feature contribution in the prediction process, and the Monte Carlo dropout method is used to achieve interval prediction. Finally, the empirical results in China’s Guangdong and Shanghai carbon markets show that the proposed model significantly outperforms benchmark models, and the coverage probability of the obtained prediction intervals significantly outperforms the confidence level. The Shapley additive explanation analysis reveals regional heterogeneity drivers. In addition, the proposed model is also intensively validated in the European carbon market and the U.S. natural gas market, which also demonstrate an excellent prediction performance, indicating that the model has good robustness and applicability.

1. Introduction

Carbon emissions from fossil fuels contribute to global warming [1], which poses substantial challenges to environmental conservation, economic stability, and social equity. To address this issue, the European Union launched the world’s first large-scale carbon market, the European Union Emissions Trading System (EU-ETS), in 2005, employing a cap-and-trade mechanism [2]. Carbon trading has been increasingly adopted by various countries and regions as an effective mechanism to control carbon emissions. As a responsible major economy, China has been expanding its carbon emissions trading pilot programs since 2011 in Beijing, Shanghai, Tianjin, Chongqing, Shenzhen, and provinces including Hubei, Guangdong, and Fujian [3,4]. The carbon price serves as the core economic tool of carbon markets, incentivizing corporate emissions reductions. Therefore, accurate carbon price forecasting is crucial for governments to formulate evidence-based policies and for enterprises to participate effectively. However, the nonlinearity and complexity of carbon markets pose significant forecasting challenges [5].

Currently, carbon price prediction research primarily covers two aspects: the analysis of influencing factors and the improvement of prediction models. Before the advent of deep learning, econometric models were commonly employed for a univariate carbon price prediction based solely on historical data. However, with a deeper analysis of data characteristics, it became evident that carbon price exhibits nonlinear and non-stationary properties [6], making it difficult to achieve accurate predictions using historical data alone. As the superiority of machine learning (ML) techniques has been demonstrated across various domains, artificial intelligence (AI)-based models leveraging ML methods have proven effective in capturing nonlinear features [7]. Consequently, an increasing number of scholars have integrated ML approaches with external factors to enhance carbon price prediction accuracy [8].

Regarding influencing factor analysis, the existing carbon price forecasting studies primarily focus on structural determinants, including macroeconomic indicators, energy price fluctuations, and international carbon market linkages; there remains a notable research gap in the systematic incorporation and analysis of non-structural data sources [9,10]. One the one hand, numerous scholars emphasize the substantial influence of energy prices on carbon price fluctuations [11,12]. Wang and Guo (2018) [13] identified that oil and natural gas prices exert significant influences on carbon price dynamics. Wang et al. (2023) [14] further dissected the transmission mechanisms through which energy prices influence carbon prices. On the other hand, in the macroeconomic context, stock prices have become a crucial factor influencing carbon prices [15]. Shi et al. (2023) [16] found that macroeconomic fluctuations significantly impact carbon prices in their study of China’s carbon market. Song and Liu (2024) [17] employed a vector autoregression model to study the Chinese market, revealing that stock prices significantly influence carbon prices. In addition, monetary policy tools such as interest rates and government bonds exert a substantial influence on carbon market prices [18,19]. Additionally, carbon price fluctuations may be influenced by environmental factors [20,21]. Zhou et al. (2024) [22] found through their research that environmental variables such as air quality not only influence short-term fluctuations in carbon prices but also participate in the long-term price formation of carbon markets. With the advancement of big data technologies, internet search behaviors have increasingly become a crucial component of online information. Unstructured data are playing an ever more significant role in predictive analytics. Zhao et al. (2025) [23] found that combining Baidu search index data with energy prices and economic factors can significantly improve the accuracy of carbon price forecasting. Zhou and Du (2025) [24] proposed a multivariate event-enhanced pre-trained large language model (LLM) that integrates unstructured text data through sentiment analysis, demonstrating an exceptional predictive accuracy and robustness in the Hubei and Shanghai carbon markets.

As for the carbon price forecasting models, they can be broadly categorized into three approaches: traditional statistical models, AI models, and hybrid models [25]. Traditional statistical models have been widely employed in early carbon price prediction studies [26,27]. However, these models often rely on linear assumptions, making it challenging to handle the nonlinear and highly volatile characteristics of carbon prices. In AI models, long short-term memory (LSTM) [28], convolutional neural networks (CNNs) [29], and temporal convolutional networks (TCNs) [30] have gained increasing attention in recent years. These models can autonomously learn complex carbon price patterns and effectively capture long-term dependencies in time series data. Nevertheless, they also face challenges including overfitting, insufficient interpretability, and parameter randomness [31]. To address these challenges, researchers have developed hybrid prediction models by integrating intelligent algorithms [32]. Duan et al. (2024) [33] employed the whale optimization algorithm (WOA) to optimize the parameters of the extreme gradient boosting (XGBoost) model. Building on this, researchers have explored integrating feature selection methods and decomposition techniques to further improve prediction accuracy [34]. Liu et al. (2024) [35] combined multi-stage decomposition with interval multilayer perceptron models enhanced by a sparrow search algorithm to obtain final carbon price predictions. Although the aforementioned models have achieved certain research progress, most of them are based on a single prediction model. Given that carbon prices are influenced by multiple factors and exhibit significant variations across different markets, it is difficult for a single prediction model to fit all carbon price components [36]. Consequently, hybrid models comprising multiple prediction techniques can fully integrate the advantages of each constituent model through strategic combination, leveraging their respective strengths in handling different data characteristics to achieve more robust and adaptable prediction outcomes [37]. Cui and Niu (2024) [38] proposed a hybrid prediction framework integrating an attention–temporal convolutional network–bidirectional gated recurrent unit and LSTM for a model ensemble, with the entropy method assigning weights to their predictions, demonstrating a superior prediction performance. Zhao et al. (2025) [39] developed an adaptive multi-factor integrated hybrid model based on periodic reconstruction and random forest techniques, demonstrating an outstanding predictive performance in empirical studies. Moreover, for complex hybrid models, the emergence of interpretability enhances transparency by visualizing decision-making principles, aiding users in understanding model logic and enabling stakeholders to grasp the key factors driving predictions, which is now widely applied in fields such as crude oil price and electricity load forecasting [40,41,42].

Inspired by the preceding discussion, this study combines feature screening algorithms, deep learning models, and interpretable explanatory analytics to construct an interpretable hybrid system for carbon market price prediction. First, multidimensional data sources, including macroeconomic indicators and the Baidu Index, are considered. The Boruta feature selection algorithm is then employed to construct a feature subspace, ensuring the inclusion of the most relevant predictive variables. Next, this study proposes a hybrid architecture of BiTCN and the Informer model, where BiTCN is used to extract local spatio-temporal dependent features, while the Informer captures the global features of the long sequences through the connectivity mechanism, which enables phased feature extraction and improves the prediction accuracy. Then, in order to improve the interpretability of the model and quantify the uncertainty, this study introduces the Shapley additive explanations (SHAP) to analyze the feature contributions in the prediction process and the Monte Carlo dropout method to achieve interval prediction, which provides a more interpretable prediction framework. Moreover, the contributions of this study are summarized below. (1) Previous studies have largely focused solely on structured data, neglecting unstructured information such as market sentiment. This study integrates twenty-one influential factors, including environmental variables such as weather and air quality, as well as macroeconomic indicators such as government bond yields and stock prices. Additionally, it also incorporates non-structural data, such as the Baidu Index, which can reflect real-time market sentiment and public attention, thereby enhancing the accuracy and timeliness of the predictions. (2) Traditional methods often employ linear ensembles, which struggle to uncover synergies between different models and provide only point predictions lacking interpretability analysis. This paper proposes a hybrid model that combines the strengths of multiple deep learning models. It preserves the original features without complex data decomposition, significantly improving prediction accuracy and enabling interval predictions. Simultaneously, it achieves interpretable predictive analysis using the SHAP method. (3) Previous studies lacked cross-regional, multi-scenario experimental validation. This paper conducts comparative experiments across multiple carbon markets, including Shanghai, Guangdong, and the EU. The results demonstrate the model’s significant predictive advantages and robustness across diverse market environments.

2. Methods

2.1. Framework of the Proposed Hybrid System

This study builds a proposed hybrid system for multi-carbon price prediction tasks, consisting of data collection, feature selection, hybrid model construction, and a further discussion and application of the model, as presented in Figure 1.

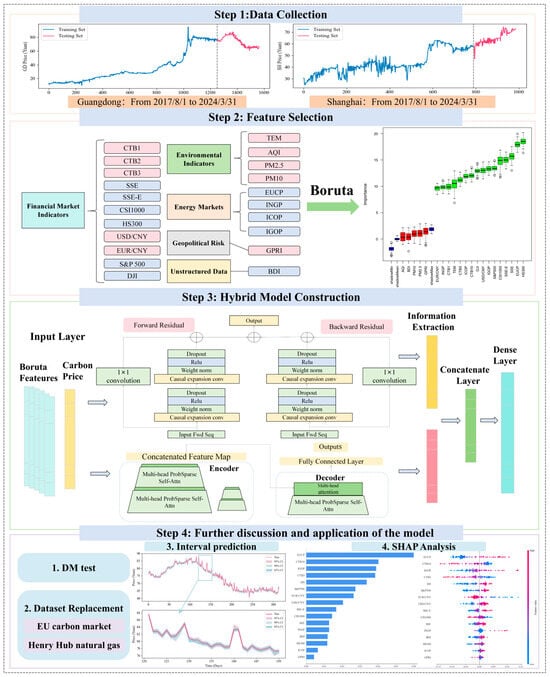
Figure 1. The detailed prediction framework of this study.

(1)

Data collection: Daily carbon price data from the Guangdong and Shanghai carbon emissions trading markets are selected for empirical analysis, covering the period from 1 August 2017 to 31 March 2024.

(2)

Feature selection: The Boruta method is first applied to reduce the dimensionality of 21 commonly used carbon prices and influencing factor data across five dimensions. These factors encompass both structured and unstructured data. Subsequently, Experiment I is conducted to validate the effectiveness of the Boruta method in enhancing prediction accuracy.

(3)

Hybrid model construction: This step first constructs common baseline models (LSTM, GRU, TCN, and Transformer) and their enhanced variants (BiLSTM, BiGRU, BiTCN, and Informer). Through Experiment II, the optimal models, i.e., Informer and Transformer, are selected via comparative analysis. Subsequently, the Informer and Transformer models are combined to build a hybrid model, namely BiTCN-Informer. Finally, Experiment III is also conducted to validate the predictive performance of the proposed hybrid model through comparative analysis.

(4)

Further discussion and application of the model: Statistical hypothesis testing and experiments with additional datasets are employed to further validate the predictive efficacy of the proposed models. Concurrently, the SHAP method is also introduced to elucidate the predictive mechanisms of the hybrid model, while Monte Carlo dropout is utilized to quantify uncertainty and enable interval prediction. This fully demonstrates the practical value of the hybrid model, whose rich insights provide robust support for corporate and governmental decision-making.

2.2. Boruta Algorithm

Boruta is a wrapper-based feature selection algorithm that builds upon the random forest model [43]. It employs the Z-score as its benchmark criterion, aiming to identify all features that contribute significantly to the response variable. The core idea of Boruta is to introduce randomness into the system and assess the importance of each feature by comparing it with its randomly permuted counterpart, known as “shadow features.” This approach effectively mitigates misleading effects caused by correlations and stochastic fluctuations, ensuring a more reliable selection of influential factors. The Boruta algorithm follows an iterative process that can be summarized as follows:

(1)

Shadow feature construction: Duplicate the original features and randomly shuffle their values to create “shadow features”, which serve as a baseline for comparison.

(2)

Random forest-based voting: Train a random forest model on the augmented dataset and compute the feature importance scores. Features that consistently outperform their shadow counterparts are retained, while those with lower importance are removed.

(3)

Convergence and feature selection: The process continues until all features are classified as “important”, “unimportant”, or “tentatively important”.

2.3. The Hybrid BiTCN-Informer Model

This study proposes a hybrid model for carbon price prediction, called BiTCN-Informer, where the Informer serves as the primary model and BiTCN complements the Informer’s long-term forecasting capability by extracting local features.

2.3.1. Bidirectional Temporal Convolutional Network (BiTCN)

The BiTCN is an advanced deep learning architecture proposed in 2023 [44], which is designed to enhance long time series prediction. It is structured into three main components: bidirectional temporal blocks, the feature fusion layer, and residual connections.

(1)

Bidirectional temporal blocks

BiTCN retains dilation convolution as a core operation. Among them, backward convolution, which is an important component of the bidirectional temporal blocks, introduces an additional pathway that enables the network to incorporate both historical dependencies and future covariates. The mathematical formulation of forward and backward dilated convolutions in BiTCN is as follows:

$$H_f\left(t\right)=\sum _{i=0}^{k-1}{h}_f\left(i\right)·x_{t-d_m·i}$$

(1)

$$H_b\left(t\right)=\sum _{i=0}^{k-1}{h}_b\left(i\right)·x_{t+d_m·i}$$

(2)

where $H_f\left(t\right)$ and $H_b\left(t\right)$ represent the forward and backward outputs of BiTCN, $h_f\left(i\right)$ and $h_b\left(i\right)$ denote the forward and backward elements in the convolution kernel, k is the kernel size, $x_t$ is the input, and $d_m·i$ is the expansion factor. Moreover, Batch Normalization and the ReLU activation function are applied to stabilize training and enhance feature representation.

(2)

Feature fusion layer

The feature fusion layer aims to integrate forward and backward outputs into a unified representation. This layer ensures that the model effectively leverages information from both temporal perspectives, enhancing feature extraction and improving predictive performance. The fused output $H\left(t\right)$ can be calculated by Equation (3).

$$H_b\left(H\left(t\right)=\mathsf{\alpha }{·H}_f\left(t\right)+(1-\mathsf{\alpha })·H_b\left(t\right)\right)=\sum _{i=0}^{k-1}{h}_b\left(i\right)·x_{t+d_m·i}$$

(3)

(3)

Residual connections

The main effect of residual connections is to stabilize training and facilitate gradient flow, linking the input directly to the output of each layer. This prevents vanishing gradients in deep networks and helps preserve essential features from earlier layers. The final output $y_{BiTCN}$ is mathematically expressed as follows:

$$y_{BiTCN}=ReLU\left(H\right(t)+x_t)$$

(4)

2.3.2. Staged Feature Extraction

Due to single models frequently lacking the capability to extract complex features, this study proposes a connection mechanism to develop a hybrid model to achieve hierarchical feature extraction. This mechanism employs linear projection to facilitate dimensional adaptation between models. Subsequent to the connection mechanism, the local features extracted by BiTCN can be augmented with the long-term dependencies identified by Informer. While reducing noise, it can effectively improve the global modeling ability of Informer [45,46]. Firstly, as Equation (5) shows, the BiTCN output features are projected to the Informer input dimension via linear transformation:

$$h_{adapt}=W_{proj}·h_{BiTCN}{+b}_{proj}$$

(5)

where $h_{adapt}\in {\mathbb{R}}^{B\times T\times 2D}$ (B: batch size, T: time steps, D: feature dimension) is the BiTCN output and $W_{proj}$ and $b_{proj}$ are learnable parameters for dimension adaptation.

Then, the bidirectional features from BiTCN are fused with global dependencies from Informer:

$$h_{fused}=LayerNorm(h_{adapt}+Informer(h_{adapt}\left)\right)$$

(6)

where LayerNorm stabilizes the gradient flow through residual connections and $h_{fused}$ represents the resulting fusion feature.

2.3.3. Informer

Informer is an advanced time series prediction model derived from Transformer, specifically designed to handle long-sequence prediction tasks efficiently [47]. While the standard Transformer model suffers from quadratic complexity O(L²) in self-attention, Informer introduces three key improvements, ProbSparse self-attention, self-attention distilling, and a generative style decoder, significantly reducing computational cost and improving prediction accuracy. Informer excels in carbon price prediction, significantly outperforming LSTMs and TCNs [48]. The architecture of Informer consists of an encoder–decoder structure, where the encoder extracts long-range dependencies with sparse self-attention, and the decoder generates future sequences non-autoregressively. The following sections provide a detailed description of each component.

(1)

ProbSparse self-attention

The standard self-attention is defined as follows:

$$\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(\mathrm{Q},\mathrm{K},\mathrm{V})=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}({\displaystyle \frac{\mathrm{Q}{\mathrm{K}}^{\mathrm{T}}}{\sqrt{d_k}}})$$

(7)

where $Q{ϵ\mathbb{R}}^{L_Q\times d_k}$, $K{ϵ\mathbb{R}}^{L_K\times d_k}$, and $V{ϵ\mathbb{R}}^{L_V\times d_V}$ are the query, key, and value matrices; and $d_k$ is the scaling factor.

ProbSparse self-attention identifies dominant queries through a sparsity measurement to reduce the quadratic complexity. For the i-th query q_i, the divergence between its attention distribution $q\left(k_j\right|q_i)$ and a uniform distribution $q\left(k_j\right|q_i)=1/L_K$ is quantified by Kullback–Leibler (KL) divergence:

$$\mathrm{K}\mathrm{L}(\mathrm{q}||\mathrm{p})=\mathrm{l}\mathrm{n}\sum _{\mathrm{l}=1}^{\mathrm{L}}{\mathrm{e}}^{{\displaystyle \frac{{\mathrm{q}}_{\mathrm{i}}{\mathrm{k}}_{\mathrm{l}}^{\mathrm{T}}}{\sqrt{\mathrm{d}}}}}-{\displaystyle \frac{1}{\mathrm{L}}}\sum _{\mathrm{j}=1}^{\mathrm{L}}{\displaystyle \frac{{\mathrm{q}}_{\mathrm{i}}{\mathrm{k}}_{\mathrm{l}}^{\mathrm{T}}}{\sqrt{\mathrm{d}}}}-\mathrm{l}\mathrm{n}\mathrm{L}$$

(8)

Dropping the constant term $ln{L}_K$, the sparsity score $M(q_i,K)$ is simplified as follows:

$$\mathrm{M}({\mathrm{q}}_{\mathrm{i}},\mathrm{K})=\mathrm{l}\mathrm{n}\sum _{\mathrm{l}=1}^{\mathrm{L}}{\mathrm{e}}^{{\displaystyle \frac{{\mathrm{q}}_{\mathrm{i}}{\mathrm{k}}_{\mathrm{l}}^{\mathrm{T}}}{\sqrt{\mathrm{d}}}}}-{\displaystyle \frac{1}{\mathrm{L}}}\sum _{\mathrm{j}=1}^{\mathrm{L}}{\displaystyle \frac{{\mathrm{q}}_{\mathrm{i}}{\mathrm{k}}_{\mathrm{l}}^{\mathrm{T}}}{\sqrt{\mathrm{d}}}}$$

(9)

Only the top $u=c·ln{L}_Q$ queries with the highest sparsity scores are retained, forming a sparse query matrix $\overline{Q}ϵ{\mathbb{R}}^{u\times d_K}$. The ProbSparse attention is then computed as follows:

$$\mathrm{Attention}(\mathrm{Q},\mathrm{K},\mathrm{V})=\mathrm{softmax}({\displaystyle \frac{\mathrm{Q}{\mathrm{K}}^{\mathrm{T}}}{\sqrt{{\mathrm{d}}_{\mathrm{k}}}}})$$

(10)

(2)

Self-attention distilling in encoder

The encoder employs a distilling operation that hierarchically compresses features and removes redundant combinations. After each ProbSparse self-attention layer, a distillation step is applied:

$$X_{j+1}^t=Maxpool\left(ELU\right(Convld\left({\left[X_j^t\right]}_{AB}\right)\left)\right)$$

(11)

where $Convld\left(·\right)$ uses a kernel width of 3, and MaxPool downsamples the sequence by a stride of 2. This operation reduces the temporal dimension by half at each layer. Multiple encoder stacks with progressively halved inputs are concatenated to preserve multi-scale features, enhancing robustness for long sequences.

(3)

Generative style decoder

Traditional autoregressive decoders suffer from slow inference and error accumulation. Instead, the Informer adopts a non-autoregressive generative decoder that predicts the entire output sequence in a single forward pass. The decoder input combines a start token (historical sequence segment $X_{token}^t$) and a placeholder $X_{token}^t$ for target timestamps:

$${\mathrm{X}}_{\mathrm{d}\mathrm{e}}^{\mathrm{t}}=\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{c}\mathrm{a}\mathrm{t}(X_{token}^t,X_o^t)\in {\mathbb{R}}^{({\mathrm{L}}_{\mathrm{t}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{n}}+{\mathrm{L}}_{\mathrm{y}\mathrm{e}\mathrm{l}})\times {\mathrm{d}}_{\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}}}$$

(12)

Masked multi-head attention ensures each position attends only to prior positions. The decoder leverages the encoder’s distilled features to generate predictions in one step, eliminating step-by-step latency and error propagation.

2.4. Shapley Additive Explanations (SHAP)

SHAP originates from the concept of Shapley values in game theory [49] and has been widely adopted to interpret machine learning model predictions [50], providing interpretability for complex black-box models. SHAP shows important value in predicting carbon price, and reveals the nonlinear influence and interaction effect of carbon price drivers through global and local explanations [51]. The Shapley value for feature i is computed as follows:

$${\varphi }_i=\sum _{S\subseteq N\backslash \left\{i\right\}}{\displaystyle \frac{\left|S\right|!\left(\right|N|-|S|-1)!}{\left|N\right|!}}\left(v\right(S\cup \left\{i\right\})-v(S\left)\right)$$

(13)

where ${\varphi }_i$ represents the Shapley value of feature i, indicating its average marginal contribution to the model output; N is the set of all features and S is a subset of N that does not include i; v(S) denotes the model’s prediction when only the feature subset S is used; ${\displaystyle \frac{\left|S\right|!\left(\right|N|-|S|-1)!}{\left|N\right|!}}$ assigns a fair weighting to different subsets; and $\left(v\right(S\cup \left\{i\right\})-v(S\left)\right)$ calculates the marginal contribution of feature i to the model output.

2.5. Monte Carlo Dropout

Monte Carlo dropout is a variational inference technique that approximates BNN by retaining dropout layers during both training and inference [52]. By sampling multiple stochastic forward passes, it estimates the predictive distribution and quantifies uncertainty [53,54]. Monte Carlo dropout provides a practical Bayesian approach for interval prediction, which balances computational efficiency and theoretical rigor, making it widely applicable in time series prediction. The quantification of uncertainty is through predictive distribution, which is computed as Equation (14):

$$p(y|x,D)\approx {\displaystyle \frac{1}{S}}{\sum }_{s=1}^{S}p\left(y\right|x,{\theta }_s),{\theta }_s~q\left(\theta \right|D)$$

(14)

where S is the number of dropout samples and θ_s denotes parameters with dropout masks.

$$\mu ={\displaystyle \frac{1}{S}}\sum _{s=1}^S{y}_s$$

(15)

$${\sigma }^2={\displaystyle \frac{1}{S}}\sum _{s=1}^S{(y_s-\mu )}^2$$

(16)

$$Interval=\mu \pm z·\sigma$$

(17)

where μ and σ² are the mean and standard deviation across samples. Z = 1.96 corresponds to a 95% confidence level under a Gaussian assumption.

3. Data Sources

This section primarily introduces the data sources for this study, including carbon prices and their influencing factors, and presents the results of the feature selection.

3.1. Carbon Prices

Two daily carbon price datasets from Guangdong and Shanghai carbon markets, named GD and SH, are selected as study cases to test the prediction performance of the proposed model. Each dataset spans 1 August 2017 to 31 March 2024, with the first 80% allocated as the training set and the remaining 20% as the testing set. Figure 2 shows the trend changes in the two carbon price series.

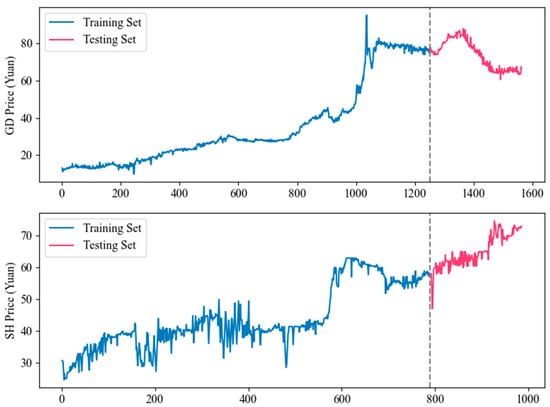
Figure 2. The trend changes in GD and SH datasets.

3.2. Influencing Factors

Based on the existing related literature [55,56,57,58], this study collects the influencing factors of carbon price from the following five dimensions. Among these, the environmental indicator data originate from the China Stock Market & Accounting Research Database (https://data.csmar.com/), while other data come from the Investing website (https://cn.investing.com/). Table 1 summarizes the influencing factors of the GD and SH datasets.

Table 1. Features used in datasets GD and SH and their abbreviations.

Factor Group	Name	Acronym
Environmental Indicators	Temperature	TEM
	Air Quality Index	AQI
	PM2.5 Concentration	PM2.5
	PM10 Concentration	PM10
Energy Markets	EU-ETS Carbon Price	EUCP
	International Natural Gas Price	INGP
	International Crude Oil Price	ICOP
	International Gasoline Price	IGOP
Financial Market Indicators	China Treasury Bond 1-year	CTB1
	China Treasury Bond 5-year	CTB5
	China Treasury Bond 10-year	CTB10
	USD/CNY	USD/CNY
	EUR/CNY	EUR/CNY
	Shanghai Stock Exchange Index	SSE
	Shanghai Stock Exchange Energy Sector Index	SSE-E
	China Securities Index 1000	CSI1000
	S&P 500 Index	S&P500
	Shanghai and Shenzhen 300 Index	HS300
	Dow Jones Index	DJI
Geopolitical Risk	Geopolitical Risk Index	GPRI
Unstructured Data	Baidu Index	BDI

(1) Environmental indicators: Environmental indicators are one of the most commonly used variables in the field of carbon price prediction. Researchers tend to select either temperature or air quality as the primary variable in order to investigate the environmental impact on carbon prices. In more detail, four kinds of environmental indicators are chosen in this study: temperature (TEM), air quality index (AQI), and PM_2.5 and PM₁₀ concentration. (2) Energy markets: The prices of energy commodities have often been shown in studies to have a large impact on carbon prices. In addition to the most commonly used EU-ETS carbon price (EUCP), we take the international market prices of natural gas (INGP), crude oil (ICOG), and gasoline (IGOP) in order to study their impact on China’s carbon price. (3) Financial market indicators: This study selects more financial market indicators as features to be selected, which can be roughly divided into the following three categories: firstly, the bond market, including China’s 1-year, 5-year, and 10-year government bonds (CTB1, CTB5 and CTB10); secondly, the exchange rate market, including the exchange rates of the US dollar and the euro against the CNY; thirdly, the stock market, including the Shanghai Composite Index (SSE), Shanghai Stock Exchange Energy Sector Index (SSE-E), China Securities Index 1000 (CSI1000), Shanghai and Shenzhen 300 Index (HS300), Shanghai Composite Energy, S&P 500 Index (S&P500), and Dow Jones Index (DJI). (4) Geopolitical risk: The Geopolitical Risk Index (GPRI) offers a data-driven approach to study geopolitical developments, which is a widely recognized quantitative indicator designed to capture the daily fluctuations of global geopolitical risks. (5) Unstructured data: Studies have shown that the integration of unstructured data, such as the Baidu Index (BDI), with structured data has been shown to enhance prediction accuracy. A total of 30 keywords related to carbon prices, such as “carbon sinks”, “carbon neutrality”, “low carbon”, “energy conservation”, and “new energy”, are integrated into Baidu’s daily search volume. By principal component analysis (PCA), the initial principal component of BDI data (from https://index.baidu.com/ by crawlers, accessed on 1 May 2024) is then extracted as a daily time series.

3.3. Feature Selection Results

In the Boruta method, a feature is typically rejected when its importance is lower than the maximum importance of all shadow features [55,56]. After inputting GD and SH datasets into Boruta, five features are identified as “unimportant”. Figure 3 displays the importance of each feature in the GD and SH datasets. Finally, the prediction models are populated with sixteen important features from both datasets, in conjunction with their carbon price series. Table 2 shows the selected influencing factors of two datasets.

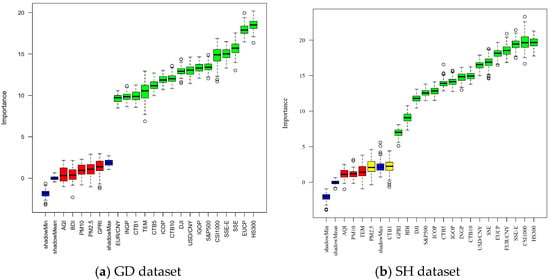
Figure 3. The importance of each feature in GD and SH datasets.

Table 2. The feature selecting results from Boruta.

Features	GD Dataset	SH Dataset
TEM	confirmed	rejected
AQI	rejected	rejected
PM2.5	rejected	rejected
PM10	rejected	rejected
EUCP	confirmed	confirmed
INGP	confirmed	confirmed
ICOP	confirmed	confirmed
IGOP	confirmed	confirmed
CTB1	confirmed	rejected
CTB5	confirmed	confirmed
CTB10	confirmed	confirmed
USD/CNY	confirmed	confirmed
EUR/CNY	confirmed	confirmed
SSE	confirmed	confirmed
SSE-E	confirmed	confirmed
CSI1000	confirmed	confirmed
S&P500	confirmed	confirmed
HS300	confirmed	confirmed
DJI	confirmed	confirmed
GPRI	rejected	confirmed
BDI	rejected	confirmed

4. Experimental Results and Analysis

This section presents the experimental results and analysis of this study. In addition to the conventional point predictions for the GD and SH datasets, this study also implements interval prediction using the Bayesian method introduced earlier. First, this section outlines the evaluation metrics used for both point and interval predictions. Subsequently, three comparative experiments are conducted for point predictions. Finally, interval prediction is performed based on the point forecasting results.

4.1. Performance Measures

Four performance measures, including the mean absolute error (MAE), mean absolute percentage error (MAPE), root mean square error (RMSE), and Theil inequality coefficient (TIC), are adopted to evaluate the predictive performances of models [58].

$$MAE={\displaystyle \frac{1}{T}}\sum _{t=1}^T\left|y_t-\widehat{y_t}\right|$$

(18)

$$MAPE={\displaystyle \frac{1}{T}}\sum _{t=1}^T\left|{\displaystyle \frac{\widehat{y_t}-y_t}{y_t}}\right|$$

(19)

$$RMSE=\sqrt{{\displaystyle \frac{1}{T}}\sum _{t=1}^T{(y_t-\widehat{y_t})}^2}$$

(20)

$$TIC={\displaystyle \frac{\sqrt{\frac{1}{T}{\sum }_{t=1}^T{(y_t-\widehat{y_t})}^2}}{\sqrt{\frac{1}{T}{\sum }_{t=1}^T{y}_t^2}+\sqrt{\frac{1}{T}{\sum }_{t=1}^T{\widehat{y_t}}^2}}}$$

(21)

where $y_t$ and $\widehat{y_t}$ represent the t-th actual and predicted values.

As for the interval prediction, three performance criteria, including the prediction interval coverage probability (PICP), prediction interval normalized average width (PINAW), and coverage width-based criterion (CWC), are used in this study [30].

$$PICP={\displaystyle \frac{1}{T}}\sum _{t=1}^{T}I(y_t\in \left[L_t,U_t\right])$$

(22)

$$PINAW={\displaystyle \frac{1}{T}}\sum _{t=1}^T{\displaystyle \frac{U_t-L_t}{max\left(y_t\right)-min\left(y_t\right)}}$$

(23)

$$CWC=PINAW(1+\gamma (PICP\left)e^{-\eta (PICP-\mu )}\right)$$

(24)

where $L_t$ and $U_t$ are the lower and upper limit of the t-th prediction interval. $I(·)$ is an indicator function. If $y_t$ is within the prediction interval, then $I=1$; otherwise, it is 0. $\gamma (·)$ is also an indicator function. If PICP is lower than μ = (1 − α) %, then γ(PICP) = 1; otherwise, it is 0. η is a parameter used to determine the degree of punishment, which controls the degree of amplification of the difference between PICP and μ.

4.2. Parameter Setting

All experiments are executed using Python 3.8 on a Windows 11 system with a 64-bit 3.20 GHz AMD Ryzen 7 5800H CPU and 16 GB RAM. The data normalization is implemented using the MinMaxScaler function. The parameter settings of the proposed model are shown in Table 3.

Table 3. The hyperparameter settings of the proposed model.

Hyperparameters	Value
kernel size	3
channels	[64, 64]
dropout rate	0.1
encoder layers	2
decoder layers	1
dmodel	4
feedforward	64
multi heads	4
activation	gelu
criterion	MSE
optimizer	Adam
learning rate	0.0005
epochs	100
batch size	64

4.3. Point Prediction

In this study, three comparative point prediction experiments are designed on the GD and SH datasets. The details are presented in the following subsections.

4.3.1. Experiment I: Comparisons of Benchmark Models

Experiment I aims to validate the impact of the Boruta feature selection algorithm on the model performance. It compares the prediction performance differences between models using all variables and those using Boruta-filtered features, further exploring the interference effects of redundant features in multi-source data. First, four common models, including LSTM, GRU, TCN, and Transformer, are selected for experiments using the GD and SH datasets. Subsequently, all-variable models and models with Boruta-selected variables are constructed to compare and analyze their predictive performance. Figure 4 and Table 4 show the prediction results of these models.

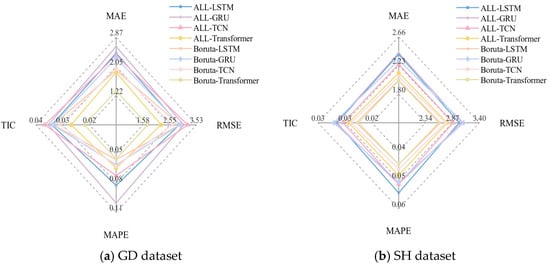
Figure 4. The point prediction results in Experiment I using GD and SH datasets.

Table 4. Results of the comparison before and after selecting features using Boruta.

Dataset	Models	MAE	RMSE	MAPE	TIC
GD	ALL-LSTM	2.4261	2.9045	0.0790	0.0301
	ALL-GRU	2.6121	3.0625	0.0974	0.0314
	ALL-TCN	2.3600	3.2102	0.0689	0.0327
	ALL-Transformer	1.8817	2.2367	0.0611	0.0230
	Boruta-LSTM	1.9362	2.9223	0.0521	0.0296
	Boruta-GRU	2.2868	2.9397	0.0575	0.0297
	Boruta-TCN	2.0005	2.6557	0.0588	0.0271
	Boruta-Transformer	1.3523	1.7503	0.0515	0.0181
SH	ALL-LSTM	2.3988	2.9981	0.0537	0.0304
	ALL-GRU	2.4207	3.0462	0.0507	0.0306
	ALL-TCN	2.2508	2.8800	0.0508	0.0292
	ALL-Transformer	2.1215	2.7614	0.0477	0.0281
	Boruta-LSTM	2.0081	2.6302	0.0440	0.0266
	Boruta-GRU	2.3100	3.0892	0.0500	0.0310
	Boruta-TCN	2.0653	2.7299	0.0456	0.0276
	Boruta-Transformer	1.9994	2.5960	0.0440	0.0262

(1)

For the GD dataset, the prediction accuracy of the model using all variables as inputs is lower than that of the same model using the features selected by the Boruta method. For instance, the MAE, RMSE, MAPE, and TIC values of the ALL-LSTM model are 2.4261, 2.9045, 0.0790, and 0.0301, respectively, which significantly underperforms for the prediction accuracy of the LSTM model with Boruta feature selection, i.e., Boruta-LSTM. Moreover, the same conclusion holds true for the vast majority of other models, demonstrating the positive impact of the Boruta algorithm on enhancing the model prediction performance.

(2)

For the SH dataset, the improvement in model performance after variable selection using the Boruta algorithm can also be observed. For instance, the MAE of the ALL-LSTM model is 2.3988, while that of the Boruta-LSTM model is 2.0081, further validating Boruta’s effectiveness in enhancing predictive performance. In comparison, the Boruta-Transformer model demonstrates the best performance among all models, exhibiting lower prediction errors than the other comparison models.

Based on the results of Experiment I and the above analysis and discussion, the following can be demonstrated: (1) After removing the unimportant features through Boruta, the prediction performance of each model has generally been enhanced. This indicates that feature selection effectively removes weakly correlated variables, significantly improving the prediction accuracy. (2) Among the four common time series prediction models, Transformer exhibits the best prediction performance, as its attention mechanism efficiently captures complex dependencies among multiple features.

4.3.2. Experiment II: Comparisons of Single Models with and Without Boruta Algorithm

The purpose of Experiment II is to compare the performances of different benchmark models based on the Boruta algorithm in the carbon price prediction task to identify the optimal predictive model. The baseline models include LSTM, GRU, TCN, BiLSTM, BiGRU, BiTCN, Transformer, and Informer. Table 5 presents the prediction error results for these models.

Table 5. Results of the comparison between the benchmark models.

Dataset	Models	MAE	RMSE	MAPE	TIC
GD	Boruta-LSTM	1.9362	2.9223	0.0521	0.0296
	Boruta-GRU	2.2868	2.9397	0.0575	0.0297
	Boruta-TCN	2.0005	2.6557	0.0588	0.0271
	Boruta-BiLSTM	1.6912	2.1446	0.0551	0.0219
	Boruta-BiGRU	1.7232	2.3095	0.0525	0.0236
	Boruta-BiTCN	1.5041	1.9718	0.0431	0.0201
	Boruta-Transformer	1.3523	1.7503	0.0515	0.0182
	Boruta-Informer	1.3171	1.7904	0.0352	0.0181
SH	Boruta-LSTM	2.0081	2.6302	0.0440	0.0266
	Boruta-GRU	2.3100	3.0892	0.0500	0.0310
	Boruta-TCN	2.0653	2.7299	0.0456	0.0276
	Boruta-BiLSTM	2.1941	2.8853	0.0470	0.0295
	Boruta-BiGRU	1.9982	2.5772	0.0443	0.0261
	Boruta-BiTCN	1.8486	2.4820	0.0412	0.0251
	Boruta-Transformer	1.9994	2.5960	0.0440	0.0262
	Boruta-Informer	1.7424	2.5141	0.0365	0.0256

(1)

For the GD dataset, measured by MAE, Boruta-Informer achieves a value of 1.3171, significantly outperforming Boruta-LSTM (1.9362), Boruta-GRU (2.2868), and the other models. Across the other evaluation metrics, Boruta-Informer also demonstrated lower prediction errors than the competing models, exhibiting a superior predictive capability. For instance, Boruta-Informer’s MAPE value was only 0.0352, lower than other models such as Boruta-LSTM (0.0521) and Boruta-GRU (0.0575). The results show that Boruta-Informer exhibits a low prediction error, minimal deviation between predicted and actual values, and high prediction accuracy when forecasting carbon market prices. The TIC of Boruta-Informer is 0.0181, which is also at a relatively low level. This series of data shows that Boruta-Informer has a small average error, a low deviation between the predicted value and the actual value, and a high prediction accuracy when predicting the carbon market price. Furthermore, comparative analysis reveals that Boruta-BiTCN achieves an MAE of 1.5041, RMSE of 1.9718, and MAPE of 0.0431, with a TIC of 0.0201, indicating a slightly inferior predictive performance compared to the Boruta-Informer model.

(2)

For the SH dataset, the Boruta-Informer model can obtain MAE, RMSE, MAPE, and TIC values of 1.7424, 2.5141, 0.0365, and 0.0256, respectively, maintaining its status as the optimal prediction model. Similarly, the Boruta-BiTCN model demonstrates an outstanding predictive performance on the Shanghai dataset, second only to the Boruta-Informer model, with corresponding MAE, RMSE, MAPE, and TIC values of 1.8486, 2.4820, 0.0412, and 0.0251, respectively.

(3)

Furthermore, comparing unidirectional and bidirectional deep learning models reveals that bidirectional mechanisms offer superior predictive advantages. Taking the GD dataset as an example, Boruta-BiLSTM achieves an MAE of 1.6912, lower than Boruta-LSTM’s 1.9362, an RMSE of 2.1446, lower than Boruta-LSTM’s 2.9223, an MAPE of 0.0551, lower than Boruta-LSTM’s 0.0521, and a TIC of 0.0219, lower than Boruta-LSTM’s 0.0296. Moreover, the Boruta-BiGRU and Bo-ruta-BiTCN models also outperform their respective unidirectional counterparts. These models demonstrate similar performances for Shanghai data.

Based on the analysis and discussion, the following conclusions can be drawn: (1) Among unidirectional deep learning models, Informer can perform best across multiple metrics, followed by Boruta-BiTCN. This is primarily because Informer and BiTCN demonstrate strong feature capture and predictive capabilities when handling multivariate time series forecasting. (2) Deep learning models with bidirectional mechanisms (e.g., BiLSTM, BiGRU, and BiTCN) significantly outperform standard unidirectional models. This advantage likely stems from the bidirectional mechanisms’ ability to learn sequence information simultaneously from both forward and backward directions, enabling a more comprehensive extraction of sequence features and thereby enhancing prediction accuracy.

4.3.3. Experiment III: Comparisons of Hybrid Models

Based on the discussion and analysis from Experiment II, to further enhance prediction accuracy, this experiment constructs a hybrid prediction model by integrating the complementary strengths of the Boruta algorithm, BiTCN, and the Informer model. Additionally, several comparative models are also constructed in this experiment. Figure 5 and Figure 6, along with Table 6, present the prediction error results for these models.

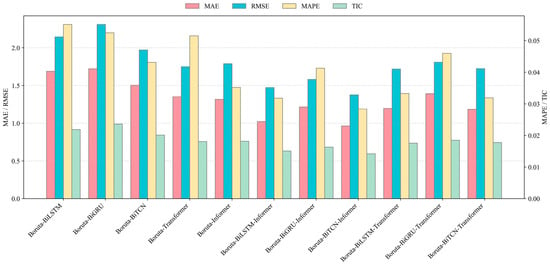
Figure 5. The point prediction results in Experiment III uisng GD dataset.

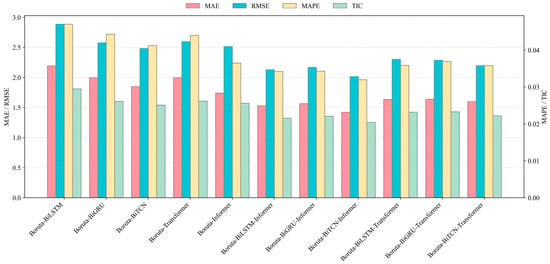
Figure 6. The point prediction results in Experiment III using SH dataset.

Table 6. Results of the comparison between the benchmark models and the hybrid models.

Dataset	Models	MAE	RMSE	MAPE	TIC
GD	Boruta-BiLSTM	1.6912	2.1446	0.0551	0.0219
	Boruta-BiGRU	1.7232	2.3095	0.0525	0.0236
	Boruta-BiTCN	1.5041	1.9718	0.0431	0.0201
	Boruta-Transformer	1.3523	1.7503	0.0515	0.0181
	Boruta-Informer	1.3171	1.7904	0.0352	0.0182
	Boruta-BiLSTM-Informer	1.0221	1.4725	0.0318	0.0151
	Boruta-BiGRU-Informer	1.2180	1.5829	0.0413	0.0163
	Boruta-BiTCN-Informer	0.9642	1.3788	0.0284	0.0142
	Boruta-BiLSTM-Transformer	1.1975	1.7199	0.0333	0.0176
	Boruta-BiGRU-Transformer	1.3933	1.8090	0.0460	0.0185
	Boruta-BiTCN-Transformer	1.1846	1.7246	0.0319	0.0178
SH	Boruta-BiLSTM	2.1941	2.8853	0.0470	0.0295
	Boruta-BiGRU	1.9982	2.5772	0.0443	0.0261
	Boruta-BiTCN	1.8486	2.4820	0.0412	0.0251
	Boruta-Transformer	1.9994	2.5960	0.0440	0.0262
	Boruta-Informer	1.7424	2.5141	0.0365	0.0256
	Boruta-BiLSTM-Informer	1.5307	2.1308	0.0342	0.0216
	Boruta-BiGRU-Informer	1.5672	2.1679	0.0343	0.0221
	Boruta-BiTCN-Informer	1.4213	2.0154	0.0320	0.0204
	Boruta-BiLSTM-Transformer	1.6344	2.3028	0.0359	0.0232
	Boruta-BiGRU-Transformer	1.6399	2.2865	0.0369	0.0233
	Boruta-BiTCN-Transformer	1.6001	2.1975	0.0358	0.0222

(1)

For the GD dataset, the proposed Boruta-BiTCN-Informer model demonstrates significantly lower prediction errors than other benchmark models, particularly outperforming single deep learning models based on the Boruta algorithm across all evaluation metrics. For instance, in terms of RMSE, Boruta-BiTCN-Informer achieves a value of 1.3788, whereas single models like Boruta-BiTCN record an RMSE of 1.9718. Additionally, Boruta-BiTCN-Informer’s MAPE value is 0.0284, substantially lower than the MAPE values of the other single models. Moreover, for the SH dataset, the Boruta-BiTCN-Informer model also demonstrates an outstanding predictive performance, with an MAE of 1.4213, lower than those of the benchmark models. The MAPE and MAE values of the proposed model are 2.0154 and 0.0320, respectively, demonstrating a higher predictive precision compared to the other models.

(2)

Comparing hybrid models built upon the same single model, it can be seen that the hybrid models based on Informer generally outperform those using Transformer. For instance, as for the prediction of the GD dataset, Boruta-BiLSTM-Informer achieves an MAE of 1.0221, lower than the 1.1975 (MAE) of the Boruta-BiLSTM-Transformer. Similar conclusions can be drawn from the model performance comparisons on the SH dataset.

The results of Experiment III show the following: (1) Hybrid models generally perform better than single benchmark models. By combining different models, the hybrid models can make use of the advantages of each model, thereby improving the overall prediction performance. (2) The proposed Boruta-BiTCN-Informer model performs best on different datasets, with a high prediction accuracy. It can effectively capture the characteristics of carbon price time series data and make more accurate predictions. (3) The hybrid models with Informer as the main model have a better performance than those based on Transformer. This indicates that Informer has stronger feature-capturing and prediction capabilities, providing superior support for the model.

4.4. Interval Prediction

In the experimental comparison analysis of the preceding subsections, the superior predictive performance of the proposed model has been fully validated. However, in practical applications, point predictions often fall short of interval predictions due to their lack of utility. Therefore, this study additionally uses the Monte Carlo dropout method in Bayesian deep learning to achieve interval prediction. Table 7 and Figure 7 and Figure 8 present the interval prediction results for the two datasets. The results indicate that, under different confidence levels, the PICP values predicted by the model are higher than the corresponding confidence level, while maintaining very low PINAW values. This indicates that the proposed interval prediction method is effective, yielding interval predictions with a strong predictive performance. This conclusion is further supported by the CWC metric. Furthermore, comparing the prediction results across the two datasets reveals that the model performs better on the GD dataset than on the SH dataset, exhibiting higher PICP values and smaller PINAW values.

Table 7. Interval prediction results of Bouruta-BiTCN-Informer for GD and SH datasets.

Dataset	Confidence Level	PICP	PINAW	CWC
GD	95%	0.9693	0.0918	0.0918
	90%	0.9201	0.0922	0.0922
	85%	0.8775	0.0830	0.0830
SH	95%	0.9553	0.1252	0.1252
	90%	0.9137	0.0905	0.0905
	85%	0.8690	0.0856	0.0856

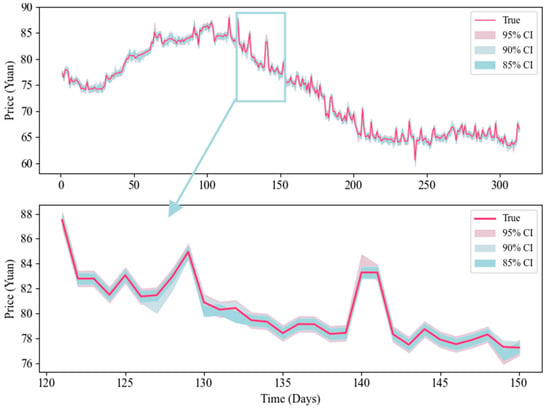
Figure 7. The interval prediction results of Bouruta-BiTCN-Informer using GD dataset.

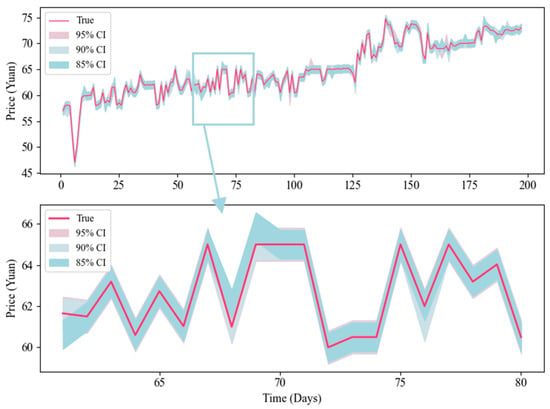
Figure 8. The interval prediction results of Bouruta-BiTCN-Informer using SH dataset.

5. Further Discussions

This section is the discussion part of this study. Firstly, the superiority of the proposed model is verified once again using the Diebold–Mariano (DM) test. Then, the European Union carbon emission trading price and natural gas price datasets are adopted in order to verify the robustness of the proposed model. Finally, the interpretability analysis of the model predictions is performed by the SHAP method.

5.1. Diebold–Mariano (DM) Test

In this study, the DM test proposed by Diebold–Mariano in 1995 [59] is utilized for the validation of the superiority of the proposed model. The DM test is capable of determining whether there is a significant difference between the two models in terms of their predictive performance at a given level of significance α. Models are compared according to the DM value. If the absolute value of the DM value is greater than Z_α/2, the null hypothesis, that there is no significant difference in the predictive performance of the two models, will be rejected. Otherwise, it is considered that there is no significant difference. Table 8 presents the DM test values between the proposed model and comparison models.

Table 8. Results of the DM test between the proposed model and comparison models.

Models	GD		SH
	DM Values	p Values	DM Value	p Values
ALL-LSTM	18.0025	0.0000	8.4444	0.0000
ALL-GRU	16.9374	0.0000	8.2741	0.0000
ALL-TCN	11.7515	0.0000	7.2461	0.0000
ALL-Transformer	13.1003	0.0000	6.8333	0.0000
Boruta-LSTM	7.6524	0.0000	5.7215	0.0000
Boruta-GRU	12.3830	0.0000	6.2337	0.0000
Boruta-TCN	10.7836	0.0000	5.8182	0.0000
Boruta-BiLSTM	9.6713	0.0000	6.1093	0.0000
Boruta-BiGRU	8.9538	0.0000	5.7404	0.0000
Boruta-BiTCN	7.5704	0.0000	4.7411	0.0000
Boruta-Transformer	5.1523	0.0000	5.8533	0.0000
Boruta-Informer	3.8973	0.0000	2.8206	0.0048
Boruta-BiLSTM-Informer	1.3081	0.1908	3.5452	0.0004
Boruta-BiGRU-Informer	5.3844	0.0000	2.6843	0.0073
Boruta-BiLSTM-Transformer	2.2441	0.0248	2.4700	0.0135
Boruta-BiGRU-Transformer	7.0809	0.0000	3.2378	0.0012
Boruta-BiTCN-Transformer	4.4931	0.0000	2.9128	0.0036

Note: Z_0.01/2 = 2.58, Z_0.05/2 = 1.96, Z_0.10/2 = 1.64.

As demonstrated in Table 8, except for Boruta-BiLSTM-Informer model, all DM values exceed Z_0.05/2 = 1.96. This indicates that, at the 0.05 confidence level, the proposed model exhibits a significant difference in predictive performance relative to the other models. Furthermore, the vast majority of DM values also exceed Z_0.01/2 = 2.58, further demonstrating that the Boruta-BiTCN-Informer model exhibits a significantly superior predictive performance compared to benchmark models at the 0.01 confidence level. In summary, the DM test results confirm that the proposed model’s predictive performance differs significantly from the comparison models, exhibiting markedly superior predictive capabilities and achieving outstanding prediction results in carbon price forecasting tasks.

5.2. Further Study of the Model Performance Based on Other Datasets

To further validate the applicability and robustness of the proposed model, this study selects the European carbon trading price (EU) and the natural gas price from Henry Hub (NG) as supplementary datasets to test the model [56,60]. The experimental results are shown in Table 9.

Table 9. The prediction results of the developed models and benchmarks using EU and NG.

Dataset	Models	MAE	RMSE	MAPE	TIC
EU	Boruta-BiLSTM	2.1648	2.9568	0.0599	0.0274
	Boruta-BiGRU	2.4188	3.3225	0.0645	0.0310
	Boruta-BiTCN	2.0665	2.7930	0.0567	0.0259
	Boruta-Transformer	2.0581	2.7620	0.0538	0.0256
	Boruta-Informer	1.8360	2.5661	0.0510	0.0241
	Boruta-BiLSTM-Informer	1.7082	2.2612	0.0512	0.0210
	Boruta-BiGRU-Informer	1.7714	2.3277	0.0525	0.0216
	Boruta-BiTCN-Informer	1.6336	2.2556	0.0444	0.0210
	Boruta-BiLSTM-Transformer	1.8402	2.4559	0.0538	0.0230
	Boruta-BiGRU-Transformer	1.8613	2.4817	0.0555	0.0231
	Boruta-BiTCN-Transformer	1.6780	2.3185	0.0459	0.0216
NG	Boruta-BiLSTM	0.2900	0.4414	0.0827	0.0592
	Boruta-BiGRU	0.3185	0.4845	0.0916	0.0650
	Boruta-BiTCN	0.3135	0.5008	0.0892	0.0672
	Boruta-Transformer	0.2447	0.3795	0.0689	0.0509
	Boruta-Informer	0.2205	0.3550	0.0598	0.0482
	Boruta-BiLSTM-Informer	0.1731	0.2621	0.0496	0.0347
	Boruta-BiGRU-Informer	0.1907	0.2762	0.0572	0.0370
	Boruta-BiTCN-Informer	0.1526	0.2355	0.0435	0.0316
	Boruta-BiLSTM-Transformer	0.1843	0.2548	0.0561	0.0340
	Boruta-BiGRU-Transformer	0.2168	0.3078	0.0645	0.0412
	Boruta-BiTCN-Transformer	0.2008	0.3010	0.0570	0.0403

For the EU dataset, the Boruta-BiTCN-Informer model achieves an MAE value of 1.6336, lower than the those of the other models. Similarly, across the other model evaluation metrics, the proposed model can also demonstrate significantly lower prediction errors than the comparison models. This conclusion can also be validated using the NG dataset. For instance, the proposed Boruta-BiTCN-Informer model achieves an MAPE value of 0.0435, significantly smaller than the 0.0561 recorded by Boruta-BiLSTM-Transformer. Overall, the proposed Boruta-BiTCN-Informer model demonstrates a robust performance and strong prediction stability across all datasets. This also validates that the hybrid model framework proposed in this study is not only applicable to carbon price forecasting but also holds promise for other energy price prediction tasks, providing a reference for future research.

5.3. Interpretability Analysis

This study also adopts the SHAP method to quantitatively assess the impact of input features on carbon price predictions, thereby further elucidating the decision-making process of the BiTCN-Informer model. Figure 9 presents the corresponding SHAP analysis results of the proposed model when predicting carbon prices in Guangdong and Shanghai. As illustrated in Figure 9, taking Shanghai carbon price prediction as an example, the left-hand bar chart displays the global feature importance ranking based on the average absolute SHAP value, where the length of each horizontal bar indicates the contribution of that feature to the model’s prediction. The right-hand SHAP summary plot provides a more granular feature impact analysis. Each point in this plot represents a point sample, with the x-axis denoting SHAP values. Positive SHAP values indicate a positive contribution of the corresponding feature to carbon price prediction, while negative SHAP values indicate a negative contribution. Additionally, the color of each point represents the magnitude of the feature value, ranging from red (high value) to blue (low value).

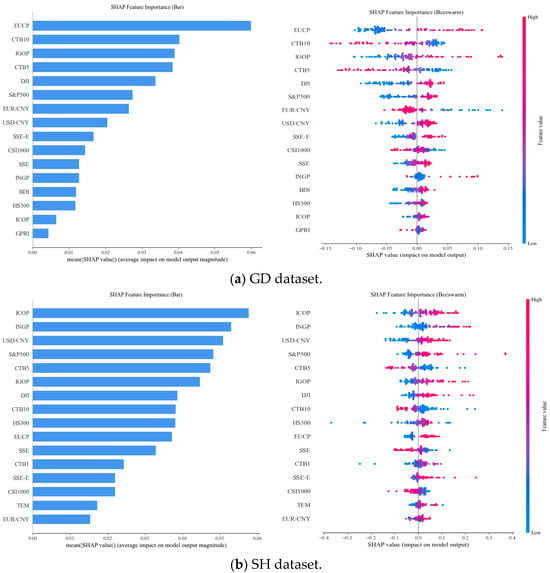
Figure 9. The SHAP analysis using GD and SH datasets.

From the bar chart, in the Guangdong carbon trading market, the five most influential factors driving carbon price fluctuations are the EU-ETS carbon price, China Treasury Bond (10-year), international crude oil price, China Treasury Bond (5-year), and the Dow Jones Index. Notably, the EU-ETS carbon price exerts a significantly stronger impact than the other factors, surpassing the second-ranked feature by a SHAP value margin of 0.01. This pronounced influence is likely attributed to Guangdong’s export-oriented economic structure. As China’s largest export hub, Guangdong accommodates numerous energy-intensive manufacturing enterprises whose carbon cost accounting is directly influenced by the EU Carbon Border Adjustment Mechanism (CBAM). Consequently, the EU-ETS carbon price transmits cross-regional policy spillover effects to the Guangdong carbon market, reinforcing its susceptibility to external regulatory and market dynamics. In contrast, the Shanghai carbon trading market exhibits a different set of key drivers. The five most influential factors are the international crude oil price, international natural gas price, USD/CNY exchange rate, S&P 500 Index, and China Treasury Bond (5-year). This indicates that energy market prices and financial market indicators play a dominant role in shaping carbon price dynamics in Shanghai. A plausible explanation is Shanghai’s status as a global financial hub, where market participants are more inclined to incorporate global energy supply–demand shifts and cross-border capital flows into their carbon asset pricing strategies.

A deeper examination of the SHAP summary plot reveals a notable heterogeneity in the impact of the EUR/CNY exchange rate across these two markets. In Shanghai, a higher EUR/CNY value is associated with positive SHAP values, indicating a positive correlation between the exchange rate and carbon prices. Conversely, in the Guangdong market, an increase in EUR/CNY corresponds to negative SHAP values, suggesting that the exchange rate exerts a suppressive effect on carbon price increases in Guangdong. These findings demonstrate that the depreciation of the Chinese yuan (CNY) relative to the euro (EUR) exerts heterogeneous impacts across different carbon markets. In the Shanghai market, participants predominantly focus on the transmission mechanism of exchange rate fluctuations, foreign capital flows, and carbon asset allocation. Concurrently, CNY depreciation may elevate imported energy costs or enhance market liquidity. Conversely, in the Guangdong market, participants prioritize the trade cost transmission pathway. An appreciation of the EUR amplifies carbon compliance costs transferred by EU importers, incentivizing local enterprises to adopt quota reservation strategies to suppress short-term carbon prices.

Based on the above analysis, different decision-makers may formulate rules or schemes for specific application scenarios: (1) For export-oriented, high-energy-consuming enterprises in Guangdong (e.g., home appliance manufacturers), when the SHAP value of EUCP exceeds a specific threshold (e.g., 0.04) over a continuous period, they may procure annual carbon allowances in advance to lock in compliance costs. When quoting export orders, convert the SHAP contribution from EUCP into a cost coefficient to hedge against carbon cost volatility. (2) For energy-dependent enterprises in Shanghai (e.g., steel producers), when the SHAP value of INGP exceeds a specific threshold (e.g., 0.03), prioritize low-energy production lines to reduce current-period carbon emissions. During carbon asset inventory, consider the heterogeneous impact of USD/CNY (positive in Shanghai markets). When the CNY depreciates, increase carbon allowance holdings modestly. (3) For the newly established national carbon market coordination department, set distinct weightings for different regions: Guangdong market allowances should reference the SHAP value from the EUCP (0.3–0.4), while Shanghai market allowances should reference the SHAP value from energy/financial indicators (0.25–0.35), thereby avoiding the bias inherent in uniform rules. Monitor the SHAP values for ICOP and USD/CNY and concurrently implement short-term exchange rate stabilization measures to mitigate carbon price volatility.

6. Conclusions and Future Outlook

This study constructs an interpretable hybrid carbon price prediction system integrating feature selection, deep learning, and interpretability analysis methods. An extensive experimental analysis and discussion demonstrate the proposed model’s superior predictive performance, significantly enhancing carbon price forecasting accuracy while providing interpretability references. The specific conclusions are as follows.

(1)

The proposed Boruta-BiTCN-Informer model demonstrates an outstanding predictive performance and high robustness across diverse market environments. In the Guangdong carbon market, the model achieves a mean absolute error of only 0.9642, representing a 26.7937% reduction compared to the Boruta-Informer model and an average decrease of 27.3809% relative to all benchmark models. Similarly, in the Shanghai carbon market, the proposed model achieves a mean absolute percentage error of 0.0320, representing a 12.3288% reduction compared to Boruta-Informer and an average decrease of 16.9507% relative to all comparison models, fully demonstrating its superior performance in carbon price forecasting.

(2)

Regarding model interpretability and practicality, this study employs the SHAP method to deeply reveal nonlinear interactions among carbon price drivers. The findings indicate that energy prices dominate carbon price fluctuations in the Shanghai carbon market, while EU carbon prices exert a significant influence on the Guangdong carbon market. Furthermore, the proposed model maintains its advantage in both the EU carbon market and the U.S. Henry Hub natural gas market. For instance, in the EU market, the proposed model achieved an MAE of 1.6336, representing an 11.0240% reduction compared to the Boruta-Informer model. In the natural gas market, the MAE improvement over the Boruta-Informer model reaches 30.7937%. Moreover, the interval prediction capability of the proposed model provides practical risk boundaries, offering robust support for enterprises and decision-makers in formulating strategic plans within uncertain market environments.

(3)

From the perspective of methodological innovation, the bidirectional architecture of BiTCN effectively mitigates the feature loss problem in traditional hybrid models, and the sparse attention mechanism of the Informer model optimizes the long-sequence modeling process. The synergy of the two not only provides an efficient solution for carbon price prediction but also serves as a reference for predicting other energy commodity prices.

Overall, the proposed model in this study demonstrates an exceptional predictive performance, significantly enhancing the accuracy of carbon market price forecasting. It also provides a methodological framework for reference in the field of time series forecasting. Future research will further explore the dynamic changes in carbon market price characteristics, focusing on cutting-edge deep learning technology research, thereby providing information references for carbon market development and decision-making.