A Hybrid Fuzzy Multi-Criteria Framework for Sustainable Product Selection in Chemical Supply Chains Under Uncertainty

Abstract

This study develops a comprehensive decision-making approach to sustainable product selection for chemical industry supply chains under uncertainty. Five product categories -enamel, ceramics, pigments, non-stick coatings, and glass- were evaluated through fifteen criteria along environmental, economic, and social sustainability dimensions. The hybrid methodology combines Fuzzy SWARA, which weights criteria based on expert opinion, with Fuzzy ARAS, which ranks the alternatives accordingly. The study found that occupational health and safety, consumer safety and health, and water usage are the most important criteria, reflecting a human-centered approach to sustainability decision-making. Ceramics had the best performance score, followed by enamel and non-stick coating. Sensitivity analysis confirmed the robustness of these rankings across various weighting scenarios. The findings indicate that decision-makers in the chemical industry prioritize worker and consumer protection alongside environmental resource stewardship. This framework provides practitioners with a structured method for integrating sustainability considerations into supply chain product portfolio decisions, balancing environmental impact, economic performance, and social responsibility.

1. Introduction

A sustainable supply chain is crucial for organizations seeking a competitive edge and optimal utilization of resources. Supply chain management, however, is an involved process with numerous variables to address, extending far beyond cost control to include factors such as product demand, delivery lead time, and environmental considerations. In this context, Multi-Criteria Decision-Making (MCDM) methods enable the simultaneous evaluation of diverse criteria to support more informed and effective strategic decisions [1,2]. In particular, for supply chain management to be sustainable, there must be a requirement that, alongside basic criteria like price, demand, and delivery time, sub-criteria such as product type, wear and tear, and damage risk also be considered [3].

Green supply chain management becomes an essential aspect in the current modern business environment because it integrates various factors in terms of the environment, society, and economy. There are different criteria that stand out in green supply chain management in an attempt to improve efficiency while lessening negative impacts on the environment. These criteria include green supply chain management practices, waste management, efficient use of energy, and reduction in emissions. Green supply chain management specifically focuses on limiting negative impacts on the environment in the entire process, such as purchasing, production, transportation, and recycling [4]. Secondly, environmental criteria in green supply chain management—such as the negative impact of products across organizations—form the foundation of sustainability in supply chain processes. On the other hand, criteria related to sustainability in terms of society include management of relationships with stakeholders in general. These criteria include working conditions, responsibility to society through different projects, and conducting ethical business [5]. The management of the entire supply chain process should be based on meeting the needs of all stakeholders [6]. Thirdly, criteria associated with sustainability in terms of economy in terms of control, efficiency, and profitability are essential in the process. Sustainability in supply chain management should allow organizations to meet goals associated with the environment and society while being able to achieve efficiency in terms of reduced costs [7,8]. Supply chain managers should, in fact, develop strategies in decision-making focused on improving economic performance in the process. Moreover, as organizations seek to manage risks related to society and the environment to meet sustainability goals, risk management becomes a critical component of sustainable supply chain management. The process involves identifying risks in supply chain management in organizations, understanding the impacts associated with risks, and creating mechanisms in place to reduce risks in organizations [3,9].

MCDM methods can be used by decision makers to manage the trade-offs between different criteria, while considering their relationships [10,11]. In such methods, weights of the criteria are determined based on expert opinions and literature, hence bringing more systematic decision-making practice [10]. A sustainable supply chain must incorporate environmental and social factors. In particular, criteria such as product environmental impact, safety of transport, and compliance with delivery specifications would turn into critical parts of the decision-making process [3,11]. For example, product wear and tear and damage risk are critical cost drivers and customer satisfaction factors. Thus, it is important for businesses to evaluate such criteria in order to achieve their sustainability goals [3].

Additionally, there is a need to take into consideration the needs of the different stakeholders in multi-criteria decision-making processes. Current sustainability efforts can be undermined if stakeholder needs are not considered, especially in decision-making processes dominated by a single individual. The importance of group decision-making processes in decision-making should not be underestimated because it promotes equality in decision-making [12].

MCDM models let businesses make more informed and effective decisions in sustainable supply chains by simultaneously considering environmental, social, and economic objectives. Such methods enhance sustainability across supply chain processes by allowing the integrated evaluation of diverse criteria. The following section will discuss the key MCDM models and their application areas in this context [2,13]. First, common MCDM methods include Fuzzy Stepwise Weight Assessment Ratio Analysis (Fuzzy SWARA) and Fuzzy Additive Ratio Assessment (Fuzzy ARAS), which are often adopted for supply chain decision-making problems. Fuzzy SWARA follows a structured approach to evaluate the importance weights of criteria using expert opinions within the framework of fuzzy logic. Fuzzy ARAS enables the calculation of the performance of alternatives against these criteria, which enables the identification of the most suitable option.

These techniques are very useful in the amalgamation of environmental and societal aspects in sustainable supply chain management, which involves coordinating material, information, and capital flows with respect to the environmental, societal, and economic aspects of sustainability [5]. In this context, the application of MCDM techniques assumes the utmost importance in terms of supplier choice, product design, and inventory management. For instance, criteria such as environmental concerns, cost, quality, and time can be efficiently addressed through the application of MCDM techniques, resulting in more informed sustainability choices [5,14]. Another imperative aspect of sustainability in supply chain management is risk management. The application of MCDM techniques can aid in identifying risks associated with supply chain uncertainty to quantify the effect of strategies on sustainability in an analytical manner, thereby facilitating the formulation of relevant decisions to counter risks and ensure sustainability [15,16].

Ultimately, the effective use of multi-criteria decision-making methods enables sustainable supply chain management. By evaluating key criteria such as price, demand, and delivery time—alongside critical sub-criteria like environmental impact, wear and tear risk, and transport safety—businesses can better achieve their sustainability goals. Numerous studies in the literature provide valuable insights for optimizing these decision-making processes [1,3]. Decision-making is a crucial strategic undertaking for companies, a process that grows increasingly complex when multiple criteria must be evaluated. The growing emphasis on sustainability has further heightened the critical nature of this process, particularly in high-impact sectors like the chemical industry. In this context, sustainability-oriented decision models support the balanced evaluation of environmental and social factors in product selection, contributing meaningfully to the industry’s sustainable future.

The purpose of this study is to address the challenge of sustainable product choices in chemical supply chain networks in uncertain scenarios. Based on the challenges and literature gaps presented above, the primary questions being addressed in the current study are:

• RQ1: What is the complete list of criteria to select products that encompass environmental, economic, and social sustainability in the chemical industry?
• RQ2: How can fuzzy techniques, employed to represent uncertainty in the judgment process, identify the most prominent criteria in sustainable product choice?
• RQ3: How are five different chemical product groups, namely enamel, ceramic, pigment, non-stick coating, and glass, prioritized with the help of fuzzy multi-criteria decision-making techniques in terms of sustainability performance, and what is the best alternative solution?
• RQ4: How robust and dependable can the proposed hybrid model framework with respect to variations in criteria weights be?

In this respect, the MCDM models act as essential enablers to realize sustainable development goals within the industry. A structured way of incorporating environmental, social, and economic criteria provides comprehensive sustainability; therefore, robust risk management and participatory approaches are also important. Application of effective MCDM methods is thus a must for progressing toward successful sustainable supply chain management practices.

2. Theoretical Background

Effective management of resources is necessary to achieve development goals. Therefore, this study aims to evaluate fuzzy decision-making methods in supply chain management [17]. This study systematically examines and compares fuzzy logic-based decision processes.

The Fuzzy Analytical Hierarchy Process (FAHP) analyzes complex decision problems within a hierarchical structure and prioritizes criteria. It is a well-known decision-making method [18]. To support the advantages of this method with an example, a notable study was conducted by Serpa et al. (2023) [19]. The study used Fuzzy AHP (FAHP) and Fuzzy TOPSIS methods to improve process and product quality. The research demonstrated how effectively Multi-Criteria Decision-Making (MCDM) methods streamline decision-making processes. It revealed that they provide valuable insights for managers. However, the FAHP method faces significant challenges as the number of criteria increases, creating practical limitations.

Fundamental research in cognitive psychology, particularly focusing on Miller’s (2014) [20] study of the “magic number seven, plus or minus two,” suggests that the human brain has a limited capacity to process information simultaneously and coherently. This cognitive limit must be taken into account when using fuzzy linguistic scales; otherwise, the risk of participant fatigue and cognitive overload increases significantly. Sustainable supply chain practices encompass both environmental and economic objectives and focus on these two criteria. Althaqafi’s research on electric vehicle production is an example of this [21]. Ahmed et al. (2020) [22] proposed a process to make concrete mix design more sustainable by applying MCDM approaches for quality management.

Fuzzy TOPSIS utilizes the ideal solution and the negative-ideal solution when ranking decision alternatives. The method evaluates alternatives based on their closeness to these two reference points. Althaqafi’s research emphasizes that the application of fuzzy TOPSIS in Green Supply Chain Management effectively supports decision-making processes involving uncertain data [21].

The F-ARAS method, like the F-TOPSIS method, is a ranking method. The ARAS method ranks alternatives based on their relative proximity to the optimal solution. By incorporating fuzzy logic into this ranking process, Fuzzy ARAS is capable of modeling the uncertainty inherent in subjective evaluations. In the F-ARAS method, the ratio of the utility of each alternative to the utility of the optimal alternative is calculated. Ranking is performed based on this ratio.

Various methods are available in the literature to support decision-making under uncertainty. For instance, Komatina et al. (2025) [23] proposed the Fuzzy RADAR (FRADAR) method for Process Failure Mode and Effects Analysis (PFMEA) in the automotive industry. The method models the uncertainty in expert assessments and integrates fuzzy logic.

The use of hybrid models is common in fuzzy MCDM methods. For example, an application was conducted in the furniture sector for green supplier selection, where the weights of 10 green criteria were determined using the F-SWARA method. The F-ARAS method was used for supplier evaluation, and the developed hybrid model provided a more reliable supplier selection process [24].

SWARA (Step-wise Weight Assessment Ratio Analysis) is a relatively new and easy-to-apply weighting method, and F-SWARA integrates linguistic variables into this process. The Fuzzy SWARA method offers a deeper perspective in determining criterion weights, without requiring direct consensus, and enables systematic analysis of expert input.

This approach offers broader application in decision-making [25]. The SWARA method has gained a place in studies thanks to its straightforward structure. It has high applicability due to its effectiveness in gathering expert opinions and its ability to facilitate expert collaboration [26].

Although FAHP has theoretical superiority in criteria weighting, F-SWARA has an advantage over FAHP in terms of practical applicability.

Similarly, F-TOPSIS and F-ARAS offer different logical approaches to ranking alternatives; F-TOPSIS is distance-based, while F-ARAS performs a ratio-based evaluation. This difference influences method selection depending on the structure of the decision problem and the preferences of the decision-makers.

In conclusion, the selection of fuzzy MCDM methods in green supply chain management varies depending on the complexity of the decision problem, the number of available experts, and the nature of data uncertainty. Hybrid approaches (e.g., F-SWARA + F-ARAS) have the potential to overcome the limitations of a single method and produce more reliable results. Findings from the literature review reveal that the F-SWARA method imposes less cognitive load compared to FAHP in criterion weighting, and the F-ARAS method offers performance similar to F-TOPSIS in alternative evaluation while providing more easily interpretable results. Therefore, a hybrid approach combining F-SWARA and F-ARAS methods has been adopted in this study. The F-TOPSIS method was also used to test the robustness of the model. This choice provides an optimal balance in terms of both methodological robustness and practical applicability.

3. Materials and Methods

To achieve sustainability goals, businesses should not only focus on costs but also on environmental and social factors. This study proposes a hybrid model to solve a product line selection problem in the chemical industry.

Fuzzy SWARA method:

The Stepwise Weight Assessment Ratio Analysis (SWARA) method was developed by Keršuliene in 2010 [27]. Expert opinion is a foundational component of the method, as it directly shapes the weighting of the criteria.

Mavi et al. [28] noted that real-life decision-making processes are often characterized by uncertainty and linguistic expressions rather than precise judgments. To model these uncertainties more effectively, they proposed an extension of the classical SWARA method, developing a fuzzy SWARA approach [28]. Fuzzy SWARA process steps are specified below [29]:

Step 1:	Ranking the Criteria in Order of Priority: Decision makers rank the evaluation criteria from most to least important, based on the decision objective. This ranking is based on expert opinions.
Step 2:	$\mathrm{Determining}\mathrm{Relative}\mathrm{Importance}\mathrm{Levels}\left({\tilde{s}}_j\right)$$:\mathrm{The}\mathrm{relative}\mathrm{importance}\mathrm{of}\mathrm{each}\mathrm{criterion}\mathrm{compared}\mathrm{to}\mathrm{the}\mathrm{previous}\mathrm{criterion}\left(j-1\right)$, which is more important than itself, is determined by verbal expressions based on expert opinions and converted into fuzzy numbers in Table 1, with the help of the appropriate table.
Step 3:	$\mathrm{Fuzzy}\mathrm{Coefficients}\left({\tilde{k}}_j\right)$	${\tilde{k}}_j=\left\{\begin{array}{ll}1& j=1\\ {\tilde{S}}_j+1,& j>1\end{array}\right.$	(1)
Step 4:	$\mathrm{Initial}\mathrm{Fuzzy}\mathrm{Weights}\left({\tilde{q}}_{\dot{j}}\right)$	${\tilde{q}}_j=\left\{\begin{array}{ll}1,& j=1\\ {\displaystyle \frac{{\tilde{q}}_{j-1}}{{\tilde{k}}_j}},& j>1\end{array}\right.$	(2)
Step 5:	$\mathrm{Fuzzy}\mathrm{Criteria}\mathrm{Weights}\left({\tilde{w}}_j\right)$	${\tilde{w}}_j={\displaystyle \frac{{\tilde{q}}_j}{{\sum }_{k=1}^n{\tilde{q}}_k}}$	(3)
Step 6:	Converting Weights to (De-Fuzzified) Values	$w_j={\displaystyle \frac{\left(w_j^l+2·w_j^m+w_j^u\right)}{4}}$	(4)

It is important to note that various linguistic scale variations, including trapezoidal fuzzy numbers [30], are available in the literature for F-SWARA applications. Although different scale types follow similar principles, the final choice often depends on application-specific convenience and established methodological practices. In this study, a triangular fuzzy number scale was preferred due to its clarity and ease of use for experts during the direct evaluation process of the 15 criteria, and because of its strong precedent in prior foundational studies [31].

Table 1. F-SWARA [31] (a) and F-ARAS [32] (b) fuzzy linguistic expression equivalents.

(a)
Linguistic Variable	Abbreviation
Absolutely less significant	(ALS)	(1; 1; 1)
Dominantly less significant	(DLS)	(0.50; 0.67; 1)
Much less significant	(MLS)	(0.40; 0.50; 0.67)
Really less significant	(RLS)	(0.33; 0.40; 0.50)
Less significant	(LS)	(0.29; 0.33; 0.40)
Moderately less significant	(MDLS)	(0.25; 0.29; 0.33)
Weakly less significant	(WLS)	(0.22; 0.25; 0.29)
Equally significant	(ES)	(0; 0; 0)
(b)
Linguistic Variable	Abbreviation
Very Poor	(VP)	(0; 1; 2)
Poor	(P)	(1; 2; 3)
Medium Poor	(MP)	(2; 3.5; 5)
Fair	(F)	(4; 5; 6)
Medium Good	(MG)	(5; 6.5; 8)
Good	(G)	(7; 8; 9)
Very Good	(VG)	(8; 9; 10)

Table 1. F-SWARA [31] (a) and F-ARAS [32] (b) fuzzy linguistic expression equivalents.

(a)
Linguistic Variable	Abbreviation
Absolutely less significant	(ALS)	(1; 1; 1)
Dominantly less significant	(DLS)	(0.50; 0.67; 1)
Much less significant	(MLS)	(0.40; 0.50; 0.67)
Really less significant	(RLS)	(0.33; 0.40; 0.50)
Less significant	(LS)	(0.29; 0.33; 0.40)
Moderately less significant	(MDLS)	(0.25; 0.29; 0.33)
Weakly less significant	(WLS)	(0.22; 0.25; 0.29)
Equally significant	(ES)	(0; 0; 0)
(b)
Linguistic Variable	Abbreviation
Very Poor	(VP)	(0; 1; 2)
Poor	(P)	(1; 2; 3)
Medium Poor	(MP)	(2; 3.5; 5)
Fair	(F)	(4; 5; 6)
Medium Good	(MG)	(5; 6.5; 8)
Good	(G)	(7; 8; 9)
Very Good	(VG)	(8; 9; 10)

Fuzzy ARAS method:

The Fuzzy ARAS method was introduced by Turskis and Zavadskas in 2010. It adapts the classical ARAS model to uncertain decision environments using a fuzzy logic approach [33]. This method calculates their relative effectiveness and allows decision makers to systematically determine the most suitable option [29]. Fuzzy ARAS process steps are summarized below [29]:

Creating the Fuzzy Decision Matrix: In the first step, a decision matrix is created containing the alternatives (m) and criteria (n). The evaluation of each alternative with respect to each criterion is performed using the verbal expressions and corresponding fuzzy numbers given in Table 1.

Step 1:	A decision matrix:	In this way, a decision matrix is obtained whose cells consist of fuzzy values:	$\tilde{X}=\left[\begin{array}{cccc}...& ...& ...& ...\\ {\tilde{X}}_{i1}& ...& {\tilde{X}}_{ij}& {\tilde{X}}_{in}\\ {\tilde{X}}_{m1}& ...& {\tilde{X}}_{mj}& {\tilde{X}}_{mn}\end{array}\right]$ $i=0.1\dots \dots m j=1\dots n$	(5)
Step 2:	Creating the expanded decision matrix (adding the ideal alternative row):	If criterion j is benefit (maximization) oriented:	${\tilde{x}}_{0j}={max}_i{\tilde{x}}_{ij}$	(6)
		If criterion j is cost (minimization) oriented:	${\tilde{x}}_{0i}={\mathit{min}}_i{\tilde{x}}_{ij}$	(7)
Step 3:	Fuzzy decision matrix normalization:	(For benefit criteria)	${\tilde{r}}_{ij}={\displaystyle \frac{{\tilde{x}}_{ij}}{{\sum }_{i=0}^m{\tilde{x}}_{ij}}}$	(8)
		(For cost criteria)	${\tilde{r}}_{ij}={\displaystyle \frac{1/{\tilde{x}}_{ij}}{{\Sigma }_{\mathrm{i}=0}^{m}1/{\tilde{x}}_{ij}}}$	(9)
Step 4	Creating the weighted normalized decision matrix:	The normalized values are multiplied by the criteria weights to obtain the weighted matrix	${\tilde{v}}_{ij}={\tilde{r}}_{ij}\times {\tilde{\omega }}_j$	(10)
Step 5:	Calculating the function values of the alternatives:	The weighted value (optimality function) is calculated for each alternative	$\widetilde{s_i}={\sum }_{j=1}^n{\tilde{v}}_{ij}$	(11)
Step 6:	Finalizing fuzzy scores:	Defuzzification	$S_i={\displaystyle \frac{l_i+4\times m_i+u_i}{6}}$	(12)
Step 7:	Calculating the benefit ratings of the alternatives:	benefit ratings	$K_i={\displaystyle \frac{S_i}{S_0}}$	(13)

4. The Development of the Sustainability Product Selection Decision Model

This study addresses the critical challenge of selecting sustainable product groups within the chemical industry. The proposed model was developed through a comprehensive literature review and structured consultations with field experts. Figure 1 shows a flowchart of the proposed hybrid MCDM model for sustainable product selection.

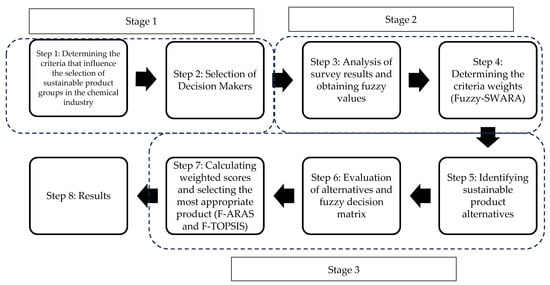
Figure 1. Flowchart of MCDM model.

• Step 1: Determining the criteria affecting the selection of sustainable product groups in the chemical industry:

This study established its evaluation criteria through a synthesis of existing literature and insights from supply chain experts. Table 2 shows the resulting criteria and detailed explanations. Three main criteria were identified for sustainable product groups: Environmental Sustainability, Economic Performance and Commercial Value, and Social Responsibility and Ethics. Each was analyzed from a distinct sustainability perspective: reducing environmental impact, enhancing economic efficiency, and promoting social responsibility. This approach aims to guide companies toward long-term sustainable success.

Table 2. Criteria and Definitions.

	Sub-Criteria	Description
Environmental Sustainability	Energy Consumption C1	- The amount of energy used in production - Energy efficiency (kWh/kg product) - Renewable energy usage rate	[34,35,36]
	Carbon Footprint/Emissions C2	- CO2 and other greenhouse gas emissions - Emissions from transport - Environmental pollution during the production process	[34,35,36,37,38,39,40]
	Raw Material Consumption C3	- Use of recycled/renewable raw materials - Critical raw material dependency	[35,36]
	Waste Management C4	- Recyclability - Waste reduction performance - Hazardous waste generation	[34,35,38]
	Water Use C5	- Water consumption per product - Wastewater treatment capacity	[34,35,36]
Economic Performance and Commercial Value	Life Cycle Cost (LCC) C6	- Supply, production, use and disposal costs	[34,35,38,39,41]
	Quality and Reliability C7	- Failure rates - Warranty period - Product lifespan	[36,41,42,43]
	Manufacturability C8	- Ease of production - Technology compatibility - Process efficiency	[41,42]
	Market Potential/Profitability C9	- Sales volume - Margin rate - ROI (Return on Investment)	[39,42,44]
	Supplier Cost and Availability C10	- Supply chain stability - Raw material price fluctuations	[45]
Social Responsibility and Ethics	Occupational Health and Safety C11	- Worker safety in the production process - Accident rate/prevention systems	[35,36,38]
	Consumer Safety and Health C12	- Product safety (certificates, test results) - Risk factors in use	[41]
	Ethical Production C13	- No child labor - Fair wages and working conditions	[36,40,41]
	Social Contribution C14	- Local employment - Social responsibility practices - Disability-friendly products/processes	[5,36]
	Education and Awareness Raising C15	- User information - Sustainability labeling (eco-labels)	[36,38,39,41]

• Step 2: Selection of Decision Makers

The identified criteria were developed based on a literature review and validated by supply chain management experts. Information regarding their roles, industry experience, and education levels is shown in Table 3.

Table 3. Characteristics of decision makers.

	Position/Title	Experience	Education
DM1	Director	21 Years	M.Sc. in Industrial Engineering
DM2	Purchasing Manager	26 Years	B.Sc. in Chemical Engineering
DM3	Planning Manager	13 Years	B.Sc. in Industrial Engineering
DM4	Logistics and Warehouse Specialist	6 Years	B.Sc. in Logistics Management
DM5	Purchasing Specialist (Indirect)	4 Years	B.Sc. in Chemical Engineering

• Step 3: Analysis of survey results and obtaining fuzzy values

Figure 2 presents the criteria for sustainable product selection, organized under the three main sustainability categories: Environmental Sustainability, Economic Performance and Commercial Value, and Social Responsibility and Ethics.

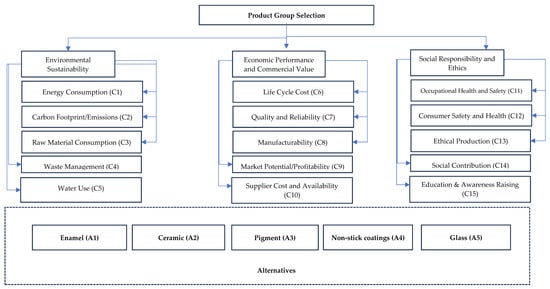
Figure 2. MCDM model.

Under Environmental Sustainability, five criteria assess the product’s environmental impact: energy consumption, carbon footprint/emissions, raw material consumption, waste management, and water usage.

The Economic Performance and Commercial Value category assesses financial benefits using five criteria: life cycle cost, quality and reliability, manufacturability, market potential/profitability, and supplier cost and availability.

The final category, Social Responsibility and Ethics, evaluates social impact and ethical compliance using five criteria: occupational health and safety, consumer safety and health, ethical production, social contribution, and education and awareness.

Within this framework, five product groups were selected for sustainability evaluation and analysis.

In the second phase of the study, decision-makers evaluated all criteria individually using the fuzzy linguistic scale presented in Table 1 to determine their relative importance. The Fuzzy SWARA methodology was systematically applied to derive criteria weights. Initially, criteria were ranked in descending order of importance based on expert consensus. Subsequently, each decision-maker expressed the relative importance of criterion j compared to the preceding criterion j-1 using triangular fuzzy numbers corresponding to the linguistic terms provided in Table 1. The individual evaluation results obtained from the five decision-makers are documented in Table A1, Table A2, Table A3, Table A4 and Table A5 in Appendix A.

• Step 4: Determining the Criteria Weights (Fuzzy SWARA)

To obtain average fuzzy weight values for all criteria, the arithmetic average of the evaluation results of five decision makers was calculated. The average weights obtained are given in Table 4.

Table 4. Fuzzy SWARA average criteria weights.

					F-SWARA
	CRITERIA	L	M	U	Weight	Ranking
C1	Energy Consumption	0.061	0.074	0.093	0.076	5
C2	Carbon Footprint/Emissions	0.042	0.051	0.062	0.051	11
C3	Raw Material Consumption	0.032	0.042	0.056	0.043	14
C4	Waste Management	0.074	0.085	0.103	0.087	4
C5	Water Use	0.097	0.106	0.122	0.108	3
C6	Life Cycle Cost (LCC)	0.052	0.063	0.078	0.064	7
C7	Quality and Reliability	0.047	0.058	0.073	0.059	8
C8	Manufacturability	0.061	0.072	0.088	0.073	6
C9	Market Potential/Profitability	0.043	0.053	0.066	0.053	9
C10	Supplier Cost & Availability	0.033	0.043	0.056	0.044	13
C11	Occupational Health and Safety	0.100	0.113	0.132	0.114	1
C12	Consumer Safety and Health	0.099	0.111	0.129	0.113	2
C13	Ethical Production	0.038	0.049	0.064	0.050	12
C14	Social Contribution	0.040	0.051	0.066	0.052	10
C15	Education & Awareness Raising	0.010	0.015	0.022	0.015	15

In this study, the Fuzzy SWARA method was used to determine the criteria weights. A meeting was held with the participation of five supply chain experts. The results obtained from expert opinions were systematically evaluated using triangular fuzzy numbers. The fuzzy values were then defuzzified to determine the relative weight of each criterion. According to the findings, the criterion with the highest weight, 0.114, was determined to be C11—Occupational Health and Safety. This result indicates that decision-makers adopt a human-centered approach within the framework of sustainability. This was followed by C12—Consumer Safety and Health (0.113) and C5—Water Use (0.108). The top three criteria are concerned with the importance placed on human health, safety, and natural resource use. Criteria such as C4—Waste Management (0.087) and C1—Energy Consumption (0.076) also carry significant weight. When analyzed from an environmental perspective, they stand out as key components. Furthermore, criteria such as C8—Manufacturability (0.073) and C6—Life Cycle Cost (0.064) demonstrate importance from an economic perspective.

According to Figure 3, Occupational Health and Safety ranked first, and Consumer Safety and Health ranked second. The placement of these criteria in the first rank indicates that safety and health for both employees and consumers are priorities in product group selection. The fuzzy triangle membership function graph provides a more in-depth analysis. For example, the L, M, and U values for the Education criterion are very close. This indicates very low uncertainty and that experts agree on the weighting of this criterion. Similarly, the relatively narrow triangles of criteria C2 (Carbon Footprint) and C14 (Social Contribution) are similarly explained. Overall, the results obtained from the Fuzzy SWARA method provide guidance on which areas should be prioritized to achieve sustainability goals.

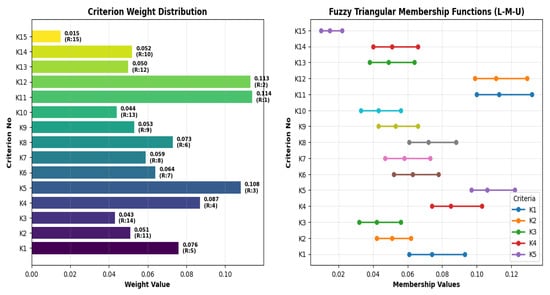
Figure 3. Criterion weighting with Fuzzy SWARA.

• Step 5: Identifying sustainable product alternatives

There are five main material groups available. Enamel (A1): This product group is used for household applications—including ovens, cooking utensils, barbecues, ranges, and stovetops—as well as in industrial manufacturing for water heaters, architectural applications, reactor enamel, and specialty uses. Enamel coatings provide applied surfaces with aesthetic appeal, high wear resistance, strong mechanical strength, and chemical resistance [46]. Ceramics (A2) offer a wide range of finishes, from frits to composite glazes, digital inks to effects. These coatings provide smooth, silky, and flawless surfaces, strong color perception, aesthetic appeal, increased chemical resistance, and easy-to-clean surfaces [47]. Pigments (A3) consist of innovative, high-temperature and chemical-resistant products used in many areas, particularly in the plastics, paint, and ceramics industries. As a result of R&D studies, it offers excellent dispersion quality, high stability, a wide color range, particle size options, and environmentally friendly properties [48]. Non-Stick Coatings (A4) include 1, 2 and 3-layer spray PTFE, roller PTFE, industrial PFA, 1 and 2-layer Sol–Gel ceramic, 1 and 2-layer decorative silicone coating options, as well as acrylic coatings used in small appliances and high-strength vitreous aluminum frits [49]. Glass (A5): Glass-coating solutions with high chemical and physical resistance serve the white goods, construction, automotive, glass packaging, and glassware sectors. Color options, surface properties, and gloss levels adapt to diverse needs [50].

• Step 6: Evaluation of alternatives and fuzzy decision matrix (F-ARAS)

In this phase, the sustainable product groups were structured according to the evaluation framework established in the previous steps, which involved the criteria weights from the Fuzzy SWARA method and the resulting decision matrix. Five experts evaluated the alternatives using the scale provided in Table 1. Their assessments form the fuzzy decision matrix presented in Table 5. Table 6 was then created by calculating the average of these expert opinions.

Table 5. Fuzzy values of decision makers.

		C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12	C13	C14	C15
		(Min)	(Min)	(Min)	(Min)	(Min)	(Min)	(Max)	(Max)	(Max)	(Min)	(Max)	(Max)	(Max)	(Max)	(Max)
A1	DM1	(2; 3.5; 5)	(4; 5; 6)	(2; 3.5; 5)	(4; 5; 6)	(7; 8; 9)	(4; 5; 6)	(7; 8; 9)	(8; 9; 10)	(8; 9; 10)	(7; 8; 9)	(5; 6.5; 8)	(7; 8; 9)	(8; 9; 10)	(8; 9; 10)	(8; 9; 10)
	DM2	(2; 3.5; 5)	(2; 3.5; 5)	(5; 6.5; 8)	(5; 6.5; 8)	(7; 8; 9)	(7; 8; 9)	(7; 8; 9)	(7; 8; 9)	(8; 9; 10)	(7; 8; 9)	(7; 8; 9)	(7; 8; 9)	(7; 8; 9)	(7; 8; 9)	(5; 6.5; 8)
	DM3	(1; 2; 3)	(4; 5; 6)	(7; 8; 9)	(5; 6.5; 8)	(5; 6.5; 8)	(7; 8; 9)	(2; 3.5; 5)	(5; 6.5; 8)	(7; 8; 9)	(2; 3.5; 5)	(4; 5; 6)	(2; 3.5; 5)	(7; 8; 9)	(7; 8; 9)	(7; 8; 9)
	DM4	(2; 3.5; 5)	(5; 6.5; 8)	(1; 2; 3)	(0; 1; 2)	(7; 8; 9)	(5; 6.5; 8)	(1; 2; 3)	(7; 8; 9)	(8; 9; 10)	(7; 8; 9)	(8; 9; 10)	(8; 9; 10)	(7; 8; 9)	(7; 8; 9)	(7; 8; 9)
	DM5	(2; 3.5; 5)	(2; 3.5; 5)	(2; 3.5; 5)	(5; 6.5; 8)	(4; 5; 6)	(5; 6.5; 8)	(7; 8; 9)	(2; 3.5; 5)	(2; 3.5; 5)	(2; 3.5; 5)	(4; 5; 6)	(8; 9; 10)	(5; 6.5; 8)	(7; 8; 9)	(5; 6.5; 8)
A2	DM1	(2; 3.5; 5)	(4; 5; 6)	(5; 6.5; 8)	(4; 5; 6)	(7; 8; 9)	(5; 6.5; 8)	(7; 8; 9)	(8; 9; 10)	(5; 6.5; 8)	(4; 5; 6)	(5; 6.5; 8)	(7; 8; 9)	(7; 8; 9)	(8; 9; 10)	(8; 9; 10)
	DM2	(1; 2; 3)	(5; 6.5; 8)	(7; 8; 9)	(5; 6.5; 8)	(2; 3.5; 5)	(7; 8; 9)	(7; 8; 9)	(8; 9; 10)	(8; 9; 10)	(7; 8; 9)	(7; 8; 9)	(7; 8; 9)	(7; 8; 9)	(7; 8; 9)	(8; 9; 10)
	DM3	(0; 1; 2)	(5; 6.5; 8)	(4; 5; 6)	(4; 5; 6)	(0; 1; 2)	(5; 6.5; 8)	(5; 6.5; 8)	(7; 8; 9)	(5; 6,5; 8)	(5; 6.5; 8)	(5; 6.5; 8)	(5; 6.5; 8)	(5; 6.5; 8)	(4; 5; 6)	(4; 5; 6)
	DM4	(1; 2; 3)	(2; 3.5; 5)	(5; 6.5; 8)	(2; 3.5; 5)	(1; 2; 3)	(4; 5; 6)	(4; 5; 6)	(5; 6.5; 8)	(2; 3.5; 5)	(8; 9; 10)	(7; 8; 9)	(7; 8; 9)	(5; 6.5; 8)	(5; 6.5; 8)	(5; 6.5; 8)
	DM5	(1; 2; 3)	(7; 8; 9)	(1; 2; 3)	(7; 8; 9)	(0; 1; 2)	(4; 5; 6)	(4; 5; 6)	(7; 8; 9)	(1; 2; 3)	(7; 8; 9)	(7; 8; 9)	(5; 6.5; 8)	(8; 9; 10)	(8; 9; 10)	(7; 8; 9)
A3	DM1	(4; 5; 6)	(5; 6.5; 8)	(5; 6.5; 8)	(4; 5; 6)	(7; 8; 9)	(7; 8; 9)	(7; 8; 9)	(7; 8; 9)	(4; 5; 6)	(4; 5; 6)	(7; 8; 9)	(4; 5; 6)	(7; 8; 9)	(7; 8; 9)	(4; 5; 6)
	DM2	(4; 5; 6)	(4; 5; 6)	(4; 5; 6)	(2; 3.5; 5)	(4; 5; 6)	(7; 8; 9)	(5; 6.5; 8)	(5; 6.5; 8)	(7; 8; 9)	(4; 5; 6)	(4; 5; 6)	(4; 5; 6)	(7; 8; 9)	(7; 8; 9)	(4; 5; 6)
	DM3	(4; 5; 6)	(2; 3.5; 5)	(1; 2; 3)	(2; 3.5; 5)	(1; 2; 3)	(4; 5; 6)	(1; 2; 3)	(2; 3.5; 5)	(1; 2; 3)	(4; 5; 6)	(1; 2; 3)	(4; 5; 6)	(1; 2; 3)	(2; 3.5; 5)	(2; 3.5; 5)
	DM4	(4; 5; 6)	(4; 5; 6)	(4; 5; 6)	(4; 5; 6)	(2; 3.5; 5)	(2; 3.5; 5)	(7; 8; 9)	(2; 3.5; 5)	(5; 6.5; 8)	(4; 5; 6)	(1; 2; 3)	(1; 2; 3)	(2; 3.5; 5)	(2; 3.5; 5)	(4; 5; 6)
	DM5	(4; 5; 6)	(4; 5; 6)	(4; 5; 6)	(4; 5; 6)	(7; 8; 9)	(1; 2; 3)	(2; 3.5; 5)	(4; 5; 6)	(7; 8; 9)	(4; 5; 6)	(2; 3.5; 5)	(2; 3.5; 5)	(4; 5; 6)	(4; 5; 6)	(4; 5; 6)
A4	DM1	(4; 5; 6)	(5; 6.5; 8)	(4; 5; 6)	(4; 5; 6)	(7; 8; 9)	(7; 8; 9)	(8; 9; 10)	(7; 8; 9)	(7; 8; 9)	(4; 5; 6)	(7; 8; 9)	(7; 8; 9)	(7; 8; 9)	(7; 8; 9)	(7; 8; 9)
	DM2	(7; 8; 9)	(7; 8; 9)	(1; 2; 3)	(1; 2; 3)	(7; 8; 9)	(1; 2; 3)	(7; 8; 9)	(4; 5; 6)	(7; 8; 9)	(7; 8; 9)	(1; 2; 3)	(1; 2; 3)	(7; 8; 9)	(7; 8; 9)	(7; 8; 9)
	DM3	(5; 6.5; 8)	(1; 2; 3)	(2; 3.5; 5)	(0; 1; 2)	(2; 3.5; 5)	(1; 2; 3)	(4; 5; 6)	(8; 9; 10)	(4; 5; 6)	(0; 1; 2)	(2; 3.5; 5)	(0; 1; 2)	(4; 5; 6)	(5; 6.5; 8)	(5; 6.5; 8)
	DM4	(7; 8; 9)	(1; 2; 3)	(2; 3.5; 5)	(1; 2; 3)	(5; 6.5; 8)	(0; 1; 2)	(2; 3.5; 5)	(4; 5; 6)	(7; 8; 9)	(1; 2; 3)	(0; 1; 2)	(0; 1; 2)	(1; 2; 3)	(1; 2; 3)	(2; 3.5; 5)
	DM5	(7; 8; 9)	(1; 2; 3)	(5; 6.5; 8)	(1; 2; 3)	(5; 6.5; 8)	(0; 1; 2)	(1; 2; 3)	(1; 2; 3)	(5; 6.5; 8)	(1; 2; 3)	(1; 2; 3)	(0; 1; 2)	(1; 2; 3)	(1; 2; 3)	(1; 2; 3)
A5	DM1	(7; 8; 9)	(5; 6.5; 8)	(4; 5; 6)	(4; 5; 6)	(7; 8; 9)	(7; 8; 9)	(8; 9; 10)	(4; 5; 6)	(7; 8; 9)	(4; 5; 6)	(7; 8; 9)	(8; 9; 10)	(7; 8; 9)	(8; 9; 10)	(7; 8; 9)
	DM2	(5; 6.5; 8)	(7; 8; 9)	(2; 3.5; 5)	(4; 5; 6)	(7; 8; 9)	(4; 5; 6)	(2; 3.5; 5)	(1; 2; 3)	(4; 5; 6)	(1; 2; 3)	(7; 8; 9)	(7; 8; 9)	(4; 5; 6)	(7; 8; 9)	(4; 5; 6)
	DM3	(2; 3.5; 5)	(0; 1; 2)	(5; 6.5; 8)	(1; 2; 3)	(4; 5; 6)	(2; 3.5; 5)	(7; 8; 9)	(4; 5; 6)	(0; 1; 2)	(1; 2; 3)	(7; 8; 9)	(1; 2; 3)	(2; 3.5; 5)	(8; 9; 10)	(8; 9; 10)
	DM4	(5; 6.5; 8)	(7; 8; 9)	(7; 8; 9)	(5; 6.5; 8)	(4; 5; 6)	(1; 2; 3)	(8; 9; 10)	(1; 2; 3)	(4; 5; 6)	(5; 6.5; 8)	(4; 5; 6)	(4; 5; 6)	(4; 5; 6)	(4; 5; 6)	(1; 2; 3)
	DM5	(5; 6.5; 8)	(5; 6.5; 8)	(7; 8; 9)	(2; 3.5; 5)	(1; 2; 3)	(7; 8; 9)	(8; 9; 10)	(5; 6.5; 8)	(8; 9; 10)	(5; 6.5; 8)	(5; 6.5; 8)	(7; 8; 9)	(2; 3.5; 5)	(8; 9; 10)	(8; 9; 10)

Table 6. Fuzzy decision matrix.

	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12	C13	C14	C15
AO	(1; 2.1; 3.2)	(2.8; 4.1; 5.2)	(2.8; 4.1; 5.4)	(1.4; 2.4; 3.4)	(2; 3.1; 4.2)	(1.8; 2.8; 3,8)	(6.6; 7.7; 8.8)	(7; 8.1; 9.2)	(6.6; 7.7; 8.8)	(2.6; 3.6; 4; 6)	(6.2; 7.4; 8.6)	(6.4; 7.5; 8.6)	(6.8; 7.9; 9)	(7.2; 8.2; 9.2)	(6.4; 7.6; 8.8)
A1	(1.8; 3.2; 4.6)	(3.4; 4.7; 6)	(3.4; 4.7; 6)	(3.8; 5.1; 6.4)	(6; 7.1; 8.2)	(5.6; 6.8; 8)	(4.8; 5.9; 7)	(5.8; 7; 8.2)	(6.6; 7.7; 8.8)	(5; 6.2; 7.4)	(5.6; 6.7; 7.8)	(6.4; 7.5; 8.6)	(6.8; 7.9; 9)	(7.2; 8.2; 9.2)	(6.4; 7.6; 8.8)
A2	(1; 2.1; 3.2)	(4.6; 5.9; 7.2)	(4.4; 5.6; 6.8)	(4.4; 5.6; 6.8)	(2; 3.1; 4.2)	(5; 6.2; 7.4)	(5.4; 6.5; 7.6)	(7; 8.1; 9.2)	(4.2; 5.5; 6.8)	(6.2; 7.3; 8.4)	(6.2; 7.4; 8.6)	(6.2; 7.4; 8.6)	(6.4; 7.6; 8.8)	(6.4; 7.5; 8.6)	(6.4; 7.6; 8.8)
A3	(4; 5; 6)	(3.8; 5; 6.2)	(3.6; 4.7; 5.8)	(3.2; 4.4; 5.6)	(4.2; 5.3; 6.4)	(4.2; 5.3; 6.4)	(4.4; 5.6; 6.8)	(4; 5.3; 6.6)	(4.8; 5.9; 7)	(4; 5; 6)	(3; 4.1; 5.2)	(3; 4.1; 5.2)	(4.2; 5.3; 6.4)	(4.4; 5.6; 6.8)	(3.6; 4.7; 5.8)
A4	(6; 7.1; 8.2)	(3,4.1; 5.2)	(2.8; 4.1; 5.4)	(1.4; 2.4; 3.4)	(5.2; 6.5; 7.8)	(1.8; 2.8; 3.8)	(4.4; 5.5; 6.6)	(4.8; 5.8; 6.8)	(6; 7.1; 8.2)	(2.6; 3.6; 4,6)	(2.2; 3.3; 4.4)	(1.6; 2.6; 3.6)	(4; 5; 6)	(4.2; 5.3; 6.4)	(4.4; 5.6; 6.8)
A5	(4.8; 6.2; 7.6)	(4.8; 6; 7.2)	(5; 6.2; 7.4)	(3.2; 4.4; 5.6)	(4.6; 5.6; 6.6)	(4.2; 5.3; 6.4)	(6.6; 7.7; 8.8)	(3; 4.1; 5.2)	(4.6; 5.6; 6.6)	(3.2; 4.4; 5.6)	(6; 7.1; 8.2)	(5.4; 6.4; 7.4)	(3.8; 5; 6.2)	(7; 8; 9)	(5.6; 6.6; 7.6)

• Step 7: Calculating weighted scores and selecting the most appropriate product

Table 7 presents the final rankings obtained from the Fuzzy ARAS and Fuzzy TOPSIS methods. Alternative A2 was identified as the most suitable sustainable product group, as it has the closest value to the ideal solution. The remaining alternatives are ranked according to their relative priorities, offering decision-makers a comparative perspective on their sustainability performance.

Table 7. Determining the most suitable alternative.

		F-ARAS		F-TOPSIS
		Ki (Sİ/So)	Ranking	d+	d−	(CCi)	Ranking
A1	0.174	0.720	2	12,439	0.579	0.044	2
A2	0.198	0.817	1	12,394	0.632	0.049	1
A3	0.143	0.590	5	12,557	0.460	0.035	5
A4	0.160	0.660	3	12,518	0.510	0.039	4
A5	0.159	0.654	4	12,491	0.524	0.040	3

A1 (Enamel), A2 (Ceramic), A3 (Pigment), A4 (Non-stick Coatings), A5 (Glass), S_o = 0.242. d⁺ represents the distance from the Ideal Solution, while d⁻ represents the distance from the Negative-Ideal Solution. (CCi) is the Closeness Coefficient.

To test the accuracy of the ranking, a comparative analysis was conducted using Fuzzy TOPSIS (Similarity to Ideal Solution Preference Ranking Technique), a leading MCDM method. As shown in Table 7, the results of both methods show a high level of agreement. Both methods (F-ARAS and F-TOPSIS) consistently ranked alternatives A2 (Ceramic) and A1 (Enamel) as the two best alternatives, while alternative A3 (Pigment) was ranked as the least preferred. They have different underlying calculation philosophies, with ARAS using a benefit rating relative to an ideal alternative, while TOPSIS measures the geometric distance from ideal and anti-ideal solutions. This strong agreement significantly supports the reliability of the main findings. A small difference was observed between the third and fourth positions for alternatives A4 (Non-Stick Coating) and A5 (Glass). The main conclusion is that ceramic (A2) coating is the most sustainable option is consistent across both methodological approaches. During the analysis, an overall performance value (Si) was calculated for each alternative. These values were then compared with the overall performance of the ideal alternative. From this comparison, the relative closeness of each alternative to the optimal solution (Ki) was calculated. A Ki value closer to 1 indicates that an alternative is closer to the ideal. Consequently, the alternatives were ranked according to their Ki values, thus determining the most suitable coating material.

• Step 8: Results

According to the findings, the highest Ki value of 0.817 belongs to the A2 (Ceramic) alternative. This result indicates that the ceramic coating is the alternative closest to the ideal solution according to the evaluation criteria. It exhibited high performance in the environmental, economic, and technical dimensions, ranking first. The ceramic alternative is followed by A1 (Enamel) and A4 (Non-Stick Coating) in second and third places, with Ki values of 0.720 and 0.660, respectively. These options represent competitive performance in terms of their relative closeness to the optimal solution. The A5 (Glass) alternative ranked fourth with a value of 0.654, and A3 (Pigment) ranked fifth with a Ki value of 0.590.

This study calculated the ranking of five coating alternatives (A1—Enamel, A2—Ceramic, A3—Pigment, A4—Non-Stick, and A5—Glass) using a hybrid model. The AO alternative was used as the optimal reference point for all comparisons. According to benefit scores, A2 (Ceramic) was the highest performing alternative with a score of 0.198. This was followed by A1 (0.174), A4 (0.160), and A5 (0.159), respectively, while A3 (0.143) received the lowest score. According to fuzzy analysis, the AO (Optimal) alternative with a Ki value of 1.00 was selected as the reference point. With a Ki value of 0.817, A2 (Ceramic) was determined to be the alternative that performed closest to this reference. The consistent distribution of Si values supports the reliability of the methodology. Based on the analyses summarized in Figure 4, A2 (Ceramic) is the alternative that performs closest to the ideal (AO). The horizontal bar chart shows the Closeness Coefficient (CCi) values calculated for the alternatives using the F-TOPSIS method. A higher CCi value means the option is closer to the ideal solution. Consistent with the F-ARAS results, A2 (Ceramic) has the highest CCi score of 0.049, making it the best option according to F-TOPSIS. A1 (Enamel) follows immediately with a score of 0.044. A3 (Pigment) has the lowest score of 0.035, making it the least preferred alternative.

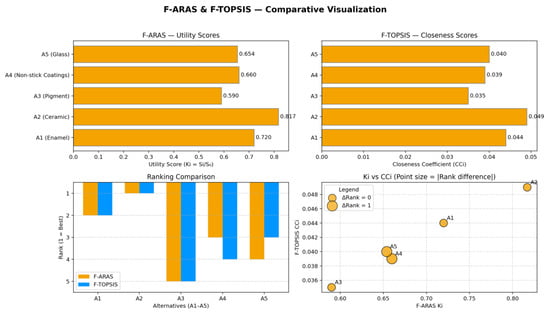
Figure 4. F-ARAS and F TOPSIS analysis results.

The only slight difference is in the middle positions (third and fourth). This difference stems from the fundamental philosophy behind the methods’ evaluation approaches: F-ARAS measures an alternative’s benefit by its ratio to the optimal solution, while F-TOPSIS considers each alternative’s geometric distance from both the best and worst solutions. However, the fact that both methods agree on the best and worst options demonstrates the robustness of our decision-making process. Ultimately, ceramic coatings are the best option from a technical and usable perspective. Enamel coatings are the second-best choice due to their affordability and aesthetic appeal. While nonstick and glass coatings are suitable for certain applications, pigment coatings are more appealing for visual applications. This entire analysis demonstrates that options A2 and A1 are highly beneficial for making smart and environmentally sound decisions, providing objective and scientific guidance to decision-makers on which coating to choose. Finally, we examined the reliability and stability of the Fuzzy TOPSIS and Fuzzy ARAS methods. We analyzed how changing the criteria weights determined from expert opinions with Fuzzy SWARA affected the final rankings of F-ARAS and F-TOPSIS. We systematically increased and decreased the weights, and the resulting ranking changes were visualized graphically to understand the robustness of the model.

Sensitivity analysis demonstrates that our decision model is quite robust; the top-ranked options performed well across all scenarios in Figure 5. Ceramic (A2) ranked best in four of the five scenarios, while Enamel (A1) consistently ranked second. Therefore, both options can be considered good alternatives overall.

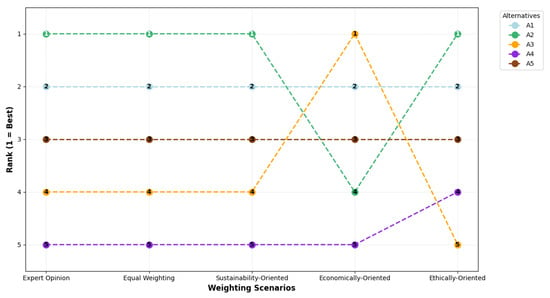
Figure 5. Alternative ranking changes based on criteria weights.

When focusing on the Economic Scenario, the situation changed significantly. Pigment (A3) rose to first place, while Ceramic (A2) fell to fourth. This result suggests that while Ceramic is normally the best option in terms of overall sustainability, pigment may be more advantageous if cost is the primary priority.

Non-Stick Coating (A4) and Glass (A5) showed less variation in ranking, with the smaller differences observed occurring mostly in scenarios where the ethical dimension was emphasized. Essentially, the performance of these two options can vary depending on the sustainability dimension being focused on.

As a result, the sensitivity analysis supports the validity of the model and shows decision makers that the prioritized criteria have a decisive impact on the final results.

5. Managerial Implications

The chemical sector is a cornerstone of the global economy, providing raw materials for many industries. However, improper production techniques and waste management can cause serious environmental damage.

Some of the products produced by the chemical industry (from plastics to cosmetics, pharmaceuticals to dyes) reach consumers directly, while others are used as intermediate goods or raw materials in other sectors (textiles, electrical appliances, metals, mineral products, construction, automotive, paper, and the service sector). This makes the chemical industry an indispensable industry for both our lives and other sectors. The chemical sector boasts a wide range of products. In addition to consumer goods such as cleaning products, paints, cosmetics, and pharmaceuticals, it also produces fertilizers and pesticides for the agricultural sector, organic and inorganic chemicals needed by the manufacturing industry, including the chemical industry, dyes, laboratory chemicals, thermoplastics, and similar products.

Many chemicals produced by the sector have negative impacts on the environment and human health, and such chemicals are considered hazardous. Sustainable chemistry encompasses the design, production, and use of efficient, effective, safe, and environmentally friendly chemical products and processes. Sustainability is crucial in the chemical industry, as it is in every sector, for protecting both the present and the future.

The study has a number of managerial implications that provide managers in the chemical industry with practical knowledge and strategic suggestions, especially those in charge of sustainable supply chain and product portfolio decisions.

In the chemical industry, choices about which products to use have a big influence on long-term financial viability, strategic management, and overall business performance. Environmental performance, market competitiveness, and financial well-being depend upon the choice of chemical products, along with production efficiency and cost structures. Cost-effectiveness, environmental concerns, compliance with regulations, and technical suitability must be weighed against each other by managers in order to maintain profitability.

Consistent quality products can improve customer satisfaction, cut costs of production, maximize stock control, and prevent wasteful use of raw material. Product options also make investment easy planning, enhance the robustness of the firm to market volatility, and create long-term value. On the other hand, bad product decisions can lead to financial exposures, regulatory fines, reputation loss, and operational inefficiencies.

The combination of Fuzzy SWARA and Fuzzy ARAS gives you a systematic, transparent, and effective approach to comparing sustainable product options. This model can help managers balance environmental, economic and social rules in a more organized way, which will make decisions less subjective and increase strategic alignment.

The fact that Ceramics (A2) is at the top of the ranking suggests that managers should invest more in ceramic product lines, R&D, and market positioning. This product category scores very high on every dimension of sustainability and can be used as a benchmark to create future products.

6. Conclusions

This work introduces an integrated model based on the Fuzzy SWARA and Fuzzy ARAS approaches to handling the product group selection issue in the chemical industry, in accordance with the rising trend towards sustainability principles. The hybrid application of these methods makes it possible to carry out more flexible and realistic analyses in uncertain decision-making environments. The model supports the integrated assessment of both qualitative and quantitative criteria, thereby improving the comprehensiveness of the decision-making process. The results highlight the significance and application of MCDM methods in sustainability-oriented decision-making processes.

In the study, 15 criteria were considered through the three primary sustainability criteria. The hybrid model provides a solution to the complex procedure involved in decision-making, giving industry players an integrated outlook with an extensive roadmap in the process. The criteria assignment of priority in the study conducted by Fuzzy SWARA indicated that the most essential criteria were Occupational Health and Safety with a priority score of 0.114, consumer safety and health with 0.113, followed by Water Use with 0.108.

The results on the basis of utility degree Ki, calculated by the Fuzzy ARAS approach to evaluate alternatives, showed that the Ceramic (A2) solution was the most sustainable one with the highest score of 0.817, followed by Enamel with 0.720, Non-Stick Coatings with 0.660, Glass with 0.654, and Pigment with 0.590. The highest rank in the ceramic product group indicates the well-rounded performance of the group in terms of sustainability criteria and strong alignment with sustainability goals. The results imply that investments in ceramic technology can inform strategic decision-making on sustainability and efficiency in performance. To ensure the reliability of the Fuzzy ARAS outcome, a comparative study was performed by implementing the Fuzzy TOPSIS methodology. The outcome of the Fuzzy TOPSIS study revealed that there was no considerable difference in the ranking results of the methods with respect to closeness coefficients, where Enamel (A1) scored the highest closeness coefficient (CCi) of 0.049, followed by Ceramic (A2) with 0.044, Pigment (A5) with 0.040, Glass (A4) with 0.039, and Non-Stick Coatings (A3) with 0.035 indicators. The values of the positive distances d+ were measured between 12.394 and 12.557, while the negative distances d- were measured between 0.460 and 0.632. Despite the slight difference in the rank ordering in terms of sustainability criteria in the two methods, the results successfully revealed that Ceramic and Enamel scored the highest rank in sustainability performance via Fuzzy ARAS and Fuzzy TOPSIS methods, respectively, ensuring the reliability and competence of the proposed decision-making model in identifying the product group on sustainability performance criteria.

The findings from the study offer key implications for businesses in the chemical industry. For instance, it is clear that it is imperative to consider human health and safety aspects in the process of selecting sustainable products. It is recommended that companies pursue integrated and holistic solutions that cover different aspects to garner a sustained competitive advantage.

This study has several limitations. First, the research is developed based on data from a specific chemical company, and validation based on a larger population is required for broad applicability. Second, the weights and criteria used include subjective decisions based on expert opinions. Third, the examination employs a static analysis that neglects dynamic market conditions or technological innovation.

This study has imperative relevance in the effective deployment of MCDM methods towards sustainable supply chain management and performs a realistic application towards the chemical sector. Integration of both Fuzzy ARAS and Fuzzy TOPSIS methods is important in strengthening the methodological power of the study and demonstrating the utility of hybrid MCDM methods towards complex decision-making scenarios. The results highlight the critical importance of structured decision-making approaches to achieving corporate sustainability goals and provide a solid platform for ongoing research.

The most significant contribution of this work is the development of an overall decision support system that includes all sustainability dimensions. This model is a contribution to sustainable development goals by providing decision-makers with a theoretical framework and an operational tool. The comparative validation with Fuzzy TOPSIS also enhances the applicability of this decision-making system by guaranteeing consistency of results according to different methodological frameworks. It is hoped that through the use of this model, chemical industry enterprises can optimize their economic performance and meet their environmental commitment.

The MCDM study has determined the most preferred product group to implement the sustainable supply chain in the chemical industry. To utilize the outcome in the formulation of company strategies, there is a great need to formulate a plan on how to implement the outcome within the corporate strategy context. Within the context of corporate strategy, there should be an overhaul of the production planning process to favor ceramic products, with related R&D and investment strategies to be developed along the way. Taking into consideration the consistent performance of both Ceramic and Enamel product groups in different methods of MCDM analysis, there should also be related formulation strategies in corporate planning related to Enamels, acting as alternatives in the process of diversification and risk management in company strategies.