Original Solution of Coupled Nonlinear Schrödinger Equations for Simulation of Ultrashort Optical Pulse Propagation in a Birefringent Fiber
Abstract
1. Introduction
2. Coupled Nonlinear Schrödinger Equations System
3. Initial Conditions and Boundary Terms
4. Dimensionless Equations
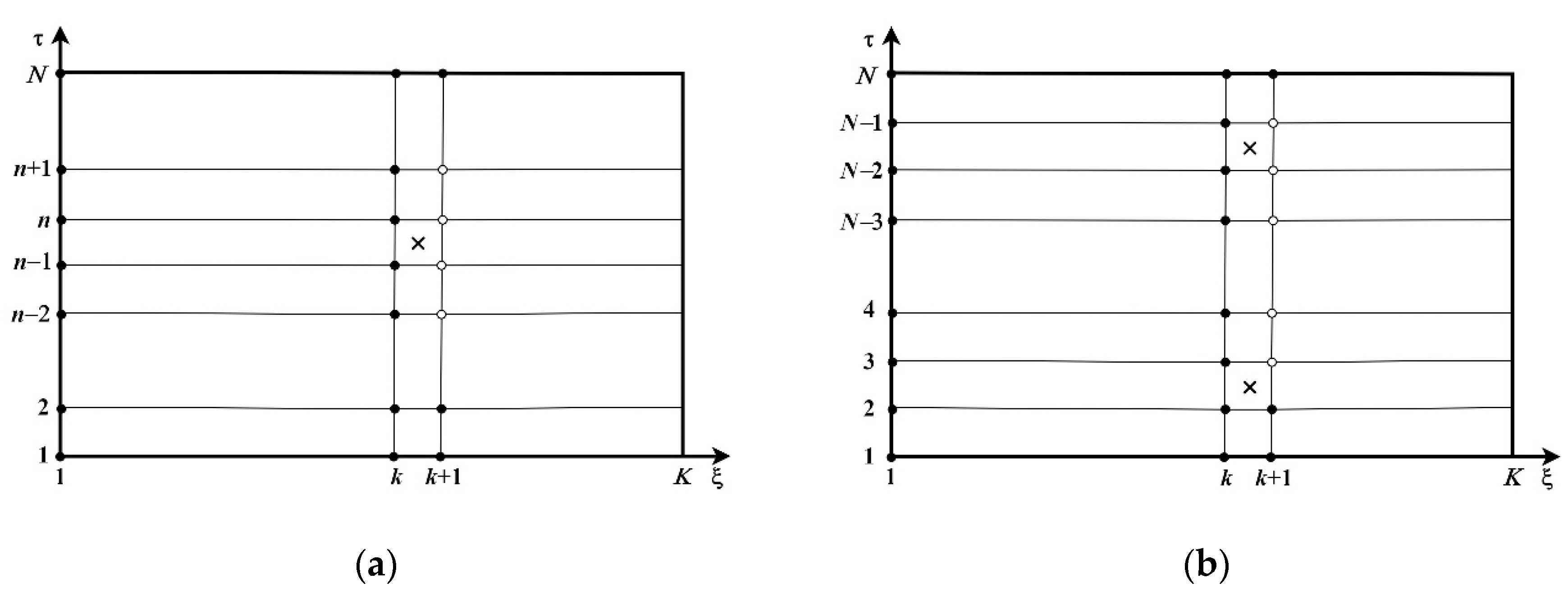
5. The Finite-Difference Scheme
6. Boundary Conditions
7. The Line Equation System in Classic Form
8. Numerical Solution Refining Algorithm
9. Method Verification on Some Classic Tasks
9.1. Heat Diffusion in a Solid Rod Task
9.2. The Korteweg–De Vries and Linear Tasks
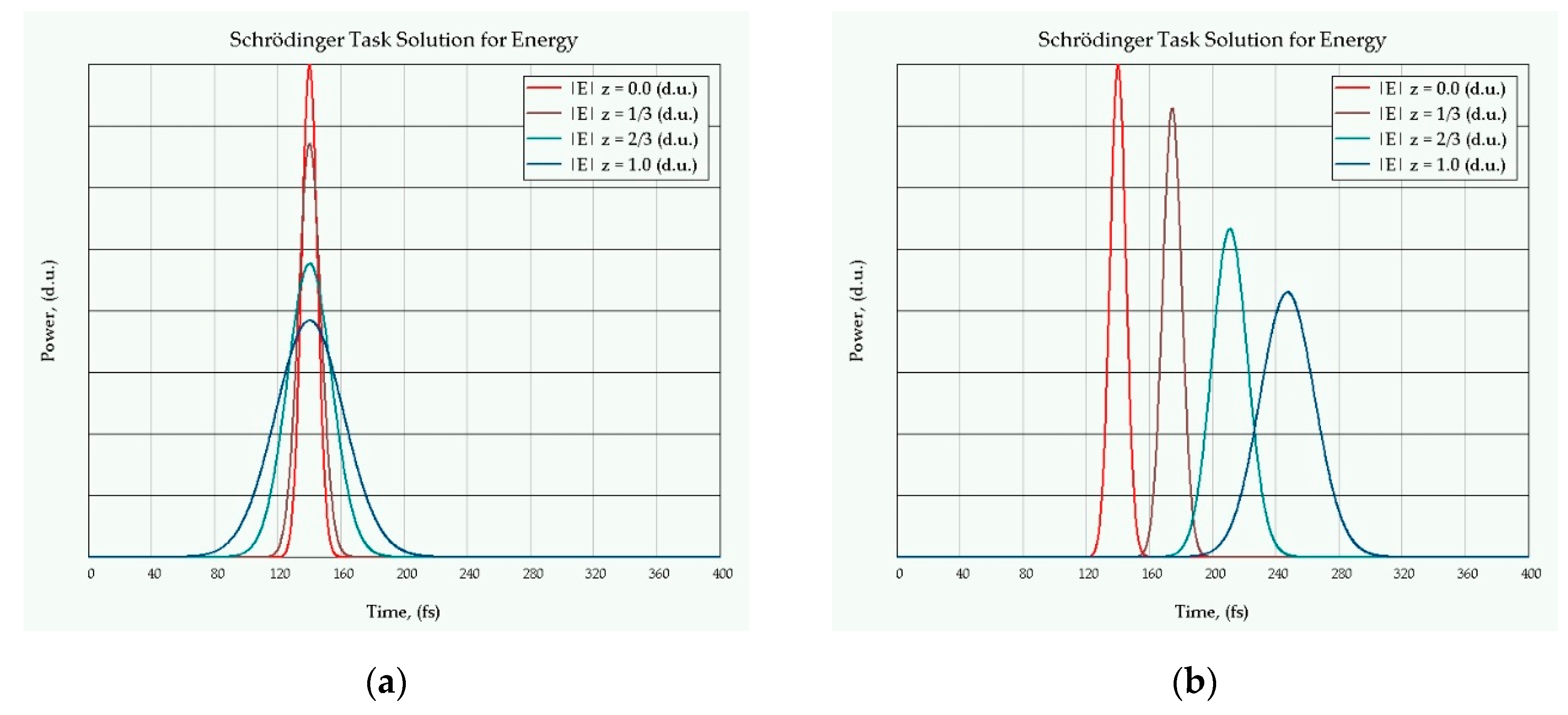
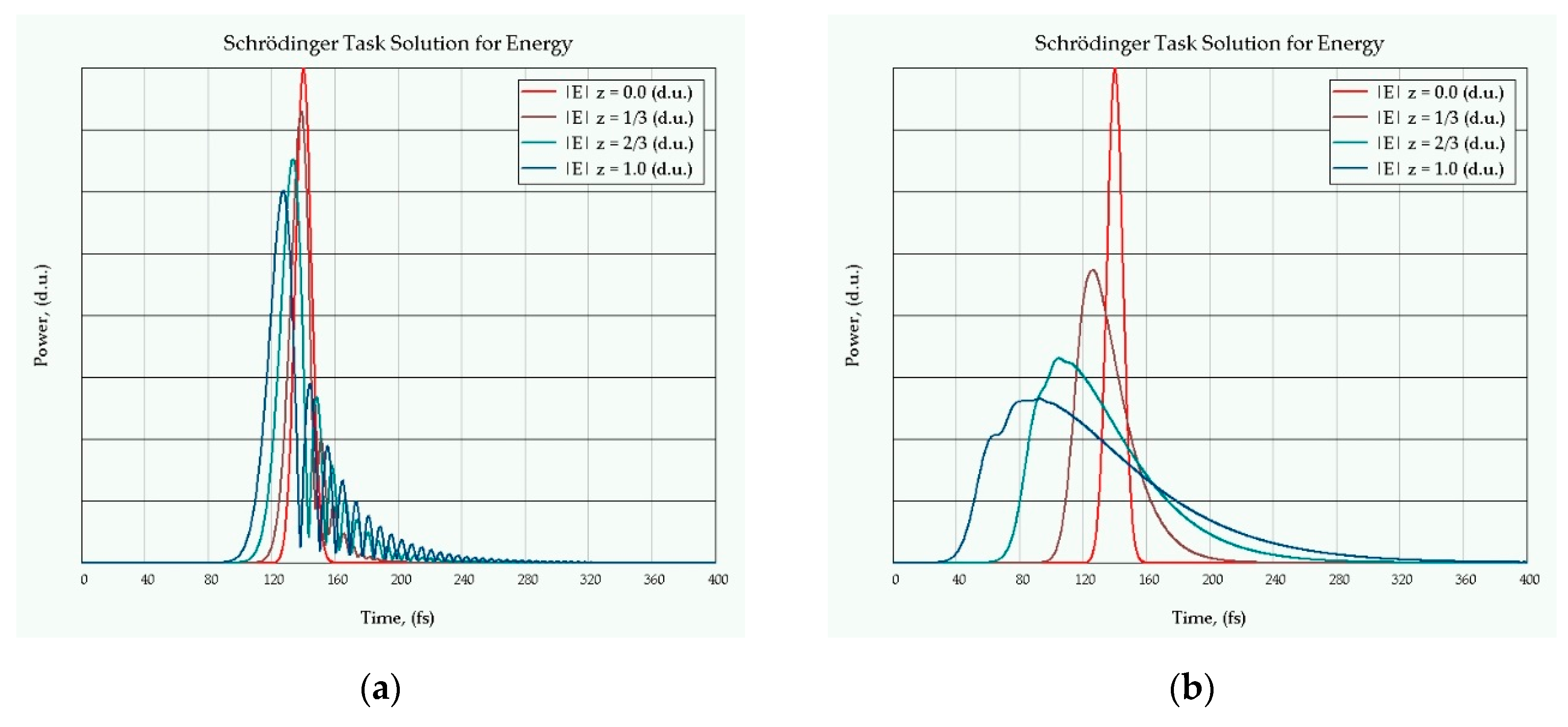
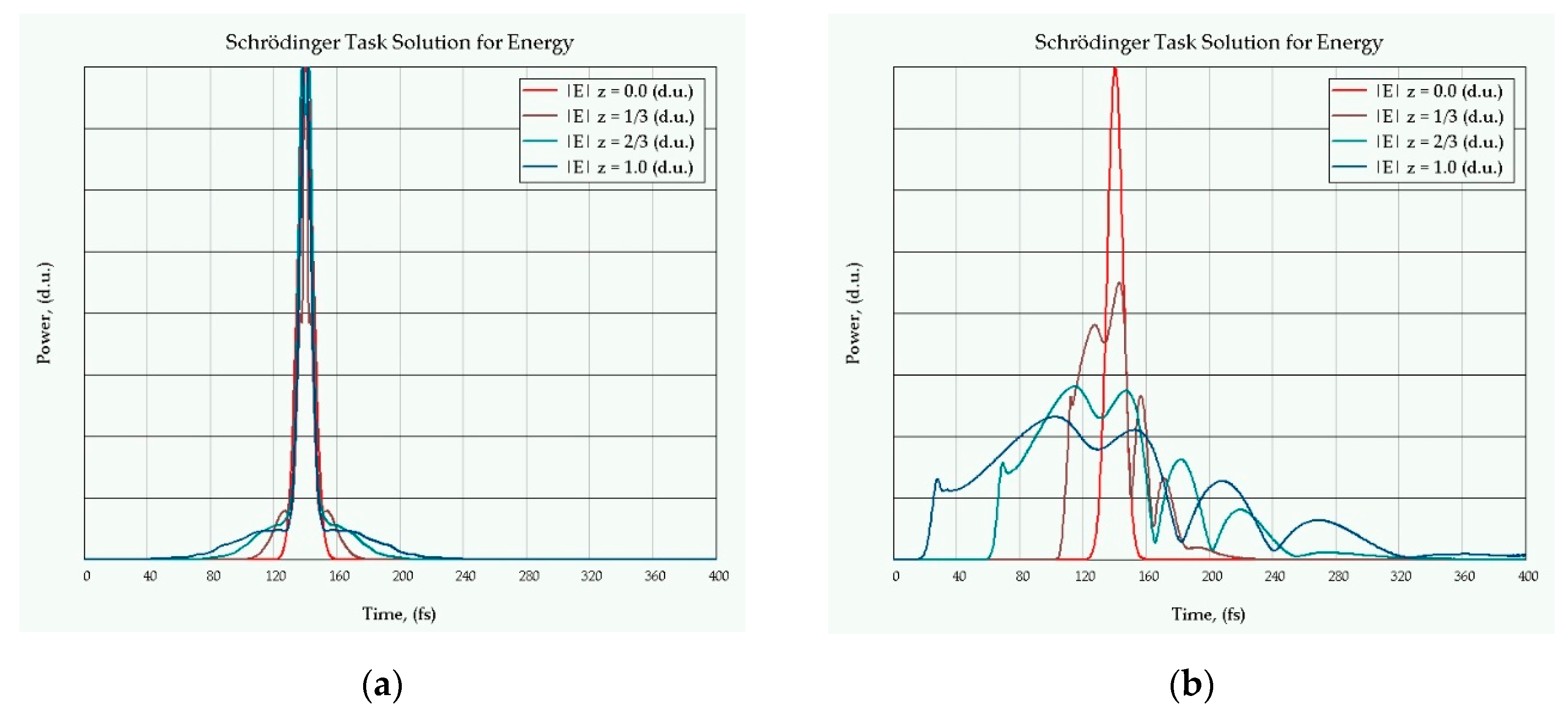
9.3. The Ultra-Short Pulse Evolution in Fiber
10. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Samad, R.; Courrol, L.; Baldochi, S.; Vieira, N. Ultrashort Laser Pulses Applications, Coherence and Ultrashort Pulse Laser Emission; IntechOpen: Lodon, UK, 2010; pp. 663–688. [Google Scholar]
- Sugioka, K.; Cheng, Y. Ultrafast lasers—Reliable tools for advanced materials processing. Light Sci. Appl. 2014, 3, e149. [Google Scholar] [CrossRef]
- Sugioka, K. Progress in ultrafast laser processing and future prospects. Nanophotonics 2017, 6, 393–413. [Google Scholar] [CrossRef]
- Hodgson, N.; Laha, M. Industrial Femtosecond Lasers and Material Processing; Industrial Laser Solutions, PennWell Publishing: Tulsa, OK, USA, 2019. [Google Scholar]
- Göbel, W.; Nimmerjahn, A.; Helmchen, F. Distortion-free delivery of nanojoule femtosecond pulses from a Ti:sapphire laser through a hollow-core photonic crystal fiber. Opt. Lett. 2004, 29, 1285–1287. [Google Scholar] [CrossRef] [PubMed]
- Michieletto, M.; Lyngsø, J.K.; Jakobsen, C.; Lægsgaard, J.; Bang, O.; Alkeskjold, T.T. Hollow-core fibers for high power pulse delivery. Opt. Express 2016, 24, 7103–7119. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Sun, B.; Luo, J.; Lee, E. Optical Fibers for High-Power Lasers. In Handbook of Optical Fibers; Peng, G.D., Ed.; Springer: Singapore, 2018. [Google Scholar]
- Poumellec, B.; Lancry, M.; Chahid-Erraji, A.; Kazansky, P. Modification thresholds in femtosecond laser processing of pure silica: Review of dependencies on laser parameters [Invited]. Opt. Mater. Express 2011, 1, 766. [Google Scholar] [CrossRef]
- Kim, D.; Choi, H.; Yazdanfar, S.; So, P.T.C. Ultrafast optical pulse delivery with fibers for nonlinear microscopy. Microsc. Res. Tech. 2008, 71, 887–896. [Google Scholar] [CrossRef]
- Larson, A.M.; Yeh, A.T. Delivery of sub-10-fs pulses for nonlinear optical microscopy by polarization-maintaining single mode optical fiber. Opt. Express 2008, 16, 14723–14730. [Google Scholar] [CrossRef]
- Le, T.; Tempea, G.; Cheng, Z.; Hofer, M.; Stingl, A. Routes to fiber delivery of ultra-short laser pulses in the 25 fs regime. Opt. Express 2009, 17, 1240–1247. [Google Scholar] [CrossRef]
- Zhou, S.; Takamido, T.; Bhandari, R.; Chong, A.; Wise, F.W. All polarization-maintaining fiber chirped-pulse amplification system for microjoule femtosecond pulses. In Proceedings of the International Society for Optics and Photonicsons, San Jose, CA, USA, 24–29 January 2009. [Google Scholar]
- Eichhorn, F.; Olsson, R.K.; Buron, J.C.D.; Grüner-Nielsen, L.; Pedersen, J.E.; Jepsen, P.U. Optical fiber link for transmission of 1-nJ femtosecond laser pulses at 1550 nm. Opt. Express 2010, 18, 6978–6987. [Google Scholar] [CrossRef]
- Kogelnik, H. Ultrashort pulse propagation in optical fibers. In New Directions in Guided Wave and Coherent Optics; Springer: Dordrecht, The Netherlands, 1984. [Google Scholar]
- Kodama, Y.; Hasegawa, A. Nonlinear pulse propagation in a monomode dielectric guide. IEEE J. Quantum Electron. 1987, 23, 510–524. [Google Scholar] [CrossRef]
- Mamyshev, P.V.; Chernikov, S.V. Ultrashort-pulse propagation in optical fibers. Opt. Lett. 1990, 15, 1076. [Google Scholar] [CrossRef] [PubMed]
- Zayed, E.M.E.; Alurrfi, K.A.E. The G′G,1G-expansion method and its applications to two nonlinear Schrödinger equations describing the propagation of femtosecond pulses in nonlinear optical fibers. Optik 2016, 127, 1581–1589. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Amer, Y.A. Many exact solutions for a higher-order nonlinear schrödinger equation with non-kerr terms describing the propagation of femtosecond optical pulses in nonlinear optical fibers. Comput. Math. Model. 2016, 28, 118–139. [Google Scholar] [CrossRef]
- Liu, W.; Hu, W.; Xie, Z.; Liu, Y. The research on propagation of ultrashort pulse in normal group-velocity dispersion fiber. In Proceedings of the 2019 2nd International Conference on Sustainable Energy, Environment and Information Engineering (SEEIE 2019), Beijing, China, 24–25 March 2019. [Google Scholar]
- Agrawal, G.P. Nonlinear Fiber Optic; Academic Press: New York, NY, USA, 2013. [Google Scholar]
- Fedoruk, M.P.; Paasonen, V.I. Kompaktnaya dissipativnaya skhema dlya nelinejnogo uravneniya Shredingera. Comput. Technol. 2011, 16, 68–73. (In Russian) [Google Scholar]
- Karpik, P.A. Investigation of difference schemes for solving the nonlinear Schrödinger equation. Bull. SSUGIT 2019, 24, 68–73. (In Russian) [Google Scholar]
- Karasawa, N.; Nakamura, S.; Morita, R.; Shigekawa, H.; Yamashita, M. Comparison between theory and experiment of nonlinear propagation for 4.5-cycle optical pulses in a fused-silica fiber. Nonlinear Opt. 2000, 24, 133–138. [Google Scholar]
- Nakamura, S.; Li, L.; Karasawa, N.; Morita, R.; Shigekawa, H.; Yamashita, M. Measurements of third-order dispersion effects for generation of high-repetition-rate, sub-three-cycle transform-limited pulses from a glass fiber. Jpn. J. Appl. Phys. 2002, 41, 1369–1373. [Google Scholar] [CrossRef][Green Version]
- Nakamura, S.; Koyamada, Y.; Yoshida, N.; Karasawa, N.; Sone, H.; Ohtani, M.; Mizuta, Y.; Morita, R.; Shigekawa, H.; Yamashita, M. Finite-difference time-domain calculation with all parameters of Sellmeier’s fitting equation for 12-fs laser pulse propagation in a silica fiber. IEEE Photon. Technol. Lett. 2002, 14, 480–482. [Google Scholar] [CrossRef][Green Version]
- Nakamura, S.; Takasawa, N.; Koyamada, Y. Comparison between finite-difference time-domain calculation with all parameters of Sellmeier’s fitting equation and experimental results for slightly chirped 12-fs laser pulse propagation in a silica fiber. J. Light. Technol. 2005, 23, 855–863. [Google Scholar] [CrossRef]
- Nakamura, S.; Takasawa, N.; Koyamada, Y.; Sone, H.; Xu, L.; Morita, R.; Yamashita, M. Extended finite difference time domain analysis of induced phase modulation and four-wave mixing between two-color femtosecond laser pulses in a silica fiber with different initial delays. Jpn. J. Appl. Phys. 2005, 44, 7453–7459. [Google Scholar] [CrossRef]
- Nakamura, S. Comparison between finite-difference time-domain method and experimental results for femtosecond laser pulse propagation. Coherence Ultrashort Pulse Laser Emiss. 2010, 442–449. [Google Scholar] [CrossRef][Green Version]
- Burdin, V.A.; Bourdine, A.V. Simulation results of optical pulse non-linear few-mode propagation over optical fiber. Appl. Photon. 2016, 3, 309–320. (In Russian) [Google Scholar] [CrossRef]
- Burdin, V.A.; Bourdine, A.V. Model for a few-mode nonlinear propagation of optical pulse in multimode optical fiber. In Proceedings of the OWTNM, Warsaw, Poland, 20–21 May 2016. [Google Scholar]
- Burdin, V.A.; Bourdine, A.V. Simulation of an ultrashort optical pulse propagation in a polarization-maintaining optical fiber. Appl. Photon. 2019, 6, 93–108. (In Russian) [Google Scholar]
- Marcuse, D.; Manyuk, C.; Wai, P.K.A. Application of the Manakov-PMD equation to studies of signal propagation in optical fibers with randomly varying birefringence. J. Light. Technol. 1997, 15, 1735–1746. [Google Scholar] [CrossRef]
- Kalithasan, B.; Nakkeeran, K.; Porsezian, K.; Dinda, P.T.; Mariyappa, N. Ultra-short pulse propagation in birefringent fibers—The projection operator method. J. Opt. A Pure Appl. Opt. 2008, 10, 85102. [Google Scholar] [CrossRef]
- Mumtaz, S.; Essiambre, R.-J.; Agrawal, G.P. Nonlinear propagation in multimode and multicore fibers: Generalization of the manakov equations. J. Light. Technol. 2012, 31, 398–406. [Google Scholar] [CrossRef]
- Hardin, R.; Tappert, F.D. Applications of the split-step Fourier method to the numerical solution of nonlinear and variable coefficient wave equations. SIAM Rev. 1973, 15, 423. [Google Scholar]
- Lake, B.M.; Yuen, H.C.; Rungaldier, H.; Ferguson, W.E. Nonlinear deep-water waves: Theory and experiment. Part 2. Evolution of a continuous wave train. J. Fluid Mech. 1977, 83, 49–74. [Google Scholar] [CrossRef]
- Wang, T. Maximum norm error bound of a linearized difference scheme for a coupled nonlinear Schrödinger equations. J. Comput. Appl. Math. 2011, 235, 4237–4250. [Google Scholar] [CrossRef]
- Wang, D.; Xiao, A.; Yang, W. A linearly implicit conservative difference scheme for the space fractional coupled nonlinear Schrödinger equations. J. Comput. Phys. 2014, 272, 644–655. [Google Scholar] [CrossRef]
- Dehghan, M.; Taleei, A. A Chebyshev pseudospectral multidomain method for the soliton solution of coupled nonlinear Schrödinger equations. Comput. Phys. Commun. 2011, 182, 2519–2529. [Google Scholar] [CrossRef]
- Dehghan, M.; Abbaszadeh, M.; Mohebbi, A. Numerical solution of system of n-coupled nonlinear Schrödinger equations via two variants of the meshless local Petrov-Galerkin (MLPG) method. Comput. Model. Eng. Sci. 2014, 100, 399–444. [Google Scholar]
- Chen, Y.; Zhu, H.; Song, S. Multi-symplectic splitting method for the coupled nonlinear Schrödinger equation. Comput. Phys. Commun. 2010, 181, 1231–1241. [Google Scholar] [CrossRef]
- Ma, Y.; Kong, L.; Hong, J.; Cao, Y. High-order compact splitting multisymplectic method for the coupled non-linear Schrödinger equations. Comput. Math. Appl. 2011, 61, 319–333. [Google Scholar] [CrossRef]
- Taha, T.R.; Xu, X. Parallel split-step fourier methods for the coupled nonlinear Schrödinger type equations. J. Supercomput. 2005, 32, 5–23. [Google Scholar] [CrossRef]
- Wang, S.; Wang, T.; Zhang, L. Numerical computations for N-coupled nonlinear Schrödinger equations by split step spectral methods. Appl. Math. Comput. 2013, 222, 438–452. [Google Scholar] [CrossRef]
- Deiterding, R.; Glowinski, R.; Oliver, H.; Poole, S. A reliable split-step fourier method for the propagation equation of ultra-fast pulses in single-mode optical fibers. J. Light. Technol. 2013, 31, 2008–2017. [Google Scholar] [CrossRef]
- Sakhabutdinov, A.Z.; Anfinogentov, V.I.; Morozov, O.G.; Gubaidullin, R.R. Numerical approaches to solving a nonlinear system of Schrödinger equations for wave propagation in an optical fiber. Comput. Technol. 2020, 25, 42–54. [Google Scholar] [CrossRef]
- Crank, J.; Nicolson, P.; Hartree, D.R. A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1947. [Google Scholar]
- Novik, Y.F. Analysis of the results of computer simulation N-soliton solutions of the Korteweg-de Vries equation. Informatics 2017, 1, 11–15. (In Russian) [Google Scholar]
- Fedoruk, M.P.; Sidelnikov, O.S. Algorithms for numerical simulation of optical communication links based on multimode fiber. Comput. Technol. 2015, 20, 105–119. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhavdatovich Sakhabutdinov, A.; Ivanovich Anfinogentov, V.; Gennadievich Morozov, O.; Alexandrovich Burdin, V.; Vladimirovich Bourdine, A.; Mudarrisovich Gabdulkhakov, I.; Anatolievich Kuznetsov, A. Original Solution of Coupled Nonlinear Schrödinger Equations for Simulation of Ultrashort Optical Pulse Propagation in a Birefringent Fiber. Fibers 2020, 8, 34. https://doi.org/10.3390/fib8060034
Zhavdatovich Sakhabutdinov A, Ivanovich Anfinogentov V, Gennadievich Morozov O, Alexandrovich Burdin V, Vladimirovich Bourdine A, Mudarrisovich Gabdulkhakov I, Anatolievich Kuznetsov A. Original Solution of Coupled Nonlinear Schrödinger Equations for Simulation of Ultrashort Optical Pulse Propagation in a Birefringent Fiber. Fibers. 2020; 8(6):34. https://doi.org/10.3390/fib8060034
Chicago/Turabian StyleZhavdatovich Sakhabutdinov, Airat, Vladimir Ivanovich Anfinogentov, Oleg Gennadievich Morozov, Vladimir Alexandrovich Burdin, Anton Vladimirovich Bourdine, Ildaris Mudarrisovich Gabdulkhakov, and Artem Anatolievich Kuznetsov. 2020. "Original Solution of Coupled Nonlinear Schrödinger Equations for Simulation of Ultrashort Optical Pulse Propagation in a Birefringent Fiber" Fibers 8, no. 6: 34. https://doi.org/10.3390/fib8060034
APA StyleZhavdatovich Sakhabutdinov, A., Ivanovich Anfinogentov, V., Gennadievich Morozov, O., Alexandrovich Burdin, V., Vladimirovich Bourdine, A., Mudarrisovich Gabdulkhakov, I., & Anatolievich Kuznetsov, A. (2020). Original Solution of Coupled Nonlinear Schrödinger Equations for Simulation of Ultrashort Optical Pulse Propagation in a Birefringent Fiber. Fibers, 8(6), 34. https://doi.org/10.3390/fib8060034







