Optical Characterization of Non-Stoichiometric Silicon Nitride Films Exhibiting Combined Defects
Abstract
1. Introduction
2. Theory
2.1. Structural Model
- The ambient is formed by vacuum with the refractive index equal to unity.
- The substrate is silicon single crystal wafer, i.e., the substrate is optically homogeneous and isotropic.
- The films are uniform in thickness inside the areas used for spectrophotometric and ellipsometric measurements.
- The non-stoichiometric silicon nitride thin films are inhomogeneous with profiles of the optical constants across these films.
- These films exhibit uniaxial anisotropy with the optical axis perpendicular to the boundaries.
- Random roughness was assumed on the upper boundaries of the films. It was assumed that this roughness corresponds to the Gaussian stochastic process.
2.2. Optical Quantities of Inhomogeneous Films
2.3. Roughness of the Upper Boundaries
2.4. Reflection on the Back Sides of the Substrates
2.5. Dispersion Model
2.6. Imaging Spectroscopic Reflectometry
3. Experiment
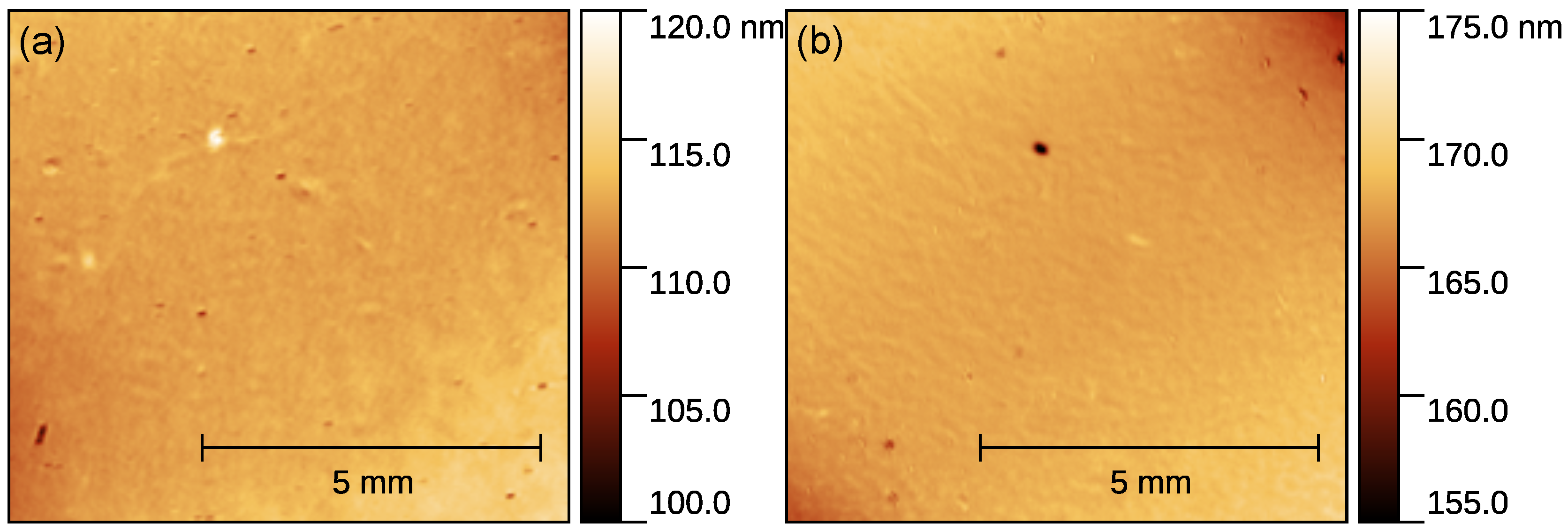
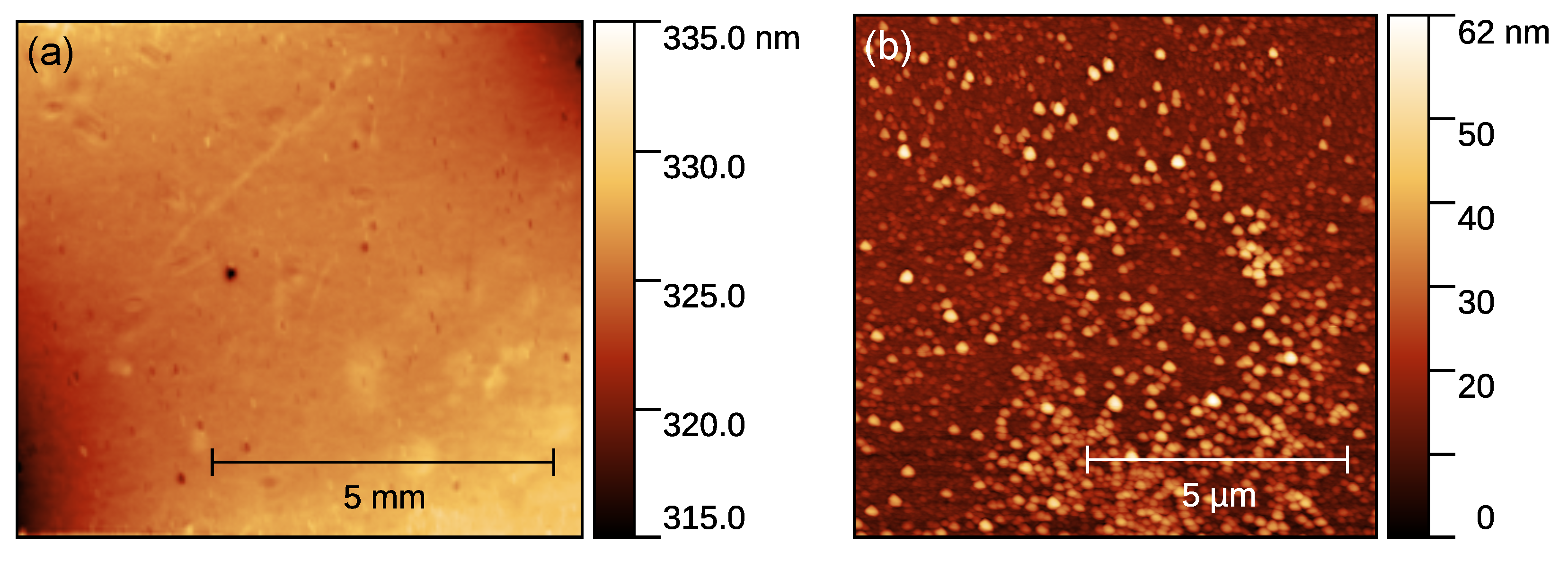
3.1. Sample Preparation
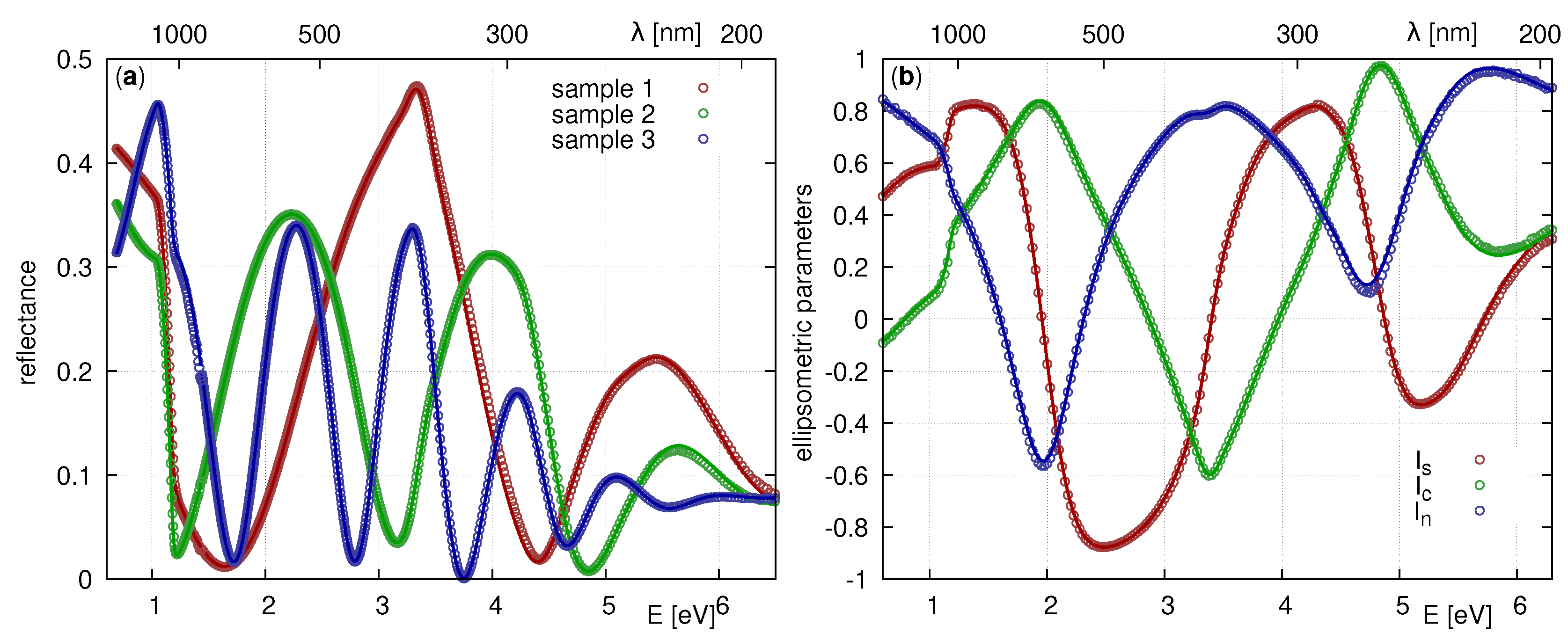
3.2. Experimental Data
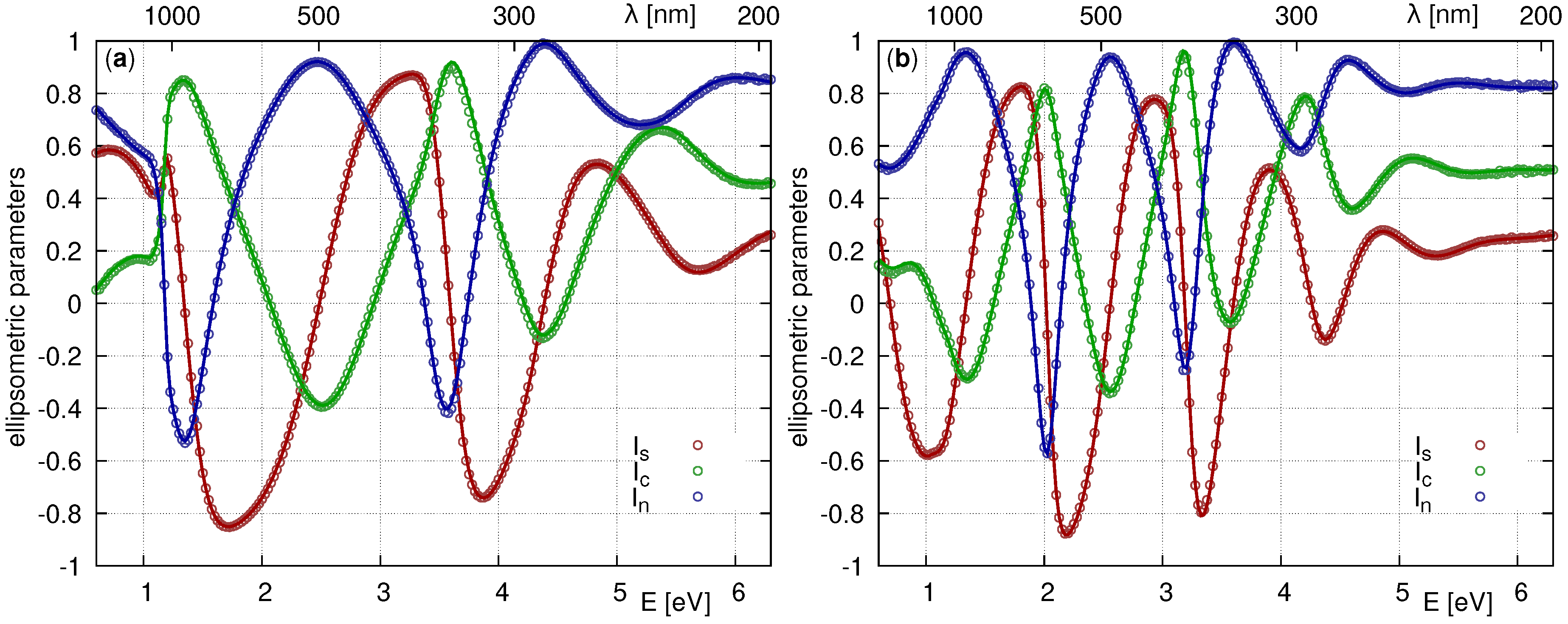
3.3. Data Processing
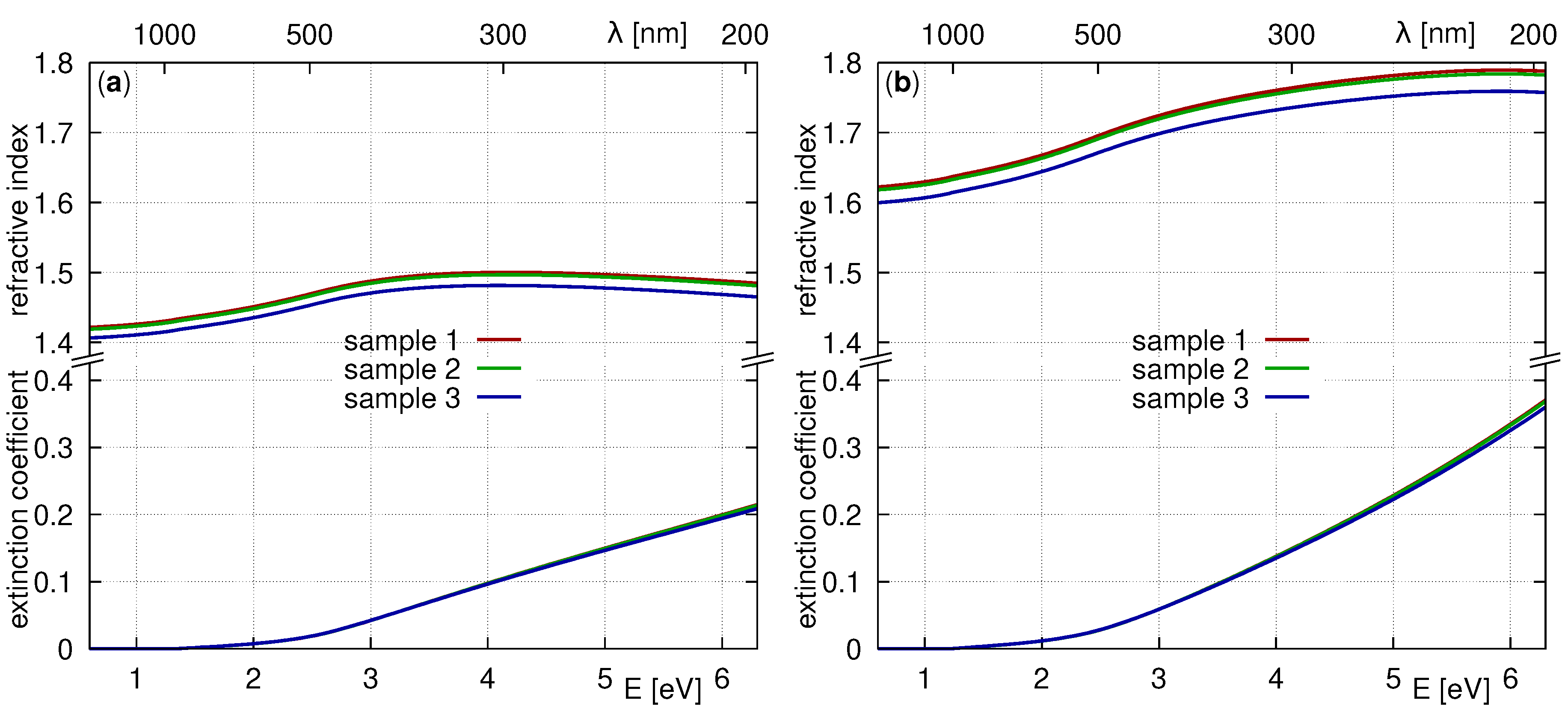
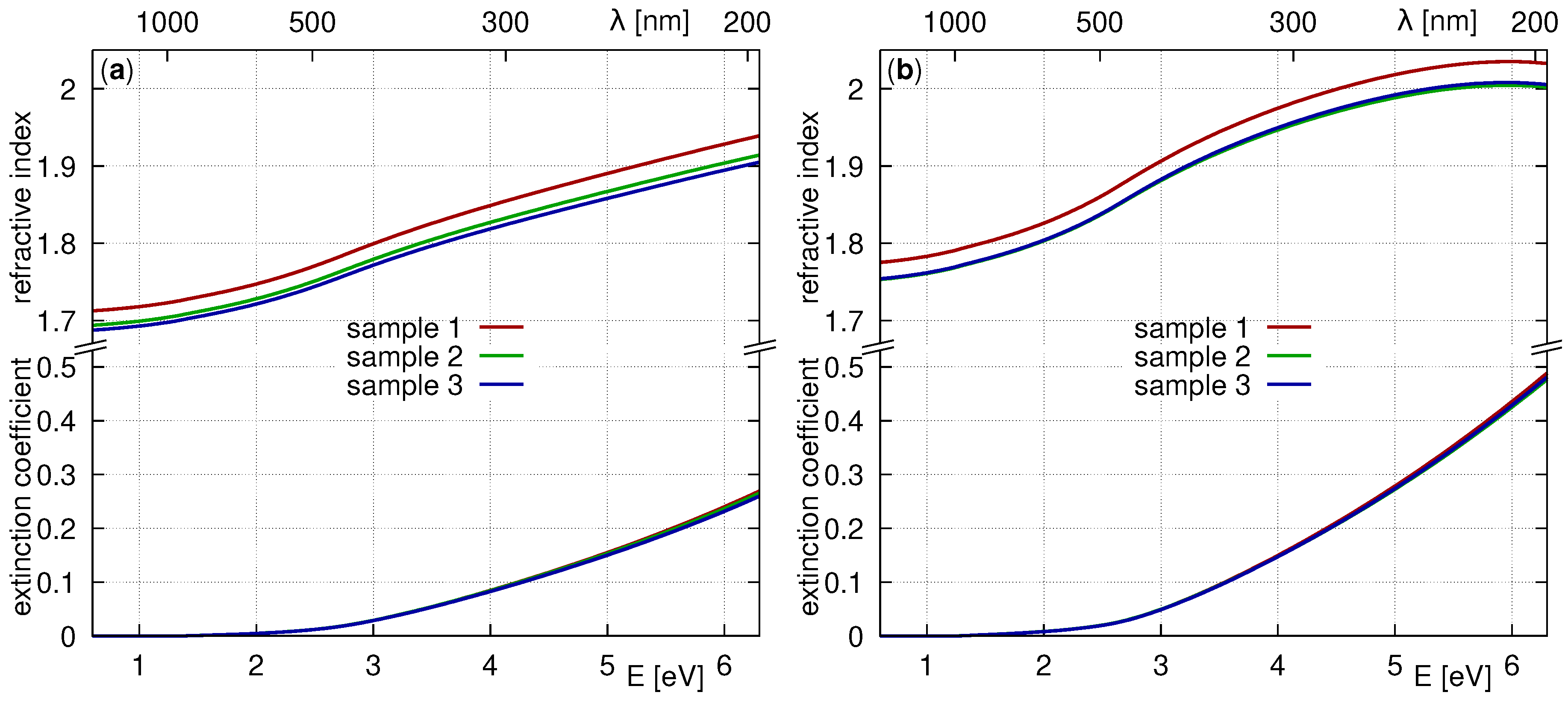
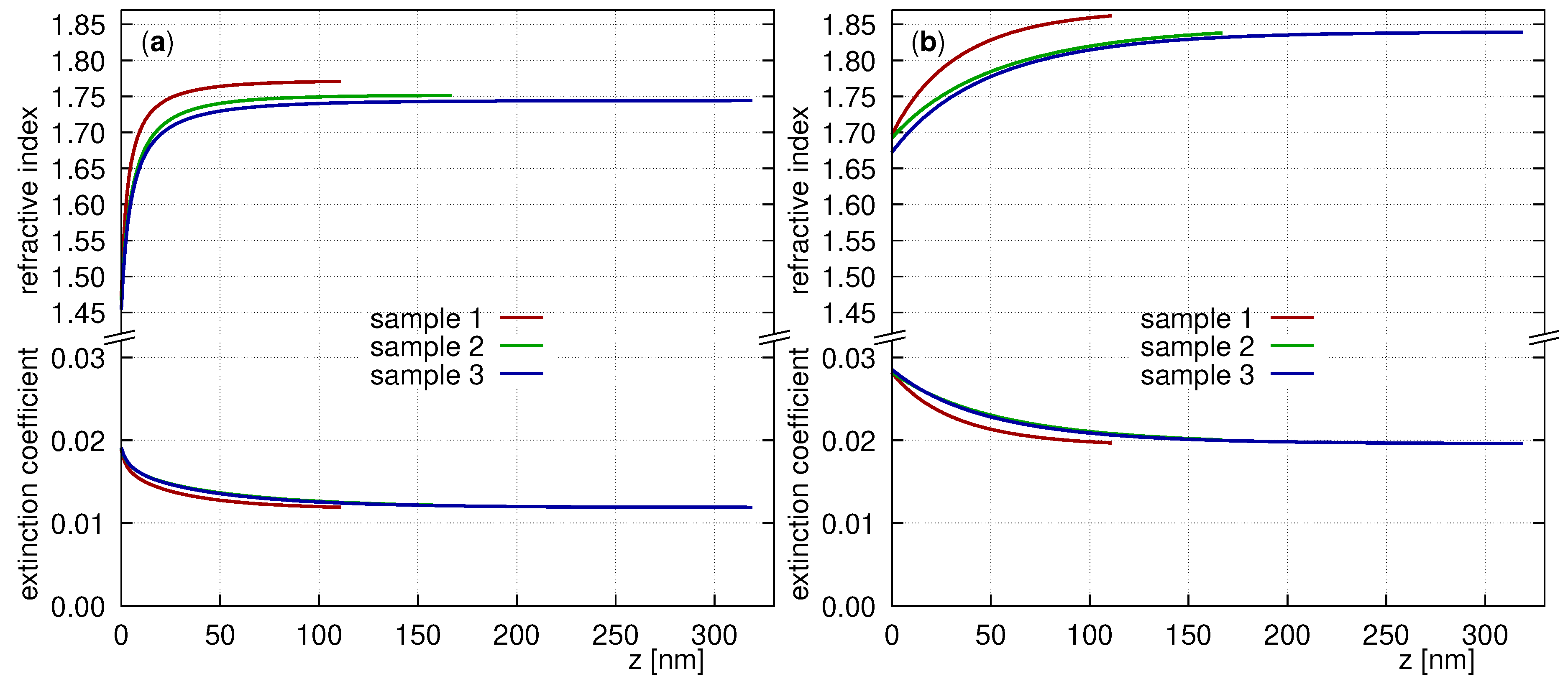
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ghosh, H.; Mitra, S.; Saha, H.; Datta, S.K.; Banerjee, C. Argon plasma treatment of silicon nitride (SiN) for improved antireflection coating on c-Si solar cells. Mater. Sci. Eng. B Adv. 2017, 215, 29–36. [Google Scholar] [CrossRef]
- Kishore, R.; Singh, S.; Das, B. PECVD grown silicon nitride AR coatings on polycrystalline silicon solar cells. Sol. Energy Mater. Sol. Cells 1992, 26, 27–35. [Google Scholar] [CrossRef]
- Cai, L.; Rohatgi, A.; Yang, D.; El-Sayed, M.A. Effects of rapid thermal anneal on refractive index and hydrogen content of plasma-enhanced chemical vapor deposited silicon nitride films. J. Appl. Phys. 1996, 80, 5384–5388. [Google Scholar] [CrossRef]
- Doshi, P.; Jellison, G.E.; Rohatgi, A. Characterization and optimization of absorbing plasma-enhanced chemical vapor deposited antireflection coatings for silicon photovoltaics. Appl. Opt. 1997, 36, 7826–7837. [Google Scholar] [CrossRef] [PubMed]
- Misiakos, I.; Tsoi, E.; Halmagean, E.; Kakabakos, S. Monolithic integration of light emitting diodes, detectors and optical fibers on a silicon wafer: A CMOS compatible optical sensor. In Proceedings of the International Electron Devices Meeting 1998, San Francisco, CA, USA, 6–9 Decemeber 1998; pp. 25–28. [Google Scholar]
- Adams, A. Dielectric and polysilicon film deposition. In VLSI technology; Sze, S.H., Ed.; McGraw-Hill Higher Education: New York, NY, USA, 1988. [Google Scholar]
- Vernhes, R.; Zabeida, O.; Klemberg-Sapieha, J.E.; Martinu, L. Single-material inhomogeneous optical filters based on microstructural gradients in plasma-deposited silicon nitride. Appl. Opt. 2004, 43, 97–103. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Arai, K.; Usami, K.; Oda, S. Toward long-term retention-time single-electron-memory devices based on nitrided nanocrystalline silicon dots. IEEE Trans. Nanotechnol. 2004, 3, 210–214. [Google Scholar] [CrossRef]
- Yang, M.S.; Cho, K.S.; Jhe, J.H.; Seo, S.Y.; Shin, J.H.; Kim, K.J.; Moon, D.W. Effect of nitride passivation on the visible photoluminescence from Si-nanocrystals. Appl. Phys. Lett. 2004, 85, 3408–3410. [Google Scholar] [CrossRef]
- Arora, W.J.; Nichol, A.J.; Smith, H.I.; Barbastathis, G. Membrane folding to achieve three-dimensional nanostructures: Nanopatterned silicon nitride folded with stressed chromium hinges. Appl. Phys. Lett. 2006, 88, 053108. [Google Scholar] [CrossRef]
- Debieu, O.; Nalini, R.P.; Cardin, J.; Portier, X.; Perrière, J.; Gourbilleau, F. Structural and optical characterization of pure Si-rich nitride thin films. Nanoscale Res. Lett. 2013, 8, 31. [Google Scholar] [CrossRef]
- Kim, J.H.; Chung, K.W. Microstructure and properties of silicon nitride thin films deposited by reactive bias magnetron sputtering. J. Appl. Phys. 1998, 83, 5831–5839. [Google Scholar] [CrossRef]
- Asinovsky, L.; Shen, F.; Yamaguchi, T. Characterization of the optical properties of PECVD SiNx films using ellipsometry and reflectometry. Thin Solid Films 1998, 313–314, 198–204. [Google Scholar] [CrossRef]
- Jellison, G.E., Jr.; Modine, F.A.; Doshi, P.; Rohatgi, A. Spectroscopic ellipsometry characterization of thin-film silicon nitride. Thin Solid Films 1998, 313–314, 193–197. [Google Scholar] [CrossRef]
- Franta, D.; Ohlídal, I. Ellipsometric parameters and reflectances of thin films with slightly rough boundaries. J. Mod. Opt. 1998, 45, 903–934. [Google Scholar] [CrossRef]
- Ohlídal, I.; Vohánka, J.; Čermák, M.; Franta, D. Optical characterization of randomly microrough surfaces covered with very thin overlayers using effective medium approximation and Rayleigh–Rice theory. Appl. Surf. Sci. 2017, 419, 942–956. [Google Scholar] [CrossRef]
- Ohlídal, I.; Vohánka, J.; Mistrík, J.; Čermák, M.; Franta, D. Different theoretical approaches at optical characterization of randomly rough silicon surfaces covered with native oxide layers. Surf. Interface Anal. 2018, 50, 1230–1233. [Google Scholar] [CrossRef]
- Ohlídal, I.; Navrátil, K.; Lukeš, F. Reflection of light by a system of nonabsorbing isotropic film–Nonabsorbing isotropic substrate with randomly rough boundaries. J. Opt. Soc. Am. 1971, 61, 1630–1639. [Google Scholar] [CrossRef]
- Ohlídal, I.; Lukeš, F. Ellipsometric parameters of rough surfaces and of a system substrate-thin film with rough boundaries. Opt. Acta 1972, 19, 817–843. [Google Scholar] [CrossRef]
- Ohlídal, I. Approximate formulas for the reflectances, transmittances, and scattering losses of nonabsorbing multilayers systems with randomly rough boundaries. J. Opt. Soc. Am. A 1993, 10, 158–170. [Google Scholar] [CrossRef]
- Ohlídal, I.; Navrátil, K.; Ohlídal, M. Scattering of light from multilayer systems with rough boundaries. In Progress in Optics; Wolf, E., Ed.; Elsevier: Amsterdam, The Netherlands, 1995; Volume 34, pp. 249–331. [Google Scholar]
- Ohlídal, I.; Franta, D.; Nečas, D. Improved combination of scalar diffraction theory and Rayleigh-Rice theory and its application to spectroscopic ellipsometry of randomly rough surfaces. Thin Solid Films 2014, 571, 695–700. [Google Scholar] [CrossRef]
- Ohlídal, I.; Vižďa, F.; Ohlídal, M. Optical analysis by means of spectroscopic reflectometry of single and double layers with correlated randomly rough boundaries. Opt. Eng. 1995, 34, 1761–1768. [Google Scholar] [CrossRef]
- Yeh, P. Optics of anisotropic layered media: A new 4 × 4 matrix algebra. Surf. Sci. 1980, 96, 41–53. [Google Scholar] [CrossRef]
- Knittl, Z. Optics of Thin Films; Wiley: London, UK, 1976. [Google Scholar]
- Ohlídal, I.; Vohánka, J.; Čermák, M.; Franta, D. Ellipsometry of layered systems. In Optical Characterization of Thin Solid Films; Stenzel, O., Ohlídal, M., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 233–267. [Google Scholar]
- Vohánka, J.; Ohlídal, I.; Ženíšek, J.; Vašina, P.; Čermák, M.; Franta, D. Use of the Richardson extrapolation in optics of inhomogeneous layers: Application to optical characterization. Surf. Interface Anal. 2018, 50, 757–765. [Google Scholar] [CrossRef]
- Franta, D.; Dubroka, A.; Wang, C.; Giglia, A.; Vohánka, J.; Franta, P.; Ohlídal, I. Temperature-dependent dispersion model of float zone crystalline silicon. Appl. Surf. Sci. 2017, 421, 405–419. [Google Scholar] [CrossRef]
- Franta, D.; Nečas, D.; Ohlídal, I.; Giglia, A. Optical characterization of SiO2 thin films using universal dispersion model over wide spectral range. In Proceedings of the SPIE Photonics Europe, Brussels, Belgium, 3–7 April 2016; Volume 9890, p. 989014. [Google Scholar]
- Franta, D.; Nečas, D.; Ohlídal, I. Universal dispersion model for characterization of optical thin films over wide spectral range: Application to hafnia. Appl. Opt. 2015, 54, 9108–9119. [Google Scholar] [CrossRef] [PubMed]
- Franta, D.; Vohánka, J.; Čermák, M. Universal dispersion model for characterisation of thin films over wide spectral range. In Optical Characterization of Thin Solid Films; Stenzel, O., Ohlídal, M., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 31–82. [Google Scholar]
- Franta, D.; Nečas, D.; Zajíčková, L. Application of Thomas–Reiche–Kuhn sum rule to construction of advanced dispersion models. Thin Solid Films 2013, 534, 432–441. [Google Scholar] [CrossRef]
- Franta, D.; Nečas, D.; Zajíčková, L.; Ohlídal, I.; Stuchlík, J.; Chvostová, D. Application of sum rule to the dispersion model of hydrogenated amorphous silicon. Thin Solid Films 2013, 539, 233–244. [Google Scholar] [CrossRef]
- Ohlídal, M.; Vodák, J.; Nečas, D. Optical characterization of thin films by means of imaging spectroscopic reflectometry. In Optical Characterization of Thin Solid Films; Stenzel, O., Ohlídal, M., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 107–141. [Google Scholar]
- Ohlídal, I.; Ohlídal, M.; Nečas, D.; Franta, D.; Buršíková, V. Optical characterisation of SiOxCyHz thin films non-uniform in thickness using spectroscopic ellipsometry, spectroscopic reflectometry and spectroscopic imaging reflectometry. Thin Solid Films 2011, 519, 2874–2876. [Google Scholar] [CrossRef]
- Nečas, D.; Ohlídal, I.; Franta, D.; Ohlídal, M.; Čudek, V.; Vodák, J. Measurement of thickness distribution, optical constants, and roughness parameters of rough nonuniform ZnSe thin films. Appl. Opt. 2014, 53, 5606–5614. [Google Scholar] [CrossRef]
- Nečas, D.; Čudek, V.; Vodák, J.; Ohlídal, M.; Klapetek, P.; Benedikt, J.; Rügner, K.; Zajíčková, L. Mapping of properties of thin plasma jet films using imaging spectroscopic reflectometry. Meas. Sci. Technol. 2014, 25, 115201. [Google Scholar] [CrossRef]
- Nečas, D.; Ohlídal, I.; Franta, D.; Čudek, V.; Ohlídal, M.; Vodák, J.; Sládková, L.; Zajíčková, L.; Eliáš, M.; Vižďa, F. Assessment of non-uniform thin films using spectroscopic ellipsometry and imaging spectroscopic reflectometry. Thin Solid Films 2014, 571, 573–578. [Google Scholar] [CrossRef]
- Berg, S.; Nyberg, T. Fundamental understanding and modeling of reactive sputtering processes. Thin Solid Films 2005, 476, 215–230. [Google Scholar] [CrossRef]
- Franta, D.; Ohlídal, I.; Klapetek, P. Analysis of slightly rough thin films by optical methods and AFM. Mikrochim. Acta 2000, 132, 443–447. [Google Scholar] [CrossRef]
- Franta, D.; Ohlídal, I. Analysis of thin films by optical multi-sample methods. Acta Phys. Slov. 2000, 50, 411–421. [Google Scholar]
- Franta, D.; Zajíčková, L.; Ohlídal, I.; Janča, J.; Veltruská, K. Optical characterization of diamond like carbon films using multi-sample modification of variable angle spectroscopic ellipsometry. Diam. Relat. Mater. 2002, 11, 105–117. [Google Scholar] [CrossRef]

| Parameters | Exhibit Profile | Different for and | Different for Each Sample |
|---|---|---|---|
| yes | no | yes | |
| , , | yes | yes | no |
| , , , | no | no | no |
| Parameter | Sample 1 | Sample 2 | Sample 3 | ||
|---|---|---|---|---|---|
| deposition time | t | [min] | 30 | 45 | 90 |
| thickness ellipsometry | [nm] | ||||
| thickness reflectance | [nm] | ||||
| roughness (rms) | [nm] | ||||
| profile parameter | w | [nm] |
| Parameter | |||||||
| [eV] | |||||||
| [eV] | |||||||
| [eV] | |||||||
| [eV] | |||||||
| Parameters without profile which are identical for the ordinary and extraordinary dielectric functions | |||||||
| Parameter | Upper Boundary | ||||||
| [eV] | Sample 1 | ||||||
| Sample 2 | |||||||
| Sample 3 | |||||||
| Parameters with profile which are identical for the ordinary and extraordinary dielectric functions | |||||||
| Upper Boundary | |||||||
| Parameter | Ordinary | Extraordinary | Ordinary | Extraordinary | |||
| [eV] | |||||||
| [eV] | |||||||
| Parameters with profile which are different for the ordinary and extraordinary dielectric functions | |||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vohánka, J.; Ohlídal, I.; Ohlídal, M.; Šustek, Š.; Čermák, M.; Šulc, V.; Vašina, P.; Ženíšek, J.; Franta, D. Optical Characterization of Non-Stoichiometric Silicon Nitride Films Exhibiting Combined Defects. Coatings 2019, 9, 416. https://doi.org/10.3390/coatings9070416
Vohánka J, Ohlídal I, Ohlídal M, Šustek Š, Čermák M, Šulc V, Vašina P, Ženíšek J, Franta D. Optical Characterization of Non-Stoichiometric Silicon Nitride Films Exhibiting Combined Defects. Coatings. 2019; 9(7):416. https://doi.org/10.3390/coatings9070416
Chicago/Turabian StyleVohánka, Jiří, Ivan Ohlídal, Miloslav Ohlídal, Štěpán Šustek, Martin Čermák, Václav Šulc, Petr Vašina, Jaroslav Ženíšek, and Daniel Franta. 2019. "Optical Characterization of Non-Stoichiometric Silicon Nitride Films Exhibiting Combined Defects" Coatings 9, no. 7: 416. https://doi.org/10.3390/coatings9070416
APA StyleVohánka, J., Ohlídal, I., Ohlídal, M., Šustek, Š., Čermák, M., Šulc, V., Vašina, P., Ženíšek, J., & Franta, D. (2019). Optical Characterization of Non-Stoichiometric Silicon Nitride Films Exhibiting Combined Defects. Coatings, 9(7), 416. https://doi.org/10.3390/coatings9070416





