Plasmonic Nanoparticles and Island Films for Solar Energy Harvesting: A Comparative Study of Cu, Al, Ag and Au Performance
Abstract
1. Introduction
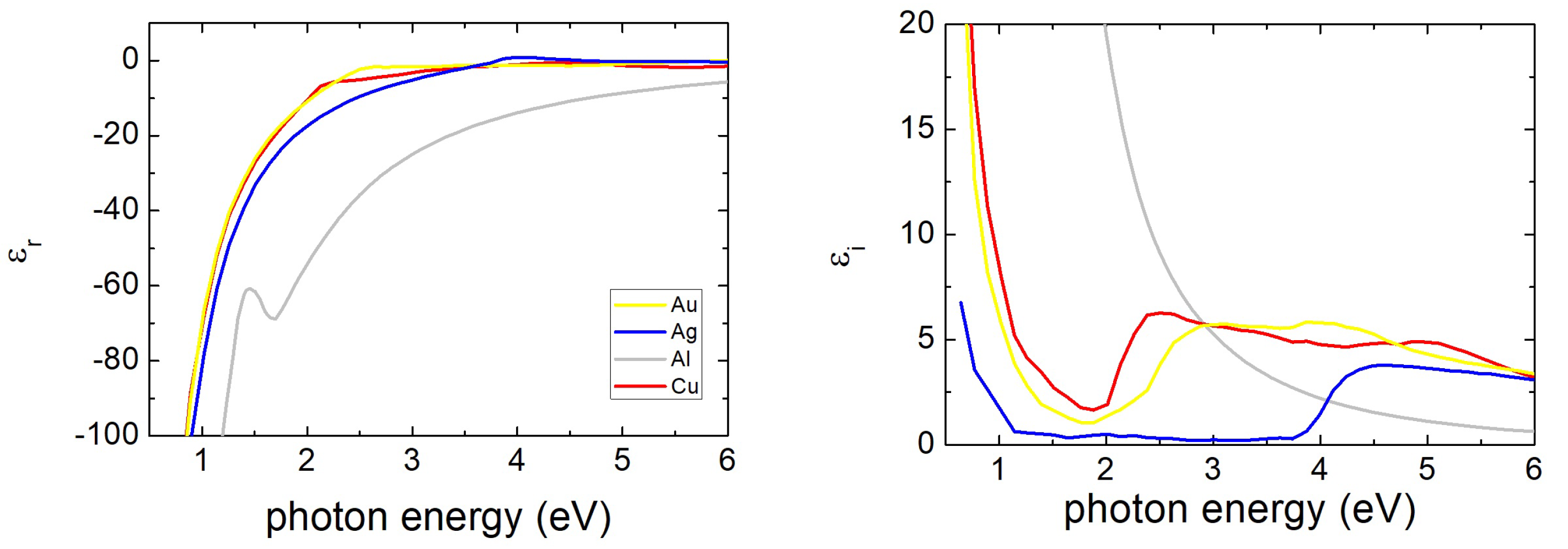
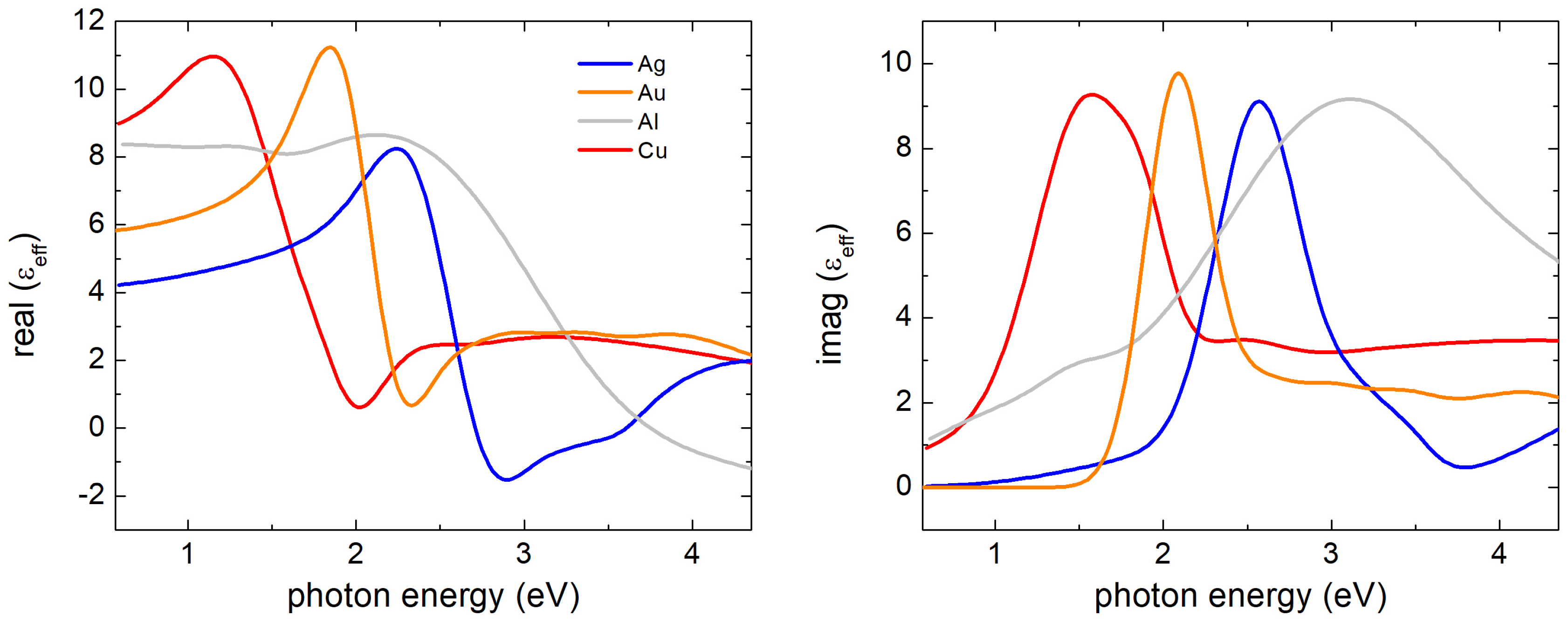
2. Plasmonic Response of Ag, Au, Cu and Al Nanoparticles
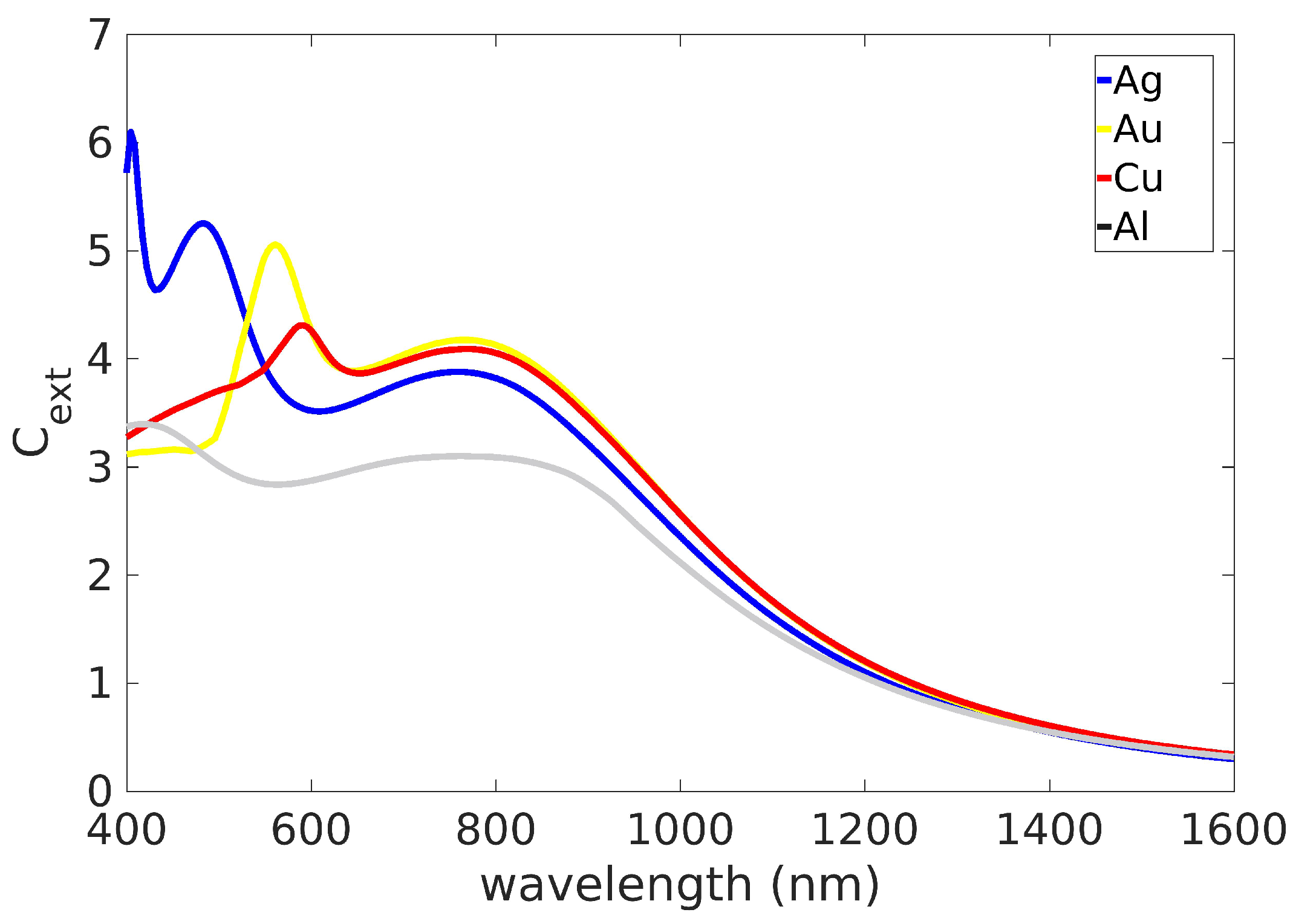
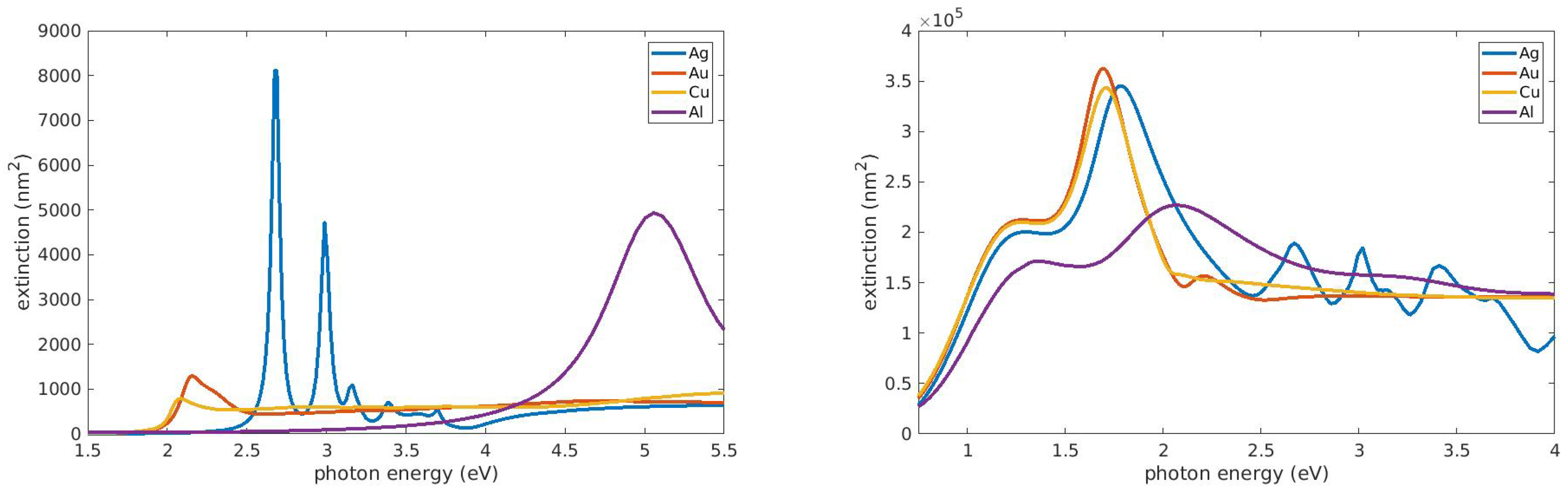
2.1. Spherical Particles: Small Particle Limit and Size Effects
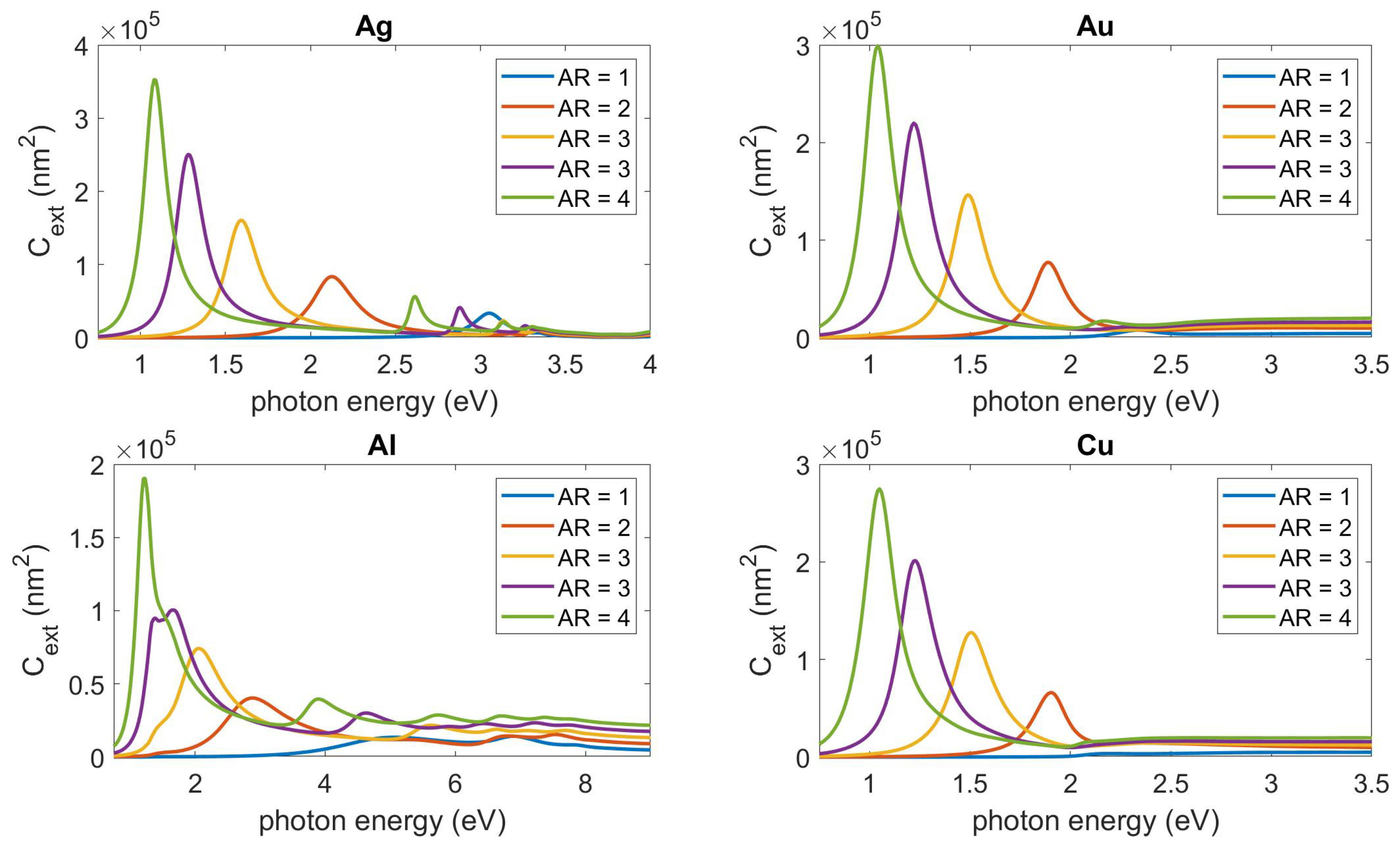
2.2. Shape Effects
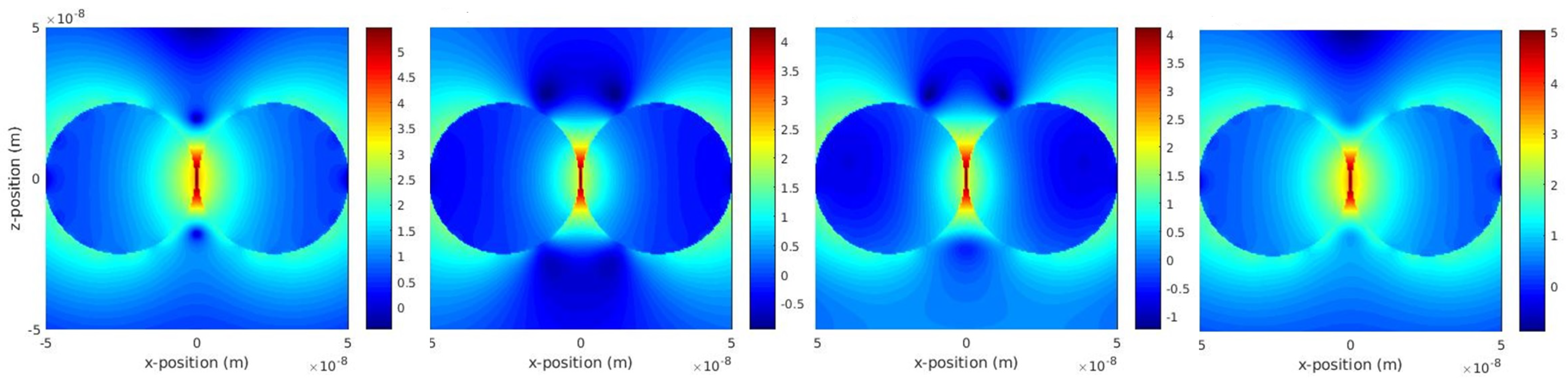
2.3. Plasmon Hybridisation: Dimers
2.4. Effect of Oxidisation
3. Metal Island Films for Solar Energy Harvesting
3.1. Fabrication and Characterisation of Metal Island Films
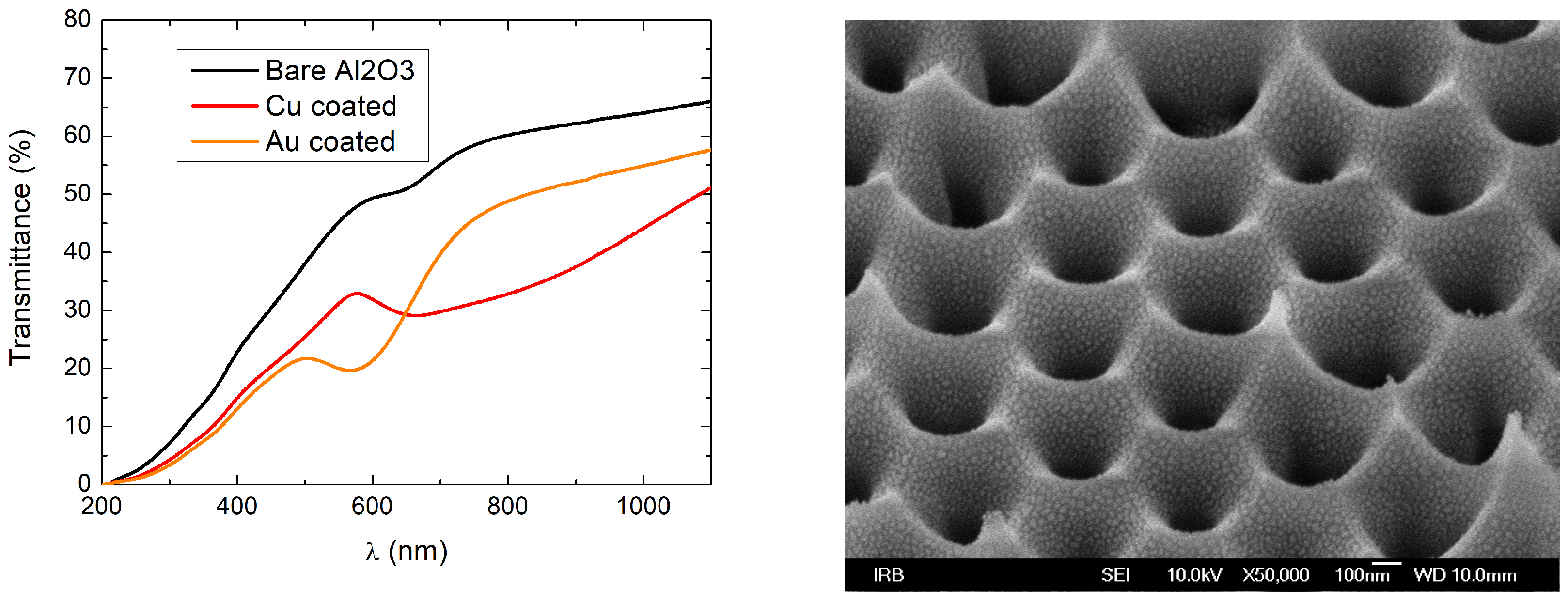
3.2. Metal Island Films in Porous AlO Templates for Water Vapour Generation
4. Conclusions
5. Materials and Methods
5.1. Numerical Methods
5.2. Fabrication and Characterisation of Metal Island Films
5.3. Nanoporous Alumina Templates and Water Vapour Generation Experiments
Author Contributions
Funding
Conflicts of Interest
References
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Stockman, M.I.; Kneipp, K.; Bozhevolnyi, S.I.; Saha, S.; Dutta, A.; Ndukaife, J.; Kinsey, N.; Reddy, H.; Guler, U.; Shalaev, V.M.; et al. Roadmap on plasmonics. J. Opt. 2018, 20, 043001. [Google Scholar] [CrossRef]
- Maradudin, A.A.; Sambles, J.R.; Barnes, W.L. Modern Plasmonics; Elsevier: Amsterdam, The Netherlands, 2014; Volume 4. [Google Scholar]
- West, P.R.; Ishii, S.; Naik, G.V.; Emani, N.K.; Shalaev, V.M.; Boltasseva, A. Searching for better plasmonic materials. Laser Photonics Rev. 2010, 4, 795–808. [Google Scholar] [CrossRef]
- Naik, G.V.; Shalaev, V.M.; Boltasseva, A. Alternative plasmonic materials: Beyond gold and silver. Adv. Mater. 2013, 25, 3264–3294. [Google Scholar] [CrossRef] [PubMed]
- Palik, E. Handbook of Optical Constants of Solids; Handbook Series; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Chan, G.H.; Zhao, J.; Hicks, E.M.; Schatz, G.C.; Van Duyne, R.P. Plasmonic properties of copper nanoparticles fabricated by nanosphere lithography. Nano Lett. 2007, 7, 1947–1952. [Google Scholar] [CrossRef]
- Ghodselahi, T.; Vesaghi, M.; Shafiekhani, A.; Baghizadeh, A.; Lameii, M. XPS study of the Cu@ Cu2O core-shell nanoparticles. Appl. Surf. Sci. 2008, 255, 2730–2734. [Google Scholar] [CrossRef]
- Sun, Q.C.; Ding, Y.; Goodman, S.M.; Funke, H.H.; Nagpal, P. Copper plasmonics and catalysis: Role of electron–phonon interactions in dephasing localized surface plasmons. Nanoscale 2014, 6, 12450–12457. [Google Scholar] [CrossRef] [PubMed]
- Kravets, V.; Jalil, R.; Kim, Y.J.; Ansell, D.; Aznakayeva, D.; Thackray, B.; Britnell, L.; Belle, B.; Withers, F.; Radko, I.; et al. Graphene-protected copper and silver plasmonics. Sci. Rep. 2014, 4, 5517. [Google Scholar] [CrossRef] [PubMed]
- Susman, M.D.; Feldman, Y.; Vaskevich, A.; Rubinstein, I. Chemical deposition and stabilization of plasmonic copper nanoparticle films on transparent substrates. Chem. Mater. 2012, 24, 2501–2508. [Google Scholar] [CrossRef]
- Sancho-Parramon, J.; Okorn, B.; Salamon, K.; Janicki, V. Plasmonic resonances in copper island films. Appl. Surf. Sci. 2019, 463, 847–853. [Google Scholar] [CrossRef]
- Peña-Rodríguez, O.; Pal, U. Effects of surface oxidation on the linear optical properties of Cu nanoparticles. J. Opt. Soc. Am. B 2011, 28, 2735–2739. [Google Scholar] [CrossRef][Green Version]
- Gérard, D.; Gray, S.K. Aluminium plasmonics. J. Phys. D Appl. Phys. 2014, 48, 184001. [Google Scholar] [CrossRef]
- Knight, M.W.; Liu, L.; Wang, Y.; Brown, L.; Mukherjee, S.; King, N.S.; Everitt, H.O.; Nordlander, P.; Halas, N.J. Aluminum plasmonic nanoantennas. Nano Lett. 2012, 12, 6000–6004. [Google Scholar] [CrossRef] [PubMed]
- Knight, M.W.; King, N.S.; Liu, L.; Everitt, H.O.; Nordlander, P.; Halas, N.J. Aluminum for plasmonics. ACS Nano 2013, 8, 834–840. [Google Scholar] [CrossRef] [PubMed]
- Martin, J.; Plain, J. Fabrication of aluminium nanostructures for plasmonics. J. Phys. D Appl. Phys. 2014, 48, 184002. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical constants of the noble metals. Phys. Rev. B 1972, 6, 4370. [Google Scholar] [CrossRef]
- Kreibig, U.; Vollmer, M. Optical Properties of Metal Clusters; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 25. [Google Scholar]
- Scholl, J.A.; Koh, A.L.; Dionne, J.A. Quantum plasmon resonances of individual metallic nanoparticles. Nature 2012, 483, 421–427. [Google Scholar] [CrossRef] [PubMed]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Nicoletti, O.; de La Peña, F.; Leary, R.K.; Holland, D.J.; Ducati, C.; Midgley, P.A. Three-dimensional imaging of localized surface plasmon resonances of metal nanoparticles. Nature 2013, 502, 80–84. [Google Scholar] [CrossRef] [PubMed]
- Zheng, P.; Tang, H.; Liu, B.; Kasani, S.; Huang, L.; Wu, N. Origin of strong and narrow localized surface plasmon resonance of copper nanocubes. Nano Res. 2019, 12, 63–68. [Google Scholar] [CrossRef]
- Kelly, K.L.; Coronado, E.; Zhao, L.L.; Schatz, G.C. The optical properties of metal nanoparticles: The influence of size, shape, and dielectric environment. J. Phys. Chem. B 2003, 1073, 668–677. [Google Scholar] [CrossRef]
- Sönnichsen, C.; Franzl, T.; Wilk, T.v.; von Plessen, G.; Feldmann, J.; Wilson, O.; Mulvaney, P. Drastic reduction of plasmon damping in gold nanorods. Phys. Rev. Lett. 2002, 88, 077402. [Google Scholar] [CrossRef]
- Aizpurua, J.; Bryant, G.W.; Richter, L.J.; De Abajo, F.G.; Kelley, B.K.; Mallouk, T. Optical properties of coupled metallic nanorods for field-enhanced spectroscopy. Phys. Rev. B 2005, 71, 235420. [Google Scholar] [CrossRef]
- Chen, H.; Shao, L.; Li, Q.; Wang, J. Gold nanorods and their plasmonic properties. Chem. Soc. Rev. 2013, 42, 2679–2724. [Google Scholar] [CrossRef] [PubMed]
- Cubukcu, E.; Capasso, F. Optical nanorod antennas as dispersive one-dimensional Fabry–Pérot resonators for surface plasmons. Appl. Phys. Lett. 2009, 95, 201101. [Google Scholar] [CrossRef]
- Dorfmuller, J.; Vogelgesang, R.; Weitz, R.T.; Rockstuhl, C.; Etrich, C.; Pertsch, T.; Lederer, F.; Kern, K. Fabry-Perot resonances in one-dimensional plasmonic nanostructures. Nano Lett. 2009, 9, 2372–2377. [Google Scholar] [CrossRef] [PubMed]
- Novotny, L. Effective wavelength scaling for optical antennas. Phys. Rev. Lett. 2007, 98, 266802. [Google Scholar] [CrossRef] [PubMed]
- Nordlander, P.; Oubre, C.; Prodan, E.; Li, K.; Stockman, M. Plasmon hybridization in nanoparticle dimers. Nano Lett. 2004, 4, 899–903. [Google Scholar] [CrossRef]
- Grillet, N.; Manchon, D.; Bertorelle, F.; Bonnet, C.; Broyer, M.; Cottancin, E.; Lermé, J.; Hillenkamp, M.; Pellarin, M. Plasmon coupling in silver nanocube dimers: Resonance splitting induced by edge rounding. ACS Nano 2011, 5, 9450–9462. [Google Scholar] [CrossRef]
- Sancho-Parramon, J.; Janicki, V.; Zorc, H. On the dielectric function tuning of random metal-dielectric nanocomposites for metamaterial applications. Opt. Express 2010, 18, 26915–26928. [Google Scholar] [CrossRef]
- Lončarić, M.; Sancho-Parramon, J.; Zorc, H. Optical properties of gold island films—A spectroscopic ellipsometry study. Thin Solid Films 2011, 519, 2946–2950. [Google Scholar] [CrossRef]
- Stenzel, O. Optical Coatings: Material Aspects in Theory and Practice; Springer Science & Business: Berlin/Heidelberg, Germany, 2014; Volume 54. [Google Scholar]
- Singer, R.; Leitner, A.; Aussenegg, F. Structure analysis and models for optical constants of discontinuous metallic silver films. JOSA B 1995, 12, 220–228. [Google Scholar] [CrossRef]
- Stenzel, O.; Macleod, A. Metal-dielectric composite optical coatings: Underlying physics, main models, characterization, design and application aspects. Adv. Opt. Technol. 2012, 1, 463–481. [Google Scholar] [CrossRef]
- Sancho-Parramon, J.; Janicki, V.; Zorc, H. Tuning the effective dielectric function of thin film metal-dielectric composites by controlling the deposition temperature. J. Nanophotonics 2011, 5, 051805. [Google Scholar] [CrossRef]
- Martin, J.; Proust, J.; Gérard, D.; Plain, J. Localized surface plasmon resonances in the ultraviolet from large scale nanostructured aluminum films. Opt. Mater. Express 2013, 3, 954–959. [Google Scholar] [CrossRef]
- Lebedev, A.; Stenzel, O.; Quinten, M.; Stendal, A.; Röder, M.; Schreiber, M.; Zahn, D. A statistical approach for interpreting the optical spectra of metal island films: Effects of multiple scattering in a statistical assembly of spheres. J. Opt. A Pure Appl. Opt. 1999, 1, 573. [Google Scholar] [CrossRef]
- Held, M.; Stenzel, O.; Wilbrandt, S.; Kaiser, N.; Tünnermann, A. Manufacture and characterization of optical coatings with incorporated copper island films. Appl. Opt. 2012, 51, 4436–4447. [Google Scholar] [CrossRef] [PubMed]
- Dalacu, D.; Martinu, L. Optical properties of discontinuous gold films: Finite-size effects. JOSA B 2001, 18, 85–92. [Google Scholar] [CrossRef]
- Neumann, O.; Urban, A.S.; Day, J.; Lal, S.; Nordlander, P.; Halas, N.J. Solar vapor generation enabled by nanoparticles. ACS Nano 2012, 7, 42–49. [Google Scholar] [CrossRef]
- Bae, K.; Kang, G.; Cho, S.K.; Park, W.; Kim, K.; Padilla, W.J. Flexible thin-film black gold membranes with ultrabroadband plasmonic nanofocusing for efficient solar vapour generation. Nat. Commun. 2015, 6, 10103. [Google Scholar] [CrossRef]
- Zhou, L.; Tan, Y.; Ji, D.; Zhu, B.; Zhang, P.; Xu, J.; Gan, Q.; Yu, Z.; Zhu, J. Self-assembly of highly efficient, broadband plasmonic absorbers for solar steam generation. Sci. Adv. 2016, 2, e1501227. [Google Scholar] [CrossRef]
- Baffou, G.; Quidant, R.; García de Abajo, F.J. Nanoscale control of optical heating in complex plasmonic systems. ACS Nano 2010, 4, 709–716. [Google Scholar] [CrossRef]
- Gérardy, J.; Ausloos, M. Absorption spectrum of clusters of spheres from the general solution of Maxwell’s equations. II. Optical properties of aggregated metal spheres. Phys. Rev. B 1982, 25, 4204. [Google Scholar] [CrossRef]
- Myroshnychenko, V.; Rodríguez-Fernández, J.; Pastoriza-Santos, I.; Funston, A.M.; Novo, C.; Mulvaney, P.; Liz-Marzan, L.M.; de Abajo, F.J.G. Modelling the optical response of gold nanoparticles. Chem. Soc. Rev. 2008, 37, 1792–1805. [Google Scholar] [CrossRef] [PubMed]
- De Abajo, F.G.; Howie, A. Retarded field calculation of electron energy loss in inhomogeneous dielectrics. Phys. Rev. B 2002, 65, 115418. [Google Scholar] [CrossRef]
- Hohenester, U.; Trügler, A. MNPBEM–A Matlab toolbox for the simulation of plasmonic nanoparticles. Comput. Phys. Commun. 2012, 183, 370–381. [Google Scholar] [CrossRef]
- Lee, W.; Park, S.J. Porous anodic aluminum oxide: Anodization and templated synthesis of functional nanostructures. Chem. Rev. 2014, 114, 7487–7556. [Google Scholar] [CrossRef] [PubMed]
- Vojkuvka, L.; Santos, A.; Pallarès, J.; Ferré-Borrull, J.; Marsal, L.F.; Celis, J.P. On the mechanical properties of nanoporous anodized alumina by nanoindentation and sliding tests. Surf. Coat. Technol. 2012, 206, 2115–2124. [Google Scholar] [CrossRef]




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fabijanić, I.; Janicki, V.; Ferré-Borrull, J.; Bubaš, M.; Blažek Bregović, V.; Marsal, L.F.; Sancho-Parramon, J. Plasmonic Nanoparticles and Island Films for Solar Energy Harvesting: A Comparative Study of Cu, Al, Ag and Au Performance. Coatings 2019, 9, 382. https://doi.org/10.3390/coatings9060382
Fabijanić I, Janicki V, Ferré-Borrull J, Bubaš M, Blažek Bregović V, Marsal LF, Sancho-Parramon J. Plasmonic Nanoparticles and Island Films for Solar Energy Harvesting: A Comparative Study of Cu, Al, Ag and Au Performance. Coatings. 2019; 9(6):382. https://doi.org/10.3390/coatings9060382
Chicago/Turabian StyleFabijanić, Ivana, Vesna Janicki, Josep Ferré-Borrull, Matej Bubaš, Vesna Blažek Bregović, Lluis F. Marsal, and Jordi Sancho-Parramon. 2019. "Plasmonic Nanoparticles and Island Films for Solar Energy Harvesting: A Comparative Study of Cu, Al, Ag and Au Performance" Coatings 9, no. 6: 382. https://doi.org/10.3390/coatings9060382
APA StyleFabijanić, I., Janicki, V., Ferré-Borrull, J., Bubaš, M., Blažek Bregović, V., Marsal, L. F., & Sancho-Parramon, J. (2019). Plasmonic Nanoparticles and Island Films for Solar Energy Harvesting: A Comparative Study of Cu, Al, Ag and Au Performance. Coatings, 9(6), 382. https://doi.org/10.3390/coatings9060382






