Spectral Modulation of Optofluidic Coupled-Microdisk Lasers in Aqueous Media
Abstract
1. Introduction
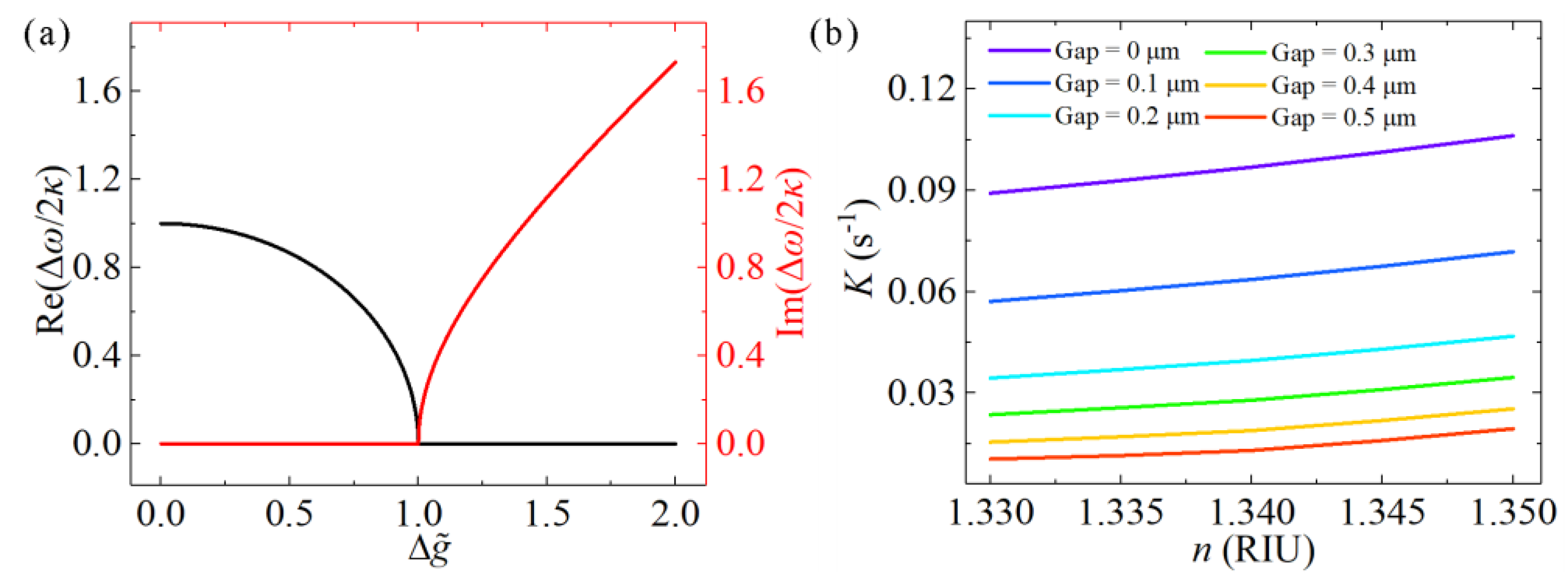
2. Coupled-Mode Analysis
3. Optofluidic Microdisk Lasers
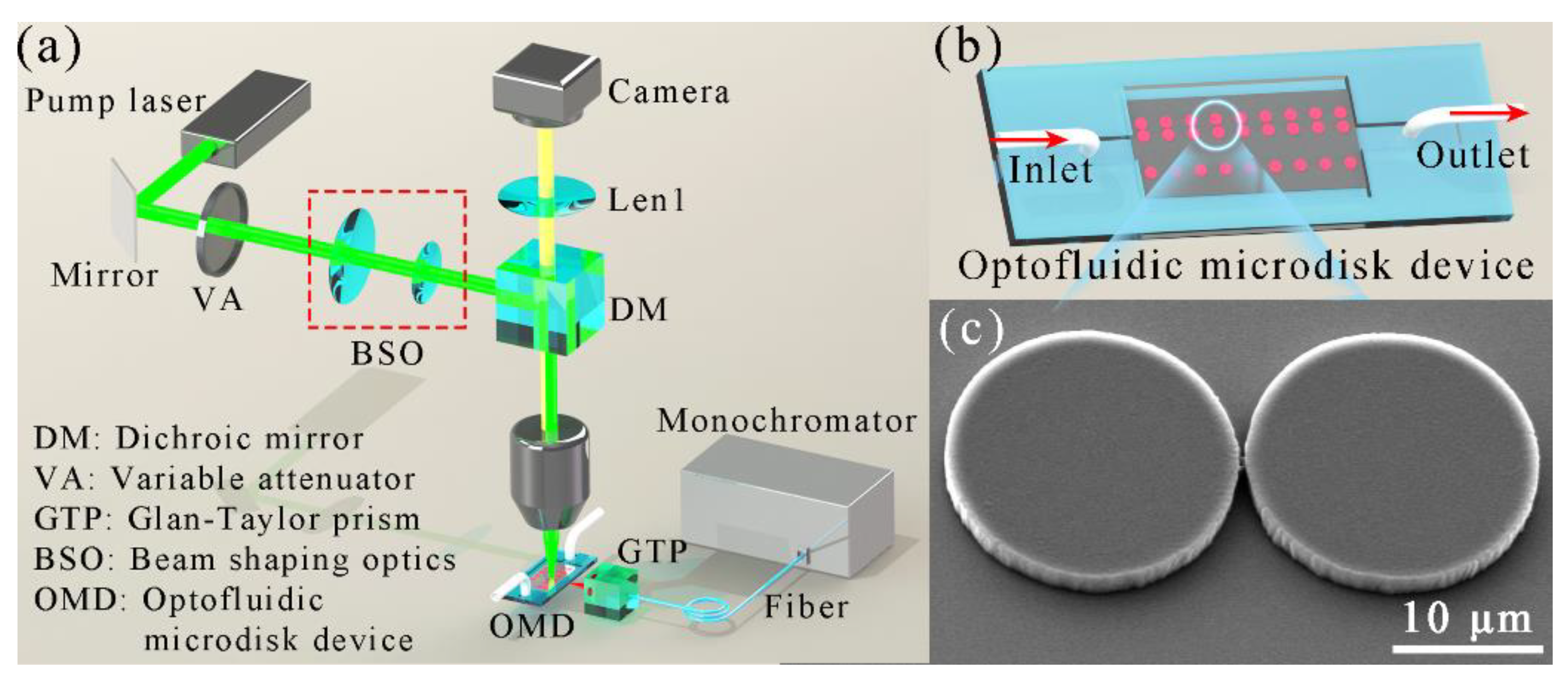
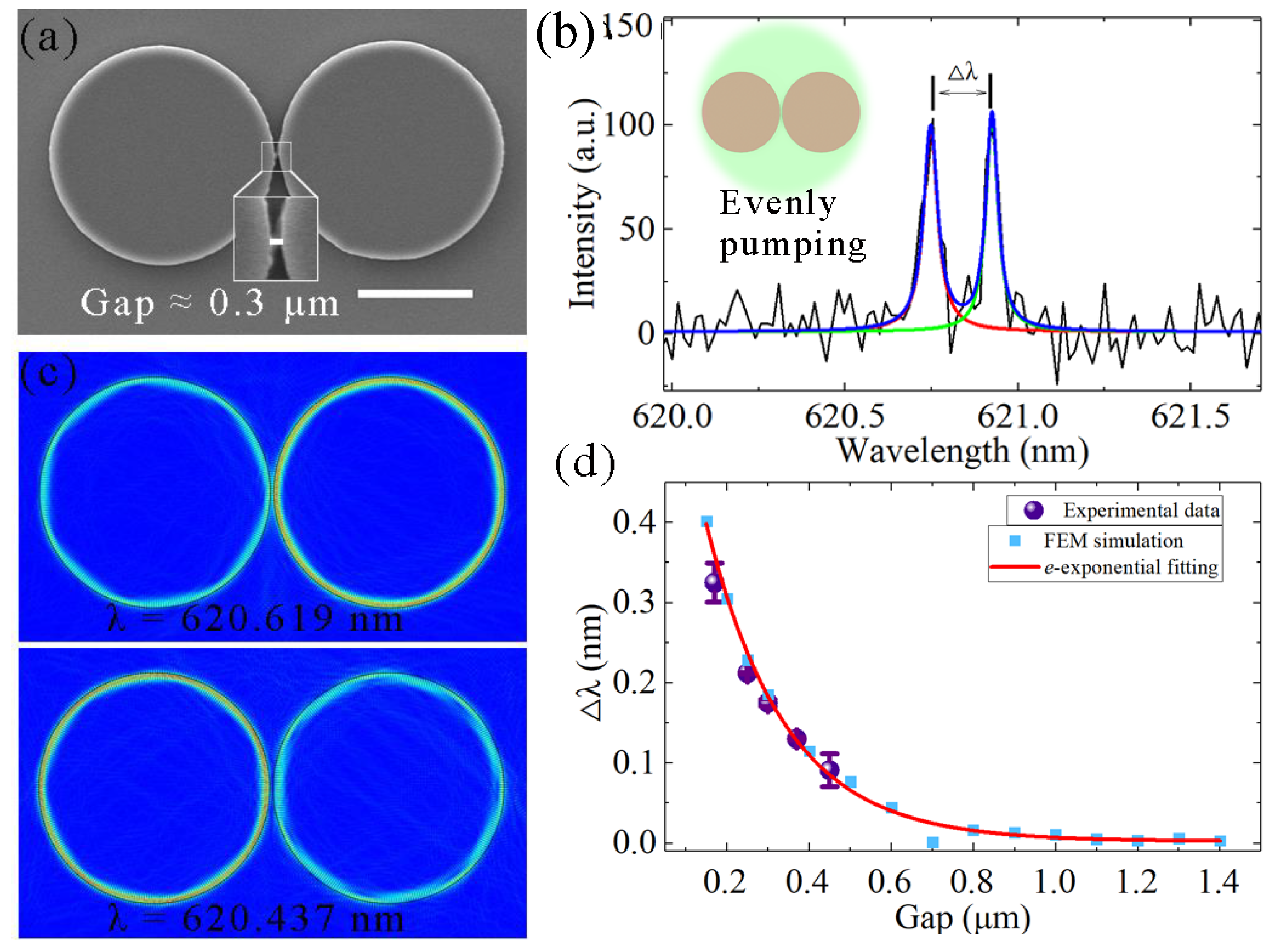
3.1. Fabrication of the Optofluidic Microdisk Device and Experimental Setup
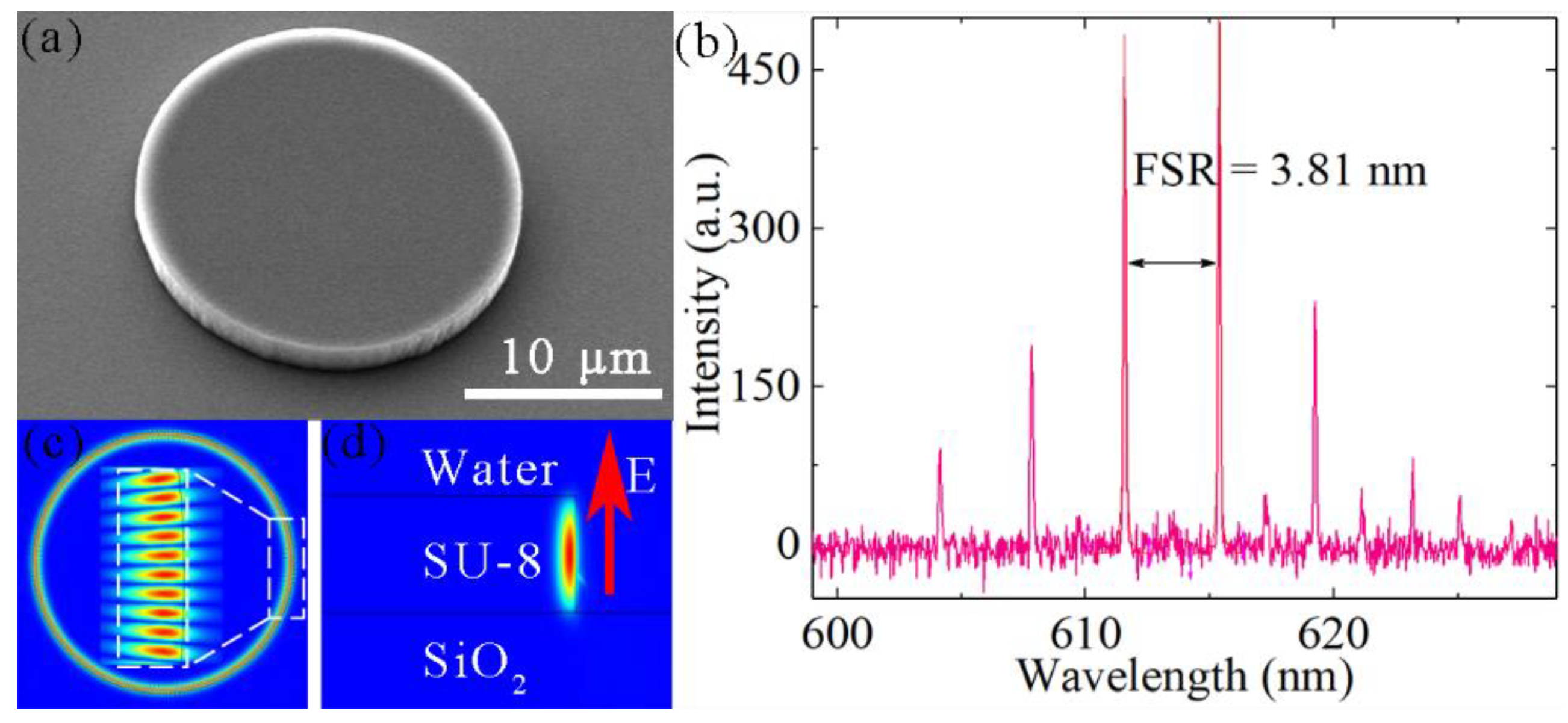
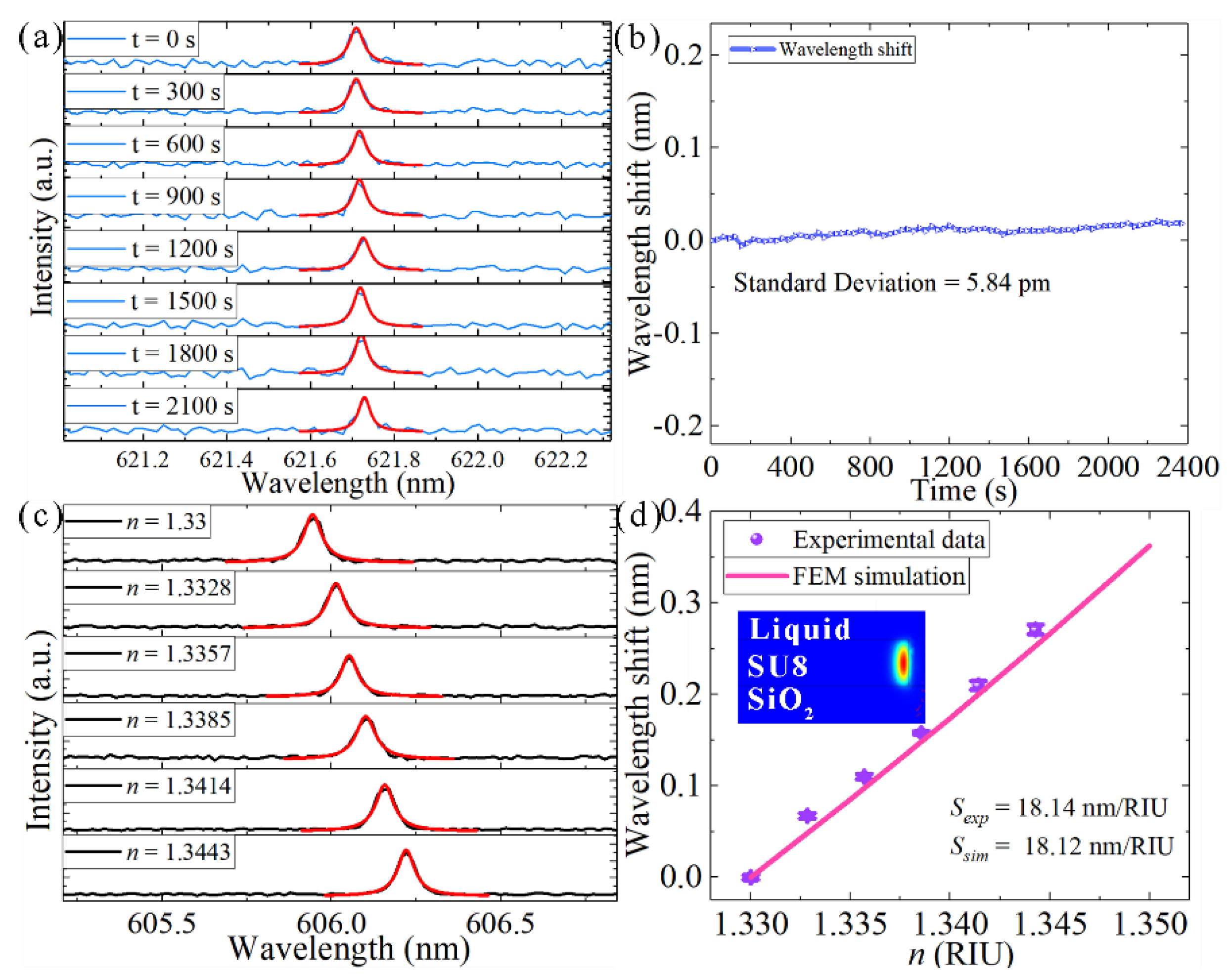
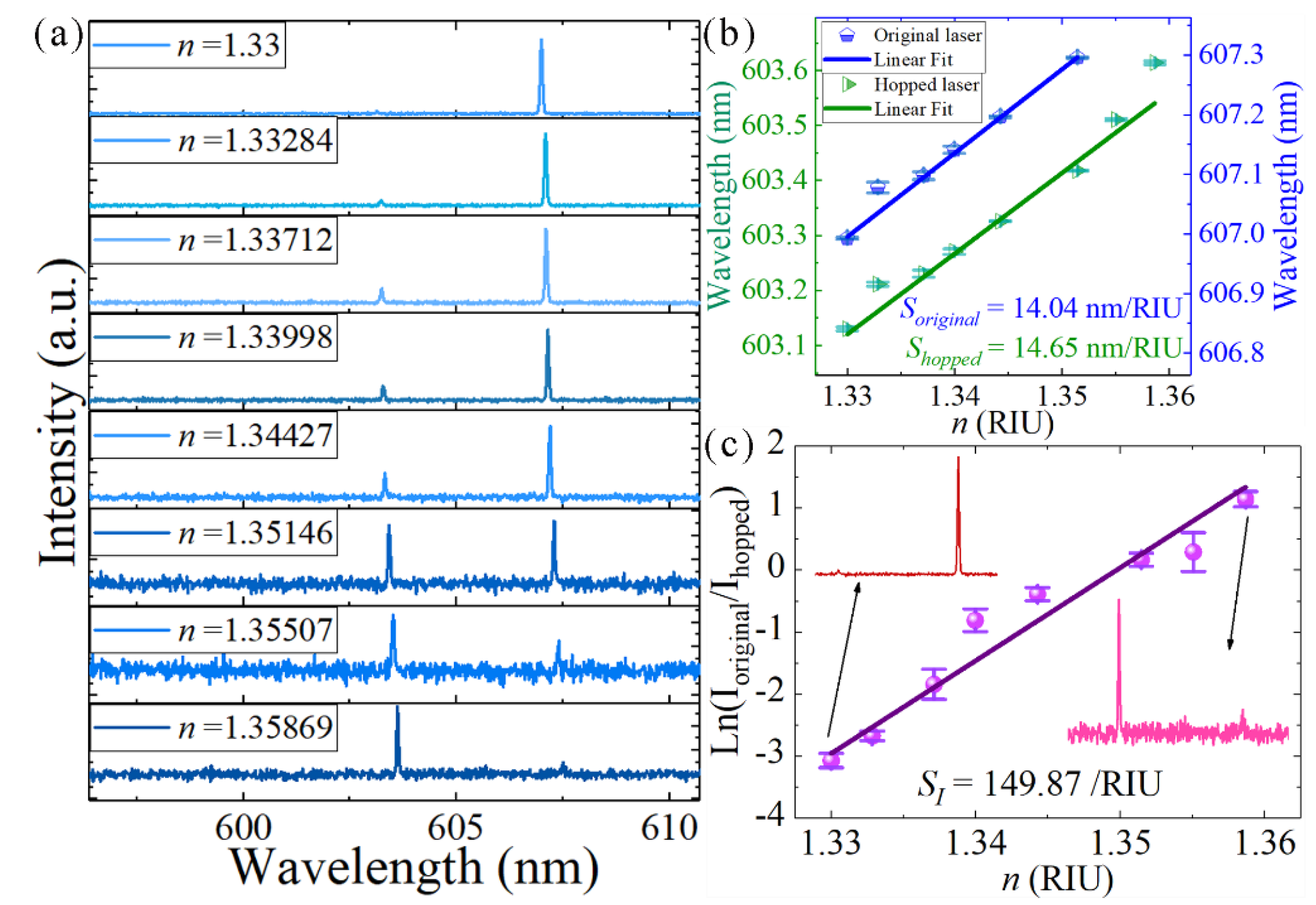
3.2. Modulation of the Microdisk Laser in Aqueous Media
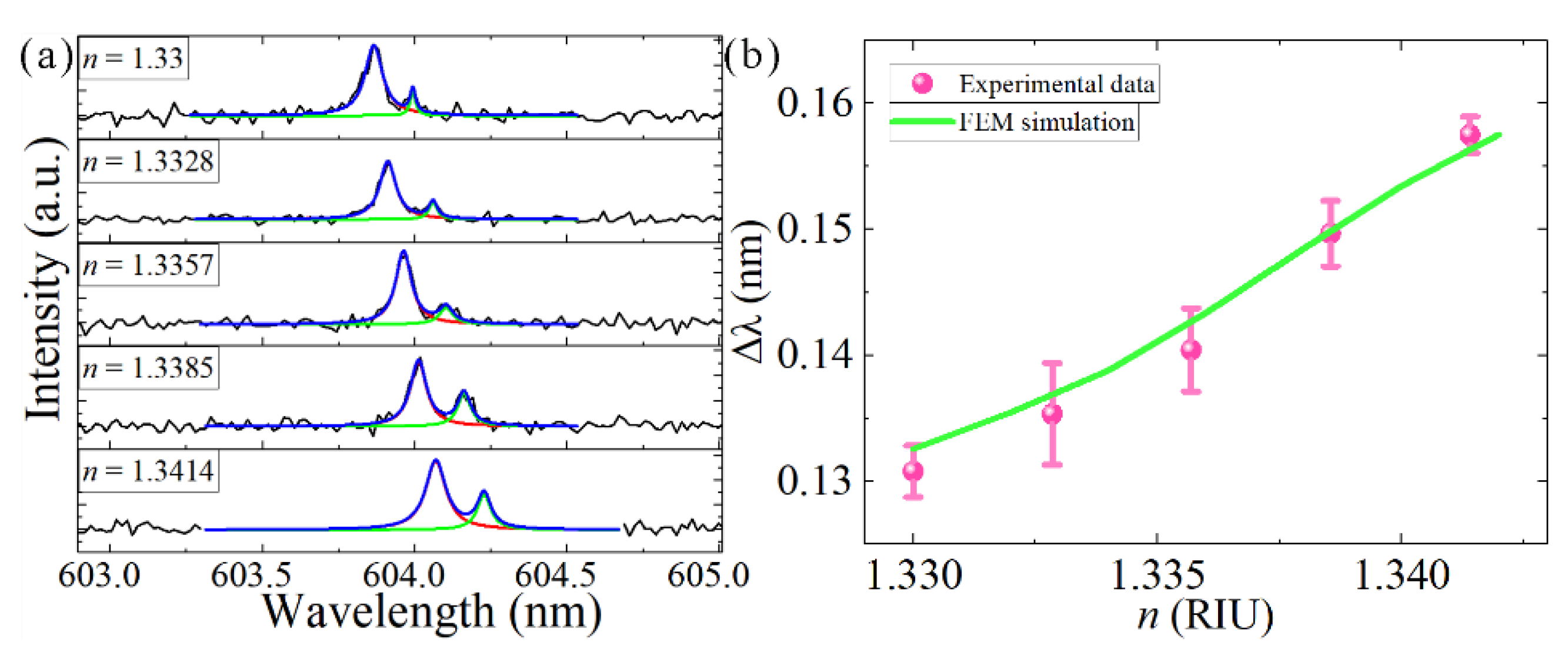
3.3. Mode Splitting from the Coupled-Microdisk Laser in Aqueous Media
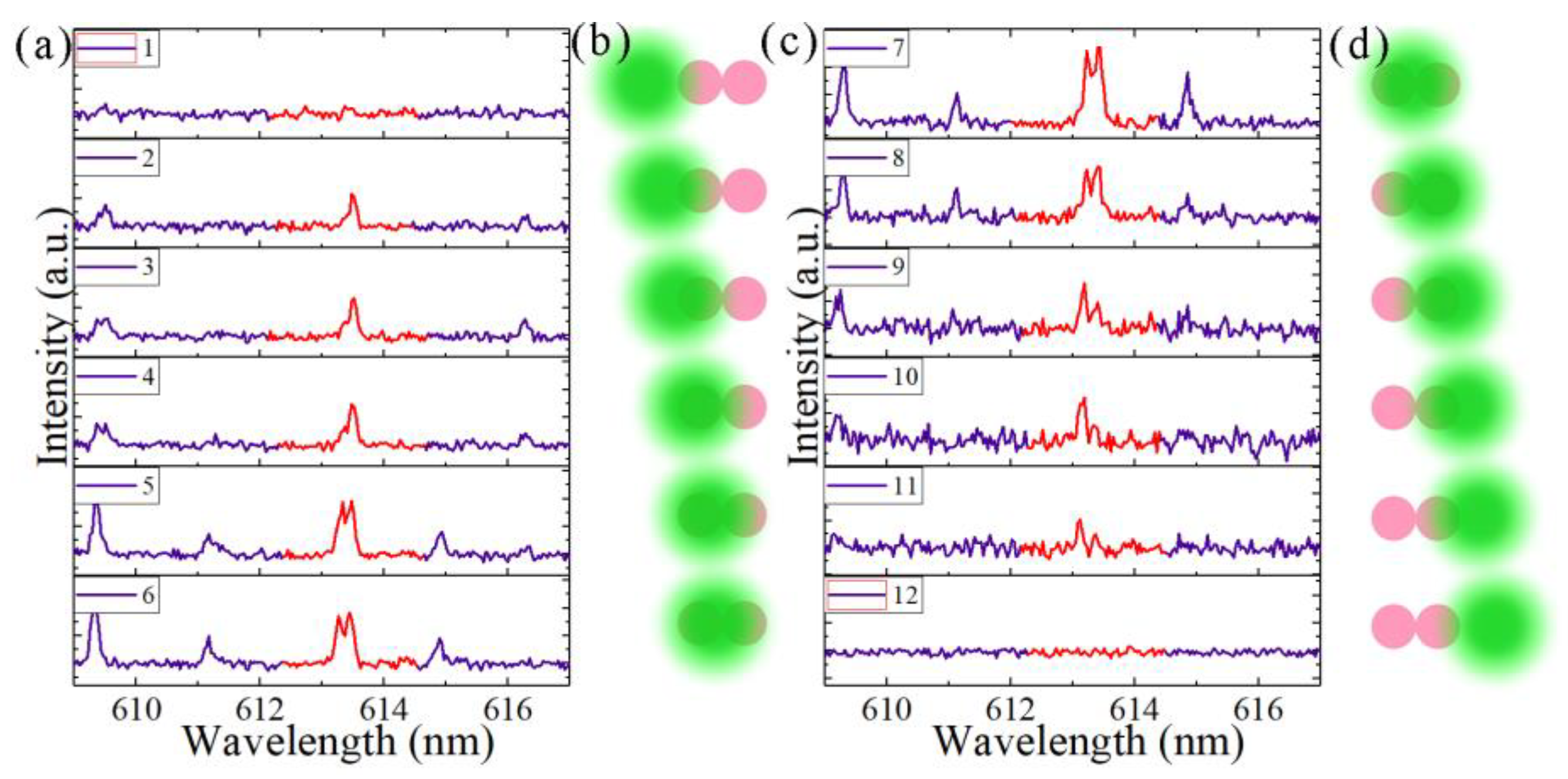
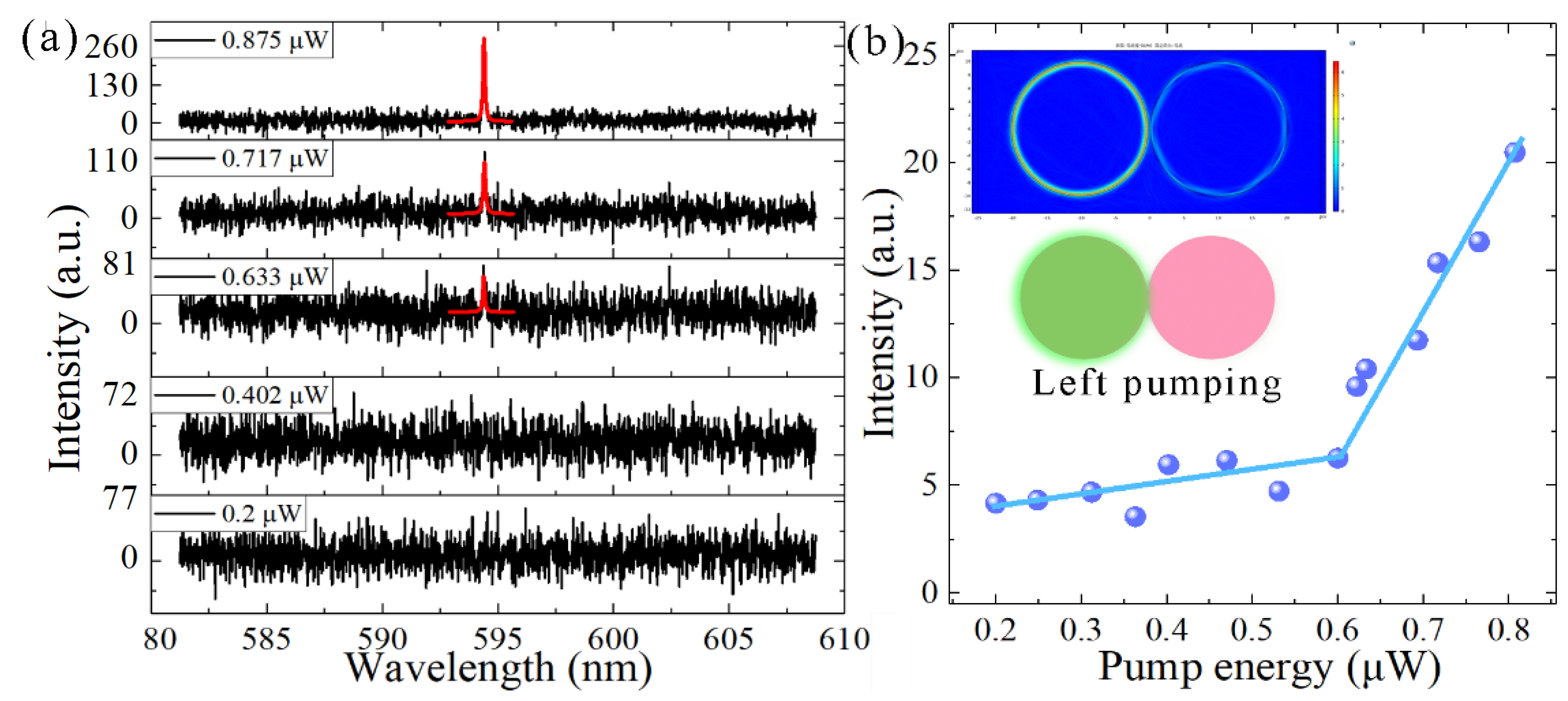
3.4. Single-Frequency Lasing from the Coupled Microdisk in Aqueous Media
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Yang, S.; Wang, Y.; Sun, H. Advances and Prospects for Whispering Gallery Mode Microcavities. Adv. Opt. Mater. 2015, 3, 1136–1162. [Google Scholar] [CrossRef]
- Helbo, B.; Kristensen, A.; Menon, A. A micro-cavity fluidic dye laser. J. Micromech. Microeng. 2003, 13, 307–311. [Google Scholar] [CrossRef]
- Shopova, S.I.; Zhou, H.; Fan, X.; Zhang, P. Optofluidic ring resonator based dye laser. Appl. Phys. Lett. 2007, 90, 221101. [Google Scholar] [CrossRef]
- Vahala, K.J. Optical microcavities. Nature 2003, 424, 839–846. [Google Scholar] [CrossRef] [PubMed]
- Gu, F.; Xie, F.; Lin, X.; Linghu, S.; Fang, W.; Zeng, H.; Tong, L.; Zhuang, S. Single whispering-gallery mode lasing in polymer bottle microresonators via spatial pump engineering. Light. Sci. Appl. 2017, 6, e17061. [Google Scholar] [CrossRef] [PubMed]
- Shang, L.; Liu, L.; Xu, L. Single-frequency coupled asymmetric microcavity laser. Opt. Lett. 2008, 33, 1150–1152. [Google Scholar] [CrossRef] [PubMed]
- Arbabi, A.; Kang, Y.M.; Lu, C.-Y.; Chow, E.; Goddard, L.L. Realization of a narrowband single wavelength microring mirror. Appl. Phys. Lett. 2011, 99, 91105. [Google Scholar] [CrossRef]
- Li, M.; Zhang, N.; Wang, K.; Li, J.; Xiao, S.; Song, Q. Inversed Vernier effect based single-mode laser emission in coupled microdisks. Sci. Rep. 2015, 5, 13682. [Google Scholar] [CrossRef]
- Wang, H.; Liu, S.; Chen, L.; Shen, D.; Wu, X. Dual-wavelength single-frequency laser emission in asymmetric coupled microdisks. Sci. Rep. 2016, 6, 38053. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H.; Tu, X.; Wu, X.; Liu, L.; Xu, L. Suppression and hopping of whispering gallery modes in multiple-ring-coupled microcavity lasers. J. Opt. Soc. Am. B 2011, 28, 483. [Google Scholar] [CrossRef]
- Wu, X.; Sun, Y.; Suter, J.D.; Fan, X. Single mode coupled optofluidic ring resonator dye lasers. Appl. Phys. Lett. 2009, 94, 241109. [Google Scholar] [CrossRef]
- Miri, M.-A.; Alù, A. Exceptional points in optics and photonics. Science 2019, 363, eaar7709. [Google Scholar] [CrossRef] [PubMed]
- Brandstetter, M.; Liertzer, M.; Deutsch, C.; Klang, P.; Schöberl, J.; Türeci, H.E.; Strasser, G.; Unterrainer, K.; Rotter, S. Reversing the pump dependence of a laser at an exceptional point. Nat. Commun. 2014, 5, 4034. [Google Scholar] [CrossRef] [PubMed]
- Chang, L.; Jiang, X.; Hua, S.; Yang, C.; Wen, J.; Jiang, L.; Li, G.; Wang, G.; Xiao, M. Parity–time symmetry and variable optical isolation in active–passive-coupled microresonators. Nat. Photon. 2014, 8, 524–529. [Google Scholar] [CrossRef]
- Peng, B.; Özdemir, Ş.K.; Lei, F.; Monifi, F.; Gianfreda, M.; Long, G.L.; Fan, S.; Nori, F.; Bender, C.M.; Yang, L. Parity–time-symmetric whispering-gallery microcavities. Nat. Phys. 2014, 10, 394–398. [Google Scholar] [CrossRef]
- Gao, Z.; Fryslie, S.T.M.; Thompson, B.J.; Carney, P.S.; Choquette, K.D. Parity-time symmetry in coherently coupled vertical cavity laser arrays. Optica 2017, 4, 323. [Google Scholar] [CrossRef]
- Regensburger, A.; Bersch, C.; Miri, M.-A.; Onishchukov, G.; Christodoulides, D.N.; Peschel, U. Parity–time synthetic photonic lattices. Nature 2012, 488, 167–171. [Google Scholar] [CrossRef]
- Guo, A.; Salamo, G.J.; Duchesne, D.; Morandotti, R.; Volatier-Ravat, M.; Aimez, V.; Siviloglou, G.A.; Christodoulides, D.N. Observation ofPT-Symmetry Breaking in Complex Optical Potentials. Phys. Rev. Lett. 2009, 103, 093902. [Google Scholar] [CrossRef]
- Peng, B.; Özdemir, Ş.K.; Liertzer, M.; Chen, W.; Kramer, J.; Yılmaz, H.; Wiersig, J.; Rotter, S.; Yang, L. Chiral modes and directional lasing at exceptional points. Proc. Natl. Acad. Sci. USA 2016, 113, 6845–6850. [Google Scholar] [CrossRef]
- Hodaei, H.; Hassan, A.U.; Wittek, S.; Garcia-Gracia, H.; El-Ganainy, R.; Christodoulides, D.N.; Khajavikhan, M. Enhanced sensitivity at higher-order exceptional points. Nature 2017, 548, 187–191. [Google Scholar] [CrossRef]
- Chen, W.; Özdemir, Ş.K.; Zhao, G.; Wiersig, J.; Yang, L. Exceptional points enhance sensing in an optical microcavity. Nature 2017, 548, 192–196. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Li, H.; Liu, L.; Xu, L. Unidirectional single-frequency lasing from a ring-spiral coupled microcavity laser. Appl. Phys. Lett. 2008, 93, 81105. [Google Scholar] [CrossRef]
- Hodaei, H.; Miri, M.-A.; Heinrich, M.; Christodoulides, D.N.; Khajavikhan, M. Parity-time-symmetric microring lasers. Science 2014, 346, 975–978. [Google Scholar] [CrossRef] [PubMed]
- Feng, L.; Wong, Z.J.; Ma, R.-M.; Wang, Y.; Zhang, X. Single-mode laser by parity-time symmetry breaking. Science 2014, 346, 972–975. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Jiang, X.; Hua, Q.; Hua, S.; Chen, Y.; Ma, J.; Xiao, M. Realization of controllable photonic molecule based on three ultrahigh-Q microtoroid cavities. Laser Photon. Rev. 2017, 11, 1600178. [Google Scholar] [CrossRef]
- Chen, Y.; Lei, L.; Zhang, K.; Shi, J.; Wang, L.; Li, H.; Zhang, X.M.; Wang, Y.; Chan, H.L.W. Optofluidic microcavities: Dye-lasers and biosensors. Biomicrofluidics 2010, 4, 043002. [Google Scholar] [CrossRef]
- Lu, Q.; Chen, X.; Fu, L.; Xie, S.; Wu, X. On-Chip Real-Time Chemical Sensors Based on Water-Immersion-Objective Pumped Whispering-Gallery-Mode Microdisk Laser. Nanomaterials 2019, 9, 479. [Google Scholar] [CrossRef]
- Ren, L.; Wu, X.; Li, M.; Zhang, X.; Liu, L.; Xu, L. Ultrasensitive label-free coupled optofluidic ring laser sensor. Opt. Lett. 2012, 37, 3873–3875. [Google Scholar] [CrossRef]
- Zhang, X.; Ren, L.; Wu, X.; Li, H.; Liu, L.; Xu, L. Coupled optofluidic ring laser for ultrahigh-sensitive sensing. Opt. Express 2011, 19, 22242–22247. [Google Scholar] [CrossRef]
- Li, H.; Shang, L.; Tu, X.; Liu, L.; Xu, L. Coupling Variation Induced Ultrasensitive Label-Free Biosensing by Using Single Mode Coupled Microcavity Laser. J. Am. Chem. Soc. 2009, 131, 16612–16613. [Google Scholar] [CrossRef]
- Li, M.; Wu, X.; Liu, L.; Fan, X.; Xu, L. Self-Referencing Optofluidic Ring Resonator Sensor for Highly Sensitive Biomolecular Detection. Anal. Chem. 2013, 85, 9328–9332. [Google Scholar] [CrossRef] [PubMed]
- Testa, G.; Persichetti, G.; Bernini, R. Liquid Core ARROW Waveguides: A Promising Photonic Structure for Integrated Optofluidic Microsensors. Micromachines 2016, 7, 47. [Google Scholar] [CrossRef]
- Wu, X.; Oo, M.K.K.; Reddy, K.; Chen, Q.; Sun, Y.; Fan, X. Optofluidic laser for dual-mode sensitive biomolecular detection with a large dynamic range. Nat. Commun. 2014, 5, 3779. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Chen, Q.; Sun, Y.; Fan, X. Bio-inspired optofluidic lasers with luciferin. Appl. Phys. Lett. 2013, 102, 203706. [Google Scholar] [CrossRef]
- Oxborrow, M. Traceable 2-D finite element simulation of the whispering gallery modes of axisymmetric elec- tromagnetic resonators. IEEE Trans. Microw. Theory Tech. 2007, 55, 1209–1218. [Google Scholar] [CrossRef]
- Guo, Y.; Ye, J.Y.; Divin, C.; Huang, B.; Thomas, T.P.; Baker, J.J.R.; Norris, T.B.; Baker, J.R. Real-Time Biomolecular Binding Detection Using a Sensitive Photonic Crystal Biosensor. Anal. Chem. 2010, 82, 5211–5218. [Google Scholar] [CrossRef] [PubMed]
- Aminabhavi, T.M. Use of mixing rules in the analysis of data for binary liquid mixtures. J. Chem. Eng. Data 1984, 29, 54–55. [Google Scholar] [CrossRef]
- Chandrahalim, H.; Fan, X. Reconfigurable Solid-state Dye-doped Polymer Ring Resonator Lasers. Sci. Rep. 2015, 5, 18310. [Google Scholar] [CrossRef]
- Zhu, H.; White, I.M.; Suter, J.D.; Dale, P.S.; Fan, X. Analysis of biomolecule detection with optofluidic ring resonator sensors. Opt. Express 2007, 15, 9139–9146. [Google Scholar] [CrossRef] [PubMed]
- Xie, F.; Yao, N.; Fang, W.; Wang, H.; Gu, F.; Zhuang, S. Single-mode lasing via loss engineering in fiber-taper-coupled polymer bottle microresonators. Photon Res. 2017, 5, B29. [Google Scholar] [CrossRef]
- Grossmann, T.; Wienhold, T.; Bog, U.; Beck, T.; Friedmann, C.; Kalt, H.; Mappes, T. Polymeric photonic molecule super-mode lasers on silicon. Light. Sci. Appl. 2013, 2, e82. [Google Scholar] [CrossRef]
- Ta, V.D.; Chen, R.; Sun, H. Coupled polymer microfiber lasers for single mode operation and enhanced refractive index sensing. Adv. Opt. Mater. 2014, 2, 220–225. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Z.; Wang, H.; Zhao, C.; Chen, L.; Liu, S.; Hu, J.; Zhou, Y.; Wu, X. Spectral Modulation of Optofluidic Coupled-Microdisk Lasers in Aqueous Media. Nanomaterials 2019, 9, 1439. https://doi.org/10.3390/nano9101439
Guo Z, Wang H, Zhao C, Chen L, Liu S, Hu J, Zhou Y, Wu X. Spectral Modulation of Optofluidic Coupled-Microdisk Lasers in Aqueous Media. Nanomaterials. 2019; 9(10):1439. https://doi.org/10.3390/nano9101439
Chicago/Turabian StyleGuo, Zhihe, Haotian Wang, Chenming Zhao, Lin Chen, Sheng Liu, Jinliang Hu, Yi Zhou, and Xiang Wu. 2019. "Spectral Modulation of Optofluidic Coupled-Microdisk Lasers in Aqueous Media" Nanomaterials 9, no. 10: 1439. https://doi.org/10.3390/nano9101439
APA StyleGuo, Z., Wang, H., Zhao, C., Chen, L., Liu, S., Hu, J., Zhou, Y., & Wu, X. (2019). Spectral Modulation of Optofluidic Coupled-Microdisk Lasers in Aqueous Media. Nanomaterials, 9(10), 1439. https://doi.org/10.3390/nano9101439





