Nanopillar Diffraction Gratings by Two-Photon Lithography
Abstract
1. Introduction
2. Experimental
2.1. Two-Photon Lithography (TPL)
2.2. Scanning Electron Microscopy (SEM)
2.3. Optical Microscopy
3. Numerical Simulations
3.1. Voxel Sizes
3.2. Optical Spectra
4. Results and Discussion
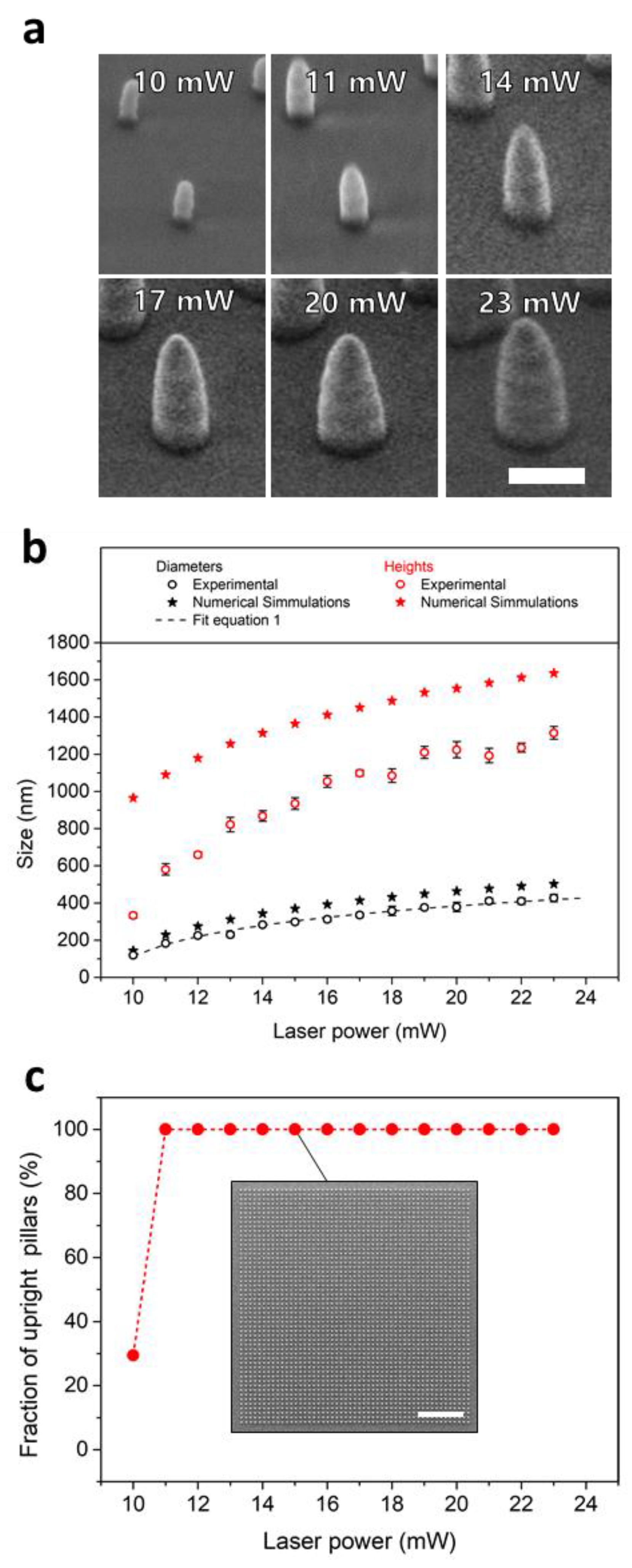
4.1. Nanopillar Sizes
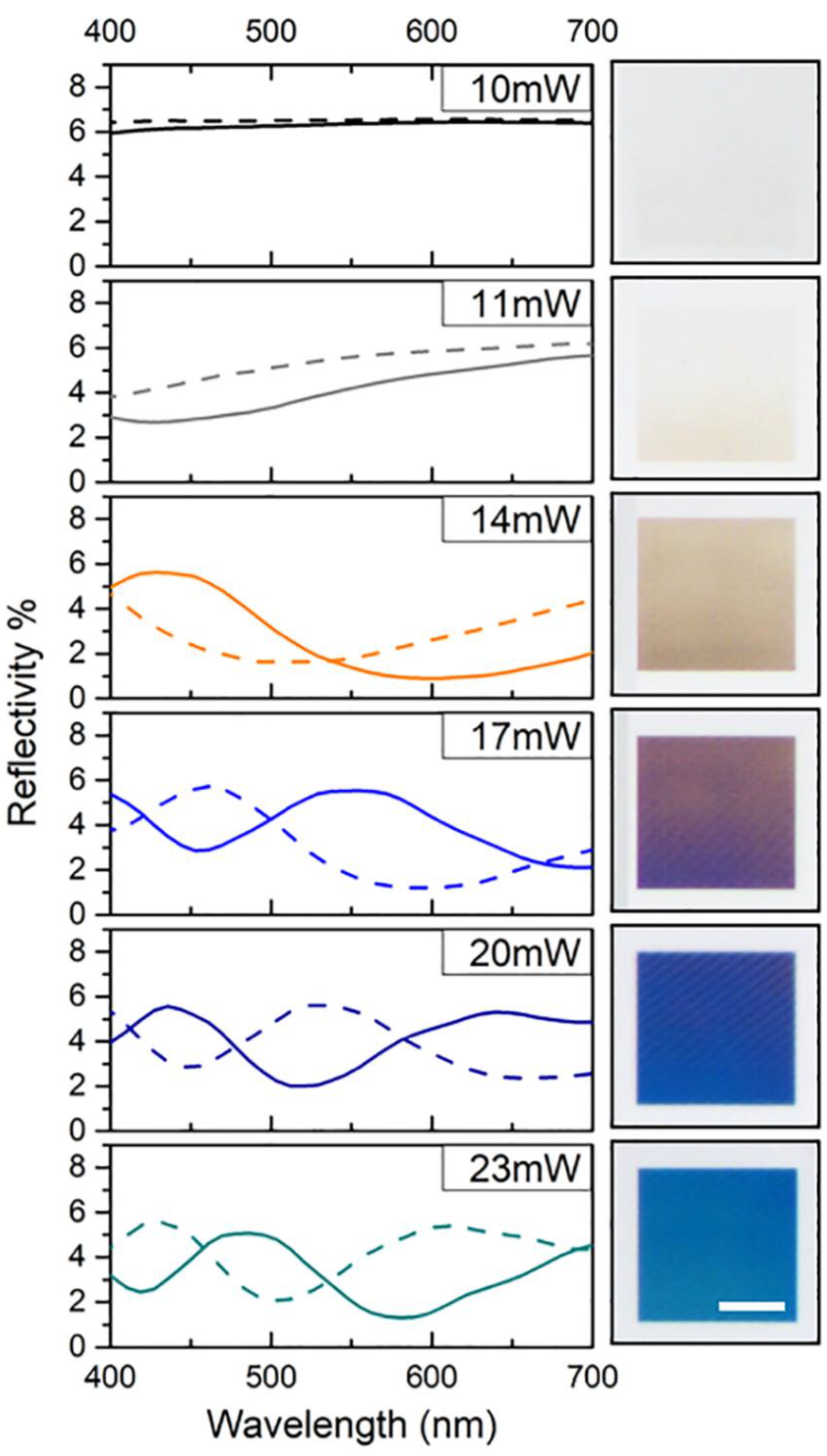
4.2. Optical Properties
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Catchpole, K.R.; Green, M.A. A conceptual model of light coupling by pillar diffraction gratings. J. Appl. Phys. 2007, 101, 063105. [Google Scholar] [CrossRef]
- Chong, T.K.; Wilson, J.; Mokkapati, S.; Catchpole, K.R. Optimal wavelength scale diffraction gratings for light trapping in solar cells. J. Opt. 2012, 14, 024012. [Google Scholar] [CrossRef]
- Yan, H.; Huang, L.; Xu, X.; Chakravarty, S.; Tang, N.; Tian, H.; Chen, R.T. Unique surface sensing property and enhanced sensitivity in microring resonator biosensors based on subwavelength grating waveguides. Opt. Express 2016, 24, 29724–29733. [Google Scholar] [CrossRef] [PubMed]
- Mao, X.; Zeng, L. Design and fabrication of crossed gratings with multiple zero-reference marks for planar encoders. Meas. Sci. Technol. 2018, 29, 025204. [Google Scholar] [CrossRef]
- Kim, D.Y.; Tripathy, S.K.; Li, L.; Kumar, J. Laser-induced holographic surface relief gratings on nonlinear optical polymer films. Appl. Phys. Lett. 1995, 66, 1166–1168. [Google Scholar] [CrossRef]
- Gale, M.T.; Knop, K.; Morf, R.H. Zero-Order Diffractive Microstructures for Security Applications; SPIE: Bellingham, WA, USA, 1990; Volume 1210. [Google Scholar]
- Wang, Y.; Lu, N.; Xu, H.; Shi, G.; Xu, M.; Lin, X.; Li, H.; Wang, W.; Qi, D.; Lu, Y.; et al. Biomimetic corrugated silicon nanocone arrays for self-cleaning antireflection coatings. Nano Res. 2010, 3, 520–527. [Google Scholar] [CrossRef]
- Dewan, R.; Fischer, S.; Meyer-Rochow, V.B.; Özdemir, Y.; Hamraz, S.; Knipp, D. Studying nanostructured nipple arrays of moth eye facets helps to design better thin film solar cells. Bioinspiration Biomim. 2011, 7, 016003. [Google Scholar] [CrossRef]
- Ji, S.; Park, J.; Lim, H. Improved antireflection properties of moth eye mimicking nanopillars on transparent glass: Flat antireflection and color tuning. Nanoscale 2012, 4, 4603–4610. [Google Scholar] [CrossRef]
- Lora Gonzalez, F.; Chan, L.; Berry, A.; Morse, D.E.; Gordon, M.J. Simple colloidal lithography method to fabricate large-area moth-eye antireflective structures on Si, Ge, and GaAs for IR applications. J. Vac. Sci. Technol. B 2014, 32, 051213. [Google Scholar] [CrossRef]
- Chigrin, D.N.; Lavrinenko, A.V. Nanopillar Coupled Periodic Waveguides: From Basic Properties to Applications; SPIE: Bellingham, WA, USA, 2006; Volume 6393. [Google Scholar]
- Farsari, M.; Chichkov, B.N. Materials processing: Two-photon fabrication. Nat. Photonics 2009, 3, 450–452. [Google Scholar] [CrossRef]
- Gissibl, T.; Thiele, S.; Herkommer, A.; Giessen, H. Two-photon direct laser writing of ultracompact multi-lens objectives. Nat. Photonics 2016, 10, 554–560. [Google Scholar] [CrossRef]
- Hohmann, J.K.; Renner, M.; Waller, E.H.; von Freymann, G. Three-Dimensional μ-Printing: An Enabling Technology. Adv. Opt. Mater. 2015, 3, 1488–1507. [Google Scholar] [CrossRef]
- Kawata, S.; Sun, H.B.; Tanaka, T.; Takada, K. Finer features for functional microdevices. Nature 2001, 412, 697. [Google Scholar] [CrossRef] [PubMed]
- Waheed, S.; Cabot, J.M.; Macdonald, N.P.; Lewis, T.; Guijt, R.M.; Paull, B.; Breadmore, M.C. 3D printed microfluidic devices: Enablers and barriers. Lab Chip 2016, 16, 1993–2013. [Google Scholar] [CrossRef] [PubMed]
- Fischer, S.C.L.; Groß, K.; Torrents Abad, O.; Becker, M.M.; Park, E.; Hensel, R.; Arzt, E. Funnel-Shaped Microstructures for Strong Reversible Adhesion. Adv. Mater. Interfaces 2017, 4, 1700292. [Google Scholar] [CrossRef]
- Hensel, R.; Moh, K.; Arzt, E. Engineering Micropatterned Dry Adhesives: From Contact Theory to Handling Applications. Adv. Funct. Mater. 2018, 28, 1800865. [Google Scholar] [CrossRef]
- Marino, A.; Filippeschi, C.; Mattoli, V.; Mazzolai, B.; Ciofani, G. Biomimicry at the nanoscale: Current research and perspectives of two-photon polymerization. Nanoscale 2015, 7, 2841–2850. [Google Scholar] [CrossRef]
- Wolfenson, H.; Meacci, G.; Liu, S.; Stachowiak, M.R.; Iskratsch, T.; Ghassemi, S.; Roca-Cusachs, P.; O’Shaughnessy, B.; Hone, J.; Sheetz, M.P. Tropomyosin controls sarcomere-like contractions for rigidity sensing and suppressing growth on soft matrices. Nat. Cell Biol. 2015, 18, 33. [Google Scholar] [CrossRef]
- Marino, A.; Ciofani, G.; Filippeschi, C.; Pellegrino, M.; Pellegrini, M.; Orsini, P.; Pasqualetti, M.; Mattoli, V.; Mazzolai, B. Two-Photon Polymerization of Sub-micrometric Patterned Surfaces: Investigation of Cell-Substrate Interactions and Improved Differentiation of Neuron-like Cells. ACS Appl. Mater. Interfaces 2013, 5, 13012–13021. [Google Scholar] [CrossRef]
- Klein, F.; Striebel, T.; Fischer, J.; Jiang, Z.; Franz, C.M.; von Freymann, G.; Wegener, M.; Bastmeyer, M. Elastic Fully Three-dimensional Microstructure Scaffolds for Cell Force Measurements. Adv. Mater. 2010, 22, 868–871. [Google Scholar] [CrossRef]
- Thiele, S.; Arzenbacher, K.; Gissibl, T.; Giessen, H.; Herkommer, A.M. 3D-printed eagle eye: Compound microlens system for foveated imaging. Sci. Adv. 2017, 3. [Google Scholar] [CrossRef] [PubMed]
- von Freymann, G.; Ledermann, A.; Thiel, M.; Staude, I.; Essig, S.; Busch, K.; Wegener, M. Three-Dimensional Nanostructures for Photonics. Adv. Funct. Mater. 2010, 20, 1038–1052. [Google Scholar] [CrossRef]
- Nawrot, M.; Zinkiewicz, Ł.; Włodarczyk, B.; Wasylczyk, P. Transmission phase gratings fabricated with direct laser writing as color filters in the visible. Opt. Express 2013, 21, 31919–31924. [Google Scholar] [CrossRef] [PubMed]
- Mueller, J.B.; Fischer, J.; Mayer, F.; Kadic, M.; Wegener, M. Polymerization Kinetics in Three-Dimensional Direct Laser Writing. Adv. Mater. 2014, 26, 6566–6571. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.B.; Maeda, M.; Takada, K.; Chon, J.W.M.; Gu, M.; Kawata, S. Experimental investigation of single voxels for laser nanofabrication via two-photon photopolymerization. Appl. Phys. Lett. 2003, 83, 819–821. [Google Scholar] [CrossRef]
- Fischer, J.; Wegener, M. Three-dimensional optical laser lithography beyond the diffraction limit. Laser Photonics Rev. 2013, 7, 22–44. [Google Scholar] [CrossRef]
- Xing, J.F.; Dong, X.Z.; Chen, W.Q.; Duan, X.M.; Takeyasu, N.; Tanaka, T.; Kawata, S. Improving spatial resolution of two-photon microfabrication by using photoinitiator with high initiating efficiency. Appl. Phys. Lett. 2007, 90, 131106. [Google Scholar] [CrossRef]
- Tanaka, T.S.; Sun, H.B.; Kawata, S. Rapid sub-diffraction-limit laser micro/nanoprocessing in a threshold material system. Appl. Phys. Lett. 2002, 80, 312–314. [Google Scholar] [CrossRef]
- Fischer, J.; Mueller, J.B.; Quick, A.S.; Kaschke, J.; Barner-Kowollik, C.; Wegener, M. Exploring the Mechanisms in STED-Enhanced Direct Laser Writing. Adv. Opt. Mater. 2015, 3, 221–232. [Google Scholar] [CrossRef]
- Sun, H.B.; Takada, K.; Kim, M.S.; Lee, K.S.; Kawata, S. Scaling Laws of Voxels in Two-Photon Photopolymerization Nanofabrication. Appl. Phys. Lett. 2003, 83, 1104–1106. [Google Scholar] [CrossRef]
- Sun, H.B.; Suwa, T.; Takada, K.; Zaccaria, R.P.; Kim, M.S.; Lee, K.S.; Kawata, S. Shape precompensation in two-photon laser nanowriting of photonic lattices. Appl. Phys. Lett. 2004, 85, 3708–3710. [Google Scholar] [CrossRef]
- LaFratta, C.; Baldacchini, T. Two-Photon Polymerization Metrology: Characterization Methods of Mechanisms and Microstructures. Micromachines 2017, 8, 101. [Google Scholar] [CrossRef]
- Hu, Y.; Lao, Z.; Cumming, B.P.; Wu, D.; Li, J.; Liang, H.; Chu, J.; Huang, W.; Gu, M. Laser printing hierarchical structures with the aid of controlled capillary-driven self-assembly. Proc. Natl. Acad. Sci. USA 2015, 112, 6876–6881. [Google Scholar] [CrossRef] [PubMed]
- Purtov, J.; Verch, A.; Rogin, P.; Hensel, R. Improved development procedure to enhance the stability of microstructures created by two-photon polymerization. Microelectron. Eng. 2018, 194, 45–50. [Google Scholar] [CrossRef]
- Roca-Cusachs, P.; Rico, F.; Martínez, E.; Toset, J.; Farré, R.; Navajas, D. Stability of Microfabricated High Aspect Ratio Structures in Poly(dimethylsiloxane). Langmuir 2005, 21, 5542–5548. [Google Scholar] [CrossRef] [PubMed]
- Chandra, D.; Yang, S. Capillary-Force-Induced Clustering of Micropillar Arrays: Is It Caused by Isolated Capillary Bridges or by the Lateral Capillary Meniscus Interaction Force? Langmuir 2009, 25, 10430–10434. [Google Scholar] [CrossRef]
- Liu, V.; Fan, S. S4: A free electromagnetic solver for layered periodic structures. Comput. Phys. Commun. 2012, 183, 2233–2244. [Google Scholar] [CrossRef]
- Available online: https://web.stanford.edu/group/fan/S4/ (accessed on 24 Nov 2018).
- Lim, T.W.; Son, Y.; Yang, D.Y.; Pham, T.A.; Kim, D.P.; Yang, B.I.; Lee, K.S.; Park, S.H. Net Shape Manufacturing of Three-Dimensional SiCN Ceramic Microstructures Using an Isotropic Shrinkage Method by Introducing Shrinkage Guiders. Int. J. Appl. Ceram. Technol. 2008, 5, 258–264. [Google Scholar] [CrossRef]
- Kuznetsov, A.I.; Miroshnichenko, A.E.; Brongersma, M.L.; Kivshar, Y.S.; Luk’yanchuk, B. Optically resonant dielectric nanostructures. Science 2016, 354, aag2472. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Purtov, J.; Rogin, P.; Verch, A.; Johansen, V.E.; Hensel, R. Nanopillar Diffraction Gratings by Two-Photon Lithography. Nanomaterials 2019, 9, 1495. https://doi.org/10.3390/nano9101495
Purtov J, Rogin P, Verch A, Johansen VE, Hensel R. Nanopillar Diffraction Gratings by Two-Photon Lithography. Nanomaterials. 2019; 9(10):1495. https://doi.org/10.3390/nano9101495
Chicago/Turabian StylePurtov, Julia, Peter Rogin, Andreas Verch, Villads Egede Johansen, and René Hensel. 2019. "Nanopillar Diffraction Gratings by Two-Photon Lithography" Nanomaterials 9, no. 10: 1495. https://doi.org/10.3390/nano9101495
APA StylePurtov, J., Rogin, P., Verch, A., Johansen, V. E., & Hensel, R. (2019). Nanopillar Diffraction Gratings by Two-Photon Lithography. Nanomaterials, 9(10), 1495. https://doi.org/10.3390/nano9101495





