Polarization and Dielectric Properties of BiFeO3-BaTiO3 Superlattice-Structured Ferroelectric Films
Abstract
:1. Introduction
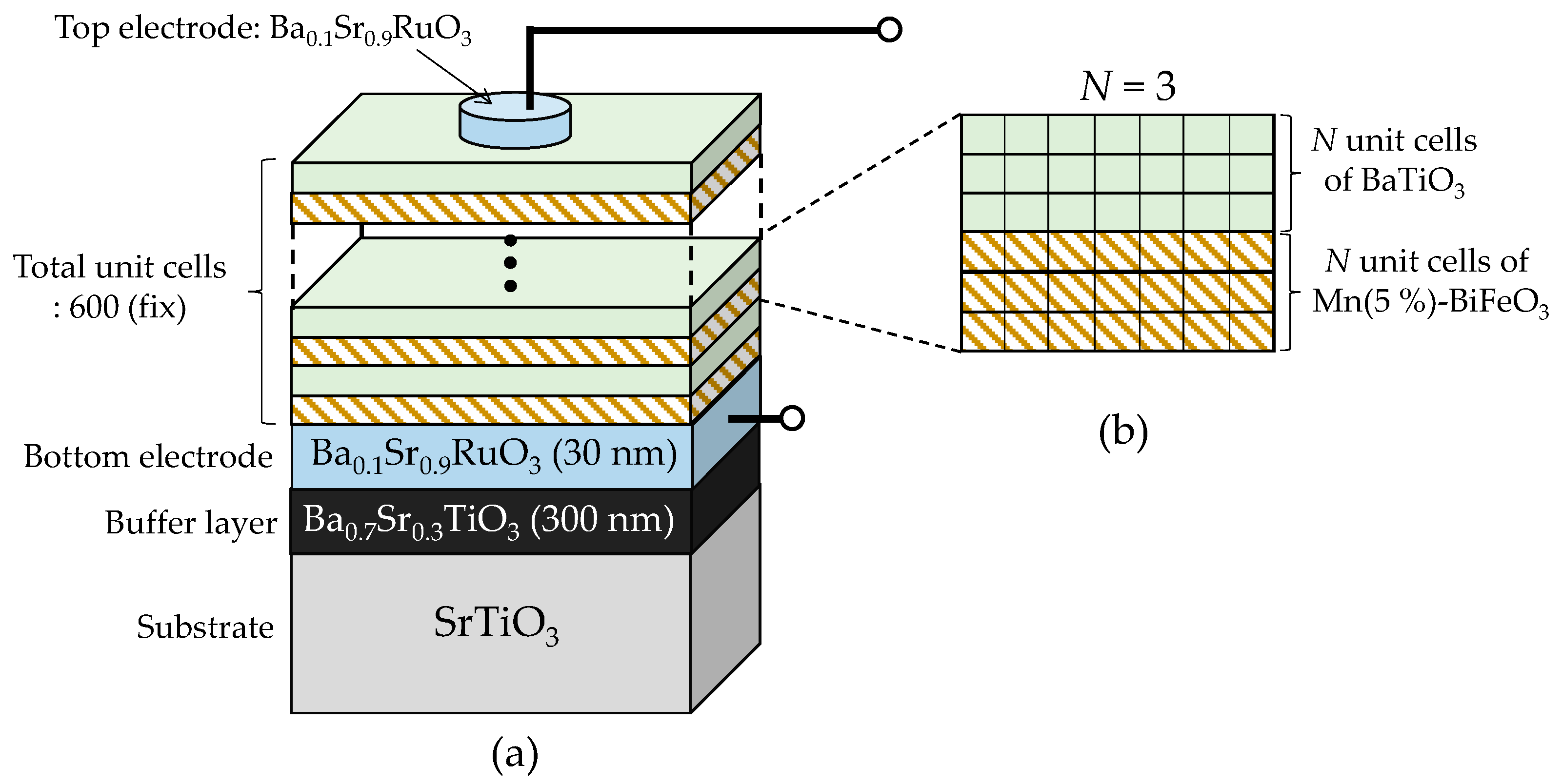
2. Materials and Methods
2.1. Experimental
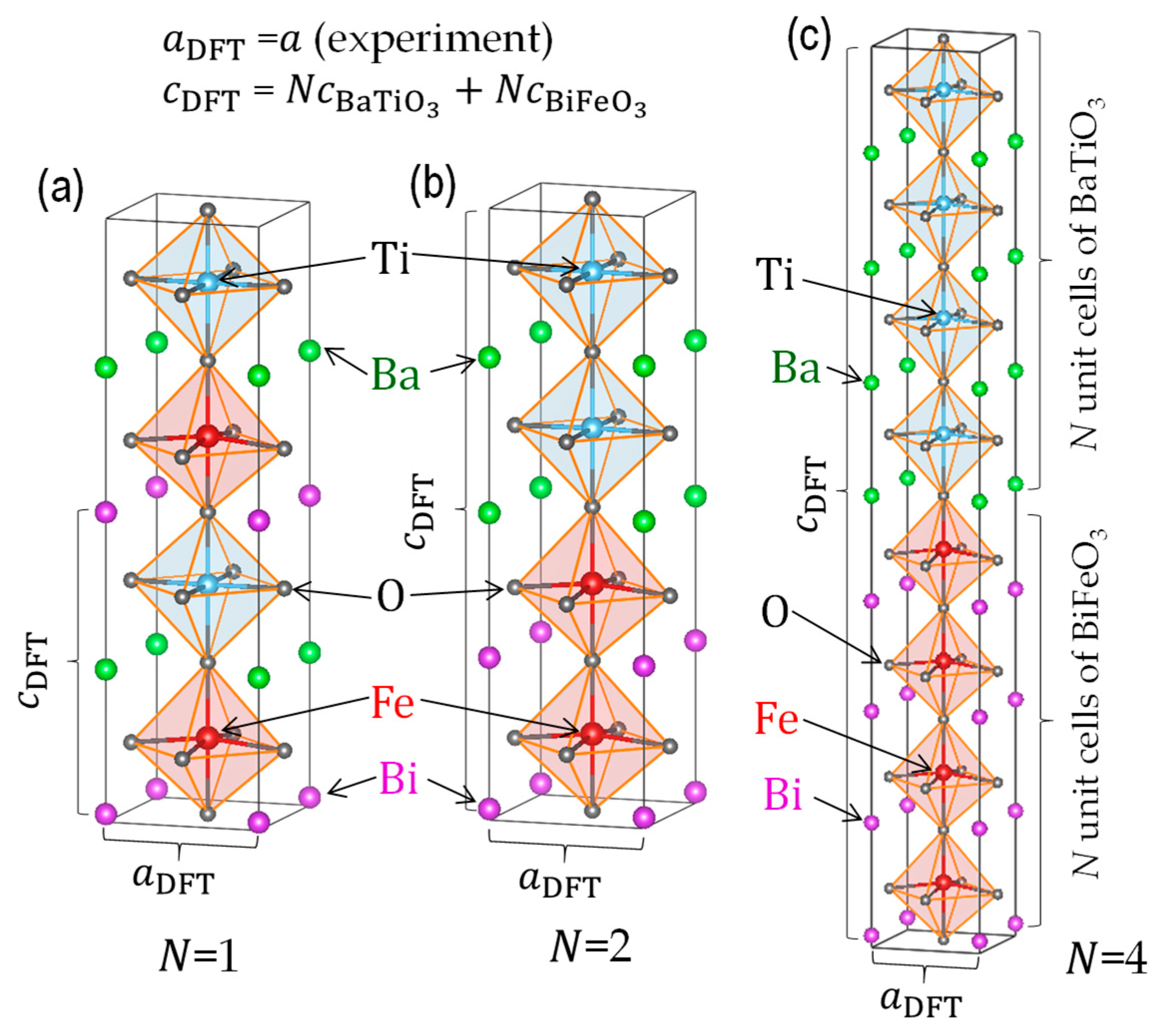
2.2. DFT Calculations
3. Results
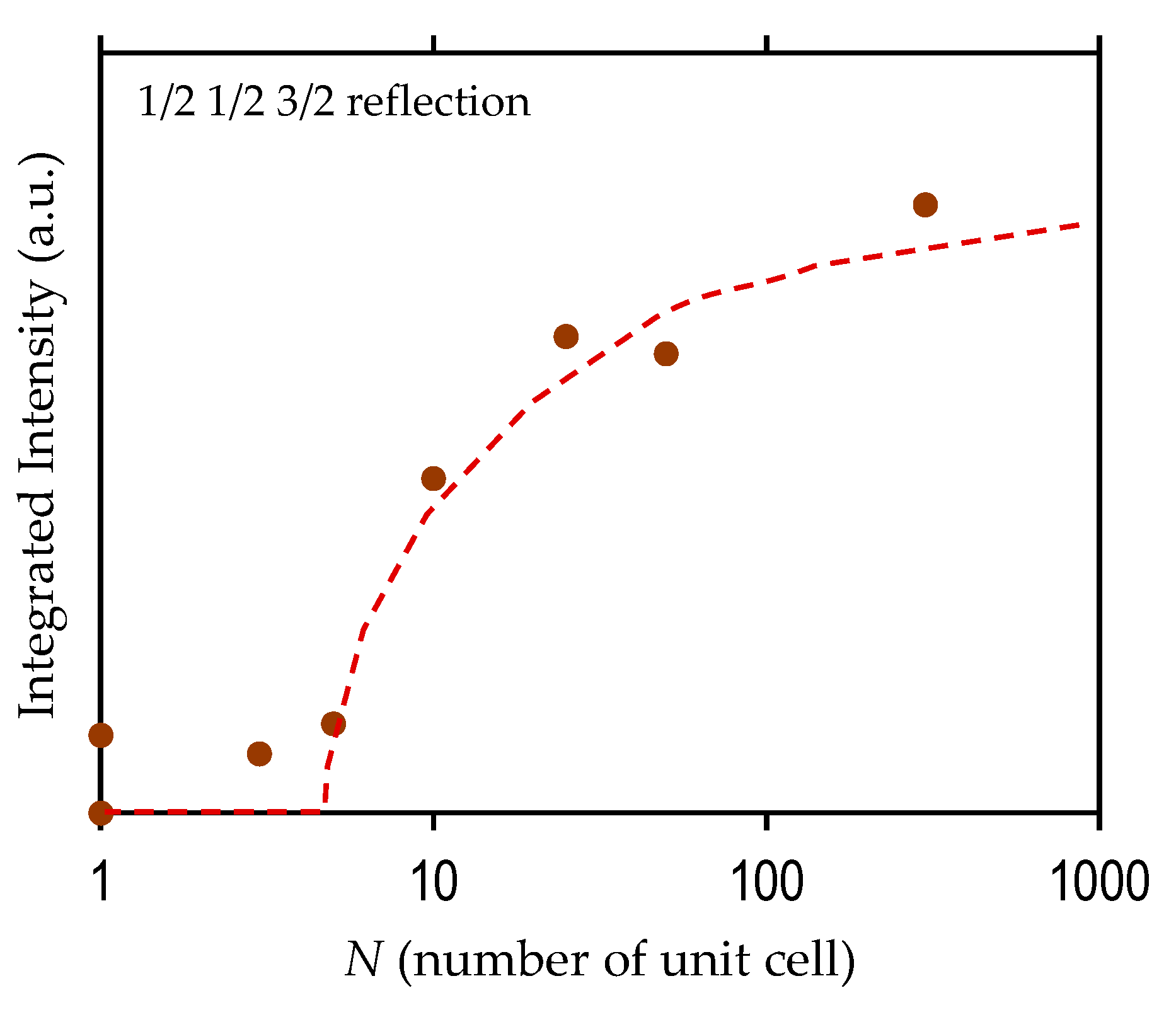
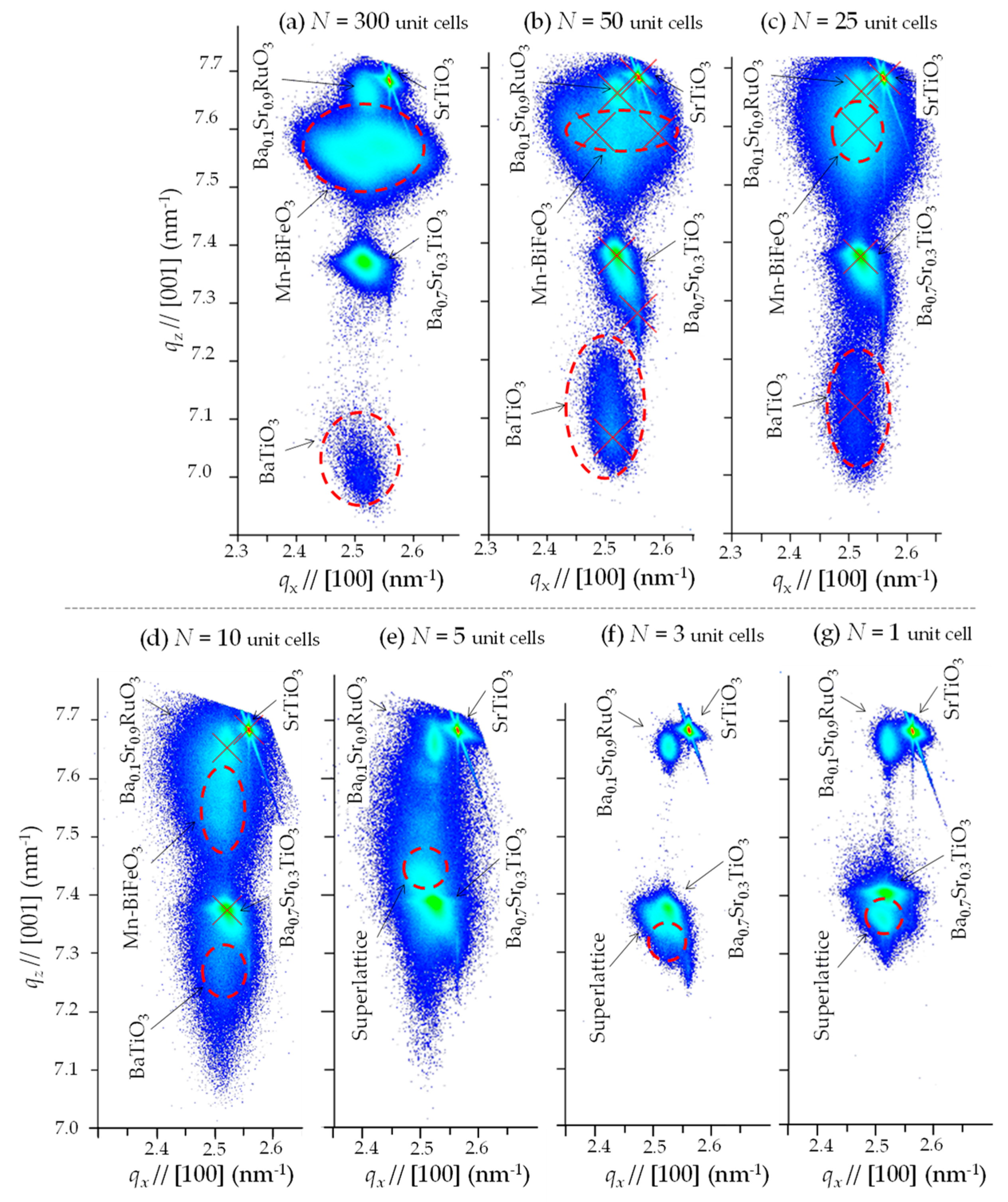
3.1. Crystal Structure
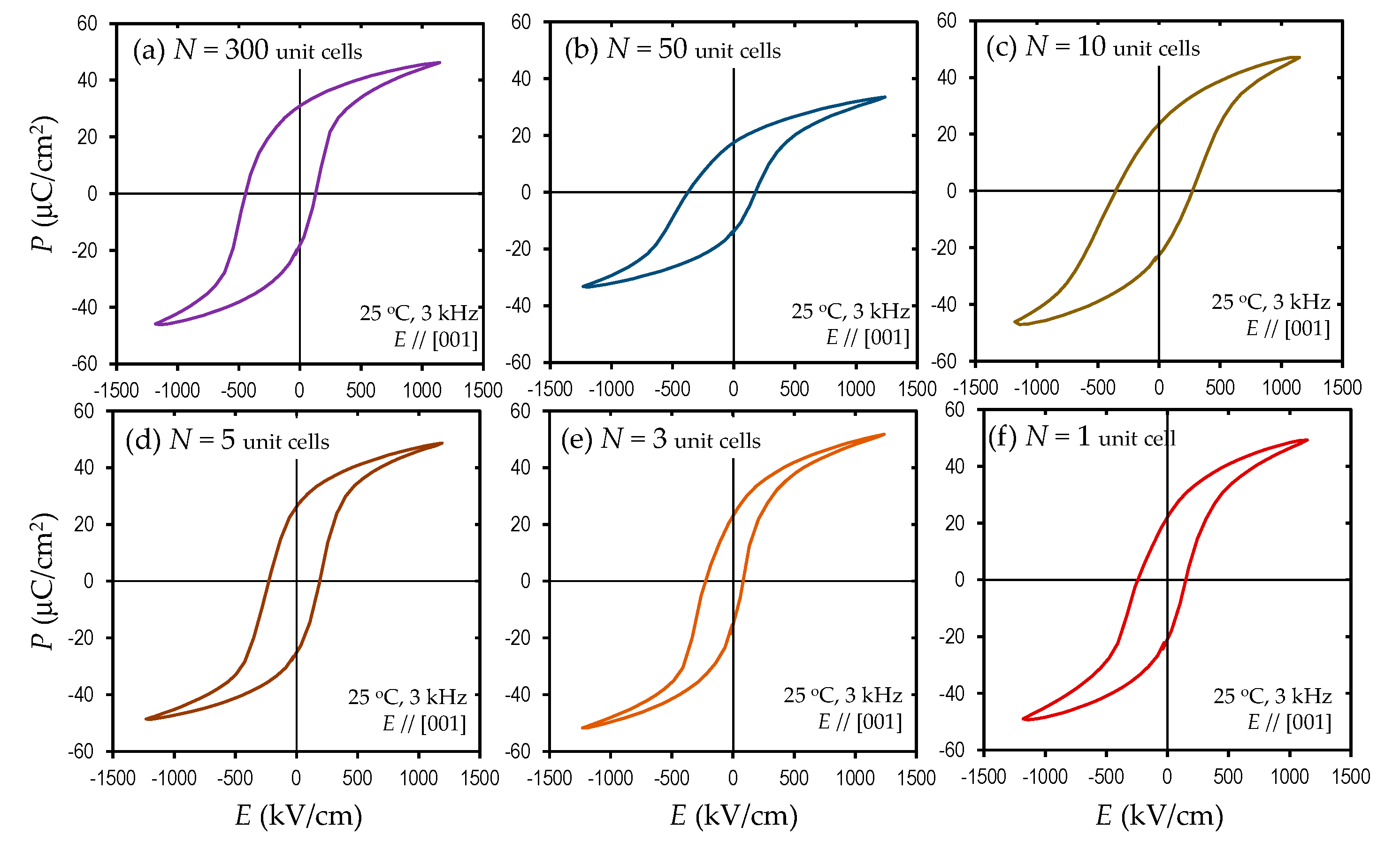
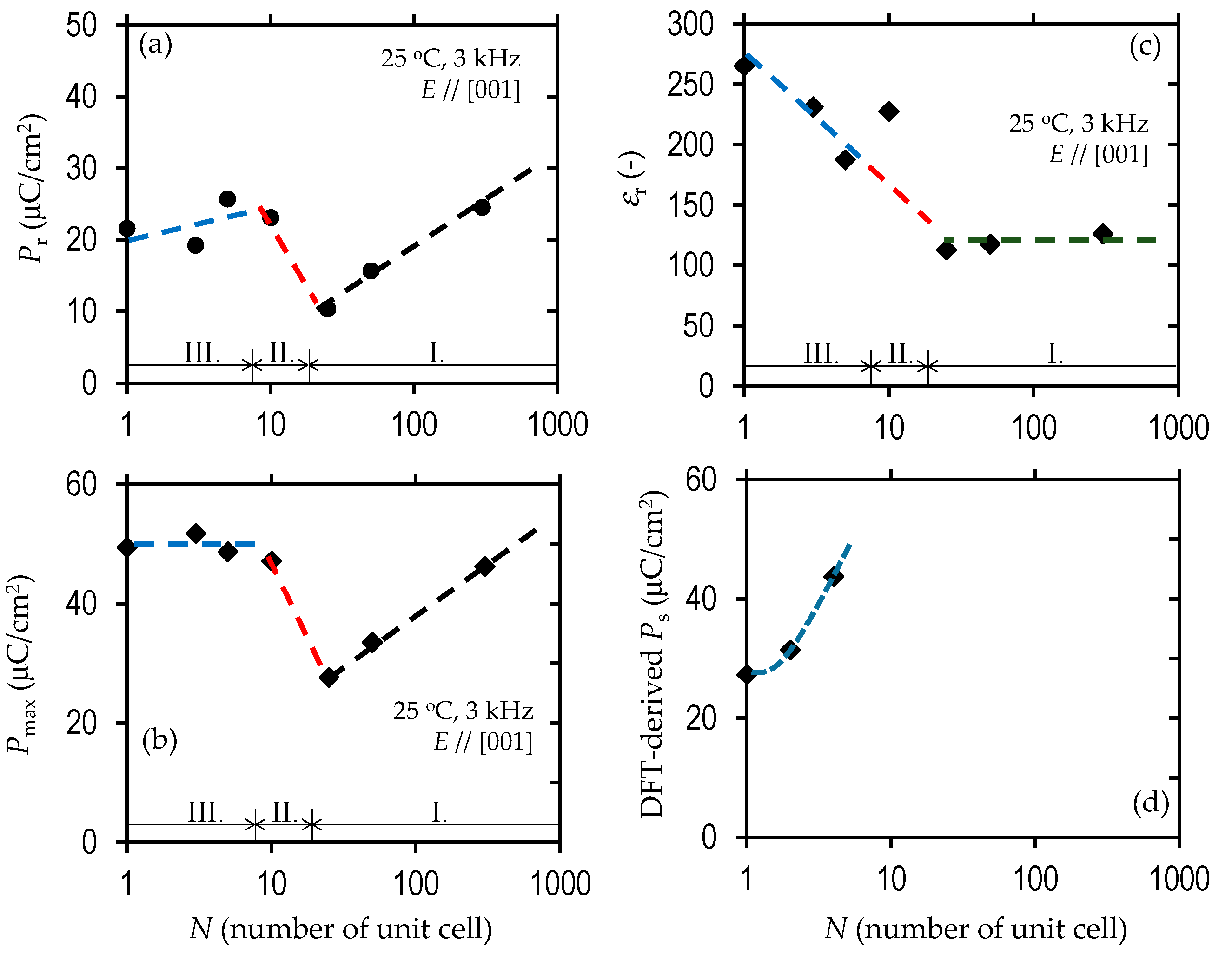
3.2. Polarization and Dielectric Properteis
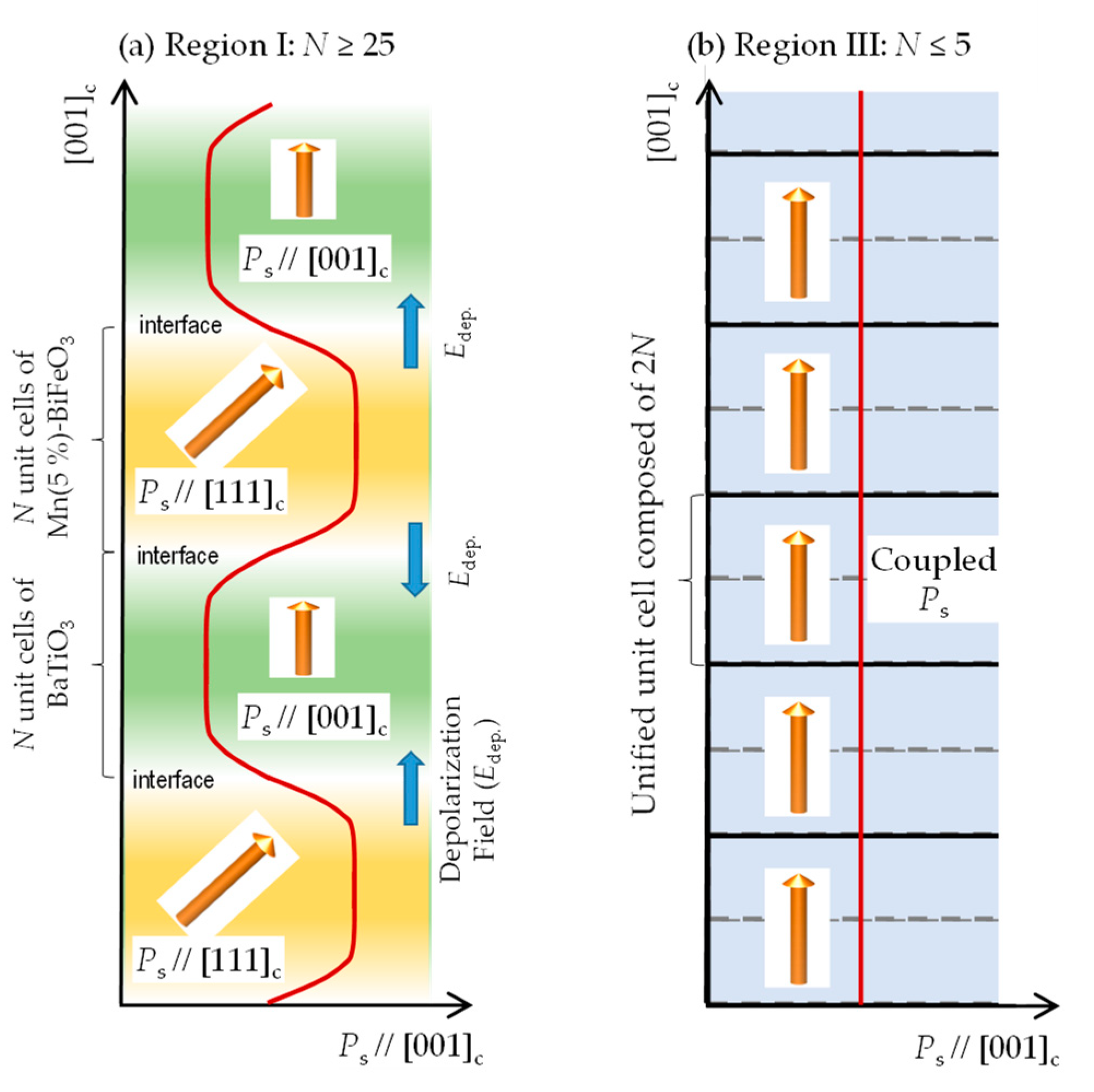
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sawaguchi, E. Ferroelectricity versus Antiferroelectricity in the Solid Solutions of PbZrO3 and PbTiO3. J. Phys. Soc. Jpn. 1953, 8, 615–629. [Google Scholar] [CrossRef]
- Jaffe, B.; Roth, R.S.; Marzullo, S. Piezoelectric properties of Lead zirconate-Lead titanate solid-solution ceramics. J. Appl. Phys. 1954, 25, 809–810. [Google Scholar] [CrossRef]
- Noheda, B.; Gonzalo, J.; Cross, L.; Guo, R.; Park, S. Tetragonal-to-monoclinic phase transition in a ferroelectric perovskite: The structure of PbZr0.52Ti0.48O3. Phys. Rev. B 2000, 61, 8687–8695. [Google Scholar] [CrossRef] [Green Version]
- Park, S.-E.; Shrout, T.R. Ultrahigh strain and piezoelectric behavior in relaxor based ferroelectric single crystals. J. Appl. Phys. 1997, 82, 1804. [Google Scholar] [CrossRef]
- Sun, E.; Cao, W. Relaxor-based ferroelectric single crystals: Growth, domain engineering, characterization and applications. Prog. Mater. Sci. 2014, 65, 124–210. [Google Scholar] [CrossRef] [Green Version]
- Fu, H.; Cohen, R.E. Polarization rotation mechanism for ultrahigh electromechanical response in single-crystal piezoelectrics. Nature 2000, 403, 281–283. [Google Scholar] [CrossRef]
- Wang, J.; Neaton, J.B.; Zheng, H.; Nagarajan, V.; Ogale, S.B.; Liu, B.; Viehland, D.; Vaithyanathan, V.; Schlom, D.G.; Waghmare, U.V.; et al. Epitaxial BiFeO3 Multiferroic Thin Film Heterostructures. Science 2003, 299, 1719–1722. [Google Scholar] [CrossRef]
- Fiebig, M. Revival of the magnetoelectric effect. J. Phys. D Appl. Phys. 2005, 38, R123. [Google Scholar] [CrossRef]
- Ramesh, R.; Spaldin, N.A. Multiferroics: Progress and prospects in thin films. Nat. Mater. 2007, 6, 21–29. [Google Scholar] [CrossRef]
- Ederer, C.; Spaldin, N.A. Weak ferromagnetism and magnetoelectric coupling in bismuth ferrite. Phys. Rev. B Condens. Matter Mater. Phys. 2005, 71, 060401(R). [Google Scholar] [CrossRef] [Green Version]
- Michel, C.; Moreau, J.M.; Achenbach, G.D.; Gerson, R.; James, W.J. The atomic structure of BiFeO3. Solid State Commun. 1969, 7, 701–704. [Google Scholar] [CrossRef]
- Kubel, F.; Schmid, H. Structure of a ferroelectric and ferroelastic monodomain crystal of the perovskite BiFeO3. Acta Crystallogr. Sect. B Struct. Sci. 1990, 46, 698–702. [Google Scholar] [CrossRef] [Green Version]
- Kumar, M.M.; Srinivas, A.; Suryanarayana, S.V. Structure property relations in BiFeO3/BaTiO3 solid solutions. J. Appl. Phys. 2000, 87, 855–862. [Google Scholar] [CrossRef]
- Kitagawa, S.; Ozaki, T.; Horibe, Y.; Yoshii, K.; Mori, S. Ferroelectric domain structures in BiFeO3-BaTiO3. Ferroelectrics 2008, 376, 122–128. [Google Scholar] [CrossRef]
- Wang, T.H.; Ding, Y.; Tu, C.S.; Yao, Y.D.; Wu, K.T.; Lin, T.C.; Yu, H.H.; Ku, C.S.; Lee, H.Y. Structure, magnetic, and dielectric properties of (1−x)BiFeO3-xBaTiO3 ceramics. J. Appl. Phys. 2011, 109, 07D907. [Google Scholar] [CrossRef]
- Wei, Y.; Jin, C.; Zeng, Y.; Wang, X.; Xu, G.; Wang, X. Polar Order Evolutions near the Rhombohedral to Pseudocubic and Tetragonal to Pseudocubic Phase Boundaries of the BiFeO3-BaTiO3 System. Materials 2015, 8, 8355–8365. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, S.; Khanal, G.P.; Nam, H.W.; Fujii, I.; Ueno, S.; Moriyoshi, C.; Kuroiwa, Y.; Wada, S. Structural and electrical characteristics of potential candidate lead-free BiFeO3-BaTiO3 piezoelectric ceramics. J. Appl. Phys. 2017, 122, 164105. [Google Scholar] [CrossRef]
- Leontsev, S.O.; Eitel, R.E. Dielectric and Piezoelectric Properties in Mn-Modified (1−x)BiFeO3-xBaTiO3 Ceramics. J. Am. Ceram. Soc. 2009, 92, 2957–2961. [Google Scholar] [CrossRef]
- Ohtomo, A.; Muller, D.A.; Grazul, J.L.; Hwang, H.Y. Artificial charge-modulation in atomic-scale perovskite titanate superlattices. Nature 2002, 419, 378–380. [Google Scholar] [CrossRef]
- Lee, H.N.; Christen, H.M.; Chisholm, M.F.; Rouleau, C.M.; Lowndes, D.H. Strong polarization enhancement in asymmetric three-component ferroelectric superlattices. Nature 2005, 433, 395–399. [Google Scholar] [CrossRef] [PubMed]
- Lorenz, M.; Wagner, G.; Lazenka, V.; Schwinkendorf, P.; Modarresi, H.; Van Bael, M.J.; Vantomme, A.; Temst, K.; Oeckler, O.; Grundmann, M. Correlation of magnetoelectric coupling in multiferroic BaTiO3-BiFeO3 superlattices with oxygen vacancies and antiphase octahedral rotations. Appl. Phys. Lett. 2015, 106, 012905. [Google Scholar] [CrossRef] [Green Version]
- Lorenz, M.; Lazenka, V.; Schwinkendorf, P.; Van Bael, M.J.; Vantomme, A.; Temst, K.; Grundmann, M.; Höche, T. Epitaxial Coherence at Interfaces as Origin of High Magnetoelectric Coupling in Multiferroic BaTiO3–BiFeO3 Superlattices. Adv. Mater. Interfaces 2016, 3, 1500822. [Google Scholar] [CrossRef]
- Matsuo, H.; Noguchi, Y.; Miyayama, M.; Kiguchi, T.; Konno, T.J. Enhanced photovoltaic effects in ferroelectric solid solution thin films with nanodomains. Appl. Phys. Lett. 2020, 116, 132901. [Google Scholar] [CrossRef]
- Hohenberger, S.; Jochum, J.K.; Van Bael, M.J.; Temst, K.; Patzig, C.; Höche, T.; Grundmann, M.; Lorenz, M. Enhanced magnetoelectric coupling in BaTiO3-BiFeO3 multilayers-an interface effect. Materials 2020, 13, 197. [Google Scholar] [CrossRef] [Green Version]
- Hohenberger, S.; Lazenka, V.; Selle, S.; Patzig, C.; Temst, K.; Lorenz, M. Magnetoelectric Coupling in Epitaxial Multiferroic BiFeO3–BaTiO3 Composite Thin Films. Phys. Status Solidi Basic Res. 2020, 257, 1900613. [Google Scholar] [CrossRef]
- Matsuo, H.; Kitanaka, Y.; Inoue, R.; Noguchi, Y.; Miyayama, M. Cooperative effect of oxygen-vacancy-rich layer and ferroelectric polarization on photovoltaic properties in BiFeO3 thin film capacitors. Appl. Phys. Lett. 2016, 108, 032901. [Google Scholar] [CrossRef]
- Matsuo, H.; Kitanaka, Y.; Noguchi, Y.; Miyayama, M. Electrical conduction mechanism in BiFeO3-based ferroelectric thin-film capacitors: Impact of Mn doping. J. Asian Ceram. Soc. 2015, 3, 426–431. [Google Scholar] [CrossRef] [Green Version]
- Noguchi, Y.; Matsuo, H.; Kitanaka, Y.; Miyayama, M. Ferroelectrics with a controlled oxygen-vacancy distribution by design. Sci. Rep. 2019, 9, 4225. [Google Scholar] [CrossRef]
- Noguchi, Y.; Maki, H.; Kitanaka, Y.; Matsuo, H.; Miyayama, M. Control of misfit strain in ferroelectric BaTiO3 thin-film capacitors with SrRuO3-based electrodes on (Ba, Sr)TiO3-buffered SrTiO3 substrates. Appl. Phys. Lett. 2018, 113, 012903. [Google Scholar] [CrossRef]
- Matsuo, H.; Noguchi, Y.; Miyayama, M. Gap-state engineering of visible-light-active ferroelectrics for photovoltaic applications. Nat. Commun. 2017, 8, 207. [Google Scholar] [CrossRef] [Green Version]
- Noguchi, Y.; Tada, M.; Kitanaka, Y.; Miyayama, M. Fabrication and characterization of (Ba, Sr)RuO3 ceramic targets and thin films for ferroelectric BaTiO3 thin-film capacitors. AIP Adv. 2018, 8, 115135. [Google Scholar] [CrossRef] [Green Version]
- Langreth, D.C.; Perdew, J.P. Theory of nonuniform electronic systems. I. Analysis of the gradient approximation and a generalization that works. Phys. Rev. B 1980, 21, 5469–5493. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [Green Version]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [Green Version]
- Anisimov, V.I.; Zaanen, J.; Andersen, O.K. Band theory and Mott insulators: Hubbard U instead of Stoner I. Phys. Rev. B 1991, 44, 943–954. [Google Scholar] [CrossRef] [Green Version]
- Neaton, J.B.; Ederer, C.; Waghmare, U.V.; Spaldin, N.A.; Rabe, K.M. First-principles study of spontaneous polarization in multiferroic BiFeO3. Phys. Rev. B 2005, 71, 014113. [Google Scholar] [CrossRef] [Green Version]
- Gonze, X.; Lee, C. Dynamical matrices, Born effective charges, dielectric permittivity tensors, and interatomic force constants from density-functional perturbation theory. Phys. Rev. B Condens. Matter Mater. Phys. 1997, 55, 10355–10368. [Google Scholar] [CrossRef]
- Chen, Z.; Qi, Y.; You, L.; Yang, P.; Huang, C.W.; Wang, J.; Sritharan, T.; Chen, L. Large tensile-strain-induced monoclinic MB phase in BiFeO3 epitaxial thin films on a PrScO3 substrate. Phys. Rev. B Condens. Matter Mater. Phys. 2013, 88, 054114. [Google Scholar] [CrossRef] [Green Version]
- Zubko, P.; Catalan, G.; Tagantsev, A.K. Flexoelectric effect in solids. Annu. Rev. Mater. Res. 2013, 43, 387–421. [Google Scholar] [CrossRef] [Green Version]
- Maki, H.; Noguchi, Y.; Kutsuna, K.; Matsuo, H.; Kitanaka, Y.; Miyayama, M. Crystal structure and polarization hysteresis properties of ferroelectric BaTiO 3 thin-film capacitors on (Ba,Sr)TiO3-buffered substrates. Jpn. J. Appl. Phys. 2016, 55, 10TA03. [Google Scholar] [CrossRef] [Green Version]
- Imura, R.; Kitanaka, Y.; Oguchi, T.; Noguchi, Y.; Miyayama, M. Polarization properties and crystal structures of ferroelectric (Ba,Ca)TiO3 single crystals. J. Adv. Dielectr. 2014, 04, 1450003. [Google Scholar] [CrossRef] [Green Version]
- Meyer, B.; Vanderbilt, D. Ab initio study of ferroelectric domain walls in PbTiO3. Phys. Rev. B 2002, 65, 104111. [Google Scholar] [CrossRef] [Green Version]
- Catalan, G.; Seidel, J.; Ramesh, R.; Scott, J.F. Domain wall nanoelectronics. Rev. Mod. Phys. 2012, 84, 119–156. [Google Scholar] [CrossRef] [Green Version]
- Farokhipoor, S.; Noheda, B. Conduction through 71° Domain Walls in BiFeO3 Thin Films. Phys. Rev. Lett. 2011, 107, 127601. [Google Scholar] [CrossRef] [Green Version]
- Dennis, M.D.; Bradt, R.C. Thickness of 90° ferroelectric domain walls in (Ba,Pb)TiO3 single crystals. J. Appl. Phys. 1974, 45, 1931–1933. [Google Scholar] [CrossRef]
- Yang, S.Y.; Seidel, J.; Byrnes, S.J.; Shafer, P.; Yang, C.-H.; Rossell, M.D.; Yu, P.; Chu, Y.-H.; Scott, J.F.; Ager, J.W.; et al. Above-bandgap voltages from ferroelectric photovoltaic devices. Nat. Nanotechnol. 2010, 5, 143–147. [Google Scholar] [CrossRef] [Green Version]
- Inoue, R.; Ishikawa, S.; Imura, R.; Kitanaka, Y.; Oguchi, T.; Noguchi, Y.; Miyayama, M. Giant photovoltaic effect of ferroelectric domain walls in perovskite single crystals. Sci. Rep. 2015, 5, 14741. [Google Scholar] [CrossRef]
- Matsuo, H.; Kitanaka, Y.; Inoue, R.; Noguchi, Y.; Miyayama, M.; Kiguchi, T.; Konno, T.J.T.J. Bulk and domain-wall effects in ferroelectric photovoltaics. Phys. Rev. B 2016, 94, 214111. [Google Scholar] [CrossRef]
- Noguchi, Y.; Inoue, R.; Matsuo, H. Domain-wall photovoltaic effect in Fe-doped BaTiO3 single crystals. J. Appl. Phys. 2021, 129, 084101. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noguchi, Y.; Matsuo, H. Polarization and Dielectric Properties of BiFeO3-BaTiO3 Superlattice-Structured Ferroelectric Films. Nanomaterials 2021, 11, 1857. https://doi.org/10.3390/nano11071857
Noguchi Y, Matsuo H. Polarization and Dielectric Properties of BiFeO3-BaTiO3 Superlattice-Structured Ferroelectric Films. Nanomaterials. 2021; 11(7):1857. https://doi.org/10.3390/nano11071857
Chicago/Turabian StyleNoguchi, Yuji, and Hiroki Matsuo. 2021. "Polarization and Dielectric Properties of BiFeO3-BaTiO3 Superlattice-Structured Ferroelectric Films" Nanomaterials 11, no. 7: 1857. https://doi.org/10.3390/nano11071857
APA StyleNoguchi, Y., & Matsuo, H. (2021). Polarization and Dielectric Properties of BiFeO3-BaTiO3 Superlattice-Structured Ferroelectric Films. Nanomaterials, 11(7), 1857. https://doi.org/10.3390/nano11071857





