Transition Metal-Hyperdoped InP Semiconductors as Efficient Solar Absorber Materials
Abstract
1. Introduction
2. Computational Methodology
3. Results
3.1. Crystal Structure
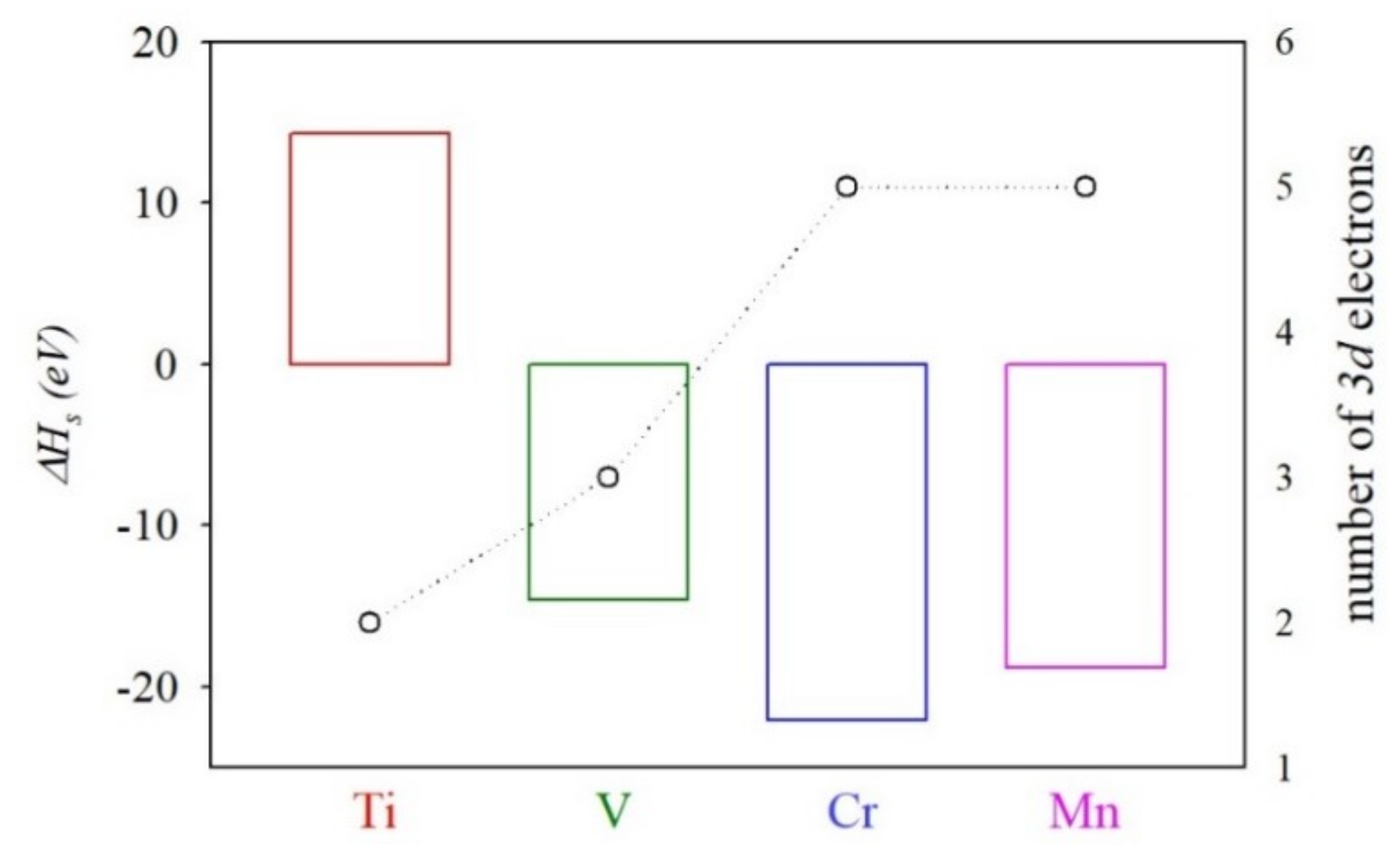
3.2. Heat of Solution of TM@InP
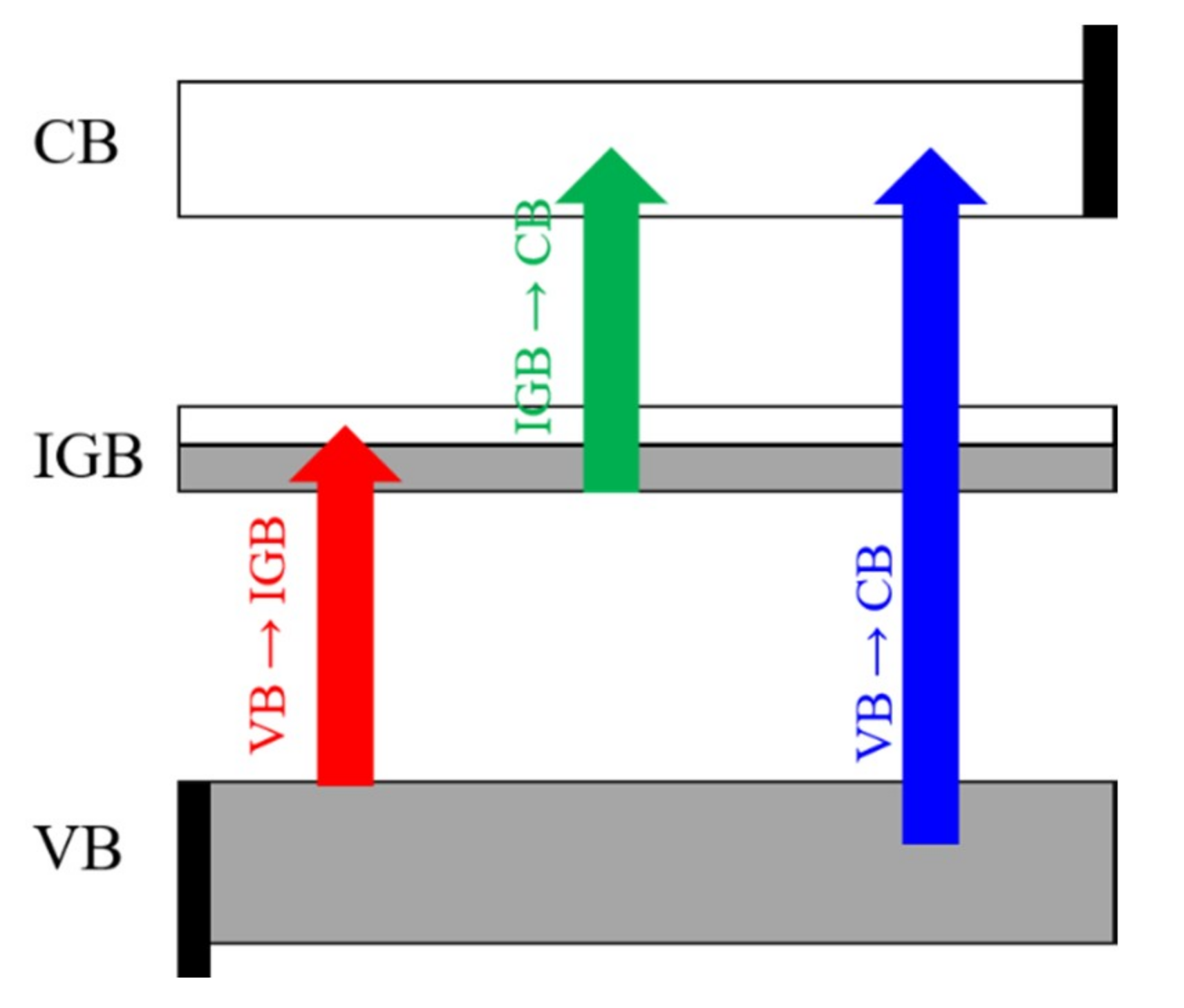
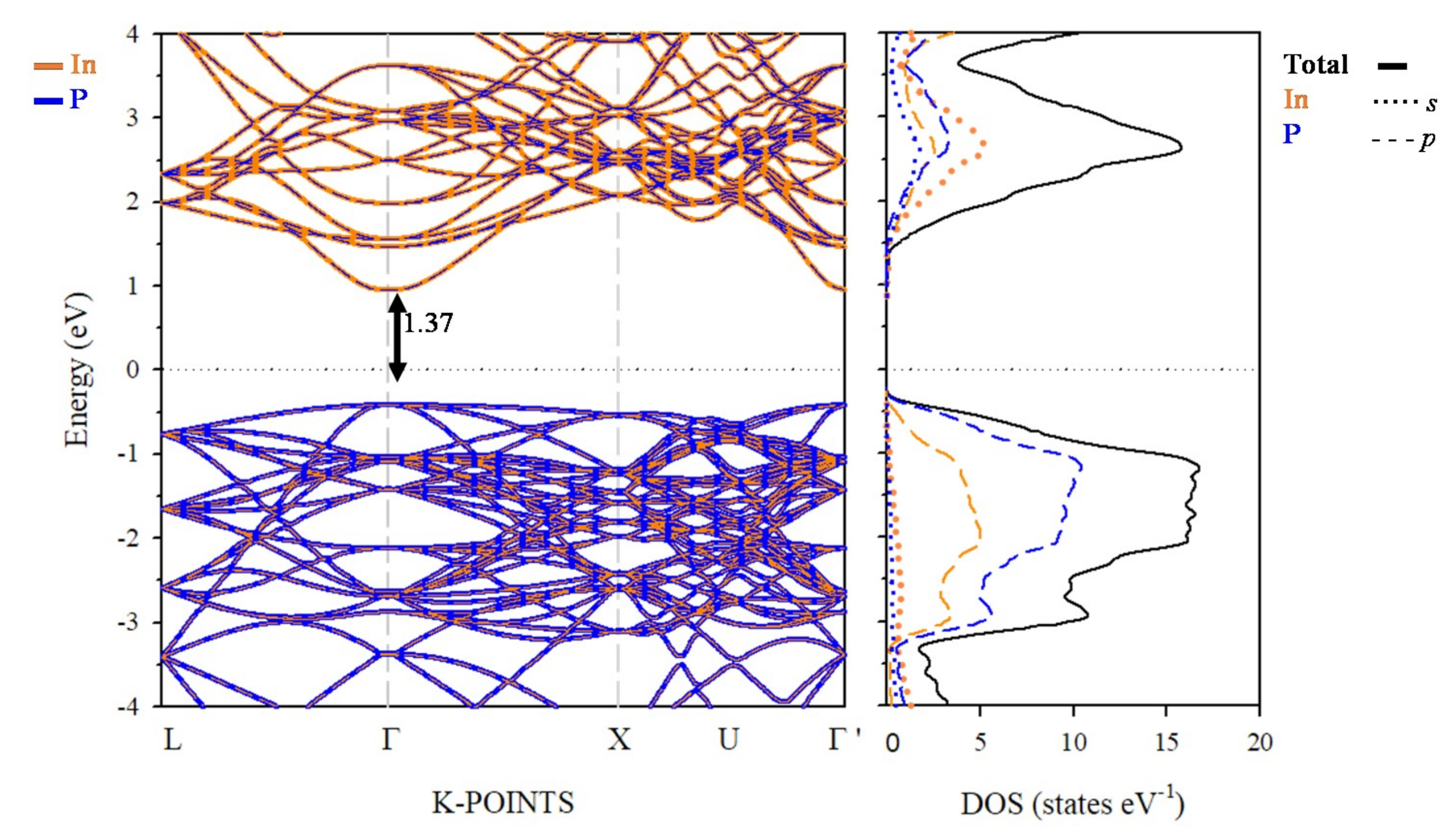
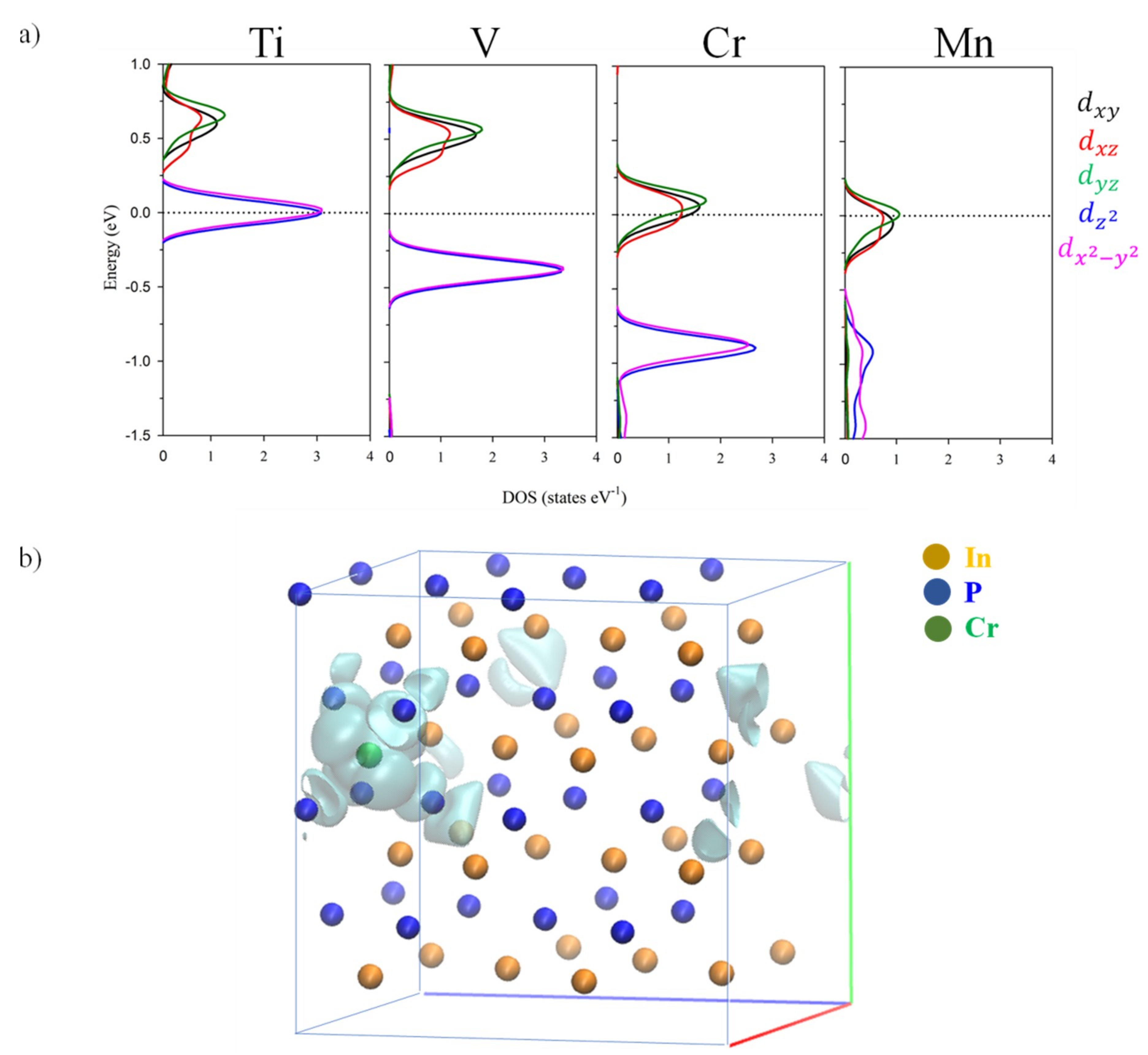
3.3. Electronic Band Structure
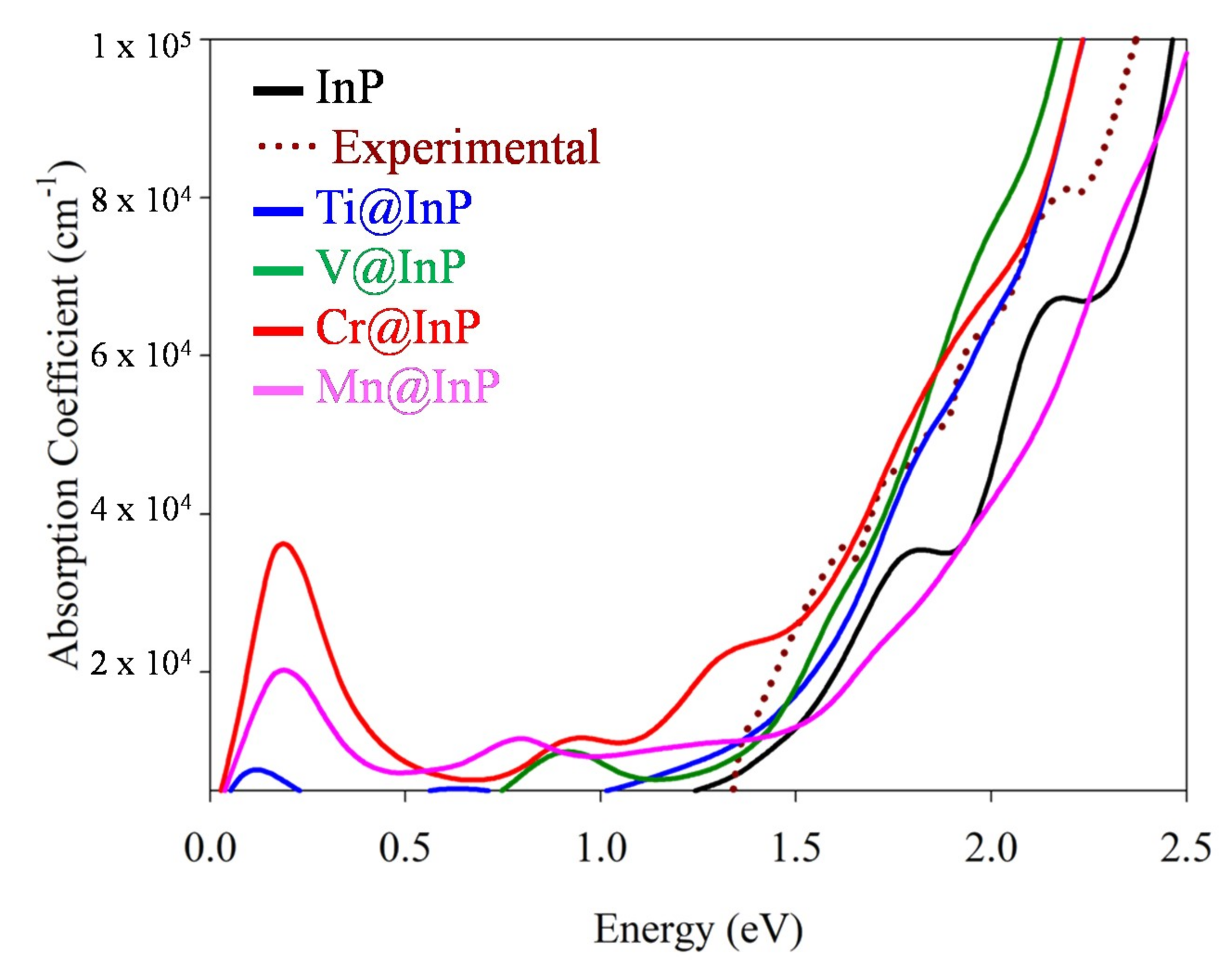
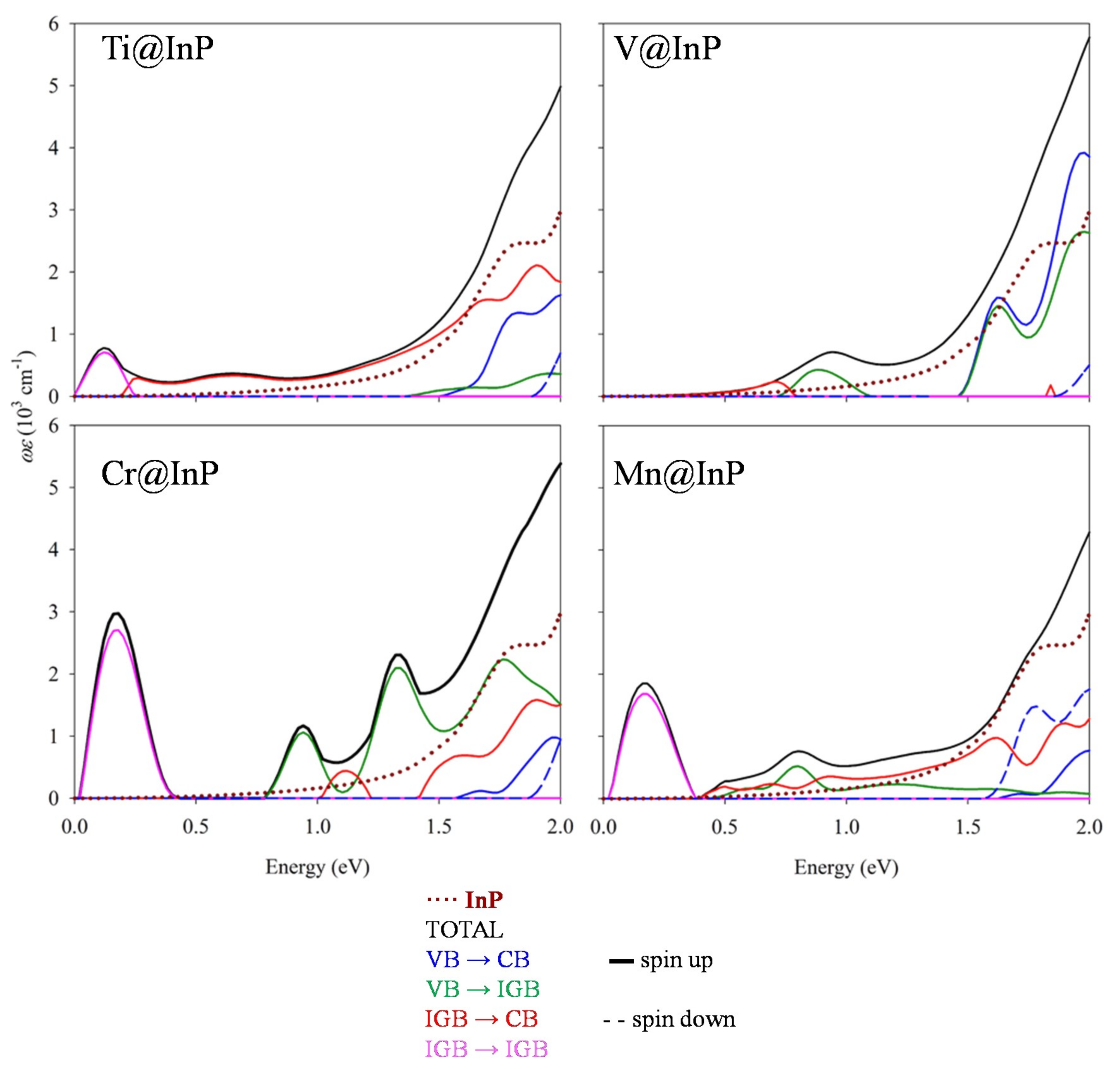
3.4. Optical Absorption Features
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rasukkannu, M.; Velauthapillai, D.; Bianchini, F.; Vajeeston, P. Properties of Novel Non-Silicon Materials for Photovoltaic Applications: A First-Principle Insight. Materials 2018, 11, 2006. [Google Scholar] [CrossRef]
- Unold, T.; Schock, H.W. Nonconventional (Non-Silicon-Based) Photovoltaic Materials. Annu. Rev. Mater. Res. 2011, 41, 297–321. [Google Scholar] [CrossRef]
- Henry, C.H. Limiting efficiencies of ideal single and multiple energy gap terrestrial solar cells. J. Appl. Phys. 1980, 51, 4494–4500. [Google Scholar] [CrossRef]
- Yuan, L.D.; Deng, H.X.; Li, S.S.; Wei, S.H.; Luo, J.W. Unified theory of direct or indirect band-gap nature of conventional semiconductors. Phys. Rev. B 2018, 98, 245203. [Google Scholar] [CrossRef]
- Tanabe, K. A Review of Ultrahigh Efficiency III-V Semiconductor Compound Solar Cells: Multijunction Tandem, Lower Dimensional, Photonic Up/Down Conversion and Plasmonic Nanometallic Structures. Energies 2009, 2, 504–530. [Google Scholar] [CrossRef]
- Friedman, D.J. Progress and challenges for next-generation high-efficiency multijunction solar cells. Curr. Opin. Solid State Mater. Sci. 2010, 14, 131–138. [Google Scholar] [CrossRef]
- Mokkapati, S.; Jagadish, C. III-V compound SC for optoelectronic devices. Mater. Today 2009, 12, 22–32. [Google Scholar] [CrossRef]
- Teran, A.S.; Lim, W.; Lee, I.; Philips, J.D. Energy Harvesting for GaAs Photovoltaics Under Low-Flux Indoor Lighting Conditions. IEEE Trans. Electron Devices 2016, 63, 2820–2825. [Google Scholar] [CrossRef]
- Keavney, C.J.; Haven, V.E.; Vernon, S.M. Emitters structures in MOCVD InP solar cells. IEEE Conf. Photovolt. Spec. 1990, 141–144. [Google Scholar]
- Yin, X.; Battaglia, C.; Lin, Y.; Chen, K.; Hettick, M.; Zheng, M.; Chen, C.Y.; Kiriya, D.; Javey, A. 19.2% Efficient InP Heterojunction Solar Cell with Electron-Selective TiO2 Contact. ACS Photonics 2014, 1, 1245–1250. [Google Scholar] [CrossRef]
- Coutts, T.J.; Naseem, S. High efficiency indium tin oxide/indium phosphide solar cells. Appl. Phys. Lett. 1985, 46, 164–166. [Google Scholar] [CrossRef]
- Wagner, S.; Shay, J.L.; Bachmann, K.J.; Buehler, E. p−InP/n−CdS solar cells and photovoltaic detectors. Appl. Phys. Lett. 1975, 26, 229–230. [Google Scholar] [CrossRef]
- Sai Gautam, G.; Senftle, T.P.; Alidoust, N.; Carter, E.A. Novel Solar Cell Materials: Insights from First-Principles. J. Phys. Chem. C 2018, 122, 27107–27126. [Google Scholar] [CrossRef]
- Luque, A.; Martí, A. Increasing the Efficiency of Ideal Solar Cells by Photon Induced Transitions at Intermediate Levels. Phys. Rev. Lett. 1997, 78, 5014–5017. [Google Scholar] [CrossRef]
- Luque, A.; Marti, A. Photovoltaics: Towards the intermediate band. Nat. Photon. 2011, 5, 137–138. [Google Scholar] [CrossRef]
- Luque, A.; Marti, A.; Stanley, C. Understanding intermediate-band solar cells. Nat. Photon. 2012, 6, 146–152. [Google Scholar] [CrossRef]
- Palacios, P.; Fernández, J.J.; Sánchez, K.; Conesa, J.C.; Wahnón, P. First-principles investigation of isolated band formation in half-metallic TixGa1-xP (x = 0.3125–0.25). Phys. Rev. B 2006, 73, 085206. [Google Scholar] [CrossRef]
- Tablero, C.; Palacios, P.; Fernández, J.J.; Wahnón, P. Properties of intermediate band materials. Sol. Energy Mater. Sol. Cells 2005, 87, 323–331. [Google Scholar] [CrossRef]
- Palacios, P.; Sánchez, K.; Conesa, J.C.; Wahnón, P. First principles calculation of isolated intermediate bands formation in a transition metal-doped chalcopyrite-type semiconductor. Phys. Stat. Sol. 2006, 203, 1395–1401. [Google Scholar] [CrossRef]
- Palacios, P.; Sánchez, K.; Conesa, J.C.; Fernández, J.J.; Wahnón, P. Theoretical modelling of intermediate band solar cell materials based on metal-doped chalcopyrite compounds. Thin Solid Film 2007, 515, 6280–6284. [Google Scholar] [CrossRef]
- Aguilera, I.; Palacios, P.; Wahnón, P. Optical properties of chalcopyrite-type intermediate transition metal band materials from first principles. Thin Solid Film 2008, 516, 7055–7059. [Google Scholar] [CrossRef]
- Lucena, R.; Aguilera, I.; Palacios, P.; Wahnón, P.; Conesa, J.C. Synthesis and Spectral Properties of Nanocrystalline V-Substituted In2S3, a Novel Material for More Efficient Use of Solar Radiation. Chem. Mater. 2008, 20, 5125–5127. [Google Scholar] [CrossRef]
- Wahnón, P.; Conesa, J.C.; Palacios, P.; Lucena, R.; Aguilera, I.; Seminovski, Y.; Fresno, F. V-doped SnS2: A new intermediate band material for a better use of the solar spectrum. Phys. Chem. Chem. Phys. 2011, 13, 20401–20407. [Google Scholar] [CrossRef] [PubMed]
- Lucena, R.; Conesa, J.C.; Aguilera, I.; Palacios, P.; Wahnón, P. V-substituted In2S3: An intermediate band material with photocatalytic activity in the whole visible light range. J. Mater. Chem. A 2014, 2, 8236–8245. [Google Scholar] [CrossRef]
- Seminóvski, Y.; Palacios, P.; Conesa, J.C.; Wahnón, P. Thermodynamics of zinc insertion in CuGaS2:Ti, used as a modulator agent in an intermediate-band photovoltaic material. Comput. Theor. Chem. 2011, 975, 134–137. [Google Scholar] [CrossRef]
- Seminóvski, Y.; Palacios, P.; Wahnón, P. Intermediate band position modulated by Zn addition in Ti doped CuGaS2. Thin Solid Film 2011, 519, 7517–7521. [Google Scholar] [CrossRef]
- Seminovski, Y.; Palacios, P.; Wahnón, P. Obtaining an intermediate band photovoltaic material through the Bi insertion in CdTe. Sol. Energy Mater. Sol. Cells 2013, 114, 99–103. [Google Scholar] [CrossRef]
- Seminovski, Y.; Palacios, P.; Wahnón, P. Analysis of SnS2 hyperdoped with V proposed as efficient absorber material. J. Phys. Condens. Matter 2014, 26, 395501. [Google Scholar] [CrossRef][Green Version]
- Castellanos-Águila, J.E.; Palacios, P.; Conesa, J.C.; Arriaga, J.; Wahnón, P. Theoretical band alignment in an intermediate band chalcopyrite based material. Appl. Surf. Sci. 2017, 424, 132–136. [Google Scholar] [CrossRef]
- Palacios, P.; Aguilera, I.; Wahnón, P.; Conesa, J.C. Thermodynamics of the Formation of Ti- and Cr-doped CuGaS2 Intermediate-band Photovoltaic Materials. J. Phys. Chem. C 2008, 112, 9525–9529. [Google Scholar] [CrossRef]
- Sánchez, K.; Aguilera, I.; Palacios, P.; Wahnón, P. Assessment through first-principles calculations of an intermediate-band photovoltaic material based on Ti-implanted silicon: Interstitial versus substitutional origin. Phys. Rev. B 2009, 79, 165203. [Google Scholar] [CrossRef]
- Sánchez, K.; Aguilera, I.; Palacios, P.; Wahnón, P. Formation of a reliable intermediate band in Si heavily coimplanted with chalcogens (S, Se, Te) and group III elements (B, Al). Phys. Rev. B 2010, 82, 165201. [Google Scholar] [CrossRef]
- Aguilera, I.; Palacios, P.; Wahnón, P. Understanding Ti intermediate-band formation in partially inverse thiospinel MgIn2S4 through many-body approaches. Phys. Rev. B 2011, 84, 115106. [Google Scholar] [CrossRef]
- García, G.; Casanova-Páez, M.; Palacios, P.; Menéndez-Proupin, E.; Wahnón, P. First principle study of V-implantation in highly-doped silicon materials. Comput. Mater. Sci. 2017, 136, 207–215. [Google Scholar] [CrossRef]
- Garcia-Hemme, E.; García, G.; Palacios, P.; Montero, D.; García-Hernansanz, R.; González-Díaz, G.; Wahnón, P. Vanadium supersaturated silicon system: A theoretical and experimental approach. J. Phys. D Appl. Phys. 2017, 50, 495101. [Google Scholar] [CrossRef]
- García, G.; Palacios, P.; Menéndez-Proupin, E.; Montero-Alejo, A.L.; Conesa Wahnón, P. Influence of chromium hyperdoping on the electronic structure of CH3NH3PbI3 perovskite: A first-principles insight. Sci. Rep. 2018, 8, 2511. [Google Scholar]
- Olea, J.; del Prado, A.; García-Hemme, E.; García-Hernansanz, R.; Montero, D.; González-Díaz, G.; Gonzalo, J.; Siegel, J.; López, E. Strong subbandgap photoconductivity in GaP implanted with Ti. Prog. Photovolt. Res. Appl. 2018, 26, 214–222. [Google Scholar] [CrossRef]
- Palacios, P.; Wahnón, P.; Tablero, C. Ab initio phonon dispersion calculations for TixGanAsm and TixGanPm compounds. Comput. Mater. Sci. 2005, 33, 118–124. [Google Scholar] [CrossRef]
- Palacios, P.; Wahnón, P.M.; Pizzinato, S.; Conesa, J.C. Energetics of formation of TiGa3As4 and TiGa3P4 intermediate band materials. J. Chem. Phys. 2006, 124, 014711. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.M.; Wang, D.; Zhao, W.M.; Gu, Y.; Bu, K.; Pan, J.; Quin, P.; Zhang, X.; Huang, F. Intermediate Band Material of Titanium-Doped Tin Disulfide for Wide Spectrum Solar Absorption. Inorg. Chem. 2018, 57, 3956–3962. [Google Scholar] [CrossRef]
- Palacios, P.; Aguilera, I.; Sánchez, K.; Conesa, J.C.; Wahnón, P. Transition-Metal-Substituted Indium Thiospinels as Novel Intermediate-Band Materials: Prediction and Understanding of Their Electronic Properties. Phys. Rev. Lett 2008, 101, 046403. [Google Scholar] [CrossRef] [PubMed]
- Palacios, P.; Sánchez, K.; Wahnón, P.; Conesa, J.C. Characterization by Ab Initio Calculations of an Intermediate Band Material Based on Chalcopyrite Semiconductors Substituted by Several Transition Metals. J. Sol. Energy Eng. 2006, 129, 314–318. [Google Scholar] [CrossRef]
- Aguilera, I.; Palacios, P.; Wahnón, P. Enhancement of optical absorption in Ga-chalcopyrite-based intermediate-band materials for high efficiency solar cells. Sol. Energy Mater. Sol. Cells 2010, 94, 1903–1906. [Google Scholar] [CrossRef]
- Ullah, S.; Ullah, H.; Bouhjar, F.; Mollar, M.; Marí, B. Synthesis of in-gap band CuGaS2:Cr absorbers and numerical assessment of their performance in solar cells. Sol. Energy Mater. Sol. Cells 2018, 180, 322–327. [Google Scholar] [CrossRef]
- Chan, M.K.Y.; Ceder, G. Efficient Band Gap Prediction for Solids. Phys. Rev. Lett. 2010, 105, 196403. [Google Scholar] [CrossRef] [PubMed]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
- Oba, F.; Kumagai, Y. Design and exploration of semiconductors from first principles: A review of recent advances. Appl. Phys. Express 2018, 11, 060101. [Google Scholar] [CrossRef]
- Hedin, L. New Method for Calculating the One-Particle Green’s Function with Application to the Electron-Gas Problem. Phys. Rev. 1965, 139, A796–A823. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio} molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [PubMed]
- Luque, A.; Martí, A.; Antolín, E.; Tablero, C. Intermediate bands versus levels in non-radiative recombination. Phys. B Condens. Matter. 2006, 382, 320–327. [Google Scholar] [CrossRef]
- Bahuguna, B.P.; Sharma, R.O.; Saini, L.K. The LDA+U calculation of electronic band structure of GaAs. AIP Conf. Proc. 2016, 1728, 020601. [Google Scholar]
- Iandelli, A. Sulla struttura dei composti InP, InAs e InSb. Gazz. Chim. Ital. 1941, 71, 58–62. [Google Scholar]
- Zhang, S.B.; Northrup, J.E. Chemical potential dependence of defect formation energies in GaAs: Application to Ga self-diffusion. Phys. Rev. Lett. 1991, 67, 2339–2342. [Google Scholar] [CrossRef]
- Karki, V.; Bhattachary, D.; Rao, T.V.C.; Alamelu, D. Depth distribution of Mn in Mn doped GaAs using secondary ion mass spectrometry. Vac. Sci. Technol. B 2016, 34, 03H125. [Google Scholar] [CrossRef]
- Cotton, F.A. I-Ligand field theory. J. Chem. Educ. 1964, 41, 466. [Google Scholar] [CrossRef]
- Deng, F.; Cao, H.; Liang, L.; Li, J.; Gao, J.; Zhang, H.; Qin, R.; Liu, C. Determination of the basic optical parameters of ZnSnN2. Opt. Lett. 2015, 40, 1282–1285. [Google Scholar] [CrossRef]
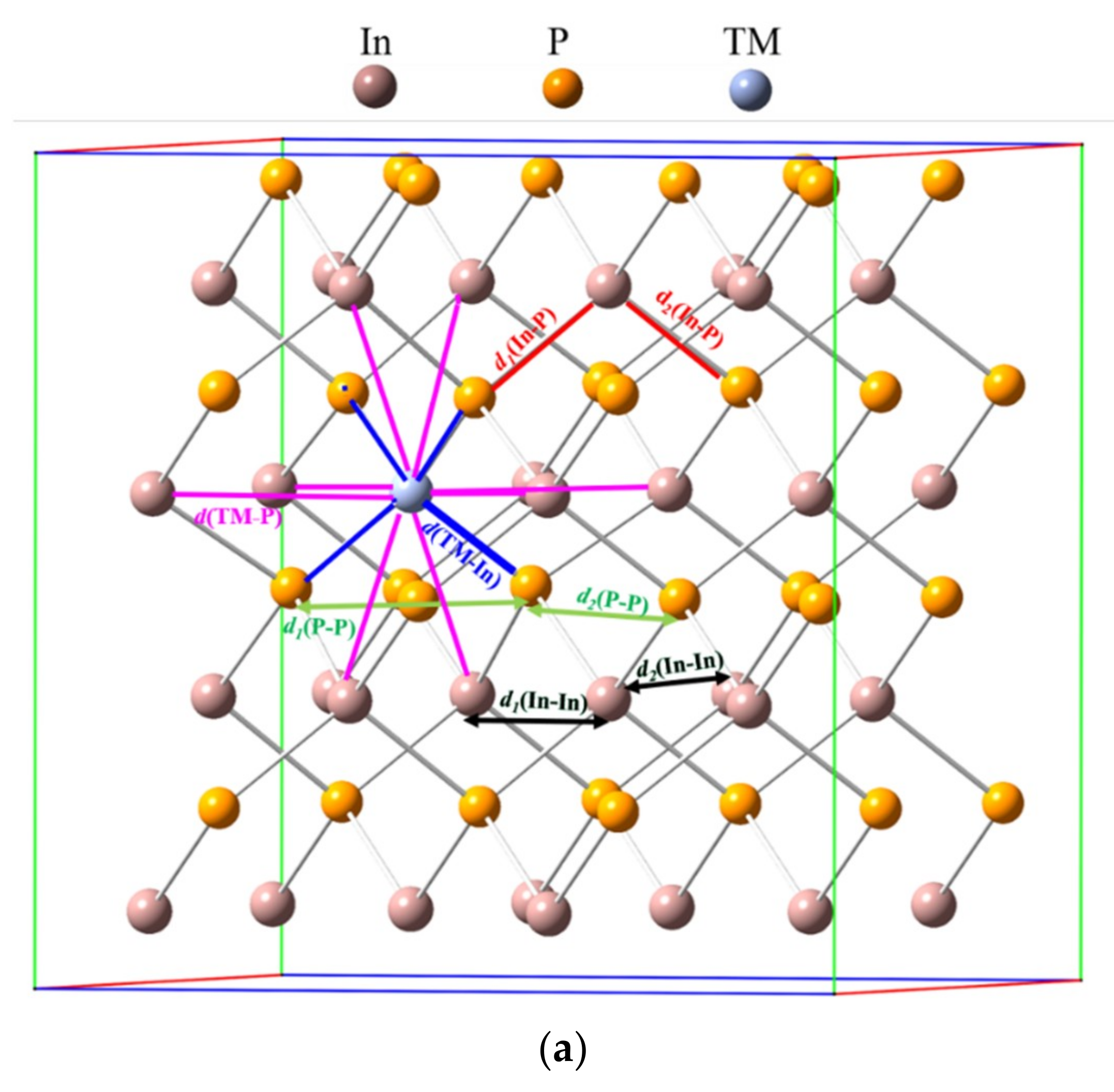
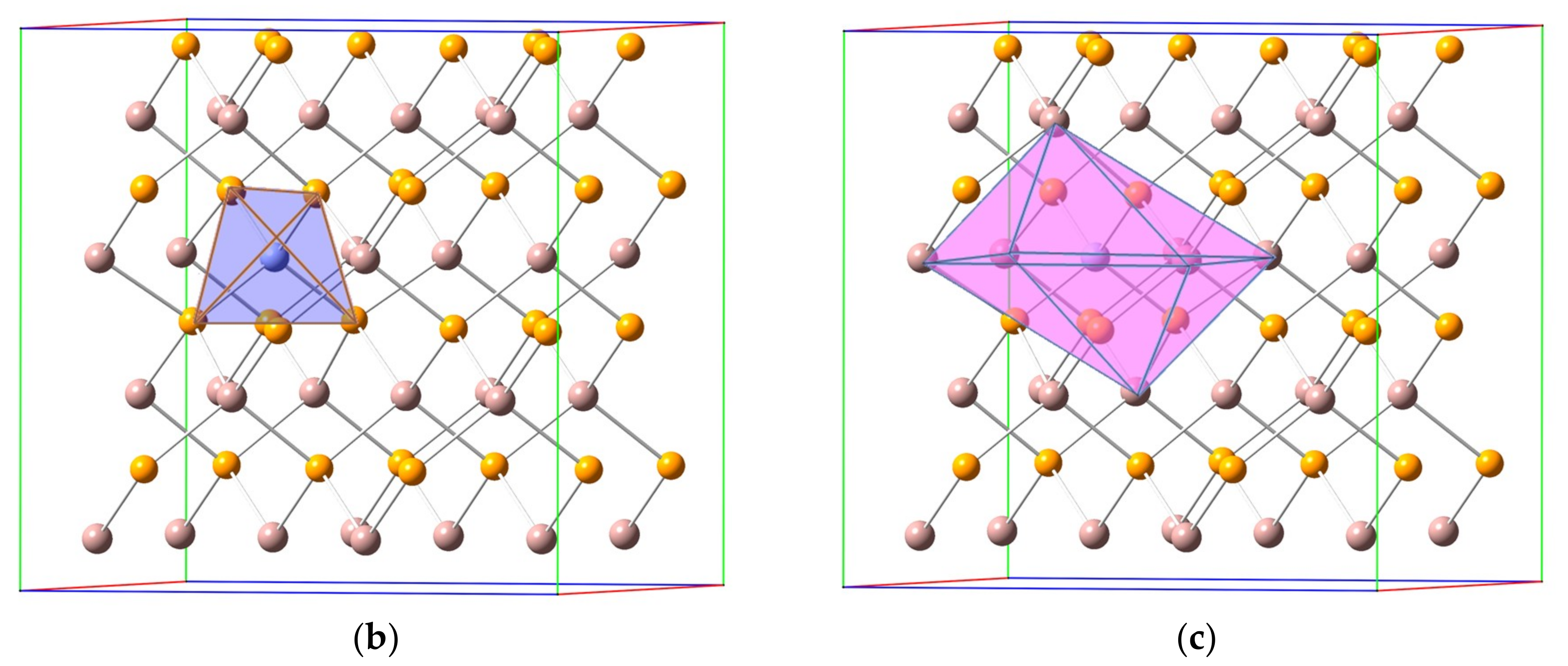
| TM@InP | ||||||
|---|---|---|---|---|---|---|
| InP a | InP | TM = Ti | TM = V | TM = Cr | TM = Mn | |
| a | 5.87 | 5.87 | 5.86 | 5.86 | 5.86 | 5.86 |
| d(In-P) | 2.54 | 2.54 | ||||
| d1(In-P) b | 2.55 | 2.56 | 2.56 | 2.56 | ||
| d2(In-P) b | 2.54 | 2.54 | 2.54 | 2.54 | ||
| d(P–P) | 4.15 | 4.15 | ||||
| d1(P–P) b | 4.16 | 4.16 | 4.16 | 4.16 | ||
| d2(P–P) b | 4.14 | 4.14 | 4.14 | 4.14 | ||
| d(In–In) b | 4.15 | 4.15 | ||||
| d1(In–In) b | 4.19 | 4.19 | 4.19 | 4.19 | ||
| d2(In–In) b | 4.15 | 4.15 | 4.15 | 4.15 | ||
| d(TM–P) | 2.53 | 2.53 | 2.53 | 2.53 | ||
| d(TM–In) | 4.14 | 4.14 | 4.14 | 4.14 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
García, G.; Sánchez-Palencia, P.; Palacios, P.; Wahnón, P. Transition Metal-Hyperdoped InP Semiconductors as Efficient Solar Absorber Materials. Nanomaterials 2020, 10, 283. https://doi.org/10.3390/nano10020283
García G, Sánchez-Palencia P, Palacios P, Wahnón P. Transition Metal-Hyperdoped InP Semiconductors as Efficient Solar Absorber Materials. Nanomaterials. 2020; 10(2):283. https://doi.org/10.3390/nano10020283
Chicago/Turabian StyleGarcía, Gregorio, Pablo Sánchez-Palencia, Pablo Palacios, and Perla Wahnón. 2020. "Transition Metal-Hyperdoped InP Semiconductors as Efficient Solar Absorber Materials" Nanomaterials 10, no. 2: 283. https://doi.org/10.3390/nano10020283
APA StyleGarcía, G., Sánchez-Palencia, P., Palacios, P., & Wahnón, P. (2020). Transition Metal-Hyperdoped InP Semiconductors as Efficient Solar Absorber Materials. Nanomaterials, 10(2), 283. https://doi.org/10.3390/nano10020283







